
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Energy Res. , 11 January 2022
Sec. Wave and Tidal Energy
Volume 9 - 2021 | https://doi.org/10.3389/fenrg.2021.818118
Pump as Turbine (PAT) is a technically and economically effective technology to utilize small/mini/micro/pico hydropower, especially in rural areas. There are two main subjects that influence the selection and application of PAT. On the one hand, manufacturers of pumps will not provide their characteristics under the turbine mode, which requires performance prediction methods. On the other hand, PAT efficiency is always slightly lower than that of pump, which requires further geometry optimization. This literature review summarized published research studies related to performance prediction and geometry optimization, aimed at guiding for selection and optimization of PAT. Currently, there exist four categories of performance prediction methods, namely, using BEP (Best Efficiency Point), using specific speed, loss modeling, and polynomial fitting. The using BEP and loss modeling methods are based on theoretical analysis, while using specific speed and polynomial fitting methods require statistical fitting. The prediction errors of published methods are within ±10% mostly. For geometry optimization, investigations mainly focus on impeller diameter and blade geometry. The influence of impeller trimming, blade rounding, blade wrap angle, blade profile, blade number, blade trailing edge position, and guide vane number has been studied. Among published methods, the blade rounding and forward-curved impellers are the most effective and feasible techniques.
• The performance prediction methods of PAT are summarized in four categories: using BEP, using specific speed, loss modeling, and polynomial fitting.
• Present geometry optimization methods for impeller diameter and blade geometry of PAT are reviewed, and the blade rounding and forward-curved impellers prove to be effective.
• Based on the comparison and summary of published articles, the prospects of future studies are proposed.
The conversion and utilization of energy play a vital role in the process of human civilization. With the rapid development of social productivity, the growing energy demand and the scarcity of fossil fuels have increasingly become a widely concerned global issue. Renewable and clean energy sources to replace traditional fossil fuels have attracted much attention. Among alternatives to conventional energy sources, the hydropower system is one of the most mature technologies and widely applied in the past decades. The installed hydropower capacity has constituted 19.2% of total installed capacity until the end of 2017, which takes up the largest fraction of renewable energy (Liu, 2019). However, the engineering applications of hydropower have also encountered several challenges. The construction of large hydropower stations can result in a negative impact on the environment and the resettlement of local residents, which is a quite complex social issue (Li et al., 2018). In consideration of the shortcomings of large hydropower stations, the small/mini/micro/pico hydropower plants with a capacity no more than 25 MW become a popular solution to harness the potential of hydropower in rural areas (Binama et al., 2017). As the crucial component in the hydropower system, cost-effective turbines with acceptable performance are the guarantee for financial benefits. Compared to conventional full-scale turbines, the cost of small-scale turbines is relatively high regarding the budget of the whole hydropower system project. As an alternative, the Pump as Turbine (PAT) technology is a feasible choice to replace conventional turbines. The design, production, and manufacture of pumps in various scales are quite mature, which is effective to balance hydraulic performance and financial cost. The annual life cycle cost analysis between PAT technology and Francis turbine has validated less cost of PAT (Motwani et al., 2013).
For PAT, pumps operate under the reverse rotation direction to serve as turbines. The early attempts of investigation in PAT start from the 1930s, and it attracts much attention in recent decades (Singh and Nestmann, 2011; Agarwal, 2012). Ramos regarded PAT as an unconventional but attractive solution to produce energy from waterfalls in isolated rural communities, with advantages of decentralization, low-cost, and reliability (Ramos and Borga, 1999). Arriaga estimated the feasibility of PAT for rural electrification of isolated communities in Lao People’s Democratic Republic and proposed a 2 kW PAT scheme for a community in Xiagnabouli Province (Arriaga, 2010). Senpanich proposed a concept that a centrifugal pump was used as an impulse turbine, which can not only widen the working range but also simplify the control system (Senpanich et al., 2019). Besides the application in hydropower stations, the PAT technology is also introduced into the water distribution network. Conventionally, pressure reducing valves (PRV) are applied for pressure management and leakage reduction in a water distribution network (Araujo et al., 2006). Even though a pressure reducing valve is a cheap and simple solution, there is inevitable energy loss, and PAT is a better solution to recover this energy (Carravetta et al., 2013; Buono et al., 2015; Rossi et al., 2016). Lydon carried out three case studies to compare the performance of PRV and PAT, and results showed that up to 40% gross power potential can be recovered by using PAT (Lydon et al., 2017a; Lydon et al., 2017b). Besides the advantage in energy recovery, the economic benefit of applying PAT in the water distribution network is also considerable; a case study in Italy shows that it can pay back within about 2.5 years (De Marchis et al., 2014). In order to maximize PAT performance in the water distribution network, the variable operating strategy (Carravetta et al., 2013) and particle swarm optimization (Lima et al., 2017; Lima et al., 2018) are proposed for guiding the selection of PAT (Novara and McNabola, 2018a). Recently, the PAT technology is even applied in oil refineries to recover energy from sewers, and a case study shows that the payback period is only about 1 year and 10 months (Renzi et al., 2019).
Due to the considerable performance and superior economy of the PAT technology in various engineering practices (Morabito and Hendrick, 2019), studies are carried out to establish principles for the selection and optimization of PAT. Usually, the performance of pump under the turbine mode is not available, and hence, it is essential to predict PAT performance to serve as the selection basis. After selection, structural optimization can be useful to further improve PAT performance. So far, PAT research related to performance prediction and geometry optimization is abundant. It is meaningful to look back to present studies, serving as a summary of proposed prediction and optimization methods. Previous reviews on PAT technology have covered various aspects (Nautiyal et al., 2010; Jain and Patel, 2014), while the emphasis on performance prediction and geometry optimization is still limited. It is of great importance to summary present investigation on performance prediction and geometry optimization, which can help a lot on the selection and modification of Pump as Turbine. The objective of the present review is to focus on these two aspects, and it is organized as follows:
a) A brief literature review about the steady and unsteady performance of PAT is carried out in Section 2, which describes their hydraulic characteristics.
b) The performance prediction methods of PAT are summarized into four categories in Section 3, namely, using the best efficiency point, using specific speed, loss modeling, and polynomial fitting. Their strength and weakness are discussed after reviewing these methods.
c) The influence of geometry parameters on PAT performance is collected in Section 4, which is clarified by impeller diameter, blade parameters, and blade profiles. Suggestions about how geometry optimization should be applied are offered at the end of this part.
Since the PAT technology is proposed and promoted, the investigation on its energy performance is fundamental. Both experimental measurements and numerical simulations have been employed in various types of pumps operating as turbines, including centrifugal pumps (Ns < 100) (Santolaria Morros et al., 2011; Raman et al., 2013; Pugliese et al., 2016; Su et al., 2016), mixed flow pumps (100 < Ns < 300) (Hao and Tan, 2018; Liu and Tan, 2018; Han and Tan, 2020), and axial flow pumps (Ns > 300) (Bozorgi et al., 2013; Derakhshan and Kasaeian, 2014; Qian et al., 2016), where specific speed Ns = n√Q/H3/4.
When centrifugal pumps run as turbines, experimental investigation shows that PAT can operate under larger flow rates with a higher head at the best efficiency point (BEP), while the maximum efficiency is lower than that under the pump mode (Raman et al., 2013). Experimental results of axial PAT performance also indicate that the flow rate and head become higher under the turbine mode (Derakhshan and Kasaeian, 2014), and axial PAT can work in a wide range with a negligible decline in efficiency (Bozorgi et al., 2013). The working range of axial PAT can even be extended with the installation of adjustable guide vanes (Qian et al., 2016). Considering the relatively low performance under the turbine mode, an incorporated inlet flow control is equipped, including spiral casing and guide vane. With this inlet flow control component, the maximum efficiency of PAT is enhanced marginally, and PAT performances under off-design conditions are improved considerably (Giosio et al., 2015). The energy conversion characteristic of PAT in different impeller regions is investigated through numerical simulations, and the results show that the energy of fluids is converted mainly in the front and middle parts of the impeller (Miao et al., 2018). The effect of fluid viscosity on PAT performance is also studied experimentally with water–glycerin mixtures. As viscosity increases, the PAT efficiency declines under the partial flow rate but increases under BEP and large flow rates (Abazariyan et al., 2018).
The unsteady performance, especially pressure fluctuations inside the PAT, is another significant aspect, which is always related to the safe and stable operation of hydraulic machinery (Zuo et al., 2015). Numerical simulations show that the radial force almost linearly grows as flow rate increases, and the amplitude of radial force is about 24–54 percent of its mean value (Fernández et al., 2010). Another numerical study also shows that the amplitude of the unsteady radial force is up to 25% of steady components in PAT with spiral casing (Santolaria Morros et al., 2011).
The accurate prediction on the performance of pumps running under the turbine mode is the most important and difficult issue since PAT technology is established and applied. At the early stages, there are two main categories on performance prediction of PAT, namely, using BEP and using specific speed (Williams, 1994). In these two kinds of methods, pump performance and turbine performance are correlated by a relation expressed by BEP or specific speed. The prediction accuracy of these methods is determined by the correlation, and many efforts have been made to obtain a better correlation. In recent years, the performance prediction method based on loss modeling in hydraulic machinery, which has achieved success in pumps (Bing et al., 2012), is also introduced in determining PAT performance. These three types of methods mainly focus on PAT performance at BEP, and there is another method based on polynomial fitting to calculate performance under full flow rates.
The early attempt to predict PAT performance using BEP is based on two assumptions (Williams, 1994): 1) the best efficiency under the turbine mode is approximately equal to the best efficiency under pump mode; 2) the turbine output power is the same as the pump input power. With another assumption that the ratio of turbine and pump flow rate is equal to the ratio of turbine and pump head, the following relations of the flow rate and head under turbine and pump modes are obtained by Childs (1962):
where Q, H, and η denote the flow rate, head, and efficiency, respectively, subscript b denotes BEP, and subscripts T and P represent the turbine mode and pump mode, respectively. Afterward, researchers have established various functions to calculate the flow rate ratio QbT/QbP and the head ratio HbT/HbP, as summarized in Table 1.
In order to estimate the prediction accuracy of these methods, a prediction criterion is proposed by Williams based on an acceptable ellipse range (Williams, 1994), as displayed in Figure 1. The criterion C is calculated as follows:
where Δa is the proportional difference parallel to the major axis of the ellipse in Figure 1, and Δb is the proportional difference parallel to the minor axis of the ellipse in Figure 1. The value of C estimates the deviation degree of predicted results to actual results. The predicted results are more accurate if the C value is smaller. The calculated C values of the above five methods are listed in Table 1. It can be found that Sharma’s method shows the best performance on prediction accuracy among the others. Yang’s prediction method, which assumes the same Euler head under pump and turbine modes, shows a better performance than Sharma and Stepanoff’s methods, with an average prediction error of 6.0% (Yang et al., 2012a).
More factors have been introduced in PAT performance prediction using BEP. Fernandez considered the slip phenomenon (Fernández et al., 2004), and the ratio of turbine and pump heads becomes
where σ is the slip coefficient. The average error of the head ratio is 2.27% according to Fernandez’ method.
Since the performance of hydraulic machinery is clearly related to internal flow fields, the rotor–volute matching principle is employed to consider the effect of flow fields by Huang (Huang et al., 2017). The operation condition is regarded as BEP when flow fields in impeller and volute match well, and the flow coefficient φ and head coefficient ψ are determined by characteristic and geometry parameters. The geometry parameters of impeller and volute are used in the function as follows, and the involved geometry and operation parameters and corresponding calculation formulas are listed in Table 2.
The predicted BEP values from this method using BEP based the on rotor–volute matching principle and other conventional performance prediction methods are compared with experimental results under three types of pumps (GDD80-20, IS100-65, and GD100-21), with specific speed varying from 58.7 to 129.6. The average error of this prediction method is only 2.44%, which is quite limited among the others, as shown in Figure 2. In addition, this method does not rely on empirical values entirely, which is of higher universality and practicality.
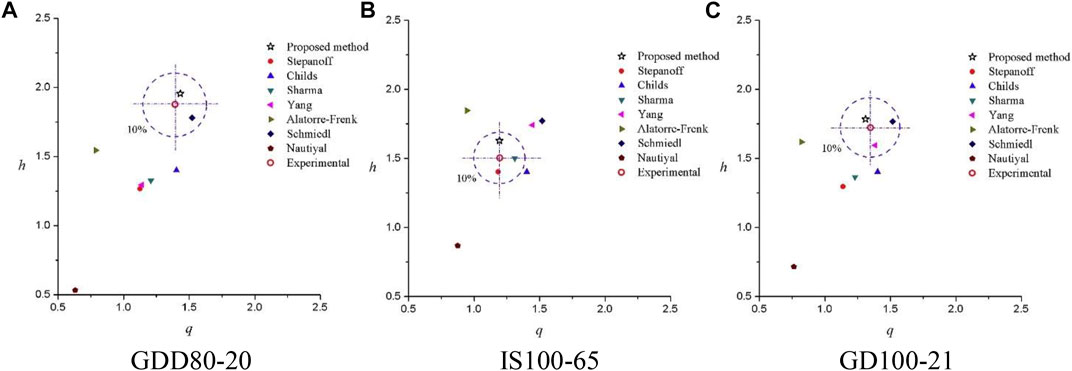
FIGURE 2. Comparisons between experimental and predicted results from various methods (Huang et al., 2017). (A) GDD80-20, (B) IS100-65, (C) GD100-21.
For such centrifugal pumps with low specific speed designed by increasing the flow rate, Shi proposed a PAT performance prediction method considering amplification coefficients (Shi et al., 2017). This method assumes the same Euler heads under pump and turbine modes, and the following correlations can be derived:
where Hp’, Qp’, and NsP’ are pump head, flow rate, and specific speed after amplification, Hp’ = ε1Hp, Qp’ = ε2Qp, and NsP’ = ε2Nsp, with amplification coefficients ε1, ε2, ε3, and u2 as the circumferential velocity at pump impeller outlet, and F1 is the area of axial surface at the impeller inlet. The average error to experimental data is 2.81% when applying this prediction method in three low specific speed centrifugal pumps, NsP = 33, 47, 66.
The PAT performance prediction method using specific speed is similar to that using BEP. The major difference lies in that the function to determine the flow rate ratio and the head ratio is expressed by specific speed. Table 3 lists classical PAT performance prediction methods using specific speed and corresponding accuracy estimated by Williams (Williams, 1994).
Comparing the prediction accuracy of methods using BEP in Table 1 and using specific speed in Table 3, the results from methods using BEP are generally better than those using specific speed. Therefore, several modified specific speeds are employed to obtain a higher accuracy. Derakshan applied dimensionless specific speed to establish the following relations for centrifugal pumps with specific speed NsP < 60 (Derakhshan and Nourbakhsh, 2008a):
The prediction error of the flow rate ratio and head ratio is 2.99% according to Derakshan’s method, which is significantly limited compared with the results from conventional Stepanoff, Sharma, and Alatorre-Frenk’ methods in the same pumps.
Nautiyal proposed a new parameter to serve as values in the function to determine the flow rate ratio and head ratio (Nautiyal et al., 2011):
The maximum deviation of predicted results to experimental measurements is within 11%, which is reduced compared to more than 20% of conventional methods. Since both maximum efficiency and specific speed have been employed in Nautiyal’s method, it can be regarded as an initial trial to combine PAT performance prediction methods using BEP and specific speed.
There is another type of the PAT performance prediction method using specific speed, which establishes the correlation between the specific speed of the pump mode and turbine mode. Singh proposed a correlation based on 13 pumps as follows, and applied the correlation for PAT selection (Singh and Nestmann, 2010).
Tan tested the hydraulic performance of centrifugal pumps under pump and turbine modes, and found several linear relations between pump and turbine parameters, as follows (Tan and Engeda, 2016):
where Ds is the specific diameter calculated by DHb0.25/Qb0.5. With the aforementioned linear relation, the average prediction error of specific speed, flow rate, head, efficiency, and power at BEP under the turbine mode is 3.95%.
A similar study has also been conducted by Stefanizzi to establish a relation between specific speed under pump and turbine modes (Stefanizzi et al., 2017).
The above correlation is determined based on performance data of 27 pumps, and it is employed to predict the PAT performance of 11 new pumps. The comparison shows that the predicted head errors of seven pumps and the predicted flow rate errors of eight pumps are within 10%. Capurso further considered the slip phenomenon in Stefanizzi’s method and found that the prediction accuracy can be improved obviously (Capurso et al., 2018).
The combined artificial neural networks (ANN) and evolutionary polynomial regression (EPR) algorithms proposed by Balacoo have also been applied to obtain an accurate correlation (Balacco, 2018). Totally, 33 pumps are tested to determine correlations listed in Table 4. The flow rate, head, efficiency at BEP, and specific speed under the pump mode are employed as input parameters, and parameters of PAT performance are output values. The models with various function forms have been established by means of the ANN–EPR algorithms. It can be found that the specific speed, flow rate, head, and efficiency at BEP under the turbine mode can be predicted with acceptable accuracy through models established by ANN–EPR algorithms. However, the ANN–EPR algorithms fail to establish a reliable correlation to predict flow rate ratio QT/QH and head ratio HT/HP.
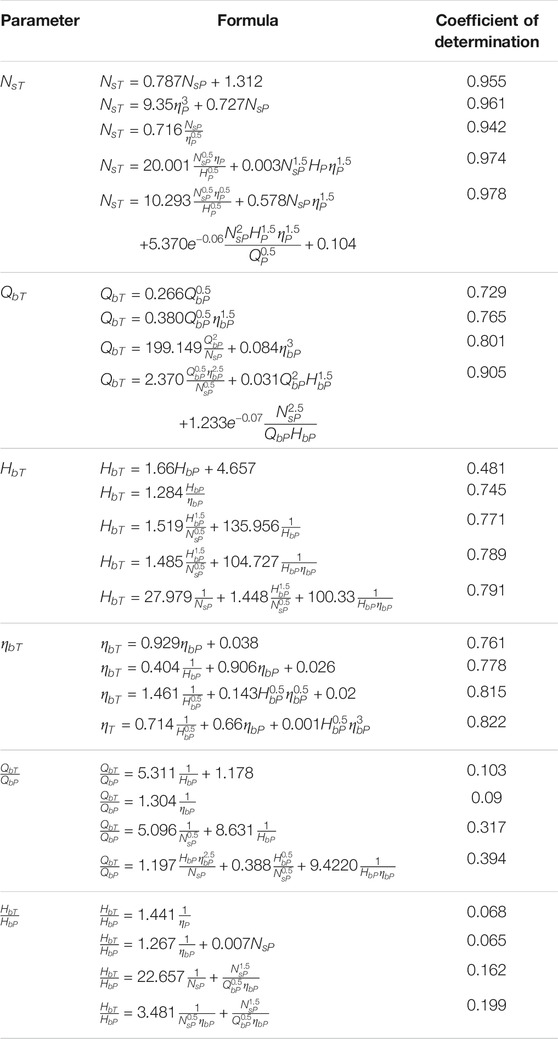
TABLE 4. Models established by ANN–EPR algorithms (Balacco, 2018).
The methods using BEP and specific speed have become the most widely used approaches to predict PAT performance, and another concept based on loss modeling also catches the attention of researchers. The loss modeling prediction method is similar to the method using BEP, which is established from the theoretical analysis of internal flow fields.
Derakhshan carried out a relatively rough theoretical analysis on internal flow fields at BEP and established a performance prediction method based on the estimation of volute losses, leakage losses, kinetic losses, hydraulic losses, and mechanical losses (Derakhshan and Nourbakhsh, 2008b). After calculating different losses components, the PAT efficiency can be determined as follows, and the calculation methods of each loss are listed in Table 5:

TABLE 5. Formulas to calculate losses (Derakhshan and Nourbakhsh, 2008b).
This prediction method proves to be useful for the tested centrifugal pump in Derakhshan’s study, and the errors between predicted and experimental results on dimensionless flow rate, head, power, and efficiency are −1.1%, −4.7%, −5.3%, and −2.1%, respectively.
A more detailed analysis of losses inside PAT has been conducted by Barbarelli (Barbarelli et al., 2016) and Liu (Liu et al., 2019). Barbarelli’s method starts from geometry components provided by pump manufacturers and employs these geometry parameters to calculate friction loss and dynamic losses in each component, namely, inlet pipe, volute, vaneless diffuser, impeller, and discharge pipe (Barbarelli et al., 2016). The whole process of performance calculation is illustrated by a flowchart in Figure 3. The calculation procedure is iterative because the leakage flow rate and volumetric efficiency are unknown at the beginning. From an assumed flow rate, the theoretical Euler head is calculated. Subsequently, friction and dynamic loess are estimated. Therefore, the real turbine head and corresponding turbine efficiency can be determined, and the final flow rate is checked whether it agrees with the assumed value. Application of this method in six centrifugal pumps with specific speed varied from 9 to 65 shows that the highest relative error at BEP is 21.4%, and it can be further reduced to 7.2% if more detailed geometry parameters are available.
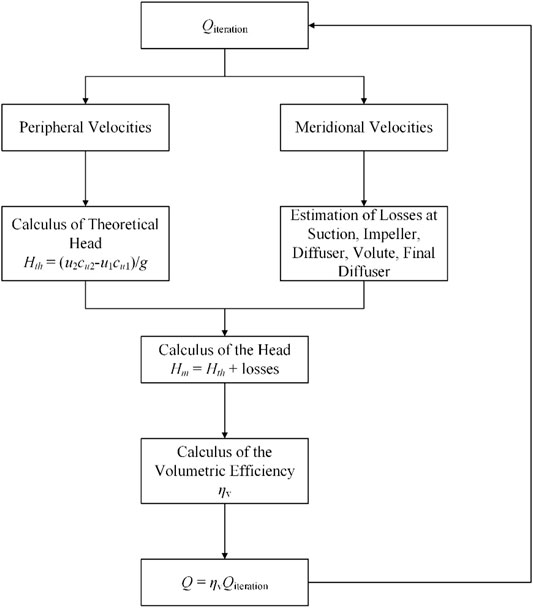
FIGURE 3. Flowchart of performance calculation in Barbarelli’s method (Barbarelli et al., 2016).
Liu conducted a comprehensive investigation on predicting the performance of the centrifugal pump under pump and turbine modes (Liu et al., 2019). In order to improve prediction accuracy, various losses in each component are calculated precisely. Table 6 lists the employed formulas for loss calculation in Liu’s method. Due to the universality and accuracy of these loss models, the performances under design and off-design conditions can be determined, which makes the acquirement of characteristic curves under full flow rates possible. Therefore, a flow rate–based iteration method to determine BEP is also proposed based on characteristic curves. Compared with the loss modeling method of Barbarelli, the prediction accuracy can be significantly improved. The average relative errors for head and efficiency under the pump mode are 6.12 and 5.31%, respectively, and they are 5.40 and 3.63% for head and efficiency, respectively, under the turbine mode. The predicted error for BEP of PAT is only 1.28% on average, which validates the effectiveness of this method.

TABLE 6. Losses modeling in Liu’s method (Liu et al., 2019).
The PAT performance prediction methods using BEP and specific speed always focus on the performance at BEP, while the PAT performance under off-design conditions is also important for long-term stable operation. There are several attempts to predict PAT performance under full flow rates using polynomial fitting.
Fecarotta proposed a prediction method for PAT performance curves based on affinity law as follows (Fecarotta et al., 2016):
where Ω and T are rotation speed and torque, respectively, and subscript b denotes the best efficiency point. It is reported that the functions WH(θ) and WT(θ) are unique for similar hydraulic machinery so that the values of turbine head H and efficiency η can be calculated based on these functions. To improve prediction accuracy, the relaxation factors are introduced to establish the following empirical formulas:
The mean errors of this semi-empirical method with relaxation factors for turbine efficiency, head, and power are 2.52, 3.93, and 7.93%, respectively.
The concept of relating dimensionless parameters through polynomial functions has also been adopted by Barbarelli (Barbarelli et al., 2017) and Novara (Novara and McNabola, 2018b). Barbarelli established the following dimensionless relations based on 12 pumps (Barbarelli et al., 2017).
Novara further established advanced polynomial functions in consideration of the specific speed using a database of a totally of 113 PAT performance curves (Novara and McNabola, 2018b).
As reported by Novara, the R2 values for data fitting of Fecarotta, Barbarelli, and Novara’s methods are 0.9295, 0.9236, and 0.9701 for PAT head, and 0.9611, 0.9551, and 0.9776 for PAT power. This comparison validates the superior prediction accuracy of Novara’s method.
A similar method has also been employed by Li to predict centrifugal PAT handling fluids with various viscosities (Li, 2017). The major difference lies in that the Reynolds number rather than the dimensionless flow rate is used as input parameters in 3rd- and 4th-order polynomial functions. The relations between PAT performance (head, power, and efficiency) and Reynolds number under five typical operating conditions such that zero-power point, 0.8 part-load points, best efficiency point, 1.2 over-load, and maximum flow rate point are established, and the average errors are 1.67, 2.57, and 6.76% in head, power, and efficiency, respectively.
In order to investigate the influence of impeller diameter and rotation speed, Jain established the following polynomial function in a logarithm form (Jain et al., 2015):
where subscript r denotes the rated value. The predicted errors according to this correlation are within the band of ±10%.
So far, PAT performance prediction methods are reviewed from different perspectives. The methods using BEP are based on theoretical analysis with complicated forms, which requires basic knowledge of pump geometry. As a contrast, the methods using specific speed are based on statistical fitting, which requires sufficient data as samples. Even though the function form of prediction methods using specific speed is similar, the function coefficients are different from each other, which indicates that the universality of this type of method is an obvious weakness.
The methods using loss modeling are similar to the methods using BEP, and they are even more theoretical. It requires comprehensive and detailed information of pumps, and its accuracy mainly depends on the reliability of employed loss models. By comparison, the methods using polynomimal fitting are similar to the methods using specific speed, and they are more statistical than the methods using the specific method. The prediction using polynomial fitting should be restricted in certain ranges since the prediction error may increase when it differs from the samples.
The aforementioned four categories of prediction methods can be summarized by theoretical and statistical characteristics. For theoretical characteristics, it is sorted by loss modeling > using BEP > using specific speed > polynomial fitting. For statistical characteristics, it is sorted by polynomial fitting > using specific speed > using BEP > loss modeling, which is exactly the inverse sortation. Theoretical approaches show better generality but require a lot of information. The statistical approaches do not require a lot of information but are less versatile.
The performance prediction plays a vital role in the selection of PAT, which is the first stage during the application. According to the previous investigation on energy performance, the PAT efficiency is always lower than that of the pump, and the high-efficiency region is relatively narrow. It is essential to carry out geometry optimization to further improve PAT performance. Considering the cost and difficulty of processing, present studies mainly focus on three aspects: impeller diameter, blade parameter, and blade profile.
The impeller diameter is one of the most important design parameters in hydraulic machinery, which can determine its capacity. Yang studied the influence of impeller diameter on the performance of centrifugal PAT through experimental, numerical, and theoretical research (Yang et al., 2013). It is found that as impeller diameter rises from 215 to 255 mm, the flow rate, PAT efficiency, required pressure head, and shaft power at the BEP are increased by 26.14, 10.26, 36.16, and 89.39%, respectively. Numerical analysis of flow fields shows that performance improvement results from the reduction of hydraulic loss within the radial gap between impeller and volute.
However, when a certain pump has been selected, it is not practical to extend impeller diameter. As a consequence, the impeller trimming method is applied to reduce impeller diameter. Yang cut down the impeller diameter of a centrifugal PAT from 255 to 235 mm and 215 mm (Yang et al., 2012b). The measured efficiency, head, and shaft power are displayed in Figure 4. The results show that as impeller diameter decreases from 255 to 215 mm, the flow rate and maximum efficiency are reduced by 20 m3/h and 2.17%, respectively. In addition, the head curves become increasingly steep, while the shaft power curves become relatively flat after impeller trimming. Jain applied 10% trimming and 20% trimming to an original impeller of 250 mm (Jain et al., 2015), and similar PAT characteristic curves to Yang’s study are also obtained. It is confirmed that when impeller trimming is adopted, the BEP of PAT shifts toward the partial flow rate at first, and backshifts toward a larger flow rate after further trimming.
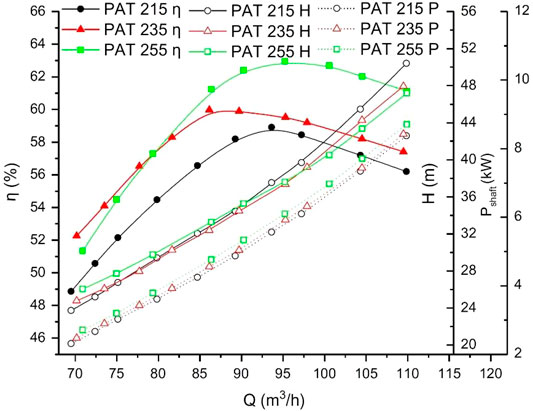
FIGURE 4. Performance curves of PAT with different impeller diameters (Yang et al., 2012b).
The geometry of impeller blade is vital for energy conversion, and various studies have been conducted to figure out the influence of blade geometry on PAT performance, including blade angle, blade number, and blade thickness.
Yang investigated the performance of centrifugal PAT with three specific speeds under different blade wrap angles experimentally and numerically (Yang et al., 2012c). The results show that there exists an optimal blade wrap angle to achieve the best efficiency, and the optimal blade wrap angle decreases as specific speed increases. With the decline of blade wrap angle, the BEP shifts toward a larger flow rate, and both PAT head and generated shaft power will become lower. Numerical analysis on flow fields indicates that smaller blade wrap angle can lead to a shorter length of impeller flow passage and smaller velocity gradient in the impeller, which induces less hydraulic loss. The same results have also been reported in Yang’s another research (Yang et al., 2012b).
The influence of blade thickness on PAT performance has also been investigated (Yang et al., 2014). The results show that increasing blade thickness can lead to decline of efficiency and rise of head and shaft power. It is recommended that the blade should be as thin as possible from the perspective of PAT efficiency.
The aforementioned research studies mainly focus on the influence of blade geometry on PAT energy performance, and there are also studies that concern unsteady performance of PAT. The numerical investigation about blade number shows that there is an optimal value of the blade number to obtain the highest efficiency, and the amplitude of pressure fluctuations can be reduced by increasing the blade number (Yang et al., 2012d). For PAT with variable guide vanes, Shi analyzed the effect of guide vane number on unsteady performance (Shi et al., 2018). After the installation of guide vanes, the radial force is not only reduced but also becomes more symmetrical and homogeneous. The optimal guide vane number is recommended to be 9, which can result in the lowest and most uniform radial force, and the minimum power losses at the same time.
Binama studied the unsteady flow fields inside centrifugal PATs under partial flow rates with three blade trailing edge hub position (15 mm, 20 mm, and 25 mm) (Binama et al., 2019). The impeller rotating frequency and its multiples are found to be the dominant frequency in centrifugal PAT. It is reported that the highest and lowest pressure fluctuations appear at the position of 20 and 15 mm, respectively, and a regular rule on the relation between blade trailing edge position and pressure fluctuations is still unknown.
Parameterizing the blade profile through the non-uniform B-spline curve, Miao optimized the blade profile by means of the back propagation neural network and genetic algorithm (Miao et al., 2015). Figure 5 shows the comparison of blade profile and performance curves of initial and optimal PAT models. The maximum PAT efficiency is improved by 2.91% after optimization because hydraulic loss in impeller has been reduced.
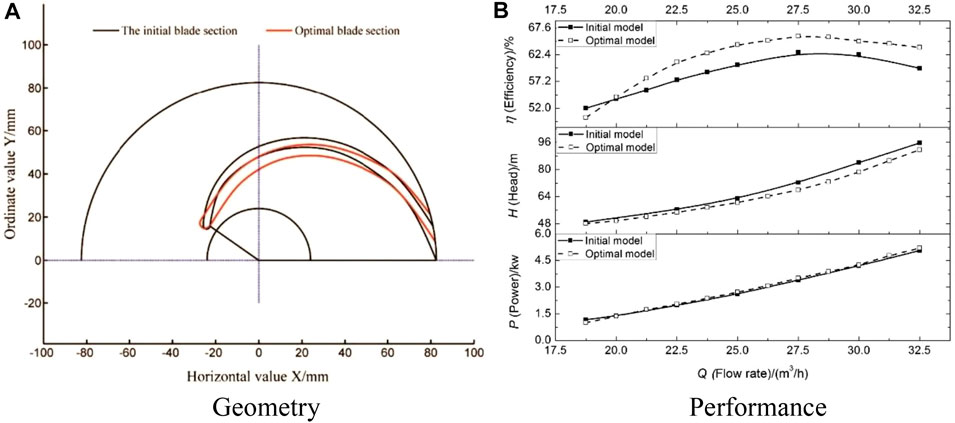
FIGURE 5. Geometry and performance of initial and optimal PAT models (Miao et al., 2015). (A) Geometry, (B) Performance.
For a given centrifugal pump, the blade rounding technique to avoid sharp edges of impeller has been introduced for PAT performance enhancement. The rounding radius equal to half of blade thickness is adopted in seven radial-flow or mixed-flow pumps, and improvements in the range of 1–3% for overall efficiency under various operating conditions have been obtained (Singh and Nestmann, 2011). Figure 6 illustrates the physical understanding on how blade rounding improves internal flow fields. After blade rounding, the wake region at the inlet due to sharp edge is suppressed so that hydraulic loss is reduced. At the same time, an exit circulation with a larger flow angle is induced at the outlet, which can lead to a higher generated power. Further detailed experimental study confirms that blade rounding can bring on a great degree of hydraulic loss reduction than increase of output power, and hence, the overall efficiency is improved (Doshi et al., 2017).
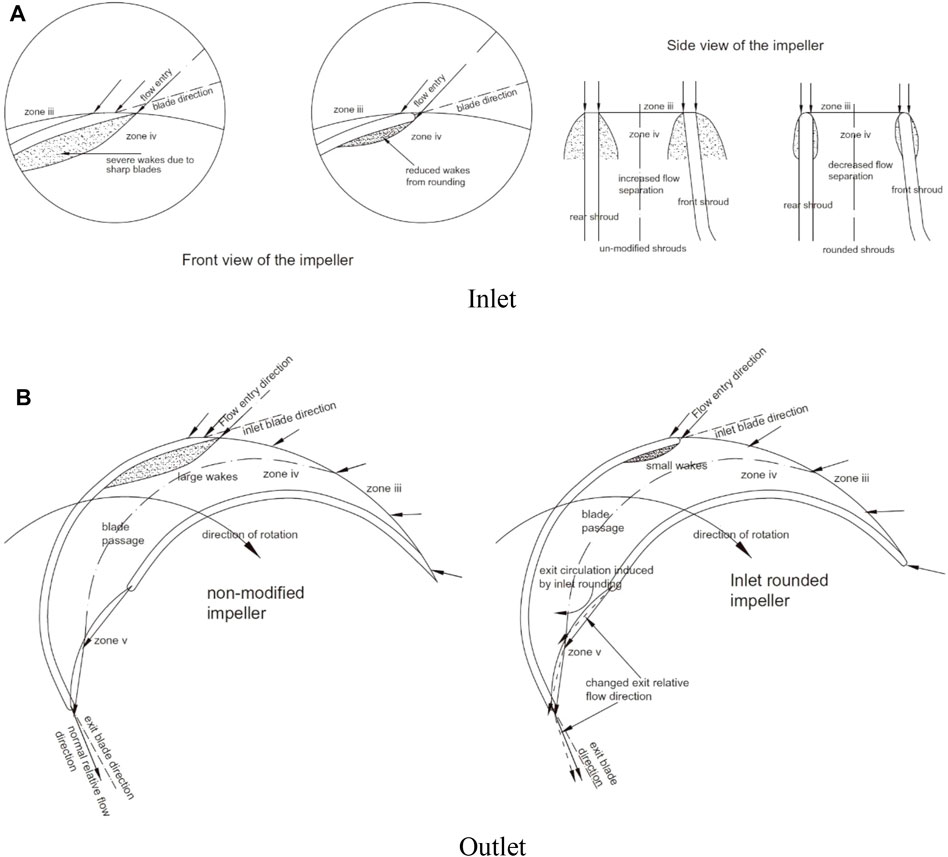
FIGURE 6. Physical understanding of blade rounding effects at inlet and outlet (Singh and Nestmann, 2011). (A) Inlet, (B) Outlet.
Since conventional backward-curved centrifugal impellers cannot match the turbine running condition well, the forward-curved centrifugal impellers are designed to improve PAT performance. Wang proposed a design method for special forward-curved impeller based on angular momentum conservation, and non-impingement velocity inlet and normal velocity outlet conditions are employed to determine inlet and outlet blade angles (Wang et al., 2017a). Figure 7 depicts the performance curves of PAT with original backward-curved impeller and special forward-curved impeller. The PAT efficiency is significantly improved with forward-curved impeller, and high efficiency scope is also extended. Comparison of three centrifugal pumps with different specific speeds (18.1, 36.4, and 52.8) shows average rise of 7.15% in efficiency, which validates the superiority of the proposed design method. Further analysis on blade inlet angle shows that a range of 70°–135° is recommended for low specific speed centrifugal pump, and larger inlet angle will match the higher rated flow rate (Wang et al., 2017b).
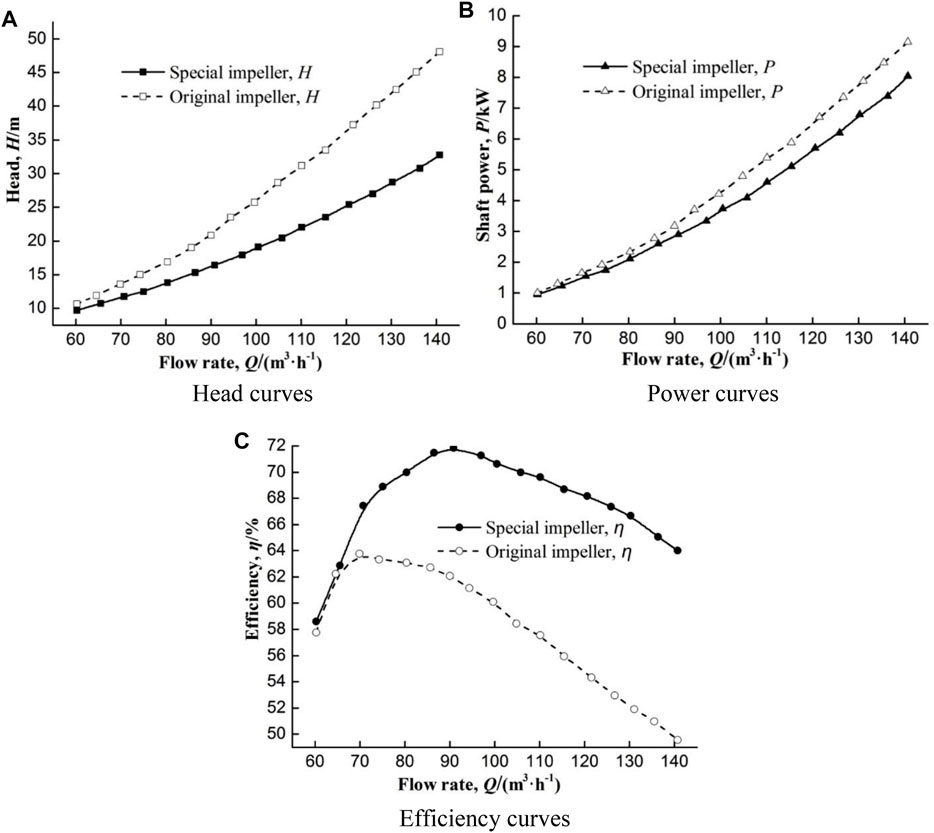
FIGURE 7. Performance curves of PAT with original and special impellers (Wang et al., 2017a). (A) Head, (B) Power, (C) Efficiency.
Present studies related to geometry optimization are reviewed in this section. Among these methods, the impeller trimming and blade rounding are the most practical methods to modify geometry after pumps have been selected. Although it is useful to adjust BEP using impeller trimming, it can also lead to head decline. By comparison, blade rounding is more reliable since PAT performance can be further improved after applying this method.
Apart from impeller trimming and blade rounding, the other geometry optimization methods are only useful when selecting certain type of pumps. These investigations about blade number and blade thickness, which indicate the influence of structural parameters, can serve as a guide to select pumps, while it is difficult to modify such structural parameters after pump selection.
A literature review on the progress in Pump as Turbine is presented in this study, with the emphasis on performance prediction and geometry optimization. The following conclusions can be drawn:
(1) Commonly, when pump operates as turbines, the BEP will shift toward a larger flow rate, and the maximum efficiency under the turbine mode is somewhat lower than that under pump mode. The unsteady radial force almost grows linearly as the flow rate increases.
(2) Current PAT performance prediction methods can be divided into four categories, namely, using BEP, using specific speed, loss modeling, and polynomial fitting. The using BEP and loss modeling methods are based on theoretical analysis, which is of a complicated form but with better universality. These two methods require many geometry parameters of pump before performance predictions. The using specific speed and polynomial fitting methods require statistical fitting, which is of a simple form but with weak universality. These two methods require sufficient data samples to establish a reliable relationship. On the basis of great efforts on improving accuracy, most prediction methods can reach the level where errors are within ±10%.
(3) The investigation on influence of geometry parameters mainly focuses on impeller diameter and blade geometry currently. The impeller trimming will lead to performance decline, but it is useful to adjust BEP. Studies show that there exist optimal blade wrap angle, blade number, blade trailing edge position, and guide vane number to achieve the highest efficiency. The blade rounding and forward-curved impeller are two effective techniques to improve PAT performance, and optimization of blade profile is also worth implementing.
According to the aforementioned conclusions, some remarks with regard to further investigation are listed:
(1) In the consideration of the advantages of each category of the performance prediction method, it will be a useful attempt to establish a combined method using BEP and specific speed. The combined performance prediction method may start from theoretical analysis of flow fields and employ some commonly used statistical relation for simplification, which is semi-theoretical and semi-empirical. This type of combined method can be of both conciseness and universality, which is more meaningful for engineering practice.
(2) Present performance prediction under off-design conditions relies on polynomial fitting mostly, which is quite case-sensitive. The expansion of conventional performance prediction methods using BEP and specific speed to off-design conditions is another meaningful subject. A two-stage performance prediction method may be proposed in the future. First, the PAT performance at BEP is predicted using the theoretical prediction method (using BEP or loss modeling), which may only require several key parameters. Second, the PAT performances at off-design conditions are determined based on performance at BEP using the statistical prediction method (using specific speed or polynomial fitting), which establishes a more general function to relate design and off-design conditions.
(3) Among published geometry optimization methods, the blade rounding is the most effective and practical technique, which can modify a given pump impeller directly. However, present investigation on blade rounding for PAT is relatively few, and the achieved efficiency improvement is no more than 3%. More in-depth research is required on the application of blade rounding. Different rounding schemes including circular type and ellipse type, the influence of rounding radius, still deserve further attempt and analysis.
(4) It will be a meaningful work to combine performance prediction and geometry optimization together. Since geometry optimization can definitely influence PAT performance, a performance prediction method considering structural parameters should be built so that PAT performance after geometry modification can also be determined. Using this method, the PAT performance after optimization can be predicted immediately, which can improve optimization efficiency and save its costs.
LT, SC, and ML contributed to conceptualization and methodology; ML contributed to writing—original draft preparation; LT and SC contributed to writing—review and editing; LT contributed to supervision, project administration, and funding acquisition. All authors have read and agreed to the published version of the manuscript.
This work has been supported by the National Key R&D Program of China (2020YFB1901401) and the State Key Laboratory of Hydroscience and Engineering (2021-KY-04).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abazariyan, S., Rafee, R., and Derakhshan, S. (2018). Experimental Study of Viscosity Effects on a Pump as Turbine Performance. Renew. Energ. 127, 539–547. doi:10.1016/j.renene.2018.04.084
Agarwal, T. (2012). Review of Pump as Turbine (PAT) for Micro-hydropower. Int. J. Emerging Tech. Adv. Eng. 2 (11), 163–169.
Alatorre-Frenk, C. (1994). Cost Minimisation in Micro-hydro Systems Using Pumps-Asturbines. Coventry, UK: University of Warwick.
Araujo, L. S., Ramos, H., and Coelho, S. T. (2006). Pressure Control for Leakage Minimisation in Water Distribution Systems Management. Water Resour. Manage. 20, 133–149. doi:10.1007/s11269-006-4635-3
Arriaga, M. (2010). Pump as Turbine - A Pico-Hydro Alternative in Lao People's Democratic Republic. Renew. Energ. 35, 1109–1115. doi:10.1016/j.renene.2009.08.022
Balacco, G. (2018). Performance Prediction of a Pump as Turbine: Sensitivity Analysis Based on Artificial Neural Networks and Evolutionary Polynomial Regression. Energies 11, 3497. doi:10.3390/en11123497
Barbarelli, S., Amelio, M., and Florio, G. (2017). Experimental Activity at Test Rig Validating Correlations to Select Pumps Running as Turbines in Microhydro Plants. Energ. Convers. Manag. 149, 781–797. doi:10.1016/j.enconman.2017.03.013
Barbarelli, S., Amelio, M., and Florio, G. (2016). Predictive Model Estimating the Performances of Centrifugal Pumps Used as Turbines. Energy 107, 103–121. doi:10.1016/j.energy.2016.03.122
Binama, M., Su, W.-T., Cai, W.-H., Li, X.-B., Muhirwa, A., Li, B., et al. (2019). Blade Trailing Edge Position Influencing Pump as Turbine (PAT) Pressure Field under Part-Load Conditions. Renew. Energ. 136, 33–47. doi:10.1016/j.renene.2018.12.077
Binama, M., Su, W.-T., Li, X.-B., Li, F.-C., Wei, X.-Z., and An, S. (2017). Investigation on Pump as Turbine (PAT) Technical Aspects for Micro Hydropower Schemes: A State-Of-The-Art Review. Renew. Sust. Energ. Rev. 79, 148–179. doi:10.1016/j.rser.2017.04.071
Bing, H., Tan, L., Cao, S., and Lu, L. (2012). Prediction Method of Impeller Performance and Analysis of Loss Mechanism for Mixed-Flow Pump. Sci. China Technol. Sci. 55 (7), 1988–1998. doi:10.1007/s11431-012-4867-9
Bozorgi, A., Javidpour, E., Riasi, A., and Nourbakhsh, A. (2013). Numerical and Experimental Study of Using Axial Pump as Turbine in Pico Hydropower Plants. Renew. Energ. 53, 258–264. doi:10.1016/j.renene.2012.11.016
Buono, D., Frosina, E., Mazzone, A., Cesaro, U., and Senatore, A. (2015). Study of a Pump as Turbine for a Hydraulic Urban Network Using a Tridimensional CFD Modeling Methodology. Energ. Proced. 82, 201–208. doi:10.1016/j.egypro.2015.12.020
Capurso, T., Stefanizzi, M., Torresi, M., Pascazio, G., Caramia, G., Camporeale, S. M., et al. (2018). How to Improve the Performance Prediction of a Pump as Turbine by Considering the Slip Phenomenon. Proceedings 2, 683. doi:10.3390/proceedings2110683
Carravetta, A., Del Giudice, G., Fecarotta, O., and Ramos, H. (2013). Pump as Turbine (PAT) Design in Water Distribution Network by System Effectiveness. Water 5, 1211–1225. doi:10.3390/w5031211
Childs, S. (1962). Convert Pumps to Turbines and Recover HP. Hydrocarb Process. Pet. Refin 41, 173–174.
De Marchis, M., Fontanazza, C. M., Freni, G., Messineo, A., Milici, B., Napoli, E., et al. (2014). Energy Recovery in Water Distribution Networks. Implementation of Pumps as Turbine in a Dynamic Numerical Model. Proced. Eng. 70, 439–448. doi:10.1016/j.proeng.2014.02.049
Derakhshan, S., and Kasaeian, N. (2014). Optimization, Numerical, and Experimental Study of a Propeller Pump as Turbine. ASME J. Energ. Resour. Tech. 136, 012005. doi:10.1115/1.4026312
Derakhshan, S., and Nourbakhsh, A. (2008). Experimental Study of Characteristic Curves of Centrifugal Pumps Working as Turbines in Different Specific Speeds. Exp. Therm. Fluid Sci. 32, 800–807. doi:10.1016/j.expthermflusci.2007.10.004
Derakhshan, S., and Nourbakhsh, A. (2008). Theoretical, Numerical and Experimental Investigation of Centrifugal Pumps in Reverse Operation. Exp. Therm. Fluid Sci. 32, 1620–1627. doi:10.1016/j.expthermflusci.2008.05.004
Doshi, A., Channiwala, S., and Singh, P. (2017). Inlet Impeller Rounding in Pumps as Turbines: An Experimental Study to Investigate the Relative Effects of Blade and Shroud Rounding. Exp. Therm. Fluid Sci. 82, 333–348. doi:10.1016/j.expthermflusci.2016.11.024
Fecarotta, O., Carravetta, A., Ramos, H. M., and Martino, R. (2016). An Improved Affinity Model to Enhance Variable Operating Strategy for Pumps Used as Turbines. J. Hydraulic Res. 54 (3), 332–341. doi:10.1080/00221686.2016.1141804
Fernández, J., Barrio, R., Blanco, E., Parrondo, J. L., and Marcos, A. (2010). Numerical Investigation of a Centrifugal Pump Running in Reverse Mode. Proc. Inst. Mech. Eng. A: J. Power Energ. 224, 373–381. doi:10.1243/09576509jpe757
Fernández, J., Blanco, E., Parrondo, J., Stickland, M. T., and Scanlon, T. J. (2004). Performance of a Centrifugal Pump Running in Inverse Mode. Proc. Inst. Mech. Eng. Part A: J. Power Energ. 218, 265–271. doi:10.1243/0957650041200632
Giosio, D. R., Henderson, A. D., Walker, J. M., Brandner, P. A., Sargison, J. E., and Gautam, P. (2015). Design and Performance Evaluation of a Pump-As-Turbine Micro-hydro Test Facility with Incorporated Inlet Flow Control. Renew. Energ. 78, 1–6. doi:10.1016/j.renene.2014.12.027
Han, Y., and Tan, L. (2020). Dynamic Mode Decomposition and Reconstruction of Tip Leakage Vortex in a Mixed Flow Pump as Turbine at Pump Mode. Renew. Energ. 155, 725–734. doi:10.1016/j.renene.2020.03.142
Hao, Y., and Tan, L. (2018). Symmetrical and Unsymmetrical Tip Clearances on Cavitation Performance and Radial Force of a Mixed Flow Pump as Turbine at Pump Mode. Renew. Energ. 127, 368–376. doi:10.1016/j.renene.2018.04.072
Huang, S., Qiu, G., Su, X., Chen, J., and Zou, W. (2017). Performance Prediction of a Centrifugal Pump as Turbine Using Rotor-Volute Matching Principle. Renew. Energ. 108, 64–71. doi:10.1016/j.renene.2017.02.045
Jain, S. V., and Patel, R. N. (2014). Investigations on Pump Running in Turbine Mode: A Review of the State-Of-The-Art. Renew. Sust. Energ. Rev. 30, 841–868. doi:10.1016/j.rser.2013.11.030
Jain, S. V., Swarnkar, A., Motwani, K. H., and Patel, R. N. (2015). Effects of Impeller Diameter and Rotational Speed on Performance of Pump Running in Turbine Mode. Energ. Convers. Manag. 89, 808–824. doi:10.1016/j.enconman.2014.10.036
Lewinsky-Kesslitz, H. (1987). Pumpen Als Turbinen Fur Kleinkraftwerke. Wasserwirtschaft 77, 531–537.
Li, W.-G. (2017). Optimising Prediction Model of Centrifugal Pump as Turbine with Viscosity Effects. Appl. Math. Model. 41, 375–398. doi:10.1016/j.apm.2016.09.002
Li, X.-z., Chen, Z.-j., Fan, X.-c., and Cheng, Z.-j. (2018). Hydropower Development Situation and Prospects in China. Renew. Sust. Energ. Rev. 82, 232–239. doi:10.1016/j.rser.2017.08.090
Lima, G. M., Luvizotto, E., and Brentan, B. M. (2017). Selection and Location of Pumps as Turbines Substituting Pressure Reducing Valves. Renew. Energ. 109, 392–405. doi:10.1016/j.renene.2017.03.056
Lima, G. M., Luvizotto, E., Brentan, B. M., and Ramos, H. M. (2018). Leakage Control and Energy Recovery Using Variable Speed Pumps as Turbines. J. Water Resour. Plann. Manage. 144 (1), 04017077. doi:10.1061/(asce)wr.1943-5452.0000852
Liu, J. (2019). China's Renewable Energy Law and Policy: A Critical Review. Renew. Sust. Energ. Rev. 99, 212–219. doi:10.1016/j.rser.2018.10.007
Liu, M., Tan, L., and Cao, S. (2019). Theoretical Model of Energy Performance Prediction and BEP Determination for Centrifugal Pump as Turbine. Energy 172, 712–732. doi:10.1016/j.energy.2019.01.162
Liu, Y., and Tan, L. (2018). Tip Clearance on Pressure Fluctuation Intensity and Vortex Characteristic of a Mixed Flow Pump as Turbine at Pump Mode. Renew. Energ. 129, 606–615. doi:10.1016/j.renene.2018.06.032
Lydon, T., Coughlan, P., and McNabola, A. (2017). Pressure Management and Energy Recovery in Water Distribution Networks: Development of Design and Selection Methodologies Using Three Pump-As-Turbine Case Studies. Renew. Energ. 114, 1038–1050. doi:10.1016/j.renene.2017.07.120
Lydon, T., Coughlan, P., and McNabola, A. (2017). Pump-As-Turbine: Characterization as an Energy Recovery Device for the Water Distribution Network. J. Hydraul. Eng. 143 (8), 04017020. doi:10.1061/(asce)hy.1943-7900.0001316
Miao, S., Yang, J., Shi, F., Wang, X., and Shi, G. (2018). Research on Energy Conversion Characteristic of Pump as Turbine. Adv. Mech. Eng. 10 (4), 1–10. doi:10.1177/1687814018770836
Miao, S., Yang, J., Shi, G., and Wang, T. (2015). Blade Profile Optimization of Pump as Turbine. Adv. Mech. Eng. 7 (9), 1–9. doi:10.1177/1687814015605748
Morabito, A., and Hendrick, P. (2019). Pump as Turbine Applied to Micro Energy Storage and Smart Water Grids: A Case Study. Appl. Energ. 241, 567–579. doi:10.1016/j.apenergy.2019.03.018
Motwani, K. H., Jain, S. V., and Patel, R. N. (2013). Cost Analysis of Pump as Turbine for Pico Hydropower Plants - A Case Study. Proced. Eng. 51, 721–726. doi:10.1016/j.proeng.2013.01.103
Nautiyal, H., Kumar, A., and Yadav, S. (2011). Experimental Investigation of Centrifugal Pump Working as Turbine for Small Hydropower Systems. Energ. Sci. Tech. 1 (1), 79–86.
Nautiyal, H., Varun, Kumar. A., and Kumar, A. (2010). Reverse Running Pumps Analytical, Experimental and Computational Study: A Review. Renew. Sust. Energ. Rev. 14, 2059–2067. doi:10.1016/j.rser.2010.04.006
Novara, D., and McNabola, A. (2018). A Model for the Extrapolation of the Characteristic Curves of Pumps as Turbines from a Datum Best Efficiency Point. Energ. Convers. Manag. 174, 1–7. doi:10.1016/j.enconman.2018.07.091
Novara, D., and McNabola, A. (2018). The Development of a Decision Support Software for the Design of Micro-hydropower Schemes Utilizing a Pump as Turbine. Proceedings 2, 678. doi:10.3390/proceedings2110678
Pugliese, F., De Paola, F., Fontana, N., Giugni, M., and Marini, G. (2016). Experimental Characterization of Two Pumps as Turbines for Hydropower Generation. Renew. Energ. 99, 180–187. doi:10.1016/j.renene.2016.06.051
Qian, Z., Wang, F., Guo, Z., and Lu, J. (2016). Performance Evaluation of an Axial-Flow Pump with Adjustable Guide Vanes in Turbine Mode. Renew. Energ. 99, 1146–1152. doi:10.1016/j.renene.2016.08.020
Raman, N., Hussein, I., Palanisamy, K., and Foo, B. (2013). An Experimental Investigation of Pump as Turbine for Micro Hydro Application. IOP Conf. Ser. Earth Environ. Sci. 16, 012064. doi:10.1088/1755-1315/16/1/012064
Ramos, H., and Borga, A. (1999). Pumps as Turbines: an Unconventional Solution to Energy Production. Urban Water 1, 261–263. doi:10.1016/s1462-0758(00)00016-9
Renzi, M., Rudolf, P., Štefan, D., Nigro, A., and Rossi, M. (2019). Installation of an Axial Pump-As-Turbine (PaT) in a Wastewater Sewer of an Oil Refinery: A Case Study. Appl. Energ. 250, 665–676. doi:10.1016/j.apenergy.2019.05.052
Rossi, M., Righetti, M., and Renzi, M. (2016). Pump-as-Turbine for Energy Recovery Applications: the Case Study of an Aqueduct. Energ. Proced. 101, 1207–1214. doi:10.1016/j.egypro.2016.11.163
Santolaria Morros, C., Fernández Oro, J. M., and Argüelles Díaz, K. M. (2011). Numerical Modelling and Flow Analysis of a Centrifugal Pump Running as a Turbine: Unsteady Flow Structures and its Effects on the Global Performance. Int. J. Numer. Meth. Fluids 65, 542–562. doi:10.1002/fld.2201
Senpanich, K., Bohez, E. L. J., Thongkruer, P., and Sakulphan, K. (2019). New Mode to Operate Centrifugal Pump as Impulse Turbine. Renew. Energ. 140, 983–993. doi:10.1016/j.renene.2019.03.116
Sharma, R. K. (1984). Small Hydroelectric Projects-Use of Centrifugal Pumps as Turbines. Bangalore, India: Kirloskar Electric Co.
Shi, F., Yang, J., and Wang, X. (2018). Analysis on the Effect of Variable Guide Vane Numbers on the Performance of Pump as Turbine. Adv. Mech. Eng. 10 (6), 1–9. doi:10.1177/1687814018780796
Shi, G., Liu, X., Wang, Z., and Liu, Y. (2017). Conversion Relation of Centrifugal Pumps as Hydraulic Turbines Based on the Amplification Coefficient. Adv. Mech. Eng. 9 (3), 1–8. doi:10.1177/1687814017696209
Singh, P., and Nestmann, F. (2010). An Optimization Routine on a Prediction and Selection Model for the Turbine Operation of Centrifugal Pumps. Exp. Therm. Fluid Sci. 34, 152–164. doi:10.1016/j.expthermflusci.2009.10.004
Singh, P., and Nestmann, F. (2011). Internal Hydraulic Analysis of Impeller Rounding in Centrifugal Pumps as Turbines. Exp. Therm. Fluid Sci. 35, 121–134. doi:10.1016/j.expthermflusci.2010.08.013
Stefanizzi, M., Torresi, M., Fortunato, B., and Camporeale, S. M. (2017). Experimental Investigation and Performance Prediction Modeling of a Single Stage Centrifugal Pump Operating as Turbine. Energ. Proced. 126, 589–596. doi:10.1016/j.egypro.2017.08.218
Stepanoff, A. J. (1957). Centrifugal and Axial Flow Pumps, Design and Applications. New York: John Wiley & Sons.
Su, X., Huang, S., Zhang, X., and Yang, S. (2016). Numerical Research on Unsteady Flow Rate Characteristics of Pump as Turbine. Renew. Energ. 94, 488–495. doi:10.1016/j.renene.2016.03.092
Tan, X., and Engeda, A. (2016). Performance of Centrifugal Pumps Running in Reverse as Turbine: Part Ⅱ- Systematic Specific Speed and Specific Diameter Based Performance Prediction. Renew. Energ. 99, 188–197. doi:10.1016/j.renene.2016.06.052
Wang, T., Kong, F., Xia, B., Bai, Y., and Wang, C. (2017). The Method for Determining Blade Inlet Angle of Special Impeller Using in Turbine Mode of Centrifugal Pump as Turbine. Renew. Energ. 109, 518–528. doi:10.1016/j.renene.2017.03.054
Wang, T., Wang, C., Kong, F., Gou, Q., and Yang, S. (2017). Theoretical, Experimental, and Numerical Study of Special Impeller Used in Turbine Mode of Centrifugal Pump as Turbine. Energy 130, 473–485. doi:10.1016/j.energy.2017.04.156
Williams, A. A. (1994). The Turbine Performance of Centrifugal Pumps: a Comparison of Prediction Methods. Proc. Inst. Mech. Eng. Part A: J. Power Energ. 208, 59–66. doi:10.1243/pime_proc_1994_208_009_02
Yang, S., Kong, F., Chen, H., and Su, X. (2012). Effects of Blade Wrap Angle Influencing a Pump as Turbine. ASME J. Fluids Eng. 134, 061102. doi:10.1115/1.4006677
Yang, S., Kong, F., Qu, X., and Jiang, W. (2012). Influence of Blade Number on the Performance and Pressure Pulsations in a Pump Used as a Turbine. ASME J. Fluids Eng. 134, 124503. doi:10.1115/1.4007810
Yang, S.-S., Derakhshan, S., and Kong, F.-Y. (2012). Theoretical, Numerical and Experimental Prediction of Pump as Turbine Performance. Renew. Energ. 48, 507–513. doi:10.1016/j.renene.2012.06.002
Yang, S.-S., Kong, F.-Y., Jiang, W.-M., and Qu, X.-Y. (2012). Effects of Impeller Trimming Influencing Pump as Turbine. Comput. Fluids 67, 72–78. doi:10.1016/j.compfluid.2012.07.009
Yang, S.-S., Liu, H.-L., Kong, F.-Y., Dai, C., and Dong, L. (2013). Experimental, Numerical, and Theoretical Research on Impeller Diameter Influencing Centrifugal Pump-As-Turbine. J. Energ. Eng. 139 (4), 299–307. doi:10.1061/(asce)ey.1943-7897.0000128
Yang, S.-S., Wang, C., Chen, K., and Yuan, X. (2014). Research on Blade Thickness Influencing Pump as Turbine. Adv. Mech. Eng. 6, 190530. doi:10.1155/2014/190530
Zuo, Z., Liu, S., Sun, Y., and Wu, Y. (2015). Pressure Fluctuations in the Vaneless Space of High-Head Pump-Turbines-A Review. Renew. Sust. Energ. Rev. 41, 965–974. doi:10.1016/j.rser.2014.09.011
PAT: Pump as Turbine
BEP: Best efficiency point
PRV: Pressure reducing valves
ANN: Artificial neural networks
EPR: Evolutionary polynomial regression
QbT: Flow rate at BEP under turbine mode
QbP: Flow rate at BEP under pump mode
HbT: Head at BEP under turbine mode
HbP: Head at BEP under pump mode
ηbT: Efficiency at BEP under turbine mode
ηbP: Efficiency at BEP under pump mode
ηbh: Hydraulic efficiency at BEP
C: Criterion
Δa: Proportional difference parallel to the major axis of the ellipse
Δb: Proportional difference parallel to the minor axis of the ellipse
σ: Slip coefficient
φ: Flow coefficient
ψ: Head coefficients
D1: Inlet impeller diameter
D2: Outlet impeller diameter
b1: Inlet passage width
b2: Outlet passage width
F: The eight cross-sectional areas of volute
β1: Inlet impeller blade angle
ξ1: Inlet blockage coefficient
ξ2: Outlet blockage coefficient
σ1: Inlet slip factor
σ2: Outlet slip factor
n: Rotation speed
Ns: Specific speed
ηv: Volumetric efficiency
ηh: Hydraulic efficiency
ε: Amplification coefficient
u2: Circumferential velocity at pump impeller outlet
F1: Area of axial-surface at impeller inlet
NsT: Specific speed under turbine mode
NsP: Specific speed under pump mode
Ds: Specific diameter
PvT: Volute power losses under turbine mode
PlT: Leakage power losses under turbine mode
PeT: Kinetic power losses under turbine mode
PiT: Hydraulic losses in impeller under turbine mode
PmT: Mechanical power losses under turbine mode
Δhinf,P: Hydraulic loss in pipe under pump mode
ΔhOuf,P: Hydraulic loss in pipe under turbine mode
Δhinc,P: Incidence loss in impeller under pump mode
Δhinc,T: Incidence loss in impeller under turbine mode
Δhsf,P: Surface friction loss in impeller under pump mode
Δhsf,T: Surface friction loss in impeller under turbine mode
Δhbl,P: Blade loading loss in impeller under pump mode
Δhbl,T: Blade loading loss in impeller under turbine mode
Δhsep,P: Separation loss in impeller under pump mode
Δhmix,P: Wake mixing loss in impeller under pump mode
ΔPrec,P: Recirculation loss in impeller under pump mode
ΔPdf,P: Disk friction loss in impeller under pump mode
ΔPdf,T: Disk friction loss in impeller under turbine mode
ΔPlk,P: Leakage loss in impeller under pump mode
ΔPlk,T: Leakage loss in impeller under turbine mode
ΔhVmix,P: Incidence loss in volute under pump mode
ΔhVdsf,P: Friction loss in diffuser of volute under pump mode
ΔhVdsf,T: Friction loss in diffuser of volute under turbine mode
ΔhVsf,P: Friction loss in volute under pump mode
ΔhVsf,T: Friction loss in volute under turbine mode
ΔhVdiff,P: Separation loss in volute under pump mode
Ω: Rotation speed
T: Torque
Keywords: pump as turbine, performance prediction, geometry optimization, best efficiency point, hydropower
Citation: Liu M, Tan L and Cao S (2022) Performance Prediction and Geometry Optimization for Application of Pump as Turbine: A Review. Front. Energy Res. 9:818118. doi: 10.3389/fenrg.2021.818118
Received: 19 November 2021; Accepted: 10 December 2021;
Published: 11 January 2022.
Edited by:
Wei Shi, Dalian University of Technology, ChinaReviewed by:
Wei Yang, China Agricultural University, ChinaCopyright © 2022 Liu, Tan and Cao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lei Tan, dGFubGVpQG1haWwudHNpbmdodWEuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.