Adaptive Droop Control of the VSC-MTDC Distribution Network Considering Power–Voltage Deviation

In order to realize the unbalanced power optimally allocated and the DC voltage stably controlled after disturbance, an adaptive droop control method considering power and voltage deviation is proposed based on the traditional voltage–power droop control of a voltage source converter-based multi-terminal direct current (VSC-MTDC) distribution network. The inherent constraint that the unbalanced power is proportionally distributed according to its capacity under the traditional droop control is broken in the proposed method to realize the reasonable transfer of unbalanced power and to reduce the overload risk of smaller capacity VSCs; the “dead zone” is appropriately set to relax the operating range of the VSC to a certain extent by a power deviation factor being introduced in the droop characteristic curve. The corresponding MATLAB/Simulink simulation model of the five-terminal DC power distribution network is established and compared with the electromagnetic transient model under the traditional droop control. Finally, the simulation results verify the effectiveness and control effects of the proposed control method.

Introduction

The continuous maturity of flexible DC equipment and control technologies in the field of electricity transmission has greatly promoted the development of DC power distribution (Li and Lao, 2017; Liao et al., 2018). Compared with the traditional AC power distribution network, the DC power distribution network has many advantages, such as lower loss, larger transmission capacity, higher power quality and power supply reliability, and easier power control, regardless of the frequency and voltage phase, more convenient for large-scale access to clean energy and lower environmental pollution (Yang et al., .2015; Jaynendra et al., 2019; Li et al., 2021a), and can effectively isolate AC side faults and disturbances in parallel with the AC system (Xu et al., 2019; Zhao et al., 2019). As an important basis of the energy internet and smart grids, a reliable, flexible, and efficient flexible DC power distribution network has gradually become an important guarantee for the safe and economic operation of the power system and power supply at a high service level (Gao et al., 2019). Therefore, the construction and development of the flexible DC power distribution network is of great significance to meet the needs of energy conservation, emission reduction, and comprehensive energy utilization in various countries, to improve the intelligent level of power supply, to promote the transition from traditional power grids to the energy internet, and to build a green and environmentally friendly energy society (Li et al., 2021b; Li et al., 2022).

The three-level VSC-MTDC power distribution network has the characteristics of multi-source power transmission, multi-drop power reception, and system power flow flexibly regulation and control and has become an effective solution to develop and reform the power supply mode in the future (Li et al., 2019). The power flow of the DC power distribution network has frequent fluctuations, and the transient process is very short, so it brings great challenges to the coordination of VSCs, the power optimal dispatching, and the voltage stability control (Beerten and Belmans, 2013; Wang and Barnes, 2014). Therefore, as a typical multi-point control, the droop control has become the hot point of the current research for the fast response capability to the change of power flow. In the aspect of the control strategy, Pedram and Mohsen, 2018 proposed a distributed control method of the DC system based on the main controller and low-bandwidth communication and realized accurate power allocation by setting droop gain, but this method depends on the communication between VSCs to a certain extent. Chen et al., 2018 proposed an adaptive droop control method for the multi-terminal DC system based on the compensation governor with synthetically considering the dynamic voltage and power deviation of the DC network, which improved the system steady-state characteristics and dynamic response. Wang et al., 2019a addressed the problem that a fixed droop control coefficient will reduce the DC voltage control capability of the entire MTDC system and proposed an adaptive droop control scheme based on the DC voltage deviation factor and power distribution factor to ensure that the MTDC system maintains a high power sharing capability. Wang et al., 2020a derived the VDM model related to the DC voltage through the VSC-MTDC generalized linear model and proposed a droop coefficient adaptive method, which can realize the effective control of the system DC voltage. Wang et al., 2020b proposed a structure-changed master–slave control method based on the equal load rate based on the master–slave control method of DC distribution systems, which can reduce the DC voltage deviation when disturbance occurs. In Qusay and Xie, 2018, a transformer less H-bridge inverter with a series power flow controller is designed to control the transmission power of PCC, and its power supply connection interface adopted the U–P droop control strategy, which improved the control flexibility of the system, but the DC transient overvoltage is high in the process of fluctuation. Li et al., 2017 basically realized the reasonable distribution of active power and the stable control of AC side voltage of each VSC according to the unified adaptive droop control based on dynamic reactive power limiter, but the DC side voltage of VSC had not been deeply analyzed and verified by simulation. In the aspect of model analysis, Rouzbehi et al., 2014 realized the economic operation of the DC system by an improved optimal power flow algorithm, but to some extent, this way of accurately controlling voltage and power by modifying the droop coefficient accordance with power flow optimization results reduced the response speed of droop control to power flow change. Han et al., 2016 proposed a hybrid MTDC system decentralized autonomous control based on the consensus algorithm considering actual requirements of wind power grid connection and power transmission; the model convergence performed well, and the global information acquired fast under power fluctuation. The above documents were the necessary combination and improvement of the traditional droop control at different angles, which improved the distribution accuracy of the active power assumed by each VSC, but none of them really realized the isochronous control of DC voltage.

In terms of VSC-MTDC system stability modeling, Wang et al., 2019b proposed a construction method of the characteristic equation for the microgrid system composed of phase-locked loop DG. Compared with the traditional state-space matrix research method, this method can determine the phase angle margin and stability margin of the system stability, and the Routh criterion can be used to simply judge the stability. In reference to the independent power supply system composed of multiple batteries, Wang et al., 2021a constructed a forbidden zone criterion based on the regression ratio matrix accordingly to establish a state matrix and a rate of return matrix and proposed a sag coefficient stable area analysis method. Wang et al., 2021b, on the basis of Wang et al., 2021a, proposed a reduced-order aggregation model based on the Routh criterion and the balanced truncation method, which can solve the problem of large input–output mapping errors between the original system and the reduced-order system. Ma et al., 2021 proposed a dual-predictive control method based on adaptive error correction (DPCEC) applied to FW-VSIs for AC microgrids, which can deal with and correct the influence of different negative factors and realize the voltage source inverter real-time tracking of the reference value and the accurate value.

At present, the research on the control strategies of the MTDC power network mostly focuses on the transmission network, and the load fluctuation and power flow change of the distribution network are more complex, which puts forward higher requirements for the design of the control system.

On the basis of traditional droop control, an adaptive droop control of the VSC-MTDC distribution network considering power–voltage deviation is proposed in this article, and the electromagnetic transient model of the five-terminal VSC-MTDC distribution network based on the MATLAB/Simulink platform is built to verify the effectiveness of the proposed adaptive control strategy by simulation according to different system operating conditions. The main contributions of this article are as follows:

1) The proposed control strategy can break the traditional droop control restriction of the active power distribution according to a fixed ratio under system disturbance; it can adaptively adjust the droop coefficient to realize the optimal distribution of power and effectively prevent the overload of the smaller-capacity converters.

2) By superimposing the constant voltage control link in the improved adaptive droop control strategy, the system voltage stability before and after the transient process can be effectively guaranteed, and the error adjustment can be realized without relying on communication.

Typical Structure of the VSC-MTDC Power Distribution

The typical structure of the VSC-MTDC distribution network is shown in Figure 1. Taking the five-terminal power system as an example, the AC system is connected to the DC network with equivalent load through the corresponding VSC. One of the VSCs is set up as the main station and adopts the constant DC voltage control to maintain the DC bus voltage stability. The other four VSCs are slave converters, which adopt the adaptive droop control strategy considering the power–voltage deviation to realize the system power optimal distribution and to ensure the stable operation of the DC system according to the requirement of VSCs, the equipment connected to the AC side, the topology of the VSC-MTDC system, and the dispatching plan. The following will carry on the detailed analysis to the VSCs which adopt the droop control.

FIGURE 1

FIGURE 1. Typical structure of five-terminal DC power distribution-based VSC.

Adaptive Droop Control of VSC-MTDC

The adaptive control of the VSC-MTDC distribution network requires that each VSC can make independent decisions and update the decision value in real time. When the loads, power flow direction, and grid structure of the network change, each VSC controller should be able to maintain the system stable and reliable operation between the allowable power and voltage regions.

DC Voltage Droop Characteristic Analysis

For the traditional voltage droop control, set the positive direction as the absorption power of VSC, so the relationship between DC voltage $U_{\text{DC}i}$ and output current $I_{\text{DC}i}$ can be expressed as follows

$I_{\text{DC}i}^{ref}-I_{\text{DC}i}+K_{\text{droop}i}^0\left(U_{\text{DC}}^{ref}-U_{\text{DC}i}\right)=0,(1)$

where $U_{\text{DC}}^{ref}$ is the DC side voltage reference value of VSC; $I_{\text{DC}i}^{ref}$ is the internal loop current reference value of VSC_i; and$K_{\text{droop}i}^0$ is the droop coefficient defined by the U–I relationship, $K_{\text{droop}i}^0>0$. Also, $P_{\text{DC}i}=U_{\text{DC}i}{I}_{\text{DC}i}$, so the output power of the VSC is

$P_{\text{DC}i}=-K_{\text{droop}i}^0{U}_{\text{DC}i}^2+\left(K_{\text{droop}i}^0{U}_{\text{DC}}^{ref}+I_{\text{DC}i}^{ref}\right)U_{\text{DC}i}.(2)$

The U–P characteristic curve of the VSC drawn by Eq. 2 is shown in Figure 2. As can be seen from Figure 2, the operating characteristic curve of the VSC is a parabola opening to the left (only taking the upper half of the symmetrical axis according to the physical meaning). The limit operating point $M\left(P_{i\text{MAX}},U_{i\text{MIN}}\right)$, respectively, corresponds to the power maximum value and the voltage minimum value, and there is

$\{\begin{array}{l}{P}_{i\text{MAX}}=\frac{1}{4}{K}_{\text{droop}i}^0{U}_{\text{DC}}^{2r\mathit{e}f}+\frac{1}{2}{P}_{\text{DC}i}^{ref}+\frac{I_{\text{DC}\mathit{i}}^{2r\mathit{e}f}}{4K_{\text{droop}i}^0}\\ U_{i\text{MIN}}=\frac{1}{2}{U}_{\text{DC}}^{ref}+\frac{I_{\text{DC}i}^{r\mathit{e}f}}{2K_{\text{droop}i}^0}.\end{array}(3)$

where $P_{\text{DC}i}^{ref}$ is the output power reference value of VSC, $P_{\text{DC}i}^{ref}=U_{\text{DC}}^{ref}{I}_{\text{DC}i}^{ref}$; $P_{\text{DCH}i}$ and $P_{\text{DCL}i}$ are the upper and lower limits of the operating power of VSCs, respectively; and $U_{\text{DCH}i}$ and $U_{\text{DCL}i}$ are the upper and lower limits of the DC side voltage of VSCs, respectively. The tangent point $N\left(P_{\text{DC}i}^{ref},U_{\text{DC}}^{ref}\right)$ of the operation characteristic curve and the drooping characteristic curve 1 is the optimal operation state point of VSC.

FIGURE 2

FIGURE 2. Characteristic curves of U–P operating.

From Eq. 2 and Eq. 3, it can be seen that the DC voltage regulation and power allocation of the VSC-MTDC power distribution network are determined by the droop coefficient. The selection of its value affects the dynamic performance and stability of the whole VSC-MTDC distribution network, so it is necessary to optimize the droop characteristic curve according to the characteristics of the power node (VSC) and the DC network.

At the same time, the voltage safety margin and power security margin should be considered in the operation of the VSC-MTDC distribution network (i.e., the AB section of the operating characteristic curve in Figure 2), which not only satisfies the power balance equation of the DC network but also satisfies the fixed boundary conditions of DC nodes’ voltage amplitude and VSCs’ operating power, that is,

$P_{\text{DC}i}-U_{\text{DC}i}{\displaystyle \sum _{j\in i}{Y}_{ij}}{U}_{\text{DC}j}=0,(4)$

$\{\begin{array}{l}{U}_{\text{DCL}i}\le U_{\text{DC}i}\le U_{\text{DCH}i}\\ P_{\text{DCL}i}\le P_{\text{DC}i}\le P_{\text{DCH}i}.\end{array}(5)$

where $j\in i$ represents the node connected to node i.

Droop Characteristic Optimization of VSC Considering Power–Voltage Deviation

According to the droop characteristic of the VSC-MTDC power distribution network, the output error signal $\chi$ of the controller is set as follows:

$\chi =P_{\text{DC}i}^{ref}-P_{\text{DC}i}+K_{\text{droop}i}\left(U_{\text{DC}}^{ref}-U_{\text{DC}i}\right).(6)$

At steady-state operation, the error signal output by the VSC controller is 0 (that is $\chi =0$). We respectively set the upper limit of operating power of the VSC_i and VSC_j in the network as $P_{i\text{MAX}}$ and $P_{j\text{MAX}}$; meanwhile, there is $P_{i\text{MAX}}<P_{j\text{MAX}}$. In the case of ignoring the DC line resistance, it can be considered that the power loss of the DC network is 0 and the voltage drop is 0. When disturbance occurs, the stable operating point of the VSC_i changes from $E\left(P_{\text{DC}i},U_{\text{DC}}\right)$ to $F\left(P_{\text{DC}i}^{\text{'}},U_{\text{DC}}^{\text{'}}\right)$, as shown in Figure 3.

FIGURE 3

FIGURE 3. Characteristic curves of U–P droop control.

It can be seen from Eq. 6 that the DC side voltage change variable of the VSC is

$\mathrm{\Delta }{U}_{\text{DC}}=U_{\text{DC}}^{\text{'}}-U_{\text{DC}}=-\frac{P_{\text{DC}i}^{\text{'}}-P_{\text{DC}i}}{K_{\text{droop}i}}=-\frac{\mathrm{\Delta }{P}_{\text{DC}i}}{K_{\text{droop}i}}.(7)$

After ignoring the DC line resistance, the whole DC network can be regarded as an equipotential point. Therefore, the total increment of the VSC output power can be expressed as

$\mathrm{\Delta }{P}_{\text{DC}}={\displaystyle \sum _{i=1}^n\mathrm{\Delta }{P}_{\text{DC}i}}=-\mathrm{\Delta }{U}_{\text{DC}}{\displaystyle \sum _{i=1}^n{K}_{\text{droop}i}}=\frac{\mathrm{\Delta }{P}_{\text{DC}j}}{K_{\text{droop}j}}{\displaystyle \sum _{i=1}^n{K}_{\text{droop}i}},(8)$

where $K_{\text{droop}j}$ is the droop coefficient of VSC_j.

Therefore, the output power increment $\Delta P_{\text{DC}j}$ of VSC_j is

$\mathrm{\Delta }{P}_{\text{DC}j}=K_{\text{droop}j}\frac{\mathrm{\Delta }{P}_{\text{DC}}}{{\displaystyle \sum _{i=1}^n{K}_{\text{droop}i}}}.(9)$

It can be seen from Eq. 9 that when the total unbalanced power $\Delta P_{\text{DC}}$ of the VSC-MTDC power distribution system is constant, the unbalanced power borne by each VSC is proportional to its droop coefficient.

For conventional droop control, the droop coefficient is set proportional to the capacity of the VSC and remains constant during the operation process. When a considerable large disturbance occurs in the system, the VSC with a smaller capacity can be overloaded (corresponding to the operation point $G\left(P_{i\text{MAX}},U_{\text{DC}}^{"}\right)$), while the VSC with a larger capacity still has a certain margin (corresponding to the operation point $G\left(P_{\text{DC}j}^{"},U_{\text{DC}}^{"}\right)$). If the power balance of each VSC is broken, make the droop coefficient set by each VSC disobey the strict proportional relation, and the droop coefficient of the VSC with a larger power margin is improved to assume more unbalanced power during the disturbance, the droop coefficient of the VSC with a smaller power margin is appropriately reduced to assume less unbalanced power during the disturbance, then the unbalanced power is reasonably transferred, and the response capability of the VSC adopting the droop control strategy to the DC power flow disturbance can be indirectly promoted. In addition, the traditional droop control can realize the real-time regulation of the DC side voltage of the VSC with power changing according to the droop characteristic. However, when there is no power fluctuation in the transmittance VSC, the acceptance VSC still performs the differential adjustment according to droop characteristics, and it is impossible to reasonably realize the power distribution and to cause the DC voltage to fluctuate. Consequently, this article proposes an adaptive droop control strategy of the VSC-MTDC power distribution network taking into account the power–voltage deviation, which can improve the response capability to DC power flow disturbance and at the same time can realize the isochronous control of DC voltage.

An improved droop coefficient that takes into account the power margin of the VSC is defined as

$K_{\text{droop}i}^{\text{'}}=\{\begin{array}{l}\frac{\mu \left(P_{i\text{MAX}}-\left|P_{\text{DC}i}\right|\right)}{P_{i\text{MAX}}}{K}_{\text{droop}i},U_{\text{DC}i}\ge U_{\text{DC}i}^{ref}\\ \frac{\mu \left|P_{\text{DC}i}\right|}{P_{i\text{MAX}}}{K}_{\text{droop}i},U_{\text{DC}i}<U_{\text{DC}i}^{ref}.\end{array}(10)$

and satisfies that

${\displaystyle \sum _{i=1}^n{K}_{\text{droop}i}^{\text{'}}}={\displaystyle \sum _{i=1}^n{K}_{\text{droop}i}}.(11)$

In Eq. 10, $\mu$ is as a constant, responsible for the proper scaling of $K_{\text{droop}i}^{\text{'}}$, and its values are generally ranging within the region (Liao et al., 2018; Li et al., 2021a) according to the actual operation state of the power network (Tao et al., 2018); in this article, $\mu$ is equal to 3; $K_{\text{droop}i}$ is the traditional droop control coefficient, and that

$K_{\text{droop}i}=\frac{P_{i\text{MAX}}-P_{\text{DC}i}}{U_{\text{DC}}-U_{\text{DCL}}}.(12)$

After the optimization by Eq. 10, the droop coefficient of VSC_i decreases and the droop coefficient of VSC_j becomes larger. Under the condition of a constant reference voltage, the optimal operating state points of the two VSCs, respectively, correspond to the points of $M\left(P_{\text{DC}i}^{\text{'}ref},U_{\text{DC}}^{ref}\right)$ and $M^{\text{'}}\left(P_{\text{DC}j}^{\text{'}ref},U_{\text{DC}}^{ref}\right)$ in Figure 3, thus realizing the optimal allocation of unbalanced power.

However, when the droop coefficient of the VSC with a smaller power margin is too low, the slight power fluctuation will lead to a large deviation between $U_{\text{DC}i}$ and $U_{\text{DC}}^{ref}$, which greatly increases the difficulty of DC voltage control and is not conducive to system stability, so a reasonable limit should be imposed on $K_{\text{droop}i}^{\text{'}}$, thus setting that (Tao et al., 2018)

$\{\begin{array}{l}{K}_{\text{droop}i\text{MAX}}^{\text{'}}=\mu K_{\text{droop}i},\\ K_{\text{droop}i\text{MIN}}^{\text{'}}=\frac{1}{3}{K}_{\text{droop}i},\\ K_{\text{droop}i\text{MIN}}^{\text{'}}\le K_{\text{droop}i}^{\text{'}}\le K_{\text{droop}i\text{MAX}}^{\text{'}}.\end{array}(13)$

At the same time, in order to ensure the continuity of DC voltage in the process of droop controlling, a power deviation factor ${\zeta }_i$ ($0<{\zeta }_i<1$) is introduced, and the “dead zone” is properly set in the droop characteristic curve, perpendicular to the voltage shaft in Figure 3, so

$\mathrm{\Delta }{P}_{\text{DC}}={\displaystyle \sum _{i=1}^n\mathrm{\Delta }{P}_{\text{DC}i}^{"}}={\displaystyle \sum _{i=1}^n{\zeta }_i\mathrm{\Delta }{P}_{\text{DC}}}.(14)$

For VSC_i in Figure 3, the adjusted droop characteristic curve is equivalent to translating the original curve to the right for ${\zeta }_i\Delta P_{\text{DC}}$, its assumed power increment becomes $\Delta P_{\text{DC}i}^{"}$, the steady operating state point is $M\left(P_{\text{DC}i}^{\text{'}ref},U_{\text{DC}}^{ref}\right)$, which only considers that the power margin is shifted to the point $K\left(P_{\text{DC}i}^{"ref},U_{\text{DC}}^{ref}\right)$ without the reference voltage changing; at present, the corresponding reference power increase is ${\zeta }_i\Delta P_{\text{DC}}$ up to $P_{\text{DC}i}^{"ref}$, where the inflection point C is a voltage deviation control enabling node, and

$P_{\text{DC}i}^{"ref}=-\frac{U_{\text{DC}}^{ref}-U_{\text{DCL}}}{{K_{\text{droop}i}^{\text{'}}|}_{U_{\text{DC}i}=U_{\text{DC}}^{ref}}}+P_{\text{DC}i}^{ref}+{\zeta }_i\Delta P_{\text{DC}},(15)$

where

${K_{\text{droop}i}^{\text{'}}|}_{U_{\text{DC}i}=U_{\text{DC}}^{ref}}=\frac{\mu {\left(P_{i\text{MAX}}-P_{\text{DC}i}^{ref}\right)}^2}{P_{i\text{MAX}}\left(U_{\text{DC}}^{ref}-U_{\text{DCL}}\right)}.$

After the additional DC voltage deviation control, the droop coefficient of the controller (corresponding to the slope of the characteristic curve of droop control) holds in line, and the power reference value of the optimal operating state point increases, which expands the operation range of VSC to a certain extent, alleviates the power margin decrease of the VSC in the case of only adopting power margin control, and can obviously enhance system voltage stability. The adaptive droop control block diagram of the double closed loop based on the PI link is shown in Figure 4.Here, $U_{\text{DC}r}$ is the DC voltage modulation value; $K_{\text{P}i}$, $K_{\text{I}i}$, $K_{\text{P}i}^{\text{'}}$, and $K_{\text{I}i}^{\text{'}}$ are the PI controller coefficients; $K_{\text{GU}i}$ and $K_{\text{GD}i}$ are the control identification bits; and the corresponding control mode is enabled when the value is 1.

FIGURE 4

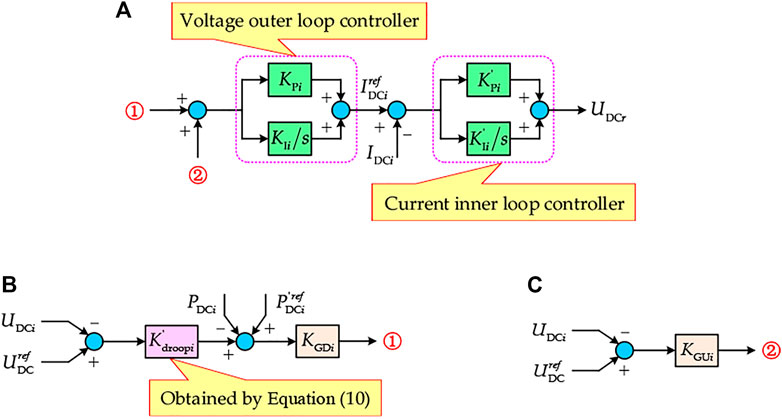
FIGURE 4. Block diagram of the control strategy: (A) voltage and current double closed loop control; (B) power deviation control; (C) additional DC voltage deviation control.

Response Characteristic Analysis of Adaptive Droop Control

To clarify the relationship between the output DC voltage and power of each VSC under the adaptive droop control in the VSC-MTDC distribution network, it is necessary to analyze the U–P response characteristics of VSCs. Figure 4 shows that when the control identification bit coefficient $K_{\text{GU}i}$ and $K_{\text{GD}i}$ are both 1, the output power–voltage relationship of the VSC is

$P_{\text{DC}i}^{\text{'}ref}-P_{\text{DC}i}+\left(K_{\text{droop}i}^{\text{'}}+1\right)\left(U_{\text{DC}}^{ref}-U_{\text{DC}i}\right)=\frac{1}{K_{\text{P}i}+\frac{K_{\text{I}i}}{s}}\left(\frac{1}{K_{\text{P}i}^{\text{'}}+\frac{K_{\text{I}i}^{\text{'}}}{s}}{U}_{\text{DC}r}+I_{\text{DC}i}\right).(16)$

Because the response speed of outer loop voltage control and inner loop current control is much higher than that of droop control, the DC voltage stability of the system is less affected by the parameters of the PI controller and more significantly affected by the droop coefficient (Liu et al., 2019). Therefore, assuming that the closed loop transfer function of DC voltage is 1, there is

$U_{\text{DC}r}=U_{\text{DC}i}.(17)$

With the introduction of unit step response into the steady operation of the VSC-MTDC distribution network, that is, the system power demand suddenly increases to 1 kW, the response relationship of the VSC-MTDC distribution system under different droop coefficients $K_{\text{droop}i}^{\text{'}}$ is obtained by Eqs. 16, 17 and shown in Figure 5, and the response relationship scheme is segmented with the DC voltage reference value ($U_{\text{DC}}^{ref}=750\text{V}$) as the critical point. In the limiting range of the droop coefficient $K_{\text{droop}i}^{\text{'}}$, the DC side voltage of the VSC can basically change in the range of ±5% of $U_{\text{DC}}^{ref}$, and for any VSC, the larger the droop coefficient is, the stronger the stability of the system is.

FIGURE 5

FIGURE 5. Control system response relationship of VSC-MTDC power distribution.

The set VSC-MTDC distribution network control parameters for response characteristic analysis are shown in Table 1. Here, the outer and inner loop control coefficients are calculated according to the method of Wang et al., 2018, $U_{\text{DC}}$ and $P_{\text{DC}i}$ are chosen according to their reference values, the maximum operating power of the VSC is selected by 70% of the reference capacity, and the lower limit of DC voltage of the VSC is less than 30% of the reference voltage; therefore,

$K_{\text{droop}i}=\frac{80000\times \left(1+70\text{\%}\right)-80000}{750-750\times \left(1-30\%\right)}=106.67,(18)$

$\{\begin{array}{l}{K}_{\text{droop}i\text{MAX}}^{\text{'}}=\mu K_{\text{droop}i}=3\times 106\text{.}67=320\\ K_{\text{droop}i\text{MIN}}^{\text{'}}=\frac{1}{3}{K}_{\text{droop}i}=\frac{1}{3}\times 106\text{.}67=\mathrm{35.56.}\end{array}(19)$

Therefore, the limiting interval of the droop coefficient is determined to be [35, 320].

TABLE 1

TABLE 1. Parameters of response characteristic analysis.

When the power fluctuation occurs, to ignore the quadratic disturbance term and to linearize Eq. 16, the small-signal closed-loop transfer function $T\left(s\right)$ of adaptive droop control can be expressed as follows

$T\left(s\right)=\frac{\mathrm{\Delta }{U}_{\text{DC}i}\left(s\right)}{\mathrm{\Delta }{P}_{\text{DC}i}\left(s\right)}=\frac{b_2{s}^2+b_{1}s}{a_2{s}^2+a_{1}s+a_0},(20)$

where

$\{\begin{array}{l}{a}_0=K_{\text{I}i}{K}_{\text{I}i}^{\text{'}}\left(U_{\text{DC}}^{ref}{K}_{\text{droop}i}^{\text{'}}+U_{\text{DC}}^{ref}+P_{\text{DC}i}^{\text{'}ref}\right),\\ a_1=\left(K_{\text{I}i}{K}_{\text{P}i}^{\text{'}}+K_{\text{P}i}{K}_{\text{I}i}^{\text{'}}\right)\left(U_{\text{DC}}^{ref}{K}_{\text{droop}i}^{\text{'}}+U_{\text{DC}}^{ref}+P_{\text{DC}i}^{\text{'}ref}\right),\\ a_2=K_{\text{P}i}{K}_{\text{P}i}^{\text{'}}\left(U_{\text{DC}}^{ref}{K}_{\text{droop}i}^{\text{'}}+U_{\text{DC}}^{ref}+P_{\text{DC}i}^{\text{'}ref}\right)-U_{\text{DC}}^{ref},\\ b_1=K_{\text{I}i}^{\text{'}},\\ b_2=K_{\text{P}i}^{\text{'}}.\end{array}$

Figure 6 shows the zero-pole distribution map of the transfer function $T\left(s\right)$. In the limiting range of the droop coefficient $K_{\text{droop}i}^{\text{'}}$, all poles are in the left half of the complex plane and on the real axis, so the VSC-MTDC power distribution network is always stable, and the system stability is independent of the inner and outer loop control coefficients and the power and voltage reference values. Only when $K_{\text{droop}i}^{\text{'}}$ reduces to a value far below its minimum value, the poles may appear to the right of the imaginary axis, at which point the system will be unstable. As shown in Figure 7, when the inner or outer loop control coefficients change, the pole will shift on the negative half axis of the real axis, and the larger the pole value is, the farther away the pole is from the virtual axis and the faster the response speed of the system is.

FIGURE 6

FIGURE 6. Zero-pole distribution map of $T\left(s\right)$ under droop coefficient variation.

FIGURE 7

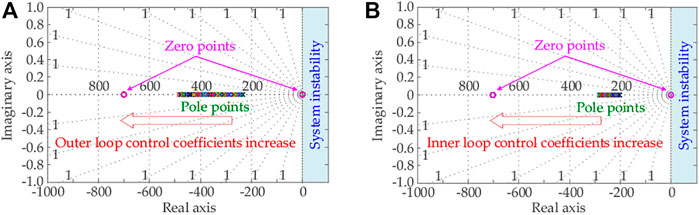
FIGURE 7. Zero-pole distribution map of $T\left(s\right)$: (A) zero-pole distribution map of outer loop control coefficient variation; (B) zero-pole distribution map of inner loop control coefficient variation.

Simulation Verification and Analysis

Parameters of the Simulation Model

In order to verify the effectiveness and control effect of adaptive droop control proposed in this article, the electromagnetic transient model of the five-terminal VSC-MTDC distribution network is established on the MATLAB/Simulink software platform, in which the other four VSCs all perform adaptive droop control considering the power–voltage deviation from the constant DC voltage control adopted in VSC₅. In this section, the simulation experiments are carried out for three operating conditions, including the equivalent load fluctuation of the DC network, VSC₃ with droop control exiting operation, and VSC₅ with fixed DC voltage control exiting operation, and the simulation results are compared and analyzed in detail with traditional droop control. The main parameters of the simulation model are shown in Table 2.

TABLE 2

TABLE 2. Parameters of response characteristic analysis.

Analysis of Simulation Results

Operating Condition 1: Equivalent Load Fluctuation in the DC Network

When $t=1.4\text{s}$ was set, the equivalent load of the DC network increased from 500kW to 545kW, the resulting power shortage led to the decrease of DC bus voltage, and then each VSC increased power output to maintain the stability of DC bus voltage.

Under the traditional droop control, the power shortage of the system should be allocated strictly according to the capacity of the VSC. As shown in Figure 8A, each VSC, that is, VSC₁, VSC₂, VSC₃, and VSC₄, which adopted the droop control strategy, respectively, increased the power output by 6.67 kwW, 13.33 kwW, 10.62 kW, and 9.38 kW, and the homologous load rates were 82.72, 60.49, 56.10, and 49.67% apart; VSC₁ operated with heavy load. The time for the system to recover stability is more than 1.6s, and there was a DC bus voltage deviation of 8.52 V compared with 1.4s ago, and the voltage deviation rate was 1.14%. During the period, the peak voltage fluctuation of the DC bus reached 54.55V, accounting for 7.27% of the rated voltage. As shown in Figure 8B, under the adaptive droop control, the unbalanced power borne by each VSC with droop control broke the fixed proportional constraint and, respectively, increased the power output of 3.27 kW, 21.16 kW, 10.63 kW, and 8.65 kW, and the corresponding load rates were 80.20, 63.39, 56.11, and 49.29%, respectively, and the load rate of VSC₁ obviously reduced. The system restored stability after 0.14s, during which the peak voltage fluctuation of the DC bus reached 14.10V, accounting for 1.88% of the rated voltage.

FIGURE 8

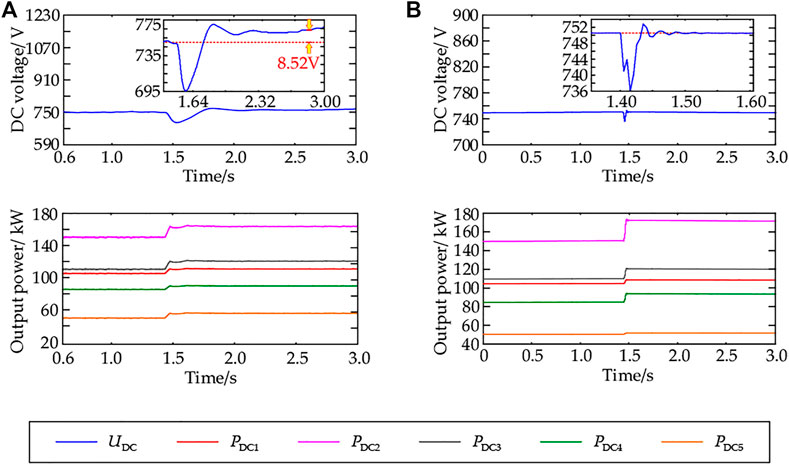
FIGURE 8. Simulation waveforms of equivalent load fluctuation in the DC network: (A) simulation waves based on traditional droop control; (B) simulation waves based on adaptive droop control.

Operating Condition 2: VSC With Droop Control Exiting Operation

When $t=1.4\text{s}$ was set, with VSC₃ with droop control exited operation, its power output reduced to 0, the resulting power shortage of 110 kW substantially led to the decrease of DC bus voltage, and then other VSCs increased the power output to maintain the stability of DC bus voltage.

As shown in Figure 9A, under the traditional droop control, the power output increments of the VSC₁, VSC₂, and VSC₄ adopted droop control strategies were 22.96kW, 45.95, and 32.34kW apart, and the homologous load rates were 94.79, 72.57, and 61.76%, respectively, VSC₁ is close to the full load, and there is a great operational risk. There was a DC bus voltage deviation of about 9.55 V between 1.4s before and after, and the voltage deviation rate was 1.27%. During the period, the peak voltage fluctuation of the DC bus reached 95.45V, accounting for 12.73% of the rated voltage. As shown in Figure 9B, under the adaptive droop control, the power output increments of the VSC₁, VSC₂, and VSC₄ adopted droop control strategies were 12.49kW, 56.16 and 38.55kW, respectively, and the corresponding load rates were 87.03, 76.36, and 65.03%, respectively, and the load rate of VSC₁ obviously reduced. The system restored stability after 0.19 s, during which the peak voltage fluctuation of the DC bus reached 30.60V, accounting for 4.08% of the rated voltage.

FIGURE 9

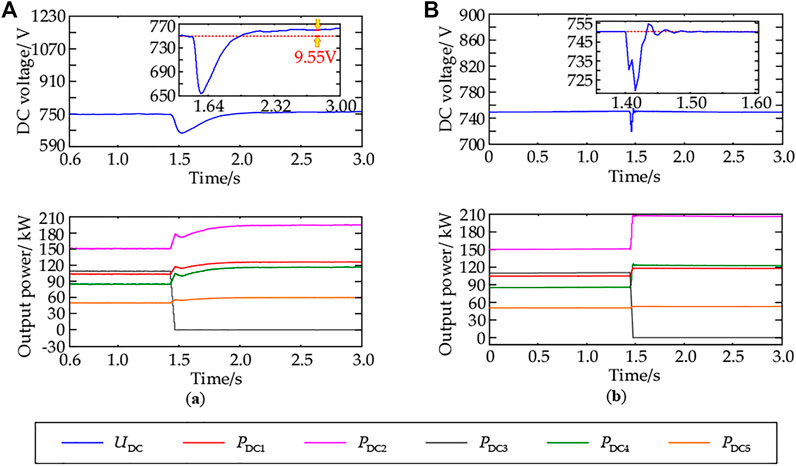
FIGURE 9. Simulation waveforms of the VSC with droop control exiting operation: (A) simulation waves based on traditional droop control; (B) simulation waves based on adaptive droop control.

Operating Condition 3: VSC With Fixed DC Voltage Control Exiting Operation

When $t=1.4\text{s}$ was set, with VSC₅ with fixed DC voltage control exited operation, its power output reduced to 0, the resulting power shortage of 50 kW substantially led to the decrease of DC bus voltage, and then other four VSCs increased the power output to maintain the stability of DC bus voltage.

As shown in Figure 10A, under the traditional droop control, the power output increments of the VSC₁, VSC₂, VSC₃, and VSC₄ adopted droop control strategies were 8.33kW, 16.67kW, 13.27kW, and 11.73kW apart and the homologous load rates were 83.95, 61.73, 57.33, and 50.91%, respectively; VSC₁ operated with heavy load. The time for the system to recover stability is more than 1.6 s due to the loss of DC voltage support; after stabilization, there will still be a certain deviation from that before 1.4s. During the period, the DC bus voltage fluctuated violently with a peak value of 156.82V, accounting for 20.91% of the rated voltage. As shown in Figure 10B, under the adaptive droop control, the power output increments of VSC₁, VSC₂, VSC₃, and VSC₄ were 4.76kW, 25.32kW, 11.98kW, and 7.94kW, respectively, and the corresponding load rates were 81.30, 64.93, 56.73, and 48.92%; the load rate of the VSC₁ obviously reduced. Because of the addition of the DC voltage deviation control in the droop characteristic, the ability to restore the system’s stable state obviously enhanced, the time consumption is about 0.39s, and the peak value of the DC bus voltage fluctuation during the period is 14.70V, accounting for 1.96% of the rated voltage.

FIGURE 10

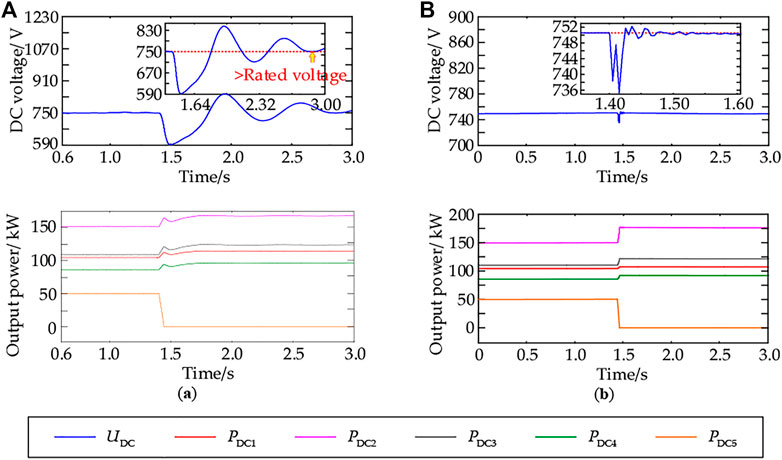
FIGURE 10. Simulation waveforms of the VSC with fixed DC voltage control exiting operation: (A) simulation waves based on traditional droop control; (B) simulation waves based on adaptive droop control.

Conclusion

In this article, the adaptive drooping characteristic optimization method considering power–voltage deviation is applied to the VSC-MTDC distribution network. The proposed control strategy is modeled and simulated based on MATLAB/Simulink under different system operation conditions and compared with the traditional droop control. The conclusions are as follows:

1) Based on the analysis of the response characteristics of the VSC-MTDC distribution network under the proposed control strategy, the stability of the control system in the limiting range of droop coefficient is verified.

2) The active power optimal allocation is realized between each VSC, and when the system is disturbed, the average load rate of the VSC with a small capacity reduces by about 6.59%, the overload risk debases, and the response ability of the VSC to DC power flow disturbance obviously improves.

3) The system DC voltage deviation before and after disturbance caused by the differential control characteristic of the conventional droop control is basically eliminated, and the isochronous control to DC voltage is achieved. At the same time, the average recovery time of the system is shortened more than 78.74% and the average transient voltage peak value during the period reduces about 76.71%, which greatly improves the reliability and power quality of power supply to users.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

YL and ZW contributed to conceptualization. YZ and LC contributed to methodology. YZ contributed to software. ZW contributed to validation. JZ and HL contributed to formal analysis. YL and QK contributed to resources. YL and YZ contributed to data curation. YL and ZW contributed to project administration.

Funding

This study received funding from Science and Technology Project of State Grid Corporation (No. SGTYHT/21-JS-225). The funder had the following involvement with the study: conceptualization, formal analysis, resources, data curation and project administration.

Conflict of Interest

Authors YL, JZ, HL and QK are employed by Smart Distribution Network Center, State Grid Jibei Electric Power Co., Ltd & State Grid Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

References

Beerten, J., and Belmans, R. (2013). Analysis of Power Sharing and Voltage Deviations in Droop-Controlled DC Grids. IEEE Trans. Power Syst. 28, 4588–4597. doi:10.1109/tpwrs.2013.2272494

CrossRef Full Text | Google Scholar

Chen, J. K., Dong, F. F., Wang, Z. H., Li, G. Q., and Zhang, C. (2018). Research on Improved Droop Control Method of Multi–Terminal MMC–HVDC System Suitable for Power Fluctuation. J. Power Syst. Tech. 42, 3708–3717.

Google Scholar

Gao, Y., Ai, Q., Yousif, M., and Wang, X. (2019). Source-load-storage Consistency Collaborative Optimization Control of Flexible DC Distribution Network Considering Multi-Energy Complementarity. Int. J. Electr. Power Energ. Syst. 107, 273–281. doi:10.1016/j.ijepes.2018.11.033

CrossRef Full Text | Google Scholar

Han, M. X., Xu, D., and Wan, L. (2016). Consensus Algorithm Based Decentralized Autonomous Control of Hybrid Multi–Terminal Direct Current System. J. Automation Electric Power Syst. 40, 130–136.

Google Scholar

Jaynendra, K., Anshul, A., and Vineeta, A. (2019). A Review on Overall Control of DC Microgrids. J. J. Energ. Storage 21, 113–138.

Google Scholar

Li, B., Liu, T., and Zhang, Y. (2017). Unified Adaptive Droop Control Design Based on Dynamic Reactive Power Limiter in VSC-MTDC. Electric Power Syst. Res. 148, 18–26. doi:10.1016/j.epsr.2017.03.010

CrossRef Full Text | Google Scholar

Li, H. L., Jiang, J. G., Zhou, Z. Z., and Zhang, D. (2019). Scheme and Control Method of MMC Based Medium–Voltage and High–Power DC Distribution System. J. Automation Electric Power Syst. 43, 83–88.

Google Scholar

Li, W. G., and Lao, X. T. (2017). Optimized Distribution for Active Power in Parallel AC/DC Transmission Systems. J. J. Northeast Electric Power Univ. 37, 24–30.

Google Scholar

Li, Y., Han, M., Yang, Z., and Li, G. (2021). Coordinating Flexible Demand Response and Renewable Uncertainties for Scheduling of Community Integrated Energy Systems with an Electric Vehicle Charging Station: A Bi-level Approach. IEEE Trans. Sustain. Energ. 12, 2321–2331. doi:10.1109/tste.2021.3090463

CrossRef Full Text | Google Scholar

Li, Y., Li, K., Yang, Z., Yu, Y., Xu, R., and Yang, M. (2022). Stochastic Optimal Scheduling of Demand Response-Enabled Microgrids with Renewable Generations: An Analytical-Heuristic Approach. J. Clean. Prod. 330, 129840. doi:10.1016/j.jclepro.2021.129840

CrossRef Full Text | Google Scholar

Li, Y., Wang, C., Li, G., and Chen, C. (2021). Optimal Scheduling of Integrated Demand Response-Enabled Integrated Energy Systems with Uncertain Renewable Generations: A Stackelberg Game Approach. Energ. Convers. Manag. 235, 113996. doi:10.1016/j.enconman.2021.113996

CrossRef Full Text | Google Scholar

Liao, J. Q., Zhou, N. C., Wang, Q. G., Li, C. Y., and Yang, J. (2018). Definition and Correlation Analysis of Power Quality index of DC Distribution Network. J. Proc. CSEE 38, 6847–6860.

Google Scholar

Liu, Z. W., Miao, S. H., Fan, Z. H., Chao, K. Y., and Kang, Y. L. (2019). Accurate Power Allocation and Zero Steady–State Error Voltage Control of the Islanding DC Microgird Based on Adaptive Droop Characteristics. J. Trans. China Electrotechnical Soc. 34, 795–806.

Google Scholar

Ma, D., Cao, X., Sun, C., Wang, R., Sun, Q., Xie, X., et al. (2021). “Dual-predictive Control with Adaptive Error Correction Strategy for AC Microgrids,” in IEEE Trans. Power Delivery (IEEE), 1. doi:10.1109/TPWRD.2021.3101198

CrossRef Full Text | Google Scholar

Pedram, G., and Mohsen, N. (2018). A Distributed Control Strategy Based on Droop Control and Low–Bandwidth Communication in DC Microgrids with Increased Accuracy of Load Sharing. J. Sust. Cities Soc. 40, 155–164.

Google Scholar

Qusay, S., and Xie, J. (2018). Decentralized Power Control Management with Series Transformer Less H–Bridge Inverter in Low–Voltage Smart Microgrid Based P–V Droop Control. J. Electr. Power Energ. Syst. 99, 500–515.

Google Scholar

Rouzbehi, K., Miranian, A., Luna, A., and Rodriguez, P. (2014). DC Voltage Control and Power Sharing in Multiterminal DC Grids Based on Optimal DC Power Flow and Voltage-Droop Strategy. IEEE J. Emerg. Sel. Top. Power Electron. 2, 1171–1180. doi:10.1109/jestpe.2014.2338738

CrossRef Full Text | Google Scholar

Tao, Y., Liu, T. Q., Li, B. H., Miao, D., Dong, Y. Q., and Lu, Z. X. (2018). Hierarchical Coordinated Adaptive Droop Control in Flexible HVDC Grid. J. Automation Electric Power Syst. 42, 70–79.

Google Scholar

Wang, R., Sun, Q., Hu, W., Li, Y., Ma, D., and Wang, P. (2021). SoC-based Droop Coefficients Stability Region Analysis of the Battery for Stand-Alone Supply Systems with Constant Power Loads. IEEE Trans. Power Electron. 36, 7866–7879. doi:10.1109/tpel.2021.3049241

CrossRef Full Text | Google Scholar

Wang, R., Sun, Q., Ma, D., and Liu, Z. (2019). The Small-Signal Stability Analysis of the Droop-Controlled Converter in Electromagnetic Timescale. IEEE Trans. Sustain. Energ. 10, 1459–1469. doi:10.1109/tste.2019.2894633

CrossRef Full Text | Google Scholar

Wang, R., Sun, Q., Tu, P., Xiao, J., Gui, Y., and Wang, P. (2021). Reduced-order Aggregate Model for Large-Scale Converters with Inhomogeneous Initial Conditions in DC Microgrids. IEEE Trans. Energ. Convers. 36, 2473–2484. doi:10.1109/tec.2021.3050434

CrossRef Full Text | Google Scholar

Wang, W., and Barnes, M. (2014). Power Flow Algorithms for Multi-Terminal VSC-HVDC with Droop Control. IEEE Trans. Power Syst. 29, 1721–1730. doi:10.1109/tpwrs.2013.2294198

CrossRef Full Text | Google Scholar

Wang, Y., He, J., Zhao, Y., Liu, G., Sun, J., Li, H., et al. (2020). Equal Loading Rate Based Master-Slave Voltage Control for VSC Based DC Distribution Systems. IEEE Trans. Power Deliv. 35, 2252–2259. doi:10.1109/tpwrd.2020.2964706

CrossRef Full Text | Google Scholar

Wang, Y., Li, B., Zhou, Z., Chen, Z., Wen, W., Li, X., et al. (2020). DC Voltage Deviation‐dependent Voltage Droop Control Method for VSC‐MTDC Systems under Large Disturbances. IET Renew. Power Generation 14, 891–896. doi:10.1049/iet-rpg.2019.0394

CrossRef Full Text | Google Scholar

Wang, Y., Wen, W., Wang, C., Liu, H., Zhan, X., and Xiao, X. (2019). Adaptive Voltage Droop Method of Multiterminal VSC-HVDC Systems for DC Voltage Deviation and Power Sharing. J. IEEE Trans. Power Deliv. 34, 169–176.

Google Scholar

Wang, Z. X., Li, Y. Z., and Li, G. Q. (2018). Parameters Optimization of Double Closed–Loop for LCL–type Inverter Based on Genetic Algorithm. J. Power Syst. Prot. Control. 46, 1–7.

Google Scholar

Xu, F., Guo, Q., Sun, H., Zhang, B., and Jia, L. (2019). A Two-Level Hierarchical Discrete-Device Control Method for Power Networks with Integrated Wind Farms. J. Mod. Power Syst. Clean. Energ. 7, 88–98. doi:10.1007/s40565-018-0417-1

CrossRef Full Text | Google Scholar

Yang, N., Paire, D., Gao, F., Miraoui, A., and Liu, W. (2015). Compensation of Droop Control Using Common Load Condition in DC Microgrids to Improve Voltage Regulation and Load Sharing. Int. J. Electr. Power Energ. Syst. 64, 752–760. doi:10.1016/j.ijepes.2014.07.079

CrossRef Full Text | Google Scholar

Zhao, X. S., Peng, K., Zhang, X. H., Xu, B. Y., Chen, Y., and Zhao, Y. H. (2019). Analysis on Dynamic Performance of Droop Control for Multi–Terminal VSC Based DC Distribution System. J. Automation Electric Power Syst. 43, 89–96.

Google Scholar