P2H Modeling and Operation in the Microgrid Under Coupled Electricity–Hydrogen Markets

The uncertainty and volatility of wind power have led to large-scale wind curtailment during grid connections. The adoption of power-to-hydrogen (P2H) system in a microgrid (MG) can mitigate the renewable curtailment by hydrogen conversion and storage. This paper conducts unified modeling for different types of P2H systems and considers the multi-energy trading in a hydrogen-coupled power market. The proposed bi-level equilibrium model is beneficial to minimize the energy cost of microgrids. Firstly, a microgrid operation model applied to different P2H systems including an alkaline electrolysis cell (AEC), a proton exchange membrane electrolysis cell (PEMEC), or a solid oxide electrolysis cell (SOEC) is proposed at the upper level. Secondly, an electricity market–clearing model and a hydrogen market model are constructed at the lower level. Then, the diagonalization algorithm is adopted to solve the multi-market equilibrium problem. Finally, case studies based on an IEEE 14-bus system are conducted to validate the proposed model, and the results show that the microgrid with a P2H system could gain more profits and help increase the renewable penetration.

1 Introduction

Renewable energy (RE) is helpful to alleviate energy and environmental pressures, but the uncertainty and randomness of wind power have led to large-scale wind curtailment at present (Xie et al., 2019). Hydrogen energy has the advantages of high density, cleanliness, and efficiency. Electro-hydrogen coupling is conducive to the cascade utilization of energy, which has a better effect on improving the accommodation of RE than the widely used electrochemical energy storage. Thus, it is significant to study the operation and transaction methods of microgrid (MG) with a power-to-hydrogen (P2H) system (Pan et al., 2020). However, there are three difficulties at present: the first is to propose a reasonable method of flexible resource allocation in an MG (Murty and Kumar, 2020), the second is to propose a unified model suitable for multiple types of P2H systems, and the third is to solve the problem of multi-market equilibrium (ME) caused by multi-energy coupling.

With the development of P2H technology, the potential application of hydrogen as a terminal energy source is gradually developed. There are three main types of mainstream P2H cells: alkaline electrolysis cell (AEC), proton exchange membrane electrolysis cell (PEMEC), and solid oxide electrolysis cell (SOEC). Among the three, the AEC has the highest maturity, the lowest equipment cost, and the longest lifespan. However, the security of AEC is poor because of the corrosive liquid inside. The PEMEC has good adaptability to RE, and its dynamic response ability is the strongest. However, its electrode is made of precious metal, and the proton exchange membrane needs to be replaced frequently, which makes it more costly. The SOEC has the highest energy utilization efficiency. However, the choice of materials is rare for its high-temperature working environment. Moreover, its speed of start and shut is slow (Mathiesen et al., 2013; Ban et al., 2017; Reddy et al., 2018; Wang et al., 2019; IEA, 2020).

The current research on P2H-containing microgrids (P2H-MGs) mainly includes three aspects: the operation characters and models of P2H, the optimization for hydrogen storage (HS) configuration, and the market operation of P2H-MG. Firstly, the state-of-art for three P2H models is discussed in details. The AEC is used to consider the coupling between electricity and heat and between electricity and hydrogen (Li et al., 2019). For the PEMEC model, the non-linear relationship between hydrogen production and power accommodation also needs to be considered (Gahleitner, 2013). Moreover, it is necessary to consider the multiple physical coupling for building the SOEC model (Cheng et al., 2017). The second aspect is the optimization for hydrogen storage (HS) configuration. For its operation configuration, the characteristics of the multi-energy federation of HS in energy storage (ES) systems are non-negligible (Shao et al., 2021). Moreover, the most utilized scenario for HS is helping RE’s grid connection like the wind. Thus, its ability to smooth wind power fluctuation needs to be considered as well (Wen et al., 2020). For HS capacity configuration, the evaluation indicators are important. The total net present value and used RE utilization and load loss rate will be two appropriate indicators (Yanzhe et al., 2020). The unit electricity cost and energy surplus rate are another proper consideration (Zhou et al., 2005). The last aspect is to carry out the market operation of P2H-MG. Hydrogen production, power generation, and hydrogen sales are the three main aspects of studying P2H-MG economic dispatch in the market environment (Maroufmashat et al., 2016). However, the bidding behavior for HS is a game against other entities and markets. Thus, it is necessary to consider game theory for HS participating in the market. On the one hand, HS was configured to improve bidding ability for optimal scheduling. On the other hand, the Stackelberg game was adopted to solve the game between HS and other entities in the market (Xianshan and Yuxiang, 2020). Furthermore, environmental operating costs must be laid on stress to study the impact of hydrogen production and storage on the system economy (Petrecca and Decarli, 2008; Dickinson et al., 2017). In summary, for different kinds of P2H systems, the unified method of modeling remains to be researched and the constraints of the P2H equipment’s start–stop and climbing characteristics remain to be taken into consideration.

Multiple energy coupling helps to optimize the resource configuration more efficiently and promote the integration of multi-energy markets (Chen et al., 2019). Meanwhile, as multiple markets are involved in the joint operation, equilibrium constraints will make it complicated for the optimization problem. The strategic behavior of multiple microgrids’ joint operation was studied by Liu et al. (2017), Liu et al. (2020), and Zhou et al. (2021). To transform the mathematical programming problem with equilibrium constraints (MPEC) into a mixed-integer linear programming model, the Karush–Kuhn–Tucker (KKT) condition, strong duality theorem, and binary expansion method are mostly used (Sadat and Fan, 2017; Guo et al., 2020). However, when there are multiple MPECs, their joint solution scheme will constitute an equilibrium problem with equilibrium constraints (EPEC). The heuristic algorithm is a feasible method to solve an EPEC via obtaining the market equilibrium with multiple producers submitting a stepped quotation curve (Ruiz et al., 2012). Though the computational burden will be small, the result still might be different such as Nash equilibrium, partial equilibrium, or saddle point, which needs to be selected based on experts’ judgment to meet the demand. The diagonalization algorithm (DA) is another method to solve the EPEC with strategic participants of wind turbines via obtaining their bidding strategies (Dai and Qiao, 2017). However, the equilibrium problem of electric hydrogen multi-market including P2H participation remains to be researched.

To optimize the scheduling of the multi-market economy, realizing ME is the key. Several aspects need to be considered. Using different energy equivalent prices to stimulate integrated energy system service providers to participate in the proposed new cross-commodity arbitrage, cross-regional (city) arbitrage, inter-period arbitrage, and future arbitrage trading models is one feasible method (Jianxiao et al., 2021). A relatively new method is to use the bi-level particle swarm algorithm to solve the ME (Jiang et al., 2021a). Moreover, the Nash-Cournot equilibrium solution can achieve the water–heat balance by applying the Nikaido–Isoda function (Molina et al., 2011). Using the energy center modeling method, the market equilibrium problem including electricity, gas, and heat multi-energy systems can be described as a game problem in which each energy center changes its energy purchase plans in different markets to maximize profits (Bahrami et al., 2018). In addition, by combining equality constraints with penalty functions and using distributed methods, inequality constraints can be transformed into feasible action sets (Du et al., 2015). Then, the power economic dispatch problem can be transformed into an unconstrained optimization problem, and it can be described as a potential game formula. Moreover, the solution of ME can be transformed into a convex optimization problem by introducing the demand response trading market to deal with the market bidding deviation caused by wind power due to its characteristics and constructing an oligopoly game equilibrium model (Xian et al., 2018). Yue et al. (2018) used the CES-type utility function to transform the consumer decision-making model into a bi-level Stackelberg-Nash game problem. The upper-level describes the relationship between the thermal market and the electricity market. The lower level describes the relationship between the markets and consumers. Using KKT conditions and linear programming, the market-clearing conditions can be obtained. Then, the pattern search algorithm can be used to solve the problem. However, the solution process of this method is complicated, and the dimensionality of the slack variable is high. So is the swarm algorithm. Thus, the DA with a more understandable principle is adopted in this paper to highlight the research focus.

This paper proposes a bi-level equilibrium model that incorporates hydrogen energy into multi-market transactions based on the traditional electric energy market and takes three types of P2H systems into account to solve the problems of ME and inconsistent P2H models while promoting RE accommodation. First, the electric energy market–clearing model and the hydrogen energy market transaction model are built in the lower level. The demand side is seen as price takers and only offers capacities. The locational marginal prices (LMPs) and time-of-use (ToU) hydrogen prices are calculated by the system operator (STO). Then, the MG in the upper level formulates its trading strategies according to the LMPs and ToU hydrogen prices generated from the lower level. The main contributions of this paper are as follows:

1) A unified P2H mathematical model is formulated considering the start–stop and climbing performance of the equipment. The advantages and disadvantages of different P2H systems are compared in the market environment.

2) Considering the interaction and transaction modes of P2H, electricity and hydrogen storage, hydrogen sales, and hydrogen-to-power (H2P), a bi-level equilibrium model of MG, EM, and hydrogen energy market has been established. The model can be used under different P2H technologies and provide a simulation evaluation platform for the comparison of market equilibrium states.

3) The EPEC is converted into multiple MPECs by using the diagonalization algorithm. Additionally, the iterative method is adopted to formulate the operation strategies and trading strategies of MG.

The remainder of this paper is organized as follows: Section 2 proposes a bi-level equilibrium model. The solution algorithm is introduced in Section 3. The simulation and result analysis are carried out based on IEEE 14 nodes in Section 4. Finally, the conclusion is presented in Section 5.

2 Model Building

The assumptions of the bi-level model are summarized and illustrated as follows:

1) P2H start-up delay assumptions. The shutdown response of P2H is very rapid, and hydrogen production stops immediately once the power supply circuit is cut off. In the start-up process of the electrolysis cell, the time delays of the two low-temperature electrolysis technologies, AEC and PEMEC, are relatively small, which has little effect on the results when ignored. Therefore, this paper assumes that the start-up delays of the two P2H technologies are 0. However, the SOEC is a high-temperature electrolysis technology, which does not produce hydrogen before the stack is heated to a certain temperature. The heating process generally takes more than 1 h which cannot be ignored, so this article assumes it is 2 h.

2) Microgrid assumptions in the upper level. Except for some large market users with self-supplied power plants, DERs are mainly used to meet the electricity demand of market players themselves, and only the excess electricity can be sold to the utility grid. Therefore, to highlight the main contribution of this article, the upper level adopts an MG assumption that it cannot sell electricity to the utility grid.

3) Other assumptions for model simplification. Other model assumptions including linear marginal generation costs, direct current optimal power flow, one-hour time interval, and zero marginal costs for renewable energy power generation are all common assumptions widely used in a large number of literature studies for model simplification. This article assumes that the reserve of the system is a linear function of net load and renewable energy accommodation.

2.1 Unified Operation Model of P2H System

Different technologies applied to the electrolytic cell will have different effects on the operation of MG. Thus, this paper constructs a unified operation model of the P2H system to describe the working characteristics of different P2H systems. The start–stop, output of the electrolytic cell, hydrogen storage tank, and fuel battery model are built in this section.

This paper sets three types of 0–1 variables: switch states $s_{i,t}^W$, start action $y_{i,t}^W$, and shutdown action $z_{i,t}^W$. All three types of P2H systems can quickly shut down. However, there is no hydrogen production in the heating stage of the SOEC high-temperature electrolysis process, and the length is generally greater than 1 h, which should not be ignored. Thus, the start-up delay needs to be considered, that is, the electrolytic cell enters the power-on state in the ${\epsilon }_i^W$ period after $y_{i,t}^W$ start. Moreover, the initial state $s_{i,t}^W$ is consistent with the last state of the day. Eqs. 1–5 are the description of the electrolytic cell’s operating characteristics. Eqs. 6–9 describe the operation process inside the electrolytic cell. Eqs. 10–13 make constraints on the capacity of the hydrogen storage tank and the internal operating process of the fuel cell. The outputs of the electrolytic cell, the hydrogen storage tank, and the fuel cell should be subjected to their output limits (Zhang et al., 2021):

$y_{i.\left(t-s_i^W\right)}^W-z_{i.t}^W=s_{i.t}^W-s_{i.\left(t-1\right)}^W,(1)$

$y_{i,t}^W\le 1-s_{i,\left(t-1\right)}^W,(2)$

$z_{i.t}^W\le s_{i.\left(t-1\right)}^W,(3)$

${\displaystyle \sum _{t=1}^T{y}_{i.t}^W}\le Y^{W\cdot \max },(4)$

${\displaystyle \sum _{t=1}^T{z}_{i.t}^W}\le Z^{W.\max },(5)$

where $Y^{W.\max }$, $Z^{W.\max }$, respectively, represent the upper limits of starting and shutdown times of electrolytic cells. Eq. 1 describes that the change of the electrolytic cell’s state is determined by the startup action at time $t-{\epsilon }_i^W$ and shutdown action at time t, which reflects the effect of time delay. Eq. 2 indicates that the startup action will not act when the electrolytic cell is turned on. Eq. 3 indicates that the shutdown action will not act when the electrolytic cell is turned off. Taking into account that frequent start and stop will damage the life of the equipment, Eqs. 4, 5 make constraints on the number of starts and stops of the electrolytic cell.

$P_{i,t}^{W.et}\ge s_{i.t}^W{P}^{W\text{.et}\text{.min }}+{\displaystyle \sum _{\tau =0}^{{\epsilon }_i^W-1}{y}_{i,t-\tau }^W}{P}_i^{W\text{.boot }},(6)$

$P_{i,t}^{W.et}\le s_{i.t}^W{P}^{\text{W}\text{.et}\text{.max }}+{\displaystyle \sum _{\tau =0}^{s_i^W-1}{y}_{i,t-\tau }^W}{P}_i^{W\cdot \text{ boot }},(7)$

$P_{i.t}^{W\cdot H_2}={\eta }_i^{W.et}{P}_{i,t}^{W_{.}et},(8)$

$\left|P_{i.t}^{W.et}-P_{i.\left(t-1\right)}^{W_{i}et}\right|\le s_{i,t}^W{\gamma }_i^W+\left(1-s_{i.t}^W\right)P^{\text{W}\text{.et}\text{.max}},(9)$

where $P_{i,t}^{W.H_2}$, ${\eta }_i^{W.et}$, respectively, represent the hydrogen production power and hydrogen production efficiency of the electrolytic cell, ${\gamma }_i^W$ is the maximum climbing power in the power-on state, and $P_{i,t}^{W.et}$ is the power of the electrolytic cell, restricted by Eqs. 6, 7. During the start-up process, it needs to consume per unit period time but does not produce hydrogen. Once the electrolytic cell is turned on, it will run within the upper and lower limits. Eqs. 8, 9, respectively, describe the electricity–hydrogen conversion relationship in the electrolytic cell and the climbing constraint.

$S_{i,t}^{W.hs}-S_{i,\left(t-1\right)}^{W.hs}={\eta }_{i.\alpha }^{W.H_2}{P}_{i,t}^{W.H_2}-\frac{P_{i,t}^{W.fc.H_2}}{{\eta }_{i.\beta }^{W.H_2}}-H_{2_{i,t}^{W.sell}},(10)$

$SO{C}_i^{H_{2.\min }}\le \frac{s_{i,t}^{W,hs}}{{\text{CES}}^{H_2}}\le SO{C}_i^{H_{2.\text{m}ax}},(11)$

$0\le H_{2_{i,t}}^{sell}\le H_{2_t}^{sell.\max },(12)$

$P_{i,t}^{W.fc}={\eta }_i^{W.fc}{P}_{i,t}^{W.fc.H_2},(13)$

where $S_{i,t}^{W.hs}$, $CE{S}^{H_2}$, ${\eta }_{i.\alpha }^{W.H_2}$, ${\eta }_{i.\beta }^{W.H_2}$, respectively, represent the real-time capacity, rated capacity, hydrogen storage efficiency, and hydrogen discharge efficiency of the hydrogen storage tank. $P_{i,t}^{W.fc.H_2}$ is the hydrogen accommodation power of the fuel cell. $H_{2_{i,t}}^{W.sell}$, $H_{2_{i,t}}^{W.sell.\max }$, respectively, represent the amount of hydrogen sold and its upper limit. $SO{C}_i^{H_2.\max }$, $SO{C}_i^{H_2.\min }$, respectively, represent the upper and lower limits of the SOC of the hydrogen storage tank. The HS tank cannot be charged and discharged at the same time according to the assumption. Thus, the hydrogen sales and the hydrogen accommodation of the fuel cell cannot be carried out at the same time as the hydrogen production of the electrolytic cell. Eq. 10 describes that the change in hydrogen storage in the hydrogen storage tank is composed of three parts: hydrogen storage, hydrogen sales, and hydrogen entering the fuel cell. Eq. 11 is the constraint of the SOC of the hydrogen storage tank. Eq. 12 limits the amount of hydrogen sold. Eq. 13 describes the hydrogen–electricity conversion relationship inside the fuel cell.

2.2 MG Model

The MG formulates strategies based on LMPs and ToU hydrogen prices to minimize costs:

$\min C_i^{LD}-I_i^{H_2},(14)$

$C_i^{LD}={\displaystyle \sum _{t=1}^T{\lambda }_{i,t}^E}{P}_{i,t}^{NLD},(15)$

$P_{i,t}^{NLD}=P_{i,t}^{LD}+P_{i,t.\alpha }^{ESS}-P_{i,t.\beta }^{ESS}-P_{i,t}^{WT}+P_{i,t}^{W.et}-P_{i.t}^{W.fc},(16)$

$0\le P_{i,t}^{WT}\le P_{i,t}^{AWT},(17)$

$E_{i,t}^{ESS}=E_{i,\left(t-1\right)}^{ESS}+\left({\eta }_{i.\alpha }^{ESS}{P}_{i,t.\alpha }^{ESS}-{\eta }_{i.\beta }^{ESS}{P}_{i,t.\beta }^{ESS}\right),(18)$

$SO{C}_i^{ESS.min}\le \frac{E_{i,t}^{ESS}}{C_i^{ESS}}\le {\mathrm{SOC}}_i^{ESS.\max },(19)$

$0\le P_{i,t.\alpha }^{ESS}\le P_{i.\alpha }^{ESS.\max }B,(20)$

$0\le P_{i,t.\beta }^{ESS}\le P_{i.\beta }^{ESS.\max }\left(1-B\right),(21)$

where the objective function (Eq. 14) consists of two parts, the MG purchase cost $C_i^{LD}$ and the hydrogen sales revenue $I_i^{H_2}$. Eq. 16 is the MG internal power balance constraint, and $P_{i,t}^{LD}$, $P_{i,t}^{NLD}$, respectively, represent the original load and net load. $P_{i,t}^{WT}$, $P_{i,t}^{AWT}$, respectively, represent the distributed wind power output and its upper limit. Eq. 18 uses $E_{i,t}^{ESS}$ to describe the change in the capacity of ES system. $C_i^{ESS}$ is the rated capacity of ES system. $SO{C}_i^{ESS.\max }$ and $SO{C}_i^{ESS.\min }$, respectively, represent the upper and lower limits of the SOC. $P_{i,t.\alpha }^{ESS}$, $P_{i,t.\beta }^{ESS}$ are, respectively, the charging and discharging power of ES. $P_{i.\alpha }^{ESS.\max }$, $P_{i.\beta }^{ESS.\max }$ are, respectively, the charging and discharging power upper limits. ${\eta }_{i.\alpha }^{ESS}$, ${\eta }_{i.\beta }^{ESS}$ are, respectively, the charging and discharging efficiency. Eqs. 20, 21 use 0–1 variable B to limit the energy storage that cannot be charged and discharged at the same time.

2.3 Market Model

2.3.1 Electric Energy Market–Clearing Model

LMP is the dominant method in the power market to calculate electricity price and to manage transmission congestion (Li and Bo, 2008). The power market entities include thermal power units $P_{i,t}^G$ and centralized wind power–generating units $P_{i,t}^{RG}$. The system must provide sufficient backup $P_{i,t}^R$ to ensure the safe operation of the system in case of emergencies. An independent system operator (ISO) performs clearing calculations based on the net load demand transmitted by each MG in the upper model to obtain the node marginal electricity prices:

$\min {\displaystyle \sum _{i=1}^{N^G}{\displaystyle \sum _{t=1}^T{c}_i^G{P}_{i,t}^G}},(22)$

$c_i^G=a_{2i}{P}_{i,t}^G+b_{2i},(23)$

${\displaystyle \sum _{i=1}^{N^G}{P}_{i,t}^G}+{\displaystyle \sum _{i=1}^{N=1}{P}_{i,t}^{RG}}={\displaystyle \sum _{i=1}^{N^{MG}}{P}_{i,t}^{NLD}},(24)$

$-P_k^{LN\cdot \max }\le {\displaystyle \sum _{i\in {\Omega }^G\cup {\Omega }^{RG}\cup {\Omega }^{MG}}{G}_{k-i}}\left(P_{i,t}^G+P_{i,t}^{RG}+P_{i,t}^R-P_{i,t}^{NLD}\right)\le P_k^{LN.\max },(25)$

${\displaystyle \sum _{i\in {\Omega }^G}{P}_{i,t}^R}\ge {\mu }_1{\displaystyle \sum _{i\in {\Omega }^{MG}}{P}_{i,t}^{NLD}}-{\mu }_2{\displaystyle \sum _{i\in {\Omega }^{RG}}{P}_{i,t}^{RG}},(26)$

$0\le P_{i,t}^R\le P_i^{R.\max },(27)$

$P_i^{G.min}\le P_{i,t}^G+P_{i,t}^R\le P_i^{G.\max },(28)$

$\left(P_{i,t}^G+P_{i,t}^R\right)-P_{i,\left(t-1\right)}^G\le P_i^{U.\max },(29)$

$P_{i,t}^G-\left(P_{i,\left(t-1\right)}^G+P_{i,\left(t-1\right)}^R\right)\ge P_i^{D.\max },(30)$

$0\le P_{i,t}^{RG}\le P_i^{ARG},(31)$

${\lambda }_{i,t}^E={\lambda }_{i,t}+{\displaystyle \sum _k{G}_{k-i}}\left({\mu }_{i,t}^{+}-{\mu }_{i,t}^{-}\right),(32)$

where $P_i^{R.\max }$ is the upper limit of reserve power. ${\mu }_1$, ${\mu }_2$ are the weights. $G_{k-i}$ represents the node power transfer distribution factor. $P_k^{LN.\max }$ represents the maximum transmission power of the kth line. $P_i^{G.\max }$, $P_i^{G.\min }$, respectively, represent the upper and lower limits of the output of thermal power units. $P_i^{U.\max }$, $P_i^{D.\max }$, respectively, represent the upper and lower limits of climbing power. $P_i^{ARG}$ represents the maximum output of the RE unit determined by natural resources. Eq. 22 describes the objective function of market-clearing to minimize the operating cost of thermal power units, and the unit power generation cost $c_i^G$ can be expressed by a linear function as Eq. 23. Eqs. 24–31 are constraints on power balance, line flow, unit operation, unit climbing, and centralized wind power output. Eq. 26 is the assumption made in this paper for system backup, namely, $P_{i,t}^R$ is a linear function of the net load $P_{i,t}^{NLD}$ and $P_{i,t}^{RG}$. Eq. 32 indicates that LMP can pass the Lagrange multiplier $\left\{{\lambda }_{i,t},{\mu }_{i,t}^{+},{\mu }_{i,t}^{-}\right\}$ through the power balance and line flow constraint in the market-clearing optimization to get.

2.3.2 Hydrogen Market Transaction Model

The remaining high-purity hydrogen in the HS tank in 1 day can be used for sale as a new profit model to improve the economic benefits of MG. This article draws on the Cournot model formula based on quantity competition (Molina et al., 2011) to establish a hydrogen market transaction model:

$I_i^{H_2}={\displaystyle \sum _t{\lambda }_t^{H_2}}{H}_{2_{i,t}}^{W.sell},(33)$

${\lambda }_t^{H_2}=a_1-b_1{\displaystyle \sum _i{S}_{i,t}^{hs}},(34)$

where ${\lambda }_t^{H_2}$ represents the time-sharing hydrogen price. Based on the Cournot competition hypothesis, the relationship between the price of hydrogen sold and its quantity should be linear, as written in Eq. 34. a₁, b₁ are two positive coefficients of the inverse price function, which can be calculated according to market parameters.

3 Solving Algorithm

Microgrids dispatch their internal load according to the previous price, calculate the net load, and report it to the ISO. Then, the ISO will calculate a new LMP based on the power balance constraint, the line flow constraint, and the price reported by the thermal power units, with the goal of minimizing the market cost.

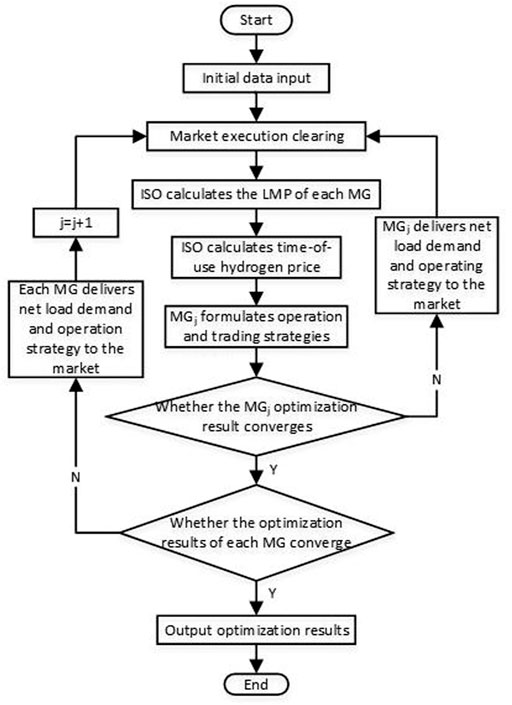
The EPEC is generated because there are multiple MGs and markets in the two-layer model. In order to achieve market equilibrium, they must formulate different trading and operating strategies. In addition, there will be another MPEC in every single two-layer model composed of the MG and ISO. Therefore, this paper uses the DA to decompose the EPEC into multiple MPECs. In each solution process, only one MPEC is solved, while the transaction and operation strategies of other microgrids are fixed. The iteration is repeated until all MG strategies converge (Jiang et al., 2021b). The specific process is shown in Figure 1.

FIGURE 1

FIGURE 1. DA flow chart.

4 Case Study

4.1 Basic Data

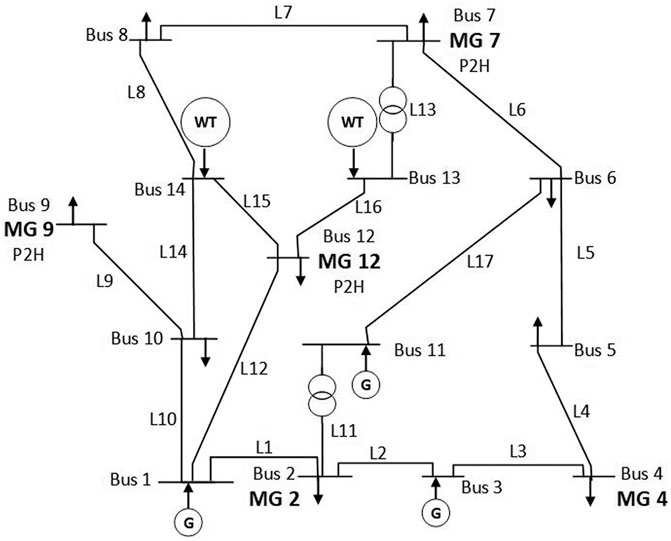
The validity of the proposed model is verified based on the IEEE 14-node system. MATLAB 2016b and CPLEX 12.6 are used to carry out simulation analysis. The system includes three traditional thermal power plants, two centralized wind farms, and five microgrids. The location distribution is shown in Figure 2. The relevant unit data and load demands can be found in the study of Yang et al. (2015) and Jiang et al. (2021b). The output limit is obtained according to the average data of a random period time combined with the model.

FIGURE 2

FIGURE 2. Node system diagram.

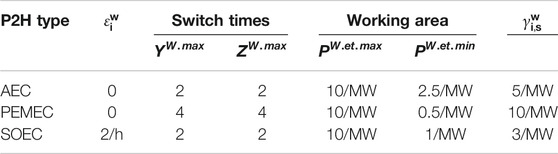
Each microgrid contains a distributed wind farm and electric energy storage system. The ES parameters are shown in Table 1. Some MGs are equipped with P2H systems, which are set according to the use of 50 P2H modules, and the power of each type of module is unified to 0.2 MW (Xing et al., 2020). The spare capacity weights μ₁, μ₂ are 0.3 and 0.1. Table 2 shows the P2H parameters used in the electrolytic cell. Table 3 shows the equipment parameters of the HS tank in the P2H system. The efficiency of P2H and H2P production is both 0.6.

TABLE 1

TABLE 1. Energy storage parameters.

TABLE 2

TABLE 2. P2H technical parameters.

TABLE 3

TABLE 3. Hydrogen storage tank parameters.

4.2 Result Analysis

The calculation example is divided into four scenarios according to whether the P2H system is configured and its configuration type, namely, no P2H, AEC type, PEMEC type, and SOEC type. Taking MG12 as an example, the different effects of its internal power output, hydrogen energy flow, load optimization, wind power accommodation, and cost are analyzed.

4.2.1 MG’s Internal Power Output Analysis

MG12’s internal equipment output and LMP curve are shown in Figure 3. As shown, the LMP is low during 00:00–05:00 and 20:00–24:00. Thus, the MG will purchase electricity to meet the load demand and allocate it to ES and the electrolytic cell for hydrogen production. Due to high electricity prices during the period from 7:00 to 19:00, the MG will reduce the electricity purchases. Correspondingly, it will use ES discharge or fuel cell hydrogen production to make up for the shortfall. During this process, the P2H system can stabilize the fluctuation of wind power output through charging and discharging cooperated with ES.

FIGURE 3

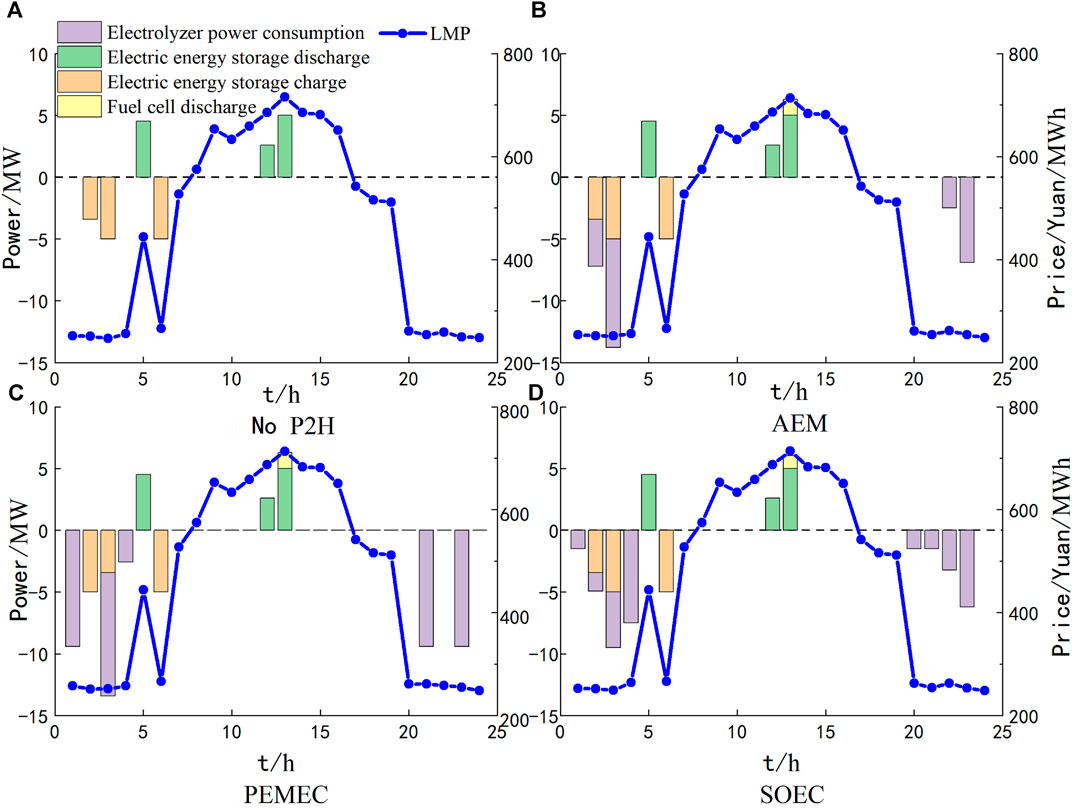
FIGURE 3. Internal equipment output of MG12 and LMP. (A) means No P2H, (B) means AEM, (C) means PEMEC, (D) means SOEC.

4.2.2 Comparative Analysis of Multiple Types of P2H Systems

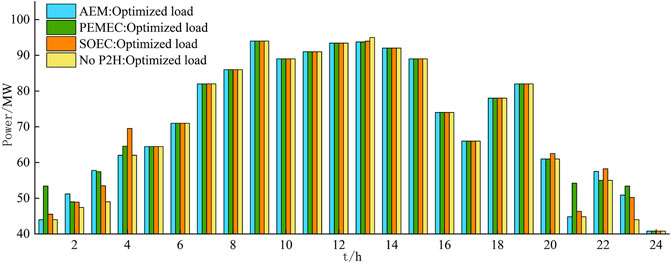
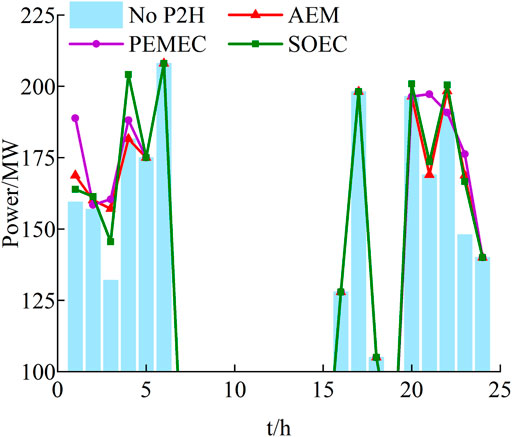
The optimized load curves under different P2H technologies are shown in Figure 4. The inner distributed wind power plants of MGs will fully output in all four scenarios to reduce load demand and power purchase costs. The differences in load optimization situation in the four cases were caused by the differences in the output of centralized wind power, P2H systems, and ES during 0:00–05:00 and 20:00–24:00. The curtailment occurs when the line power flow is restricted. However, wind power that cannot be absorbed can be used to produce hydrogen via the configuration of P2H. Figure 5 shows the accommodation of centralized wind power output. Table 4 shows the working status of the electrolytic cell under different P2H technologies. Figure 6 shows the hydrogen energy flow and the time-sharing hydrogen price curve within the MG during the optimization process.

FIGURE 4

FIGURE 4. MG12 optimized load curve under different P2H systems.

FIGURE 5

FIGURE 5. Centralized wind farm output diagram.

TABLE 4

TABLE 4. MG12 electrolysis pool status under different P2H systems.

FIGURE 6

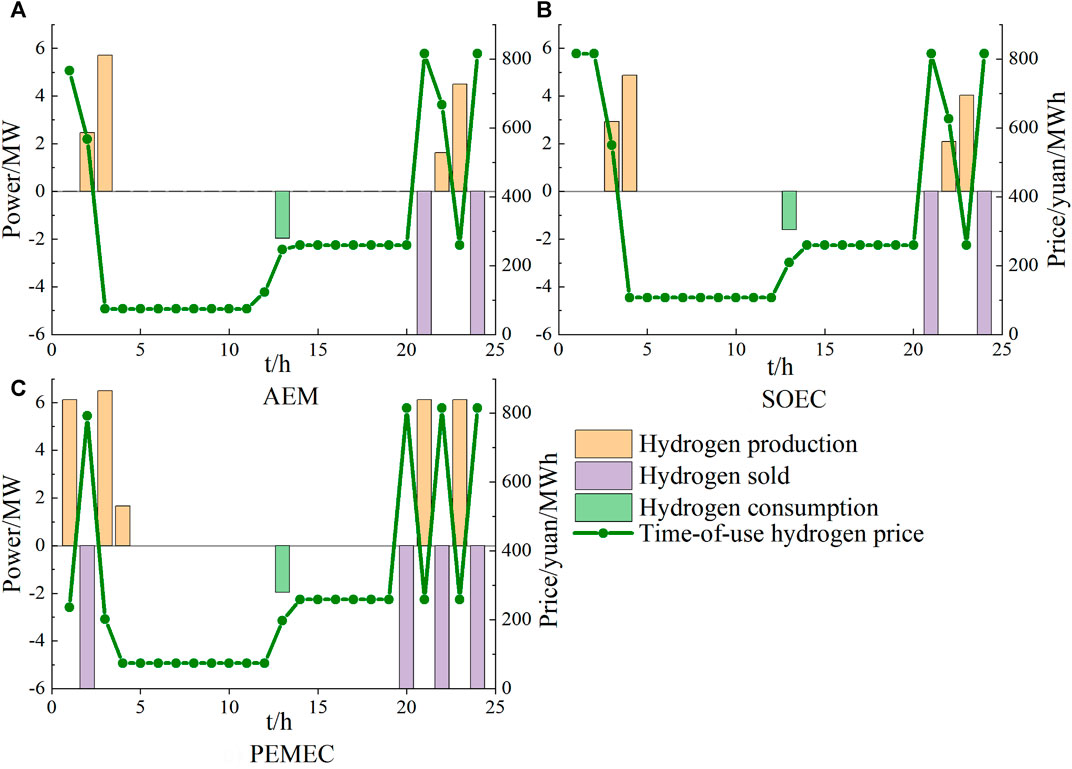
FIGURE 6. Hydrogen energy flow diagram under different P2H systems in the MG and time-sharing hydrogen price curve. (A) means AEM, (B) means PEMEC, (C) means SOEC.

As shown in Figures 3, 6, the peak and valley periods of LMP are exactly the opposite of those of the time-sharing hydrogen price. When the electricity price is high and the hydrogen price is low, the wind power accommodation is the same in four cases, like 06:00–19:00. During these periods, there is no hydrogen produced. Correspondingly, hydrogen will be used to produce electricity because selling hydrogen directly is more beneficial to the MG than reducing electricity purchase costs by H2P. Thus, MGs will sell hydrogen as much as possible. For the AEC and SOEC, the number of start and stop times is limited, which restricts their hydrogen production to sell. Oppositely, the PEMEC is flexible to start and stop frequently, which makes it possible that hydrogen can be produced and sold in multiple periods. Conversely, when the price of electricity is low, fuel cells will purchase electricity to produce hydrogen. When the price of hydrogen is high, fuel cells will sell hydrogen to increase revenue.

According to Table 4 and Figure 6, there is no start-up time delay for the AEC and PEMEC, and they enter the start-up state immediately after start-up. In contrast, for the SOEC, there is a time delay when it enters the start-up state. For example, the electrolytic cell can only produce hydrogen at 03:00 as shown in Figure 6. However, from Figure 4, it is seen that the electrolytic cell still consumes electricity during the period from 01:00 to 03:00. According to Figure 5, the use of three P2H technologies can significantly increase the accommodation of RE. Compared with the daily wind power accommodation without P2H, the use of AEC can consume 65.945 MW more, while the PEMEC can consume 122.46 MW more and SOEC can consume 82.27 MW more. The PEMEC has the highest flexibility; thus, it can improve the accommodation of RE the most. To change the P2H system configuration location from nodes 7, 9, and 12 to nodes 2, 4, and 9 which are far away from the centralized wind farm, the wind power accommodation will be reduced. For instance, for the PEMEC, after the change, the accommodation is reduced by 39.82 MW. Thus, the closer the renewable energy location, the better the effect of the P2H system in improving accommodation.

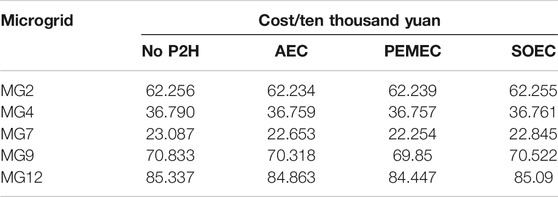
The costs of each microgrid under different P2H technologies are shown in Table 5. As shown, all three P2H technologies can achieve the goal of reducing MG costs. For MG7, MG9, and MG12, the reduction of costs is more than that for the other two MGs. Each MG can formulate trading and operating strategies to obtain revenue from the sale of hydrogen based on the LMPs and ToU hydrogen prices. When the SOEC is used, although electricity is consumed during the start-up process, there is a small reduction in MG cost because there is no hydrogen production. Oppositely, the reduction of costs by using the PEMEC is the most due to a large amount of hydrogen selling. Moreover, while the wind is used in P2H to increase its accommodation, the output of thermal power units will increase. Therefore, it can be inferred that the output of thermal power units can support the accommodation of RE after the P2H system is configured.

TABLE 5

TABLE 5. MG costs.

5 Conclusion

This paper mainly studies the equilibrium problem of electric hydrogen multi-market under different P2H technologies. The results show that the three P2H systems, AEC, PEMEC, and SOEC, all can promote the accommodation of RE after reasonable configuration, and the PEMEC has the best effect. The effect of promoting RE accommodation will be more obvious when the equipment is installed near the renewable energy node. Additionally, it is found that the output of thermal power units can support the accommodation of RE after the P2H system is configured to a certain extent. According to the economic analysis, it can be seen that multi-market transactions considering the coupling of electricity and hydrogen are beneficial to reduce the energy purchase cost of MG and increase its income.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

HL conceptualized the research idea and performed the methodology. YW ran the software and wrote the original draft. FX was involved in investigation and data validation. MW visualized the data. KJ curated the data. XY reviewed and edited the paper. NL supervised the work.

Conflict of Interest

The authors HL, FX, and MW are employed by State Grid Zhejiang Electric Power Co., Ltd., Lishui Power Supply Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bahrami, S., Toulabi, M., Ranjbar, S., Moeini-Aghtaie, M., and Ranjbar, A. M. (2018). A Decentralized Energy Management Framework for Energy Hubs in Dynamic Pricing Markets. IEEE Trans. Smart Grid 9 (6), 6780–6792. doi:10.1109/TSG.2017.2723023

CrossRef Full Text | Google Scholar

Ban, M., Yu, J., Shahidehpour, M., and Yao, Y. (2017). Integration of Power-To-Hydrogen in Day-Ahead Security-Constrained Unit Commitment with High Wind penetrationJournal of Modern Power Systems and Clean Energy. J. Mod. Power Syst. Clean. Energ. 5 (3), 337–349. doi:10.1007/s40565-017-0277-0

CrossRef Full Text | Google Scholar

Chen, H., Wang, X., Li, Z., Chen, W., and Cai, Y. (2019). Distributed Sensing and Cooperative Estimation/detection of Ubiquitous Power Internet of Things. Prot. Control. Mod. Power Syst. 4, 13. doi:10.1186/s41601-019-0128-2

CrossRef Full Text | Google Scholar

Cheng, T., Jiang, J., Xu, M., and Li, X. (2017). “Performance Evaluation and Optimization of a Solid Oxide Fuel Cell System Combined with Solid Oxide Electrolysis Cell,” in 2017 Chinese Automation Congress (CAC), 2473–2477. doi:10.1109/CAC.2017.8243191

CrossRef Full Text | Google Scholar

Dai, T., and Qiao, W. (2017). Finding Equilibria in the Pool-Based Electricity Market with Strategic Wind Power Producers and Network Constraints. IEEE Trans. Power Syst. 32 (1), 389–399. doi:10.1109/TPWRS.2016.2549003

CrossRef Full Text | Google Scholar

Dickinson, R. R., Lymperopoulos, N., Le Duigou, A., Lucchese, P., Mansilla, C., Tlili, O., et al. (2017). “Fower-to-hydrogen and Hydrogen-To-X Pathways: Opportunities for Next Generation Energy Systems,” in 2017 14th International Conference on the European Energy Market (EEM), 1–6. doi:10.1109/EEM.2017.7981882

CrossRef Full Text | Google Scholar

Du, L., Grijalva, S., and Harley, R. G. (2015). Game-Theoretic Formulation of Power Dispatch with Guaranteed Convergence and Prioritized BestResponse. IEEE Trans. Sustain. Energ. 6 (1), 51–59. doi:10.1109/TSTE.2014.2358849

CrossRef Full Text | Google Scholar

Gahleitner, G. (2013). Hydrogen from Renewable Electricity: An International Review of Power-To-Gas Pilot Plants for Stationary Applications. Int. J. Hydrogen Energ. 38 (5), 2039–2061. doi:10.1016/j.ijhydene.2012.12.010

CrossRef Full Text | Google Scholar

Guo, H., Chen, Q., Xia, Q., and Kang, C. (2020). Modeling Strategic Behaviors of Renewable Energy with Joint Consideration on Energy and Tradable Green Certificate Markets. IEEE Trans. Power Syst. 35 (3), 1898–1910. doi:10.1109/TPWRS.2019.2953114

CrossRef Full Text | Google Scholar

IEA (2020). The Future of Hydrogen [EB/OL]. Available at: https://www.iea.org/reports/the-future-of-hydrogen (Accessed 01 04, 2020).

Google Scholar

Jiang, J.-J., Wei, W.-X., Shao, W.-L., Liang, Y.-F., and Qu, Y.-Y. (2021). Research on Large-Scale Bi-level Particle Swarm Optimization Algorithm. IEEE Access 9, 56364–56375. doi:10.1109/ACCESS.2021.3072199

CrossRef Full Text | Google Scholar

Jiang, K., Wang, P., Wang, J., and Liu, N. (2021). “Reserve Cost Allocation Mechanism in Renewable Portfolio Standard-Constrained Spot Market,” in IEEE Trans. Sustain. Energy, 1. doi:10.1109/TSTE.2021.3103853

CrossRef Full Text | Google Scholar

Jianxiao, W., Qing, X., Gengyin, L., Qi, A., Zhaoyuan, W., and Tiance, Z. (2021). “Mechanism Design for Integrated Energy Markets Based on Multi-Market Equilibrium[J],” in Proceedings of the CSEE, 1-15[2021-09-11]. doi:10.13334/j.0258-8013.pcsee.210349

CrossRef Full Text | Google Scholar

Li, F., and Bo, R. (2008). “DCOPF-based LMP Simulation: Algorithm, Comparison with ACOPF, and Sensitivity,” in 2008 IEEE/PES Transmission and Distribution Conference and Exposition, 1. doi:10.1109/TDC.2008.4517062

CrossRef Full Text | Google Scholar

Li, J., Lin, J., Song, Y., Xing, X., and Fu, C. (2019). Operation Optimization of Power to Hydrogen and Heat (P2HH) in ADN Coordinated with the District Heating Network. IEEE Trans. Sustain. Energ. 10 (4), 1672–1683. doi:10.1109/TSTE.2018.2868827

CrossRef Full Text | Google Scholar

Liu, N., Tan, L., Zhou, L., and Chen, Q. (2020). Multi-party Energy Management of Energy Hub: A Hybrid Approach with Stackelberg Game and Blockchain. J. Mod. Power Syst. Clean Energ. 8 (5), 919–928. doi:10.35833/MPCE.2019.000545

CrossRef Full Text | Google Scholar

Liu, N., Wang, J., and Wang, L. (2017). Distributed Energy Management for Interconnected Operation of Combined Heat and Power-Based Microgrids with Demand Response. J. Mod. Power Syst. Clean. Energ. 5 (3), 478–488. doi:10.1007/s40565-017-0267-2

CrossRef Full Text | Google Scholar

Maroufmashat, A., Mukherjee, U., Ranisau, J., Barbouti, M., Trainor, A., El-Shayeb, H., et al. (2016). “Optimization of Renewable Powered Hydrogen Micro-grid; Taking in to Account Economic Criteria,” in 2016 IEEE Smart Energy Grid Engineering (SEGE), 252–256. doi:10.1109/SEGE.2016.7589534

CrossRef Full Text | Google Scholar

Mathiesen, B. V., Ridjan, I., Connolly, D., Nielsen, M. P., Hendriksen, P. V., Mogensen, M. B., et al. (2013). Technology Data for High Temperature Solid Oxide Electrolyser Cells, Alkali and PEM Electrolysers.

Google Scholar

Molina, J. P., Zolezzi, J. M., Contreras, J., Rudnick, H., and Reveco, M. J. (2011). Nash-Cournot Equilibria in Hydrothermal Electricity Markets. IEEE Trans. Power Syst. 26 (3), 1089–1101. doi:10.1109/TPWRS.2010.2077313

CrossRef Full Text | Google Scholar

Murty, V. V. S. N., and Kumar, A. (2020). Multi-objective Energy Management in Microgrids with Hybrid Energy Sources and Battery Energy Storage Systems. Prot. Control. Mod. Power Syst. 5, 2. doi:10.1186/s41601-019-0147-z

CrossRef Full Text | Google Scholar

Pan, G., Gu, W., Lu, Y., Qiu, H., Lu, S., and Yao, S. (2020). Optimal Planning for Electricity-Hydrogen Integrated Energy System Considering Power to Hydrogen and Heat and Seasonal Storage. IEEE Trans. Sustain. Energ. 11 (4), 2662–2676. doi:10.1109/TSTE.2020.2970078

CrossRef Full Text | Google Scholar

Petrecca, G., and Decarli, M. (2008). “A Review of Hydrogen Applications: Technical and Economic Aspects,” in MELECON 2008 - The 14th IEEE Mediterranean Electrotechnical Conference, 658–662. doi:10.1109/MELCON.2008.4618510

CrossRef Full Text | Google Scholar

Reddy, G. N., Shrestha, S., Acharya, B., Bangi, V. K. T., and Guduru, R. (2018). “Analysis of Hydrogen Dry Cell for Alkaline Water Electrolysis,” in 2018 7th International Conference on Renewable Energy Research and Applications (ICRERA), 687–692. doi:10.1109/ICRERA.2018.8566705

CrossRef Full Text | Google Scholar

Ruiz, C., Conejo, A. J., and Smeers, Y. (2012). Equilibria in an Oligopolistic Electricity Pool with Stepwise Offer Curves. IEEE Trans. Power Syst. 27 (2), 752–761. doi:10.1109/TPWRS.2011.2170439

CrossRef Full Text | Google Scholar

Sadat, S. A., and Fan, L. (2017). “Mixed Integer Linear Programming Formulation for Chance Constrained Mathematical Programs with Equilibrium Constraints,” in 2017 IEEE Power & Energy Society General Meeting, 1–5. doi:10.1109/PESGM.2017.8273875

CrossRef Full Text | Google Scholar

Shao, C., Feng, C., Shahidehpour, M., Zhou, Q., Wang, X., and Wang, X. (2021). Optimal Stochastic Operation of Integrated Electric Power and Renewable Energy with Vehicle-Based Hydrogen Energy System. IEEE Trans. Power Syst. 36 (5), 4310–4321. doi:10.1109/TPWRS.2021.3058561

CrossRef Full Text | Google Scholar

Wang, T., Zhu, X., Ge, P., Hu, Q., Wu, Q., Dou, X., et al. (2019). “Expanding Flexibility with P2H for Integrated Energy Systems,” in 8th Renewable Power Generation Conference (RPG 2019), 1–6. doi:10.1049/cp.2019.0670

CrossRef Full Text | Google Scholar

Wen, T., Zhang, Z., Lin, X., Li, Z., Chen, C., and Wang, Z. (2020). Research on Modeling and the Operation Strategy of a Hydrogen-Battery Hybrid Energy Storage System for Flexible Wind Farm Grid-Connection. IEEE Access 8, 79347–79356. doi:10.1109/ACCESS.2020.2990581

CrossRef Full Text | Google Scholar

Xian, W., Kai, Z., and Shaohua, Z. (2018). Joint Equilibrium Analysis of Day-Ahead Electricity Market and DRX Market Considering Wind Power Bidding[J]. Proc. CSEE 38 (19), 5738–5750+5930.

Google Scholar

Xianshan, L., and Yuxiang, Y. (2020). Optimization Dispatching for Joint Operation of Hydrogen Storage-Wind Power and Cascade Hydropower Station Based on Bidirectional Electricity Price Compensation. Powe Syst. Tech. 44 (09), 3297–3306.

Google Scholar

Xie, K., Hui, H., and Ding, Y. (2019). Review of Modeling and Control Strategy of Thermostatically Controlled Loads for Virtual Energy Storage System. Prot. Control. Mod. Power Syst. 4, 23. doi:10.1186/s41601-019-0135-3

CrossRef Full Text | Google Scholar

Xing, X., Lin, J., Song, Y., Song, J., and Mu, S. (2020). Intermodule Management within a Large-Capacity High-Temperature Power-To-Hydrogen Plant. IEEE Trans. Energ. Convers. 35 (3), 1. doi:10.1109/TEC.2020.2978552

CrossRef Full Text | Google Scholar

Yang, H., Wei, H., and Li, C. (2015). Day-ahead Generation Scheduling Plan Modes for Large-Scale Wind-Storage Combined Power Generation System Based on Two-Stage Optimization[J]. Automation Electric Power Syst. 39 (24), 8–15.

Google Scholar

Yanzhe, L., Xiaojia, G., Haiying, D., and Zheng, G. (2020). Optimal Capacity Configuration of Wind/PV/Storage Hybrid Energy Storage System in Microgrid[J]. Automation Electric Power Syst. 32 (06), 123–128.

Google Scholar

Yue, C., Wei, W., Feng, L., Shengwei, M., and Tiejiang, Y. (2018). CES Utility Function Based Consumer Optimal Decision Making in Heat-Power Market[J]. Automation Electric Power Syst. 42 (13), 118–126. doi:10.7500/AEPS20171225004

CrossRef Full Text | Google Scholar

Zhang, K., Zhou, B., Or, S. W., Li, C., Chung, C. Y., and Voropai, N. I. (2021). “Optimal Coordinated Control of Multi-Renewable-To-Hydrogen Production System for Hydrogen Fueling Stations,” in IEEE Trans. on Ind. Applicat., 1. doi:10.1109/TIA.2021.3093841

CrossRef Full Text | Google Scholar

Zhou, B., Zou, J., Yung Chung, C., Wang, H., Liu, N., Voropai, N., et al. (2021). Multi-microgrid Energy Management Systems: Architecture, Communication, and Scheduling Strategies. J. Mod. Power Syst. Clean Energ. 9 (3), 463–476. doi:10.35833/MPCE.2019.000237

CrossRef Full Text | Google Scholar

Zhou, H., Chen, S., Kang, J., and Zhang, F. (2005). “A Statistical Model for Setting Price Cap in Electricity Market,” in 2005 IEEE/PES Transmission & Distribution Conference & Exposition: Asia and Pacific, 1–5. doi:10.1109/TDC.2005.1546866

CrossRef Full Text | Google Scholar