An Investigation of the Kinetic Modeling and Ignition Delay Time of Methanol—Syngas Fuel

The recycling of exhaust heat in internal combustion engines to dissociate the methanol, followed by its blending with methanol to produce engine fuel, is promising for improving the efficiency of engines, and reducing emissions. The kinetic model MEOHSYNGAS1.0 for the methanol–syngas fuel is proposed by reducing the detailed chemical kinetic model (Mech15.34). Shock tube experiments are conducted to measure the ignition delay time of methanol blended with dissociated methanol gas at different dissociated methanol ratios (0, 30, 50, and 100%). The model is validated by the experimental data of the present work and with data from the literature. The effects of the equivalence ratio, pressure, and dissociated methanol ratio on the ignition delay time are investigated through reaction path analysis and sensitivity analysis. When the dissociated methanol ratio does not surpass 50%, the ignition delay time increases with the increase in the dissociated methanol ratio, which is more obvious in the low temperature range, and but decreases with the increase in temperature.

Introduction

Methanol is a promising fuel for internal combustion engines because it can be efficiently and cleanly burned (Verhelst et al., 2019). In addition, methanol is used as an energy carrier for transportation vehicles (Jaspers et al., 2021). Carbon neutrality can be achieved by capturing carbon dioxide (CO₂) to produce methanol with renewable energy (Borisut and Nuchitprasittichai, 2019). Methanol can be used in either the spark-ignition engine or the compression-ignition engine, burning either pure methanol directly or a blend of methanol with gasoline or diesel (Li et al., 2021). To improve the thermal efficiency of the engine, the method of blending methanol with dissociated methanol gas was proposed (Xie, 2016; Wen, 2018). Specifically, the methanol is vaporized by the exhaust heat of the internal combustion engine through a methanol dissociation device, and then dissociated using a catalyst to generate a mixture of hydrogen (H₂) and carbon monoxide (CO) with a ratio of 2:1. The resulting syngas is added to the engine cylinder to improve combustion, as Figure 1 shows.

FIGURE 1

FIGURE 1. Blending methanol and syngas as a fuel for the internal combustion engine.

The thermal decomposition global reaction is

$\mathrm{C}{\mathrm{H}}_3\mathrm{OH}=2{\mathrm{H}}_2+\mathrm{CO},(1)$

This method can not only recycle the exhaust heat, but also enable the engine to be closer to the constant volume cycle, and, thus, the thermal efficiency of the engine is improved (Ji et al., 2013). In addition, dissociated methanol gas is rich in hydrogen, and mixing hydrogen with a hydrocarbon fuel for combustion can increase the flame speed (Zhao et al., 2019), and extend the lean-burn limit (Jaimes et al., 2018). Lean combustion enables the fuel to burn completely, which further increases the thermal efficiency, and may reduce the emissions of CO (Liu and Dumitrescu, 2019). In addition, lean-burn can reduce the combustion temperature, thus reducing NO_x emissions (Yao et al., 2014). Considering the research of Nguyen and Verhelst (2017), Gong et al. (2019), Zhang et al. (2014), and other scholars on the use of methanol blended with hydrogen as a fuel for internal combustion engines, as well as our previous research (Jiang et al., 2019), the results show that under suitable working conditions and parameters, blending methanol and dissociated methanol gas as a fuel can improve the efficiency and reduce emissions of internal combustion engines.

At present, there are very few direct studies on the kinetic modeling of methanol–syngas fuel where hydrogen (H₂) and carbon monoxide (CO) are mixed at a ratio of 2:1. This section will review the oxidation mechanism of methanol and syngas. Sun et al. (2007) constructed the oxidation mechanism of CO/H₂/air, and the flame speed was measured by the constant-pressure spherical flame technique. Combined with previous ignition temperatures results, the mechanism proved to be accurate. Some of the mechanism parameters were determined by ab initio calculations. Kalitan et al. (2007) studied the combustion characteristics of syngas by a shock tube with a temperature range of 809–1300 K, a pressure of 1.0, 2.5, and 15.0 atm, and an equivalence ratio of 0.5. Thi et al. (2014) investigated the ignition delay time of syngas at different equivalence ratios by a shock tube at 870–1350 K, a pressure 0.2, 1.0, and 2.0 MPa, and equivalence ratios of 0.3, 1.0, and 1.5. Kéromnès et al. (2013) updated the kinetic model of the H₂/CO/O₂/N₂/AR system and verified the accuracy of the mechanism by various experiments including a shock tube, a rapid compression machine (RCM), a spherical bomb facility, etc. It had a pressure range of 1–70 bar, a temperature range of 914–2220 K, and an equivalence ratio range of 0.1–4.0. Mansfield and Wooldridge (2014) studied the ignition characteristics of syngas at a low temperature with a RCM. The H₂/CO mole ratio was 0.7, the temperature range was 870–1150 K, the pressure range was 3–15 atm, and the equivalence ratios were 0.1 and 0.5.

The mechanism of methanol oxidation proposed by Held and Dryer (1998) was verified by many experiments, in which the temperature range was 633–2050 K, the pressure range was 0.26–20 atm, and the equivalence ratio range was 0.05–2.6. The experimental verification included a shock tube, a flow reactor, a burner-stabilized flame, a laminar premixed flame, etc. Although some radicals, such as CH and CH₂, are neglected in this mechanism, it is consistent with the experimental data. Li et al. (2007) updated some of the reaction rate constants and thermodynamic data in the methanol oxidation process. According to the H₂/O₂/CO/HCO/CH₂O/CH₃/CH₄/CH₂OH/CH₃O/CH₃OH reaction pathway, the mechanism of the methanol oxidation was constructed. The mechanism proposed by Li et al. (2007) was verified by experimental results using a shock tube, a laminar premixed flame, a burner-stabilized flame, and a flow reactor, where the temperature range was 300–2200 K, the pressure range was 1–20 atm, and the equivalence ratio range was 0.05–6.0. Liao et al. (2011) simplified the methanol mechanism proposed by Held and Dryer (1998), from 22 species and 89 reactions to 17 species and 40 elementary reactions. The mechanism was verified by ignition delay time, premixed laminar flame speeds, and the radicals in static reactors and flow reactors. The temperature ranged from 823 to 2180 K, the pressure ranged from 0.005 to 2.0 MPa, and the equivalence ratio ranged from 0.2 to 2.6. The error between the simulation and experimental results was acceptable. Pinzón et al. (2019) undertook a shock tube experiment for methanol oxidation and measured water time-history profiles. The experimental temperature range was 940–1540 K, the pressure was 1.3 and 14.9 atm, and the equivalence ratios were 0.5, 1.0, and 2.0. The methanol oxidation process was analyzed by the rate of production (ROP) and sensitivity analysis, focusing on the effect on water production. The error between the simulation and experimental data was analyzed. Christensen et al. (2016) updated the Konnov mechanism, version 0.6 (Konnov, 2009). According to the latest theoretical research and experimental results, Christensen et al. (2016) systematically updated the rate constants and compared the simulation results with the experimental results of the shock tube, flow reactors, burner stabilized flame, and freely propagating flames. The results indicate that the new mechanism shows an obvious improvement in predicting the flame propagation speed of methanol.

Burke et al. (2016) summarized the previous studies on the mechanism of methanol oxidation and, based on new experimental data, presented the detailed kinetic model of methanol oxidation Mech15.34, and verified the new mechanism by the experimental results and previous data. Its verification methods include a shock tube, rapid compression machine, and jet-stirred reactor under a pressure range of 1–50 atm, a temperature range of 800–1650 K, and an equivalence ratio range of 0.2–2.0. In addition, the simulation of the laminar premixed flame speed was also verified by previous experimental data (Vancoillie et al., 2012). This mechanism is a detailed and well-validated mechanism of methanol oxidation, but it contains 173 components and 1,011 elementary reactions, and is not suitable for the three-dimensional simulation of combustion in internal combustion engines under the current computational conditions. Aramcomech 3.0 (Zhou et al., 2018) is a detailed mechanism for the oxidation of hydrocarbon fuels, based on 1,3-butadiene, including CH₃OH. It was verified by a shock tube, RCM, and laminar flame speed. It contains 581 components and 3,037 elementary reactions, so it needs to be simplified for the application in the methanol–syngas engine. Zhang and Zhang (2019) constructed the methanol-based toluene reference fuel mechanism, which has a high accuracy in the temperature range of 300–2500 K, and an equivalence ratio range of 0.375–2.0, and contains the submechanisms of methanol. Pichler and Nilsson (2020) analyzed the oxidation pathway of small alcohol in the internal combustion engine, and proposed a simplified mechanism of methanol, ethanol, and n-propanol. The mechanism is based on the equivalence ratio range of 0.7–1.4, pressure range of 1–40 atm, temperature range of 700–1700 K, and their errors are within 5% for the ignition delay times, laminar burning velocity, and extinction strain rate (Pichler and Nilsson, 2018).

In summary, the current research on the combustion kinetic modeling of the methanol–syngas mixture mainly focuses on syngas and methanol. There is no specific study on the dissociated methanol gas and methanol-dissociated methanol gas, and there is also a lack of experimental data on the mixture of methanol and dissociated methanol gas. In addition, the most recent comprehensive methanol mechanism that covers the interactions among CH₃OH, CO, H₂, and their intermediate species was proposed by Burke et al. (2016), and contains 173 species and 1,011 elementary reactions. It is too large for a three-dimensional simulation of the combustion in internal combustion engines under the current computational conditions. In this study, the combustion characteristics of dissociated methanol gas and methanol blended with the dissociated methanol gas are analyzed, and a kinetic model, MEOHSYNGAS1.0, for the methanol–syngas fuel is proposed, and verified experimentally.

Methodology

Shock Tube Experiments

The shock tube used in this research was validated using various studies and the results were similar to those of other research institutions. Part of the research on fuel ignition delay times has been published (Liu et al., 2019). The shock tube used in this study was 12 m in total, of which the high-pressure section was 4 m, the low-pressure section was 5 m, and the inner diameter was 100 mm. The driving section and the driven section were separated by a polyethylene terephthalate (PET) diaphragm. Considering the reliability and repeatability, the PET diaphragm was burst by a built-in spring needle to produce a shock wave, which is shown in Figure 2.

FIGURE 2

FIGURE 2. Polyethylene terephthalate (PET) diaphragm is burst by a built-in spring needle to produce a shock wave.

The mixing tank was first degassed and purged with Ar, followed by degassing again to remove the residual gas. The pressure in a 300 L mixing tank was first reduced below 3,000 Pa using a TRIVAC D40T vacuum pump and then below 1 Pa using a Ruwauvac 501 pump. The fuel, oxidant, and dilute gas were added. Finally, the mixture was left for more than 12 h to ensure complete mixing. For the methanol, it was necessary to first vacuum the tank and then inject the methanol so it vaporizes. Following this, the other gases were added. The fuels and gases used in the experiment, including CH₃OH, H₂, CO, O₂, Ar, He, N₂, had a purity of ≥99.9%. The compositions of the mixtures used in the experiment are given in Table 1. The dissociated ratio is used to define the composition of the methanol–syngas blended fuel, which is the percentage of methanol dissociated to H₂ and CO in the blended fuel. The dissociated methanol gas had a mole fraction of 67% H₂ and 33% CO. To determine the interaction between the methanol and syngas, the experimental pressure was set at 1.6 atm.

TABLE 1

TABLE 1. Mixture composition for the shock tube experiments.

Five PCB 111A24 piezoelectric pressure transducers were uniformly distributed near the end wall of the driven segment, between which the distance was 20 cm. The nearest pressure transducer was 0.2 cm from the end wall to obtain a shock velocity. A Kistler 603B1 piezoelectric pressure transducer was also used to measure the pressure, which was 0.2 cm from the end wall. Finally, the temperature was calculated by the program Gaseq (Moley, 2003). The experimental bench was equipped with a band-pass filter with a wavelength of 307 ± 10 nm, which was connected to the photomultiplier through a QP600-2-SR fiber with a length of 2 m and a diameter of 0.6 mm. All optical and pressure signals were converted into digital signals with an amplifier and exported. The ignition delay time was identified based on the pressure.

Numerical Model

A homogeneous 0-D reactor model was used to simulate the chemical reactions in the shock tube for the combustion study. The equations used to calculate the ignition delay time include the mass conservation equations, gas-phase species equations, gas energy equations, and gas equation of state. The simulation was conducted with the software ANSYS Chemkin.

The chemical rate of the fuel oxidation was calculated based on the Arrhenius equation. The rate constants of each elementary reaction are expressed as

$k=\mathit{A}{\mathit{T}}^b\exp \left(\frac{-E}{\mathit{RT}}\right),(2)$

where $k$ is the reaction rate constant, A is the pre-exponential factor, T is the temperature, b is the temperature exponent, E is the activation energy, and R is the gas constant.

Since the MEOHSYNGAS1.0 model needs to reflect the oxidation processes of CH₃OH, H₂, and CO, as well as the interactions among them and the intermediates, a comprehensive mechanism incorporating all these elementary reactions was selected at the beginning. Based on the Mech15.34 model proposed by Burke et al. (2016), mechanism reduction methods of directed relation graph with error propagation (Pepiot-Desjardins and Pitsch, 2008), and a full species sensitivity analysis (Turányi, 1997) were applied. The initial working condition range covers a pressure of 1–50 atm, a temperature of 800–1650 K, an equivalence ratio (φ) of 0.5–2.0, and a dissociated methanol ratio of 0–50%. As a result, the MEOHSYNGAS1.0 mechanism is able to predict the interaction among CH₃OH, H₂, CO, and the intermediates.

Sensitivity Analysis

Sensitivity analysis was performed to investigate the level of significance of a certain elementary reaction to the chemical reaction. The influence of the elementary reaction on the ignition delay time was evaluated by the sensitivity coefficient

$S_i=\frac{{\tau }_{2\mathit{ki}}-{\tau }_{\left(\mathrm{1}/2\right)\mathit{ki}}}{{\tau }_{\mathit{ki}}},(3)$

where $S_i$ is the sensitivity coefficient, ${\tau }_{2\mathrm{ki}}$ is the ignition time when the rate constant of the certain elementary reaction increases by two folds, ${\tau }_{\left(1/2\right)\mathrm{ki}}$ is the ignition time when the rate constant of the certain elementary reaction decreases by half, and ${\tau }_{\mathrm{ki}}$ is the original ignition delay time of the certain elementary reaction.

The normalized sensitivity coefficient was obtained by

$S_{i,\mathit{normalized}}=\frac{S_i}{S_{i,\mathit{max}}},(4)$

where $S_{i,\mathrm{normalized}}$ is the normalized sensitivity coefficient, $S_i$ is the sensitivity coefficient, and $S_{i,\max }$ is the maximum sensitivity coefficient among all elementary reactions in a specific condition. A positive sensitivity coefficient means that the elementary reaction inhibits the reactivity, while a negative sensitivity coefficient means that the elementary reaction promotes the reactivity.

Fuel Reaction Path Analysis

Figure 3 shows the reaction pathways of the methanol fuel. The initial reaction conditions were a temperature of 1200 K, a pressure of 1.6 atm, and an equivalence ratio of 1.0. The analyses were performed at the time when 20% of the methanol had been consumed. The percentage indicates the amount of a species consumed in the reaction, as a proportion of the total consumption of the substance at this time.

FIGURE 3

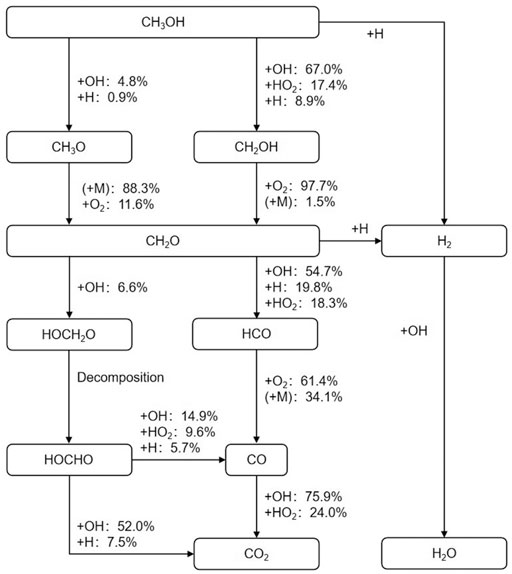
FIGURE 3. Reaction pathways for methanol at T = 1200 K, p = 1.6 atm, φ = 1.0, and 20% fuel consumption.

Methanol first undergoes a dehydrogenation reaction, mainly by the reaction between methyl and radicals such as OH, HO₂, and H to form CH₂OH. Moreover, a small amount of the reaction consists of the removal of hydrogen on the hydroxyl through OH, H to produce CH₃O. Meanwhile, H₂ is produced by the dehydrogenation reaction of methanol. CH₂OH mainly reacts with O₂ and also collides with a third body M to form CH₂O, while CH₃O mainly collides with the M, and also reacts with O₂ to form CH₂O. CH₂O is an important intermediate product in the process of methanol oxidation. It may become a pollutant in the combustion process of an internal combustion engine and be finally released into the atmosphere.

The main oxidation path of CH₂O is to produce HCO by reacting with OH, H, HO₂, and other radicals. HCO then reacts with O₂ or collides with the M to generate CO. H₂ is also produced in the CH₂O dehydrogenation reaction. The other reaction path of CH₂O is to react with OH to form HOCH₂O, which subsequently decomposes into HOCHO. HOCHO mainly reacts with OH or H to form CO₂ and partially reacts with OH, HO₂, and H to form CO.

The main way that CO is oxidized to CO₂ is by reacting with OH and HO₂, though the amount of CO is very small at this time, because when the methanol consumption ratio is 20%, a large number of hydrocarbons are still in the process of producing and consuming CH₂O.

At this stage, a small amount of H₂O is generated, which mainly originates from the reaction of OH with CH₃OH and CH₂O, respectively. In addition, CH₃OH and CH₂O react with H to form H₂. The oxidation of H₂ was the main source of water in the later stage of the reaction.

Figure 4 shows the variation of the mole fraction of different species with time at 1200 K, 1.6 atm, a 30% dissociated ratio (Mixture 2), and an equivalence ratio of 1.0. The reaction time signifies the reaction process. At the initial stage, before the peak of the hydrogen fraction, the main reaction is dehydrogenation, and so the fraction of methanol gradually decreases with time. The oxidation of hydrocarbon fuels follows the path of CH₃OH-CH₂O-CO. Before 2 ms, CH₂O consumption was less than CH₂O production, so CH₂O increased. CO was mainly produced by the reaction between HCO and O₂ and the collision between HCO and M. The oxidation of CO to CO₂ was not carried out on a large scale, so the increase rate of CO₂ was slow. At this stage, both CH₃OH and CH₂O undergo dehydrogenation. They react with H to form H₂, and with OH to form H₂O. At this stage, the production of H₂ is more than the consumption of H₂, and so H₂ increases. The main sources of H₂O are the reaction of OH with H₂, CH₃OH, and CH₂O respectively.

FIGURE 4

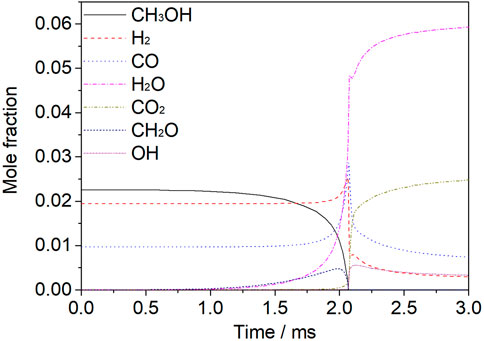
FIGURE 4. Mole fraction analysis of species for a mixture of 30% dissociated methanol (Mixture 2) at T = 1200 K, p = 1.6 atm, φ = 1.0, and Ar = 0.9.

Figure 5 shows the rate of production of H₂ and CO for a mixture of 30% dissociated methanol (Mixture 2) at T = 1200 K, p = 1.6 atm, φ = 1.0, and Ar = 0.9. When the reaction reaches a certain point, after the peak of H₂, the temperature rises, the radical OH is accumulated, and the chain branching reaction increases the oxidation rate rapidly. The reaction rate is further increased by the increasing temperature and the chain branching reaction; therefore, hydrogen is consumed rapidly. Before H₂ peaks, CO increases because of the continuous formation, and when the production of CH₃OH and CH₂O is almost complete, CO begins to be consumed rapidly, mainly by the reaction between CO and OH.

FIGURE 5

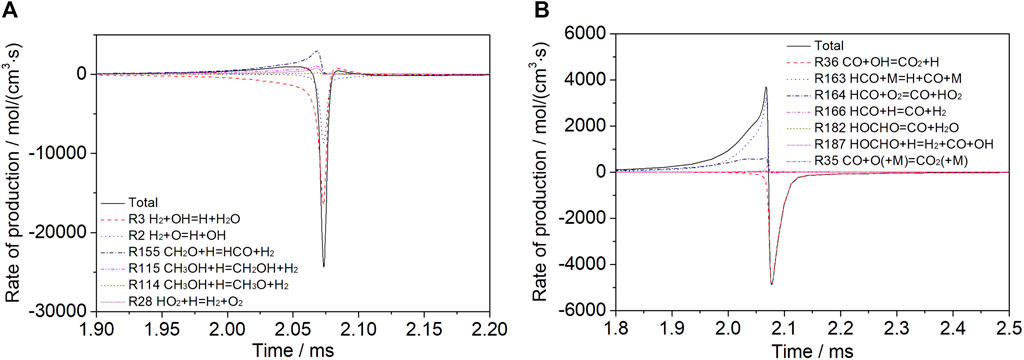
FIGURE 5. Rate of production analysis for a mixture of 30% dissociated methanol (Mixture 2) at T = 1200 K, p = 1.6 atm, φ = 1.0, and Ar = 0.9 for (A) H₂ and (B) CO.

Figure 6 shows the H₂O rate of production analysis for a mixture of 30% dissociated methanol (Mixture 2) at T = 1200 K, p = 1.6 atm, φ = 1.0, and Ar = 0.9. In the early stage of the reaction, the main sources of water production are the dehydrogenation of CH₃OH, the dehydrogenation of CH₂O, and the reaction between H₂ and OH. In the later stage, the main source of water is the reaction of H₂ with OH.

FIGURE 6

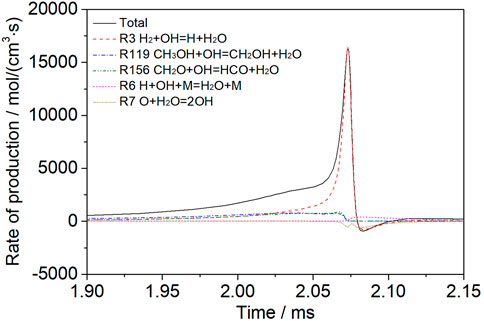
FIGURE 6. Analysis of the H₂O rate of production for a mixture of 30% dissociated methanol (Mixture 2) at T = 1200 K, p = 1.6 atm, φ = 1.0, and Ar = 0.9.

According to the oxidation process of methanol, hydrogen, carbon monoxide, and other main intermediate species, the important elementary reactions can be determined. A reduced mechanism consisting of 28 species and 146 elementary reactions was constructed and named MEOHSYNGAS1.0.

Results and Discussion

This section analyzes the effect of equivalence ratios, pressures, and dissociated ratios on the ignition delay time of the methanol–syngas fuel under different conditions. The simulation was conducted based on the mechanism of MEOHSYNGAS1.0 and the results are compared with experiments. The experimental results refer to the data from both this study and the literature.

Effect of the Equivalence Ratio

The effects of different equivalence ratios on the ignition delay times of methanol and dissociated methanol gas are investigated. According to Figure 7, the equivalence ratio does not have a significant effect on the activation energy. The symbols represent the experimental data from Burke et al. (2016). The experimental results show that the increase in the equivalence ratio reduces the ignition delay time of methanol at 0.5–1.0 equivalence ratio, 950–1450 K, 20 atm, and N₂ = 0.8. The simulation results also show this trend and fit well with the experimental data.

FIGURE 7

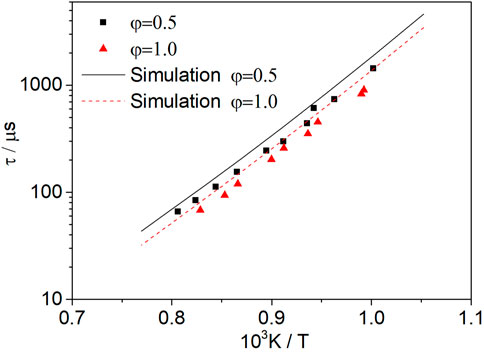
FIGURE 7. Influence of the equivalence ratio on mixtures of methanol at 20 atm. The symbols represent the experimental data from Burke et al. (2016).

The concentration of methanol is higher with the increase in the equivalence ratio. There is a higher probability of collisions among the molecules and radicals, and the heat release is faster, which further promotes the reaction of methanol with oxygen molecules and radicals, and the shortening of the ignition delay time.

Figure 8 shows the ignition delay times measured at φ = 1.0 (Mixture 4) and φ = 0.6 (Mixture 5) for dissociated methanol gas (67% H₂/33% CO). When the pressure is 1.6 atm, the equivalence ratio range is 0.6–1.0 and the temperature range is 950–1450 K, and the equivalence ratio has little effect on the activation energy in this range. However, when the temperature is below 950 K, there is a significant change in the slope, since the dominant reaction in the H₂-O₂ system is not the same at high and low temperatures (Kéromnès et al., 2013).

FIGURE 8

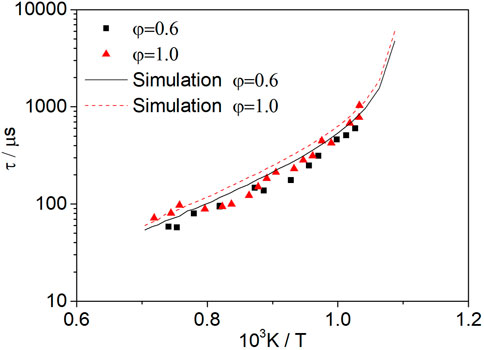
FIGURE 8. Ignition delay times measured at φ = 1.0 (Mixture 4) and φ = 0.6 (Mixture 5) for dissociated methanol gas (67% H₂/33% CO) at 1.6 atm.

The measured ignition delay time is slightly shorter than the simulation, which is consistent with the phenomenon that an increase in the equivalence ratio can increase the ignition delay time, as shown by the simulation. For dissociated methanol gas, the ignition delay time increases with the increase in the equivalence ratio in the certain temperature and pressure range, which is significantly different from methanol fuel (Figure 7). The reason for this phenomenon is explained through a sensitivity analysis of the ignition delay time.

Figure 9 shows the normalized sensitivity coefficients of each elementary reaction in the oxidation process of dissociated methanol gas fuel at p = 1.6 atm, φ = 1.0, Ar = 0.9, and a temperature of 950, 1050, and 1300 K, respectively. The pressure, equivalence ratio, and fuel are the same as those for Mixture 4. At 950 K, only the elementary reaction R5 O₂+H=O + OH has a significant effect on the ignition delay time, whereas the other elementary reactions have a negligible effect. When the temperature reaches 1050 K, the elementary reaction R2 H₂+O=H + OH and R3 H₂+OH = H + H₂O also begins to have an influence. When the temperature rises to 1300 K, the elementary reaction R5 O₂+H=O + OH is still dominant, though other elementary reactions, such as R2 H₂+O=H + OH, R6 H + OH + M = H₂O + M, R8 O + H + M = OH + M, and R24 CO + OH = CO₂+H, begin to play important roles. The reaction rate of R5 O₂+H=O + OH, R2 H₂+O=H + OH, and R3 H₂+OH = H + H₂O will increase with the increase in the temperature; thus, the ignition process will be accelerated, and the ignition delay time will be shortened. The change in the sensitivity coefficient of the elementary reaction shows that the increase in the temperature not only accelerates the reaction rate, but also changes the relative importance of the elementary reaction in the ignition process and alters the reaction path of the fuel.

FIGURE 9

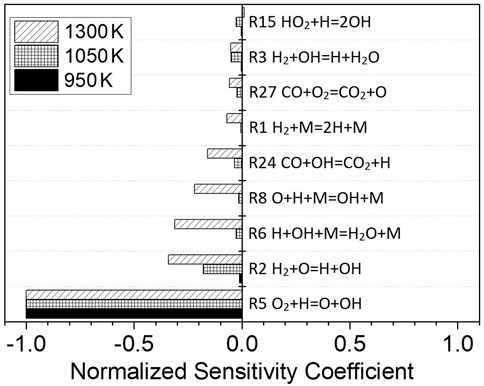
FIGURE 9. Sensitivity analysis for dissociated methanol gas (67% H₂/33% CO) at different temperatures; p = 1.6 atm, φ = 1.0, and Ar = 0.9.

From 950 to 1300 K, the reaction that promotes oxidation the most and shortens the ignition delay time is R5 O₂+H=O + OH. When the equivalence ratio of dissociated methanol gas increases, the oxygen concentration will decrease; hence, the reaction rate of R5 O₂+H=O + OH will also decrease, and, as a result, the ignition delay time will increase.

Figure 10 shows the normalized sensitivity coefficients of the elementary reactions in the ignition process of methanol at p = 1.6 atm, φ = 1.0, Ar = 0.9, and temperatures of 1050, 1300, and 1500 K, respectively. The pressure, equivalence ratio, and fuel are the same as Mixture 1. The most important elementary reaction in the ignition process changes with the increase in temperature. At 1050 and 1300 K, the elementary reaction R85 CH₃OH + HO₂ = CH₂OH + H₂O₂ is the most sensitive elementary reaction. At 1500 K, the reaction R5 O₂+H=O + OH becomes the most significant, and though the reaction R85 CH₃OH + HO₂ = CH₂OH + H₂O₂ still occupies an important position.

FIGURE 10

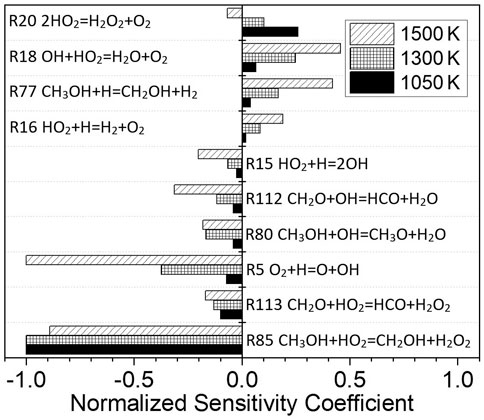
FIGURE 10. Sensitivity analysis for methanol fuel at different temperatures; p = 1.6 atm, φ = 1.0, and Ar = 0.9.

From 1050 to 1500 K, R85 CH₃OH + HO₂ = CH₂OH + H₂O₂ plays a dominant role in the ignition process. Therefore, the decrease in the methanol equivalence ratio will decrease the CH₃OH concentration. Consequently, this will decrease the reaction rate of R85 CH₃OH + HO₂ = CH₂OH + H₂O₂ and ultimately increase the ignition delay time. Thus, the fuel equivalence ratio has different effects on methanol and dissociated methanol gas.

Effect of the Pressure

Figure 11 shows the change in the methanol ignition delay time with temperature at φ = 1.0, Ar = 0.92, and pressures of 2.2 and 10.5 atm. The symbols represent the experimental data from Noorani et al. (2010). When the pressure is increased from 2.2 to 10.5 atm, the ignition delay time is shortened because the increase in pressure leads to higher concentrations of molecules and radicals; thus, the reaction rate is increased, resulting in a shorter ignition delay time. The experimental results show that increasing the pressure can shorten the ignition delay time.

FIGURE 11

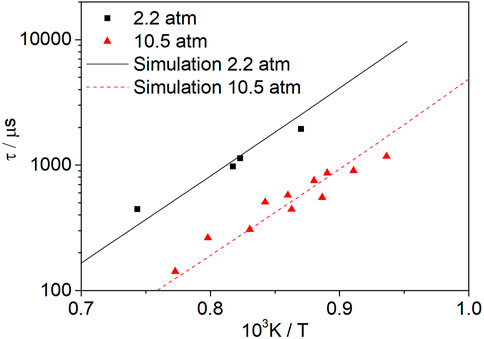
FIGURE 11. Influence of pressure on mixtures of methanol at an equivalence ratio of 1.0. The symbols represent the experimental data from Noorani et al. (2010).

Figure 12 shows the change of the syngas ignition delay time with temperature at φ = 0.5, Ar = 0.93, and pressures of 1.0 atm, 4.0 atm, and 16.0 atm. The symbols represent the experimental data from Kéromnès et al. (2013). The variation of the ignition delay time with temperature at different pressures is predicted well with the present model. The ignition delay time is shortened with the increase in pressure at high temperature, whereas this is not the case at low temperature.

FIGURE 12

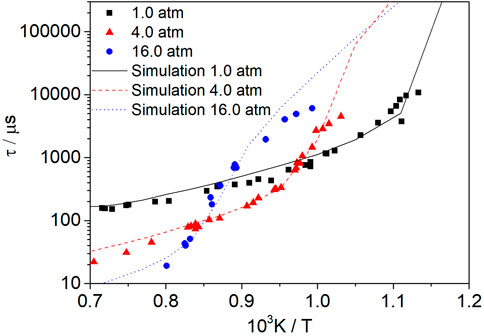
FIGURE 12. Influence of pressure on mixtures of syngas (50% H₂/50% CO) at an equivalence ratio of 1.0. The symbols represent the experimental data from Kéromnès et al. (2013).

According to literature (Konnov, 2008; Hong et al., 2011), at low pressures, oxidation is mainly controlled by the competition between R22H + O₂ (+M) = HO₂(+M) and R5 O₂+H=O + OH. At high pressures, the reaction is mainly controlled by R9 H₂O₂(+M) = 2OH(+M), and R11 H₂O₂+H=H₂+HO₂. As the activation energy at high pressure differs from that at low pressure, the shapes of the three curves are different. In the high-temperature range, the dominant chain-branching reaction R5 O₂+H=O + OH is not a pressure-dependent reaction. Thus, a pressure increase can increase the concentrations of radicals and decrease the ignition delay time. In the low-temperature range, it is the pressure-dependent reaction R22H + O₂ (+M) = HO₂(+M) instead of R5 O₂+H=O + OH that plays an important role in the reactivity. Hence, the influence of the temperature and pressure is complicated in the low-temperature range.

Effect of the Dissociated Ratio

Figure 13 shows the effect of the dissociated methanol ratio on the ignition delay time of methanol–syngas fuel at p = 1.6 atm, φ = 1.0, Ar = 0.9, and dissociated methanol ratios of 0% (Mixture 1), 30% (Mixture 2), and 50% (Mixture 3). With the increase in the dissociated ratio, the ignition delay time of the mixture fuel increases, and this effect is more obvious at the low-temperature range; however, with the increase in the temperature, this effect is weakened. Regarding the experimental data, the ignition delay time can even be shortened if the dissociated methanol gas is mixed at a high-temperature range. This can be explained by sensitivity analysis.

FIGURE 13

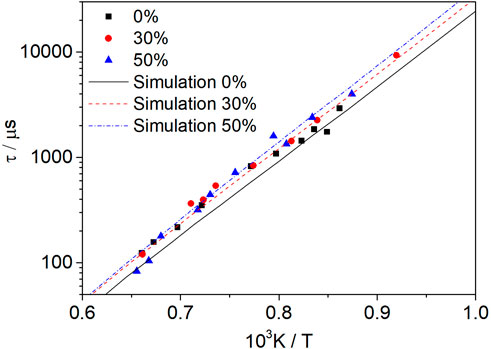
FIGURE 13. Influence of the dissociated methanol ratio (0, 30, and 50%) on methanol–syngas mixtures at an equivalence ratio of 1.0 and a pressure of 1.6 atm.

According to the sensitivity analysis in Figure 14, similar to pure methanol, the most important reaction for the mixture fuel at 1050 and 1300 K is R85 CH₃OH + HO₂ = CH₂OH + H₂O₂, and at 1500 K it is R5 O₂+H=O + OH. However, due to the presence of H₂ in the mixture, H₂-related elementary reactions, such as R3 H₂+OH = H + H₂O and R77 CH₃OH + H=CH₂OH + H₂, begin to play a more important role in the oxidation process. The influence of CO is relatively small, mainly including the elementary reaction R119 HCO + M = H + CO + M.

FIGURE 14

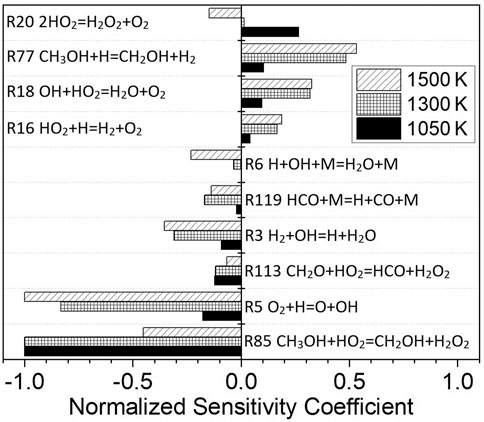
FIGURE 14. Sensitivity analysis for different temperatures at a dissociated methanol ratio of 30%, p = 1.6 atm, and φ = 1.0.

The reaction with the greatest influence on the ignition delay time at low temperature is R85 CH₃OH + HO₂ = CH₂OH + H₂O₂. The concentration of CH₃OH will be decreased by mixing with dissociated methanol gas, so the reaction rate will decrease, and the ignition delay time will be prolonged. With the increase in the temperature, the importance of the R5 O₂ + H=O + OH reaction increases, and so the effect of increasing the ignition delay time is not so obvious. In addition, the sensitivity coefficient of the reaction R77 CH₃OH + H=CH₂OH + H₂ becomes higher, and this reaction increases the ignition delay time. The addition of hydrogen inhibits the R77 CH₃OH + H=CH₂OH + H₂ reaction and, therefore, shortens the ignition delay time. This is the reason why the influence of blending-dissociated methanol gas is different at high and low temperatures.

Conclusion

Using the exhaust heat of the internal combustion engine to dissociate methanol to produce dissociated methanol gas, and sending it into the cylinder to be blended with methanol for combustion is a promising energy utilization method. This research investigated the combustion characteristics and kinetic model of the methanol–syngas fuel and the main conclusions are as follows.

1) The ignition delay time of dissociated methanol gas with a H₂ to CO ratio of 2:1 at equivalence ratios of 0.6 and 1.0 was measured with a shock tube. The ignition delay time of the methanol–syngas fuel with a dissociated ratio of 0, 30, and 50% was measured.

2) By analyzing the oxidation path of the fuel and the concentration change of species, the mechanism MEOHSYNGAS1.0 for the methanol–syngas fuel is proposed based on the reduction of the detailed chemical kinetic model (Mech15.34). Its working condition range covers a temperature of 800–1650 K, a pressure of 1–50 atm, an equivalence ratio of 0.5–2.0, and a dissociated ratio of 0–50%.

3) The effect of the equivalence ratio on the ignition delay time of methanol and the dissociated methanol gas was studied. Over a certain range, the ignition delay time of methanol is decreased with the increase in the equivalence ratio, while the ignition delay time of dissociated methanol gas is increased. This is due to the difference between the elementary reaction influencing the ignition delay time of methanol and the elementary reaction influencing the ignition delay time of dissociated methanol gas.

4) The ignition delay time of methanol decreases with the increase in the pressure, due to the collision frequency between reactants increasing with the increase in pressure. For the dissociated methanol gas the relationship between the ignition delay time and pressure is complex, because the elementary reaction that has the biggest influence on the ignition delay time is different at low pressure and high pressure.

5) Through simulations and experiments, the effect of blending syngas into methanol on the ignition delay time was studied when the dissociated ratio was not greater than 50%. The ignition delay time increases with the increase in the dissociated ratio, which is more obvious at the low temperature range, but the effect decreases with the increase in temperature.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

YC: conceptualization, investigation, writing—original draft; YJ: funding acquisition, writing—review and editing; XW: investigation; HL: supervision, writing—review and editing.

Funding

This work was supported by the Department of Science and Technology of Hubei Province, China (Grant numbers 2016AAA045 and 2020BAB127).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.812522/full#supplementary-material

References

Borisut, P., and Nuchitprasittichai, A. (2019). Methanol Production via CO2 Hydrogenation: Sensitivity Analysis and Simulation-Based Optimization. Front. Energ. Res. 7, 1–10. doi:10.3389/fenrg.2019.00081

CrossRef Full Text | Google Scholar

Burke, U., Metcalfe, W. K., Burke, S. M., Heufer, K. A., Dagaut, P., and Curran, H. J. (2016). A Detailed Chemical Kinetic Modeling, Ignition Delay Time and Jet-Stirred Reactor Study of Methanol Oxidation. Combustion and Flame 165, 125–136. doi:10.1016/j.combustflame.2015.11.004

CrossRef Full Text | Google Scholar

Christensen, M., Nilsson, E. J. K., and Konnov, A. A. (2016). A Systematically Updated Detailed Kinetic Model for CH2O and CH3OH Combustion. Energy Fuels 30, 6709–6726. doi:10.1021/acs.energyfuels.6b00049

CrossRef Full Text | Google Scholar

Gong, C., Li, Z., Chen, Y., Liu, J., Liu, F., and Han, Y. (2019). Influence of Ignition Timing on Combustion and Emissions of a Spark-Ignition Methanol Engine with Added Hydrogen under Lean-Burn Conditions. Fuel 235, 227–238. doi:10.1016/j.fuel.2018.07.097

CrossRef Full Text | Google Scholar

Held, T. J., and Dryer, F. L. (1998). A Comprehensive Mechanism for Methanol Oxidation. Int. J. Chem. Kinet. 30, 805–830. doi:10.1002/(sici)1097-4601(1998)30:11<805:aid-kin4>3.0.co;2-z

CrossRef Full Text | Google Scholar

Hong, Z., Davidson, D. F., and Hanson, R. K. (2011). An Improved H2/O2 Mechanism Based on Recent Shock Tube/laser Absorption Measurements. Combustion and Flame 158, 633–644. doi:10.1016/j.combustflame.2010.10.002

CrossRef Full Text | Google Scholar

Jaimes, D., McDonell, V. G., and Samuelsen, G. S. (2018). Lean Flammability Limits of Syngas/Air Mixtures at Elevated Temperatures and Pressures. Energy Fuels 32, 10964–10973. doi:10.1021/acs.energyfuels.8b02031

CrossRef Full Text | Google Scholar

Jaspers, B. C., Kuo, P.-C., Amladi, A., van Neerbos, W., and Aravind, P. V. (2021). Negative CO2 Emissions for Transportation. Front. Energ. Res. 9, 1–5. doi:10.3389/fenrg.2021.626538

CrossRef Full Text | Google Scholar

Ji, C., Dai, X., Wang, S., Liang, C., Ju, B., and Liu, X. (2013). Experimental Study on Combustion and Emissions Performance of a Hybrid Syngas-Gasoline Engine. Int. J. Hydrogen Energ. 38, 11169–11173. doi:10.1016/j.ijhydene.2013.02.101

CrossRef Full Text | Google Scholar

Jiang, Y., Mei, Z., and Wang, R. (2019). Study on Combustion Characteristics of Gasoline Engine Blending with Dissociated Methanol. Huazhong Keji Daxue Xuebao (Ziran Kexue Ban)/journal Huazhong Univ. Sci. Technol. (Natural Sci. Ed.) 47, 1–6. doi:10.13245/j.hust.190901

CrossRef Full Text | Google Scholar

Kalitan, D. M., Mertens, J. D., Crofton, M. W., and Petersen, E. L. (2007). Ignition and Oxidation of Lean CO/H2 Fuel Blends in Air. J. Propulsion Power 23, 1291–1301. doi:10.2514/1.28123

CrossRef Full Text | Google Scholar

Kéromnès, A., Metcalfe, W. K., Heufer, K. A., Donohoe, N., Das, A. K., Sung, C.-J., et al. (2013). An Experimental and Detailed Chemical Kinetic Modeling Study of Hydrogen and Syngas Mixture Oxidation at Elevated Pressures. Combustion and Flame 160, 995–1011. doi:10.1016/j.combustflame.2013.01.001

CrossRef Full Text | Google Scholar

Konnov, A. A. (2009). Implementation of the NCN Pathway of Prompt-NO Formation in the Detailed Reaction Mechanism. Combustion and Flame 156, 2093–2105. doi:10.1016/j.combustflame.2009.03.016

CrossRef Full Text | Google Scholar

Konnov, A. A. (2008). Remaining Uncertainties in the Kinetic Mechanism of Hydrogen Combustion. Combustion and Flame 152, 507–528. doi:10.1016/j.combustflame.2007.10.024

CrossRef Full Text | Google Scholar

Li, J., Zhao, Z., Kazakov, A., Chaos, M., Dryer, F. L., and Scire, J. J. (2007). A Comprehensive Kinetic Mechanism for CO, CH2O, and CH3OH Combustion. Int. J. Chem. Kinet. 39, 109–136. doi:10.1002/kin.20218

CrossRef Full Text | Google Scholar

Li, R., Wang, Z., Tang, C., and Meng, X. (2021). Study on Particulate Structure Characteristics of Diesel Engines Fueled with a Methanol/Biodiesel Blend. ACS Omega 6, 6081–6087. doi:10.1021/acsomega.0c04371

PubMed Abstract | CrossRef Full Text | Google Scholar

Liao, S.-Y., Li, H.-M., Mi, L., Shi, X.-H., Wang, G., Cheng, Q., et al. (2011). Development and Validation of a Reduced Chemical Kinetic Model for Methanol Oxidation. Energy Fuels 25, 60–71. doi:10.1021/ef101335q

CrossRef Full Text | Google Scholar

Liu, J., and Dumitrescu, C. E. (2019). Numerical Investigation of Methane Number and Wobbe Index Effects in Lean-Burn Natural Gas Spark-Ignition Combustion. Energy Fuels 33, 4564–4574. doi:10.1021/acs.energyfuels.8b04463

CrossRef Full Text | Google Scholar

Liu, Y., Cheng, J., Zou, C., Lu, L., and Jing, H. (2019). Ignition Delay Times of Ethane under O2/CO2 Atmosphere at Different Pressures by Shock Tube and Simulation Methods. Combustion and Flame 204, 380–390. doi:10.1016/j.combustflame.2019.03.031

CrossRef Full Text | Google Scholar

Mansfield, A. B., and Wooldridge, M. S. (2014). High-pressure Low-Temperature Ignition Behavior of Syngas Mixtures. Combustion and Flame 161, 2242–2251. doi:10.1016/j.combustflame.2014.03.001

CrossRef Full Text | Google Scholar

Moley, C. (2003). GASEQ A Chemical Equilibrium Program for Windows. Version 0.79 12, 1–2. Available at: http://www.gaseq.co.uk/.

Google Scholar

Nguyen, D.-K., and Verhelst, S. (2017). Computational Study of the Laminar Reaction Front Properties of Diluted Methanol-Air Flames Enriched by the Fuel Reforming Product. Energy Fuels 31, 9991–10002. doi:10.1021/acs.energyfuels.7b00691

CrossRef Full Text | Google Scholar

Noorani, K. E., Akih-Kumgeh, B., and Bergthorson, J. M. (2010). Comparative High Temperature Shock Tube Ignition of C1−C4 Primary Alcohols. Energy Fuels 24, 5834–5843. doi:10.1021/ef1009692

CrossRef Full Text | Google Scholar

Pepiotdesjardins, P., and Pitsch, H. (2008). An Efficient Error-Propagation-Based Reduction Method for Large Chemical Kinetic Mechanisms. Combustion and Flame 154, 67–81. doi:10.1016/j.combustflame.2007.10.020

CrossRef Full Text | Google Scholar

Pichler, C., and Nilsson, E. J. K. (2020). Pathway Analysis of Skeletal Kinetic Mechanisms for Small Alcohol Fuels at Engine Conditions. Fuel 275, 117956. doi:10.1016/j.fuel.2020.117956

CrossRef Full Text | Google Scholar

Pichler, C., and Nilsson, E. J. K. (2018). Reduced Kinetic Mechanism for Methanol Combustion in Spark-Ignition Engines. Energy Fuels 32, 12805–12813. doi:10.1021/acs.energyfuels.8b02136

CrossRef Full Text | Google Scholar

Pinzón, L. T., Mathieu, O., Mulvihill, C. R., Schoegl, I., and Petersen, E. L. (2019). Ignition Delay Time and H2O Measurements during Methanol Oxidation behind Reflected Shock Waves. Combustion and Flame 203, 143–156. doi:10.1016/j.combustflame.2019.01.036

CrossRef Full Text | Google Scholar

Sun, H., Yang, S. I., Jomaas, G., and Law, C. K. (2007). High-pressure Laminar Flame Speeds and Kinetic Modeling of Carbon Monoxide/hydrogen Combustion. Proc. Combustion Inst. 31, 439–446. doi:10.1016/j.proci.2006.07.193

CrossRef Full Text | Google Scholar

Thi, L. D., Zhang, Y., and Huang, Z. (2014). Shock Tube Study on Ignition Delay of Multi-Component Syngas Mixtures - Effect of Equivalence Ratio. Int. J. Hydrogen Energ. 39, 6034–6043. doi:10.1016/j.ijhydene.2014.01.170

CrossRef Full Text | Google Scholar

Turányi, T. (1997). Applications of Sensitivity Analysis to Combustion Chemistry. Reliab. Eng. Syst. Saf. 57, 41–48. doi:10.1016/S0951-8320(97)00016-1

CrossRef Full Text | Google Scholar

Vancoillie, J., Christensen, M., Nilsson, E. J. K., Verhelst, S., and Konnov, A. A. (2012). Temperature Dependence of the Laminar Burning Velocity of Methanol Flames. Energy Fuels 26, 1557–1564. doi:10.1021/ef2016683

CrossRef Full Text | Google Scholar

Verhelst, S., Turner, J. W., Sileghem, L., and Vancoillie, J. (2019). Methanol as a Fuel for Internal Combustion Engines. Prog. Energ. Combustion Sci. 70, 43–88. doi:10.1016/j.pecs.2018.10.001

CrossRef Full Text | Google Scholar

Wen, X. (2018). Study on the Ignition Characteristics of Methanol Syngas. [dissertation/master's thesis]. Wuhan: Huazhong University of Science and Technology.

Google Scholar

Xie, M. (2016). Experimental Study on Mixed Combustion of Dissociated Methanol in SI Engine. [dissertation/master's thesis]. Wuhan: Huazhong University of Science and Technology.

Google Scholar

Yao, C., Li, X., Zang, R., and Xu, Y. (2014). Research on the Performance of an Electronically Controlled Spark Ignition Engine Fuelled with Hydrogen-Rich Gases. Proc. Inst. Mech. Eng. D: J. Automobile Eng. 228, 1084–1094. doi:10.1177/0954407014525360

CrossRef Full Text | Google Scholar

Zhang, B., Ji, C., Wang, S., and Liu, X. (2014). Combustion and Emissions Characteristics of a Spark-Ignition Engine Fueled with Hydrogen-Methanol Blends under Lean and Various Loads Conditions. Energy 74, 829–835. doi:10.1016/j.energy.2014.07.055

CrossRef Full Text | Google Scholar

Zhang, J., and Zhang, Y. (2019). Reduced Mechanism Generation for Methanol-Based Toluene Reference Fuel with Combined Reduction Methods. Fuel 247, 135–147. doi:10.1016/j.fuel.2019.03.028

CrossRef Full Text | Google Scholar

Zhao, T., Zhang, J., Ju, D., Huang, Z., and Han, D. (2019). Exergy Losses in Premixed Flames of Dimethyl Ether and Hydrogen Blends. Front. Energ. 13, 658–666. doi:10.1007/s11708-019-0645-8

CrossRef Full Text | Google Scholar

Zhou, C.-W., Li, Y., Burke, U., Banyon, C., Somers, K. P., Ding, S., et al. (2018). An Experimental and Chemical Kinetic Modeling Study of 1,3-butadiene Combustion: Ignition Delay Time and Laminar Flame Speed Measurements. Combustion and Flame 197, 423–438. doi:10.1016/j.combustflame.2018.08.006

CrossRef Full Text | Google Scholar