Optimal PID Tuning of PLL for PV Inverter Based on Aquila Optimizer

Phase-locked loop (PLL) is a fundamental and crucial component of a photovoltaic (PV) connected inverter, which plays a significant role in high-quality grid connection by fast and precise phase detection and lock. Several novel critical structure improvements and proportional-integral (PI) parameter optimization techniques of PLL were proposed to reduce shock current and promote the quality of grid connection at present. However, the present techniques ignored the differential element of PLL and did not acquire ideal results. Thus, this paper adopts Aquila optimizer algorithm to regulate the proportional-integral-differential (PID) parameters of PLL for smoothing power fluctuation and improving grid connection quality. Three regulation strategies (i.e., PLL regulation, global regulation, and step regulation) are carefully designed to systematically and comprehensively evaluate the performance of the proposed method based on a simulation model in MATLAB/Simulink, namely, “250-kW Grid-Connected PV Array”. Simulation results indicate that PLL regulation strategy can effectively decrease power fluctuation and overshoot with a short response time, low complexity, and time cost. Particularly, the Error(P) and the maximum deviation of output power under optimal parameters obtained by PLL strategy are decreased by 418 W and 12.5 kW compared with those under initial parameters, respectively.

Introduction

The rapid growth and development of the world economy and society are accompanied by the consumption and utilization of enormous non-renewable energy (Yang et al., 2018a; Zhang et al., 2021), especially fossil fuel, which leads to a great challenge for uninterrupted energy supply and environmental protection (Gan et al., 2019; Pabitra and Abhik, 2020). Solar energy, as a representative of renewable energy (Zhou et al., 2021), has attracted extensive attention in recent years (Yang et al., 2018b; Wang et al., 2020). Furthermore, photovoltaic (PV) generation is considered one of the most efficient, promising, and reliable exploitation and application methods of solar energy (Yang et al., 2019a; Yang et al., 2019b; Yang et al., 2020).

Photovoltaic grid-connected inverter is a critical bridge of connecting photovoltaic power and power grid systems, whose performance significantly determines power factor and shock current of the power grid (Liu et al., 2020). Therefore, phase lock technology is immensely applied to improve the performance of photovoltaic grid-connected inverters via fast and accurately extracting and tracking the phase angle information of grid voltage (Se-Kyo, 2000). Several structural improvement techniques of conventional PLL have been suggested in the past few years. Specifically, Rodriguez et al. (2007) designed a decoupled double synchronous reference frame phase-locked loop (PLL) to efficiently detect positive sequence voltage under unbalanced and distorted grid conditions. Note that the proposed method successfully separated utility voltage into positive and negative sequence components and eliminated voltage detection errors of conventional PLL. Besides, Guo et al. (2011) adopt a multiple-complex coefficient-filter to filter harmonic components of grid voltage and significantly enhance the dynamic response of PLL. Additionally, Kong et al. (2020) proposed a novel self-adjusting double second-order generalized integrator PLL (SOGI-PLL) strategy with the ideal low-pass filter, which acquired desirable performance in the PV grid with high harmonic content. Meanwhile, SOGI-PLL controller was reported to detect phase angle jumps and magnitude variations of voltage and current in the literature (Pazhanimuthu et al., 2021). Similarly, Han et al. (2009), Chittora et al. (2019),and Çelik and Meral (2019) developed adaptive PLL to implement synchronization of PV source, load balance, and harmonics reduction. In the literature (Musengimana et al., 2021), a low-frequency damping strategy was presented to mitigate low-frequency oscillations related to PLL, which improved the performance of PV-connected inverter and outer loop controller.

In addition, several researchers focused to identify the best control parameters of PLL to track phase angle with high accuracy and fast speed in various complex operation conditions. A mutated hybrid firefly algorithm was proposed to optimize the control parameters of second-order PLL in a microgrid system to improve the system stability in the literature (Satapathy et al., 2016). Ikken et al. (2016) proposed a fuzzy logic control methodology to adaptively justify proportional-integral (PI) parameters of PLL. Furthermore, several meta-heuristic algorithms are used to extract the optimal control PI parameters of PLL for improving the performance of three-phase grid-connected PV inverter, such as genetic algorithm (GA) (Farhat et al., 2020), moth flame optimization (MFO), antlions optimization algorithm (ALO), grey wolf optimization (GWO), and whales optimization algorithm (WOA) (Aouchiche, 2020).

However, the above structural improvements inevitably increased the cost and complexity of the whole system, while the present parameter optimization strategies only optimized the PI parameters of PLL and ignored the influences of the differential element of PLL on extracting phase angle and suppressing PV output power fluctuation. Therefore, this paper proposes a novel PLL regulation method based on Aquila optimizer (AO) algorithm for PV inverter to decrease PV output power fluctuation and improve system stability, which deals with a comprehensive optimal PID parameter identification of PLL.

The rest of the sections of this paper are organized as follows: Grid-Connected PV System indicates the modelling of the PV system under study, especially PV inverter and PLL; the main working principle of AO algorithm in optimal PID parameter identification of PLL is \ investigated in detail in Description of PID Parameter Optimization with AO Algorithm; Case Study provides a typical case study based on three regulation strategies to evaluate the performance of the proposed method; Conclusions and Perspectives summarizes two significant conclusions of this paper.

Grid-Connected PV System

A 250 kW PV system under this study is mainly composed of a power transformation system and a control system (Aouchiche, 2020). The former system includes seven components, i.e., PV array, boost converter, three-phase inverter, filter, transformer, grid, and load while the latter one is divided into maximum power point tracking (MPPT) control and inverter control (Li et al., 2020), shown in Figure 1. In addition, the perturbation observation (P and O) method is used to implement MPPT control while voltage regulator, current regulator as well as PLL controller accomplish precise and fast three-phase inverter control through coordinate and efficient cooperation.

FIGURE 1

FIGURE 1. The structure of the 250 kW PV system.

Modelling of PV Cell

PV cell works as a current source to convert solar energy into direct current through the photovoltaic effect (Mokhtar et al., 2020; Li et al., 2021), whose power generation characteristics can be explained as

$I_{\text{PV}}=I_{ph}-I_o\{e^{\left[\frac{q(V_{\text{PV}}+R_{\text{s}}\cdot I_{\text{PV}})}{N\cdot K\cdot T}\right]}-1\}-\frac{V+R_{\text{s}}\cdot I_{\text{PV}}}{R_{sh}}(1)$

$I_{\text{d}}=I_o{e}^{\left[\frac{q(V+R_S\cdot I_{\text{PV}})}{N\cdot K\cdot T}\right]}(2)$

where $V_{\text{PV}}$ and $I_{\text{PV}}$ are the output voltage and current of PV cell, respectively; $I_{ph}$ represents photo-generated current; $I_o$ stands for reverse saturation current; $I_{\text{d}}$ is defined as junction current of the diode; $q$ is electron charge ($1.6\times {10}^{-19}C$); $R_{\text{s}}$ and $R_{\text{sh}}$ is determined as the series resistance and parallel resistance, respectively; N denotes the diode characteristic coefficient (2.8 for T = 300 K); K represents Boltzmann constant ($1.38\times {10}^{-23 }J/K$); and T is the working temperature.

Modelling of Grid-Connected PV Inverter

The grid-connected PV inverter is applied to convert DC voltage from the DC/DC converter in Figure 1 into grid-connected alternating voltage, whose schematic configuration is illustrated as Figure 2, which is mainly consisted of a grid-connected inverter and power grid (Zhao et al., 2021).

FIGURE 2

FIGURE 2. Schematic diagram of a three-phase grid-connected PV inverter.

According to Figure 2, three-phase alternating voltage for PV inverter can be calculated by (Wang et al., 2020; Zhao et al., 2021):

$\{\begin{array}{c}{v}_{\mathrm{a}}=R_{\mathrm{a}}{i}_{\mathrm{a}}+L_{\mathrm{a}}\frac{\mathrm{d}{i}_{\mathrm{a}}}{\mathrm{d}t}+e_{\mathrm{a}}\\ v_{\mathrm{b}}=R_{\mathrm{b}}{i}_{\mathrm{b}}+L_{\mathrm{b}}\frac{\mathrm{d}{i}_{\mathrm{b}}}{\mathrm{d}t}+e_{\mathrm{b}}\\ v_{\mathrm{c}}=R_{\mathrm{c}}{i}_{\mathrm{c}}+L_{\mathrm{c}}\frac{\mathrm{d}{i}_{\mathrm{c}}}{\mathrm{d}t}+e_{\mathrm{c}}\end{array}(3)$

Besides, the stationary abc voltage and current can be transferred to synchronous rotating dq voltage and current through Park’s transformation as follows:

$\{\begin{array}{c}{v}_{\mathrm{d}}=e_{\mathrm{d}}+R{i}_{\mathrm{d}}+L\frac{\mathrm{d}{i}_{\mathrm{d}}}{\mathrm{d}t}+{\omega }_{\text{s}}L{i}_{\mathrm{q}}\\ v_{\mathrm{q}}=e_{\mathrm{q}}+R{i}_{\mathrm{q}}+L\frac{\mathrm{d}{i}_{\mathrm{q}}}{\mathrm{d}t}-{\omega }_{\text{s}}L{i}_{\mathrm{d}}\end{array}(4)$

where $v_{\text{d}}$, and $v_{\text{q}}$, $e_{\text{d}}$, $e_{\text{q}}$, $i_{\text{d}}$, $i_{\text{q}}$ stands for PV inverter voltage, grid voltage, as well as grid current under dq-axis, respectively; R and L are defined as the equivalent grid resistance and grid inductance, respectively; and ${\omega }_{\text{s}}$ denotes the angular speed of the grid. Moreover, PV inverter must follow the power balance principle during power transformation, which can be described as Equation (5) if ignoring power losses of switches.

$V_{\text{dc}}{I}_{\text{dc}}=e_{\text{d}}{i}_{\text{d}}+e_{\text{q}}{i}_{\text{q}}(5)$

where $V_{\text{dc}}$ and $I_{\text{dc}}$ denote the input voltage and current of the grid-connected inverter, respectively. Lastly, DC link dynamics are determined as

$C\frac{\mathrm{d}{V}_{\text{dc}}}{\mathrm{d}t}=I_{\mathrm{dc}0}-I_{\mathrm{dc}}=I_{\mathrm{dc}0}-\frac{e_{\mathrm{d}}{i}_{\mathrm{d}}+e_{\mathrm{q}}{i}_{\mathrm{q}}}{V_{\mathrm{dc}}}(6)$

where $I_{\text{dc}0}$ represents the output current of DC/DC convert; and $C$ means DC link capacitor.

Modelling of PLL

Particularly, PLL plays a significant role in reducing shock current and power fluctuation, ensuring high-quality grid connection, as well as improving grid stability by accurately detecting and adjusting the frequency and phase of connected voltage (Aouchiche, 2020; Zhu et al., 2020). Figure 3 demonstrates its basic structure mainly including a phase detector, a low pass filter, and a voltage-controlled oscillator (VCO).

FIGURE 3

FIGURE 3. The basic structure of three-phase PLL.

For the first step, three-phase grid voltage $V_{\text{a},\text{s}}$, $V_{\text{b},\text{s}}$, $V_{\text{c},\text{s}}$ are transferred into straight-axis voltage ($V_{\text{d},\text{s}}$) and cross-axis voltage ($V_{\text{q},\text{s}}$) through Clark transformation and Park transformation (Chen et al., 2019), as follows:

$\left[\begin{array}{c}{V}_{\mathrm{\alpha }}\\ V_{\mathrm{\beta }}\\ V_{\text{γ}}\end{array}\right]=\frac{2}{3}\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& -\frac{\sqrt{3}}{2}& \frac{\sqrt{3}}{2}\\ \frac{1}{2}& \frac{1}{2}& \frac{1}{2}\end{array}\right]\left[\begin{array}{c}{V}_{\mathrm{a},\text{s}}\\ V_{b,s}\\ V_{\mathrm{c},\mathrm{s}}\end{array}\right]$

$=\frac{2}{3}V\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& -\frac{\sqrt{3}}{2}& \frac{\sqrt{3}}{2}\\ \frac{1}{2}& \frac{1}{2}& \frac{1}{2}\end{array}\right]\left[\begin{array}{c}sin\left(w_{\mathrm{s}}t\right)\\ sin(w_{\mathrm{s}}t-\frac{2\pi }{3})\\ sin(w_{\mathrm{s}}t+\frac{2\pi }{3})\end{array}\right]=V\left[\begin{array}{c}sin\left(w_{\mathrm{s}}t\right)\\ -cos\left(w_{\mathrm{s}}t\right)\\ 0\end{array}\right] (7)$

$\left[\begin{array}{c}{V}_{\mathrm{d},\mathrm{s}}\\ V_{\mathrm{q},\mathrm{s}}\end{array}\right]=\left[\begin{array}{cc}\cos \left(w_{\mathrm{vco}}t\right)& \sin \left(w_{\mathrm{vco}}t\right)\\ -\sin \left(w_{\mathrm{vco}}t\right)& \cos \left(w_{\mathrm{vco}}t\right)\end{array}\right]\left[\begin{array}{c}{V}_{\mathrm{\alpha }}\\ V_{\mathrm{\beta }}\end{array}\right]=V\left[\begin{array}{c}cos(w_{\mathrm{s}}t+w_{\mathrm{vco}}t)\\ sin(w_{\mathrm{s}}t-w_{\mathrm{vco}}t)\end{array}\right](8)$

where $w_{\text{s}}$ and $w_{\text{vco}}$ stand for the angular speed of grid and VCO. Note that if $w_{\text{s}}$ is equal to $w_{\text{vco}}$, $V_{\text{q},\text{s}}$ will become zero, which means the input of the PID controller is also zero and the PLL system keeps steady (i.e., a successful phase lock).

Besides, a conventional PID controller (ShenYao et al., 2019) can be mathematically described as

$w_{\mathrm{vco}}\left(t\right)=K_{\mathrm{p}}\cdot \overline{X}\left(t\right)+K_{\mathrm{i}}\cdot \underset{0}{\overset{t}{{\displaystyle \int }}}\overline{X}\left(\tau \right)d\tau +K_{\mathrm{d}}\cdot \frac{d\overline{X}\left(t\right)}{dt}(9)$

where $K_{\text{p}}$, $K_{\text{i}}$, $K_{\text{d}}$ represent the gains of proportional element, integral element, and differential element, respectively, which will be significantly optimized via the AO algorithm. In addition, Equation (9) should be discretized into Equation (10) in actual application, as follows:

$w_{\mathrm{vco}}\left(k\right)=K_{\mathrm{p}}\cdot \overline{X}\left(k\right)+K_{\mathrm{i}}\cdot {\displaystyle \sum }_{n=0}^k\overline{X}\left(n\right)+K_{\mathrm{d}}\cdot (\overline{X}\left(k\right)-\overline{X}(k-1))(10)$

Fitness Function

Aiming to smooth power fluctuation, the fitness function is determined as the error between ideal output power and actual power of the PV system, calculated by

$F\left(X_i\right)=\underset{0}{\overset{T_{\text{s}}}{{\displaystyle \int }}}\left|P_{\mathrm{act}}-P_{\mathrm{ideal}}\right|dt(11)$

where $F\left(X_i\right)$ stands for fitness value of the ith solution vector, $X_i$; $T_{\text{s}}$ denotes simulation time; and $P_{\mathrm{act}}$ and $P_{\mathrm{ideal}}$ represent the actual and ideal power of PV system, respectively.

Description of PID Parameter Optimization with AO Algorithm

Inspired by the prey behaviors of Aquila, Laith (Abualigah et al., 2021) proposed the AO algorithm in 2021, which effectively acquired wanted optimization results both in test functions and engineering problems. Note that the optimization procedures of the AO algorithm are mainly composed of population initialization, search space selection, short glide attack, slow descent attack, and grab prey.

Population Initialization

For this PID parameter optimization problem, current positions of N Aquilas form the candidate solution matrix which can be initialized as

$X=\left[\begin{array}{c}{x}_{\mathrm{1,1}}\\ x_{\mathrm{2,1}}\\ ⋮\\ x_{i,1}\\ ⋮\\ x_{(N-1),1}\\ x_{N,1}\end{array}\begin{array}{c}{x}_{\mathrm{1,2}}\\ x_{\mathrm{2,2}}\\ ⋮\\ x_{i,2}\\ ⋮\\ x_{(N-1),2}\\ x_{N,2}\end{array}\begin{array}{c}{x}_{\mathrm{1,3}}\\ x_{\mathrm{2,3}}\\ ⋮\\ x_{i,3}\\ ⋮\\ x_{(N-1),3}\\ x_{N,3}\end{array}\right](12)$

where the ith row of candidate solution matrix $X$ represents a current location (corresponding to a solution) of the ith Aquila, which can be presented as

$X_i=\left(U_{\mathrm{B}}-L_{\mathrm{B}}\right)\cdot rand+L_{\mathrm{B}}=\left[x_{i,1},x_{i,2},x_{i,3}\right]=\left[K_{\mathrm{p}},K_{\mathrm{i}},K_{\mathrm{d}}\right](13)$

where $K_{\text{p}},K_{\text{i}},K_{\text{d}}$ denotes control parameters corresponding to proportional element, integral element, and differential element of PLL, respectively; $U_B=[K_{p\max },K_{i\max },K_{d\max }]$ is defined as the upper bound vector of control parameters while $L_{\mathrm{B}}=[K_{p\min },K_{\mathrm{imin}},K_{d\min }]$ stands for the lower bound vector; and $rand$ is equal to a random number from 0 to 1.

Search Space Selection

Each initialized solution will be updated in the iteration processes, Equations (14) and (15) provide the search space selection rule of the ith candidate solution in the (t+1)th iteration.

$X_i\left(t+1\right)=X_{\mathrm{best}}\left(t\right)\cdot \left(1-\frac{t}{T_{\max }}\right)+(X_{\mathrm{M}}\left(t\right)-X_{\mathrm{best}}\left(t\right)\cdot rand)(14)$

$X_{\mathrm{M}}\left(t\right)=\frac{1}{N}{\sum }_{i=1}^N{X}_i\left(t\right)(15)$

where $X_{\text{best}}\left(t\right)$ represents the best solution of the tth iteration, which performs the minimum fitness value; $X_{\text{M}}\left(t\right)$ is determined as the mean solution of the tth iteration; t and $T_{\max }$ are considered as the current iteration and the max iteration, respectively.

Short Glide Attack

After determining the search space of each Aquila, a narrowed exploration should be implemented by a short glide attack, which can be mathematically described as:

$X_i\left(t+1\right)=X_{\mathrm{best}}\left(t\right)\cdot Levy\left(D\right)+X_{\mathrm{R}}\left(t\right)+(y-x)\cdot rand(16)$

where $D$ stands for the dimension space; $X_{\text{R}}\left(t\right)$ denotes a random solution vector in the tth iteration; and $Levy\left(D\right)$ is defined as levy flight distribution function, which is calculated by

$Levy\left(D\right)=s\cdot \frac{\mu \cdot \sigma }{{\left|v\right|}^{\frac{1}{\beta }}}(17)$

where $s$ represents a constant value which is fixed to 0.01; $\mu$ and $v$ are two random numbers from 0 to 1; and $\sigma$ can be determined as

$\sigma =\left(\frac{Г(1+\beta )\cdot \sin \left(\frac{\pi \beta }{2}\right)}{Г\left(\frac{1+\beta }{2}\right)\cdot \beta \cdot 2^{\left(\frac{\beta -1}{2}\right)}}\right)(18)$

where $\beta$ is fixed to 1.5.

Besides, $x$ and $y$ stand for spiral shape searches, which can be presented by Equations (19)–(23).

$y=r\cdot \cos \left(\theta \right)(19)$

$x=r\cdot \sin \left(\theta \right)(20)$

$r=r_1+U\cdot D_1(21)$

$\theta =-\omega \cdot D_1+{\theta }_1(22)$

${\theta }_1=\frac{3\pi }{2}(23)$

where $r_1$ is a number from 1 to 20 and $D_1$ takes an integer number between 1 and $D$; $U$ and $\omega$ are fixed to 0.00565 and 0.005 respectively.

Slow Descent Attack

When accurately specifying the prey area, Aquila will land and implement a preliminary attack, namely a slow descent attack. This behavior can be presented as

$X_i\left(t+1\right)=X_{\mathrm{best}}\left(t\right)-X_{\mathrm{M}}\left(t\right)\cdot \alpha -rand+(\left(U_{\mathrm{B}}-L_{\mathrm{B}}\right)\cdot rand+L_{\mathrm{B}})\cdot \delta (24)$

Here, $\alpha$ and $\delta$ refer to two exploitation adjustment parameters both fixed to 0.1.

Grab Prey

For the last step, Aquila attacks and grabs the prey when they are close enough, which can be mathematically described as

$X_i\left(t+1\right)=QF\left(t\right)\cdot X_{\mathrm{best}}\left(t\right)-(G_1\cdot X_i\left(t\right)\cdot rand)-G_2\cdot Levy\left(D\right)+rand\cdot G_1(25)$

where $QF\left(t\right)$ is applied to equilibrium search strategies called quality function, which is calculated by

$QF\left(t\right)=t^{\frac{G_1}{{(1-T_{\text{max}})}^2}}(26)$

$G_1=2\cdot rand-1(27)$

$G_2=2\cdot (1-\frac{t}{T_{\max }})(28)$

where $G_1$ and $G_2$ denote various motions and flight stops of Aquila, respectively.

Procedure for PID Parameter Optimization of PLL with AO Algorithm

According to Subsection 3.1 to Subsection 3.5, a whole procedure for PID parameter optimization of PLL with AO algorithm can be depicted in Figure 4.

FIGURE 4

FIGURE 4. Flow chat for PID parameter optimization of PLL with AO algorithm..

Case Study

In this section, AO algorithm with 4 individuals is used to identify the best PID parameters of PLL through 15 times iteration. Additionally, three regulation strategies are taken into consideration to evaluate the influence of parameters of PLL for smoothing output power fluctuation, as follows: 1) only optimizing PID parameters of PLL; 2) global regulation, i.e., simultaneously regulating PI parameters of voltage controller and current controller as well as PID parameters of PLL; 3) step regulation strategy, e.g., optimizing the PI gains of controller voltage and current controller in the first step, then regulating PID parameters of PLL. Furthermore, the irradiance of PV system drops from 1000 W/m² to 200 W/m² at 1 S point and then rises to 1000 W/m² at 2 S point with slopes of 6000 (W/m²)/S for both changes to approximately simulate actual illumination variations in engineering applications.

Note that all case studies are undertaken by a Simulink model, namely “250-kW Grid-Connected PV Array” in MATLAB 2019b via a personal computer with Intel(R) Core(TM) i5 CPU at 2.9 GHz and 16 GB of RAM. The simulation time is set to 3 S. Furthermore, relevant crucial parameters of AO algorithm and search scopes of all optimized parameters are tabulated in Tables 1 and 2.

TABLE 1

TABLE 1. Crucial parameters of AO algorithm

TABLE 2

TABLE 2. Upper bound and lower bound of optimized parameters.

Table 3 provides optimization results under various regulation strategies, where $K_{\mathrm{p}\_\mathrm{V}}$, $K_{\text{i}\_\_\text{V}}$ and $K_{\text{p}\_\text{I}}$, $K_{\text{i}\_\_\text{I}}$ stand for the gains of the proportional element and integral element of voltage controller and current controller, respectively; Error(P) is defined as the integral value of error power between actual power and ideal power of the PV system, which is directly determined by the fitness function.

TABLE 3

TABLE 3. Optimization results under different regulation strategies

One can easily observe that Error(P) is decreased by 418 W from 28.7069 to 28.2889 kW via regulating control parameters of PLL, while it is only reduced to 28.6037 kW when adding the optimization of voltage controller and current controller parameters. In other words, the global optimization and adjustment of controller parameters does not acquire satisfactory results, which results in a 314.8 W increase of Error(P) compared to that of PLL regulation strategy, which illustrates that optimizing PID parameters of PLL plays a crucial and main role in decreasing Error(P) and limiting power fluctuation. Additionally, the step optimization strategy can obtain the least Error(P), i.e., 27.6045 kW in the cost of more calculation time and higher solving complexity.

Furthermore, Figure 5 clearly depicts the comparison results of output power responding curves under different control parameter regulation strategies, upon which the step regulation strategy acquires the best performance that performs the fastest response speed and the least overshoot, followed by the PLL regulation strategy, global regulation strategy, and initial condition. Particularly, the maximum deviation of output power acquired by step optimization strategy is reduced around 19.1 kW, while those obtained by only regulating PLL and global optimization strategy are decreased by about 12.5 kW and 11.1 kW, respectively. However, the step regulation strategy extensively increases the solving complexity and time cost. It also indicates that optimizing PID parameters of PLL is an efficient and reliable method to prevent output power of PV systems from excessive fluctuation through fast and accurately detecting and locking the grid phase angle.

FIGURE 5

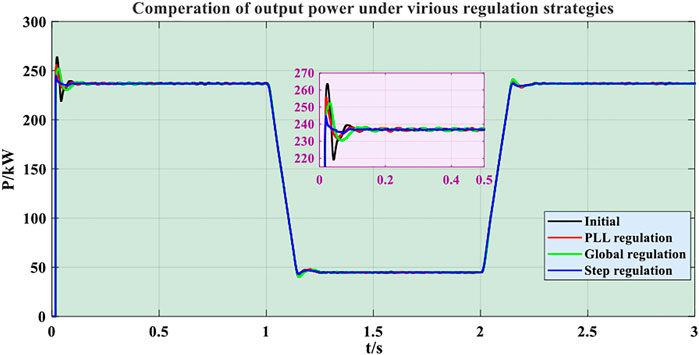
FIGURE 5. Comparison results of output power responding curves under different regulation strategies.

At last, Figure 6 provides an optimization performance radar map, which systematically and comprehensively compared the Error(P), response time, maximum deviation of output power, complexity, and time cost of various regulation strategies. From Figure 6, the radar curve of PLL regulation strategy is most regular and its area extremely approaches to that of step regulation strategy but is far less than that obtained by global regulation strategy. Therefore, PLL regulation performs the best comprehensive and global optimization performances.

FIGURE 6

FIGURE 6. Radar map of optimization performance under different regulation strategies.

Conclusions and Perspectives

A novel PID parameter tuning technique of PLL with AO algorithm is proposed to dramatically ensure a high-quality connection grid of a PV system. Besides, two critical conclusions are summarized as follows:

1) Three AO algorithm-based regulation strategies are carefully designed to evaluate the performance of the proposed method, i.e., PLL regulation strategy, global regulation strategy, and step regulation strategy.

2) PLL regulation strategy can effectively decrease power fluctuation and overshoot with a short response time, low complexity, and time cost through a fast and accurate phase detection and lock. Compared with global regulation strategy and step regulation strategy, PLL regulation strategy performs the lower complexity and time cost, because it only needs to optimize three parameters, which is more suitable for actual engineering applications that require fast time response. In particular, the Error(P) and the maximum deviation of output power obtained by the PLL strategy are smaller 418 W and 12.5 kW than those of the initial strategy, respectively.

Lastly, PLL regulation strategy based on AO algorithm acquires satisfactory results in PV connected grid system. Thus, it could be applied in other new energy grid connection systems in the future, such as wind, tidal, fuel cell, etc.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

Z.G.: Conceptualization, writing-original draft, formal analysis; B.Y.: Supervision, writing-review and editing; Y.H.: Formal analysis, software, supervision; T.H.: Project administration, resources; P.H.: Investigation, validation; X.M.: Writing-reviewing and editing, methodology; X.H.: Visualization, validation.

Funding

This study received funding from Key Project of China Southern Power Grid Co., Ltd. (YNKJXM20191240).

Conflict of Interest

Authors T.H., P.H., X.M., and X.H. are employed by Electric Power Research Institute of Yunnan Power Grid Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors gratefully acknowledge the support of Key Project of China Southern Power Grid Co., Ltd. (YNKJXM20191240).

References

Abualigah, L., Yousri, D., Abd Elaziz, M., Ewees, A. A., Al-qaness Mohammed, A. A., and Gandomi, A. H. (2021). Aquila Optimizer: A Novel Meta-Heuristic Optimization Algorithm. Comput. Ind. Eng. 157, 107250. doi:10.1016/j.cie.2021.107250

CrossRef Full Text | Google Scholar

Aouchiche, N. (2020). Meta-heuristic Optimization Algorithms Based Direct Current and DC Link Voltage Controllers for Three-phase Grid Connected Photovoltaic Inverter. Solar Energy 207, 683–692. doi:10.1016/j.solener.2020.06.086

CrossRef Full Text | Google Scholar

Çelik, D., and Meral, M. E. (2019). Current Control Based Power Management Strategy for Distributed Power Generation System. Control. Eng. Pract. 82, 72–85.

Google Scholar

Chen, J., Yao, W., Zhang, C. K., Ren, Y., and Jiang, L. (2019). Design of Robust MPPT Controller for Grid-Connected PMSG-Based Wind Turbine via Perturbation Observation Based Nonlinear Adaptive Control. Renew. Energ. 134, 478–495. doi:10.1016/j.renene.2018.11.048

CrossRef Full Text | Google Scholar

Chittora, P., Singh, A., and Singh, M. (2019). Adaptive EPLL for Improving Power Quality in Three-phase Three-Wire Grid-Connected Photovoltaic System. IET Renew. Power Generation 13 (9), 1595–1602. doi:10.1049/iet-rpg.2018.5261

CrossRef Full Text | Google Scholar

Farhat, M., Hussein, M., and Atallah, A. M. (2017). “Enhancement Performance of a Three Phase Grid Connected Photovoltaic System Based on Pi-Genetic Algorithm (PI-GA) Controller,” in 19th International Middle East Power Systems Conference (New Jersey, NJ: Menoufia Univ, Fac Engn, Elect Engn, Shibin Al Kawm, EGYPT), 19–21.

CrossRef Full Text | Google Scholar

Gan, W., Ai, X., Fang, J., Yan, M., Yao, W., Zuo, W., et al. (2019). Security Constrained Co-planning of Transmission Expansion and Energy Storage. Appl. Energ. 239, 383–394. doi:10.1016/j.apenergy.2019.01.192

CrossRef Full Text | Google Scholar

Guo, X. Q., Wu, W. Y., and Chen, Z. (2011). Multiple-complex Coefficient-Filter-Based Phase-Locked Loop and Synchronization Technique for Three-phase Grid-Interfaced Converters in Distributed Utility Networks. IEEE Trans. Ind. Electro. 58 (4), 1194–1204. doi:10.1109/tie.2010.2041738

CrossRef Full Text | Google Scholar

Han, Y., Xu, L., Khan, M. M., Yao, G., Zhou, L. D., and Chen, C. (2009). A Novel Synchronization Scheme for Grid-Connected Converters by Using Adaptive Linear Optimal Filter Based PLL (ALOF-PLL). Simulation Model. Pract. Theor. 17 (7), 1299–1345. doi:10.1016/j.simpat.2009.05.004

CrossRef Full Text | Google Scholar

Ikken, N., Bouknadel, A., El Omari, H., and El Omari, H. (2016). Design and Implementation of Intelligent PI-Fuzzy Logic Control for Grid Connected Inverters. in” IEEE 2016 International Renewable and Sustainable Energy Conference (IRSEC), 14-17. New Jersey, NJ: Marrakech, MOROCCO, 1111–1117. doi:10.1109/irsec.2016.7984022

CrossRef Full Text | Google Scholar

Kong, L. G., Shi, Z. Y., Cai, G. W., Liu, C., and Xiong, C. N. (2020). Phase-locked Strategy of Photovoltaic Connected to Distribution Network with High Proportion Electric Arc Furnace. IEEE Access 8, 86012–86023. doi:10.1109/access.2020.2989896

CrossRef Full Text | Google Scholar

Li, R. S., Wong, P., Wang, K., Li, B., and Yuan, F. F. (2020). Power Quality Enhancement and Engineering Application with High Permeability Distributed Photovoltaic Access to Low-Voltage Distribution Networks in Australia. Prot. Control. Mod. Power Syst. 5 (3), 183–189. doi:10.1186/s41601-020-00163-x

CrossRef Full Text | Google Scholar

Li, Z., Cheng, Z., Si, J., Zhang, S., Dong, L., Li, S., et al. (2021). Adaptive Power point Tracking Control of PV System for Primary Frequency Regulation of AC Microgrid with High PV Integration. IEEE Trans. Power Syst. 36 (4), 3129–3141. doi:10.1109/tpwrs.2021.3049616

CrossRef Full Text | Google Scholar

Liu, J., Yao, W., Wen, J., Fang, J., Jiang, L., He, H., et al. (2020). Impact of Power Grid Strength and PLL Parameters on Stability of Grid-Connected DFIG Wind Farm. IEEE Trans. Sust. Energ. 11(1): 545–557. doi:10.1109/tste.2019.2897596

CrossRef Full Text | Google Scholar

Mokhtar, B., Antonio, B., Pierluigi, C., Guido, C., Mauro, C., and Pasquale, D. F. (2020). Bayesian Bootstrap Quantile Regression for Probabilistic Photovoltaic Power Forecasting. Prot. Control. Mod. Power Syst. 5 (3), 218–229. doi:10.1186/s41601-020-00167-7

CrossRef Full Text | Google Scholar

Musengimana, A., Li, H., Zheng, X., and Yu, Y. (2021). Small-signal Model and Stability Control for Grid-Connected PV Inverter to a Weak Grid. Energies 14 (13), 3907. doi:10.3390/en14133907

CrossRef Full Text | Google Scholar

Pabitra, K. G., and Abhik, B. (2020). Stability Enhancement of Wind Energy Integrated Hybrid System with the Help of Static Synchronous Compensator and Symbiosis Organisms Search Algorithm. Prot. Control. Mod. Power Syst. 5 (2), 138–150. doi:10.1186/s41601-020-00158-8

CrossRef Full Text | Google Scholar

Pazhanimuthu, C., Baranilingesan, I., and Karthick, A. (2021). An Improved Control Algorithm for Series Hybrid Active Power Filter Based on SOGI-PLL under Dynamic Load Conditions. Solid State. Commun. 333, 114357. doi:10.1016/j.ssc.2021.114357

CrossRef Full Text | Google Scholar

Rodriguez, P., Pou, J., Bergas, J., Candela, J. I., Burgos, R. P., and Boroyevich, D. (2007). Decoupled Double Synchronous Reference Frame PLL for Power Converters Control. IEEE Trans. Power Electro. 22 (2), 584–592. doi:10.1109/tpel.2006.890000

CrossRef Full Text | Google Scholar

Satapathy, P., Dhar, S., and Dash, P. K. (2016). A Mutated Hybrid Firefly Approach to Mitigate Dynamic Oscillations of Second Order PLL Based PV-Battery System for Microgrid Applications. Sustainable Energ. Tech. Assessments 16, 69–83. doi:10.1016/j.seta.2016.05.004

CrossRef Full Text | Google Scholar

Se-Kyo, C. (2000). A Phase Tracking System for Three Phase Utility Interface Inverters. IEEE Trans. Power Electro. 15 (3), 431–438. doi:10.1109/63.844502

CrossRef Full Text | Google Scholar

ShenYao, Y. W. J., Wen, Y. H., He, B., and Jiang, L. (2019). Resilient Wide-Area Damping Control Using GrHDP to Tolerate Communication Failures. IEEE Trans. Smart Grid 10 (3), 2547–2557. doi:10.1109/tsg.2018.2803822

CrossRef Full Text | Google Scholar

Wang, Q., Yao, W., Fang, J., Ai, X., Wen, J., Yang, X., et al. (2020). Dynamic Modeling and Small Signal Stability Analysis of Distributed Photovoltaic Grid-Connected System with Large Scale of Panel Level DC Optimizers. Appl. Energ. 259, 114132. doi:10.1016/j.apenergy.2019.114132

CrossRef Full Text | Google Scholar

Yang, B., Wang, J., Zhang, X., Yu, T., Yao, W., Shu, H., et al. (2020). Comprehensive Overview of Meta-Heuristic Algorithm Applications on PV Cell Parameter Identification. Energ. Convers. Manag. 208, 112595. doi:10.1016/j.enconman.2020.112595

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H., Dong, J., and Jiang, L. (2018). Robust Sliding-Mode Control of Wind Energy Conversion Systems for Optimal Power Extraction via Nonlinear Perturbation Observers. Appl. Energ. 210, 711–723. doi:10.1016/j.apenergy.2017.08.027

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H., Zhang, Y., Chen, J., Sang, Y., et al. (2018). Passivity-based Sliding-Mode Control Design for Optimal Power Extraction of a PMSG Based Variable Speed Wind Turbine. Renew. Energ. 119, 577–589. doi:10.1016/j.renene.2017.12.047

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Zhang, X., Li, H., Shu, H., Sang, Y., et al. (2019). Dynamic Leader Based Collective Intelligence for Maximum Power point Tracking of PV Systems Affected by Partial Shading Condition. Energ. Convers. Manag. 179, 286–303. doi:10.1016/j.enconman.2018.10.074

CrossRef Full Text | Google Scholar

Yang, B., Zhong, L., Zhang, X., Shu, H., Yu, T., Li, H., et al. (2019). Novel Bio-Inspired Memetic Salp Swarm Algorithm and Application to MPPT for PV Systems Considering Partial Shading Condition. J. Clean. Prod. 215, 1203–1222. doi:10.1016/j.jclepro.2019.01.150

CrossRef Full Text | Google Scholar

Zhang, K., Zhou, B., Or, S. W., Li, C., Chung, C. Y., and Voropai, N. I. (2021). Optimal Coordinated Control of Multi-Renewable-To-Hydrogen Production System for Hydrogen Fueling Stations. IEEE Trans. Ind. Applicat., 1. doi:10.1109/tia.2021.3093841

CrossRef Full Text | Google Scholar

Zhao, Y. Y., An, A. M., Xu, Y. F., Wang, Q. Q., and Wang, M. M. (2021). Model Predictive Control of Grid-Connected PV Power Generation System Considering Optimal MPPT Control of PV Modules. Prot. Control. Mod. Power Syst. 6 (4), 407–418. doi:10.1186/s41601-021-00210-1

CrossRef Full Text | Google Scholar

Zhou, B., Fang, J. K., Ai, X. M., Yang, C. X., Yao, W., and Wen, J. Y. (2021). Dynamic Var reserve-constrained Coordinated Scheduling of LCC-HVDC Receiving-End System Considering Contingencies and Wind Uncertainties. IEEE Trans. Sust. Energ. 12 (01), 469–481. doi:10.1109/tste.2020.3006984

CrossRef Full Text | Google Scholar

Zhu, D. H., Zhou, S. Y., Zou, X. D., and Kang, Y. (2020). Improved Design of PLL Controller for $LCL$-Type Grid-Connected Converter in Weak Grid. IEEE Trans. Power Electro. 35 (5), 4715–4727. doi:10.1109/tpel.2019.2943634

CrossRef Full Text | Google Scholar

Nomenclature

Variables

${\mathit{V}}_{\mathbf{PV}}$ output voltage of photovoltaic cell, V

${\mathit{I}}_{\mathbf{PV}}$ output current of photovoltaic cell, A

${\mathit{I}}_{\mathit{p}\mathit{h}}$ photo-generated current, A

${\mathit{I}}_{\mathbf{o}}$ reverse saturation current, A

${\mathit{I}}_{\mathbf{d}}$ junction current of diode, A

$\mathit{T}$ temperature of photovoltaic cell, °C

${\mathit{V}}_{\mathit{a}}$ a phase voltage of PV inverter, V

${\mathit{V}}_{\mathit{b}}$ b phase voltage of PV inverter, V

${\mathit{V}}_{\mathbf{c}}$ c phase voltage of PV inverter, V

${\mathit{V}}_{\mathit{a},\mathit{s}}$ a phase voltage of grid, V

${\mathit{V}}_{\mathit{b},\mathit{s}}$ b phase voltage of grid, V

${\mathit{V}}_{\mathbf{c},\mathbf{s}}$ c phase voltage of grid, V

$\mathit{L}$ equivalent grid inductance, H

R equivalent grid resistance, Ω

${\mathit{w}}_{\mathbf{vco}}$ angular speed of voltage-controlled oscillator, rad/s

${\mathit{\omega }}_{\mathbf{s}}$ angular speed of grid, rad/s

Abbreviations

AO aquila optimizer

PLL phase-locked loop

PV photovoltaic

PI proportional-integral

PID proportional-integral-differential

VCO voltage-controlled oscillator