- 1College of Electrical and Information Engineering, Hunan University of Technology, Zhuzhou, China
- 2Hunan Creator Information Technologies Co., Ltd., Changsha, China
To solve the problems that a large number of random and uncontrolled electric vehicles (EVs) connecting to the distribution network, resulting in a decrease in the performance and stability of the grid and high user costs, in this study, a multi-objective comprehensive charging/discharging scheduling strategy for EVs based on improved particle swarm optimization (IPSO) is proposed. In the distribution network, the minimum root-mean-square error and the minimum peak valley difference of system load are first designed as objective functions; on the user side, the lowest charge and discharge cost of electric vehicle users and the lowest battery loss cost are used as objective functions, then a multi-objective optimization scheduling model for EVs is established, and finally, the optimization through IPSO is performed. The simulation results show that the proposed method is effective, which enhances the peak regulating capacity of the power grid, and it optimizes the system load and reduces the user cost compared with the conventional methods.
Introduction
The new energy source has made a great contribution to solving the increasingly serious energy shortage and environmental degradation. It will gradually replace non-renewable energy sources that cannot be recycled or reused (Teng et al., 2021). Electric vehicles (EVs) have gradually gained popularity in recent years due to their energy-saving (Xiong et al., 2020; Huang et al., 2021; Zhang et al., 2021) and environmentally friendly features. However, a large number of EVs connected to the distribution network increase the load of the power grid, which may lead to problems such as the increase of the peak-valley difference of the load, the local overload of the grid load, the increase of the line loss, and the over-limit of the transformer capacity of the distribution network (Wang et al., 2020). In addition, the electricity consumption of residents is increasing, and unreasonable charging costs will limit the popularization of EVs. EVs with vehicle to grid (V2G) capability can feed electricity back to the grid when their state of charge (SOC) is high. The maturity of the V2G technology and autonomous vehicle communication technology enables EVs to participate in optimal dispatch and reduce the load pressure on the distribution network. In addition, the charging/discharging of EVs are similar and clustered. EVs in the same street or community have similar charging behaviors, which increases the dispatch ability of EVs (Badawy and Sozer, 2017). The dispatching strategy of EVs is mainly to study the load balancing factors and distribution capacity on the distribution network side, while the user side aims to improve user satisfaction, battery loss costs, and the charging/discharging costs of EVs. The optimal charging/discharging scheduling of EVs was used to eliminate the influence of a large number of EVs connected to the grid, reduce the fluctuation of the grid load, and reduce user costs.
At present, intelligent scheduling has become one of the research hotspots. The economic cost is minimized, but the power grid load fluctuation is not considered (Habib et al., 2020). When a large number of EV users charge during the valley period, an “avalanche effect” will occur (Gottwalt et al., 2011). In the study by Jin et al. (2020), a probability mass function (PMF)-based model is proposed to provide more accurate forecasts of future EV behaviors. In addition, it developed an EV aggregator (EVA) optimization schedule model that combines a day-ahead optimization schedule and a real-time optimization schedule to reduce EVA operation costs and maximize the travel utility for users participating in this service of EVs. So as to resolve the conflict of interest between customers and system operators during the implementation of the vehicle to the grid, it proposed to use an augmented epsilon constrain-based technique to implement two-way and three-way multi-objective optimization (Maigha and Crow 2018). Amamra and Marco (2019) established an optimization strategy for V2G scheduling, which solved the problems of EV’s plug in time, adjustment price, EV’s expected leaving time, battery degradation cost, and vehicle charging demand, but the article does not optimize the load on the distribution grid. Hadian et al. (2020) similarly used a multi-objective particle swarm optimization (PSO) algorithm to control the charging/discharging rate and time of EVs to achieve the peak shaving, valley filling, and flattening goals of the grid load curve. The power routing strategy for EVs was proposed in the study by Esfahani and Mohammed (2019); the objective function involves minimization of power loss and the power imbalance factor along with improved system load ability as well as voltage profile. PSO reoptimized the received sub-optimal solution (site and the size of the station), which leads to an improvement in the algorithm functionality and enhances quality of the solution; the author shows the superior performance of the proposed method on the genetic algorithm and PSO in terms of improvement in the voltage profile and quality through simulation (Awasthi et al., 2017). Ma et al, (2019) studied the load fluctuation of the distribution network and the charge/discharge cost of EVs on the basis of the peak-valley time-of-use (TOU) price, and finally, a coordinated dispatch strategy and an optimized dispatch model were proposed to reduce the peak-valley difference of the power grid and improve the economic benefits of users.
The PSO algorithm requires fewer parameters and has low requirements on the objective function, which is widely used. Many literature studies use PSO to solve the scheduling problem (Yousif et al., 2019), but when the problem dimension is high, the algorithm is prone to precocity. Contrastively, in the study by Kang et al. (2017), it established a multi-objective optimization model and used the improved particle swarm optimization (IPSO) algorithm to find out the solution with the minimum electricity cost; the results verify that this method can better meet the economic benefits and environmental protection requirements of microgrid power generation than PSO, but it does not consider the optimization of the grid side.
To summarize, this study mainly conducts the following research on the basis of the above research work and combined with the background of an odd–even license plate restriction policy:
1) The charging/discharging cost and battery loss cost of EVs are constructed as objective functions on the user side of EVs, and the two objective functions of load mean square deviation and load peak-valley difference are established in terms of power grid load.
2) The influence of the current odd–even license plate restriction policy on EV scheduling is considered, and the charging power and state of charge/charging quantity of EVs are constrained.
3) An IPSO algorithm is proposed, which can effectively avoid the premature phenomenon of particles.
4) Finally, experiments have verified that the algorithm has better EV scheduling performance, and it reduces the user cost of EVs and plays the role of peak shaving and valley filling for the system load.
The rest of this article is organized as follows: the first section introduces the scheduling system, objective function, and model constraints of V2G; the second section describes the dispatching strategy scheme of EVs; the third section gives simulation results to prove that the proposed IPSO algorithm has a better power grid peak regulating ability and is beneficial to reducing user costs; finally, the fourth part gives the conclusion.
Vehicle to Grid and the Scheduling Model
Vehicle to Grid Dispatching System
The V2G dispatching system is divided into five parts: the distribution network, information collection system, V2G dispatching center, intelligent charging module, and EVs. The structure of the V2G scheduling system is shown in Figure 1.
Lithium Ion Battery Model
Battery aging is mainly caused by EV’s cyclic charge and discharge, which is also related to the type of battery. In this study, a linear model proportional only to the total number of battery cycles is used to study lithium ion batteries. The curve diagram of cycle times and life as shown in Figure 2 is presented in the study by Neubauer and Wood (2014), and the value is given by the battery manufacturer. The model is related to the battery replacement cost, and the battery aging cost is obtained.
Objective Function
Battery Aging Cost
The battery aging cost includes the charge and discharge power and the cost caused by the fluctuation of charge and discharge power. The battery aging cost caused by charging/discharging power is expressed as
where
The battery aging cost caused by charge and discharge power fluctuation in adjacent periods is expressed as
where
The aging cost of the battery is expressed as
where N is the total number of EVs.
Charging Cost
The charging cost of EVs participating in the V2G program depends on the charging consumption and discharge income. When the discharge revenue of EVs is higher than the charging consumption, the charging cost may be negative. The reducing charging cost is the most important incentive factor for EV owners to participate in the V2G program, but a high-frequency discharge will cause irreversible loss of the battery, which limits the enthusiasm of EV owners to feed the power grid.
The electricity price is designed as a linear function of the instantaneous load of the grid:
where
Under the real-time electricity price, EV charging cost is expressed as
Mean Square Error of Power Grid Load
The smaller the load mean square error, the more stable the load fluctuation. The charge and discharge power of each EV in 24 periods of a day is regarded as the control variable:
where
Peak and Valley Difference of Power Grid Load
Peak load is expressed as
The peak and valley difference of the load curve is expressed as
where
Objective Function
The optimized objective function is expressed as
From the perspective of comprehensive indicators, only considering a single target does not truly reflect the actual cost of users. The four costs represent the interests of the power grid and vehicle owners. When setting the weight coefficient, the importance of the four costs is the same, which is closer to the actual use cost of users. If only the charging cost is considered, the charging cost is the smallest near the load valley, but a too long charging time increases the battery aging cost, and the charge and discharge power under the constraint of charging cost will produce a short-term peak, so the cost in this period is not necessarily the smallest. Considering comprehensively, set the same weight for the four objectives.
Constraints of the Model
SOC Constraints
Reasonable upper and lower limits of state of charge can delay battery aging as
where
Charging/Discharging Power Constraints
When the EVs support V2G,
When the EVs do not support V2G,
where
Battery Power Constraints
where
Equation 13 ensures that the battery power can meet the requirements when the EVs leave, and Eq. 14 ensures that the power in the dispatching section is always within the allowable range, neither excessive discharge nor overcharge.
Even–Odd License Plate Method
In order to alleviate urban traffic pressure and environmental pollution, it is imperative to implement a restriction policy on odd and even numbers. On the other hand, the traffic restriction policy can improve the enthusiasm of EV owners to participate in power grid dispatching and alleviate the burden of the distribution network. However, not all EV owners are willing to participate in the scheduling during the travel restriction period, so the probability of participating in the scheduling is selected as 0.95 in this study. In addition, most unrestricted EVs are actually idle almost 95% of the time in a day (Shen et al., 2021). This part of EVs can participate in the scheduling under the condition of meeting the model constraints. In this study, the probability of unrestricted driving participating in the scheduling is 0.8.
Solution of the Scheduling Policy
It is difficult to solve the multi-variable, non-linear, multi-constrained, and high-dimensional EV charging/discharging scheduling optimization problem by using classical optimization algorithms such as linear programming (Liu et al., 2020). Considering that the standard PSO algorithm is prone to fall into local optimum, this study adopts the IPSO algorithm for optimization.
Particle Swarm Optimization
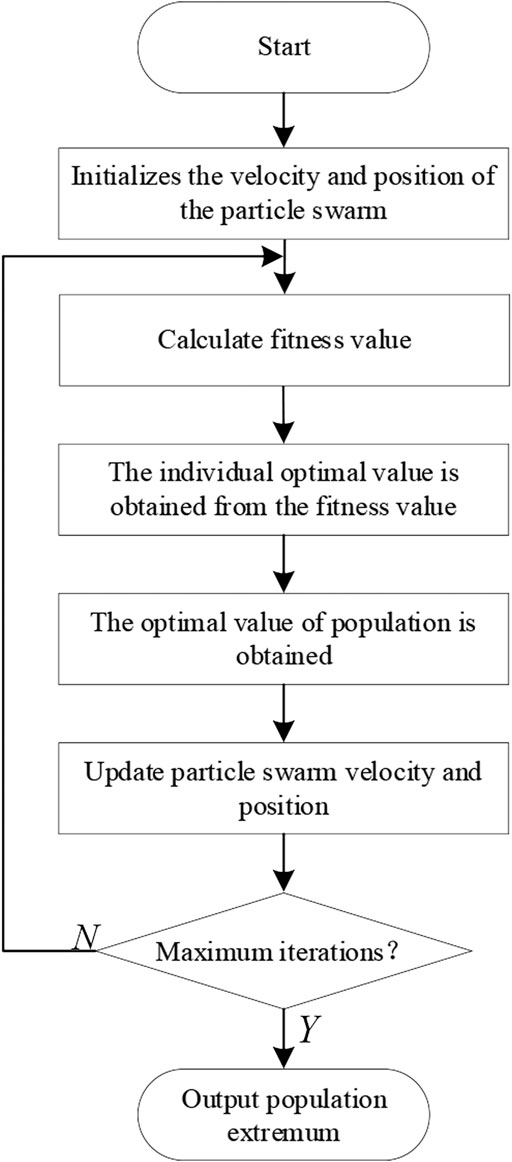
PSO needs a certain amount of initial solution and then through iteration to find the optimal solution. In the process of each iteration and update, the particle needs to update two quantities, which are the individual optimal position and the population optimal position.
Supposing that in a D-dimensional solution space, the population is composed of N particles, where the position of particle i can be expressed as follows
The velocity of particle i can also be represented as follows:
The optimal position searched by particle i is called the individual optimal position, denoted as
The optimal position found by the whole particle swarm is called the optimal position of the population, denoted as
The whole particle swarm is described as
where
The flow chart of the PSO algorithm is shown in Figure 3.
Improved Particle Swarm Optimization Algorithm
If the particle velocity is too divergent, it will lead to slow convergence in the later stage. In order to solve this problem, a simplified PSO algorithm is proposed in the literature (Lin et al., 2020). In this algorithm, the velocity term is omitted, and the evolutionary direction of particles is controlled only by the position term; Eq. 19 in the standard PSO algorithm can be simplified as
Levy Flight
Levy flight is a random search path between short-distance walking and occasionally long-distance walking obeying Levy distribution. After a lot of research, it is in line with the foraging trajectory of many insects in nature, such as bees and fruit flies (Yao et al., 2020). If the algorithm falls into the local optimum, the particle position can be readjusted by Levy’s flight formula to make it jump out of the local optimum. Levy’s flight position update equation is expressed as
where
The step length of Levy flight conforms to Levy distribution which is often simulated by the Mantegna algorithm, and the calculation formula of step s is expressed as
where
where
If all particles gather near the optimal particle, the algorithm will stagnate with the iteration. If it is the local optimum, the obtained solution is not the global optimum. In order to make the particles escape the local optimum and improve the population diversity, Levy flight is carried out to update the position of the particles. The adaptive adjustment strategy is written as
Random Inertia Weight
In the PSO algorithm, a large value of inertia weight can be conducive to more extensive search, and a small inertia weight can improve the accurate local search ability of the algorithm. Therefore, the value of the inertia weight is very important. Based on this, a non-linear decreasing inertia weight with randomness is proposed. The inertia weight is as follows:
where
Simulated Annealing Algorithm
Aiming at the problem that PSO is easy to fall into local optimum, the idea of simulated annealing (SA) is introduced in PSO to improve PSO by using the characteristic that SA can accept inferior solutions under a certain probability.
The operation steps of simulated annealing are as follows:
1) The solution optimized by PSO is used as the initial solution to determine the initial annealing temperature;
2) Calculate the fitness function difference between the new solution and the old solution:
3) Calculate the annealing temperature according to Eq. (26):
4) If the convergence criterion is reached, the final accepted state is output, otherwise turn to step 2.
Through the research of a PSO improvement strategy, when the next position of the particle is better than the current position, the particle moves to the next position. Instead, particles move with the probability controlled by temperature instead of directly moving to the next position. When the temperature drops slowly enough, the algorithm will not easily jump out of the “promising” search area. This way can enhance the local search ability of the PSO.
Calculation Example Analysis
Simulation Parameter Setting
Taking a microgrid as an example for simulation analysis, the scale of EVs in the planning area is 600, and 50 EVs do not support V2G; the scheduling period ranges from 0 to 24 points. The simulation step
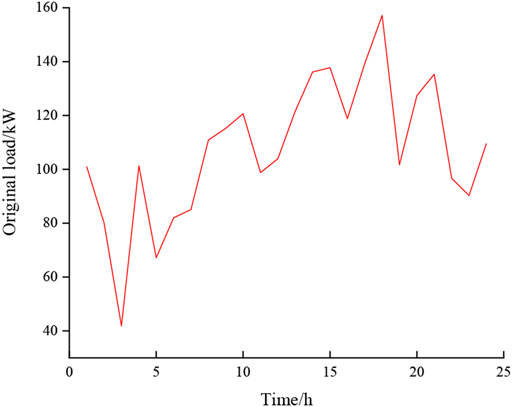
The typical daily electricity load of the grid is shown in Figure 4.
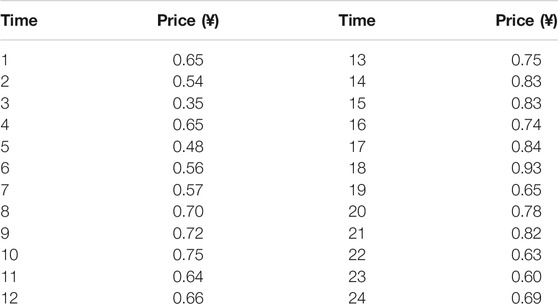
In this study, load scheduling is dispatched under the condition of the TOU price. TOU price data obtained through Eq. 4 are shown in Table 1.
In order to illustrate the effectiveness of IPSO in solving the economic dispatching of the microgrid, the solution results will be compared with those of standard PSO and adaptive particle swarm optimization (APSO). The specific parameter settings are as follows:
The maximum iteration times of each algorithm were set to 1,000 times. The population number was 100;
Analysis of Simulation Results.
The 1-day charging load demand of a single EV is obtained by Monte Carlo simulation, and the total charging load demand of 600 EV clusters is superimposed with the basic load to form the 1-day total load demand. We took the objective function
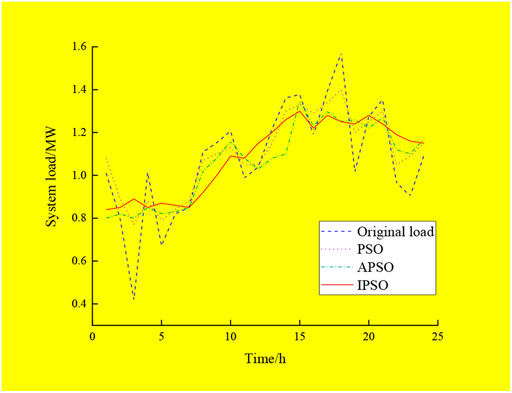
The load curve optimized by the three methods and the original load curve are shown in Figure 6.
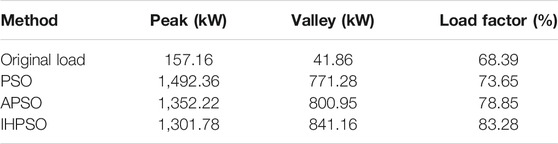
The load curve optimization values of the three methods and the objective function optimization values are shown in Table 2 and Table 3.
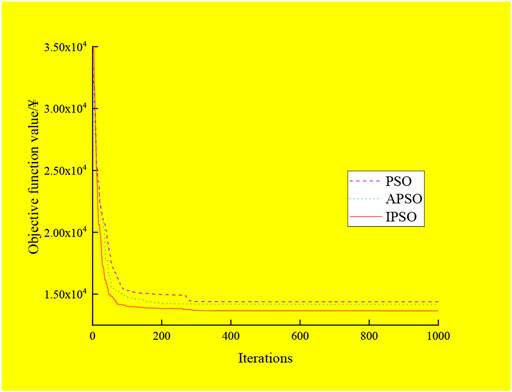
It can be seen from Figure 5 that the objective function value of PSO in 280 generations is stable at 14,385.39 ¥, and the algebra of APSO converging to this value is generation 163. When it is stable, the objective function value is 14,186.32, and the cost is reduced by 199.07 ¥/day. In addition, according to the data in Table 2 and Table 3, the load rate of APSO is 5.2% higher than that of PSO and the load mean square deviation is 4.87% lower than that of PSO and 23.55% lower than the peak valley difference of PSO, indicating that APSO is conducive to the safe and stable operation of the power grid and reducing cost. It can be seen from Figure 5 and Figure 6 that IPSO performs better, and it can converge to the optimal value of APSO in generation 80. Its final objective function value is 13,654.27 ¥, the cost is 532.05 ¥/day lower than that of APSO, and the effect of peak cutting and valley filling is more obvious. Meanwhile, according to the data in Table 2 and Table 3, the load rate is 4.43% higher than that of APSO, the load mean square deviation is 8.08% lower than that of APSO, and the peak valley difference is 16.44% better than that of APSO. It shows that the IPSO algorithm has strong optimization ability for multi-constraint, strong coupling, and high-dimensional scheduling problems of the microgrid, and its convergence is better than that of other algorithms, so it is more suitable for the scheduling problems of the microgrid.
The numerical example shows that EVs can participate in the peak shaving and valley filling of the power grid as a flexible energy storage device on the premise of ensuring the regular vehicle demand of vehicle owners. The scheduling model based on IPSO can well enable family EVs to participate in the interaction of the power grid, actively respond to the price incentive on the power grid side, and achieve the purpose of optimizing user costs and power energy. At the same time, the example results also verify that the IPSO algorithm scheduling not only saves the economic costs of users but also can indirectly reduce the peak valley difference of the load curve, plays a better role in peak shifting and valley filling, and can effectively maintain the stability of the power grid.
Conclusion
Aiming at the problems of large load fluctuations and high user costs caused by a large number of EVs connected to the grid, a multi-objective comprehensive charging/discharging scheduling strategy for EVs based on IPSO is proposed in this study. The strategy uses a multi-objective control scheme to simulate a typical power grid and carries on the optimization with the IPSO algorithm. The following conclusion is obtained by analyzing the results of the simulation:
1) The IPSO algorithm proposed in this study has a better search ability than the standard PSO algorithm and the APSO algorithm. This method avoids premature convergence, and the optimization iteration task is completed better.
2) This method has a good response on the price incentives on the grid side and reduces the cost of EVs for users. Meanwhile, the example also shows that the model has a good effect on the load curve.
3) Taking the comprehensive optimization of load mean square deviation, peak-valley difference, and user economic cost as the overall objective function of the scheduling model, the objective function of the scheduling model is no longer single, which is beneficial to take into account the needs of various aspects. In addition, the even–odd license plate method is considered to improve the comprehensive performance of the scheduling policy.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
BF: conceptualization, software, and methodology. BL: data curation and writing–original draft preparation. XL: visualization and investigation. YJ: writing—review and editing. WX: supervision. YL: software and validation.
Funding
This project was supported by the Hunan High-tech Industry Science and Technology Innovation Leading Foundation of China (2022GK4055).
Conflict of Interest
YJ was employed by the company Hunan Creator Information Technologies Co., Ltd.
The remaining authors stated that the research was conducted in the absence of any commercial or financial relationships that could be considered as potential conflicts of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
References
Amamra, S.-A., and Marco, J. (2019). Vehicle-to-Grid Aggregator to Support Power Grid and Reduce Electric Vehicle Charging Cost. IEEE Access 7, 178528–178538. doi:10.1109/ACCESS.2019.2958664
Awasthi, A., Venkitusamy, K., Padmanaban, S., Selvamuthukumaran, R., Blaabjerg, F., and Singh, A. K. (2017). Optimal Planning of Electric Vehicle Charging Station at the Distribution System Using Hybrid Optimization Algorithm. Energy 133, 70–78. doi:10.1016/j.energy.2017.05.094
Badawy, M. O., and Sozer, Y. (2017). Power Flow Management of a Grid Tied PV-Battery System for Electric Vehicles Charging. IEEE Trans. Ind. Applicat. 53 (2), 1347–1357. doi:10.1109/TIA.2016.2633526
Esfahani, M. M., and Mohammed, O. (2019). Real-time Distribution of En-Route Electric Vehicles for Optimal Operation of Unbalanced Hybrid AC/DC Microgrids. eTransportation 1, 100007. doi:10.1016/j.etran.2019.100007
Gottwalt, S., Ketter, W., Block, C., Collins, J., and Weinhardt, C. (2011). Demand Side Management-A Simulation of Household Behavior under Variable Prices. Energy Policy 39 (12), 8163–8174. doi:10.1016/j.enpol.2011.10.016
Habib, H. U. R., Subramaniam, U., Waqar, A., Farhan, B. S., Kotb, K. M., and Wang, S. (2020). Energy Cost Optimization of Hybrid Renewables Based V2G Microgrid Considering Multi Objective Function by Using Artificial Bee Colony Optimization. IEEE Access 8, 62076–62093. doi:10.1109/ACCESS.2020.2984537
Hadian, E., Akbari, H., Farzinfar, M., and Saeed, S. (2020). Optimal Allocation of Electric Vehicle Charging Stations with Adopted Smart Charging/Discharging Schedule. IEEE Access 8, 196908–196919. doi:10.1109/ACCESS.2020.3033662
Huang, S., Wu, Q., Liao, W., Wu, G., Li, X., and Wei, J. (2021). Adaptive Droop-Based Hierarchical Optimal Voltage Control Scheme for VSC-HVDC Connected Offshore Wind Farm. IEEE Trans. Ind. Inf. 17 (12), 8165–8176. 10.1109/TII.2021.3065375.
Jin, Y., Yu, B., Seo, M., and Han, S. (2020). Optimal Aggregation Design for Massive V2G Participation in Energy Market. IEEE Access 8, 211794–211808. doi:10.1109/ACCESS.2020.3039507
Kang, Q., Feng, S., Zhou, M., Ammari, A. C., and Sedraoui, K. (2017). Optimal Load Scheduling of Plug-In Hybrid Electric Vehicles via Weight-Aggregation Multi-Objective Evolutionary Algorithms. IEEE Trans. Intell. Transport. Syst. 18 (9), 2557–2568. doi:10.1109/TITS.2016.2638898
Lin, M., Wang, Z., Wang, F., and Chen, D. (2020). Improved Simplified Particle Swarm Optimization Based on Piecewise Nonlinear Acceleration Coefficients and Mean Differential Mutation Strategy. IEEE Access 8, 1. doi:10.1109/ACCESS.2020.2994984
Liu, W.-L., Gong, Y.-J., Chen, W.-N., Liu, Z., Wang, H., and Zhang, J. (2020). Coordinated Charging Scheduling of Electric Vehicles: A Mixed-Variable Differential Evolution Approach. IEEE Trans. Intell. Transport. Syst. 21 (12), 5094–5109. doi:10.1109/TITS.2019.2948596
Ma, Y., Chen, Y., Chen, X., Deng, F., and Song, X. (2019). Optimal Dispatch of Hybrid Energy Islanded Microgrid Considering V2G under TOU Tariffs. E3S Web of Conferences 107, 2007–2013. doi:10.1051/e3sconf/201910702007
Maigha, M. L., and Crow, M. L. (2018). Electric Vehicle Scheduling Considering Co-optimized Customer and System Objectives. IEEE Trans. Sustain. Energ. 9 (1), 410–419. doi:10.1109/TSTE.2017.2737146
Neubauer, J., and Wood, E. (2014). The Impact of Range Anxiety and home, Workplace, and Public Charging Infrastructure on Simulated Battery Electric Vehicle Lifetime Utility. J. Power Sourc. 257 (3), 12–20. doi:10.1016/j.jpowsour.2014.01.075
Shen, J., Wang, L., and Zhang, J. (2021). Integrated Scheduling Strategy for Private Electric Vehicles and Electric Taxis. IEEE Trans. Ind. Inf. 17 (3), 1637–1647. doi:10.1109/TII.2020.2993239
Teng, W., Wang, Y., Sun, S., Cheng, Y., Yu, P., and Wang, S. (2021). Robust Stability Control for Electric Vehicles Connected to DC Distribution Systems. Front. Energ. Res. 9, 100–108. doi:10.3389/fenrg.2021.740698
Wang, W., Liu, L., Liu, J. Z., and Chen, Z. (2020). Energy Management and Optimization of Vehicle-To-Grid Systems for Wind Power Integration. CSEE J. Power Energ. Syst. 7 (1), 172–180. doi:10.17775/CSEEJPES.2020.01610
Xiong, L., Liu, X., Liu, Y., and Zhuo, F. (2020). Modeling and Stability Issues of Voltage-Source Converter Dominated Power Systems: a Review. Csee Jpes. doi:10.17775/CSEEJPES.2020.03590
Yao, L., You, S., Xiaodong, L., and Bo, G. (2020). Control Allocation for a Class of Morphing Aircraft with Integer Constraints Based on Lévy Flight. J. Syst. Eng. Electron. 31 (4), 826–840. doi:10.23919/JSEE.2020.000056
Yousif, M., Ai, Q., Gao, Y., Wattoo, W. A., Jiang, Z., and Hao, R. (2019). An Optimal Dispatch Strategy for Distributed Microgrids Using PSO. CSEE J. Power Energ. Syst. 6 (3). 10.17775/CSEEJPES.2018.01070.
Keywords: electric vehicle, multi-objective optimization, improved particle swarm algorithm, grid peak shaving, charging/discharging scheduling
Citation: Fang B, Li B, Li X, Jia Y, Xu W and Liao Y (2021) Multi-Objective Comprehensive Charging/Discharging Scheduling Strategy for Electric Vehicles Based on the Improved Particle Swarm Optimization Algorithm. Front. Energy Res. 9:811964. doi: 10.3389/fenrg.2021.811964
Received: 09 November 2021; Accepted: 24 November 2021;
Published: 21 December 2021.
Edited by:
Bin Zhou, Hunan University, ChinaReviewed by:
Ling Yang, Guangdong University of Technology, ChinaHui Cai, Changsha University of Science and Technology, China
Copyright © 2021 Fang, Li, Li, Jia, Xu and Liao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Baling Fang, NTkxMTg2NkBxcS5jb20=
 Baling Fang
Baling Fang Bo Li1
Bo Li1