The Influence of Humidity on Electron Transport Parameters and Insulation Performance of Air

The environmental conditions affect the external insulation performance of power equipment. In order to study the physical characteristics of air discharge, the microscopic process of electron–molecule collision in the air based on the Boltzmann equation has been studied in this paper. The influence of humidity on the air gap insulation performance was also analyzed. The calculation results show that with the temperature 300 K and the pressure 1.0 atm, the electron energy distribution function and electron transport parameters varied with the air relative humidity. As the air relative humidity is increased by each 30%, the average electron energy decreases by about 0.2 eV, the reduced electron mobility decreases by about 0.25 × 10²³ [1/(V·m·s)], the reduced electron diffusion coefficient decreases by about 0.2 × 10²⁴ [1/(m s)], and the effective ionization coefficient decreases by about 4 × 10⁻²⁴ m². As the air relative humidity increases from 0% to 60%, the critical breakdown electric field increases by 1.22 kV/cm.

1 Introduction

In order to transmit a large-capacity power supply by long transmission distance, a UHV power grid has been constructed and developed rapidly in China (Zhao et al., 2015; Xun et al., 2020a; Xun et al., 2021a). For high voltage level and large span of UHV transmission line, it inevitably leads to power loss, and noise pollution and equipment corrosion (Zhenya, 2005a; Zhenya, 2005b; Muniappan, 2021). The terrain conditions, altitude, and meteorological conditions along UHV transmission lines are complex and changeable, which may affect the external insulation characteristics (Xun et al., 2017; Xun et al., 2020b; Weichen et al., 2021). The characteristics of air discharge can be significantly affected by air humidity (Wenliang et al., 2007; Yang et al., 2021a; Yang et al., 2021b), which has become one of the focuses in the field of power system external insulation.

At present, most researches are committed to the development process of air discharge (Prasad and Craggs, 1960; Abdel-Salam, 1985; Xun et al., 2021b; Xun and Pongsathorn, 2021). Bian Xingming and other scholars (Xingming et al., 2010) studied the physical characteristics of negative DC corona in a rod-plate electrode. They applied the charge simulation method and surface photoelectron calculation method to achieve the inception voltage of negative DC corona, and to study the influence of humidity. Cai Xinjing and other scholars (Xinjing et al., 2015) used fluid model to simulate the propagation process of bi-directional streamer in air gaps with different water vapor. It was concluded that humidity had little effect on the propagation characteristics of a streamer under the same background electric field, but the influence of air humidity on the inception characteristics of a streamer was not studied. To design the structure of EHV transmission lines in high altitude areas, Liu Youwei and other scholars (Liu et al., 1990) analyzed the characteristics of corona around the conductor with different humidity in detail. Their experimental results showed that humidity had a significant impact on the corona inception electrical field of the conductor. Li Kelin (Kelin, 2019) built the corresponding discharge chamber to simulate different climate conditions. The change of negative DC corona discharge mode under different humidity conditions was analyzed in detail, and the influence mechanism was analyzed combined with the simulation results. Yuke, (2017) used the self-designed experimental platform that can adjust humidity to study the influence of different air humidity on corona discharge with the internal electrode of converter valve as an example. The above studies were mostly focused on the influence of humidity on corona inception electric field and corona discharge process, and rarely considered the influence of humidity on electron transport parameters. The electron transport parameters are not only the basis for the plasma hydrodynamics model of air discharge but also can reflect the insulation performance of air gaps (Wen et al., 2016; Roostaee et al., 2017; Xinyu et al., 2018; Xun and Raksincharoensak, 2021; Yuanchao et al., 2021). The external insulation of power equipment exposed to air will be affected by air humidity. The variation of air humidity will affect the electronic transport parameters during air discharge that lead to different insulation performance of air gaps and may threaten the operation characteristics of external insulation of power equipment.

In this paper, the motion collision processes between electrons and molecules in air under different humidity are simulated in detail. The Boltzmann two approximation method is used to solve the electron transport parameters of air. The air electron transport parameters under different reduced electric fields are calculated and analyzed. The calculation results are compared with the results of Morrow (Morrow and Lowke, 1997) and Nikonov (Nikonov et al., 2001) to verify the model reasonability in this paper. The effect of humidity on electron energy distribution function (EEDF), reduced electron mobility (μ/N), reduced electron diffusion coefficient (D/N), and critical breakdown electric field are simulated and analyzed.

2 Calculation Method of Electron Transport Parameters

2.1 Binomial Approximation Expansion

Electron energy distribution function is calculated by Boltzmann binomial approximation. The electron collision process plays a major role during the air discharge. In the numerical simulation of fluid dynamics of gas discharge, the accuracy of electron collision section data is the key to accurately solve the transport parameters using Boltzmann equation. In order to simplify the calculation, only four types of collision sections are considered in this paper, including elasticity, ionization, adhesion, and excitation (Su et al., 2019).

During air discharge, the electron distribution function can be described by Boltzmann Eq. 1:

$\frac{\partial f}{\partial t}+\overrightarrow{v}.\nabla f-\frac{e}{m}\left(\overrightarrow{E}.\nabla \overrightarrow{v}.f\right)=C\left[f\right](1)$

where f is the distribution function of electrons in the six-dimensional phase space; e is the amount of electron charge; v is an electron velocity vector; E is the field strength, V m⁻¹; $\nabla$ is a velocity gradient operator; m is electronic quality; and C is a collision term, which represents the variation rate of distribution function.

Since it is very difficult to solve the Boltzmann equation directly, the equation can be expanded into spherical coordinates as Eq. 2.

$\frac{\partial f}{\partial t}+v\cos \theta \frac{\partial f}{\partial z}-\frac{e}{m}E\left(\cos \theta \frac{\partial f}{\partial v}+\frac{{\sin }^2\theta }{v}\frac{\partial f}{\partial \cos \theta }\right)=C\left[f\right](2)$

Based on the uniform spatial electric field, elastic collision plays a major role when the electric field intensity is not high (generally less than 1000Td). The binomial approximation method can be used to reduce the complexity. Here, f is expanded as Eq. 3.

$f\left(v,t,z,\cos \theta \right)\approx f_0\left(v,t,z\right)+f_1\left(v,t,z\right)\cos \theta (3)$

where θ is the angle between the electron velocity vector and the direction of the electric field, and f₀ and f₁ correspond to the respective homogeneity and heterogeneity of the electron energy distribution function, respectively.

Take Eq. 3 into Eq. 2, and the Legendre polynomial expansion is performed. Then the following two equations are obtained by integrating θ:

$\{\begin{array}{l}\frac{\partial f_{\text{0}}}{\partial t}+\frac{\gamma }{3}{\epsilon }^{\frac{1}{2}}\frac{\partial f_1}{\partial t}-\frac{\gamma }{3}{\epsilon }^{\frac{1}{2}}\frac{\partial }{\partial \epsilon }\epsilon E{f}_1=C_0\\ \frac{\partial f_1}{\partial t}+\gamma {\epsilon }^{\frac{1}{2}}\frac{\partial f_0}{\partial t}-E\gamma {\epsilon }^{\frac{1}{2}}\frac{\partial f_0}{\partial \epsilon }=-N{\sigma }_m\gamma {\epsilon }^{\frac{1}{2}}{f}_1\\ {\sigma }_m={\displaystyle \sum _k{x}_k{\sigma }_k},\gamma ={\left(2e/m\right)}^{0.5},\epsilon ={\left(v/\gamma \right)}^2\end{array}(4)$

Here, C₀ is the variation of f₀ caused by collision; σ_m and σ_k are the total collision cross section and the collision cross section of reaction k, where reaction k represents any collision reaction, m².

According to the separation variable method, Eq. 4 can be combined as Eq. 5:

$\{\begin{array}{l}\frac{\partial }{\partial \epsilon }\left[\frac{\epsilon }{3{\sigma }_m}\frac{\partial f_0}{\partial \epsilon }{\left(\frac{E}{N}\right)}^2+{\epsilon }^2\left({\text{f}}_0+\frac{k_{b}T}{e}\frac{\partial f_0}{\partial \epsilon }\right)\right]=S\\ {\text{f}}_1=\frac{E}{N}\frac{1}{{\sigma }_m}\frac{\partial f_0}{\partial \epsilon },{\sigma }_{\epsilon }={\displaystyle \sum 2\frac{\text{m}}{M}{\sigma }_k},S={\displaystyle \sum _{\text{k}=i_n}{C}_k-\gamma \lambda {\epsilon }^{\frac{1}{2}}f}\end{array}(5)$

In Eq. 5, N denotes the number density of neutral gas molecules, m⁻³; T represents temperature, K; k_b represents Boltzmann constant; M represents particle mass; σ_ε is the effective cross section of the total elastic collision; k = i_n represents all inelastic collision reactions, S represents loss term for inelastic collisions.

The electron energy distribution function can be obtained by solving f₀ and f₁, which provides the basis data for the subsequent solution of various electron transport parameters.

2.2 Calculation of Electronic Collapse Parameters

The electron energy distribution function in charged air is determined by the Boltzmann equation. According to its EEDF, the reduced ionization coefficient (α/N), reduced attachment coefficient (η/N), and effective ionization coefficient[(α-η)/N] in air can be calculated. The reduced ionization coefficient and reduced attachment coefficient (Morrow and Lowke, 1997) are obtained by Eq. 6.

$\{\begin{array}{l}\frac{\alpha }{N}=\sqrt{\frac{2e}{m}}\frac{1}{V}{\displaystyle {\int }_{{\epsilon }_i}^{\infty }\epsilon Q_i\left(\epsilon \right)F_0\left(\epsilon \right)d\epsilon }\\ \frac{\eta }{N}=\sqrt{\frac{2e}{m}}\frac{1}{V}{\displaystyle {\int }_{{\epsilon }_{\text{a}}}^{\infty }\epsilon Q_a\left(\epsilon \right)F_0\left(\epsilon \right)d\epsilon }\end{array}(6)$

where, F₀ represents the stable energy distribution function by applying Boltzmann binomial approximation method to f; V represents the electron drift velocity; Q_i and ε_i represent the effective cross section and critical energy of ionization reaction, respectively; Q_a and ε_a represent the effective cross section and critical energy of the adhesion reaction, respectively; and ε is the electron energy, J.

2.3 Applied Reactions and Cross-Sectional Data

In order to simplify the calculation, air components are considered as 80% nitrogen and 20% oxygen, and H₂O is considered to study the effect of humidity on air gap discharge processes. The applied electron collision reactions are shown in Table 1. Their cross-sectional data are from the LAXCAT database. The parameters set in this paper are as follows: standard atmospheric pressure, background temperature 300 K, and reduced electric field 50Td–300Td (1Td = 10⁻²¹ Vm²).

TABLE 1

TABLE 1. Applied electron collision reactions.

3 Analysis of Electron Transport Parameters and Insulation Performance of Air

3.1 Verification of Simulation Model in Dry Air

In this section, the dry air pressure is the standard atmospheric pressure, the relative humidity is 0%, and the air temperature is 300 K. The collision reactions include reactions 1–43 in Table 1.

3.1.1 Electron Energy Distribution Function Distribution

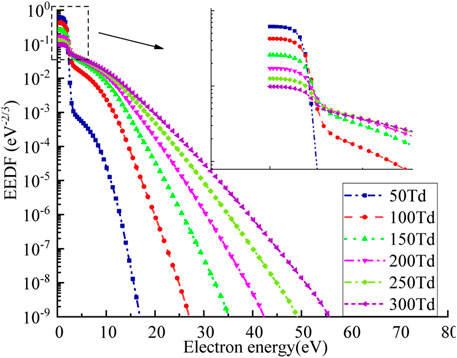
The calculated electron energy distribution is shown in Figure 1. The number of low-energy electrons is much higher than that of high-energy electrons under the same electric field; the number of low-energy electrons decreases with reduced electric field while the number of high-energy electrons increases. When the electron energy is 0–3 eV, the average electron energy decreases with the reduced electric field; when the electron energy is greater than 3 eV, the average electron energy increases with the reduced electric field. The increase of electric field increases the electrons speed and their kinetic energy. Electrons are more likely to collide and ionize with molecules in the air.

FIGURE 1

FIGURE 1. Electron energy distribution function (EEDF) distribution of dry air.

3.1.2 Electron Transport Parameters Calculation

The reduced ionization coefficient and reduced adhesion coefficient calculated according to Eq. 6 are shown in Figure 2. As shown in Figure 2, as the reduced electric field exceeds 100 Td, the reduced ionization coefficient increases exponentially with the reduced electric field, which has the same tendency with results by Morrow and Nikonov. The variation of ionization coefficient is mainly caused by the high electric field. The high electric field can greatly increase the number of high energy electrons in air that leads to the increasing number of collision ionization between electrons and molecules.

FIGURE 2

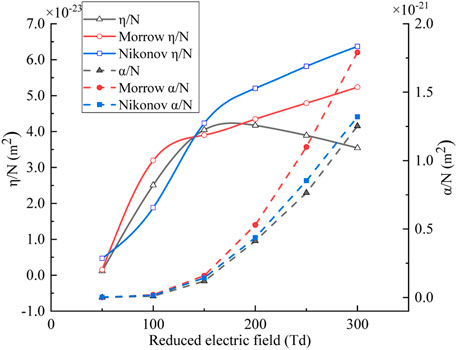
FIGURE 2. The variation of ionization coefficient and attachment coefficient with reduced electric field.

The reduced adhesion coefficient increases first and then decreases with the reduced electric field. As the reduced electric field is below 150 Td, the variation curve of attachment coefficient with reduced electric field calculated is between those obtained by Morrow and Nikonov. When the reduced electric field is below 200 Td, the adhesion coefficient increases with the reduced electric field. Hence, under the low reduced electric field, the energy of electrons is low, and the adhesion process is easy to occur. When the reduced electric field exceeds 200 Td, the adhesion coefficient decreases with the reduced electric field. The electrons are accelerated by obtaining more energy at such high electric field that make them difficult to be attached.

3.2 The Effect of Humidity on Electron Transport Parameters and Insulation Performance of Air

To study the effect of humidity on electron transport parameters and insulation performance of air, the relative humidity in the air is set as 0%, 30%, and 60%, respectively.

3.2.1 Effect of Humidity on Electron Transport Parameters

The reduced electron mobility (μ/N) and reduced electron diffusion coefficient (D/N) are important parameters during air discharges, which can be obtained from the electron energy distribution. Figure 3 shows the variation of the approximate electron mobility and approximate electron diffusion coefficient with the approximate electric field under different relative humidity conditions calculated based on Boltzmann’s equation.

FIGURE 3

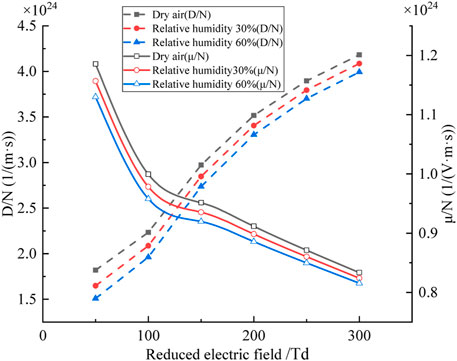
FIGURE 3. The variation of electron transport parameters with reduced field strength under different humidity.

As shown in Figure 3, μ/N decreases with the reduced electric field, and the reduction rate is faster with lower electric field. The increasing electric field can increase the kinetic energy of electrons, which accelerates the irregular movement of electrons and inhibits the directional migration of electrons. Thus, the reduced electron mobility decreases. Under the same reduced electric field, the reduced electron mobility decreases with the air humidity. For every 30% increase in relative humidity, the reduced electron mobility decreases by about 0.25 × 10²³ [1/(V·m·s)] indicating that the presence of water molecules hinders the electron mobility. The influence of humidity on D/N is similar, the electron diffusion coefficient increases with the reduced electric field. Under the same reduced electric field, the reduced electron diffusion coefficient decreases with the air relative humidity. For every 30% increase in air humidity, the reduced electron diffusion coefficient decreases by about 0.2 × 10²⁴ [1/(m.s)] showing that water molecules can weaken the diffusion of electrons.

3.2.2 Effect of Humidity on Effective Ionization Coefficient and Insulation Performance of Air

In the Thomson discharge theory, the ionization coefficient or the attachment coefficient is defined as the average number of ionizations or attachments per unit length of electrons moving along the electric field. It is used to characterize the collision ionization and electron adsorption ability of particles and electrons (Prasad, 1959; Chen, 2016). During air discharges, the Thomson ionization coefficient is mainly affected by the collision ionization between electrons and nitrogen molecules, and oxygen molecules and water molecules. The Thomson attachment coefficient is affected by the adhesion between electrons and molecules. Since the adsorption coefficient of N₂ approximately is equal to 0, the adsorption reaction here mainly considers the adsorption of electrons and O₂ molecules (Xingliang et al., 2009; Xiaobo et al., 2010).

Considering the effect of water molecules, the calculation of ionization coefficient and adhesion coefficient should be modified accordingly. The reduced ionization coefficient and adhesion coefficient in wet air can be calculated by Eq. 7.

$\{\begin{array}{l}\alpha =H{P}_w\left(0.001{\left(\frac{E}{P}\right)}^2-0.06\left(\frac{E}{P}\right)+1.0\right)+P_d\left(4.7786{\text{e}}^{-211P/E}\right)\\ \eta =H\frac{P_w}{P}{\eta }_s+P_d\left(0.01298-0.54\times {10}^{-3}\left(\frac{E}{P}\right)+0.87\times {10}^{-5}{\left(\frac{E}{P}\right)}^2\right)\end{array}(7)$

Here, H represents the relative humidity in the air. P_d is dry air partial pressure, P_w is saturated vapor partial pressure, and unit is Torr. η_s is the adhesion coefficient of water vapor, in m². When E/p ≤ 37.6 V/(cm.Torr), η_s/p = 3.67 × 10⁻⁵ (E/P)² + 0.026 (E/P)−0.273. When E/p ≥ 37.6 V/(cm.Torr), η_s/p = −2.5 × 10⁻⁵ (E/P)²–2.5 × 10⁻⁴ (E/P) + 0.23. E is the electric field intensity, and the unit is V/cm.

According to the above formulas, the reduced ionization coefficient and the reduced attachment coefficient are mainly affected by the electric field, and the relative humidity has little effect on them. The density of water molecules in the air increases accordingly with the relative humidity. Collision ionization between electrons and water molecules in the air increases with humidity, resulting in an increasing reduced ionization coefficient. However, for the low electric field and low electron energy, the effect of humidity on ionization is not obvious. The water molecules adsorb electrons to form negative ions, which plays a leading role in the total collision process. The increase in relative humidity increases the density of water molecules in the air, and the adhesion will be more obvious. Therefore, the adhesion coefficient increases with the humidity.

Due to the adsorption effect of air, the ionization coefficient will be weakened in collision ionization process. The effective ionization coefficient is applied for the difference between the reduced ionization coefficient and the reduced attachment coefficient. Figure 4 shows the effective ionization coefficient variation under different air relative humidity conditions. The effective ionization coefficient first decreases and then increases with the reduced electric field. The effective ionization coefficient decreases slightly with the relative humidity. Under the same reduced electric field, the effective ionization coefficient decreases about 4 × 10⁻²⁴ m² for each 30% increase of air relative humidity.

FIGURE 4

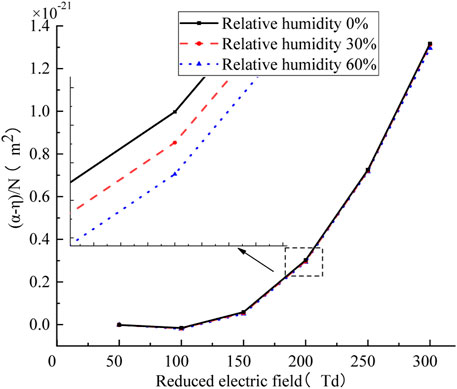
FIGURE 4. Variation of effective ionization coefficient with reduced electric field under different humidity.

As shown in Table 2, the critical breakdown electric field increases with the air relative humidity. This is caused by the increasing electron attachment velocity and the decreasing collision ionization velocity. More water molecules capturing free electrons in the air become negative ions, inhibiting the occurrence of collision ionization. Therefore, the increasing relative humidity of the air will increase the critical breakdown electric field and improve the air insulation performance.

TABLE 2

TABLE 2. Critical breakdown electric field under different humidity.

4 Conclusion

According to the collision cross-section data of different electron collision reactions, the reduced ionization coefficient, reduced attachment coefficient, and effective ionization coefficient under different humidity are studied with Boltzmann equation. Conclusions are as follows:

1) The electron energy distribution is mainly affected by the reduced electric field. With the increasing reduced electric field, the proportion of low-energy electrons decreases, and the proportion of high-energy electrons increases, while the reduced ionization coefficient increases, and the reduced adhesion coefficient increases first and then decreases.

2) When the reduced electric field remains unchanged, the electron transport parameters are affected by the relative humidity of the air. As the air relative humidity is increased from 0% to 60%, the reduced electron mobility decreases by about 0.5 × 10²³ [1/(V·m·s)], the reduced electron diffusion coefficient decreases by about 0.4 × 10²⁴ [1/(m·s)], and the effective ionization coefficient decreases by about 8 × 10⁻²⁴ m².

3) With the increasing relative humidity, the number of low-energy electrons increases and the number of high-energy electrons decreases, resulting in the increasing critical breakdown electric field of the air gap. The simulation results show that when the temperature is 300 K, the pressure is 1.0 atm, the relative humidity increases from 0% to 60%, and the critical breakdown electric field increases by 4%.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

YA contributed to the conceptualization, preparation, writing, and preparation of the original draft and handled the software. MH was in charge of the software. SM ensured project administration. YH handled the funding acquisition and validation. TH and MY supervised the study. BH was involved in the revision of the manuscript. KY validated the study. YL handled the figures.

Funding

This manuscript was supported, in part, by the Natural Science Foundation of China under Grant 51807113 and, in part, by the Natural Science Foundation of Shandong Province under Grant ZR202103040796, the Natural Science Foundation of Jiangsu Province under Grant BK20200111, the Key Laboratory of Special Machine and High Voltage Apparatus (Shenyang University of Technology), and the Ministry of Education under Grant KFKT202111.

Conflict of Interest

TH was employed by the State Grid Jiangsu Power Engineering Consulting Limited Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdel-Salam, M. (1985). Positive Wire-To-Plane Coronas as Influenced by Atmospheric Humidity. IEEE Trans. Ind. Applicat. IA-21 (1), 35–40. doi:10.1109/tia.1985.349640

CrossRef Full Text | Google Scholar

Chen, X. (2016). Study on Micro-physical Characteristics and Propagation Law of corona Discharge Pulse in corona Cage. Hubei: Wuhan University.

Google Scholar

Kelin, L. I. (2019). Study on the Influence of Humidity and Air Pressure on the Mode Conversion of DC corona Discharge. Hunan: Hunan University.

Google Scholar

Liu, Y., Jihong, L., and Bin, L. (1990). Influence of Air Density and Humidity on corona Characteristics of Conductor. Power Syst. Tech. 45 (4), 46–50.

Google Scholar

Morrow, R., and Lowke, J. J. (1997). Streamer Propagation in Air. J. Phys. D: Appl. Phys. 30 (4), 614–627. doi:10.1088/0022-3727/30/4/017

CrossRef Full Text | Google Scholar

Muniappan, M. (2021). A Comprehensive Review of DC Fault protection Methods in HVDC Transmission Systems. Prot. Control. Mod. Power Syst. 6 (1), 1–20. doi:10.1186/s41601-020-00173-9

CrossRef Full Text | Google Scholar

Nikonov, V., Bartnikas, R., and Wertheimer, M. R. (2001). Surface Charge and Photoionization Effects in Short Air Gaps Undergoing Discharges at Atmospheric Pressure. J. Phys. D: Appl. Phys. 34 (19), 2979–2986. doi:10.1088/0022-3727/34/19/308

CrossRef Full Text | Google Scholar

Prasad, A. N., and Craggs, J. D. (1960). Measurement of Ionization and Attachment Coefficients in Humid Air in Uniform fields and the Mechanism of Breakdown. Proc. Phys. Soc. 76 (2), 223–232. doi:10.1088/0370-1328/76/2/306

CrossRef Full Text | Google Scholar

Prasad, A. N. (1959). Measurement of Ionization and Attachment Coefficients in Dry Air in Uniform Fields and the Mechanism of Breakdown. Proc. Phys. Soc. 74 (1), 33–41. doi:10.1088/0370-1328/74/1/306

CrossRef Full Text | Google Scholar

Roostaee, S., Thomas, M. S., and Mehfuz, S. (2017). Experimental Studies on Impedance Based Fault Location for Long Transmission Lines. Prot. Control. Mod. Power Syst. 2 (1), 16. doi:10.1186/s41601-017-0048-y

CrossRef Full Text | Google Scholar

Su, Z., Yunkun, D., Ruishuang, Z., and Dengming, X. (2019). The Synergistic Effect Analysis of CF₃I Mixed Gas Based on Boltzmann Equation. Trans. China Electrotechnical Soc. 34 (7), 1554–1557. doi:10.19595/j.cnki.1000-6753.tces.180373

CrossRef Full Text | Google Scholar

Weichen, Y., Yunzhu, A., Yuanchao, H., Jiang, Z., Gao, X., and Zhou, L. (2021). Research on cylinder Flexible Graphite Earth Electrode (FGEE) Used to Reduce tower Earth Resistance. Electric Power Syst. Res. 196 (3), 107268. doi:10.1016/j.epsr.2021.107268

CrossRef Full Text | Google Scholar

Wen, X., Yuan, X., Lan, L., Long, M., and Hao, L. (2016). Study on the Effective Ionization Rate of Atmospheric Corona Dicharge Plasmas by Considering Humidity. IEEE Trans. Plasma Sci., 3386–3891. doi:10.1109/tps.2016.2623805

CrossRef Full Text | Google Scholar

Wenliang, Z., Yongqing, Y., Guangfan, L., and Fan, J. B. (2007). Research on UHVDC Technology. Proc. CSEE 27 (22), 1–7. doi:10.3321/j.issn:0258-8013.2007.22.001

CrossRef Full Text | Google Scholar

Xiaobo, M., Xingming, B., Zhao, X., and Cao, J. (2010). Influence of Environmental Factors on corona Inception Voltage of DC Overhead Conductors. High Voltage Eng. 36 (8), 1916–1922. doi:10.1016/j.puhe.2013.08.003

CrossRef Full Text | Google Scholar

Xingliang, J., Rui, L., Qin, H., Zhijin, Z., and Jianlin, H. (2009). DC Positive Corona Inception Performances of Stranded Conductors and its Affecting Factors. Proc. CSEE 29 (34), 108–114.

Google Scholar

Xingming, B., Jianfeng, H., Huang, H., and Wang, L.-M. (2010). Study on the Influence of Air Pressure and Humidity on the Characteristics of Negative DC corona. Proc. CSEE 30 (4), 118–123. doi:10.1021/j100398a017

CrossRef Full Text | Google Scholar

Xinjing, C., Kaiqi, W., Xinxin, W., Xiaobing, Z., and Zhiwei, L. (2015). Flow Discharge Characteristics of Air under Different Humidity. High Voltage Eng. 41 (2), 633–638. doi:10.13336/j.1003-6520.hve.2015.02.041.org6

CrossRef Full Text | Google Scholar

Xinyu, D., Xiaoyue, C., Wei, L., Guozhou, X., Lei, L., Xishan, W., et al. (2018). Study on Air Insulation Performance at Different Altitude Based on Boltzmann Equation. Water Resour. Power 36 (12), 167–170.

Google Scholar

Xun, S., Ouyang, T., Khajorntraidet, C., Li, Y., Li, S., Zhuang, J., et al. (2021). Mixture Density Networks-Based Knock Simulator. IEEE/ASME Trans. Mechatronics (99), 1. doi:10.1109/TMECH.2021.3059775

CrossRef Full Text | Google Scholar

Xun, S., Ouyang, T., Nan, Y., and Zhuang, J. (2021). Sample-based Neural Approximation Approach for Probabilistic Constrained Programs. IEEE Trans. Neural Networks Learn. Syst., 1–8. doi:10.1109/TNNLS.2021.3102323

CrossRef Full Text | Google Scholar

Xun, S., and Pongsathorn, R. (2021). Pedestrian-aware Statistical Risk Assessment. IEEE Trans. Intell. Transportation Syst., 1–9. doi:10.1109/TITS.2021.3074522

CrossRef Full Text | Google Scholar

Xun, S., and Raksincharoensak, P. (2021). Statistical Models of Near-Accident Event and Pedestrian Behavior at Non-signalized Intersections. J. Appl. Stat., 1–21. doi:10.1080/02664763.2021.1962263

CrossRef Full Text | Google Scholar

Xun, S., Zhang, X., Ouyang, T., Li, Y., and Raksincharoensak, P. (2020). Cooperative Comfortable-Driving at Signalized Intersections for Connected and Automated Vehicles. IEEE Robotics Automation Lett. 5 (4), 6247–6254. doi:10.1109/lra.2020.3014010

CrossRef Full Text | Google Scholar

Xun, S., Zhang, Y., Kota, S., and Shen, T. (2020). Gaussian Mixture Model Clustering-Based Knock Threshold Learning in Automotive Engines. IEEE/ASME Trans. Mechatronics 25 (99), 2981–2991. doi:10.1109/TMECH.2020.3000732

CrossRef Full Text | Google Scholar

Xun, S., Zhang, Y., Tielong, S., and Khajorntraidet, C. (2017). Spark advance Self-Optimization with Knock Probability Threshold for Lean-Burn Operation Mode of SI Engine. Energy 122 (MAR.1), 1–10. doi:10.1016/j.energy.2017.01.065

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Wu, L., Shen, X., Jia, J., Li, Z., et al. (2021). Intelligent Data-Driven Decision-Making Method for Dynamic Multi-Sequence: An E-Seq2Seq Based SCUC Expert System. IEEE Trans. Ind. Inform., 1. doi:10.1109/tii.2021.3107406

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Xing, C., Yi, D., Jia, J., Chen, D., et al. (2021). Deep Learning-Based SCUC Decision-Making: An Intelligent Data-Driven Approach with Self-Learning Capabilities. IET Generation, Transmation&Distribution, 1–12. doi:10.1049/gtd2.12315

CrossRef Full Text | Google Scholar

Yuanchao, H., Yitong, L., Yunzhu, A., Wen, X., Li, H., Su, M., et al. (2021). Laboratory Study on Negative Spark Inception Direction and Breakdown Characteristics in Rod–Rod Air Gaps. Electric Power Syst. Res. 201, 107498. doi:10.1016/j.epsr.2021.107498

CrossRef Full Text | Google Scholar

Yuke, F. (2017). Experimental Study on Influence of Air Pressure and Humidity on corona Characteristics of High Voltage Electrode under Compound Voltage. Beijing: North China Electric Power University.

Google Scholar

Zhao, M., Xiaoxin, Z., Yuwei, S., and Limei, Z. (2015). Form and Development Trend of Future Distribution System. Proc. CSEE 35 (6), 1289–1298. doi:10.13140/RG.2.1.3664.4004

CrossRef Full Text | Google Scholar

Zhenya, L. (2005). Special Album of Research Results of UHVDC Transmission Technology. Beijing: China electric power Press.

Google Scholar

Zhenya, L. (2005). UHV Power Grid. Beijing: China economic publishing house.

Google Scholar