Power Grid Frequency Regulation Strategy for Photovoltaic Plant Based on Multi-Objective Harris Hawks Optimization

To settle the issue of balance between two objectives, i.e., photovoltaic (PV) power station output power maximization and frequency regulation (FR) signals response, a novel PV reconfiguration strategy is proposed in this work, which maximizes the output power through PV reconfiguration, and meanwhile utilizes the energy storage system (ESS) to decrease the PV plant generated power’ deviation from FR signals. Above all, a model of PV-storage power station reconfiguration is designed to minimize the power bias of both rated power and FR signals. Then, the multi-objective Harris hawks optimization (MHHO) is used to obtain the Pareto front which can optimize the above two objectives due to its high optimization efficiency and speed. Subsequently, the optimal compromise solution is selected by the decision-making method of VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR). Aiming to substantiate the efficacy of the proposed technique, the case studies are carried out under partial shading condition (PSC) with constant and time-varying FR signals. The simulation results show that, compared with the situation without optimization, the power deviations of the two objectives are reduced by 25.11 and 75.76% under constant FR signals and 23.27 and 55.81% under time-varying FR signals by proposed method, respectively.

Introduction

Nowadays, major countries in the world are committed to developing the application technology of renewable energy resources to tackle the incoming traditional energy crisis. With respect to its abundant reserves and environmentally-friendly quality, solar energy has become the most widespread energy resource (Gan et al., 2019; Mahidin et al., 2021). In general, photovoltaic (PV) arrays operate at the maximum power point by maximum power point tracking (MPPT) (Salam et al., 2013; Yang et al., 2016) technique to maximize the outputs of PV station. However, in the field application of large-scale PV power generation system, the bypass diodes of PV panel will be activated under partial shading condition (PSC), resulting in inconformity of output characteristic between various PV array rows (Sai Krishna and Moger, 2019; Zhang et al., 2021a). And further consequence of multi-peak with power-voltage (P-V) curve is caused which can prominently decrease PV plant power generation and make it more difficult for MPPT. Besides, PSC could lead to hot spot phenomenon which may break PV panels and even cause a fire. In addition, PSC is mostly attributed to clouds, building shadows, dust, birds’ feces, manufacturing defect and non-uniform aging of PV components (Yang et al., 2018a; Laudani et al., 2018).

For the purpose of mitigating the effects of PSC as well as enhancing the power generation of PV station, altering the topological structure of PV components is employed, which could equivalently disperse the originally-centralized shadow on the array surface to the whole array. In recent years, researchers have developed multiple methods of PV arrays reconfiguration, which are classified mainly into static reconfiguration techniques and dynamic techniques (Kaushika and Gautam, 2003; Yang et al., 2021).

Three different topological structures of PV arrays, i.e., series–parallel (SP), bridge linked (BL), and total-cross-tied (TCT), are studied and compared under PSC in literature (Kaushika and Gautam, 2003; Ajmal et al., 2020), of which the performance of TCT is ascertained the best topological configuration theoretically for its robustness. But TCT has higher wiring losses for its longer cable. Literature (Rani et al., 2013) reconfigures the PV components based on Sudoku patterns, and a variant of sudoku-based arrangement (Horoufiany and Ghandehari, 2018) is proposed to tackle with mutual shadows (Horoufiany and Ghandehari, 2017; Yang et al., 2020a). By introducing mixed integer quadratic programming, literature (Shams el-Dein et al., 2013) utilizes the mathematical formulation to dissipate the shadow of PV array. TomTom puzzle divides the PV array into irregular pieces with particular calculation rule assigned for each piece, and then accomplishes the reconfiguration of PV array (Tatabhatla et al., 2019; Yang et al., 2019). The essential characteristic of static reconfiguration is that only the physical location of the PV module but not the electrical connection will change. Moreover, as a one-time reconstruction technique, static method is not able to automatically alter reconfiguration schema to meet various shadow pattern. Therefore, the PV system with static method must artificially constructs a new configuration when a new shadow appears. In practice, shadow patterns frequently change, hence static method is not universally applicable, nor is it suitable for real-time scenarios.

Dynamic PV array reconfiguration techniques come into being in response to the aforementioned drawback of static techniques. Different from static methods, dynamic methods can dynamically change the electrical connection of PV modules in real time by switching matrix according to the shadow change (La Manna et al., 2014; Yang et al., 2018b). Literature (Vicente et al., 2015) applies rough set theory to PV array reconfiguration. Literature (Sanseverino et al., 2015) builds a control system embedded with Munkres algorithm to alter the switches layout. Feed forward artificial neural network is utilized to alter the switch matrix by training irradiance data and short-circuit currents (Karakose et al., 2014). Nowadays, meta-heuristic algorithms has become a prevailing tendency in applicating to PV array reconfiguration, such as genetic algorithm (GA) (Deshkar et al., 2015), flow regime algorithm (FRA) (Babu et al., 2020), particle swarm optimization (PSO) (Babu et al., 2018), grasshopper optimization algorithm (GOA) (Fathy, 2018), butterfly optimization algorithm (BOA) (Fathy, 2020), artificial ecosystem-based optimization (AEO) (Yousri et al., 2020) and so forth.

However, existing researches take little account of the combination of PV array reconfiguration and power grid frequency regulation (FR) (Xi et al., 2018), nor do they take the power fluctuation balance of energy storage system (ESS) (Jin et al., 2017; Zhou et al., 2021) into consideration. Hence, this work proposes a novel technique of PV array associating power grid FR, to promote the dynamic-response performance of the entire regional power grid.

Given the confliction between power outputs maximization and minimizing FR signals’ deviation from the output power, this work employs the efficient multi-objective Harris hawks optimization (MHHO) to obtain the Pareto front promptly, then Visekriterijumska Optimizacija I Kompromisno Resenje (VIKOR) strategy is adopted to determine the optimum compromising solution based on aforementioned Pareto front.

Mathematical Model of PV-Storage Power Station Reconfiguration

Modeling of PV Array

Each PV module is formed by multiple of PV cell strings connected in parallel, while PV array is comprised of several PV modules connected in series and parallel. Accordingly, multiple PV arrays make up a PV system. The most frequently employed model is the single diode PV cell model (Jacob et al., 2015; Humada et al., 2016; Yang et al., 2020b), illustrated as Figure 1A.

FIGURE 1

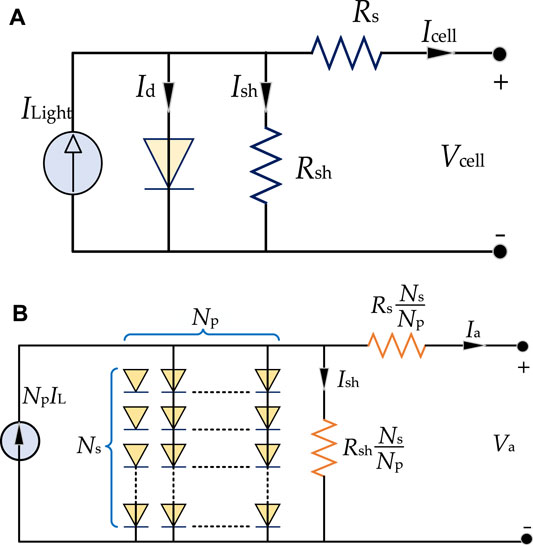
FIGURE 1. (A) Equivalent circuit of single diode PV cell and (B) equivalent circuit of a PV component with N_s × N_p modules.

Calculated by Kirchhoff’s Current Law (KCL), the operation current of PV cell $I_{\text{cell}}$ is given below:

$I_{\text{cell}}=I_{\text{Light}}-I_{\text{d}}-I_{\text{sh}}(1)$

where $I_{\text{Light}}$ denotes the photo-generated current; $I_{\text{d}}$ is the current of diode; $I_{\text{sh}}$ represents the current of shunt resistor.

By replacing the $I_{\text{d}}$ and $I_{\text{sh}}$, the Eq. 1 can be rewritten as Eq. (2).

$I_{\text{cell}}=I_{\text{Light}}-I_{\text{o}}\left[\text{exp}\left(q\frac{V_{\text{cell}}+I_{\text{cell}}{R}_{\text{s}}}{B\sigma T_{\text{c}}}-1\right)\right]-\frac{V_{\text{cell}}+I_{\text{cell}}{R}_{\text{s}}}{R_{\text{sh}}}(2)$

where $I_{\text{o}}$ and q denote the leakage current and electronic charge of the diode, respectively; $T_{\text{c}}$, $V_{\text{cell}}$, $R_{\text{sh}}$, $R_{\text{s}}$, $\sigma$ and $\text{B}$ are the operation temperature and voltage, shunt and series resistance of PV cells, ideality factor and Boltzmann’s constant.

The output current $I_{\text{m}}$ of one PV module comprised of $n_{\text{s}}$ PV cells in series can be calculated as follows:

$I_{\text{m}}=I_{\text{Light}}-I_{\text{o}}\left[\text{exp}\left(q\frac{V_{\text{m}}+I_{\text{m}}{R}_{\text{S}}}{n_{\text{s}}b\sigma T_{\text{c}}}-1\right)\right]-\frac{V_{\text{m}}+I_{\text{m}}{R}_{\text{S}}}{R_{\text{SH}}}(3)$

where $I_{\text{m}}$ denotes the PV module current output; $V_{\text{m}}$ represents the operation voltage of PV module; $R_{\text{SH}}$ and $R_{\text{S}}$ separately refer to the parallel and series resistor of PV module.

Moreover, $I_{\text{Light}}$ represents the photo-generated current of PV module which is caused by photoelectric effect, and its formula is given below:

$I_{\text{Light}}=\frac{G}{G_0}\left[I_{\text{stc}}+K_{\text{sc}}\left(T_{\text{c}}-T_0\right)\right](4)$

where $G$ and $G_0$, $I_{\text{stc}}$, $T_{\text{c}}$ and $T_0$, $K_{\text{sc}}$ represent the actual and reference irradiance, the photo-generated current under standard environment condition, the operating and standard temperature, and the short-circuit current factor, respectively.

Thus, as demonstrated in Figure 1B, it can be further deduced the output current $I_{\text{a}}$ of the PV component formed by N_s×N_p PV modules can be described as:

$I_{\text{a}}=N_{\text{p}}{I}_{\text{L}}-N_{\text{p}}{I}_{\text{o}}\left[\text{exp}\left(q\frac{V_{\text{a}}+\frac{N_{\text{s}}}{N_{\text{p}}}{I}_{\text{a}}{R}_{\text{S}}}{N_{\text{s}}{n}_{\text{s}}b\sigma T_{\text{c}}}-1\right)\right]-\frac{V_{\text{a}}+\frac{N_{\text{s}}}{N_{\text{p}}}{I}_{\text{a}}{R}_{\text{S}}}{\frac{N_{\text{s}}}{N_{\text{p}}}{R}_{\text{SH}}}(5)$

where $V_{\text{a}}$ and $I_{\text{a}}$ respectively refer to the operation current and operation voltage of PV components.

Modeling of PV Array in TCT Structure

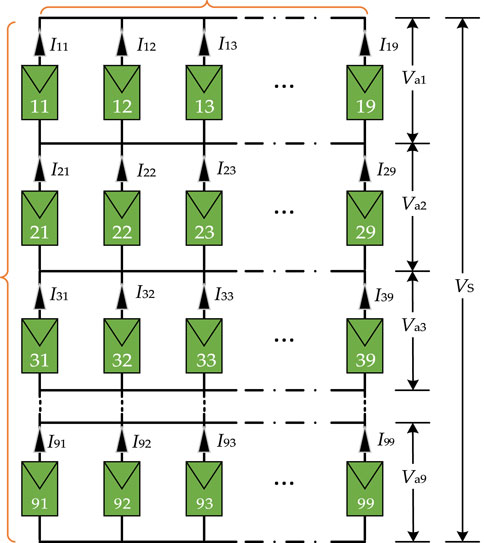
Because of the better stability of TCT topology under PSC, it is widely applied to the theoretical research of PV reconfiguration (Bingöl and Özkaya, 2018). As depicted in Figure 2, the 9 × 9 PV array is connected in TCT configuration, the output voltage and current of which can be calculated by:

$V_{\text{S}}={\displaystyle \sum _{i=1}^9{V}_{\text{a}i}}(6)$

$I_{\text{S}}={\displaystyle \sum _{j=0}^9\left(I_{ij}-I_{\left(i+1\right)j}\right)}=0, i=\mathrm{0,1,2},\dots ,8(7)$

where $V_{\text{S}}$ represents the entire voltage of PV system; $V_{\text{a}i}$ represents the row voltage at the $i$ th row; $I_{\text{S}}$ represents the entire current; and $I_{ij}$ is the flowing current at the $i$ th row and the $j$ th column.

FIGURE 2

FIGURE 2. One 9 × 9 TCT array in a PV station.

Optimization Objective

This work features two sets of assignments: one is to reduce the power deviation y₁ of real PV power generation average value from the rated PV power; while the other aims to minimize average value y₂ of the power difference between the outputs of PV station and FR signals. Meanwhile, the peak-to-valley deviation of the power curve is taken into consideration to control its fluctuation. In consequence the proposed objective function can be computed as follows:

$\{\begin{array}{c}\min f_1=P_{\text{pv}}^{\text{rate}}-\frac{1}{T}{\displaystyle \sum _{t\in T}{P}_{\text{pv}}\left(t\right)}\\ \min f_2=\frac{1}{T}{\displaystyle \sum _{t\in T}\left|P_{\text{FR}}\left(t\right)-\left[P_{\text{pv}}\left(t\right)-P_{\text{ESS}}\left(t\right)\right]\right|}+\underset{t\in T}{\max }\left[P_{\text{pv}}\left(t\right)-P_{\text{ESS}}\left(t\right)\right]-\underset{t\in T}{\min }\left[P_{\text{pv}}\left(t\right)-P_{\text{ESS}}\left(t\right)\right] \end{array}(8)$

where $P_{\text{pv}}^{\text{rate}}$ represents the rated output power of PV plant; T denotes the duration of FR; $P_{\text{pv}}\left(t\right)$, $P_{\text{ESS}}\left(t\right)$, $P_{\text{FR}}\left(t\right)$ respectively denote the generated power of the PV station with ESS, the charging power of ESS, and the FR signals in the $t$ th control time period.

Constraint Condition

Each PV module can only switch to other row in the same column to reconfigure PV system via switching matrix, which is called constraint condition of the electrical switch states.

The power and capability constraints should be satisfied in the ESS, shown as follows:

$P_{\text{ESS}}^{\text{min}}\le P_{\text{ESS}}\left(t\right)\le P_{\text{ESS}}^{\text{max}}, t\in T(9)$

$SO{C}_{\text{ESS}}^{\text{min}}\le SO{C}_{\text{ESS}}\left(t\right)\le SO{C}_{\text{ESS}}^{\text{max}}, t\in T(10)$

$SO{C}_{\text{ESS}}\left(t\right)=\{\begin{array}{c}SO{C}_{\text{ESS}}\left(t-1\right)+P_{\text{ESS}}\left(t\right)\cdot \Delta t\cdot {\eta }_{\text{ch}}/E_{\text{ESS}},\text{ if} P_{\text{ESS}}\left(t\right)\ge 0 \\ SO{C}_{\text{ESS}}\left(t-1\right)+P_{\text{ESS}}\left(t\right)\cdot \Delta t/\left({\eta }_{\text{dis}}\cdot E_{\text{ESS}}\right), otherwise \end{array}(11)$

where $P_{\text{ESS}}^{\text{max}}$, $P_{\text{ESS}}^{\text{min}}$, $SO{C}_{\text{ESS}}^{\text{max}}$, $SO{C}_{\text{ESS}}^{\text{min}}$ severally represent the maximum and minimum charging power, and the maximum, minimum state of charge (SOC) of ESS; ${\eta }_{\text{ch}}$ and ${\eta }_{\text{dis}}$ are the charging and discharging efficiency; $\Delta t$ denotes the control period; and $E_{\text{Ess}}$ denotes the rated capacity of ESS.

Optimization for PV-Storage Station Reconfiguration Based on MHHO and VIKOR

Design of MHHO

MHHO simulates the cooperation mechanism and pounce style in the hunting of Harris hawk’s predation. The purpose of this research is to integrate the non-dominated rank sorting with MHHO, evolving into a multi-objective optimization algorithm.

Exploration Stage of MHHO

In MHHO, the Harris hawks can be seen as the candidate solution, and in each iteration process the optimal solution is considered as the prey. Harris hawks apply two types of inhabitation tactics with equally mathematical probability, the specific model of which is demonstrated as follows:

$X\left(t+1\right)=\{\begin{array}{c}{X}_{\text{rand}}\left(t\right)-r_1\left|X_{\text{rand}}\left(t\right)-2r_{2}X\left(t\right)\right|q\ge 0.5\\ (X_{\text{prey}}\left(t\right)-X_{\text{m}}\left(t\right))r_3(X_{\text{rand}}\left(t\right)-r_3\left(\text{Ub}-\text{Lb}\right) q<0.5\end{array}(12)$

where $X\left(t+1\right)$ and $X\left(t\right)$ respectively denote the hawk’s position vector in the next iteration and in the present; $X_{\text{prey}}\left(t\right)$ is the position vector of the prey; $r_1$, $r_2$, $r_3$, $q$ are random numbers between 0 and 1; $U_b$ and $L_b$ represent search bounds; $X_{\text{rand}}\left(t\right)$ denotes the stochastic individual in the present population; and $X_{\text{m}}\left(t\right)$ denotes the population’s average position vector.

Exploitation Stage of MHHO

The flock of hawks round up the prey softly or strongly from all directions by tracing the left escape energy of prey. MHHO algorithm introduces the parameter of E: the flock performs soft besiegement based on Eq. 13, 14 if |E| $<$ 0.5, otherwise the hard encirclement would be executed based on Eq. 15.

$X\left(t+1\right)=\Delta X\left(t\right)-E\times |J{X}_{\text{prey}}\left(t\right)-X\left(t\right)|(13)$

$\Delta X\left(t\right)=X_{\text{prey}}\left(t\right)-X\left(t\right)(14)$

where $J=2(1-r_5)$, and J represents the prey’s leaping distance when they act on escaping; and $r_5$ is a digit randomly generated by the computer between 0 and 1.

$X\left(t+1\right)=X_{\text{prey}}\left(t\right)-E\left|\Delta X\left(t\right)\right|(15)$

Multi-Objective Non-dominated Sorting and Archive Management

MHHO selects an optimal Pareto front via non-dominated rank sorting, then introduces archive management to control Pareto solutions.

When a new solution is created, it is to be compared with the ones in the archive. Were it dominated by those, the new solution would not be collected into archive; Were a few individuals in the archive dominated by new solution, those would be replaced by the new one; if it is none of the above, this new solution would also be collected. Additionally, when the quantity of solutions exceeds the archive’ capacity, the roulette shall roll out the more crowded solutions.

Fitness Function

On the basis of the penalty function technique, the fitness function of MHHO is calculated by Eqs 16, 17.

$\{\begin{array}{c}{g}_1=f_1+{\displaystyle \sum }_{t\in T}Pe\left(t\right)\\ g_2=f_2+{\displaystyle \sum }_{t\in T}Pe\left(t\right)\end{array}(16)$

$Pe\left(t\right)=\{\begin{array}{c}\varphi , \mathrm{i}\mathrm{f} \mathrm{v}\mathrm{i}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}\\ 0, \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}(17)$

where $Pe\left(t\right)$ denotes the penalty part of the restraint conditions in Eq. 10 in the $t$ th dispatching period of FR signals; and $\varphi$ denotes the penalty factor that usually employs a large positive number.

Design of VIKOR

The optimal compromise solution can be impersonally chosen by VIKOR (Lin et al., 2021) decision-making approach from the Pareto front solutions obtained by MHHO, the design process of which is elaborated below:

Step 1: Define the plus-minus ideal solutions on the basis of the obtained Pareto front, as given:

$\{\begin{array}{c}{\mathit{v}}^{+}=\left\{v_1^{+},v_2^{+}\right\}\\ {\mathit{v}}^{-}=\left\{v_1^{-},v_2^{-}\right\}\end{array}(18)$

$\{\begin{array}{c}{v}_j^{+}=\underset{i=\mathrm{1,2},\dots ,n}{\min }{v}_j^i,j=\mathrm{1,2};\\ v_j^{-}=\underset{i=\mathrm{1,2},\dots ,n}{\max }{v}_j^i,j=\mathrm{1,2};\end{array}(19)$

where $v_j^i$ is the corresponding $i$ th Pareto numerical solution of the $j$ th objective function; and ${\mathit{v}}^{+}$ and ${\mathit{v}}^{-}$ respectively represent the plus and minus perfect solutions.

Step 2: Calculate the values of the cluster effect and single regret:

$U_i={\displaystyle \sum }_{j=\mathrm{1,2}}{\phi }_j\frac{v_j^{+}-v_j^i}{v_j^{+}-v_j^{-}}, i=\mathrm{1,2},\dots ,n(20)$

$R_i=\underset{j=\mathrm{1,2}}{\max }\left({\phi }_j\frac{v_j^{+}-v_j^i}{v_j^{+}-v_j^{-}}\right), i=\mathrm{1,2},\dots ,n(21)$

where ${\phi }_j$ is the weighting factor of the $j$ th objective function; and $U_i$, $R_i$ denote the cluster effect value and single regret value corresponding to $i$ th Pareto front solution, separately.

Step 3: Determine the integrated valuation of all the Pareto front solutions:

$Q_i=\gamma \cdot \frac{U_i-U^{+}}{U^{-}-U^{+}}+\left(1-\gamma \right)\cdot \frac{R_i-R^{+}}{R^{-}-R^{+}}, i=\mathrm{1,2},\dots ,n(22)$

$\{\begin{array}{c}{U}^{+}=\underset{i=\mathrm{1,2},\dots ,n}{\min }{U}_i\\ U^{-}=\underset{i=\mathrm{1,2},\dots ,n}{\max }{U}_i\end{array}(23)$

$\{\begin{array}{c}{R}^{+}=\underset{i=\mathrm{1,2},\dots ,n}{\min }{R}_i\\ R^{-}=\underset{i=\mathrm{1,2},\dots ,n}{\max }{R}_i\end{array}(24)$

where $\gamma$ means the weighting factor of the cluster effect value; $Q_i$ denotes the integrated valuation value of the $i$ th Pareto front solution; $U^{+}$, $U^{-}$ denote the minimum and maximum values of cluster effect; and $R^{+}$, $R^{-}$ represent the minimum and maximum values of single regret.

Step 4: Find the optimal eclectic solution on the basis of integrated valuation value, as follows:

${\mathit{x}}_{\text{opti}}=\arg \underset{i=\mathrm{1,2},\dots ,n}{\min }{Q}_i\left({\mathit{x}}_i^{\ast }\right)(25)$

where ${\mathit{x}}_i^{\ast }$ represents the $i$ th Pareto solution; ${\mathit{x}}_{\text{opti}}$ is the optimal eclectic solution.

Procedure Steps

With regard to the PV station array reconfiguration, the procedure that MHHO executes is demonstrated in the following Table 1.

TABLE 1

TABLE 1. The procedure pseudocode of MHHO for PV station array reconfiguration.

Case Studies

The simulation experiment conducted herein designs a 40 MW PV power plant comprised of 50 identical 9 × 9 sub-systems, to test the MHHO performance in the experiment of PV power plant’ response to FR signals. The parameters of the sub-systems are derived from literature (Zhang et al., 2021b), and the specific parameter settings of PV module are tabulated in Table 2. This work supposes all PV arrays’ operation temperature to be at 25°C, and the shadow distribution of each sub-system to be consistent. Figure 3A illustrates sub-system’s shadow distribution in 10 min, while Table 3 gives the main parameters of ESS.

TABLE 2

TABLE 2. Specific parameter settings of PV modules.

FIGURE 3

FIGURE 3. Irradiance distribution of PV array before and after reconfiguration: (A) shadow distribution for every sub-system of PV station with ESS, (B) optimal shadow distribution under constant FR signals obtained by MHHO and (C) optimal shadow distribution under time-varying FR signals obtained by MHHO.

TABLE 3

TABLE 3. Main parameters of ESS.

The number of agents (N_pop) is 200. Meanwhile the termination number of iterations (Max_itera) is set as 100. Moreover, all of the weighting factor in VIKOR are set as: ${\phi }_j$ = 0.5. All simulation tests are conducted on Matlab R2019b.

Constant FR Signals

To testify the effectiveness of the proposed algorithm under the constant FR signals, the constant FR signals are designed as follows:

$P_{\text{FR}}\left(t\right)=35 \text{MW}(26)$

The shadow distribution of PV array after reconfiguration under constant FR signals is depicted in Figure 3B. Obviously, MHHO commendably disperse the originally-centralized shadow to the whole array. Meanwhile, the optimal compromise and eclectic solution obtained by VIKOR exhibits more balance among two objectives than other Pareto front solutions, as it is shown in Figure 4A. In particular, the results of optimal eclectic solution are: the power deviation between the average generated power of PV array and the rated value is 9.128MW; the average power deviation between the output power of PV-storage station and constant FR signals is 2.903MW.

FIGURE 4

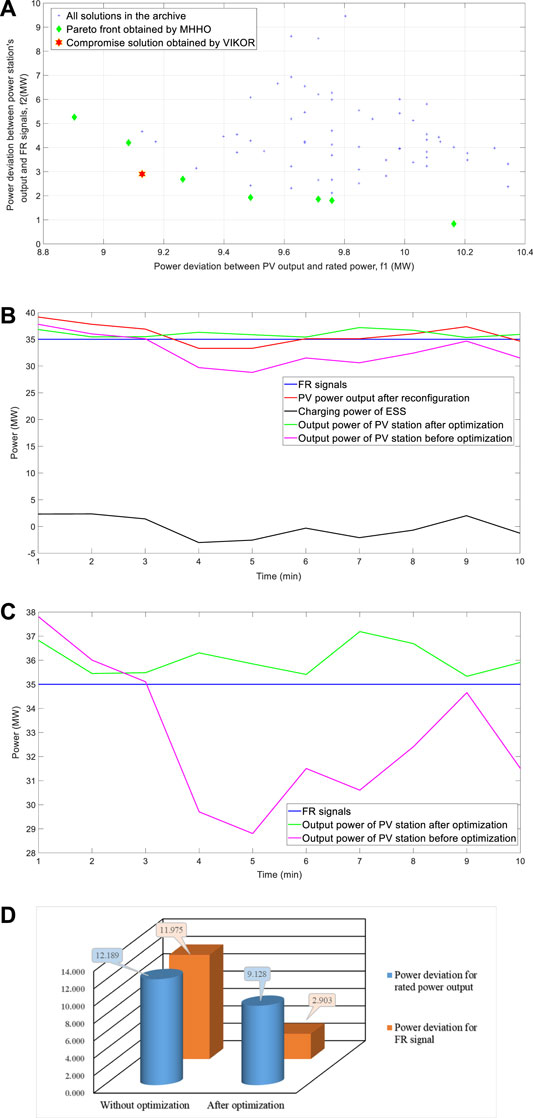
FIGURE 4. The optimal solution and the comparison between the optimized results and original ones for constant FR signals test: (A) Pareto front obtained by MHHO and optimal compromise solution by VIKOR, (B) output results responding to FR signals, (C) power output curve of PV power station before and after optimization and (d) comparison of optimized power deviation with those of the original.

Figure 4B illustrates the output power with optimization under constant FR signals of PV array, PV power plant, and ESS. With the help of ESS, the output power of PV plant is higher than that without optimization and gets closer to FR signal. The power outputs of PV power plant before and after optimization are given in Figure 4C and Figure 4D. After optimization by the proposed method, the objective f₁ drops sharply by 25.11%, while the objective f₂ drops by 75.76%. In addition, the output power with optimization experiences less power fluctuation.

Time-Varying FR Signals

The time-varying FR signals are designed to testify the effect of the proposed approach under the condition of it, as follows:

$P_{\text{FR}}\left(t\right)=\{\begin{array}{c}36, 0min\le t<3min\\ 32, 4min\le t<7min\\ 35, 7min\le t<10min\end{array}(27)$

Figure 3C shows the irradiation distribution of PV array after reconfiguration under time-varying FR signals, of which the shadow distribution is more uniform compared to that without optimization. In the meantime, the compromise solution obtained by VIKOR shows better equilibrium among multiple targets than other Pareto front solutions, as demonstrated in Figure 5A. Particularly, the results of optimal compromise solution are: the power deviation between the average generated power of PV array and the rated value is 9.353MW; the average power deviation between the output power of PV-storage station and constant FR signals is 4.708MW.

FIGURE 5

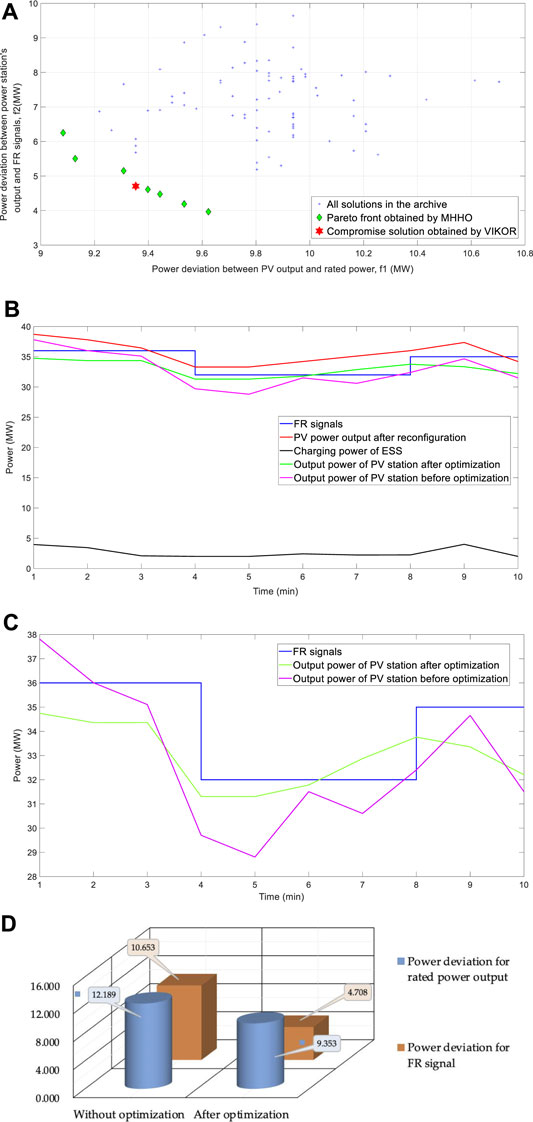
FIGURE 5. The optimal solution and the comparison between the optimized results and original ones for time-varying FR signals test: (a) Pareto front obtained by MHHO and optimal compromise solution by VIKOR, (b) output results responding to FR signals, (c) power output curve of PV power station before and after optimization and (d) comparison of optimized power deviation with those of the original.

Figure 5B depicts the output power with optimization of PV array, PV power plant, and ESS. It can be deduced that due to the coordination of ESS, the output power of PV plant gets closer to FR signal. Figures 5C, D gives the results of PV power plant’s power output before and after optimization. After optimization by the proposed method, the general deviation between the output power of PV plant and FR signals drops sharply by 55.81%, while the power deviation between the PV plant output power and rated power drops by 23.27%. Compared with constant FR signals, the optimization effect of objective f₂ slightly drops while that of objective f₁ is close. And the possible reason is that time-varying FR signals are more complicated. Also, the output power with optimization experiences less power fluctuation.

Conclusions and Perspectives

Founded on PV array reconfiguration, a new technique of PV station participating grid FR is presented in this work. The proposed technique contributes to effective power response of PV plant to FR signals, and is consequently conducive to improving the frequency stability of the regional grid. The main contributions of this work are summed up as follows:

1) Not only can the proposed MHHO algorithm optimize two conflicted objectives simultaneously, but reconfigure PV array for FR expeditiously. Moreover, MHHO can find a series of solutions that fit simultaneously two objectives to meet the different dispatch needs;

2) To entail the balance of each objective function, VIKOR decision-making technique is adopted to select the optimal eclectic solution, which gives a guarantee of the balance between PV power station’s economical operation and its security;

3) By virtue of the proposed method of PV array reconfiguration coordinated with ESS, the PV station is able to track the maximum power point as possible under any irradiance distribution, reducing the abandoned solar energy. In the meanwhile, the proposed method increases both economic benefit and security of the PV station.

However, it needs many independent runs to find the optimal solution due to the high randomness and local convergence of MHHO. Moreover, the implementation of ESS increase the cost of FR response. In addition, the proposed strategy cannot work in the condition of no shadow. Besides, The future work will focus on the following perspectives:

• Except for simulation test, hardware-in-the-loop (HIL) experiments should be performed to examine the practical effect of proposed method;

• More studies on larger scales of PV array are urgent to testify the universal applicability of proposed approach.

• Weighting parameters are difficult to adjust which significantly affect the convergence speed of meta-heuristic algorithms and the spatial distribution of the optimal solution and hence deserve deeper research;

• In addition to meta-heuristic algorithms, hybrid algorithm and AI algorithm should be applied in this field of PV array reconfiguration participating grid FR;

• In addition to VIKOR, more attention should be paid to other decision-making technique to find more reasonable compromise solution.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

LW: Conceptualization, Writing- Reviewing and Editing. XC: Writing-Original draft preparation, Investigation. XL: Writing-Reviewing and Editing. WH: Supervision. YJ: Supervision.

Funding

This work was supported by the Key Technologies R&D Program of Henan Province (No. 202102210335/212102210026); the Key Scientific Research Projects of Institutions of Higher Education in Henan Province (No. 20B413007).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ajmal, A. M., Sudhakar Babu, T., Ramachandaramurthy, V. K., Yousri, D., and Ekanayake, J. B. (2020). Static and Dynamic Reconfiguration Approaches for Mitigation of Partial Shading Influence in Photovoltaic Arrays. Sustainable Energ. Tech. Assessments 40, 100738. doi:10.1016/j.seta.2020.100738

CrossRef Full Text | Google Scholar

Babu, T. S., Yousri, D., and Balasubramanian, K. (2020). Photovoltaic Array Reconfiguration System for Maximizing the Harvested Power Using Population-Based Algorithms. IEEE Access 8, 2169–3536. doi:10.1109/access.2020.3000988

CrossRef Full Text | Google Scholar

Babu, T. S., Ram, J. P., Dragicevic, T., Miyatake, M., Blaabjerg, F., and Rajasekar, N. (2018). Particle Swarm Optimization Based Solar PV Array Reconfiguration of the Maximum Power Extraction under Partial Shading Conditions. IEEE Trans. Sustain. Energ. 9 (1), 74–85. doi:10.1109/tste.2017.2714905

CrossRef Full Text | Google Scholar

Bingöl, O., and Özkaya, B. (2018). Analysis and Comparison of Different PV Array Configurations under Partial Shading Conditions. Solar Energy 160, 336–343.

Google Scholar

Deshkar, S. N., Dhale, S. B., Mukherjee, J. S., Babu, T. S., and Rajasekar, N. (2015). Solar PV Array Reconfiguration under Partial Shading Conditions for Maximum Power Extraction Using Genetic Algorithm. Renew. Sust. Energ. Rev. 43, 102–110. doi:10.1016/j.rser.2014.10.098

CrossRef Full Text | Google Scholar

Fathy, A. (2020). Butterfly Optimization Algorithm Based Methodology for Enhancing the Shaded Photovoltaic Array Extracted Power via Reconfiguration Process. Energ. Convers. Manag. 220, 113115. doi:10.1016/j.enconman.2020.113115

CrossRef Full Text | Google Scholar

Fathy, A. (2018). Recent Meta-Heuristic Grasshopper Optimization Algorithm for Optimal Reconfiguration of Partially Shaded PV Array. Solar Energy 171, 638–651. doi:10.1016/j.solener.2018.07.014

CrossRef Full Text | Google Scholar

Gan, W., Ai, X., Fang, J., Yan, M., Yao, W., Zuo, W., et al. (2019). Security Constrained Co-planning of Transmission Expansion and Energy Storage. Appl. Energ. 239, 383–394. doi:10.1016/j.apenergy.2019.01.192

CrossRef Full Text | Google Scholar

Horoufiany, M., and Ghandehari, R. (2017). Optimal Fixed Reconfiguration Scheme for PV Arrays Power Enhancement under Mutual Shading Conditions. IET Renew. Power Generation 11, 1456–1463. doi:10.1049/iet-rpg.2016.0995

CrossRef Full Text | Google Scholar

Horoufiany, M., and Ghandehari, R. (2018). Optimization of the Sudoku Based Reconfiguration Technique for PV Arrays Power Enhancement under Mutual Shading Conditions. Solar Energy 159, 1037–1046. doi:10.1016/j.solener.2017.05.059

CrossRef Full Text | Google Scholar

Humada, A. M., Hojabri, M., Mekhilef, S., and Hamada, H. M. (2016). Solar Cell Parameters Extraction Based on Single and Double-Diode Models: a Review. Renew. Sust. Energ. Rev. 56, 494–509. doi:10.1016/j.rser.2015.11.051

CrossRef Full Text | Google Scholar

Jacob, B., Balasubramanian, K., Babu T, S., Azharuddin, S. M., and Rajasekar, N. (2015). Solar PV Modelling and Parameter Extraction Using Artificial Immune System. Energ. Proced. 75, 331–336. doi:10.1016/j.egypro.2015.07.375

CrossRef Full Text | Google Scholar

Jin, X., Mu, Y., Jia, H., Wu, J., Jiang, T., and Yu, X. (2017). Dynamic Economic Dispatch of a Hybrid Energy Microgrid Considering Building Based Virtual Energy Storage System. Appl. Energ. 194, 386–398. doi:10.1016/j.apenergy.2016.07.080

CrossRef Full Text | Google Scholar

Karakose, M., Baygin, M., and Parlak, K. S. (2014). “A New Real-Time Reconfiguration Approach Based on Neural Network in Partial Shading for PV Arrays,” in 3rd International Conference on Renewable Energy Research and Applications (USA: Milwakuee), 633–637. doi:10.1109/icrera.2014.7016462

CrossRef Full Text | Google Scholar

Kaushika, N. D., and Gautam, N. K. (2003). Energy Yield Simulations of Interconnected Solar PV Arrays. IEEE Trans. Energ. Convers. 18 (1), 127–134. doi:10.1109/tec.2002.805204

CrossRef Full Text | Google Scholar

La Manna, D., Li Vigni, V., Riva Sanseverino, E., Di Dio, V., and Romano, P. (2014). Reconfigurable Electrical Interconnection Strategies for Photovoltaic Arrays: a Review. Renew. Sust. Energ. Rev. 33, 412–426. doi:10.1016/j.rser.2014.01.070

CrossRef Full Text | Google Scholar

Laudani, A., Lozito, G. M., Maria Lozito, G., Lucaferri, V., Radicioni, M., and Riganti Fulginei, F. (2018). On Circuital Topologies and Reconfiguration Strategies for PV Systems in Partial Shading Conditions: a Review. AIMS Energy 6 (5), 735–763. doi:10.3934/energy.2018.5.735

CrossRef Full Text | Google Scholar

Lin, M., Chen, Z., Xu, Z., Gou, X., and Herrera, F. (2021). Score Function Based on Concentration Degree for Probabilistic Linguistic Term Sets: An Application to TOPSIS and VIKOR. Inf. Sci. 551, 270–290. doi:10.1016/j.ins.2020.10.061

CrossRef Full Text | Google Scholar

Mahidin, E., Husin, H., and Zaki, N. M. (2021). A Critical Review of the Integration of Renewable Energy Sources with Various Technologies. Prot. Control. Mod. Power Syst. 6 (1), 37–54.

Google Scholar

Rani, B. I., Ilango, G. S., and Nagamani, C. (2013). Enhanced Power Generation from PV Array under Partial Shading Conditions by Shade Dispersion Using Su Do Ku Configuration. IEEE Trans. Sustain. Energ. 4 (3), 594–601. doi:10.1109/tste.2012.2230033

CrossRef Full Text | Google Scholar

Sai Krishna, G., and Moger, T. (2019). Reconfiguration Strategies for Reducing Partial Shading Effects in Photovoltaic Arrays: State of the Art. Solar Energy 182, 429–452. doi:10.1016/j.solener.2019.02.057

CrossRef Full Text | Google Scholar

Salam, Z., Ahmed, J., and Merugu, B. S. (2013). The Application of Soft Computing Methods for MPPT of PV System: a Technological and Status Review. Appl. Energ. 107, 135–148. doi:10.1016/j.apenergy.2013.02.008

CrossRef Full Text | Google Scholar

Sanseverino, E. R., Ngoc, T. N., Cardinale, M., Li, V., Musso, D., Romano, P., et al. (2015). Dynamic Programming and Munkres Algorithm for Optimal Photovoltaic Arrays Reconfiguration. Solar Energy 122, 347–358. doi:10.1016/j.solener.2015.09.016

CrossRef Full Text | Google Scholar

Shams El-Dein, M. Z., Kazerani, M., and Salama, M. M. A. (2013). Optimal Photovoltaic Array Reconfiguration to Reduce Partial Shading Losses. IEEE Trans. Sustain. Energ. 4 (1), 145–153. doi:10.1109/tste.2012.2208128

CrossRef Full Text | Google Scholar

Tatabhatla, V. M. R., Agarwal, A., and Kanumuri, T. (2019). Minimising the Power Loss of Solar Photo Voltaic Array through Efficient Reconfiguration of Panels. Proc. Inst. Mech. Eng. A: J. Power Energ. 234 (5), 690–708. doi:10.1177/0957650919871864

CrossRef Full Text | Google Scholar

Vicente, P. S., Pimenta, T. C., and Ribeiro, E. R. (2015). Photovoltaic Array Reconfiguration Strategy for Maximization of Energy Production. Int. J. Photoenergy 2015, 59283. doi:10.1155/2015/592383

CrossRef Full Text | Google Scholar

Xi, L., Chen, J., Huang, Y., Xu, Y., Liu, L., Zhou, Y., et al. (2018). Smart Generation Control Based on Multi-Agent Reinforcement Learning with the Idea of the Time Tunnel. Energy 153, 977–987. doi:10.1016/j.energy.2018.04.042

CrossRef Full Text | Google Scholar

Yang, B., Jiang, L., Wang, L., Yao, W., and Wu, Q. H. (2016). Nonlinear Maximum Power point Tracking Control and Modal Analysis of DFIG Based Wind Turbine. Int. J. Electr. Power Energ. Syst. 74, 429–436. doi:10.1016/j.ijepes.2015.07.036

CrossRef Full Text | Google Scholar

Yang, B., Wang, J., Zhang, X., Yu, T., Yao, W., Shu, H., et al. (2020). Comprehensive Overview of Meta-Heuristic Algorithm Applications on PV Cell Parameter Identification. Energ. Convers. Manag. 208, 112595. doi:10.1016/j.enconman.2020.112595

CrossRef Full Text | Google Scholar

Yang, B., Ye, H., Wang, J., Li, J., Wu, S., Li, Y., et al. (2021). PV Arrays Reconfiguration for Partial Shading Mitigation: Recent Advances, Challenges and Perspectives. Energ. Convers. Manag. 247, 114738. doi:10.1016/j.enconman.2021.114738

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H., Dong, J., and Jiang, L. (2018). Robust Sliding-Mode Control of Wind Energy Conversion Systems for Optimal Power Extraction via Nonlinear Perturbation Observers. Appl. Energ. 210, 711–723. doi:10.1016/j.apenergy.2017.08.027

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H., Zhang, Y., Chen, J., Sang, Y., et al. (2018). Passivity-based Sliding-Mode Control Design for Optimal Power Extraction of a PMSG Based Variable Speed Wind Turbine. Renew. Energ. 119, 577–589. doi:10.1016/j.renene.2017.12.047

CrossRef Full Text | Google Scholar

Yang, B., Zhong, L., Zhang, X., Shu, H., Yu, T., Li, H., et al. (2019). Novel Bio-Inspired Memetic Salp Swarm Algorithm and Application to MPPT for PV Systems Considering Partial Shading Condition. J. Clean. Prod. 215, 1203–1222. doi:10.1016/j.jclepro.2019.01.150

CrossRef Full Text | Google Scholar

Yang, B., Zhu, T., Wang, J., Shu, H., Yu, T., Zhang, X., et al. (2020). Comprehensive Overview of Maximum Power point Tracking Algorithms of PV Systems under Partial Shading Condition. J. Clean. Prod. 268, 121983. doi:10.1016/j.jclepro.2020.121983

CrossRef Full Text | Google Scholar

Yousri, D., Babu, T. S., Mirjalili, S., Rajasekar, N., and Elaziz, M. A. (2020). A Novel Objective Function with Artificial Ecosystem-Based Optimization for Relieving the Mismatching Power Loss of Large-Scale Photovoltaic Array. Energ. Convers. Manag. 225, 113385. doi:10.1016/j.enconman.2020.113385

CrossRef Full Text | Google Scholar

Zhang, K., Zhou, B., Or, S. W., Li, C., Chung, C. Y., and Voropai, N. I. (2021). Optimal Coordinated Control of Multi-Renewable-To-Hydrogen Production System for Hydrogen Fueling Stations. IEEE Trans. Ind. Applicat. 1, 1. doi:10.1109/TIA.2021.3093841

CrossRef Full Text | Google Scholar

Zhang, X., Li, C., Li, Z., Yin, X., Yang, B., Gan, L., et al. (2021). Optimal Mileage-Based PV Array Reconfiguration Using Swarm Reinforcement Learning. Energ. Convers. Manag. 232, 113892. doi:10.1016/j.enconman.2021.113892

CrossRef Full Text | Google Scholar

Zhou, B., Fang, J. K., Ai, X. M., and Yang, C. (2021). Dynamic Var reserve-constrained Coordinated Scheduling of LCC-HVDC Receiving-End System Considering Contingencies and Wind Uncertainties. IEEE Trans. Sust. Energ. 12 (01), 469–481. doi:10.1109/tste.2020.3006984

CrossRef Full Text | Google Scholar