Primary Frequency Stability Support of a DFIG in Association With Pitch Angle Control

For an electric power grid that has large penetration levels of variable renewable energy including wind generation and photovoltaics, the system frequency stability is jeopardized, which is manifest in lowering frequency nadir and settling frequency. This paper suggests an enhanced primary frequency response strategy of a doubly-fed induction generator (DFIG) in association with pitch angle control. The DFIG works in de-loaded operation with a certain reserve power via pitch angle control prior to disturbances for frequency regulation. To address this, a function of the pitch angle is employed that decreases the pitch angle with time to slowly feed the active power to the power gird. The simulation results demonstrate the effectiveness and feasibility of the proposed primary frequency response strategy including the settling frequency and frequency nadir.

Introduction

When disturbances occur in a power system, the conventional synchronous generators (CSGs) intrinsically release kinetic energy in the rotor to compensate for the power imbalance as an inertial response; as a result, the system frequency declines (Kundur, 1994; Yang et al., 2018). Once the system frequency decreases beyond the deadband, the primary frequency response (PFR) is activated to arrest the frequency decline and stabilize the system frequency (which calls the settling frequency) (Bevrani, 2009; North American Electric R, 2015). To restore the system frequency to the nominal value, secondary frequency responses (SFRs) of CSGs are activated (Eto et al., 2010). During the frequency regulation process, if the maximum frequency nadir exceeds the threshold, low frequency relays are activated to avoid the system frequency decline; in addition, if the settling frequency is not located in the acceptable range, the SFRs would not be activated (Li et al., 2018; Sarasúa et al., 2021).

As the increasing problems of environmental pollution, renewable energy power generation has developed rapidly (Li et al., 2021; Zhang et al., 2021). As one of the most popular variable renewable energies, wind generation with power electronics has developed rapidly in recent years (Nasirpour et al., 2021; Wang et al., 2021). As a result, doubly-fed induction generators (DFIGs) replace the CSGs in power systems for generating active power (Hansen et al., 2016). However, since the DFIG is connected to the electric power grid via back-to-back power electronic devices with DC-link, it is unable to participate in frequency responses including inertia response and primary frequency response (Aziz et al., 2018; Yang et al., 2022). As a result, the high wind power penetration integrated in a power system might result in a severe challenge on frequency stability (Hydro Québec TransÉnergie, 2009; Kim et al., 2019). This means that the high wind power penetration increases the possibility for activation the relays and inactivation of SFR. To solve this, additional defense plans should be deployed, e.g., interruptible loads, energy storage systems, and quick-starting generators (Eto et al., 2010; Shi et al., 2021); nevertheless, these plans require additional investments.

The DFIG can temporarily increase its output power to emulate inertia response by releasing the kinetic energy to the gird (Vidyanandan and Senroy, 2014; Zhong et al., 2021), thereby reducing the possibility for activation the relays. In (Attya et al., 2018; Ye et al., 2019), the schemes increase the output power based on the frequency deviation, rate of change of frequency, and both of them. The schemes in (Yang et al., 2018; Kheshti et al., 2019; Yang et al., 2022) increase the output power based on the predefined reliable function, temporary function, and adaptive function. However, the maximum power point tracking operation is implemented prior to disturbances, even though the DFIG has a large potential for frequency regulation; in the case of a low wind speed condition or decreasing wind speed condition, the available kinetic energy is insufficient (Vidyanandan and Senroy, 2013).

This study suggests an enhanced PFR strategy of a DFIG based on pitch angle control to boost the settling frequency and maximum frequency deviation. To address this, a function of the pitch angle is employed that decreases the pitch angle with time to generate the additional active power. The DFIG works in de-loaded operation with a certain reserve power for frequency regulation prior to disturbances. The enhanced PFR strategy performance is indicated using EMTP-RV simulator under various scenarios with different wind speed conditions and wind penetrations.

Modeling and Control of a Doubly-Fed Induction Generator

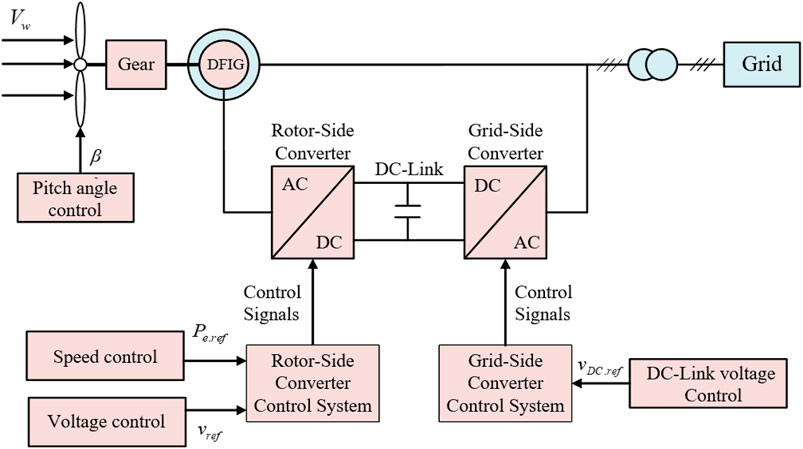
Figure 1 illustrates the typical configuration of the DFIG including wind turbine model, induction generator model, and back-to-back power electronic devices (Lee et al., 2016; Zhu et al., 2021).

FIGURE 1

FIGURE 1. Typical configuration of the DFIG.

The wind turbine model is used to capture the mechanical power from the wind. The captured power (P_m) is depicted by:

$P_m=0.5\rho \pi R^2{v}_w^3{c}_P\left(\lambda ,\beta \right)(1)$

where ρ and A respectively indicate the air density and swept area; β and λ respectively are pitch angle and the tip-speed ratio; c_p and v_w respectively indicate the power coefficient and wind speed.

In this paper, the expression of the power coefficient c_p is given as:

$c_P\left(\lambda ,\beta \right)=0.645\left\{0.00912\lambda +\frac{-5-0.4\left(2.5+\beta \right)+116{\lambda }_i}{e^{21{\lambda }_i}}\right\}(2)$

where

${\lambda }_i=\frac{1}{\lambda +0.08\left(2.5+\beta \right)}-\frac{0.035}{1+{\left(2.5+\beta \right)}^3}(3)$

$\lambda =\frac{{\omega }_{r}R}{v_w}.(4)$

During MPPT control, c_p is at the maximum value (c_P,max) when λ is regulated at the optimal λ (λ_opt). Hence, the reference for MPPT control is derived via substituting (4) in (Eq. 1), as in (Eq. 5).

${\mathit{P}}_{\mathrm{MPT}}=\frac{1}{2}\rho \pi R^2{\left(\frac{{\omega }_{r}R}{{\lambda }_{\mathrm{opt}}}\right)}^3{c}_{p,\max }=k_g{\omega }_r^3(5)$

$k_g=\frac{1}{2{\mathit{\lambda }}_{\text{opt}}^3}{C}_{p\text{,max}}\left({\mathit{\lambda }}_{\text{opt}}\mathit{,}0\right)\mathit{\rho }\mathrm{\pi }{R}^5(6)$

where k_g is constant coefficient of MPPT control calculated by (Eq. 6).

Figures 2A–C display the controllers of rotor-side converter, gird-side converter, and pitch angle, respectively. The aims of RSC controller are to regulate active power (torque) of the DFIG injected to the power grid and the voltage of the DFIG, respectively, as displayed in Figure 2A. The objective of the GSC controller is to keep DC-link voltage at reference values, as displayed in Figure 2B. The aim of the pitch angle controller is to achieve the de-loaded operation of the DFIG in the study, as shown in Figure 2C (Muljadi and Butterfield, 2001).

FIGURE 2

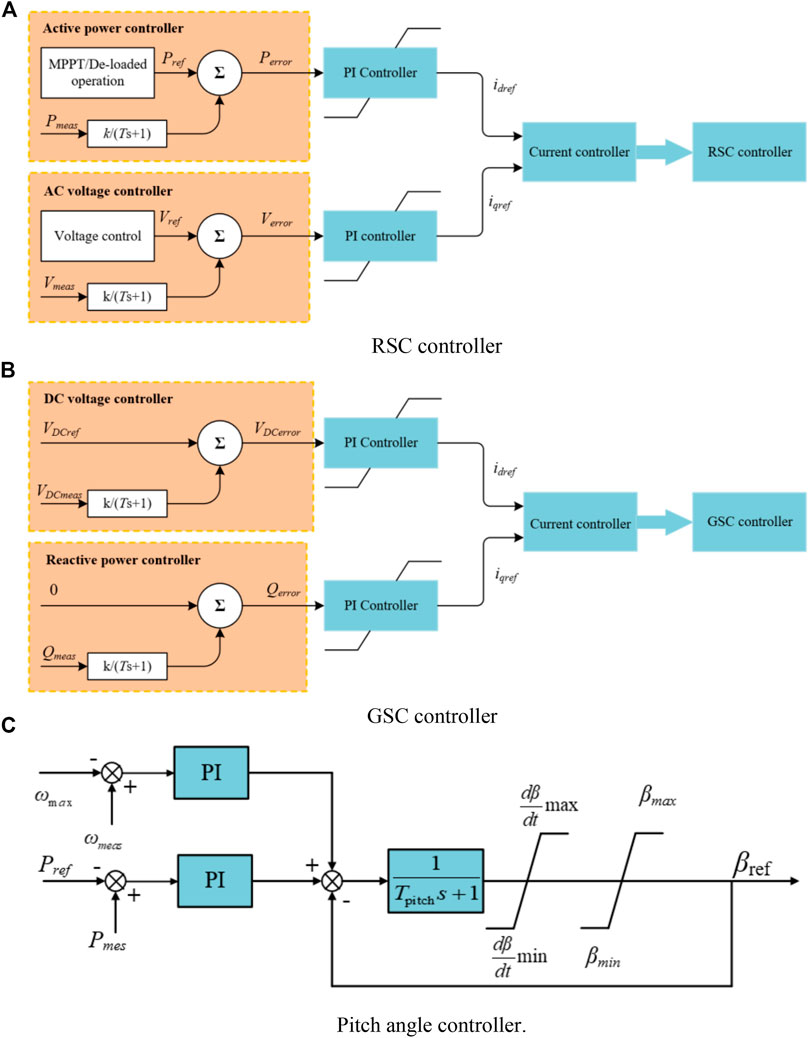
FIGURE 2. Control diagram of the DFIG. (A) RSC controller. (B) GSC controller. (C) Pitch angle controller.

Proposed Enhanced Primary Frequency Response Strategy of a Doubly-Fed Induction Generator

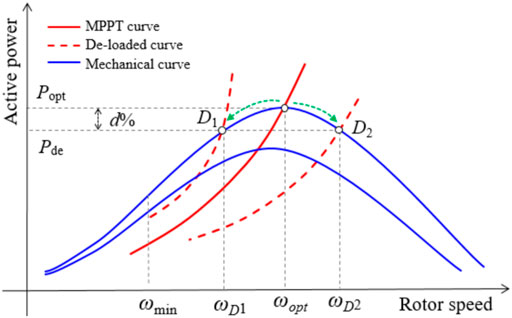
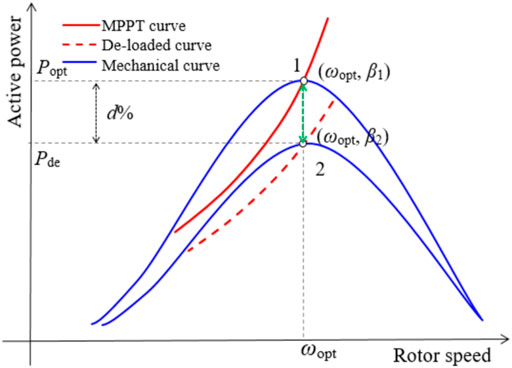
Figure 3 and Figure 4 illustrate the control concepts of the overspeed and pitch angle control strategies for de-loaded operation, respectively. The red solid line and blue solid line indicate the electrical output power of MPPT operation and mechanical power curves, respectively. The mechanical power retains an optimal value (P_opt) achieved by the MPPT operation at the optimal rotor speed (ω_opt). Generally, the DFIG can implement pitch angle control and over-speed control to ensure the de-loaded operation (Kheshti et al., 2019), as represented by the red dotted lines in Figures 3, 4. The green dotted line means the moving trajectory for de-loaded operation.

FIGURE 3

FIGURE 3. Control concept of overspeed strategy.

FIGURE 5

FIGURE 5. Control diagram of the proposed enhanced PFR strategy of the DFIG based pitch angle.

As in Figure 3, de-loaded operation of the DFIG is able to be achieved by either acceleration or deceleration of the rotor speed, as indicated the left and right hand operating points of D₁ and D₂ in Figure 3. In the case of decreasing wind speed conditions, the operating point of D₁ trends to decrease to the minimum rotor speed so as to result in stalling of the rotor speed. On the other hand, the operating point of D₂ trends to increase to the maximum rotor speed so as to store more kinetic energy for frequency regulation. As a result, to ensure the safe and stable operation of the DFIG, overspeed control should be chosen for the WTG rather than low-speed control (Hu et al., 2019).

Based on (Eq. 1), the DFIG can increase the pitch angle to achieve de-loaded operation, as shown in Figure 4. Since β₂ is larger than β₁, the power coefficient decreases so as to reduce the captured mechanical power and accomplish the spinning reserve power (Fu et al., 2017). Even though the overspeed control strategy has more rapid response and results less mechanical wear, but is suitable for part of wind speed conditions, the pitch angle control is able to implement for full wind speed conditions.

The spinning reserve power (d%) of the DFIG can be calculated by

$d\%=\raisebox{1ex}{$\left(P_{opt}-P_{de}\right)$}\!\left/ \!\raisebox{-1ex}{$P_{opt}$}\right.\times 100\%(7)$

Based on (Eq. 7), the power coefficient for de-loaded operation (C_{p, deload}) can be derived as in:

${\mathit{C}}_{\mathit{p,deload}}=\left(\mathrm{1}-\mathit{d\%}\right){\mathit{C}}_{\mathit{p,max}}(8)$

Thus, the power reference during de-loaded operation mode (P_de) is represented as

$P_{de}=0.5\rho \pi R^2{C}_{p,deload}(9)$

As in (Fu et al., 2017), based on the low-order system frequency response model, the expressions of the maximum frequency deviation and settling frequency are given as:

$\mathrm{\Delta }{\mathit{f}}_{\mathit{nadir}}=\frac{\mathit{K}\mathrm{\Delta }\mathit{P}}{\mathrm{DK}\mathit{+}\mathrm{1}}\left(\mathrm{1}\mathit{+}\sqrt{\mathrm{1}\mathit{+}{\mathit{\varsigma }}^{\mathit{2}}}\right){\alpha }^{-\varsigma {\omega }_{\mathit{n}}{\mathit{t}}_{\mathit{nadir}}}(10)$

${\mathit{f}}_{\mathit{settling}}\mathit{=}{\mathit{f}}_{\mathit{nom}}\mathit{-}\frac{\mathit{K-}\mathrm{\Delta }\mathit{P}}{\mathit{D}}(11)$

where Δf_nadir and f_settling are the maximum frequency deviation and settling frequency, respectively. K and D are the setting of PFR and damping of the CSGs, respectively. α and ς are the coefficient during the derived process and damping ratio, respectively. t_nadir is the instant of the maximum frequency deviation. ΔP is the power imbalance calculated by the difference between the power variation of the DFIG and size of disturbance.

Based on (Eqs. 10, 11), if the DFIG increases the output power following a disturbance, the equivalent power imbalance becomes small so that the maximum frequency deviation and settling frequency become better. This means that the DFIG can provide the capability of PFR.

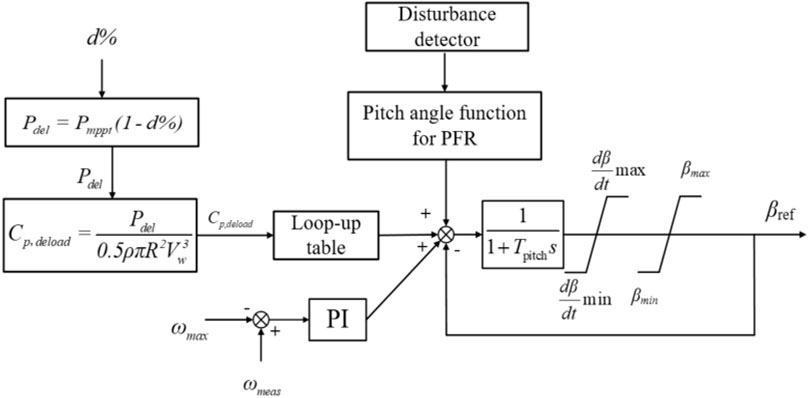
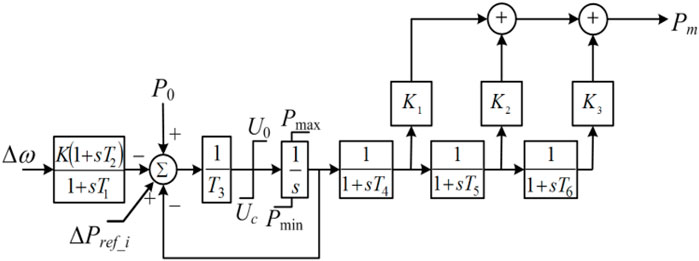
Figure 5 illustrates the control diagram of the enhanced PFR strategy of the DFIG. If the DFIG decreases the pitch angle to capture more wind power by the wind turbine. The output power of the DFIG can be increased to compensate for the power imbalance. Thus, after the system frequency exceeds the deadband (detecting a disturbance), this study suggests a function related to pitch angle and time to participate in PFR, as in (Eq. 12). As time goes on, the pitch angle decreases, the DFIG captures more mechanical power from the wind so as to generate more active power to the grid for frequency support.

${\beta }_{ref}\left(t\right)=\beta \left(t_0\right)\times \left[1-\frac{1}{\mathrm{\Delta }t}\left(t-t_0\right)\right](12)$

where β_ref is the reference of pitch angle, β(t₀) is the pitch angle at the instant when a disturbance is detected, Δt means the duration for decreasing pitch angle.

FIGURE 4

FIGURE 4. Control concept of pitch angle control strategy.

As in (Eq. 12), the setting of Δt decides on the performances in terms of improvement of the frequency nadir and settling frequency. With a large settling of Δt, the pitch angle gradually decreases so that the output power of the DFIG gradually increases to P_opt; meanwhile, even though the large Δt is better for causing less mechanical stress on the pitch angle, the benefit for improving the maximum frequency deviation becomes less. On the other hand, the small Δt is better for improving the PFR capability, however, it might cause mechanical stresses on the pitch angle control system. Normally, the setting should be in second-scale so as to be unable to result in mechanical fatigue of the pitch angle control system.

As shown in Figure 5, after detecting a disturbance, the output power of the DFIG increases toward to P_opt with the decreasing pitch angle from operating point 2 to operating point 1; thereafter, the DFIG converges at ω_opt while the pitch angle decreases to zero. Since the output power increases in comparison with MPPT operation, the maximum frequency deviation and settling frequency are able to be enhanced.

System Layout

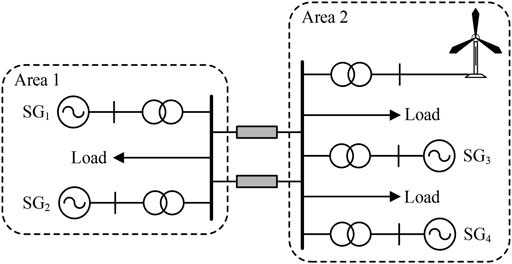
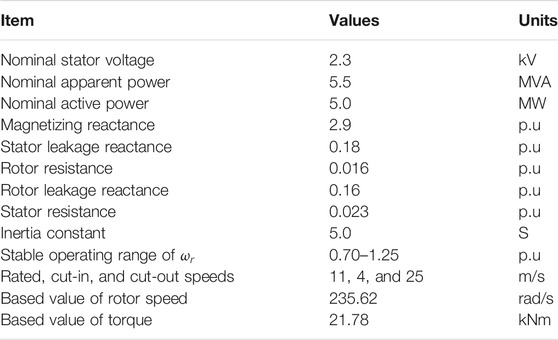
Figure 6 displays a model system with two areas and four CSGs to investigate the performance of the enhanced PFR strategy. CSGs are: two 200-MVA with the inertia time constant of 5.0 s, and two 150-MVA with the inertia time constant of 4.3 s. They are assumed as steam turbine generators for modeling low ramping capability (5% of PFR). Figure 7 illustrates the configuration of the type B steam governor model, as modeled in (Byerly et al., 1973). The specific parameters of the IEEEG1 steam governor model are shown in Table 1. In addition, a DFIG based wind farm is integrated into the model system though a transformer. The detailed parameters are referred in (Lee et al., 2016) (Table 2).

FIGURE 6

FIGURE 6. Test model system with four CSGs two areas.

FIGURE 7

FIGURE 7. IEEEG1 steam governor model.

TABLE 1

TABLE 1. Parameters of the IEEEG1 steam governor model.

TABLE 2

TABLE 2. Parameters of the DFIG.

To explore the effectiveness and feasible of the proposed enhanced PFR strategy, three cases with different wind speed conditions and wind power penetration levels are carried out. Wind power penetration levels are respectively 15% for Case 1 and Case 2, and 30% for Case 3.

Case 1: Wind Speed of 8.0 m/s With 10% De-Loaded Operation, Wind Power Penetration Level of 15%

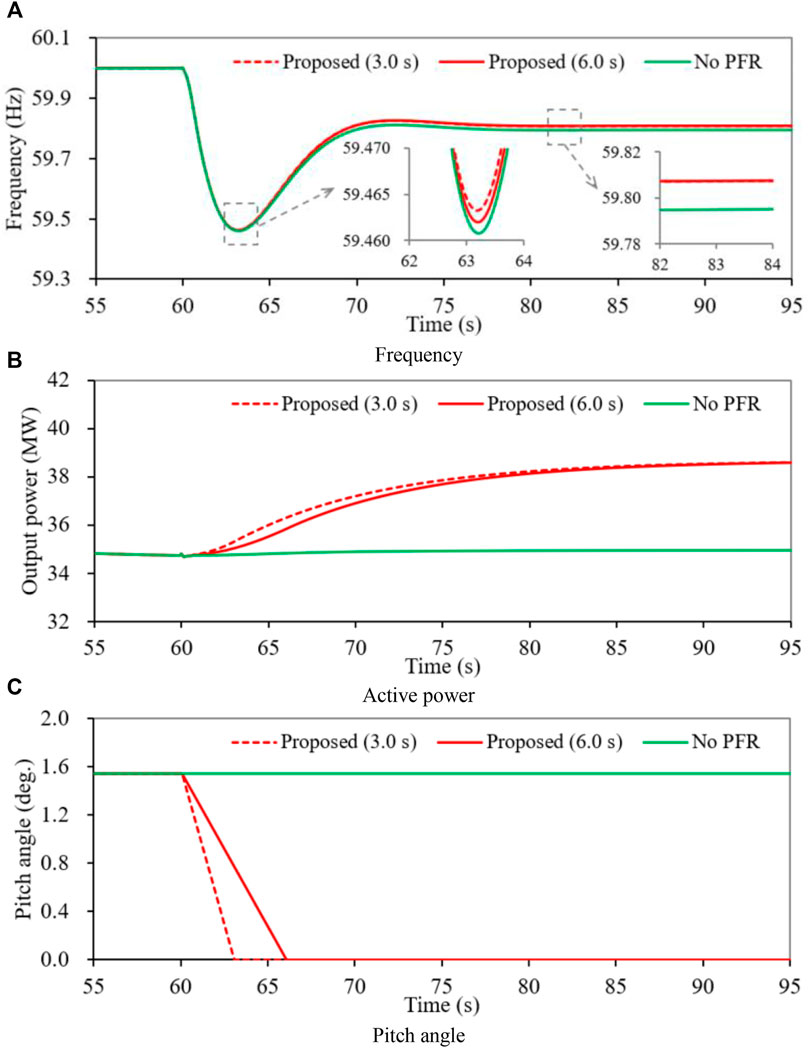
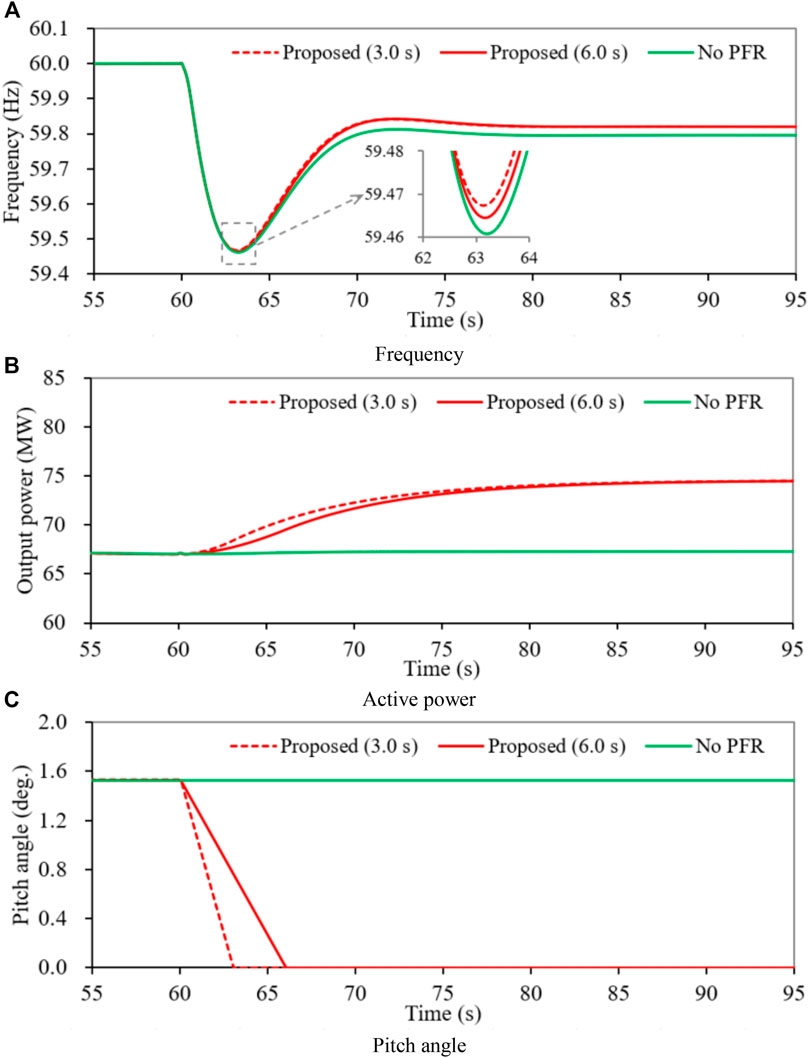
Figure 8 illustrates the simulation results for Case 1. To achieve spinning reserve power of 10%, the pitch angle control increases the pitch angle to 1.54°. When CSG₄ generates 65 MW is tripped out from the electric power gird, the maximum frequency deviation for the DFIG without PFR is 0.539 Hz; in this case, there is no change on the pitch angle and the output of the DFIG. When the DFIG implements the proposed PFR strategies with a small Δt and with a large Δt, the maximum frequency deviations are 0.537 Hz and 0.538 Hz, respectively, as shown in Figure 8A. The improvements of the maximum frequency nadir for the proposed enhanced PFR strategies with different Δt are higher by 0.002 and 0.001 Hz in comparison with no PFR strategy, respectively, since the output power of the DFIG gradually increases and the rate of output power of the DFIG for the proposed PFR strategy with a small Δt is more than in the proposed PFR strategy with a large Δt (Figure 8C). The settling frequency for the proposed PFR strategy is 59.808 Hz; this is more than that of no PFR strategy by 0.013 Hz due to the more power generation of 3.7 MW.

FIGURE 8

FIGURE 8. Results for case 1. (A) Frequency. (B) Active power. (C) Pitch angle.

As shown in Figure 8B, the DFIG decreases the pitch angle from 1.53 to 0° during 3.0 and 6.0 s for the proposed enhanced PFR strategy, respectively. Thus, the DFIG increases it output power gradually from 34.7 to 38.4 MW for compensating the power deficit. On the other hand, there is no change for the pitch angle and output power of the DFIG based wind farm in no PFR.

Case 2: Wind Speed of 10.0 m/s With 10% De-Loaded Operation, Wind Power Penetration Level of 15%

Figure 9 illustrates the simulation results for Case 2. Similar to previous case, to achieve 10% spinning reserve power, the pitch angle control almost increases the pitch angle to 1.53°. The maximum frequency deviation for the DFIG without PFR is 0.539 Hz, which is almost the same as in Case 1 due to the same size of disturbance and no response from the DFIG.

FIGURE 9

FIGURE 9. Results for case 2. (A) Frequency. (B) Active power. (C) Pitch angle.

The maximum frequency deviation of the proposed PFR strategy with a small Δt and with a large Δt, the maximum frequency deviations are 0.533 and 0.536 Hz, respectively, as shown in Figure 8A. The improvements of the maximum frequency nadir for the proposed enhanced PFR strategies with different Δt are higher by 0.006 and 0.003 Hz in comparison with no PFR strategy, respectively, since the rate of output power of the DFIG for the proposed PFR strategy with a small Δt is more than in the proposed PFR strategy with a large Δt (Figure 8C). The settling frequency for the proposed PFR strategy is 59.820 Hz; this is more than that of no frequency regulation strategy by 0.025 Hz due to the more power generation of 7.5 MW.

Compared with Case 1, as in Case 1, the DFIG decreases the pitch angle from 1.53° to 0° during 3.0 and 6.0 s for the proposed enhanced PFR strategy, respectively. However, the amount of increase power of the DFIG is 7.5 MW, which is more than that of Case 1 so that the settling frequency is 0.012 Hz higher and the maximum frequency deviations are less. Thus, as the wind speed increases, the proposed enhanced PFR strategy can improve the performance in terms of reducing the maximum frequency deviation and increasing the settling frequency.

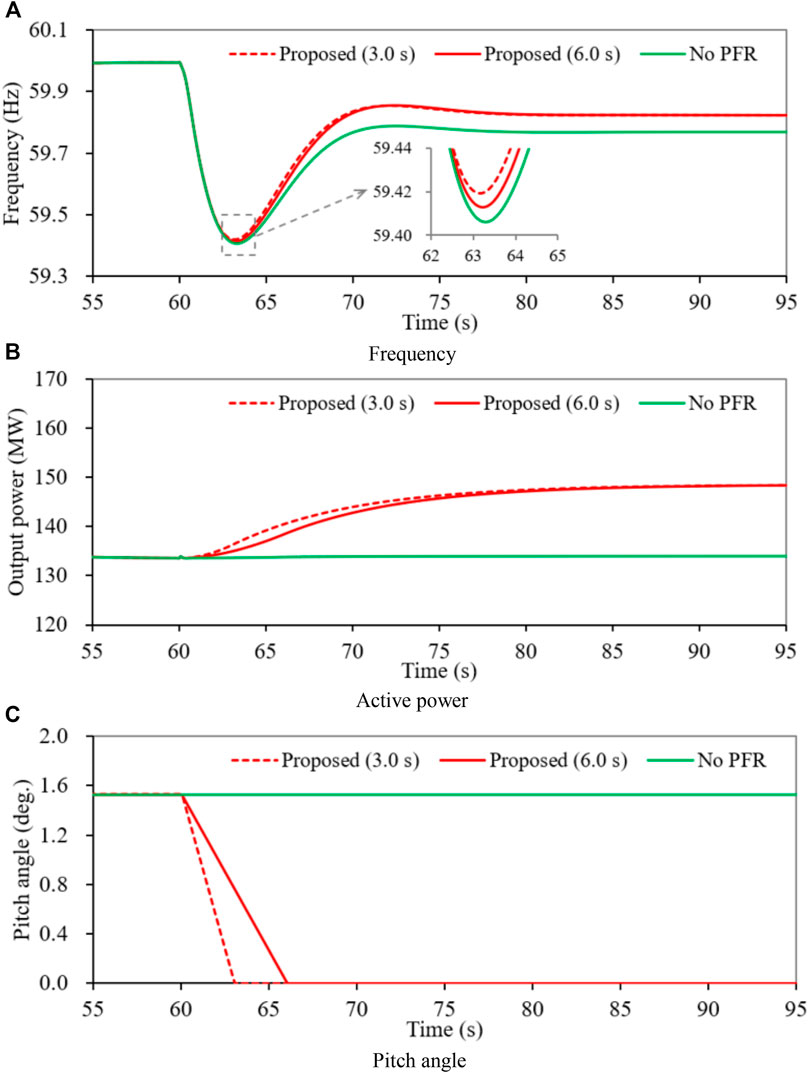
Case 3: Wind Speed of 10.0 m/s With 10% De-Loaded Operation, Wind Power Penetration Level of 30%

Figure 10 illustrates the simulation results for Case 3 with a high wind power penetration compared to Case 2. The maximum frequency deviation for the DFIG without PFR is 0.594 Hz and is less than Case 1 and Case 2 due to the reduced frequency support capability. The DFIG with the proposed enhanced PFR strategy increases it output power from 133.6 to 148.4 MW with various rates by decreasing the pitch angle from 1.53° to 0° during 3.0 and 6.0 s, respectively. As a result, the maximum frequency deviation of the proposed PFR strategy with a small Δt is 0.581 Hz, which is 0.006 Hz more than that of the proposed PFR strategy with a large Δt. Furthermore, the improvement of the maximum frequency deviation is more than that of Case 2 because of the higher wind power penetration level. In addition, the settling frequencies for the proposed PFR strategy are the same due to the same amount of increase output power of the DFIG; moreover, it is 0.054 Hz more than in no frequency regulation strategy and 0.003 Hz more than that of Case 2, even though the PFR of the CSGs becomes worse.

FIGURE 10

FIGURE 10. Results for case 3. (A) Frequency. (B) Active power. (C) Pitch angle.

As the growing wind power penetration levels, the proposed PFR strategy can improve the frequency maximum frequency deviation and settling frequency in comparison with low wind penetration levels.

Conclusion

This paper suggests an improved PFR strategy of the DFIG based on the pitch angle control to reduce the maximum frequency deviation and improve the settling frequency. To address this, a function of the pitch angle is employed that decreases the pitch angle with time to feed the active power to the power gird. The DFIG works in de-loaded operation with a certain reserve power for frequency regulation via pitch angle control prior to disturbances. The contributions of the proposed PFR are as follows:

1) The function of the pitch angle is defined in the time domain so as to regulate the participating time of the PFR.

2) The proposed PFR scheme can smoothly increase the output power to improve the PFR capability.

Simulation results on various wind speed conditions and penetration levels successfully illustrated that the proposed PFR strategy can reduce the maximum frequency deviation and improve the settling frequency. As the increasing wind speed conditions and wind power penetration level, the improvement of the maximum frequency deviation and settling frequency become better.

In future, the authors would focus on designing the optimal primary frequency response of the DFIG with the maximum rotor kinetic energy (Shi et al., 2018).

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

XS and XW conducted the back ground research of the project. FY, HY, and DJ proposed the methodology of the project. XS, XW, YX, and DJ completed the main theory and simulation content. XS and XW completed the writing of the paper. The work was supported by the fund of XS, FY, and HY.

Funding

This work was supported by the Technology Project of Alpha ESS Co., Ltd. (21ZH479).

Conflict of Interest

XS, FY, and HY were employed by the company Alpha ESS Co., Ltd. The authors declare that this study received funding from Alpha ESS Co., Ltd. (21ZH479). The company had the following involvement in the study: back ground research, methodology and writing—original draft preparation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Attya, A. B., Dominguez-Garcia, J. L., and Anaya-lara, O. (2018). A Review on Frequency Support Provision by Wind Power Plants: Current and Future Challenges. Renew. Sust. Energ. Rev. 81, 2071–2087. doi:10.1016/j.rser.2017.06.016

CrossRef Full Text | Google Scholar

Aziz, A., Than Oo, A., and Stojcevski, A. (2018). Frequency Regulation Capabilities in Wind Power Plant. Sustainable Energ. Tech. Assessments 26, 47–76. doi:10.1016/j.seta.2017.10.002

CrossRef Full Text | Google Scholar

Bevrani, H. (2009). “Real Power Compensation and Frequency Control,” in Robust Power System Frequency Control (New York: Springer Science Business Media, LLC), 15–37.

Google Scholar

Byerly, R. T., Aanstad, O., Berry, D. H., Dunlop, R. D., Ewart, D. N., Fox, B. M., et al. (1973). Dynamic Models for Steam and Hydro Turbines in Power System Studies. IEEE Trans. Power App. Syst. PAS-92 (6), 1904–1915.

Google Scholar

Eto, J. H., Undrill, J., Mackin, P., Daschmans, R., Williams, B., Haney, B., et al. (2010). Use of Frequency Response Metrics to Assess the Planning and Operating Requirements for Reliable Integration of Variable Renewable Generation. Berkeley, CA, USA: Lawrence Berkeley National Laboratory. Tech. Rep. LBNL-4142E.

Google Scholar

Fu, Y., Zhang, X., Hei, Y., and Wang, H. (2017). Active Participation of Variable Speed Wind Turbine in Inertial and Primary Frequency Regulations. Electric Power Syst. Res. 147, 174–184. doi:10.1016/j.epsr.2017.03.001

CrossRef Full Text | Google Scholar

Hansen, A. D., Altin, M., and Iov, F. (2016). Provision of Enhanced Ancillary Services from Wind Power Plants - Examples and Challenges. Renew. Energ. 97, 8–18. doi:10.1016/j.renene.2016.05.063

CrossRef Full Text | Google Scholar

Hu, J., Shao, C., Wang, W., Xu, G., Dong, C., and Bi, T. (2019). “A Fast Frequency Control Strategy for Deloaded WTG in the 303 Power System with High Penetration of Renewable Energy,” in Proceeding of the 2019 IEEE Innovative Smart Grid Technologies - Asia 304 (ISGT Asia), Chengdu, China, May 2019 (IEEE), 4036–4041.

Google Scholar

Hydro Québec TransÉnergie (2009). Transmission Provider Technical Requirements for the Connection of Power Plants to the Hydro Québec Transmission System. Québec: Montréal.

Google Scholar

Kheshti, M., Ding, L., Nayeripour, M., Wang, X., and Terzijia, V. (2019). Active Power Support of Wind Turbines for Grid Frequency Events Using a Reliable Power Reference Scheme. Renew. Energ. 139, 1421–1454. doi:10.1016/j.renene.2019.03.016

CrossRef Full Text | Google Scholar

Kim, J., Muljadi, E., Gevorgian, V., and Hoke, A. F. (2019). Dynamic Capabilities of an Energy Storage-Embedded DFIG System. IEEE Trans. Ind. Applicat. 55 (4), 4124–4134. doi:10.1109/tia.2019.2904932

CrossRef Full Text | Google Scholar

Kundur, P. (1994). Power System Stability and Control Electric Power Research Institute. New York: McGraw-Hill.

Google Scholar

Lee, J., Jang, G., Muljadi, E., Blaabjerg, F., Chen, Z., and Cheol Kang, Y. (2016). Stable Short-Term Frequency Support Using Adaptive Gains for a DFIG-Based Wind Power Plant. IEEE Trans. Energ. Convers. 31 (3), 1068–1079. doi:10.1109/tec.2016.2532366

CrossRef Full Text | Google Scholar

Li, W., Du, P., and Lu, N. (2018). Design of a New Primary Frequency Control Market for Hosting Frequency Response reserve Offers from Both Generators and Loads. IEEE Trans. smart grid 9, 4883–4892. in press. doi:10.1109/tsg.2017.2674518

CrossRef Full Text | Google Scholar

Li, Y., Gao, W., Yan, W., Huang, S., Wang, R., Gevorgian, V., et al. (2021). Data-driven Optimal Control Strategy for Virtual Synchronous Generator via Deep Reinforcement Learning Approach. J. Mod. Power Syst. 9 (4), 919–929. doi:10.35833/mpce.2020.000267

CrossRef Full Text | Google Scholar

Muljadi, E., and Butterfield, C. P. (2001). Pitch-controlled Variable-Speed Wind Turbine Generation. IEEE Trans. Ind. Applicat. 37 (1), 240–246. doi:10.1109/28.903156

CrossRef Full Text | Google Scholar

Nasirpour, N., Madani, S. M., Niroomand, M., and Muljadi, E. (2021). Closed-loop Fast Primary Frequency-Response of Type-3 Wind Power Plants in Low Inertia Grids. IET Renew. Power Gener. 15, 2931–2943. doi:10.1049/rpg2.12226

CrossRef Full Text | Google Scholar

North American Electric Reliability Corporation (2015). Reliability Guideline: Primary Frequency Control.

Google Scholar

Sarasúa, J. I., Pérez-Díaz, J. I., Martínez-Lucas, G., and Fernández-Muñoz, D. (2021). Simplified Event-Based Load Shedding Scheme for Frequency Stability in an Isolated Power System with High Renewable Penetration. El Hierro: A Case Study. Front. Energ. Res. 9, 698081. doi:10.3389/fenrg.2021.698081

CrossRef Full Text | Google Scholar

Shi, Q., Li, F., and Cui, H. (2018). Analytical Method to Aggregate Multi-Machine SFR Model with Applications in Power System Dynamic Studies. IEEE Trans. Power Syst. 33 (6), 6355–6367. doi:10.1109/tpwrs.2018.2824823

CrossRef Full Text | Google Scholar

Shi, Q., Liu, L., Wang, Y., Lu, Y., Zou, Q., Zhang, Q., et al. (2021). Cooperative Synthetic Inertia Control for Wind Farms Considering Frequency Regulation Capability. Front. Energ. Res. 9, 738857. doi:10.3389/fenrg.2021.738857

CrossRef Full Text | Google Scholar

Vidyanandan, K. V., and Senroy, N. (2014). Closure to Discussion on “Primary Frequency Regulation by Deloaded Wind Turbines Using Variable Droop”. IEEE Trans. Power Syst. 29 (1), 414–415. doi:10.1109/tpwrs.2013.2290822

CrossRef Full Text | Google Scholar

Vidyanandan, K. V., and Senroy, N. (2013). Primary Frequency Regulation by Deloaded Wind Turbines Using Variable Droop. IEEE Trans. Power Syst. 28 (2), 837–846.

CrossRef Full Text | Google Scholar

Wang, R., Sun, Q., Tu, P., Xiao, J., Gui, Y., and Wang, P. (2021). Reduced-Order Aggregate Model for Large-Scale Converters with Inhomogeneous Initial Conditions in DC Microgrids. IEEE Trans. Energ. Convers. 36 (3), 2473–2484. doi:10.1109/tec.2021.3050434

CrossRef Full Text | Google Scholar

Yang, D., Jin, Z., Zheng, T., and Jin, E. (2022). An Adaptive Droop Control Strategy with Smooth Rotor Speed Recovery Capability for Type III Wind Turbine Generators. Int. J. Electr. Power Energ. Syst. 135, 107532. doi:10.1016/j.ijepes.2021.107532

CrossRef Full Text | Google Scholar

Yang, D., Kim, J., Kang, Y. C., Muljadi, E., Zhang, N., Hong, J., et al. (2018). Temporary Frequency Support of a DFIG for High Wind Power Penetration. IEEE Trans. Power Syst. 33 (3), 3428–3437. doi:10.1109/tpwrs.2018.2810841

CrossRef Full Text | Google Scholar

Ye, Y., Qiao, Y., and Lu, Z. (2019). Revolution of Frequency Regulation in the Converter-Dominated Power System. Renew. Sust. Energ. Rev. 111, 145–156. doi:10.1016/j.rser.2019.04.066

CrossRef Full Text | Google Scholar

Zhang, N., Sun, Q., Wang, J., and Yang, L. (2021). Distributed Adaptive Dual Control via Consensus Algorithm in the Energy Internet. IEEE Trans. Ind. Inform. 17, 4848–4860. in press. doi:10.1109/tii.2020.3031437

CrossRef Full Text | Google Scholar

Zhong, C., Lv, Y., Zhou, Y., and Li, H. (2021). An Equivalent Rotor Speed Compensation Control of PMSG-Based Wind Turbines for Frequency Support in Islanded Microgrids. Front. Energ. Res. 9, 717327. doi:10.3389/fenrg.2021.717327

CrossRef Full Text | Google Scholar

Zhu, Q., Wang, Y., Song, J., Jiang, L., and Li, Y. (2021). Coordinated Frequency Regulation of Smart Grid by Demand Side Response and Variable Speed Wind Turbines. Front. Energ. Res. 9, 754057. doi:10.3389/fenrg.2021.754057

CrossRef Full Text | Google Scholar