Short-Lived Interfaces in Energy Materials

Borgschulte, Andreas; Terreni, Jasmin; Fumey, Benjamin; Sambalova, Olga; Billeter, Emanuel

doi:10.3389/fenrg.2021.784082

REVIEW article

Front. Energy Res., 03 January 2022

Sec. Hydrogen Storage and Production

Volume 9 - 2021 | https://doi.org/10.3389/fenrg.2021.784082

This article is part of the Research Topic Horizons in Energy Research View all 4 articles

Short-Lived Interfaces in Energy Materials

Andreas Borgschulte^1,2*

Jasmin Terreni^1,2

Benjamin Fumey³

Olga Sambalova^1,2

Emanuel Billeter^1,2

1Laboratory for Advanced Analytical Technologies, Empa—Swiss Federal Laboratories for Materials Science and Technology, Dübendorf, Switzerland
2Department of Chemistry, University of Zurich, Zürich, Switzerland
3Urban Energy Systems Laboratory, Empa—Swiss Federal Laboratories for Materials Science and Technology, Dübendorf, Switzerland

The kinetics of most chemical energy storage/conversion systems depend on the mass transport through matter, which is rate-limited by various kinetic barriers. The distinction of the barriers by static and dynamic interfaces helps in reducing their impact and therefore enhancing the overall kinetics. The concept is introduced along examples of static and dynamic interfaces in hydrogen storage, thermal energy storage in absorptive media, and electrochemical water splitting and CO₂ reduction. In addition to the description of analysis methods to probe static and dynamic interfaces, the general strategy as well as concrete examples to overcome them are discussed.

1 Introduction

Energy storage is pivotal for a swift implementation of a renewable energy economy, but still awaits a technically and economically feasible large scale solution. Primary physical parameter used to assess the suitability of a specific technology is the total amount of stored energy, e.g., energy storage density. Secondary parameter is the kinetics, i.e., the minimum time to extract the energy, often expressed by the power density. The latter is defined by the specific physical and chemical processes. In this review, we discuss the corresponding parameters along three archetypal examples of different energy storage technologies highlighted in Figure 1.

FIGURE 1

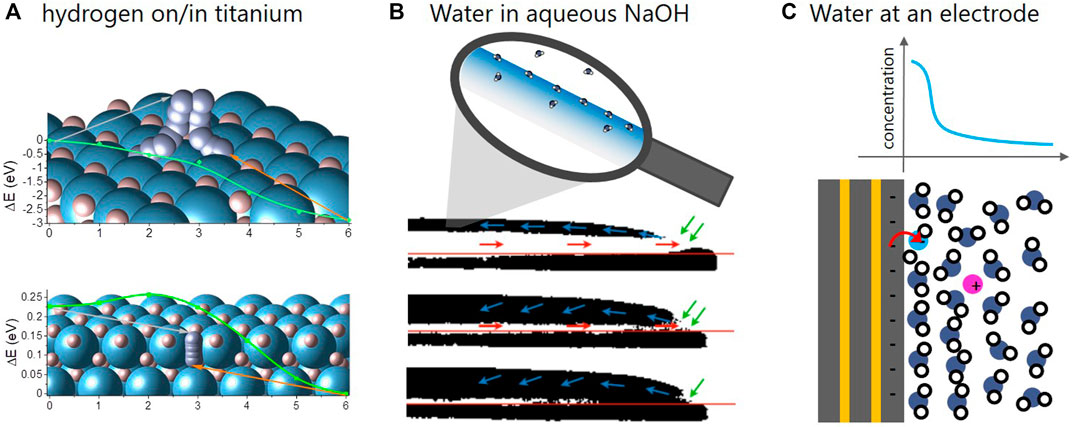
FIGURE 1. Schemes of the archetypal energy storage/conversion systems, in which short-lived interfaces play an important role. (A): Hydrogen dissociation/recombination (top) and surface-subsurface hopping (bottom) on Ti [adapted from Billeter et al. (2021)]. The y-axis is the energy of hydrogen molecule and atom, respectively, while the x-axis is the reaction coordinate describing the pathway of the molecule and atom. (B): Water absorption into aqueous NaOH visualized by neutron imaging [adapted from Fumey et al. (2022)]. Highly concentrated aqueous NaOH absorbs water vapor. The process was made visible by neutron imaging showing the absorbed H₂O in the original NaOD-D₂O droplet in black and white, respectively. (C): Scheme of electrode-electrolyte interface during water splitting [adapted from Sambalova et al. (2021)]. A specific analysis method based on magneto-optics was developed to probe the water/OH⁻ gradient in the vicinity of the electrode.

Although fundamentally different, the chosen systems are similar in that all processes are governed by molecular reactions taking place at an interface. In metal hydrides, stored hydrogen is split/recombined at the surface of the metal hydrides before it diffuses through the solid (Borgschulte et al., 2006). The power density of heat storage is determined by the water uptake kinetics in liquid sorbents, which is limited both by diffusion as well as surface phenomena (Fumey et al., 2020). And electrochemical conversion relies on the efficiency of the electrocatalytic reactions at the electrode-electrolyte interface. Needless to say that the improvement of these interface reactions gained great attention by scientists, resulting in huge effort dedicated to research and development of new catalysts. There are limitations of this approach, though: referring to catalysts for electrochemical CO₂ reduction, Chan, 2020 provokes with the following statement: “To date, I am not aware of a new catalyst with intrinsic activity towards C₂ products that unequivocally exceeds that of Cu foil.” This statement should be discussed in the light of the great achievements, which have recently been made in this field: the father of the electrochemical CO₂ conversion Hori et al., 1987 reports current densities of around 5 mA cm⁻² with a Faraday efficiency of around 20% percent towards C₂H₄ using a copper foil. Recently, current densities as high as 750 mA cm⁻² with a Faraday efficiency above 60% using polycrystalline copper surfaces were achieved by Dinh et al., 2018, i.e., with basically the same electrocatalyst as used by Hori et al., 1987. The secret to this great success lies in a sophisticated design of the electrochemical interface, i.e., the controlled transport of reactants and products from and to the active Cu sites (Dinh et al., 2018; Nesbitt et al., 2020); while the phenomena on the molecular level at the interface play a minor role only.

The question arises, whether this approach is similarly successful in other areas of energy storage, and what is its limitation. In a simplified way, one may argue that the ultimate limit is the fundamental turnover frequency (TOF) of the catalyst, namely of its active sites (“intrinsic catalytic activity”). However, there are systems, in which the TOF depends on the applied conditions (see, e.g., Borgschulte et al., 2013). This, in turn, can be used to tailor the interface properties. Alternatively, one may circumvent a rate-limiting interface to improve the overall kinetics. In any case, an improvement relies on the knowledge of interface structure on the microscopic as well as macroscopic dimension. Despite the clarity of the goal, analysis of such interfaces is challenging, in particular, if they are impermanent. In this review, we will summarize the state-of-the-art of three archetypal energy storage/conversion systems with respect to the importance of the underlying active interface, conceptualize the chosen approaches, address the analytical challenges that need to be overcome, and give an outlook for future research and development.

2 Interfaces in Energy Conversion and Storage

A renewable energy scenario must consider the renewable primary energy input as well as the demand and consumption pathways. The latter are mechanical work, electricity, and heat. The sun delivers light and heat, and only indirectly mechanical work (wind, precipitation, waves). This means that most of the incoming energy must be converted to the desired forms of energy. Although heat appears to be readily available, there is a mismatch between the availability and the demand peaks. This seasonal energy variation is a challenge in general, in particular at higher latitudes of earth’s hemispheres (Mulder, 2014). Energy storage is thus inevitable. The debate about which forms of energy storage are most suitable is ongoing. A description of them is beyond the scope of this review (see, e.g., Züttel et al., 2010). Great potential is seen in converting solar light into hydrogen either directly (photo-catalytic or photo-electrochemical energy conversion (Reece et al., 2011; Berardi et al., 2014; Dogutan and Nocera, 2019), or indirectly via photovoltaics and water electrolysis (Züttel et al., 2010; Jacobsson, 2018). Water electrolysis in alkaline electrolyzers is an established technology with very high conversion efficiencies without using precious metals (Ni, Fe; see, e.g., Zeng and Zhang, 2010; Phillips and Dunnill, 2016). We discuss the ingenious design of the electrochemical cell (“zero-gap geometry”) in subsection 2.3. The underlying physical principle is based on the approach “improving the dynamic interface”. This approach has been shown to be equally successful in heat storage in aqueous sodium hydroxide solution (Fumey et al., 2020; Fumey et al., 2022), and is discussed in detail in subsection 2.2. Hydrogen as an energy carrier requires safe and efficient storage strategy, which is still an obstacle for its widespread introduction (Andersson and Grönkvist, 2019). Hydrogen storage in metal hydrides is a promising solution to this problem (e.g., Schlapbach and Züttel, 2001; Yang et al., 2010; Modi and Aguey-Zinsou, 2021). From a didactic point of view, it is the simplest model system to demonstrate the importance of “short-lived interfaces” for kinetics and its quantitative description. We thus start with this system.

2.1 Hydrogen Sorption in Metal Hydrides

The qualitative picture of hydrogen sorption in (transition) metal hydrides is relatively simple and thus allows an in-depth modeling of the kinetics. During hydrogen absorption in metal hydrides there are two main steps involved (Schlapbach, 1992; Fukai, 2005): the dissociation of the hydrogen molecule and the transport of the chemisorbed hydrogen towards the subsurface and adjacent diffusion in the bulk (see Figure 2).

FIGURE 2

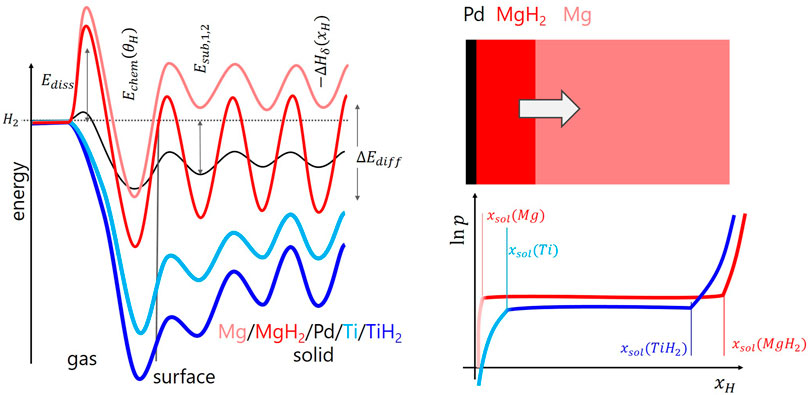
FIGURE 2. Left graph: characteristic solid-gas interaction steps pictured by the dependence of the potential energy on the distance z from the surface for Mg, MgH₂, Pd, Ti, and TiH₂ [adapted from Refs. Fukai (2005); Borgschulte et al. (2006); Billeter et al. (2021)]. Top right shows a simplified model of the hydrogenation of a Mg thin film capped with a catalyst. Bottom right is the sketch of the pressure-composition isotherms of Mg and Ti. See text for details.

Since physisorption of gas molecules on surfaces requires no activation energy and the impingement rate of H₂ onto the surface is high, the gas phase can be assumed to be in equilibrium with the physisorbed state. Furthermore, the heat of formation ΔH_phys is very small and the molecule remains in its entity. This step is thus neglected in most cases. For chemisorption, the hydrogen molecule has to dissociate (see, e.g., for Ti Figure 1A), and for that it has to overcome a dissociation barrier of 0 ≤ E_diss < 2 eV which, in most cases, e.g. in case of Mg, is high (Figure 2), and only few materials such as Ti and Pd have negligible E_diss. The hydrogen atoms are then in practically all relevant cases strongly chemisorbed (Fukai, 2005; Borgschulte et al., 2006; Billeter et al., 2021). Figure 2 emphasizes the importance of “catalysis” in hydrogen storage and hydrogen permeable membranes: the static surface barrier E_diss is the main barrier for hydrogen uptake in promising materials such as Mg, and reducing it by adding a “catalyst” such as Pd or Ti without a significant E_diss on the surface of the storage material is straightforward.

Hydrogen storage in metal hydrides relies on hydrogen sorption in the bulk of the metal/alloy. The prerequisite for hydrogen storage is the hopping of hydrogen chemisorbed on the surface into a subsurface sites (Figure 1A), and adjacent layers. After two to three monolayers, the potential-energy surface is bulk-like (Figure 2), i.e., hoping between layers corresponds to bulk diffusion in the metal/alloy from minimum to minimum in the potential-energy surface. This corresponds to the heat of solution (−ΔH_sol) governed by the activation energy of diffusion ΔE_diff. However, relevant amount of hydrogen is absorbed in the hydride phase only (e.g., in TiH₂, MgH₂). The physics is usually discussed along so-called pressure composition isotherms, sketched in Figure 2. At low pressures, hydrogen is dissolved up to a maximum concentration x_sol(M). At this concentration, it is energetically beneficial to form the hydride phase, which grows on expense of the solubility phase, until reaching again a single phase at x_sol(MH₂). It is worth noting here that hydrogen uptake is thus inherently linked to the formation and annihilation of (short-lived) interfaces.

The details of these interfaces define growth of the phases and thus eventually hydrogen uptake kinetics (Førde et al., 2007; Lai et al., 2019), and are beyond the scope of this work. We refer to Fukai (2005), Schlapbach (1992) and others. Some key features may be listed: changes into a new phase are associated with modifications of the surface potential energy. For Ti going from the α-phase to the δ-phase, the changes are moderate as the heat of solution (ΔH_sol) is similarly negative as is the heat of hydride formation (compare light and dark blue curves in Figure 2). The activation energies of diffusion do not differ markedly either (Billeter et al., 2021). This leads to relatively high boundary solubility both for the hydrogen as well as vacancy solubility in the solid solution and hydride phase, respectively. Hydrogen uptake kinetics is thus mainly determined by transport phenomena, i.e., diffusion. The situation is different in the hydrogen - magnesium system. The heat of solution in Mg is positive and thus x_sol is extremely small. This leads to very marked interfaces. Furthermore, diffusion of hydrogen requires the availability of empty sites. They exist in TiH₂, as also the hydride vacancy solubility is high, but hardly in MgH₂ (Töpler et al., 1982; Uchida et al., 2015). This results in the formation of a blocking layer on the surface of a Mg layer (grain) upon hydrogenation (Zhdanov et al., 1993; see Figure 2).

Eventually, the motivation for elucidating the mechanism of hydrogen sorption in metal hydrides lies in improvement of the kinetics by development of a fast hydrogen storage material (Lai et al., 2019).¹ The line of thought is well explained on the example of MgH₂. Earth-abundant and cheap, MgH₂ has been recognized as a promising material, and although the equilibrium thermodynamics of this material are suboptimal (Zhou et al., 2021a), much research has been performed on its kinetics (see, e.g., Sun et al., 2020). The surface of Mg and MgH₂ grains as smallest unit in a technical hydrogen storage material is usually covered by oxides, drastically reducing the dissociation kinetics (see, e.g., Friedrichs et al., 2006; Borgschulte et al., 2008; Lai et al., 2019). Metal particles with low dissociation barrier and fast hydrogen diffusion such as Pd (Zhdanov et al., 1993) and TiH₂ (Zhang et al., 2019; Zhou et al., 2021b) are attached to the metal hydride to lower the static interface. Many other materials than Pd and Ti have been found to be active catalyst (Sun et al., 2020). However, removing the rate-limiting step at the surface, means that the rate limiting step occurs at the inner layers. Zhdanov et al., 1993 found that the hydride blocking layer slows down the hydrogenation kinetics markedly. The velocity of this moving (dynamic) interface depends on the diffusion of hydrogen in the hydride layer, which is much slower than in α − Mg (Töpler et al., 1982; Uchida et al., 2015).

One solution to reducing the effect of the blocking layer is to improve the hydrogen diffusion in it by additives (Hao and Sholl, 2008; Koteski et al., 2015). However, various trials were not very effective. Using thermodynamic conditions, under which the blocking layer is not formed (Zhdanov et al., 1993; Uchida et al., 2015), is possible, but unpractical. Alternatively, the bulk material is broken up into small grains by, e.g., ball milling (Zaluski et al., 1997; Lai et al., 2019). If the grains are below a critical size, the blocking layer cannot be formed. Additives added during ball-milling prevent grain growth during hydrogen cycling (Aguey-Zinsou et al., 2006), and facilitate hydrogen dissociation and hydrogen transport along the grain boundaries (Barkhordarian et al., 2006; Lai et al., 2019).

Using alloys instead of pure metals is an established concept to tailor thermodynamics for efficient hydrogen storage (Fukai, 2005; Schlapbach, 1992). Alternatively, composites can be used to optimize the heat of reaction (Reilly and Wiswall, 1967; Bösenberg et al., 2007). In general, various so-called complex metal hydride systems are composites at least in one hydrogenation state (Frankcombe, 2012; Orimo et al., 2007; Ikeda et al., 2021), complicating the description of sorption kinetics and underlying morphology changes.

2.2 Water Absorption Into Aqueous NaOH

The supply of the heat demand of buildings located at high latitudes with renewable energy is challenging, as for about quarter of the year the energy must come from stored energy (Pinel et al., 2011; Shah et al., 2018). Liquid sorption heat storage is a promising technology, providing loss-free storage over time, high energy density, and relatively low cost (Hadorn, 2008). The concept is based on a sorption heat pump equipped with liquid sorbent and sorbate storage. Typical hygroscopic fluids studied are aqueous solutions of lithium bromide, lithium chloride, calcium chloride, and sodium hydroxide (Zhang et al., 2014; Weber and Dorer, 2008), with sodium hydroxide showing superior potential with respect to high energy density and low material price (Fumey et al., 2017). Recently, functional storage systems became available. These reach performance values near to the anticipated and required temperature swing, power- and energy density (Fumey et al., 2022). The reason for this is not of technical nature, but due to the detrimental relation between power- and energy density. It is special for this kind of energy storage, and thus worth to illuminate in greater detail.

The water vapor pressure p of the aqueous sodium hydroxide solution is concentration and temperature-dependent. An increase in the water vapor pressure or a decrease in the solution temperature leads to absorption of water, thus increasing water concentration c at the gas-liquid interface. A decrease in the water vapor pressure triggers the reversed process. The resulting chemical current density of water molecules j (molar flux $\dot{M}$ per area A) is linked to the resulting heat flow $\dot{q}$ via the heat of water absorption ΔH (Fumey et al., 2020):

\dot{M} = A \cdot j = \dot{q} \cdot {(Δ H)}^{- 1} (1)

If this process takes place in a mass and heat exchanger (Figure 3), the heat flux will not lead to a significant increase of the temperature (assuming that the heat removal is sufficient and that the applied water vapor pressure is a step-like function, i.e., constant after initial increase/decrease). For heat release, the vapor pressure is increased (Figure 3A, C). The solution with low water concentration is water enriched from c_low to c_high while passing the mass- and heat exchanger. The maximum water concentration c_high depends on T_l and on the kinetics: Δc^h > Δc^s, where the indices h, and s stand for high and slow kinetics. However, the concentration difference defines the total storage density, which now depends on the kinetics. During heat absorption (i.e., high T = T_u, Figure 3B, D), the process is reversed, but exhibits the same detrimental relation between kinetics and storage density. For slow kinetics, we start already at a lower maximum concentration $c_{h i g h}^{s}$ giving a smaller maximum temperature swing ΔT = T_u − T_l. This is in contrast to, e.g., energy storage in batteries. Here, the voltage (corresponds to the temperature swing in thermal energy storage) may be reduced at high current densities/slow kinetics, but the terminal voltage is generally not affected.

FIGURE 3

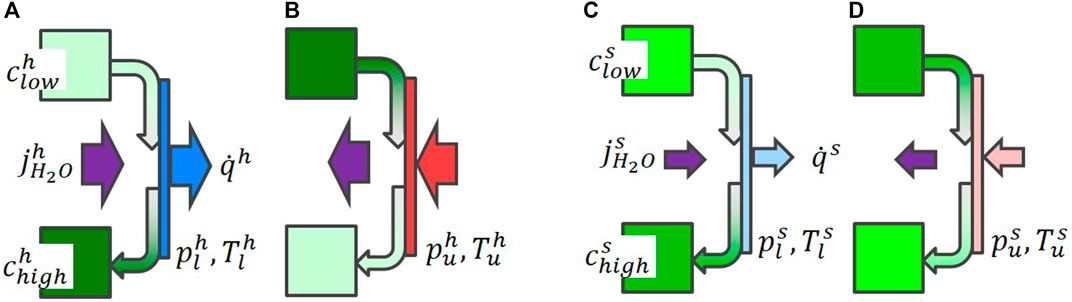
FIGURE 3. Scheme illustrating the heat storage in aqueous NaOH. Two reservoirs with low and high water concentrations c_low, c_high are connected via a heat and mass exchanger. For heat release [schemes (A), C)], water vapor is absorbed $(j_{H_{2} O})$ at the water vapor pressure p and temperature T, generating heat $(\dot{q})$ and increasing the water concentration; for heat uptake [schemes (B, D)], water desorbs and thereby cools the liquid. The indices h and s denote fast and slow kinetics. The final concentrations and thus the total amount of heat stored/released depends on the kinetics.

Because of the importance of kinetics in thermal energy storage, Fumey et al., 2020 studied the gas-liquid interface under operation conditions. For this, a confocal Raman setup was designed allowing the temporally and spatially resolved measurement of the water concentration upon absorption/desorption. The measurement brought to the fore that the measured water gradient is well fitted to solutions of 2nd Ficks law using the literature diffusion coefficient of water in aqueous NaOH. This means that diffusion is rate-limiting. From a scientific point of view, this is a satisfying result. However, it is the most difficult outcome from an applied perspective: the intrinsic diffusion coefficient of H₂O in aqueous NaOH cannot be easily altered. Furthermore, the diffusion gradient extends over 100–200 μm. The thickness of the floating aqueous NaOH is much thicker, but cannot be thinned markedly due to the low viscosity of aqueous NaOH (Smith, 1956; Kim et al., 1996; Li et al., 2016). An improvement of the performance of a mass and heat exchanger by lowering the diffusion barrier seemed to be unpromising.

In addition to mass transport on a microscopic scale, mass transport occurs on a macroscopic scale via convection (Fujita, 1993; Li et al., 2016). Neutron imaging gave indication that this convection can be induced by buoyancy (Fumey et al., 2022, see Figure 1B). With appropriate design, the convection flux provides continuously fresh NaOH solution to the gas-liquid interface. Based on these observations, Fumey et al. (2022) constructed a mass and heat exchanger with an area specific power of 1.28 kWm⁻² with an extrapolated thermal energy storage density of 243 kWh m⁻³, near to the theoretical limit of 360 kWhm⁻³. This solution may be generalized by the approach “separation of interface and mass transport”: at the interface, reaction is fast; to guarantee fast uptake into the bulk, the material at the interface is transported by convection (Figure 1B).

An open research question is, whether the Marangoni-effect plays a role in the increase of the convection [for basics of the Marangoni effect we refer to Leal (2007)]. However, the effect is based on a gradient of the surface tension, e.g., generated by a point source (Roché et al., 2014). This gradient may exist in heat and mass exchanger under certain conditions. However, under steady state conditions, the influence of the surface gradient can be considered to be small.

2.3 Short-Lived Interfaces in Electrochemical Energy Conversion

Alkaline water electrolysis is an established technology, which has been optimized over 100 years (see, e.g., Zeng and Zhang, 2010; Phillips and Dunnill, 2016). Accordingly, there is not much room for further optimization. However, various technical challenges have been successfully overcome over the course of development. These challenges are common in electrochemical conversion associated with the evolution of gases. Having a closer look may thus help optimizing other electrochemical reactions, such as CO₂ reduction.

In liquid alkaline electrolysis, the desired high current densities translate into a relatively large pH gradient between the electrodes. At the oxygen evolution electrode

4 O H^{-} \to O_{2} + 2 H_{2} O + 4 e^{-} (2)

OH⁻ is consumed and water produced, while water is consumed and OH⁻ produced at the hydrogen evolution electrode:

4 H_{2} O + 4 e^{-} \to 2 H_{2} + 4 O H^{-} (3)

This gradient adds to the overpotentials from electro-catalysis at the electrodes. To lower it, the distance between the electrode (“gap”) d should be as small as possible (Figure 4), because the electrolyte resistance R₀ increases with it:

R_{0} = ρ_{0} (c_{O H}) \frac{d}{A} (4)

A is the electrode surface; ρ₀(c_OH) is the resistivity of the electrolyte, which depends on its pH (concentration of OH⁻). However, in addition to the ion transport, the formed hydrogen and oxygen bubbles have to be removed as quickly as possible, because they block the ion transport. Tobias (1959) proposed Bruggemann’s equation

ρ / ρ_{0} = {(1 - v)}^{- 3 / 2} (5)

to correlate the bubble induced resistivity ρ/ρ₀ to gas void fraction v in electrolytic cells. The gas void fraction is closely related to the number and size of the bubbles, which depend on a number of parameters such as pressure, temperature, and surface tension of electrolyte and electrode. In practice, the distribution is determined experimentally. The important fact is that the void- (simplified bubble-) concentration decreases, if the volume, i.e., the gap between the electrode increases. Figure 4 shows some empirical results of the bubble induced resistivity R/R₀, with R₀ the resistance of the electrolyte without bubbles (Hine and Murakami, 1980). The resistance increases with applied current, as it is the origin of the produced bubbles; however, the main effect is the gap: the resistivity increases extremely for gaps smaller than 0.5 cm [Figure 4, from Hine and Murakami (1980)]. The behavior is reciprocal to the behavior of electrolyte resistance R₀ with distance (Eq. 4), and apparently only a bad compromise is possible.

FIGURE 4

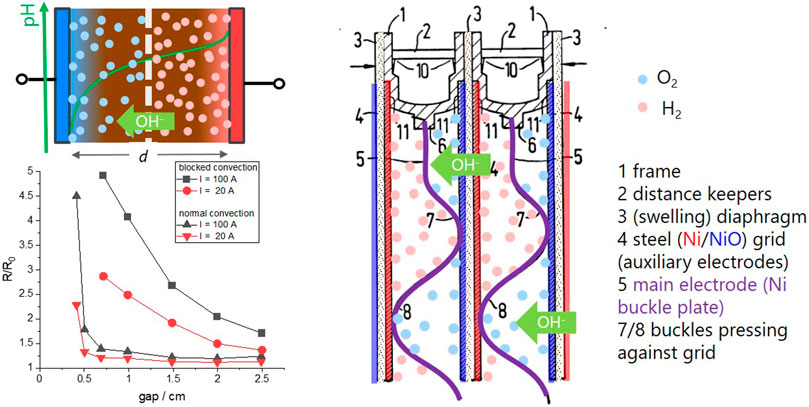
FIGURE 4. Left: simple sketch of an electrolyzer with bubbles formed between the electrodes (top). The bottom graph shows the normalized bubble resistivity of a model electrolyzer with normal convection and blocked convection as a function of the electrode gap (from Hine and Murakami (1980)). Right: technical drawing of the bipolar electrodes in an alkaline zero-gap electrolyzer (adapted from Zdansky (1977)).

To solve this challenge, Zdansky invented the so-called “zero-gap” geometry (Zdansky, 1959): he reduced the gap to basically zero, i.e., to the minimum distance defined by the obligatory porous diaphragm, which prevents a mixing of hydrogen and oxygen gas. As the electrode meshes (or grids) touch the diaphragm, the bubbles cannot be formed between the electrodes, and thus do not block the ion current in the electrolyte. Instead, they are formed at the other side of the meshes, where there is enough space to purge the bubbles away by the flow of the electrolyte (see the bipolar configuration of a zero-gap alkaline electrolyzer in Figure 4). At the same time, the electrolyte resistance R₀ is minimized given a diaphragm with proper porosity/tortuosity is used (Ju et al., 2018).

This 60 year old design has become the standard in alkaline (liquid) electrolyzers with only minor further improvements mainly addressing materials properties of the diaphragm and electrodes (Zeng and Zhang, 2010; Phillips and Dunnill, 2016; Ju et al., 2018). Some new concepts are the so-called hybrid electrolyzers with a gas diffusion electrode as anode and a conventional immersed porous cathode (Koj et al., 2019).

Apart from the bubble resistivity, Zdansky (1959) reports an improvement of the diffusion layer properties in zero-gap electrolyzers. On the other hand, a recent publication challenges this statement arguing that the electrode area facing the diaphragm is not active, a depletion of OH⁻ ions in the vicinity of the electrodes occurs, and the supersaturation of the electrodes increases the equilibrium potential at elevated current densities (Haverkort and Rajaei, 2021).

Inherent to electrochemistry is the dependence of the reaction on external parameters such as applied potential. The potential determines the electron transfer reaction, and with it the species and number of adsorbed molecules. If ions, i.e., charged species, are involved, the corresponding electric field will determine the gradient built up (Figure 1C, see discussion above). Can the species be influenced by other external fields as well? Recently, a markedly increased electrochemical efficiency of the oxygen evolution reaction in water splitting was achieved by applying a uniform magnetic field to the oxygen evolution electrode Garcés-Pineda et al., 2019. Magnetic enhancement was observed also for the hydrogen evolution reaction at different electrodes Zhou et al., 2020; Lin et al., 2012. The effect is surprising, if one considers only spin-spin interactions at the interface as the origin of the effect. Typical magnetic energies are orders of magnitude lower than chemical energies (energy of spin-spin interactions $< μ$ J mol⁻¹, Steiner and Ulrich, 1989). Using magneto-optical spectroscopy, Sambalova et al., 2021 demonstrated that the effect on hydrogen evolution can at least partially be traced back to the magnetic properties of the species near to the electrode (OH⁻ and H₂O). The thermodynamic force f_mag induced by a homogeneous magnetic field is restricted to the interface with a steep gradient of the susceptibility χ:

f_{m a g} = - \frac{\partial}{\partial x} μ_{m a g} = - \frac{1}{2 μ_{0}} B^{2} \cdot \frac{\partial χ}{\partial x} (6)

The susceptibility of an alkaline solution depends on the concentration of OH⁻ ions, i.e., the effect depends on the pH-gradient as a result of the electrochemical double layer (EDL) built up during electrolysis.

Apart from demonstrating the impact of a magnetic field on the EDL, the authors report a time dependence of the effect indicating a redistribution of ions as a response to the thermodynamic force. This effect can be utilized: modulating the external fields can alter the overall reaction mechanism. In so-called pulse-electrolysis (Liu et al., 2021), the time to accumulate a certain coverage of intermediates and/or products and corresponding changes of the electrode-electrolyte interface is used to enhance efficiency of the water splitting reaction (Vincent et al., 2018) as well as to control the selectivity of the products in electrochemical CO₂ reduction (Kumar et al., 2016). It is too early to assess the success of these ideas in practical applications; however, they are a beautiful demonstration of “short-lived interfaces for energy conversion”.

2.4 Concepts to Improve Interfaces in Energy Materials

Aim of this review is to conceptualize how to overcome kinetic barriers from interfaces in energy materials/systems. The various different concepts used to overcome the kinetic barriers may be simplified by:

1. removing the static interface

2. improving the static interface

3. removing the dynamic interface

4. improving the dynamic interface

A static interface is often the surface such as the oxide skin on MgH₂ blocking hydrogen dissociation and transport. Its removal [concept 1)] is only a theoretical option, as there are always contaminants in technical hydrogen (Delmelle et al. (2014)). Concept 2) is the only option. An electrode surface is a static interface with function. Thus, it cannot be removed [concept 1)], and its performance must be optimized [concept 2)]. The surface of liquids is a static interface, too, but there is no kinetic barrier at least for water uptake in aqueous NaOH.

With the surface removed or properly optimized, other reaction steps may be rate-limiting. We focus here on the dynamic (“short-lived”) interfaces being built only under certain circumstances. This makes analysis difficult, because they only exist under operando conditions (see subsection 2.5). However, already knowing their existence is helpful. Basically, the same concepts as for the static interface may be applied.

To explain the relevance of interfaces in hydrogenation reactions, we chose the well studied example of MgH₂, because discussion of the effectiveness of additives is often led only along their sorption rate enhancement. This results in a multitude of often contradicting papers, simply because an additive improving the static interface may not help to reduce the barrier of the dynamic one. The case MgH₂ is well studied, in contrast to hydrogen sorption kinetics in NaAlH₄. In particular the role of additives such as TiH_x as a hydrogenation catalyst in Al + NaH to form NaAlH₄ remains elusive (Bogdanović and Schwickardi, 1997; Frankcombe, 2012). There is consensus that the effective catalysts affect the static interface, i.e., they enable hydrogen dissociation and recombination (concept 1). The additional properties that make catalysts such as Ti better than classical hydrogenation catalysts, such as Pd, is not fully understood (Frankcombe, 2012). Reducing the dynamic interface by improving the transport of alane species has been suggested (concept 4, here called zipper model, see Marashdeh et al., 2007), although experimental evidence is lacking. The difficulty of complex hydrides is the formation of at least two solid phases during decomposition, which generates additional short-lived interfaces with mass transport of hydrogen and even metal atoms. Here, a fast interface reaction has been identified as prerequisite for the functioning of reactive hydride composites (Kato et al., 2012; Ali et al., 2021). Further research is needed for deeper insight into the dynamic interfaces during formation and decomposition.

The diffusion layer built upon water uptake in aqueous NaOH is not a sharp interface on a microscopic scale. As the system boundaries are much larger, it is the rate-limiting interface on a macroscopic scale. Both concepts (3 and 4) have been tested in the past: improving diffusion by additives (concept 4), and removing the interface by separating interface reaction and mass transport by introducing convection (concept 3).

The dynamic interface in electrochemistry is by far the most complex one. Although known since 100 years, research focuses on the improvement of the static interface by, e.g., developing electrocatalysts, while the dynamic interface is neglected probably due to the apparently simple measures to overcome it. Simple measures such as “stirring” to eliminate the impact of the diffusion (concept 3) are established techniques in analytical research (“rotating disc electrode”, see Baur (2007)). Similar to the case water uptake in a liquid, the challenge lies in the development of a design, where this idea is implemented into the confined and optimized technical device. The Zdansky “zero-gap” electrolyzer is a compelling example for this. The introductory example of electro-chemical CO₂ reduction to ethylene highlights concept 4): one can make use of the interface to control the mass transport of reactants to the interface (Nesbitt et al., 2020). The electro-chemical double layer (Figure 1C) is an interesting hybrid interface: it is always there (i.e., it is static), but depends on external parameters (i.e., it is dynamic) posing both a challenge for fundamental analysis as well as technical improvements.

In this review, we omitted the discussion of battery systems as important electro-chemical energy storage systems. The reason for this is not that short-lived interfaces do not exist here. On the contrary, the concept is directly applicable to nickel - metal hydride batteries with hydrogen diffusion processes in the metal hydride (Feng and Northwood, 2004), and the critical electrode-electrolyte interface (Han et al., 1999). Similar processes are relevant in Li-ion batteries as well (e.g., Li-ion diffusion, see Zhu and Wang, 2010). However, additional topics such as the stability of electrolyte, electrode, and interfaces are challenges in battery research (see, e.g., Xiao et al., 2020), which go beyond the scope of this review.

2.5 Analysis of Short-Lived Interfaces

Most statements on the existence of specific rate-limiting steps are made on the basis of kinetic measurements, e.g., hydrogen sorption kinetics (Førde et al., 2007; Zhou et al., 2021a; Lai et al., 2019; heat exchange kinetics (Zhang et al., 2014), current—voltage relationships, impedance spectroscopy and their modelling (Dau and Pasquini, 2019; Mukouyama and Nakanishi, 2020). There is an uncertainty of the interface models, if solely gained from a kinetic analysis. Direct proof of the corresponding dynamic interface is required to unambiguously assign the best kinetic model.

Hydrogen sorption kinetics in MgH₂ is an archetypal example. First hints of a dynamic interface built up during hydrogenation (“blocking layer”) date back to Stampfer et al. (1960), with indications substantiating using kinetic analyses by Rudman (1979) and Zhdanov et al. (1993). Convincing evidence was then provided by the visualisation of the hydrogen distribution using the N15-method (Rydén et al., 1989). It is worth mentioning that the proof relies on thin Mg films capped with Pd to remove the static interface barrier (i.e., successful realization of concept 1). Furthermore, hydrogen diffusion is slow and can be quenched by cooling allowing the use of the post-mortem nuclear N15-method. These boundary conditions cannot always be met. Below we give an overview of the state-of-the-art analysis methods and future developments with particular emphasis on operando methods.

Perhaps the most direct method of probing a surface is photoelectron spectroscopy. As it is an established technique, we refer to the various books and reviews describing the potential of the method (Briggs and Seah, 1983; Hüfner, 2003). In a nutshell: X-ray photoelectron spectroscopy and related techniques reveal qualitative and quantitative elemental composition of a surface. The small mean free path length of photoelectrons limits the information depth to few monolayers, and restricts the analysis to ultra-high vacuum environments. New developments extend the information depth up to around 10 nm, allowing to probe buried interface even when using laboratory apparatus using hard X-rays (Regoutz et al., 2018; Sambalova et al., 2020, see also Figure 5A, B). Sophisticated engineering pushed the maximum allowed gas pressure up to the bars range (near ambient pressure photoelectron spectroscopy, see, e.g., Knudsen et al., 2016; Roy et al., 2018; Amann et al., 2019; Novotny et al., 2020).

FIGURE 5

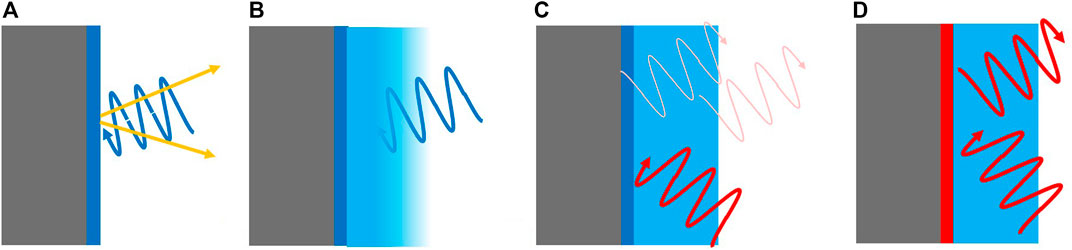
FIGURE 5. (A) Typical surface science analysis: nm mean free path length of electrons (yellow arrows, waves stand for photons) guarantees surface sensitivity. (B) Short mean free path length (of electrons and/or photons) impedes the analysis of buried interfaces. (C) Unrestricted mean free path length allows the measurement of buried interfaces, but spatial resolution is usually limited. (D) resonant interaction of the probe beam with the interface scales the spatial resolution down to the interface region.

The direct measurement of the ion gradients in the electrolyte in the vicinity of the interface is extremely challenging (Zaera, 2012), because the water layers above it absorb (photo-)electrons (Figure 5B). Recent technical developments (see refs. above) have made it possible to probe water and a spectator molecule (pyrazine) in an alkaline electrolyte in the vicinity of an electrode by photoelectron spectroscopy (Favaro et al., 2016). The results verify the shape of the potential in the EDL with nanometer resolution as function of applied potential and electrolyte concentration in a beautiful way, as predicted by the established theoretical framework (Helmholtz/Debye theory of the EDL, see, e.g., Devanathan and Tilak, 1965).

Other analysis techniques utilize photons to circumvent the challenges associated with electrons (e.g., X-ray absorption spectroscopy, de Groot, 2001; Newton and Dent, 2013; Nachtegaal et al., 2017). An established optical technique is diffusive reflectance infrared Fourier transform spectroscopy (DRIFTS Terreni et al., 2020; Negahdar et al., 2020). In general, operando investigations using probes with small mean free path lengths are usually limited to changes of the surface of materials, or adsorbates on it (Li and Gong, 2020).

Probing technical electrode/electrolyte interfaces such as in measurement of electro-chemical gradients on a mesoscopic length scale is difficult with photoemission spectroscopy (Figure 5B). Here optical methods such as spatially resolved Raman spectroscopy similar to the one described in section 2.2 have high potential. Visible light is hardly absorbed by typical electrolytes, and Raman spectroscopy is sensitive to molecular vibrations such as OH and ${C O}_{3}^{2 -}$ . Lu et al. (2020) applied the method to probe the pH gradient and CO₂—OH⁻ neutralization reaction near to a CO₂ reduction electrode. They find that the ${H C O}_{3}^{-}$ concentration profile extends a distance of 120 μm into the electrolyte at zero current. The pH gradient layer narrows with increasing CO₂ reduction current densities. These findings are highly relevant for the development of novel electrochemical CO₂ electrolyzers (Nesbitt et al., 2020). However, the space resolution of confocal Raman spectroscopy and related optical microscopy methods is of the order of 200 nm (Sil and Umapathy, 2014) limited by the Abbe-limit (see also Figure 5C). If sub-micrometer resolution is sufficient, Raman microscopy and generally optical methods are powerful tools to visualise particularly dynamic phenomena (hydrogen sorption: Borgschulte et al., 2010; Duan et al., 2018, diffusion gradients in liquids: Fumey et al., 2020; Lu et al., 2020), particularly because of the good time resolution. New developments push the resolution limits down to 20 nm using scanning near field optical microscopy (Karst et al., 2020). The latter study highlights the importance of spatial resolution by differentiating the hydrogen dynamics in small grains from the one in macroscopic behavior: the nm-sized grains transform individually, i.e., the hydrogen sorption kinetics does not follow a continuous diffusion as may be drawn from macroscopic observations with micrometer resolution.

To enhance the interface sensitivity in optical spectroscopy, resonance effects can be exploited, e.g., in surface plasmon enhanced Raman spectroscopy. Here, the surface enhances locally (nm range) the signal intensity (Dieringer et al., 2006). This means that although excitation and collection take place on a much larger scale, the measured signal can be associated to the adjacent interface layers (Figure 5D); e.g., to the EDL in the vicinity of a hydrogen evolution electrode (Yonezawa et al., 2017). The same principle applies to second-harmonic and sum-frequency generation spectroscopy (Shen, 1989), which have been employed in catalysis (Roiaz et al., 2016), surface characterization of liquids (Yamaguchi et al., 2012), electrochemical interfaces (Rey and Dlott, 2017).

Electron microscopy has traditionally been the method with highest spatial resolution. Surfaces and interfaces can be investigated with atomic resolution (e.g., de Graaf et al., 2020). Due to the high energies of the electrons used, operando conditions are possible, allowing the measurement of pressure composition isotherms of individual palladium nano-particles (Baldi et al., 2014).

Still, the operando, i.e., time resolved measurement under reaction conditions of elemental distribution over a wide range with nm precision is an open research question. Nuclear methods such as the above mentioned N15-nuclear resonance analysis can measure the hydrogen concentration in thin films with a typical depth resolution of 5–10 nm, over a depth of several microns (Lanford et al., 1976; Wilde and Fukutani, 2008; Wilde and Fukutani, 2014)). A related nuclear method is elastic recoil detection (ERD, Barbour and Doyle, 1995). Nuclear methods are in general very well suited for depth profiling, such as neutron imaging. The spatial resolution of neutron imaging is only in the micrometer range (Morgano et al., 2018), but its great advantages are the time resolution (Zboray and Trtik, 2018) and the compatibility to the harsh conditions as is relevant in catalysis (Terreni et al., 2018), heat storage (Fumey et al., 2022), and fuel cells (Boillat et al., 2017; Minnaar et al., 2020).

Finally, we would like to emphasise the importance of simultaneously good time and space resolution for the analysis of dynamic interfaces. Figure 6 shows a times series of neutron radiography images of water absorption into Ni-loaded zeolite beads [from Terreni et al. (2018)]. The time resolution of 1 min is (here) given by the time required to take an image with an appropriate signal to noise ratio. The spatial resolution was approximately 50 μm. However, this value is misleading, because it was measured on a static interface (at the bead’s outer surface). The interface of interest moves while the camera accumulates counts, here with a maximum velocity of around 80 μm per min. Thus, the “dynamic” spatial resolution deteriorates to more than double the static value. Terreni et al. (2018) repeated the measurements at higher temperatures, where the diffusion of water in zeolites is faster, and the total uptake smaller than at lower temperatures. The latter worsens the contrast ratio, and thus the signal to noise ratio, both effects impeding the measurement of meaningful diffusion gradients at higher temperatures.

FIGURE 6

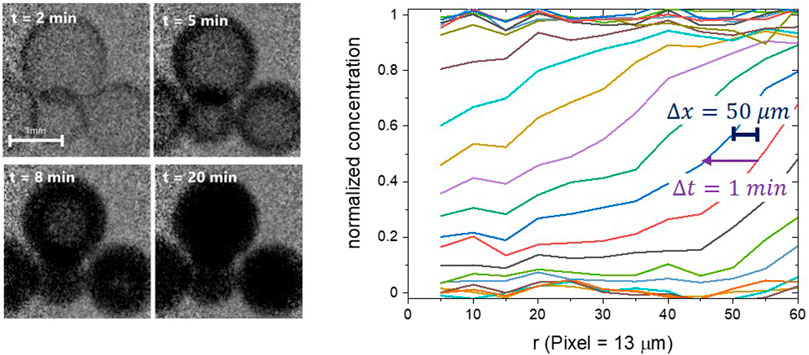
FIGURE 6. Left: times series of neutron radiography images of water absorption into Ni-loaded zeolite beads at 50°C [from Terreni et al. (2018)]. Right: normalized radial water concentration extracted from the times series. The spatial resolution was approximately 50 μm, with the time resolution of 1 min. The true gradient can be expected to be much steeper.

3 Conclusion

In this review, we discuss the kinetics of chemical energy storage/conversion systems alongside the concept of static and dynamic interfaces as rate-limiting steps. The review omits the importance of physical and chemical properties of energy materials, which may be found elsewhere. However, having identified the rate-limiting interface, the appropriate materials science should be applied to overcome them. In particular, a static interface must be treated differently from a dynamic one. At this point, material science comes back into play.

In detail, we give an overview of static and dynamic interfaces in hydrogen storage, sorption based thermal energy storage, electrochemical water splitting and electrochemical CO₂ reduction. We show successful examples, both historical and very recent ones, of how to lower the detrimental effect that stem from these interfaces. Emphasis is laid on the description of analysis methods suitable to probe static and dynamic interfaces.

The given examples are not exhaustive: similar effects of static and dynamic interfaces are expected to occur in other electrochemical applications such as fuel-cells (PEM-electrolyzers), batteries, etc.

In this review, we omit the description of numerical simulations for further insights into short-lived interfaces in energy materials due to practical reasons. Without doubt, theoretical approaches can bridge cases, which are difficult to access experimentally, and are important to generalize the usually specific technical systems.

Author Contributions

AB is the originator of the conceptual design, all authors contributed to writing of the manuscript, and reviewed and commented on it.

Funding

Financial support from the Swiss National Science Foundation (grant Nos. 172662 and 182987) is greatly acknowledged. Additional funding from the UZH-UFSP program LightChEC was received. This research work is financially supported by the Swiss Innovation Agency Innosuisse grant Nr. 1155002545 and is part of the Swiss Competence Centre for Energy Research SCCER HaE. Supplementary funding is received from the Swiss Federal Office of Energy SFOE grant Nr. SI/501605-01 in the frame of the IEA SHC Task 58/ECES Annex 33 participation.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Additional technical measures may be needed, such as tank design taking into account heat transfer, chemical and mechanical stress, etc., which we omit here.

References

Aguey-Zinsou, K.-F., Ares Fernandez, J. R., Klassen, T., and Bormann, R. (2006). Using mgo to Improve the (de)Hydriding Properties of Magnesium. Mater. Res. Bull. 41, 1118–1126. doi:10.1016/j.materresbull.2005.11.011