Perturbation Observer Based Fractional-Order Control for SMES Systems Based on Jellyfish Search Algorithm

The electric energy storage system (EESS) is considered as an efficient and promising tool to alleviate the power imbalance of grid-connected microgrid with distributed generation (DG). This work develops a perturbation observer-based fractional-order control (POFOC) strategy for superconducting magnetic energy storage (SMES) system. Initially, a high-gain state and perturbation observer (HGSPO) is designed for reliable estimation of the combined impact of the nonlinearities, parameter uncertainties, unmodeled dynamics, and external disturbances of SMES. Then the storage function of an SMES system is designed, which takes favorable terms into serious consideration to sufficiently utilize the physical properties of the SMES system. Moreover, a fractional-order control framework is applied for complete compensation for the estimated perturbation and adopted as the attached input to boost its dynamical responses. Furthermore, a newly proposed jellyfish search algorithm (JSA) is utilized to realize optimization and tuning of control gains of the developed strategy, upon which high-quality global optimum can be obtained to ensure prominent controlling performance. Case studies, e.g., active power and reactive power supply and system restoration capability under power grid fault effectively validate the effectiveness and reliability of the POFOC strategy compared with traditional PID control and interconnection and damping assignment passivity-based controller (IDA-PBC). In particular, the overshoot of PID is 115.264% of the rated value, while POFOC has no overshoot.

1 Introduction

Large-scale exploitation and application of renewable energy are significant to our future energy transformation and sustainable development, thanks to their outstanding environment-friendly characteristics (Yan, 2020), which can effectively help in the global energy crisis and ecosystem deterioration (Zhang et al., 2021a). In general, distributed generation (DG) is always deemed as an insightful solution, which can satisfy the demand for both uninterrupted electricity supply and zero pollution (Yang et al., 2019a; Xi et al., 2020). Nevertheless, the inherent intermittence and randomness of DGs often lead to fluctuation of output power, which may severely threaten microgrid operation stability and reliability. Electric energy storage system (EESS) serves as a promising strategy to solve this tricky problem.

In general, EESS owns various distinctive advantages, such as boosting power supply stability and reliability with fast responses, balancing power supply and demand under low costs, enhancing power generation efficiency, and decreasing pollution emissions. EESS systems can be generally divided into two main subsystems (Yang et al., 2018; Sara et al., 2020), i.e., i) high-energy storage systems and ii) high-power storage systems. In particular, the second can be further categorized into more different types, among which one of the most representative one is superconducting magnetic energy storage (SMES) (Shi et al., 2019). It is worth noting that SMES receive vast research attention, thanks to their merits of high-energy conversion efficiency via superconductors, and also low cost and high current intensity (Yang et al., 2016). Moreover, it can also achieve rapid regulation of active power/reactive power, which is beneficial to power transfer control (Shima et al., 2018). Currently, pulse-width modulated current source converter (PWM-CSC) is extensively adopted to restrain harmonic distortion and decrease the complexity of a system component (Yang et al., 2020).

As for SMES, a critical task during its operation is the design of an appropriate control system, which is crucial to ensure that SMES can obtain optimal operation performance under various applications. Thus far, traditional linear control method, for instance, proportional-integral-derivative (PID) control is extensively utilized due to its easy implementation and satisfactory effectiveness (Yang et al., 2017). However, SMES is a typical high nonlinear system, such that control gains of PID control that are acquired via single-point linearization cannot realize a globally consistent control. Therefore, many nonlinear control strategies are proposed to solve such an obstacle. For example, in the literature (Lin et al., 2018), an energy-shaping mechanism on the basis of port-controlled Hamiltonian (PCH) models was devised for a rapid power command response. Furthermore, a fuzzy logic control was adopted by Shanchuan Wang and Jianxun Jin (2014) to boost the dynamical responses of SMES systems under different operating scenarios.

However, SMES is usually prone to various uncertainties that are caused by renewable energy stochastic features (Montoya et al., 2018; Trilochan et al., 2018; Yang et al., 2019b). To boost the robustness and response speed of SMES under various operating scenarios at the same time, a perturbation observer-based fractional-order control (POFOC) strategy is devised in this work, which combines the benefits of high-gain state perturbation observer (HGPO) and fractional-order sliding-mode control (FOC) (Montoya et al., 2018). Furthermore, a novel jellyfish search algorithm (JSA) (Chou and Truong, 2021) is adopted to realize the optimization and tuning of control gains of the developed strategy, upon which high-quality global optimum can be obtained to ensure a consistently remarkable performance. The main novelties are outlined as follows:

• System nonlinearities, parameter uncertainties, unmodeled dynamics, as well as external disturbances are combined to one perturbation. Then, an HGPO is employed to estimate the perturbation, while the controller is then adopted for complete compensation for the estimated perturbation. Therefore, the proposed POFOC control can maintain high robustness against different uncertainties.

• Due to the employed two fractional orders by POFOC, its response speed can be significantly boosted compared with PID control and damping assignment passivity-based controller (IDA-PBC). Meanwhile, the perturbation compensation mechanism can efficiently ensure that the proposed method obtains a consistently optimal global control performance.

• JSA can effectively avoid falling into local optimal solutions, which can ensure that the control gains can be properly optimized and tuned in a relatively short time.

The remaining of this paper is organized as follows: Section 2 develops the SMES system modeling. Section 3 develops the POFOC. In Section 4, the jellyfish search algorithm is described. In Section 5, the POFOC design for SMES systems is described. Comprehensive case studies are undertaken in Section 6. Last, Section 7 summarizes the main contributions of the paper.

2 Superconducting magnetic energy storage system modeling

Energy storage devices have bidirectional power regulation ability. The power response characteristics of different energy storage devices have various time scales and recycling efficiency due to their different energy storage forms. SMES is a kind of power-type energy storage device, which has the characteristics of fast-response speed and high-power grade. As one of the typical superconducting devices, SMES owns great potential to be widely used in microgrids with the continuous development of superconducting technology.

According to the literature (Espinoza and Joos, 1998; Montoya et al., 2018), the modeling of one typical SMES system is able to be expressed by:

$L_{\text{T}}\frac{\mathrm{d}}{\mathrm{dt}}{i}_{\text{d}}=-R_{\text{T}}{i}_{\text{d}}-\omega L_{\text{T}}{i}_{\text{q}}+v_{\text{d}}-E_{\text{d}}(1)$

$L_{\mathrm{T}}\frac{\mathrm{d}}{\mathrm{d}t}{i}_{\mathrm{q}}=-R_{\mathrm{T}}{i}_{\mathrm{q}}+\omega L_{\mathrm{T}}{i}_{\mathrm{d}}+v_{\mathrm{q}}-E_{\mathrm{q}}(2)$

$C\frac{\mathrm{d}}{\mathrm{d}t}{v}_{\mathrm{d}}=-i_{\mathrm{d}}-\omega C{v}_{\mathrm{q}}+m_{\mathrm{d}}{i}_{\mathrm{dc}}(3)$

$C\frac{\mathrm{d}}{\mathrm{d}t}{v}_{\mathrm{q}}=-i_{\mathrm{q}}+\omega C{v}_{\mathrm{d}}+m_{\mathrm{q}}{i}_{\mathrm{dc}}(4)$

$\frac{1}{2}{L}_{\mathrm{sc}}\frac{\mathrm{d}}{\mathrm{d}t}{i}_{\mathrm{dc}}^2=-E_{\mathrm{d}}{i}_{\mathrm{d}}-E_{\mathrm{q}}{i}_{\mathrm{q}}(5)$

where all the variables can be referred to in the Nomenclature, while the basic framework of PWM-CSC-based SMES system is demonstrated in Figure 1.

FIGURE 1

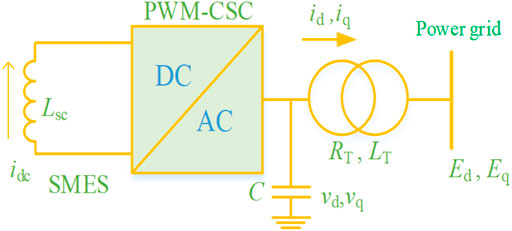
FIGURE 1. Pulse-width modulated current source converterPWM-CSC)-based superconducting magnetic energy storage (SMES) system connected to an AC power grid.

In particular, $P_{\text{ac}}$ and $Q_{\text{ac}}$ can be expressed by (Espinoza and Joos, 1998; Montoya et al., 2018):

$P_{\mathrm{ac}}=E_{\mathrm{d}}{i}_{\mathrm{d}}+E_{\mathrm{q}}{i}_{\mathrm{q}}(6)$

$Q_{\mathrm{ac}}=E_{\mathrm{q}}{i}_{\mathrm{d}}-E_{\mathrm{d}}{i}_{\mathrm{q}}(7)$

3 Perturbation observer-based fractional-order control

3.1 High-gain state and perturbation observer design

An uncertain nonlinear system can be written in a standard form, as follows:

$\{\begin{array}{c}\dot{x}=Ax+B\left(a\left(x\right)+b\left(x\right)u+d\left(t\right)\right)\\ y=x_1\end{array}(8)$

where $x={\left[x_1,x_2,\cdots ,x_n\right]}^{\mathrm{T}}\in {\mathrm{ℛ}}^n$ means the state variable vector, while the other variables and parameters can be referred to in the literature (Espinoza and Joos, 1998; Elsisi et al., 2017). State matrix A and control matrix B are described by:

$A= {\left[\begin{array}{ccc}\begin{array}{c}0\\ 0\\ \cdots \end{array}& \begin{array}{c}1\\ 0\\ \cdots \end{array}& \begin{array}{c}\begin{array}{ccc}0& \cdots & 0\end{array}\\ \begin{array}{ccc}1& \cdots & 0\end{array}\\ \begin{array}{ccc}\cdots & \cdots & \cdots \end{array}\end{array}\\ 0& 0& \begin{array}{ccc}0& \cdots & 1\end{array}\\ 0& 0& \begin{array}{ccc}0& \cdots & 0\end{array}\end{array}\right]}_{n\times n},B={\left[\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ 1\end{array}\right]}_{n\times 1}(9)$

The perturbation of the system is represented by literature (Shtessel et al., 2008; Zhu et al., 2015; Elsisi et al., 2017):

$\psi \left(x,u,t\right)=a\left(x\right)+\left(b\left(x\right)-b_0\right)u+d\left(t\right)(10)$

where b₀ denotes a control gain that is set by the users, which is a constant.

Furthermore, x_n in the system is written as:

${\dot{x}}_n=a\left(x\right)+\left(b\left(x\right)-b_0\right)u+d\left(t\right)+b_{0}u=\psi \left(x,u,t\right)(11)$

Now, $x_{n+1}=\psi \left(x,u,t\right)$. Hence, the system (Eq. 8) can be further expressed as:

$\{\begin{array}{c}y=x_1\\ {\dot{x}}_1=x_2\\ ⋮\\ {\dot{x}}_n=x_{n+1}+b_{0}u\\ {\dot{x}}_{n+1}=\dot{\psi }(\cdot )\end{array}(12)$

Thus, $x_{\text{e}}={\left[x_1,x_2,\cdots ,x_n,x_{n+1}\right]}^{\text{T}}$ and two following assumptions can be defined by (Shtessel et al., 2008; Zhu et al., 2015; Elsisi et al., 2017):

A.1 Inequality $\left|\mathit{b}\left(\mathit{x}\right)/{\mathit{b}}_0-1\right|\le \mathit{\theta }<1$ must always be satisfied by b₀, in which θ means a positive constant.

A.2 Perturbation $\mathit{\psi }\left(\mathit{x},\mathit{u},\mathit{t}\right):{\mathbf{ℛ}}^{\mathit{n}}\times \mathit{ℛ}\times {\mathbf{ℛ}}^{+}\mapsto \mathbf{ℛ}$ and its first-order derivative $\dot{\mathit{\psi }}\left(\mathit{x},\mathit{u},\mathit{t}\right):{\mathbf{ℛ}}^{\mathit{n}}\times \mathbf{ℛ}\times {\mathbf{ℛ}}^{+}\mapsto \mathbf{ℛ}$ are limited as $\left|\mathit{\psi }\left(\mathit{x},\mathit{u},\mathit{t}\right)\right|\le {\mathit{\gamma }}_{1 },\left|\dot{\mathit{\psi }}\left(\mathit{x},\mathit{u},\mathit{t}\right)\right|\le {\mathit{\gamma }}_2$ with $\mathit{\psi }\mathrm{0,0,0}=0$, and $\dot{\mathit{\psi }}(\mathrm{0,0,0}=0)$, in which ${\mathit{\gamma }}_{1 }$ and ${\mathit{\gamma }}_2$ denote the limits of perturbation and its first-order derivative, which are two positive constants, respectively.

The estimation error of x is defined as $\tilde{x}=x-\widehat{x}$, while $\widehat{x}$ is the estimation of x, and the reference of x is represented by x*. Based on this, an (n + 1)th-order HGSPO is designed for states and perturbation estimation (Espinoza and Joos, 1998; Elsisi et al., 2017):

${\dot{\widehat{x}}}_{\text{e}}=A_0{\widehat{x}}_{\text{e}}+B_{1}u+H\left(x_1-{\widehat{x}}_1\right)(13)$

with

$A_0={\left[\begin{array}{ccc}\begin{array}{c}0\\ 0\\ \cdots \end{array}& \begin{array}{c}1\\ 0\\ \cdots \end{array}& \begin{array}{c}\begin{array}{ccc}0& \cdots & 0\end{array}\\ \begin{array}{ccc}1& \cdots & 0\end{array}\\ \begin{array}{ccc}\cdots & \cdots & \cdots \end{array}\end{array}\\ 0& 0& \begin{array}{ccc}0& \cdots & 1\end{array}\\ 0& 0& \begin{array}{ccc}0& \cdots & 0\end{array}\end{array}\right]}_{(n+1)\times (n+1)},B_1={\left[\begin{array}{c}0\\ 0\\ ⋮\\ 1\\ 0\end{array}\right]}_{(n+1)\times 1}(14)$

where observer gain $H={\left[{\alpha }_1/\epsilon ,{\alpha }_2/{\epsilon }^2,\dots ,{\alpha }_n/{\epsilon }^n,{\alpha }_{n+1}/{\epsilon }^{n+1}\right]}^T$ decides the rate of estimation, while the other variables and parameters can be referred to in the literature (Espinoza and Joos, 1998; Elsisi et al., 2017):

${\alpha }_i=C_{n+1}^i{\lambda }_{\alpha }^i,i =\mathrm{1,2},\cdots ,n+1.(15)$

where λ_α represents the observer root that can ensure the convergence of the observer. Particularly, $C_{n+1}^i=\frac{\left(n+1\right)!}{i!\ast \left(n+1-i\right)!}$.

3.2 Fractional-order control

Fractional calculus is based on integral calculus. Based on its order in the field of fractions or complex numbers, it is the traditional differential and integral unified form of expression. The process from integral to differential can be expressed as the ordered set of fractional calculus to order. Therefore, using fractional calculus instead of integer calculus can better describe the actual physical system and natural phenomena. For integer calculus, there is a relatively clear physical meaning and geometric interpretation, for example, the first derivative of a variable can be used to express the speed in the physical sense, and the second derivative is the corresponding acceleration. If many problems are described by integer derivative, then the appropriate differential equation cannot be obtained, or the obtained differential equation is not complex, and the results are not necessarily very consistent with the actual situation. However, the differential equation obtained by fractional derivative is not only very concise, but also the results obtained by fractional derivative are closer to the reality. Sometimes, a problem is complex not because it is really complex, but because no suitable method has been found. The fractional differential equation generated by fractional derivative is such a powerful tool to study complex problems. Hence, it has become a powerful tool for mathematical modeling of complicated mechanical and physical processes.

In particular, the basic operator ${}_a{{\displaystyle D}}_t^{\alpha }$ is expressed as (Wei Yao et al., 2015; Yang et al., 2015; Zhang et al., 2021b):

${}_a{{\displaystyle D}}_t^{\alpha }=\{\begin{array}{c}\frac{{\mathrm{d}}^{\alpha }}{\mathrm{d}{t}^{\alpha }}, \alpha >0\\ 1, \alpha =0\\ \underset{a}{\overset{t}{\int }}{\left(\mathrm{d}\tau \right)}^{-\alpha }, \alpha <0 \end{array}(16)$

where $a$ and t mean the lower and upper boundaries, and $\alpha \in R$ means the order of operation.

The definition of Riemann–Liouville (RL) is on the basis of Gamma function $\Gamma (\cdot )$ and yields:

${}_a{{\displaystyle D}}_t^{\alpha }f\left(t\right)=\frac{1}{\Gamma \left(n-\alpha \right)}\frac{{\mathrm{d}}^n}{\mathrm{d}{t}^n}\underset{a}{\overset{t}{{\displaystyle \int }}}\frac{f\left(\tau \right)}{{\left(t-\tau \right)}^{\alpha -n+1}}\mathrm{d}\tau (17)$

where $n$ denotes the first integer that is larger than or equal to $\alpha$, e.g., $n-1\le \alpha <n$.

In particular, $G\left(s\right)$ of the POFOC method is expressed as:

$G\left(s\right)=K_P+\frac{K_I}{s^{\mu }}+K_D{s}^{\lambda }(18)$

where $K_P$, $K_I$, and $K_D$can be found in Figure 2.

FIGURE 2

FIGURE 2. Parameter ranges for different controllers.

3.3 Overall perturbation observer-based fractional-order control design

Thus, POFOC can be illustrated by (Wei Yao et al., 2015; Zhang et al., 2015; Xi et al., 2016; Zhang et al., 2016):

$u=\frac{1}{b_0}\left[x_1^{\ast \left(n\right)}-\widehat{\psi }(\cdot )+K_P\left(x_1-x_1^{\ast }\right)+\frac{K_{\mathrm{I}}}{s^{\mu }}\left(x_1-x_1^{\ast }\right)+K_D{s}^{\lambda }\left(x_1-x_1^{\ast }\right)\right](19)$

where $x_1^{\text{*}}$ means the reference of state $x_1$, while $x_1^{\ast \left(n\right)}$ is the nth-order derivative of $x_1^{\ast }$.

4 Jellyfish search algorithm

4.1 Jellyfish search algorithm overview

Jui-Sheng Chou et al. (Chou and Truong, 2021) recently proposed a JSA via emulating the predation process of jellyfish, which involves three behaviors. Figure 3 presents the steps of JSA.

FIGURE 3

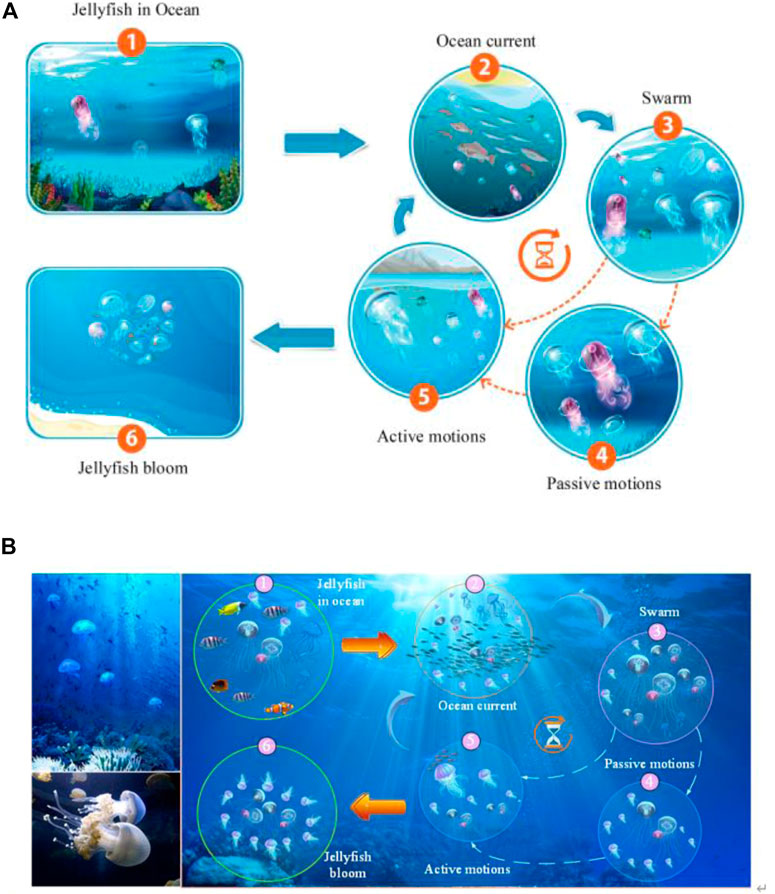
FIGURE 3. Jellyfish’s behavior in the ocean. (A) the original figure source and (B) redecorated figure with citation.

4.2 The principle of jellyfish search algorithm

4.2.1 Population initialization

The initialization of population in JSA is conducted based on a logical graph (May 1976), which eliminates the negative effects of random initialization that are often adopted by traditional metaheuristic algorithms, e.g., low convergence rate and easy to fall into local optima due to the lack of population diversity. The JSA-based logical graph is expressed as:

$X_{i+1}=\vartheta X_i\left(1-X_i\right), 0\le X_0\le 1(20)$

where $X_i$ denotes the location chaotic value of the ith jellyfish, $X_0$ means the initial population of the jellyfish, while the parameter $\vartheta$ is set to 4.0 (Chou and Truong, 2021).

4.2.2 Ocean current

Jellyfishes are attracted by ocean currents that contain large amounts of nutrients, which update their location according to the $\overrightarrow{\mathrm{trend}}$ of ocean currents, as shown in Figure 4A. It can be modeled by:

$X_i\left(t+1\right)=X_i\left(t\right)+\mathrm{rand}\left(\mathrm{0,1}\right)\times \left(X^{\ast }-\beta \times \mathrm{rand}\left(\mathrm{0,1}\right)\times \mu \right)(21)$

where $X^{\ast }$ is defined as the best location of jellyfish in the swarm, $\mu$ represents the mean location of the population, and β means the coefficient corresponding to distribution, whose value is set to 3.

FIGURE 4

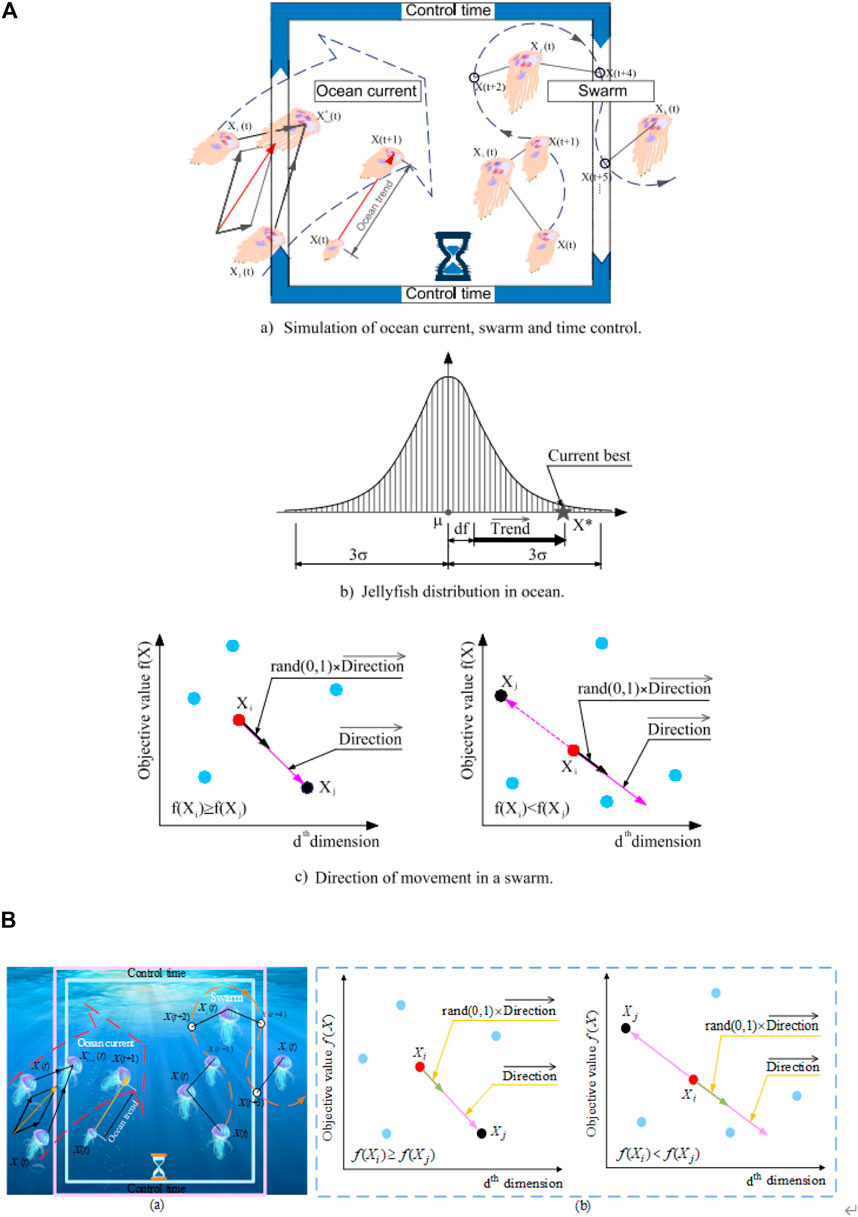
FIGURE 4. Simulation of Jellyfish behavior. (A) the original figure source and (B) redecorated figure with citation.

4.2.3 Jellyfish swarm

The movements of jellyfishes in the swarm can be segmented into two types: passive motion and active motion. The location of one specific jellyfish is updated during iterations as:

$X_i\left(t+1\right)=X_i\left(t\right)+\gamma \times \mathrm{rand}\left(\mathrm{0,1}\right)\times \left(U_b-L_b\right)(22)$

where $U_{\text{b}}$ and $L_{\text{b}}$ denote the upper and lower boundaries of the searching space, and $\gamma$ means the coefficient corresponding to motion, which is set to 0.1.

The active motion of jellyfishes in the swarm is determined by:

$X_i\left(t+1\right)=X_i\left(t\right)+\mathrm{rand}\left(\mathrm{0,1}\right)\times \overrightarrow{\mathrm{direction}}(23)$

Figure 4B illustrates the direction of the movements of jellyfishes inside the swarm: jellyfishes always move toward the direction of greater food availability. The corresponding movement direction of each jellyfish is given by:

$\overrightarrow{\mathrm{direction}}=\{\begin{array}{c}{X}_j\left(t\right)-X_i\left(t\right), \mathrm{if} f\left(X_j\right)\ge f\left(X_i\right) \\ X_i\left(t\right)-X_j\left(t\right), \mathrm{if} f\left(X_j\right)<f\left(X_i\right)\end{array}(24)$

where $f$ is the objective function of location X.

4.2.4 Time control mechanism

In JSA, the time control mechanism is adapted to govern the movements of jellyfishes following ocean currents and inside jellyfish swarm. The implementation of JSA mainly depends on the time controlling function $\text{c}\left(t\right)$, which randomly fluctuates within the range of 0–1, which is depicted as:

$c\left(t\right)=\left|\left(1-\frac{k}{k_{\max }}\right)\times \left(2\times \mathrm{Rand}\left(\mathrm{0,1}\right)-1\right)\right|(25)$

where k denotes the total number of iterations, $k_{\max }$ is the maximum number of iterations, and the executive procedure of JSA is given in Figure 5.

FIGURE 5

FIGURE 5. Executive procedure of jellyfish search algorithm (JSA).

5 Perturbation observer-Based fractional-order control design for superconducting magnetic energy storage systems

Define state vector as $x={\left(x_1,x_2,x_3,x_4,x_5\right)}^{\text{T}}={\left(i_{\text{d}},i_{\text{q}},v_{\text{d}},v_{\text{q}},i_{\text{dc}}\right)}^{\text{T}}$, output $y={\left(y_1,y_2\right)}^{\text{T}}={\left(i_{\text{d}},i_{\text{q}}\right)}^{\text{T}}$, and control input $u={\left(u_1,u_2\right)}^{\text{T}}={\left(m_{\text{d}},m_{\text{q}}\right)}^{\text{T}}$. Next, Eqs 1–7 are able to be expressed as:

$\dot{x}=f\left(x\right)+g\left(x\right)u(26)$

where

$f\left(x\right)=\left(\begin{array}{c}\begin{array}{c}{f}_1\\ f_2\\ f_3\end{array}\\ f_4\\ f_5\end{array}\right)=\left(\begin{array}{c}-\frac{R_{\text{T}}}{L_{\text{T}}}{x}_1-\omega x_2+\frac{x_3}{L_{\text{T}}}-\frac{E_{\text{d}}}{L_{\text{T}}}\\ -\frac{R_{\text{T}}}{L_{\text{T}}}{x}_2+\omega x_2+\frac{x_4}{L_{\text{T}}}-\frac{E_{\text{q}}}{L_{\text{T}}}\\ -\frac{1}{C}{x}_1-\omega x_4\\ -\frac{1}{C}{x}_2+\omega x_3\\ \frac{-E_{\text{d}}{x}_1-E_{\text{q}}{x}_2}{L_{\text{sc}}{x}_5}\end{array}\right);g\left(x\right)=\left(\begin{array}{c}\begin{array}{cc}0& 0\\ 0& 0\\ \frac{x_5}{C}& 0\end{array}\\ 0 \frac{x_5}{C}\\ 0 0\end{array}\right)(27)$

Differentiating y until u explicitly appeared, gives:

$\{\begin{array}{c}{\ddot{y}}_1=\left(\frac{R_{\text{T}}^2}{L_{\text{T}}^2}-{\omega }^2-\frac{1}{C{L}_{\text{T}}}\right)i_{\text{d}}+\frac{2\omega R_{\text{T}}}{L_{\text{T}}}{i}_{\text{q}}+\frac{R_{\text{T}}}{L_{\text{T}}^2}\left(E_{\text{d}}-v_{\text{d}}\right)+\frac{w}{L_{\text{T}}}{E}_{\text{q}}-\frac{2w}{L_{\text{T}}}{v}_{\text{q}}-\frac{1}{L_{\text{T}}}{\dot{E}}_{\text{d}}+\frac{1}{C{L}_{\text{T}}}{i}_{\text{dc}}{m}_{\text{d}}\\ {\ddot{y}}_2=\left(\frac{R_{\text{T}}^2}{L_{\text{T}}^2}-{\omega }^2-\frac{1}{C{L}_{\text{T}}}\right)i_{\text{q}}-\frac{2\omega R_{\text{T}}}{L_{\text{T}}}{i}_{\text{d}}+\frac{R_{\text{T}}}{L_{\text{T}}^2}\left(E_{\text{q}}-v_q\right)-\frac{w}{L_{\text{T}}}{E}_{\text{d}}+\frac{2w}{L_{\text{T}}}{v}_{\text{d}}-\frac{1}{L_{\text{T}}}{\dot{E}}_{\text{q}}+\frac{1}{C{L}_{\text{T}}}{i}_{\text{dc}}{m}_{\text{q}}\end{array}(28)$

Thus, the system (Eq. 28) can be further described by a matrix, as follows:

$\left[\begin{array}{c}{\ddot{y}}_1\\ {\ddot{y}}_2\end{array}\right]=\left[\begin{array}{c}{h}_1\left(x\right)\\ h_2\left(x\right)\end{array}\right]+B\left(x\right)\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right](29)$

where

$h_1\left(x\right)=\left(\frac{R_{\text{T}}^2}{L_{\text{T}}^2}-{\omega }^2-\frac{1}{C{L}_{\text{T}}}\right)i_{\text{d}}+\frac{2\omega R_{\text{T}}}{L_{\text{T}}}{i}_{\text{q}}+\frac{R_{\text{T}}}{L_{\text{T}}^2}\left(E_{\text{d}}-v_{\text{d}}\right)+\frac{w}{L_{\text{T}}}{E}_{\text{q}}-\frac{2w}{L_{\text{T}}}{v}_{\text{q}}-\frac{1}{L_{\text{T}}}{\dot{E}}_{\text{d}}(30)$

$h_2\left(x\right)=\left(\frac{R_{\text{T}}^2}{L_{\text{T}}^2}-{\omega }^2-\frac{1}{C{L}_{\text{T}}}\right)i_{\text{q}}-\frac{2\omega R_{\text{T}}}{L_{\text{T}}}{i}_{\text{d}}+\frac{R_{\text{T}}}{L_{\text{T}}^2}\left(E_{\text{q}}-v_q\right)-\frac{w}{L_{\text{T}}}{E}_{\text{d}}+\frac{2w}{L_{\text{T}}}{v}_{\text{d}}-\frac{1}{L_{\text{T}}}{\dot{E}}_{\text{q}}(31)$

with

$B\left(x\right)=\left[\begin{array}{cc}\frac{i_{\text{dc}}}{C{L}_{\text{T}}}& 0\\ 0& \frac{i_{\text{dc}}}{C{L}_{\text{T}}}\end{array}\right](32)$

Furthermore, to ensure that the linearization of input–output is effective, B(x) needs to be nonsingular under all the operating circumstances, e.g.,

$\det \left[B\left(x\right)\right]=\frac{i_{\text{dc}}^2}{C^2{L}_{\text{T}}^2}\ne 0(33)$

Due to $i_{\text{dc}}$ is always not equal to zero, Eq. 36 can always be satisfied

Perturbations ${\psi }_1(\cdot )$ and ${\psi }_2(\cdot )$ for the SMES system (32) are described by:

$\left[\begin{array}{c}{\psi }_1(\cdot )\\ {\psi }_2(\cdot )\end{array}\right]=\left[\begin{array}{c}{h}_1\left(x\right)\\ h_2\left(x\right)\end{array}\right]+\left(B\left(x\right)-B_0\right)\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right](34)$

Moreover, B₀ can be described by:

$B_0=\left[\begin{array}{cc}{b}_{11}& 0\\ 0& b_{22}\end{array}\right](35)$

where b₁₁ and b₂₂ mean constant control gains that are set by users.

Tracking error is e = [e₁, e₂]^T = [$i_{\text{d}}$-$i_{\text{d}}^{\ast }$,$i_{\text{q}}$-$i_{\text{q}}^{\ast }$]^T, while differentiating e until input u explicitly appears, yields:

$\left[\begin{array}{c}{\ddot{e}}_1\\ {\ddot{e}}_2\end{array}\right]=\left[\begin{array}{c}{\psi }_1(\cdot )\\ {\psi }_2(\cdot )\end{array}\right]+B_0\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right]-\left[\begin{array}{c}{\ddot{i}}_{\text{q}}^{\ast }\\ {\ddot{i}}_{\text{d}}^{\ast }\end{array}\right](36)$

Therefore, a third-order HGPO is designed for the estimation of perturbation ${\psi }_1(\cdot )$ as:

$\{\begin{array}{c}{\dot{\widehat{\dot{i}}}}_{\text{d}}={\widehat{\dot{\dot{i}}}}_{\text{d}}+\frac{{\alpha }_{11}}{{\mathit{ϵ}}_1}\left({\dot{i}}_{\text{d}}-{\widehat{\dot{i}}}_{\text{d}}\right)\\ {\dot{\widehat{\dot{\dot{i}}}}}_{\text{d}}={\widehat{\psi }}_2(\cdot )+\frac{{\alpha }_{12}}{{\mathit{ϵ}}_1^2}\left({\dot{i}}_{\text{d}}-{\widehat{\dot{i}}}_{\text{d}}\right)+b_{11}{u}_1\\ {\dot{\widehat{\dot{i}}}}_{\text{d}}(\cdot )=\frac{{\alpha }_{13}}{{\mathit{ϵ}}_1^3}\left({\dot{i}}_{\text{d}}-{\widehat{\dot{i}}}_{\text{d}}\right)\end{array}(37)$

where α_11, α₁₂, and α₁₃ mean three positive constants, with $0\le {\mathit{ϵ}}_1\ll 1$.

Besides, a third-order HGSPO is adopted to realize the estimation of perturbation ${\psi }_2(\cdot )$ and the first-order derivative of mechanical rotation speed, as follows:

$\{\begin{array}{c}{\dot{\widehat{\dot{i}}}}_{\text{q}}={\widehat{\dot{\dot{i}}}}_{\text{q}}+\frac{{\alpha }_{21}}{{\mathit{ϵ}}_2}\left({\dot{i}}_{\text{q}}-{\widehat{\dot{i}}}_{\text{q}}\right)\\ {\dot{\widehat{\dot{\dot{i}}}}}_{\text{q}}={\widehat{\psi }}_2(\cdot )+\frac{{\alpha }_{22}}{{\mathit{ϵ}}_2^2}\left({\dot{i}}_{\text{q}}-{\widehat{\dot{i}}}_{\text{q}}\right)+b_{22}{u}_2\\ {\dot{\widehat{\dot{i}}}}_{\text{q}}(\cdot )=\frac{{\alpha }_{23}}{{\mathit{ϵ}}_2^3}\left({\dot{i}}_{\text{q}}-{\widehat{\dot{i}}}_{\text{q}}\right)\end{array}(38)$

where observer gains α₂₁, α₂₂, and α₂₃ are all positive constants, with $0\le {\mathit{ϵ}}_2\ll 1$.

Tracking error dynamics of the POFOC method is written as:

$\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right]=B_0^{-1}\left[\begin{array}{c}{\dot{i}}_d^{\ast }-{\widehat{\psi }}_1(\cdot )+K_{P1}\left(i_d-i_d^{\ast }\right)+\frac{K_{I1}}{s^{{\mu }_1}}\left(i_d-i_d^{\ast }\right)+K_{D1}{s}^{{\lambda }_1}\left(i_d-i_d^{\ast }\right)\\ {\dot{i}}_q^{\ast }-{\widehat{\psi }}_2(\cdot )+K_{P2}\left({\dot{i}}_q-{\dot{i}}_q^{\ast }\right)+\frac{K_{I2}}{s^{{\mu }_2}}\left({\dot{i}}_q-{\dot{i}}_q^{\ast }\right)+K_{D2}{s}^{{\lambda }_2}\left({\dot{i}}_q-{\dot{i}}_q^{\ast }\right)\end{array}\right](39)$

where control gains $K_{\text{P}1}$, $K_{\text{P}2}$, $K_{\text{I}1}$, $K_{\text{I}2}$, $K_{\text{D}1}$, $K_{\text{D}2}$, fractional integrator order ${\mu }_1$ and ${\mu }_2$, and differentiator order ${\lambda }_1$ and ${\lambda }_2$ are chosen to realize a satisfactory dynamic tracking error.

Then, JSA is used to optimize POFOC control gains. The optimization goal is to minimize active power and reactive power tracking errors and minimize the overall controlling cost, as follows:

Minimize F(x) = ${\displaystyle \sum }_{Two cases}\underset{0}{\overset{T}{{\displaystyle \int }}}\left(\left|P_{ac}-P_{ac}^{\ast }\right|+\left|Q_{ac}-Q_{ac}^{\ast }\right|+{\omega }_1\left|u_1\right|+u_2\left|m_q\right|\right)\mathrm{d}t$

$\mathrm{subject to} \{\begin{array}{c}0\le K_{\mathrm{P}\mathrm{i}}\le 300\\ 0\le K_{\mathrm{I}\mathrm{i}}\le 200\\ 0\le K_{\mathrm{D}\mathrm{i}}\le 50\\ 0\le {\lambda }_i\le 2\\ 0\le {\mu }_i\le 2\\ -1\le m_{\mathrm{d}}\le 1\\ -1\le m_{\mathrm{q}}\le 1\end{array};i=\mathrm{1,2}.(40)$

where the weights ${\omega }_1$ and ${\omega }_2$ mean the scaling coefficients that are designed as 0.2, while T = 10 s. The overall control framework of POFOC control is given in Figure 6.

FIGURE 6

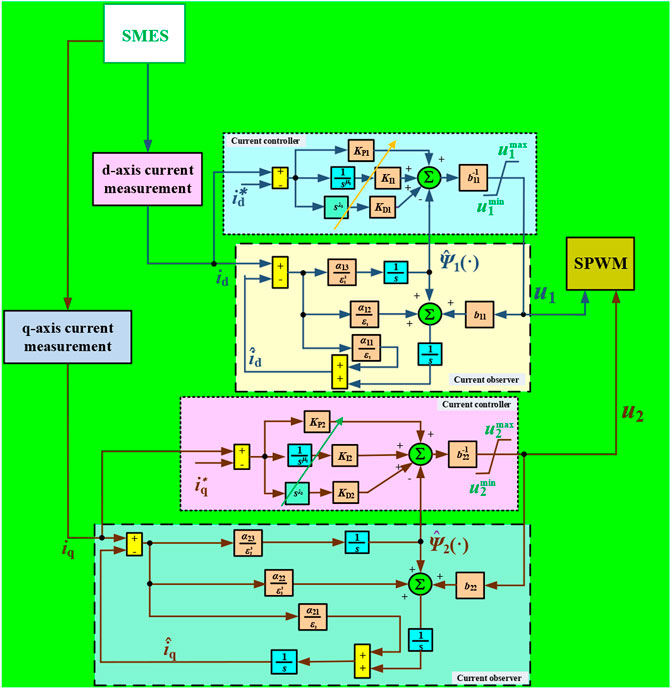
FIGURE 6. The overall control framework of a perturbation observer-based fractional-order control (POFOC).

6 Case studies

The configuration of a typical SMES system is illustrated in Figure 7, while related parameters are specifically shown in Table 1. To testify the control performance and robustness of the POFOC strategy, it is compared against the traditional PID control and IDA-PBC under two cases. In addition, the simulation is executed on Matlab/Simulink 7.10 using a personal computer with an Intel^R CoreTMi7 CPU at 2.2 GHz and 8 GB of RAM.

FIGURE 7

FIGURE 7. The configuration of an SMES system in a microgrid.

TABLE 1

TABLE 1. The superconducting magnetic energy storage (SMES) system parameters and microgrid parameters.

6.1 Active power and reactive power supply

The purpose of this case is to verify the ability to regulate the output of active power and reactive power when the system is under disturbance. In this case, the reference of power is constantly changing, and the main purpose is to track them accurately. In addition, the detailed system response is demonstrated in Figure 8, which indicates that POFOC can adjust the active power and reactive power in the shortest time, and the tracking effect is the best. In addition, serious overshoot occurs in PID control, which might lead to a decrease in the operating stability and reliability of the system. The system cannot be quickly restored to the stable state due to the slow adjustment speed of IDA-PBC.

FIGURE 8

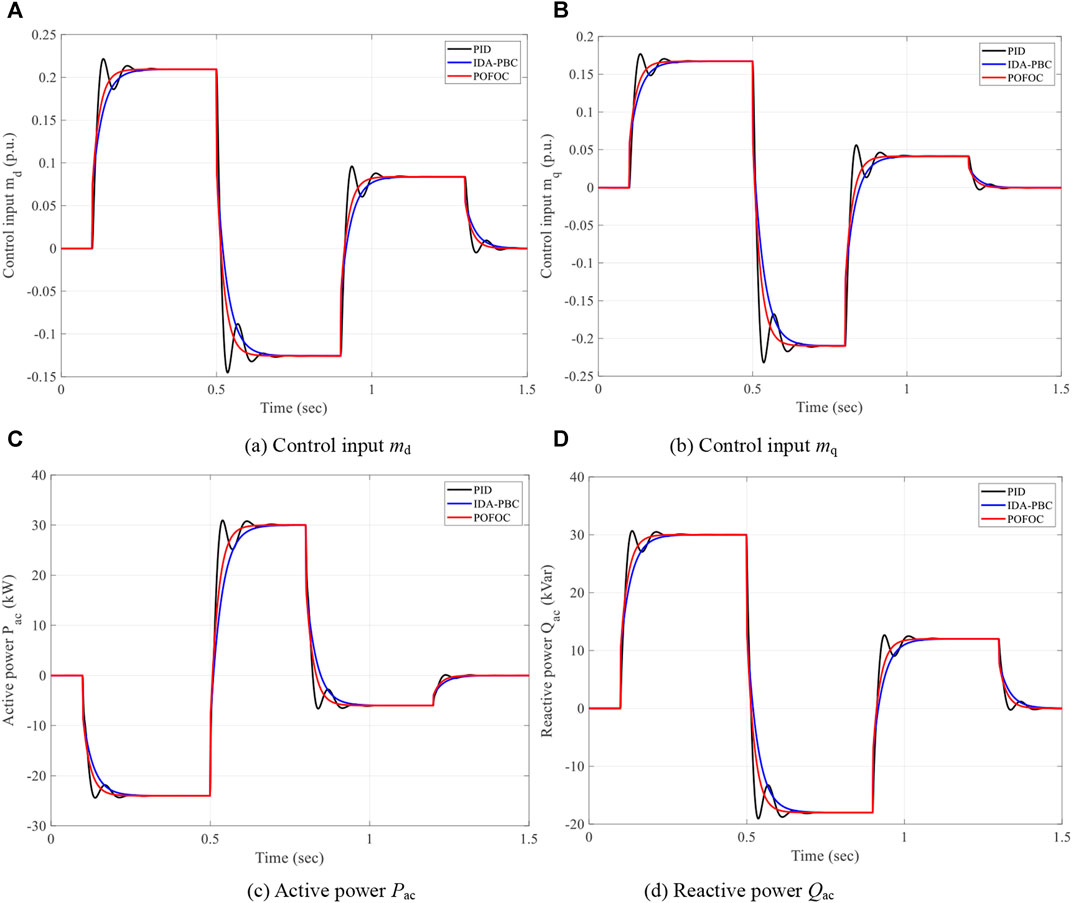
FIGURE 8. System responses under power support. (A) Control input m_d. (B) Control input m_q. (C) Active power P_ac. (D) Reactive power Q_ac.

6.2 System restoration ability under power grid fault

This section aims to verify whether the control system can recover the disturbance system quickly and effectively. Suppose at t = 0.5 s between Bus 2 and infinite bus, there is a three-phase short-circuit fault that occurs on a transmission line. In addition, when t = 0.6 s, the fault line is disconnected, and the automatic re-closing device is turned on, and the normal supply of electric power is restored after the fault is cleared. Figure 9 shows the recovery performance achieved by various controllers when a failure happens, which indicates that POFOC can effectively and significantly mitigate power oscillations caused by faults, ensuring that unstable systems return to normal operation at the highest speed. Compared with PID control, the proposed POFOC method can always maintain a relatively stable tracking performance, and the restore speed is much faster after the fault on the transmission line.

FIGURE 9

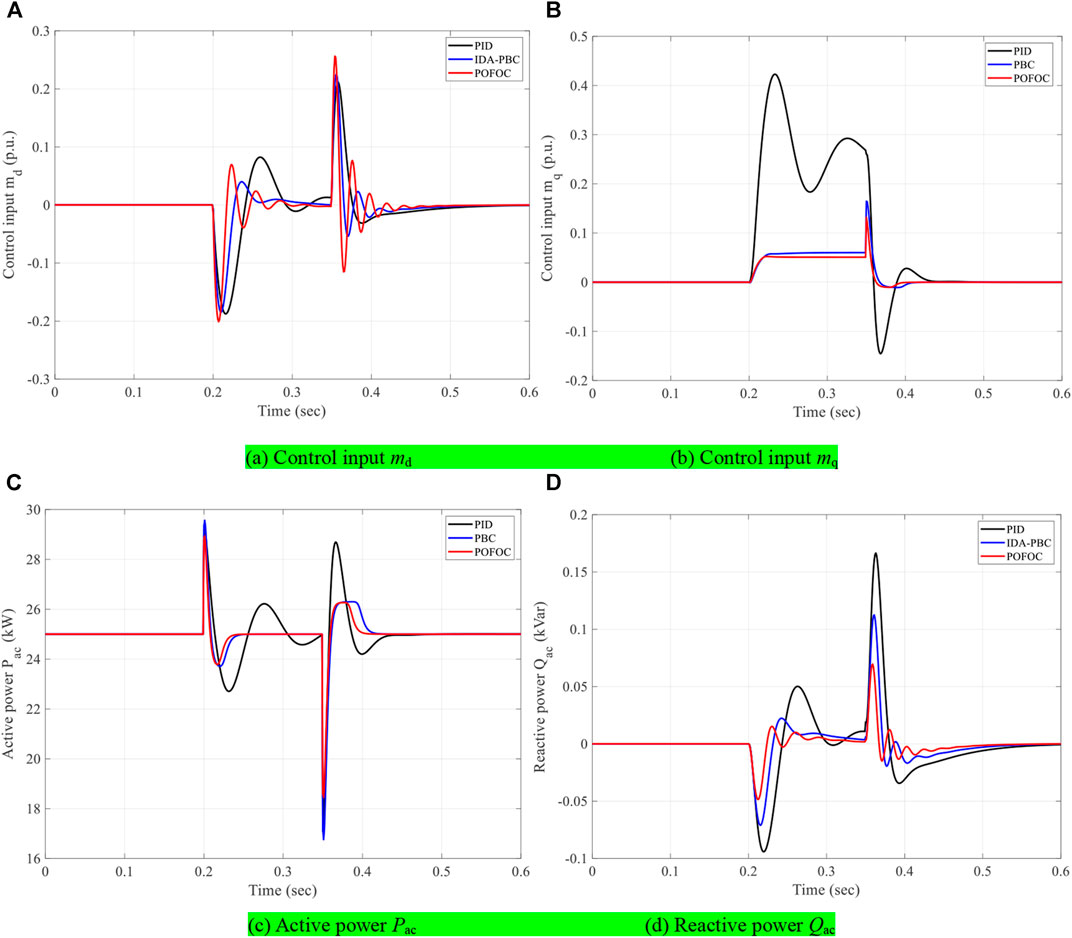
FIGURE 9. System responses under power system fault. (A) Control input m_d. (B) Control input m_q. (C) Active power P_ac. (D) Reactive power Q_ac.

7 Conclusion

A novel POFOC scheme combined with JSA is developed in this work for SMES systems, which main novelties are outlined as:

1) HGPO is first employed to estimate the combined impact of SMES system modeling uncertainties, unknown parameters, and external disturbances. Then, the control strategy fully compensates the estimated perturbation for consistent global control, which leads to stronger robustness.

2) A novel JSA is employed to optimize and tune the control gains based on its powerful global searching ability, which can effectively avoid the algorithm falling into local optimal solutions.

3) Case studies testify the practical performance of the proposed POFOC scheme compared against traditional PID control and IDA-PBC. Experimental results indicate that POFOC control can significantly enhance the overall control performance of SMES system in comparison with PID control in terms of tracking ability and control costs. In particular, the overshoot of PID is 115.264% of the rated value, while POFOC and IDA-PBC has no overshoot.

In future studies, a more advanced controller and algorithm will be devised to solve this problem.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

KL conceptualized the study, wrote and prepared the original draft, wrote, reviewed, and edited the manuscript. YJ wrote, reviewed, and edited the manuscript. JZ supervised the study and conducted the investigation.

Funding

This work is supported by the National Natural Science Foundation of China (NSFC) under grant number 61902039.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chou, J.-S., and Truong, D.-N. (2021). A Novel Metaheuristic Optimizer Inspired by Behavior of Jellyfish in Ocean. Appl. Math. Comput. 389, 125535. doi:10.1016/j.amc.2020.125535

CrossRef Full Text | Google Scholar

Elsisi, M., Soliman, M., Aboelela, M. A. S., and Mansour, W. (2017). Optimal Design of Model Predictive Control with Superconducting Magnetic Energy Storage for Load Frequency Control of Nonlinear Hydrothermal Power System Using Bat Inspired Algorithm. J. Energ. Storage 12, 311–318. doi:10.1016/j.est.2017.05.009

CrossRef Full Text | Google Scholar

Espinoza, J. R., and Joos, G. (1998). State Variable Decoupling and Power Flow Control in PWM Current-Source Rectifiers. IEEE Trans. Ind. Electron. 45 (1), 78–87. doi:10.1109/41.661308

CrossRef Full Text | Google Scholar

Lin, X., Lei, Y., and Zhu, Y. (2018). A Novel Superconducting Magnetic Energy Storage System Design Based on a Three-Level T-type Converter and its Energy-Shaping Control Strategy. Electric Power Syst. Res. 162, 64–73. doi:10.1016/j.epsr.2018.05.006

CrossRef Full Text | Google Scholar

May, R. M. (1976). Simple Mathematical Models with Very Complicated Dynamics. Nature 261, 459–467. doi:10.1038/261459a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Montoya, O. D., Garcés, A., and Espinosa-Pérez, G. (2018). A Generalized Passivity-Based Control Approach for Power Compensation in Distribution Systems Using Electrical Energy Storage Systems. J. Energ. Storage 16, 259–268. doi:10.1016/j.est.2018.01.018

CrossRef Full Text | Google Scholar

Sara, M., Ahmed, E., Tamou, N., and Badr, B. I. (2020). NA Direct Power Control of a DFIG Based-WECS during Symmetrical Voltage Dips. Prot. Control. Mod. Power Syst. 5 (1), 36–47. doi:10.1186/s41601-019-0148-y

CrossRef Full Text | Google Scholar

Shanchuan Wang, S., and Jianxun Jin, J. (2014). Design and Analysis of a Fuzzy Logic Controlled SMES System. IEEE Trans. Appl. Supercond. 24 (5), 1–5. doi:10.1109/tasc.2014.2348562

CrossRef Full Text | Google Scholar

Shi, J., Xu, Y., Liao, M., Guo, S., Li, Y., Ren, L., et al. (2019). Integrated Design Method for Superconducting Magnetic Energy Storage Considering the High Frequency Pulse Width Modulation Pulse Voltage on Magnet. Appl. Energ. 248, 1–17. doi:10.1016/j.apenergy.2019.04.079

CrossRef Full Text | Google Scholar

Shima, Y., Mahdi, D., and Erfan, S. (2018). Designing and Analyzing an Electric Energy Storage System Based on Reversible Solid Oxide Cells. Energ. Convers. Manage. 159, 381–395. doi:10.1016/j.enconman.2017.12.082

CrossRef Full Text | Google Scholar

Shtessel, Y., Baev, S., and Biglari, H. (2008). Unity Power Factor Control in Three-phase AC/DC Boost Converter Using Sliding Modes. IEEE Trans. Ind. Electron. 55 (11), 3874–3882. doi:10.1109/tie.2008.2003203

CrossRef Full Text | Google Scholar

Trilochan, P., Anup, K. P., and Sunil, K. S. (2018). Implementing Dynamic Evolution Control Approach for DC-link Voltage Regulation of Superconducting Magnetic Energy Storage System. Electr. Power Energ. Syst. 95, 275–286. doi:10.1016/j.ijepes.2017.08.022

CrossRef Full Text | Google Scholar

Wei Yao, W., Lin Jiang, L., Jinyu Wen, J. Y., Qinghua Wu, Q. H., and Shijie Cheng, S. J. (2015). Wide-Area Damping Controller for Power System Interarea Oscillations: A Networked Predictive Control Approach. IEEE Trans. Contr. Syst. Technol. 23 (1), 27–36. doi:10.1109/tcst.2014.2311852

CrossRef Full Text | Google Scholar

Xi, L., Wu, J., Xu, Y., and Sun, H. (2020). Automatic Generation Control Based on Multiple Neural Networks with Actor-Critic Strategy. IEEE Trans. Neural Netw. Learn. Syst. PP (6), 2483–2493. doi:10.1109/TNNLS.2020.3006080

PubMed Abstract | CrossRef Full Text | Google Scholar

Xi, L., Yu, T., Yang, B., Zhang, X., and Qiu, X. (2016). A Wolf Pack Hunting Strategy Based Virtual Tribes Control for Automatic Generation Control of Smart Grid. Appl. Energ. 178, 198–211. doi:10.1016/j.apenergy.2016.06.041

CrossRef Full Text | Google Scholar

Yan, X. (2020). A Review of Cyber Security Risks of Power Systems: from Static to Dynamic False Data Attacks. Prot. Control. Mod. Power Syst. 5 (3), 8–19. doi:10.1186/s41601-020-00164-w

CrossRef Full Text | Google Scholar

Yang, B., Jiang, L., Wang, L., Yao, W., and Wu, Q. H. (2016). Nonlinear Maximum Power point Tracking Control and Modal Analysis of DFIG Based Wind Turbine. Int. J. Electr. Power Energ. Syst. 74, 429–436. doi:10.1016/j.ijepes.2015.07.036

CrossRef Full Text | Google Scholar

Yang, B., Jiang, L., Yao, W., and Wu, Q. H. (2015). Perturbation Estimation Based Coordinated Adaptive Passive Control for Multimachine Power Systems. Control. Eng. Pract. 44, 172–192. doi:10.1016/j.conengprac.2015.07.012

CrossRef Full Text | Google Scholar

Yang, B., Wang, J., Zhang, X., Yu, T., Yao, W., Shu, H., et al. (2020). Comprehensive Overview of Meta-Heuristic Algorithm Applications on PV Cell Parameter Identification. Energ. Convers. Manage. 208, 112595. doi:10.1016/j.enconman.2020.112595

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H., Zhang, Y., Chen, J., Sang, Y., et al. (2018). Passivity-based Sliding-Mode Control Design for Optimal Power Extraction of a PMSG Based Variable Speed Wind Turbine. Renew. Energ. 119, 577–589. doi:10.1016/j.renene.2017.12.047

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Zhang, X., Li, H., Shu, H., Sang, Y., et al. (2019b). Dynamic Leader Based Collective Intelligence for Maximum Power point Tracking of PV Systems Affected by Partial Shading Condition. Energ. Convers. Manage. 179, 286–303. doi:10.1016/j.enconman.2018.10.074

CrossRef Full Text | Google Scholar

Yang, B., Zhang, X., Yu, T., Shu, H., and Fang, Z. (2017). Grouped Grey Wolf Optimizer for Maximum Power point Tracking of Doubly-Fed Induction Generator Based Wind Turbine. Energ. Convers. Manage. 133, 427–443. doi:10.1016/j.enconman.2016.10.062

CrossRef Full Text | Google Scholar

Yang, B., Zhong, L., Zhang, X., Shu, H., Yu, T., Li, H., et al. (2019a). Novel Bio-Inspired Memetic Salp Swarm Algorithm and Application to MPPT for PV Systems Considering Partial Shading Condition. J. Clean. Prod. 215, 1203–1222. doi:10.1016/j.jclepro.2019.01.150

CrossRef Full Text | Google Scholar

Zhang, K., Zhou, B., Or, S. W., Li, C., Chung, C. Y., and Voropai, N. I. (2021a). Optimal Coordinated Control of Multi-Renewable-To-Hydrogen Production System for Hydrogen Fueling Stations. IEEE Trans. Ind. Applicat. 1. doi:10.1109/TIA.2021.3093841

CrossRef Full Text | Google Scholar

Zhang, X., Tan, T., Zhou, B., Yu, T., Yang, B., and Huang, X. (2021b). Adaptive Distributed Auction-Based Algorithm for Optimal Mileage Based AGC Dispatch with High Participation of Renewable Energy. Int. J. Electr. Power Energ. Syst. 124, 106371. doi:10.1016/j.ijepes.2020.106371

CrossRef Full Text | Google Scholar

Zhang, X., Yu, T., Yang, B., and Li, L. (2016). Virtual Generation Tribe Based Robust Collaborative Consensus Algorithm for Dynamic Generation Command Dispatch Optimization of Smart Grid. Energy 101, 34–51. doi:10.1016/j.energy.2016.02.009

CrossRef Full Text | Google Scholar

Zhang, X., Yu, T., Yang, B., Zheng, L., and Huang, L. (2015). Approximate Ideal Multi-Objective Solution Q(λ) Learning for Optimal Carbon-Energy Combined-Flow in Multi-Energy Power Systems. Energ. Convers. Manage. 106, 543–556. doi:10.1016/j.enconman.2015.09.049

CrossRef Full Text | Google Scholar

Zhu, J., Yuan, W., Qiu, M., Wei, B., Zhang, H., Chen, P., et al. (2015). Experimental Demonstration and Application Planning of High Temperature Superconducting Energy Storage System for Renewable Power Grids. Appl. Energ. 137, 692–698. doi:10.1016/j.apenergy.2014.07.022

CrossRef Full Text | Google Scholar

Glossary

E_d d-axis voltage of AC equivalent node

E_q q-axis voltage of AC equivalent node

$\mathit{\omega }$ electrical frequency of AC equivalent node

i_d d-axis current flowing across the transformer

i_q q-axis current flowing across the transformer

v_d d-axis voltage at PWM-CSC terminal

v_q q-axis voltage at PWM-CSC terminal

i_dc DC current flowing across superconducting coil

m_d d-axis modulation indicatrix

m_q q-axis modulation indicatrix

P_ac active power

Q_ac reactive power

ς_i, φ_iλ_ci (i = 1,2) controller gains

α_ij, k_ij (i = 1,2; j = 1,2,3) observer gains

${\epsilon }_o$ the thickness layer boundary of the observer

${\epsilon }_c$ the thickness layer boundary of controller

$\alpha 1$,$\alpha 2$ fractional differential order

C capacitor used as low-pass filter

L_sc inductance of superconducting coil device

L_T inductance of transformer

R_T resistance of transformer

${\mathit{S}}_{\mathrm{SMES}}^{\mathrm{rated}}$ rated apparent power of SMES system

SMES superconductor magnetics energy storage

DG distributed generation

FOSMC fractional-order SMC

AFOSMC adaptive fractional-order SMC

PID proportional-integral-derivative

SMSPO sliding-mode state and perturbation observer

PWM-CSC pulse-width modulated current source converter

HIL hardware-in-the-loop

IDA-PBC interconnection and damping assignment passivity-based control

JSA jellyfish search algorithm

EESS electric energy storage systems

SCES super-capacitor energy storage

FWES super-capacitor energy storage

HESS hybrid energy storage system

TES thermal energy system

CAES compressed air energy system

PHES pumped hydroelectric energy storage

PCU power converter unit

PCC point of common coupling

PCH port-controlled Hamiltonian

MPC model predictive control

PO perturbation observer

PERSFC perturbation estimation based robust state feedback control

DFIG doubly-fed induction generator

PoFoPID perturbation observer based fractional-order PID