A Hierarchical Modeling Framework for Cyber-Physical Micro Energy Grid System

This paper proposes a hierarchical modeling framework for micro energy grid (MEG) from the perspective of cyber-physical integration, including three layers: object layer, integration layer and decision layer. This modeling framework can fully reveal the interplay of the information flow and energy flow in MEG. The energy hub approach is used to uniformly describe the conversion and distribution of different energy sources in the object layer. The state machine is used to describe the characteristics of energy flow and information flow and their dynamic relationships in the integration layer, where the energy flow describes the dynamic balance of energy between the supply side and demand side and the energy changes of each unit in MEG, and the information flow describes the transferring process of each unit’s operating state and the conditions triggering the state transformation. The optimization objective of the decision layer is established based on the actual requirements with optimal operation. The combination of the three-layer model forms the overall model of the MEG. Finally, a typical MEG system is taken as an example to verify the proposed modeling approach, and the results show that the proposed modeling method effectively improves the observability and optimal operation of the MEG.

Introduction

Micro energy grid (MEG), as an extension of the microgrid (Xu et al., 2020), integrates the functions of interconnection, conversion, coupling and storage of multiple energy sources (cooling, heating, electricity and gas), which can effectively improve the comprehensive utilization efficiency of energy and reduce environmental pollution through multi-energy complementation and the cascade utilization of energy (Liu et al., 2019a; Zhao et al., 2021). As an essential part of the energy internet, MEG is one of future energy system development (Zhang et al., 2021).

The current domestic and foreign research on MEG mainly focuses on modeling (Lu et al., 2020; Martinez Cesena et al., 2020), planning and design (Chen et al., 2019a; Wei et al., 2019), optimal operation strategy (Qin et al., 2020) and demand response (Mohseni et al., 2021). Among them, modeling is the basis of MEG for planning and design, optimal operation, etc. It is also a research hotspot in recent years, and this paper is also mainly devoted to the modeling research of MEG. There is a body of research that has focused extensively on the modeling of the MEG, which can be divided into two categories: building up model for MEG from the holistic perspective (Geidl et al., 2007; Chicco and Mancarella, 2008; Almassalkhi and Towle, 2016; Wang et al., 2019a; Liu et al., 2019b; Huo et al., 2019; Li et al., 2020a) and the local perspective (Ma et al., 2017; Li et al., 2018; Chen et al., 2019b; Wang et al., 2019b; Ju et al., 2020).

The first type proposes MEG models from the holistic perspective. It mainly describes the MEG from a holistic perspective without focusing on modeling the individual devices in the MEG. The typical representative is the energy hub (EH) method proposed in (Geidl et al., 2007; Liu et al., 2019b; Li et al., 2020a). EH abstracts the MEG as a multi-port network with multiple inputs and output ports and attempts to describe the coupling relationship between energy inputs and outputs in terms of conversion, distribution and transmission, etc., by using a coupling matrix. The EH model has been widely used in the planning and design, optimization operation of MEG, etc. The difficulty of its application is the coupling matrix formulation. Therefore, a coupling matrix generation scheme based on the path searching method was proposed in (Chicco and Mancarella, 2008). However, the coupling matrix formulation will become complicated as the number of devices in the MEG increases. The reference (Huo et al., 2019) proposed a method to generate automatically coupling matrix for small-scale triple-supply MEGs. Due to the introduction of dispatch factor variables in the coupling matrix, the established EH model optimization problem becomes a nonlinear optimization problem, which leads to difficulty in obtaining the global optimal solution for the EH model. In order to eliminate the nonlinear issue caused by the dispatch factor in the EH model, a method using variable substitution was proposed in (Almassalkhi and Towle, 2016), which avoids the multiplication of variables. The reference (Wang et al., 2019a) proposed a normalized matrix modeling method without dispatch factors based on graph theory to achieve automatically coupling matrix formulation.

The second type proposes MEG models from the local perspective and it builds up models for each type of device and each type of energy system separately. The typical representative is the idea of modeling MEG based on energy bus architecture proposed in Ma et al. (2017), which divides the MEG into electric, thermal and cooling systems and then builds up models for each system separately. Unlike the EH model that focuses on the system port characteristics and abstracts the system’s internal structure, the model based on the energy bus architecture tries to clarify the system’s internal structure and energy flow relationship. That is to say, this model focuses on the internal structure of the system and the conversion relationship of energy flow and is also widely used at present. For example, the references (Li et al., 2018; Wang et al., 2019b) discussed the optimal operation and planning of MEG based on this model, respectively. Reference (Chen et al., 2019b) proposed MEG model by taking the devices of source-network-load-storage links into account. In Ju et al. (2020), the photovoltaic (PV), wind turbine (WT), electric chiller (EC), and gas turbine (GT) devices in the MEG were modeled in detail based on the construction of the MEG, respectively.

The above two types of modeling methods have been well applied in different fields. However, the above modeling methods mainly focus on modeling the MEG physical system and not taking the cyber system into account to develop the MEG model. As MEG is a typical cyber-physical system (CPS) (Deng et al., 2021), the cyber and physical systems of MEG should be studied as an integrated system for modeling analysis. On the one hand, this will help to fully reveal the interplay of the information flow and energy flow in MEG and thoroughly explore the ability improvement brought by the integration of the two systems; on the other hand, it can also point out the direction for the planning and information construction of MEG. Although a large number of papers have combined CPS and power grid and proposed various modeling methods for power grid CPS (Xin et al., 2015; Fu et al., 2019; Li et al., 2020b), very few papers study the modeling of MEG CPS.

Therefore, the research in this paper attempts to introduce CPS into MEG and propose a modeling method for MEG from the perspective of CPS. To the best of our knowledge, the original contributions of this paper are summarized as follows:

1) A hierarchical modeling framework for MEG is proposed, divided into object layer, integration layer and decision layer. The proposed modeling framework is universal and can be applied to arbitrarily complex MEG modeling.

2) The EH-based approach develops the model of object layer for a unified description of the coupling relationship between different energy sources. The state machine approach is used to develop the model of integration layer for describing the characteristics of information flow and energy flow in the MEG and their dynamic relationships. The optimization objective of decision layer is established based on the actual requirements of the system for determining the optimal operation strategy of the system.

The rest of this paper is organized as follows. In The Architecture of MEG Base on CPS, the CPS and CPS-based architecture of MEG is presented. In Modeling Framework for MEG Based on CPS, a hierarchical modeling framework for MEG is proposed, and the modeling approach of MEG is discussed in CPS-Based Modeling of MEG. Modeling verification is presented in Model Verification. Finally, Conclusion concludes this paper.

The Architecture of MEG Base on CPS

The Introduction of CPS

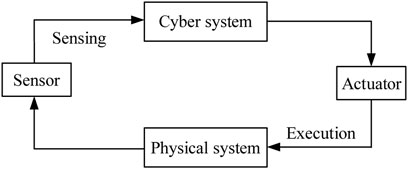
The CPS consists of the cyber system and the physical system and the interface (sensors and actuators) connecting with the two systems, as shown in Figure 1. The sensors are mainly responsible for sensing the environmental information and the physical system and transmitting the sensed information to the cyber system, which analyzes and calculates the information and generates control instructions to send to the actuators. The actuators control the physical entities according to the control instructions issued by the cyber system. This closed-loop process ensures that the CPS can control the physical entities in a safe, efficient, reliable and real-time way.

FIGURE 1

FIGURE 1. Structure of the cyber-physical system.

The Architecture of MEG Based on CPS

In this section, the CPS-based architecture of MEG is proposed, as shown in Figure 2. The MEG CPS mainly consists of an energy network layer and a cyber network layer. The energy network layer consists of the following parts:

FIGURE 2

FIGURE 2. The CPS-based architecture of MEG.

1) Energy input: including WT, PV, power grid and natural gas; 2) Energy conversion: to complete the conversion from primary energy source to energy and the conversion between different forms of secondary energy, such as GT (to complete the conversion from natural gas to electricity), absorption chiller (AC) (to complete the conversion from thermal energy to cooling energy); 3) Energy storage: to achieve the storage of different forms of energy, including battery storage (BS), thermal storage (TS) and ice storage conditioner (ISC); 4) Energy collection: three types of energy buses (electrical bus, heating bus and cooling bus) are used to achieve the collection of different forms of energy; 5) Energy delivery: three different energy networks (electric network, heating network and cooling network) are used to deliver different forms of energy for users.

The cyber network layer consists of information devices such as information collection and extraction, analysis and control devices of sources and loads to provide the economically optimal energy supply to the users.

The architecture of MEG in Figure 2 can intuitively and distinctly illustrate the energy conversion, the energy flow of MEG and the connection between various devices.

Modeling Framework for MEG Based on CPS

The Modeling Principles

From the perspective of general applicability, in this section, we set up the MEG model based on the following principles.

1) Independence: To meet the scalability of the model, a modular and hierarchical modeling approach should be utilized, with modules being independent of each other and different layers interacting with each other through information.

2) Generic: The model establishment should be conducted from the perspective of general applicability and can describe arbitrarily complex MEG.

3) Accuracy: The established model should accurately describe the interplay of the information flow and energy flow in the MEG and fully reflect the integration relationship between the two.

Hierarchical Modeling Framework for MEG Based on CPS

Based on the above modeling principles, this section abstracts MEG architecture in Figure 2 and proposes a hierarchical modeling framework for MEG from the functional perspective of CPS as shown in Figure 3, dividing the MEG modeling into three layers: object layer, integration layer and decision layer. The internal functions of each layer are relatively independent, and different layers interact through information flow.

1) Object layer: The coupling matrix approach is used to provide a unified description of the relationships between the input and output variables of different energy sources. This layer focus on describing the static characteristics of the system, including the conversion, storage and distribution of energy.

2) Integration layer: The information flow, energy flow and their dynamic relationships in the MEG are described based on the hybrid system theory. Here, the energy flow describes the dynamic balance of energy between the supply-side and demand-side and the energy change of each unit in the MEG. The information flow describes the transferring process of each unit’s operating state and the conditions triggering the state transformation. The conditions include the control instructions issued from the decision layer and the state transfer events generated when the evolution of internal state variables exceeds a specific threshold value.

3) Decision layer: This layer, as the top layer of the MEG, mainly completes the global optimization management decision of the system. The global optimal management strategy of the system can be designed by taking the operational constraints of each device in the object layer into account on the basis of the different optimization objectives of the system.

FIGURE 3

FIGURE 3. The hierarchical modeling framework for the MEG.

CPS-Based Modeling of MEG

The Object Layer

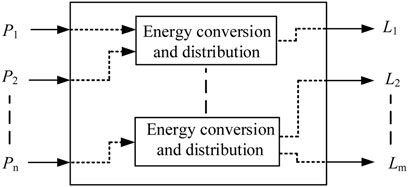
MEG is a system composed of multiple energy sources, such as cooling, heat, electricity and gas. The conversion between different energy sources can be represented by the multi-input and multi-output port network, as shown in Figure 4.

FIGURE 4

FIGURE 4. The multi-inputs and multi-output ports model for object layer.

In Figure 4, P and L denote the energy input and energy output of the system, respectively. C denotes the coupling matrix. Thus, the object layer at the mathematical level is a function of the input P to the output L.

$\mathbf{L}=f\left(\mathbf{P}\right)(1)$

The function f (^.) can represent the transmission, conversion and storage of different energy sources. Further, the coupling matrix can be used to describe the relationship between output and input, as shown in Eq. 2.

$\left[\begin{array}{c}{L}_1\\ L_2\\ ⋮\\ L_m\end{array}\right]=\left[\begin{array}{cccc}{c}_{11}& c_{12}& \cdots & c_{1n}\\ c_{21}& c_{22}& \cdots & c_{2n}\\ ⋮& ⋮& & ⋮\\ c_{m1}& c_{m2}& \cdots & c_{mn}\end{array}\right]\left[\begin{array}{c}{P}_1\\ P_2\\ ⋮\\ P_n\end{array}\right](2)$

In Eq. 2, P_i denotes the ith energy source input to the system, L_j denotes the jth energy source output from the system and c_ij is the coupling factor, which denotes the ratio of L_j to P_i. The c_ij consists of two parts: the energy distribution factor α_ij and the energy conversion efficiency factor β_ij.

The α_ij represents the percentage of input power P_i converted to output power L_j, as shown in Eq. 3.

$L_j={\mathit{\alpha }}_{ij}{P}_i(3)$

The value of α_ij in Eq. 3 is determined by the decision layer and the following constraints need to be satisfied.

$0\le {\mathit{\alpha }}_{ij}\le 1,{\displaystyle \sum _{j=1}^m{\mathit{\alpha }}_{ij}}=1(4)$

The (4) indicates that the energy allocated to convert to energy source j should be less than or equal to the energy of energy source i. The sum of the energy allocated to energy source j should be equal to the total energy of energy source i.

The β_ij represents the efficiency of converting the input power P_i into the output power L_j, as shown in Eq. 5.

$L_j={\mathit{\beta }}_{ij}{P}_i(5)$

Then the coupling matrix C can be expressed as

$\mathbf{C}=\mathbf{\beta }\times \mathbf{\alpha }\mathit{= }\left[\begin{array}{cccc}{\mathit{\beta }}_{11}& {\mathit{\beta }}_{12}& \cdots & {\mathit{\beta }}_{1n}\\ {\mathit{\beta }}_{21}& {\mathit{\beta }}_{22}& \cdots & {\mathit{\beta }}_{2n}\\ ⋮& ⋮& & ⋮\\ {\mathit{\beta }}_{m1}& {\mathit{\beta }}_{m2}& \cdots & {\mathit{\beta }}_{mn}\end{array}\right]\times \mathit{ }\left[\begin{array}{cccc}{\mathit{\alpha }}_{11}& {\mathit{\alpha }}_{12}& \cdots & {\mathit{\alpha }}_{1n}\\ {\mathit{\alpha }}_{21}& {\mathit{\alpha }}_{22}& \cdots & {\mathit{\alpha }}_{2n}\\ ⋮& ⋮& & ⋮\\ {\mathit{\alpha }}_{n1}& {\mathit{\alpha }}_{n2}& \cdots & {\mathit{\alpha }}_{nn}\end{array}\right](6)$

Where β denotes the efficiency matrix and α denotes the dispatch matrix. Then the model of the object layer can be represented by the following equation.

$\mathbf{L}=\mathbf{\beta }\times \mathbf{\alpha }\times \mathbf{P}=\mathbf{C}\times \mathbf{P}(7)$

The Integration Layer

The devices in the MEG exhibit a hybrid system characteristic during operation. The interplay of the information flow and energy flow in the MEG cannot be accurately described by a single continuous or discrete modeling method. Therefore, this section employs hybrid system theory to model the integration layer, i.e., state equation and algebraic equation are used to describe the energy flow. The state machines are used to describe the information flow.

The energy flow in the integration layer describes the dynamic balance of energy between the supply-side and demand-side and the energy change of each unit in the MEG. Since there are three systems with different time scale characteristics in MEG: electrical system, heating system and cooling system, energy flow needs to be able to characterize these multi-time scale characteristics. Therefore, the following state equations are established to characterize the slow, medium and fast response characteristics, as shown in Eq. 8.

$\{\begin{array}{l}{\dot{x}}_e=f_e(x_e,y,u,s,t_e)\\ {\dot{x}}_h=f_h(x_h,y,u,s,t_h)\\ {\dot{x}}_c=f_c(x_c,y,u,s,t_c)\\ 0=EHC(x,y,u,s,t)\end{array}(8)$

Where x_e, x_h and x_c denote the state variables related to the electric, heating and cooling systems, respectively, t_e, t_h and t_c denote the corresponding time scales, respectively. The functions f_e, f_h and f_c denote the continuous dynamic change characteristics of the three subsystems, respectively. u denotes the control input variables of the system y denotes the output of the system and s denotes the current operating state of the system. The function EHC represents the real-time balance equation of energy between the supply-side and demand-side, including the real-time balance equations of electrical power, heating power and cooling power.

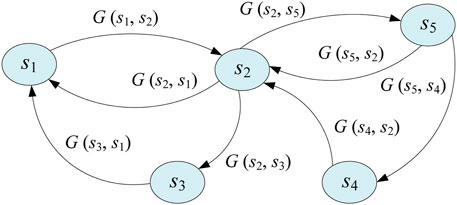
The information flow in the integration layer adopts the state machine model shown in Figure 5 to describe the transferring process of each unit’s operating state and the conditions triggering the state transformation.

FIGURE 5

FIGURE 5. Illustration of information flow using state machine.

The circles in Figure 5 indicate the operating states of the system. The system can be electric, heating, cooling system or a single device. In each operating state, there is a function that describes how the continuous state variables change, as shown in Table 1.

TABLE 1

TABLE 1. Illustration of energy flow in each operating state.

In Figure 5, the directed arcs between the circles represent the transformation relationships between the states of the system. The function G (s_i, s_j) labeled on the edges of the directed arcs represents the conditions that trigger the transfer of the system between the states. The triggering conditions here include state transfer commands from the decision layer and state transfer events triggered by the change of state variables within the system beyond a certain threshold.

The state machine model shown in Figure 5 can sense the signals in MEG and the automatic transformation between different states. The sensing system collects information and triggers the state transformation condition and the operation state of MEG changes accordingly when the external environment or user demand changes. At the same time, the differential equation that characterizes the system state also changes accordingly to respond to the external environment or demand.

The Decision Layer

As the top layer of the MEG, the primary function of the decision layer is to formulate the global optimization operation strategy of the system and issue task objectives, which are executed and completed by the object layer. Considering the characteristics of the decision layer, the model of this layer is built by building the objective function that takes the system’s operation constraints into account, as shown in Eq. 9.

$\{\begin{array}{l}\mathit{max or min}\{obj1,obj2,\cdots ,obji\}\\ s.t.\{\begin{array}{l}h\left(x\right)=0\\ w\left(x\right)\le 0\end{array}\end{array}(9)$

In Eq. 9, obji denotes the optimization objective of the system, which is set according to the actual requirements of the system. h(x) and w(x) represent the equality and inequality constraints that the system requires to satisfy, respectively.

Model Verification

System Description

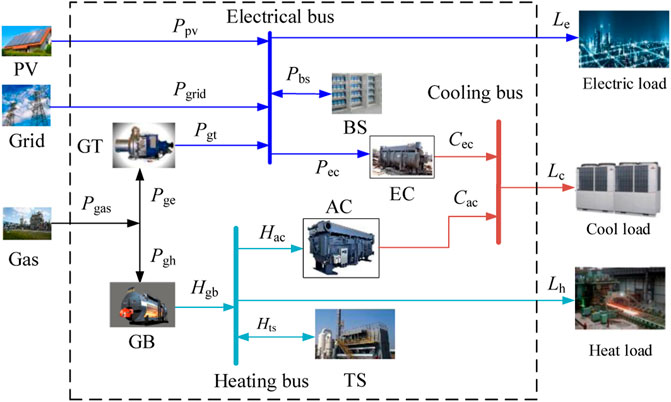
Figure 6 shows a simple MEG consisting of PV, GT, gas boiler (GB), EC, BS, TS, and AC. The input energy sources include PV input power P_pv, power grid input power P_grid and natural gas input power P_gas. The output energy is electrical load L_e, heat load L_h, and cooling load L_c. The electrical bus and heating bus are connected with energy storage devices, respectively, to maintain the real-time power balance of the system, the energy storage devices will charge when the energy is surplus; otherwise, they will discharge.

FIGURE 6

FIGURE 6. The topology structure of MEG.

The Model Implementation of MEG

The Object Layer

To build a unified model of the input-output for the object layer, define η_gt and η_gb as the conversion efficiency of the GT and GB, respectively. Define v_gt and v_gb as the ratio of natural gas used in the GT and GB for electricity generation and heat generation, respectively. Define v_ec as the ratio of electrical energy used in the EC for cooling. Define v_ac as the ratio of heating energy used in the AC for cooling. The following Eq. 10 describes the conversion relationship between different energy sources.

$\{\begin{array}{l}{P}_{gas}=P_{ge}+P_{gh}\\ P_{gt}={\mathit{\eta }}_{gt}{P}_{ge}={\mathit{\eta }}_{gt}{v}_{gt}{P}_{gas}\\ H_{gb}={\mathit{\eta }}_{gb}{P}_{gh}={\mathit{\eta }}_{gb}{v}_{gb}{P}_{gas}\\ C_{ec}=P_{ec}{k}_{ec}=v_{ec}(P_{pv}+P_{grid}+P_{gt})k_{ec}\\ C_{ac}=H_{ac}{k}_{ac}={\mathit{\eta }}_{gb}{v}_{ac}{v}_{gb}{P}_{gas}{k}_{ac}\end{array}(10)$

Where P_ge and P_gh denote the natural gas fired by the GT and GB, respectively. P_gt, denotes the electricity generated by GT, H_gb denotes the heat generated by GB, H_ac denotes the heat fed into the AC. C_ec and C_ac denote the cooling energy generated by EC and AC, respectively. k_ec and k_ac denote coefficients for the performance of EC and AC, respectively.

Taking energy storage devices into account, the input-output unified model of the object layer can be described as follows.

$\left[\begin{array}{c}{L}_e\\ L_h\\ L_c\end{array}\right]=\left[\begin{array}{ccc}1-v_{ec}& 1-v_{ec}& (1-v_{ec}){\mathit{\eta }}_{gt}{v}_{gt}\\ 0& 0& {\mathit{\eta }}_{gb}(1-v_{ac})v_{gb}\\ v_{ec}{k}_{ec}& v_{ec}{k}_{ec}& {\mathit{\eta }}_{gb}{v}_{gb}{v}_{ac}{k}_{ac}+v_{ec}{\mathit{\eta }}_{gt}{v}_{gt}{k}_{ec}\end{array}\right]\times \left[\begin{array}{c}\begin{array}{l}{P}_{pv}\\ P_{grid}\end{array}\\ P_{gas}\end{array}\right]+\left[\begin{array}{c}{P}_{bs}\\ H_{ts}\\ 0\end{array}\right](11)$

Where P_bs and H_ts indicate the power of the BS and TS, respectively, specifying that the discharge power of the energy storage devices is positive and the charging power is negative.

The Decision Layer

Objective Function

The decision layer formulates the global optimization operation strategy of the system according to the operating status and operating constraints of each unit in the integration layer and the object layer based on the actual requirements of the system. In this section, the following objective function is established to minimize the daily operation cost of MEG.

$C_{\text{r}}=\min (C_{pe}+C_{pg})(12)$

Where C_r denotes the total daily operating cost of the MEG, which consists of two parts: electricity purchasing cost C_pe from the grid and natural gas purchasing cost C_pg.

a) The electricity purchasing cost C_pe.

$C_{pe}={\displaystyle \sum _{t=1}^{24}(c_{eb,t}}\cdot P_{grid,t}^{buy}-c_{es,t}\cdot P_{grid,t}^{sell}\cdot \Delta t(13)$

$c_{eb,t}$ and $P_{grid,t}^{buy}$ denote the electricity purchase price and the purchasing power at time t, respectively. $c_{es,t}$ and $P_{grid,t}^{sell}$ denote the electricity sales price and the selling power at time t, respectively. $\Delta t$ is the time interval.

b) The natural gas purchasing cost C_pg.

$C_{pg}=c_{pg,t}\cdot {\displaystyle \sum _{t=1}^{24}(\Delta P_{ge,t}+P_{gh,t})\cdot \Delta t}=c_{pg,t}\cdot {\displaystyle \sum _{t=1}^{24}(\frac{P_{gt,t}}{{\eta }_{gt}}+}\frac{H_{gb,t}}{{\eta }_{gb}})\cdot \Delta t(14)$

In Eq. 14, $c_{pg,t}$ denote the price of natural gas at time t.

Constraints

a) Energy balance constraints.

1) Electrical power balance.

$P_{\mathit{pv,t}}+P_{gt,t}+P_{grid,t}^{buy}+P_{bs,d}^t=P_{\mathit{ec,t}}+P_{grid,t}^{sell}+P_{bs,c}^t+L_{\mathit{e,t}}(15)$

Where $P_{bs,c}^t$ and $P_{bs,d}^t$ represent the BS charging and discharging power at time t, respectively. $P_{\mathit{ec,t}}$ represents the power consumption of EC at time t. $L_{\mathit{e,t}}$ represents the electric load demand of users at time t.

2) Heating energy balance.

$H_{\text{gb,t}}+H_{\text{ts},\text{d}}^t=H_{\text{ts},\text{c}}^t+H_{ac,t}+L_{h,t}(16)$

$H_{\text{ts},\text{c}}^t$ and $H_{\text{ts},\text{d}}^t$ denote the TS heating charging and discharging power at time t, respectively. $L_{h,t}$ represents the heating load demand of users at time t.

3) Cooling energy balance.

$C_{\text{ec,t}}+C_{\text{ac,t}}=L_{\text{c,t}}(17)$

$L_{\text{c,t}}$ represents the cooling load demand at time t.

b) Device output constraints.

All the devices must work within the allowable range, i.e., the following constraints need to be satisfied.

$P_{i,\min }\le P_{i,t}\le P_{i,\max }(18)$

In Eq. 18, $P_{i,\min }$ and $P_{i,\max }$ denote the maximum and minimum output power of the i-type device, respectively, and $P_{i,t}$ denotes the output power of the i-type device at time t.

c) Constraints for the electricity exchanged with the power grid.

$\{\begin{array}{l}0\le P_{grid,t}^{buy}\le v_{g,t}{P}_{grid,\max }^{buy}\\ 0\le P_{grid,t}^{sell}\le (1-v_{g,t})P_{grid,\max }^{sell}\\ v_{g,t}\in \left\{\mathrm{0,1}\right\}\end{array}(19)$

In Eq. 19, $P_{grid,\max }^{buy}$ and $P_{grid,\max }^{sell}$ are the maximum purchasing power and selling power, respectively. $v_{g,t}$ is 0–1 variable introduced to constrain MEG not purchasing and selling electricity to the grid simultaneously.

d) Constraints for the gas exchanged with natural gas network.

$0\le P_{gas,t}\le P_{gas,\max }(20)$

$P_{gas,\max }$ denotes the maximum power of MEG to purchase gas from the natural gas network.

Case Study

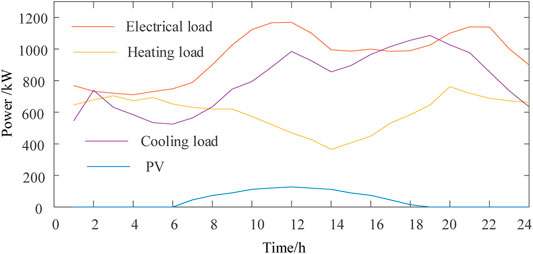
In this section, the built MEG model is applied to the optimal operation of the MEG, i.e., the above Eq. 19 is solved by MATLAB. Figure 7 shows the typical daily loads (electrical, cooling, and heating loads) and the PV day-ahead predicted output power curves of the MEG.

FIGURE 7

FIGURE 7. Predicted output power of electrical, heating, cooling load and PV.

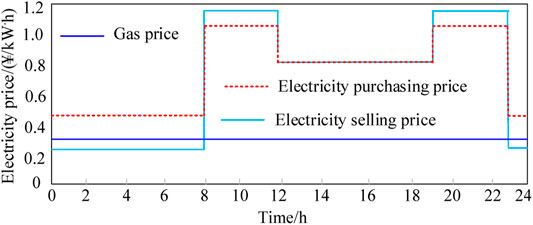
To promote the participation of MEG in grid operation and encourage more and full generation during peak hours to alleviate the grid power supply tension, the electricity sales price is set higher than the electricity purchase price during peak hours, equal to the electricity purchase price during the flat period, and lower than the electricity purchase price during valley period in this paper, as shown in Figure 8. Assume that the price of natural gas is fixed at 0.35 ¥/(kW^.h).

FIGURE 8

FIGURE 8. Time-of-use price of the MEG.

The parameters of the energy storage devices in the simulation are shown in Table 2 and Table 3.

TABLE 2

TABLE 2. Parameters for energy storage devices.

TABLE 3

TABLE 3. Other main devices parameters of MEG.

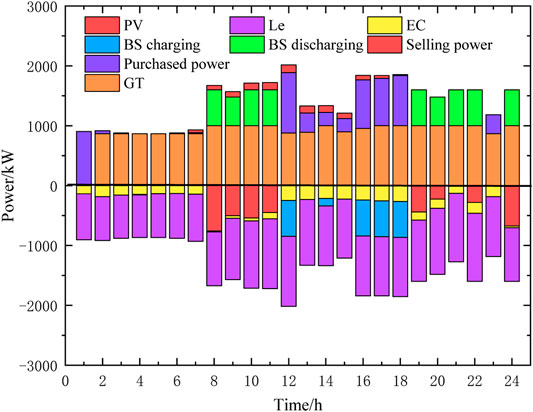
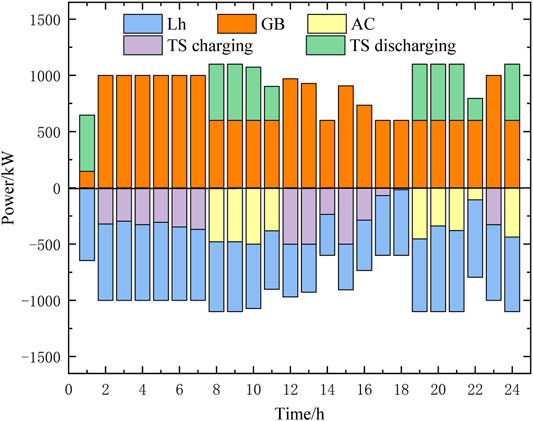
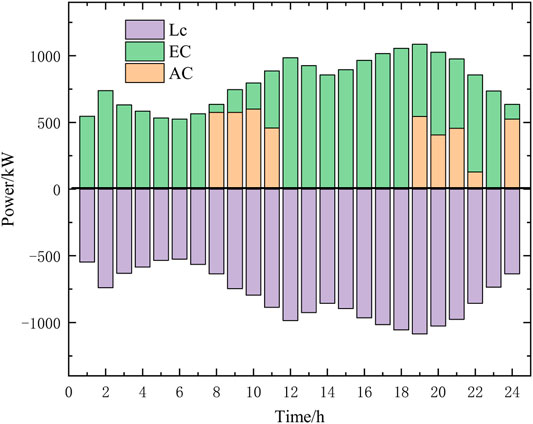
Figures 9–11 show the optimal dispatch results of electric power, heating power, and cooling power of each device in the MEG, respectively.

FIGURE 9

FIGURE 9. Optimal dispatch results of the electric power.

FIGURE 10

FIGURE 10. Optimal dispatch results of the heating power.

FIGURE 11

FIGURE 11. Optimal dispatch results of the cooling power.

In Figures 9–11, the upper part of the horizontal axis denotes the energy flowing into the energy bus, while the lower part denotes the energy flowing out from the energy bus. Since the MEG can maintain the real-time balance of electric power, heating power, and cooling power during operation, the optimization results are symmetric about the horizontal axis. The daily operational cost of the optimized MEG is ¥1244.4. The optimized dispatching results have the following characteristics.

1) During the valley period, most of the electric load is supplied by the GT and is purchased from the power grid since the electricity price is low and the price of natural gas is lower than the electricity price. During peak hours, the electricity price is relatively high; in addition to the electricity supplied by PV, the electric load is supplied by BS discharging and GT and the redundant electricity is sold to the grid to bring some revenues. During the flat period, the electric load is mainly supplied by GT, PV, and power grid. The electricity flowing into the electrical bus first meets the electric load, and the surplus electricity is used to generate cooling energy for the EC and charge the BS.

2) Since the system does not contain the heat recovery steam generator, the heating load is mainly supplied by the GB, and the redundant heat is used to store heat for the TS. When the electricity price is high, the TS will release heat to supply the heating load and the AC to generate cooling energy.

3) The cooling load is supplied by AC and EC. When electricity price is high, the cooling load is mainly supplied by AC to reduce system operating costs. Limited by the maximum power of AC, the EC assists in providing surplus cooling energy.

Conclusion

This paper proposes a hierarchical modeling framework for MEG modeling from the perspective of CPS, including object layer, integration layer and decision layer. The models of each layer are developed separately based on the design of the functions of the three layers. The combination of the three-layer model forms the overall model of the MEG. The model developed in this paper can clearly describe the interplay of the information flow and energy flow and can present the operation state of each unit in the MEG and the transfer process of the state. This is not only helpful to design the optimal operation state trajectory of the system but also can fully explore the ability improvement brought by the integration of the two systems, which can point out the direction for the planning and information construction of MEG and thus dramatically improving observable, controllable ability and optimal operation level of the MEG.

However, due to the focus of this paper, the limitation of the current study is that only the feasibility of the built MEG model has been verified and no specific application has been carried out. How to use the established MEG model to design the optimal operating state trajectory to obtain the optimal configuration of the system and how to plan the optimal capacity of the system is what we need to consider in our future work.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

YY carried out the establishment of model, presentation of strategies, data analysis, and wrote the first draft. GL assisted in establishment of model and improvement of strategies. ZL assisted in data analysis and polished the manuscript. YT helped the revision of the manuscript and help to collect sample data and write programs.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Almassalkhi, M. R., and Towle, A. (2016). “Enabling City-Scale Multi-Energy Optimal Dispatch with Energy Hubs,” in Proc. IEEE Power Syst. Comput. Conf., Genoa, Italy, 20-24 June 2016 (IEEE), 1–7. doi:10.1109/pscc.2016.7540981

CrossRef Full Text | Google Scholar

Chen, C., Sun, H., Shen, X., Guo, Y., Guo, Q., and Xia, T. (2019). Two-stage Robust Planning-Operation Co-optimization of Energy Hub Considering Precise Energy Storage Economic Model. Appl. Energ. 252. doi:10.1016/j.apenergy.2019.113372

CrossRef Full Text | Google Scholar

Chen, Z., Zhang, Y., Tang, W., Lin, X., and Li, Q. (2019). Generic Modelling and Optimal Day-Ahead Dispatch of Micro-energy System Considering the price-based Integrated Demand Response. Energy 176, 171–183. doi:10.1016/j.energy.2019.04.004

CrossRef Full Text | Google Scholar

Chicco, G., and Mancarella, P. (2008). Matrix Modelling of Small-Scale Trigeneration Systems and Application to Operational Optimization. Energy 34 (3), 261–273.

Google Scholar

Deng, C., Wang, Y., Wen, C., Xu, Y., and Lin, P. (2021). Distributed Resilient Control for Energy Storage Systems in Cyber-Physical Microgrids. IEEE Trans. Ind. Inf. 17 (2), 1331–1341. doi:10.1109/tii.2020.2981549

CrossRef Full Text | Google Scholar

Fu, R., Huang, X., Xue, Y., Wu, Y., Tang, Y., and Yue, D. (2019). Security Assessment for Cyber Physical Distribution Power System under Intrusion Attacks. IEEE Access 7, 75615–75628. doi:10.1109/access.2018.2855752

CrossRef Full Text | Google Scholar

Geidl, M., Koeppel, G., Favre-Perrod, P., Klockl, B., Andersson, G., and Frohlich, K. (2007). Energy Hubs for the Future. IEEE Power Energ. Mag. 5 (1), 24–30. doi:10.1109/mpae.2007.264850

CrossRef Full Text | Google Scholar

Huo, D., Gu, C., Ma, K., Wei, W., Xiang, Y., and Le Blond, S. (2019). Chance-Constrained Optimization for Multienergy Hub Systems in a Smart City. IEEE Trans. Ind. Electron. 66 (2), 1402–1412. doi:10.1109/tie.2018.2863197

CrossRef Full Text | Google Scholar

Ju, L., Tan, Q., Lin, H., Mei, S., Li, N., Lu, Y., et al. (2020). A Two-Stage Optimal Coordinated Scheduling Strategy for Micro Energy Grid Integrating Intermittent Renewable Energy Sources Considering Multi-Energy Flexible Conversion. Energy 196, 117078. doi:10.1016/j.energy.2020.117078

CrossRef Full Text | Google Scholar

Li, M., Xue, Y., Ni, M., and Li, X. (2020). Modeling and Hybrid Calculation Architecture for Cyber Physical Power Systems. IEEE Access 8 (22), 138251–138263. doi:10.1109/access.2020.3011213

CrossRef Full Text | Google Scholar

Li, P., Sheng, W., Duan, Q., Li, Z., Zhu, C., and Zhang, X. (2020). A Lyapunov Optimization-Based Energy Management Strategy for Energy Hub with Energy Router. IEEE Trans. Smart Grid 11 (6), 4860–4870. doi:10.1109/tsg.2020.2968747

CrossRef Full Text | Google Scholar

Li, Y., Zou, Y., Tan, Y., Cao, Y., Liu, X., Shahidehpour, M., et al. (2018). Optimal Stochastic Operation of Integrated Low-Carbon Electric Power, Natural Gas, and Heat Delivery System. IEEE Trans. Sustain. Energ. 9 (1), 273–283. doi:10.1109/tste.2017.2728098

CrossRef Full Text | Google Scholar

Liu, N., Wang, J., and Wang, L. (2019). Hybrid Energy Sharing for Multiple Microgrids in an Integrated Heat-Electricity Energy System. IEEE Trans. Sustain. Energ. 10 (3), 1139–1151. doi:10.1109/tste.2018.2861986

CrossRef Full Text | Google Scholar

Liu, T., Zhang, D., Dai, H., and Wu, T. (2019). Intelligent Modeling and Optimization for Smart Energy Hub. IEEE Trans. Ind. Electron. 66 (12), 9898–9908. doi:10.1109/tie.2019.2903766

CrossRef Full Text | Google Scholar

Lu, S., Gu, W., Meng, K., Yao, S., Liu, B., and Dong, Z. Y. (2020). Thermal Inertial Aggregation Model for Integrated Energy Systems. IEEE Trans. Power Syst. 35 (3), 2374–2387. doi:10.1109/tpwrs.2019.2951719

CrossRef Full Text | Google Scholar

Ma, T., Wu, J., and Hao, L. (2017). Energy Flow Modeling and Optimal Operation Analysis of the Micro Energy Grid Based on Energy Hub. Energ. Convers. Manag. 133, 292–306. doi:10.1016/j.enconman.2016.12.011

CrossRef Full Text | Google Scholar

Martinez Cesena, E. A., Loukarakis, E., Good, N., and Mancarella, P. (2020). Integrated Electricity- Heat-Gas Systems: Techno-Economic Modeling, Optimization, and Application to Multienergy Districts. Proc. IEEE 108 (9), 1392–1410. doi:10.1109/jproc.2020.2989382

CrossRef Full Text | Google Scholar

Mohseni, S., Brent, A. C., Kelly, S., Browne, W. N., and Burmester, D. (2021). Strategic Design Optimisation of Multi-Energy-Storage-Technology Micro-grids Considering a Two-Stage Game-Theoretic Market for Demand Response Aggregation. Appl. Energ. 287 (3), 116563.

CrossRef Full Text | Google Scholar

Qin, Y., Wu, L., Zheng, J., Li, M., Jing, Z., Wu, Q. H., et al. (2020). Optimal Operation of Integrated Energy Systems Subject to Coupled Demand Constraints of Electricity and Natural Gas. CSEE J. Power Energ. Syst. 6 (2), 444–457.

Google Scholar

Wang, Y., Wang, Y., Huang, Y., Yu, H., Du, R., Zhang, F., et al. (2019). Optimal Scheduling of the Regional Integrated Energy System Considering Economy and Environment. IEEE Trans. Sustain. Energ. 10 (4), 1939–1949. doi:10.1109/tste.2018.2876498

CrossRef Full Text | Google Scholar

Wang, Y., Zhang, N., Kang, C., Kirschen, D. S., Yang, J., and Xia, Q. (2019). Standardized Matrix Modeling of Multiple Energy Systems. IEEE Trans. Smart Grid 10 (1), 257–270. doi:10.1109/tsg.2017.2737662

CrossRef Full Text | Google Scholar

Wei, J., Zhang, Y., Wang, J., Cao, X., and Khan, M. A. (2019). Multi-period Planning of Multi-Energy Microgrid with Multi-type Uncertainties Using Chance Constrained Information gap Decision Method. Appl. Energ. 260, 1–19.

Google Scholar

Xin, S., Guo, Q., Sun, H., Zhang, B., Wang, J., and Chen, C. (2015). Cyber-Physical Modeling and Cyber-Contingency Assessment of Hierarchical Control Systems. IEEE Trans. Smart Grid 6 (5), 2375–2385. doi:10.1109/tsg.2014.2387381

CrossRef Full Text | Google Scholar

Xu, D., Wu, Q., Zhou, B., Li, C., Bai, L., and Huang, S. (2020). Distributed Multi-Energy Operation of Coupled Electricity, Heating, and Natural Gas Networks. IEEE Trans. Sustain. Energ. 11 (4), 2457–2469. doi:10.1109/tste.2019.2961432

CrossRef Full Text | Google Scholar

Zhang, S., Gu, W., Yao, S., Lu, S., Zhou, S., and Wu, Z. (2021). Partitional Decoupling Method for Fast Calculation of Energy Flow in a Large-Scale Heat and Electricity Integrated Energy System. IEEE Trans. Sustain. Energ. 12 (1), 501–513. doi:10.1109/tste.2020.3008189

CrossRef Full Text | Google Scholar

Zhao, P., Gu, C., Cao, Z., Hu, Z., Zhang, X., Chen, X., et al. (2021). Economic-Effective Multi-Energy Management Considering Voltage Regulation Networked with Energy Hubs. IEEE Trans. Power Syst. 36 (3), 2503–2515. doi:10.1109/tpwrs.2020.3025861

CrossRef Full Text | Google Scholar