ACCRUE—An Integral Index for Measuring Experimental Relevance in Support of Neutronic Model Validation

A key challenge for the introduction of any design changes, e.g., advanced fuel concepts, first-of-a-kind nuclear reactor designs, etc., is the cost of the associated experiments, which are required by law to validate the use of computer models for the various stages, starting from conceptual design, to deployment, licensing, operation, and safety. To achieve that, a criterion is needed to decide on whether a given experiment, past or planned, is relevant to the application of interest. This allows the analyst to select the best experiments for the given application leading to the highest measures of confidence for the computer model predictions. The state-of-the-art methods rely on the concept of similarity or representativity, which is a linear Gaussian-based inner-product metric measuring the angle—as weighted by a prior model parameters covariance matrix—between two gradients, one representing the application and the other a single validation experiment. This manuscript emphasizes the concept of experimental relevance which extends the basic similarity index to account for the value accrued from past experiments and the associated experimental uncertainties, both currently missing from the extant similarity methods. Accounting for multiple experiments is key to the overall experimental cost reduction by prescreening for redundant information from multiple equally-relevant experiments as measured by the basic similarity index. Accounting for experimental uncertainties is also important as it allows one to select between two different experimental setups, thus providing for a quantitative basis for sensor selection and optimization. The proposed metric is denoted by ACCRUE, short for Accumulative Correlation Coefficient for Relevance of Uncertainties in Experimental validation. Using a number of criticality experiments for highly enriched fast metal systems and low enriched thermal compound systems with accident tolerant fuel concept, the manuscript will compare the performance of the ACCRUE and basic similarity indices for prioritizing the relevance of a group of experiments to the given application.

1 Introduction

Model validation is one of the key regulatory requirements to develop a scientifically-defendable process in support of establishing confidence in the results of computerized physics models for the various developmental stages starting from conceptual design to deployment, licensing, operation, and safety. To ensure that model predictions can be trusted for a given application, e.g., the domain envisaged for code usage, the regulatory process requires the consolidation of two independent sources of knowledge, one from measurements collected from experimental conditions that are similar to the application, and the other from code predictions that model the same experimental conditions. For criticality safety applications, representing the focus of this manuscript, model validation plays a critical role in supporting design changes, e.g., the introduction of high burnup fuel, high assay low enrichment fuel, etc., or new fuel designs, e.g., accident tolerant fuel, both typically challenged by the scarcity of experimental data.

It is thus paramount to devise a methodology that can consolidate knowledge from both the experimental and computational domains in some optimal manner. The optimality of this consolidation process needs to recognize the possible scarcity of relevant experimental data expected with new designs, the cost for constructing new validation experiments, and the infeasibility of duplicating of all application conditions in the experimental domain. Ideally, the consolidation methodology should be able to optimally leverage existing experimental data in order to minimize the need for new experiments.

In our context, model validation entails a mapping process in which the experimental biases (differences between measurements and model predictions) are to be mapped to the application’s responses of interest in the form of calculational (i.e., best-estimate) biases along with their uncertainties. The goal is to improve the analyst’s confidence in the calculated application response. Mathematically, the confidence is measured in terms of the response uncertainty. The initial uncertainty propagated throughout the model is referred to as the prior uncertainty which accounts for parameter uncertainties, modeling assumptions, numerical approximations, initial, and boundary conditions, etc. The consolidation of experimental biases with the prior uncertainties results in a calculational bias that is intended to correct for the prior uncertainties. A successful consolidation process would result in a reduced bias uncertainty, i.e., as compared to the prior uncertainty, implying increased confidence in the calculated response.

The prior uncertainties are often grouped into two categories, aleatory, and epistemic. This manuscript will focus on epistemic uncertainties resulting from the lack of knowledge of the true values of the nuclear cross-section data. The implied assumption here is that cross-sections constitute the major source of uncertainty in neutronic calculations (Glaeser, 2008; Avramova and Ivanov, 2010; Abdel-Khalik et al., 2013; Wieselquist, 2016). Specifically, we focus on a single consolidation methodology for reducing the impact of epistemic uncertainties, the so-called generalized linear least-squares (GLLS) methodology which may be derived using Bayesian estimation theory (Williams et al., 2016). It is designed to calculate an optimal bias for any calculated response based on an optimal adjustment of the nuclear cross-sections.

In the neutronic community, the GLLS methodology has been independently developed by various researchers (Gandini, 1967; Salvatores, 1973; Broadhead et al., 2004; Cacuci and Ionescu-Bujor, 2010) with varying levels of generalization and mathematical formulation, e.g., Gaussianity assumption of the uncertainty source, degree of nonlinearity of the response variations with cross-sections, mathematical formulation in the cross-section space or the response space, etc. Under the same set of assumptions however, one can show the equivalence of these various formulations. For example, for Gaussian prior cross-section uncertainties and assumed linear approximations, the noted GLLS optimality criterion reduces to an L₂ minimization of the sum of two terms, see Eq. 4. The first term minimizes the L₂ norm of the adjustments of the cross-sections to ensure their consistency with their prior values, and the second term minimizes the discrepancy between the measurements and predictions for the selected experimental responses. The GLLS methodology is briefly discussed in Section 2.

A prerequisite for the GLLS methodology is to select the experiments that are most relevant to the application conditions¹. The premise is that with higher relevance biases with higher confidence, i.e., reduced uncertainties, can be calculated. In the neutronic community, sensitivity methods have been adopted to determine experimental relevance using a scalar quantity, denoted by the similarity index c_k (Broadhead et al., 2004)—also called representativity factor by other researchers (Palmiotti and Salvatores, 2012)—which can be used to prioritize/rank the experiments and possibly judge the value of a new experiment before it is constructed.

To measure the similarity index c_k, sensitivity methods are first employed to calculate the first-order variations in select quantities of interest that can be experimentally measured, e.g., critical eigenvalue, reaction rate ratios, etc., with respect to the cross-section variations by isotope, reaction type, and incident neutron energy. This is done with both the experimental models as well as the application model of interest, e.g., calculating the criticality conditions for a new fuel design, resulting in one sensitivity vector per model. The sensitivity vector comprises the first-order derivatives, i.e., sensitivity coefficients, of a given response with respect to all cross-sections. Next, the sensitivity vector of the experiment is folded with that of the application and the prior cross-section covariance matrix to calculate the similarity index.

The result of this folding process, see Eq. 5, is an integral quantity (c_k) taken to measure the degree of similarity between the first order derivatives of a single quantity of interest with respect to all cross-sections as calculated from both the experiment and the application models². The prior uncertainties are used as weighting parameters, assigning more weight to cross-sections with higher uncertainties. The resulting similarity index c_k is thus expected to be heavily influenced by cross-sections exhibiting both high prior uncertainties as well as strong sensitivities. This helps the GLLS methodology find the optimal adjustments for cross-sections with strong sensitivities as well as high uncertainties. This is justified as follows: cross-sections with weak sensitivities would require large adjustments to change the response, potentially rendering them statistically inconsistent with their prior values. Similarly, adjusting low-uncertainty cross-sections would violate their prior values, also considered a form of fudging that cannot be mathematically justified as it violates the basic assumption of the GLLS methodology, that is the observed discrepancies are mainly originating from the prior cross-section uncertainties.

The resulting similarity index c_k is a scalar quantity which lies between −1.0 and 1.0 and may be interpreted as follows: a zero value implies no correlations, i.e., cross-sections with strong sensitivities and high uncertainties, exist between the application, and the experimental conditions. This implies that experimental bias cannot be used to infer the application bias, i.e., it cannot be used to improve the prior estimate of the application response and hence the experiment is judged to have no value to the given application. Conversely, a high similarity value, i.e., close to 1.0, implies that the associated experimental bias can be reliably used to infer the application bias. More important, the bias uncertainty can be reduced with highly relevant experiments. Theoretically, the inclusion of a zero-similarity experiment would keep the prior uncertainty for the application unchanged—not increasing the confidence—while a perfectly similar experiment, e.g., c_k $=$ 1.0, would result in the minimum bias uncertainty, i.e., the maximum attainable confidence³.

One key limitation of the similarity index is that it does not account for the impact of measurement uncertainties. Essentially, the c_k value is obtained by normalizing the covariance matrix for the calculated responses. This further implies that the measurements uncertainties have no impact on the c_k value calculation. To explain this, consider two experiments with analogous similarity as measured by the c_k value but with different measurement uncertainties. The experiment with the lower uncertainty would result in the calculation of lower bias uncertainty, i.e., more confidence. This implies that an experiment with a lower c_k value and a low measurement uncertainty could result in a lower bias uncertainty than that obtained from an experiment with higher c_k value and higher measurement uncertainty. Thus, it is important to include the measurement uncertainty in the definition of relevance. This brings value to the design of future experiments, often involving an optimization of sensors’ types and placements. Inclusion of measurement uncertainty would allow the analyst to compare the value of different experiments (and sensors selection) prior to the conduction of the experiment.

Another limitation of the similarity index is that it does not consider the impact of past experiments. As the c_k value is calculated by normalizing the weighted inner product of two sensitivity vectors, with more experiments involved in the relevance evaluation process, the c_k value cannot be employed to capture a weighted relevance between two subspaces. To explain this, consider that the analyst has calculated the application bias using ideal conditions, i.e., with a highly relevant experiment and near zero measurement uncertainty. In this scenario, the inclusion of additional experiments, even if highly relevant, is unlikely to lead to further noticeable reduction in the bias uncertainty. Thus, two experiments with the same c_k value should be assigned different relevance depending on which experiment is employed first. This provides a lot of value when designing new experiments by quantifying the maximum possible increase in confidence while accounting for past experiments. Addressing these two limitations will help analysts determine the minimum number of experiments required to meet a preset level of increased confidence as well as compare the value of planned experiments, providing a quantitative approach for their optimization.

In response to these limitations, this manuscript employs the concept of experimental relevance as opposed to similarity in order to distinguish between the possible added value of a new experiment, if any, and the value available from past experiments. This is possible by extending the definition of the c_k similarity index⁴ via a new analytical expression for experimental relevance, denoted by the ACCRUE index, designed to account for the experiment’s measurement uncertainty and the prior confidence associated with past experiments. The symbol j_k is used to distinguish the ACCRUE index from the similarity index c_k, where the j denotes the ability to jointly assess the relevance of an experiment with past experiments. The ACCRUE index is short for Accumulated Correlation Coefficient for Relevance of Uncertainties in Experimental validation.

The TSURFER code, representing the GLLS rendition under the ORNL’s SCALE code suite, is employed to exemplify the application of the ACCRUE index j_k. Specifically, we develop three sorting methods for the available experiments based respectively on the similarity index c_k, the ACCRUE index j_k, and pure random sampling. Two different sets of experiments are employed to compare the performance of the various sorting methods. The first set involves low-enriched uranium thermal compound systems with the accident-tolerant fuel (ATF) concept BWR assembly, and the second comprises highly enriched uranium fast metal systems. Finally, numerical experiments will be employed to verify the analytically-calculated values for j_k.

This manuscript is organized as follows. Section 2 provides a background on sensitivity theory and the details of mathematical description of the GLLS nuclear data adjustment methodology. Section 3 introduces ACCRUE algorithm and an extension of the non-intrusive stochastic verification with mathematical details. Section 4 verifies the performance of the proposed algorithm by numerical experiments to compare the results made by one of the conventional integral similarity indices, c_k¸ and the ACCRUE index, j_k. Concluding remarks and further research are summarized in Section 5.

2 Background and Relevance

This section presents a brief background on three key topics: 1) sensitivity methods employed for the calculation of first-order derivatives; 2) the GLLS adjustment theory, employed to calculate the application bias; and 3) the extant similarity index c_k definition. The material in this section may be found in the literature, however compiled here to help set the stage for the proposed ACCRUE index.

2.1 Sensitivity Theory

Sensitivity coefficients are the key ingredients for the GLLS methodology, as they are used to relate the response variations to the model parameter variations, with the latter assumed to represent the dominant sources of uncertainties. A sensitivity coefficient measures the first-order variation of a response that is caused by a change in one input model parameter. For the numerical experiments employed in this paper, we focus on the multiplication factor, k_eff, i.e., critical eigenvalue, as the response of interest and the reaction-wise cross-sections by isotope and energy group as the model parameters.

While sensitivity coefficients can be readily evaluated using finite differencing, the adjoint-based perturbation theory methodology (Usachev, 1964; Gandini, 1967; Stacey, 1974; Oblow, 1976; Cacuci and Ionescu-Bujor, 2010) has been adopted as the most efficient way to calculate derivatives. This follows because adjoint-based sensitivity theory requires one adjoint solution per response, implying that one can calculate the first-order derivatives of the given response with respect to all cross-sections using a single adjoint model evaluation, whereas finite differencing requires an additional forward model evaluation for each cross-section. The general idea behind adjoint-based sensitivity analysis is summarized below for the evaluation of the first order derivatives of the critical eigenvalue.

The Boltzmann transport equation for an assembly containing fissionable material, referred to as the forward model, can be symbolically expressed as (Williams, Broadhead and Parks, 2001):

$\begin{array}{c}\left(\mathit{M}\left(\alpha \right)-\frac{1}{k}\mathit{F}\left(\alpha \right)\right)\psi =0\end{array}(1)$

where

$\mathit{M}\left(\alpha \right)=$ Multigroup form of the Boltzmann loss operator.

$\mathit{F}\left(\alpha \right)=$ Multigroup form of the Boltzmann production operator.

$\psi =\psi \left(r,\text{Ω},g\right)=$ Multigroup angular flux. where $\psi$ is a function of

$r=$ position.

$\text{Ω}=$ neutron moving direction.

$g=$ energy group.

The two operators $\mathit{M}\left(\alpha \right)$ and $\mathit{F}\left(\alpha \right)$ are functions of the reference multi-group cross-section data which may be described by an n-dimensional vector, $\alpha ={\left[\begin{array}{cccc}{\alpha }_1& {\alpha }_2& \cdots & {\alpha }_n\end{array}\right]}^T$ whose n components are the reaction-wise cross-sections by energy-group and isotope⁵. Thus, the solution of this equation yielding the eigenvalue may be compactly written as follows:

$k_j=f_j\left(\alpha \right)$

where $k_j$ is the code-predicted eigenvalue⁶, i.e., k_eff, of jth critical experiment model and $f_j$ is a compact representation of the solution of Eq. 1 implying its dependence on $\alpha$. Analytically, the first-order derivatives of k_eff with respect to each cross-section can be expressed in a relative sense—referred to as the sensitivity coefficients—using a first-order Taylor series expansion:

$\begin{array}{c}{S}_{k_j,{\alpha }_i}=\frac{{\alpha }_i}{k_j}\frac{f_j\left({\alpha }_1,\dots ,{\alpha }_i+\text{Δ}{\alpha }_i,\dots ,{\alpha }_n\right)-f_j\left({\alpha }_1,\dots ,{\alpha }_i,\dots ,{\alpha }_n\right)}{\text{Δ}{\alpha }_i}\end{array}(2)$

and aggregated in a vector (referred to as the sensitivity vector or profile) with the superscript “T” representing vector/matrix transpose:

$s_j={\left[\begin{array}{cccc}{S}_{k_j,{\alpha }_1}& S_{k_j,{\alpha }_2}& \cdots & S_{k_j,{\alpha }_n}\end{array}\right]}^T$

Eq. 2 implies that a finite-difference-based sensitivity analysis would require $n+1$ forward model executions, one with the reference cross-section values, and one additional execution per cross-section. For most practical neutronic problems, this is computationally infeasible because cross-sections often number in the 10⁴ to 10⁵ range.

The adjoint formulation of sensitivity coefficients may be described by the following equation:

$\begin{array}{c}{S}_{k_j{\alpha }_i}=\frac{{\alpha }_i}{k_j}\frac{\langle {\psi }^{\ast }\frac{\partial }{\partial {\alpha }_i}\left(\frac{1}{k}\mathit{F}-\mathit{M}\right)\psi \rangle }{\langle {\psi }^{\ast }\mathit{F}\psi \rangle }\end{array}(3)$

The brackets represent an inner product operation corresponding to an integration over entire phase-space (e.g., energy groups, direction of neutron travel, and space) using the forward solution obtained from Eq. 1 and a new quantity, called the adjoint solution, obtained from:

$\left({\mathit{M}}^{\ast }-\frac{1}{k}{\mathit{F}}^{\ast }\right){\psi }^{\ast }=0$

where ${\mathit{M}}^{\ast }$ and ${\mathit{F}}^{\ast }$ are the adjoint operators of the forward operators $\mathit{M}$ and $\mathit{F}$, evaluated at the reference cross-section values. The $\frac{\partial }{\partial {\alpha }_i}$ term differentiates the operators $\mathit{M}$ and $\mathit{F}$ with respect to the ith cross-section, with the derivative taken around the reference cross-section values. Since the mathematical expressions for $\mathit{M}$ and $\mathit{F}$ are known, these changes can be analytically calculated. More importantly, they do not require re-execution of the forward or the adjoint model. The implication is that one can evaluate the derivatives with respect to all cross-sections using a single forward and a single adjoint model evaluation.

Several computer codes have embodied the adjoint methodology to calculate sensitivity coefficients (Lucius et al., 1981; Becker et al., 1982; Gerald; Rimpault et al., 2002). Of interest to us is the SCALE TSUNAMI methodology (Rearden and Jessee, 2016) which is used as a basis for the evaluation of the sensitivity coefficients for the GLLS-based TSURFER code, discussed in the next section.

2.2 GLLS Adjustment Methodology

As discussed earlier, the main goal of GLLS is to consolidate knowledge from computations and experiments. This is illustrated in Figure 1 using two representative PDFs describing the best available knowledge about the k_eff from the experiments (shown in red) and model predictions (blue). The spread of each PDF is taken as a measure of confidence. The confidence in the model predictions is determined by the propagated prior uncertainties, and the experiment’s confidence is tied to its measurement uncertainties. The GLLS methodology represents a disciplined mathematical approach to consolidate these two PDFs into one (yellow) that provides higher confidence for the calculated response as compared to the prior confidence from model predictions.

FIGURE 1

FIGURE 1. k_eff consolidated confidence from experiment and prior calculations.

To achieve that, GLLS assumes that the uncertainties originate from the cross-sections. Therefore, it attempts to identify the optimal cross-section adjustments which minimize the discrepancies between measured and predicted responses. Based on the optimal adjustments, one can calculate the corresponding change in the application’s response, with the application representing the conditions for which no experimental values exist. The change in the code-calculated application response, i.e., from its prior value, is denoted by the application bias.

Considering that the analyst is interested in calculating the bias for the k_eff value for a given application, and there exist $M$ available experiments, the corresponding prior values may be aggregated in a vector $k\in {\mathrm{ℝ}}^{M+1}$ such that:

$k={\left[k_1{k}_2\cdots k_{M+1}\right]}^T$

where the last component is the prior value for the application k_eff. The corresponding measurements for the first $M$ values are designated by another vector $m\in {\mathrm{ℝ}}^{M+1}$. In this formulation, the last element of $m$ is set to the prior value of k_eff, assumed to have no corresponding experimental value.

The prior cross-section uncertainties are described by a multi-variable Gaussian PDF with a vector of means representing the reference multi-group cross-sections and a covariance matrix given by:

${\mathit{C}}_{\mathit{\alpha \alpha }}=\left[\begin{array}{cccc}cov\left({\alpha }_1,{\alpha }_1\right)& cov\left({\alpha }_1,{\alpha }_2\right)& \cdots & cov\left({\alpha }_1,{\alpha }_n\right)\\ cov\left({\alpha }_2,{\alpha }_1\right)& cov\left({\alpha }_2,{\alpha }_2\right)& \cdots & cov\left({\alpha }_2,{\alpha }_n\right)\\ ⋮& ⋮& \ddots & ⋮\\ cov\left({\alpha }_n,{\alpha }_1\right)& cov\left({\alpha }_n,{\alpha }_2\right)& \cdots & cov\left({\alpha }_n,{\alpha }_n\right)\end{array}\right]\in {\mathrm{ℝ}}^{n\times n}$

The adjusted cross-sections are calculated as the minimizer of the following minimization problem subject to the constraint $k^{\prime }\left({\alpha }^{\prime }\right)=m\prime$:

$\begin{array}{c}{\alpha }^{\ast }=\underset{{\alpha }^{\prime }}{\text{argmin}}{\left[{\alpha }^{\prime }-\alpha \right]}^T{\mathit{C}}_{\mathit{\alpha \alpha }}^{-1}\left[{\alpha }^{\prime }-\alpha \right]+{\left[m^{\prime }-m\right]}^T{\mathit{C}}_{\mathit{mm}}^{-1}\left[m^{\prime }-m\right]\end{array}(4)$

where ${\mathit{C}}_{\mathit{mm}}\in {\mathrm{ℝ}}^{\left(M+1\right)\times \left(M+1\right)}$ is the covariance matrix for the measured k_eff. The constraint implies that the adjusted cross-sections ${\alpha }^{\prime }$ will update the best-estimated values (the components of $m\prime$) for all $M$ experiments as well as the application. The last element of the vector $m\prime$ is taken to represent the best-estimate for the application k_eff value, and the last component of $m\prime -m$ is referred to as the application bias. Note that $k_j-m_j$ represents the initial discrepancy between the prior code-calculated and measured k_eff values for the jth experiment, and $m\prime -m$ represents the discrepancy after the cross-sections are adjusted.

The objective function in Eq. 4 may be re-written in terms of the calculated and adjusted k_eff values as:

${\chi }_M^2={\left[k^{\prime }-k\right]}^T{\mathit{C}}_{\mathit{kk}}^{-1}\left[k^{\prime }-k\right]+{\left[m^{\prime }-m\right]}^T{\mathit{C}}_{\mathit{mm}}^{-1}\left[m^{\prime }-m\right]$

where ${\chi }_M^2$ is the $M$ -degrees of freedom chi-square value describing the discrepancies between the prior and adjusted k_eff values. The ${\mathit{C}}_{\mathit{kk}}\in {\mathrm{ℝ}}^{\left(M+1\right)\times \left(M+1\right)}$ matrix denotes the prior covariance matrix for the calculated k_eff values given by:

$\begin{array}{c}{\mathit{C}}_{\mathit{kk}}={\mathit{S}}_{\mathit{k\alpha }}{\mathit{C}}_{\mathit{\alpha \alpha }}{\mathit{S}}_{\mathit{k\alpha }}^{\mathit{T}}\end{array}(5)$

and ${\mathit{S}}_{\mathit{k\alpha }}\in {\mathrm{ℝ}}^{\left(M+1\right)\times n}$ matrix aggregates the sensitivity profiles for all $M$ experiments and the application:

${\mathit{S}}_{\mathit{k\alpha }}=\left[\begin{array}{cccccc}{S}_{\mathrm{1,1}}& S_{\mathrm{1,2}}& \cdots & S_{1,i}& \cdots & S_{1,n}\\ S_{\mathrm{2,1}}& S_{\mathrm{2,2}}& \cdots & S_{2,i}& \cdots & S_{2,n}\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ S_{j,1}& S_{j,2}& \cdots & S_{j,i}& \cdots & S_{j,n}\\ ⋮& ⋮& \cdots & ⋮& \ddots & ⋮\\ S_{M,1}& S_{M,2}& \cdots & S_{M,i}& \cdots & S_{M,n}\\ S_{M+\mathrm{1,1}}& S_{M+\mathrm{1,2}}& \cdots & S_{M+1,i}& \cdots & S_{M+1,n}\end{array}\right]$

where (j, i) element represents the relative sensitivity coefficient of the jth experiment [or application, $\left(M+1\right)$th row] with respect to the ith multi-group cross-section.

Assuming that the linearization of the constraint $k\prime \left({\alpha }^{\prime }\right)=m\prime$ is sufficiently accurate within the limitations of first-order sensitivity theory, the minimizer of the objective function in Eq. 4 may be given by:

$\text{Δ}k=-{\mathit{C}}_{\mathit{kk}}{\left({\mathit{C}}_{\mathit{kk}}+{\mathit{C}}_{\mathit{mm}}\right)}^{-1}d$

where $\text{Δ}k=k^{\prime }-k$ and $d\in {\mathrm{ℝ}}^{M+1}$ is the discrepancy vector, $d=k-m$

The posterior (i.e., post the consolidation of experimental and prior values) covariance matrix for the k_eff values is given by:

$\begin{array}{c}{\mathit{C}}_{{\mathit{k}}^{\mathit{\prime }}{\mathit{k}}^{\mathit{\prime }}}={\mathit{C}}_{\mathit{kk}}-{\mathit{C}}_{\mathit{kk}}{\left({\mathit{C}}_{\mathit{kk}}+{\mathit{C}}_{\mathit{mm}}\right)}^{-1}{\mathit{C}}_{\mathit{kk}}\end{array}(6)$

The diagonal elements of this matrix describe the confidence one has in the posterior k_eff values. The $\left(M+1\right)$th diagonal element of the ${\mathit{C}}_{\mathit{kk}}$ matrix (${\mathit{C}}_{\mathit{kk}}\left[M+1,M+1\right]$) measures the prior confidence one has in the calculated application k_eff value. If the experiments are relevant to the application, the posterior confidence, (${\mathit{C}}_{{\mathit{k}}^{\prime }{\mathit{k}}^{\prime }}\left[M+1,M+1\right]$) should provide higher confidence, i.e., ${\mathit{C}}_{{\mathit{k}}^{\prime }{\mathit{k}}^{\prime }}\left[M+1,M+1\right]<{\mathit{C}}_{\mathit{kk}}\left[M+1,M+1\right]$.

2.3 Similarity Index, c_k

The definition of the similarity index c_k naturally appears in the GLLS formulation of the prior covariance matrix. Specifically, one can expand Eq. 5 as follows:

$\begin{array}{c}{\mathit{C}}_{\mathit{kk}}=\left[\begin{array}{cccc}{s}_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_1& s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_2& \cdots & s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_{M+1}\\ s_2^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_2& s_2^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_2& \cdots & s_2^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_{M+1}\\ ⋮& ⋮& \ddots & ⋮\\ s_{M+1}^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_1& s_{M+1}^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_2& \cdots & s_{M+1}^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_{M+1}\end{array}\right]\end{array}(7)$

The diagonal entries of this matrix represent the uncertainty (in the units of variance) of the prior k_eff values and the off-diagonal entries are the correlations between these uncertainties. Ideally, one would want to maximize the correlations between the application and all experiments, described by the last row or last column of the matrix. A standardized form of this matrix may be obtained by multiplying it from both sides by the inverse of the square root of its diagonal elements to produce the matrix $\mathit{R}\in {\mathrm{ℝ}}^{(M+1)\times (M+1)}$:

$\mathit{R}=\left[\begin{array}{cccc}1& \frac{s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_2}{\sqrt{s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_1}\sqrt{s_2^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_2}}& \cdots & \frac{s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_{M+1}}{\sqrt{s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_1}\sqrt{s_{M+1}^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_{M+1}}}\\ \frac{s_2^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_1}{\sqrt{s_2^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_2}\sqrt{s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_1}}& 1& \cdots & \frac{s_2^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_{M+1}}{\sqrt{s_2^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_2}\sqrt{s_{M+1}^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_{M+1}}}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{s_{M+1}^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_1}{\sqrt{s_{M+1}^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_{M+1}^{ }}\sqrt{s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_1}}& \frac{s_{M+1}^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_2}{\sqrt{s_{M+1}^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_{M+1}}\sqrt{s_2^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_2}}& \cdots & 1\end{array}\right]$

In this representation, the value of any off-diagonal terms is standardized between $-1$.0 and $1$.0 which is equivalent to the definition of the standard correlation coefficient between two random variables. Appearing naturally in the GLLS formulation, these off-diagonal terms have been adopted as to measure experimental relevance. Specifically, the similarity index c_k between the application and the jth experiment is given by:

$\begin{array}{c}{c}_k\left(k_j,k_{M+1}\right)=\frac{s_j^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_{M+1}}{\sqrt{s_j^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_j}\sqrt{s_{M+1}^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_{M+1}}}\end{array}(8)$

This equation may be used to pre-calculate the similarities of all available experiments with respect to the given application. To achieve that one needs to calculate the corresponding sensitivity profiles for the experiments and the application which are readily calculated using the adjoint sensitivity theory presented in Section 2.1. In our work, the SCALE TSUNAMI code is employed to calculate the sensitivity profiles as well as the similarity indices.

Next, it is instructive to give a geometric interpretation of the similarity index. To do that, rewrite the expressions in Eq. 8 using the Cholesky decomposition of ${\mathit{C}}_{\mathit{kk}}$ as:

${\mathit{C}}_{\mathit{kk}}={\mathbf{\Gamma }}^T\mathbf{\Gamma }$

where $\mathbf{\Gamma }=\left[\begin{array}{cccc}{\gamma }_1& {\gamma }_2& \cdots & {\gamma }_{M+1}\end{array}\right]$, where the inner-product of any of two columns of $\mathbf{\Gamma }$ gives:

${\gamma }_i^T{\gamma }_j={\mathit{C}}_{\mathit{kk}}\left[i,j\right],i,j=\mathrm{1,2},\dots , M+1$

Performing this transformation for both the numerator and denominator in Eq. 8, the c_k index reduces to:

$\begin{array}{c}{c}_k\left(k_j,k_{M+1}\right)=\frac{{\gamma }_j^T{\gamma }_{M+1}}{\sqrt{{\gamma }_j^T{\gamma }_j}\sqrt{{\gamma }_{M+1}^T{\gamma }_{M+1}}}=\frac{{\mathit{C}}_{\mathit{kk}}\left[j,M+1\right]}{\sqrt{{\mathit{C}}_{\mathit{kk}}\left[j,j\right]}\sqrt{{\mathit{C}}_{\mathit{kk}}\left[M+1,M+1\right]}}=\cos \theta \left({\gamma }_j,{\gamma }_{M+1}\right)\end{array}(9)$

As illustrated in Figure 2, this expression is interpreted as cosine angle between two vectors, one related to the application and the other to an experiment.

FIGURE 2

FIGURE 2. Geometrical interpretation for the similarity index, c_k.

Further, it has been shown in earlier research (Huang et al., 2020) that one can calculate c_k using randomized forward model evaluations taking advantage of the equivalence between the c_k definition and the standard correlation coefficient. This requires sampling of the cross-sections within their prior uncertainties a few hundred times to obtain sufficiently approximate estimates of the similarity index, as shown below. As demonstrated in earlier work using the Sampler code under the SCALE environment (Wieselquist, 2016), this forward-based approach provides two advantages; first, it allows one to calculate similarity indices when the adjoint solver is not available; and second, it provides a way to verify the results of adjoint-based calculations.

It has been shown in earlier work that these two vectors may be interpreted as the directional sensitivity profiles with respect to the dominant eigen directions of the prior covariance matrix. To illustrate the mechanics of the forward-based approach for calculating the similarity index, first consider re-writing the cross-section covariance matrix decomposed by Cholesky methodology as follows:

$\begin{array}{c}{\mathit{C}}_{\mathit{\alpha \alpha }}=\mathit{U}{\mathbf{\Lambda }}^2{\mathit{U}}^{\mathit{T}}\end{array}(10)$

where $\mathit{U}\in {\mathrm{ℝ}}^{n\times n}$ a unitary matrix; ${\mathit{U}}^T\mathit{U}=\mathit{U}{\mathit{U}}^T=\mathit{I}$ and $\mathbf{\Lambda }\in {\mathrm{ℝ}}^{n\times n}$ is a diagonal matrix whose elements are square root of the singular values of ${\mathit{C}}_{\mathit{\alpha \alpha }}$.

If ${\xi }^{\left(p\right)}\in {\mathrm{ℝ}}^n$ is a Gaussian variable, one can generate $N$ random samples for the cross-sections which respect their covariance structure, such that:

$\text{Δ}{\alpha }^{\left(p\right)}=\mathit{U}\mathbf{\Lambda }{\xi }^{\left(p\right)},p=\mathrm{1,2},\dots ,N$

By the law of large numbers, one can show that as $N$ increases (Stark and Woods, 2012)

$\underset{N\to \infty }{\lim }\left(\frac{1}{N}{\displaystyle \sum }_{p=1}^N{\xi }^{\left(p\right)}{\xi }^{{\left(p\right)}^T}\right)=\mathit{I}$

This limit is readily reached with a few hundred samples. Verification with numerical experiments is provided in the following section.

Then, Eq. 10 can be re-written by the cross-section samples, such as:

${\mathit{C}}_{\mathit{\alpha \alpha }}=\underset{N\to \infty }{\text{lim}}\mathit{U}\mathbf{\Lambda }\left(\frac{1}{N}{\displaystyle \sum }_{p=1}^N{\xi }^{\left(p\right)}{\xi }^{{\left(p\right)}^T}\right){\mathbf{\Lambda }}^T{\mathit{U}}^T=\underset{N\to \infty }{\text{lim}}\left(\frac{1}{N}{\displaystyle \sum }_{p=1}^N\text{Δ}{\alpha }^{\left(p\right)}\text{Δ}{\alpha }^{{\left(p\right)}^T}\right)$

With the linearity assumption valid, e.g., ${\mathit{S}}_{\mathit{k\alpha }}\text{Δ}{\alpha }^{\left(p\right)}=\text{Δ}{k}^{\left(p\right)}$, samples for the code-calculated responses also can be calculated by the sandwich rule in Eq. 5, and thus the covariance matrix for calculated responses can be re-written as:

${\mathit{C}}_{\mathit{kk}}={\mathit{S}}_{\mathit{k\alpha }}\mathit{U}{\mathbf{\Lambda }}^2{\mathit{U}}^{\mathit{T}}{\mathit{S}}_{\mathit{k\alpha }}^{\mathit{T}}=\underset{N\to \infty }{\text{lim}}\left(\frac{1}{N}{\displaystyle \sum }_{p=1}^N{\mathit{S}}_{\mathit{k\alpha }}\text{Δ}{\alpha }^{\left(p\right)}\text{Δ}{\alpha }^{\left(p\right)T}{\mathit{S}}_{\mathit{k\alpha }}^T\right)=\underset{N\to \infty }{\text{lim}}\left(\frac{1}{N}{\displaystyle \sum }_{p=1}^N\text{Δ}{k}^{\left(p\right)}\text{Δ}{k}^{\left(p\right)T}\right)$

where $\text{Δ}k$ transforms the sensitivity matrix ${\mathit{S}}_{\mathit{k\alpha }}$ using the Chelosky factor of ${\mathit{C}}_{\mathit{\alpha \alpha }}$.

Thus, the construction of the ${\mathit{C}}_{\mathit{kk}}$ matrix effectively reduces to the following three steps; first, it transforms the original variables into a set that are uncorrelated; second, it calculates the sensitivities along the directions of the transformed variables (referred to as directional sensitivity in the calculus literature); and third, it weighs each directional sensitivity by its corresponding prior uncertainty.

The deviation vector of jth experiment (or application denoted by subscript $M+1$) code-calculated samples from its reference value can be written as:

$\text{Δ}{k}_j=\left[\begin{array}{c}\frac{k_j^{\left(1\right)}-k_j^{\left(ref\right)}}{k_j^{\left(ref\right)}}\\ \frac{k_j^{\left(2\right)}-k_j^{\left(ref\right)}}{k_j^{\left(ref\right)}}\\ ⋮\\ \frac{k_j^{\left(N\right)}-k_j^{\left(ref\right)}}{k_j^{\left(ref\right)}}\end{array}\right],j=\mathrm{1,2},\dots ,M+1$

Each term in $\text{Δ}{k}_j$ may be considered as a sample resulting from executing the forward model with a random cross-section perturbation. Thus, $\text{Δ}{k}_j$ is a vector of $N$ sampled perturbations of the jth response. Graphically, these perturbation vectors can be displayed via a scatter plot. For example, Figure 3 shows a representative scatter plot of the perturbation vectors for the jth experiment and the application.

FIGURE 3

FIGURE 3. Representative scatter plot of two perturbation vectors.

Their similarity index thus reduces to the standard correlation coefficient between the two vectors $\text{Δ}{k}_j$ and $\text{Δ}{k}_{M+1}$ similarly to Eq. 9 such that:

$\cos \theta \left(\text{Δ}{k}_j,\text{Δ}{k}_{M+1}\right)=\frac{\text{Δ}{k}_j^{\text{T}}\text{Δ}{k}_{M+1}}{\sqrt{\text{Δ}{k}_j^T\text{Δ}{k}_j}\sqrt{\text{Δ}{k}_{M+1}^T\text{Δ}{k}_{M+1}}}$

With a large number of samples, the inner-products of any two sample vectors reduce to the elements of the ${\mathit{C}}_{\mathit{kk}}$ matrix, such that:

$\underset{N\to \infty }{\lim }\text{Δ}{k}_i^T\text{Δ}{k}_j={\mathit{C}}_{\mathit{kk}}\left[i,j\right]$

Thus,

$c_k\left(k_j,k_{M+1}\right)=\underset{N\to \infty }{\lim }\frac{\text{Δ}{k}_j^{\text{T}}\text{Δ}{k}_{M+1}}{\sqrt{\text{Δ}{k}_j^T\text{Δ}{k}_j}\sqrt{\text{Δ}{k}_{M+1}^T\text{Δ}{k}_{M+1}}}$

In this manuscript, the ACCRUE index will be calculated using both the analytical definition, presented in Section 3, as well as the noted forward-based approach for verification.

3 ACCRUE Index and Verification Algorithm

This section details the theoretical derivation of the ACCRUE index j_k, discusses its relationship to the c_k index, and shows how it can be calculated both analytically using the adjoint approach and statistically using the forward approach. The j_k index is designed to address two limitations of the c_k index, first the impact of measurement uncertainty on the relevance of a given experiment, and second, the diminished value of an experiment resulting from its similarity with previously consolidated experiments. With regard to the first limitation, the c_k index bases the similarity on the code-calculated values only. In practice however, an experiment with a high c_k index could prove less valuable to estimating the application bias if its measurements have high uncertainties. The second limitation calls for an approach to identify experimental redundancy. The high level premise of any inference procedure is that additional measurements will result in more confidence in the calculated application bias. In practice however, the confidence gleaned from multiple highly relevant experiments could be equally obtained from a smaller number of experiments if high level of redundancy exists between the experiments, a common phenomenon observed in many fields, often referred to as the law of diminished return. The c_k index does not capture this effect because it is based on a single experiment.

3.1 Impact of Measurement Uncertainty

Different from the c_k index which relies on the ${\mathit{C}}_{\mathit{kk}}$ matrix, the j_k index leverages the ${\mathit{C}}_{\mathit{kk}}+{\mathit{C}}_{\mathit{mm}}$ matrix which appears in the GLLS procedure to weigh the prior values and the experimental measurements. This matrix can be shown to be the covariance matrix for the discrepancies between the calculated and measured values, whereas the ${\mathit{C}}_{\mathit{kk}}$ matrix is the covariance matrix for the calculated values only.

The discrepancies can be aggregated in a vector such that:

$d={\left[\begin{array}{ccccc}{k}_1-m_1& k_2-m_2& \cdots & k_M-m_M& k_{M+1}\end{array}\right]}^T$

where the last element, $k_{M+1}$, of the discrepancy vector remains the same as $k$, since measurement uncertainty for the application is not applicable.

Then the covariance matrix for the discrepancy vector, $d$, is:

$\begin{array}{c}{\mathit{C}}_{\mathit{dd}}=\left[\begin{array}{ccccc}{D}_{\mathrm{1,1}}& D_{\mathrm{1,2}}& \cdots & D_{1,M}& D_{1,M+1}\\ D_{\mathrm{2,1}}& D_{\mathrm{2,2}}& \cdots & D_{2,M}& D_{2,M+1}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ D_{M,1}& D_{M,2}& \cdots & D_{M,M}& D_{M,M+1}\\ D_{M+\mathrm{1,1}}& D_{M+\mathrm{1,2}}& \cdots & D_{M+1,M}& D_{M+1,M+1}\end{array}\right]\in {\mathrm{ℝ}}^{\left(M+1\right)\times \left(M+1\right)}\end{array}(11)$

where $D_{i,j}={\mathit{C}}_{\mathit{kk}}\left[i,j\right]+{\mathit{C}}_{\mathit{mm}}\left[i,j\right]$ and ${\mathit{C}}_{\mathit{mm}}\left[i,j\right]$ describes the possible correlations between the experimental measurements. The elements of the last column or the last row of the ${\mathit{C}}_{\mathit{dd}}$ are the same as those of the ${\mathit{C}}_{\mathit{kk}}$ matrix since no measurement is applicable for the application. If the experiments are independent, then the ${\mathit{C}}_{\mathit{mm}}$ matrix reduces to a diagonal matrix.

Similarly to before, consider the expressions in Eq. 11 using the Cholesky decomposition of ${\mathit{C}}_{\mathit{dd}}$ as:

${\mathit{C}}_{\mathit{dd}}={\mathit{D}}^T\mathit{D}$

where $\mathit{D}=\left[\begin{array}{cccc}{\delta }_1& {\delta }_2& \cdots & {\delta }_{M+1}\end{array}\right]$, where the inner-product of any of two columns of $\mathit{D}$ gives:

$7{\delta }_i^T{\delta }_j={\mathit{C}}_{\mathit{dd}}\left[i,j\right],i,j=\mathrm{1,2},\dots ,M+1$

Geometrically, the ACCRUE index j_k with a single experiment thus is defined as the cosine angle defined by two vectors of $\mathit{D}$, specifically one related to the application and the other to an experiment as:

$\begin{array}{c}{j}_k\left(d_j;d_{M+1}\right)=\frac{{\delta }_j^T{\delta }_{M+1}}{\sqrt{{\delta }_j^T{\delta }_j}\sqrt{{\delta }_{M+1}^T{\delta }_{M+1}}}=\frac{{\mathit{C}}_{\mathit{dd}}\left[j,M+1\right]}{\sqrt{{\mathit{C}}_{\mathit{dd}}\left[j,j\right]}\sqrt{{\mathit{C}}_{\mathit{dd}}\left[M+1,M+1\right]}}=\cos \theta \left({\delta }_j,{\delta }_{M+1}\right)\end{array}(12)$

Figure 4 graphically shows how the measurement uncertainty impacts on the j_k value with a single experiment (the jth experiment denoted by subscript “j”) as compared to the c_k value. Due to the measurement uncertainty, the cosine angles estimated by c_k and j_k respectively change from $\cos {\theta }_j$ to $\cos {\phi }_j$. If the associate measurement uncertainty of the given experiment is zero, the j_k value reduces to the c_k value. In any other cases where the measurement uncertainty of the given experiment is not zero, the cosine angle given by j_k is always smaller than that by c_k as illustrated, e.g., $\cos {\phi }_j<\cos {\theta }_j$ or ${\phi }_j>{\theta }_j$. This can be readily proved by comparing the analytical expressions for each c_k and j_k value shown in Eqs. 9, 12, respectively.

FIGURE 4

FIGURE 4. Impact of measurement uncertainty inclusion.

With regard to the matrix notations of both equations, ${\mathit{C}}_{\mathit{kk}}\left[j,M+1\right]$ and ${\mathit{C}}_{\mathit{dd}}\left[j,M+1\right]$, ${\mathit{C}}_{\mathit{kk}}\left[M+1,M+1\right]$ and ${\mathit{C}}_{\mathit{dd}}\left[M+1,M+1\right]$ are the same respectively since measurement is not applicable for the application, while ${\mathit{C}}_{\mathit{dd}}\left[j,j\right]$ is always greater than ${\mathit{C}}_{\mathit{kk}}\left[j,j\right]$ since ${\mathit{C}}_{\mathit{dd}}\left[j,j\right]={\mathit{C}}_{\mathit{kk}}\left[j,j\right]+{\mathit{C}}_{\mathit{mm}}\left[j,j\right]$. As a result, the cosine angle is reduced proportional to $\sqrt{{\mathit{C}}_{\mathit{kk}}\left[j,j\right]/{\mathit{C}}_{\mathit{dd}}\left[j,j\right]}$ with experimental measurement uncertainty present.

As discussed in Section 2.3, the covariance matrix, ${\mathit{C}}_{\mathit{mm}}$, can be written as:

${\mathit{C}}_{\mathit{mm}}=\mathit{L}{\mathit{L}}^{\mathit{T}}=\underset{N\to \infty }{\lim }\left(\mathit{L}\frac{1}{N}{\displaystyle \sum }_{i=1}^N{\zeta }^{\left(p\right)}{\zeta }^{\left(p\right)T}{\mathit{L}}^{\mathit{T}}\right)=\underset{N\to \infty }{\text{lim}}\left(\frac{1}{N}{\displaystyle \sum }_{p=1}^N\text{Δ}{m}^{\left(p\right)}\text{Δ}{m}^{\left(p\right)T}\right)$

where $\mathit{L}\in {\mathrm{ℝ}}^{M\times M}$ a low triangular matrix.

Then the measurement sample vector for jth experiment, $\text{Δ}{m}_j\in {\mathrm{ℝ}}^N$, is defined as:

$\text{Δ}{m}_j=\left[\begin{array}{c}\frac{m_j^{\left(1\right)}-m_j^{\left(ref\right)}}{m_j^{\left(ref\right)}}\\ \frac{m_j^{\left(2\right)}-m_j^{\left(ref\right)}}{m_j^{\left(ref\right)}}\\ ⋮\\ \frac{m_j^{\left(N\right)}-m_j^{\left(ref\right)}}{m_j^{\left(ref\right)}}\end{array}\right],j=\mathrm{1,2},\dots ,M$

Thus, the discrepancy sample vector for jth experiment, $\text{Δ}{d}_j\in {\mathrm{ℝ}}^N$, is:

$\text{Δ}{d}_j=\text{Δ}{k}_j-F_j\text{Δ}{m}_j$

where $F_j$ is a scalar quantity representing a ratio of experimental to calculated response values of jth experiment

$\underset{N\to \infty }{\lim }\text{Δ}{d}_i^T\text{Δ}{d}_j={\mathit{C}}_{\mathit{dd}}\left[i,j\right]$

Thus,

$j_k\left(d_j;d_{M+1}\right)=\underset{N\to \infty }{\lim }\frac{\text{Δ}{d}_j^{\text{T}}\text{Δ}{d}_{M+1}}{\sqrt{\text{Δ}{d}_j^T\text{Δ}{d}_j}\sqrt{\text{Δ}{d}_{M+1}^T\text{Δ}{d}_{M+1}}}$

3.2 Impact of Multiple Experiments

The ACCRUE index may be viewed as the similarity between a group of experiments and the application of interest when the experimental uncertainties are excluded from the analysis. Its true value however is in assessing the relevance of a new experiment by taking into account both the experiment’s measurement uncertainty and the value gleaned from past experiments. In this section, the detailed analytical derivation for j_k value with multiple experiments is provided with the $\delta$ vectors. However, if analysts are not interested in including the impact of measurement uncertainties, they can work directly with the $\gamma$ vectors instead of $\delta$ vectors.

Analytically, the j_k index for the first $L$ experiments is given using the elements of the ${\mathit{C}}_{\mathit{dd}}$ matrix in Eq. 11 by:

$\begin{array}{c}{j}_k=\sqrt{{\displaystyle \sum }_{i=1}^L\frac{{\left(E_{i,M+1}\right)}^2}{E_{i,i} D_{M+1,M+1}}}\end{array}(13)$

where the $E$ terms are defined by the following recurring relation:

$E_{1,j}=D_{1,j}$

$E_{i,j}=D_{i,j}-{\displaystyle \sum }_{k=1}^{i-1}\frac{E_{k,i}}{E_{k,k}}{E}_{k,j}$

These terms can be evaluated analytically given access to the sensitivity coefficients, the prior cross-section covariance matrix, and the measurement uncertainties. By way of an example, consider the simple case with $L=1$, i.e., a single experiment, where the j_k reduces to:

$\begin{array}{c}{j}_k\left(d_1;d_{M+1}\right)=\sqrt{\frac{{\left(D_{1,M+1}\right)}^2}{D_{\mathrm{1,1}} D_{M+1,M+1}}}=\frac{s_1{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_{M+1}^T}{\sqrt{s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_1+{\sigma }_{m_1}^2}\sqrt{s_{M+1}^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_{M+1}}}\end{array}(14)$

This expression equivalent to the c_k index assuming zero measurement uncertainty, i.e., ${\sigma }_{m_1}^2=0.0$. The implication is the j_k will always have a lower value than the corresponding c_k value for any realistic non-zero experimental uncertainties. With $L=2$, and assuming the measurement uncertainties are uncorrelated, i.e., ${\mathit{C}}_{\mathit{mm}}\left[\mathrm{1,2}\right]={\mathit{C}}_{\mathit{mm}}\left[\mathrm{2,1}\right]=0$, the j_k value becomes:

$j_k\left(d_1,d_2;d_{M+1}\right)=\sqrt{\frac{{\left(E_{1,M+1}\right)}^2}{E_{\mathrm{1,1}} D_{M+1,M+1}}+\frac{{\left(E_{2,M+1}\right)}^2}{E_{\mathrm{2,2}} D_{M+1,M+1}}}$

$=\sqrt{\frac{{\left(D_{1,M+1}\right)}^2}{D_{\mathrm{1,1}} D_{M+1,M+1}}+\frac{{\left(D_{2,M+1}-\frac{D_{\mathrm{1,2}}}{D_{\mathrm{1,1}}}{D}_{1,M+1}\right)}^2}{\left(D_{\mathrm{2,2}}-\frac{D_{\mathrm{1,2}}}{D_{\mathrm{1,1}}}{D}_{\mathrm{1,2}}\right) D_{M+1,M+1}}}$

$\begin{array}{c}=\sqrt{\frac{{\left(s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_a\right)}^2}{\left(s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_1+{\sigma }_{m_1}^2\right)\left(s_a^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_a\right)}+\frac{{\left(s_2^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_a-\frac{s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_2}{s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_1+{\sigma }_{m_1}^2}{s}_2^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_a\right)}^2}{\left(s_2^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_2+{\sigma }_{m_2}^2-\frac{s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_2}{s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_1+{\sigma }_{m_1}^2}{s}_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_2\right)s_a^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_a}}\end{array}(15)$

Eq. 15 shows that the relevance of two experiments may be expressed as the sum of two terms, one very similar to the c_k index representing the relevance of the first experiment, and the other subtracting away the impact of the first experiment. To help interpret the j_k index for $L$ experiments, we resort to the geometrical and statistical interpretations provided earlier in Section 3.1.

Consider the case with two experiments (denoted by the subscripts “1” and “2”, respectively) as illustrated in Figure 5, where j_k calculates the angle between the ${\delta }_{M+1}$ vector (representing the application) and the subspace formed by ${\delta }_1$ and ${\delta }_2$ (representing the two experiments). As long as the second experiment provides additional information which is not duplicated by the first experiment, the j_k value is expected to increase as compared to the value obtained with a single experiment, i.e., $j_k\left({\delta }_1,{\delta }_2;{\delta }_{M+1}\right)>j_k\left({\delta }_1;{\delta }_{M+1}\right)$ or ${\phi }_2<{\phi }_1$ as shown in Figure 5. In the case that the second experiment carries no additional information, e.g., the j_k value remains the same. The implication is that the second experiments provides no value to the GLLS inference procedure, and hence can be excluded.

FIGURE 5

FIGURE 5. Geometrical interpretation of j_k value with two experiments.

The cosine angle between any two subspaces can be calculated by orthogonal projection techniques, e.g., QR decomposition or Singular Value Decomposition (SVD). For example, consider the j_k value of the first $L$ experiments and the application, the corresponding $\delta$ vectors can be aggregated as:

${\mathit{D}}_L=\left[\begin{array}{cccc}{\delta }_1& {\delta }_2& \cdots & {\delta }_L\end{array}\right]$

Then, the associated j_k expression can be written as:

$j_k\left({\mathit{D}}_L;{\delta }_{M+1}\right)=\cos \theta \left({\mathit{D}}_L,{\delta }_{M+1}\right)=\cos \theta \left({\mathit{Q}}_{\mathit{L}},v\right)=\left|\left|{\mathit{Q}}_{\mathit{L}}^{\mathit{T}}v\right|\right|=\sqrt{{\left(q_1^{T}v\right)}^2+{\left(q_2^{T}v\right)}^2+\cdots {\left(q_L^{T}v\right)}^2}$

where $q_j \left(j=\mathrm{1,2},\dots ,L\right)$ is jth $q$ vector of the ${\mathit{Q}}_{\mathit{L}}$ matrix from QR decomposition and $v$ is a normalized ${\delta }_{M+1}$ vector for the application such as $v={\delta }_{M+1}/\left|\left|{\delta }_{M+1}\right|\right|$.

For example, consider the case where $D_1$ contains only ${\delta }_1$ vector corresponding to the first experiment, i.e., $D_1={\delta }_1$, then the j_k value is calculated as:

$j_k\left(D_1,{\delta }_{M+1}\right)=\sqrt{{\left(q_1^{T}v\right)}^2}$

where $q_1$ is a normalized directional vector of ${\delta }_1$:

$q_1=\frac{{\delta }_1}{\left|\left|{\delta }_1\right|\right|}$

Thus, the j_k value is

$j_k=\sqrt{\frac{{\left({\delta }_1^T{\delta }_{M+1}\right)}^2}{{\delta }_1^T{\delta }_1{\delta }_{M+1}^T{\delta }_{M+1}}}=\frac{{\delta }_1^T{\delta }_{M+1}}{\sqrt{{\delta }_1^T{\delta }_1}\sqrt{{\delta }_{M+1}^T{\delta }_{M+1}}}=\frac{s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_a}{\sqrt{s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_1+{\sigma }_{m_1}^2}\sqrt{s_a^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_a}}$

which is equivalent to Eq. 14

If ${\mathit{D}}_2$ contains two $\delta$ vectors (${\delta }_1$ and ${\delta }_2$) corresponding to the first two experiments, then the j_k value is calculated as:

$j_k\left({\mathit{D}}_2,{\delta }_{M+1}\right)=\sqrt{{\left(q_1^{T}v\right)}^2+{\left(q_2^{T}v\right)}^2}$

where $q_2$ is defined by Gram-Schmidt process such as:

$q_2=\frac{\left({\delta }_2-\frac{{\delta }_1^T{\delta }_2}{{\delta }_1^T{\delta }_1}{\delta }_1\right)}{\sqrt{{\delta }_2^T{\delta }_2\left(1-\frac{{\delta }_1^T{\delta }_2{\delta }_1^T{\delta }_2}{{\delta }_1^T{\delta }_1{\delta }_2^T{\delta }_2} \right)}}$

Thus, the j_k value is:

$j_k=\sqrt{\frac{{\left({\delta }_1^T{\delta }_{M+1}\right)}^2}{{\delta }_1^T{\delta }_1{\delta }_{M+1}^T{\delta }_{M+1}}+\frac{{\left({\delta }_2{\gamma }_a-\frac{{\delta }_1^T{\delta }_2}{{\delta }_1^T{\delta }_1}{\delta }_1{\delta }_{M+1}\right)}^2}{\left({\delta }_2^T{\delta }_2-{\delta }_2^T{\delta }_1\frac{{\delta }_1^T{\delta }_2}{{\delta }_1^T{\delta }_1}\right){\delta }_{M+1}^T{\delta }_{M+1}}}$

$=\sqrt{\frac{{\left(s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_a\right)}^2}{\left(s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_1+{\sigma }_{m_1}^2\right)\left(s_a^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_a\right)}+\frac{{\left(s_2^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_a-s_2^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_a\frac{s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_2}{s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_1+{\sigma }_{m_1}^2}\right)}^2}{\left(s_2^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_2+{\sigma }_{m_2}^2-s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_2\frac{s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_2}{s_1^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_1+{\sigma }_{m_1}^2}\right)s_a^T{\mathit{C}}_{\mathit{\alpha \alpha }}{s}_a}}$

which is equivalent to Eq. 15

Consequently, the general expression for j_k value can be written as:

$j_k=\sqrt{{\displaystyle \sum }_{i=1}^L\frac{{\left(u_i^T{\delta }_{M+1}\right)}^2}{u_i^T{u}_i {\delta }_{M+1}^T{\delta }_{M+1}}}$

where

$u_1={\delta }_1$

$u_i={\delta }_i-{\displaystyle \sum }_{k=1}^{i-1}\frac{u_k^T{\delta }_i}{u_k^T{u}_k}{u}_k, i=\mathrm{2,3},\dots ,L$

which evaluates the same scalar quantity as that calculated by the matrix element notations in earlier this section.

3.3 Overall Process

Figure 6 shows the overall process for evaluating the similarity or relevance of an experiment to a given application. The similarity accounts for the correlation between two responses, e.g., one from the application and the other from the experiment, as calculated by a computer code. The ACCRUE index extends the concept of similarity to quantify the relevance, as measured by the added value of the experiment, taking into account both the experiment’s measurement uncertainties as well as past experiments. As shown in this figure, the first step is to check if an adjoint solver is available which allows one to employ sensitivity coefficients. If no experimental measurement uncertainty is available and only a single experiment is available, the ACCRUE index j_k reduces to the similarity index c_k. If the experimental uncertainty is available, Eq. 12 is employed to evaluate the j_k index. If additional experiments are available, then the most general expression for j_k is employed per Eq. 13.

FIGURE 6

FIGURE 6. Approach for evaluating experimental relevance.

4 Numerical Experiments

Numerical experiments have been conducted with two different case studies. The first case study assumes that the applications have low c_k values for all available experiments which are in the order of 0.7, referred to as the low relevance applications, and the second case study considers applications with high c_k values that are greater than 0.9. An application with low relevant experiments represents a realistic scenario expected with first-of-a-kind designs, i.e., advanced reactor designs and new fuel concepts, with no prior or rare strongly relevant experiments. It also highlights the expected high cost of new experiments, and the need to employ modeling and simulation to design a minimal number of targeted validation experiments. When the c_k values are low for the given application, it is important to figure out a way to prioritize the selection of past available experiments, as well as judge the value of new/planned experiments. We compare the performance of the j_k and c_k indices for both the high relevance and low relevance applications for a range of assumed values for the experimental uncertainties. This is also important when designing new experiments, as it provides quantitative value for different types of instrumentations with varying levels of measurement uncertainties.

The low relevance case study employs 17 critical benchmark experiments from the low enriched uranium thermal compound systems (LCT-008-001—LCT-008-017) in the ICSBEP handbook (NEA, 2011) as experiments and the accident-tolerant fuel (ATF) concept BWR assembly as an application. The selected LCT benchmark experiment set (LCT-008) cases are critical lattices with UO₂ fuel rods of 2.9% enrichment and perturbing rods in borated water in common, but have different boron concentrations and various rods arrangements. Their similarity indices, c_k, to the BWR ATF model are all around 0.7 as reported by TSUNAMI-IP. The BWR ATF model is a $10\times 10$ GE14 dominant lattice with UO₂ fuel and FeCrAl cladding. This model comprises 92 UO₂ fuel pins, 78 out of which are fuel with various enrichments from 2 to 4% and the remaining are 14 rods with gadolinium, surrounded by water coolant in a channel box structure (Jessee, 2020). The layouts of a representative LCT benchmark experiment (LCT-008-001) and the application model are shown in Figure 7. The high relevance case study employs 42 critical experiments from highly enriched uranium fast metal systems (HMF set, short for HEU-MET-FAST) in ICSBEP handbook. In this study, application models are selected among these benchmark experiments and similarity indices are in the 0.9 range (NEA, 2011). All the critical benchmarks employ highly enriched uranium fuel with a variety of design configurations and different enrichments. Figure 8 shows two representative benchmark experiments one of which is used as an experiment (HMF-020-001, Polyethylene-reflected spherical assembly of ²³⁵U) and the other as an application (HMF-019-001, Graphite-reflected spherical assembly of ²³⁵U).

FIGURE 7

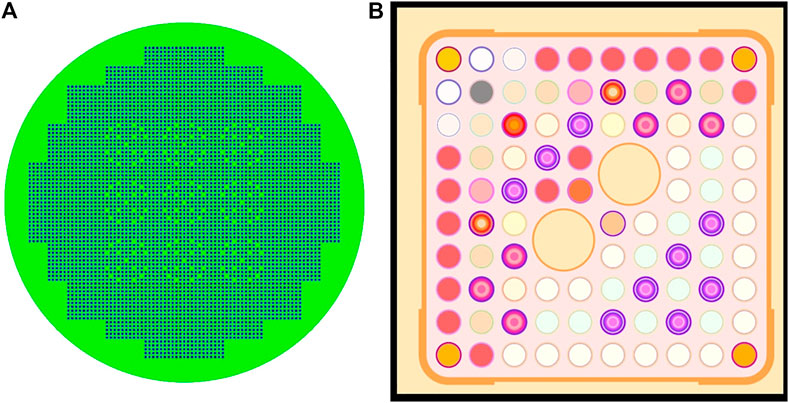
FIGURE 7. Low-relevant case layouts of the representative models. (A) Experiment model: LCT-008-001 (B) Application model: ATF assembly.

FIGURE 8

FIGURE 8. High-relevant case layouts of the representative models. (A) Experiment model: HMF-020-001 (B) Application model: HMF-019-001.

To identify the possible impact of initial discrepancies, i.e., differences between calculated and measured responses, on the GLLS-estimated biases, three critical experiments having different biases (high, intermediate, and low) are selected as applications and the remaining experiments are used as validation experiments. The high bias application is selected to have an initial k_eff discrepancy in the order of 1,000 pcm, while the intermediate in the order of 300–500 pcm, and the low 200 pcm.

4.1 Comparison of j_k vs. c_k-Sorting

Figure 9 shows representative results for the high relevance case study for three different applications with high, intermediate, and low biases. The x-axis explores the change in the GLLS-estimated biases when adding one experiment at a time, wherein the experiments are ordered according to their c_k values (top graphs), and j_k values (bottom graphs). The c_k-sorting is straightforward as each experiment is employed once in conjunction with the given application. Markedly different, the j_k value depends on the number and order of experiments included, hence each sorting is expected to give rise to different profiles for j_k and the associated bias and bias uncertainty. The goal is thus to identify the order that allows the analyst to reach a certain level of confidence in the calculated bias with minimal number of experiments. In the current study, the search for this optimal order is initiated with the experiment having the highest c_k value, with the second experiment selected to maximize the j_k value among all remaining experiments, and so on. In practice, one may start with any experiment, and adds experiments as they become available, or may employ the j_k value to quantify the value of new/planned experiments. For each added experiment, the GLLS bias and bias uncertainty are calculated to help compare the c_k and j_k-sorting. The goal is to achieve a stable prediction of the bias with minimal uncertainty.

FIGURE 9

FIGURE 9. Bias and uncertainty estimation for high relevance case.

These results show that the bias stabilizes quicker with the j_k sorting. More important, the c_k-sorting could show sudden changes after a period of stable behavior. For all considered applications using the c_k-sorting, the biases continue to experience sudden or gradual changes following a period of stable behavior. For example, for the low bias application, the estimated bias exhibits an upward trend after the 20th experiment. The implication is that the additional experiments continue to provide value to the GLLS procedure despite their lower relevance. With the j_k-sorting, a more explainable trend is achieved whereby the bias trend shows stable behavior after the 20th experiment.

Regarding the bias uncertainties, shown in Figure 9 as error bars, they are plotted in Figures 10, 11 as a function of the number of experiments using both the c_k and j_k-sorting for, respectively, one application with high relevance experiments and one application with low relevance experiments. The results highlight a key limitation of the c_k-sorting, that is the addition of low relevance experiments could change the trend of both the bias and the bias uncertainty. The j_k-sorting however does not suffer from this limitation, implying that one can select the minimal number of experiments required to reach a certain pre-determined level of confidence for the calculated bias. Comparison of the uncertainty values in both figures indicate that the impact is much less pronounced when highly relevant experiments are available. This highlights the value of the j_k-sorting when limited number of experiments are available, as is the case with first-of-a-kind designs.

FIGURE 10

FIGURE 10. Bias uncertainty reduction for a low relevance application.

FIGURE 11

FIGURE 11. Bias uncertainty reduction for a high relevance application.

These results are compared in Figure 12 with randomized orders (shown as multi-color solid lines) for one of the low relevance applications at different levels of measurement uncertainty, specifically 10 pcm (representing a highly accurate measurement), 100 pcm (a realistic measurement), and 500 pcm (a low confidence measurement) for the measured k_eff values. The results show that pure random sampling could be superior to c_k-sorting, with the j_k sorting still exhibiting the best behavior in terms of reducing the bias uncertainty with minimal number of experiments. When the measurement uncertainty is too high, the ordering of the experiments is no longer important. This is a key observation highlighting the value of ordering experiments as experimentalists continue to improve their measurements in support of model validation.

FIGURE 12

FIGURE 12. Bias uncertainty reduction with random orders.

To help understand the changes in the bias and bias uncertainty associated with the c_k-sorting, the left plot in Figure 13 orders the experiments according to their c_k values, and the middle plot calculates the corresponding j_k values using the c_k-sorting. Notice that although the first few experiments, i.e., #15, #13, #12, …, to #4 have higher relevance than later experiments, they do not change the j_k value, and hence the bias and bias uncertainty as shown in the earlier figures. The j_k values start to show larger increase when additional lower relevance experiments are added, explaining the sudden or gradual change in the bias and its uncertainty. However, when the experiments are ordered according to their j_k values, as shown in the right plot, a smoother j_k profile is obtained which is consistent with the bias and bias uncertainty profiles obtained using the GLLS procedure. The implication is that one can employ the j_k profile to develop insight into the amount of experimental effort necessary to reach a target confidence in the calculated bias, even before the actual measurements are recorded. This follows because j_k only requires access to the prior uncertainties and the expected measurement uncertainty, not the actual measured bias.

FIGURE 13

FIGURE 13. Comparison of the c_k and j_k profiles.

4.2 Stochastic Non-Intrusive Verification

As mentioned earlier, the analytical expressions for the similarity or relevance metrics such as c_k and j_k require access to derivatives which may not be readily available. To address this challenge, earlier work has developed an alternative to the estimation of c_k value using a non-intrusive forward-based stochastic method (Huang et al., 2020). In this section, we present numerical results comparing the results of the analytically-calculated j_k value to that estimated by the noted stochastic method. This will serve two purposes: the first is to provide a simple approach for the calculation of the j_k value when derivatives are unavailable, and the second to help verify the calculated j_k value using the stochastic method by comparing it to the analytically-calculated value. To achieve that, two benchmark experiments (HMF-005-001 and 005-002) are selected to calculate the j_k value. Their calculated response uncertainties are 1,492 pcm and 1721 pcm respectively, and measurement uncertainties are 360 pcm. A total of 1,000 samples are generated to examine the convergence of forward-based j_k value, whose corresponding analytical value is 0.9445 as given by Eq. 15, shown in Figure 14 as a horizontal line. The results indicate that the forward-based approach produces acceptable approximation of the analytical value using few hundred simulations, which is consistent with the results reported previously for the c_k value (Huang et al., 2020).

FIGURE 14

FIGURE 14. Non-intrusive stochastic estimation of j_k.

5 Conclusion and Further Research

This manuscript has introduced an extension of the basic similarity metric, denoted by the ACCRUE metric and mathematically symbolized by the j_k index to distinguish it from the c_k similarity metric. The ACCRUE metric takes into account the impact of multiple experiments and the associated experimental uncertainties, both currently missing from the extant similarity definition. The results show that the ACCRUE metric is capable of finding the optimal sorting of the experiments, the one that leads to the most stable variation in the GLLS calculated bias and bias uncertainty. When the experiments available are highly relevant and numerous, the performance of the c_k metric approaches that of the j_k metric. However, when highly-relevant experiments are scarce and when experimental uncertainties are low, the j_k metric is capable of identifying the minimal number of experiments required to reach a certain confidence for the calculated bias, whereas the c_k metric may be outperformed by random sorting of the experiments. The results of this work are expected to be valuable to the validation of computer models for first-of-a-kind designs where little or rare experimental data exist. Another important value for the j_k metric is that it can be calculated using forward samples of the model responses, thereby precluding the need for derivatives, which allows one to extend the concept to non-k_eff responses. This will allow one to extend its definition to models exhibiting nonlinear behavior often resulting from multi-physics coupling, e.g., different geometry, compositions, and types of reactor. This will pave the way to the development of relevance metrics that goes beyond the first-order variations currently captured by the extant similarity analysis.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

JS: Writing the original draft, methodology, investigation, visualization. HA-K: Conceptualization, methodology, writing/editing, supervision. AE: Supervision, review/editing.

Funding

This work was supported in part by an Idaho National Laboratory project (Grant no. 74000576).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to acknowledge Dr. Ugur Mertyurek of Oak Ridge National Laboratory for providing the models used in this study.

Footnotes

¹In theory the GLLS can incorporate any experimental data regardless of their relevance to the application conditions. In practice however, one limits the analysis to the most relevant experiments for various practical considerations. For example, inclusion of many weakly-relevant experiments may adversely impact the χ² value making it difficult to interpret the GLLS results.

²Other empirical forms for the similarity index have been proposed, but are not covered here. (Broadhead et al., 2004). Examples include the use of the absolute difference in the sensitivity coefficients, D, and the inner products of two sensitivity profiles, E, etc.

³In this hypothetical scenario, the minimum uncertainty would be controlled by the measurement uncertainty and other administrative uncertainties that are typically added for unaccounted sources of uncertainties.

⁴The development here will be limited to the GLLS methodology; it is thus implicitly assumed that the GLLS assumptions are satisfied, i.e., Gaussianity of the cross-section prior uncertainty and linearity of the response variation with cross-section perturbations.

⁵Other dependencies for the two operators, such as geometry, composition, etc., are suppressed in the current discussion, since GLLS focuses only on the epistemic uncertainties associated with nuclear cross-sections.

⁶The subscript j (denoting the jth experiment) will be suppressed for other quantities in Eqs. 2, 3 to reduce notational clutter, and because they do not contribute to the discussion.

References

Abdel-Khalik, H. S., Bang, Y., and Wang, C. (2013). Overview of Hybrid Subspace Methods for Uncertainty Quantification, Sensitivity Analysis. Ann. Nucl. Energ. 52, 28–46. doi:10.1016/j.anucene.2012.07.020

CrossRef Full Text | Google Scholar

Avramova, M. N., and Ivanov, K. N. (2010). Verification, Validation and Uncertainty Quantification in Multi-Physics Modeling for Nuclear Reactor Design and Safety Analysis. Prog. Nucl. Energ. 52, 601–614. doi:10.1016/j.pnucene.2010.03.009

CrossRef Full Text | Google Scholar

Becker, M., Henley, E. J., and Oshima, K. (1982). Advances in Nuclear Science and Technology.

Google Scholar

Broadhead, B. L., Rearden, B. T., Hopper, C. M., Wagschal, J. J., and Parks, C. V. (2004). Sensitivity- and Uncertainty-Based Criticality Safety Validation Techniques. Nucl. Sci. Eng. 146, 340–366. doi:10.13182/NSE03-2

CrossRef Full Text | Google Scholar

Cacuci, D. G., and Ionescu-Bujor, M. (2010). Best-Estimate Model Calibration and Prediction through Experimental Data Assimilation-I: Mathematical Framework. Nucl. Sci. Eng. 165, 18–44. doi:10.13182/NSE09-37B

CrossRef Full Text | Google Scholar

Gandini, A. (1967). A Generalized Perturbation Method for Bi-linear Functionals of the Real and Adjoint Neutron Fluxes. J. Nucl. Energ. 21, 755–765. doi:10.1016/0022-3107(67)90086-X

CrossRef Full Text | Google Scholar

Glaeser, H. (20082008). GRS Method for Uncertainty and Sensitivity Evaluation of Code Results and Applications. Sci. Tech. Nucl. Installations 2008, 1–7. doi:10.1155/2008/798901

CrossRef Full Text | Google Scholar

Huang, D., Mertyurek, U., and Abdel-Khalik, H. (2020). Verification of the Sensitivity and Uncertainty-Based Criticality Safety Validation Techniques: ORNL's SCALE Case Study. Nucl. Eng. Des. 361, 110571. doi:10.1016/j.nucengdes.2020.110571

CrossRef Full Text | Google Scholar

Jessee, M. (2020). SCALE Lattice Physics Code Assessments of Accident-Tolerant Fuel.

Google Scholar

Lucius, J. L., Weisbin, C. R., Marable, J. H., Drischler, J. D., Wright, R. Q., and White, J. E. (1981). Users Manual for the FORSS Sensitivity and Uncertainty Analysis Code System. Oak Ridge, TN. doi:10.2172/6735933

CrossRef Full Text | Google Scholar

NEA (2011). International Handbook of Evaluated Criticality Safety Benchmark Experiments 2015.

Google Scholar

Oblow, E. M. (1976). Sensitivity Theory from a Differential Viewpoint. Nucl. Sci. Eng. 59, 187–189. doi:10.13182/nse76-a15688

CrossRef Full Text | Google Scholar

Palmiotti, G., and Salvatores, M. (20122012). Developments in Sensitivity Methodologies and the Validation of Reactor Physics Calculations. Sci. Tech. Nucl. Installations 2012, 1–14. doi:10.1155/2012/529623

CrossRef Full Text | Google Scholar

Rearden, B. T., and Jessee, M. A. (2016). TSUNAMI Utility Modules. Ornl/Tm-2005/39.

Google Scholar

Rimpault, G., Plisson, D., Tommasi, J., Jacqmin, R., Rieunier, J-M., Verrier, D., et al. (2002). The ERANOS Code and Data System for Fast Reactor Neutronic Analysis.

Google Scholar

Salvatores, M. (1973). Adjustment of Multigroup Neutron Cross Sections by a Correlation Method. Nucl. Sci. Eng. 50, 345–353. doi:10.13182/nse73-a26569

CrossRef Full Text | Google Scholar

Stacey, W. B. (1974). Variational Methods in Nuclear Reactor Physics. Academic Press. doi:10.1016/b978-0-12-662060-3.x5001-2

CrossRef Full Text | Google Scholar

Stark, H., and Woods, J. W. (2012). Probability, Statistics, and Random Processes for Engineers. Fourth Edition4th editio. Upper Saddle River: Pearson.

Google Scholar

Usachev, L. N. (1964). Perturbation Theory for the Breeding Ratio and for Other Number Ratios Pertaining to Various Reactor Processes. J. Nucl. Energ. Parts A/B. Reactor Sci. Tech. 18, 571–583. doi:10.1016/0368-3230(64)90142-9

CrossRef Full Text | Google Scholar

Wieselquist, W. A., 2016. SAMPLER: A Module for Statistical Uncertainty Analysis with SCALE Sequences, 6.2.3. ed. Ornl/Tm-2005/39.

Google Scholar

Williams, M. L., Broadhead, B. L., Jessee, M. A., Wagschal, J. J., and Lefebvre, R. A., 2016. TSURFER: An Adjustment Code to Determine Biases and Uncertainties in Nuclear System Responses by Consolidating Differential Data and Benchmark Integral Experiments, 6.2.3. ed.

Google Scholar