Abstract
In this paper, the stability of load frequency control (LFC) for delayed power systems with an electric vehicle (EV) aggregator is studied based on Lyapunov theory and linear matrix inequalities (LMIs). Through mechanism analysis, the LFC of power systems with an EV aggregator based on a proportional–integral–differential (PID) controller is modeled. By constructing a delay interval information correlation functional and estimating its derivative using Wirtinger inequality and extended reciprocally convex matrix inequality, a new stability analysis criterion is proposed. Finally, in order to verify its advantage, the proposed method is used to discuss the influence of EV aggregator gains and PID controller gains on the delay margins for LFC of power systems with EV aggregator participation in frequency regulation.
1 Introduction
Under the guidance of sustainable development concept, the generation of renewable energy sources (RESs) such as wind power, hydropower, and photovoltaic power has developed rapidly in recent years, and part of traditional thermal power generation will be gradually replaced (). However, the grid connection of these RESs also brings some problems, especially the wind power generation with great intermittency and volatility (; ). These problems aggravate the imbalance between generation and load consumption in the power systems, resulting in obvious frequency fluctuation. Therefore, load frequency control (LFC) is widely used in power systems (; ). The frequency deviation caused by an intermittent energy grid connection is difficult to be eliminated by traditional generator sets. With the grid connection of controllable loads such as electric vehicles (EVs) and the rapid response characteristics of batteries, some studies paid attention to vehicle-to-grid technology, which provides frequency regulation services with a large number of converging EVs (; ; ; ).
In traditional power systems, the time delay phenomenon of the LFC system is not obvious. However, modern power systems tend to use flexible and open communication networks for information exchange (). For power systems with EVs and intermittent wind power connected, the EV aggregator needs to transmit the control command to the EVs through open communication networks (; ). The use of such networks will inevitably bring unreliable factors, such as time delay, packet loss, and potential failure, which may lead to instability of LFC for power systems (; ). Therefore, it is very important to analyze the influence of time delays on the LFC of power systems with an EV aggregator. In addition, in order to ensure the stability of power system LFC, it is necessary to calculate the delay margins and determine all parameters of the proportional–integral–differential (PID) controller (; ).
In recent years, EVs have been widely used in power systems, and there are also some studies on the influence of time delays and EV aggregator on LFC stability. The Rekasius substitution method is used to determine the stability delay margins of LFC with constant communication delays for an EV aggregator (). Then, Naveed et al. presented a graphical method to describe the trajectory of the stable boundary and studied the influence of EV aggregators with communication delays on the stability regions and stability delay margins of the LFC system (). Based on Lyapunov theory and linear matrix inequalities (LMIs), stability criteria for time-varying delays using the Wirtinger-based improved integral inequality are proposed to calculate the delay margins for LFC with EVs, and the relationship between the gains and the delay margins of the PI controller is given in detail (). Two stability criteria are derived, respectively, using Bessel–Legendre inequality and model reconstruction technique, and the interregional delay interaction and the effect of EV gain on the delay margins are discussed (). Khalil et al. proposed a microgrid model of photovoltaic power generation and EVs considering communication delay, and the maximum allowable delay bound for the stable operation of microgrids is calculated by solving the LMIs (). Dong et al. characterized the asymptotic stability of EV aggregation delays by using the delay distortion matrix structure of infinite operator dimension reduction and proved that convergence delay affects frequency stability in the form of low-frequency oscillation through three unstable modes (). Although there have been some studies on the stability of delayed LFC systems with an EV aggregator, there are few studies on LFC of renewable energy power systems with an EV aggregator. Also, how to obtain more accurate delay margins remains a challenge.
In this paper, the stability of LFC for power systems with EV aggregator participation in frequency regulation is considered, and the influence of EV aggregator and controller gains on the delay margins is studied. Firstly, based on the PID controller, the LFC of power systems with an EV aggregator is modeled. Then, a new delay stability criterion using Wirtinger inequality and extended reciprocally convex matrix inequalities is proposed. Finally, according to the proposed stability criterion, the delay margins of LFC for power systems with an EV aggregator are obtained, and case studies are performed to show the advantage of the proposed method.
2 Model of LFC for Power System With EV Aggregator
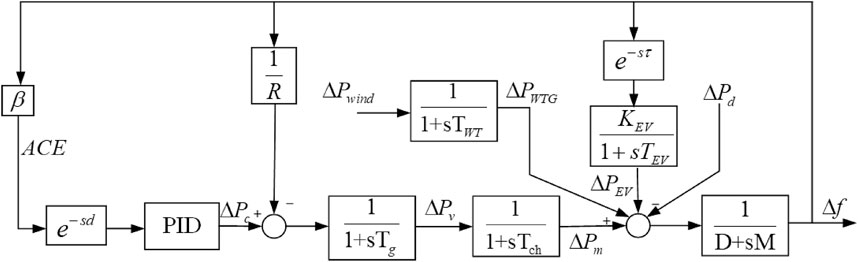
The block diagram of the LFC for power systems with an EV aggregator is given in Figure 1, and the controller is the PID controller. e−sτ and e−sd denote the time delay of the frequency regulation circuit involved in the EV aggregator and the secondary frequency regulation circuit, respectively; KEV is the gain of the EV aggregator; Δf, ΔPEV, ΔPWTG, ΔPm, ΔPv, and ΔPd are the deviation of frequency, EV aggregator power output, wind turbine generator (WTG) power output, mechanical output of the generator, valve position, and load disturbance, respectively. Definitions of other related symbols in the figure are shown in Table 1.
FIGURE 1
TABLE 1
| Parameter | Value | Description |
|---|---|---|
| M | 10 | Inertia constant |
| D | 1 | Generator damping coefficient |
| Tg | 0.1 | Time constant of the governor |
| Tch | 0.3 | Time constant of the turbine |
| TWTG | 1.5 | Time constant of the wind turbine generator |
| TEV | 0.1 | Time constant of the battery |
| R | 0.05 | Speed regulation |
| β | 21 | Frequency bias factor |
Parameter of the LFC model.
Select the following state variables, output variables, disturbance, and control input:
Then, the following system state space model can be obtained:where
The controller is designed as
Define the new vectors , and K = [KpKiKd]. The system (Eq. 5) is rewritten aswhere , , , , , and .
In order to simplify the analysis, it is assumed that the delay τ(t) of the frequency regulation circuit involved in the EV aggregator is consistent with the delay d(t) of the secondary frequency regulation circuit. Then, the closed-loop state space equation of LFC for the delayed power system with an EV aggregator can be obtained as follows:where A = A1, Ad = A2 – BKC, and Fw = F − BKD.
3 Delay-Dependent Stability Analysis
When discussing the internal stability of the power system, the influence of external disturbance can be ignored. The model of LFC for the delayed power system with an EV aggregator is obtained as follows:where h1 ≤ d(t) ≤ h2 and ∀t > t0.
The following stability criterion for system (Eq. 9) is derived by using Wirtinger inequality () and extended reciprocally convex matrix inequality ().
For given scalars α > 0, h2 > h1 > 0, the LFC of the closed-loop power system with an EV aggregator (Eq. 9) is exponentially stable, if there exist matrices P > 0, Qi > 0, Z > 0, R > 0, i = 1, 2, and any matrix S1 or S2 with appropriate dimension, satisfyingwhere
h12 = h2 − h1, es = Ae1 + Ade3.
Proof: Construct the following Lyapunov–Krasovskii functional:where .
Calculating the derivative of V(t), we get
where
Based on Wirtinger inequality, we havewhere
Using extended reciprocally convex matrix inequality to estimate Eq. 15 yieldswhere
Then, we can get
Applying Eq. 14 and Eq. 17 to Eq. 13, the following holds:
By using the Schur complement, Eqs 10, 11 are equal to the following inequalities:which implies
Thus, it follows from Eq. 21 that , which further leads to
Noting that V(t) ≥ ρ‖x(t)‖2, , ρ > 0, and β > 0, we havewhich implies the system (Eq. 9) is exponentially stable ().
According to the above, system (Eq. 9) is exponentially stable if Eqs 10, 11 hold. The proof is completed.
Remark 1The method proposed in this section establishes the constraint relation between the delay information and the exponential stability of the LFC for power systems with an EV aggregator, which can be used to analyze the influence of delays on the stability of the system and calculate the delay margins. The margins represent the time delay tolerance range of the system to ensure exponential stability, which is composed of the delay lower bound h1 and delay upper bound h2.
Remark 2
In
Theorem 1, the LFC for power systems with an EV aggregator is exponentially stable if
Eqs 10,
11are satisfied. The calculation steps of the delay margins for the stability of the system can be briefly summarized as follows:
1) Construct the LFC closed-loop model for power systems with an EV aggregator and a PID controller.
2) Choose the values of α, the EV aggregator gain KEV, and the allowable lower bound h1.
3) Calculate the delay margin h2 of the power system by using the binary search technique () and MATLAB/LMI toolbox to solve the LMIs in Theorem 1.
4 Case Studies
Case studies of LFC for power systems with an EV aggregator are presented to verify the advantage of the proposed method and study the influence of PID controller and EV aggregator gains on the delay margins. The related parameters of the system are shown in Table 1.
4.1 Comparison With the Existing Research
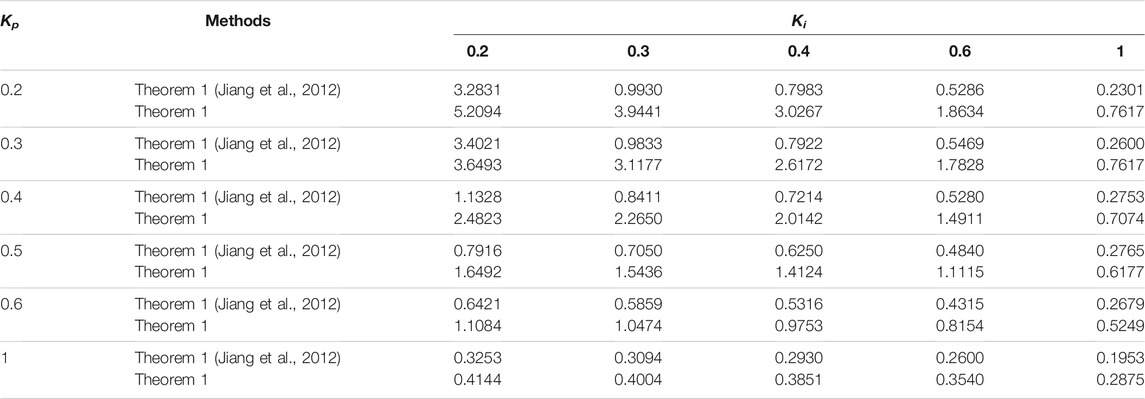
The method proposed by ) is used to verify the advantage of the proposed method. Set h1 = 0, α = 0, Kd = 0, and kEV = 1, and the system can be considered asymptotically stable if the conditions in Theorem 1 are true. Then, the delay margins of the method proposed in this paper are compared with the delay margins of time-varying delay (μ = 0.9) in the study of ). It is clear from Table 2 that the results of the proposed method are less conservative.
TABLE 2
| Kp | Methods | Ki | ||||
|---|---|---|---|---|---|---|
| 0.2 | 0.3 | 0.4 | 0.6 | 1 | ||
| 0.2 | Theorem 1 () | 3.2831 | 0.9930 | 0.7983 | 0.5286 | 0.2301 |
| Theorem 1 | 5.2094 | 3.9441 | 3.0267 | 1.8634 | 0.7617 | |
| 0.3 | Theorem 1 () | 3.4021 | 0.9833 | 0.7922 | 0.5469 | 0.2600 |
| Theorem 1 | 3.6493 | 3.1177 | 2.6172 | 1.7828 | 0.7617 | |
| 0.4 | Theorem 1 () | 1.1328 | 0.8411 | 0.7214 | 0.5280 | 0.2753 |
| Theorem 1 | 2.4823 | 2.2650 | 2.0142 | 1.4911 | 0.7074 | |
| 0.5 | Theorem 1 () | 0.7916 | 0.7050 | 0.6250 | 0.4840 | 0.2765 |
| Theorem 1 | 1.6492 | 1.5436 | 1.4124 | 1.1115 | 0.6177 | |
| 0.6 | Theorem 1 () | 0.6421 | 0.5859 | 0.5316 | 0.4315 | 0.2679 |
| Theorem 1 | 1.1084 | 1.0474 | 0.9753 | 0.8154 | 0.5249 | |
| 1 | Theorem 1 () | 0.3253 | 0.3094 | 0.2930 | 0.2600 | 0.1953 |
| Theorem 1 | 0.4144 | 0.4004 | 0.3851 | 0.3540 | 0.2875 | |
Delay margins for different methods.
4.2 Effect of PID Controller and EV Aggregator Gains
The gains of the PID controller and EV aggregator have an important effect on the delay margins of the LFC for power systems with an EV aggregator. Firstly, let h1 = 0, α = 0.01, kEV = 1, and PID controller parameters K be different; the delay margins of the system are obtained, and the related results are shown in Tables 3–5.
TABLE 3
| Kp − Ki | 0.05 | 0.1 | 0.15 | 0.2 | 0.3 | 0.4 |
|---|---|---|---|---|---|---|
| 0.1 | 15.8185 | 11.2262 | 8.2007 | 6.2970 | 4.1388 | 2.9816 |
| 0.2 | 7.3389 | 6.7004 | 5.9119 | 5.1477 | 3.9001 | 2.9550 |
| 0.3 | 4.1736 | 4.0625 | 3.8623 | 3.6151 | 3.0890 | 2.5940 |
| 0.4 | 2.6349 | 2.5977 | 2.5397 | 2.4573 | 2.2430 | 1.9946 |
| 0.6 | 1.1597 | 1.1414 | 1.1194 | 1.0938 | 1.0333 | 0.9625 |
Delay margins for Kd = 0.
TABLE 4
| Kp − Ki | 0.05 | 0.1 | 0.15 | 0.2 | 0.3 | 0.4 |
|---|---|---|---|---|---|---|
| 0.1 | 1.5466 | 1.5955 | 1.6443 | 1.6943 | 1.7902 | 1.8616 |
| 0.2 | 1.4648 | 1.5125 | 1.5607 | 1.6101 | 1.7096 | 1.7920 |
| 0.3 | 1.3391 | 1.3818 | 1.4258 | 1.4722 | 1.5674 | 1.6571 |
| 0.4 | 1.1835 | 1.2177 | 1.2537 | 1.2915 | 1.3721 | 1.4563 |
| 0.6 | 0.8734 | 0.8887 | 0.9039 | 0.9198 | 0.9540 | 0.9900 |
Delay margins for Kd = 0.2.
TABLE 5
| Kp − Ki | 0.05 | 0.1 | 0.15 | 0.2 | 0.3 | 0.4 |
|---|---|---|---|---|---|---|
| 0.1 | 0.4761 | 0.4785 | 0.4810 | 0.4834 | 0.4889 | 0.4944 |
| 0.2 | 0.4663 | 0.4688 | 0.4712 | 0.4736 | 0.4791 | 0.4840 |
| 0.3 | 0.4559 | 0.4578 | 0.4602 | 0.4626 | 0.4675 | 0.4730 |
| 0.4 | 0.4443 | 0.4462 | 0.4486 | 0.4510 | 0.4553 | 0.4602 |
| 0.6 | 0.4193 | 0.4211 | 0.4230 | 0.4248 | 0.4285 | 0.4327 |
Delay margins for Kd = 0.5.
As shown in Table 3, when Kd = 0 (PI controllers), for fixed Kp, the delay margins decrease gradually with the increase of Ki. For fixed Ki, with the increase of Kp, the delay margins decrease gradually. As can be seen from Tables 3–5, when Kd is not 0 (PID controllers), the delay margins gradually become smaller with the gradual increase of Kd. For fixed Kp, the delay margins increase gradually with the increase of Ki; for fixed Ki, the delay margins decrease as Kp increases. To sum up, the delay margins under PI controllers are larger than that under the PID controller. The larger Kp or Kd is, the smaller delay margins are.
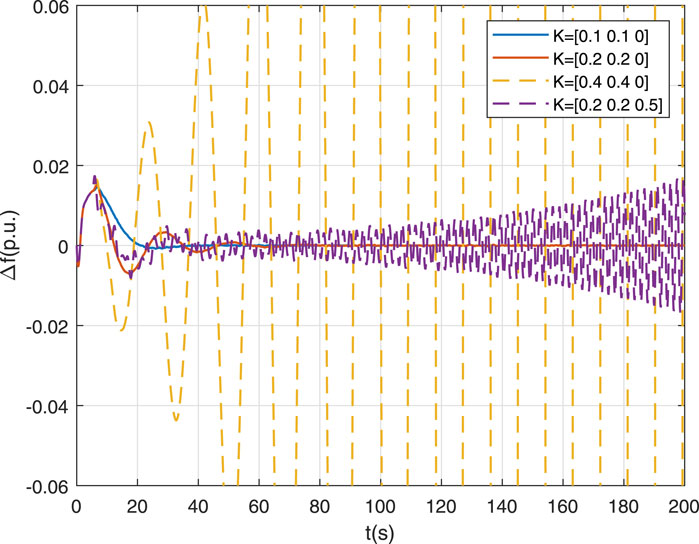
Then, the frequency deviations of LFC for power systems with an EV aggregator under the delay of 5.15s and different PID controller gains are simulated. It is assumed that the power deviations of load and WTG fluctuate randomly in the range of 0.19–0.21 p. u. and 0.49–0.51 p. u., respectively. As shown in Figure 2, when K = [0.2 0.2 0], the system is stable. When Kp and Ki decrease (K = [0.1 0.1 0]), the frequency deviation also tends to zero. But when Kp and Ki are increased (K = [0.4 0.4 0]), or Kd is increased (K = [0.2 0.2 0.5]), it is clear that the frequency deviations do not converge in these cases. Therefore, Figure 2 validates the analysis in Tables 3–5, and appropriate selection of PID controller gains K is very important for the stability of LFC for power systems with an EV aggregator.
FIGURE 2
Finally, the gain of the EV aggregator KEV is also an important factor affecting the delay margins of LFC for power systems with an EV aggregator. As shown in Table 6, regardless of how the gains of the PID controller change, the delay margins of the delayed LFC system with an EV aggregator and intermittent wind energy decrease with the increase of KEV.
TABLE 6
| KEV − K | [0.1 0.05 0] | [0.1 0.1 0] | [0.1 0.1 0.2] | [0.2 0.2 0.2] |
|---|---|---|---|---|
| 1 | 15.8185 | 11.2262 | 1.5955 | 1.6101 |
| 2 | 13.3228 | 10.4242 | 1.4941 | 1.5259 |
| 3 | 8.9191 | 7.7698 | 1.3904 | 1.4270 |
| 4 | 6.3446 | 5.7806 | 1.2891 | 1.3226 |
| 5 | 4.8284 | 4.5056 | 1.1969 | 1.2250 |
Delay margins for different values of KEV and K.
5 Conclusion
In this paper, the LFC stability of delayed power systems with an EV aggregator was studied. The LFC of the power system was modeled as a delayed linear system with an EV aggregator. Based on Lyapunov stability theory and the linear matrix inequality approach, a new stability criterion was proposed by using Wirtinger inequality and improved inverse convex matrix inequality. Finally, the influence of EV aggregator gains and PID controller gains on the delay margins was studied, and some case studies have shown the advantage of the results. The research of this paper can solve the delay margins more accurately and guide the design of PID controllers of LFC for power systems with an EV aggregator effectively.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by the China Postdoctoral Science Foundation–funded project under Grant No. 2021M692992.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1
DongC.XiaoQ.WangM.MorstynT.McCullochM. D.JiaH. (2020). Distorted Stability Space and Instability Triggering Mechanism of Ev Aggregation Delays in the Secondary Frequency Regulation of Electrical Grid-Electric Vehicle System. IEEE Trans. Smart Grid11, 5084–5098. 10.1109/TSG.2020.3008333
2
JiaH.LiX.MuY.XuC.JiangY.YuX.et al (2018). Coordinated Control for Ev Aggregators and Power Plants in Frequency Regulation Considering Time-Varying Delays. Appl. Energ.210, 1363–1376. 10.1016/j.apenergy.2017.05.174
3
JiangL.YaoW.WuQ. H.WenJ. Y.ChengS. J. (2012). Delay-dependent Stability for Load Frequency Control with Constant and Time-Varying Delays. IEEE Trans. Power Syst.27, 932–941. 10.1109/TPWRS.2011.2172821
4
JinL.HeY.ZhangC.-K.ShangguanX.-C.JiangL.WuM. (2021a). Novel Structure-Exploiting Techniques Based Delay-dependent Stability Analysis of Multi-Area Lfc with Improved Numerical Tractability. IEEE Trans. Power Syst.36, 4194–4211. 10.1109/TPWRS.2021.3056594
5
JinL.HeY.ZhangC.-K.ShangguanX.-C.JiangL.WuM. (2021b). Robust Delay-dependent Load Frequency Control of Wind Power System Based on a Novel Reconstructed Model. IEEE Trans. Cybernetics, 1, 12. 10.1109/TCYB.2021.3051160
6
JinL.ZhangC.-K.HeY.JiangL.WuM. (2019). Delay-dependent Stability Analysis of Multi-Area Load Frequency Control with Enhanced Accuracy and Computation Efficiency. IEEE Trans. Power Syst.34, 3687–3696. 10.1109/TPWRS.2019.2902373
7
KhalilA.RajabZ.AlferganiA.MohamedO. (2017). The Impact of the Time Delay on the Load Frequency Control System in Microgrid with Plug-In-Electric Vehicles. Sustain. Cities Soc.35, 365–377. 10.1016/j.scs.2017.08.012
8
KoK. S.SungD. K. (2019). The Effect of Cellular Network-Based Communication Delays in an Ev Aggregator’s Domain on Frequency Regulation Service. IEEE Trans. Smart Grid10, 65–73. 10.1109/TSG.2017.2731846
9
KoK. S.SungD. K. (2018). The Effect of Ev Aggregators with Time-Varying Delays on the Stability of a Load Frequency Control System. IEEE Trans. Power Syst.33, 669–680. 10.1109/TPWRS.2017.2690915
10
LiX.YuX.JiaH.MuY.WuJ.WangM.et al (2019). Structure Constrained Controller Design for Power Plants and Ev Aggregator in Frequency Regulation Considering Time Delays. Energ. Proced.158, 2966–2971. 10.1016/j.egypro.2019.01.961
11
NaveedA.SönmezԶ.AyasunS. (2019a). Identification of Stability Delay Margin for Load Frequency Control System with Electric Vehicles Aggregator Using Rekasius Substitution. IEEE Milan PowerTech. 1, 6. 10.1109/PTC.2019.8810662
12
NaveedA.SönmezԶ.AyasunS. (2021). Impact of Electric Vehicle Aggregator with Communication Time Delay on Stability Regions and Stability Delay Margins in Load Frequency Control System. J. Mod. Power Syst. Clean Energ.9, 595–601. 10.35833/MPCE.2019.000244
13
NaveedA.ZerdaliE.SönmezԶ.AyasunS. (2019b). “Optimization of Pi Controller Gains Using Genetic Algorithm for Time-Delayed Load Frequency Control Systems with Electric Vehicles Aggregator,” in 2019 11th International Conference on Electrical and Electronics Engineering (ELECO), 28-30 November, 2019, Bursa, Turkey. 10.23919/ELECO47770.2019.8990434
14
PengC.ZouJ.LianL.LiL. (2017). An Optimal Dispatching Strategy for V2g Aggregator Participating in Supplementary Frequency Regulation Considering Ev Driving Demand and Aggregator’s Benefits. Appl. Energ.190, 591–599. 10.1016/j.apenergy.2016.12.065
15
PintoJ.CarvalhoA.MoraisV. (2021). Power Sharing in Island Microgrids. Front. Energ. Res.8, 360. 10.3389/fenrg.2020.609218
16
SeuretA.GouaisbautF. (2013). Wirtinger-based Integral Inequality: Application to Time-Delay Systems. Automatica49, 2860–2866. 10.1016/j.automatica.2013.05.030
17
ShangGuanX.-C.HeY.ZhangC.-K.JinL.JiangL.WuM.et al (2021). Switching System-Based Load Frequency Control for Multi-Area Power System Resilient to Denial-Of-Service Attacks. Control. Eng. Pract.107, 104678. 10.1016/j.conengprac.2020.104678
18
ShangguanX.-C.HeY.ZhangC.-K.JinL.YaoW.JiangL.et al (2021a). Control Performance Standards-Oriented Event-Triggered Load Frequency Control for Power Systems under Limited Communication Bandwidth. IEEE Trans. Control. Syst. Tech.1, 9. 10.1109/TCST.2021.3070861
19
ShangguanX.-C.ZhangC.-K.HeY.JinL.JiangL.SpencerJ. W.et al (2021b). Robust Load Frequency Control for Power System Considering Transmission Delay and Sampling Period. IEEE Trans. Ind. Inform.17, 5292–5303. 10.1109/TII.2020.3026336
20
ShiQ.LiuL.WangY.LuY.ZouQ.ZhangQ.et al (2021). Cooperative Synthetic Inertia Control for Wind Farms Considering Frequency Regulation Capability. Front. Energ. Res.9, 501. 10.3389/fenrg.2021.738857
21
TekB.SönmezԶ.AyasunS. (2020). “Delay-dependent Stability Analysis of a Two-Area Load Frequency Control System Including Electric Vehicle Aggregator and Dynamic Demand Response,” in 2020 12th International Conference on Electrical and Electronics Engineering (ELECO), 26-28 November, 2019, Bursa, Turkey, 178–182. 10.1109/ELECO51834.2020.00035
22
TengW.WangY.SunS.ChengY.YuP.WangS. (2021). Robust Stability Control for Electric Vehicles Connected to Dc Distribution Systems. Front. Energ. Res.9, 423. 10.3389/fenrg.2021.740698
23
YangB.HaoM.WangR.ZhaoX.ZongG. (2020). Exponential Stability of Delayed Generalized Neural Networks with Intermittent Large-Delay Periods. IEEE Trans. Syst. Man, Cybernetics: Syst.1, 11. 10.1109/TSMC.2020.2967506
24
ZhangC.-K.HeY.JiangL.WuM.WangQ.-G. (2017). An Extended Reciprocally Convex Matrix Inequality for Stability Analysis of Systems with Time-Varying Delay. Automatica85, 481–485. 10.1016/j.automatica.2017.07.056
25
ZhangC.-K.JiangL.WuQ. H.HeY.WuM. (2013). Delay-dependent Robust Load Frequency Control for Time Delay Power Systems. IEEE Trans. Power Syst.28, 2192–2201. 10.1109/TPWRS.2012.2228281
26
ZhouB.XuD.LiC.ChungC. Y.CaoY.ChanK. W.et al (2018). Optimal Scheduling of Biogas–Solar–Wind Renewable Portfolio for Multicarrier Energy Supplies. IEEE Trans. Power Syst.33, 6229–6239. 10.1109/TPWRS.2018.2833496
27
ZhouS.-J.ZengH.-B.XiaoH.-Q. (2020). Load Frequency Stability Analysis of Time-Delayed Multi-Area Power Systems with Ev Aggregators Based on Bessel-Legendre Inequality and Model Reconstruction Technique. IEEE Access8, 99948–99955. 10.1109/ACCESS.2020.2997002
Summary
Keywords
power system, load frequency control, electric vehicles, stability analysis, time delay
Citation
Yuan Z-L, Xu D, Jin L and Wang H-Z (2021) Delay-Dependent Stability Analysis of Load Frequency Control for Power System With EV Aggregator. Front. Energy Res. 9:771465. doi: 10.3389/fenrg.2021.771465
Received
06 September 2021
Accepted
23 September 2021
Published
26 October 2021
Volume
9 - 2021
Edited by
Yaxing Ren, University of Warwick, United Kingdom
Reviewed by
Jian Chen, Yancheng Institute of Technology, China
Hong-Bing Zeng, Hunan University of Technology, China
Wen-Juan Lin, Qingdao University, China
Updates
Copyright
© 2021 Yuan, Xu, Jin and Wang.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Da Xu, xuda@cug.edu.cn
This article was submitted to Smart Grids, a section of the journal Frontiers in Energy Research
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.