- Yaroslavl State Technical University, Yaroslavl, Russia
The additional operation of deaeration (compaction) of powders affects the quality of many products of chemical industries, the conditions for their delivery. Otherwise, energy consumption increases significantly. The aim of this work is the modeling of the deaeration of solid finely dispersed media in a gap with perforated hemispherical shapes on the surfaces of the shaft and conveyor belt within the framework of the mechanics of heterogeneous systems. A plane-deformation model is described, neglecting the forces of interphase interaction and taking into account the compressibility of a solid-particle-gas mixture without elastoplastic deformations. The model assumes consideration of the movement of (1) the components of the solid skeleton together with the carrying phase as a whole; (2) gas in an isothermal state through the pores of a finely dispersed material. This work is devoted to the study of part (a), i.e., behavior of the solid particle-gas system as a whole. The efficiency of the seal-deaerator is estimated using the obtained analytical dependencies for the main strength and speed indicators. The change in the degree of compaction of a spherical granule made of kaolin with given strength characteristics is investigated. It is shown that for the initial time interval up to 3.7⨯10−2 s, the growth of the porosity value relative to the horizontal coordinate along the conveyor belt is exponential and increases by a factor of 1.1. After eight such time intervals, the porosity values stabilize along the indicated coordinate with an increase of more than 1.4 times from the initial value.
Introduction
Preliminary deaeration (compaction) of powder components (Akiyama et al., 1986; Kapranova and Zaitzev, 2011; Francis, 2016), including soot and kaolin, affects the strength characteristics of the finished product, for example, car tires, and other polymer products. Transportation of sealed containers with a powder product with a high content of gas in its pores, in particular, for construction or food purposes, violates the principles of energy saving and energy efficiency. In contrast to the pressing of powders (Pizette et al., 2010; Bayle et al., 2016; Seong et al., 2020) or larger particles (Gai et al., 2005), deaeration refers to its initial stage, when there is no destruction of particles of the compacting medium. If it is necessary to obtain a special structure of a dispersed medium with given strength characteristics, it is advisable to use a mechanical deaeration method (Akiyama et al., 1986; Kapranova and Zaitzev, 2011) in particular, when obtaining granules from bitumen and mineral powder (Zaitsev et al., 2010), dry dye mixtures.
The design of roller devices for the deaeration of dispersed media is associated with the formation of theoretical foundations (Kapranova et al., 2000; Kapranova, 2010; Kapranova et al., 2015) for the engineering calculation of the parameters of these devices (Kapranova et al., 2001; Kapranova et al., 2006a; Kapranova et al., 2006b). For example, this is relevant in the manufacture of granules (Zaitsev et al., 2010) from bitumen (Santos et al., 2014; Fingas and Fieldhouse, 2009) and mineral powder (Renner et al., 2007). For these purposes, as a rule, the mechanics of heterogeneous systems are used (Nigmatulin, 1978; Generalov, 2002). The analytical results (Kapranova et al., 2000; Kapranova, 2010; Kapranova et al., 2015) when describing the behavior of the system solid particles-gas have some advantages over numerical solutions, (Pizette et al., 2010; Bayle et al., 2016; Seong et al., 2020) for example, when choosing rational ranges for changing the main parameters of the compaction process or when evaluating their optimal values (Kapranova et al., 2001; Kapranova et al., 2006a; Kapranova et al., 2006b). The importance of understanding the mechanism of the behavior of compacted materials is obvious for any type of modeling methods: analytical (Kapranova and Zaitzev, 2011; Kapranova et al., 2015; Udalov et al., 2019) or numerical (Khoei, 2005; Pizette et al., 2010; Bayle et al., 2016; Seong et al., 2020).
There are two sufficiently developed classical approaches to the formation of the initial model for calculating the main indicators of the powder compaction process. In the first method (roller rolling of metal powders) (Generalov, 2002; Wang et al., 2015), the conditions of air outflow from volumes are experimentally investigated depending on the shape of the constituent particles during their granulometric analysis (Vinogradov et al., 1969; Pimenov et al., 2015). In this case, scaling methods are used (Pimenov et al., 2015) within the framework of the Pi-Buckingham theorem (Buckingham, 1915; Annenkov et al., 2005); equilibrium equations (Generalov, 2002; Misic et al., 2010) and the limit state in the linearized representation (Tselikov et al., 1980; Generalov et al., 1984); indicators of changes in the volume of the specified workpiece (Generalov and Chainikov, 1972; Tselikov et al., 1980; Hu et al., 2021). The second method of description (Torner, 1977) does not make it possible to consider the compressibility of the system solid particles - gas when air is removed from the pores.
Two factors here are two factors that determine the modeling approach to modeling based on (Nigmatulin, 1978): (1) a significant content of the carrier phase in the composition of the specified system of solid particles—gas; (2) the maximum possible value of the degree of compaction of the material. This method makes it possible to carry out analytical calculations for the main indicators of the process under study, depending on the coordinates, time, design, and operating parameters, in particular, for the porosity of the mixture of solid particles-gas and the components of the velocity of the phases.
Theory
Hemispherical shaft and belt surfaces are used to obtain deaerated portions of powder (Figure 1) with radius
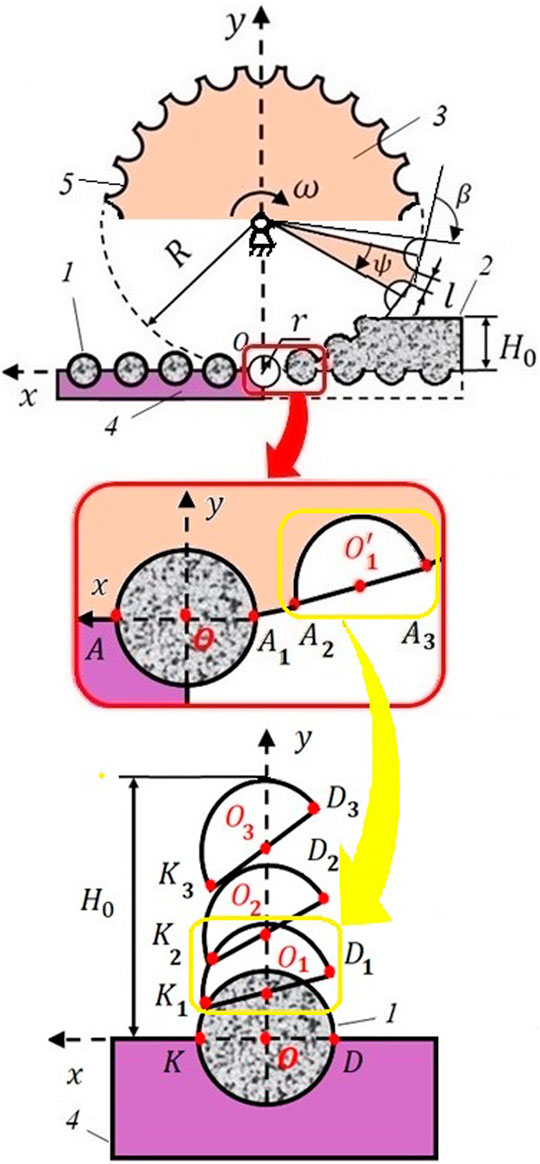
FIGURE 1. Conditional scheme for the movement of the compacted finely dispersed medium in the gap of the shaft-conveyor belt: 1—deaerated granule-sphere; 2—solid finely dispersed material; 3—shaft; 4—conveyor belt; 5—hemispherical shapes (cells).
Let the total number of flat cells on the rim of the shaft section be
Here it is indicated:
Let for a dispersed system solid particles-gas in further designations the subscript “2” corresponds to the dispersed phase (solid skeleton), the subscript “1”-to the carrier phase. The classical conditions for the proportionality of the reduced
This work is devoted to the study of part (1), i.e., motion at a speed
The following assumptions are made:
where
where
In addition, for shear stresses, the vertical component of the velocity of the solid skeleton along the
where coefficient
The system of Equations 4–6 in Cartesian coordinates is supplemented by the equations of motion of the medium with the true density of the solid phase
and the following equation of continuity of the solid
System (8)–(10) allows you to obtain analytical approximations for the main indicators of the process. The applied solution methods include a combination of the method of model equations and the method of substitution of constants instead of variable parameters (Kapranova et al., 2010; Kapranova et al., 2011; Kapranova et al., 2009).
By Equations 8–10, taking into account the slow nature of powder deaeration, we have
Here are the first approximations for tangential stresses
The auxiliary functions included in Expressions (11)–(14) are
In this case, the constants
Thus, expressions (11)–(14) can be used to form engineering methods for calculating the swath device (Kapranova et al., 2010; Kapranova et al., 2011; Kapranova et al., 2009).
Results and Discussion
The calculation of the basic characteristics of the process of mechanical compaction of a dispersed medium
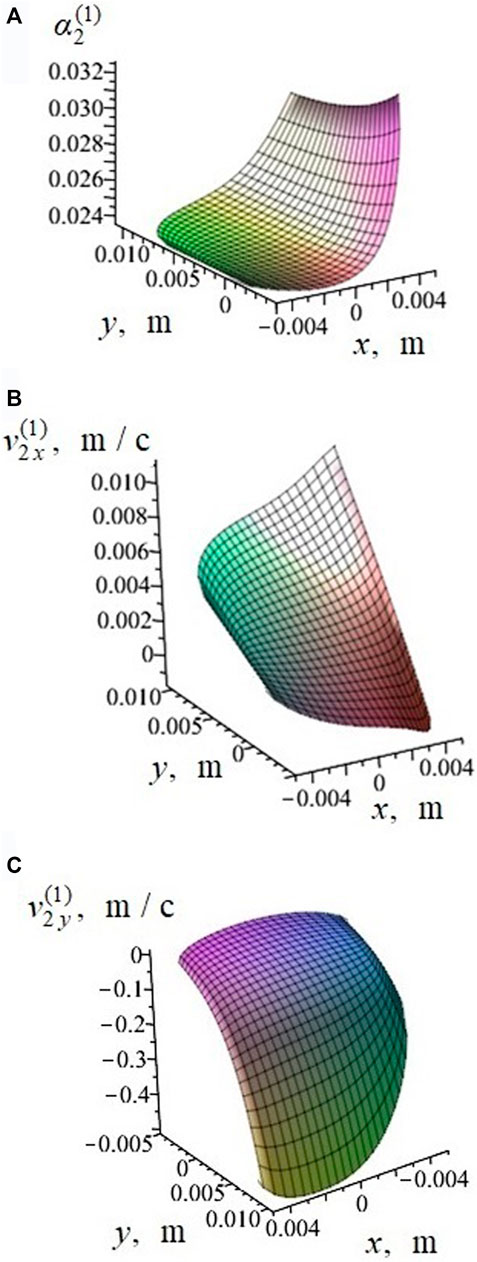
FIGURE 2. Dependencies for the main indicators of the deaeration process of kaolin GOST 21235-75 in a spherical matrix of a roll-type apparatus on Cartesian coordinates and time during:
The surfaces shown in Figure 2 correspond to a fixed point in time
According to the results obtained for the porosity function from Equation (11) (Figure 2A), the process of deaeration of the powder in the specified gap begins from the area surrounding the point
Analysis of surfaces for
Key Findings and Results
• The plane-deformation modeling of the movement of the solid skeleton of the dispersed medium together with the carrier phase as a whole in the working volume of the specified roller apparatus is carried out, as part (1) for the complete deaeration model (Kapranova and Zaitzev, 2011). The description of the movement of gas in an isothermal state through the pores of a finely dispersed material, as part (2) of this model, is discussed in the works of the authors (Kapranova et al., 2010; Kapranova et al., 2011; Kapranova et al., 2009).
• The theoretical substantiation of the possibility of realizing deaeration of dispersed media in a roller device with a spherical matrix on the surfaces of the shaft and conveyor is obtained based on the results of the performed simulation.
• The proposed plane-deformation model contributes to the development of methods for modeling the behavior of dispersed media in the working volumes of seals-deaerators, identifying the main information variables of the deaeration process, for example, according to the approaches, tested for the processing of solid dispersed materials (Kapranova et al., 2020a; Kapranova et al., 2020b) or when transporting liquid media (Kapranova et al., 2020c; Kapranova et al., 2020d).
Conclusion
An analytical method is proposed for assessing the efficiency of the deaeration process of solid dispersed components in a gap with perforated hemispherical shapes on the surfaces of the shaft and conveyor belt within the framework of the mechanics of heterogeneous systems taking into account the compressibility. It is noted that the porosity of the finished granule-sphere at the final stage of deaeration in the described gap of the conveyor shaft with a spherical matrix almost uniformly reaches its limiting value. In this case, the difference between the maximum and minimum porosity values does not exceed
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
All authors contributed to manuscript revision, and read and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akiyama, T., Miyamoto, Y., Yamanaka, N., and Zhang, J. Q. (1986). Densification of Powders by Means of Air, Vibratory and Mechanical Compactions. Powder Technol. 46 (2-3), 173–180. Available from: https://www.sciencedirect.com/science/article/abs/pii/0032591086800249?via%3Dihub (Accessed November 12, 2021). doi:10.1016/0032-5910(86)80024-9
Alcoverro, J. (2003). The Effective Stress Principle. Math. Comp. Model. 37 (5), 457–467. doi:10.1016/S0895-7177(03)00038-4
Andrianov, E. I. (1982). Methods for Determining the Structural - Mechanical Characteristics of Powdered Materials. Moscow: Khimiya Chemistry, 256.
Annenkov, U. M., Ivaschutenko, A. S., and Kondratyuk, A. A. (2005). “Comparative Analysis of Alumina-Zirconium Powders Compressibility with Different Dispersibility,” in Proceedings. The 9th Russian-Korean International Symposium on Science and Technology, Novosibirsk, Russia, July 2005 (KORUS), 415–417. doi:10.1109/KORUS.2005.1507746
Bayle, J.-P., Reynaud, V., Gobin, F., Brenneis, C., Tronche, E., Ferry, C., et al. (2016). Modelling of powder die compaction for press cycle optimization. EPJ Nucl. Sci. Technol. 2 (25), 25–29. doi:10.1051/epjn/2016018
Bessonov, A. I., Kutuzova, O. A., and Toporov, Y. P. (2001). A Cell for Measuring Shear Strength of Powdered Disperse Systems. Colloid J. 63, 788–789. doi:10.1023/A:1013244524903
Fingas, M., and Fieldhouse, B. (2009). Studies on Crude Oil and Petroleum Product Emulsions: Water Resolution and Rheology. Colloids Surf. A: Physicochemical Eng. Aspects 333 (1-3), 67–81. doi:10.1016/j.colsurfa.2008.09.029
Francis, L. F. (2016). “Powder Processes,” in Materials Processing. A Unified Approach to Processing of Metals, Ceramics and Polymers (University of Minnesota), 343–414. Available at: https://www.sciencedirect.com/science/article/pii/B9780123851321000057?via%3Dihub/ (Accessed November 12, 2021). doi:10.1016/B978-0-12-385132-1.00005-7
Gai, G.-S., Yang, Y.-F., Fan, S.-M., and Cai, Z.-F. (2005). Preparation and Properties of Composite mineral Powders. Powder Technol. 153 (3), 153–158. doi:10.1016/j.powtec.2005.03.013
Generalov, M. B., and Chainikov, N. A. (1972). Rolling of Powders onto Parts. Powder Metall. Met. Ceram. 11, 525–531. doi:10.1007/BF00798188
Generalov, M. B., Klassen, P. V., Stepanova, A. R., and Shomin, I. P. (1984). Design of Mineral Fertilizer Granulation Equipment [Raschet Oborudovaniya Dlya Granulirovaniya mineral’nykh Udobrenii]. Moscow: Mashinostroenie, 191.
Generalov, M. B. (2002). Mechanics of Particulate Media in Chemical Processes [Mekhanika Tverdykh Dispersnykh Sred V Protsessakh Khimicheskoi Tekhnologii]. Kaluga: Izd. N. Bochkarevoi 592.
Hu, Y., Sun, J., Peng, W., and Zhang, D. (2021). A Novel Forecast Model Based on CF-PSO-SVM Approach for Predicting the Roll gap in Acceleration and Deceleration Process. Eng. Computations 38 (3), 1117–1133. doi:10.1108/EC-08-2019-0370
Kapranova, A. B., and Zaitzev, A. I. (2011). Mechanical Compaction of Finely Dispersed Materials. Moscow: Ekon-inform, 247. Available from: https://search.rsl.ru/ru/record/01004975377 (Accessed November 12, 2021).
Kapranova, A. V., Zaitsev, A. I., and Nikitina, T. P. (2000). Taking into Account wall Slip and Friction in Calculating the Degree of Compaction of a Powder in a Screw Machine. Theor. Found. Chem. Eng. 34 (6), 592–599. Available from: https://www.researchgate.net/publication/225827276_Taking_into_Account_Wall_Slip_and_Friction_in_Calculating_the_Degree_of_Compaction_of_a_Powder_in_a_Screw_Machine (Accessed November 12, 2021). doi:10.1023/A:1005233226377
Kapranova, A. V., Zaitsev, A. I., and Nikitina, T. P. (2001). Design of a Screw Powder Compactor. Theor. Found. Chem. Eng. 35 (1), 90–94. Available from: https://link.springer.com/article/10.1023/A:1005233205559?error=cookies_not_supported&code=27bd158d-2c37-42a7-8884-90f3327e41d1 (Accessed November 12, 2021). doi:10.1023/A:1005233205559
Kapranova, A., Zaitzev, A. I., Bushmelev, A. V., and Lebedev, A. E. (2006a). “The Optimization Problem of the Curvilinear Blades from in the Powder Densification Set-Up,” in 17-th Int. Congr of Chem. and Process Eng. – CHISA’2006, Prague, Czech. Republic, 27 August 2006 - 31 August 2006. ISBN 8086059456, 978-808605945-7. Available at: https://www.scopus.com/record/display.uri?eid=2-s2.0-34748857979&origin=resultslist, 878 Book of abstracts.
Kapranova, A., Zaitzev, A. I., Bushmelev, A. V., and Kuzmin, I. O. (2006b). “The Investigation of the Densification Powder Sliding Effect in the Cell of the Set-Up with the Curvilinear Blades,” in 17-th Int. Congr of Chem. and Process Eng. – CHISA’2006, Prague, Czech. Republic, 27 August 2006 - 31 August 2006. ISBN 8086059456, 978-808605945-7. Available at: https://www.scopus.com/authid/detail.uri?authorId=22034771200, 875 Book of abstracts. (Accessed November 12, 2021).
Kapranova, A. B., Lebedev, A. E., and Vasiliev, A. M. (2010). On the Movement of the Carrying Phase of a Dispersed Medium during its Degassing in the gap of a Roll Deaerator with a Spherical Matrix [Ekspress-Metod Otsenki Odnorodnosti Smesey Sypuchikh Materialov] Russian Journal of Chemistry and Chemical Technology [Izvestiya Vysshikh Uchebnykh Zavedeniy. Seriya: Khimiya I Khimicheskaya Tekhnologiya]. Elibrary 53 (6), 101–103. Available from: https://www.elibrary.ru/download/elibrary_15125889_14369485.pdf (Accessed November 12, 2021).
Kapranova, A. B., Zaitsev, A. I., Dubrovin, A. V., Vasiliev, A. M., and Nikitina, Y. V. (2011). Movement Model of Carrying Phase of Bulk Mixture in Rolling gap with Spherical Matrix [Ekspress-Metod Otsenki Odnorodnosti Smesey Sypuchikh Materialov] Russian Journal of Chemistry and Chemical Technology [Izvestiya Vysshikh Uchebnykh Zavedeniy. Seriya: Khimiya I Khimicheskaya Tekhnologiya. Elibrary 54 (8), 97–99. Available from: https://www.elibrary.ru/download/elibrary_16388583_98787057.pdf (Accessed November 12, 2021).
Kapranova, A. B., Dubrovin, A. V., and Zaisev, A. I. (2009). To the Question of Evaluating the External Pressure in the gap of the Roller Deaerator of Powders with a Spherical Matrix [Ekspress-Metod Otsenki Odnorodnosti Smesey Sypuchikh Materialov] Russian Journal of Chemistry and Chemical Technology [Izvestiya Vysshikh Uchebnykh Zavedeniy. Seriya: Khimiya I Khimicheskaya Tekhnologiya]. Elibrary 52 (12), 116–118. Available from: https://www.elibrary.ru/download/elibrary_12971400_26424233.pdf (Accessed November 12, 2021).
Kapranova, A. B., Zaitsev, A. I., and Kuz’min, I. O. (2015). Studying the Porosity of Powders under Pressure Compaction in Deaeration Mixers. Theor. Found. Chem. Eng. 49 (4), 436–446. Available from: https://link.springer.com/article/10.1134/S0040579515040272?error=cookies_not_supported&code=7b22ff21-cb92-4ddb-b226-46340f3125b9 (Accessed November 12, 2021). doi:10.1134/S0040579515040272
Kapranova, A., Verloka, I., Bahaeva, D., Tarshis, M., and Cherpitsky, S. (2020a). To the Calculation of the Average Value of the Volume Fraction of the Key Bulk Component at the Intermediate Stage of Mixing with an Inclined Bump. Front. Energ. Res. 8, 1–11. doi:10.3389/fenrg.2020.00135
Kapranova, A. B., Verloka, I. I., and Bahaeva, D. D. (2020b). “About Preparation of the Analytical Platform for Creation of a Cyber-Physical System of Industrial Mixture of Loose Components,” in Cyber-Physical Systems: Advances in Design & Modelling. Studies in Systems, Decision and Control. Editors A. Kravets, A. Bolshakov, and M. Shcherbakov (Cham: Springer), 259, 81–91. doi:10.1007/978-3-030-32579-4_7
Kapranova, A., Neklyudov, S., Lebedev, A., Meltser, A., and Voronin, D. (2020c). Engineering Method for Calculating of an Axial Valve Separator with an External Location of the Locking Part. Front. Energ. Res. 8, 1–17. doi:10.3389/fenrg.2020.00032
Kapranova, A. B., Lebedev, A. E., Melzer, A. M., and Neklyudov, S. V. (2020d). “About Formation of Elements of a Cyber-Physical System for Efficient Throttling of Fluid in an Axial Valve,”in Cyber-Physical Systems: Advances in Design & Modelling. Studies in Systems, Decision and Control. Editors A. Kravets, A. Bolshakov, and M. Shcherbakov (Cham: Springer), 259, 109–119. doi:10.1007/978-3-030-32579-4_9
Kapranova, A. B. (2010). Powder Densification Process in a Centrifugal Apparatus with Curvilinear Blades. Math. Models Comput. Simul 2 (1), 63–75. Available from: https://link.springer.com/article/10.1134/S2070048210010072?error=cookies_not_supported&code=202ef76c-3a51-483a-9a76-ee9c2b1f041a (Accessed November 12, 2021). doi:10.1134/S2070048210010072
Khoei, A. R. (2005). “Finite Element Model,” in Computational Plasticity in Powder Forming Processes (Elsevier), 19–43. Available at: https://www.sciencedirect.com/science/article/pii/B978008044636350002X (Accessed November 12, 2021). doi:10.1016/B978-008044636-3/50002-X
Misic, T., Najdanovic-Lukic, M., and Nesic, L. (2010). Dimensional Analysis in Physics and the Buckingham Theorem. Eur. J. Phys. 31 (4), 893–906. doi:10.1088/0143-0807/31/4/019
Nigmatulin, R. I. (1978). Fundamentals of Heterogeneous Medium Mechanics [Osnovy Mekhaniki Geterogennykh Sred]. Moscow: Nauka, 336.
Pimenov, V. A., Babushko, Y. Y., and Bakhtin, S. V. (2015). Reversible Cold Rolling of Thin High-Silicon Steel Strip. Steel Transl. 44 (10), 764–768. doi:10.3103/S0967091214100131
Pizette, P., Martin, C. L., Delette, G., Sornay, P., and Sans, F. (2010). Compaction of Aggregated Ceramic Powders: From Contact Laws to Fracture and Yield Surfaces. Powder Technol. 198 (2), 240–250. Available from: https://www.researchgate.net/publication/244157915_Compaction_of_Aggregated_Ceramic_Powders_From_Contact_Laws_to_Fracture_and_Yield_Surfaces (Accessed November 12, 2021). doi:10.1016/j.powtec.2009.11.013
Renner, J., Siddiqi, G., and Evans, B. (2007). Plastic Flow of Two-Phase Marbles. J. Geophys. Res. 112 (B7). doi:10.1029/2005JB004134
Santos, R. G., Loh, W., Bannwart, A. C., and Trevisan, O. V. (2014). An Overview of Heavy Oil Properties and its Recovery and Transportation Methods. Braz. J. Chem. Eng. 31 (3), 571–590. doi:10.1590/0104-6632.20140313s00001853
Seong, Y., Yim, D., Jang, M. J., Park, J. M., Park, S. J., and Kim, H. S. (2020). Physics-Based Constitutive Model of Porous Materials for Die/Isostatic Compaction of Metallic Powders. Met. Mater. Int. 26, 221–229. doi:10.1007/s12540-019-00317-z
Torner, R. V. (1977). “Theoretical Foundations of Polymer Processing [Teoreticheskie Osnovy Pererabotki Polimerov], Khimiya, Moscow,” in Theoretical Foundations of Polymer Processing (Moscow: Khimiya Chemistry), 462.
Tselikov, A. I., Nikitin, G. S., and Rokotyan, S. E. (1980). Lengthwise Rolling Theory [Teoriya Prodol’noi Prokatki]. Moscow: Metallurgiya, 319.
Udalov, A. A., Parshin, S. V., Udalov, A. V., and Vasilevykh, S. L. (2019). Power Parameters of the Process of Hardening of Cylindrical Parts by a Toroidal Roller by the Method of Surface Plastic Deformation. J. Phys. Conf. Ser. 1210, 012150. doi:10.1088/1742-6596/1210/1/012150
Vinogradov, G. A., Semenov, Y. N., Katrus, O. A., and Katashinskii, V. N. (1969). Metal Wire Rolling [Prokatka Metallicheskikh Poroshkov]. Moscow: Metallurgiya, 382.
Wang, Z.-L., and Xiao, H. (2015). “A Study of Metal Fatigue Failure as Inherent Features of Elastoplastic Constitutive Equations,” in From Creep Damage Mechanics to Homogenization Methods Advanced Structured Materials. Editors H. Altenbach, T. Matsuda, and D. Okumura (Cham: Springer), 64, 529–540. doi:10.1007/978-3-319-19440-0_23
Zaitsev, A. I., Lebedev, A. E., Dubrovin, A. V., and Gotovtsev, V. M. (2010). Aggregate for Obtaining Coated Granular Material. Patent 2385762 Russian Federation, IPC C 10 C 3/14. Bull. N. 10, 1 4. Available at: https://fips.ru/registers-doc-view/fips_servlet?DB=RUPAT&rn=5649&DocNumber=2385762&TypeFile=html (Accessed September 03, 2020).
Keywords: model, deaeration (densification), finely dispersed medium, roller, porosity
Citation: Kapranova A, Tarshis M, Badaeva N and Sheronina I (2021) Mathematical Model of the Deaeration of Finely Dispersed Solid Media in a Spherical Matrix of a Roller-Type Apparatus. Front. Energy Res. 9:769940. doi: 10.3389/fenrg.2021.769940
Received: 02 September 2021; Accepted: 27 October 2021;
Published: 24 November 2021.
Edited by:
Zheng Li, Vanderbilt University, United StatesReviewed by:
Xiaoyu Zhang, Vanderbilt University, United StatesBo Jiang, Nanjing University of Science and Technology, China
Copyright © 2021 Kapranova, Tarshis, Badaeva and Sheronina. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Anna Kapranova, a2FwcmFub3ZhX2FubmFAbWFpbC5ydQ==
 Anna Kapranova
Anna Kapranova Mikhail Tarshis
Mikhail Tarshis