- 1Mechanical and Electrical Engineering College, Hainan University, Hainan, China
- 2School of Robotics, Xi’an Jiaotong-Liverpool University, Jiangsu, China
Aiming at the state estimation error caused by inaccurate battery model parameter estimation, a model-based state of charge (SOC) estimation method of lithium-ion battery is proposed. This method is derived from parameter identification using an adaptive genetic algorithm (AGA) and state estimation using fractional-order unscented Kalman filter (FOUKF). First, the fractional-order model is proposed to simulate the characteristics of lithium-ion batteries. Second, to tackle the problem of fixed values of probabilities of crossover and mutation in the genetic algorithm (GA) in model parameter identification, an AGA has been proposed. Then, the FOUKF method is used to assess battery SOC. For the data redundancy problem caused by the fractional-order algorithm, a time window is set to enhance the computational efficiency of the fractional-order operator. Finally, the experimental results show that the developed AGA-FOUKF algorithm can increase the correctness of SOC estimation.
Introduction
Lithium (Li)–ion batteries are an essential energy source for new energy electric vehicles, and the precise estimation of state of charge (SOC) can effectively estimate the vehicle’s mileage (Shen et al., 2019). The accurate estimation of Li battery SOC is very vital for the battery management system (BMS) (Wang et al., 2021). Nevertheless, it is challenge to accurately estimate the battery SOC accurately, as the battery is a highly irregular system, and the model parameters, such as SOC, temperature, and battery aging degree, will change with time (Tian et al., 2017).
In order to address this problem, researchers have been presented many SOC estimation methods, including the ampere-hour (Ah) counting (Cano et al., 2018), open-circuit voltage (OCV) method (Chen et al., 2019), Kalman filter (Shrivastava et al., 2019), extended Kalman filter (EKF) (Guo et al., 2019), nonlinear observers (Zhu et al., 2017), neural network (He et al., 2014; Li et al., 2019), and so on. However, each method and technology have their own advantages and limitations. The Ah counting and the OCV method are easy to implement, but the Ah counting will produce cumulative errors and decrease the veracity of SOC estimation. The OCV of the battery needs to stand for a long time to obtain it exactly. To solve the shortcomings of traditional algorithms, Plett adopted EKF to assess the battery SOC (Plett, 2004). Nonetheless, the EKF algorithm adopted Taylor’s first-order formula to linearize the nonlinear system, ignoring higher-order terms, which will reduce the estimation authenticity of the nonlinear battery system. Therefore, researchers have been proposed the unscented Kalman filter (UKF) algorithm (He et al., 2013). compares the SOC estimation results of EKF and UKF, demonstrating that the UKF algorithm has a faster convergence speed and higher verity. Meng et al. (2016) proposed an accurate Li battery SOC estimation algorithm based on adaptive UKF and least-squares (LS) support vector machine. Key to the success of the algorithm is its ability to correctly estimate the battery SOC. Sun et al. (2018) proposed an SOC evaluation algorithm based on adaptive correntropy UKF, which can precisely estimate the actual measurement data in the case of non-Gaussian system noise. The above proves that UKF has higher estimation accuracy than EKF.
In recent years, model-based estimation methods are commonly used in battery SOC estimation. Because of its simplicity, the equivalent circuit model has been widely used in battery SOC estimation (Wang et al., 2018). Hu et al. (2012) compares and discusses some integer-order models and studies the effectiveness of these models through comprehensive evaluation. Notwithstanding, because of the fractional nature of capacitors, the integer-order model will produce errors when describing the internal conditions of the battery. Specifically, the low-order model has a small amount of calculation but low accuracy, and the high-order model has a higher accuracy but a large amount of calculation. Liu et al. (2016) proposed a fractional-order model (FOM) based on the Partnership for a New Generation of Vehicle model and compared it with the integer-order model (iom). Xu et al. (2013) established a battery equivalent circuit model based on electrochemical impedance spectroscopy (EIS) technology and realized the SOC estimation of the battery, but the EIS model also has the disadvantage of a large amount of calculation. The key to the equivalent circuit model’s success is closely related to the identification of the model parameters (Wang et al., 2021). For the identification of nonlinear system parameters, some algorithms have been presented to identify parameters in the equivalent circuit, including the LS method (Chen et al., 2017), particle swarm optimization algorithm (Zhou et al., 2021; Wang et al., 2015), and genetic algorithm (GA) (Zhu et al., 2019). Chen et al. (2017) utilized the LS method to assess the model parameters and achieved the effect of model identification. Compared with the LS method, the GA method has many advantages, including searching from the string set, covering a large area, being conducive to global optimization, and being easier to implement. The model parameters are identified using a GA and experimental data of dynamic driving cycles (Mu et al., 2017). Pizarro-Carmona et al. (2021) put forward an identification method of Li-ion battery model based on GA. The results show that the identification results based on the GA can accurately represent the highly dynamic characteristics of Li-ion batteries, although the GA has the disadvantage of fixed probabilities of crossover and mutation. Specifically, both good individuals and inferior individuals have undergone the exact probabilities of crossover and mutation operations, which affect the efficiency of the algorithm to a certain extent. To sum up, the primary contributions of this article are made as follows: 1) Based on fractional calculus theory, an FOM is put forward. 2) Aiming at the optimization problem of the equivalent circuit model parameter identification, to overcome the disadvantage that simple GA and some improved GA have fixed values of probabilities of crossover and mutation, the adaptive genetic algorithm (AGA) is proposed to identify model parameters, and the concept of fractional-order is applied to the AGA, so as to improve the accuracy and speed of model identification. At the same time, it is compared with the results of integer-order LS method and fractional-order GA identification. 3) In addition, this article used pulse experimental data to identify the order and parameters in the model through AGA, instead of the individually identified order in references (Xu et al., 2013; Wang et al., 2015), so that the parameters can more fully show the features of the battery. 4) Based on fractional calculus theory, the UKF algorithm is used to estimate the battery SOC, and the time window is set to enhance the computational efficiency of fractional-order operator. 5) Compared with LSM-UKF based on iom and GA–fractional-order UKF (FOUKF) based on FOM, it reveals the feasibility and superiority of AGA-FOUKF.
The rest of this article is organized as follows: In Battery Modeling, a battery model is described. In SOC Estimation Method, an FOUKF technique is presented to estimate the battery SOC. The model parameters are identified in Model Parameter Identification. Validation and Discussion is the verification and discussion process is given. Finally, conclusions are given in the last section.
Battery Modeling
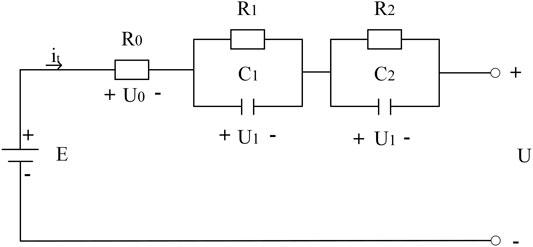
The equivalent circuit model can describe the relationship between the external characteristics and internal parameters of the battery. The establishment of a precise model is the basis for SOC appraisement, and the correctness of the equivalent circuit model will directly affect the precision of SOC evaluation. This section studies the second-order RC model based on the fractional-order theory.
Fractional Calculus
With the development of computing power, many researchers have provided theories and methods for studying the theory of fractional calculus theory. As fractional-order theory can more faultlessly and honestly describe physical systems than integer-order theory, fractional calculus is widely used to deal with problems in engineering practice, such as electronics, bioengineering, and robotics (Liu et al., 2018), (Richard, 2010). Fractional calculus is defined as follows:
where α is the fractional-order; a and t are the upper and lower limits of calculus, respectively. Fractional calculus has three methods: Riemann-Liouville definition, Caputo definition, and Grünwald-Letnikov (GL) definitions (Yang et al., 2020). GL calculus Eq. 2 is as follows:
where h is the sampling interval. The factors
It should be noted that the result of fractional calculus at a specific time is related to the information of the past time and has memory, although considering all the past states will increase the amount of BMS calculations. Hence, pursuant to the principle of short memory, the past state is shortened to avoid the computational burden and alleviate the problems caused by it. Hence, Eq. 3 can be rewritten as:
where L is the memory length.
Definition of Fractional Capacitance
Studies have shown that the capacitors have fractional-order characteristics (Westerlund and Ekstam, 1994). Therefore, an FOM is established to more veraciously approximate the actual variable characteristics of the Li-ion battery more accurately. The fractional capacitance is defined as follows:
where
Fractional-Order Model
The structure of the FOM is illustrated in Figure 1. E is the OCV source, U is the terminal voltage, and R0 is the ohmic resistance. The fractional capacitance is used to replace the integer-order capacitance to describe the impedance created by the internal polarization influence and concentration polarization effect. The state-space Eq. 5 can be gained as follows:
Generally, SOC is obtained by Ah counting method, which is usually expressed as follows:
where
where
The association between OCV and SOC can be fitted through a polynomial fitting formula. In this article, the sixth-order polynomial formula is adopted, and OCV can be expressed as a function including SOC:
where
SOC Estimation Method
The FOM can more precisely describe the internal state of the battery since the existence of the fractional order. Even so, the traditional UKF becomes inapplicable under the FOM. Therefore, it is necessary to make specific improvements to the traditional UKF. The UKF method is developed for the FOUKF for solve the FOM, and the detailed process of FOUKF is introduced.
System Description
For irregular discrete-time systems, the state and observation Eq. 9 can be expressed as:
where
Fractional-Order Unscented Kalman Filter
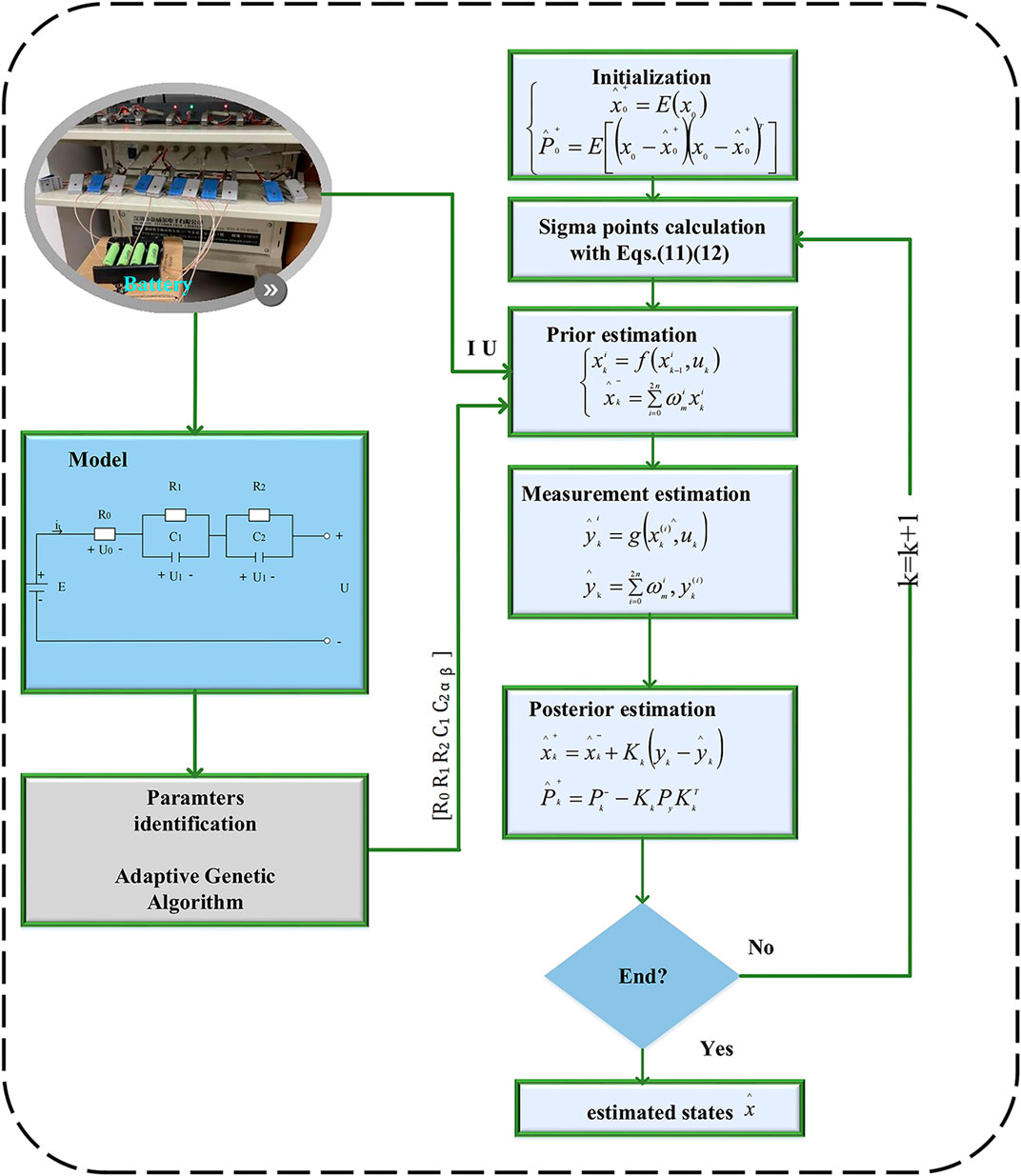
The UKF algorithm abandons the traditional approach of linearizing nonlinear functions and adopts Kalman linear filtering framework. Unscented transform is applied to deal with the nonlinear transfer problem of mean and covariance (Zhang et al., 2015). Compared with the UKF, the FOUKF has no intrinsic distinction apart from the initial estimation process of the states. The implementation process of the FOUKF method is as follows:
Step 1 Initialization: the state vector and the state error covariance matrix.
where
Step 2 For k = 1, 2, … , calculate:A priori estimate update.
1) Calculate 2j+1 Sigma points
where j refers to the dimension of the state;
2) Calculate the weight
3) Status estimation time update:
4) Time update of covariance matrix:
Measurement update.
1) Convert the sigma point to the measurement estimated point:
2) Calculate the average of the measurement estimates:
3) Calculate the covariance and Kalman gain:
Posterior estimate update.
1) Update status and covariance:
Step 3 Skip to Step 2, k = k + 1The battery current and voltage measured by the CT-4008 battery test platform are transmitted to the algorithm for estimation. The flowchart of the algorithm is shown in Figure 2.
Model Parameter Identification
Before the battery states were estimated, the parameters of the battery model must first be obtained. The exactitude of battery SOC estimation depends strongly on the precise model parameter identification. As the BMS cannot directly measure battery parameters, it is necessary to identify and calculate unknown parameters to obtain equivalent circuit model information. In this section, an AGA is used to identify the fractional order and other parameters in the model simultaneously. Moreover, it is compared with the identification result of the LS method based on the IOM and the GA identification result based on the FOM.
Test for the Model Parameter Identification
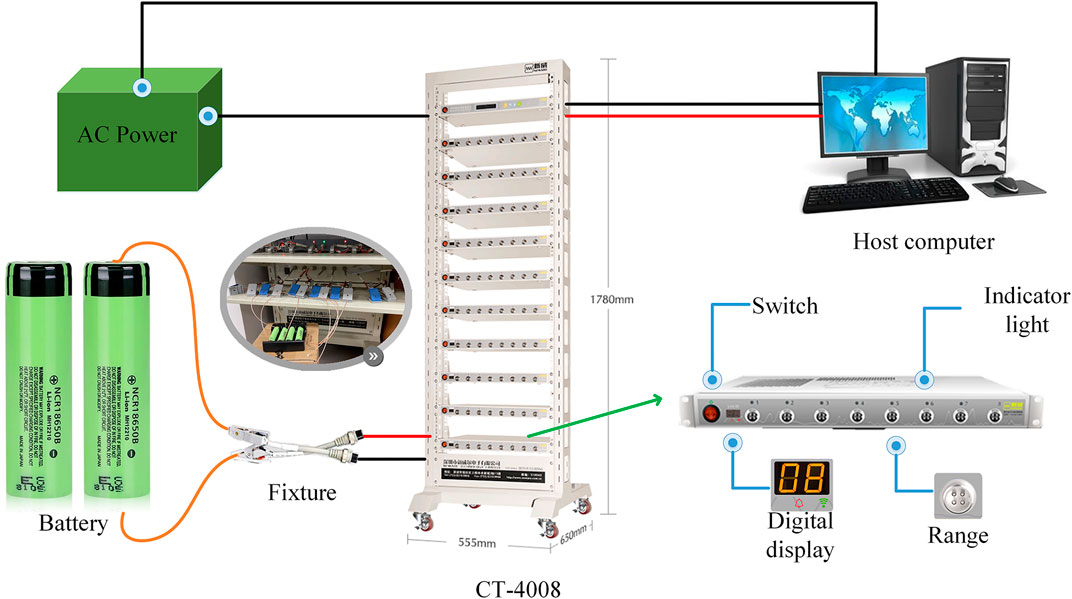
The battery test platform based on CT-4008 can be used to verify the effectiveness of this method. The composition of the bench is shown in Figure 3. It comports a test system CT-4008, fixtures, a host, and test objects. The measuring current precision of the equipment is ±0.05% full scale (FS), the voltage precision is ±0.05% FS, the temperature range is 040°C, and the sampling frequency is 10 Hz. The test object in this article is Panasonic NCR18650B, with a nominal capacity of 3.4 Ah, a nominal voltage of 3.7 V, a charge cutoff voltage of 4.2 V, and a discharge cutoff voltage of 2.5 V. The corresponding performance parameters are shown in Table 1.
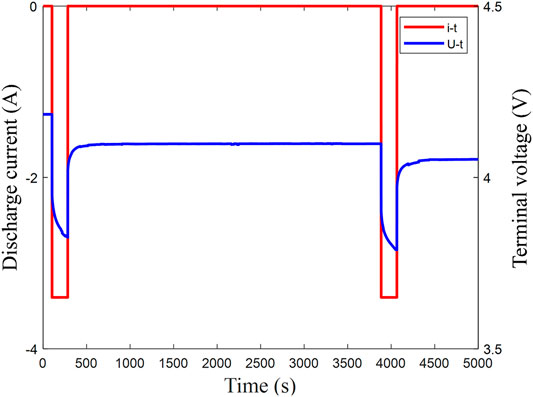
The general method to identify model parameters is the battery pulse characterization experiment. The pulse test process is as follows: First, fully charge the battery and let it stand for 3,600 s, and then, release a discharge pulse with a pulse current of 1°C. Continue the pulse discharge for 180 s to reduce the SOC value of the battery by approximately 0.05. Let the battery standstill fully. In the experiment, set the battery standing time to be 3,600 s. Repeat the above steps until the voltage reaches the set voltage, as shown in Figure 4.
Parameter Identification Based on AGA
In comparison with the LS method, the superiority of the GA is that the optimal solution can be obtained only by determining the value of the goal function, despite the disadvantage that GA has fixed values of probabilities of crossover and mutation. Therefore, an AGA is presented to identify the parameters of the battery model.
Crossover and Mutation
In the initial population, select a part of the parent individuals who can be used for mating and performing the chromosome crossover operation. Specifically, it refers to the process of selecting two of these individuals to mate with each other and exchanging some of their chromosomes with each other in a certain way to form two new individuals. In this article, a single-point crossover is selected in AGA. In this kind of crossover, only one crossover point is randomly set in the individual coding string, and the chromosomes are divided into two parts in this kind of crossover. The left and right sides of the offspring chromosomes are derived from the parent chromosomes, respectively.
The new individuals were formed after the crossover operation; there is a certain probability that gene variation will occur in this process. As the selection operation, this operation is based on probability. This probability becomes the mutation probability (
Probabilities of Crossover and Mutation
In the application of the GA, the reasonable probability of crossover (
where k1, k2, k3, and k4 are all less than 1.
Fitness Function
In the GA, the function that measures each chromosome introduced to reflect the adaptability of the chromosome is called the fitness function. The fitness value of an individual is calculated using a fitness function, and the optimal solution is searched according to the fitness value. The objective function is defined as:
where
where
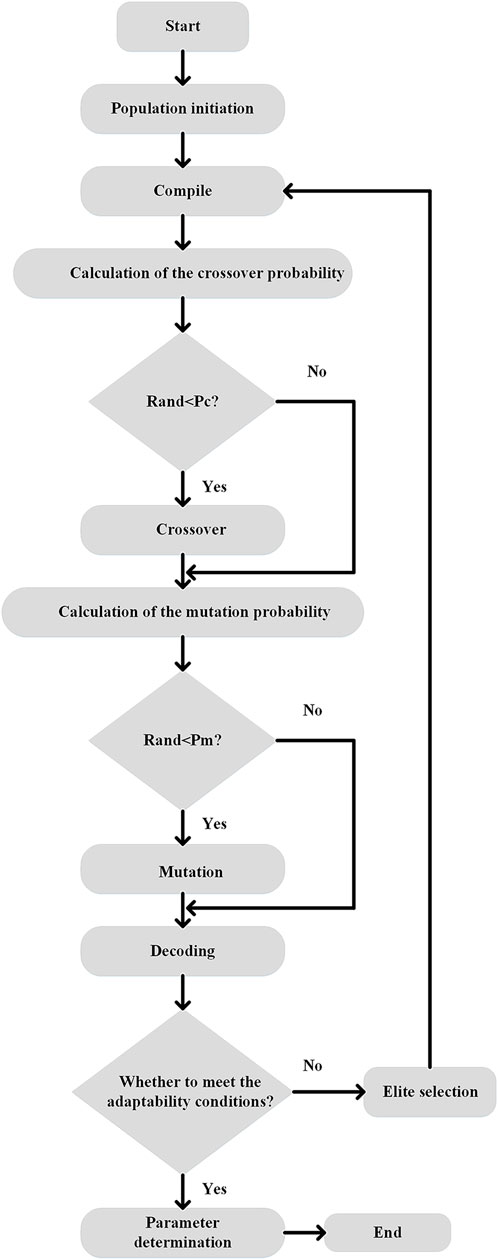
By applying the above genetic operator and fitness function to find the optimal value, the AGA flowchart is shown in Figure 5. The specific steps are as follows:
1) The initial population is generated randomly as the initial value of the parameter.
2) The initial value generated in the first step is encoded and converted into the corresponding binary code, representing the individual gene.
3) The current population is crossed, and some gene fragments (the binary code of the exchange part) are exchanged, and the new individuals produced after the exchange are the offspring.
4) Simulate the mutation behavior in the biological evolution process, and randomly generate mutations in the genes of the offspring. This step aims to prevent the identified parameters from falling into the local optimal solution range.
5) The value of offspring can be obtained by decoding the offspring after hybridization and variation.
6) Substitute the decoded offspring in Step 5 input into the fitness function to determine whether the individual meets the set requirements. If there was an individual that meets the set conditions, the most eligible individual was used as the model identification parameter; if the set conditions were not met, the offspring produced in the fifth step would be selected by elites (the closer the individual is to the set conditions, the greater the probability of being retained), so as to generate a new population, and then loop the second to sixth steps “Operate to simulate the next round of biological evolution,” until there is an individual that meets the adaptability conditions, or the number of reproduction algebra exceeds the set algebra.
Validation and Discussion
To prove the effectiveness of AGA identification results, it is compared with the LS method based on IOM and the GA based on FOM. In addition, to prove the effectiveness of the AGA-FOUKF algorithm, comparing the parameter identification and SOC estimation results under distinct methods and models, it is verified that the established AGA-FOUKF algorithm can improve the prediction authenticity.
Results of Model Parameter Identification
Data simulation was performed using the MATLAB R2018 software. The AGA was run by setting the initial population size at 200, the initial value of adaptive
To certify the accuracy of AGA identification, the battery terminal voltage estimated based on the AGA identification result is compared with the measured data. At the same time, it is compared with the LS method based on the IOM and the GA based on the FOM. The comparison of the results is shown in Figure 6A. In Figure 6B, it can be seen that the model voltage estimated by the AGA identification result better follows the measured terminal voltage of the battery. The error between the model voltage and the measured voltage is basically within 0.01 V. When the discharge pulse appears and ends, the load current changes sharply. Because of the modeling error, it will be a short-time error spike. But the error will gradually converge over time. In addition, the AGA obviously suppresses this phenomenon better than the other two algorithms.
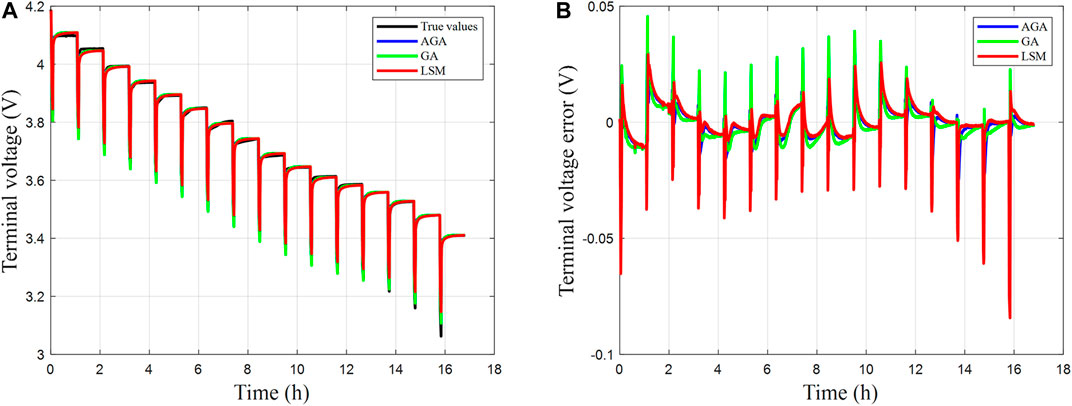
FIGURE 6. Model identification results. (A) Comparison of measured values and model predictions. (B) Terminal voltage curve.
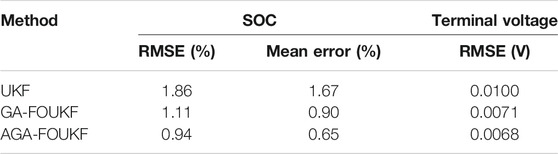
In Table 3, the terminal voltage estimation of the AGA identification based on the fractional second-order RC model is more accurate. The root mean square error (RMSE) of the terminal voltage identified by AGA and GA based on the fractional second-order RC model is 0.68 and 0.78%, respectively. The RMSE of the terminal voltage estimated by the LS method based on the integer second-order RC model is 0.10%. To certify the stability and robustness of the terminal voltage estimation, the average error is used as an indicator. The average error of terminal voltage estimation of LS method, GA, and AGA is 0.58, 0.56, and 0.48%, respectively. It can be seen that the AGA improves the precision of the model.
SOC Estimation Results
SOC Estimation Under the Discharging Process of OCV Test
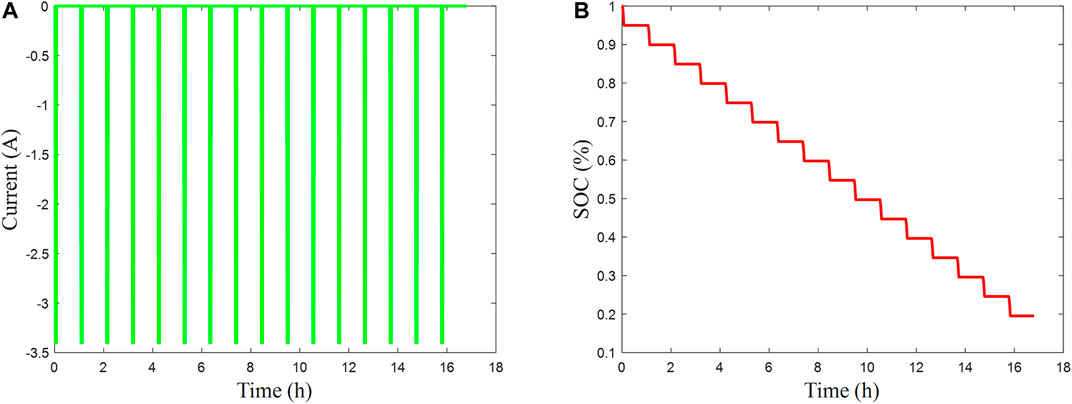
To certify the validity of the AGA-FOUKF, the data of the pulse test discharge process is used, and the current and SOC curve are shown in Figure 7. In this article, the SOC initial value error of 0.2 is artificially introduced. It means that there is an error in the initial SOC value. From the topical enlargement of Figure 8A, it is clear that the SOC prediction results of AGA-FOUKF and GA-FOUKF are similar, which also appears in the model parameter identification results. After the AGA-FOUKF converges, the SOC prediction error can be restrained within 2%, as shown in Figure 8B. It can be seen from the partially enlarged view of Figure 8C that the predicted terminal voltage can track the measured value well after the three methods converge. The AGA-FOUKF algorithm shows a better convergence effect, as shown in Figure 8D.
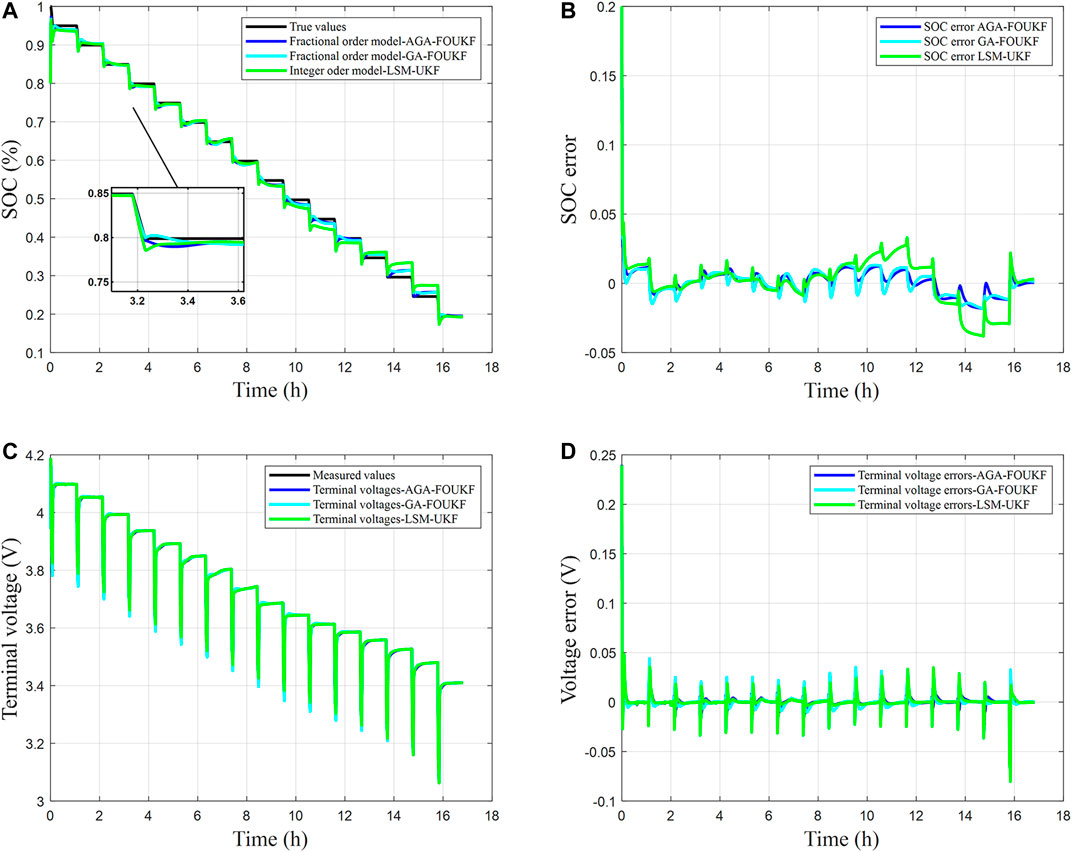
FIGURE 8. Under the charging procedure of the pulse test, the SOC estimation and the terminal voltage estimation are compared. (A) SOC estimation result; (B) the errors of SOC estimation; (C) terminal voltage estimation result; (D) the errors of terminal voltage.
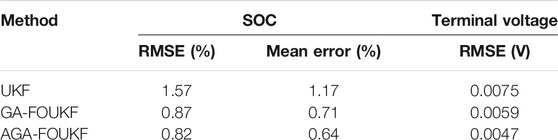
It can be seen from Table 4 that the estimation of the AGA-FOUKF algorithm based on the FOM is more accurate. The RMSE of SOC and terminal voltage estimated by AGA-FOUKF based on the FOM are 0.82 and 0.47%, respectively. The RMSE of SOC and terminal voltage estimated by GA-FOUKF based on the FOM are 0.87 and 0.59%, respectively. The SOC and terminal voltage RMSE estimated by the UKF algorithm based on the IOM are 1.57 and 0.75%, respectively. The average error of SOC estimation of LSM-UKF algorithm, GA-FOUKF algorithm, and AGA-FOUKF algorithm is 1.17, 0.71, and 0.64%, respectively. The estimation results show that the overall performance of the FOM and battery SOC estimation has been improved.
SOC Estimation Under the Dynamic Discharge Experiment
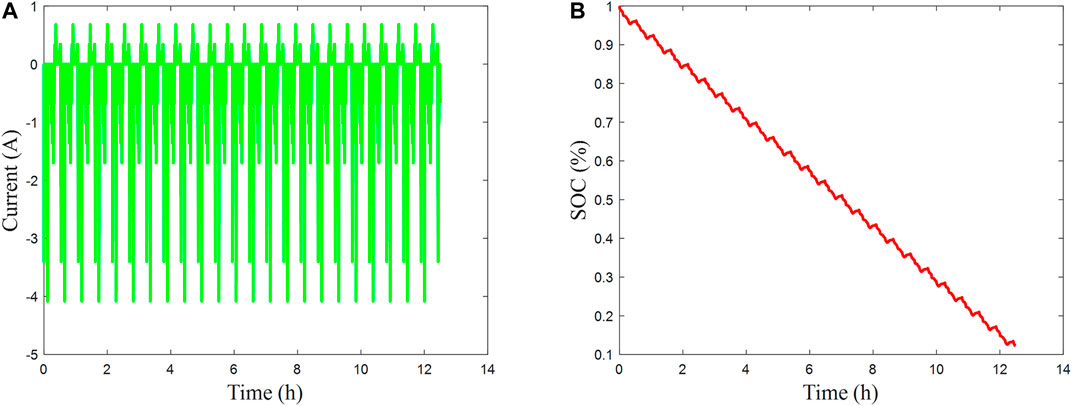
In order to certify the dynamic characteristic of AGA-FOUKF, the dynamic pulse status is used. The current and SOC curve are shown in Figure 9. The results under dynamic discharge experiment are given as Figure 10. The dynamic discharge experiment results of the three methods are shown in Table 5.
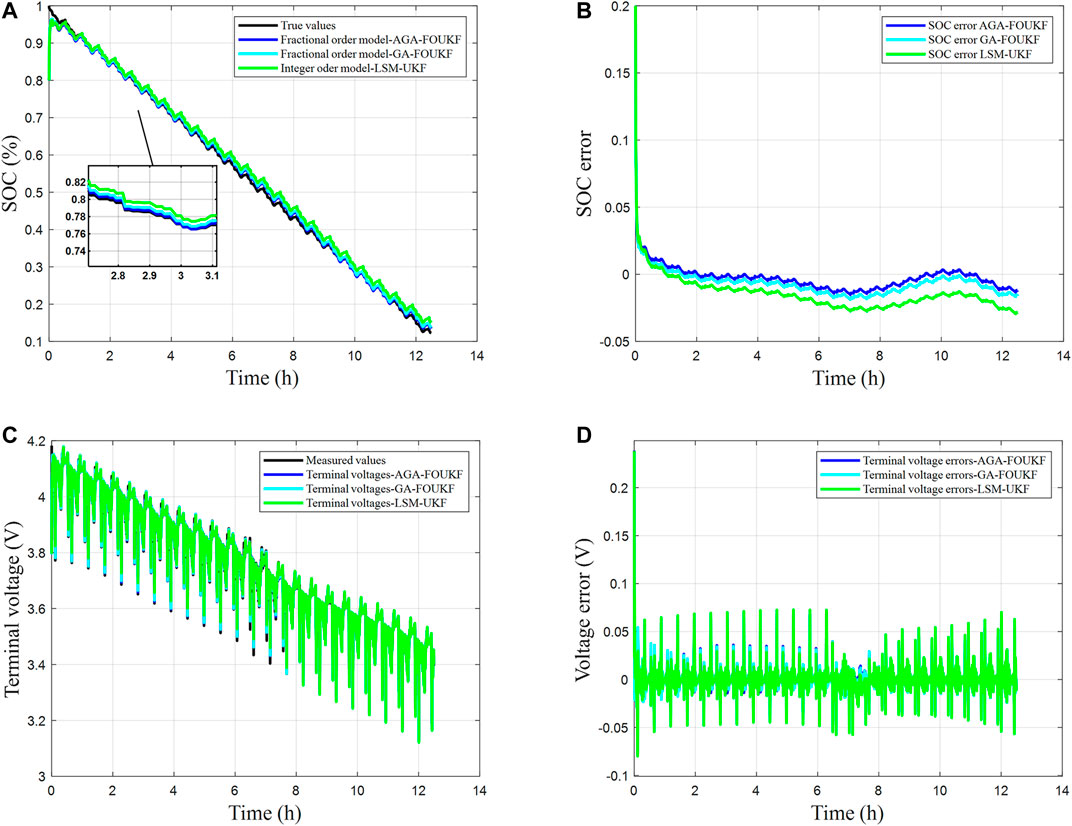
FIGURE 10. The results of dynamic discharge experiment. (A) SOC estimation result; (B) the errors of SOC estimation; (C) terminal voltage estimation result; (D) the errors of terminal voltage.
Conclusion
The SOC prediction of Li-ion batteries is an indispensable and vital part of BMS. In this article, considering the fractional-order nature of capacitors, an FOM is established. To overcome the disadvantage that GA has fixed values of probabilities of crossover and mutation, the AGA is proposed to distinguish the FOM parameters, and its FOM parameter identification performance is better than the other two methods. In addition, taking 18650 Li-ion batteries as the test object, the method of combining AGA and FOUKF is applied to estimate battery SOC. Using the experimental data of the CT-4008 battery test platform for simulation, under pulse conditions, the RMSE of the battery SOC and terminal voltage estimated by AGA-FOUKF are within 1 and 0.7%, respectively. The average error of AGA identification based on the FOM is less than 0.7%. The performance of the above method is verified by simulation.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
Full-paper design, JW, ZJ, and CF; writing-review and editing, CF, ZJ, and JW; funding acquisition, ZJ and JW; software, ZJ, and CF; formal analysis, ZJ, CF, and JW; data curation, CL; writing—original draft preparation, CF, and JW; supervision, JW; All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the scientific research fund of Hainan University (No. kyqd(ZR)1934), Application research project of Henan Transportation Department (No. 2016-2-5), Innovative scientific research project of Hainan Province (No. Hys2020-77) and Research project of Hainan Research Institute of China Engineering Science and technology development strategy (No. 19-HN-XZ-08).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Cano, Z. P., Banham, D., Ye, S., Hintennach, A., Lu, J., Fowler, M., et al. (2018). Batteries and Fuel Cells for Emerging Electric Vehicle Markets. Nat. Energ. 3 (4), 279–289. doi:10.1038/s41560-018-0108-1
Chen, Y., Huang, D., Zhu, Q., Liu, W., Liu, C., and Xiong, N. (2017). A New State of Charge Estimation Algorithm for Lithium-Ion Batteries Based on the Fractional Unscented Kalman Filter. Energies 10 (9), 1313. doi:10.3390/en10091313
Chen, Y., Yang, G., Liu, X., and He, Z. (2019). A Time-Efficient and Accurate Open Circuit Voltage Estimation Method for Lithium-Ion Batteries. Energies 12 (9), 1803. doi:10.3390/en12091803
Guo, L., Li, J., and Fu, Z. (2019). Lithium-Ion Battery SOC Estimation and Hardware-In-The-Loop Simulation Based on EKF. Energ. Proced. 158, 2599–2604. doi:10.1016/j.egypro.2019.02.009
He, H., Qin, H., Sun, X., and Shui, Y. (2013). Comparison Study on the Battery SoC Estimation with EKF and UKF Algorithms. Energies 6 (10), 5088–5100. doi:10.3390/en6105088
He, W., Williard, N., Chen, C., and Pecht, M. (2014). State of Charge Estimation for Li-Ion Batteries Using Neural Network Modeling and Unscented Kalman Filter-Based Error Cancellation. Int. J. Electr. Power Energ. Syst. 62, 783–791. doi:10.1016/j.ijepes.2014.04.059
Hu, X., Li, S., and Peng, H. (2012). A Comparative Study of Equivalent Circuit Models for Li-Ion Batteries. J. Power Sourc. 198, 359–367. doi:10.1016/j.jpowsour.2011.10.013
Li, X., Zhang, L., Wang, Z., and Dong, P. (2019). Remaining Useful Life Prediction for Lithium-Ion Batteries Based on a Hybrid Model Combining the Long Short-Term Memory and Elman Neural Networks. J. Energ. Storage 21, 510–518. doi:10.1016/j.est.2018.12.011
Liu, C., Liu, W., Wang, L., Hu, G., Ma, L., and Ren, B. (2016). A New Method of Modeling and State of Charge Estimation of the Battery. J. Power Sourc. 320, 1–12. doi:10.1016/j.jpowsour.2016.03.112
Liu, H., Li, S., Wang, H., and Sun, Y. (2018). Adaptive Fuzzy Control for a Class of Unknown Fractional-Order Neural Networks Subject to Input Nonlinearities and Dead-Zones. Inf. Sci. 454-455, 30–45. doi:10.1016/j.ins.2018.04.069
Meng, J., Luo, G., and Gao, F. (2016). Lithium Polymer Battery State-Of-Charge Estimation Based on Adaptive Unscented Kalman Filter and Support Vector Machine. IEEE Trans. Power Elect. 31 (3), 2226–2238. doi:10.1109/TPEL.2015.2439578
Mu, H., Xiong, R., Zheng, H., and Chang, Y. (2017). A Novel Fractional Order Model Based State-Of-Charge Estimation Method for Lithium-Ion Battery. Appl. Energ. 207, 384–393. doi:10.1016/j.apenergy.2017.07.003
Peng, S., Zhu, X., Yinjiao, X., Hongbing, S., Cai, X., and Pecht, M. (2018). An Adaptive State of Charge Estimation Approach for Lithium-Ion Series-Connected Battery System. J. Power Sourc. 392, 48–59. doi:10.1016/j.jpowsour.2018.04.101
Pizarro-Carmona, V., and Castano-Solis, S. (2021). GA-based Approach to Optimize an Equivalent Electric Circuit Model of a Li-Ion Battery-Pack. Expert Syst. Appl. 172 (8), 114647. doi:10.1016/j.eswa.2021.114647
Plett, G. L. (2004). Extended Kalman Filtering for Battery Management Systems of LiPB-Based HEV Battery Packs. J. Power Sourc. 134 (2), 277–292. doi:10.1016/j.jpowsour.2004.02.033
Richard, L. M. (2010). Fractional Calculus Models of Complex Dynamics in Biological Tissues. Comput. Math. Appl. 59, 1586–1593. doi:10.1016/j.camwa.2009.08.039
Shen, J.-N., Shen, J.-J., He, Y.-J., and Ma, Z.-F. (2019). Accurate State of Charge Estimation with Model Mismatch for Li-Ion Batteries: A Joint Moving Horizon Estimation Approach. IEEE Trans. Power Elect. 34 (5), 4329–4342. doi:10.1109/TPEL.2018.2861730
Shrivastava, P., Soon, T. K., Idris, M. Y. I. B., and Mekhilef, S. (2019). Overview of Model-Based Online State-Of-Charge Estimation Using Kalman Filter Family Forlithium-Ion Batteries. Renew. Sust. Energ. Rev. 113, 109233. doi:10.1016/j.rser.2019.06.040
Srinivas, M., and Patnaik, L. M. (2002). Adaptive Probabilities of Crossover and Mutation in Genetic Algorithms. IEEE Trans. Syst. Man, Cybernetics, C. 24 (4), 656–667. doi:10.1109/21.286385
Sun, Q., Zhang, H., Zhang, J., and Ma, W. (2018). Adaptive Unscented Kalman Filter with Correntropy Loss for Robust State of Charge Estimation of Lithium-Ion Battery. Energies 11 (11), 3123. doi:10.3390/en11113123
Tian, Y., Li, D., Tian, J., and Xia, B. (2017). State of Charge Estimation of Lithium-Ion Batteries Using an Optimal Adaptive Gain Nonlinear Observer. Electrochimica Acta 225, 225–234. doi:10.1016/j.electacta.2016.12.119
Wang, B., Li, S. E., Peng, H., and Liu, Z. (2015). Fractional-order Modeling and Parameter Identification for Lithium-Ion Batteries. J. Power Sourc. 293, 151–161. doi:10.1016/j.jpowsour.2015.05.059
Wang, Y., Zhang, C., and Chen, Z. (2018). On-line Battery State-Of-Charge Estimation Based on an Integrated Estimator. Appl. Energ. 185, 2026–2032. doi:10.1016/j.apenergy.2015.09.015
Wang, Z., Feng, G., Zhen, D., Gu, F., and Ball, A. (2021). A Review on Online State of Charge and State of Health Estimation for Lithium-Ion Batteries in Electric Vehicles. Energ. Rep. 7, 5141–5164. doi:10.1016/j.egyr.2021.08.113
Westerlund, S., and Ekstam, L. (1994). Capacitor Theory. Dielectrics & Electrical Insulation IEEE Transactions on, 827–839. doi:10.1109/94.326654
Xu, J., Mi, J. C., Cao, B., and Cao, J. (2013). A New Method to Estimate the State of Charge of Lithium-Ion Batteries Based on the Battery Impedance Model. J. Power Sourc. 233, 277–284. doi:10.1016/j.jpowsour.2013.01.094
Yang, Q., Xu, J., Li, X., Xu, D., and Cao, B. (2020). State-of-health Estimation of Lithium-Ion Battery Based on Fractional Impedance Model and Interval Capacity. Int. J. Electr. Power Energ. Syst. 119, 105883. doi:10.1016/j.ijepes.2020.105883
Zhang, W., Shi, W., and Ma, Z. (2015). Adaptive Unscented Kalman Filter Based State of Energy and Power Capability Estimation Approach for Lithium-Ion Battery. J. Power Sourc. 289, 50–62. doi:10.1016/j.jpowsour.2015.04.148
Zhou, S., Liu, X., Hua, Y., Zhou, X., and Yang, S. (2021). Adaptive Model Parameter Identification for Lithium-Ion Batteries Based on Improved Coupling Hybrid Adaptive Particle Swarm Optimization- Simulated Annealing Method. J. Power Sourc. 482, 228951. doi:10.1016/j.jpowsour.2020.228951
Zhu, Q., Xiong, N., Yang, M. L., Huang, R.-S., and Hu, G.-D. (2017). State of Charge Estimation for Lithium-Ion Battery Based on Nonlinear Observer: An H∞ Method. Energies 10 (5), 679. doi:10.3390/en10050679
Keywords: lithium-ion battery, fractional-order model, fractional order unscented kalman filter, state of charge, adaptive genetic algorithm
Citation: Fang C, Jin Z, Wu J and Liu C (2021) Estimation of Lithium-Ion Battery SOC Model Based on AGA-FOUKF Algorithm. Front. Energy Res. 9:769818. doi: 10.3389/fenrg.2021.769818
Received: 02 September 2021; Accepted: 18 October 2021;
Published: 05 November 2021.
Edited by:
Xianming Ye, University of Pretoria, South AfricaReviewed by:
Jiangwei Shen, Kunming University of Science and Technology, ChinaHuan Xi, Xi’an Jiaotong University, China
Copyright © 2021 Fang, Jin, Wu and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jingjin Wu, amluZ2ppbi53dUBoYWluYW51LmVkdS5jbg==
†These authors have contributed equally to this work and share first authorship
 Chao Fang
Chao Fang Zhiyang Jin1†
Zhiyang Jin1† Jingjin Wu
Jingjin Wu Chenguang Liu
Chenguang Liu