Numerical Simulation of Magnetic Dipole Flow Over a Stretching Sheet in the Presence of Non-Uniform Heat Source/Sink

The main objective of current communication is to present a mathematical model and numerical simulation for momentum and heat transference characteristics of Maxwell nanofluid flow over a stretching sheet. Further, magnetic dipole, non-uniform heat source/sink, and chemical reaction effects are considered. By using well-known similarity transformation, formulated flow equations are modelled into OD equations. Numerical solutions of the governing flow equations are attained by utilizing the shooting method consolidated with the fourth-order Runge-Kutta with shooting system. Graphical results are deliberated and scrutinized for the consequence of different parameters on fluid characteristics. Results reveal that the temperature profile accelerates for diverse values of space dependent parameter, but it shows opposite behaviour for escalated integrity of temperature dependent parameter.

Introduction

Fluids exhibiting non-Newtonian behavior were used in many engineering applications such as hydraulic fracturing, remediation, and solar heating applications and in several industrial processes. The motion of non-Newtonian fluids equations is extremely nonlinear when compared to Navier–Stokes’s equations. The models of non-Newtonian fluids are mainly parted into 3 groups: rate, integral, and differential type fluids. The model of fluid considered here is a sub-category of a rate type fluid which is called Maxwell fluid. The model of Maxwell fluid forecasts the impacts of relaxation time. These impacts cannot be projected by other fluid types. Nano-science is the specified excellent way of altering the personality of a liquid. Deportation of heat characteristics through nanofluid flow plays a major role in industrial and technological applications. Motivated by these applications, several researchers examined the Maxwell nano liquid stream past diverse surfaces. Irfan et al. (Irfan et al., 2018) explored the aspects of heat generation or sink and magnetic field on the Maxwell liquid wrapped up a cylinder. Prasannakumara et al. (Prasannakumara et al., 2018) studied the nanoparticles suspension on Maxwell fluid stream through stretchy geometry with Soret and Dufour effects. Ahmed et al. (Ahmed et al., 2019) used Maxwell nanofluid to scrutinize the impact of radiation effect. Ijaz and Ayub (Ijaz and Ayub, 2019) scrutinized the two-dimensional stream of a Maxwell nano liquid with the effect of activation energy. Ahmed et al. (Ahmed et al., 2020) studied the stream of Maxwell fluid impelled through gyrating disks on taking account of mixed convection and Karmann’s swirling flow of rate type nano liquid. The boundary layer stream with magnetic dipole has extensive applications in several engineering fields. Given this, recently, several researchers are showing keen interest in exploring the magnetic dipole effect on diverse liquid streams over different geometries. Initially, Khan et al. (Khan et al., 2021) studied the magnetic dipole and thermal radiation impacts on stagnation point flow of micropolar-based nanofluids over a vertical stretching sheet. Ali et al. (Ali et al., 2021) investigated the magnetic dipole and thermal radiation effects on hybrid base micropolar CNTs flow over a stretching sheet: Finite element method approach. Veeranna et al. (Veeranna et al., 2021) discussed the effect of Stefan blowing and magnetic dipole on chemically reactive second-grade nanomaterial flow over a stretching sheet. Prasannakumara (Prasannakumara, 2021) analyzed the numerical simulation of heat transport in Maxwell nanofluid flow over a stretching sheet considering the magnetic dipole effect. Waqas et al. (Waqas et al., 2021) studied the numerical simulation for a magnetic dipole in bioconvection flow of Jeffrey nanofluid with swimming motile microorganisms.

The non-uniform heat source/sink effect in the heat transference is another excellent consideration in several realistic issues. The various types of fluids through different surfaces with the impact of inhomogeneous reaction were argued by various researchers. Basha et al. (Basha et al., 2018) examined the irregular uniform heat sink/generation effect on chemically reacting nano liquid stream through a cone and plate. Elgazery (Elgazery, 2019) explored the nano liquid flow past a porous instable stretchy surface with in homogeneous heat source/sink. Irfan et al. (Irfan et al., 2020) deliberated the heat sink/source features on Maxwell nano liquid stream through an extended cylinder. Recently, Tawade et al. (Tawade et al., 2021) discussed the radiant heat and non-uniform heat source on MHD Casson fluid flow of thin liquid film beyond a stretching sheet. Xu et al. (Xu et al., 2021) investigated the non-uniform heat source/sink features for enhancing the thermal efficiency of third-grade nano fluid containing microorganisms. Shi et al. (Shi et al., 2021) discussed the heat and mass transfer analysis in the MHD flow of radiative Maxwell nanofluid with a non-uniform heat source/sink.

A chemical reaction is a spacious range of applications in the fields of chemical engineering and industries. It is necessary to concentrate the flow of heat or mass, subjected with components in the same or different phases of chemical reactions. Khan et al. (Khan et al., 2020) deliberate the consequence of Arrhenius energy in the chemical gyrating stream by considering non-linear heat flux. Asma et al. (Asma et al., 2020) scrutinized the MHD stream of nano liquid due to a gyrating disc with the significant impact of activation reaction. Santhi et al. (Santhi et al., 2021) studied the heat and mass transfer characteristics of radiative hybrid nanofluid flow over a stretching sheet with a chemical reaction. Reddy et al. (Reddy et al., 2021) discussed the chemical reaction impact on MHD natural convection flow through porous medium past an exponentially stretching sheet in presence of heat source/sink and viscous dissipation. Sandhya et al. (Sandhya et al., 2021) studied the Casson nanofluid thin film flow over a stretching sheet with viscous dissipation and chemical reaction.

In fluid mechanics, the scrutiny of the various physical and chemical phenomenon on the flow of different liquids over a stretching surface has assisted many researchers in developing numerous applications related to real-life problems and industrial areas. This inspection helps us to study the control rate of heat flow and is applicable in the areas like production of paper sheets, extruding polymers, crystals, glass, fibers, electronic chips, and metallic sheets. Abbas et al. (Abbas et al., 2020) explored the stream of micropolar fluid with hybrid nanoparticles over a stretching sheet. Asghar et al. (Asghar et al., 2020) delineated the mixed convective stream of a Williamson liquid caused by an elastic surface. Ramadevi et al. (Ramadevi et al., 2019) discussed the non-uniform heat source/sink on the three-dimensional magnetohydrodynamic Carreau fluid flow past a stretching surface with modified Fourier’s law. Kumaran and Sandeep (Kumaran and Sandeep, 2017) studied the thermophoresis and Brownian moment effects on parabolic flow of MHD Casson and Williamson fluids with cross diffusion. Kumar et al. (Kumar et al., 2019a) investigated the simultaneous solutions for MHD flow of Williamson fluid over a curved sheet with non-uniform heat source/sink. Kumar et al. (Kumar et al., 2019b) discussed the MHD stagnation point flow of Williamson and Casson fluids past an extended cylinder: a new heat flux model. Many related publications can be found also in the references (Saha et al., 2012; Bhattacharyya et al., 2016; Bhattacharyya et al., 2018; Bhattacharyya et al., 2019; Bhattacharyya, 2020a; Bhattacharyya et al., 2020a; Bhattacharyya, 2020b; Bhattacharyya et al., 2020b; Souayeh et al., 2021).

The detailed literature survey delivered that no study exists in the literature dealing with the analysis of magnetic dipole flow suspended with Nimonic 80 A–AA7075 nanoparticles. Hence, a sincere effort has been made to analyse such a flow numerically through RKF −45 with shooting system. The basic PDEs are developed with the help of boundary layer theory and reduced into highly nonlinear ODEs with the guidance of transforming variables. Numerical solutions for the considered investigation are achieved. The heat transfer properties, mass transfer properties, and flow features under the influence of various physical parameters are also studied.

Mathematical Formulation

Consider a steady, incompressible, and two-dimensional flow of Maxwell nanofluid in the presence of magnetic dipole, chemical reaction, and non-uniform heat source/sink over a stretching sheet. Two equal and opposite forces are applied along the x-axis so that the wall is stretched, keeping the origin fixed. The steady two-dimensional boundary layer equations for this fluid in usual notation are (Sarada et al., 2021):

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0(1)$

$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{{\mu }_{nf}}{{\rho }_{nf}}\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\right)+\frac{{\mu }_{0}M}{{\rho }_{nf}}\frac{\partial H}{\partial x}+\mathrm{\Gamma }\left\{u^2\frac{{\partial }^{2}u}{\partial x^2}+2uv\frac{{\partial }^{2}u}{\partial x\partial y}+v^2\frac{{\partial }^{2}u}{\partial y^2}\right\}(2)$

$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_{nf}}{{\left(\rho C_p\right)}_{nf}}\left(\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial y^2}\right)-\frac{{\mu }_{0}T}{{\left(\rho C_p\right)}_{nf}}\frac{\partial M}{\partial T}\left(u\frac{\partial H}{\partial x}+v\frac{\partial H}{\partial y}\right)+\frac{q‴}{{\left(\rho C_p\right)}_{nf}}\}(3)$

$u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D_{nf}\left(\frac{{\partial }^{2}C}{\partial x^2}+\frac{{\partial }^{2}C}{\partial y^2}\right)-k_r\left(C-C_c\right)(4)$

where ${\mu }_{0}M\frac{\partial H}{\partial x}$ signifies the ferromagnetic force per unit volume.

The corresponding boundary constraints are as follow:

$\begin{array}{l}y=0:u=cx,v=0,T=T_w,C=C_w,\\ y\to \infty :u=0,T=T_c,C=C_c.\end{array}\}(5)$

where the non-dimensional form of $q^{‴}$ is given by (Gireesha et al., 2019; Kumar et al., 2020).

$\mathit{q}‴=\frac{{\mathit{k}}_{nf}c}{{\mathit{\nu }}_{nf}}\left[{\mathit{A}}^{\ast }\left(T_w-T_c\right){\mathit{f}}^{\prime }+{\mathit{B}}^{\ast }\left(T-T_c\right)\right]$

Moreover, $A^{\ast }>0$ and $B^{\ast }>0$ defines the heat generation state, while $A^{\ast }<0$ and $B^{\ast }<0$ resembles to the internal heat absorption of the system.

Due to the magnetic dipole, the assumed liquid flow is affected by the magnetic field, whose magnetic scalar potential is given by (Everts et al., 2020):

${\varphi }_1=\frac{x}{{\left(y+a\right)}^2+x^2}\frac{\alpha }{2\pi }(6)$

and the corresponding magnetic field $H$ has the components

$H_y=-\frac{\partial {\varphi }_1}{\partial y}=\frac{2\left(y+a\right)x}{{\left({\left(y+a\right)}^2+x^2\right)}^2}\frac{\gamma }{2\pi }(7)$

$H_x=-\frac{\partial {\varphi }_1}{\partial x}=-\frac{{\left(y+a\right)}^2-x^2}{{\left({\left(y+a\right)}^2+x^2\right)}^2}\frac{\gamma }{2\pi }.(8)$

Since the magnetic body force is proportional to the gradient of the magnitude of $H$ and using

$H={\left[{\left(\frac{\partial {\varphi }_1}{\partial y}\right)}^2+{\left(\frac{\partial {\varphi }_1}{\partial x}\right)}^2\right]}^{1/2},(9)$

we attain that

$\frac{\partial H}{\partial y}=\left[\frac{4x^2}{{\left(y+a\right)}^5}-\frac{2}{{\left(y+a\right)}^3}\right]\frac{\gamma }{2\pi }(10)$

$\frac{\partial H}{\partial x}=\left[-\frac{2x}{{\left(y+a\right)}^4}\right]\frac{\gamma }{2\pi }(11)$

Assuming that the applied field $H$ is sufficiently strong to saturate the assumed fluid and the variation of magnetization M with temperature T is approximated by the linear equation

$M=K\left(T_c-T\right)(12)$

We introduce the following the dimensionless coordinates and dimensionless variables as follows:

$\left(\eta ,\xi \right)=\sqrt{\frac{c}{{\nu }_f}}\left(y,x\right),\psi \left(\xi ,\eta \right)=\left(\frac{{\mu }_f}{{\rho }_f}\right)\xi .f\left(\eta \right),$

$T=T_c-\left(T_c-T_w\right)\theta \left(\xi ,\eta \right)=T_c-\left(T_c-T_w\right)\left[{\theta }_1\left(\eta \right)+{\xi }^2{\theta }_2\left(\eta \right)\right]C=C_c-\left(C_c-C_w\right)\chi \left(\xi ,\eta \right)$

The velocity components $u$ and $v$ are related to the physical stream function $\psi$ according to

$u=\frac{\partial \psi }{\partial y}=cx{f}^{\prime }(\eta ),v=-\frac{\partial \psi }{\partial x}=-\sqrt{c{\nu }_f}f\left(\eta \right)$

where the dynamic viscosity, density, specific heat capacity, and thermal conductivity of nanofluid are given by:

${\mu }_{nf}=\frac{{\mu }_f}{{\left(1-\varphi \right)}^{2.5}}$

${\rho }_{nf}=\left(1-\varphi \right){\rho }_f+\varphi {\rho }_s,$

${\left(\rho C_p\right)}_{nf}=\left(1-\varphi \right){\left(\rho C_p\right)}_f+\varphi {\left(\rho C_p\right)}_s,$

$\frac{k_{nf}}{k_f}=\frac{k_s+2k_f-2\varphi \left(k_f-k_s\right)}{k_s+2k_f+\varphi \left(k_f-k_s\right)}.$

The equation of continuity is trivially satisfied, whereas moment and thermal equations are converted to corresponding set of ordinary differential equations:

${\epsilon }_{1}f‴-{\mathrm{f\prime }}^2+ff″-{\epsilon }_2\frac{2\beta {\theta }_1}{{\left(\eta +\alpha \right)}^4}+{\Gamma }_1\left\{-2f″f^{\prime }f+f^{2}f‴\right\}=0,(13)$

${\epsilon }_3\frac{k_{nf}}{k_f}\frac{1}{\mathrm{Pr}}{\theta }_1^{″}+f{\theta }_1^{\prime }+\frac{2{\theta }_2}{\mathrm{Pr}}+{\epsilon }_3\frac{1}{\mathrm{Pr}}\frac{2\lambda \beta }{{\left(\eta +\alpha \right)}^3}f\left({\theta }_1-\epsilon \right)+\frac{k_{nf}}{k_f}\frac{{\epsilon }_3}{{\epsilon }_1}\frac{1}{\mathrm{Pr}}\left[A^{\ast }{f}^{\prime }+B^{\ast }{\theta }_1\right]=0,(14)$

$\begin{array}{l}{\epsilon }_3\frac{k_{nf}}{k_f}\frac{1}{\mathrm{Pr}}{\theta }_2^{″}+f{\theta }_2^{\prime }-2f^{\prime }{\theta }_2+{\epsilon }_3\frac{1}{\mathrm{Pr}}\frac{2\lambda \beta }{{\left(\eta +\alpha \right)}^3}f{\theta }_2-{\epsilon }_3\frac{\lambda \beta \left({\theta }_1-\epsilon \right)}{\mathrm{Pr}}\left[\frac{4f}{{\left(\eta +\alpha \right)}^5}+\frac{2f^{\prime }}{{\left(\eta +\alpha \right)}^4}\right]\\ +\frac{k_{nf}}{k_f}\frac{{\epsilon }_3}{{\epsilon }_1}\frac{1}{\mathrm{Pr}}{B}^{\ast }{\theta }_2=0,\end{array}\}(15)$

${\left(1-\varphi \right)}^{2.5}\frac{1}{Sc}{\chi }_1^{″}+f{\chi }_1^{\prime }+{\left(1-\varphi \right)}^{2.5}\frac{2{\chi }_2}{Sc}-\sigma {\chi }_1=0(16)$

where

${\epsilon }_1=\frac{1}{{\left(1-\varphi \right)}^{2.5}\left[1-\varphi +\varphi \frac{{\rho }_s}{{\rho }_f}\right]},{\epsilon }_2=\frac{1}{\left[1-\varphi +\varphi \frac{{\rho }_s}{{\rho }_f}\right]},{\epsilon }_3=\frac{1}{\left[1-\varphi +\varphi \frac{{\left(\rho C_p\right)}_s}{{\left(\rho C_p\right)}_f}\right]}.$

Corresponding reduced boundary conditions

$\begin{array}{l}f\left(0\right)=0,f^{\prime }\left(0\right)=1,{\theta }_1\left(0\right)=1,{\theta }_2\left(0\right)=0,{\chi }_1\left(0\right)=1,{\chi }_2\left(0\right)=0,\\ f^{\prime }\left(\infty \right)\to 0,{\theta }_1\left(\infty \right)\to 0,{\theta }_2\left(\infty \right)\to 0,{\chi }_1\left(\infty \right)\to 0,{\chi }_2\left(\infty \right)\to 0.\end{array}\}(17)$

where

$\alpha =\sqrt{\frac{c}{{\nu }_f}}a,{\mathrm{\Gamma }}_1=\mathrm{\Gamma }c,\beta ={\mu }_{0}K\frac{\gamma {\rho }_f}{2\pi {\mu }_f^2}\left(T_c-T_w\right),\epsilon =\frac{T_c}{\left(T_c-T_w\right)},\lambda =\frac{c{\mu }_f^2}{k_f{\rho }_f\left(T_c-T_w\right)},\mathrm{Pr}=\frac{{\mu }_f{C}_p}{k_f},\sigma =\frac{k_r}{c},Sc=\frac{{\nu }_f}{D_f},\mathrm{Re}=\frac{c{x}^2}{{\nu }_f}$

Physical quantities of practical interest in their dimensionless form are as follows (Abel and Nandeppanavar, 2009; Rehman et al., 2017; Aleem et al., 2020):

$\sqrt{\mathrm{Re}}{C}_f=-\frac{\left(1+{\mathrm{\Gamma }}_1\right)f^{″}\left(0\right)}{{\left(1-\varphi \right)}^{2.5}}(18)$

${\mathrm{Re}}^{-1/2}Nu=-\frac{k_{nf}}{k_f}\left[{\theta }_1^{\prime }\left(0\right)+{\xi }^2{\theta }_2^{\prime }\left(0\right)\right](19)$

${\mathrm{Re}}^{-1/2}Sh=-{\left(1-\varphi \right)}^{2.5}\left[{\chi }_{\mathrm{1}}^{\prime }\left(0\right)\right](20)$

Numerical Method

The dimensionless arrangement of Eqs 13–16 with the conditions (17) is profoundly coupled differential conditions. One needs to turn towards numerical strategies to acquire the arrangement of such conditions. In this investigation, we have utilized the method Runge–Kutta–Fehlberg fourth–fifth order with shooting system. The calculations have been done utilizing the representative programming Maple.

The algorithm of Runge-Kutta-Fehlberg–forth-fifth order method is given by:

$k_0=F\left(\overline{x_m},\overline{y_m}\right)$

$k_1=F\left(\overline{x_m}+\frac{h}{4},\overline{y_m}+\frac{h{k}_0}{4}\right)$

$k_2=F\left(\overline{x_m}+\frac{3}{8}h,\overline{y_m}+\left(\frac{3}{32}{k}_0+\frac{9}{32}{k}_1\right)h\right)$

$k_3=F\left(\overline{x_m}+\frac{12}{13}h,\overline{y_m}+\left(\frac{1932}{2197}{k}_0-\frac{7200}{2197}{k}_1+\frac{7296}{2197}{k}_2\right)h\right)$

$k_4=F\left(\overline{x_m}+h,\overline{y_m}+\left(\frac{439}{216}{k}_0-8k_1+\frac{3860}{513}{k}_2-\frac{845}{4104}{k}_3\right)h\right)$

$k_5=F\left(\overline{x_m}+\frac{h}{2},\overline{y_m}+\left(-\frac{8}{27}{k}_0+2k_1-\frac{3544}{2565}{k}_2+\frac{1859}{4104}{k}_3-\frac{11}{40}{k}_4\right)h\right)$

$\overline{y_{m+1}}=\overline{y_m}+h\left(\frac{25}{216}{k}_0+\frac{1408}{2565}{k}_2+\frac{2197}{4109}{k}_3-\frac{1}{5}{k}_4\right)$

$\overline{y_{m+1}}=\overline{y_m}+h\left(\frac{16}{135}{k}_0+\frac{6656}{12825}{k}_2+\frac{28561}{56430}{k}_3-\frac{9}{50}{k}_4+\frac{2}{55}{k}_5\right)$

Results and Discussion

In this segment, the effects of assorted specification, namely, Maxwell parameter ${\Gamma }_1$, space dependent parameter $A^{\ast }$ , ferromagnetic interaction parameter $\beta$, temperature dependent parameter $B^{\ast }$, and reaction rate parameter $\sigma$ on the fluid profiles such as radial velocity $f^{\prime }$, temperature profile ${\theta }_1$, and concentration profile ${\chi }_1$, are explained via graphs. Also, deviation in the drag force, transfer heat rate, and Sherwood number for disparate values of corresponding specification are discussed here. The dominant nonlinear PD equations are reduced into terminated ODEs by using suitable analogy variables, and the obtained expressions are tackled numerically with the aid of RKF 45 with shooting system arrangement by employing shooting pattern. The material features of the carrier liquid engine oil and nanoparticle subsistence appropriate in this work are manifest in Table 1.

TABLE 1

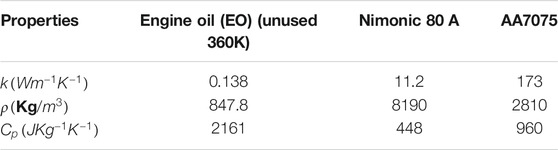
TABLE 1. The material features of the base fluid and nanoparticles (Reddy et al., 2020; Tlili et al., 2020; Raju et al., 2021).

Figure 1 elucidates the nature of radial velocity $f^{\prime }$ against diverse values of ferromagnetic interaction parameter $\beta$. It clarifies that $f^{\prime }$ declines significantly for higher values of $\beta$. Physically, the Lorentz force deviates for the augmentation of magnetic parameter and this force causes additional resistance to the transport process. The consequence of Maxwell parameter ${\Gamma }_1$ on $f^{\prime }$ for both fluids is exemplified via Figure 2. In this figure, we can perceive that radial acceleration is a developing function of Maxwell restriction and, moreover, $f^{\prime }$ heightens for augmentation of ${\Gamma }_1$.

FIGURE 1

FIGURE 1. Provocation of $\beta$ on $f^{\prime }$.

FIGURE 2

FIGURE 2. Provocation of ${\mathrm{\Gamma }}_1$ on $f^{\prime }$.

Figure 3 portrays the behavior of temperature profile ${\theta }_1$ for enhancement in the temperature dependent parameter $B^{\ast }$. It indicates that ${\theta }_1$ decreases rapidly with an improvement of $B^{\ast }$. Physically, the presence of non-uniform heat source parameters provides less heat to the system which decayed the transportation process. The impact of space dependent parameter $A^{\ast }$ on ${\theta }_1$ for both liquids is described in Figure 4. This figure explains the enhancing nature of ${\theta }_1$ for heightening values of $A^{\ast }$. It happens because of the existence of heat source specification innards the flow field transfers additional hotness, and this phenomenon is the reason for the growth of thermal boundary layer thickness.

FIGURE 3

FIGURE 3. Provocation of $B^{\ast }$ on ${\theta }_1$.

FIGURE 4

FIGURE 4. Provocation of $A^{\ast }$ on ${\theta }_1$.

The consequence of $\beta$ on ${\theta }_1$ is explained in Figure 5. It signifies that an improvement in $\beta$ values upsurges the temperature profile ${\theta }_1$ remarkably. The influence of $Sc$ on ${\chi }_1$ is explicated by Figure 6. From this figure, one can conclude that $Sc$ has a major impact on ${\chi }_1$ and it is perceived that the solute outline layer stiffness is a declining activity of $Sc$. This is because $Sc$ is the ratio of momentum diffusivity to mass diffusivity, and bulkier attitude of $Sc$ correlates to a limited mass diffusivity. Hence, concentration profile ${\chi }_1$ declines for both liquids.

FIGURE 5

FIGURE 5. Provocation of $\beta$ on ${\theta }_1$.

FIGURE 6

FIGURE 6. Provocation of $Sc$ on ${\chi }_1$.

Figure 7 illustrates the consequence of $\sigma$ on ${\chi }_1$ for both the liquid cases. This figure confirms that ${\chi }_1$ exhibits decreasing nature for diverse values of $\sigma$, and an enhancement in the reaction rate parameter $\sigma$ reduces the concentration of the liquids. Physically, as the values of reaction rate parameter heightens concentration field and associated solutal layer thickness is reduced.

FIGURE 7

FIGURE 7. Provocation of $\sigma$ on ${\chi }_1$.

Figures 8, 9 describe the variations in surface drag force $C_f$ against ${\Gamma }_1$ for diverse values of $\beta$ and $\varphi$, respectively. The deviation in the heat transfer rate $Nu$ against space dependent parameter $A^{\ast }$ for ${\Gamma }_1$ is indicated via Figure 10. Similarly, the variation in heat transfer rate $Nu$ against temperature dependent parameter $B^{\ast }$ for $\beta$ is illustrated (see Figure 11). Figure 12 demonstrates the fluctuation of Sherwood number against $\sigma$ for diverse character of $Sc$.

FIGURE 8

FIGURE 8. Change in ${\mathrm{Re}}^{-1/2}{C}_f$ for $\mathbf{\beta }$ versus ${\Gamma }_1$ .

FIGURE 9

FIGURE 9. Change in ${\mathrm{Re}}^{-1/2}{C}_f$ for $\varphi$ versus ${\Gamma }_1$.

FIGURE 10

FIGURE 10. Change in ${\mathrm{Re}}^{-1/2}Nu$ for ${\Gamma }_1$ versus $A^{\ast }$.

FIGURE 11

FIGURE 11. Change in ${\mathrm{Re}}^{-1/2}Nu$ for $\mathbf{\beta }$ versus $B^{\ast }$.

FIGURE 12

FIGURE 12. Change in ${\mathrm{Re}}^{-1/2}Sh$ for $Sc$ versus $\sigma$.

Final Remarks

In the present study, the ferromagnetic stream of a Maxwell nano liquid over a sheet with heat sink/source and chemical reaction effects is inspected. Advisable correlation transformations are occupied to attain the corresponding set of ODEs and are numerically solved with the assistance of Runge-Kutta-Fehlberg-45 with shooting system performance onward with shooting arrangement. The main outcomes of the present investigation are given below:

• The existence of heat source specification innards the flow field transfers additional hotness, and this phenomenon is the reason for the growth of temperature profile.

• The presence of non-uniform heat source parameter $\left(B^{\ast }\right)$ provides less heat to the system which decayed the temperature profile.

• $Sc$ is the ratio of momentum diffusivity to mass diffusivity. A larger value of $Sc$ decreases the concentration profile.

• Velocity profile enhances with an increment value of ${\Gamma }_1$, whereas it declines for escalation of $\beta$.

• As the values of the chemical reaction parameter enhance, the concentration profile decreases.

• Momentum boundary layer thickness is higher in larger values of ${\text{Γ}}_1$.

• Solutal boundary layer thickness is scaled back for larger values of $Sc$.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

Conceptualization, BS and MK; methodology, BS; software, BS and MK; validation, BS, MA, and SH; formal analysis, BS and SH; investigation, BS, MA, MK, and SH; writing—review and editing, BS, MA, MK, and SH.

Funding

The authors acknowledge the Deanship of Scientific Research at King Faisal University for the financial support under Nasher track (Grant No. 206099).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbas, N., Nadeem, S., and Malik, M. Y. (2020). On Extended Version of Yamada-Ota and Xue Models in Micropolar Fluid Flow under the Region of Stagnation point. Physica A: Stat. Mech. its Appl. 542, 123512. doi:10.1016/j.physa.2019.123512

CrossRef Full Text | Google Scholar

Abel, M. S., and Nandeppanavar, M. M. (2009). Heat Transfer in MHD Viscoelastic Boundary Layer Flow over a Stretching Sheet with Non-uniform Heat Source/sink. Commun. Nonlinear Sci. Numer. Simulation 14 (5), 2120–2131. doi:10.1016/j.cnsns.2008.06.004

CrossRef Full Text | Google Scholar

Ahmed, A., Khan, M., and Ahmed, J. (2020). Mixed Convective Flow of Maxwell Nanofluid Induced by Vertically Rotating cylinder. Appl. Nanosci. 2, 01320. doi:10.1007/s13204-020-01320-2

CrossRef Full Text | Google Scholar

Ahmed, J., Khan, M., and Ahmad, L. (2019). Transient Thin Film Flow of Nonlinear Radiative Maxwell Nanofluid over a Rotating Disk. Phys. Lett. A 383, 1300–1305. doi:10.1016/j.physleta.2019.01.024

CrossRef Full Text | Google Scholar

Aleem, M., Asjad, M. I., Shaheen, A., and Khan, I. (2020). MHD Influence on Different Water Based Nanofluids (TiO2, Al2O3, CuO) in Porous Medium with Chemical Reaction and Newtonian Heating, Chaos. Solitons & Fractals 130, 109437. doi:10.1016/j.chaos.2019.109437

CrossRef Full Text | Google Scholar

Ali, B., Siddique, I., Khan, I., Masood, B., and Hussain, S. (2021). Magnetic Dipole and thermal Radiation Effects on Hybrid Base Micropolar CNTs Flow over a Stretching Sheet: Finite Element Method Approach. Results Phys. 25, 104145. doi:10.1016/j.rinp.2021.104145

CrossRef Full Text | Google Scholar

Asghar, Z., Kousar, M., Waqas, M., Irfan, M., Bilal, M., and Khan, W. A. (2020). Heat Generation in Mixed Convected Williamson Liquid Stretching Flow under Generalized Fourier Concept. Appl. Nanosci 10 (12), 4439–4444. doi:10.1007/s13204-020-01500-0

CrossRef Full Text | Google Scholar

Asma, M., Othman, M., Muhammad, W. A., Mallawi, F., and Wong, B. R. (2020). Numerical Study for Magnetohydrodynamic Flow of Nanofluid Due to a Rotating Disk with Binary Chemical Reaction and Arrhenius Activation Energy. Symmetry 11 (10), 1282. doi:10.3390/sym11101282

CrossRef Full Text | Google Scholar

Basha, H. T., Sivaraj, R., Animasaun, I. L., and Makinde, O. D. (2018). Influence of Non-uniform Heat Source/sink on Unsteady Chemically Reacting Nanofluid Flow over a Cone and Plate. Ddf 389, 50–59. doi:10.4028/www.scientific.net/ddf.389.50

CrossRef Full Text | Google Scholar

Bhattacharyya, S., Benim, A. C., Chattopadhyay, H., and Banerjee, A. (2018). Experimental Investigation of Heat Transfer Performance of Corrugated Tube with spring Tape Inserts. Exp. Heat Transfer 32 (5), 411–425. doi:10.1080/08916152.2018.1531955

CrossRef Full Text | Google Scholar

Bhattacharyya, S., Chattopadhyay, H., and Benim, A. C. (2016). Heat Transfer Enhancement of Laminar Flow of Ethylene Glycol through a Square Channel Fitted with Angular Cut Wavy Strip. Proced. Eng. 157, 19–28. doi:10.1016/j.proeng.2016.08.333

CrossRef Full Text | Google Scholar

Bhattacharyya, S., Chattopadhyay, H., Guin, A., and Benim, A. C. (2019). Investigation of Inclined Turbulators for Heat Transfer Enhancement in a Solar Air Heater. Heat Transf. Eng. 40 (17–18), 1451–1460. doi:10.1080/01457632.2018.1474593

CrossRef Full Text | Google Scholar

Bhattacharyya, S. (2020). Fluid Flow and Heat Transfer in a Heat Exchanger Channel with Short-Length Twisted Tape Turbulator Inserts. Iran J. Sci. Technol. Trans. Mech. Eng. 44 (1), 217–227. doi:10.1007/s40997-018-0251-0

CrossRef Full Text | Google Scholar

Bhattacharyya, S., Hari, R. B., and Paul, A. R. (2020). The Effect of Circular Hole Spring Tape on the Turbulent Heat Transfer and Entropy Analysis in a Heat Exchanger Tube: An Experimental Study. Exp. Heat Transf 2020, 1–20. doi:10.1080/08916152.2020.1787560

CrossRef Full Text | Google Scholar

Bhattacharyya, S., Sarkar, D., Mahabaleshwar, U. S., Soni, M. K., and Mohanraj, M. (2020). Experimental Study of Thermohydraulic Characteristics and Irreversibility Analysis of Novel Axial Corrugated Tube with Spring Tape Inserts. Eur. Phys. J. Appl. Phys. 92 (3), 30901. doi:10.1051/epjap/2020200192

CrossRef Full Text | Google Scholar

Bhattacharyya, S. (2020). The Effects of Short Length and Full Length Swirl Generators on Heat Transfer and Flow Fields in a Solar Air Heater Tube. J. Therm. Anal. Calorim. 140 (3), 1355–1369. doi:10.1007/s10973-019-08764-x

CrossRef Full Text | Google Scholar

Elgazery, N. S. (2019). Nanofluids Flow over a Permeable Unsteady Stretching Surface with Non-uniform Heat Source/sink in the Presence of Inclined Magnetic Field. J. Egypt. Math. Soc. 27, 9. doi:10.1186/s42787-019-0002-4

CrossRef Full Text | Google Scholar

Everts, M., Bhattacharyya, S., Bashir, A. I., and Meyer, J. P. (2020). Heat Transfer Characteristics of Assisting and Opposing Laminar Flow through a Vertical Circular Tube at Low Reynolds Numbers. Appl. Therm. Eng. 179, 115696. doi:10.1016/j.applthermaleng.2020.115696

CrossRef Full Text | Google Scholar

Gireesha, B. J., Krishnamurthy, M. R., and Ganesh Kumar, K. (2019). Nonlinear Radiative Heat Transfer and Boundary Layer Flow of Maxwell Nanofluid Past Stretching Sheet. J. Nanofluids 8 (5), 1093–1102. doi:10.1166/JON.2019.1661

CrossRef Full Text | Google Scholar

Ijaz, M., and Ayub, M. (2019). Nonlinear Convective Stratified Flow of Maxwell Nanofluid with Activation Energy. Heliyon 5, e01121. doi:10.1016/j.heliyon.2019.e01121

PubMed Abstract | CrossRef Full Text | Google Scholar

Irfan, M., Khan, M., Khan, W. A., and Ayaz, M. (2018). Modern Development on the Features of Magnetic Field and Heat Sink/source in Maxwell Nanofluid Subject to Convective Heat Transport. Phys. Lett. A. 382 (30). doi:10.1016/j.physleta.2018.05.008

CrossRef Full Text | Google Scholar

Irfan, M., Khan, M., and Khan, W. A. (2020). Heat Sink/source and Chemical Reaction in Stagnation point Flow of Maxwell Nanofluid. Appl. Phys. A. 126 (11), 892. doi:10.1007/s00339-020-04051-x

CrossRef Full Text | Google Scholar

Khan, M. I., Nasir, T., Hayat, T., Khan, N. B., and Alsaedi, A. (2020). Binary Chemical Reaction with Activation Energy in Rotating Flow Subject to Nonlinear Heat Flux and Heat Source/sink. J. Comput. Des. Eng. 7, 279–286. doi:10.1093/jcde/qwaa023

CrossRef Full Text | Google Scholar

Khan, S. A., Ali, B., Eze, C., Lau, K. T., Ali, L., Chen, J., et al. (2021). Magnetic Dipole and thermal Radiation Impacts on Stagnation point Flow of Micropolar Based Nanofluids over a Vertically Stretching Sheet: Finite Element Approach. MDPI 9 (7), 1089. doi:10.3390/pr9071089

CrossRef Full Text | Google Scholar

Kumar, K. A., Reddy, J. R., Sugunamma, V., and Sandeep, N. (2019). Simultaneous Solutions for MHD Flow of Williamson Fluid over a Curved Sheet with Non-uniform Heat Source/sink. Heat Transfer Res. 50 (6). doi:10.1615/heattransres.2018025939

CrossRef Full Text | Google Scholar

Kumar, K. A., Sugunamma, V., Sandeep, N., and Reddy, J. R. (2019). MHD Stagnation point Flow of Williamson and Casson Fluids Past an Extended cylinder: a New Heat Flux Model. SN Appl. Sci. 1 (7), 1–11. doi:10.1007/s42452-019-0743-6

CrossRef Full Text | Google Scholar

Kumar, K. G., Reddy, M. G., Vijaya kumari, P., Aldalbahi, A., Rahimi-Gorji, M., and Rahaman, M. (2020). Application of Different Hybrid Nanofluids in Convective Heat Transport of Carreau Fluid. Chaos, Solitons & Fractals 141, 110350. doi:10.1016/j.chaos.2020.110350

CrossRef Full Text | Google Scholar

Kumaran, G., and Sandeep, N. (2017). Thermophoresis and Brownian Moment Effects on Parabolic Flow of MHD Casson and Williamson Fluids with Cross Diffusion. J. Mol. Liquids 233, 262–269. doi:10.1016/j.molliq.2017.03.031

CrossRef Full Text | Google Scholar

Prasannakumara, B. C. (2021). Numerical Simulation of Heat Transport in Maxwell Nanofluid Flow over a Stretching Sheet Considering Magnetic Dipole Effect. Partial Differential Equations Appl. Mathematics 4, 100064. doi:10.1016/j.padiff.2021.100064

CrossRef Full Text | Google Scholar

Prasannakumara, B. C., Reddy, M. G., Thammanna, G. T., and Gireesha, B. J. (2018). MHD Double-Diffusive Boundary-Layer Flow of a Maxwell Nanofluid over a Bidirectional Stretching Sheet with Soret and Dufour Effects in the Presence of Radiation. Nonlinear Eng. 7 (3), 58. doi:10.1515/nleng-2017-0058

CrossRef Full Text | Google Scholar

Raju, A., Ojjela, O., and Kambhatla, P. K. (2021). A Comparative Study of Heat Transfer Analysis on Ethylene Glycol or Engine Oil as Base Fluid with Gold Nanoparticle in Presence of thermal Radiation. J. Therm. Anal. Calorim. 145, 2647–2660. doi:10.1007/s10973-020-09757-x

CrossRef Full Text | Google Scholar

Ramadevi, B., Kumar, K. A., Sugunamma, V., and Sandeep, N. (2019). Influence of Non-uniform Heat Source/sink on the Three-Dimensional Magnetohydrodynamic Carreau Fluid Flow Past a Stretching Surface with Modified Fourier’s Law. Pramana 93 (6), 1–11. doi:10.1007/s12043-019-1847-7

CrossRef Full Text | Google Scholar

Reddy, M. G., Kumar, K. G., and Shehzad, S. A. (2020). A Static and Dynamic Approach of Aluminum Alloys (AA7072-Aa7075) over a Semi-infinite Heated Plate. Physica Scripta 95 (12), 125201. doi:10.1088/1402-4896/abbf20

CrossRef Full Text | Google Scholar

Reddy, N. N., Rao, V. S., and Reddy, B. R. (2021). Chemical Reaction Impact on MHD Natural Convection Flow through Porous Medium Past an Exponentially Stretching Sheet in Presence of Heat Source/sink and Viscous Dissipation. Case Stud. Therm. Eng. 25, 100879. doi:10.1016/j.csite.2021.100879

CrossRef Full Text | Google Scholar

Rehman, S. U. R., Zeeshan, A., Majeed, A., and Arain, M. B. (2017). Impact of Cattaneo-Christov Heat Flux Model on the Flow of Maxwell Ferromagnetic Liquid along a Cold Flat Plate Embedded with Two Equal Magnetic Dipoles. Jmag 22, 472–477. doi:10.4283/jmag.2017.22.3.472

CrossRef Full Text | Google Scholar

Saha, S. K., Bhattacharyya, S., and Pal, P. K. (2012). Thermohydraulics of Laminar Flow of Viscous Oil through a Circular Tube Having Integral Axial Rib Roughness and Fitted with Center-Cleared Twisted-Tape. Exp. Therm. Fluid Sci. 41, 121–129. doi:10.1016/j.expthermflusci.2012.04.004

CrossRef Full Text | Google Scholar

Sandhya, G., Malleswari, K., Sarojamma, G., Sreelakshmi, K., and Satya Narayana, P. V. (2021). Unsteady Casson Nanofluid Thin Film Flow over a Stretching Sheet with Viscous Dissipation and Chemical Reaction. Eur. Phys. J. Spec. Top. 230, 1–10. doi:10.1140/epjs/s11734-021-00033-z

CrossRef Full Text | Google Scholar

Santhi, M., Suryanarayana Rao, K. V., Sudarsana Reddy, P., and Sreedevi, P. (2021). Heat and Mass Transfer Characteristics of Radiative Hybrid Nanofluid Flow over a Stretching Sheet with Chemical Reaction. Heat Transfer 50 (3), 2929–2949. doi:10.1002/htj.22012

CrossRef Full Text | Google Scholar

Sarada, K., Gowda, R. J. P., Sarris, I. E., Kumar, R. N., and Prasannakumara, B. C. (2021). Effect of Magnetohydrodynamics on Heat Transfer Behaviour of a Non-newtonian Fluid Flow over a Stretching Sheet under Local thermal Non-equilibrium Condition. Fluids 6 (8), 264. doi:10.3390/fluids6080264

CrossRef Full Text | Google Scholar

Shi, Q.-H., Khan, M. N., Abbas, N., Khan, M. I., and Alzahrani, F. (2021). Heat and Mass Transfer Analysis in the MHD Flow of Radiative Maxwell Nanofluid with Non-uniform Heat Source/sink. Waves in Random and Complex Media 31, 1–24. doi:10.1080/17455030.2021.1978591

CrossRef Full Text | Google Scholar

Souayeh, B., Bhattacharyya, S., Hdhiri, N., and Waqas Alam, M. (2021). Heat and Fluid Flow Analysis and ANN-Based Prediction of A Novel Spring Corrugated Tape. Sustainability 13 (6), 3023. doi:10.3390/su13063023

CrossRef Full Text | Google Scholar

Tawade, J. V., Biradar, M., and Benal, S. S. (2021). “Influence of Radiant Heat and Non-uniform Heat Source on MHD Casson Fluid Flow of Thin Liquid Film beyond a Stretching Sheet,” in Recent Trends in Mathematical Modeling and High Performance Computing. Editors V. K. Singh, Y. D. Sergeyev, and A. Fischer, 23–36. doi:10.1007/978-3-030-68281-1_3

CrossRef Full Text | Google Scholar

Tlili, I., Nabwey, H. A., Ashwinkumar, G. P., and Sandeep, N. (2020). 3-D Magnetohydrodynamic AA7072-AA7075/methanol Hybrid Nanofluid Flow above an Uneven Thickness Surface with Slip Effect. Sci. Rep. 10 (1), 4265–4313. doi:10.1038/s41598-020-61215-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Veeranna, Y., Jayaprakash, M. C., Sreenivasa, G. T., and Lalitha, K. R. (2021). Effect of Stefan Blowing and Magnetic Dipole on Chemically Reactive Second-Grade Nanomaterial Flow over Stretching Sheet. Int. J. Ambient Energ. 12, 1–25. doi:10.1080/01430750.2021.1999325

CrossRef Full Text | Google Scholar

Waqas, H., Hussain, M., Alqarni, M. S., Eid, M. R., and Muhammad, T. (2021). Numerical Simulation for Magnetic Dipole in Bioconvection Flow of Jeffrey Nanofluid with Swimming Motile Microorganisms. Waves in Random and Complex Media 107, 1–18. doi:10.1080/17455030.2021.1948634

CrossRef Full Text | Google Scholar

Xu, Y. J., Khan, S. U., Al-Khaled, K., Khan, M. I., Alzahrani, F., and Khan, M. I. (2021). Effectiveness of Induced Magnetic Force and Non-uniform Heat Source/sink Features for Enhancing the thermal Efficiency of Third Grade Nanofluid Containing Microorganisms. Case Stud. Therm. Eng. 27, 101305. doi:10.1016/j.csite.2021.101305

CrossRef Full Text | Google Scholar

Glossary

$u,v$ Velocity components

$M$ Magnetization

$\mu$ Dynamic viscosity

$\Gamma$ Relaxation time

$H$ Magnetic field intensity

$Nu$ Nusselt number

$T$ Temperature of fluid

$\sigma$ Reaction rate parameter

$a$ Distance

$f\text{'}\left(\eta \right)$ Radial velocity

$\eta ,\xi$ Independent coordinate

$\alpha$ Dimensionless distance

$q\text{'}\text{'}\text{'}$ Non-uniform heat source/sink parameter

$f\theta$ Dimensionless temperature

${\theta }_1,{\theta }_2$ Dimensionless temperature

$A^{\ast }$ Space dependent parameter

$B^{\ast }$ Temperature dependent parameter

$\beta$ Ferromagnetic interaction parameter

$\mathrm{Pr}$ Prandtl number

${\Gamma }_1$ Maxwell parameter

$\lambda$ Viscous dissipation parameter

${\varphi }_1$ Scalar potential

$\psi$ Stream function

$\epsilon$ Dimensionless Curie temperature

$\mathrm{Re}$ Local Reynolds number

$x,y$ Coordinate axes

$\rho$ Density

${\mu }_0$ Magnetic permeability

$k$ Thermal conductivity

${\chi }_1$ Dimensionless concentration

$\rho C_p$ Heat capacitance

$\nu$ Kinematic viscosity

$C_f$ Skin friction

$Sc$ Schmidt number

$c$ Curie

$f$ fluid

$s_1$ Solid volume fraction of

$s_2$ Solid volume fraction of

$w$ Surface