- Shanghai Jiaotong University, Shanghai, China
The combined fission matrix theory is a recently-developed hybrid neutron transport method. It features high efficiency, fidelity, and resolution whole-core transport calculation. The theory is based on the assumption that the fission matrix element ai,j is dominated by the property of the destination cell i. This assumption can be well explained in thermal reactors, and the combined fission matrix method has been validated in a series of thermal neutron system benchmarks. This work examines the feasibility of the combined fission matrix theory in fast reactors. The European Sodium Fast Reactor is used as the numerical benchmark. Compared to the Monte Carlo method, the combined fission matrix theory reports a 64 pcm keff difference and 8.3% 2D RMS error. The error is much larger than that in thermal reactors, and the correction ratio cannot significantly reduce the material discontinuity error in fast reactors. Overall, the combined fission matrix theory is more suited for thermal reactor transport calculations. Its application in fast reactors needs further developments.
1 Introduction
The high-fidelity neutron transport method is a key technique in reactor design and safety analysis. There have been many such methods developed, including the deterministic MOC (Liu et al., 2011) method; the VNM method (Zhang et al., 2013, 2018); and the stochastic Monte Carlo method. Other than these traditional methods, the hybrid neutron transport method is gaining popularity in recent years. It pre-calculates a series of response functions and solves for the neutron transport deterministically relying on response functions. Such methods feature the combination of high accuracy from the Monte Carlo method and the high efficiency from the deterministic method.
The fission matrix method is originally proposed as an acceleration to the Monte Carlo neutron transport solver. A fission matrix describes the response of fission neutrons to a source neutron between spatial cells. The fission matrix element ai,j is defined as the number of fission neutrons produced in cell i per source neutron in cell j, and its detailed theory can be found in (Carney et al., 2014). The fission matrix from the neutron transport eigenmode equation can be written as:
Where k is the multiplication factor, Fj and Fi are the source and fission neutron distributions, and ai,j is the fission matrix element. The eigenvalue and the eigenvector represent the multiplication factor and fission source distribution of the system. However, the calculation of the fission matrix could be memory-challenging and time-consuming in an extensive system, such as a whole-core calculation. There are typically two methods to tally the fission matrix through Monte Carlo calculations, which are the criticality calculation and the fixed-source calculation. Taking a whole-core calculation as an example, the criticality calculation runs the iterative Monte Carlo simulation and tallies the fission matrix in each iterative cycle. Therefore, the fission matrix is tallied from a converged whole-core fission source and considered the most accurate result. On the other hand, a fission matrix can also be composed of a set of fixed-source calculations, each of which will yield a fission matrix column. However, the fixed-source calculation assumes a uniform source in each mesh cell, so the mesh used to perform the fixed-source calculation has to be fine enough to guarantee the fission matrix is not biased by the source distribution. Overall, the fission matrix derivation is time-consuming and memory-prohibitive for a whole core problem.
In order to obtain the system fission matrix efficiently, a fission matrix combination theory has been developed (Walters et al., 2018; Terlizzi and Kotlyar, 2019; Laureau et al., 2015). It assumes that the system fission matrix element ai,j is dependent only on the property of the destination cell i. Therefore, the system fission matrix can be estimated by combining a set of pre-calculated database fission matrices. The assumption relies on the fact that neutrons are thermalized before fissioning, and the thermal fission cross-section is much larger than the scattering cross-section. As a result, the destination cell property is more dominating in the number of fission neutrons than the intermediate or born cells. Based on the theory, a hybrid neutron transport code called RAPID has been developed. The combined fission matrix theory can perform high-fidelity and efficient whole-core pin-wise transport calculations. It is validated on the BEAVRS PWR benchmark (He and Walters, 2019, 2020), PSBR TRIGA reactor core (Topham et al., 2020; Rau and Walters, 2020), and UNF spent fuel cask benchmark (Mascolino et al., 2017). However, the promising methodology is mainly used and validated in thermal neutron systems. This paper will examine the validity of the combined fission matrix theory in the fast reactor whole-core transport calculations.
The paper will be organized as the following: In Section 2, a detailed overview of the combined fission matrix theory will be given for completeness of the paper. In Section 3, a Sodium Fast Reactor (SFR) numerical benchmark will be presented for the theory validation. Numerical results are shown in Section 4. Conclusions and future improvements are summarized in Section 5.
2 Overview of the Combined Fission Matrix Theory
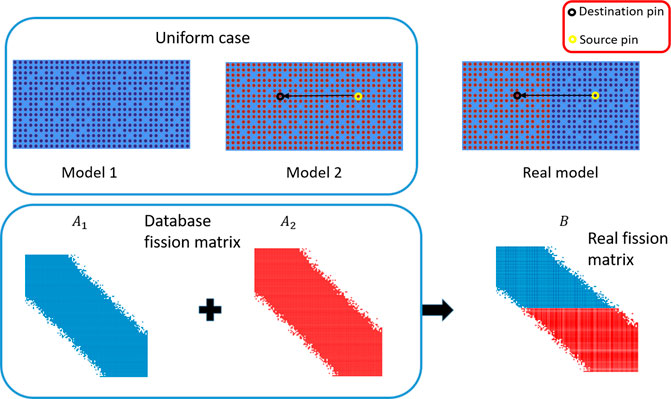
The combined fission matrix theory, as the core of the RAPID code scheme, estimates the core fission matrix instantly from pre-calculated database fission matrices. The theory states that the system fission matrix element ai,j equals to the database fission matrix element
In a whole-core transport calculation, the core fission matrix is estimated by combining database fission matrices following the above assumption. The database fission matrices are calculated in uniform-assembly loading cases, where the same assemblies fill the infinite geometry. However, as explained before, the fission matrix combination theory assumes that only the destination cell dominates the fission matrix element ai,j. The neutrons are also in a low energy range in the destination nearby cells. So a surrounding cell of different properties from the destination cell may introduce a perturbation to the fission matrix element ai,j. Taking the BEAVRS benchmark as an example, the core is composed of different enrichment assemblies shown in Figure 3. For each type of assembly, the database fission matrices are pre-calculated and combined to build to a whole-core fission matrix. The details can be found in (He and Walters, 2019). The eigenpair of the fission matrix represents the multiplication factor and the fission source distribution, respectively. The pin-wise fission rate distribution obtained with the combined fission matrix method has been compared against the Monte Carlo reference calculation, and the relative error is shown in Figure 4. The keff difference is 156 pcm and the 2D root mean square (RMS) error is 6.26%.
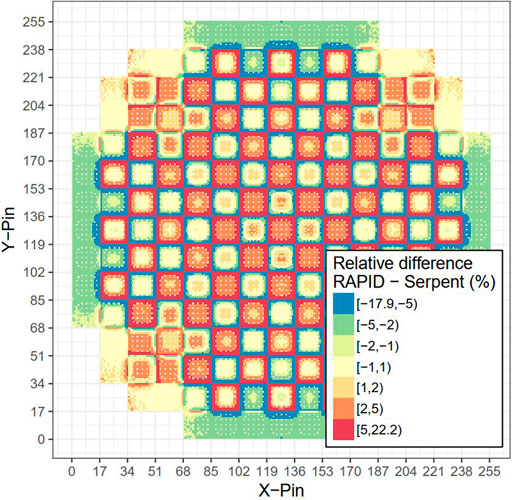
FIGURE 4. The pin-wise relative error between the combined fission matrix method and the Monte Carlo calculation.
Due to the perturbation a different surrounding cell brings to the fission matrix element ai,j, the cells at the assembly boundary have relatively large errors. In order to reduce the error the material discontinuity brings to the combined fission matrix theory, a correction ratio method has been developed. The detail of the theory can be found in (He and Walters, 2019). The correction ratio estimates the perturbation a different surrounding assembly brings to the destination assembly. The pin-wise correction ratios are defined as the fission rates with perturbation assembly divided by those in uniform cases. In thermal reactors, due to the limited transport length of neutrons, only perturbation assemblies adjacent to the destination assembly are assumed to contribute to the correction ratios. Therefore, correction ratios are calculated corresponding to different perturbation assembly locations in a mini-four assembly model, as shown in Figure 5. With the correction ratio applied to the combined fission matrix theory in the whole-core problem, the relative error is significantly reduced, as shown in Figure 6. The keff difference is 26 pcm with a 3 pcm uncertainty and the 2D RMS error is 0.54% with a 0.21% uncertainty. The Monte Carlo reference calculation takes about 80 h and the RAPID calculation can be finished within minutes. Note, the RAPID run time does not take the database preparation into account since the database does not need to be prepared again when performing additional RAPID calculations. Overall, the combined fission matrix theory with correction ratio has achieved high accuracy in thermal reactors.

FIGURE 5. The mini four assembly model to calculate the correction ratio with (A) no perturbation (B) perturbation on the upper right.
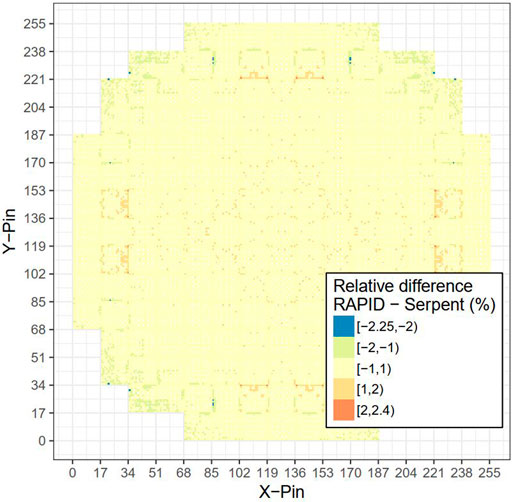
FIGURE 6. The pin-wise relative error between the combined fission matrix method and the Monte Carlo calculation.
3 Sodium Fast Reactor Benchmark
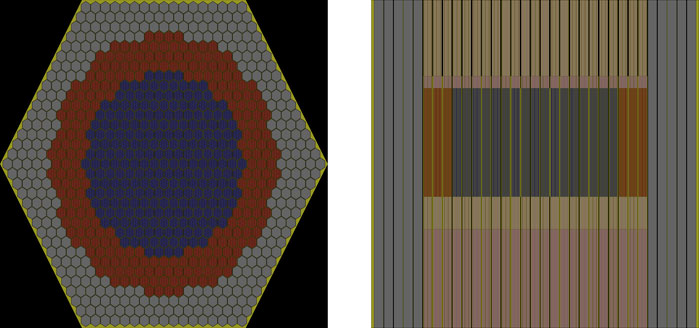
This work takes the European Sodium Fast Reactor as the benchmark problem (Fiorini and Vasile, 2011). The radial and axial cross-sections of the core are shown in Figure 7. The core is composed of three layers: the inner fuel regions, the outer fuel regions, and the outermost reflector regions. The inner and outer fuel regions have different Pu enrichment at 14.05 and 16.35%, respectively. The core is slightly modified in this work that the control and shutdown assemblies are switched with inner fuel assemblies for the convenience of fission matrix tally. Since the purpose of the work is to validate the combined fission matrix theory in a fast reactor, such a modification will not bias the conclusion. The main parameters of the reactor core and assembly are summarized in Table 1. The core is modeled at hot-zero-power condition, with the fuel and moderator temperature equal to 300K.
4 Results
The combined fission matrix method is compared against the Monte Carlo calculation on the ESFR model. The database fission matrix is composed of two fission matrices. The two fission matrices represent the cases where inner and outer fuel assemblies fill the entire core as shown in Figure 8. The database fission matrix in this study is obtained through the Monte Carlo code OpenMC (Romano and Forget, 2013) criticality calculation due to its high fidelity. The mesh to tally the fission matrix is based on assemblies, i.e., there are 487 fuel assemblies in the core, which corresponds to a 487 × 487 fission matrix. The whole-core reference calculation is also using criticality calculation. The criticality calculations use 500 inactive cycles and 2000 active cycles, with 10, 000, 000 neutron histories simulated per cycle.
Before applying the combined fission matrix theory to the whole-core problem, we will first compare the neutron transport track between the thermal and fast reactors. As shown in Figure 9, the neutron transport from born to death may cover several assemblies in a fast reactor, which is much longer than that in thermal reactors.
The whole-core fission matrix is estimated by combining two database fission matrices, and its eigenvalue and eigenvector represent the multiplication factor and assembly-wise fission rate. The fission rate calculated from the Monte Carlo reference calculation and its difference with that from the combined fission matrix method are shown in Figure 10. The 2D RMS error is 8.3% and the keff difference is 64 pcm with a roughly 4 pcm uncertainty. The relatively large error in a fast reactor can be explained from the neutron transport point of view: the neutron remains high energy from birth to death in a fast reactor. The absorption and scattering in the intermediate cells have a competing impact with the absorption and fission in the destination cell. It implies that the destination cell property is not dominating in the fission matrix element ai,j. On the other hand, because the neutron transports a long way in such a reactor, the destination is subject to perturbations from a large number of assemblies, i,e. the destination assembly is easier to be perturbed.
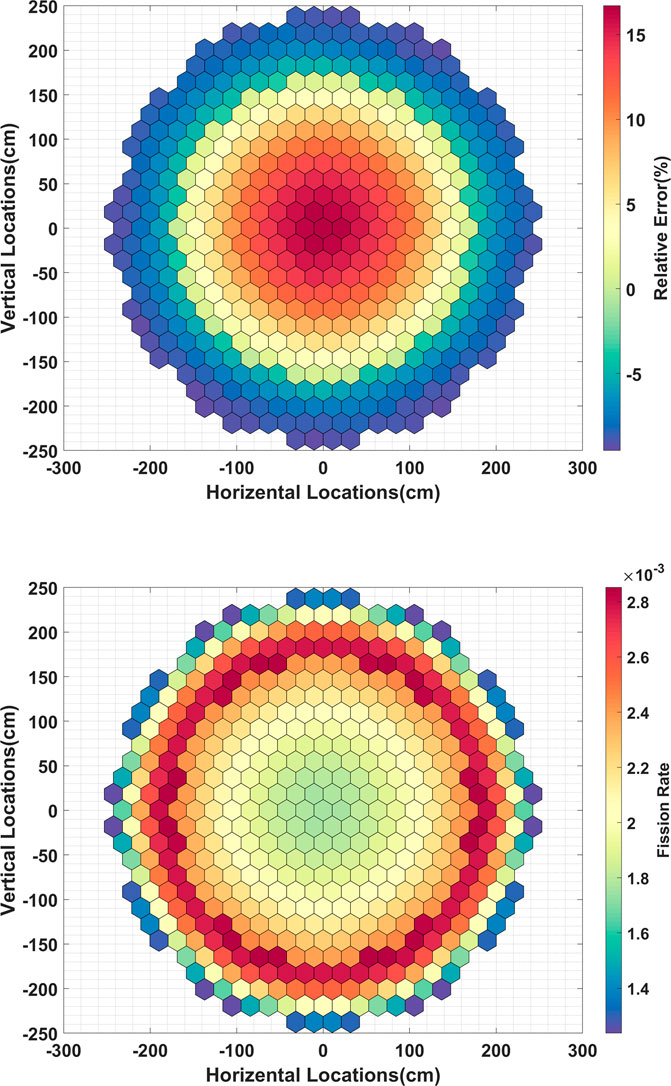
FIGURE 10. The fission rate from Monte Carlo calculation and its relative error with that from the combined fission matrix theory.
In this work, a whole-core correction ratio has also been tested. That is, the whole-core fission source from criticality calculation in the fast reactor is used to calculate the fission source in the uniform models, and then derive the correction ratios separately for the inner fuel and outer fuel assemblies as in
Where, Ri and Fi are correction ratios and fission rates in assembly i. With the correction ratio applied, the 2D relative error is shown in Figure 11. The keff difference is 48 pcm, and the 2D RMS error is 7.3%. It can be seen that the combined fission matrix method in the fast reactor has lower accuracy than in the thermal reactor. The long length of the neutron transport in a fast reactor also makes the correction ratio generation a challenging problem. Overall, the combined fission matrix theory can provide a rough estimation of keff and fission source distribution in fast reactors, but it cannot restore the high-fidelity as in thermal reactors.
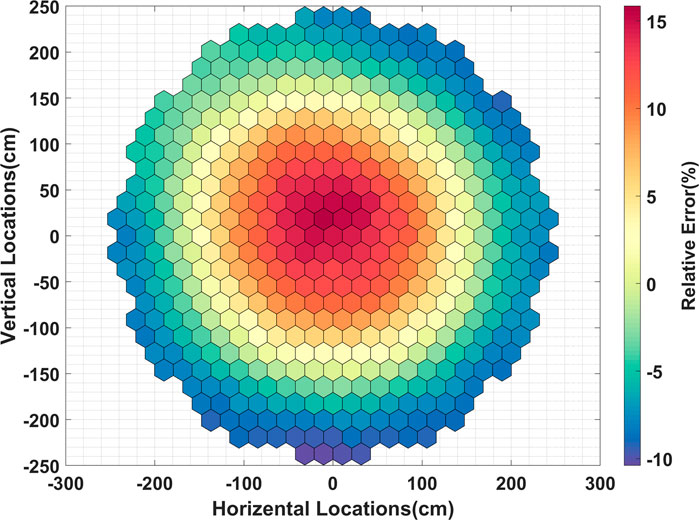
FIGURE 11. The fission rate relative error between the Monte Carlo calculation and the combined fission matrix theory with correction ratio.
5 Conclusion
The combined fission matrix theory features an efficient and high-fidelity calculation. The method has been validated in a series of thermal reactors. This paper examines its application in fast reactors. Theoretically, the mechanism of combining database fission matrices by the destination cell property is more suited for a thermal neutron system. In fast reactors, the destination cell property is no more dominating in the fission matrix element, and the fission matrix element is more affected by intermediate cells. Finally, the combined fission matrix theory is validated in an SFR benchmark problem. Compared to the Monte Carlo reference calculation, the combined fission matrix theory has a larger error in the SFR than thermal reactors. It can be concluded that the combined fission matrix theory still needs further development in fast reactor applications.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author Contributions
DH proposes the idea and finishes the calculations in this work. TZ and XL helps organizes and edit the paper.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors would like to acknowledge that this research is sponsored by Shanghai Sailing Program (21YF1421200) and Natural Science Foundation of Shanghai (21ZR1429700).
References
Carney, S., Brown, F., Kiedrowski, B., and Martin, W. (2014). Theory and Applications of the Fission Matrix Method for Continuous-Energy Monte Carlo. Ann. Nucl. Energ. 73, 423–431. doi:10.1016/j.anucene.2014.07.020
Fiorini, G. L., and Vasile, A. (2011). European Commission - 7th Framework Programme. Nucl. Eng. Des. 241, 3461–3469. doi:10.1016/j.nucengdes.2011.01.052
He, D., and Walters, W. J. (2020). A Correction Method for RAPID Fission Matrix Calculations with Control Rod Movement. Prog. Nucl. Energ. 121, 103226. doi:10.1016/j.pnucene.2019.103226
He, D., and Walters, W. J. (2019). A Local Fission Matrix Correction Method for Heterogeneous Whole Core Transport with RAPID. Ann. Nucl. Energ. 134, 263–272. doi:10.1016/j.anucene.2019.06.008
Laureau, A., Aufiero, M., Rubiolo, P. R., Merle-Lucotte, E., and Heuer, D. (2015). Transient Fission Matrix: Kinetic Calculation and Kinetic Parameters βeff and Λeff Calculation. Ann. Nucl. Energ. 85, 1035–1044. doi:10.1016/j.anucene.2015.07.023
Liu, Z., Wu, H., Cao, L., Chen, Q., and Li, Y. (2011). A New Three-Dimensional Method of Characteristics for the Neutron Transport Calculation. Ann. Nucl. Energ. 38, 447–454. doi:10.1016/j.anucene.2010.09.021
Mascolino, V., Haghighat, A., and Roskoff, N. J. (2017). Evaluation of RAPID for a UNF Cask Benchmark Problem. EPJ Web Conf. 153, 05025. doi:10.1051/epjconf/201715305025
Rau, A., and Walters, W. J. (2020). Validation of Coupled Fission Matrix - TRACE Methods for thermal-hydraulic and Control Feedback on the Penn State Breazeale Reactor. Prog. Nucl. Energ. 123, 103273. doi:10.1016/j.pnucene.2020.103273
Romano, P. K., and Forget, B. (2013). The OpenMC Monte Carlo Particle Transport Code. Ann. Nucl. Energ. 51, 274–281. doi:10.1016/j.anucene.2012.06.040
Terlizzi, S., and Kotlyar, D. (2019). Fission Matrix Decomposition Method for Criticality Calculations: Theory and Proof of Concept. Nucl. Sci. Eng. 193, 948–965. doi:10.1080/00295639.2019.1583948
Topham, T. J., Rau, A., and Walters, W. J. (2020). An Iterative Fission Matrix Scheme for Calculating Steady-State Power and Critical Control Rod Position in a TRIGA Reactor. Ann. Nucl. Energ. 135, 106984. doi:10.1016/j.anucene.2019.106984
Walters, W. J., Roskoff, N. J., and Haghighat, A. (2018). The RAPID Fission Matrix Approach to Reactor Core Criticality Calculations. Nucl. Sci. Eng. 192, 21–39. doi:10.1080/00295639.2018.1497395
Zhang, M., Cao, Z., Xie, J., Zhu, W., Zhou, P., Gu, H., et al. (2013). Mutagenesis Analysis of Porcine Reproductive and Respiratory Syndrome Virus Nonstructural Protein 7. Virus Genes 47, 467–477. doi:10.1007/s11262-013-0957-4
Keywords: fission matrix, Monte Carlo, fast reactor, neutron transport, reactor physics
Citation: He D, Zhang T and Liu X (2021) The Application of the Combined Fission Matrix Theory in Fast Reactors. Front. Energy Res. 9:766449. doi: 10.3389/fenrg.2021.766449
Received: 29 August 2021; Accepted: 18 October 2021;
Published: 17 December 2021.
Edited by:
Mingjun Wang, Xi’an Jiaotong University, ChinaReviewed by:
Guang Hu, Xi’an Jiaotong University, ChinaJiankai Yu, Massachusetts Institute of Technology, United States
Copyright © 2021 He, Zhang and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Donghao He, ZG9uZ2hhb2hlQHNqdHUuZWR1LmNu
 Donghao He
Donghao He Tengfei Zhang
Tengfei Zhang Xiaojing Liu
Xiaojing Liu