Battery Electrode Mass Loading Prognostics and Analysis for Lithium-Ion Battery–Based Energy Storage Systems

With the rapid development of renewable energy, the lithium-ion battery has become one of the most important sources to store energy for many applications such as electrical vehicles and smart grids. As battery performance would be highly and directly affected by its electrode manufacturing process, it is vital to design an effective solution for achieving accurate battery electrode mass loading prognostics at early manufacturing stages and analyzing the effects of manufacturing parameters of interest. To achieve this, this study proposes a hybrid data analysis solution, which integrates the kernel-based support vector machine (SVM) regression model and the linear model–based local interpretable model-agnostic explanation (LIME), to predict battery electrode mass loading and quantify the effects of four manufacturing parameters from mixing and coating stages of the battery manufacturing chain. Illustrative results demonstrate that the derived hybrid data analysis solution is capable of not only providing satisfactory battery electrode mass loading prognostics with over a 0.98 R-squared value but also effectively quantifying the effects of four key parameters (active material mass content, solid-to-liquid ratio, viscosity, and comma-gap) on determining battery electrode properties. Due to the merits of explainability and data-driven nature, the design data–driven solution could assist engineers to obtain battery electrode information at early production cases and understand strongly coupled parameters for producing batteries, further benefiting the improvement of battery performance for wider energy storage applications.

Introduction

Recently, the lithium-ion (Li-ion) battery has become a popular energy storage technology for many sustainable energy applications, such as transportation electrification (Su et al., 2011; Chen et al., 2016) and a smart grid (Chen and Su, 2018; Hu et al., 2020; Hu et al., 2021a), due to the advantages of a low discharge rate and high energy density (Wang et al., 2020; Xie et al., 2020). However, Li-ion battery performance would be highly influenced by its related manufacturing process especially for the electrode component (Liu et al., 2021a). To further improve battery performance and save the battery cost for wider battery applications, efforts are urgently required to accurately predict battery electrode properties in the early manufacturing stage and in-depth understand key parameters within a battery electrode manufacturing process.

Unfortunately, the battery electrode manufacturing process involves multidisciplinary operations from electrical, chemical, thermal, and mechanical engineers, which would contain numerous individual manufacturing stages with lots of strongly coupled parameters, over 600 in total (Wu et al., 2019). The current solutions to analyze the contributions and importance of these parameters are still mainly dependent on long-term experimental experiences and trial and error approaches (Kwade et al., 2018). These conventional solutions are significantly time-consuming and labor-intensive. In light of this, it is very meaningful to design a suitable data analysis solution that could efficiently and automatically perform an interpretable analysis for explaining the contributions and importance of parameters within the battery manufacturing process.

With the rapid development of artificial intelligence and machine learning technology, data-driven strategies have been widely used as an efficient tool in the field of battery management (Liu et al., 2019a; Li et al., 2019). Numerous research studies have been carried out to design suitable data-driven solutions to benefit battery internal-state estimation (Feng et al., 2020; Zhang et al., 2020), lifetime, or future aging prognostics in both cycling (Lucu et al., 2020; Tang et al., 2020) and calendar modes (Liu et al., 2019b), fault diagnostics (Yang et al., 2018; Wang et al., 2021), cell equalization (Ouyang et al., 2019; Liu et al., 2020; Song et al., 2020), charging control (Ban et al., 2021; Wei et al., 2021), thermal management (Xie et al., 2021a; Xie et al., 2021b), and energy management (Liu et al., 2019c; Wu et al., 2020; Chen et al., 2021). Overall, after deriving these data-driven solutions, a more efficient and smarter battery management can be achieved. However, these research studies mainly focus on the performance improvement of battery products, while relatively little has been carried out to benefit their related production chain. It should be known that battery performance actually is determined or affected by its manufacturing stage, which should be also well analyzed and managed (Kwade et al., 2018; Liu et al., 2021a).

In comparison with battery management activities with fruitful achievements, just a few research studies have been carried out so far through deriving advanced data–based strategies to improve battery manufacturing (Zwicker et al., 2020). For instance, using the cross industry standard process (CISP), a linear data–driven model and a neural network–based data-driven model are derived by Schnell et al. (2019) for predicting battery properties and identifying dependencies of the battery manufacturing chain. Turetskyy et al. (2019) adopted the tree-based techniques to analyze the importance of manufacturing parameters and predict the maximum capacity of the manufactured battery. In Cunha et al. (2020), after plotting 2D graphs from data-driven models and experiment data, the dependencies of three mixing parameters are analyzed. After designing a random forest–based framework, an interpretable data-driven model is designed in Liu et al. (2021b) to analyze parameters within a battery manufacturing chain. For the aforementioned studies, through designing data-driven solutions, reasonable analyses of parameters within the battery manufacturing chain can be obtained. However, most research studies still use the conventional data-driven methods without explainability to only achieve battery property predictions. Moreover, few studies have been carried out through deriving data-driven solutions to quantify and explain the effects of manufacturing parameters from key stages such as mixing and coating on battery electrode property predictions. In order to obtain battery electrode property information at the battery’s early production stages and optimize the related manufacturing parameters for smarter battery production, it is vital to perform an effective parameter effect analysis with respect to the mixing and coating specifications of battery manufacturing.

Given the aforementioned consideration, this study proposes a hybrid data analysis solution by combining the benefits of the SVM and LIME to benefit battery electrode property predictions and a parameter effect analysis. The main focus of this study is on two early but important manufacturing stages: mixing and coating. Several main objectives of this study are 1) to perform accurate battery electrode mass loading predictions at the battery’s early manufacturing stage via an effective data-driven model and 2) to evaluate the contributions of some manufacturing parameters of interest from mixing and coating on electrode mass loading predictions, where their contributions and importance will also be quantified and explained effectively. All these efforts could help engineers to better understand their manufactured battery, further benefiting the improvement of battery performance, and achieve smarter battery production for wider battery-based applications.

The reminder of this article is organized as follows: Battery Early Manufacturing Stages and Electrode gives a brief introduction to the battery early manufacturing stages, especially for electrode production. Methodology details the fundamental of the SVM with different kernel functions, the LIME with the linear model to explain parameter contributions and effects, the derived hybrid data–driven model structure, and some typical performance indicators to quantify the performance of battery electrode mass loading predictions. Then, the detailed results and discussion of mass loading predictions and the parameter effect analysis are given in Results and Discussions. Finally, Conclusion concludes this study.

Battery Early Manufacturing Stages and Electrodes

As a complicated progress that involves many electrical, chemical, thermal, and mechanical operations, battery electrode manufacturing plays a vital role in determining the electrode’s properties, further affecting battery performance in energy storage applications. In light of this, the parameters and variables in the early manufacturing stages of the battery must be well monitored and analyzed.

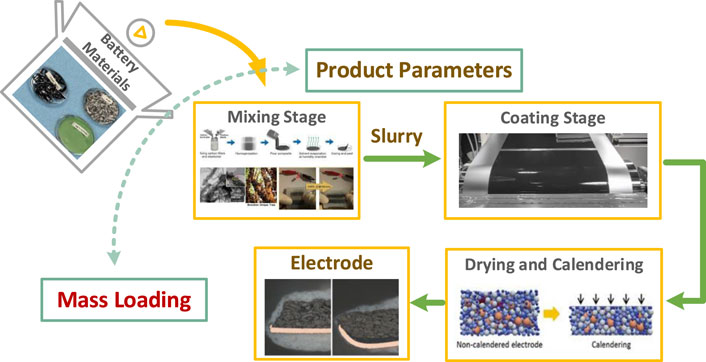
Figure 1 summarizes several key individual battery early manufacturing stages to produce battery electrodes. Specifically, proper materials such as active materials (Li–NCM oxide and graphite), conductive additives (carbon black), a solvent (N-methyl-2-pyrrolidone), and a binder (polyvinylidene-difluoride, hydrogenated-nitrile, or ethyl-acrylate-co-maleic anhydride) will be first prepared. Then, these materials will be mixed within soft blenders to produce slurries during the mixing stage. After that, a coating stage will be performed to coat these slurries onto the surface of metal foil. In general, the anode electrode would use the copper foil and the cathode electrode will adopt the aluminum foil. The coating speed would be set to a constant value, and the coater’s comma-gap will be adjusted to generate the shear force which could mainly determine the coating thickness. Then, the wet coating product would be dried within ovens through presetting suitable temperature. After that, a calendering stage will be conducted to further evaporate the residual solvent of the dry-coated product. Finally, after cutting the calendered products into suitable sizes for different types of batteries, the battery electrode could be obtained.

FIGURE 1

FIGURE 1. Key early stages during the battery electrode manufacturing progress.

It should be noted that all these individual stages (mixing, coating, drying, calendaring, and cutting) require the specific equipment (i.e., mixer, coater, and dryer) and would involve numerous process parameters and variables. Some parameters particularly from battery electrode early manufacturing stages such as mixing and coating are crucial for determining electrode property and must be well monitored and analyzed. Therefore, to explore the effects and contributions of some interested battery early manufacturing parameters on predicting battery key electrode properties, three parameters including the active material mass content (MC) with the unit of %, solid to liquid-ratio (StLR) with the unit of %, and viscosity with the unit of Pas from the mixing stage and a process parameter called comma-gap (CG) with the unit of mm from the coating stage are chosen as the explored parameters of interest. Then, a hybrid data analysis solution would be designed to perform battery electrode mass loading predictions at early manufacturing stages and also quantify the contributions of these selected manufacturing parameters. Theoretically, the mass ratio between a solid component and slurry mass can be reflected by StLR. The coating stage, especially for the coating shear rate, would be highly affected by the viscosity of slurries. CG represents the gap between comma and coating rolls. This parameter could highly affect both weights and thickness of the coated product. Electrode mass loading has a unit of $mg/c{m}^2$. In order to perform effective battery mass loading predictions and analyze these important battery manufacturing parameters, the well-collected dataset from Franco Laboratoire-de-Reactivite-et-Chimie-des-Solides (LRCS) is explored in this study. It should be known that the effectiveness of this type of dataset has been verified by Cunha et al. (2020). Due to page limitations, detailed information regarding the related design of experiments and data descriptions are provided in Cunha et al. (2020) for readers of interest. Based upon this dataset, the hybrid data analysis solution combining the kernel-based SVM and linear model–based LIME could be derived to predict battery electrode mass loading at the early manufacturing stage, where the contributions of these four battery manufacturing parameters of interest could also be explained.

Methodology

In this section, the fundamental of the support vector machine regression model with three different kernels are first presented, followed by the descriptions of a linear model–based local interpretable model-agnostic explanation technique. Some performance indicators to evaluate the prediction performance are also given.

Support Vector Machine Regression Model With Different Kernels

The support vector machine (SVM) belongs to the supervised machine learning method and is powerful for classification and regression (Pisner and Schnyer, 2020). To achieve effective regression, a structural risk minimization way is utilized in the SVM to generate the upper bound on the generalization error (Zendehboudi et al., 2018). Using a high-dimension linear function, the approximated regression function of the SVM could be expressed as follows:

$\mathit{Y}=\omega \cdot \theta \left(\mathit{X}\right)+\mathit{c,}(1)$

where $Y$ and $X$ represent the output and input vectors, respectively; $\theta \left(X\right)$ means the higher dimension feature spaces; and $\omega$ stands for the weight vector, while $c$ is a constant parameter to reflect bias. Both these parameters could be identified through minimizing a regularized risk function ($Rrf$) as follows:

$\mathit{Rrf}={\Vert \omega \Vert }^2/2+\mathit{Cp}{\displaystyle \sum _{\mathit{k}=1}^{\mathit{M}}{L}_{\epsilon }\left({\mathit{x}}_{\mathit{k}},{\mathit{y}}_{\mathit{k}},\mathit{f}\right)},(2)$

with

${\mathit{L}}_{\epsilon }\left({\mathit{x}}_{\mathit{k}},{\mathit{y}}_{\mathit{k}},\mathit{f}\right)=\{\begin{array}{c}\begin{array}{cc}\left|{\mathit{y}}_{\mathit{k}}-f\left({\mathit{x}}_{\mathit{k}}\right)\right|-\epsilon , & \left|{\mathit{y}}_{\mathit{k}}-\mathit{f}\left({\mathit{x}}_{\mathit{k}}\right)\right|\ge \epsilon \end{array}\\ \begin{array}{cc}0,& \mathit{otherwise}\end{array}\end{array},(3)$

where ${\Vert \omega \Vert }^2/2$ is a regularization term to measure the function flatness; $Cp$ represents a cost parameter to determine the trade-off between training errors and model flatness; $\epsilon$ means tube sizes; and $L_{\epsilon }\left(x_k,y_k,f\right)$ is an $\epsilon$-insensitive cost function to penalize the errors larger than $\epsilon$. After involving slack variables ${\xi }_k$ and ${\xi }_k^{\ast }$, Eq. 2 could be further expressed with the constrained formation as follows:

$\mathit{min}\left[{\Vert \omega \Vert }^2/2+\mathit{Cp}{\displaystyle \sum _{\mathit{k}=1}^{\mathit{M}}\left({\xi }_{\mathit{k}}+{\xi }_{\mathit{k}}^{\ast }\right)}\right].(4)$

subject to

$\{\begin{array}{c}{\mathit{y}}_{\mathit{k}}-\left[\left(\omega \times {\mathit{x}}_{\mathit{k}}\right)+\mathit{c}\right]\le \epsilon +{\xi }_{\mathit{k}}\\ \left[\left(\omega \times {\mathit{x}}_{\mathit{k}}\right)+\mathit{c}\right]-{\mathit{y}}_{\mathit{k}}\le \epsilon +{\xi }_{\mathit{k}}^{\ast }\\ {\xi }_{\mathit{k}}, {\xi }_{\mathit{k}}^{\ast }\ge 0\end{array}.(5)$

For this quadratic programming issue, the way of adopting the Lagrangian multiplier $\beta$ could be utilized to handle the issue. Then, $f\left(x\right)$ could be finally obtained with the explicit form as follows:

$\mathit{f}\left(\mathit{x}\right)={\displaystyle \sum _{\mathit{k}=1}^{\mathit{M}}\left({\beta }_{\mathit{k}}-{\beta }_{\mathit{k}}^{\ast }\right)\mathit{K}\left({\mathit{x}}_{\mathit{k}},\mathit{x}\right)+\mathit{c}},(6)$

where ${\beta }_k{\beta }_k^{\ast }=0$, ${\beta }_k,{\beta }_k^{\ast }\ge 0$, and $K\left(x_k,x\right)$ represents a kernel function that could be formulated by $K\left(x_k,x\right)=\theta {\left(x_k\right)}^T\theta \left(x\right)$ in feature spaces.

It should be noted that for various real applications, different kernel functions could provide various performances and need to be carefully determined. In this study, to perform satisfactory battery electrode mass loading predictions, three classical and effective kernel functions are derived. The first kernel function is a typical Gaussian kernel as follows:

${\mathit{K}}_{\mathit{Gaussian}}\left({\mathit{x}}_{\mathit{k}},\mathit{x}\right)=\mathit{exp}\left[-\Vert {\mathit{x}}_{\mathit{k}}-{\mathit{x}}^2\Vert /2{\sigma }^2\right],(7)$

where $\sigma$ is the hyperparameter of the Gaussian kernel.

Next, two polynomial kernel functions including the cubic-based kernel and quadratic-based kernel are also adopted with the following forms as:

${\mathit{K}}_{\mathit{Cubic}}\left({\mathit{x}}_{\mathit{k}},\mathit{x}\right)={\left({\mathit{a}}_{\mathit{c}}\cdot {\mathit{x}}_{\mathit{k}}^{\mathit{T}}\cdot \mathit{x}+{\mathit{b}}_{\mathit{c}}\right)}^3,(8)$

${\mathit{K}}_{\mathit{Quadratic}}\left({\mathit{x}}_{\mathit{k}},\mathit{x}\right)={\left({\mathit{a}}_{\mathit{q}}\cdot {\mathit{x}}_{\mathit{k}}^{\mathit{T}}\cdot \mathit{x}+{\mathit{b}}_{\mathit{q}}\right)}^2,(9)$

where $a_c$ and $b_c$ are the hyperparameters for the cubic-based kernel and $a_q$ and $b_q$ stand for the hyperparameters of the quadratic-based kernel

Local Interpretable Model-Agnostic Explanations

After deriving the SVM-based regression model for battery electrode mass loading prediction, to further explain these related predictions, the local interpretable model-agnostic explanation (LIME) is utilized. It should be known that LIME belongs to a model-agnostic solution which could mimic the underlying behaviors of a black box model for generating the explanation of the related prediction (Zafar and Khan, 2021). Based upon the derived SVM-regression model, detailed workflow to develop related LIME is shown in Table 1.

TABLE 1

TABLE 1. Detailed workflow to develop LIME for prediction explanation.

To sum up, LIME would perform four key steps to provide the explanation of an instance as follows: 1) LIME would randomly generate samples around the observation of interest, as illustrated in line 3; 2) LIME would adopt the SVM-based regression model to perform predictions of the generated random samples, as shown in line 4; 3) LIME would construct a local regression model based on the generated random samples and related prediction points from the SVM-based regression model, as illustrated in line 5; and 4) the coefficients from the local regression model within LIME quantify the contributions and importance of parameters of interest on the predictions of observation from the SVM-based regression model.

Model Structure and Performance Indicator

For battery electrode production, key parameters from mixing and coating stages would highly affect the performance and property of the manufactured battery electrode. In this study, to effectively analyze the contributions and effects of mixing and coating’s parameters of interest on the early manufacturing predictions of battery electrode mass loading, a hybrid SVM-LIME–based data-driven model is derived, with the structure shown in Figure 2. Specifically, four battery manufacturing parameters including MC, StLR, CG, and viscosity are utilized as SVM-based regression model inputs, while their related electrode mass loading is adopted as the model output. The linear model–based LIME is integrated within the SVM to give the explanation of these predictions.

FIGURE 2

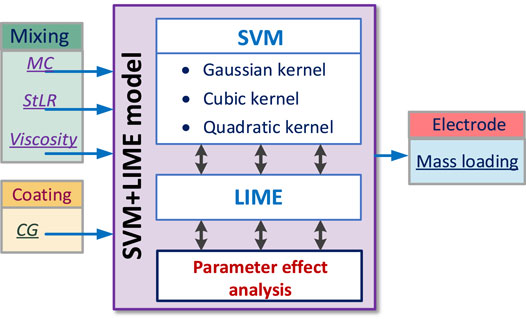
FIGURE 2. Hybrid data–driven model through combining the SVM and LIME to predict battery electrode mass loading and analyze parameter effects.

In order to quantify battery electrode mass loading prediction results of using various kernel-based SVM regression models, several classical performance indicators (Hu et al., 2021b) are utilized in this study.

1) Mean absolute error (MAE): suppose $N$ stands for the total number of observations, $Mas{s}_i$ represents the real tested battery electrode mass loading values, and ${\widehat{Mass}}_i$ stands for the predicted mass loading points from the SVM, then the MAE to quantify the accuracy of the SVM can be expressed as follows:

$\mathit{MAE}=\frac{1}{\mathit{N}}{\displaystyle \sum _{\mathit{i}=1}^{\mathit{N}}\left|\mathit{Mas}{\mathit{s}}_{\mathit{i}}-{\widehat{\mathit{Mass}}}_{\mathit{i}}\right|}.(10)$

2) Mean square error (MSE): following the same assumption, the MSE could be calculated with the following form to reflect the deviation between predicted electrode mass loading and real values as follows:

$\mathit{MSE}=\frac{1}{\mathit{N}}{\displaystyle \sum _{\mathit{i}=1}^{\mathit{N}}{\left(\mathit{Mas}{\mathit{s}}_{\mathit{i}}-{\widehat{\mathit{Mass}}}_{\mathit{i}}\right)}^2}.(11)$

3) Root mean square error (RMSE): The RMSE is a popular performance indicator derived from the MSE as follows:

$\mathit{RMSE}=\sqrt{\frac{1}{\mathit{N}}{\displaystyle \sum _{i=1}^{\mathit{N}}{\left(\mathit{Mas}{\mathit{s}}_{\mathit{i}}-{\widehat{\mathit{Mass}}}_{\mathit{i}}\right)}^2}}.(12)$

4) R-squared: suppose $\overline{M_{ }ass}$ means the average point of all predicted electrode mass loadings, R-squared can be calculated with the following form to reflect how much the predicted electrode mass loading gets close to the real values as follows:

$\mathit{R}-\mathit{Squared}=1-{\displaystyle \sum _{\mathit{i}=1}^{\mathit{N}}{\left(\mathit{Mas}{\mathit{s}}_{\mathit{i}}-{\widehat{\mathit{Mass}}}_{\mathit{i}}\right)}^2}/{\displaystyle \sum _{\mathit{i}=1}^{\mathit{N}}{\left(\mathit{Mas}{\mathit{s}}_{\mathit{i}}-\overline{\mathit{Mas}{\mathit{s}}_{\mathit{i}}}\right)}^2}.(13)$

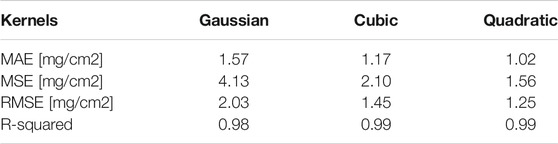
For our battery electrode mass loading prediction cases, when the predicted mass loading points match well with the real test points, MAE, MSE, and RMSE would become close to 0, while R-squared would get close to 1. Based on these performance indicators, the electrode mass loading predictions from SVM regression models with different kernels can be evaluated.

Results and Discussion

In this section, to evaluate the prediction performance of the derived SVM models with different kernel functions, the battery electrode mass loading predictions are first carried out using three kernel-based SVM regression models. To further analyze the parameter effects, the case studies of using LIME to quantify the importance of three mixing parameters and one coating parameter are then carried out and discussed.

Battery Electrode Mass Loading Prediction Results

We first consider the results and discussion of battery electrode mass loading predictions. Based upon the model structure as illustrated in Figure 3, three mixing parameters, including slurry MC, StLR, and viscosity, and one coating parameter, CG, are inputted into the SVM regression model, while battery electrode mass loading is used as the output of the SVM model. Without the loss of generality, sevenfold cross-validation solution is utilized to evaluate battery electrode mass loading prediction performance of all SVMs. Their corresponding predicted response versus actual response plots are also presented.

FIGURE 3

FIGURE 3. Prediction results for battery electrode mass loading using different kernel-based SVMs.

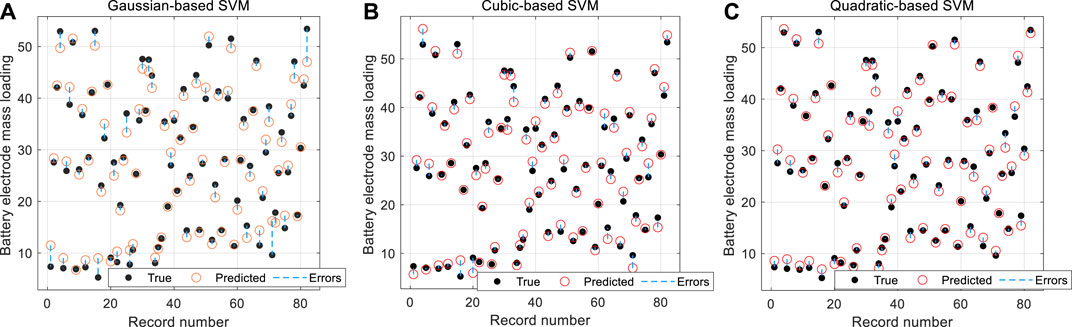
Figure 3 and Table 2 illustrate the mass loading prediction results and the corresponding performance indicators for all three kernel-based SVMs, respectively. Obviously, the most predicted battery electrode mass loading points from these three SVMs in Figure 3 agree well with the real observations. Quantitatively, the SVM regression model with the cubic kernel achieves the best performance for electrode mass loading prediction with 1.02 $mg/c{m}^2$ MAE, 4.13 $mg/c{m}^2$ MSE, and 2.03 $mg/c{m}^2$ RMSE, which are 12.8, 25.7, and 13.8% smaller than those from the SVM regression model with the quadratic kernel, respectively. In contrary, the SVM regression model with the Gaussian kernel gives the worst prediction results of battery electrode mass loading with 1.57 $mg/c{m}^2$ MAE, 1.56 $mg/c{m}^2$ MSE, and 1.25 $mg/c{m}^2$ RMSE. However, the R-squared values of all these three SVMs are all larger than 0.98, which implies that Gaussian, quadratic, and cubic kernels could provide enough prediction accuracy for battery electrode mass loading. In summary, using MC, StLR, viscosity, and CG as the inputs of SVM regression models, satisfactory battery electrode mass loading prediction could be obtained.

TABLE 2

TABLE 2. Performance indicators for mass loading prediction using different kernel-based SVMs.

To further evaluate the deviation results of battery electrode mass loading prediction, the predicted response versus actual response plots (PvAPs) for all three SVMs with different kernels are illustrated in Figure 4. Theoretically, for the observations on both the left and right of PvAP, the furthest from the mean point will generate the most leverages and make the prediction line close to that observation. In this context, the observations should become close to the perfect prediction line for a good prediction model. From Figure 4, almost all observations become close to their perfect prediction lines for all these three SVM models with different kernels. These results signify that the Gaussian-based SVM model, cubic-based SVM model, and quadratic-based SVM model could all give satisfactory performance without outliers for battery electrode mass loading prediction.

FIGURE 4

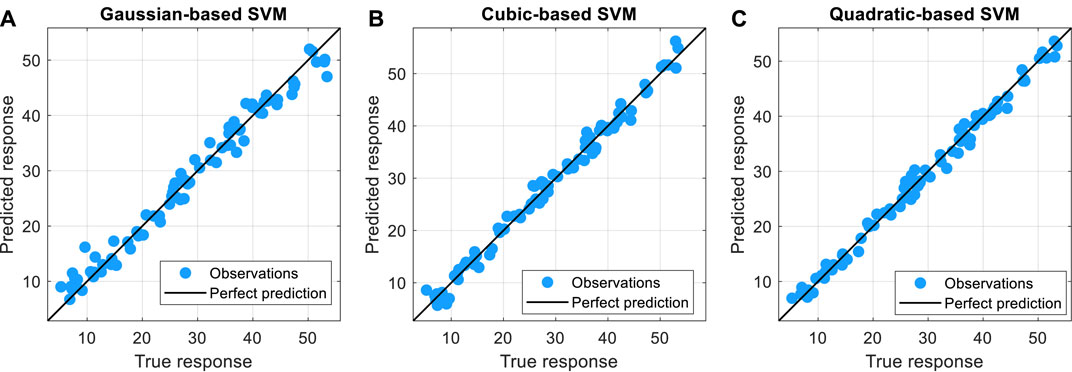
FIGURE 4. Predicted versus actual plots using different kernel-based SVMs: (A) Gaussian kernel, (B) quadratic kernel, and (C) cubic kernel.

Parameter Effect Analysis

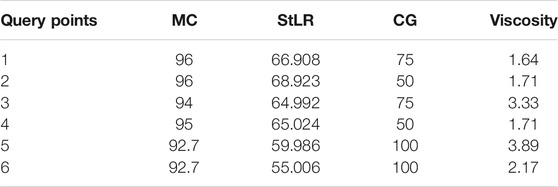
After deriving SVM models with three different kernel functions for the predictions of battery electrode mass loading, this part would then focus on the effect analysis of four battery manufacturing parameters of interest toward determining battery electrode mass loading. To perform the parameter effect analysis of different battery electrode manufacturing cases, six randomly selected observations listed in Table 3 are selected as the query points for further investigation in this study. Then, the LIME with the linear model is integrated with the most accurate SVM regression model with the quadratic kernel to explain the parameter effects on battery electrode mass loading predictions of these six query points.

TABLE 3

TABLE 3. Case studies of randomly selecting query points to analyze parameter effects.

To reflect the effects of these four battery manufacturing parameters (MC, StLR, viscosity, and CG) on determining mass loading of these six query points, their parameter effect analysis results using LIME with the linear model are shown in Figure 5. The predicted results of using the SVM regression model and a simple model within LIME are also given to reflect the output difference between these two models. From Figure 5, it can be observed that all these query points provide the same parameter effect trends of four predictors. Quantitatively, CG achieves the largest negative effect with around −9$\times {10}^{-3}$, which is over ten times larger than that from slurry viscosity (the parameter gives the smallest negative effect). Slurry StLR provides the second largest positive effect with around 2.5$\times {10}^{-3}$, which is 13.6% larger than MC (the parameter gives the third largest positive effect). These results signify that the effects of all four key manufacturing parameters can be successfully obtained by LIME. Besides, it can be noted that the mass loading prediction results from the LIME’s simple model get close to the prediction results from the quadratic kernel–based SVM model, indicating that the LIME with the linear model can present the accurate predictions of mass loading for all query points. Therefore, our proposed hybrid solution could also well explain the effects of all these four manufacturing parameters.

FIGURE 5

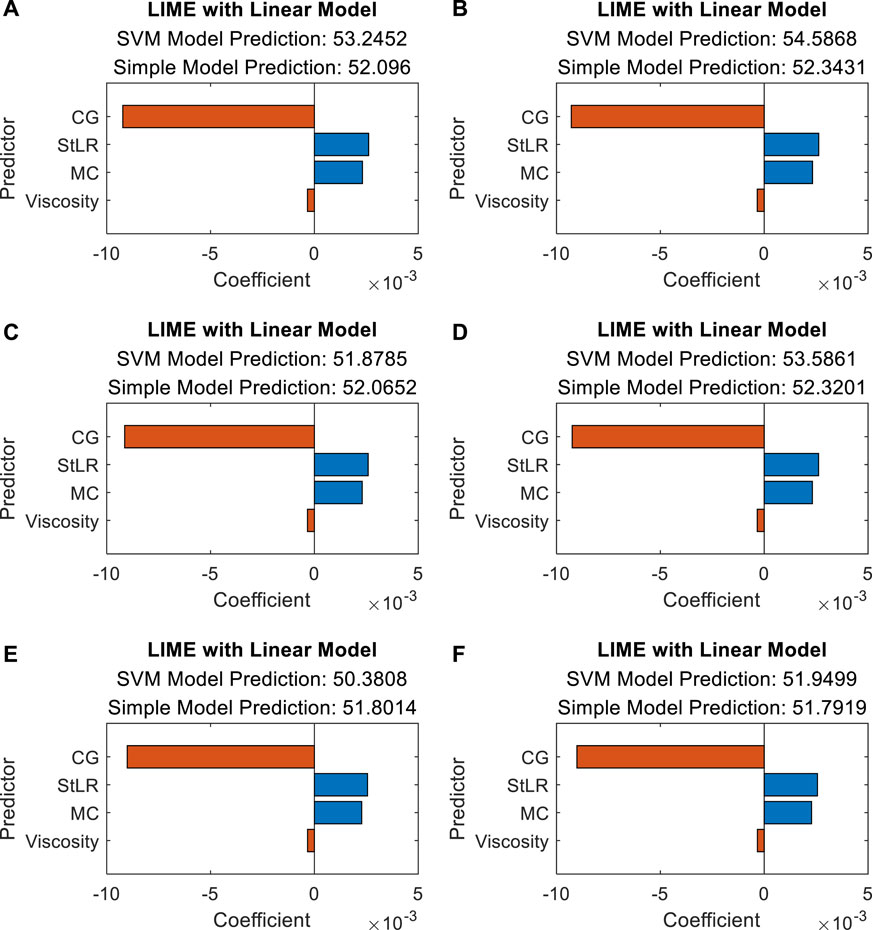
FIGURE 5. Parameter effect analysis results using LIME with the linear model for six query points: (A) query point 1, (B) query point 2, (C) query point 3, (D) query point 4, (E) query point 5, and (F) query point 6.

On the other hand, in this study, we follow the same flow from some feature engineering applications (Dong and Liu, 2018; Liu et al., 2021c) to derive a hybrid data analysis solution for analyzing four key battery manufacturing parameters from mixing and coating stages. Based upon MATLAB 2020 with a 2.40 GHz Intel Pentium 4 CPU, the efficient calculation process can be achieved with a low computational burden of less than 5s computational time for all tests. Then, the derived hybrid method is capable of providing effective battery electrode mass loading predictions and reliable effect analyses of interested manufacturing variables. As battery manufacturing is a highly nonlinear and strongly coupled process with numerous parameters in total, monitoring and controlling all these parameters are significantly time-consuming and laborious. In the light of this, the merits of using our proposed hybrid data analysis solution will be more obvious when more datasets to reflect other parameters within battery manufacturing become available. Then, this hybrid solution could assist engineers to predict battery electrode properties with satisfactory accuracy and understand the effects of battery manufacturing parameters of interest.

Conclusion

As battery electrode manufacturing plays a pivotal role in determining the performance of related battery products, the reliable electrode mass loading predictions and effect analysis of manufacturing parameters of interest are presented in this article. An explainable data-driven solution, based on the integration of different kernel-based SVM models and LIME with the linear model, is derived to perform effective battery electrode mass loading predictions. Besides, the effects of four involved manufacturing parameters from mixing and coating stages are also analyzed. Based upon the comparative prediction results and parameter effects analysis, some conclusions could be obtained as follows: 1) The SVM regression models could well predict battery electrode mass loading with over a 0.98 R-squared value after inputting four key manufacturing parameters, while the quadratic kernel–based one is able to achieve the best prediction performance with only 1.25 $mg/c{m}^2$ RMSE. 2) The LIME could generate similar parameter effect trends for all six selected query points. CG would give the largest effect, while viscosity provides the smallest effect. 3) The outputs from the linear model within LIME get close to the predicted values from the quadratic kernel–based SVM regression model for all six query points, indicating the effectiveness of integrated LIME. This is the first known application by combining the SVM regression model and LIME to design a hybrid data analysis solution for accurately predicting battery electrode mass loading and analyzing key battery manufacturing parameter effects of interest. As the derived data analysis solution in this study has merits of data-driven characteristics, flexibility, and explainability, it could be extended to predict other battery properties and analyze other manufacturing parameter effects when the related dataset becomes available.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

TC, MS, and HL contributed to conception and design of the study. TC and HH performed the data-driven analysis. TC wrote the first draft of the manuscript. MS, HH, and HL wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work is supported by the National Natural Science Foundation of China under Grant No. 52107079, No. 51807023 and No. 52007030.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank Dr. Kailong Liu from WMG, University of Warwick, for fruitful discussions and proof reading.

References

Ban, M., Zhang, Z., Li, C., Li, Z., and Liu, Y. (2021). Optimal Scheduling for Electric Vehicle Battery Swapping-Charging System Based on Nanogrids. Int. J. Electr. Power Energ. Syst. 130, 106967. doi:10.1016/j.ijepes.2021.106967

CrossRef Full Text | Google Scholar

Chen, T., and Su, W. (2018). Indirect Customer-To-Customer Energy Trading with Reinforcement Learning. IEEE Trans. Smart Grid 10 (4), 4338–4348. doi:10.1109/tsg.2018.2857449

CrossRef Full Text | Google Scholar

Chen, T., Zhang, B., Pourbabak, H., Kavousi-Fard, A., and Su, W. (2016). Optimal Routing and Charging of an Electric Vehicle Fleet for High-Efficiency Dynamic Transit Systems. IEEE Trans. Smart Grid 9 (4), 3563–3572. doi:10.1109/tsg.2016.2635025

CrossRef Full Text | Google Scholar

Chen, T., Cui, Q., Gao, C., Hu, Q., Lai, K., Yang, J., et al. (2021). Optimal Demand Response Strategy of Commercial Building‐based Virtual Power Plant Using Reinforcement Learning. IET Gener. Transm. Distrib. 15 (16), 2309–2318. doi:10.1049/gtd2.12179

CrossRef Full Text | Google Scholar

Cunha, R. P., Lombardo, T., Primo, E. N., and Franco, A. A. (2020). Artificial Intelligence Investigation of NMC Cathode Manufacturing Parameters Interdependencies. Batteries & Supercaps 3 (no. 1), 60–67. doi:10.1002/batt.201900135

CrossRef Full Text | Google Scholar

Dong, G., and Liu, H. (2018). Feature Engineering for Machine Learning and Data Analytics. Boca Raton: CRC Press.

Feng, F., Teng, S., Liu, K., Xie, J., Xie, Y., Liu, B., et al. (2020). Co-estimation of Lithium-Ion Battery State of Charge and State of Temperature Based on a Hybrid electrochemical-thermal-neural-network Model. J. Power Sourc. 455, 227935. doi:10.1016/j.jpowsour.2020.227935

CrossRef Full Text | Google Scholar

Hu, Q., Ding, H., Chen, X., Chen, T., and Ding, Y. (2020). Analysis on Rotating Power Outage in California USA in 2020 and its Enlightenment to Power Grid of China. Autom. Electric Power Syst. 44 (22), 11–18. doi:10.7500/AEPS20201016002

CrossRef Full Text | Google Scholar

Hu, Q., Zhang, N., Quan, X., Bai, L., Wang, Q., and Chen, X. (2021). A User Selection Algorithm for Aggregating Electric Vehicle Demands Based on a Multi‐armed Bandit Approach. IET Energ. Syst. Integr. 3 (3), 295–305. doi:10.1049/esi2.12027

CrossRef Full Text | Google Scholar

Hu, T., Li, K., Ma, H., Sun, H., and Liu, K (2021). Quantile Forecast of Renewable Energy Generation Based on Indicator Gradient Descent and Deep Residual BiLSTM. Control. Eng. Pract. 114, 104863. doi:10.1016/j.conengprac.2021.104863

CrossRef Full Text | Google Scholar

Kwade, A., Haselrieder, W., Leithoff, R., Modlinger, A., Dietrich, F., and Droeder, K. (2018). Current Status and Challenges for Automotive Battery Production Technologies. Nat. Energ. 3 (4), 290–300. doi:10.1038/s41560-018-0130-3

CrossRef Full Text | Google Scholar

Li, Y., Liu, K., Foley, A. M., Zülke, A., Berecibar, M., Nanini-Maury, E., et al. (2019). Data-driven Health Estimation and Lifetime Prediction of Lithium-Ion Batteries: A Review. Renew. Sustainable Energ. Rev. 113, 109254. doi:10.1016/j.rser.2019.109254

CrossRef Full Text | Google Scholar

Liu, K., Li, K., Peng, Q., and Zhang, C. (2019). A Brief Review on Key Technologies in the Battery Management System of Electric Vehicles. Front. Mech. Eng. 14 (1), 47–64. doi:10.1007/s11465-018-0516-8

CrossRef Full Text | Google Scholar

Liu, K., Li, Y., Hu, X., Lucu, M., and Widanage, W. D. (2019). Gaussian Process Regression with Automatic Relevance Determination Kernel for Calendar Aging Prediction of Lithium-Ion Batteries. IEEE Trans. Ind. Inform. 16 (6), 3767–3777. doi:10.1109/tii.2019.2941747

CrossRef Full Text | Google Scholar

Liu, K., Hu, X., Yang, Z., Xie, Y., and Feng, S. (2019). Lithium-ion Battery Charging Management Considering Economic Costs of Electrical Energy Loss and Battery Degradation. Energ. Convers. Manag. 195, 167–179. doi:10.1016/j.enconman.2019.04.065

CrossRef Full Text | Google Scholar

Liu, K., Yang, Z., Tang, X., and Cao, W. (2020). Automotive Battery Equalizers Based on Joint Switched-Capacitor and Buck-Boost Converters. IEEE Trans. Vehicular Technol. 69 (11), 12716–12724. doi:10.1109/tvt.2020.3019347

CrossRef Full Text | Google Scholar

Liu, Y., Zhang, R., Wang, J., and Wang, Y. (2021). Current and Future Lithium-Ion Battery Manufacturing. Iscience 24, 102332. doi:10.1016/j.isci.2021.102332

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, K., Hu, X., Zhou, H., Tong, L., Widanalage, D., and Marco, J. (2021). Feature Analyses and Modelling of Lithium-Ion Batteries Manufacturing Based on Random forest Classification. IEEE/ASME Trans. Mechatron., 1. doi:10.1109/TMECH.2020.3049046

CrossRef Full Text | Google Scholar

Liu, K., Wei, Z., Yang, Z., and Li, K.. Mass Load Prediction for Lithium-Ion Battery Electrode Clean Production: a Machine Learning Approach. J. Clean. Prod. 289 (2021), 125159. doi:10.1016/j.jclepro.2020.125159

CrossRef Full Text | Google Scholar

Lucu, M., Martinez-Laserna, E., Gandiaga, I., Liu, K., Camblong, H., Widanage, W. D., et al. (2020). Data-driven Nonparametric Li-Ion Battery Ageing Model Aiming at Learning from Real Operation Data-Part B: Cycling Operation. J. Energ. Storage 30, 101410. doi:10.1016/j.est.2020.101410

CrossRef Full Text | Google Scholar

Ouyang, Q., Wang, Z., Liu, K., Xu, G., and Li, Y. (2019). Optimal Charging Control for Lithium-Ion Battery Packs: A Distributed Average Tracking Approach. IEEE Trans. Ind. Inform. 16, 3430–3438. doi:10.1109/tii.2019.2951060

CrossRef Full Text | Google Scholar

Pisner, D. A., and Schnyer, D. M. (2020). “Support Vector Machine,” in Machine Learning (Boca Raton: Academic Press), 101–121. doi:10.1016/b978-0-12-815739-8.00006-7

CrossRef Full Text | Google Scholar

Schnell, J., Nentwich, C., Endres, F., Kollenda, A., Distel, F., Knoche, T., et al. (2019). Data Mining in Lithium-Ion Battery Cell Production. J. Power Sourc. 413, 360–366. doi:10.1016/j.jpowsour.2018.12.062

CrossRef Full Text | Google Scholar

Song, L., Liang, T., Lu, L., and Ouyang, M. (2020). Lithium-ion Battery Pack Equalization Based on Charging Voltage Curves. Int. J. Electr. Power Energ. Syst. 115, 105516. doi:10.1016/j.ijepes.2019.105516

CrossRef Full Text | Google Scholar

Su, W., Eichi, H., Zeng, W., and Chow, M. Y. (2011). A Survey on the Electrification of Transportation in a Smart Grid Environment. IEEE Trans. Ind. Inform. 8, 1–10. doi:10.1109/tii.2011.21724541

CrossRef Full Text | Google Scholar

Tang, X., Liu, K., Wang, X., Gao, F., Macro, J., and Widanage, W. D. (2020). Model Migration Neural Network for Predicting Battery Aging Trajectories. IEEE Trans. Transp. Electrification 6 (2), 363–374. doi:10.1109/tte.2020.2979547

CrossRef Full Text | Google Scholar

Turetskyy, A., Thiede, S., Thomitzek, M., Drachenfels, N. V., Pape, T., and Herrmann, C. (2019). Toward Data‐Driven Applications in Lithium‐Ion Battery Cell Manufacturing. Energ. Technol. 8, 1900136. doi:10.1002/ente.201900136

CrossRef Full Text | Google Scholar

Wang, Y., Tian, J., Sun, Z., Wang, L., Xu, R., Li, M., et al. (2020). A Comprehensive Review of Battery Modeling and State Estimation Approaches for Advanced Battery Management Systems. Renew. Sustainable Energ. Rev. 131, 110015. doi:10.1016/j.rser.2020.110015

CrossRef Full Text | Google Scholar

Wang, J., Zhang, S., and Hu, X. (2021). A Fault Diagnosis Method for Lithium-Ion Battery Packs Using Improved RBF Neural Network. Frontier Energ. Res. doi:10.3389/fenrg.2021.702139

CrossRef Full Text | Google Scholar

Wei, Z., Quan, Z., Wu, J., Li, Y., Pou, J., and Zhong, H. (2021). Deep Deterministic Policy Gradient-Drl Enabled Multiphysics-Constrained Fast Charging of Lithium-Ion Battery. IEEE Trans. Ind. Electron., 1. doi:10.1109/TIE.2021.3070514

CrossRef Full Text | Google Scholar

Wu, X., Song, K., Zhang, X., Hu, N., Li, L., Li, W., et al. (2019). Safety Issues in Lithium Ion Batteries: Materials and Cell Design. Front. Energ. Res. 7, 65. doi:10.3389/fenrg.2019.00065

CrossRef Full Text | Google Scholar

Wu, J., Wei, Z., Liu, K., Quan, Z., and Li, Y. (2020). Battery-involved Energy Management for Hybrid Electric Bus Based on Expert-Assistance Deep Deterministic Policy Gradient Algorithm. IEEE Trans. Vehicular Technol. 69 (11), 12786–12796. doi:10.1109/tvt.2020.3025627

CrossRef Full Text | Google Scholar

Xie, Y., Li, B., Hu, X., Lin, X., Zhang, Y., and Zheng, J. (2020). Improving the Air-Cooling Performance for Battery Packs via Electro-Thermal Modelling and Particle Swarm Optimization. IEEE Trans. Transp. Electrification 7 (3), 1285–1302. doi:10.1109/tte.2020.3046735

CrossRef Full Text | Google Scholar

Xie, Y., Wang, X., Hu, X., Lin, X., Li, W., and Zhang, Y. (2021). An Enhanced Electro-thermal Model for EV Battery Packs Considering Current Distribution in Parallel Branches. IEEE Trans. Power Electron. doi:10.1109/tpel.2021.3102292

CrossRef Full Text | Google Scholar

Xie, Y., Guo, H., Li, W., Zhang, Y., Chen, B., and Zhang, K.. Improving Battery thermal Behavior and Consistency by Optimizing Structure and Working Parameter. Appl. Therm. Eng. 196 (2021), 117281. doi:10.1016/j.applthermaleng.2021.117281

CrossRef Full Text | Google Scholar

Yang, R., Xiong, R., He, H., and Chen, Z. (2018). A Fractional-Order Model-Based Battery External Short Circuit Fault Diagnosis Approach for All-Climate Electric Vehicles Application. J. Clean. Prod. 187, 950–959. doi:10.1016/j.jclepro.2018.03.259

CrossRef Full Text | Google Scholar

Zafar, M. R., and Khan, N. (2021). Deterministic Local Interpretable Model-Agnostic Explanations for Stable Explainability. Machine Learn. Knowl. Extr. 3, 525–541. doi:10.3390/make30300273

CrossRef Full Text | Google Scholar

Zendehboudi, A., Baseer, M. A., and Saidur, R. (2018). Application of Support Vector Machine Models for Forecasting Solar and Wind Energy Resources: A Review. J. Clean. Prod. 199, 272–285. doi:10.1016/j.jclepro.2018.07.164

CrossRef Full Text | Google Scholar

Zhang, D., Couto, L. D., and Moura, S. J. (2020). Electrode-Level State Estimation in Lithium-Ion Batteries via Kalman Decomposition. IEEE Control. Syst. Lett. 5 (5), 1657–1662. doi:10.1109/LCSYS.2020.3042751

CrossRef Full Text | Google Scholar

Zwicker, M. F. R., Moghadam, M., Zhang, W., and Nielsen, C. V. (2020). Automotive Battery Pack Manufacturing–A Review of Battery to Tab Joining. J. Adv. Joining Process. 1, 100017. doi:10.1016/j.jajp.2020.100017

CrossRef Full Text | Google Scholar