Coordinated Frequency Regulation of Smart Grid by Demand Side Response and Variable Speed Wind Turbines

Frequency stability of the power system is impacted by the increasing penetration of wind power because the wind power is intermittent. Meanwhile, sometimes the demand side loads increase quickly to require more power than total power produced. So balancing the active power in the power system to maintain the frequency is the main challenge of the high penetration of wind power to the smart grid. This paper proposes coordination rotor speed control (RSC), pitch angle control (PAC) and inertial control (IC) to control wind turbines, together with demand side response (DSR) participating in frequency regulation to balance active power in the power system. Firstly, the model of a single area load frequency control (LFC) system is obtained, which includes variable-speed wind turbines (VSWT) and DSR containing aggregated air conditioners and plug-in electric vehicles (PEVs). Then the RSC, PAC and IC, which controls wind turbines participating in frequency regulation in the power system, are introduced, respectively. Finally, the coordination of these three methods for wind turbines in different wind speeds is proposed. Case studies are carried out for the single area LFC system with a wind farm and DSR supported grid frequency. Coordination RSC and PAC combined IC are used to control wind turbines with DSR to balance active power in the power system. The proposed method used in the power system with high penetration of wind power and fluctuation of demand load is tested, respectively. Coordinated RSC or PAC with DSR can increase penetration of wind power and reduce peak load.

1 Introduction

Due to environmental pressures and increasing fossil fuel prices, intermittent renewable energy has been developed rapidly in recent years, especially wind energy. With the low penetration of wind power in the power system, i.e., less than 20% of the total power system capacity, thermal plants with abundant regulating capability can balance the active power of the power system. However, when the penetration of wind power is increased, the frequency stability will be progressively influenced due to the uncertainty of wind power and insufficient thermal power reserves (Zhang et al., 2011; Khoo et al., 2020; Yang et al., 2020). Moreover, it may even cause one situation that the total power produced by the power system is less than the demand load required. Therefore, balancing the active power in the power system is a challenging problem when the high penetration of wind power level increases to a certain level.

Many methods can be used to solve this imbalance problem caused by intermittent wind power. Traditionally, the spinning generation reserves with enough capacity and the grid-scale energy storage system can be used to meet this task. However, these solutions require expensive auxiliary equipment and high installation and operation cost. Thus it will increase the operation cost and reduces the advantages of wind power (Dui et al., 2018; Oshnoei et al., 2020; Paul et al., 2020). The advance load frequency control (LFC) scheme is an alternative way to provide the robustness against to the disturbances caused by the intermittent wind power (Zhang et al., 2016; Soliman et al., 2019). However, an advanced LFC scheme usually makes the power system a little complex and can not maintain the power system balance if the high penetration of wind power participates in the power system.

With the increasing penetration of wind power in the power system, variable-speed wind turbines (VSWTs) are required to participate in frequency regulation via augmented additional controllers, such as inertial control (IC), pitch angle control (PAC) and rotor speed control (RSC) (Margaris et al., 2012; Ravanji et al., 2020). When the grid frequency changes, not only the synchronous generators will respond to this change, but also wind turbines will quickly change their output active power to follow this disturbance change (Ma and Chowdhury, 2010). The IC method used for frequency regulation can transiently release the large kinetic energy stored in the rotating mass to emulate inertia of wind generators for providing frequency regulation (Ma and Chowdhury, 2010; Ravanji et al., 2020; Prasad and Padhy, 2020). The PAC and RSC used in the VSWT to participate in the frequency control for an extended period are investigated (Ma and Chowdhury, 2010; Zhang et al., 2011; Chau et al., 2018). In this paper, the VSWTs participate in frequency regulation via coordination of IC, RSC and PAC control methods under different wind speeds in the LFC system.

Because the wind power and demand side load are all uncertain, sometimes the total produced power is less than the demand loads required. In this situation, the demand side response (DSR), which can control or shift the controllable loads, has become a promising smart grid technology for accommodating intermittent renewable generations (Zhu et al., 2014; Esther and Kumar, 2016; Zhu et al., 2016a; Hosseini et al., 2020). In recent years, the PEVs have drawn increasing attention to the transportation electrification and suppressed the fluctuation in renewable energy sources have been investigated in lots of literature (Kariminejad et al., 2018; Nunna et al., 2018; Liu et al., 2020; Wang et al., 2020). The dynamic demand control (DDC) method, which controls the thermostatically controlled appliances (TCAs), such as electric water heaters (Vivekananthan and Mishra, 2015), refrigerators (Algarni et al., 2021) and air conditioners (Jay and Swarup, 2011), can self-adjust the usage of appliances based on frequency deviation of the power system (Hosseini et al., 2020). In this paper, DSR which includes aggregated air conditioners and PEVs participates in frequency regulation to reduce peak loads and to help the power system in stable.

This paper investigates combination wind turbines and DSR participating in frequency regulation in the power system to solve the imbalance problem caused by high penetration of wind power. Combination wind turbines and DSR participates in frequency regulation to deal with high wind power penetration and the DSR can remit frequency fluctuation when the total produced power is not enough for demand load required. Finally, wind turbines with different capacity of DSR supporting grid frequency are tested. This combination method has several advantages over other resources used for energy balancing and ancillary services, including providing enough capacity to adopt the high penetration of wind power and fluctuation of demand load problems.

2 Dynamic Model of Smart Grid for Frequency Regulation

The model of a signal area LFC system is proposed. A wind farm which contains several VSWTs participates in frequency regulation. The DSR which includes several PEVs and air conditioners is used to reduce the peak load and compensate for imbalance problem caused by wind power. Figure 1 shows the structure of the frequency regulation of the smart grid.

FIGURE 1

FIGURE 1. The structure of the frequency regulation of the power system.

From Figure 1, the relationship between the energy imbalance and the corresponding frequency deviation can be given as follows:

$\begin{array}{ccc}\hfill & \hfill & \mathrm{\Delta }{P}_m(s)+\mathrm{\Delta }{P}_{wind}(s)-\mathrm{\Delta }{P}_L(s)-\mathrm{\Delta }{P}_{DDC}(s)-\mathrm{\Delta }{P}_{V2G}(s)\hfill \\ \hfill & \hfill & =2Hs\mathrm{\Delta }f(s)+D\mathrm{\Delta }f(s)\hfill \end{array}(1)$

where ΔP_m is the generator mechanical output, ΔP_wind is the deviation of the wind power from the wind farm, ΔP_DDC is the power deviation from the DDC based on air conditioners, ΔP_V2G is the power deviation from the PEVs, ΔP_L is the load change, 2H is the equivalent inertia constant, D is the equivalent load-damping coefficient, and Δf is the frequency deviation of smart grid. K(s) is usually a PID controller.

2.1 The Model of a Variable Speed Wind Turbine

Wind power is developing very fast in recent years and its intermittent characteristic may cause energy imbalance for the smart grid. The details of VSWT model is introduced in (Thomsen and Poulsen, 2007; Boukhezzar and Siguerdidjane, 2011; Zhu et al., 2016b). The VSWT model is a complex nonlinear system, which consists of aerodynamics model, turbine mechanics model, generator model, and pitch actuator model.

The aerodynamic blades on the rotor convert the kinetic energy of the wind into mechanical energy, effectively providing the torque, T_r, on the rotor:

$T_r=\frac{P_r}{{\omega }_r}(2)$

where ω_r is the rotor speed, and the mechanical power absorbed from the wind P_r is shown as:

$P_r=\frac{1}{2}\rho \pi R_{wind}^2{v}^3{C}_p(3)$

where ρ is the air density, R_wind is the wind radius, v is the effective wind speed, and C_p is the power coefficient.

The blade pitch angle, θ, is changed by a hydraulic/mechanical actuator. A simplified model of the dynamics in this paper is presented by the following first order linear model:

$\dot{\theta }=-\frac{1}{{\tau }_{\theta }}\theta +\frac{1}{{\tau }_{\theta }}{\theta }_r(4)$

where θ_r is the reference and the one control input for the wind turbine.

The generator power, P_e, is given by:

$P_e=T_g{\omega }_g(5)$

where T_g is controlled, however, it cannot be changed instantaneously.

A wind farm represents a number of aggregated individual wind turbines. It assumes the wind speed for each wind turbine is same at the same time. Considering the clustering effect of wind turbines, the deviation of the active power from the wind farm is expressed as:

$\mathrm{\Delta }{P}_{wind}=\sum _{j=1}^{N_{wind}}(P_{e,j}-P_{wind,desired})(6)$

where P_{wind, desired} is the desired active power output of the wind farm, ΔP_wind is the deviation of the actual power out from the desired value, P_e,j is active power output of the jth wind turbines and N_wind is the total number of wind turbines in the wind farm (Chang-Chien et al., 2014).

2.2 Plug-In Electric Vehicles Model

The PEVs participating in frequency regulation contain several small capacity batteries. Therefore, large scale PEVs have potential to provide frequency support to the grid. The battery of the PEV comprising parallel/series connected battery cells is connected to the distribution grid through the DC/AC inverter (Hajizadeh and Golkar, 2007). The PEV model is introduced in (Zhu et al., 2016b).

In this paper, the active power losses in the inverter and the transformer are ignored, thus the active V2G power injected into the grid, P_V2G, can be given as

$P_{V2G,i}=I_{dc,i}{V}_{dc,i}(7)$

Linearizing (Eq. 7) yields the incremental active power as follows

$\mathrm{\Delta }{P}_{V2G,i}=V_{dc,i}^o\mathrm{\Delta }{I}_{dc,i}+I_{dc,i}^o\mathrm{\Delta }{V}_{dc,i}s(8)$

where $V_{dc,i}^o$ and $I_{dc,i}^o$ represent for the DC voltage and current of the battery at the initial time, respectively.

Similar to the BESS, the partial adjustment of battery voltage is used to compensate the power change resulting from current deviation (Xia et al., 2018). Thus, the V2G power of PEV_i responding to frequency regulation is

$\mathrm{\Delta }{P}_{V2G,i}=\frac{k_{b,i}}{1+s{T}_{b,i}}\mathrm{\Delta }f(9)$

where $k_{b,i}=-k_{v,i}{I}_{dc,i}^o$ is the battery gain, which represents the sensitivity of V2G power with respect to frequency deviation.

Assume that there are N PEVs in the smart grid discussed in this paper can be used to provide frequency support, and consider that the T_b,i in (Eq. 9) is not very sensitive to frequency deviation, then the aggregated V2G power can be approximately presented as following:

$\mathrm{\Delta }{P}_{V2G}=\sum _{i=1}^N\mathrm{\Delta }{P}_{V2G,i}=\frac{k_{ev}}{1+s{T}_{ev}}\mathrm{\Delta }f(10)$

where the aggregated PEVs gain $k_{ev}={\sum }_{i=1}^N{k}_{b,i}$, and the aggregated time constant $T_{ev}={\sum }_{i=1}^N\frac{T_{b,i}}{N}$.

2.3 Controllable Air-Conditioner Based Dynamic Demand Control Model

Domestic electric appliances of the user can be classified into five different groups based on their characteristics (Trovato et al., 2017), in which the TCAs can be used as a controllable load for frequency regulation, since they are relevant directly to the frequency derivation. In this paper, a typical TCA, air conditioner, is considered as the DDC loads. The detail of this model is introduced in (Zhu et al., 2016b). The frequency dependent characteristic of air conditioner can be shown as:

$\mathrm{\Delta }{P}_{\text{DDC}}=\mathrm{\Delta }{P}_{LC}+D_{ac}\mathrm{\Delta }\omega =\frac{m{c}_p}{EER}\mathrm{\Delta }{T}_{st}+D_{ac}\mathrm{\Delta }\omega (11)$

where m is the mass of air flow, c_p is the specific heat capacity of air, EER is the energy efficient ratio (EER) (Ruelens et al., 2017), D_ac is the reheat coefficient of the air conditioner, Δω = 2πΔf is the deviation of the speed, and ΔP_LC is the controllable change in power consumed, which depends on the characteristic of the air conditioner and the set point of a smart thermostat (ΔT_st). ΔT_st can be expressed as follows:

$\mathrm{\Delta }{T}_{st}=\frac{\bar{K}}{s}\alpha \mathrm{\Delta }f(12)$

where $\bar{K}$ is integral gain and α is a coefficient (given as 0.5 R/Hz in this paper). The temperature set-point is bounded and varies based on the weather condition and different time interval in a day.

From the aforementioned discussion, the load model with respect to frequency deviation of air conditioner is given as:

$\mathrm{\Delta }{P}_{\text{ddc,\hspace{0.17em}i}}=\left(\frac{0.5K_{ddc,i}}{s}+2\pi D_{ac,i}\right)\mathrm{\Delta }f(13)$

where $K_{ddc}=\frac{m{c}_p\bar{K}}{EER}$ is the combined integral gain.

Due to the small capacity of an individual air conditioner, it is necessary to aggregate several small domestic loads into a relatively large and lumped DDC load to participate the LFC scheme. Assume that there are M air conditioners in the smart homes of the grid, then the aggregated power of the DDC can be presented as follows:

$\mathrm{\Delta }{P}_{DDC}=\sum _{i=1}^M\mathrm{\Delta }{P}_{ddc,i}=\left(\frac{0.5K_{DDC}}{s}+2\pi D_{ac}\right)\mathrm{\Delta }f(14)$

where $K_{DDC}={\sum }_{i=1}^M{K}_{ddc,i}$, and $D_{ac}={\sum }_{i=1}^M{D}_{ac,i}$.

3 Control Design of the Wind Turbine Supported in Frequency Regulation

The wind turbines can be controlled by IC, RSC and PAC control methods to participate in frequency regulation in the smart grid. The IC is used for short-time grid frequency restoration. Meanwhile, RSC and PAC are used for grid frequency restoration.

3.1 Inertial Control for Short-Time Grid Frequency Restoration

For a synchronous generator, the kinetic energy is released automatically from the rotating mass when the frequency drops. In the VSWT, the IC utilizes the kinetic energy of wind turbine’s rotor during grid frequency excursion (Ma and Chowdhury, 2010). The kinetic energy is stored in the wind generator as shown in (Eq. 15).

$E_k=\frac{1}{2}J{\omega }_r^2(15)$

where J is the equivalent moment of inertia.

The power from the rotating mass is expressed as follows:

$\mathrm{\Delta }{P}_{ic}=\frac{d{E}_k}{dt}=J{\omega }_r\frac{d{\omega }_r}{dt}(16)$

To couple the grid frequency change, dω_r/dt is replaced by the grid frequency change df_sys/dt for the inertial control loop. So extracted power from the inertial controller is described as:

$\mathrm{\Delta }{P}_{ic}=K_{ic}\frac{d{f}_{sys}}{dt}(17)$

where control coefficient K_ic has replaced the coefficient Jω_r.

3.2 Rotor Speed Control for Grid-Frequency Regulation

The wind turbine is controlled by RSC based on the frequency drop characteristic. The controller adjusts the active power output in proportion to the frequency deviation with the ratio of $-\frac{1}{R}$ (Parizy et al., 2019) as following:

$\mathrm{\Delta }{P}_{wind}=-\frac{1}{R}(f_{sys}-f_{ref})=-\frac{1}{R}\mathrm{\Delta }f(18)$

where f_ref is the nominal frequency and f_sys is the measured system frequency.

The wind power P_e,ref is the initial wind plant output power and it is held constant during the grid frequency restoration period.

3.3 Pitch Angle Control for Grid-Frequency Regulation

PAC of the wind turbine is designed much like the governor control of the synchronous machine. The PAC is used for preventing the rotor speed from exceeding the nominal value (Zhang et al., 2011).

The input signal is Δf. The ΔP_wind can achieve according (Eq. 17) and output is the pitch angle. By using the PAC method, the wind farm provides either higher or lower power to share in the frequency restoration strategy in the long term. This method achieves the coordinated control strategies which will be discussed in Section 3.4.

3.4 Coordinated Control Strategies

Figure 2 shows the wind turbine power output curve at different wind speeds. In region 1, the wind turbine blades cannot rotate in very low wind speeds. While the wind turbine will start to rotate and generate the maximum electrical power from the wind when the wind speed rises in region 2. In region 3, as the power generated by the wind turbine is higher than its rated output power, the wind turbine starts to regulate the pitch angle to limit the electrical power to its rated value. Finally, at the cut-out wind speed, a braking system is used to stop the wind turbine for the sake of protecting the wind turbine in region 4. In this paper, it presents a novel frequency regulation by VSWT to coordinate IC, RSC and PAC under low or high wind speed.

FIGURE 2

FIGURE 2. The wind turbine power output curve with different wind speed.

When the wind speed is in the range [5 m/s, 12 m/s] (in region 2), the output power can be achieved following the trajectory of the 90% sub-optimal operation curve. The PAC does not need to be activated to down-regulate the wind turbine (Zhang et al., 2011). So the RSC is used to control wind turbine and the pitch angle is equal to 0. When the frequency drops, the RSC will control the wind turbine to produce more active output power. On the contrary, the RSC will control the wind turbine to produce less active output power.

When the wind speed is in the range [12 m/s, 25 m/s] (in region 3), the RSC is impossible to control the wind turbines because the MPPT speed has been over maximum rotor speed. Therefore PAC is the only way to down-regulate the wind turbine. When the wind speed is above the rated, the pitch angle is increased to limit the mechanical power of a wind turbine to output its rated value (Ma and Chowdhury, 2010). However, if the power grid requires less power than the rate power, the pitch angle is further increased to satisfy the grid side power demand in order to minimise the frequency deviation of the power system.

The IC can support frequency control in transient. So the IC combined RSC or PAC controls wind turbines to participate in frequency regulation to maintain grid frequency in stable more quickly with smaller fluctuation. When wind turbines produce the rated power but the total power is less than the demand load need, the DSR will shift controllable load to other time used or reduce controllable load using to solve these imbalance problems. On the contrary, the DSR will move the controllable load to use in this time or add controllable load using to solve these imbalance problems. Coordinated frequency regulation of smart grid by DSR and variable speed wind turbines will increase the stability of the power system and allow more wind turbines to connect to the power system.

4 Case Study

The proposed frequency regulation methods are tested on a single area LFC scheme which includes a wind farm, aggregated DDC based on air conditioners and PEVs. The micro generation equips with a non-heat turbine with a capacity of 800 MW. The wind turbine’s capacity is around 2.25 MW. Assume that all wind turbines are identical and the cut-in wind speed, the rated wind speed, and the cut-out speed are 5, 12, and 25 m/s, respectively (Algarni et al., 2021). The related parameters are recalled from literatures (Jay and Swarup, 2011; Xia et al., 2018). The following three cases are studied.

4.1 The High Penetration of Wind Power in the Smart Grid

In this section, the LFC scheme with the high penetration of wind power and DSR is tested. The wind farm consists 400 wind turbines and the total wind farm output power is 900 MW (about 52.94% of the total output power). The DSR and a part of wind turbines joining in frequency regulation. Three scenarios shown in below are tested.

Scenario 1: 40 wind turbines participate in frequency regulation and 360 wind turbines directly connect to the power system.

Scenario 2: 200 wind turbines participate in frequency regulation and 200 wind turbines directly connect to the power system.

Scenario 3: 360 wind turbines participate in frequency regulation and 40 wind turbines directly connect to the power system.

Frequency deviation from three scenarios in the variable low and high wind speed is shown in Figure 3. When the wind speed is low (7 m/s-10 m/s), the wind turbines participating in frequency regulation based on the RSC method (shown in subfigures Figures 3A–C), in which the dash-dot line, the dashed line and the solid line represent three different control methods to control wind turbine participating in frequency regulation, respectively. Frequency deviation is the fastest convergent to schedule values with the smallest fluctuation by combined RSC and DSR approach. While fluctuation of frequency deviation is the biggest and recovering time is longest by RSC method. Compared to the same control method used in these three scenarios, the Scenario 3 can be obtained the best performance in these three scenarios. When the wind speed is high (16 m/s-20 m/s), the wind turbines participating in frequency regulation based on the PAC method. Subfigures Figures 3D–F show frequency deviation in three scenarios in variable high wind speed, in which dash-dot line, dash line and solid line represent for PAC method, PAC combined IC method and combined PAC and DSR method, respectively. Similar results can be obtained from the simulation study. The combined PAC and DSR method is the best method to maintain frequency deviation in desired value with the smallest fluctuation and fastest response time in variable wind speed.

FIGURE 3

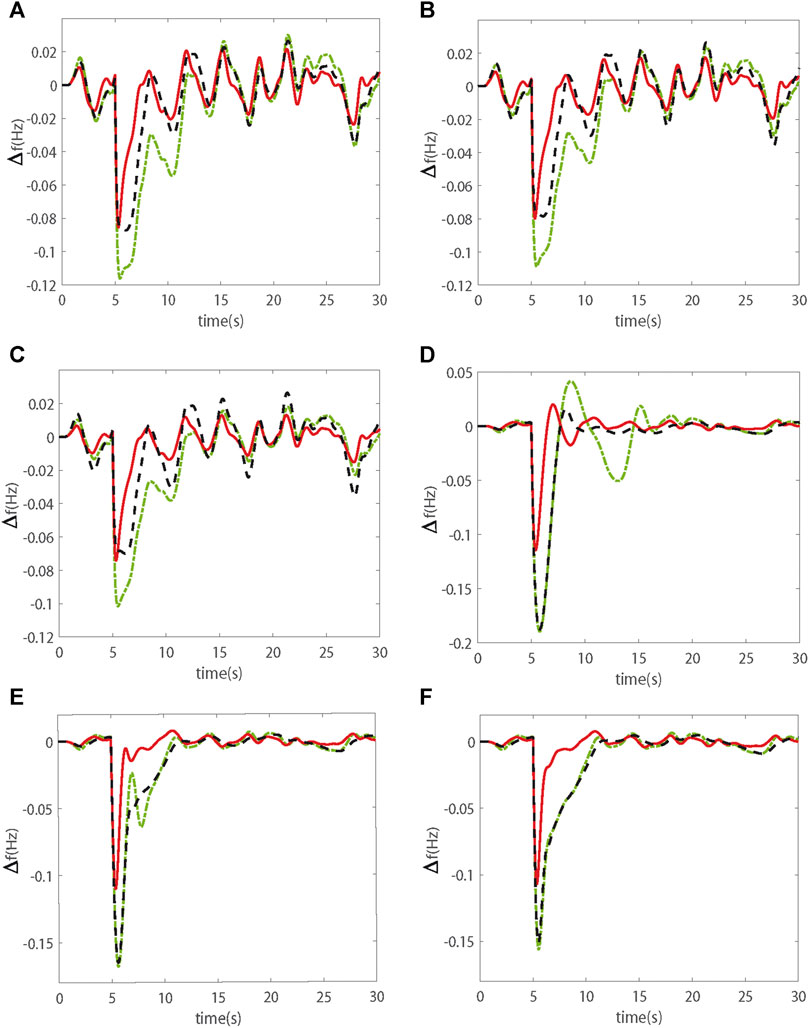
FIGURE 3. Frequency deviation from different control methods under three scenarios in variable low and high wind speed, (A) is Scenario 1 in low wind speed, (B) is Scenario 2 in low wind speed, (C) is Scenario 3 in low wind speed, (D) is Scenario 1 in high wind speed, (E) is Scenario 2 in high wind speed, (F) is Scenario 3 in high wind speed.

4.2 The Demand Load Required Power Exceeds Produced Power

When the high penetration of wind power connects in the power system, it will cause the total produced power insufficient to demand load required because the wind power is intermittent and time-varying. On the other hand, the demand load change may suddenly increase sometimes in a year. Due to these two reasons, the demand side load may need more power than total produced power during some periods. In this section, three scenarios are introduced in the above are simulates with significant demand load change in variable low and high wind speed. The power system required grid frequency in the range 50 ± 0.5 HZ.

A step demand load change is 0.56pu at t = 5 s in the power system. When wind speed is in [7 m/s, 10 m/s], frequency deviation from three scenarios is shown in Figure 4. In these three scenarios, the combined RSC and DSR method can recover the frequency deviation in desired range with the smallest fluctuation and the fastest response time. The fluctuation of frequency deviation from wind turbines controlled by the RSC is the biggest. When more wind turbines participate in frequency regulation, the fluctuation of frequency deviation is smaller. When wind speed is in [16 m/s, 20 m/s], results are similar as above. Wind turbines together with DSR participating in frequency regulation can improve the power system stability and can balance the power system when the demand load change suddenly change. Meanwhile, the more wind turbines participating in the frequency regulation can reduce the fluctuation of the frequency deviation.

FIGURE 4

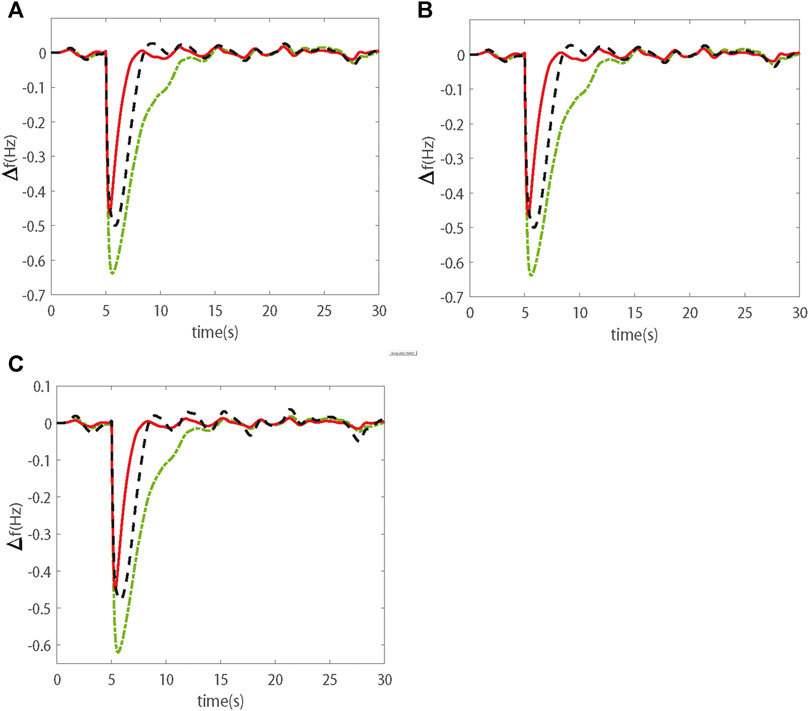
FIGURE 4. Frequency deviation from different control methods in three scenarios with big load change in variable high wind speed, (A) is Scenario 1, (B) is Scenario 2 and (C) is Scenario 3: dash-dot (RSC), dashed (RSC with IC), solid (RSC with DSR).

5 Conclusion

With the increasing penetration of wind power, wind turbines are required to participate in frequency regulation. This paper discusses coordination frequency regulation via VSWTs and DSR in different wind speeds. The VSWTs participating in frequency regulation are controlled by coordinated RSC, PAC and IC in different wind speeds, together with DSR for the LFC of the power system under intermittent wind power and demand load suddenly increasing. Combined RSC or PAC with DSR can contribute to increase penetration of wind power and also slash peak load.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

QZ and LJ was responsible for the design and revision of the thesis proposal, YW and JS was responsible for writing the introduction and dynamic model of smart grid for frequency regulation, and YL was responsible for writing the case study and conclusion.

Funding

This work was jointly supported by the Scientific Research Program Funded by Shaanxi Provincial Education Department (Program No. 21JK0843) and Natural Science Basic Research Program of Shaanxi (Program No. 2020JM-542).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.754057/full#supplementary-material

References

Algarni, A. S., Suryanarayanan, S., Siegel, H. J., and Maciejewski, A. A. (2021). Combined Impact of Demand Response Aggregators and Carbon Taxation on Emissions Reduction in Electric Power Systems. IEEE Trans. Smart Grid 2 (12), 1825–1827. doi:10.1109/TSG.2020.3023586

CrossRef Full Text | Google Scholar

Boukhezzar, B., and Siguerdidjane, H. (2011). Nonlinear Control of a Variable-Speed Wind Turbine Using a Two Mass Model. IEEE Trans. Energ. Convers. 1 (2), 149–162. doi:10.1109/TEC.2010.2090155

CrossRef Full Text | Google Scholar

Chang-Chien, L., Sun, C., and Yeh, Y. (2014). Modeling of Wind Farm Participation in AGC. IEEE Trans. Power Syst. 3 (29), 1204–1211. doi:10.1109/TPWRS.2013.2291397

CrossRef Full Text | Google Scholar

Chau, T. K., Yu, S. S., Fernando, T. L., Iu, H. H., and Small, M. (2018). A Novel Control Strategy of DFIG Wind Turbines in Complex Power Systems for Enhancement of Primary Frequency Response and LFOD. IEEE Trans. Power Syst. 2 (33), 1811–1823. doi:10.1109/TPWRS.2017.2726160

CrossRef Full Text | Google Scholar

Dui, X. W., Zhu, G. P., and Yao, L. Z. (2018). Two-Stage Optimization of Battery Energy Storage Capacity to Decrease Wind Power Curtailment in Grid-Connected Wind Farms. IEEE Trans. Power Syst. 3 (33), 3296–3305. doi:10.1109/TPWRS.2017.2779134

CrossRef Full Text | Google Scholar

Esther, B. P., and Kumar, K. S. (2016). A Survay on Residential Demand Side Management Architercture, Approaches, Optimization Models and Methods. ENTSO-E 59, 342–351. doi:10.1016/j.rser.2015.12.282

CrossRef Full Text | Google Scholar

Hajizadeh, A., and Golkar, M. A. (2007). Intelligent Power Management Strategy of Hybrid Distributed Generation System. Int. J. Electr. Power Energ. Syst. 10 (29), 783–795. doi:10.1016/j.ijepes.2007.06.025

CrossRef Full Text | Google Scholar

Hosseini, S. A., Toulabi, M., Dobakhshari, A. S., Ashouri-Zadeh, A., and Ranjbar, A. M. (2020). Delay Compensation of Demand Response and Adaptive Disturbance Rejection Applied to Power System Frequency Control. IEEE Trans. Power Syst. 3 (35), 2037–2046. doi:10.1109/TPWRS.2019.2957125

CrossRef Full Text | Google Scholar

Jay, D., and Swarup, K. S. (2011). “Frequency Restoration Using Dynamic Demand Control under Smart Grid Environment,” in Proc. IEEE PES ISGT, Kollam, India, 1–3 December 2011, 311–315. doi:10.1109/ISET-India.2011.6145408

CrossRef Full Text | Google Scholar

Kariminejad, N., Taher, S. A., Shahidehpour, M., and Khateri, K. (2018). A Hierarchical Governor/Turbine and Electric Vehicles Optimal Control Framework for Primary Frequency Support in Power Systems. IEEE Trans. Smart Grid. 6 (9), 6702–6712. doi:10.1109/TSG.2017.2718557

CrossRef Full Text | Google Scholar

Khoo, W. C., Teh, J. S., and Lai, C. (2020). Integration of Wind and Demand Response for Optimum Generation Reliability, Cost and Carbon Emission. IEEE Access 8, 183606–183618. doi:10.1109/ACCESS.2020.3029273

CrossRef Full Text | Google Scholar

Liu, P., Wang, C. Y., Hu, J., Fu, T. T., Cheng, N., Zhang, N., et al. (2020). Joint Route Selection and Charging Discharging Scheduling of EVs in V2G Energy Network. IEEE Trans. Veh. Technol. 10 (69), 10630–10641. doi:10.1109/TVT.2020.3018114

CrossRef Full Text | Google Scholar

Ma, H. T., and Chowdhury, B. H. (2010). Working towards Frequency Regulation with Wind Plants: Combined Control Approaches. IET Renew. Power Gener. 4 (4), 308–316. doi:10.1049/iet-rpg.2009.0100

CrossRef Full Text | Google Scholar

Margaris, I. D., Papathanassious, S. A., Hatziargyriou, N. D., Hansen, A. D., and Sorensen, P. (2012). Frequency Control in Autonomous Power Systems with High Wind Power Penetration. IEEE Trans. Sustain. Energ. 2 (3), 189–199. doi:10.1109/TSTE.2011.2174660

CrossRef Full Text | Google Scholar

Nunna, H. S. V. S. K., Battula, S., Doolla, S., and Srinivasan, D. (2018). Energy Management in Smart Distribution Systems with Vehicle-To-Grid Integrated Microgrids. IEEE Trans. Smart Grid. 5 (9), 4004–4016. doi:10.1109/TSG.2016.2646779

CrossRef Full Text | Google Scholar

Oshnoei, A., Kheradmandi, M., and Muyeen, S. M. (2020). Robust Control Scheme for Distributed Battery Energy Storage Systems in Load Frequency Control. IEEE Trans. Power Syst. 6 (35), 4781–4791. doi:10.1109/TPWRS.2020.2997950

CrossRef Full Text | Google Scholar

Parizy, E. S., Bahrami, H. R., and Choi, S. (2019). A Low Complexity and Secure Demand Response Technique for Peak Load Reduction. IEEE Trans. Smart Grid. 3 (10), 259–265. doi:10.1109/TSG.2018.2822729

CrossRef Full Text | Google Scholar

Paul, S., Nath, A. P., and Rather, Z. H. (2020). A Multi-Objective Planning Framework for Coordinated Generation from Offshore Wind Farm and Battery Energy Storage System. IEEE Trans. Sustain. Energ. 4 (11), 2087–2097. doi:10.1109/TSTE.2019.2950310

CrossRef Full Text | Google Scholar

Prasad, R., and Padhy, N. P. (2020). Synergistic Frequency Regulation Control Mechanism for DFIG Wind Turbines with Optimal Pitch Dynamics. IEEE Trans. Power Syst. 4 (35), 3181–3191. doi:10.1109/TPWRS.2020.2967468

CrossRef Full Text | Google Scholar

Ravanji, M. H., Canizares, C. A., and Parniani, M. (2020). Modeling and Control of Variable Speed Wind Turbine Generators for Frequency Regulation. IEEE Trans. Sustain. Energ. 2 (11), 916–927. doi:10.1109/TSTE.2019.2912830

CrossRef Full Text | Google Scholar

Ruelens, F., Claessens, B. J., Vandael, S., Schutter, B. D., Babuka, R., and Belmans, R. (2017). Residential Demand Response of Thermostatically Controlled Loads Using Batch Reinforcement Learning. IEEE Trans. Smart Grid. 5 (8), 2149–2159. doi:10.1109/TSG.2016.2517211

CrossRef Full Text | Google Scholar

Soliman, M. A., Hasanien, H. M., Azazi, H. Z., El-Kholy, E. E., and Mahmoud, S. A. (2019). An Adaptive Fuzzy Logic Control Strategy for Performance Enhancement of a Grid-Connected PMSG-Based Wind Turbine. IEEE Trans. Ind. Informat. 6 (15), 3163–3173. doi:10.1109/TII.2018.2875922

CrossRef Full Text | Google Scholar

Thomsen, S. C., and Poulsen, N. K. (2007). “A Disturbance Decoupling Nonlinear Control Law for Variable Speed Wind Turbines,” in TProc.15th Meditereanean Confernece, Athens, Greece, 27–29 June 2007, 1–6. doi:10.1109/MED.2007.4433869

CrossRef Full Text | Google Scholar

Trovato, V., Sanz, I. M., Chaudhuri, B., and Strbac, G. (2017). Advanced Control of Thermostatic Loads for Rapid Frequency Response in Great Britain. IEEE Trans. Power Syst. 3 (32), 2106–2117. doi:10.1109/TPWRS.2016.2604044

CrossRef Full Text | Google Scholar

Vivekananthan, C., and Mishra, Y. (2015). Stochastic Ranking Method for Thermostatically Controllable Appliances to Provide Regulation Services. IEEE Trans. Power Syst. 4 (30), 1987–1996. doi:10.1109/TPWRS.2014.2353655

CrossRef Full Text | Google Scholar

Wang, M. S., Mu, Y. F., Shi, Q. X., Jia, H. J., and Li, F. X. (2020). Electric Vehicle Aggregator Modeling and Control for Frequency Regulation Considering Progressive State Recovery. IEEE Trans. Smart Grid 5 (11), 4176–4189. doi:10.1109/TSG.2020.2981843

CrossRef Full Text | Google Scholar

Xia, S. W., Bu, S. Q., Luo, X., Chan, K. W., and Lu, X. (2018). An Autonomous Real-Time Charging Strategy for Plug-In Electric Vehicles to Regulate Frequency of Distribution System with Fluctuating Wind Generation. IEEE Trans. Sustain. Energ. 2 (9), 511–524. doi:10.1109/TSTE.2017.2746097

CrossRef Full Text | Google Scholar

Yang, Z., Xia, L., and Guan, X. H. (2020). Fluctuation Reduction of Wind Power and Sizing of Battery Energy Storage Systems in Microgrids. IEEE Trans. Autom. Sci. Eng. 3 (17), 1195–1207. doi:10.1109/TASE.2020.2977944

CrossRef Full Text | Google Scholar

Zhang, S. Q., Mishra, Y., and Shahidehpour, M. (2016). Fuzzy-Logic Based Frequency Controller for Wind Farms Augmented with Energy Storage Systems. IEEE Trans. Power Syst. 2 (31), 1595–1603. doi:10.1109/TPWRS.2015.2432113

CrossRef Full Text | Google Scholar

Zhang, Z. S., Sun, Y. Z., and Li, G. J. (2011). Coordinated Frequency Regulation by Doubly Fed Induction Generator-Based Wind Power Plants. IET Renew. Power Gener. 1 (6), 38–47. doi:10.1049/iet-rpg.2010.0208

CrossRef Full Text | Google Scholar

Zhu, Q., Jiang, L., Yao, W., Zhang, C. K., and Luo, C. (2016b). Robust Load Frequency Control with Dynamic Demand Response for Deregulated Power Systems Considering Communication Delays. ELECTR. POW COMPO SYS 1 (45), 75–87. doi:10.1080/15325008.2016.1233300

CrossRef Full Text | Google Scholar

Zhu, Q., Yao, W., Jiang, L., Luo, C., and Wu, Q. H. (2014). “Load Frequency Control with Dynamic Demand Control for Deregulated Power System,” in 2014 IEEE Power Energy Soc. Gen. Meet, Washington, U.S., 27-31 July 2014, 1–5. doi:10.1109/PESGM.2014.6939313

CrossRef Full Text | Google Scholar

Zhu, Q., Zhang, C. K., Yao, W., and Jiang, L. (2016a). “Chapter 8: Frequency Regulation of Smart Grid via Dynamic Demand Control and Battery Energy Storage System,” in Smarter Energy: From Smart Metering to the Smart Grid. Editors H. Sun, N. Hatziargyriou, H. V. Poor, L. Carpanini, and M. A. S. Fornie (London: The institution of engineering and technology), 209–243.

Google Scholar