
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
BRIEF RESEARCH REPORT article
Front. Energy Res. , 28 September 2021
Sec. Smart Grids
Volume 9 - 2021 | https://doi.org/10.3389/fenrg.2021.753718
This article is part of the Research Topic Advanced Optimization and Control for Smart Grids with High Penetration of Renewable Energy Systems View all 49 articles
A nonlinear control without using anemometer is proposed to achieve the maximum power of the wind turbine (WT) based on two-mass model in this paper. To track the maximum power points, the optimal tip speed ratio control strategy requiring to know the optimal rotor speed of the WT (ORS) is employed. To achieve the ORS, a torque observer is designed to estimate the aerodynamic torque, then the ORS can be obtained by the corresponding calculations based on the estimated torque. Due to the high nonlinearities of the WT and time-varying wind speed, a nonlinear control based on feedback linearization control (FLC) is adopted to track the ORS. In the FLC, the WT is linearized firstly, then the rotor speed controller is designed via linear control technique. The effectiveness of the proposed control strategy is verified by simulation studies. The simulation results show that, compared with the traditional PI control based on torque estimation and FLC based on wind speed estimation, the proposed control strategy provides better dynamic performances and higher power conversion efficiency.
With the increasingly serious energy crisis and environmental problems, renewable clean energy such as wind energy, solar energy and hydrogen energy have attracted more and more attention (Liu et al., 2020; Peng et al., 2020; Sun et al., 2020; Li et al., 2021). Among them, due to large reserves and high conversion efficiency, the total installed capacity of wind turbine (WT) is much higher than that of other renewable energy sources (Wang et al., 2020; Xiong et al., 2021). In order to reduce the relatively high operation cost, it is necessary to improve the conversion efficiency of wind power system. More than 50% energy of a typical wind turbine is captured in the operation area below the rated wind speed (Huang et al., 2015). Therefore, it is necessary to effectively improve the efficiency of wind energy conversion through the maximum power point tracking (MPPT) control strategy in this operation area (Yang et al., 2016).
The essence of the MPPT control strategy is to make the WT always operate under the optimal tip speed ratio (OTSR) (Yang et al., 2018). The traditional MPPT control strategies mainly include hill climb searching (HCS) (Youssef et al., 2019), power signal feedback (PSF) (also known as optimal torque method) (Zhang et al., 2019) and OTSR (Chen et al., 2019b). However, the general MPPT control method using HCS is mainly suitable for small and medium-sized WTs, not for large inertia WTs. The PSF control method usually needs offline training, real-time wind speed information statistics and so on. Compared with the MPPT control strategy of HCS and PSF, the MPPT control strategy based on OTSR directly adjusts the speed according to the speed error, which can obtain faster response speed (Mousa et al., 2021). The traditional OTSR needs to obtain the optimal rotor speed (ORS) through the real-time wind speed. However, in practical application, the wind speed measured by an anemometer cannot accurately represent the effective wind speed acting on the WT. Therefore, the acquisition of accurate optimal rotor speed is one of the important factors for the efficient implementation of MPPT control based on OTSR. In order to achieve the ORS, a Newton-Rafson iteration method (Mérida et al., 2014), a method based on adaptive neuro fuzzy inference system (Golnary and Moradi, 2018), and a non-standard extended Kalman filter-based estimator (Song et al., 2017) are adopted to obtain the estimated wind speed. In this paper, in order to obtain the accurate ORS, a high-gain observer investigated in Chen et al. (2014), Chen et al. (2019b), and Lu et al. (2020) is employed to estimate the aerodynamic torque accurately. Then, the accurate ORS can be obtained based on the estimated aerodynamic torque. The high-gain observer has been successfully used in power system (Chen et al., 2014) and permanent magnet synchronous motor (Chen et al., 2019a), and provides satisfactory estimation ability and strong robustness.
In order to obtain the maximum wind energy from time-varying wind speed, effective control methods need to be adopted after obtaining the accurate ORS. The traditional PI control is widely used in industry because of its simple design and high reliability. However, due to the high nonlinearities of WT and time-varying wind speed, the traditional PI control designed based on a certain operating point cannot provide satisfactory dynamic performance, which reduces the wind energy conversion efficiency. To overcome the shortcomings of traditional PI control and improve wind energy conversion efficiency, a feedback linearization control (FLC) has successfully realized the maximum wind energy capture of permanent magnet synchronous generator (Chen et al., 2019b). Meanwhile, FLC techniques have been widely used in power system, permanent magnet synchronous motor and power electronics. In this paper, in order to obtain the maximum wind energy capture of WT based on two-mass model and avoid using anemometer, the FLC based MPPT control strategy and aerodynamic torque observer will be proposed. Firstly, the aerodynamic torque observer based on the high-gain observer is designed to obtain the accurate aerodynamic torque, so as to obtain the accurate ORS. Then, the WT with two-mass model is transformed into an equivalent linear system. Finally, the ORS is tracked by the designed linear speed controller. In the simulation studies, in order to verify the effectiveness of the proposed control strategy, it will compare with the traditional PI control and FLC based on wind speed estimation (FLC-WE).
The rest of this paper is organized as follows. In Section 2, the model of WT and problem formulation are briefly recalled. Meanwhile, the design of aerodynamic torque observer and wind speed estimation technique are presented in this section. The design of the proposed MPPT control scheme is presented in Section 3. In Section 4, simulation studies are conducted to verify the performances of the proposed FLC based on torque estimation (FLC-TE), and compared with the traditional PI control and FLC-WE. Finally, conclusions are drawn in Section 5.
The state-space model of the WT (Boukhezzar and Siguerdidjane, 2011) can be obtained as
where
where, x ∈ R3, u ∈ R1 and y ∈ R1 are state vector, input vector and output vector, respectively; f(x), g(x) and h(x) are smooth vector fields. Jg is the generator inertia, Ds is the low-speed shaft stiffness, Ng is the gearbox ratio, Kr is the rotor eternal damping, Kg is the generator eternal damping, Ks is the low-speed shaft damping, Jr is the rotor inertia, ωr is the rotor speed, ωg is the generator speed, Tls is the low-speed shaft torque, and Tg is the generator torque. It comes then that
where
In this paper, an MPPT controller based on OTSR is used to capture the maximum wind power. To achieve this objective, the maximum power coefficient Cpmax should be achieved. It is obtained when the TSR λ keeps at its optimal value λopt. λopt can be achieved if the rotor speed ωr can track its optimal reference ωref (ORS), which can be calculated as
In Eq. 3, the ωref (ORS) has a linear relationship with wind speed when the λopt is constant. However, in practical application, the effective wind speed acting on the WT cannot accurately obtained (Ren et al., 2016). To obtain the wind speed, it can be estimated by using the Newton-Raphson method (Ren et al., 2016). In this paper, to achieve the ORS, the aerodynamic torque is estimated by a designed torque observer firstly. The aerodynamic torque observer is designed based on the high-gain observer theory mentioned in Chen et al. (2014), Chen et al. (2019a), and Chen et al. (2019b). In Chen et al. (2014), Chen et al. (2019a), and Chen et al. (2019b), the high-gain observer theory has successfully applied in power system, permanent magnet synchronous generator and permanent magnet synchronous motor, which provides satisfactory performance for perturbation estimation. The detailed design process of the observer can refer to the literature mentioned above. According to Eq. 2 and high-gain observer theory, the aerodynamic torque observer is designed as follows. Carry out the input/output linearization of system (2)
where
and the relative degree is ri = [1].
The following observer is designed to estimate the perturbation
where the gains are designed as
are in the open left-half complex plane.
According Eq. 5 and the estimation of F1(x) obtained from designed observer (7), the aerodynamic torque can be estimated as
The aerodynamic torque is expressed as
According to Eq. 10, the estimation of the ORS can be obtained as
To achieve the effective wind speed and avoid using anemometer, the wind speed is estimated by using the Newton-Raphson method (Mérida et al., 2014; Ren et al., 2016).
The wind speed estimator is realized by minimizing the cost function J (t, V)
where Ta(t) is the aerodynamic torque at time t, and fa(V) is the aerodynamic torque function of wind speed V.
The problem is equivalent to find the solution of
From the partial derivative equation
The iteration form of the estimator can be written as
where
At time t, the iteration will be performed until
where ɛ is a small value. The estimation of wind speed at time t is then
For system (1), choose the output of the system as y = h(x) = ωr and control input u = Tg, we have
where
where B2(x) ≠ 0 for all nominal operation points.
The feedback linearization control of system (1) is obtained as
And the original system is linearized as
where, v is input of linear system, k1 and k2 are gains of linear controller, and
The final control law represented by physical variables is given as follows:
To clearly illustrate the principle of the proposed control strategy for the WT system, a overall control block diagram is shown in Figure 1.
In simulation studies, to verify the performance of the proposed FLC-TE, it compares with the traditional PI control and FLC-WE. The detailed parameters of the WT are given in Boukhezzar and Siguerdidjane (2011). The parameters of the designed observer are α11 = 3.2 × 102, α12 = 2.56 × 104, ∈1 = 0.02. The controller parameters are k1 = 25, k2 = 10.
It can be seen from Figure 2 that, the FLC-TE achieves the best tracking performance among these three controllers. The worst performance is obtained by the traditional PI control. It is because that the PI control designed based one operation point cannot provide optimal performance during time-varying operation points. The FLC-WE achieve a worse tracking performance than the FLC-TE. Although the Newton-Raphson method can be used to estimate wind speed, it requires accurate system model. The inaccurate system model may result in large estimation error. The Cp cannot maintain around its maximum value Cpmax when the rotor cannot be well tracked. Figure 3 shows that the FLC-TE and PI achieve the highest and lowest efficiency, respectively. In Figure 4, the aerodynamic torque Ta is well estimated by the designed observer in most of the time, which is always around its optimal value
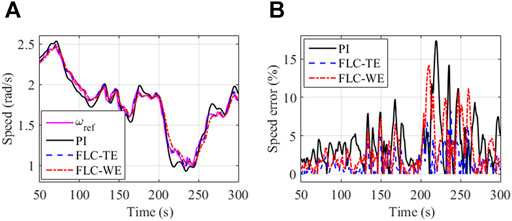
FIGURE 2. Rotor speed response to random wind speed. (A) Rotor speed; (B) relative error of the rotor speed.
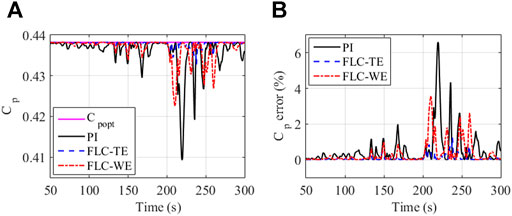
FIGURE 3. Power coefficient response to random wind speed. (A) Power coefficient; (B) relative error of power coefficient.
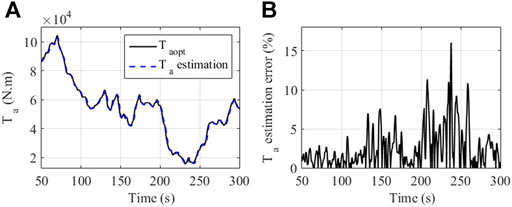
FIGURE 4. Aerodynamic torque response to random wind speed. (A) Aerodynamic torque estimation; (B) relative error of aerodynamic torque estimation.
In this paper, a FLC-TE has been proposed to relaize the MPPT control of the WT. In the proposed control strategy, a high-gain observer is designed to estimate aerodynamic torque, then the ORS can be obtained through the estimated aerodynamic torque. The FLC technique is employed to linearize the WT system, then a linear speed controller is designed for rotor speed regulation. Among the traditional PI, FLC-WE and FLC-TE controllers, the proposed FLC-TE achieves the best dynamic performance and highest efficiency. In the future work, a nonlinear adaptive control based on perturbation estimation technique will be investigated to improve the robustness of the FLC-TE against parameter uncertainties and disturbances.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
JC, QL, LC, and XD contributed to conception and controller design of the study and wrote sections of the manuscript. JC performed the analysis of the simulation results and wrote the first draft of the manuscript. LZ provides guidance. BY and WD proof reading. All authors contributed to manuscript revision, read, and approved the submitted version.
This research was supported by the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant NO.19KJB470036) and National Natural Science Foundation of China under Grant NO.62003292.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Boukhezzar, B., and Siguerdidjane, H. (2011). Nonlinear Control of a Variable-Speed Wind Turbine Using a Two-Mass Model. IEEE Trans. Energ. Convers. 26, 149–162. doi:10.1109/TEC.2010.2090155
Chen, J., Jiang, L., Yao, W., and Wu, Q. H. (2014). Perturbation Estimation Based Nonlinear Adaptive Control of a Full-Rated Converter Wind Turbine for Fault Ride-Through Capability Enhancement. IEEE Trans. Power Syst. 29, 2733–2743. doi:10.1109/TPWRS.2014.2313813
Chen, J., Yao, W., Ren, Y., Wang, R., Zhang, L., and Jiang, L. (2019a). Nonlinear Adaptive Speed Control of a Permanent Magnet Synchronous Motor: A Perturbation Estimation Approach. Control. Eng. Pract. 85, 163–175. doi:10.1016/j.conengprac.2019.01.019
Chen, J., Yao, W., Zhang, C.-K., Ren, Y., and Jiang, L. (2019b). Design of Robust Mppt Controller for Grid-Connected Pmsg-Based Wind Turbine via Perturbation Observation Based Nonlinear Adaptive Control. Renew. Energ. 134, 478–495. doi:10.1016/j.renene.2018.11.048
Golnary, F., and Moradi, H. (2018). Design and Comparison of Quasi Continuous Sliding Mode Control with Feedback Linearization for a Large Scale Wind Turbine with Wind Speed Estimation. Renew. Energ. 127, 495–508. doi:10.1016/j.renene.2018.04.081
Huang, C., Li, F., and Jin, Z. (2015). Maximum Power point Tracking Strategy for Large-Scale Wind Generation Systems Considering Wind Turbine Dynamics. IEEE Trans. Ind. Electron. 62, 2530–2539. doi:10.1109/TIE.2015.2395384
Li, Y., Wang, C., Li, G., and Chen, C. (2021). Optimal Scheduling of Integrated Demand Response-Enabled Integrated Energy Systems with Uncertain Renewable Generations: A Stackelberg Game Approach. Energ. Convers. Manag. 235, 113996. doi:10.1016/j.enconman.2021.113996
Liu, J., Yao, W., Wen, J., Fang, J., Jiang, L., He, H., et al. (2020). Impact of Power Grid Strength and Pll Parameters on Stability of Grid-Connected Dfig Wind Farm. IEEE Trans. Sustain. Energ. 11, 545–557. doi:10.1109/TSTE.2019.2897596
Lu, Q., Zhang, D., Ye, W., Fan, J., Liu, S., and Su, C.-Y. (2020). Targeting Posture Control with Dynamic Obstacle Avoidance of Constrained Uncertain Wheeled mobile Robots Including Unknown Skidding and Slipping. IEEE Trans. Syst. Man, Cybernetics: Syst. (Early Access) , 1–10. doi:10.1109/tsmc.2019.2962732
Mérida, J., Aguilar, L. T., and Dávila, J. (2014). Analysis and Synthesis of Sliding Mode Control for Large Scale Variable Speed Wind Turbine for Power Optimization. Renew. Energ. 71, 715–728. doi:10.1016/j.renene.2014.06.030
Mousa, H. H. H., Youssef, A.-R., and Mohamed, E. E. M. (2021). State of the Art Perturb and Observe Mppt Algorithms Based Wind Energy Conversion Systems: A Technology Review. Int. J. Electr. Power Energ. Syst. 126, 106598. doi:10.1016/j.ijepes.2020.106598
Peng, X., Yao, W., Yan, C., Wen, J., and Cheng, S. (2020). Two-stage Variable Proportion Coefficient Based Frequency Support of Grid-Connected Dfig-Wts. IEEE Trans. Power Syst. 35, 962–974. doi:10.1109/TPWRS.2019.2943520
Ren, Y., Li, L., Brindley, J., and Jiang, L. (2016). Nonlinear Pi Control for Variable Pitch Wind Turbine. Control. Eng. Pract. 50, 84–94. doi:10.1016/j.conengprac.2016.02.004
Song, D., Yang, J., Cai, Z., Dong, M., Su, M., and Wang, Y. (2017). Wind Estimation with a Non-standard Extended Kalman Filter and its Application on Maximum Power Extraction for Variable Speed Wind Turbines. Appl. Energ. 190, 670–685. doi:10.1016/j.apenergy.2016.12.132
Sun, K., Yao, W., Fang, J., Ai, X., Wen, J., and Cheng, S. (2020). Impedance Modeling and Stability Analysis of Grid-Connected Dfig-Based Wind Farm with a Vsc-Hvdc. IEEE J. Emerg. Sel. Top. Power Electron. 8, 1375–1390. doi:10.1109/JESTPE.2019.2901747
Wang, Q., Yao, W., Fang, J., Ai, X., Wen, J., Yang, X., et al. (2020). Dynamic Modeling and Small Signal Stability Analysis of Distributed Photovoltaic Grid-Connected System with Large Scale of Panel Level Dc Optimizers. Appl. Energ. 259, 114132. doi:10.1016/j.apenergy.2019.114132
Xiong, Y., Yao, W., Wen, J., Lin, S., Ai, X., Fang, J., et al. (2020). Two-level Combined Control Scheme of Vsc-Mtdc Integrated Offshore Wind Farms for Onshore System Frequency Support. IEEE Trans. Power Syst. 36, 1. doi:10.1109/TPWRS.2020.2998579
Yang, B., Jiang, L., Wang, L., Yao, W., and Wu, Q. H. (2016). Nonlinear Maximum Power point Tracking Control and Modal Analysis of Dfig Based Wind Turbine. Int. J. Electr. Power Energ. Syst. 74, 429–436. doi:10.1016/j.ijepes.2015.07.036
Yang, B., Yu, T., Shu, H., Zhang, Y., Chen, J., Sang, Y., et al. (2018). Passivity-based Sliding-Mode Control Design for Optimal Power Extraction of a Pmsg Based Variable Speed Wind Turbine. Renew. Energ. 119, 577–589. doi:10.1016/j.renene.2017.12.047
Youssef, A.-R., Ali, A. I. M., Saeed, M. S. R., and Mohamed, E. E. M. (2019). Advanced Multi-Sector P&O Maximum Power point Tracking Technique for Wind Energy Conversion System. Int. J. Electr. Power Energ. Syst. 107, 89–97. doi:10.1016/j.ijepes.2018.10.034
Keywords: maximum power point tracking, torque estimation, feedback linearization control, two-mass model wind turbine, high-gain observer
Citation: Chen J, Lu Q, Chen L, Duan X, Yang B, Duan W and Zhang L (2021) Nonlinear Maximum Power Point Tracking Control of Wind Turbine Based on Two-Mass Model Without Anemometer. Front. Energy Res. 9:753718. doi: 10.3389/fenrg.2021.753718
Received: 05 August 2021; Accepted: 13 September 2021;
Published: 28 September 2021.
Edited by:
Bo Yang, Kunming University of Science and Technology, ChinaReviewed by:
Wang Yao-Wei, China University of Geosciences Wuhan, ChinaCopyright © 2021 Chen , Lu , Chen, Duan , Yang, Duan and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jian Chen , Y2p5Y2l0QDE2My5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.