A Learning-Based Bidding Approach for PV-Attached BESS Power Plants

Large-scale renewable photovoltaic (PV) and battery energy storage system (BESS) units are promising to be significant electricity suppliers in the future electricity market. A bidding model is proposed for PV-integrated BESS power plants in a pool-based day-ahead (DA) electricity market, in which the uncertainty of PV generation output is considered. In the proposed model, we consider the market clearing process as the external environment, while each agent updates the bid price through the communication with the market environment for its revenue maximization. A multiagent reinforcement learning (MARL) called win-or-learn-fast policy-hill-climbing (WoLF-PHC) is used to explore optimal bid prices without any information of opponents. The case study validates the computational performance of WoLF-PHC in the proposed model, while the bidding strategy of each participated agent is thereafter analyzed.

Introduction

The share of photovoltaic (PV) installations experiences an exponential growth worldwide and accounts for most of the electricity supply of renewable energy (Zucker and Hinchliffe, 2014). However, the actual output of PV power may be different from the scheduled production, which brings an inevitable challenge in power system real-time balancing. Battery energy storage system (BESS) units can deal with the uncertainty of PV production by the flexible up-and-down regulation capability (Li et al., 2013). Hence, the combination of PV farms and BESS sets will be a promising form of virtual power plant, which will actively participate in the future energy spot market with more deregulated paradigms. Thus, it is necessary to investigate the decision making of such PV–BESS generation as prosumers in the market.

In the work of Shafie-khah and Catalao (2015) and Shafie-khah et al. (2015), bidding strategies of large-scale renewable resources in oligopoly electricity markets were formulated as mathematical programming with equilibrium constraints (MPEC) with the uncertainty of market competitors considered using incomplete information dynamic game theory. However, the equilibrium of such model is often difficult to be obtained because of the computational burden, and the complexity of these models increases with consideration of numerous complicated real-world assumptions and constraints (Ventosa et al., 2005). In this way, this complex set of equations is required to be solved again to find the market equilibrium in the new situation (Salehizadeh and Soltaniyan, 2016/04). With the development of artificial intelligence (AI) techniques in recent years, AI algorithms have been applied in the power system to deal with various problems such as renewable energy forecasting (Zeng et al., 2020), price prediction (Kebriaei et al., 2015), and energy management (Wang et al., 2019). The electricity market can be modeled as an AI-enabled energy platform, where market participants are regarded as AI agents. Agents make bidding decisions by gradually learning through repetitive communication with the AI-enabled market platform. The common AI learning technologies applied in the electricity market refer to heuristic search, artificial neural network, and reinforcement learning. Market participants make bidding decisions with shuffled frog-leaping algorithm (Jonnalagadda and DullaMallesham, 2013), genetic algorithm (Praça et al., 2003), and fuzzy adaptive gravitational search algorithm (Vijaya Kumar et al., 2013) by performing a heuristic search. Some reinforcement learning methods are used to address bidding problems, for example, the traditional Q-learning algorithms in the work of Najafi et al. (2019) and a deep reinforcement learning-based approach (Ye et al., 2019). However, market players develop the bidding strategy by using the abovementioned methods without consideration of other competitors. In the real-world electricity market, each agent achieves its purpose in response to other agents’ bidding behaviors. Considering this, a multiagent multiobjective architecture with reinforcement learning is proposed to minimize energy costs for EV owners, in which agents should communicate with all friendly agents and get their rewards functions (Da Silva et al., 2019). The Markov game approach is utilized to update multiagent competitive bidding strategies in the work of Rashedi et al. (1049), while it is necessary to obtain other agents’ previous bidding. However, market participants are not willing to share neither perfect nor part information in practice. The future research is expected to develop a bidding strategy obtained by a fully distributed online training procedure without any information communicated among agents.

Two bidding strategies are formulated considering the uncertainty of PV prediction in the work of Bo et al. (2017). The bidding strategy of battery storage systems in the secondary control reserve market is investigated in the work of Merten et al. (2020). Chen et al. (2021) studied the optimal bidding strategy of a PV-BESS VPP in frequency control ancillary services markets. A two-stage bidding strategy of households PV-BESSs is proposed in peer-to-peer market (Zhang et al., 2019). Niknam et al. (2012) introduced a bidding strategy of combined PV-storage systems in day-ahead (DA) market, in which PV-storage systems are considered as price takers. So far, to the best of the authors’ knowledge, there is little research considering PV-attached BESS power plants in a pool-based DA wholesale market as oligopolists to make their bidding decisions without any information of opponents. Furthermore, prior research studies consider aggregated PV-BESSs developing bidding strategy with either complete or part information of other strategic players. In other words, previous work cannot deal with the situation that each strategic participant of PV-BESSs does not share any information with other rivals. This challenging issue is required to be addressed properly. In this study, we propose a DA bidding strategy of PV-attached BESS power plants to maximize their benefits by self-bidding not relied on any information of competitors. A multiagent reinforcement learning win-or-learn-fast policy-hill-climbing (WoLF-PHC) is used to solve the proposed bidding problem. The main contributions of this study are summarized as follows:

1) A stochastic bidding strategy model of PV-attached BESS power plants in a pool-based DA wholesale market is developed, to maximize revenues of PV-attached BESS power plants considering the uncertainty of potential maximum PV power production

2) A multiagent stochastic game framework with incomplete information is used to describe the proposed bidding model, and the proposed model is then solved by a multiagent reinforcement learning WoLF-PHC without any opponents’ information

3) The validity of the proposed model and the WoLF-PHC algorithm is validated by the modified IEEE 6-bus and 118-bus systems

The remaining part of this article is arranged as follows. Proposed Bidding Model introduces the proposed bilevel stochastic bidding model. In Methodology, the WoLF-PHC is used to solve the proposed bidding problem. Simulation results and analysis are conducted in Case Study, while Conclusion concludes the whole article.

Proposed Bidding Model

The DA wholesale pool-based market is considered in this study. Strategic participants PV-attached BESS power plants submit bid prices and power capacities to the market operator (MO) on an hourly basis. The MO runs the market clearing process to confirm the locational marginal pricing (LMP) and scheduled power production of PV-attached BESS power plants. The overall structure figure of the proposed model is presented in Figure 1.

FIGURE 1

FIGURE 1. Overall structure figure of the proposed model.

The assumptions of the proposed market model are as follows:

1) Uncertainty of potential maximum PV power production is considered in this study, which is dealt with a scenario-based stochastic optimization method. The uncertainty is modeled as a set of scenarios derived from a scenario generation process on account of the roulette wheel mechanism in the work of Niknam et al. (2012) and an efficient scenario-reduction method in the work of Morales et al. (2009). In this way, a stochastic optimization problem can be converted into a deterministic one and solved with many methods.

2) PV-attached BESS power plants are assumed as large-scale strategic players in the wholesale market. Each PV-attached BESS power plant makes a bidding decision to increase its revenue.

3) Loads submit their bid prices to MO but not strategically. The bid prices are their marginal cost prices which are open to strategic PV-attached BESS power plants.

4) The transmission network only considers DC optimal power flow (DC-OPF) without losses.

5) Bertrand model of competition is considered in the proposed work with bidding prices as decision variables. Although the cournot model and the supply function equilibrium (SFE) model, in which a quantity and a pair of bid price and quantity are seperately chosen to bid, can be considered to make bidding decision, the cournot model and SFE model are required to be formulated using mathematical programming approaches, which makes solving difficult (Shafie-khah and Catalao, 2015; Shafie-khah et al., 2015). There is no such limitation in the Bertrand competition model, and thus, it is selected in this study.

A stochastic bidding model is introduced where the total cost is minimized for the MO completing the market clearing, while respective revenues are maximized for strategic participants PV-attached BESS power plants.

Market Clearing Model

In the market clearing process, suppliers PV-attached BESS power plants and loads first submit their bid prices ${\pi }_{co,t}^{bid}$ and ${\pi }_{d,t}^D$, respectively, to the MO. The MO then completes market clearing by minimizing the total cost relied on the OPF. At last, the dispatched power production of PV-attached BESS power plants $P_{co,\alpha ,t}^{CO}$ and LMP ${\lambda }_{n,\alpha ,t}$ will be returned to maximize revenues of strategic PV-attached BESS power plants.

Minimize

${\displaystyle \sum _{\alpha \in N_{\alpha }}{\tau }_{\alpha }}\cdot ({\displaystyle \sum _{co\in {\Omega }_n^{CO}}{\mathit{\pi }}_{co,t}^{bid}\cdot P_{co,\alpha ,t}^{CO}}-{\displaystyle \sum _{d\in {\Omega }_n^D}{\mathit{\pi }}_{d,t}^D\cdot P_{d,t}^D})(1)$

subject to

$P_{co,\alpha ,t}^{CO}-{\displaystyle \sum _{m\in {\Omega }_n^N}}{B}_{nm}\cdot ({\theta }_{n,\alpha ,t}-{\theta }_{m,\alpha ,t})=P_{d,t}^D:{\mathit{\lambda }}_{n,\alpha ,t},\forall n,t,\alpha ,(1.1)$

$P_{pv,\alpha ,t}^{PV}+P_{be,\alpha ,t}^{BE}=P_{co,\alpha ,t}^{CO},(1.2)$

$P_{co,\alpha ,t}^{CO}\ge 0.(1.3)$

$0\le P_{pv,\alpha ,t}^{PV}\le P_{pv,\alpha ,t}^{PV,\max },\forall pv,t,\alpha ,(1.4)$

$-P_{be}^{BE,\min }\le P_{be,\alpha ,t}^{BE}\le P_{be}^{BE,\max },\forall be,(1.5)$

$-f_{nm}^{\max }\le B_{nm}\cdot \left({\theta }_{n,\alpha ,t}-{\theta }_{m,\alpha ,t}\right)\le f_{nm}^{\max },\forall n,m\in {\Omega }_n^N,t,\alpha ,(1.6)$

${\theta }_{n,\alpha ,t}=0,\forall t,\alpha ,n:ref,(1.7)$

$-\pi \le {\theta }_{n,\alpha ,t}\le \pi ,\forall t,\alpha ,n\backslash n:ref,(1.8)$

$SO{C}^{\min }\le SO{C}_{be,\alpha ,t}\le SO{C}^{\max },\forall be,t,\alpha ,(1.9)$

$SO{C}_{be,\alpha ,t}=SO{C}_{be,\alpha ,t-1}-\left(P_{be,\alpha ,t}^{BE}/{\eta }_{dis}\cdot \Delta t/E_{be}^{\max }\right),\forall be,t,\alpha ,P_{be,\alpha ,t}^{BE}\ge 0,(\mathrm{1.10.1})$

$SO{C}_{be,\alpha ,t}=SO{C}_{be,\alpha ,t-1}-\left(P_{be,\alpha ,t}^{BE}.{\eta }_c\cdot \Delta t/E_{be}^{\max }\right),\forall be,t,\alpha ,P_{be,\alpha ,t}^{BE}<0.(\mathrm{1.10.2})$

The objective of Eq. 1 is to minimize the total cost. The first term is the costs of purchasing electricity from PV-attached BESS power plants ${\pi }_{co,t}^{bid}\cdot P_{co,\alpha ,t}^{CO}$, while the second term represents the revenues of selling electricity to load demands ${\pi }_{d,t}^D\cdot P_{d,t}^D$. $P_{co,\alpha ,t}^{CO}$ and $P_{d,t}^D$ are the power output of the coth PV-attached BESS power plant and the dth load in each hour. α indexes scenarios of PVs, and ${\tau }_{\alpha }$ is the corresponding probability. The constraint of Eq. 1.1 is the power production and consumption balance for node n with a dual variable ${\lambda }_{n,\alpha ,t}$ donating the LMP, where $B_{nm}$ is the susceptance of the line connecting nodes n and m, and θ is the voltage angle. Eq. 1.2 represents the scheduled power of PV-attached BESS power plants $P_{co,\alpha ,t}^{CO}$ supplied from PVs $P_{pv,\alpha ,t}^{PV}$ and BESS units $P_{be,\alpha ,t}^{BE}$. The scheduled power of PV-attached BESS power plants should be nonnegative, as shown in Eq. 1.3. Maximum and minimum capacity limitation for PV units and BESS units are considered in Eq. 1.4 and Eq. 1.5 respectively. Inequality Eq. 1.6 limits the thermal capacity of the transmission line $f_{nm}^{max}$. Eq. 1.7 and inequality Eq. 1.8 set voltage angle limits at the slack bus and other buses, respectively. Inequality Eq. 1.9 represents the SOC range of the BESS at the present hour, while constraints Eq. 1.10.1 and Eq. 1.10.2 indicate time-series SOC formulation of the BESS at present and the previous hours. η_c and η_dis are the charging and discharging efficiency of the BESS separately. $E_{be}^{max}$ refers to the maximized power capacity of BESS.

The PV-Attached BESS Power Plant Revenue Model

The strategic player revenue for the $co$th PV-attached BESS power plant is maximized and represented by scenarios α with corresponding probabilities ${\tau }_{\alpha }$ and represented in Eq. 2, where LMP ${\lambda }_{n,\alpha ,t}$ and scheduled power output of PV-attached BESS power plant $P_{co,\alpha ,t}^{CO}$ are obtained from the market clearing process. The revenue of a PV-attached BESS power plant in Eq. 2 includes the income of selling electricity to the electricity market ${\lambda }_{n,\alpha ,t}\cdot P_{co,\alpha ,t}^{CO}$ and the battery degradation cost $\left({{\rm K}}_b/{\varpi }_b\right)\cdot \left|P_{be,\alpha ,t}^E\right|$. ${{\rm K}}_b \text{and} {\varpi }_b$ are battery lifetime and battery capital cost, respectively. Absolute-value function in Eq. 2 can be addressed by a linear programming simplex method in the work of Hill and Ravindran (1975).

Maximize

$R_{co}={\displaystyle \sum _{\alpha \in N_{\alpha }}{\tau }_{\alpha }\cdot \left({\mathit{\lambda }}_{n,\alpha ,t}\cdot P_{co,\alpha ,t}^{CO}-\left({{\rm K}}_b/{\varpi }_b\right)\cdot \left|P_{be,\alpha ,t}^E\right|\right)}.(2)$

Methodology

Introduction to Multiagent Reinforcement Learning

The proposed bidding model brings fundamental problems: how the strategic market participants work as AI agents to learn and determine the optimal bid prices? This research implies that, in the electricity market, it is possible to train agents with AI algorithms to better solve the optimization of bidding problems. The common core techniques for AI are classified as the artificial neural network, reinforcement learning, genetic algorithms, and multiagent systems (Xu et al., 2019).

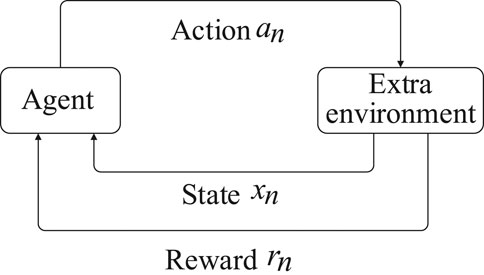
In reinforcement learning (RL), the agent makes its decision in terms of communication with the external environment as in Figure 2 (Hwang et al., 2017). First, the agent perceives a state $x_n$ and a reward $r_n$ based on its past action $a_{n-1}$ from the environment at each step n. Then, its learning is reinforced by comparing the returned scalar reward signal $r_n$ every time with the one in last round $r_{n-1}$ for evaluating the quality of its environment-based behavior. Specifically, the probability of this potential action p will be increased if the compared result is better and decreased if conversely. Last, the highest probability action $a_n$ would be chosen through the learning by itself. There are three main classes of methods that made use of RL principles, namely, dynamic programming methods, Monte Carlo techniques, and temporal difference learning methods (Tellidou and Bakirtzis, 2006). The premise of using dynamic programming is the complete availability of system information. Although Monte Carlo techniques could cope with unknown environments, the solution process is very time consuming and a long time would be needed to wait for the final outcome of learning. Temporal difference learning methods used to learn from an unknown environment after every step without the final result are more suitable for the problem presented in this study, and Q-learning is one of such most frequently used RL approaches. In Q-learning, sets of states g and actions k of each agent are represented as χ = {$x_1,x_{2 },\dots ,x_{g }$} and Λ = {$a_1,a_{2 },\dots ,a_{k }$}. Then Q values are updated in the nth step Eq. 3, in which $x_n\in$χ,$a_n\in$$\Lambda$, and $r_n$ refers to each pair $(x_n,a_n).$α and β are the learning rate and discount factor separately, which are both in the range (0,1].

$Q_{n+1}\left(x_n,a_n\right)\leftarrow \left(1-\alpha \right)Q_n\left(x_n,a_n\right)+\alpha \left(r_n+\beta \underset{a_n^{\prime }}{\max }{Q}_{n+1}\left(x_n,a_n^{\prime }\right)\right).(3)$

FIGURE 2

FIGURE 2. Reinforcement learning process of the agent.

Multiagent reinforcement learning (MARL) is developed from the single-agent RL with adding the game relationship between all agents, which are similar to strategic players in the electricity market. Let a tuple (K, χ, Λ, P, r) represent a multiagent game framework, where K = {1, 2, … , k} is a set of agents and χ is a set of states {$x_g$}. The sects of actions of each agent $a_i$ are described as $a_i$= {$a{a}_{min}$, …, $a{a}_{max}$} in Λ = {$a_1,\dots ,a_i,\dots , a_k$}. P refers to the transition function written as $\chi \times \Lambda \times \chi \to \left[\mathrm{0,1}\right]$. r = {$r_1$,…, $r_i$ …, $r_k$} is the set of reward functions of all agents, where $r_i$: ($x_g$, $a_i$)$\to \mathrm{ℛ}$ implies the ith agent’s reward function with a pair ($x_g$, $a_i)$. In each episode, the agent observes the state $x_g\in \chi$ and selects to execute the action $a_i$ relying on an appropriate policy of learning algorithm and then steps into the next state $x_g\in \chi$.

Assumptions and Definitions

The proposed bidding model in Proposed Bidding Model can be expressed as the multiagent game framework. We consider agents

$K=\left\{co\in {\Omega }_n^{CO}\right\},(4)$

where K is a set of strategic participants PV-attached BESS power plants, states

$X={\left\{x_{co}\right\}}_{co\in {\Omega }_n^{CO}},(5)$

where χ is defined as different levels of PV-attached BESS power plants’ capacities. $P_{co,\alpha ,t}^{CO}$ is obtained from the market clearing, which would show that a state $x_{co}$ is selected after the communication with the extra environment, and actions

$\mathit{\Lambda }=\left\{a_i\right\}.(6)$

Λ is used to update bid price ${\left\{{\pi }_{co,t}^{bid}\right\}}_{co\in \left\{a_j\right\}}$.

Reward function: $r_i$ ($x_{co}$, $a_i$)$\to \mathrm{ℛ}$ is the revenue of the coth player with the bid price ${\text{π}}_{co,t}^{bid}$ in the PV-attached BESS power plant’s capacity level $x_{co}$.

In this way, K, χ, Λ, and r have been defined. The optimal policy p, which is used to choose an action in current state, is required to find. Here, a suitable algorithm win-or-learn-fast policy-hill-climbing (WoLF-PHC) would be introduced in this study.

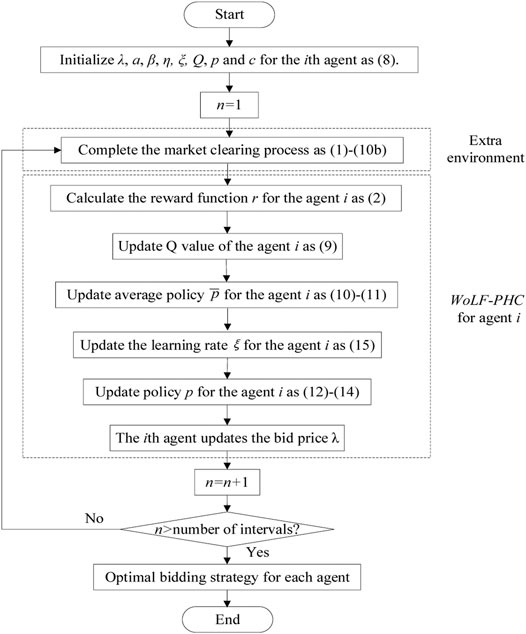
The Step-by-Step Implementation of the Proposed Model With WoLF-PHC

The WoLF-PHC is developed from the Q-learning, which requires two learning parameters with winning ${\xi }_w\text{ and losing }{\xi }_l$. The convergence is enhanced with these two learning rates. It is defined that ${\xi }_{\omega }$ should be smaller than${\xi }_l$. If the agent loses, it will learn faster with ${\xi }_l$ to update its action. On the contrary, the agent will keep caution with ${\xi }_{\omega }$ when it wins. The evaluation criterion of winning or losing is comparing the expected revenue and the average profit, in which the average strategy replaces the original equilibrium policy. The WoLF-PHC algorithm of agent i is represented as follows.

ALGORITHM 1

ALGORITHM 1. The WoLF-PHC for agent i.

Specific learning procedures for the ith PV-attached BESS power plant strategically bidding with WoLF-PHC are described in following steps. 1) Bid price ${\lambda }_i$, parameters α, β, η,${\xi }_w,\text{ and }{\xi }_l$, and $Q_i,p_i$, and $c\left(x_{co}\right)$ are initialized. 2) In the nth episode, market clearing is completed as (1)–(10b). After that, the reward function of the ith agent $r_{in}$ can be obtained as (2). Then, $Q_i$, ${\overline{p}}_i$, $\xi$, and $p_i$ are updated in sequence as (9), (10)–(11), (15), and (12)–(14), individually. Last, the bid price of ith agent ${\lambda }_i$ is updated according to the updated policy $p_i$. 3) n = n + 1 is set, and step 2) is repeated until n > number of intervals. The abovementioned implementation of WoLF-PHC for solving PV-attached BESS power plants’ bidding problems in Proposed Bidding Model is shown in Figure 3.

FIGURE 3

FIGURE 3. Flowchart of solving the proposed bidding problem with the WoLF-PHC.

Case Study

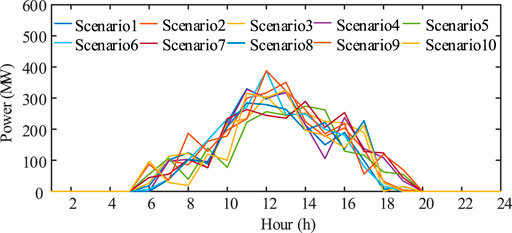
The proposed model is tested on the IEEE 6-node and 118-node systems. Scenarios for electricty output capacities of the PV unit are derived from historical data from the work of Agathokleous and Steen (2019) and represented in Figure 4 after scenario generation and deduction (Niknam et al., 2012) (Morales et al., 2009). 10 corresponding probabilities are shown in Table 1. Parameters of BESS and WoLF-PHC are shown in Table 2 and Table 3, respectively. We run all simulations in MATLAB with a 1.6 GHz Intel Core i5-5250U computer.

FIGURE 4

FIGURE 4. Scenarios for electricty output capacities of the PV unit.

TABLE 1

TABLE 1. | Parameters of the BESS.

TABLE 2

TABLE 2. Parameters of the BESS.

TABLE 3

TABLE 3. Parameters of the WoLF-PHC.

Case 1

In the 6-node system, three suppliers PV-attached BESS power plants are located in buses 1–3 separately and three loads are connected to buses 4-6 individually. Bid prices of loads are assumed as constant in 24 h, which are 59.4 $/MWh, 50.8 $/MWh, and 39.7 $/MWh (Zugno et al., 2013).

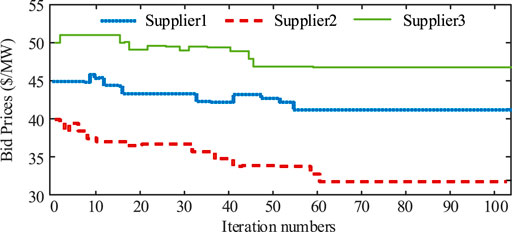
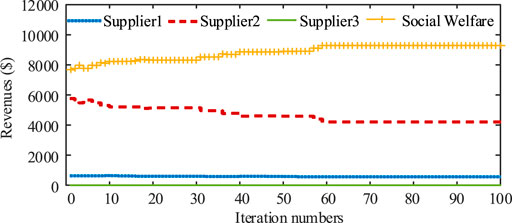
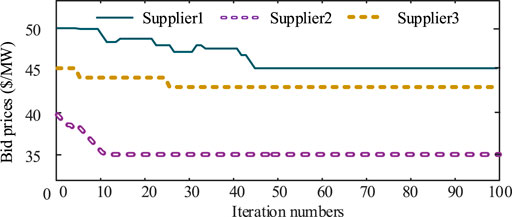
Three suppliers PV-attached BESS power plants represent three strategic participants in this case. According to the parameter setting given above, their bid prices and revenues are shown in Figure 5 and Figure 6. It demonstrates that WoLF-PHC could be used to, respectively, optimize bid prices for the competitive PV-attached BESS power plants. During this process, each strategic participant obtains optimal bid price only relying on the communication with the extra environment ISO. Rivals’ cost functions, bidding information, and historical bidding information are not open to the agent. We protect the personal information of market players with the WoLF-PHC. Three PV-attached BESS power plants’ power outputs and SOC are, respectively, shown in Figures 7–9. There is no solar power output in 1:00-5:00 and 20.00–23:00, and BESSs supply loads by discharging, while PV units satisfy the requirement of load demand and charging of BESSs during 6:00–19.00.

FIGURE 5

FIGURE 5. Bid prices of three suppliers PV-attached BESS power plants in the 6-node system.

FIGURE 6

FIGURE 6. Revenues of three suppliers PV-attached BESS power plants in the 6-node system.

FIGURE 7

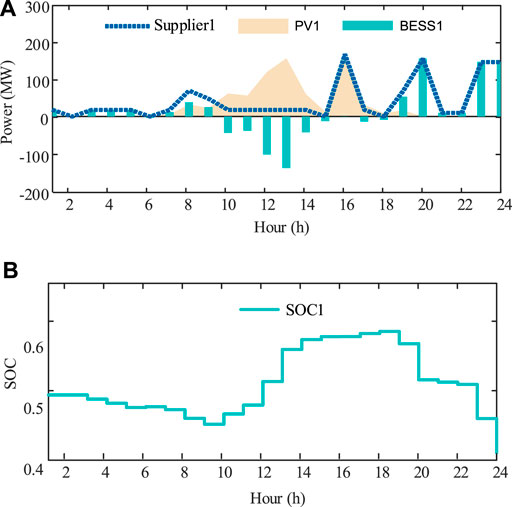
FIGURE 7. (A) Scheduled power output of PV unit 1, BESS 1, and PV-attached BESS power plant 1 in the 6-node system. (B) SOC of PV-attached BESS power plant 1 in the 6-node system.

FIGURE 8

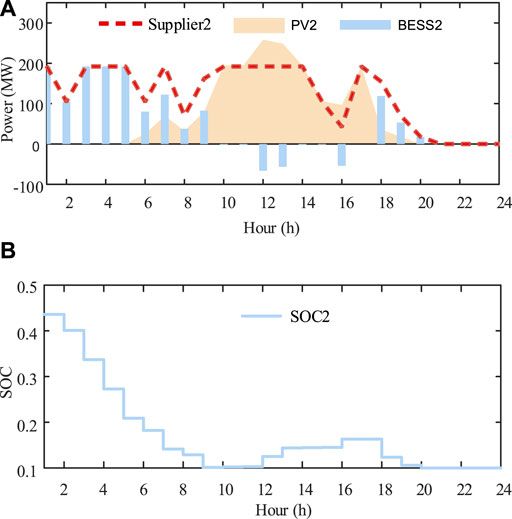
FIGURE 8. (A) Scheduled power output of PV unit 2, BESS 2, and PV-attached BESS power plant 2 in the 6-node system. (B) SOC of PV-attached BESS power plant 2 in the 6-node system.

FIGURE 9

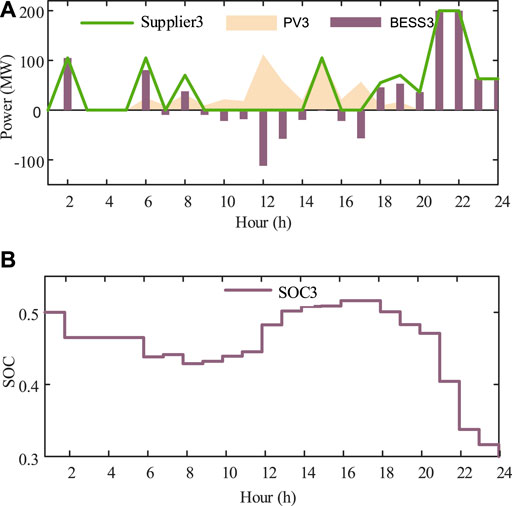
FIGURE 9. (A) Scheduled power output of PV unit 3, BESS 3, and PV-attached BESS power plant in the 6-node system. (B) SOC of PV-attached BESS power plant 3 in the 6-node system.

Comparison

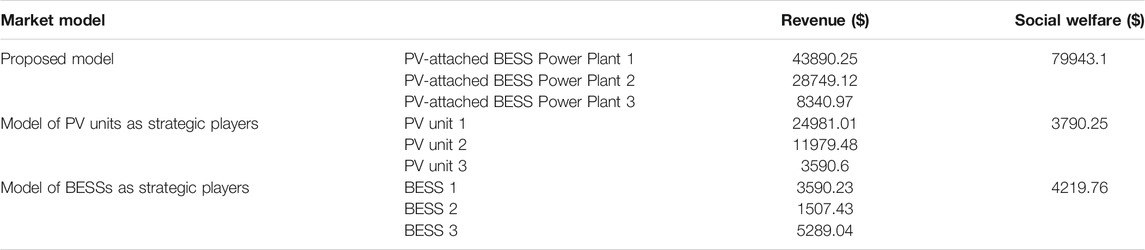
The proposed bidding model of the PV-attached BESS power plant is compared with the other two models, which consider only PV units and only BESSs as strategic market participants. Revenue comparison of the proposed model, PV unit, and BESS for 24 h is represented in Table 4. Due to the limited light time and the degradation of the battery, revenues of PV unit and BESS separately as the strategic player are both lower than the profit of the proposed model. The social welfare of the proposed model is higher than that of the other two models.

TABLE 4

TABLE 4. Revenues comparison of the proposed model, PV unit, and BESS for 24 h.

Case 2

In this case, results of bidding prices are analyzed with different load levels and different numbers of strategic players. First, the total load demand is set equal to the total capacity of the three strategic players. Figure 10 represents bid prices of three suppliers in 100 iterations. Compared with bid prices in Figure 5, bid prices of three participants are higher in Figure 10. The lack of competition among market participants shows that they are not required to lower their bid prices for selling more. On the contrary, each player tries to raise its bid price for earning more profits. Then, total demand is set as half of the load in case 1. Bidding results are shown in Figure 11. More competition drives all participants to reduce their bid prices than those in Figure 5. Last, the number of strategic players is increased to five and the corresponding curves of bidding prices in 100 iterations are represented in Figure 12. Suppliers adopt relatively conservative behaviors so that their price levels are lower than those in Figure 5.

FIGURE 10

FIGURE 10. Bid prices of three suppliers PV-attached BESS power plants within increased load in the 6-node system.

FIGURE 11

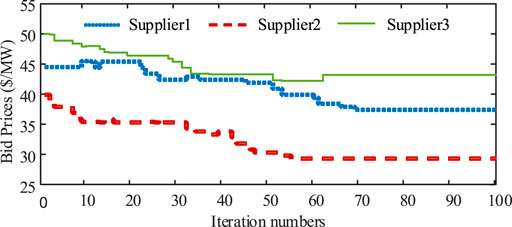
FIGURE 11. Bid prices of three suppliers PV-attached BESS power plants within reduced load in the 6-node system.

FIGURE 12

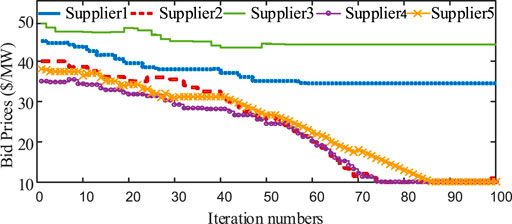
FIGURE 12. Bid prices of three suppliers PV-attached BESS power plants within increased players in the 6-node system.

Case 3

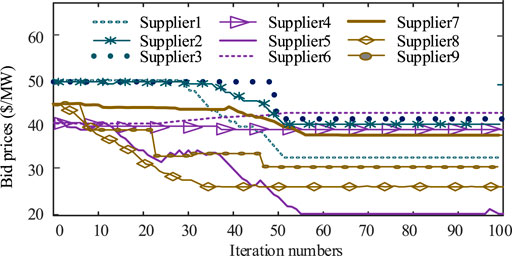
The proposed model is applied in the IEEE 118-node system with three and nine PV-attached BESS ower plants, respectively, in this case. The three suppliers of PV-attached BESS power plants are located in node 12, 29, and 98, which are then individually duplicated to be three strategic players in the same nodes and then become nine players. The convergences of bidding prices for three suppliers and nine suppliers are shown in Figure 13 and Figure 14 separately, which imply that each agent can get its convergent bid price with WoLF-PHC in a larger power system with more participants. In this process, any information of opponents is not required. Each supplier communicates just with the ISO in the clearing process, which ensures the privacy of suppliers. Additionally, the overall bid level of nine strategic suppliers in Figure 14 is lower compared with three suppliers in Figure 13,. This is because more competition compels market players to reduce bid prices for selling more.

FIGURE 13

FIGURE 13. Bid prices of three suppliers PV-attached BESS power plants in the 118-node system.

FIGURE 14

FIGURE 14. Bid prices of nine suppliers PV-attached BESS power plants in the 118-node system.

Conclusion

A bidding model with incomplete information for considering the uncertainty of generation output of PV units is proposed. A MARL algorithm WoLF-PHC is used to explore optimal bid prices for strategic PV-attached BESS power plants, and it protects personal privacy and respects the autonomy of market players. Three cases are implemented in the modified IEEE 6-node system and a larger IEEE 118-node system, with some conclusions represented as follows: 1) multiple strategic market players can obtain their bid prices individually with the WoLF-PHC in the electricity markets; 2) compared with models of PV unit and BESS as strategic participants independently, the revenue of proposed model is higher; and 3) decreased load and increased numbers of market players bring more competition, resulting in strategic suppliers bidding at lower prices.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was jointly supported by the Shenzhen Polytechnic, the Hong Kong Polytechnic University, the Natural Science Foundation of Guangdong Province, 2020A1515010461, the National Natural Science Foundation of China (52077075), and the Jiangsu Basic Research Project (BK20180284).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agathokleous, C., and Steen, D. (2019).. IEEE Milan PowerTechIEEE, 1–6. doi:10.1109/ptc.2019.8810651 Stochastic Operation Scheduling Model for a Swedish Prosumer with PV and BESS in Nordic Day-Ahead Electricity Market2019.

CrossRef Full Text | Google Scholar

Bo, T., Ishizaki, T., Koike, M., Yamaguchi, N., and Imura, J.-i. (2017). 56th Annual Conference of the Society of Instrument and Control Engineers of Japan. SICE)IEEE, 293–298. doi:10.23919/sice.2017.8105613 Optimal Bidding Strategy for Multiperiod Electricity Market with Consideration of PV Prediction Uncertainty 2017.

CrossRef Full Text | Google Scholar

Chen, W., Qiu, J., Zhao, J. H., Chai, Q., and Dong, Z. Y. (2021). IEEE Transactions on Smart Grid. doi:10.1109/tsg.2021.3053000 Bargaining Game-Based Profit Allocation of Virtual Power Plant in Frequency Regulation Market Considering Battery Cycle Life.

CrossRef Full Text | Google Scholar

Da Silva, F. L., Nishida, C. E., Roijers, D. M., and Costa, A. H. R. (2019). Coordination of Electric Vehicle Charging through Multiagent Reinforcement Learning. IEEE Trans. Smart Grid 11 (3), 2347–2356.

Google Scholar

Hill, T. W., and Ravindran, A. (1975). On Programming with Absolute-Value Functions. J. Optimization Theor. Appl. 17 (1), 181–183. doi:10.1007/bf00933924

CrossRef Full Text | Google Scholar

Hwang, K.-S., Jiang, W.-C., and Chen, Y.-J. (2017). Pheromone-Based Planning Strategies in Dyna-Q Learning. IEEE Trans. Ind. Inf. 13 (2), 424–435. doi:10.1109/tii.2016.2602180

CrossRef Full Text | Google Scholar

Jonnalagadda, V. K., and Dulla Mallesham, V. K. (2013). Bidding Strategy of Generation Companies in a Competitive Electricity Market Using the Shuffled Frog Leaping Algorithm. Turk J. Elec Eng. Comp. Sci. 21 (6), 1567–1583. doi:10.3906/elk-1109-43

CrossRef Full Text | Google Scholar

Kebriaei, H., Rahimi-Kian, A., and Ahmadabadi, M. N. (2015). Model-Based and Learning-Based Decision Making in Incomplete Information Cournot Games: A State Estimation Approach. IEEE Trans. Syst. Man. Cybern, Syst. 45 (4), 713–718. doi:10.1109/tsmc.2014.2373336

CrossRef Full Text | Google Scholar

Li, X., Hui, D., and Lai, X. (2013). Battery Energy Storage Station (BESS)-based Smoothing Control of Photovoltaic (PV) and Wind Power Generation Fluctuations. IEEE Trans. Sustain. Energ. 4 (2), 464–473. doi:10.1109/tste.2013.2247428

CrossRef Full Text | Google Scholar

Merten, M., Olk, C., Schoeneberger, I., and Sauer, D. U. (2020). Bidding Strategy for Battery Storage Systems in the Secondary Control reserve Market. Appl. Energ. 268, 114951. doi:10.1016/j.apenergy.2020.114951

CrossRef Full Text | Google Scholar

Morales, J. M., Pineda, S., Conejo, A. J., and Carrion, M. (2009). Scenario Reduction for Futures Market Trading in Electricity Markets. IEEE Trans. Power Syst. 24 (2), 878–888. doi:10.1109/tpwrs.2009.2016072

CrossRef Full Text | Google Scholar

Najafi, S., Shafie-khah, M., Siano, P., Wei, W., and Catalão, J. P. (2019).Reinforcement Learning Method for Plug-In Electric Vehicle Bidding. IET Smart Grid.

Google Scholar

Niknam, T., Zare, M., and Aghaei, J. (2012). Scenario-based Multiobjective Volt/var Control in Distribution Networks Including Renewable Energy Sources. IEEE Trans. Power Deliv. 27 (4), 2004–2019. doi:10.1109/tpwrd.2012.2209900

CrossRef Full Text | Google Scholar

Praça, I., Ramos, C., Vale, Z., and Cordeiro, M. (2003). MASCEM: a Multiagent System that Simulates Competitive Electricity Markets. IEEE Intell. Syst. 18 (6), 54–60. doi:10.1109/mis.2003.1249170

CrossRef Full Text | Google Scholar

Rashedi, N., Tajeddini, M. A., and Kebriaei, H.. Markov Game Approach for Multi-Agent Competitive Bidding Strategies in Electricity Market. IET Generation, Transm. Distribution 10, 3756–3763. Available: https://digital-library.theiet.org/content/journals/10.1049/iet-gtd.2016.0075.

Google Scholar

Salehizadeh, M. R., and Soltaniyan, S. (2016/04/01/ 2016). Application of Fuzzy Q- Learning for Electricity Market Modeling by Considering Renewable Power Penetration. Renew. Sust. Energ. Rev. 56, 1172–1181. doi:10.1016/j.rser.2015.12.020

CrossRef Full Text | Google Scholar

Shafie-khah, M., and Catalao, J. P. S. (2015). A Stochastic Multi-Layer Agent-Based Model to Study Electricity Market Participants Behavior. IEEE Trans. Power Syst. 30 (2), 867–881. doi:10.1109/tpwrs.2014.2335992

CrossRef Full Text | Google Scholar

Shafie-khah, M., Heydarian-Forushani, E., Golshan, M. E. H., Moghaddam, M. P., Sheikh-El-Eslami, M. K., and Catalão, J. P. S. (2015). Strategic Offering for a Price-Maker Wind Power Producer in Oligopoly Markets Considering Demand Response Exchange. IEEE Trans. Ind. Inf. 11 (6), 1542–1553. doi:10.1109/tii.2015.2472339

CrossRef Full Text | Google Scholar

Tellidou, A. C., and Bakirtzis, A. G. (20062006).. International IEEE Conference Intelligent Systems, 408–413. doi:10.1109/is.2006.348454 Multi-Agent Reinforcement Learning for Strategic Bidding in Power Markets.

CrossRef Full Text | Google Scholar

Ventosa, M., Baillo, A., Ramos, A., and Rivier, M. (2005). Electricity Market Modeling Trends. Energy policy 33 (7), 897–913. doi:10.1016/j.enpol.2003.10.013

CrossRef Full Text | Google Scholar

Vijaya Kumar, J., Vinod Kumar, D. M., and Edukondalu, K. (2013). Strategic Bidding Using Fuzzy Adaptive Gravitational Search Algorithm in a Pool Based Electricity Market. Appl. soft Comput. 13 (5), 2445–2455. doi:10.1016/j.asoc.2012.12.003

CrossRef Full Text | Google Scholar

Wang, S., Bi, S., and Zhang, Y. A. (2019). Reinforcement Learning for Real-Time Pricing and Scheduling Control in EV Charging Stations. IEEE Trans. Ind. Inform. 17 (2), 849–859.

Google Scholar

Xu, Y., Ahokangas, P., Louis, J.-N., and Pongrácz, E. (2019). Electricity Market Empowered by Artificial Intelligence: A Platform Approach. Energies 12 (21), 4128. doi:10.3390/en12214128

CrossRef Full Text | Google Scholar

Ye, Y., Qiu, D., Sun, M., Papadaskalopoulos, D., and Strbac, G. (2019). Deep Reinforcement Learning for Strategic Bidding in Electricity Markets. IEEE Trans. Smart Grid, 1.

Google Scholar

Zeng, B., Feng, J., Liu, N., and Liu, Y. (2020). Co-optimized Public Parking Lot Allocation and Incentive Design for Efficient PEV Integration Considering Decision-dependent Uncertainties. IEEE Trans. Ind. Inform. 20 (1)., p.

Google Scholar

Zhang, Z., Tang, H., Huang, Q., and Lee, W.-J. (2019). IEEE/IAS 55th Industrial and Commercial Power Systems Technical Conference. I&CPS)IEEE, 1–9. doi:10.1109/icps.2019.8733335 Two-stages Bidding Strategies for Residential Microgrids Based Peer-To-Peer Energy Trading2019

CrossRef Full Text | Google Scholar

Zucker, A., and Hinchliffe, T. (2014). Optimum Sizing of PV-Attached Electricity Storage According to Power Market Signals - A Case Study for Germany and Italy. Appl. Energ. 127, 141–155. doi:10.1016/j.apenergy.2014.04.038

CrossRef Full Text | Google Scholar

Zugno, M., Morales, J. M., Pinson, P., and Madsen, H. (2013). Pool Strategy of a price-maker Wind Power Producer. IEEE Trans. Power Syst. 28 (3), 3440–3450. doi:10.1109/tpwrs.2013.2252633

CrossRef Full Text | Google Scholar