Temperature-Dependent Crystallization Mechanisms of Methylammonium Lead Iodide Perovskite From Different Solvents

Hybrid perovskites are a novel type of semiconductors that show great potential for solution-processed optoelectronic devices. For all applications, the device performance is determined by the quality of the solution-processed perovskite thin films. During solution processing, the interaction of solvent with precursor molecules often leads to the formation of solvate intermediate phases that may diverge the crystallization pathway from simple solvent evaporation to a multi-step formation process. We here investigate the crystallization of methylammonium lead iodide (MAPbI₃) from a range of commonly utilized solvents, namely dimethyl sulfoxide (DMSO), N,N-dimethylformamide (DMF), N-methylpyrrolidone (NMP), and gamma-butyrolactone (GBL) at different temperatures ranging from 40°C to >100°C by in-situ grazing-incidence wide-angle X-ray scattering (GIWAXS) measurements. For all solvents but GBL, we clearly observe the formation of solvate-intermediate phases at moderate processing temperatures. With increasing temperatures, an increasing fraction of the MAPbI₃ perovskite phase is observed to form directly. From the temperature-dependence of the phase-formation and phase-decomposition rates, the activation energy to form the MAPbI₃ perovskite phase from the solvate-phases are determined as a quantitative metric for the binding strength of the solvent within the solvate-intermediate phases and we observe a trend of DMSO > DMF > NMP > GBL. These results enable prediction of processing temperatures at which solvent molecules can be effectively removed.

Introduction

Hybrid perovskites have recently become a promising choice of semiconductor material for a variety of optoelectronic applications. Hybrid perovskites offer excellent optoelectronic properties such as high absorption coefficient, long diffusion length, and bandgaps in the visible range of the solar spectrum (Wolf et al., 2014; Dong et al., 2015; Rehman et al., 2017). High-quality thin films of hybrid perovskites can be deposited from precursor solutions followed by annealing at temperatures as low as 50°C (Fu et al., 2015; Xu et al., 2015; Arain et al., 2019). The improvement of the crystalline properties of the materials and, as a result, their optoelectronic quality is often achieved by optimization of precursor solution composition and deposition procedures (Jeon et al., 2017; Haque et al., 2020).

Optimization of precursor solution is often realized by employing solvent mixtures that allow to manipulate nucleation kinetics and chemical pathways leading to the perovskite formation (Singh et al., 2017; Arain et al., 2019). To date, however, the choice of solvents is often based on empirical evidence of quality enhancement of obtained thin films or devices. Early research on precursor solutions of these materials showed that the crystallization of thin films is affected by an interaction between lead halide perovskite precursors and solvent molecules in a precursor solution (Hamill et al., 2018). In solution, this interaction leads to the formation of complexes that may act as “building blocks” for the formation of amorphous and crystalline solvate phases upon drying (Guo et al., 2016; Li et al., 2019; Valencia et al., 2020). In recent years, the application of different crystallization monitoring techniques revealed that not all solvents form intermediate phases with the perovskite precursors (Ortoll-Bloch et al., 2020). In fact, the usage of weakly coordinating solvents has been employed to avoid the formation of solvate-intermediate phases completely. In particular, layers deposited from gamma-butyrolactone (GBL), 2-methoxy ethanol (2-ME), acetonitrile (ACN), and tetrahydrofuran (THF) as solvents and co-solvents showed the direct formation of perovskite phase with enhanced optoelectronic quality (Deng et al., 2019). In contrast, it has been demonstrated that the formation of certain crystalline intermediate phases or the presence of strongly coordinating solvents is beneficial for the formation of the perovskite phase as it acts as a template or induces nucleation (Seo et al., 2017; Li et al., 2021). Interestingly, precursor solutions containing strongly coordinating solvents such as dimethyl sulfoxide (DMSO) and dimethylformamide (DMF) are still among the most commonly used. This indicates that the correlation between solvent coordination strength and quality of resulting materials is not apparent. Moreover, the choice of the solvent mixture is often dictated by the choice of the deposition technique and availability of methods for controlling nucleation and crystallization of materials.

Different strategies have been employed to ensure an efficient solvent removal and transformation of the precursor-solvent complexes or intermediate phases into semiconducting perovskite material. To date, vacuum, gas quenching, anti-solvent quenching, and annealing are the most commonly used methods for inducing crystallization and aiding solvent removal (Jeon et al., 2014; Li et al., 2016; Zhang et al., 2017). Among those, annealing is one of the most versatile methods for material crystallization as it is simple in use and allows easy scaling. Several reports have indicated that applying an annealing procedure, that is optimized for the material and processing conditions, allows to control not only material nucleation but also the transformation from solvate phase into perovskite. This is of particular importance when strongly coordinating solvents are used. In this case, removal of solvent molecules from intermediate phases determines the transformation of the intermediate phase into perovskite and, as a result, the quality of materials (Tan et al., 2019; Lin et al., 2021). It has been suggested previously that prolonged annealing of >60 min at 100°C is required for complete solvent removal for high-quality materials (Saliba et al., 2018). However, similarly to solution optimization, optimization of annealing procedures is mostly done by assessment of the optoelectronic quality of the resulting materials. Therefore, an in-depth understanding of interactions of solvent and precursor in solution, as well as in solvate intermediate phases, is required for multiparameter optimization of material deposition from various solvents.

It is important to note that the exact mechanism of the perovskite formation from the various different solvate-intermediate phases is not yet understood, however, it is plausible that the ease of the transformation depends on the strength of the chemical interaction between solvent and precursor, stability of the intermediate phase, and evaporation rate of the solvent. Therefore, identifying the parameters influencing the material’s transformation from solvate intermediate phase to perovskite phase is an important step for rationalizing this process and developing strategies for the preparation of high-quality materials.

In this work, we investigate the crystallization of methylammonium lead iodide (MAPbI₃) hybrid perovskites from commonly-used solvents with different physical and chemical properties as a function of temperature. The MAPbI₃ hybrid perovskite was chosen as a test material because 1) the coordination of solvents mostly occurs via an interaction with Pb²⁺ and 2) PbI₂ as the main component of other more complex perovskite compositions is responsible for the formation of solvate intermediate phases. The evolution of crystalline solvate intermediate and perovskite phases during drying of blade-coated MAPbI₃ hybrid perovskite films was monitored by synchrotron-based grazing-incidence wide-angle x-ray scattering technique. The crystallization process was studied in a range of processing temperatures between 40 and 100°C. Our findings indicate that at processing temperatures below 75°C, the formation of the MAPbI₃ phase from strongly coordinating solvents (dimethyl sulfoxide, dimethylformamide, n-methyl pyrrolidone) occurs dominantly via decomposition of the solvate intermediate phases. At temperatures above 75°C, the formation of perovskite and decomposition of intermediate phases can occur simultaneously. From Arrhenius plots of the formation and decomposition rate of the solvate intermediate phases as well as the formation of the MAPbI₃ perovskite phase, we determined the respective activation energies for the formation and transformation of MAPbI₃ from the different solvent systems. We observe that the activation energy for solvent removal from the solvate-intermediate phase correlates with the predicted coordination strength of solvent molecules to Pb in solution complexes. Our findings present the fundamental understanding of processes occurring during the formation of MAPbI₃ hybrid perovskites. However, the correlations found in this work can be applied to the other more complex perovskite compositions and solvents. These results indicate an important aspect for the optimization of processing conditions for temperature-controlled hybrid perovskites deposition methods.

Materials and Methods

For the temperature-dependent study of perovskite phase formation, 1 mol/L precursor solutions of MAPbI₃ were used. The solutions contained equimolar amounts of CH₃NH₃I and PbI₂ dissolved in anhydrous dimethyl sulfoxide (DMSO), dimethylformamide (DMF), N-methyl pyrrolidone (NMP), and gamma-butyrolactone (GBL). As-purchased GBL was kept over molecular sieves for 48 h before use. The solutions were prepared in an N₂-filled glovebox, heated for 12 h at 60°C, and cooled down to room temperature before use. Grazing-incidence wide-angle x-ray scattering (GIWAXS) technique was chosen for in-situ monitoring of the formation of the intermediate phase and its transformation into the perovskite phase. The synchrotron-based GIWAXS technique allows a simple differentiation between different crystalline phases and fast acquisition times. For in-situ grazing-incidence wide-angle x-ray scattering (GIWAXS), 5 µl of the precursor solutions were deposited using manual blade-coating onto a 25 × 25 mm soda-lime glass substrate placed on an Anton Paar heating stage at T = 28°C in 6 L/h N₂ flow. The wet film thickness amounted to about 8 µm for all samples resulting in about 1 µm thin films. Next, a graphite dome was attached to the heating stage over the sample. The stage was connected to a dry nitrogen bottle with 6 L/h flow of N₂ and a 50 mbar overpressure valve on the outlet of the stage as shown in Scheme 1.

SCHEME 1

SCHEME 1. Schematic representation of the experimental setup.

Data collection was done at the KMC-2 DIFFRACTION beamline at the BESSY II synchrotron (Többens and Zander, 2016), using radiation energy of 8,048 eV (λ = 1.5406 Å, equivalent to Cu Kα₁) with flux, f = 10¹¹ photon/s/mm². GIWAXS geometry with incidence angle at the sample of 1° and a Valencia et al., 2000 area detector in fixed position covering an angular range from 4.8 to 15.7° 2θ was used for collecting diffraction frame every 14.2 s. The first frame was acquired 60 s after the liquid was dispensed at room temperature. The wet films were heated to the set processing temperature with a 50 K/min rate. The detector image acquisition started prior to the heating of the stage. The data obtained in the isothermal regime was used for the analysis. A new sample was used for each processing temperature regime. To obtain diffraction patterns, the 2D detector images were azimuthally integrated using in-house developed software.

Results and Discussion

In-situ GIWAXS on MAPbI₃ Precursor Solutions at Different Annealing Temperatures

Figure 1 shows 2D contour plots of the evolution of azimuthally integrated GIWAXS patterns of MAPbI₃ thin-films processed at 40, 50, 58, 78, and 100°C as a function of time. The wet films deposited from solutions of MAPbI₃ in commonly-used organic solvents (DMSO, DMF, NMP, GBL) were investigated. These four solvents exhibit different coordination strengths to lead (DMSO > DMF > NMP > GBL) and evaporation rates (DMF > GBL > NMP > DMSO) (Stevenson et al., 2017; Hamill et al., 2018; Shargaieva et al., 2020).

FIGURE 1

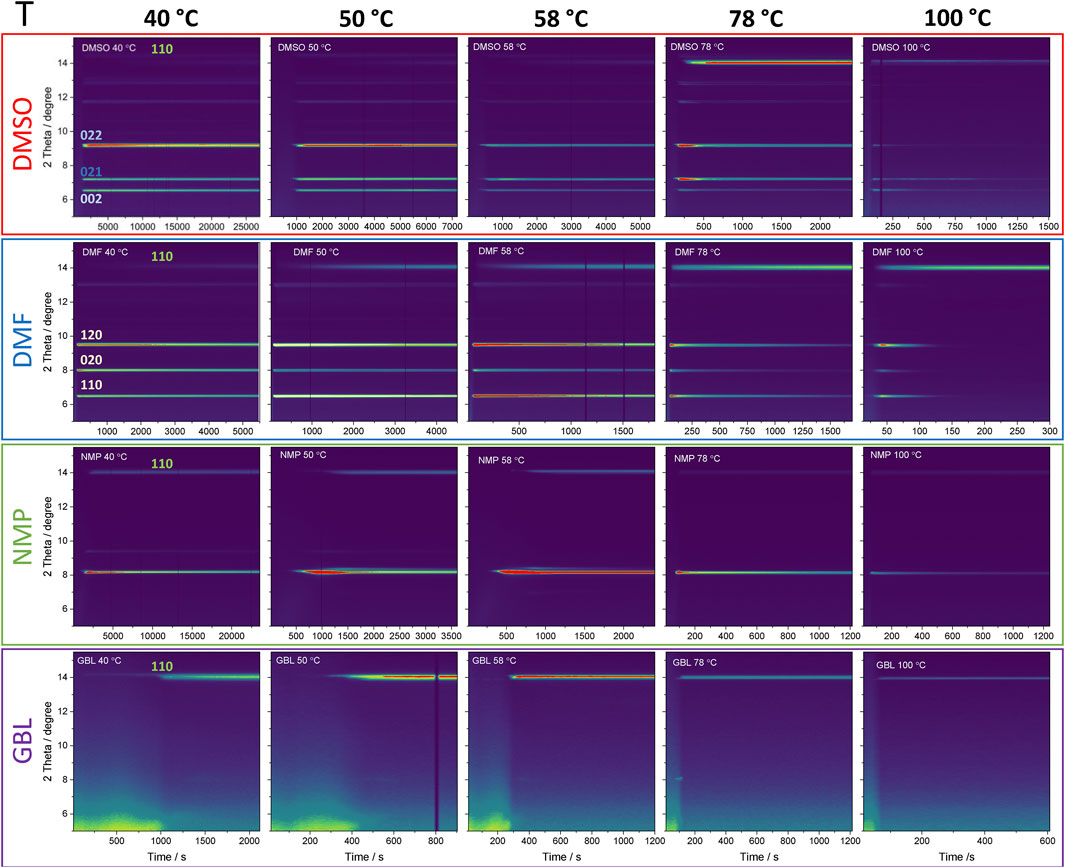
FIGURE 1. 2D contour plots of the azimuthally integrated GIWAXS detector frames obtained as a function of time during crystallization of MAPbI₃ from DMSO, DMF, NMP, GBL at 40, 50, 58, 78, and 100°C. Wavelength 1.5406 Å is equivalent to Cu K_α1.

In all solvents, significant differences were observed in terms of the structure of solvate intermediate phases as well as the onset of crystallization and transformation kinetics to MAPbI₃. The crystallization of MAPbI₃ from DMSO occurred via the solvate intermediate phase with diffraction peaks at 6.59, 7.22, 9.16° 2θ that have been previously assigned to a phase often referred to as MAPbI₃∙DMSO with the stoichiometric formula MA₂Pb₃I₈(DMSO)₂ adopting orthorhombic crystal structure with the Pbc21 space group previously reported by Cao et al. (2016). The individual diffraction pattern of the intermediate phase is shown in Supplementary Figure S2B and corresponding 2D detector images are shown in Supplementary Figure S11. The onset of crystallization of the solvate intermediate phase showed a strong dependence on the process temperature. At 40°C the onset of crystallization of MA₂Pb₃I₈(DMSO)₂ is observed after about 1,300 s, while a low-intensity perovskite phase, indicated by the peak at 14.1° 2θ is observed only after about 7,000 s. An increase of the temperature of annealing to 50°C dramatically accelerated the formation of the solvate-intermediate phase as well as transformation to the perovskite phase with onsets at 800 s and 3,000 s, respectively. Further increase of annealing temperature decreased the time difference between the crystallization of solvate intermediate phase and its transformation to perovskite phase. Annealing at 100°C led to the simultaneous evolution of both solvate-intermediate and perovskite diffraction peaks indicating the competitive formation of both phases.

The crystallization of MAPbI₃ from DMF also occurred via a solvate-intermediate phase, exhibiting diffraction peaks at 6.5, 8.0, and 9.5° 2θ that were previously attributed to a solvate intermediate phase with the stoichiometric formula MA₂Pb₃I₈(DMF)₂ adopting orthorhombic crystal structure with the Pnnm space group first reported by Petrov et al. (2017). The individual diffraction pattern is shown in Supplementary Figure S2A, the corresponding 2D detector images are shown in Supplementary Figure S11. Similarly to the crystallization from DMSO solutions, an increase in the processing temperature accelerated the crystallization and formation of both the solvate-intermediate and perovskite phases. At temperatures T ≥ 78°C, the simultaneous formation of the perovskite phase and the solvate-intermediate phase is apparent. Compared to the DMSO precursor solution, the formation of MAPbI₃ from DMF solutions via the DMF-solvate phase follows faster kinetics.

Crystallization of MAPbI₃ from NMP-based solutions also occurs via an intermediate phase with diffraction peaks at 8.2 and 9.4° 2θ. The position of the individual peaks is indicated in Supplementary Figure S2C and corresponding 2D detector images are shown in Supplementary Figure S12. The diffraction peaks were previously associated with PbI₂-NMP intermediate but its structure and stoichiometry have not yet been identified (Jo et al., 2016; Li et al., 2019; Ortoll-Bloch et al., 2020). Interestingly, the film crystallized from NMP at a processing temperature of 100°C still exhibited the presence of intermediate phase even after 1,200 s and only processing at 120°C allowed the formation of the perovskite phase without the formation of intermediate phase (see Supplementary Figure S1).

Processing of MAPbI₃ from GBL solutions exhibits the presence of an amorphous sol-gel solvate phase with a characteristic broad signal at low diffraction angles (2θ < 6) during the early stages of drying (Lee et al., 2020). Further solvent removal led to the crystallization of wet film directly to the perovskite phase with only a small amount of a crystalline solvate-intermediate phase indicated by a low-intensity diffraction peak at 8.1° 2θ. The position of the individual peaks is indicated in Supplementary Figure S2D. The corresponding 2D detector images are shown in Supplementary Figure S12. In a previous report, we show that an intermediate phase with similar lattice spacings as the DMF solvate phase (MA₂Pb₃I₈(DMF)₂) is formed also in GBL (Shargaieva et al., 2020). It was found that the GBL solvate-intermediate phase is highly sensitive to the presence of water in the precursor solution (Shargaieva et al., 2020). Therefore, the low-intensity peak of the intermediate phase from GBL might indicate the suppression of the solvate phase formation due to the presence of water. This behavior is consistent with other reports where crystallization of MAPbI₃ from GBL has been observed only through the direct formation of the perovskite phase (Ma et al., 2019).

For all precursor solutions studied, the increase of temperature facilitates the removal of solvent molecules. Solvent evaporation leads, for most cases, to the crystallization of solvate-intermediate phases indicating that these are thermodynamically more favored compared to the MAPbI₃ phase. Therefore, it is plausible that the decomposition of the intermediate phase through solvent removal is required for the formation of the perovskite phase. At higher processing temperatures, however, the formation of solvate-intermediate phases can be suppressed and the crystallization occurs through the perovskite phase likely as the kinetics of solvent removal outcompetes the formation of the solvate-intermediate phases.

Schematic Model of Competitive Formation Processes and Phase Formation Kinetics

In order to analyze the evolution of the intermediate and MAPbI₃ perovskite phases as a function of time, we distinguish the different processes occurring during perovskite crystallization as schematically shown in Scheme 2 with structures of complexes and intermediate phases of MAPbI₃ in DMSO used as an example. The crystallization from other solvents occurs via different intermediate phases, however, the generalized approach for the description of processes should be applicable for most solvent systems. The first process corresponds to the increase of concentration of complexes in the solution due to solvent evaporation. This results in the precipitation of the intermediate phase from the solution at a moment of time t₁ as shown in Scheme 2A. In our experiments, only a product of the reaction–crystalline intermediate phase–can be detected due to the nature of the measurement technique. During the second process, the formed intermediate phase undergoes decomposition due to further solvent removal which can be observed as a decrease of the peak intensity at the moment of time t₂ indicating a decrease of the amount of the phase as depicted in Scheme 2B. At the same time, the intermediate phase acts as a reagent for the formation of the perovskite phase as shown in Scheme 2C. In this case, the removal of the solvent from the intermediate phase should occur at the same rate as the formation of the perovskite phase assuming that process 1 has completely finished. However, it is possible that reconstruction of the intermediate phase into perovskite may involve a multistep process or the formation of a transition phase that due to its distorted or amorphous nature cannot be detected by diffraction-based methods. Additionally, it is plausible that the evolution of the signal intensities of the intermediate phase is affected by simultaneous processes a, b, and c. In the case of simultaneous processes, when t₂ is approaching t₁ (Scheme 2D), the intermediate phase concentration does not reach its maximum value as it is consumed at the same time as it forms. At higher processing temperatures, the perovskite phase may also form directly from the solution-precursor due to fast solvent removal. Therefore, the experimental kinetic traces discussed below may deviate from idealized representation as shown in Scheme 2.

SCHEME 2

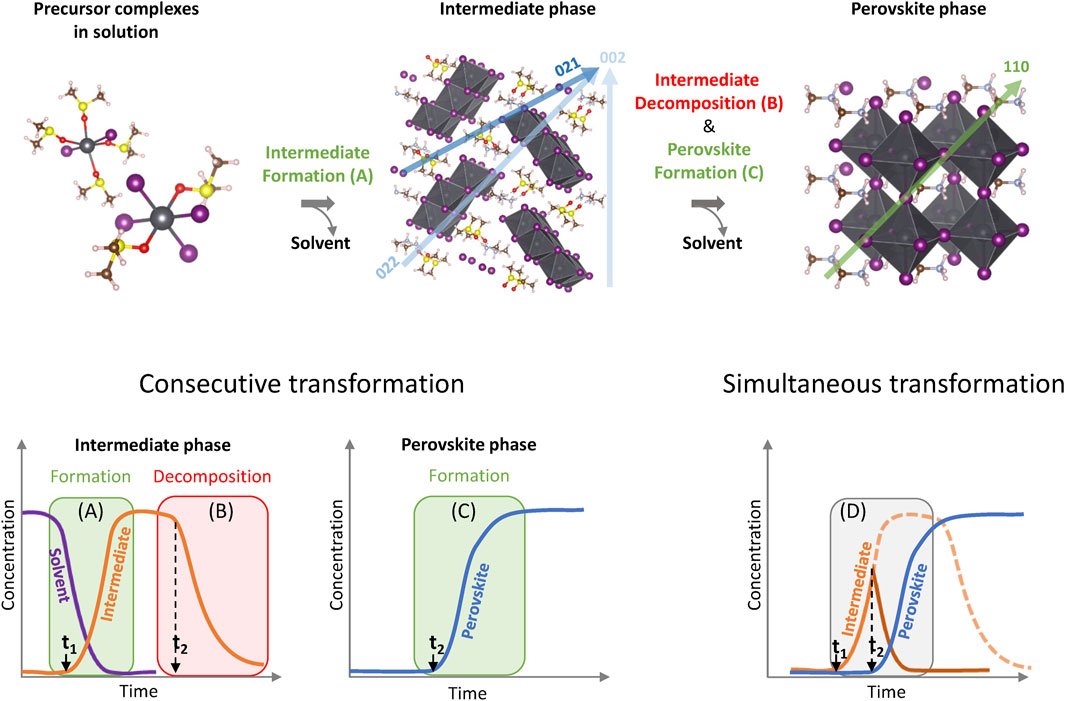
SCHEME 2. Schematic representation of processes occurring during crystallization of MAPbI₃ from solution complexes to perovskite semiconductor (top) and kinetic curves for these processes (bottom).

Kinetics of Crystallization at Different Temperatures

To assess the relationship between intermediate and perovskite phases, the rate of the intermediate phase decomposition and MAPbI₃ phase formation need to be compared. In Figure 2, we compare the evolution of intermediate and MAPbI₃ perovskite phases from different solvents as a function of time and processing temperature. The kinetic traces were derived by integration of the characteristic diffraction peaks of the intermediate (A(interm)) and perovskite (A(pero)) phases as a function of time. The full data sets are shown in Supplementary Figures S3–6. We chose to perform the analysis only on one diffraction peak for each intermediate phase. These were the peaks at 7.22, 6.5, 8.2, and 8.1° for the films deposited from DMSO, DMF, NMP, and GBL, respectively. Additionally, the analysis on three different crystallographic directions (110, 020, and 120) of the (MA)₂Pb₃I₈ (DMF)₂ phase at 6.5, 8.0, 9.5° 2θ was performed for comparison indicating similar kinetics as shown in Supplementary Figure S7.

FIGURE 2

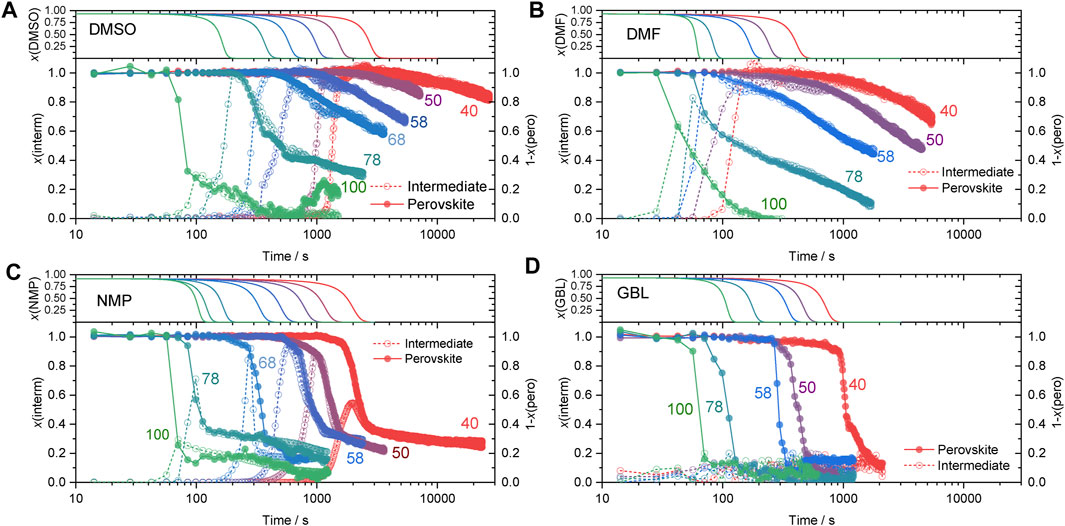
FIGURE 2. Top) Simulated evolution of the fraction of solvent over time at different temperatures. Bottom) Fraction of intermediate phase peak, x(interm), (open symbol) and fraction of perovskite phase to be formed, 1-x(pero), (solid symbol) were obtained from integration of x-ray diffraction patterns during crystallization at different temperatures noted on the graphs.

Important to note is that the diffraction peak intensity depends on a variety of parameters such as the grain size, shape, orientation, and scattering factors, which are not directly related to the amount of a crystalline phase. To define an analytical expression for the degree of transformation, the peak area was normalized by a predicted peak area corresponding to its maximum value (A_max). This way, the normalized peak intensity corresponds to a fraction of the converted material (x) and, therefore, can be compared across different processing temperatures. To obtain the maximum value of the peak area, A_max, the experimental curves in the data range corresponding to the formation of intermediate and perovskite phases were fitted with Johnson–Mehl–Avrami–Kolmogorov (JMAK) model (Avrami, 1939; Fanfoni and Tomellini, 1998) expressed as the following equation:

$\mathit{A}={\mathit{A}}_{\mathit{max}}\left(1-\exp (-\left(\mathit{k}{\left(t-t_0\right)}^{\mathit{n}}\right)\right),(1)$

where A is peak area, A_max is maximum peak area corresponding to full conversion, t-time, t₀-the onset of the process similar to t₁ and t₂ in Scheme 2, k-reaction rate constant, n-reaction order. The JMAK model (Eq. 1) is largely applied for the calculation of solid phase transformations, however, in recent reports, it has been successfully applied for the investigation of perovskite crystallization kinetics from in-situ XRD patterns (Moore et al., 2015; Pool et al., 2017; Suchan et al., 2020). The obtained values of A_max are summarized in Supplementary Table S1. The normalized peak areas (A/A_max) of the intermediate phases (x(interm)) of different solvents at different processing temperatures are shown in Figure 2 as open symbols.

To allow direct visual comparison of the decomposition of the solvate-intermediate phase and formation of the MAPbI₃ perovskite phase, the normalized peak intensity of the MAPbI₃ phase formation was plotted as 1-x(pero) corresponding to the amount of perovskite phase to be formed (Figure 2 solid symbols). If the perovskite phase is mainly formed via decomposition of the intermediate phase, the relation between the respective amount of these crystalline phases can be expressed as x(interm) = 1-x(pero).

The kinetic traces in Figure 2 clearly show a strong dependence of the onset of crystallization of the solvate-intermediate phases on the processing temperature across all studied solvents. To estimate the correlation between the onset of solvate phase crystallization and the concentration of the precursor solution, the evaporation rate of solvents was estimated based on the previously described evaporation model (Shargaieva et al., 2020). The model describes the evaporation of non-coordinated solvent molecules and, therefore, accounts solely for the physical properties of solvents. The onset of crystallization was determined as the moment of the appearance of diffraction peaks of crystalline phases.

The onset of crystallization at different temperatures often correlates with the range of a dramatic change of solvent fraction. The fraction of solvent at the moment of crystallization is increasing with the increase of the processing temperature as shown in Supplementary Figure S10. This indicates that at lower processing temperatures (e.g., RT - 50°C) solutions can reach supersaturation due to slow solvent evaporation leading to a higher concentration than the solubility limit. The estimated amount of solvent at the onset of crystallization is summarized in Supplementary Table S5. At higher processing temperatures (e.g., 100°C), when the evaporation rate of solvent is higher than solvent diffusion, spontaneous nucleation can occur locally even when large total amounts of solvent are still present. In addition, we observe that at higher processing temperatures the formation of the MAPbI₃ perovskite phase competes with the formation of solvate-intermediate phases. This is likely because, at higher solvent evaporation rates, the concentration of solvent molecules decreases dramatically preventing their incorporation into the intermediate crystal structure and, thus, leading to the direct formation of the perovskite phase.

In the solvate-intermediate phase, solvent molecules are incorporated into the crystal lattice. Hence, their removal depends on the binding strength of the solvent within the crystalline matrix rather than the evaporation rate of non-bound solvent molecules. The strength of solvent coordination within the crystalline intermediate phases can be estimated from the transformation kinetics of the solvate to the MAPbI₃ phase. At low temperatures (40, 50°C) the kinetic curves of the DMSO and DMF intermediate phases (Figures 2A,B) reached a plateau indicating that the majority of deposited material formed the crystalline intermediate phase. At higher temperatures, the curves never reach the plateau and quickly transition into the decomposition regime indicating simultaneous formation and decomposition, as well as the direct formation of MAPbI₃, as illustrated in Scheme 2D. For the DMF and DMSO precursor solutions crystallizing at low temperature, the decomposition of the solvate phase and formation of the perovskite phase correlate, as clearly visible from the comparison of x(interm) and (1-x(pero)) in Figure 2. This correlation indicates a direct transformation from the solvate to the perovskite phase. Small deviations observed in the x(interm) in the early stages of decomposition likely occur due to a rapid decrease of crystalline size upon removal of solvent.

Crystallization of MAPbI₃ from the NMP precursor solutions exhibits two different regimes of crystallization. In the first regime, a rapid decrease in the amount of the intermediate phase is observed. In the second regime, a much slower transformation rate of the intermediate phase into the perovskite phase is observed. This behavior can be interpreted as a fast nucleation step preceding a second crystal growth or ripening step. This observation suggests that perovskite formation from NMP occurs via a different mechanism than from DMSO, DMF, and GBL. This difference in the transformation behavior is probably related to the differences in the nature of the solvate intermediate phases. While DMSO and DMF have been suggested to form solvate phases incorporating both solvent and MA molecules, NMP has been suggested to form a solvate phase only incorporating the lead iodide precursors, PbI₂-NMP, as previously suggested by Jo et al. (2016). In this case, the MA cation would likely be bound in another, secondary, phase and becomes incorporated only during the transformation step.

Interestingly, different behavior can be observed during the formation of GBL-based wet thin films. Solvent removal led to the crystallization of the materials directly to the perovskite phase following fast formation kinetics. The intermediate phase was formed after the majority of the material has crystalized.

Activation Energy of Phase Transformations

From the temperature dependence of the transformation from solvate intermediate to MAPbI₃ perovskite phase, the activation energies for the formation of the solvate phases as well as solvent removal from the solvate phase can be estimated. The reaction rate constants, k, can be obtained from the JMAK fits of the experimental data similarly as it was done for the determination of A_max. In addition to the reaction rate constant, the kinetic curve is also defined by the n parameter. The parameter n, according to JMAK theory, describes the mechanism of the crystallization process in terms of dimensionality of the formed nuclei. Therefore, to compare values of k of different experiments, first, we estimate a common value of n for the kinetic curves obtained for the same solvent within the same process. Estimation of n values was done by plotting the kinetic curves in Sharp-Hancock coordinates ln(ln(1-x)) vs. ln(t-t₀). The values of n were determined from the slope of a linear fit of the data in Sharp-Hancock coordinates and rounded to the nearest integer. The Sharp-Hancock fits of the data are shown in Supplementary Figure S8. The detailed methodology, as well as the summary of the fitting parameters, are shown in Supplementary Information and Supplementary Table S2.

Using the Sharp-Hancock method, analysis was conducted for the intermediate phase formation range of the data. Estimated values of n were n = 3 for DMSO, n = 2 for DMF, and n = 3 for NMP. According to the JMAK model, the values of n of the intermediate phase formation indicate that crystallization in DMSO and NMP occurs via formation and growth of 2D platelets, while in DMF—1D rods assuming sporadic nucleation. The values of n = 1 obtained for the perovskite formation from DMF, DMSO, and NMP indicate that the process of the intermediate phase decomposition and perovskite phase formation is limited by the diffusion of the species. In GBL, the formation of the perovskite phase precedes the formation of the intermediate phase and, thus, corresponds to the nucleating species. Therefore, the process in GBL can be described by 1D crystallization of rods assuming sporadic nucleation. Using obtained n values, the experimental data was fitted with the JMAK model described in Eq. 1. The data range corresponding to the decomposition of the intermediate phase was fitted with a modified JMAK-equation for the description of the decomposition process:

$\mathit{A}={\mathit{A}}_{\mathit{max}}\left(\exp (\left(-\mathit{k}{\left(\mathit{t}-{\mathit{t}}_2\right)}^{\mathit{n}}\right)\right),(2)$

Fitting the intermediate phase decomposition and perovskite phase formation was done in the overlapping range of the data corresponding to the formation of perovskite from the solvate intermediate phase. The fitted curves and the summary of fitting parameters are shown in Supplementary Figure S9 and Supplementary Table S3. The obtained values of the reaction rate constant, k, were used for calculation of the activation energy required for the formation of perovskite phase from intermediate phase using the Arrhenius equation:

$\mathit{k}=\mathit{I}{\mathit{e}}^{-{\mathit{E}}_{\mathit{a}}/\mathit{RT}},(3)$

where k is the reaction rate constant, I is the interaction factor, E_a is the activation energy, R is gas constant, and T is temperature. Important to note that the prediction of the reaction rates with the JMAK model assumes homogeneous nucleation and is sensitive to the number of growing nuclei and their volume fraction. Thus, the model will likely deviate from the experiment when nucleation occurs via only a few growing nuclei (Todinov, 2000).

From the Arrhenius equation, activation energy can be obtained from the slope, –E_a/R, of the linear fit of the dependencies of the reaction rate constant on the temperature in Arrhenius coordinates. The fits obtained for the decomposition of the intermediate phase and formation of the perovskite phase from DMF, DMSO, NMP, and GBL are shown in Figures 3B,C. The obtained values of the activation energy are noted in Table 1, fitting parameters are shown in Supplementary Table S4. The same approach was applied for the calculation of the activation energy of the intermediate phase formation in DMSO, DMF, and NMP. The fitted values of k are shown in Figure 3A. The activation energies of the formation of the intermediate phase, E_{a(interm form)}, decomposition of the solvate intermediate phase, E_{a(interm. decomp)}, and formation of the MAPbI₃ perovskite phase, E_{a(pero form)}, are summarized in Table 1.

FIGURE 3

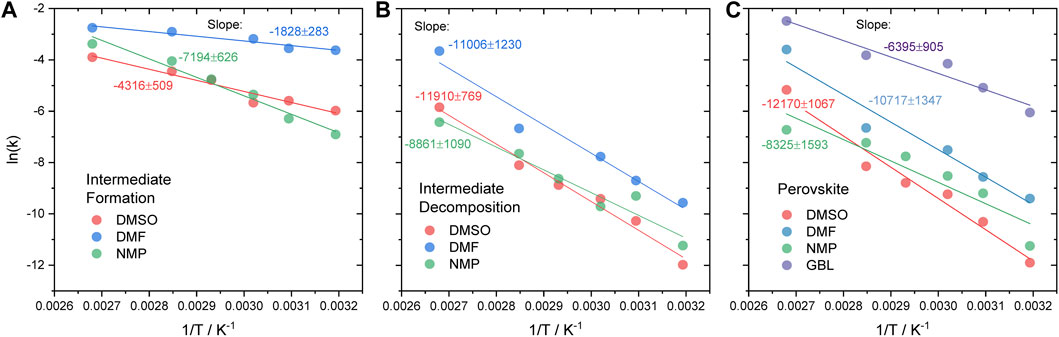
FIGURE 3. Arrhenius plot of (A) intermediate phase formation and (B) decomposition and (C) perovskite phase formation from DMSO, DMF, NMP, and GBL.

TABLE 1

TABLE 1. Calculated activation energies for the formation (E_{a(interm form)}) and decomposition (E_{a(interm. decomp)}) of intermediate phases and formation of perovskite phases (E_{a(pero form}).

As the solvate phase formation is dependent on reaching the respective critical concentration, the activation energy should reflect the thermal energy needed to facilitate solvent evaporation. As evident from Table 1, E_{a(interm form)}(DMF) < E_{a(interm form)}(DMSO) < E_{a(interm form)}(NMP). This trend indicates that both the physical properties of the solvent and their coordination ability influence the activation energy of intermediate phase crystallization. In particular, the high evaporation rate of DMF likely aids its removal from the film and promotes nucleation. Additionally, the high coordination ability of DMF likely stimulates the formation of the intermediate phase through coordination to precursor, thus, lowering the activation energy required for the formation of the intermediate phase. Similarly, DMSO exhibits low activation energy for the formation of the intermediate phase compared to NMP. This lower E_{a(interm form)} can be rationalized with the stronger coordination of DMSO molecules to the precursor in solution. However, despite higher coordination strength E_{a(interm form)} of DMSO is higher than that of DMF possibly due to substantially lower solvent evaporation rate. This trend is in good agreement with the calculated enthalpy of formation of the intermediate phase with DMSO and DMF reported by A. Petrov et al. (2017).

Crystallization from NMP shows a higher E_{a(interm form)} probably due to a combination of weak coordination strength of the solvent to precursor solution complexes and a low evaporation rate. During crystallization from GBL, only a weak peak of the intermediate phase was observed which did not allow to obtain good fitting of the data.

The activation energy of decomposition of intermediate phase E_{a(interm decomp)} and perovskite phase formation E_{a(pero form)} show similar values across different precursor solutions studied. This finding confirms our hypothesis that the MAPbI₃ phase forms by decomposition of the solvate-intermediate phase. Interestingly, the activation energy of the intermediate phase decomposition shows a strong correlation with the coordination strength of the solvent molecules to lead-halide solution complexes shown to be DMSO >> DMF > NMP > GBL (Hamill et al., 2018; Shargaieva et al., 2020). This indicates that the perovskite phase is forming much more readily from solutions containing weakly coordinating solvents.

For DMF and DMSO, the activation energy for the formation of the solvate intermediate phase is clearly much lower than the activation energy for the transformation of the solvate to the perovskite phase: E_{a(pero form)} > E_{a(interm form)}. This energetic difference experimentally manifests itself as a long delay between the appearance of the diffraction peaks from the intermediate phases and the MAPbI₃ perovskite phase in Figures 1, 2. This proves that for both these solvents, the solvate intermediate phase presents a thermodynamically favored state that can only be avoided upon kinetically controlled process conditions. The formation of a solvate phase can be avoided when the solvent evaporation rate is high enough that the precursor solution is rapidly depleted of solvent molecules. The value of the activation energy for the formation of the perovskite phase from DMF, E_a = 89.1 kJ/mol, is in good agreement with previously reported values of E_a = 97.3 and 94 kJ/mol obtained for the formation of MAPbI₃ from DMF with excess of MAI and MACl, respectively, (Moore et al., 2015; Suchan et al., 2020).

In the case of NMP, the activation energies for the formation of the perovskite and solvate intermediate phases are comparable: E_{a(pero form)} ∼ E_{a(interm form)}. This observation can be interpreted as both the intermediate and MAPbI₃ perovskite phases forming competitively and therefore simultaneously. The delay between the appearance of the diffraction peaks of the intermediate and perovskite phase, as seen in Figures 1, 2, is therefore very short.

In the experimental run shown here, only a minor amount of a solvate intermediate phase was found to form for the GBL precursor solution. This is likely due to the fairly low activation energy for the formation of the MAPbI₃ phase determined from the experimental data as summarized in Table 1. Additionally, considering the trend in the E_{a(interm form)} as a function of solvent coordination strength, it is plausible to assume that E_{a(interm form)} of GBL would be larger than that of NMP. Thus, E_{a(pero form)} in GBL is likely smaller than E_{a(interm form)} suggesting that the perovskite phase should form much more readily and faster than the intermediate phase. This effect is apparent in the experimental data shown in Figures 1, 2 where the GBL-intermediate phase is found to appear after the appearance of the diffraction peak associated with the formation of the MAPbI₃ perovskite phase. It is important to note that the formation of the GBL-intermediate phase might be suppressed due to the presence of water.

The obtained data confirms previously reported mechanisms of the formation of hybrid perovskites via crystalline intermediate phases when deposited from strongly coordinating solvents (Qin et al., 2021). When weakly-coordinating solvents are utilized, the direct formation of the perovskite crystalline phase can be observed (Deng et al., 2019). Our findings indicate that the perovskite phase can be formed even at low temperatures from solvent systems in cases where E_{a(interm decomp)} < E_{a(interm form)}. The formation from solvent systems with E_{a(interm decomp)} > E_{a(interm form)} will require a larger amount of energy supplied during annealing or usage of quenching techniques to manipulate the values of the energy barrier for the formation of the perovskite phase. This means that the formation of the intermediate phase can be suppressed in favor of the direct formation of the perovskite phase, if process conditions enable fast solvent removal. This is for instance the case, when an anti-solvent is utilized during the perovskite thin-film deposition, as demonstrated in recent reports (Dou et al., 2017; Pratap et al., 2021). The antisolvent may lower the energetic barrier for the formation of the perovskite phase by aiding solvent extraction as shown by A. Taylor et al. (2021).”

It is important to note that only crystalline phases were monitored during the crystallization process. Based on the postulated stoichiometry of the reported crystalline intermediate phases in DMSO and DMF namely (MA)₂Pb₃I₈(Solvent)₂ we conclude that only 2/3 of the materials can be formed directly through decomposition of the intermediate phase and 1/3 of the material require an additional step of incorporation of methylammonium iodide.

(MA)₂Pb₃I₈(Solvent)₂ + 1 MAI = 3 MAPbI₃—2 Solvent.

We were not able to observe any secondary phases corresponding to the process of incorporation of MAI. Moreover, the kinetic curves of the perovskite formation follow the kinetics of the intermediate phase decomposition during most of the crystallization process indicating that the majority of the material is transformed according to the proposed ratio x(interm) = 1-x(pero). Since no PbI₂ formation was observed during the process, we conclude that the incorporation process occurs either via the non-crystalline phase or on the time scale faster than what is achievable within our experimental conditions. Therefore, more insight into mechanistic processes occurring during the transformation of the solvate intermediate phases into the perovskite phase is needed in order to understand the influence of solvents on the processing of hybrid perovskite materials. This is of particular importance for understanding the crystallization process from other intermediate phases that do not include MAI in the crystal structure.

Conclusion

To summarize, we were able to rationalize the temperature-dependent crystallization process of the hybrid perovskite material MAPbI₃ from different commonly-used solvents. The nucleation of the solvate intermediate phase showed a strong dependence on both the coordination strength of solvent to lead-halide solution complexes as well as its evaporation rate. Strongly-coordinating solvents such as DMSO are found to readily form solvate-intermediate phases while for weakly coordinating solvents like GBL the MAPbI₃ phase may crystallize directly. From the temperature dependence of the intermediate phase decomposition and perovskite phase formation, the activation energy for solvent removal from the solvate-phase was estimated. We found the activation energy to correlate with the solvent coordination strength to lead iodide with a relative trend of DMSO > DMF > NMP > GBL. At higher processing temperatures, the MAPbI₃ perovskite phase can be formed directly without the intermittent formation of the intermediate phases when processing conditions enable the fast removal of solvents. Our findings contribute to a more detailed understanding of the different roles solvents play in the formation process of halide perovskite semiconductors and enable predicting processing conditions, at which the formation of solvate-intermediate phases can be circumvented.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

OS, EU–conceptualization and methodology; OS, HN–data acquisition and analysis; DT, JL–experimental setup and data acquisition. All co-authors have contributed to writing and editing the article.

Funding

OS and EU acknowledge funding from the German Science Foundation (DFG) provided in the framework of the priority program SPP 2196, “Perovskite semiconductors: From fundamental properties to devices” Project number 424394788. HN and EU acknowledge funding from the German Ministry of Education and Research (BMBF) for the Young Investigator Group Hybrid Materials Formation and Scaling (HyPerFORME) within the program “NanoMatFutur” (grant no. 03XP0091). JL acknowledges funding from the Chinese Scholarship Council (CSC, grant No. CSC201908120116).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

HN and JL acknowledge the support from the HyPerCells graduate school and HI-SCORE research school. OS thanks Rahim Munir for organizing the beamtime and allocating time for the experiments. The authors thank BESSY II synchrotron in Berlin for use of beamtime at KMC-2 DIFFRACTION beamline.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.749604/full#supplementary-material

References

Arain, Z., Liu, C., Ren, Y., Yang, Y., Mateen, M., Liu, X., et al. (2019). Low-Temperature Annealed Perovskite Films: A Trade-Off between Fast and Retarded Crystallization via Solvent Engineering. ACS Appl. Mater. Inter. 11, 16704–16712. doi:10.1021/acsami.9b02297

PubMed Abstract | CrossRef Full Text | Google Scholar

Avrami, M. (1939). Kinetics of Phase Change. I General Theory. J. Chem. Phys. 7, 1103–1112. doi:10.1063/1.1750380

CrossRef Full Text | Google Scholar

Cao, J., Jing, X., Yan, J., Hu, C., Chen, R., Yin, J., et al. (2016). Identifying the Molecular Structures of Intermediates for Optimizing the Fabrication of High-Quality Perovskite Films. J. Am. Chem. Soc. 138, 9919–9926. doi:10.1021/jacs.6b04924

PubMed Abstract | CrossRef Full Text | Google Scholar

De Wolf, S., Holovsky, J., Moon, S.-J., Löper, P., Niesen, B., Ledinsky, M., et al. (2014). Organometallic Halide Perovskites: Sharp Optical Absorption Edge and its Relation to Photovoltaic Performance. J. Phys. Chem. Lett. 5, 1035–1039. doi:10.1021/jz500279b

CrossRef Full Text | Google Scholar

Deng, Y., van Brackle, C. H., Dai, X., Zhao, J., Chen, B., and Huang, J. (2019). Tailoring Solvent Coordination for High-Speed, Room-Temperature Blading of Perovskite Photovoltaic Films. Sci. Adv. 5, eaax7537. doi:10.1126/sciadv.aax7537

PubMed Abstract | CrossRef Full Text | Google Scholar

Dong, Q., Fang, Y., Shao, Y., Mulligan, P., Qiu, J., Cao, L., et al. (2015). Electron-hole Diffusion Lengths > 175 μm in Solution-Grown CH 3 NH 3 PbI 3 Single Crystals. Science 347, 967–970. doi:10.1126/science.aaa5760

PubMed Abstract | CrossRef Full Text | Google Scholar

Dou, B., Pool, V. L., Toney, M. F., and van Hest, M. F. A. M. (2017). Radiative Thermal Annealing/In Situ X-ray Diffraction Study of Methylammonium Lead Triiodide: Effect of Antisolvent, Humidity, Annealing Temperature Profile, and Film Substrates. Chem. Mater. 29, 5931–5941. doi:10.1021/ACS.CHEMMATER.7B01467

CrossRef Full Text | Google Scholar

Fanfoni, M., and Tomellini, M. (1998). The Johnson-Mehl- Avrami-Kohnogorov Model: A Brief Review. Nouv Cim D 20, 1171–1182. doi:10.1007/BF03185527

CrossRef Full Text | Google Scholar

Fu, F., Feurer, T., Jäger, T., Avancini, E., Bissig, B., Yoon, S., et al. (2015). Low-temperature-processed Efficient Semi-transparent Planar Perovskite Solar Cells for Bifacial and Tandem Applications. Nat. Commun. 6, 1–9. doi:10.1038/ncomms9932

CrossRef Full Text | Google Scholar

Guo, X., McCleese, C., Kolodziej, C., Samia, A. C. S., Zhao, Y., and Burda, C. (2016). Identification and Characterization of the Intermediate Phase in Hybrid Organic-Inorganic MAPbI3perovskite. Dalton Trans. 45, 3806–3813. doi:10.1039/c5dt04420k

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamill, J. C., Schwartz, J., and Loo, Y.-L. (2018). Influence of Solvent Coordination on Hybrid Organic-Inorganic Perovskite Formation. ACS Energ. Lett. 3, 92–97. doi:10.1021/acsenergylett.7b01057

CrossRef Full Text | Google Scholar

Haque, M. A., Troughton, J., and Baran, D. (2020). Processing‐Performance Evolution of Perovskite Solar Cells: From Large Grain Polycrystalline Films to Single Crystals. Adv. Energ. Mater. 10, 1902762. doi:10.1002/aenm.201902762

CrossRef Full Text | Google Scholar

Jeon, N. J., Noh, J. H., Kim, Y. C., Yang, W. S., Ryu, S., and Seok, S. I. (2014). Solvent Engineering for High-Performance Inorganic-Organic Hybrid Perovskite Solar Cells. Nat. Mater 13, 897–903. doi:10.1038/nmat4014

PubMed Abstract | CrossRef Full Text | Google Scholar

Jeon, T., Kim, S. J., Yoon, J., Byun, J., Hong, H. R., Lee, T.-W., et al. (2017). Hybrid Perovskites: Effective Crystal Growth for Optoelectronic Applications. Adv. Energ. Mater. 7, 1602596. doi:10.1002/aenm.201602596

CrossRef Full Text | Google Scholar

Jo, Y., Oh, K. S., Kim, M., Kim, K.-H., Lee, H., Lee, C.-W., et al. (2016). High Performance of Planar Perovskite Solar Cells Produced from PbI2(DMSO) and PbI2(NMP) Complexes by Intramolecular Exchange. Adv. Mater. Inter. 3, 1500768. doi:10.1002/admi.201500768

CrossRef Full Text | Google Scholar

Lee, S., Tang, M.-C., Munir, R., Barrit, D., Kim, Y.-J., Kang, R., et al. (2020). In Situ study of the Film Formation Mechanism of Organic-Inorganic Hybrid Perovskite Solar Cells: Controlling the Solvate Phase Using an Additive System. J. Mater. Chem. A. 8, 7695–7703. doi:10.1039/d0ta00048e

CrossRef Full Text | Google Scholar

Li, J., Dagar, J., Shargaieva, O., Flatken, M. A., Köbler, H., Fenske, M., et al. (202120034). 20.8% Slot‐Die Coated MAPbI ₃ Perovskite Solar Cells by Optimal DMSO‐Content and Age of 2‐ME Based Precursor Inks. Adv. Energ. Mater. doi:10.1002/aenm.202003460

CrossRef Full Text | Google Scholar

Li, X., Bi, D., Yi, C., Décoppet, J.-D., Luo, J., Zakeeruddin, S. M., et al. (2016). A Vacuum Flash-Assisted Solution Process for High-Efficiency Large-Area Perovskite Solar Cells. Science 353, 58–62. doi:10.1126/science.aaf8060

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Zhi, L., Ge, G., Zhao, Z., Cao, X., Chen, F., et al. (2019). Investigation on Crystallization of CH3NH3PbI3 Perovskite and its Intermediate Phase from Polar Aprotic Solvents. Cryst. Growth Des. 19, 959–965. doi:10.1021/acs.cgd.8b01516

CrossRef Full Text | Google Scholar

Lin, P., Zhang, W., Tian, L., Zhang, F., Zhou, S., Liu, R., et al. (2021). Remanent Solvent Management Engineering of Perovskite Films for PEDOT: PSS-Based Inverted Solar Cells. Solar Energy 216, 530–536. doi:10.1016/j.solener.2021.01.044

CrossRef Full Text | Google Scholar

Ma, Y., Hangoma, P. M., Park, W. I., Lim, J.-H., Jung, Y. K., Jeong, J. H., et al. (2019). Controlled crystal Facet of MAPbI3 Perovskite for Highly Efficient and Stable Solar Cell via Nucleation Modulation. Nanoscale 11, 170–177. doi:10.1039/c8nr08344d

CrossRef Full Text | Google Scholar

Moore, D. T., Sai, H., Tan, K. W., Smilgies, D.-M., Zhang, W., Snaith, H. J., et al. (2015). Crystallization Kinetics of Organic-Inorganic Trihalide Perovskites and the Role of the lead Anion in crystal Growth. J. Am. Chem. Soc. 137, 2350–2358. doi:10.1021/ja512117e

CrossRef Full Text | Google Scholar

Ortoll-Bloch, A. G., Herbol, H. C., Sorenson, B. A., Poloczek, M., Estroff, L. A., and Clancy, P. (2020). Bypassing Solid-State Intermediates by Solvent Engineering the Crystallization Pathway in Hybrid Organic-Inorganic Perovskites. Cryst. Growth Des. 20, 1162–1171. doi:10.1021/acs.cgd.9b01461

CrossRef Full Text | Google Scholar

Petrov, A. A., Sokolova, I. P., Belich, N. A., Peters, G. S., Dorovatovskii, P. V., Zubavichus, Y. V., et al. (2017). Crystal Structure of DMF-Intermediate Phases Uncovers the Link between CH3NH3PbI3 Morphology and Precursor Stoichiometry. J. Phys. Chem. C 121, 20739–20743. doi:10.1021/acs.jpcc.7b08468

CrossRef Full Text | Google Scholar

Pool, V. L., Dou, B., Van Campen, D. G., Klein-Stockert, T. R., Barnes, F. S., Shaheen, S. E., et al. (2017). Thermal Engineering of FAPbI3 Perovskite Material via Radiative thermal Annealing and In Situ XRD. Nat. Commun. 8, 1–8. doi:10.1038/ncomms14075

PubMed Abstract | CrossRef Full Text | Google Scholar

Pratap, S., Babbe, F., Barchi, N. S., Yuan, Z., Luong, T., Haber, Z., et al. (20212021). Out-of-equilibrium Processes in Crystallization of Organic-Inorganic Perovskites during Spin Coating. Nat. Commun. 12, 1–9. doi:10.1038/s41467-021-25898-5

CrossRef Full Text | Google Scholar

Qin, M., Chan, P. F., and Lu, X. (2021). A Systematic Review of Metal Halide Perovskite Crystallization and Film Formation Mechanism Unveiled by In Situ GIWAXS. Adv. Mater., 2105290. doi:10.1002/ADMA.202105290

CrossRef Full Text | Google Scholar

Rehman, W., McMeekin, D. P., Patel, J. B., Milot, R. L., Johnston, M. B., Snaith, H. J., et al. (2017). Photovoltaic Mixed-Cation lead Mixed-Halide Perovskites: Links between Crystallinity, Photo-Stability and Electronic Properties. Energy Environ. Sci. 10, 361–369. doi:10.1039/C6EE03014A

CrossRef Full Text | Google Scholar

Saliba, M., Correa-Baena, J. P., Wolff, C. M., Stolterfoht, M., Phung, N., Albrecht, S., et al. (2018). How to Make over 20% Efficient Perovskite Solar Cells in Regular (N-i-p) and Inverted (P-i-n) Architectures. Chem. Mater. 30, 4193–4201. doi:10.1021/acs.chemmater.8b00136

CrossRef Full Text | Google Scholar

Seo, Y.-H., Kim, E.-C., Cho, S.-P., Kim, S.-S., and Na, S.-I. (2017). High-performance Planar Perovskite Solar Cells: Influence of Solvent upon Performance. Appl. Mater. Today 9, 598–604. doi:10.1016/J.APMT.2017.11.003

CrossRef Full Text | Google Scholar

Shargaieva, O., Näsström, H., Smith, J. A., Többens, D., Munir, R., and Unger, E. (2020). Hybrid Perovskite Crystallization from Binary Solvent Mixtures: Interplay of Evaporation Rate and Binding Strength of Solvents. Mater. Adv. 1, 3314–3321. doi:10.1039/d0ma00815j

CrossRef Full Text | Google Scholar

Singh, R., Suranagi, S. R., Kumar, M., and Shukla, V. K. (2017). Investigations on the Role of Mixed-Solvent for Improved Efficiency in Perovskite Solar Cell. J. Appl. Phys. 122, 235302. doi:10.1063/1.4998630

CrossRef Full Text | Google Scholar

Stevenson, J., Sorenson, B., Subramaniam, V. H., Raiford, J., Khlyabich, P. P., Loo, Y.-L., et al. (2017). Mayer Bond Order as a Metric of Complexation Effectiveness in Lead Halide Perovskite Solutions. Chem. Mater. 29, 2435–2444. doi:10.1021/acs.chemmater.6b04327

CrossRef Full Text | Google Scholar

Suchan, K., Just, J., Becker, P., Unger, E. L., and Unold, T. (2020). Optical In Situ Monitoring during the Synthesis of Halide Perovskite Solar Cells Reveals Formation Kinetics and Evolution of Optoelectronic Properties. J. Mater. Chem. A. 8, 10439–10449. doi:10.1039/d0ta01237h

CrossRef Full Text | Google Scholar

Tan, Q., Hinrichs, K., Mao-Dong, H., Fengler, S., Rappich, J., Prajongtat, P., et al. (2019). Temperature Dependent Diffusion of DMSO in CH3NH3PbI3 Precursor Films during Layer Formation and Impact on Solar Cells. ACS Appl. Energ. Mater. 2, 5116–5123. doi:10.1021/acsaem.9b00769

CrossRef Full Text | Google Scholar

Taylor, A. D., Sun, Q., Goetz, K. P., An, Q., Schramm, T., Hofstetter, Y., et al. (2021). A General Approach to High-Efficiency Perovskite Solar Cells by Any Antisolvent. Nat. Commun. 12. doi:10.1038/S41467-021-22049-8

CrossRef Full Text | Google Scholar

Többens, D. M., and Zander, S. (2016). KMC-2: an X-ray Beamline with Dedicated Diffraction and XAS Endstations at BESSY II. Jlsrf 2, 49. doi:10.17815/jlsrf-2-65

CrossRef Full Text | Google Scholar

Todinov, M. T. (2000). On Some Limitations of the Johnson-Mehl-Avrami-Kolmogorov Equation. Acta Materialia 48, 4217–4224. doi:10.1016/S1359-6454(00)00280-9

CrossRef Full Text | Google Scholar

Valencia, A. M., Shargaieva, O., Schier, R., Unger, E., and Cocchi, C. (2020). Fingerprints of Iodoplumbate Chains in the Optical Absorption of lead-halide Perovskite Solution Precursors. arXiv.

Google Scholar

Xu, M.-F., Zhang, H., Zhang, S., Zhu, H. L., Su, H.-M., Liu, J., et al. (2015). A Low Temperature Gradual Annealing Scheme for Achieving High Performance Perovskite Solar Cells with No Hysteresis. J. Mater. Chem. A. 3, 14424–14430. doi:10.1039/c5ta02730f

CrossRef Full Text | Google Scholar

Zhang, M., Yun, J. S., Ma, Q., Zheng, J., Lau, C. F. J., Deng, X., et al. (2017). High-Efficiency Rubidium-Incorporated Perovskite Solar Cells by Gas Quenching. ACS Energ. Lett. 2, 438–444. doi:10.1021/acsenergylett.6b00697

CrossRef Full Text | Google Scholar