The Output Consensus Problem of DC Microgrids With Dynamic Event-Triggered Control Scheme

In this paper, the output consensus problem of DC microgrids with dynamic event-triggered control scheme is investigated. According to the properties of DC microgrids and multi-agent systems, the multi-agent systems function model for DC microgrids is provided. For making the multi-agent systems achieve output consensus, the non-periodic and periodic dynamic event-triggered control schemes are provided, respectively, which are classified according to the style of receiving information. By using a series of analysis, it can be proved that these two control schemes not only can make systems achieve output consensus, but also can avoid the Zeno-behavior successfully. Moreover, the periodic dynamic event-triggered control scheme does not need the continuous information transfer. Finally, a numerical example is provided to support our conclusions.

1 Introduction

With the rapid development of national economy, the problems of non-renewable energy and ${\mathrm{C}\mathrm{O}}_2$ emission are getting worse. For alleviating these problems, the distributed renewable energy was investigated and used in many aspects (Zhang et al., 2014)- (Aluisio et al., 2017). Moreover, the wind energy and solar energy have been considered as the most potential renewable energy (Hu et al., 2020)- (Schfer et al., 2018). Therefore, the DC microgrids with wind and solar energy generators has attracted more and more attentions (Su et al., 2018; Liu et al., 2018; Liu et al., 2020). In (Aquila et al., 2020) for obtaining the optimal configuration strategy of DC microgrids, the hybrid programming optimization algorithm based on PL technology was provided. The control scheme for DC microgrids with embedded power supply and load changing randomly was given in (Ma et al., 2017) and the layered distributed model predictive control scheme was provided in (Kong et al., 2019), respectively.

For designing the proper control schemes of DC microgrids, the systems function modeling of DC microgrids is very important. In (Purba et al., 2019), the scalable models for DC microgrids with limited computational complexity was provided and the dynamic characteristics was analyzed, too. Moreover, the state-space function model of the converters with plug-and-play (PnP) regulator and $V-I$ droop controller for DC microgrids was built in (Zhou et al., 2020). On the other hand, DC microgrids can be seen as a complex system consist of several subsystems (wind and solar energy generators). According to this point, the function model of DC microgrids can be built with the style of multi-agent systems, which was investigated in many existing results (Zhou et al., 2020) (Wang et al., 2021).

The function model of multi-agent systems has attracted lots of attentions due to its widely applications in many aspects (Bender, 1991; Cai et al., 2016; Lawton and Beard, 2002). Among all these issues about multi-agent systems, the consensus problem for multi-agent systems is the most basic and quite important, which attracted large scholars to investigate. In (Fax and Murray, 2004), the topology structure representing the information transfer between agents was analyzed and the decision conditions of making multi-agent systems achieve consensus was also provided. In (Olfati-Saber and Murray, 2004) and (Savino et al., 2016), the consensus problem of multi-agent systems with directed topology and switching topology were studied, which further reduced the amount of information transfer. After that, in order to make multi-agent systems be more fit for the actual situation, the heterogeneous multi-agent systems that can make the agents’ system function models be different was pointed out. In (Franceschelli et al., 2010), the consensus problem for one special kind of heterogeneous multi-agent systems was investigated, which had only two different kinds of dynamic models. Then, the dynamic compensator was built for each agent to deal with the output consensus problem of general heterogeneous multi-agent systems in (Zhang et al., 2017) and (Huang and Ye, 2014).

Traditional control schemes for multi-agent systems always require that both information transfer and the update of controller should be continuous, which may cause the congestion of information and the cost of energy if the amount of agents is large enough. For overcoming this problem, the periodic sampling control scheme was proposed and used for the multi-agent systems in (Fridman, 2010; Liu and Fridman, 2012; Shen et al., 2012) which can give a fixed sampling periodic making the information communications and controller’s update occur at the periodic sampled instant. Nevertheless, this scheme only considered the ‘worst situation’, which leaded to the increase of conservativeness in the choice of sampled instant. Considering about this problem, the event-triggered control scheme making the controller’s update occur at the triggered time according to the agents’ behavior was investigated and used for multi-agent systems in (Zhu et al., 2014; Duan et al., 2017; Zhang et al., 2017). In (Zhu et al., 2014), the event-triggered control scheme was proposed to solve the consensus problem for linear multi-agent with directed topology. Moreover, the corresponding event-triggered control approaches for solving consensus problems of multi-agent systems with special models such as nonlinear and heterogeneous were provided in (Seifullaev and Fradkov, 2016) and (Duan et al., 2017), respectively.

Although the event-triggered control schemes for multi-agent systems have been investigated by many papers and achieved significant results, some points still need to be improved: 1) How to avoid the Zeno-behavior is one of the key problem for event-triggered control scheme. However, most existing works only can avoid this phenomenon before consensus, while a fixed minimum triggered interval can not be given. 2) Compare with periodic sampling control scheme, the frequency of controller’s update by using event-triggered control scheme is lower. However, because of the existing of event-triggered conditions, the continuous information transfer is always needed, which may cause the information congestion. These problems motivate us to provide this paper.

In this paper, the output consensus problem for the multi-agent systems function model of DC microgrids is investigated and the corresponding dynamic event-triggered control schemes are provided, respectively. The main contributions of this paper are given as follows:

1) According to the relevant knowledge of DC microgrids and multi-agent systems, the multi-agent systems function model of DC microgrids is built. Moreover, by utilizing this model, the control problem for DC microgrids is converted into the output consensus problem of multi-agent systems.

2) For the multi-agent systems built in this paper, the non-periodic and periodic dynamic event-triggered control schemes for achieving output consensus are provided, respectively. Compare with traditional event-triggered control scheme, these two control schemes can provide the fixed minimum triggered interval, and may have the lower conservativeness event-triggered conditions because of the existing of dynamic item. Moreover, the periodic dynamic event-triggered control scheme can also avoid the continuous information transfer.

The rest of this paper is organized as follows. In section 2, the preliminaries is given. The multi-agent systems function model of DC microgrids is provided in section 3. In section 4, the dynamic event-triggered control schemes with non-periodic and periodic event-triggered conditions are proposed, respectively. The numerical example supporting for our results is provided in section 5 and the conclusion is given in section 6.

2 Preliminaries

2.1 Notations

1) Denote $R^{m\times n}$ and $R^n$ as the sets of all $m\times n$ real matrices and $n$-dimensional Euclidean space, respectively.

2) Denote $\Vert \cdot \Vert$ as the induced 2-norm for $m\times n$ real matrices or the Euclidean norm for $n$-dimensional vectors in $R^n$.

3) Denote $co{l}_i(X)$ and $ro{w}_i(X)$ as the $i$-th column and row of matrix $X$, respectively. Moreover, $co{l}_{i,j}(X)=[co{l}_i(X),co{l}_{i+1}(X),\dots ,co{l}_j(X)]$, $ro{w}_{i,j}(X)={[ro{w}_i{(X)}^T,ro{w}_{i+1}{(X)}^T,\dots ,ro{w}_j{(X)}^T]}^T$.

4) Denote $\lambda (X)$ as the set of all eigenvalues of $n\times n$ real matrix $X$. Moreover, denote ${\lambda }_i(X)$ and $\mathrm{R}\mathrm{e}{\lambda }_i(X)$ as the $i$-th eigenvalue of $X$ and its real part for $i\in \{\mathrm{1,2},\dots ,n\}$, respectively.

5) $P>0$ ($P<0$) represents that $P$ is a symmetric positive (negative) definite matrix.

6) Denote $I$ and $O$ as the identity matrix and zero matrix with compatible dimension, respectively. Moreover, $O_{m\times n}$ represents $m\times n$ zero matrix.

2.2 Algebraic Graph Topology

Consider a system consist of one leader and $N$ agents, a directed graph $\bar{g}$ is provide to describe the relationship of the information transfer among them. Let $\bar{g}=\{0\}\cup g$, where $\{0\}$ represents the leader, and $g=(\mathcal{V},\mathcal{E},\mathcal{A})$ is the information exchange between agents with $\mathcal{V}=\{\mathrm{1,2},\dots ,N\}$, $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$ and $\mathcal{A}=\{a_{ij}\}\in R^{N\times N}$, which represent the set of agents, the set of directed edges, and the weighted adjacency matrix, respectively. If agent $i$ can obtain information from agent $j$, agent $j$ is called an in-neighbor of agent $i$ and the directed edge $(j,i)\in \mathcal{E}$, $a_{ij}>0$, $a_{ij}=0$, otherwise. Denote ${\mathcal{N}}_i=\{j|j\in \mathcal{V}(j,i)\in \mathcal{E}\}$ as the set of in-neighbor index of agent $i$. Then the Laplacian matrix $L$ about $g$ can be given as $L=\{l_{ij}\}\in R^{N\times N}$, where $l_{ij}={\sum }_{j\in {\mathcal{N}}_i}{a}_{ij}$ if $i=j$, and $l_{ij}=-a_{ij}$, otherwise. Denote $B=diag\{b_1,b_2,\dots ,b_N\}$ as the leader adjacency matrix associated with graph $\bar{g}$. $b_i>0$ means that there exists a directed edge from leader to agent $i$ and agent $i$ can take information from leader, $b_i=0$, otherwise. A series of edges $(pp,q{q}_1)(q{q}_1,q{q}_2),\dots (q{q}_m,qq)$ is called a directed path from agent $pp$ to agent $qq$ in the directed graph $\bar{g}$, where $q{q}_{ss}(ss=\mathrm{1,2},\dots ,m)$ represents the different agents. Throughout this paper, it is assumed that there does not exist self-loops or parallel edges in the directed graph $\bar{g}$.

Define $H$ as $H=L+B$, the following result can be given.

Lemma 1 (Fax and Murray, 2004) If a directed spanning tree with the leader as the root exists in the graph topology, $\mathrm{R}\mathrm{e}{\lambda }_i(H)>0$ for every ${\lambda }_i(H)\in \lambda (H)$.

3 The Multi-Agent Systems Function Modeling of DC Microgrids

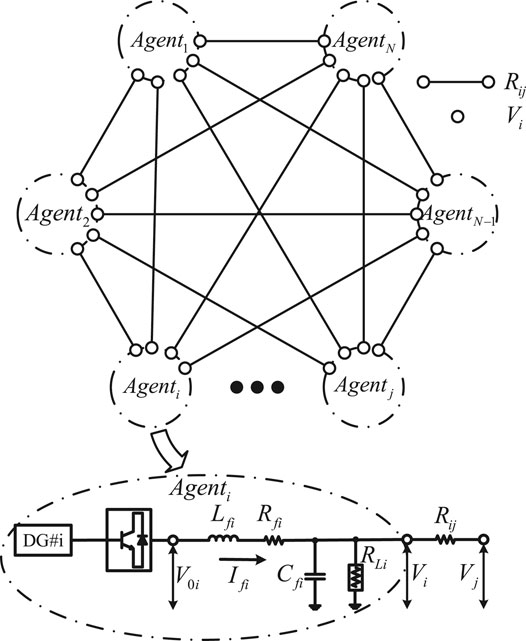
According to (Wang et al., 2021), the typical structure of DC microgrids with wind and solar energy generators is shown in Figure 1, where agent $i$ ($i=\mathrm{1,2},\dots ,N$) is the $i$-th distributed generator representing the wind or solar energy generator belong to DC microgrids. $V_i$ represents the interfaced voltage of agent $i$. $R_{fi}$, $L_{fi}$ and $C_{fi}$ represent the RLC filter of agent $i$, respectively. $I_{fi}$ and $V_{0i}$ represent the current and output voltage of agent $i$, respectively. $R_{Li}$ and $R_{ij}$ are used to describe the common resistor load and the line resistance between agents $i$ and $j$, respectively. By utilizing the results of (Wang et al., 2021), the system function model of agent $i$ can be given as follows:

$\begin{array}{ll}\hfill {\dot{x}}_i(t)& =\left(A_{ii}+\sum A_{ij}\right)x_i(t)-\sum A_{ij}{x}_j(t)+B_{ii}{u*}_i(t)\hfill \end{array}(1)$

$\begin{array}{ll}\hfill y_i(t)& =C_{ii}{x}_i(t)\hfill \end{array}(2)$

where

$\begin{array}{l}{A}_{ii}=\left(\begin{array}{cc}\hfill {\bar{A}}_{ii}+{\bar{B}}_{ii}{n}_i^p\hfill & \hfill {\bar{B}}_{ii}{n}_i^i\hfill \\ \hfill A_i^{*}\hfill & \hfill O\hfill \end{array}\right),A_{ij}=\left(\begin{array}{cc}\hfill {\bar{A}}_{ij}\hfill & \hfill O\hfill \\ \hfill O\hfill & \hfill O\hfill \end{array}\right),B_{ii}=\left(\begin{array}{c}\hfill n_i^p\hfill \\ \hfill n_i^i\hfill \end{array}\right),C_{ii}={\left(\begin{array}{c}\hfill {\bar{C}}_{i}i\hfill \\ \hfill O\hfill \end{array}\right)}^T\hfill \\ x_i(t)={({\bar{x}}_i^T(t),{\bar{z}}_i^T(t))}^T,{u*}_i(t)={\bar{u}}_i(t),y_i(t)={\bar{y}}_i(t)\hfill \\ {\bar{A}}_{ii}=\left(\begin{array}{cc}\hfill -\frac{1}{C_{fi}{R}_{Li}}\hfill & \hfill \frac{1}{C_{fi}}\hfill \\ -\frac{1}{L_{fi}}\hfill & \hfill -\frac{R_{fi}}{L_{fi}}\hfill \end{array}\right),{\bar{A}}_{ij}=\left(\begin{array}{cc}\hfill -\frac{1}{C_{fi}{R}_{ij}}\hfill & \hfill O\hfill \\ \hfill O\hfill & \hfill O\hfill \end{array}\right),{\bar{B}}_{ii}=\left(\begin{array}{c}\hfill O\hfill \\ \hfill \frac{1}{L_{fi}}\hfill \end{array}\right),{\bar{C}}_{ii}={\left(\begin{array}{c}\hfill O\hfill \\ \hfill m_i\hfill \end{array}\right)}^T\hfill \\ {\bar{x}}_i(t)={(V_i,I_{fi})}^T,{\bar{u}}_i(t)=V_{0i},{\bar{y}}_i(t)=m_i{I}_{fi},{\bar{z}}_i(t)={\int }_0^t(V_{refi}-V_i)dt\hfill \\ n_i^p=(n_{i,1},n_{i,2}),n_i^i=n_{i,3},V_{refi}=V_i^{*}-m_i{I}_i\hfill \end{array}$

FIGURE 1

FIGURE 1. The typical structure of DC microgrids.

$m_i$ represents the $V-I$ droop coefficient, $n_{i,1}$, $n_{i,2}$ and $n_{i,3}$ represent the PI controller coefficients of agent $i$, respectively, $V_i^{*}$ represents the output voltage of agent $i$ when unloading.

According to (1) and (2), the further systems function model of DC microgrids can be obtained. Take $A_i=(A_{ii}+\sum A_{ij})$, $u_i^{\prime }(t)=-\sum A_{ij}{x}_j(t)+B_{ii}{u}_i^{*}(t)$ and $C_{ii}=C_i$ for $i=\mathrm{1,2},\dots ,N$(1) and (2) can be rewritten as follows:

$\begin{array}{ll}\hfill {\dot{x}}_i(t)& =A_i{x}_i(t)+u_i^{\prime }(t)\hfill \end{array}(3)$

$\begin{array}{ll}\hfill y_i(t)& =C_i(t)x_i(t)\hfill \end{array}(4)$

Since $A_{ij}$ and $B_{ii}$ are constant matrix, $u_i^{\prime }(t)$ can be rewritten as $u_i^{\prime }(t)=B_i{u}_i(t)$, where $B_i$ is a constant matrix with compatible dimension and $u_i(t)$ is a function of $x_i(t)$ and $x_j(t)$ for $j\in {\mathcal{N}}_i$. On the other hand, for satisfying the actual demands, the power of each distributed generator is always required to be consistent with the ideal power finally. In other words, provide a control scheme to make the output of agent $i$ be the consensus with the ideal output finally is quite significant. Denote $y_0(t)$ as the ideal output and the corresponding system function model can be given as follows:

$\begin{array}{l}\hfill {\dot{x}}_0(t)=A_0{x}_0(t)\end{array}(5)$

$\begin{array}{l}\hfill y_0(t)=C_0{x}_0(t)\end{array}(6)$

where $A_0\in R^{n_0\times n_0}$ and $C_0\in R^{q\times n_0}$ are constant matrix. Assume that $y_j(t)$ have the same dimension $y_j(t)\in R^q$ for $j=\mathrm{0,1},\dots ,N$. Then, the above problem is equivalent to find the proper design scheme of $u_i(t)$ to make the following systems.

$\begin{array}{l}\hfill {\dot{x}}_i(t)=A_i{x}_i(t)+B_i{u}_i(t)\end{array}(7)$

$\begin{array}{l}\hfill y_i(t)=C_i{x}_i(t)\end{array}(8)$

Such that

$\underset{t\to \infty }{\lim }\Vert y_i(t)-y_0(t)\Vert =0(9)$

for $i=\mathrm{1,2},\dots ,N$ and any initial values of $x_i(t)$, where $A_i\in R^{n_i\times n_i}$, $B_i\in R^{n_i\times m_i}$ and $C_i\in R^{q\times n_i}$.

Therefore, the multi-agent systems function model of DC microgrid has been built by 5–8, where (5), (6) and (7), (8) represent the leader and agent systems, respectively. In the rest of this paper, the main purpose is to provide the control scheme making multi-agent systems 5–8 achieve output consensus.

4 Dynamic Event-Triggered Control Scheme for DC Microgird

4.1 The Design of Controller

For systems (5)–(8), assume that the following condition is satisfied in this paper.

Assumption 1 For $i=\mathrm{1,2},\dots ,N$, there are constant matrices ${\mathrm{\Pi }}_i\in R^{n_i\times n_0}$ and ${\mathrm{\Gamma }}_i\in R^{m_i\times n_0}$ making the following conditions hold.

$\begin{array}{l}\hfill {\mathrm{\Pi }}_i{A}_0=A_i{\mathrm{\Pi }}_i+B_i{\mathrm{\Gamma }}_i\\ \hfill 0=C_i{\mathrm{\Pi }}_i-C_0.\end{array}$

Let $a_{ij}$ ($b_i$) represent the relationship of information transfer between agent $i$ and agent $j$ (leader). According to the knowledge of algebraic graph topology and existing results (Fax and Murray, 2004)- (Huang and Ye, 2014), for making systems (5)–8) achieve output consensus (which means that condition 9) holds), the following condition should be satisfied.

Assumption 2 There exists a directed spanning tree with the leader as the root in topology $\bar{g}$. Since Assumptions 1–2 hold, the control protocol for each agent can be given as follows:

$\begin{array}{l}\hfill {\dot{z}}_i(t)=A_0{z}_i(t)+F_i\left[\sum _{j\in {\mathcal{N}}_i}{a}_{ij}{C}_0(z_i(t_k^i)-z_j(t_k^i))+b_i(C_0{z}_i(t_k^i)-x_0(t_k^i))\right]\end{array}(10)$

$\begin{array}{l}\hfill u_i(t)=K_i(y_i(t_k^i)-C_i{\mathrm{\Pi }}_i{z}_i(t_k^i))+{\mathrm{\Gamma }}_i{z}_i(t),t\in [t_k^i,t_{k+1}^i)\end{array}(11)$

For $i=\mathrm{1,2},\dots ,N$, $k=\mathrm{1,2},\dots$, where (10) represents the dynamic compensator for agent $i$ and $z_i(t)\in R^{n_0}$ represents the state of it, $K_i\in R^{m_i\times n_i}$ and $F_i\in R^{n_0\times n_0}$ represent the control gain matrices need to be solved, $t_k^i$ represents the triggered time decided by the event-triggered conditions, which will be designed in the rest of this paper.

4.2 The Design of Dynamic Event-Triggered Condition

Consider Assumptions one to two hold and the control protocol for systems (5)–(8) is (10), (11), the following conclusion can be given.

Proposition 1 Systems (5)–(8) can achieve output consensus with control protocol (10), (11) if the following systems

$\dot{\phi }(t)=A^{*}\phi (t)+\sum _{i=1}^N{D}_i(\phi (t)-\phi (t_k^i))(12)$

such that $\underset{t\to \infty }{\lim }\Vert \phi (t)\Vert =0$ for any initial value, where

$\begin{array}{l}{A}^{*}=\hat{A}+\hat{B}\hat{K}\hat{C},D_i={\left(\begin{array}{ccccc}\hfill O_{1i}\hfill & \hfill D_{1i}^T\hfill & \hfill O_{2i}\hfill & \hfill D_{2i}^T\hfill & \hfill O_{3i}\hfill \end{array}\right)}^T\hfill \\ \hat{A}=\left(\begin{array}{cc}\hfill \tilde{A}\hfill & \hfill O\hfill \\ \hfill O\hfill & \hfill {\tilde{A}}_0\hfill \end{array}\right),\hat{B}=\left(\begin{array}{cc}\hfill \tilde{B}\hfill & \hfill -\tilde{\mathrm{\Pi }}\hfill \\ \hfill O\hfill & \hfill I\hfill \end{array}\right),\hat{K}=\left(\begin{array}{cc}\hfill \tilde{K}\hfill & \hfill O\hfill \\ \hfill O\hfill & \hfill \tilde{F}\hfill \end{array}\right),\hat{C}=\left(\begin{array}{cc}\hfill \tilde{C}\hfill & \hfill O\hfill \\ \hfill O\hfill & \hfill \tilde{H}{\tilde{C}}_0\hfill \end{array}\right)\hfill \\ O_{1i}=O_{n^{*}\times {\sum }_{j=1}^i{n}_j-n_i},O_{2i}=O_{n^{*}\times {\sum }_{j=i}^N{n}_j-n_i+(i-1)n_0},O_{3i}=O_{n^{*}\times (N-i)n_0}\hfill \\ D_{1i}=\left(\begin{array}{cc}\hfill -\{{\mathcal{BKC}}_i\}\hfill & \hfill {\mathrm{\Pi }}_i{F}_i{\mathcal{H}}_i{\tilde{C}}_0\hfill \end{array}\right),D_{2i}=\left(\begin{array}{cc}\hfill O_{n_0\times {\sum }_{i=1}^N{n}_i}\hfill & \hfill -F_i{\mathcal{H}}_i{\tilde{C}}_0\hfill \end{array}\right)\hfill \\ \tilde{X}=diag\{X_1,X_2,\dots ,X_N\},X\in \{A,B,C,\mathrm{\Pi },K,F\},\hfill \\ {\tilde{A}}_0=I_N\otimes A_0,\tilde{H}=H\otimes I_q,{\tilde{C}}_0=I_N\otimes C_0\hfill \\ \{{\mathcal{BKC}}_i\}=ro{w}_{\sum _{j=1}^i{n}_j-n_i+1,\sum _{j=1}^i{n}_j}(\tilde{B}\tilde{K}\tilde{C}),{\mathcal{H}}_i=ro{w}_{(i-1)q+1,i\times q}(\tilde{H})\hfill \\ n*=\sum _{i=1}^N{n}_i+N\cdot n_0\hfill \end{array}$

for $i=\mathrm{1,2},\dots ,N$.

Proof. Take ${\phi }_{1i}(t)=x_i(t)-{\mathrm{\Pi }}_i{z}_i(t)$, ${\phi }_{2i}(t)=z_i(t)-x_0(t)$ for $i=\mathrm{1,2},\dots ,N$, ${\phi }_r(t)={({\phi }_{r1}^T(t),\dots ,{\phi }_{rN}^T(t))}^T$ for $r=\mathrm{1,2}$ and $\phi (t)={({\phi }_1^T(t),{\phi }_2^T(t))}^T$, according to (5)–(8) and (10), (11), $\phi (t)$ such that condition (12) holds. Meanwhile, since Assumption 1 holds, it can be found out that

$\begin{array}{ll}\hfill & \underset{t\to \infty }{\lim }\Vert y_i(t)-y_0(t)\Vert \hfill \\ \hfill =& \underset{t\to \infty }{\lim }\Vert C_i{x}_i(t)-C_0{x}_0(t)\Vert \hfill \\ \hfill =& \underset{t\to \infty }{\lim }\Vert C_i{x}_i(t)-C_i{\mathrm{\Pi }}_i{z}_i(t)+C_0{z}_i(t)-C_0{x}_0(t)\Vert \hfill \\ \hfill \le & \underset{t\to \infty }{\lim }\Vert C_i\Vert \Vert {\phi }_{1i}(t)\Vert +\Vert C_0\Vert \Vert {\phi }_{2i}(t)\Vert \hfill \end{array}(13)$

Therefore, we have $\underset{t\to \infty }{\lim }\Vert y_i(t)-y_0(t)\Vert =0$ for $i=\mathrm{1,2},\dots ,N$ if $\underset{t\to \infty }{\lim }\Vert \phi (t)\Vert =0$. The proof is completed.

Remark 1 According to the proof of Proposition 1, it is important to make Assumptions 1 and 2 be true. Specially, the existence of Assumption 1 makes each agent can obtain the information of leader directly or indirectly, which is a necessary condition of achieving output consensus. On the other hand, the existence of Assumption 2 makes output consensus problem of systems (5)–(8) can be turned into the stable problem of system (12), which is a necessary condition of using dynamic compensator to transfer information.According to Proposition one and some existing results, for making systems (5)–(8) achieve output consensus, assume that the following condition holds.

Assumption 3 There exists matrices $K_i\in R^{m_i\times n_i}$, $F_i\in R^{n_0\times n_0}$ and symmetric positive definite matrix $P=diag\{P_{11},P_{12},\dots ,P_{1N},P_{21},P_{22},\dots ,P_{2N}\}$ with $P_{1i}\in R^{n_i\times n_i}$, $P_{2i}\in R^{n_0\times n_0}$, $P_{1i}>0$ and $P_{2i}>0$ for $i=\mathrm{1,2},\dots ,N$, such that

$PA*+{A*}^{T}P<-\mu P(14)$

where $\mu >0$ is a constant.Since Assumption three is satisfied, $K_i$ and $F_i$ can be chosen by utilizing condition (14). Based on these, two dynamic event-triggered conditions are provided in the next part of this paper, respectively.

4.2.1 Non-periodic Dynamic Event-Triggered Condition

Consider that the triggered time $t_k^i$ is decided by the following dynamic event-triggered condition.

$t_{k+1}^i=\max \{t_{k+1}^{i*},t_{k+1}^i+h\}(15)$

where.

$\begin{array}{l}{t}_{k+1}^{i*}=\inf \left\{t>t_k^i|\right.\left.{\theta }_i\{{\delta }_i{(D_i\phi (t))}^{T}P{D}_i\phi (t)-{[D_i(\phi (t)-\phi (t_k^i))]}^{T}P{D}_i(\phi (t)-\phi (t_k^i))\}+{\eta }_i(t)<0\right\}\left.\right\}\hfill \end{array}(16)$

$\begin{array}{l}\hfill {\dot{\eta }}_i(t)=-{\lambda }_i{\eta }_i(t)+{\alpha }_i\{{\delta }_i{(D_i\phi (t))}^{T}P{D}_i\phi (t)-{[D_i(\phi (t)-\phi (t_k^i))]}^{T}P{D}_i(\phi (t)-\phi (t_k^i))\},t\in [t_k^i,t_{k+1}^{i*})\end{array}(17)$

$\begin{array}{l}\hfill {\dot{\eta }}_i(t)=-{\lambda }_i{\eta }_i(t),t\in [t_{k+1}^{i*},t_{k+1}^i)\end{array}(18)$

Furthermore, $h,{\theta }_i,{\delta }_i,{\alpha }_i,{\lambda }_i>0$ need to be designed, ${\eta }_i(t)$ represents the dynamic item such that ${\eta }_i(0)\ge 0$ for $i=\mathrm{1,2},\dots ,N$ and $P$ is given according to condition (14).

According to event-triggered condition (15), the following result can be obtained.

Theorem 1 Assume that Assumptions 1–3 hold, systems (5)–(8) can achieve output consensus with control protocol (10), (11) and event-triggered condition (15) if $P$ such that condition (14) holds, and constants $h,{\theta }_i,{\delta }_i,{\alpha }_i,{\lambda }_i,c,\ell >0$ such that the following conditions hold.

${\mathrm{\Psi }}_1<0,{\mathrm{\Psi }}_2<0,{\mathrm{\Psi }}_{3i}<0,i=\mathrm{1,2},\dots ,N(19)$

where

$\begin{array}{l}\hfill {\mathrm{\Psi }}_1=-\mu P+\sum _{i=1}^N({\alpha }_i+{\ell }^{-1}+3c{h}^2){\delta }_i{D}_i^{T}P{D}_i+\ell P+3c{h}^2{A*}^{T}PA*,\end{array}(20)$

$\begin{array}{l}\hfill {\mathrm{\Psi }}_2=-cP+\sum _{i=1}^N({\ell }^{-1}-{\alpha }_i+3c{h}^2)D_i^{T}P{D}_i,\end{array}(21)$

$\begin{array}{l}\hfill {\mathrm{\Psi }}_{3i}=\frac{1}{{\theta }_i}({\ell }^{-1}+3c{h}^2)-{\lambda }_i.\end{array}(22)$

Proof Set

$V(t)={\phi }^T(t)P\phi (t)+ch{\int }_{-h}^0{\int }_{t+v}^t{\dot{\phi }}^T(s)P\dot{\phi }(s)dsdv+\sum _{i=1}^N{\eta }_i(t),(23)$

According to (16)–(18), We Have

$\begin{array}{l}\hfill {\dot{\eta }}_i(t)\ge -\left({\lambda }_i+\frac{{\alpha }_i}{{\theta }_i}\right){\eta }_i(t),t\in [t_k^i,t_{k+1}^{i*})\\ \hfill {\dot{\eta }}_i(t)=-{\lambda }_i{\eta }_i(t),t\in [t_{k+1}^{i*},t_{k+1}^i)\end{array}$

Since ${\eta }_i(0)\ge 0$ for $i=\mathrm{1,2},\dots ,N$, ${\eta }_i(t)\ge 0$ for any $t\ge 0$. Therefore, we have $V(t)\ge 0$ and $V(t)=0$ only if $\Vert \phi (t)\Vert =0$. Meanwhile, according to Proposition 1, systems (5)–8) can achieve output consensus if $\underset{t\to \infty }{\lim }\Vert \phi (t)\Vert =0$. As a result, the original problem is changed to prove that $\dot{V}(t)<0$ for any $\Vert \phi (t)\Vert >0$.According to (23), We Have

$\dot{V}(t)=V_1(t)+V_2(t)+V_3(t)+V_4(t)+V_5(t)(24)$

where

$\begin{array}{l}\hfill V_1(t)={\phi }^T(t)(A^{*T}P+P{A}^{*})\phi (t)\end{array}(25)$

$\begin{array}{l}\hfill V_2(t)=2{\phi }^T(t)P\sum _{i=1}^N{D}_i(\phi (t)-\phi (t_k^i))\end{array}(26)$

$\begin{array}{l}\hfill V_3(t)=\sum _{i=1}^N{\dot{\eta }}_i(t)\end{array}(27)$

$\begin{array}{l}\hfill V_4(t)=c{h}^2{\dot{\phi }}^T(t)P\dot{\phi }(t)\end{array}(28)$

$\begin{array}{l}\hfill V_5(t)=-ch{\int }_{t-h}^t{\dot{\phi }}^T(s)P\dot{\phi }(s)ds\end{array}(29)$

Denote ${\mathfrak{R}}_1$ and ${\mathfrak{R}}_2$ as the index sets of agent $i$ such that ${\mathfrak{R}}_1=\{i\in \{\mathrm{1,2},\dots ,N\}|t\in [t_k^i,t_{k+1}^{i*})\}$ and ${\mathfrak{R}}_2=\{i\in \{\mathrm{1,2},\dots ,N\}|t\in [t_{k+1}^{i*},t_{k+1}^i)\}$. Then, the following results can be obtained.

$\begin{array}{l}\hfill V_1(t)\le -\mu {\phi }^T(t)P\phi (t)\end{array}(30)$

$\begin{array}{l}\hfill V_2(t)\le \ell {\phi }^T(t)P\phi (t)+{\ell }^{-1}\sum _{i=1}^N{[D_i(\phi (t)-\phi (t_k^i))]}^{T}P{D}_i(\phi (t)-\phi (t_k^i))\\ \hfill \le \ell {\phi }^T(t)P\phi (t)+{\ell }^{-1}\sum _{i\in {\mathfrak{R}}_1}\left[{\delta }_i{(D_i\phi (t))}^{T}P{D}_i\phi (t)+\frac{1}{{\theta }_i}{\eta }_i(t)\right]\\ +{\ell }^{-1}\sum _{i\in {\mathfrak{R}}_2}{[D_i(\phi (t)-\phi (t_k^i))]}^{T}P{D}_i(\phi (t)-\phi (t_k^i))\hfill \end{array}(31)$

$\begin{array}{l}\hfill V_3(t)=\sum _{i\in {\mathfrak{R}}_1}\left\{-{\lambda }_i{\eta }_i(t)+{\alpha }_i{\delta }_i{(D_i\phi (t))}^{T}P{D}_i\phi (t)-{\alpha }_i{[D_i(\phi (t)-\phi (t_k^i))]}^{T}P{D}_i(\phi (t)-\phi (t_k^i))\right\}-\sum _{i\in {\mathfrak{R}}_2}{\lambda }_i{\eta }_i(t)\end{array}(32)$

$\begin{array}{l}\hfill V_4(t)\le 3c{h}^2\left\{{\phi }^T(t)A^{*T}P{A}^{*}\phi (t)+\sum _{i=1}^N{[D_i(\phi (t)-\phi (t_k^i))]}^{T}P{D}_i(\phi (t)-\phi (t_k^i))\right\}\\ \hfill \le 3c{h}^2\left\{{\phi }^T(t)A^{*T}P{A}^{*}\phi (t)+\sum _{i\in {\mathfrak{R}}_1}\left[{\delta }_i{(D_i\phi (t))}^{T}P{D}_i\phi (t)+\frac{1}{{\theta }_i}{\ell }_i(t)\right]\right.\\ \left.+\sum _{i\in {\mathfrak{R}}_2}{[D_i(\phi (t)-\phi (t_k^i))]}^{T}P{D}_i(\phi (t)-\phi (t_k^i))\right\}\hfill \end{array}(33)$

$\begin{array}{l}\hfill V_5(t)=-\sum _{i\in {\mathfrak{R}}_2}{c}_{i}h{\int }_{t-h}^t{\dot{\phi }}^T(s)P_i\dot{\phi }(s)ds\\ \hfill \le -\sum _{i\in {\mathfrak{R}}_2}{c}_i(t-t_k^i){\int }_{t_k^i}^t{\dot{\phi }}^T(s)P_i\dot{\phi }(s)ds\\ \hfill \le -\sum _{i\in {\mathfrak{R}}_2}{(\phi (t)-\phi (t_k^i))}^T{c}_i{P}_i(\phi (t)-\phi (t_k^i))\end{array}(34)$

where $c_i{P}_i>0$ such that ${\sum }_{i=1}^N{c}_i{P}_i=cP$.Then, We Have

$\dot{V}(t)\le {\phi }^T(t){\mathrm{\Psi }}_1\phi (t)+\sum _{i\in N_2}{(\phi (t)-\phi (t_k^i))}^T{\mathrm{\Psi }}_{2i}(\phi (t)-\phi (t_k^i))+\sum _{i\in N_1}{\mathrm{\Psi }}_{3i}{\eta }_i(t)(35)$

where

${\mathrm{\Psi }}_{2i}=-c_i{P}_i+({\ell }^{-1}-{\alpha }_i+3c{h}^2)D_i^{T}P{D}_i,i=\mathrm{1,2},\dots ,N(36)$

By simple analysis, there exist $c_i$ and $P_i$ for $i=\mathrm{1,2},\dots ,N$ such that ${\mathrm{\Psi }}_{2i}<0$ if ${\mathrm{\Psi }}_2<0$. Therefore, $\dot{V}(t)<0$ for any $\Vert \phi (t)\Vert >0$ if condition 19) holds. The proof is completed.

Remark 2 Because of the existence of $h$, event-triggered condition (15) can be seen as an improved condition based on traditional event-triggered condition. Since $h>0$ is constant, the minimum triggered interval of (15) must be no less than $h$. In other words, the Zeno-behavior is avoided successfully, which is difficult to achieve in many existing works.

Remark 3 ${\eta }_i(t)$ seems to need the additional channel of information transfer. However, according to (17) and (18), the information of ${\eta }_i(t)$ can be given from the information of $z_i(t)$ and $x_i(t)$ directly. Therefore, there is no need to build external channel of information transfer for obtaining the information of ${\eta }_i(t)$.

Remark 4 Compare with the static event-triggered condition, the most obvious difference of dynamic event-triggered condition (15) is the existence of dynamic item ${\eta }_i(t)$. Moreover, how to design ${\eta }_i(t)$ is the key problem of building dynamic event-triggered condition (15). In this paper, ${\eta }_i(t)$ is designed with the following rules: i) ${\eta }_i(t)\ge 0$ for any $t\ge 0$; ii) The information of ${\eta }_i(t)$ can be given from $x_i(t)$ and $z_i(t)$. Therefore, we have ${\delta }_i{(D_i\phi (t))}^{T}P{D}_i\phi (t)-{[D_i(\phi (t)-\phi (t_k^i))]}^{T}P{D}_i(\phi (t)-\phi (t_k^i))\ge 0$ is a sufficient condition for ${\theta }_i\{{\delta }_i{(D_i\phi (t))}^{T}P{D}_i\phi (t)-{[D_i(\phi (t)-\phi (t_k^i))]}^{T}P{D}_i(\phi (t)-\phi (t_k^i))\}+{\eta }_i(t)\ge 0$, which means that the conservativeness of event-triggered condition (15) is lower than its corresponding static event-triggered condition. Moreover, according to some existing results such as (Wang et al., 2017) and (Ge and Han, 2017), condition (15) may have the bigger minimum triggered interval if the parameters are chosen well.

4.2.2 Periodic Dynamic Event-Triggered Condition

Consider that the triggered time $t_k^i$ is decided by the following dynamic event-triggered condition.

$\begin{array}{l}\hfill t_{k+1}^i=\inf \left\{t_k^i+s_{i}h|s_i\in \{\mathrm{1,2},\dots \},{\theta }_i\left\{{\delta }_i{(D_i\phi (t_k^i+s_{i}h))}^{T}P(D_i\phi (t_k^i+s_{i}h))\right.\right.\\ \left.\left.-{[D_i(\phi (t_k^i+s_{i}h)-\phi (t_k^i))]}^{T}P{D}_i(\phi (t_k^i+s_{i}h)-\phi (t_k^i))\right\}+{\eta }_i(t_k^i+s_{i}h)<0\right\},\hfill \end{array}(37)$

where

$\begin{array}{ll}\hfill {\dot{\eta }}_i(t)=& -{\lambda }_i{\eta }_i(t),t\in (t_k^i,t_k^i+h]\hfill \end{array}(38)$

$\begin{array}{ll}\hfill {\dot{\eta }}_i(t)=& -{\lambda }_i{\eta }_i(t)+{\alpha }_i\left\{{\delta }_i{(D_i\phi (t_k^i+(s_i-1)h))}^{T}P(D_i\phi (t_k^i+(s_i-1)h))\right.\hfill \\ \hfill & \left.-{[D_i(\phi (t_k^i+(s_i-1)h)-\phi (t_k^i))]}^{T}P{D}_i(\phi (t_k^i+(s_i-1)h)-\phi (t_k^i))\right\},\hfill \\ \hfill & t\in (t_k^i+(s_i-1)h,t_k^i+s_{i}h],s_i\ge 2\hfill \end{array}(39)$

Moreover, $h,{\theta }_i,{\delta }_i,{\alpha }_i,{\lambda }_i>0$ need to be designed, ${\eta }_i(t)$ represents the dynamic item such that ${\eta }_i(0)\ge 0$ for $i=\mathrm{1,2},\dots ,N$ and $P$ is given according to condition (14).

According to event-triggered condition (37), the following conclusion can be given.

Theorem 2 Assume that Assumptions 1–3 hold, systems (5)–(8) can achieve output consensus with control protocol (10), (11) and event-triggered condition (37) if $P$ such that condition (14) hold, constants $\varrho >1$ and $h,{\theta }_i,{\delta }_i,{\alpha }_i,{\lambda }_i,c,\ell >0$ such that the following conditions hold.

$\begin{array}{ll}\hfill & h\le \frac{\ln \left(1+\frac{{\theta }_i{\lambda }_i}{{\alpha }_i}\right)}{{\lambda }_i}\hfill \end{array}(40)$

$\begin{array}{ll}\hfill & {\mathrm{\Theta }}_1<0,{\mathrm{\Theta }}_2<0,{\mathrm{\Theta }}_3<0,{\mathrm{\Theta }}_{4i}<0\hfill \end{array}(41)$

where

$\begin{array}{l}\hfill {\mathrm{\Theta }}_1=-\mu P+\ell P+3c{h}^2{A}^{*T}P{A}^{*}+0.5(\varrho -1)cP\end{array}(42)$

$\begin{array}{l}\hfill {\mathrm{\Theta }}_2=\sum _{i=1}^N(2{\ell }^{-1}-{\alpha }_i+6c{h}^2)D_i^{T}P{D}_i-0.5cP\end{array}(43)$

$\begin{array}{l}\hfill {\mathrm{\Theta }}_3=\sum _{i=1}^N(2{\ell }^{-1}+{\alpha }_i+6c{h}^2){\delta }_i{D}_i^{T}P{D}_i-0.5(1-{\varrho }^{-1})cP\end{array}(44)$

$\begin{array}{l}\hfill {\mathrm{\Theta }}_{4i}=\frac{1}{{\theta }_i}(2{\ell }^{-1}+6c{h}^2)-{\lambda }_i\left[e^{-{\lambda }_{i}h}-\frac{{\alpha }_i}{{\theta }_i{\lambda }_i}(1-e^{-{\lambda }_{i}h})\right]\end{array}(45)$

Proof According to (38), (39), the following results can obtained.

$\begin{array}{l}\hfill {\eta }_i(t)\ge e^{-{\lambda }_{i}h}{\eta }_i(t_k^i),t\in (t_k^i,t_k^i+h]\\ \hfill {\eta }_i(t)\ge \left[e^{-{\lambda }_{i}h}-\frac{{\alpha }_i}{{\theta }_i{\lambda }_i}(1-e^{-{\lambda }_{i}h})\right]{\eta }_i(t_k^i+(s_i-1)h),\\ t\in \left(\right.t_k^i+(s_i-1)h,t_k^i+s_{i}h\left.\right]],s_i\ge 2\hfill \end{array}$

Since ${\eta }_i(0)\ge 0$ and condition (40) holds, we have ${\eta }_i(t)\ge 0$ for $i=\mathrm{1,2},\dots ,N$ and any $t\ge 0$. Take $V(t)$ and $V_i(t)$ ($i=\mathrm{1,2},\dots ,5$) have the same meanings as given in Theorem 1. Be similar with Theorem 1, this problem is equivalent to prove that $\dot{V}(t)<0$ for any $\Vert \phi (t)\Vert >0$. It can be found out that $V_1(t)$ still satisfies condition (30). For $V_2(t)-V_5(t)$, the following results can be obtained.

$\begin{array}{l}\hfill V_2(t)\le \ell {\phi }^T(t)P\phi (t)+{\ell }^{-1}\sum _{i=1}^N{[D_i(\phi (t)-\phi (t_k^i))]}^{T}P{D}_i(\phi (t)-\phi (t_k^i))\\ \hfill \le \ell {\phi }^T(t)P\phi (t)+2{\ell }^{-1}\sum _{i\in {\mathfrak{R}}_1}\left\{{\delta }_i{(D_i\phi (t_k^i+r_k^{i}h))}^{T}P{D}_i\phi (t_k^i+r_k^{i}h)+\frac{1}{{\theta }_i}{\eta }_i(t_k^i+r_k^{i}h)\right\}\\ \hfill +2{\ell }^{-1}\sum _{i=1}^N{[D_i(\phi (t)-\phi (t_k^i+r_k^{i}h))\left.\right)]}^{T}P{D}_i(\phi (t)-\phi (t_k^i+r_k^{i}h))\end{array}(46)$

$\begin{array}{l}\hfill V_3(t)=\sum _{i\in {\mathfrak{R}}_1}\left\{-{\lambda }_i{\eta }_i(t)+{\alpha }_i{\delta }_i{(D_i\phi (t_k^i+r_k^{i}h))}^{T}P(D_i\phi (t_k^i+r_k^{i}h))\right.\\ \left.-{\alpha }_i{[D_i(\phi (t_k^i+r_k^{i}h)-\phi (t_k^i))]}^{T}P{D}_i(\phi (t_k^i+r_k^{i}h)-\phi (t_k^i))\right\}-\sum _{i\in {\mathfrak{R}}_2}{\lambda }_i{\eta }_i(t)\hfill \\ \hfill \le \sum _{i\in {\mathfrak{R}}_1}\left\{-{\lambda }_i\left[e^{-{\lambda }_{i}h}-\frac{{\alpha }_i}{{\theta }_i{\lambda }_i}(1-e^{-{\lambda }_{i}h})\right]{\eta }_i(t_k^i+r_k^{i}h)+{\alpha }_i{\delta }_i{(D_i\phi (t_k^i+r_k^{i}h))}^{T}P(D_i\phi (t_k^i+r_k^{i}h))\right.\left.-{\alpha }_i{[D_i(\phi (t_k^i+r_k^{i}h)-\phi (t_k^i))]}^{T}P{D}_i(\phi (t_k^i+r_k^{i}h)-\phi (t_k^i))\right\}\end{array}(47)$

$\begin{array}{l}\hfill V_4(t)\le 3c{h}^2\left\{{\phi }^T(t)A^{*T}P{A}^{*}\phi (t)+\sum _{i=1}^N{[D_i(\phi (t)-\phi (t_k^i))]}^{T}P{D}_i(\phi (t)-\phi (t_k^i))\right\}\end{array}$

$\begin{array}{l}\hfill \le 3c{h}^2\left\{{\phi }^T(t)A^{*T}P{A}^{*}\phi (t)+2\sum _{i\in {\mathfrak{R}}_1}\left\{{\delta }_i{[D_i\phi (t_k^i+r_k^{i}h)]}^{T}P{D}_i\phi (t_k^i+r_k^{i}h)+\frac{1}{{\theta }_i}{\eta }_i(t_k^i+r_k^{i}h)\right\}\right.\left.+2\sum _{i=1}^N{[D_i(\phi (t)-\phi (t_k^i+r_k^{i}h))]}^{T}P{D}_i(\phi (t)-\phi (t_k^i+r_k^{i}h))\right\}\end{array}(48)$

$\begin{array}{l}\hfill V_5(t)\le -\sum _{i=1}^N{c}_i(t-t_k^i-r_k^{i}h){\int }_{t_k^i+r_k^{i}h}^t{\dot{\phi }}^T(s)P_i\dot{\phi }(s)ds\\ \hfill \le -\sum _{i=1}^N{c}_i{(\phi (t)-\phi (t_k^i+r_k^{i}h))}^T{P}_i(\phi (t)-\phi (t_k^i+r_k^{i}h))\\ \hfill \le -0.5\sum _{i=1}^N\left\{c_i{(\phi (t)-\phi (t_k^i+r_k^{i}h))}^T{P}_i(\phi (t)-\phi (t_k^i+r_k^{i}h))\right.\\ \left.-(\varrho -1)c_i{\phi }^T(t)P_i\phi (t)+(1-{\varrho }^{-1})c_i{\phi }^T(t_k^i+r_k^{i}h)P_i\phi (t_k^i+r_k^{i}h)\right\}\hfill \end{array}(49)$

Therefore, the following conclusion can be given.

$\begin{array}{l}\hfill \dot{V}(t)\le {\phi }^T(t){\mathrm{\Theta }}_1\phi (t)+\sum _{i=1}^N{[\phi (t)-\phi (t_k^i+r_k^{i}h)]}^T{\mathrm{\Theta }}_{2i}[\phi (t)-\phi (t_k^i+r_k^{i}h)]\\ +\sum _{i\in {\mathfrak{R}}_1}[{\phi }^T(t_k^i+r_k^{i}h){\mathrm{\Theta }}_{3i}\phi (t_k^i+r_k^{i}h)+{\mathrm{\Theta }}_{4i}{\eta }_i(t_k^i+r_k^{i}h)]\hfill \end{array}(50)$

where

$\begin{array}{l}\hfill {\mathrm{\Theta }}_{2i}=(2{\ell }^{-1}-{\alpha }_i+6c{h}^2)D_i^{T}D{E}_i-0.5c_i{P}_i\end{array}(51)$

$\begin{array}{l}\hfill {\mathrm{\Theta }}_{3i}=(2{\ell }^{-1}+{\alpha }_i+6c{h}^2){\delta }_i{D}_i^{T}P{D}_i-0.5(1-{\varrho }^{-1})c_i{P}_i\end{array}(52)$

$c_i$ and $P_i$ have the same meanings as given in Theorem 1. Obviously, there exist $c_i$, $P_i$ such that ${\mathrm{\Theta }}_{2i}<0$, ${\mathrm{\Theta }}_{3i}<0$ if ${\mathrm{\Theta }}_2<0$, ${\mathrm{\Theta }}_3<0$. Therefore, $\dot{V}(t)<0$ for any $\Vert \phi (t)\Vert >0$ if conditions (40)–41) hold. The proof is completed.

Remark 5 In this paper, event-triggered condition (37) is called periodic dynamic event-triggered condition because it combines periodic sampling condition with dynamic event-triggered condition. More specifically, event-triggered condition (37) makes the controller of each agent receive the systems’ information at the fixed periodic sampling instant ($s_{i}h$ for $s_i=\mathrm{1,2},\dots$) and update itself at the triggered time when the dynamic event-triggered condition ${\theta }_i\{{\delta }_i{(D_i\phi (t_k^i+s_{i}h))}^{T}P(D_i\phi (t_k^i+s_{i}h))-{[D_i(\phi (t_k^i+s_{i}h)-\phi (t_k^i))]}^{T}P{D}_i(\phi (t_k^i+s_{i}h)-\phi (t_k^i))\}+{\eta }_i(t_k^i+s_{i}h)<0$ holds. Therefore, event-triggered condition (37) not only can avoid the Zeno-behavior, but also can avoid the continuous information transfer.

Remark 6 As we know, the differences between linear and nonlinear systems are huge. Therefore, it is difficult to extend the control algorithm for linear system to the nonlinear system directly. More specifically, take this paper as an example: In this paper, the information of dynamic item ${\eta }_i(t)$ can be given according to the results of the integral of systems (5)–(8). For linear system, the integral of system can be given easily and the result is standard, which is difficult to realize for nonlinear system. Hence, the control algorithm given in this paper is hardly extended to the nonlinear system directly. This problem is quite interesting and worth considering, which will be investigated in our further work.

5 Numerical Example

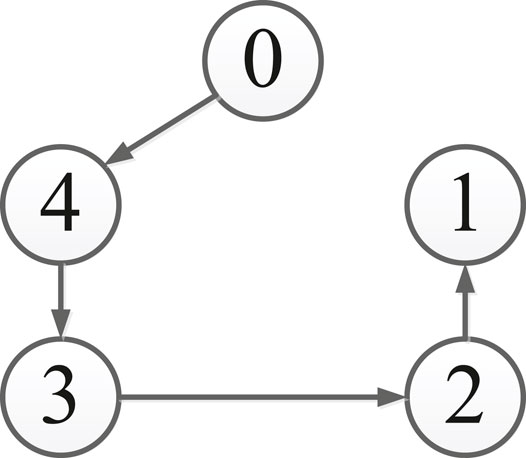
Consider systems (5)–(8) with the topology structure shown in Figure 2 and the parameters given as follows:

$\begin{array}{l}H=\left(\begin{array}{cccc}\hfill 1\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill -1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill -1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right),A_0=\left(\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right),A_1=A_2=A_3=\left(\begin{array}{cc}\hfill 0\hfill & \hfill -1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right),A_4=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill -1\hfill & \hfill 2\hfill \\ \hfill -1\hfill & \hfill 0\hfill & \hfill -1\hfill \\ \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill \end{array}\right)\hfill \\ B_1=B_2=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \end{array}\right),B_3=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill -1\hfill \end{array}\right),B_4=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill -1\hfill \\ \hfill 1\hfill \end{array}\right),C_0=0.1\times \left(\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \end{array}\right),C_1=C_2=0.1\times \left(\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \end{array}\right)\hfill \\ C_3=0.1\times \left(\begin{array}{cc}\hfill 1\hfill & \hfill -1\hfill \end{array}\right),C_4=0.1\times \left(\begin{array}{ccc}\hfill 1\hfill & \hfill -1\hfill & \hfill 1\hfill \end{array}\right)\hfill \\ {\mathrm{\Pi }}_1={\mathrm{\Pi }}_2=\left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 1\hfill \end{array}\right),{\mathrm{\Pi }}_3=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right),{\mathrm{\Pi }}_4=\left(\begin{array}{cc}\hfill 0.46\hfill & \hfill 0.46\hfill \\ \hfill -0.38\hfill & \hfill -0.38\hfill \\ \hfill 0.15\hfill & \hfill 0.15\hfill \end{array}\right),\hfill \\ {\mathrm{\Gamma }}_1={\mathrm{\Gamma }}_2={\mathrm{\Gamma }}_3=(11),{\mathrm{\Gamma }}_4=(-0.23-0.23)\hfill \end{array}$

FIGURE 2

FIGURE 2. Topology structure of network.

For satisfying Assumption 3, $K_i$ and $F_i$ can be chosen as follows:

$K_1=K_2=K_3=K_4=-10,F_1=F_2=F_3=F_4=\left(\begin{array}{c}\hfill -10\hfill \\ \hfill -10\hfill \end{array}\right)$

Then, the non-periodic and periodic dynamic event-triggered conditions can be given as follows:

1) Non-periodic dynamic event-triggered scheme: According to Theorem 1, the parameters of condition 15) can be given as $h=0.02$, ${\delta }_i=0.01$, ${\theta }_i=1$, ${\lambda }_i=1$ and ${\alpha }_i=1$ for $i=\mathrm{1,2,3,4}$. Then, through Figure 3, systems (5)–(8) has achieved output consensus. Moreover, the change process of inputs for all agents is shown in Figure 4.

2) Periodic dynamic event-triggered scheme: According to Theorem 2, the parameters of condition (37) can be given as $h=0.001$, ${\delta }_i=0.01$, ${\theta }_i=1$, ${\lambda }_i=0.1$ and ${\alpha }_i=1$ for $i=\mathrm{1,2,3,4}$. Then, through Figure 5, systems (5)–(8) has achieved output consensus. Moreover, the change process of inputs for all agents is shown in Figure 6.

FIGURE 3

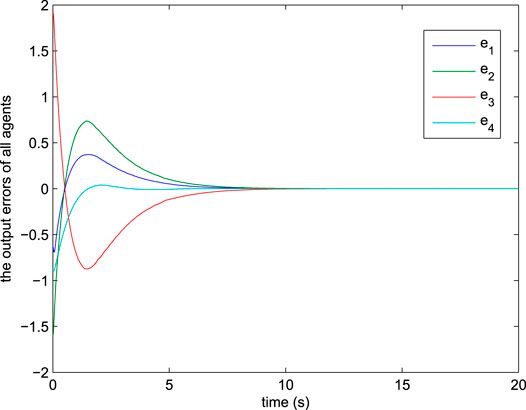
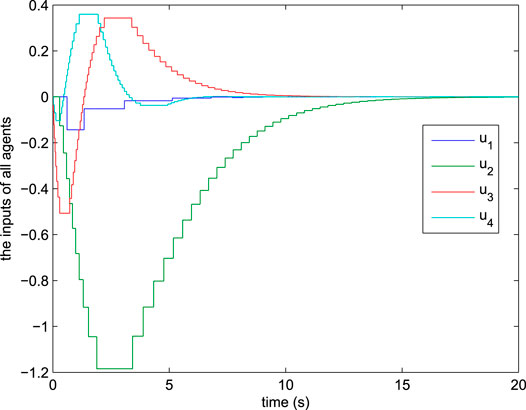
FIGURE 3. The output error between agent $i$ and leader for $i=\mathrm{1,2,3,4}$ with random initial values and event-triggered condition (15).

FIGURE 4

FIGURE 4. The inputs of all agents with event-triggered condition (15).

FIGURE 5

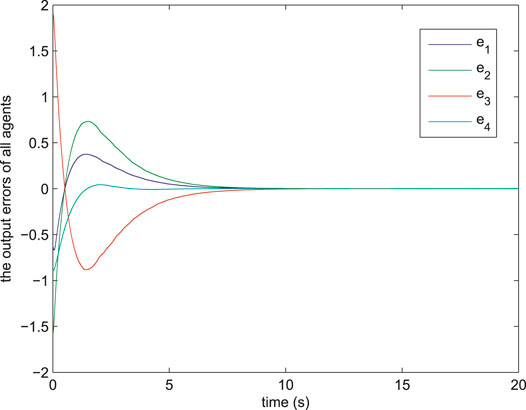
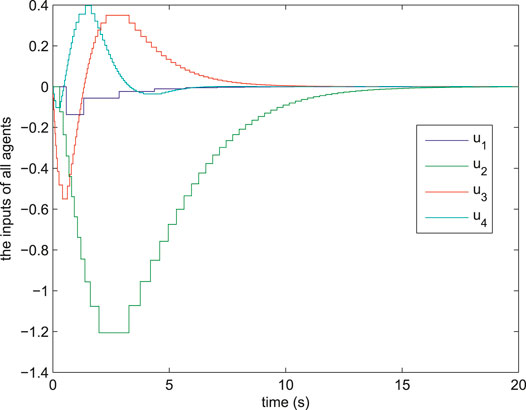
FIGURE 5. The output error between agent $i$ and leader for $i=\mathrm{1,2,3,4}$ with random initial values and event-triggered condition (37).

FIGURE 6

FIGURE 6. The inputs of all agents with event-triggered condition (37).

Remark 7 According to Figures 4, 6, compared with condition (37), the number of triggered times with condition (15) is much lower. This phenomenon is due to the differences between these two conditions. More specifically, condition (15) receive the continuous information while condition (37) only receive the information at the fixed periodic sampling instant. For avoiding the continuous information transfer, the conservativeness of condition (37) is higher than condition (15) for making up the lack of information transfer, which leads to the results that the frequency of trigger with condition (37) is higher.

6 Conclusion

In this paper, we have studied the output consensus problem of DC microgrids with dynamic event-triggered control scheme. By using the relevant knowledge of DC microgrids and multi-agent systems, and some existing results, the multi-agent systems function model for DC microgrids has been built. Then, for this system function model, the non-periodic and periodic dynamic event-triggered control scheme have been provided, respectively. By a series of analysis and the support of numerical example, it can be proved that these two control schemes both can make system achieve output consensus and avoid the Zeno-behavior successfully. Moreover, the periodic dynamic event-triggered control scheme can also avoid the continuous information transfer of system.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

YG and JJ contributed to conception and design of the study. BH organized the database and performed the statistical analysis.

Funding

The National Natural Science Foundation of China (61372195).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (61372195) and College of Information and Electrical Engineering, Shenyang Agricultural University, and Liaoning Provincial College of Communications.

References

Aluisio, B., Dicorato, M., Forte, G., and Trovato, M. (2017). An Optimization Procedure for Microgrid Day-Ahead Operation in the Presence of CHP Facilities. Sustainable Energ. Grids Networks 11, 34–45. doi:10.1016/j.segan.2017.07.003

CrossRef Full Text | Google Scholar

Aquila, G., Queiroz, A. R., Lima, L. M. M., Balestrassi, P. P., Lima, J. W. M., and Pamplona, E. O. (2020). Modelling and Design of Wind‐solar Hybrid Generation Projects in Long‐term Energy Auctions: a Multi‐objective Optimisation Approach. IET Renew. Power Generation 14 (14), 2612–2619. doi:10.1049/iet-rpg.2020.0185

CrossRef Full Text | Google Scholar

Bender, J. G. (1991). An Overview of Systems Studies of Automated Highway Systems. IEEE Trans. Veh. Technol. 40 (1), 82–99. doi:10.1109/25.69977

CrossRef Full Text | Google Scholar

Cai, Y., Tang, Z., Ding, Y., and Qian, B. (2016). Theory and Application of Multi-Robot Service-Oriented Architecture. Ieee/caa J. Autom. Sinica 3 (1), 15–25. doi:10.1109/jas.2016.7373758

CrossRef Full Text | Google Scholar

Duan, M.-M., Liu, C.-L., and Liu, F. (2017). Event-triggered Consensus Seeking of Heterogeneous First-Order Agents with Input Delay. IEEE Access 5, 5215–5223. doi:10.1109/access.2017.2696026

CrossRef Full Text | Google Scholar

Fax, J. A., and Murray, R. M. (2004). Information Flow and Cooperative Control of Vehicle Formations. IEEE Trans. Automat. Contr. 49 (9), 1465–1476. doi:10.1109/tac.2004.834433

CrossRef Full Text | Google Scholar

Franceschelli, M., Gasparri, A., Giua, A., and Ulivi, G. (2010). Decentralized Stabilization of Heterogeneous Linear Multi-Agent Systems. IEEE Int. Conf. Robotics Automation, 3556–3561. doi:10.1109/robot.2010.5509637

CrossRef Full Text | Google Scholar

Fridman, E. (2010). A Refined Input Delay Approach to Sampled-Data Control. Automatica 46, 421–427. doi:10.1016/j.automatica.2009.11.017

CrossRef Full Text | Google Scholar

Ge, X., and Han, Q.-L. (2017). Distributed Formation Control of Networked Multi-Agent Systems Using a Dynamic Event-Triggered Communication Mechanism. IEEE Trans. Ind. Electron. 64 (10), 8118–8127. doi:10.1109/tie.2017.2701778

CrossRef Full Text | Google Scholar

Hu, X., Ma, D., Zheng, J., Zhang, H., and Wang, R. (2020). An Operation State Analysis Method for Integrated Energy System Based on Correlation Information Adversarial Learning. Acta Automatica Sinica 46 (9), 1783–1797. doi:10.16383/j.aas.c200171

CrossRef Full Text | Google Scholar

Huang, C., and Ye, X. (2014). Cooperative Output Regulation of Heterogeneous Multi-Agent Systems: An $H_{\infty}$ Criterion. IEEE Trans. Automat. Contr. 59 (1), 267–273. doi:10.1109/tac.2013.2272133

CrossRef Full Text | Google Scholar

Kong, X., Liu, X., Ma, L., and Lee, K. Y. (2019). Hierarchical Distributed Model Predictive Control of Standalone Wind/solar/battery Power System. IEEE Trans. Syst. Man. Cybern, Syst. 49 (8), 1570–1581. doi:10.1109/tsmc.2019.2897646

CrossRef Full Text | Google Scholar

Lawton, J. R., and Beard, R. W. (2002). Synchronized Multiple Spacecraft Rotations. Automatica 38 (8), 1359–1364. doi:10.1016/s0005-1098(02)00025-0

CrossRef Full Text | Google Scholar

Liu, K., and Fridman, E. (2012). Wirtinger's Inequality and Lyapunov-Based Sampled-Data Stabilization. Automatica 48, 102–108. doi:10.1016/j.automatica.2011.09.029

CrossRef Full Text | Google Scholar

Liu, Z., Liu, R., Zhang, X., Su, M., Sun, Y., Han, H., et al. (2020). Feasible Power-Flow Solution Analysis of DC Microgrids under Droop Control. IEEE Trans. Smart Grid 11 (4), 2771–2781. doi:10.1109/tsg.2020.2967353

CrossRef Full Text | Google Scholar

Liu, Z., Su, M., Sun, Y., Yuan, W., Han, H., and Feng, J. (2018). Existence and Stability of Equilibrium of DC Microgrid with Constant Power Loads. IEEE Trans. Power Syst. 33 (6), 6999–7010. doi:10.1109/tpwrs.2018.2849974

CrossRef Full Text | Google Scholar

Ma, G., Xu, G., Chen, Y., and Ju, R. (2017). Multi‐objective Optimal Configuration Method for a Standalone Wind-Solar-Battery Hybrid Power System. IET Renew. Power Generation 11 (1), 194–202. doi:10.1049/iet-rpg.2016.0646

CrossRef Full Text | Google Scholar

Olfati-Saber, R., and Murray, R. (2004). Consensus Problems in Networks of Agents with Switching Topology and Time-Delays. IEEE Trans. Automatic Control. 49 (4), 1520–1533. doi:10.1109/tac.2004.834113

CrossRef Full Text | Google Scholar

Purba, V., Johnson, B. B., Rodriguez, M., Jafarpour, S., Bullo, F., and Dhople, S. V. (2019). Reduced-order Aggregate Model for Parallel-Connected Single-phase Inverters. IEEE Trans. Energ. Convers. 34 (2), 824–837. doi:10.1109/tec.2018.2881710

CrossRef Full Text | Google Scholar

Savino, H. J., dos Santos, C. R. P., Souza, F. O., Pimenta, L. C. A., de Oliveira, M., and Palhares, R. M. (2016). Conditions for Consensus of Multi-Agent Systems with Time-Delays and Uncertain Switching Topology. IEEE Trans. Ind. Electron. 63 (2), 1258–1267. doi:10.1109/tie.2015.2504043

CrossRef Full Text | Google Scholar

Schfer, B., Beck, C., Aihara, K., Witthaut, D., and Timme, M. (2018). Non-gaussian Power Grid Frequency Fluctuations Characterized by Levy-Stable Laws and Superstatistics. Nat. Energ. 3, 119–126.

Google Scholar

Seifullaev, R. E., and Fradkov, A. L. (2016). Event-Triggered Control of Sampled-Data Nonlinear Systems**This Work Was Supported by Saint Petersburg State University, (grant 6.38.230.2015) and by Government of Russian Federation, Grant 074-U01. The Lyapunov-Krasovskii Functional Based Analysis of Closed-Loop Switched System Was Performed in IPME RAS under Support of Russian Science Foundation (grant 14-29-00142). IFAC-PapersOnLine. 49 (14), 12–17. doi:10.1016/j.ifacol.2016.07.965

CrossRef Full Text | Google Scholar

Shen, B., Wang, Z., and Liu, X. (2012). Sampled-data Synchronization Control of Dynamical Networks with Stochastic Sampling. IEEE Trans. Automat. Contr. 57 (10), 2644–2650. doi:10.1109/tac.2012.2190179

CrossRef Full Text | Google Scholar

Su, M., Liu, Z., Sun, Y., Han, H., and Hou, X. (2018). Stability Analysis and Stabilization Methods of DC Microgrid with Multiple Parallel-Connected DC-DC Converters Loaded by CPLs. IEEE Trans. Smart Grid 9 (1), 132–142. doi:10.1109/tsg.2016.2546551

CrossRef Full Text | Google Scholar

Wang, R., Sun, Q., Tu, P., Xiao, J., Gui, Y., and Wang, P. (2021). Reduced-order Aggregate Model for Large-Scale Converters with Inhomogeneous Initial Conditions in DC Microgrids. IEEE Trans. Energ. Convers. 36, 2473–2484. doi:10.1109/TEC.2021.3050434

CrossRef Full Text | Google Scholar

Wang, Y., Zheng, W. X., and Zhang, H. (2017). Dynamic Event-Based Control of Nonlinear Stochastic Systems. IEEE Trans. Automat. Contr. 62 (12), 6544–6551. doi:10.1109/tac.2017.2707520

CrossRef Full Text | Google Scholar

Zhang, H., Han, J., Wang, Y., and Jiang, H. (2019). $H_\infty$ Consensus for Linear Heterogeneous Multiagent Systems Based on Event-Triggered Output Feedback Control Scheme. IEEE Trans. Cybern. 49 (6), 2268–2279. doi:10.1109/tcyb.2018.2823362

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, H., Liang, H., Wang, Z., and Feng, T. (2017). Optimal Output Regulation for Heterogeneous Multiagent Systems via Adaptive Dynamic Programming. IEEE Trans. Neural Netw. Learn. Syst. 28 (1), 18–29. doi:10.1109/tnnls.2015.2499757

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Karady, G. G., and Ariaratnam, S. T. (2014). Optimal Allocation of CHP-Based Distributed Generation on Urban Energy Distribution Networks. IEEE Trans. Sustain. Energ. 5 (1), 246–253. doi:10.1109/tste.2013.2278693

CrossRef Full Text | Google Scholar

Zhou, J., Xu, Y., Sun, H., Wang, L., and Chow, M.-Y. (2020). Distributed Event-Triggered $H_\infty$ Consensus Based Current Sharing Control of DC Microgrids Considering Uncertainties. IEEE Trans. Ind. Inf. 16 (12), 7413–7425. doi:10.1109/tii.2019.2961151

CrossRef Full Text | Google Scholar

Zhu, W., Jiang, Z.-P., and Feng, G. (2014). Event-based Consensus of Multi-Agent Systems with General Linear Models. Automatica 50 (2), 552–558. doi:10.1016/j.automatica.2013.11.023

CrossRef Full Text | Google Scholar