Optimization Design of SNS Sensor Structural Parameters for Battery Expansion Monitoring

In this article, a method to improve refractive index (RI) sensitivity of single‐mode–no core–single‐mode fiber (SNS) sensor structure is addressed by optimization of geometric parameters of no-core fiber (NCF), which could be used to accurately measure the irreversible deformation of the battery expansion state caused by temperature change. From the perspective of temperature changing RI of the electrolyte solution, the impacts of diameter, length, and waveband on the performance of the fiber sensor have been discussed as RI measurement range is 1.340–1.390. After optimization, RI sensitivity can reach approximately 2,252.7 and 2037.3 nm/RIU with the length of 6.55 and 6.75 mm when the RI is from 1.380 to 1.390.

Introduction

Optical fiber sensor is widely applied in industry, medical treatment, energy storage, aerospace, and other fields for sensing measurement due to its anti-electromagnetic interference, small size, easy access, etc. Single-mode–multimode–single-mode fiber (SMS) structure based on multimode interference (MMI) has been used for strain (May-Arrioja et al., 2016; Zhou et al., 2008), temperature (Tripathi et al., 2009; Su et al., 2014; Han et al., 2014; Zhang et al., 2013; Li et al., 2006), humidity (An et al., 2014), and RI (Zhao et al., 2015; Zhang et al., 2020; Zhao et al., 2014) measurement in harsh environment. Compared with SMS, SNS structure can directly sense changes of its surrounding RI, and there is no need to strip or corrode the cladding of multimode fiber (MMF) using hydrofluoric acid. The geometric parameters of the waveguide structure based on MMI and RI measurement range have a great effect on sensing sensitivity (Qiang et al., 2011). The RI sensitivity of SNS reflective structure with the range of 1.330–1.380 is 141 nm/RIU (Zhou et al., 2015) and 327 nm/RIU when the reflective structure is based on single-mode–multimode structure (S-M) coating gold layer with small NCF diameter (Zhou et al., 2017). It illustrates again that RI sensitivity of SNS structure can be improved by optimizing NCF’s geometric parameters.

However, there are few reports on structural parameter optimization or the analysis process of SNS sensor. Meanwhile, in view of the huge research space for expansion and deformation of lithium batteries when overcharged, lithium batteries tend to have many internal chemical reactions before and after expansion to release a large amount of heat (Wang et al., 2014; Yan et al., 2018; Zla, et al., 2020; Maleki and Howard, 2006; Shin et al., 2002). The higher the temperature, the more obvious is the bulging degree of battery. If not controlled, it is easy to evolve into the phenomenon of lithium battery thermal runaway (Feng et al., 2017; Liang et al., 2021). Since the sensitivity of SNS structure with temperature change is insufficient in this study, the real-time monitoring of fine temperature changes cannot be performed using SNS structure (Chen et al., 2015). Therefore, the idea of predicting the battery expansion degree by monitoring the variation of RI caused by surrounding temperature with SNS structure is proposed.

Materials and Methods

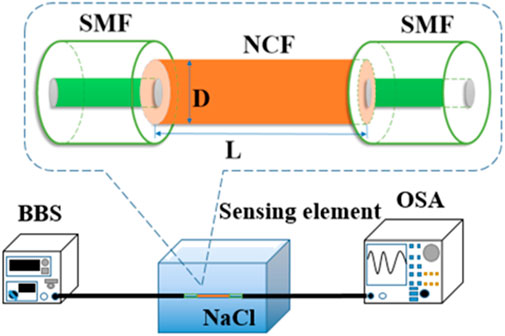
In order to improve RI sensitivity, the key point of SNS structural parameter optimization is to apply low-cost and easily accessible NaCl with concentration of 5–25%, instead of electrolyte solution to monitor the RI varying from 1.340 to 1.390 (Li et al., 2012; Wang et al., 2016). The schematic diagram of SNS structure sensing is shown in Figure 1.

FIGURE 1

FIGURE 1. Schematic diagram of SNS sensor structure.

In SNS structure, the single-mode fiber (SMF) is Corning SMF-28e with core diameter of 8.2 μm, cladding diameter of 125 μm, core RI of 1.45, and cladding RI of 1.444. Since the normalized power of SNS structure is higher when the length of NCF is a multiple of self-imaging period, the wavelength shift of the interference peak in the transmission spectrum can be easily observed at this time. And the smaller the NCF diameter, more energy will transmit into the surrounding liquid material in the form of evanescent wave (Wu et al., 2007; Tan et al., 2013). Besides, RI sensitivity is closely related to the sensing waveband. Therefore, SNS structure with higher RI sensitivity can be obtained within a certain waveband by continuously optimizing the geometric parameters of NCF.

At first, the initial diameter D_core of NCF is 125 μm, the appropriate initial length L₁ of NCF is 15 mm obtained from the self-imaging period. Then, the diameter D₁ is optimized according to RI sensitivity of SNS structure and the curve overlap of different RI in a certain diameter’s transmission spectrum. The values of L₁ and D₁ are large, and RI sensitivity is not ideal at this moment, so it is called the initial rough optimization. For the secondary meticulous optimization, the length L₂ is optimized based on the self-imaging period to achieve higher RI sensitivity of SNS structure when the diameter is D₁. On the premise of L₂ and D₁, a smaller diameter D₂ can be optimized again by analyzing RI sensitivity and the spectral line overlap phenomenon of transmission spectrum. Since SNS structure’s self-imaging period is different with different NCF diameters, length optimization is carried out again on the basis of D₂. Considering that L₂ is already short, the value of optimized length L₃ should be close to L₂, and then another diameter optimization can be avoided. After the geometrical parameters of NCF are finally determined, RI sensitivity is re-analyzed by changing waveband.

In addition, the effect of SMF parameters on RI sensitivity should also be considered. Then, the diameter of SMF and the difference of RI square between the core and cladding are finally simply analyzed according to the normalized frequency and numerical aperture.

Results and Discussion

NCF First Roughly Parameter Optimization Process

The initial diameter 125 μm is a common and easily available diameter (D_core) of NCF in SNS structure. RI of NCF’s core (n_core) changes with incident wavelength$\left(\lambda \right)$ and then n_core is 1.443989951 according to the Sellmeier function of Eq. 1 when $\text{λ}$ is 1550 nm (Malitson, 1965). Meanwhile, according to Eq. 2 (Ma et al., 2014), the length(L) of NCF is 14.556 mm when the number(P) of self-imaging period is 1, which is close to the simulation result of SNS monitor value with finite difference beam propagation method (FD-BPM) in Figure 2D. As a result, the minimum self-imaging length is approximately 15 mm.

$n_{core}^2\left(\lambda \right)=1+\frac{0.696{\lambda }^2}{{\lambda }^2-4.679\times {10}^{-3}}+\frac{0.408{\lambda }^2}{{\lambda }^2-1.351\times {10}^{-2}}+\frac{0.897{\lambda }^2}{{\lambda }^2-97.934},(1)$

$L=P\cdot \frac{n_{core}\cdot D_{core}^2}{\lambda }.(2)$

FIGURE 2

FIGURE 2. NCF normalized power of D_core variation: (A) 25 μm; (B) 30 μm; (C) 50 μm; (D) 125 μm.

Equation 2 shows that the self-imaging period increases with the increase in D_core, as shown in Figure 2. Since D_core involved in this article is less than 125 μm and L should meet the requirement that all fiber diameters mentioned have at least one self-imaging period within this length, then a multiple of 15 mm is an appropriate value and L₁ is determined to be 15 mm.

L₁ is set to be a constant, and D_core is yet to be optimized to obtain a higher RI sensitivity. RI is monitored according to wavelength shifts of interference peaks, and the diameter D₁ value is determined by the relationship between D_core and RI sensitivity.

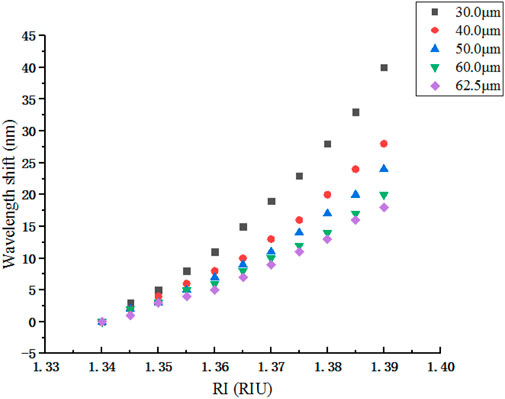
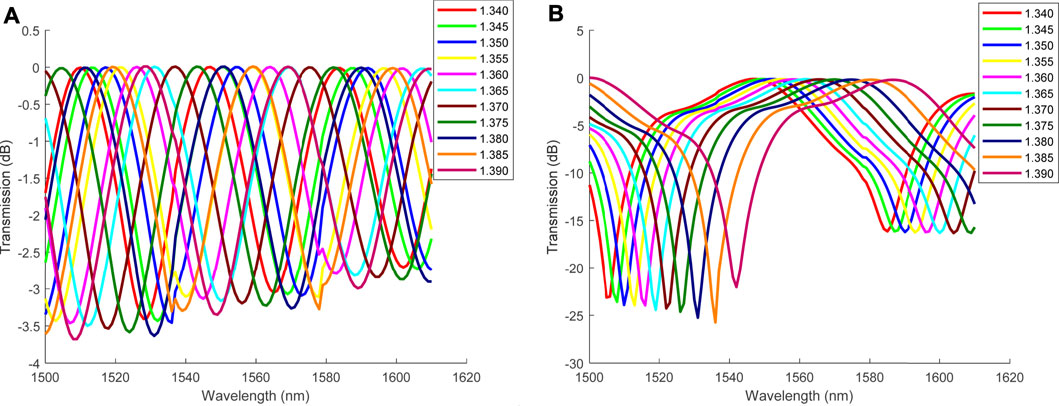
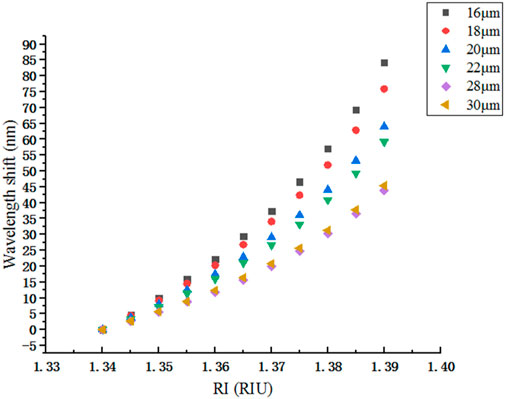
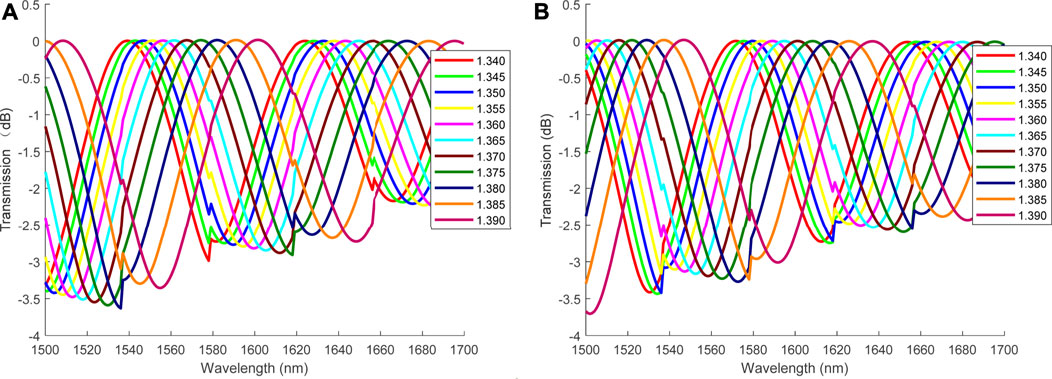
Figure 3 shows the effect of D_core on RI sensitivity when the L₁ value is 15 mm. Since the adjacent optimized diameter value varies greatly, it is difficult to find the same interference peak in a fixed waveband, but the general trend is the same, that is, the wavelength red shifts when RI increases, and RI sensitivity increases when D_core decreases. However, it is not that the smaller the D_core, the better will be the result. In the transmission spectrum of L₁ shown in Figure 4, the smaller the diameter, the higher will be the overlap ratio of different interference peaks, then it is difficult to distinguish different peaks. Therefore, D₁ is determined to be 30 μm according to Figure 4.

FIGURE 3

FIGURE 3. Wavelength shift of D_core variation when L₁ = 15 mm.

FIGURE 4

FIGURE 4. Transmission spectrum of D_core variation when L₁ = 15 mm: (A) 20 μm; (B) 30 μm.

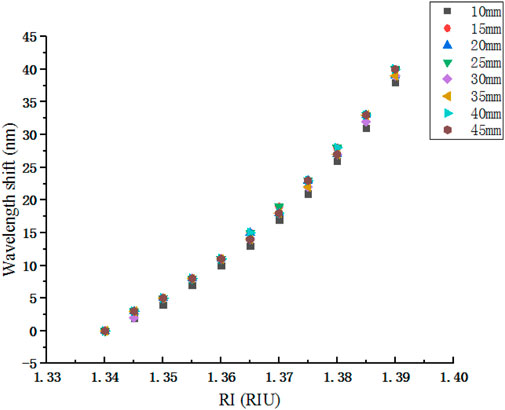
After preliminary parameter optimization, D₁ is obtained and then the effect of length on RI sensitivity is roughly analyzed. Figure 5 shows wavelength shifts of interference peaks with different lengths at D₁. It is worth noting that only appropriate but not the same interference peak is selected due to the large variation of length. The result indicated that the length has little effect on RI sensitivity when a diameter of NCF is relatively large. Then, in the next simulation process, we do not need to pay more attention to long length, just a few self-imaging periods is enough. Meanwhile, it proves that L₁ is an appropriate value in the previous simulation. This is the first rough geometric parameter optimization process of NCF in SNS structure, and then L₁ and D₁ are finally optimized to be 15 mm and 30 μm.

FIGURE 5

FIGURE 5. Wavelength shift of L variation when D₁ = 30 μm.

NCF Second Precisely Parameter Optimization Process

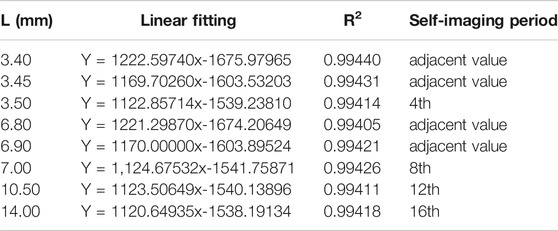
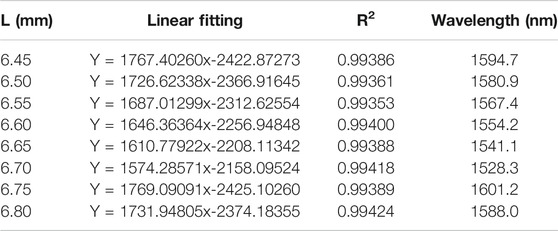
D₁ is set to be a constant, the length L₂ is yet to be optimized to make SNS structure achieve a higher RI sensitivity. The normalized power at D₁ is shown in Figure 2B, and then a multiple of self-imaging period and its adjacent values are selected to analyze the effect of NCF length on RI sensitivity, as shown in Figure 6A. Since there are many scattered points overlap in Figures 6A,B is the numerical refinement of partial RI range and linear fitting of RI sensitivity.

FIGURE 6

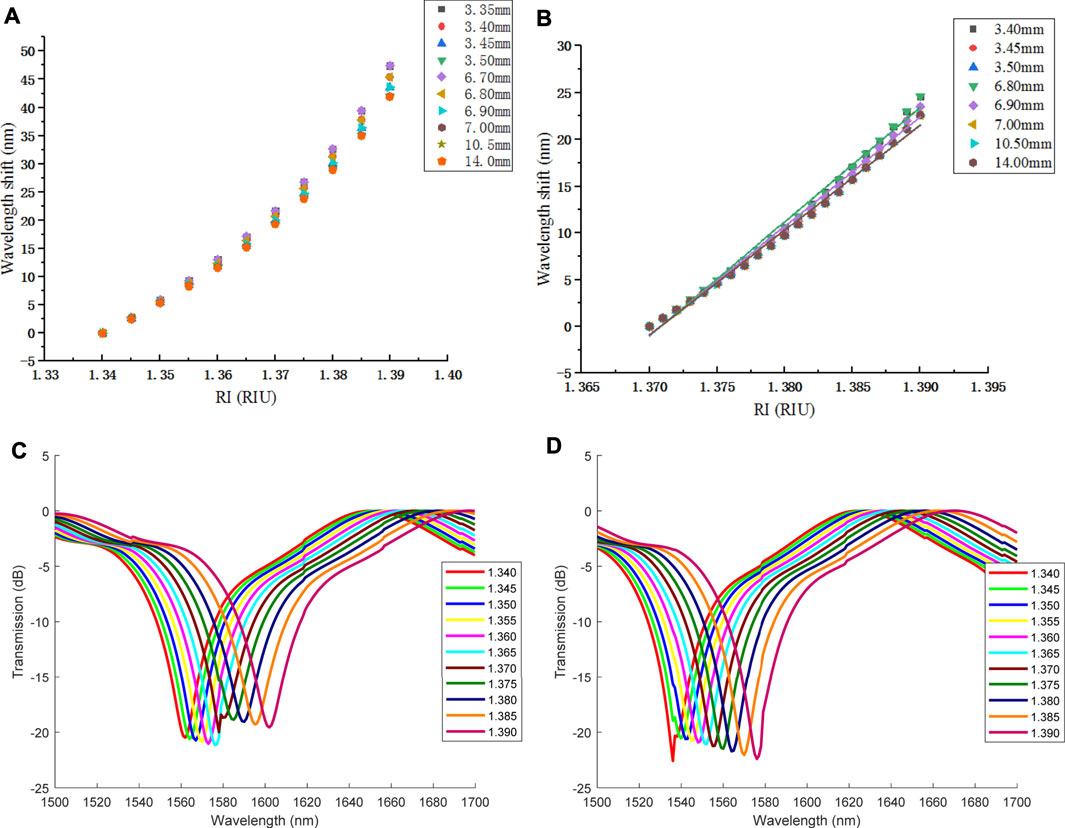
FIGURE 6. RI sensitivity of self-imaging length variation when D1 = 30 μm: (A) wavelength shift; (B) linear fitting; (C) transmission spectrum of 6.70 mm; (D) transmission spectrum of 6.80 mm.

Figure 6A shows that RI sensitivity corresponding to L of 3.35 and 6.70 mm is basically the same and relatively high, but the interference peak is approximately 1,700 nm when L is 6.70 mm in Figure 6C, which is not in an ideal waveband. For small diameter, the shorter the length, the more difficult will be to find a suitable interference peak for monitoring. Therefore, 3.35 mm is abandoned and it is considered that the length should not be too short.

In Figure 6B and Table 1 formed by linear fitting of scattered points, RI sensitivity obtained by taking the 4th, 8th, 12th, and 16th self-imaging period as L is basically identical, which is also applicable to the adjacent length of the 4th self-image period and the 8th. Therefore, SNS structures with the same normalized power value in Figure 2 have approximately consistent RI sensitivity. Although RI sensitivity of 3.40 mm is slightly higher than that of 6.80 mm, as mentioned before, the short length of 3.40 mm is abandoned in favor of 6.80 mm. Then, as shown in Figure 6D, L₂ of 6.80 mm is not a multiple of self-imaging period but an adjacent value.

TABLE 1

TABLE 1. Linear fitting of wavelength shift when D₁ = 30 μm.

Then L₂ is set to be a constant, and D₂, which is smaller than D₁, is yet to be optimized to obtain higher RI sensitivity of SNS structure. Because the smaller the NCF diameter, the more overlap occurs in the transmission spectrum. Therefore, during the re-optimization of D_core, 16 μm is selected as the minimum optical diameter of NCF. Figure 7 shows that 16 μm can achieve higher RI sensitivity.

FIGURE 7

FIGURE 7. Wavelength shift of D_core variation when L₂ = 6.80 mm.

However, in Figure 8A, there is still so much overlap that it is not easy to distinguish a complete interference peak when D_core is 16 μm. And the same as 18 μm, then D₂ is optimized to be 20 μm according to Figure 8B.

FIGURE 8

FIGURE 8. Transmission spectrum of D_core variation when L₂ = 6.80 mm: (A) 16 μm; (B) 20 μm.

D₂ is set to be a constant, and the appropriate length L₃ is yet to be optimized by calculating the self-imaging period corresponding to D₂ using Eq. 2. The length of the 18th self-imaging period is approximately 6.70 mm, which is close to L₂, so 6.70 mm is taken as the reference value for length optimization. In Figure 9A, adjacent lengths are also selected to find out the optimal length L₃ with higher RI sensitivity.

FIGURE 9

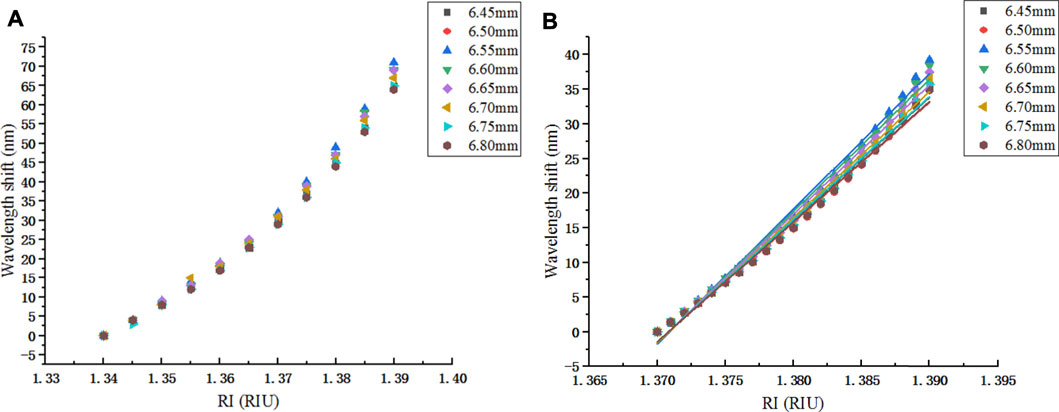
FIGURE 9. RI sensitivity of L variation at 1,500–1,700 nm when D₂ = 20 μm: (A) wavelength shift; (B) linear fitting.

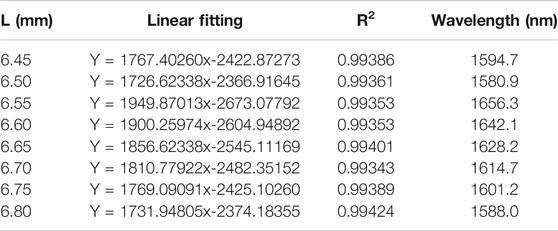
When RI is in the range of 1.340–1.370, it can be seen from Figure 9A that the change in length has little effect on RI sensitivity. So, only the RI range of 1.370–1.390 is analyzed specifically in Figure 9B. Meanwhile, the wavelength values of interference peaks corresponding to RI of 1.370 are marked in Table 2 obtained by linear fitting the data in Figure 9B. From Table 2, RI sensitivity is higher with L₃ of 6.55 mm.

TABLE 2

TABLE 2. Linear fitting of wavelength shift at 1,500–1,700 nm.

Effects of Waveband

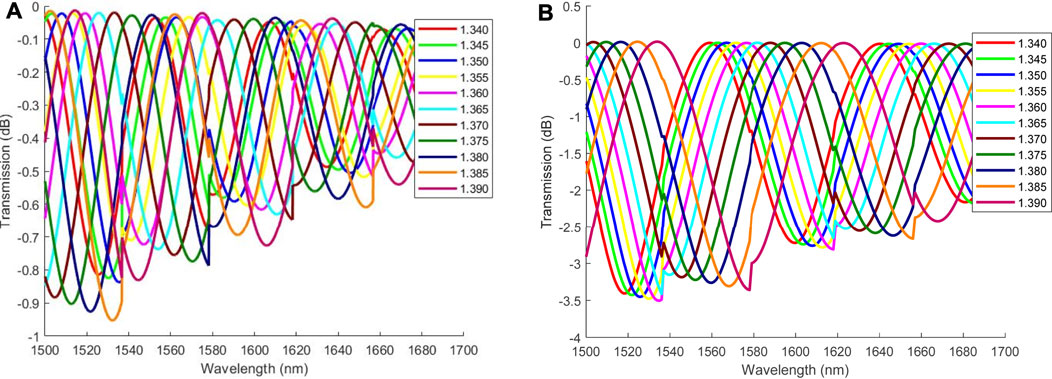
Sometimes, as shown in Figure 10A, the transmission spectrum contains more than one interference peak in the waveband of 1,500–1,700 nm. Figure 9A shows the wavelength monitoring results of the interference peak with better RI sensitivity corresponding to each length. Therefore, the next step is to analyze the effect of waveband on RI sensitivity.

FIGURE 10

FIGURE 10. Transmission spectrum of L variation when D₂ = 20 μm: (A) 6.55 mm; (B) 6.75 mm.

If the waveband is selected as 1,550–1,700 nm, only the five lengths of 6.55, 6.60, 6.65, 6.70, and 6.75 mm in Figure 9A can be used for complete RI monitoring, and RI sensitivity corresponding to L₃ of 6.55 mm is higher. If the waveband is 1,500–1,650 nm, RI sensitivity is shown in Figure 11A. Similarly, the RI range of 1.370–1.390 is analyzed in Figure 11B.

FIGURE 11

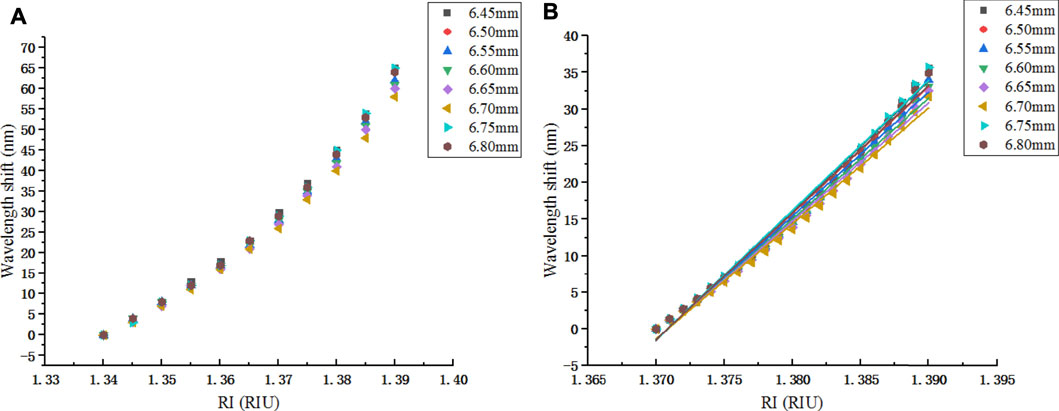
FIGURE 11. RI sensitivity of L variation at 1,500–1,650 nm when D₂ = 20 μm: (A) wavelength shift; (B) linear fitting.

Table 3 obtained by Figure 11B indicates that RI sensitivity is relatively higher when L₄ of NCF is 6.75 mm. The wavelength values with RI of 1.370 are marked in Table 3.

TABLE 3

TABLE 3. Linear fitting of wavelength shift at 1,500–1,650 nm.

Tables 2, 3 show that different wavebands limit the appearance of different interference peaks, thus affecting RI sensitivity of different lengths. In order to analyze the reason of higher RI sensitivity when the length of NCF is a certain value, the RI is set to 1.370 and wavelength is fixed to 1,656.3 and 1,601.2 nm, the self-imaging phenomenon is shown in Figures 12A,B, L₃ of 6.55 mm in Table 2, and L₄ of 6.75 mm in Table 3 are at the maximum normalized power in Figures 12A,B, so they are also consistent with the previous statement that length is related to the self-imaging period.

FIGURE 12

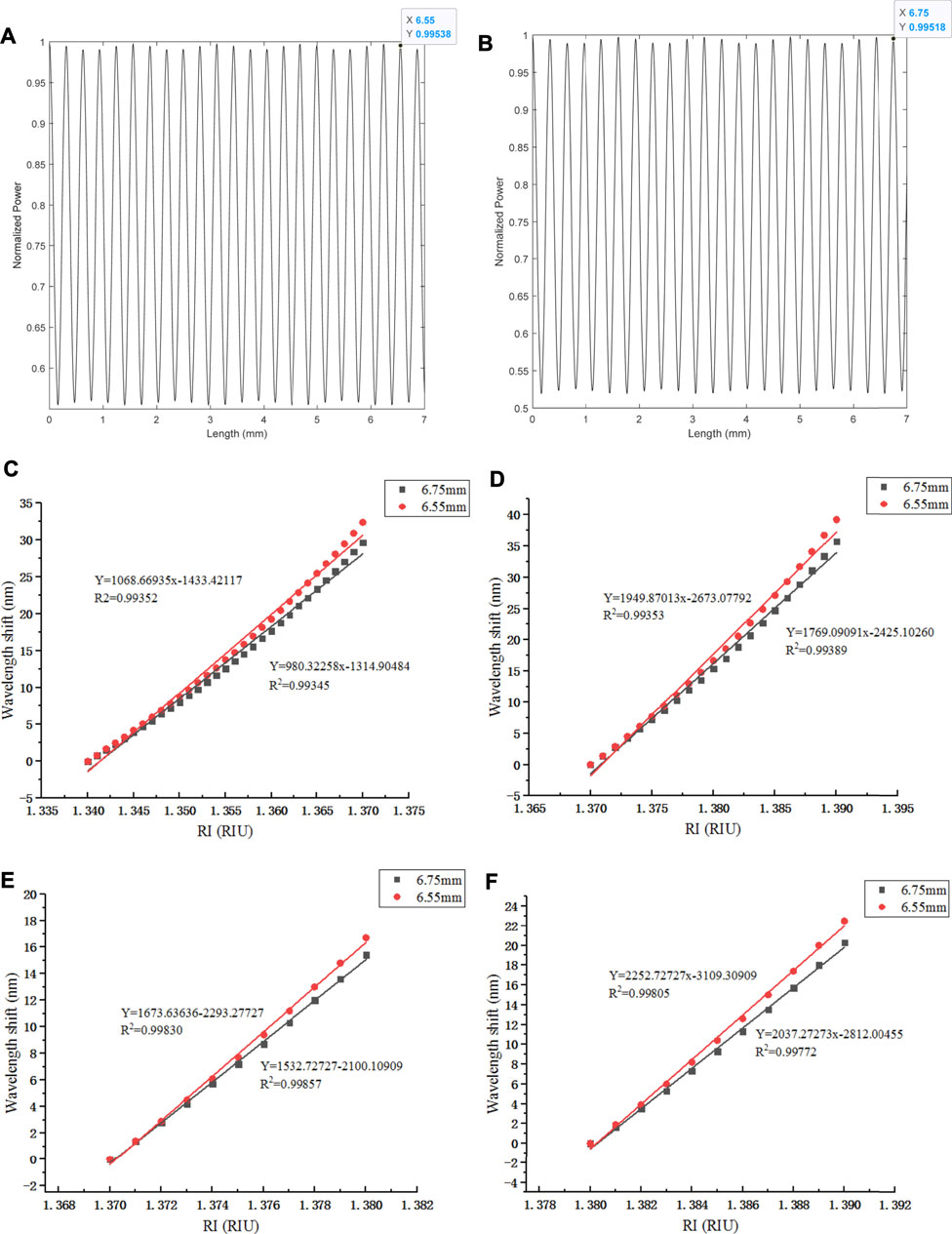
FIGURE 12. Comparison of NCF normalized power and RI sensitivity at L₃ and L₄: (A) NCF normalized power of L₃; (B) NCF normalized power of L₄; (C) comparison of RI sensitivity at 1.340–1.370; (D) comparison of RI sensitivity 1.370–1.390; (E) comparison of RI sensitivity 1.370–1.380; (F) comparison of RI sensitivity 1.380–1.390.

By comparing and analyzing L₃ and L₄ in Figures 12C,D, the results can be obtained that the RI sensitivity of L₃ and L₄ is approximately 1,068.7 and 980.3 nm/RIU when the RI range is 1.340–1.370, approximately 1949.9 and 1769.1 nm/RIU at 1.370–1.390. Because the higher the surrounding RI, the greater is the effect on RI sensitivity. Therefore, the scattered points in Figure 12D are fitted linearly again in Figures 12E,F.

RI varies from 1.380 to 1.390 and then RI sensitivity is approximately 2,252.7 nm/RIU when waveband is 1,550–1,700 nm and L₃ is 6.55 mm. Similarly, the RI sensitivity is approximately 2037.3 nm/RIU when waveband is 1,500–1,650 nm and L₄ is 6.75 mm. The resolution is 4.4 × 10⁻⁵ and 4.9 × 10⁻⁵, respectively. This is the whole process of NCF’ parameter optimization to obtain higher RI sensitivity.

SMF Parameter Optimization Process

After NCF optimization is completed, SMF parameter optimization is carried out. According to the guide mode cutoff condition in Eq. 3, in order to ensure that there is only one mode that exists in SMF, it is necessary to make the normalized frequency V < 2.405.

$V=\left(\frac{2\Pi }{{\lambda }_0}\right)a\sqrt{n_1^2-n_2^2}=k_{0}a{n}_1\sqrt{2▵}(3)$

$n_1$ and $n_2$are the RI of core and cladding, ${\text{k}}_0$ is the number of light waves in vacuum, $a$ is the diameter of core, ${\text{λ}}_0$ is wavelength in vacuum, and $\sqrt{2\text{Δ}}$ is numerical aperture (NA). Due to waveband needs to be considered and at least one interference peak is in it, the waveband is determined to be 1,500–1,700 nm to further study $a$, $n_1$, and $n_2$ of SMF.

Because the core diameter is generally between 8 and 10 μm and simulation is based on Corning SMF-28e, then the diameter varies from 8.20 to 9.00 μm when SMF is optimized. NA indicates coupling efficiency which is related to $n_1$ and $n_2$, so $n_1$ is fixed at 1.45 and $n_2$ varies in a small range from 1.444 to 1.449. Although the diameter and NA change, the transmission spectrum is basically the same as that in Figure 10. Therefore, the SMF remains Corning SMF-28e.

Conclusion

The geometric parameters of NCF are continuously optimized to obtain higher RI sensitivity. The final diameter of NCF is 20 μm when the RI range is 1.340–1.370 and 1.370–1.390, and RI sensitivity is approximately 1,068.7 and 1948.9 nm/RIU with the length of 6.55 mm, approximately 980.3 and 1769.1 nm/RIU with the length of 6.75 mm. Meanwhile, RI sensitivity can reach approximately 2,252.7 and 2037.3 nm/RIU when RI varies from 1.380 to 1.390, respectively. Although parameters of SMF are also considered to be optimized, the result shows that the effect on improving RI sensitivity of SNS structure can be ignored.

The structure optimization method proposed in this article can provide a reference for the optimal design of other mode interference structures. And SNS structure can have a great application prospect in monitoring battery expansion, especially when the surrounding RI is high.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

SX conceived the project. SX and ZW contributed to the analysis of the data. ZW, HY, and SJ performed the computations and wrote the article with support from JL and ZS. HY and SJ reviewed the article. All authors contributed to the scientific discussion and article revisions.

Funding

This work was supported by the Youth Science Found Project of National Natural Science Foundation of China (NSFC) (61703090), Enterprise Postdoctoral Innovation Project Foundation of Tianjin City No. 2016; CNPC Bohai Drilling Engineering Company Project of Long-term Fiber Sensor Monitoring for Gas Storage under Grant No. CS201607K.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors thank all the staff of the Advanced Sensor Research Institute of Northeast Electric Power University for their help in carrying out this work.

References

An, J., Jin, Y., Sun, M., and Dong, X. (2014). Relative Humidity Sensor Based on SMS Fiber Structure with Two Waist-Enlarged Tapers. IEEE Sensors J. 14 (8), 2683–2686. doi:10.1109/JSEN.2014.2313878

CrossRef Full Text | Google Scholar

Chen, Y., Wang, Y., Chen, R., Yang, W., Liu, H., Liu, T., et al. (2016). A Hybrid Multimode Interference Structure-Based Refractive index and Temperature Fiber Sensor. IEEE Sensors J. 16 (2), 331–335. doi:10.1109/JSEN.2015.2484346

CrossRef Full Text | Google Scholar

Feng, X., Ouyang, M., Liu, X., Lu, L., Xia, Y., and He, X. (2018). Thermal Runaway Mechanism of Lithium Ion Battery for Electric Vehicles: a Review. Energ. Storage Mater. 10, 246–267. doi:10.1016/j.ensm.2017.05.013

CrossRef Full Text | Google Scholar

Han, W., Tong, Z., and Cao, Y. (2014). Simultaneous Measurement of Temperature and Liquid Level Base on Core-Offset Singlemode-Multimode-Singlemode Interferometer. Opt. Commun. 321, 134–137. doi:10.1016/j.optcom.2013.12.078

CrossRef Full Text | Google Scholar

Li, B., Jiang, L., Wang, S., Mengmeng Wang, Q. C., and Yang, J. (2012). A New Mach-Zehnder Interferometer in a Thinned-Cladding Fiber Fabricated by Electric Arc for High Sensitivity Refractive index Sensing. Opt. Lasers Eng. 50 (6), 829–832. doi:10.1016/j.optlaseng.2012.01.024

CrossRef Full Text | Google Scholar

Li, E., Wang, X., and Zhang, C. (2006). Fiber-optic Temperature Sensor Based on Interference of Selective Higher-Order Modes. Appl. Phys. Lett. 89 (9), 091119. doi:10.1063/1.2344835

CrossRef Full Text | Google Scholar

Liang, H. B., Du, J. H., Hao, X., Yang, S. Z., Tu, R., and Zhang, R. C. (2021). A Review of Current Research on the Formation Mechanism of Lithium Batteries. Energ. Storage Sci. Technol. 10 (1), 647–657. doi:10.19799/j.cnki.2095-4239.2020.0358

CrossRef Full Text | Google Scholar

Liao, Z., Zhang, S., Zhao, Y., Qiu, Z., Li, K., Han, D., et al. (2020). Experimental Evaluation of Thermolysis-Driven Gas Emissions from LiPF6-Carbonate Electrolyte Used in Lithium-Ion Batteries. J. Energ. Chem. 49, 124–135. doi:10.1016/j.jechem.2020.01.030

CrossRef Full Text | Google Scholar

Ma, L., Qi, Y., Kang, Z., and Jian, S. (2014). All-Fiber Strain and Curvature Sensor Based on No-Core Fiber. IEEE Sensors J. 14 (5), 1514–1517. doi:10.1109/JSEN.2014.2298553

CrossRef Full Text | Google Scholar

Maleki, H., and Howard, J. N. (2006). Effects of Overdischarge on Performance and thermal Stability of a Li-Ion Cell. J. Power Sourc. 160 (2), 1395–1402. doi:10.1016/j.jpowsour.2006.03.043

CrossRef Full Text | Google Scholar

Malitson, I. H. (1965). Interspecimen Comparison of the Refractive Index of Fused Silica*,†. J. Opt. Soc. Am. 55, 1205–1208. doi:10.1364/JOSA.55.001205

CrossRef Full Text | Google Scholar

May-Arrioja, D. A., Ruiz-Perez, V. I., Bustos-Terrones, Y., and Basurto-Pensado, M. A. (2016). Fiber Optic Pressure Sensor Using a Conformal Polymer on Multimode Interference Device. IEEE Sensors J. 16 (7), 1956–1961. doi:10.1109/JSEN.2015.2510360

CrossRef Full Text | Google Scholar

Shin, J.-S., Han, C.-H., Jung, U.-H., Lee, S.-I., Kim, H.-J., and Kim, K. (2002). Effect of Li2CO3 Additive on Gas Generation in Lithium-Ion Batteries. J. Power Sourc. 109 (1), 47–52. doi:10.1016/S0378-7753(02)00039-3

CrossRef Full Text | Google Scholar

Su, J., Tong, Z., Cao, Y., and Zhang, W. (2014). High Sensitivity Multimode-Multimode-Multimode Structure Fiber Sensor Based on Modal Interference. Opt. Commun. 315, 112–115. doi:10.1016/j.optcom.2013.10.050

CrossRef Full Text | Google Scholar

Tan, Y. C., Lou, J., Xu, H. M., Huang, J., Shen, W. M., and Li, B. C. (2013). Simulation and Analysis of Sensitivity for Optical Fiber Evanescent Wave Absorbing Sensors. Yadian Yu Shengguang/Piezoelectrics and Acoustooptics. 35 (6), 810–813.

Google Scholar

Tripathi, S. M., Kumar, A., Varshney, R. K., Kumar, Y. B. P., Marin, E., and Meunier, J.-P. (2009). Strain and Temperature Sensing Characteristics of Single-Mode-Multimode-Single-Mode Structures. J. Lightwave Technol. 27 (13), 2348–2356. doi:10.1109/JLT.2008.2008820

CrossRef Full Text | Google Scholar

Wang, H. W., Deng, S., Xiao, H. Q., Zhao, H. F., and Wang, C. (2014). Research of Overcharge/overdischarge of Power Li-Ion Battery under Different Ambient Temperatures. Chin. J. Power Sourc. 38 (03), 431–433.

Google Scholar

Wang, Q., Li, C., Zhao, C., and Li, W. (2016). Guided-Mode-Leaky-Mode-Guided-Mode Fiber Interferometer and its High Sensitivity Refractive Index Sensing Technology. Sensors 16, 801. doi:10.3390/s16060801

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Q., Semenova, Y., Wang, P., and Farrell, G. (2011). High Sensitivity SMS Fiber Structure Based Refractometer - Analysis and experiment. Opt. Express 19 (9), 7937–7944. doi:10.1364/OE.19.007937

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Y., Deng, X., Li, F., and Zhuang, X. (2007). Less-mode Optic Fiber Evanescent Wave Absorbing Sensor: Parameter Design for High Sensitivity Liquid Detection. Sensors Actuators B: Chem. 122 (1), 127–133. doi:10.1016/j.snb.2006.05.026

CrossRef Full Text | Google Scholar

Yan, S., Deng, J., Bae, C., and Xiao, X. (2018). Thermal Expansion/shrinkage Measurement of Battery Separators Using a Dynamic Mechanical Analyzer. Polym. Test. 71, 65–71. doi:10.1016/j.polymertesting.2018.08.028

CrossRef Full Text | Google Scholar

Zhang, S., Wang, Z., Zhu, M., Li, L., Wang, S., Li, S., et al. (2020). A Compact Refractive index Sensor with High Sensitivity Based on Multimode Interference. Sensors Actuators A: Phys. 315, 112360. doi:10.1016/j.sna.2020.112360

CrossRef Full Text | Google Scholar

Zhang, Y., Tian, X., Xue, L., Zhang, Q., Yang, L., and Zhu, B. (2013). Super-High Sensitivity of Fiber Temperature Sensor Based on Leaky-Mode Bent SMS Structure. IEEE Photon. Technol. Lett. 25 (6), 560–563. doi:10.1109/LPT.2013.2245644

CrossRef Full Text | Google Scholar

Zhao, Y., Cai, L., and Hu, H.-F. (2015). Fiber-Optic Refractive Index Sensor Based on Multi-Tapered SMS Fiber Structure. IEEE Sensors J. 15, 6348–6353. doi:10.1109/JSEN.2015.245889311

CrossRef Full Text | Google Scholar

Zhao, Y., Cai, L., Li, X.-G., Meng, F.-c., and Zhao, Z. (2014). Investigation of the High Sensitivity RI Sensor Based on SMS Fiber Structure. Sensors Actuators A: Phys. 205, 186–190. doi:10.1016/j.sna.2013.10.023

CrossRef Full Text | Google Scholar

Zhou, D.-P., Wei, L., Liu, W.-K., Liu, Y., and Lit, J. W. Y. (2008). Simultaneous Measurement for Strain and Temperature Using Fiber Bragg Gratings and Multimode Fibers. Appl. Opt. 47 (10), 1668–1672. doi:10.1364/AO.47.001668

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, G., Wu, Q., Kumar, R., Ng, W. P., Liu, H., Niu, L., et al. (2017). High Sensitivity Refractometer Based on Reflective Smf-Small Diameter No Core Fiber Structure. Sensors 17, 1415. doi:10.3390/s17061415

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, X., Chen, K., Mao, X., peng, W., and Yu, Q. (2015). A Reflective Fiber-Optic Refractive index Sensor Based on Multimode Interference in a Coreless Silica Fiber. Opt. Commun. 340, 50–55. doi:10.1016/j.optcom.2014.11.030

CrossRef Full Text | Google Scholar