The Influence of Combined Turbulators on the Hydraulic-Thermal Performance and Exergy Efficiency of MWCNT-Cu/Water Nanofluid in a Parabolic Solar Collector: A Numerical Approach

The present research benefits from the finite volume method in investigating the influence of combined turbulators on the thermal and hydraulic exergy of a parabolic solar collector with two-phase hybrid MWCNT-Cu/water nanofluid. All parabolic geometries are produced using DesignModeler software. Furthermore, FLUENT software, equipped with a SIMPLER algorithm, is applied for analyzing the performance of thermal and hydraulic, and exergy efficiency. The Eulerian–Eulerian multiphase model and k-ε were opted for simulating the two-phase hybrid MWCNT-Cu/water nanofluid and turbulence model in the collector. The research was analyzed in torsion ratios from 1 to 4, Re numbers from 6,000 to 18,000 (turbulent flow), and the nanofluid volume fraction of 3%. The numerical outcomes confirm that the heat transfer and lowest pressure drop are relevant to the Re number of 18,000, nanofluid volume fraction of 3%, and torsion ratio of 4. Furthermore, in all torsion ratios, rising Re numbers and volume fraction lead to more exergy efficiency. The maximum value of 26.32% in the exergy efficiency was obtained at a volume fraction of 3% and a torsion ratio of 3, as the Re number goes from 60,000 to 18,000.

Introduction

Due to the improvements in industries, many researchers focused on boosting the heat transfer (Kalbasi, 2021; Giwa et al., 2020). The incorporation of nanomaterials or nanofluids is another important passive method that has attracted the attention of researchers owing to significant developments in the field of materials science in recent decades (Abedi et al., 2019; Keyvani et al., 2019; Parsa et al., 2020; Tian et al., 2020; Torosyan et al., 2020; Giwa et al., 2021; Parsa, 2021; Parsa et al., 2021). Vortex generators and nanofluids can be named as the passive methods. Leaking to the previous studies, employing vortex generators and nanofluids results in better efficiency of thermal systems (Sharifpur et al., 2018; Mansoury et al., 2020; Rostami et al., 2020; Yan et al., 2020; Zahmatkesh et al., 2021). Among all generators, combined turbulators are the newest forms of generators.

Pourmohamadian et al. (2019) considered the influence of Brownian movement models on the flow, the forced convection heat transfer, and entropy generations in a chamber numerically. Re numbers from 10 to 1,000 and the volume fraction of 0.04% were employed for the simulations. The finite volume method (FVM) with the SIMPLER algorithm was utilized as a solution to converge conservation equations. Rising the mean Nu number and entropy generations in all Re numbers was a clear outcome of rising the percentage of nanofluid volume fraction.

Nguyen et al. (2020) used triangular ribs as vortex generators and hybrid nanofluids to increase the heat transfer. The outcomes of simulation claimed that the heat transfer can be achieved at higher nanofluids in the presence of triangular ribs.

Aghaei et al. (2018) employed the numerical methods to see the effect of elliptical vertical and horizontal walls on entropy generation, heat transfer, and MWCNT/water nanofluid in a square chamber equipped with baffles. The finite volume method (FVM) with the SIMPLER algorithm with a Fortran code was utilized as a solution to converge conservation equations. The research was done on Re number from 0.01 to 100, the volume fraction of 0.08%, and at the constant Gr number of 104. The outputs showed that baffles result in more heat transfer and entropy generations in a horizontal position. Also, the maximum heat transfer was depicted in volume fraction of 1% and Ri = 0.01. Karimipour et al. (2020) employed hybrid nanofluids as an effective solution to enhance heat convection transfer in the presence of vortexes. They reported that there is a 79% rise in heat transfer in the maximum volume fraction of hybrid nanofluids. Fattahi et al. (2020) utilized numerical methods to investigate the various efficient types of materials to have more heat transfer in the design of heat exchangers. AlN, as a member of advanced ceramic, has a significant conductive heat transfer in the construction of heat exchanger. Small heat exchangers made by AlN were the main goals of their study. Based on the numerical outputs, AlN heat exchangers were 59% practical compared with their peers Al₂O₃.

Vajdi et al. (2020) benefited from BeO as an advanced ceramic that has a significant role in microthermal systems such as micro heat exchangers (MHE) by exerting numerical methods. These exchangers are a member of micro electrothermal systems that absorb a considerable amount of heat flux in a small volume. Owing to the high level of the MHEs, it has been proved that such applications are useful in supercomputers, optical systems, and other tools of high flux devices.

Dinesh Kumar et al. (2020) studied the thermal and hydraulic properties of a plate heat exchanger to increase heat transfer. They used a multi-objective whale optimization (MOWO) to optimize the plate heat exchanger’s parameter.

In another study, Acır et al. (2016) numerically calculated the effect of circular turbulators with different angles on the energy and exergy efficiency of a solar collector. According to the obtained results, the highest energy efficiency and exergy have been increased by 1.06 and 5.4%, respectively, when using circular turbulators.

Olfian et al. (2021) numerically considered the influence of phase change materials in a solar collector equipped with a corrugated U-shaped tube by the finite volume method. Their results show that the corrugated tube enhances the heat transfer by 21.55% compared to the smooth tube.

In addition, Hashemi Karouei et al., (2021) numerically examined the effect of a curved turbulator on the thermal performance of hybrid nanofluids in a heat exchanger. For this purpose, they used water-hybrid nanofluid (MWCNT-Fe₃O₄/water). Their results show that the thermal performance is directly proportional to the Reynolds number and nanoparticle concentration; in other words, it grows as they increase.

Panahi and Zamzamian (2017) experimentally explored the effect of a helical turbulator on the flow field and heat transfer in a heat exchanger. The results indicate that when a helical turbulator was used, the heat transfer increases significantly compared to the simple heat exchanger.

Numerically, Zhou et al. (2018) surveyed the heat transfer properties of oscillating heat pipes with graphene nanofluids by computational fluid dynamics. They found that in the presence of 2% nanofluid, the thermal resistance decreases by 83.6% compared to distilled water.

By using the finite volume method, Wongcharee and Eiamsa-ard (2011) evaluated the influence of twisted tapes with alternate axes on flow friction, heat transfer, and thermal performance in a round tube. In their study, they used Fluent to numerically simulate. Their results revealed that the heat transfer rate and friction coefficient of all twisted tapes are significantly higher than that of the channel without the twisted tape. Moreover, heat transfer increments with increasing Reynolds number and wing-chord ratios. Nguyen et al. (2020) and Yan et al. (2020) employed a wavy wall to make vortexes to improve heat transfer in a heat exchanger by hybrid nanofluids. According to their outputs, as the amplitude of wave rises, the strength of vortexes turns higher and results in more heat transfer. Júnior et al. (2019) numerically considered the performance of thermal parameters on exhaust gases of the cyclone preheater. They claim that, with the aid of heat recovery, the energy and exergy efficiency can be increased by 0.22 and 0.48, respectively. Geometric parameters also have a significant effect on the thermal performance.

Pal Singh Bhinder et al. (2012) simulated the effect of a semicircular cylinder on forced heat transfer within the channel. They found that the heat transfer grows with increasing Reynolds number and angle of incidences. In addition, the streamline curvature increases with a higher angle of incidence.

In an experimental study, Zarringhalam et al. (2016) tested the effect of nanoparticle volume fraction and Reynolds number on the heat transfer coefficient and pressure drop of nanofluid of a two-pipe reverse flow heat exchanger in a turbulent regime at Reynolds numbers 2,900–18,500. They used water–copper oxide nanofluids as the working fluid. They observed a higher heat transfer coefficient, average Nusselt number, and increase in the pressure drop in nanofluids compared with base fluids, and these increases were intensified by higher nanoparticle volume fraction. They also reported that the optimal conditions for the thermal performance factor are for 2% nanoparticle volume fraction at Reynolds number 3677. Srikanth et al. (2010) investigated the effect of triangular obstacles in a horizontal channel by applying the numerical software (Fluent). The K-epsilon turbulent model was employed for the turbulence model. The outputs reveal that the height of the obstacle results in more heat transfer.

Based on the aforementioned literature, the impact of combined turbulators has not been investigated on the hydraulic and thermal performance and exergy efficiency of two-phase hybrid MWCNT-Cu/water nanofluid of the parabolic solar collector. Consequently, in this research, a combined turbulator is checked on torsion ratios from 1 to 4, Re numbers from 6,000 to 18,000 (turbulent flow), and the nanofluid volume fraction of 1–3%.

Model Description

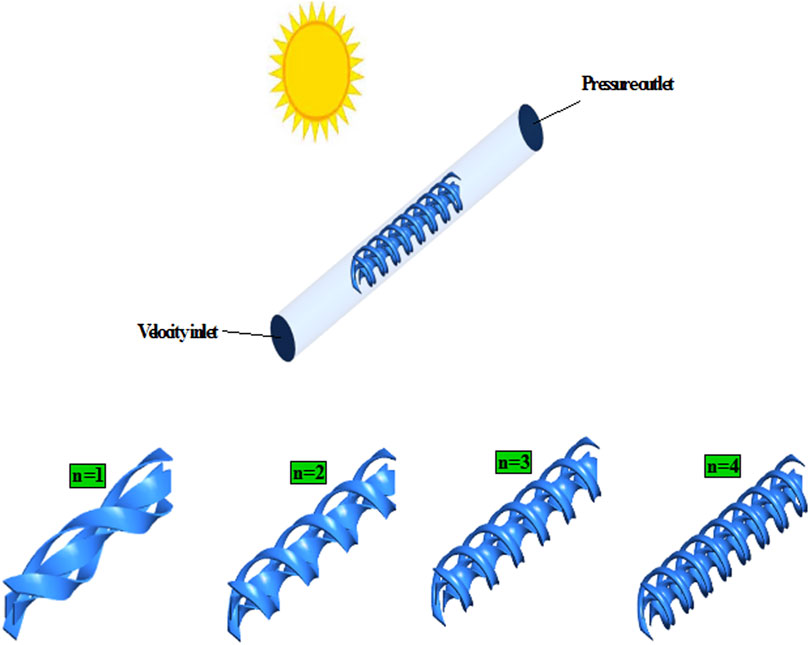
The geometry of solar collectors with combined turbulators is illustrated in Figure 1.

FIGURE 1

FIGURE 1. The geometries of various solar collector combined turbulators.

L and D are the length and diameter of the tube used in the collector, respectively. Moreover, n indicates the number of times the turbulator is twisted inside the tube.

The specification of solar collectors equipped with combined turbulators is listed in Table 1.

TABLE 1

TABLE 1. The specification of solar collector.

The Specification of Hybrid Nanofluid

The specification of the two-phase hybrid MWCNT-Cu/water nanofluid, which is passed in a solar collector, is also listed in Table 2.

TABLE 2

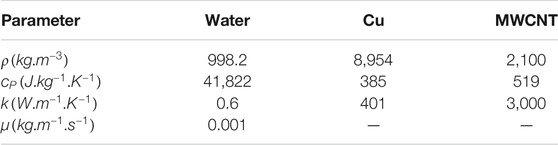
TABLE 2. The specification of water and nanoparticles (Abdollahzadeh et al., 2018; Nguyen et al., 2020).

Implication of Numerical Method

Applying numerical methods was always an affordable solution to analyze the behavior of the flow field and heat trasnfer (Razavi et al., 2019; Shiriny et al., 2019; Bahrami et al., 2020; Dinarvand et al., 2021). In the current research, FVM with the SIMPLER algorithm that couple pressure and velocity were employed to simulate. A two-phase Eulerian–Eulerian model was opted for simulating the hybrid MWCNT-Cu/water nanofluid in the collector (Behzadmehr et al., 2007; Hejazian et al., 2014). The advantage of this model is that each phase has a specific velocity field; further every volume fraction is benefited from different velocities (Sheikholeslami et al., 2016). Owing to turbulence flow, k-ε was applied for the turbulence model for the simulations. This is an appropriate model for solving the temperature and flow field of combined turbulators.

The equations that should be applied in the numerical methods are presented in Table 3 (Sheikholeslami et al., 2016):

TABLE 3

TABLE 3. Governing equations (Sheikholeslami et al., 2016).

The standard constants in the k-ε model are employed, $C_{\mu }=0.09$, $c_1=1.44$, $c_2=1.92$, ${\sigma }_k=1.00$, ${\sigma }_{\epsilon }=1.30$, and ${\sigma }_t=0.85$.

$Nu=\frac{h_f\cdot D_i}{k_f},(18)$

The pressure drop through inlet to outlet of test section is defined as follows:

$\Delta P=P_{av,inlet}-P_{av,outlet},(19)$

$f=\frac{2}{\left(\frac{L}{D_i}\right)}\frac{\Delta P}{{\rho }_{nf}\cdot u_m^2},(20)$

${\eta }_c=\frac{E_c}{I\cdot A}=\frac{Q_{in}\cdot {\rho }_{in}\cdot c_{p,in}\cdot \left(T_{out}-T_{in}\right)}{6\cdot {10}^4\cdot I\cdot A}.(21)$

Grid Independency

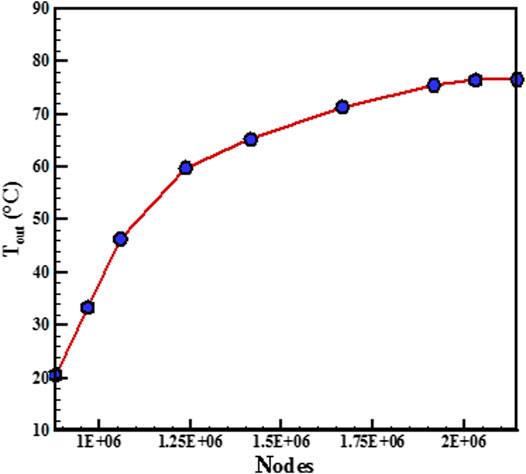
The temperature of hybrid nanofluid was calculated at the outlet of the solar collector so as to reach a suitable meshing network. The outcomes of various element numbers are exhibited in Figure 2. Based on the given outputs, the network with 1,926,154 was sufficient, since rising more elements results in a negligible change in the value of temperature.

FIGURE 2

FIGURE 2. The outcomes of various node numbers.

Verification

The geometry of Sheikholeslami et al. (2016) and their boundary conditions were utilized to validate. The consequence of their research is compared with the result of the present study in the mean Nu form in Figure 3. There is a slight 3.27% discrepancy in the outputs of the present study compared with Sheikholeslami et al. (2016), which claims that the current numerical methods can be reliable.

FIGURE 3

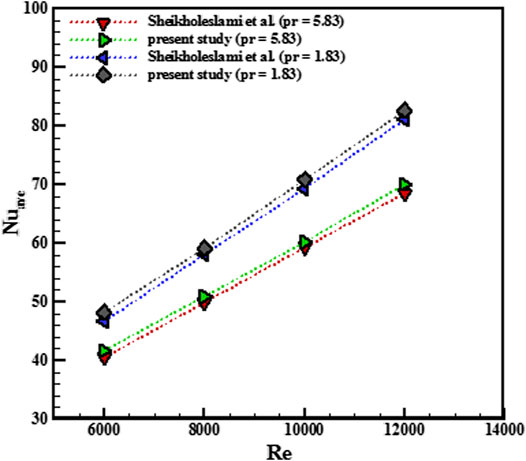
FIGURE 3. The outcomes of the present study compared with Sheikholeslami et al. (2016).

Results and Discussion

The outputs of numerical results are offered in this section. First, the contours of pressure, velocity, and temperatures are presented for various torsion ratios of combined turbulators. Then, the contours of streamlines and vectors of flow are examined. Eventually, the results of mean Nu number, pressure drop, and the variations of performance exergy are discussed in different Re numbers, volume fractions, and torsion ratios of combined turbulators in the parabolic solar collector.

The contours of pressure for Re = 18,000, φ = 3%, and torsion ratios of a) n = 1, b) n = 2, c) n = 3, and d) n = 4 are depicted in Figure 4. The density of streamlines rises with the increase of the torsion ratio of the combined turbulator in the solar collector; so this leads to a high value of pressure in the parabolic solar collector. The two-phase hybrid nanofluid rotates between the blades of the turbulator, which leads to more density of streamlines and heat transfer. There is a stagnation point in the hitting of the fluid at the combined turbulator which leads to the whole velocity transfer to the pressure. As the flow passes through the turbulators, there is a gradual decrease in the figure for the pressure.

FIGURE 4

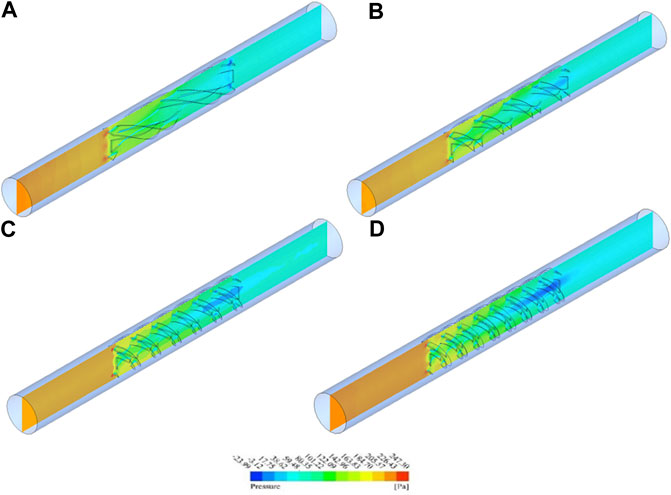
FIGURE 4. The distribution of pressure field at torsion ratios of (A)n = 1, (B)n = 2, (C)n = 3, and (D)n = 4.

The distribution of velocity for Re = 18,000, φ = 3%, and torsion ratios of a) n = 1, b) n = 2, c) n = 3 and d) n = 4 is exhibited in Figure 5. As it is obvious from the velocity field, more compression of streamlines can be achieved with the increase in the torsion ratio of the combined turbulator in the solar collector. So this leads to a considerable velocity. The separation flow occurs, as the flow impacts the combined turbulators, which leads to the formation of vortices, and these vortexes start to rotate. Consequently, heat transfer sees a considerable improvement, as the no-slip condition is considered for the whole inner wall, the fluid attached to the wall, therefore, the velocity is minimum in the vicinity of the wall of the collector and reached its maximum value at the central.

FIGURE 5

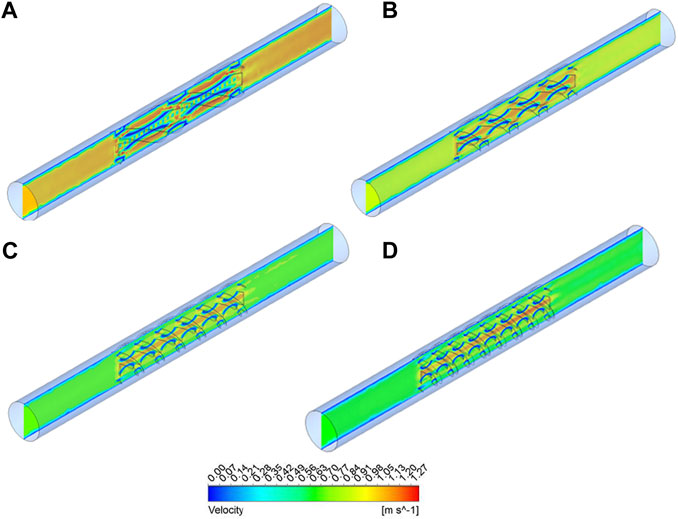
FIGURE 5. The distribution of velocity at torsion ratios of (A)n = 1, (B)n = 2, (C)n = 3, and (D)n = 4.

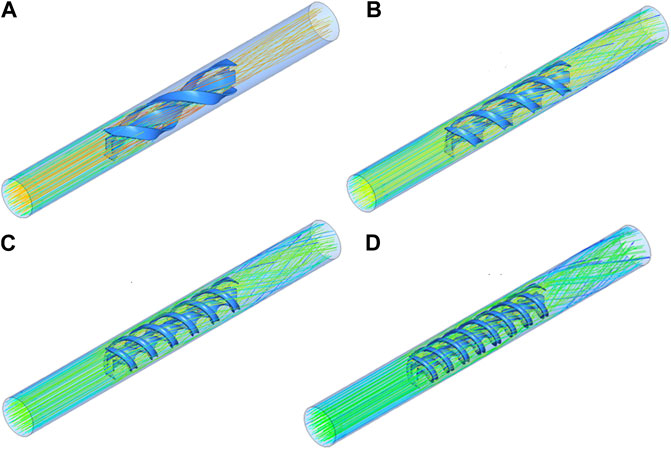
The contours of streamlines for Re = 18,000, φ = 3%, and torsion ratios of a) n = 1, b) n = 2, c) n = 3 and d) n = 4 are exhibited in Figure 6. As it is vividly shown, rising the torsion ratio of the combined turbulator brings about the lower streamlines’ density in the first time of the impact. As it was mentioned, rising the torsion ratio results in more velocity at the initial moment which hits the curved turbulator that leads to compression of more streamlines. The distribution of temperature and three-dimensional vectors that show the direction of the flow for the same conditions of the Re number, φ, and torsion ratios are illustrated in Figures 7, 8, respectively. The vectors of streamlines experience a substantial rise as a result of more torsion ratio.

FIGURE 6

FIGURE 6. The streamlines at torsion ratios of (A)n = 1, (B)n = 2, (C)n = 3, and (D)n = 4.

FIGURE 7

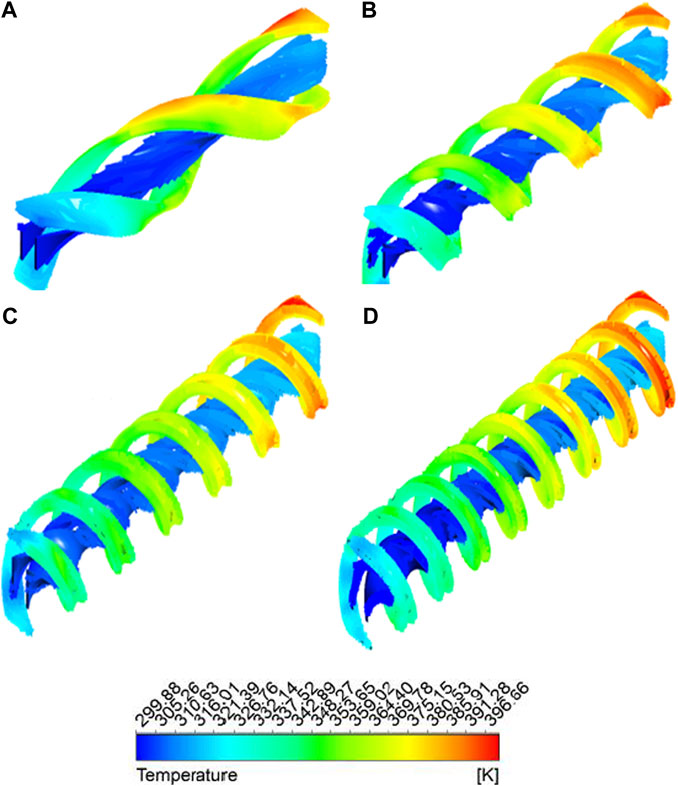
FIGURE 7. The distribution of temperature at torsion ratios of (A)n = 1, (B)n = 2, (C)n = 3, and (D)n = 4.

FIGURE 8

FIGURE 8. The vectors of flow at Re = 18,000, φ = 3%, and torsion ratios of (A)n = 1, (B)n = 2, (C)n = 3, and (D)n = 4.

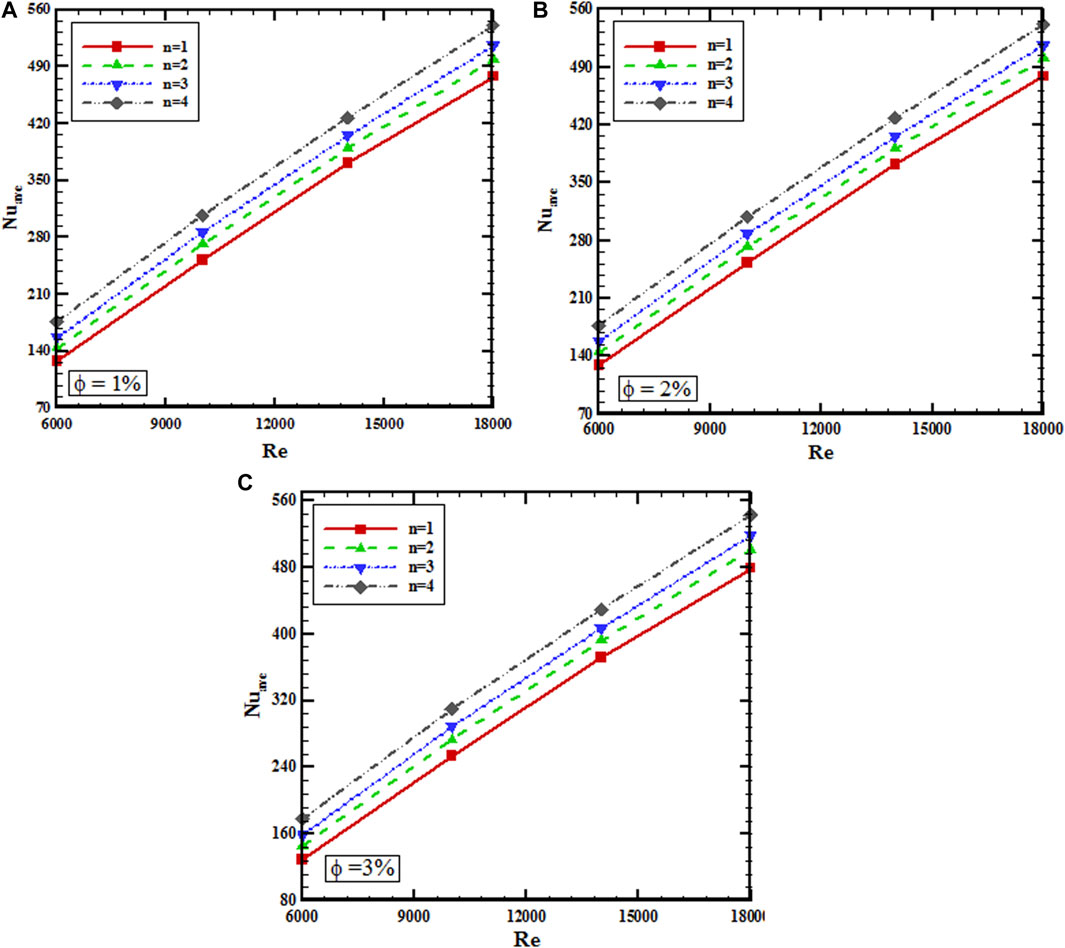
The variation of mean Nu number for different Re numbers and volume fractions is exhibited in Figure 9. The heat transfer sees a substantial improvement as a result of rising the values of Re numbers, torsion ratios, and volume fraction of hybrid nanofluids in all cases. This figure confirms that at Re = 18,000 and φ = 1%, rising the torsion ratio to 4 brings about 13.17% enhancement in heat transfer. The figure for φ = 3% at the same condition is 15.29%. For mean Nu number, rising Re numbers from 6,000 to 18,000 has a considerable growth of 269.25% at φ = 3% and a torsion ratio of 1. This growth is 244.18, 226.05, and 204.09% for torsion ratios of 2, 3, and 4, respectively.

FIGURE 9

FIGURE 9. The variations of mean Nu number at (A)φ = 1%, (B)φ = 2%, (C)φ = 3%.

Figure 10 exhibits the variation of pressure drop for different Re numbers and volume fractions. A significant pressure drop can be seen owing to increasing the figures for the Re number, torsion ratio, and volume fraction of hybrid nanofluid in all cases of combined turbulators as a result of higher flow stagnation of two-phase hybrid nanofluid, which impacts the blades at the initial time. Besides, rising the percentage of volume fraction of hybrid nanofluid causes more pressure loss in the parabolic solar collector. The highest amount of pressure loss is related to Re = 1800, φ = 3%, and a torsion ratio of 4, and the lowest extent of pressure loss is related to Re = 6,000, φ = 1%, and a torsion ratio of 1. At φ = 3%, rising Re numbers from 6,000 to 18,000 brings about 543.51, 497.79, 401.65, and 289.86% increase in pressure drop at torsion ratios of 1, 2, 3, and 4, respectively.

FIGURE 10

FIGURE 10. The variations of pressure drop at (A)φ = 1%, (B)φ = 2%, and (C)φ = 3%.

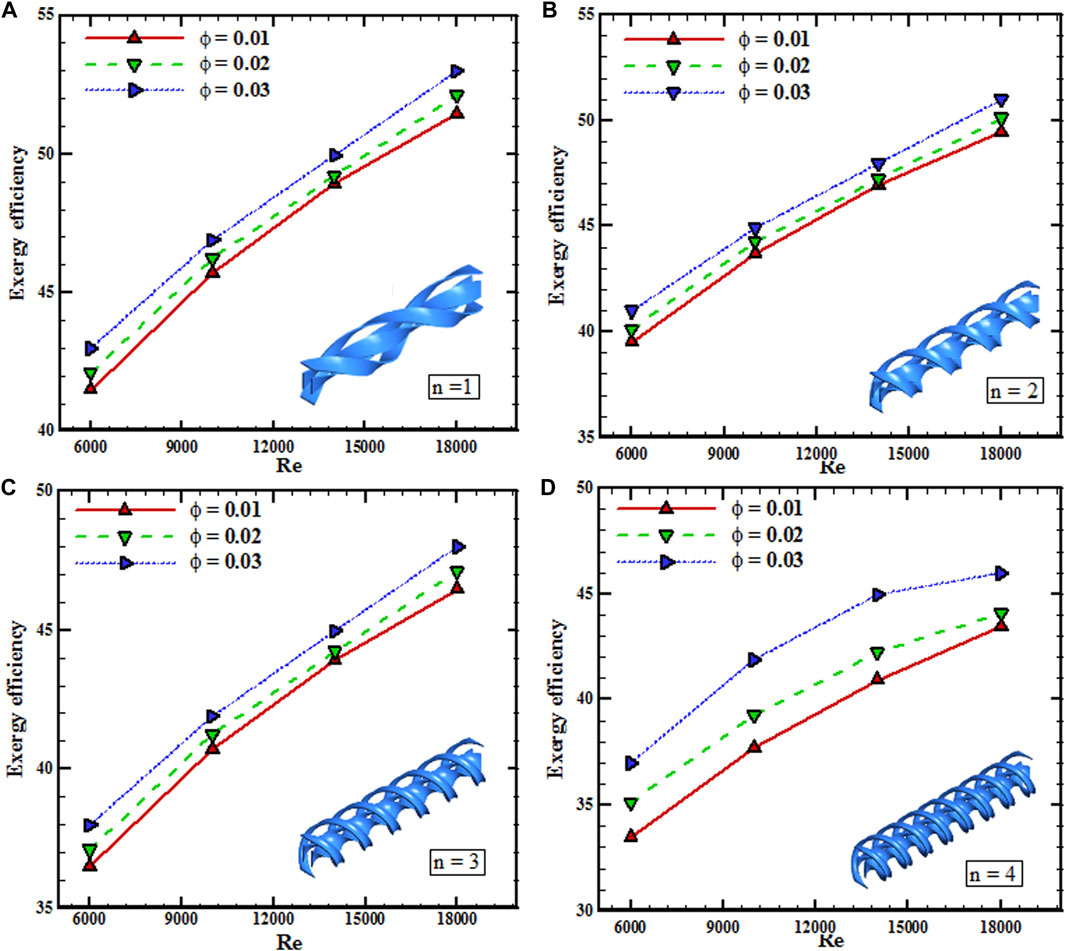
The exergy efficiency of the collector is displayed in Figure 11 at all Re numbers, volume fractions, and torsion ratios. In all torsion ratios, adding nanofluid volume fraction and rising Re numbers bring about higher exergy performance. At φ = 3%, as the Re number goes from 6,000 to 18,000, there is a 23.26, 24.4, 26.32, and 24.33% enhancement in the exergy efficiency at n = 1,2,3, and 4, respectively.

FIGURE 11

FIGURE 11. The variations of exergy efficiency (A)n = 1, (B)n = 2, (C)n = 3, and (D)n = 4.

Conclusion

The present study benefits from the finite volume method in investigating the influence of combined turbulators on the thermal and hydraulic exergy of a parabolic solar collector with two-phase hybrid MWCNT-Cu/water nanofluid. The Eulerian–Eulerian multiphase model and k-ε were opted for simulating the two-phase hybrid MWCNT-Cu/water nanofluid and turbulence model in the collector. The study was analyzed in torsion ratios from 1 to 4, Re numbers from 6,000 to 18,000 (turbulent flow), and the nanofluid volume fraction of 3%.

The highlighted outcomes from this study are as follows:

• In all torsion ratios, adding nanofluid volume fraction and rising Re numbers bring about higher exergy performance.

• The maximum value of heat transfer is related to higher Re number, torsion ratio, and volume fraction.

• The minimum value of heat transfer is related to the least Re number, torsion ratio, and volume fraction.

• Rising Re numbers from 6,000 to 18,000 has a considerable growth of 269.25% at φ = 3% and torsion ratio of 1.

• At φ = 3%, as the Re number goes from 6,000 to 18,000, there is a 23.26, 24.4, 26.32, and 24.33% enhancement in the exergy efficiency at n = 1,2,3, and 4, respectively.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

YK: writing and methodology. AM: conceptualization and software. RA: writing and validation.

Funding

This work was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under grant nos. (D1432-22–135).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors, therefore, acknowledge with thanks the Deanship of Scientific Research (DSR) technical and financial support.

References

Abdollahzadeh, M., Sedighi, A. A., and Esmailpour, M. (2018). Stagnation point Flow of Nanofluids towards Stretching Sheet through a Porous Medium with Heat Generation. J. Nanofluids 7, 149–155. doi:10.1166/jon.2018.1431

CrossRef Full Text | Google Scholar

Abedi, M., Moskovskikh, D. O., and Mukasyan, A. S. (2019). “Reactive Flash Spark Plasma Sintering of Alumina Reinforced by Silicon Carbide Nanocomposites: Physicochemical Study,” in International Symposium on Self-Propagating High-Temperature Synthesis, (XV), 8, 2018. Moscow, Russia, 10–11.

Google Scholar

Acır, A., Ata, İ., and Şahin, İ. (2016). Energy and Exergy Analyses of a New Solar Air Heater with Circular-type Turbulators Having Different Relief Angles. Int. J. Exergy 20, 11–31.

Google Scholar

Aghaei, A., Sheikhzadeh, G. A., Goodarzi, M., Hasani, H., Damirchi, H., and Afrand, M. (2018). Effect of Horizontal and Vertical Elliptic Baffles inside an Enclosure on the Mixed Convection of a MWCNTs-Water Nanofluid and its Entropy Generation. The Eur. Phys. J. Plus 133, 486. doi:10.1140/epjp/i2018-12278-4

CrossRef Full Text | Google Scholar

Bahrami, D., Nadooshan, A. A., and Bayareh, M. (2020). Numerical Study on the Effect of Planar normal and Halbach Magnet Arrays on Micromixing. Int. J. Chem. Reactor Eng. 18(9), 20200080. doi:10.1515/ijcre-2020-0080

CrossRef Full Text | Google Scholar

Behzadmehr, A., Saffar-Avval, M., and Galanis, N. (2007). Prediction of Turbulent Forced Convection of a Nanofluid in a Tube with Uniform Heat Flux Using a Two Phase Approach. Int. J. Heat Fluid Flow 28, 211–219. doi:10.1016/j.ijheatfluidflow.2006.04.006

CrossRef Full Text | Google Scholar

Dinarvand, M., Abolhasani, M., Hormozi, F., and Bahrami, Z. (2021). Cooling Capacity of Magnetic Nanofluid in Presence of Magnetic Field Based on First and Second Laws of Thermodynamics Analysis. Energy Sourc. A: Recovery, Utilization, Environ. Effects, 1–17. doi:10.1080/15567036.2021.1872746

CrossRef Full Text | Google Scholar

Dinesh Kumar, S., Chandramohan, D., Purushothaman, K., and Sathish, T. (2020). Optimal Hydraulic and thermal Constrain for Plate Heat Exchanger Using Multi Objective Wale Optimization. Mater. Today Proc. 21, 876–881. doi:10.1016/j.matpr.2019.07.710

CrossRef Full Text | Google Scholar

Fattahi, M., Vaferi, K., Vajdi, M., Sadegh Moghanlou, F., Sabahi Namini, A., and Shahedi Asl, M. (2020). Aluminum Nitride as an Alternative Ceramic for Fabrication of Microchannel Heat Exchangers: a Numerical Study. Ceramics Int. 46, 11647–11657. doi:10.1016/j.ceramint.2020.01.195

CrossRef Full Text | Google Scholar

Giwa, S. O., Sharifpur, M., Ahmadi, M. H., and Meyer, J. P. (2020). A Review of Magnetic Field Influence on Natural Convection Heat Transfer Performance of Nanofluids in Square Cavities. J. Therm. Anal. Calorim. doi:10.1007/s10973-020-09832-3

CrossRef Full Text | Google Scholar

Giwa, S. O., Sharifpur, M., Ahmadi, M. H., Sohel Murshed, S. M., and Meyer, J. P. (2021). Experimental Investigation on Stability, Viscosity, and Electrical Conductivity of Water-Based Hybrid Nanofluid of MWCNT-Fe2O3. Nanomaterials 11, 136. doi:10.3390/nano11010136

CrossRef Full Text | Google Scholar

Hashemi Karouei, S. H., Ajarostaghi, S. S. M., Gorji-Bandpy, M., and Hosseini Fard, S. R. (2021). Laminar Heat Transfer and Fluid Flow of Two Various Hybrid Nanofluids in a Helical Double-Pipe Heat Exchanger Equipped with an Innovative Curved Conical Turbulator. J. Therm. Anal. Calorim. 143, 1455–1466. doi:10.1007/s10973-020-09425-0

CrossRef Full Text | Google Scholar

Hejazian, M., Moraveji, M. K., and Beheshti, A. (2014). Comparative Study of Euler and Mixture Models for Turbulent Flow of Al2O3 Nanofluid inside a Horizontal Tube. Int. Commun. Heat Mass Transfer 52, 152–158. doi:10.1016/j.icheatmasstransfer.2014.01.022

CrossRef Full Text | Google Scholar

Júnior, E. P. B., Arrieta, M. D. P., Arrieta, F. R. P., and Silva, C. H. F. (2019). Assessment of a Kalina Cycle for Waste Heat Recovery in the Cement Industry. Appl. Therm. Eng. 147, 421–437. doi:10.1016/j.applthermaleng.2018.10.088

CrossRef Full Text | Google Scholar

Kalbasi, R. (2021). Introducing a Novel Heat Sink Comprising PCM and Air - Adapted to Electronic Device thermal Management. Int. J. Heat Mass Transfer 169, 120914. doi:10.1016/j.ijheatmasstransfer.2021.120914

CrossRef Full Text | Google Scholar

Karimipour, A., Bahrami, D., Kalbasi, R., and Marjani, A. (2020). Diminishing Vortex Intensity and Improving Heat Transfer by Applying Magnetic Field on an Injectable Slip Microchannel Containing FMWNT/water Nanofluid. J. Therm. Anal. Calorim. 144. 2235–2246. doi:10.1007/s10973-020-10261-5

CrossRef Full Text | Google Scholar

Keyvani, N., Azarniya, A., Hosseini, H. R. M., Abedi, M., and Moskovskikh, D. (2019). Thermal Stability and Strain Sensitivity of Nanostructured Aluminum Titanate (Al2TiO5). Mater. Chem. Phys. 223, 202–208. doi:10.1016/j.matchemphys.2018.10.060

CrossRef Full Text | Google Scholar

Mansoury, D., Doshmanziari, F. I., Kiani, A., Chamkha, A. J., and Sharifpur, M. (2020). Heat Transfer and Flow Characteristics of Al2O3/Water Nanofluid in Various Heat Exchangers: Experiments on Counter Flow. Heat Transfer Eng. 41, 220–234. doi:10.1080/01457632.2018.1528051

CrossRef Full Text | Google Scholar

Nguyen, Q., Bahrami, D., Kalbasi, R., and Bach, Q. V. (2020). Nanofluid Flow through Microchannel with a Triangular Corrugated wall: Heat Transfer Enhancement against Entropy Generation Intensification, Math. Methods Appl. Sci. doi:10.1002/mma.6705

CrossRef Full Text | Google Scholar

Olfian, H., Ajarostaghi, S. S. M., Farhadi, M., and Ramiar, A. (2021). Melting and Solidification Processes of Phase Change Material in Evacuated Tube Solar Collector with U-Shaped Spirally Corrugated Tube. Appl. Therm. Eng. 182, 116149. doi:10.1016/j.applthermaleng.2020.116149

CrossRef Full Text | Google Scholar

Pal Singh Bhinder, A., Sarkar, S., and Dalal, A. (2012). Flow over and Forced Convection Heat Transfer Around a Semi-circular cylinder at Incidence. Int. J. Heat Mass Transfer 55, 5171–5184. doi:10.1016/j.ijheatmasstransfer.2012.05.018

CrossRef Full Text | Google Scholar

Panahi, D., and Zamzamian, K. (2017). Heat Transfer Enhancement of Shell-And-Coiled Tube Heat Exchanger Utilizing Helical Wire Turbulator. Appl. Therm. Eng. 115, 607–615. doi:10.1016/j.applthermaleng.2016.12.128

CrossRef Full Text | Google Scholar

Parsa, S. M., Rahbar, A., Koleini, M. H., Davoud Javadi, Y., Afrand, M., Rostami, S., et al. (2020). First Approach on Nanofluid-Based Solar Still in High Altitude for Water Desalination and Solar Water Disinfection (SODIS). Desalination 491, 114592. doi:10.1016/j.desal.2020.114592

CrossRef Full Text | Google Scholar

Parsa, S. M. (2021). Reliability of thermal Desalination (Solar Stills) for Water/wastewater Treatment in Light of COVID-19 (Novel Coronavirus "SARS-CoV-2") Pandemic: What Should Consider? Desalination 512, 115106. doi:10.1016/j.desal.2021.115106

PubMed Abstract | CrossRef Full Text | Google Scholar

Parsa, S. M., Yazdani, A., Dhahad, H., Alawee, W. H., Hesabi, S., Norozpour, F., et al. (2021). Effect of Ag, Au, TiO2 Metallic/metal Oxide Nanoparticles in Double-Slope Solar Stills via Thermodynamic and Environmental Analysis. J. Clean. Prod. 311, 127689. doi:10.1016/j.jclepro.2021.127689

CrossRef Full Text | Google Scholar

Pourmohamadian, H., Sheikhzadeh, G. A., Aghaei, A., Ehteram, H., and Adibi, M. (2019). Investigating the Effect of Brownian Motion Models on Heat Transfer and Entropy Generation in Nanofluid Forced Convection. Therm. Sci. 23, 485–496.

Google Scholar

Razavi, S. E., Farhangmehr, V., and Babaie, Z. (2019). Numerical Investigation of Hemodynamic Performance of a Stent in the Main branch of a Coronary Artery Bifurcation. Bioimpacts 9, 97–103. doi:10.15171/bi.2019.13

PubMed Abstract | CrossRef Full Text | Google Scholar

Rostami, S., Aghakhani, S., Hajatzadeh Pordanjani, A., Afrand, M., Cheraghian, G., Oztop, H. F., et al. (2020). A Review on the Control Parameters of Natural Convection in Different Shaped Cavities with and without Nanofluid. Processes 8, 1011. doi:10.3390/pr8091011

CrossRef Full Text | Google Scholar

Sharifpur, M., Solomon, A. B., Ottermann, T. L., and Meyer, J. P. (2018). Optimum Concentration of Nanofluids for Heat Transfer Enhancement under Cavity Flow Natural Convection with TiO2 - Water. Int. Commun. Heat Mass Transfer 98, 297–303. doi:10.1016/j.icheatmasstransfer.2018.09.010

CrossRef Full Text | Google Scholar

Sheikholeslami, M., Gorji-Bandpy, M., and Ganji, D. D. (2016). Effect of Discontinuous Helical Turbulators on Heat Transfer Characteristics of Double Pipe Water to Air Heat Exchanger. Energ. Convers. Manage. 118, 75–87. doi:10.1016/j.enconman.2016.03.080

CrossRef Full Text | Google Scholar

Shiriny, A., Bayareh, M., Nadooshan, A. A., and Bahrami, D. (2019). Forced Convection Heat Transfer of Water/FMWCNT Nanofluid in a Microchannel with Triangular Ribs. SN Appl. Sci. 1, 1–11. doi:10.1007/s42452-019-1678-7

CrossRef Full Text | Google Scholar

Srikanth, S., Dhiman, A. K., and Bijjam, S. (2010). Confined Flow and Heat Transfer across a Triangular cylinder in a Channel. Int. J. Therm. Sci. 49, 2191–2200. doi:10.1016/j.ijthermalsci.2010.06.010

CrossRef Full Text | Google Scholar

Tian, X.-X., Kalbasi, R., Jahanshahi, R., Qi, C., Huang, H.-L., and Rostami, S. (2020). Competition between Intermolecular Forces of Adhesion and Cohesion in the Presence of Graphene Nanoparticles: Investigation of Graphene Nanosheets/ethylene Glycol Surface Tension. J. Mol. Liquids 311, 113329. doi:10.1016/j.molliq.2020.113329

CrossRef Full Text | Google Scholar

Torosyan, K. S., Sedegov, A. S., Kuskov, K. V., Abedi, M., Arkhipov, D. I., Kiryukhantsev‐Korneev, P. V., et al. (2020). Reactive, Nonreactive, and Flash Spark Plasma Sintering of Al 2 O 3/SiC Composites-A Comparative Study. J. Am. Ceram. Soc. 103, 520–530. doi:10.1111/jace.16734

CrossRef Full Text | Google Scholar

Vajdi, M., Shahedi Asl, M., Nekahi, S., Sadegh Moghanlou, F., Jafargholinejad, S., and Mohammadi, M. (2020). Numerical Assessment of Beryllium Oxide as an Alternative Material for Micro Heat Exchangers. Ceramics Int. 46, 19248–19255. doi:10.1016/j.ceramint.2020.04.263

CrossRef Full Text | Google Scholar

Wongcharee, K., and Eiamsa-ard, S. (2011). Heat Transfer Enhancement by Twisted tapes with Alternate-Axes and Triangular, Rectangular and Trapezoidal Wings. Chem. Eng. Process. Process Intensification 50, 211–219. doi:10.1016/j.cep.2010.11.012

CrossRef Full Text | Google Scholar

Yan, S.-R., Kalbasi, R., Nguyen, Q., and Karimipour, A. (2020). Sensitivity of Adhesive and Cohesive Intermolecular Forces to the Incorporation of MWCNTs into Liquid Paraffin: Experimental Study and Modeling of Surface Tension. J. Mol. Liquids 310, 113235. doi:10.1016/j.molliq.2020.113235

CrossRef Full Text | Google Scholar

Yan, S. R., Golzar, A., Sharifpur, M., Meyer, J. P., Liu, D. H., and Afrand, M. (2020). Effect of U-Shaped Absorber Tube on thermal-hydraulic Performance and Efficiency of Two-Fluid Parabolic Solar Collector Containing Two-phase Hybrid Non-newtonian Nanofluids. Int. J. Mech. Sci. 185. 105832. doi:10.1016/j.ijmecsci.2020.105832

CrossRef Full Text | Google Scholar

Zahmatkesh, I., Sheremet, M., Yang, L., Heris, S. Z., Sharifpur, M., Meyer, J. P., et al. (2021). Effect of Nanoparticle Shape on the Performance of thermal Systems Utilizing Nanofluids: A Critical Review. J. Mol. Liquids 321, 114430. doi:10.1016/j.molliq.2020.114430

CrossRef Full Text | Google Scholar

Zarringhalam, M., Karimipour, A., and Toghraie, D. (2016). Experimental Study of the Effect of Solid Volume Fraction and Reynolds Number on Heat Transfer Coefficient and Pressure Drop of CuO-Water Nanofluid. Exp. Therm. Fluid Sci. 76, 342–351. doi:10.1016/j.expthermflusci.2016.03.026

CrossRef Full Text | Google Scholar

Zhou, Y., Cui, X., Weng, J., Shi, S., Han, H., and Chen, C. (2018). Experimental Investigation of the Heat Transfer Performance of an Oscillating Heat Pipe with Graphene Nanofluids. Powder Technol. 332, 371–380. doi:10.1016/j.powtec.2018.02.048

CrossRef Full Text | Google Scholar