The Parametric Modeling and Two-Objective Optimal Design of a Downwind Blade

To cope with the future challenges to the blade that will be introduced by the development of extreme-scale wind turbines, this study focuses on the optimization design of the aerodynamic shape of a downwind blade via the inverse design method. Moreover, the genetic algorithm is used to optimize the chord, twist angle, and pre-bending parameters of the blade to maximize the energy production of the rotor and minimize the flapping bending moment of the blade root. By taking a 5-MW wind turbine as the optimization object, the two-objective optimization design of the downwind blade is carried out, and Pareto optimal solutions in line with the expectations are obtained. After analyzing four representatives of the Pareto optimal solutions, while a more ideal solution is found to sacrifice 9.41% of the energy production of the rotor, the flapping bending moment of the blade root is reduced by 42.92%, thereby achieving the lightweight optimization design of an extreme-scale wind turbine blade. Furthermore, based on the selected four sets of blades, the influence mechanisms of the chord, twist angle, and pre-bending on the optimization goal are analyzed, and it is found that the pre-bending parameter has the greatest influence on the two optimization goals.

Introduction

Global wind industry is gradually achieving the grid parity of wind power. In pursuit of lower electricity costs, both the single capacity of wind turbines and the blade length have been increasing (Zhang et al., 2021b). However, the blade design may reach a maximum size that will fail in an extreme wind regime. Therefore, some scholars have used the characteristics of palm trunks to resist aerodynamic loads, and have designed ultra-long blades in the downwind direction that have a certain cone angle and are deformed in sections along the spanwise direction (Ichter et al., 2016; Loth et al., 2017). Via the set cone angle and segmental deformation, the resultant force of each blade segment occurs only along the axial direction of the blade, and the blade only bears axial tension, which greatly reduces the cantilever load; these blades are called downwind blades (Yang et al., 2019). Although the downwind rotor will be affected by the tower shadow effect on the aerodynamics and aeroacoustics (Janajreh et al., 2010; Koh and Ng, 2016; Dose et al., 2020), the wind load of the downwind blade pushes the blade farther away from the tower; thus, due to the increased distance between the blade and the tower, there is no need to consider the interference between them. Therefore, the stiffness of the blade can be appropriately reduced to reduce costs and the weight of the rotor (Wand et al., 2018), as well as to increase the service life of the blades and the competitiveness of non-subsidized wind power (Pao et al., 2021).

Regarding the downwind blade design that is characterized by a reduced load, Rasmussen et al. (Rasmuseen et al., 1998) designed a flexible downwind rotor structure for MW-class wind turbines based on the bionic principle. The blades are bent and deformed under the action of aerodynamic loads, and the load can be reduced by 25–50%. Recently, Loth et al. (2017) (Ichter et al., 2016; Noyes et al., 2018; Pao et al., 2021) designed a 13.2-MW blade that is pre-bent downwind in sections, and used FAST platform simulations to verify its feasibility. Under constant power, the simulation results revealed that, in Class IIB winds, the performance of the two-blade downwind rotor with a 15°cone angle is comparable to that of an upwind three-blade rotor using Sandia SNL100-02 blades. Moreover, the equivalent load of blade damage is reduced by 19.0%, and the blade quality is reduced by 27.4%. Additionally, Qin et al. (Qin et al., 2020) increased the power of a two-blade downwind wind turbine system from 13.2 to 25 MW via the redesign of the aerodynamics, structure, and control system, and the system can be used as a super-large wind turbine for further development and evaluation. Furthermore, Noyes et al. (2020) studied whether the cone angle of the downwind blade can be changed with the variation of the wind speed via a deformable hinge, and found that load alignment can be achieved by using a fixed cone angle or a deformable hinge. In the case of a constant rated power, the deformable hinge can achieve a larger swept area at lower wind speeds than can a fixed cone angle, and can increase the power by up to 4.6%.

These previous studies fully demonstrate the feasibility of the application of downwind blades in large wind turbines, and have revealed their obvious advantages in blade load reduction and light weighting. However, these studies were based on increasing the length of the reference blades; the coupling relationship between the rotor power output and change of the blade root load caused by the bending of a constant-length blade was not investigated, nor were modeling methods of the geometric parameters, such as the chord, twist angle, and pre-bending of the blades, involved in the design process.

To address these problems, a two-objective optimization design method suitable for downwind blades is developed in the present study. By using an NREL 5-MW blade (Jonkman et al., 2009) as a reference, the two-objective optimization of the downwind blade is carried out based on the distributions of the blade chord, twist angle, and pre-bending parameters. The internal relationship between the output power of the rotor (P) and the blade root load is designed and investigated, and the influence mechanisms of the design parameters of the blade on the output power of the rotor and the flapping bending moment of the blade root (Mb) are discerned.

Geometric Representation and Optimization Goals of the Blade

For the geometric representation of the blade, some basic geometric models are employed to describe the aerodynamic shape of the blade with the fewest possible parameters via geometric calculations. These parameters are the design variables. The parametric modeling of the blade is the basis of the inverse design of the blade. This section establishes the mathematical model of the chord, twist angle, and pre-bending aerodynamic shape optimization variables required for the downwind blade design.

Chord Distribution

The chord distribution of the blade starts from the blade root along the spanwise direction, and first increases and then decreases. The maximum chord generally appears at 0.2 to 0.25 times the blade length. To make the chord distribution consistent with the chord change trend of large wind turbine blades, the parameterized model is simplified; the sixth-order Bezier curve (Zhu et al., 2020) is used to parametrically model the blade chord distribution, which can be expressed as

$c\left(\overline{r}\right)=P_0{(1-\overline{r})}^6+6P_1\overline{r}{(1-\overline{r})}^5+15P_2{\overline{r}}^2{(1-\overline{r})}^4+20P_3{\overline{r}}^3{\left(1-\overline{r}\right)}^3+15P_4{\overline{r}}^4{(1-\overline{r})}^2+6P_5{\overline{r}}^5\left(1-\overline{r}\right)+P_6{\overline{r}}^6,(1)$

where $\overline{r}$ is the dimensionless spanwise length of the blade, $\overline{r}=r/R$, R is the length of the blade, and $0\le \overline{r}\le 1$.

Taking the reference blade as the benchmark, the root chord and the tip chord are fixed at 2.50 and 1.53 m, respectively. When $\overline{r}=0$ and $\overline{r}=1$, P₀ and P₆ are the dimensionless lengths of the root and tip chords, so $P_0=0.0376$ and $P_6=0.0230$. According to the chord length distribution characteristics and combined with the structural reliability and the optimization range reported in previous studies (Yang et al., 2015; ViannaNeto et al., 2018), P₁, P₂, P₃, P₄, and P₅ are respectively defined as $0.032\le P_1\le 0.045$, $0.16\le P_2\le 0.25$, $-0.1\le P_3\le -0.05$, $0.09\le P_4\le 0.115$, and $0\le P_5\le 0.02$. The optimal range of the blade chord distribution is presented in Figure 1.

FIGURE 1

FIGURE 1. The chord distribution curves.

Twist Angle Distribution

The twist angle distribution of the blade generally exhibits a decreasing trend (ViannaNeto et al., 2018). However, due to the manufacturing process, the twist angle of the blade root should not be too large, and the angle of the tip requires a unique design; thus, the angles of the blade root and tip are designed separately during modeling. The remaining part of the blade twist angle distribution fits into a third-order polynomial curve, as follows.

$\beta =\dot{a}{\overline{r}}^3+\dot{b}{\overline{r}}^2+\dot{c}\overline{r}+\dot{d}(2)$

By using the trend line of the twist angle of the reference blade, and according to the limit of the stall angle of attack when running at the rated wind speed, the ranges of $\dot{a}$, $\dot{b}$, $\dot{c}$, and $\dot{d}$ in Eq. 2 can respectively be defined as $-35\le \dot{a}\le -32$, $77\le \dot{b}\le 79$, $-77.5\le \dot{c}\le -75$, and $26\le \dot{d}\le 29$. The optimized range of the blade twist angle distribution is presented in Figure 2.

FIGURE 2

FIGURE 2. The twist angle distribution curves.

Pre-bending Distribution

In general, to reduce the power generation cost of wind turbines with a large horizontal axis and avoid the collision of the blades with the tower due to elastic deformation, the blades of MW-class wind turbines are generally designed with pre-bending (Guo et al., 2017). Downwind blades do not have the risk of collision with the tower, and the pre-bending of the blades can reduce the blade flapping bending moment, which requires that the direction of the resultant force on each blade element after pre-bending be as consistent as possible with the axial direction of the blade element.

The pre-bending distribution of the blade approximately obeys a second-order monomial distribution. The blade root segment (which is 0–0.1 times the length of the blade) approximately obeys a first-order mononomial distribution due to the requirements of the blade structure. The displacement of the blade root is 0, and its deformation characteristics are determined by $\ddot{a}$:

$\{\begin{array}{c}dx\left(\overline{r}\right)=\ddot{a}{\overline{r}}_0\overline{r},\left(\overline{r}\le {\overline{r}}_0\right)\\ dx\left(\overline{r}\right)=\ddot{a}{\overline{r}}^2,(\overline{r}>{\overline{r}}_0),\end{array}(3)$

where ${\overline{r}}_0$ is the actual spanwise position of $0.1R$after pre-bending.

The pre-bending degree of the reference blade is 0.1. The increase in pre-bending degree of the blade will reduce the swept area and output power of the rotor. When $\ddot{a}=1$, the power loss caused by the reduction of the swept area of the rotor is 41.63%. The loss far exceeds the cost reduction effect brought about by weight reduction of blades, so $\ddot{a}=1$ is a reasonable larger upper limit. And combined with the empirical values of the downwind blades coning angle in Reference (Rasmuseen et al., 1998; Ichter et al., 2016; Loth et al., 2017; Noyes et al., 2018; Noyes et al., 2020; Qin et al., 2020), whose the pre-bending parameter $\ddot{a}$ are all between 0 and 1, the range of $\ddot{a}$ in Eq. 3 is defined as $0\le \ddot{a}\le 1$. The optimized range of the blade pre-bending distribution is presented in Figure 3.

FIGURE 3

FIGURE 3. The pre-bending distribution curves.

Optimization Goals

The design of wind turbine blades is not an independent process, and involves aerodynamics, the blade structure, and many other aspects. Due to the many design goals, e.g., the largest wind energy utilization factor, the greatest power generation, the smallest load, the lightest weight, etc., this is a very complicated and non-decoupled multi-objective optimization problem (Yang et al., 2015; Wang et al., 2017).

The main purpose of the downwind layout of the blades is to reduce the flapping bending moment of the blades and avoid collision with tower; moreover, via this design, the weight of the blades will also decrease. Therefore, the minimum flapping bending moment of the blade root is one of the optimization objectives. The load reduction is achieved by pre-bending, but too much pre-bending will reduce the swept area of the blades, thereby reducing the output power of the rotor. Therefore, the maximum output power of the rotor is another optimization objective. However, the two optimization objectives are contradictory, and they must be optimized via multi-objective coordination to achieve the best comprehensive benefits.

Rotor Power and Load Calculation Model

Blade Element Momentum

The blade element-momentum theory is adopted for the calculation of the aerodynamic characteristics of the blade. Eqs. 4, 5 are iteratively solved for the axial and tangential derivative coefficients$a$and $a^{\prime }$, respectively, and the normal force coefficient $C_n$ and tangential force coefficient $C_t$ of the rotor plane are then obtained.

$\frac{a}{1-a}=\frac{\sigma C_{\text{n}}}{4f{\left(\sin \varphi \right)}^2},(4)$

$\frac{a^{\prime }}{1+a^{\prime }}=\frac{\sigma C_{\text{t}}}{4f\text{sin}\varphi \text{cos}\varphi },(5)$

where $\sigma$ is the local solidity of the rotor, $\sigma =\frac{Bc}{2\pi r}$, $B$ is the number of blades, $c$ is the chord of the local blade element, $\varphi$ is the inflow angle, and $f$is the Prandtl tip loss factor (Wood et al., 2016), which is modified by Eq. 6. Moreover, $C_{\text{n}}=C_{\text{L}}\text{cos}\varphi +C_{\text{D}}\text{sin}\varphi$ and $C_{\text{t}}=C_{\text{L}}\text{sin}\varphi -C_{\text{D}}\text{cos}\varphi$, where $C_{\text{L}}$ and $C_{\text{D}}$ are respectively the lift and drag coefficients of the local blade element after correction by the Snel three-dimensional lift coefficient correction model (Snel et al., 1994) at the angle of attack $\alpha$.

$f=\frac{2}{\pi }\text{arccos}\left[\text{exp}\left(-\frac{B}{2}\frac{R-r}{r\text{sin}\varphi }\right)\right](6)$

The axial thrust $\text{d}{F}_{\text{n}}$of the blade element with thickness $\text{d}r$ can be calculated from Eq. 7, and Eqs. 8, 9 are used to calculate the overall mechanical parameters of the rotor:

$\text{d}{F}_{\text{n}}=\frac{1}{2}\rho C_{\text{n}}{v}_0^{2}c\text{d}r,(7)$

where $\rho$ is the local air density and $v_0$ is the relative speed.

$C_{\text{T,rotor}}=B\underset{0}{\overset{R}{{\displaystyle \int }}}{C}_n\frac{v_0^2}{v_1^2}\frac{c}{A}\text{d}r,(8)$

$C_{\text{M,rotor}}=B\underset{0}{\overset{R}{{\displaystyle \int }}}{C}_{\text{t}}\frac{v_0^2}{v_1^2}\frac{r}{R}\frac{c}{A}\text{d}r,(9)$

where $C_{\text{T,rotor}}$ is the thrust coefficient of the rotor, $C_{\text{M,rotor}}$ is the torque coefficient of the rotor, $v_1$ is the incident wind speed, and $A$ is the swept area of the rotor.

Rotor Load Calculation Model

As shown in Figure 4, each blade element is subjected to its own gravity, centrifugal force during operation, and thrust from the wind. However, the influence of gravity on the flapping bending moment of the blade root varies with the change of the azimuth angle during the rotation of the rotor. The resultant force $K$ of the blade element at the azimuth angle $\delta$ and the angle $\theta$ between the resultant force $K$ and the rotor shaft are respectively calculated as

$K=\sqrt{{\left(\text{d}{F}_{\text{c}}-\text{d}G\text{cos}\delta \right)}^2+\text{d}{\mathit{F}}_{\mathrm{n}}^{\mathrm{2}}},(10)$

$\theta =\text{atan}\left(\frac{\text{d}{F}_{\text{c}}-\text{d}G\text{cos}\delta }{\text{d}{F}_{\text{n}}}\right),(11)$

where $\text{d}{F}_{\text{c}}$ and $\text{d}G$ are the centrifugal force and gravity of the blade element, respectively.

FIGURE 4

FIGURE 4. The schematic diagram of the force analysis of the rotor.

Therefore, when $\delta$ is 0° and 180°, the resultant forces K and $K^{\prime }$ at the bending moments $\text{d}{M}_{\text{T}}$ and $\text{d}{M}_{\text{T}}\prime$ to the blade root are respectively

$\text{d}{M}_{\text{T}}=-K\times \text{sin}\left(\gamma -\theta \right)\times l,(12)$

$\text{d}{M}_{\text{T}}\prime =K\prime \times \text{sin}\left(\gamma -\theta \prime \right)\times l,(13)$

where “-” indicates a clockwise bending moment, $l$ is the force arm of the bending moment of the blade root, $l=\sqrt{r^2+\text{d}{x}^2}$, $\text{d}x$ is the amount of local pre-bending of the blade element control point, and $\text{γ}$ is the angle between $l$ and the rotor shaft, $\gamma =\text{atan}\left(\frac{r}{\text{d}x}\right)$.

Rotor Radius Scaling Factor After Pre-bending

Because the blade length remains constant, the swept area of the rotor decreases as the blade pre-bending increases (Sessarego et al., 2020), which results in a reduction in the rotor power under the same conditions. Therefore, to calculate the actual swept area of the rotor after pre-bending, the rotor scaling factor $L_f$ is introduced.

Because the pre-bending distribution geometry of the rotor obeys the first-type curve integral, it is expressed as

$1.0={\overline{r}}_0\sqrt{{\left(\ddot{a}{\overline{r}}_0\right)}^2+1}+\underset{{\overline{r}}_0}{\overset{L_f}{{\displaystyle \int }}}\sqrt{4{\left(\ddot{a}\overline{r}\right)}^2+1}\text{d}\overline{r},(14)$

where $0.1={\overline{r}}_0\sqrt{{\left(\ddot{a}{\overline{r}}_0\right)}^2+1}$. After solving $L_f$, the rotor radius after pre-bending is calculated as follows.

$R^{\prime }=R\times L_f(15)$

Evaluation Function Based on the Blade Element-Momentum Theory

In this study, the blade element-momentum theory modified by the Prandtl tip loss factor and the Snel three-dimensional lift coefficient correction model is used as the aerodynamic calculation model. Moreover, the centrifugal force and gravity of the blade are coupled to establish Eqs. 12, 13, 16, which constitute the rotor power and load calculation model, and the model calculation program is compiled using the C language.

$P=\frac{1}{2}{C}_{\text{P}}\rho A{v}_1^3,(16)$

where $C_{\text{P}}$ is the rotor power coefficient $C_{\text{P}}=\lambda C_{\text{M,rotor}}$, and $\lambda$ is the tip speed ratio.

Table 1 lists the parameters of the reference NREL 5-MW blade.

TABLE 1

TABLE 1. The parameters of reference 5-MW downwind wind turbine.

Aerodynamic performance calculations under the rated and operating wind speeds were performed on the benchmark example, and results were compared and analyzed with the GH Bladed simulation results, as presented in Figures 5, 6.

FIGURE 5

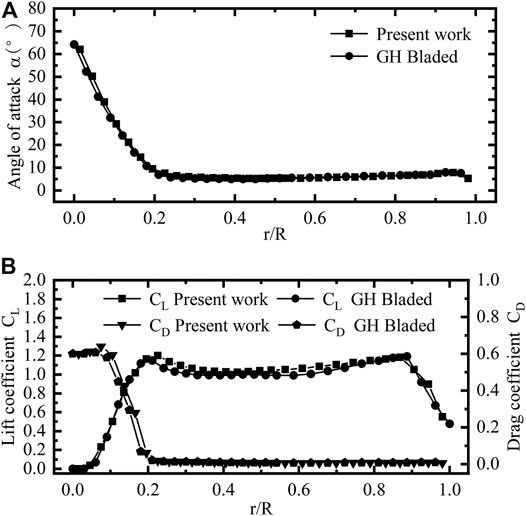
FIGURE 5. The aerodynamic characteristics of the blades along the span under the rated wind speed. (A) Angle of attack curve. (B) Lift and drag coefficient curves.

FIGURE 6

FIGURE 6. The aerodynamic characteristics of the rotor under the operating wind speed. (A) Rotor power and rotor power coefficient curves. (B) Thrust and thrust coefficient curves.

The analysis of Figures 5, 6 reveals that the calculation results of the evaluation function model are in good agreement with the simulation results under steady-state conditions, and the overall results are in line with the expectations and have high accuracy and stability. Therefore, the model can be used as a tool for the calculation of the aerodynamic performance of rotors and blades.

Genetic Algorithm

According to the laws of biological evolution in nature, the genetic algorithm (Selig and Coverstone-Carroll, 1996; Skinner and Zare-Behtash, 2018; ViannaNeto et al., 2018; Zhang et al., 2021a) was first designed and proposed by John Holland in the United States in the 1970s. This algorithm uses mathematical methods and computer simulations to transform problem-solving processes into processes similar to the crossover and mutation of chromosomal genes during biological evolution. In genetic algorithms, the design variables are usually called genes, which are encoded in a binary system, and all genes are combined to form a chromosome. The length of the chromosome is determined by the constraints of the design variables. For the variables in the present work, the blade chord c, twist angle β, and pre-bending dx are respectively constrained as follows:

${\overline{c}}_{\text{min}}\left(\overline{r}\right)<\overline{c}\left(\overline{r}\right)<{\overline{c}}_{\text{max}}\left(\overline{r}\right),(17)$

${\beta }_{\text{min}}\left(\overline{r}\right)<\beta \left(\overline{r}\right)<{\beta }_{\text{max}}\left(\overline{r}\right),(18)$

$\text{d}{x}_{\text{min}}\left(\overline{r}\right)<\text{d}x\left(\overline{r}\right)<\text{d}{x}_{\text{max}}\left(\overline{r}\right),(19)$

where $\overline{c}$ is the dimensionless chord, $\overline{c}=c/R$.

In summary, based on the genetic algorithm, a two-objective design method suitable for downwind blades is constructed by establishing geometric representations of the blade chord, twist angle, and pre-bending, determining the maximum output power of the rotor and the minimum blade root bending as optimization goals, and using the blade power and load calculation model established in the present work as an evaluation function. The optimization process is presented in Figure 7.

FIGURE 7

FIGURE 7. The flowchart of the proposed two-objective optimization design method.

Results and Analysis

By taking reference 5-MW wind turbine under the rated wind speed of 10.5 m/s as the optimization object, and in comprehensive consideration of the convergence speed of the algorithm and the stability of the results, the population size was set to 100, and the optimization generation was set to 2000. The two-objective optimization design was subsequently carried out, and the Pareto optimal solutions are shown in Figure 8.

FIGURE 8

FIGURE 8. The two-objective optimization results.

It can be seen from Figure 8 that the distribution of the optimal solutions presents a smooth, monotonically increasing curve. The curve divides the optimization goal into two parts, namely Parts I and II. Part I includes the ideal solutions that cannot be reached under the constraints of the present work, while Part II includes the feasible solutions under the constraints of the present work. The monotonic increase of the curve indicates that the increase of the output power of the rotor will be accompanied by the increase of the blade root load, which demonstrates that the two optimization goals are conflicting. Figure 8 also reveals that the slope of the curve increases with the increase of the output power of the rotor. Therefore, when a certain point on the curve is exceeded, the rate of increase of the flapping bending moment of the blade root (Mb) is much greater than that of the output power of the rotor. Thus, if the optimization of a certain goal is pursued alone, a superior design result will not be obtained.

To better explain the two-objective optimization curve, the four sets of optimized blades A, B, C, and D in Figure 8 were considered for a more detailed analysis. The comparison with the aerodynamic characteristics of the reference blade is exhibited in Table 2, and the optimal solutions of the design variables corresponding to A, B, C, and D are reported in Table 3. The flapping bending moment of the blade root of the D-blade was found to be slightly less than that of the reference blade, while the rotor output power of the D-Blade was greater. The rotor output power of the C-Blade was slightly greater than that of the reference blade, while the flapping bending moment of the blade root of the C-blade was smaller, indicating that the proposed calculation model performed well for the two-objective optimization. Compared with the reference blade, the rotor output power of the B-blade was reduced by 9.41%, but the flapping bending moment of the blade root was reduced by 42.92%, which is an ideal design scheme. However, in the totality of the optimal solutions shown in Figure 8, the optimal solution that meets the expected goal is not the only one; other optimal solutions also exhibited better performance than the reference blade, thereby providing decision-makers with more choices.

TABLE 2

TABLE 2. The comparison of the optimal solutions after two-objective optimization.

TABLE 3

TABLE 3. The variable design results after two-objective optimization.

Design Variable Sensitivity Analysis

The design parameters of the four sets of blades A, B, C, and D were compared with those of the reference blade, as shown in Figures 9–11. In addition, Figure 12 presents the distribution curves of the flapping bending moments of the blade roots at the rated wind speed.

FIGURE 9

FIGURE 9. The optimized blade chord distribution curves.

FIGURE 10

FIGURE 10. The optimized blade twist angle distribution curves.

FIGURE 11

FIGURE 11. The optimized blade pre-bending distribution curves.

FIGURE 12

FIGURE 12. The optimized flapping bending moment of the blade root along the span.

Based on the analysis of the chord distribution curves of the reference blade and the A-Blade exhibited in Figure 9, it can be concluded that under the conditions of a constant blade twist angle and pre-bending, and with the variation of only the chord parameter (${\text{A}}^{\prime }$), the output power of the ${\text{A}}^{\prime }$-Blade at the rated wind speed was 0.86% higher than that of the reference blade rotor, but the flapping bending moment of the blade root was increased by 8.19%. Therefore, with the increase of the chord of the blade, the output power of the rotor will increase, but so too will the thrust of the rotor, thereby increasing the flapping bending moment of the blade root.

The chord and pre-bending parameters of the four sets of blades A, B, C, and D were then kept consistent with those of the reference blade, and only the twist angle parameter of the blades was changed, which are denoted as ${\text{A}}^{″}$, ${\text{B}}^{″}$, ${\text{C}}^{″}$, and ${\text{D}}^{″}$. The aerodynamic characteristics were calculated at the rated wind speed, and the results are reported in Table 4. According to Figure 10, by optimizing the twist angle of the blade, the flapping bending moment of the blade root can be reduced while sacrificing a portion of the output power of the rotor, and the load distribution of the blade can be improved by reducing the angle of attack.

TABLE 4

TABLE 4. The aerodynamic characteristics of the rotor with the variation of only the twist angle.

Based on the analysis of the distribution curves of the blade chord, pre-bending, and flapping bending moment of the blade root presented in Figures 9, 11, 12, as well as the results reported in Table 3, it can be concluded that a larger degree of pre-bending can quickly reduce the flapping bending moment of the blade root. However, when the degree of pre-bending was greater than that of the C-Blade, the increase of the blade chord was not sufficient to offset the influence of the greater pre-bending on the output power of the rotor. In summary, under the condition of a constant blade length, the pre-bending parameter of the blade has the greatest influence on the output power of the rotor and the flapping bending moment of the blade root. The greater the degree of pre-bending, the smaller the swept area of the rotor, the lower its output power, and the smaller the blade root load.

Conclusion

In this paper, a 5-MW wind turbine was considered as the design optimization object, and the chord, twist angle, and pre-bending of the blade were taken as the design variables. Based on this, the two-objective optimization of the maximum output power of the rotor and the minimum flapping bending moment of the blade root was carried out. Singular optimization yielded evenly distributed Pareto optimal solutions; this verifies the stability and accuracy of the proposed model, which can meet the preliminary requirements of the inverse design of downwind blades.

Via the analysis of the Pareto optimal solutions of the calculation example, the solutions of the C-Blade and D-Blade achieved the two-objective optimization with a greater rotor output power and a smaller flapping bending moment of the blade root. Among them, at the expense of 9.41% of the rotor output power, the flapping bending moment of the blade root of the ideal B-Blade was found to be reduced by 42.92%; moreover, the root load was greatly reduced, and the lightweight and optimized design of the downwind wind turbine blade was realized.

In addition, the four sets of blades selected in the present work were combined with the Pareto optimal solutions to analyze the design variables of the blades. It was found that increasing the chord of the blade can increase the output power of the rotor, but this will also increase the flapping bending moment of the blade root. Moreover, while increasing the twist angle and pre-bending of the blade can reduce the flapping bending moment of the blade root, a portion of the rotor output power will be reduced. A comparison revealed that the blade pre-bending parameter has the greatest influence on the output power of the rotor and the flapping bending moment of the blade root.

In this paper, the optimal design results of the downwind blades are obtained under rated wind speed, and the feasibility of downwind blades is preliminarily verified. However, the performance of the blade in terms of manufacturing cost, power generation and load under realistic operating conditions requires more detailed study to verify the feasibility of the downwind blades.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

BX: methodology, writing—review and editing, and funding acquisition. ZL: formal analysis, investigation, data curation and writing—review and editing. ZiZ: investigation and data curation. XC: conceptualization and supervision. TW: conceptualization and supervision. ZhZ: conceptualization and supervision. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Fundamental Research Funds for the Central Universities (grant number B210202063); and the Open fund of Jiangsu Wind Power Engineering Technology Center of China (grant number ZK19-03-01).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Dose, B., Rahim, H., Stovesadbt, B., and Peinke, J. (2020). Fluid-structure Coupled Investigations of the NREL 5 MW Wind Turbine for Two Downwind Configurations. Renew. Energ. 146, 1113–1123. doi:10.1016/j.renene.2019.06.110

CrossRef Full Text | Google Scholar

Guo, X., Guo, S., and Yang, S., (2017). Multi-objective Optimization Design of the Pre-bending Wind Turbine Blades[J]. Renew. Energ. Resour. 35 (06), 875–883.

Google Scholar

Ichter, B., Steele, A., Loth, E., Moriarty, P., and Selig, M. (2016). A Morphing Downwind-Aligned Rotor Concept Based on a 13-MW Wind Turbine. Wind Energy 19 (4), 625–637. doi:10.1002/we.1855

CrossRef Full Text | Google Scholar

Janajreh, I., Qudaih, R., Talab, I., and Ghenai, C. (2010). Aerodynamic Flow Simulation of Wind Turbine: Downwind versus Upwind Configuration. Energ. Convers. Manag. 51 (8), 1656–1663. doi:10.1016/j.enconman.2009.12.013

CrossRef Full Text | Google Scholar

Jonkman, J., Butterfield, S., and Musial, W. (2009). Definition of a 5-MW Reference Wind Turbine for Offshore System development[R]. Golden, CO: National Renewable Energy Laboratory. Report No. NREL/TP-500-38060. doi:10.2172/947422

CrossRef Full Text

Koh, J. H., and Ng, E. Y. K. (2016). Downwind Offshore Wind Turbines: Opportunities, Trends and Technical Challenges. Renew. Sustain. Energ. Rev. 54, 797–808. doi:10.1016/j.rser.2015.10.096

CrossRef Full Text | Google Scholar

Loth, E., Steela, A., and Qin, C. (2017). Downwind Pre-aligned Rotors for Extreme-Scale Wind Turbines[J]. Wind Energy 20 (7), 1241–1259.

Google Scholar

Noyes, C., Loth, E., Martin, D., Johnson, K., Ananda, G., and Selig, M. (2020). Extreme-scale Load-Aligning Rotor: To Hinge or Not to Hinge? Appl. Energ. 257, 113985. doi:10.1016/j.apenergy.2019.113985

CrossRef Full Text | Google Scholar

Noyes, C., Qin, C., and Loth, E. (2018). Pre-aligned Downwind Rotor for a 13.2 MW Wind Turbine. Renew. Energ. 116, 749–754. doi:10.1016/j.renene.2017.10.019

CrossRef Full Text | Google Scholar

Pao, L. Y., Zalkind, D. S., and Griffith, D. T. (2021). Control Co-design of 13 MW Downwind Two-Bladed Rotors to Achieve 25% Reduction in Levelized Cost of Wind Energy[J]. Annu. Rev. Control.

Google Scholar

Qin, C., Loth, E., Zalkind, D. S., Pao, L. Y., Yao, S., Griffith, D. T., et al. (2020). Downwind Coning Concept Rotor for a 25 MW Offshore Wind Turbine. Renew. Energ. 156, 314–327. doi:10.1016/j.renene.2020.04.039

CrossRef Full Text | Google Scholar

Rasmuseen, F., Petersen, J. T., and Volund, P. (1998). Soft Rotor Design for Flexible turbines[R]. Contract JOU3-CT95-0062. Denmark: Risø National Laboratory: Roskilde.

Selig, M. S., and Coverstone-Carroll, V. L. (1996). Application of a Genetic Algorithm to Wind Turbine Design. J. Energ. Resour. Techn. 118 (1), 22–28. doi:10.1115/1.2792688

CrossRef Full Text | Google Scholar

Sessarego, M., Feng, J., Ramos-García, N., and Horcas, S. G. (2020). Design Optimization of a Curved Wind Turbine Blade Using Neural Networks and an Aero-Elastic Vortex Method under Turbulent Inflow. Renew. Energ. 146, 1524–1535. doi:10.1016/j.renene.2019.07.046

CrossRef Full Text | Google Scholar

Skinner, S. N., and Zare-Behtash, H. (2018). State-of-the-art in Aerodynamic Shape Optimisation Methods. Appl. Soft Comput. 62, 933–962. doi:10.1016/j.asoc.2017.09.030

CrossRef Full Text | Google Scholar

Snel, H., Houwink, R., and Bosschers, J. (1994). Sectional Prediction of Lift Coefficients on Rotating Wind Turbine Blades in stall[R]. Netherlands: ECN-C-93-052.

Vianna Neto, J. X., Guerrea Junior, E. J., Moreno, S. R., Hultmann Ayala, H. V., Mariani, V. C., and Coelho, L. d. S. (2018). Wind Turbine Blade Geometry Design Based on Multi-Objective Optimization Using Metaheuristics. Energy 162, 645–658. doi:10.1016/j.energy.2018.07.186

CrossRef Full Text | Google Scholar

Wand, Z., Tian, W., and Hu, H. (2018). A Comparative Study on the Aeromechanic Performances of Upwind and Downwind Horizontal-axis Wind Turbines. Energ. Convers. Manag. 163, 100–110. doi:10.1016/j.enconman.2018.02.038

CrossRef Full Text | Google Scholar

Wang, L., Wang, T., Wu, J., and Chen, G. (2017). Multi-objective Differential Evolution Optimization Based on Uniform Decomposition for Wind Turbine Blade Design. Energy 120, 346–361. doi:10.1016/j.energy.2016.11.087

CrossRef Full Text | Google Scholar

Wood, D. H., Okulovo, V. L., and Bhattacharjee, D. (2016). Direct Calculation of Wind Turbine Tip Loss. Renew. Energ. 95, 269–276. doi:10.1016/j.renene.2016.04.017

CrossRef Full Text | Google Scholar

Yang, Y., Zeng, P., and Lei, L. (2019). Concept and Development of Novel Blade Structure of Large Horizontal-axis Wind Turbine[J]. Eng. Mech. 36 (10), 1–7.

Google Scholar

Yang, Y., Chun, L. I., and Miao, W., (2015). Global Optimal Design of Wind Turbines Blade Based on Multi-Object Genetic Algorithm. J. Mech. Engineer. 51 (14), 192–198. doi:10.3901/jme.2015.14.192

CrossRef Full Text | Google Scholar

Zhang, L., Hu, T., Yang, Z., and Zhang, Z. (2021a). Elite and Dynamic Opposite learning Enhanced Sine Cosine Algorithm for Application to Plat-fin Heat Exchangers Design Problem. Neural Comput. Appl. doi:10.1007/s00521-021-05963-2

Zhang, L., Li, Y., Zhang, H., Xu, X., Yang, Z., and Xu, W. (2021b). A Review of the Potential of District Heating System in Northern China. Appl. Thermal Eng. 188, 116605. doi:10.1016/j.applthermaleng.2021.116605

Zhu, F.-W., Ding, L., Huand, B., Bao, M., and Liu, J.-T. (2020). Blade Design and Optimization of a Horizontal axis Tidal Turbine. Ocean Eng. 195, 106652. doi:10.1016/j.oceaneng.2019.106652

CrossRef Full Text | Google Scholar