A Novel Real-Coded Genetic Algorithm for Dynamic Economic Dispatch Integrating Plug-In Electric Vehicles

Massive popularity of plug-in electric vehicles (PEVs) may bring considerable opportunities and challenges to the power grid. The scenario is highly dependent on whether PEVs can be effectively managed. Dynamic economic dispatch with PEVs (DED with PEVs) determines the optimal level of online units and PEVs, to minimize the fuel cost and grid fluctuations. Considering valve-point effects and transmission losses is a complex constrained optimization problem with non-smooth, non-linear, and non-convex characteristics. High efficient DED method provides a powerful tool in both power system scheduling and PEVs charging coordination. In this study, firstly, PEVs are integrated into the DED problem, which can carry out orderly charge and discharge management to improve the quality of the grid. To tackle this, a novel real-coded genetic algorithm (RCGA), namely, dimension-by-dimension mutation based on feature intervals (GADMFI), is proposed to enhance the exploitation and exploration of conventional RCGAs. Thirdly, a simple and efficient constraint handling method is proposed for an infeasible solution for DED. Finally, the proposed method is compared with the current literature on six cases with three scenarios, including only thermal units, units with disorderly PEVs, and units with orderly PEVs. The proposed GADMFI shows outstanding advantages on solving the DED with/without PEVs problem, obtaining the effect of cutting peaks and filling valleys on the DED with orderly PEVs problem.

Introduction

The Optimization Problem

Over the last few decades, the rapid increase in the use of fossil fuel has led to a consequential worldwide reduction of the resource; thus, its optimal utilization in power generation has become an important research topic (Niu et al., 2014; Yang et al., 2015). In addition, massive popularity of PEVs may bring opportunities or challenges to the power grid. Therefore, the DED with PEVs plays an important role in power systems operation and control. Coupling with space and time, it is a complicated optimal decision problem, and its goal is to minimize the fuel cost and fluctuation of the power grid, on the premise of satisfying a series of constraints.

The DED problem was first introduced in 1971 by Bechert and Kwanty (Niu et al., 2014) and an extension of static economic dispatch (SED), taking into account ramp rate limits. Owing to the inertia of thermal units, the output from the units is not changed significantly from one operating hour to the next, which can avoid shortening the life of the units (Elaiw et al., 2013). The fuel cost function is a highly discontinuous, nonlinear, and non-convex curve, due to the valve-point effect (VPE) of the steam turbine (Shen et al., 2019), and the transmission loss should not be ignored on a large scale of the power system. As a mobile, distributed energy storage, PEVs charge from the grid through the grid to vehicle technology (G2V), and feedback to the grid through the vehicle to gird technology (V2G) (Wang et al., 2019a). So, VPE, transmission losses, and PEVs make the DED model more complicated, but more accurate.

Over the past few years, optimization methods based on artificial intelligence have been successfully and popularly applied to DED. Meta-heuristic algorithms do not care certain mathematical properties of the objective function such as continuous, differentiability, and convex, compared with traditional techniques. They include simulated annealing (SA) (Panigrahi et al., 2007), genetic algorithm (GA), particle swarm optimization (PSO) (Sawyerr et al., 2011), differential evolution (DE), artificial immune system (AIS) (Hemamalini and Simon, 2011a; Basu, 2011), cuckoo search (CS) (Mellal and Williams, 2020), artificial bee colony (ABC) (Hemamalini and Simon, 2011b; Tehzeeb-ul-Hassan et al., 2020), harmony search (HS) (Ravikumar Pandi and Panigrahi, 2011; Chakraborty et al., 2012; Li et al., 2019), an efficient fitness-based differential evolution (EFDE) (Shen et al., 2019), hybrid different evolution (DE), sequential quadratic programming (SQP), and hybrid PSO and SQP (Elaiw et al., 2013). However, few scholars integrate PEVs into the DED problem to perform effective management considering network loss. Panpan M. et al. manage the charging and discharging of PEVs through the scene method in the problem (Yang et al., 2014; Mei et al., 2019). Behera et al. (2019) ignored two important constraints: the power balance constraint and the ramp rate limit.

The Optimization Algorithm

Since GA was proposed by Holland in 1975 (Ali et al., 2018), which has undergone two revisions: the binary-coded genetic algorithm (BCGA) and real-coding genetic algorithm (RCGA). RCGA was first suggested by Herrera in 1998 (Akopov et al., 2019; Iyer et al., 2019). It is known that its performance depends heavily on crossover and mutation operators (Thakur et al., 2014), and then scholars mainly focused on the improvement of crossover and mutation operators and proposed many excellent variants of RCGA.

The crossover operator generates new individuals through interactive information among existing ones (Nakane et al., 2020). Arithmetic crossover (AX) (Naqvi et al., 2020) produces offspring through the linear combination of the parents. By flat crossover (FX) (Picek et al., 2013a), the parents exchange genes to produce offspring, but it does not destroy genetic information in the population. In LX (Deep and Thakur, 2007), Laplace distribution is used as the density function to generate genes near the parents. In 1993, Eshelman et al. used the concept of interval schemata to develop a blend crossover operator (BLX-α) (Wang et al., 2019b), which can do linear exploration around the parents. SPX is a multi-paternal crossover operator based on the nature of the simplex and is an extension of BLX (Chuang et al., 2015). SBX (Naqvi et al., 2020), as its name implies, is formed by simulating binary crossover operator; UNDX can produce two or more offspring individuals from three parents (Kwak and Lee, 2016). The comparative research results have been reported in the literature (Picek et al., 2013b; Naqvi et al., 2020) for the above-mentioned crossover operators.

Mutation is the important operation responsible for exploration in RCGA (Wang et al., 2018), especially the local development. The popular and widespread mutation operators in the literature mostly use a certain distribution as a density function to generate random numbers around the gene to vary, so as to carry out the local development of the gene, which may lead to a lot of troubles in the application of the algorithm due to the introduction of extra parameters, such as the random mutation (RM), the non-uniform mutation (NUM) (Wang et al., 2019b), the power mutation (PM), the polynomial mutation (PLM), the Gaussian mutation (GM) (Wang et al., 2019b), and Cauchy mutation (CM). In addition, the direction mutation is presented (Tang and Tseng, 2013), which mutates toward a promising area by utilizing statistical population information and has achieved good results. On the basis of previous studies, two simple and efficient mutation operators are proposed. One is the dimension-by-dimension mutation based on feature intervals (DMFI), which combines horizontal search at the component level with the rule of greed to form a directional horizontal local development strategy; what is more, the genetic characteristics of outstanding individuals are extracted as the variation interval, thereby providing a directional vertical local development capability. The other is the uniform mutation based on the interval of opposing features (UMOFI); the opposing of feature intervals of outstanding individuals is employed as the variation interval for the inferior individuals, thereby introducing new information in the population.

At present, genetic algorithms have the defects of falling into local optimal and lack of exploration capabilities for large-scale and high-dimensional problems (Sawyerr et al., 2011; Fang et al., 2014; D’Angelo and Palmieri, 2021; Sawyerr et al., 2014). In the final analysis, this is a fundamental and difficult problem faced by metaheuristics: how to balance the exploration and exploitation of the algorithm. In general, researchers design or improve an algorithm based on the idea that focuses on exploration in the early stage and later on exploitation. However, if the development capability is not enough to find the global optimal area in the early stage, it will become stuck in the local optimal. Given this, this study provides a new solution, based on the idea of collaborative optimization of the superior and inferior individuals, in which excellent individuals strengthen local search. Inferior individuals are responsible for introducing new information to increase the diversity of the population. Then, interacting information between excellent individuals and inferior individuals helps to find outstanding individuals and realizing their comprehensive development carried out in each iterative.

The characteristics of GA’s mechanisms and the new solutions mentioned above are consistent on the issue of balancing the global and local search capabilities. Therefore, an RCGA based on co-optimization of superior and inferior individuals is proposed: 1) through the rank selection and the flat crossover to realize the genetic interaction between superior and inferior populations, 2) using DMFI to obtain the ability of directed vertical and horizontal local development for excellent individuals and achieve in-depth local search, and 3) using UMOFI for the inferior individuals, which is controlled by the mutation probability $Pm$ , thereby introducing new genetic information while maintaining the diversity of the population.

Constraint Handling Methods

For constraint optimization problems, the feasibility of the solutions is more important than the objective values. The penalty function method is common and popular for handling some constraints (Shen et al., 2019). However, it is a troublesome thing to choose a suitable penalty factor. Hence, some scholars proposed several types of repair methods to meet problem constraints. Feasibility-based rules are used to lead the search toward the feasible region to handle inequality constraints effectively (Yuan et al., 2009), which is more efficient to filter feasible solutions and ease the burden of setting the penalty factor compared to the penalty function method. However, for optimization problems with equality constraints, owing to feasible solutions occupying an extremely small proportion of the solution space, it is difficult to repair by screening feasible solutions and guiding infeasible solutions. Heuristics for handling constraints perform excellently to deal with equality constraints without considering the transmission loss (Wang et al., 2011). They adjust the output power according to general experience to gradually reduce the violation of the constraint until it becomes a feasible solution, whereas this cannot efficiently solve complex equality constraints, for instance, the power balance constraint with the transmission loss, and there may be an excessive adjustment, especially when the amount of violation is not big. The forced repair technology refers to adjusting the output strictly according to the characteristics of the equation, which greatly improves repair efficiency of equality constraints (Panigrahi et al., 2007; Zou et al., 2018). Apart from equality limits, inequality constraints also influence the feasibility, and hence the forced repair technology may spend more time solving the quadratic equation of DED with transmission losses. In Li et al. (2019) and Shen et al. (2019), the constraints handling technology combining a heuristic repair technology and the forced repair technology is proposed, which enhances the capability of repairing infeasible solutions.

In summary, the methods or techniques above-mentioned have the following shortcomings in solving DED with PEVs: 1) the algorithms are difficult to solve large-scale problems or face premature phenomena and 2) constraint processing techniques are difficult to repair infeasible solutions or do not work well with the algorithm. In view of this, this study proposed GADMFI based on RCGA. Meanwhile, a simple and efficient constraint processing technique is designed.

The remainder of this study is arranged as follows: The Formulation of the Dynamic Economic Dispatch With Plug-In Electric Vehicles gives the mathematical formulation of the DED with PEVs. Genetic Algorithm Dimension Mutation Based on Feature Intervals describes GADMFI in detail. In Constraints Handling Method, the constraint handling methods are proposed. The Implementation of Genetic Algorithm Dimension Mutation Based on Feature Intervals for Dynamic Economic Dispatch With Plug-In Electric Vehicles presents the implementation of GADMFI on the DED problem. Experimental Results and Analysis designs and analyzes experiments. Finally, the study ends with conclusions and further research work.

The Formulation of the Dynamic Economic Dispatch With Plug-In Electric Vehicles

The DED integrating PEVs aims to determine the optimal generation levels of all online units and PEVs, during a specified period of time (e.g., 24 intervals a day), so as to minimize the total fuel cost and subject to a number of equality and inequality constraints.

The Optimization Objectives

There are two optimization objectives for this problem: one is to minimize fuel costs and the other is to minimize the fluctuation of the grid, that is, maximize peak shaving and valley filling. They are described in Eqs. 1, 2.

$\min f_1\left(P\right)={{\displaystyle \sum }}_{t=1}^T{\displaystyle \sum }_{i=1}^N{a}_i+b_i{P}_{t,i}+c_i{P}_{t,i}^2+\left|c_{i}sin\left[f_i\left(P_i^{min}-P_{t,i}\right)\right]\right|.(1)$

$\text{min}{f}_2\left(P,P_{PEV}\right)={\displaystyle \sum }_{t=1}^{T-1}{\left[{\displaystyle \sum }_{i=1}^N\left(P_{t+1,i}+P_{PEV,t+1}-P_{L,t+1}\right)-{\displaystyle \sum }_{i=1}^N\left(P_{t,i}+P_{PEV,t}-P_{L,t}\right)\right]}^2,(2)$

where $P$ and $P_{PEV}$ constitute the decision variables of the problem and $P_{L,t}$ is the transmission loss at time t.

Constraints

The DED with PEVs is an optimization problem containing multiple inequalities and equality constraints, including capacity constraints, ramp rate limits, PEVs charge/discharge limits, PEVs demand limits, and power balance constraints.

Capacity Constraints

The capacity limits of the thermal unit are inequality constraints, which are determined by the physical characteristics of the unit and are given as follows:

$P_i^{min}\le P_{t,i}\le P_i^{max},(3)$

where $P_i^{min}$ and $P_i^{max}$ represent the min and max output power of the ith unit, respectively.

Ramp Rate Limits

Due to the inertia of thermal power units, the ramp rate limits are considered to extend the service life of the units; that is, the output of the unit cannot be adjusted greatly in a short time, and the output of current time will affect the output of the next time:

$\{\begin{array}{c}{P}_{t,i}-P_{t-1,i}\le U{R}_i\\ P_{t-1,i}-P_{t,i}\le D{R}_i\end{array},(4)$

where $U{R}_i$ and $D{R}_i$ , respectively, represent the maximum allowable rise and fall of the ith unit, which are limited to its physical characteristics.

Plug-In Electric Vehicles Charge/Discharge Limits

The maximum charging power and discharging power of PEVs should be limited to a normal range. Because different types of electric vehicles have different models, the charging and discharging power of PEVs at t time is described as a variable $P_{PEV,t}$ :

$P_{PEV,disc}^{max}\le P_{PEV,t}\le P_{PEV,char}^{max}.(5)$

The Plug-In Electric Vehicles Demand Constraint

For users’ daily travel, the PEVs demand constraint should be met (Yang et al., 2017a), which is described as Eq. 6:

${\displaystyle \sum }_{t=1}^T{P}_{PEV,t}\le P_{PEV,total},(6)$

where $P_{PEV,total}$ is the desired power for daily use.

The Power Balance Constraint

Power balance limit is the most important and complex constraint, especially considering the transmission loss, which is defined as

${\displaystyle \sum }_{t=1}^T{P}_{t,i}=P_{D,t}+P_{L,t}+P_{PEV,t},(7)$

where $P_{D,t}$ presents the load demand at time t, $P_{L,t}$ is the transmission loss, and its mathematic model is expressed by Kron’s loss (Abdelaziz et al., 2008) as Eq. 8.

$P_{L,t}={\displaystyle \sum }_{i=1}^N{\displaystyle \sum }_{j=1}^N{P}_{t,i}{B}_{ij}{P}_{t,j}+{\displaystyle \sum }_{j=1}^N{B}_{0i}{P}_{t,i}+B_{00},(8)$

where $B_{ij}$ , $B_{0i}$ , and $B_{00}$ represent the loss coefficients of the generation units. In addition, the model of the transmission loss is usually simplified as Eq. 9 (Pan et al., 2018), which is adopted in this study:

$P_{L,t}={\displaystyle \sum }_{i=1}^N{\displaystyle \sum }_{j=1}^N{P}_{t,i}{B}_{ij}{P}_{t,j}.(9)$

Proposed Genetic Algorithm Dimension-by-Dimension Mutation Based on Feature Intervals

RCGAs generally consist of selection, crossover, mutation, and elite retention strategies, and the pseudo-code is summarized in Table 1. Without destroying its main structure and extra parameters, this study proposes a simple and efficient, superior and inferior population collaborative optimization algorithm, namely, a novel real-coded genetic algorithm: GADMFI. Its pseudo-code is shown in Table 2. It is worth noting that this study takes the minimum value of the function as the optimization objective.

TABLE 1

TABLE 1. The pseudo-code of conventional RCGA

TABLE 2

TABLE 2. The pseudo-code of the proposed GADMFI.

In the study, two novel mutation operators are proposed: the dimension-by-dimension mutation based on feature intervals (DMFI) and the uniform mutation based on the interval of opposite features (UMOFI). DMFI and UMOFI are designed based on the idea that excellent individuals strengthen local exploitation capabilities, to improve the convergence accuracy and speed of the algorithm; low-quality individuals introduce new information, to improve population diversity; and good and bad individuals exchange information by an interactive operation. Excellent individuals perform DMFI to strengthen local development in both vertical and horizontal dimensions. Inferior individuals introduce new genes through UMOFI. Then, the information of the two is exchanged through the ranking selection (RS) and FX, so as to achieve the effect of collaborative optimization.

The Selection and Crossover Operator

The selection operator is the first operator of GA. One of the most widely used selection operators is the roulette selection. The higher the fitness, the greater the probability of being selected. However, the excellent genes of the inferior individuals may be abandoned. The other most commonly used is RS (Chuang et al., 2016). Excellent individuals are used as the parent 1 to cross, and inferior individuals are used as the parent 2. All individuals participate in the crossover with the same probability, which does not affect the diversity of the population. RS is used in the study; however, the difference between this study and the literature (Chuang et al., 2016) is random matching for the individuals, thus enhancing the population diversity.

The flat crossover (FX) is rarely used due to its poor local development ability, but it has the characteristics of not changing the genetic information in the population that other operators do not have. It can maintain the diversity of the population and the interaction between individuals. The role of RS and FX is to carry out information interaction between individuals without changing the genetic information of the population.

The Mutation Operator

Strong local search capabilities should be possessed for each stochastic algorithm. At the same time, it is also indispensable to maintain the diversity of the population. In order to illustrate the design idea of the mutation operator, horizontal search and vertical search are firstly defined. If there is a comparison between the variants or a variant and ontology in an operator, it is called horizontal search of individuals. If only components are changed, it is called the vertical search of the individual. In previous related studies, local search often refers to vertical search. All the components are developed simultaneously. In this section, horizontal search and the greedy rule, vertical search, and feature intervals are combined to fulfill horizontal and vertical local search so as to obtain in-depth development for the superior population by DMFI. In addition, new population information is also introduced into the inferior population by UMOFI.

The Dimension-by-Dimension Mutation Based on Feature Intervals

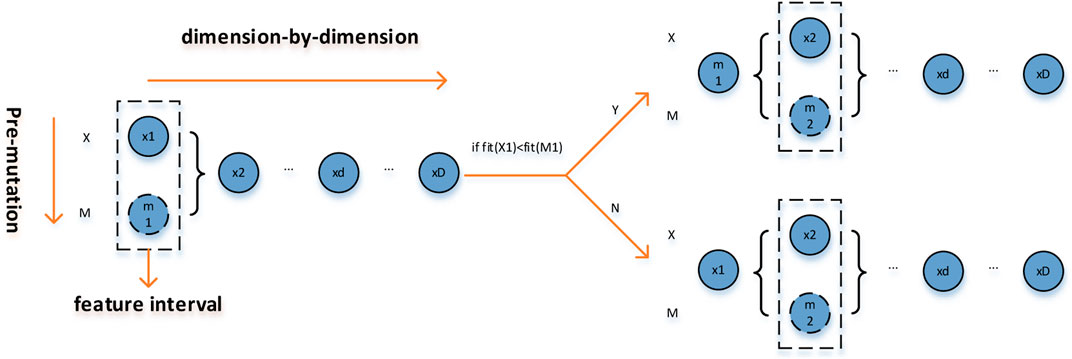
The dimension-by-dimension mutation is a dimension-by-dimension search for outstanding individuals in the characteristic interval and is combined with the greedy rule to achieve a directed horizontal search. Figure 1 shows the change from one dimension to the next dimension of DMFI. A gene $x1$ of the chromosome $X$ is pre-mutated to $m1$ in the feature interval that is formed by the minimum and maximum gene values of the excellent population individuals, which can be described as Eqs. 10, 11. Because the feature interval contains the genetic characteristics of excellent individuals, the mutation will search toward a promising area and is used to realize the vertical local development for the superior population, which is different from the previous uniform mutation in that it is not centered on the individual, but the center of the superior population:

$\left[S_{upper}\left(d\right),S_{lower}\left(d\right)\right]=\left\{min\left[S\left(d\right)\right],max\left[S\left(d\right)\right]\right\},(10)$

$m\left(d\right)=rand\times \left(S_{upper}\left(d\right)-S_{lower}\left(d\right)\right)+S_{lower}\left(d\right),(11)$

where ${\text{S}}_{\text{upper}}\left(d\right)$ and ${\text{S}}_{\text{lower}}\left(d\right)$ are the lower and upper limits of the characteristic interval of the dth dimension, $\text{S}\left(d\right)$ is the dth dimension of the superior population, $\text{m}\left(d\right)$ is the pre-mutation gene of the d-dimension, and $rand$ is a number generated randomly from 0 to 1. And then, $M$ is the chromosome after the pre-mutation, and $X$ are compared by the greedy rule. If $M$ is better, then the variation is executed and the pre-mutation of the next dimension continues; otherwise, it is not mutated. Until all dimensions have performed the process, $X$ is an excellent individual who has completed directional vertical and partial development. Its mathematical formula can be expressed as Eq. 12:

$X=M,iffit\left(M\right)<fit\left(X\right).(12)$

FIGURE 1

FIGURE 1. Diagram of dimension-by-dimension mutation based on feature intervals.

The Uniform Mutation Based on the Interval of Opposite Features

In order to obtain new genetic information without destroying the diversity of the population, the opposite feature intervals are utilized as the range of variation to carry out by Eqs. 13, 14 in UMOFI. What is more, UMOFI controls $Pm$ :

$\left[O_{L,lower}\left(d\right),O_{L,upper}\left(d\right)\right]=\left\{X_{lower}\left(d\right),min\left[S\left(d\right)\right]\right\},(13)$

$\left[O_{R,lower}\left(d\right),O_{R,upper}\left(d\right)\right]=\left\{max\left[S\left(d\right)\right],X_{upper}\left(d\right)\right\},(14)$

where $O_{L,lower}\left(d\right)$ and $O_{R,lower}\left(d\right)$ represent the lower limits of opposite feature intervals on the left and right, respectively.

Constraints Handling Method

Ramp Rate Limits Handling

$P_{t,i}^{min}=\{\begin{array}{cc}{P}_i^{min},& ift=1\\ \max \left(P_i^{min},P_{t-1,i}-D{R}_i\right),& otherwise\end{array},(15)$

$P_{t,i}^{max}=\{\begin{array}{cc}{P}_i^{max},& ift=1\\ \max \left(P_i^{max},P_{t-1,i}+U{R}_i\right),& otherwise\end{array},(16)$

where $P_{t,i}^{min}$ and $P_{t,i}^{max}$ stand for the new lower and upper bounds, considering simultaneously the ramp rate constraint and the capacity limit of the ith unit for the tth time, as Eqs 15, 16. Then, if $P_{t,i}$ is beyond its new bound, it will be limited to the bound. Namely, $P_{t,i}$ is repaired by Eq. 17. It is simpler and more efficient than the traditional penalty function method:

$P_{t,i}=\{\begin{array}{cc}{P}_{t,i}^{min},& if{P}_{t,i}\le P_{t,i}^{min}\\ P_{t,i}^{max}& if{P}_{t,i}\ge P_{t,i}^{max}\end{array}.(17)$

The Power Balance Constraint Handling

Considering the network transmission loss, the power balance constraint is the most difficult to repair among all constraints. This study proposes a simple and efficient repair technology. The overall process is designed as two stages: firstly, rough adjustment can rapidly reduce the violation and then enter the second fine adjustment stage to eliminate the violation; the detailed steps are described as Steps 1–4.

Step 1. Set the set A = $\left\{\mathrm{1,2,3},\dots ,\text{N}-1,\text{N}\right\}$ , and select randomly a unit r from A and roughly adjust the output by Eq. 18:

$P_{t,r}=P_{t,r}-Vio\left(t\right),(18)$

where $Vio\left(t\right)$ is the violation of the power balance constraint at t time. And if $P_{t,r}$ does not go beyond its new boundary, it is thought that $Vio\left(t\right)$ is so small to repair by the fine stage and thus go to the next step and reset A = $\left\{\mathrm{1,2,3},\dots ,\text{N}-1,\text{N}\right\}$ . Let $k=1$ ; otherwise, remove r unit from A. If A is an empty set, end repair; otherwise, repeat Step 1.

Step 2. Handling the power balance constraint can be converted as solving a quadratic equation, and the output of the unit is solved by Eq. 19. Here, two cases are discussed as follows:

Otherwise, it can be converted as solving a quadratic equation, and the output of the unit is solved by Eq. 19. Here, two cases are discussed as follows:

$B_{kk}{P}_{t,k}^2+\left(2{\displaystyle \sum }_{i\in A,\ne k}{B}_{ki}{P}_{t,i}-1\right)P_{t,k}+\left(P_{D,t}+{\displaystyle \sum }_{i\in A,\ne k}{\displaystyle \sum }_{j\in A,\ne k}{P}_{t,j}{B}_{ij}{P}_{t,j}-{\displaystyle \sum }_{i\in A,\ne k}{P}_{t,i}\right)=0.(19)$

Let a = $B_{kk}$ , b = $2{\displaystyle \sum }_{i\in A,\ne k}{B}_{ki}{p}_{t,i}-1$ , c = $P_{D,t}+{\displaystyle \sum }_{i\in \text{A},\ne k}{\displaystyle \sum }_{j\in A,\ne k}{P}_{t,i}{B}_{ij}{P}_{t,j}-{\displaystyle \sum }_{i\in A,\ne k}{P}_{t,i}$ ; then, if existing, the roots are calculated by $So{l}_1$ and $So{l}_2$ = $\frac{-b\pm \sqrt{b^2-4ac}}{2a}$ when $a\ne 0$ , or $So{l}_3=-\frac{c}{b}$ when $a=0$ and $b\ne 0$ .

Case 1. If no solution, let $=k+1$ ; if $k<N$ , repeat Step 2; and otherwise, end repair.

Case 2. If there are solutions, checking whether they satisfy the other constraints. If satisfied, let $P_{t,k}$ be equal to any, and end; if only a solution is satisfied, let $P_{t,k}$ be equal to the solution. Otherwise, let $k=k+1$ ; if $k<N$ , repeat Step 2; and otherwise, end repair.

Step 1 can rapidly decrease violation of the equality constraint associated with power balances, and Step 2 further decrease or eliminate the violation by fine adjustment as well as solving. And finally, if still infeasible, the feasible-rule (Yuan et al., 2009) is used to strictly screen the feasible solutions of the population.

The Implementation of Genetic Algorithm Dimension Mutation Based on Feature Intervals for Dynamic Economic Dispatch With Plug-In Electric Vehicles

The Implementation of GADMFI on DED integrating PEVs is a process that effectively combines heuristic algorithms and constraints handling methods and optimal mathematical model. The overall framework is described in Figure 2.

FIGURE 2

FIGURE 2. The flowchart of the implementation of GADMFI for the DED with PEVs.

Step 1. The initialization of the population consisted of $NP$ individuals. Each is expressed as a matrix of T rows and (N+1) columns by Eq. 20:

$\left[P,P_{PEV}\right]=\left[\begin{array}{ccccc}{P}_{\mathrm{1,1}}& P_{\mathrm{1,2}}& \cdots & P_{1,N}& P_{PEV,1}\\ P_{\mathrm{2,1}}& P_{\mathrm{2,2}}& \cdots & P_{2,N}& P_{PEV,2}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ P_{T,1}& P_{T,2}& \cdots & P_{T,N}& P_{PEV,T}\end{array}\right],(20)$

and all variables of $P_{t,i}$ are initialized by Eq. 21:

$\{\begin{array}{cc}{P}_{t,i}=P_{t,i}^{min}+rand\times \left(P_{t,i}^{max}-P_{t,i}^{min}\right),& t=\mathrm{1,2},\dots ,T,n=\mathrm{1,2},\dots ,N\\ P_{PEV,t}=P_{PEV,disc}^{max}+rand\times \left(P_{PEV,char}^{max}-P_{PEV,disc}^{max}\right),& t=\mathrm{1,2},\dots ,T\end{array}.(21)$

Step 2. Checking individuals’ feasibility. If feasible, go to the next step; otherwise, repair by constraint handling technology and go to the next step.

Step 3. Evaluate their fitness by Eq. 22, in which the objective functions $f1$ and $f2$ are combined into $f$ by a weighting factor $\lambda$ and update the optimal individual. If FEs are equal to MaxFEs, output the best solution; otherwise, go to the next step:

$f_1=f_1+\lambda f_2.(22)$

Step 4. Update individuals in the population via GADMFI, and go to Step 2

Experimental Results and Analysis

Validation of the Performance of Genetic Algorithm Dimension Mutation Based on Feature Intervals

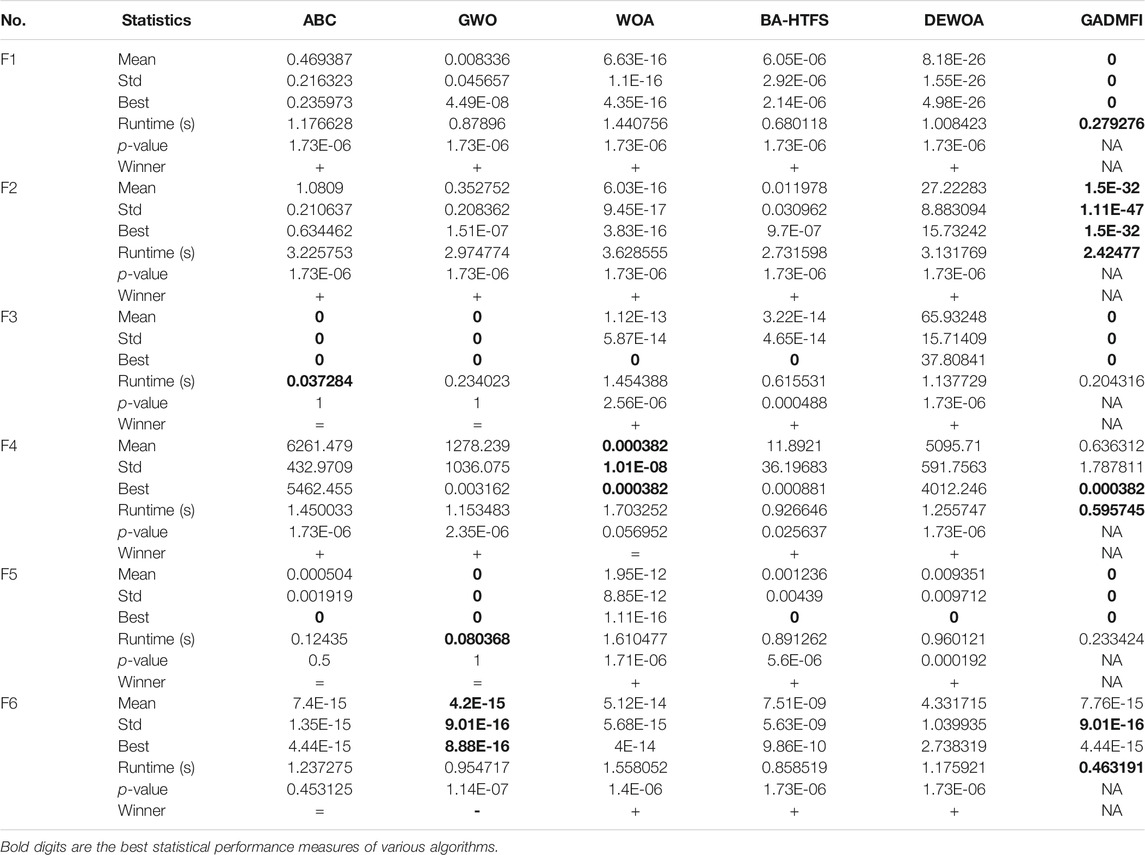
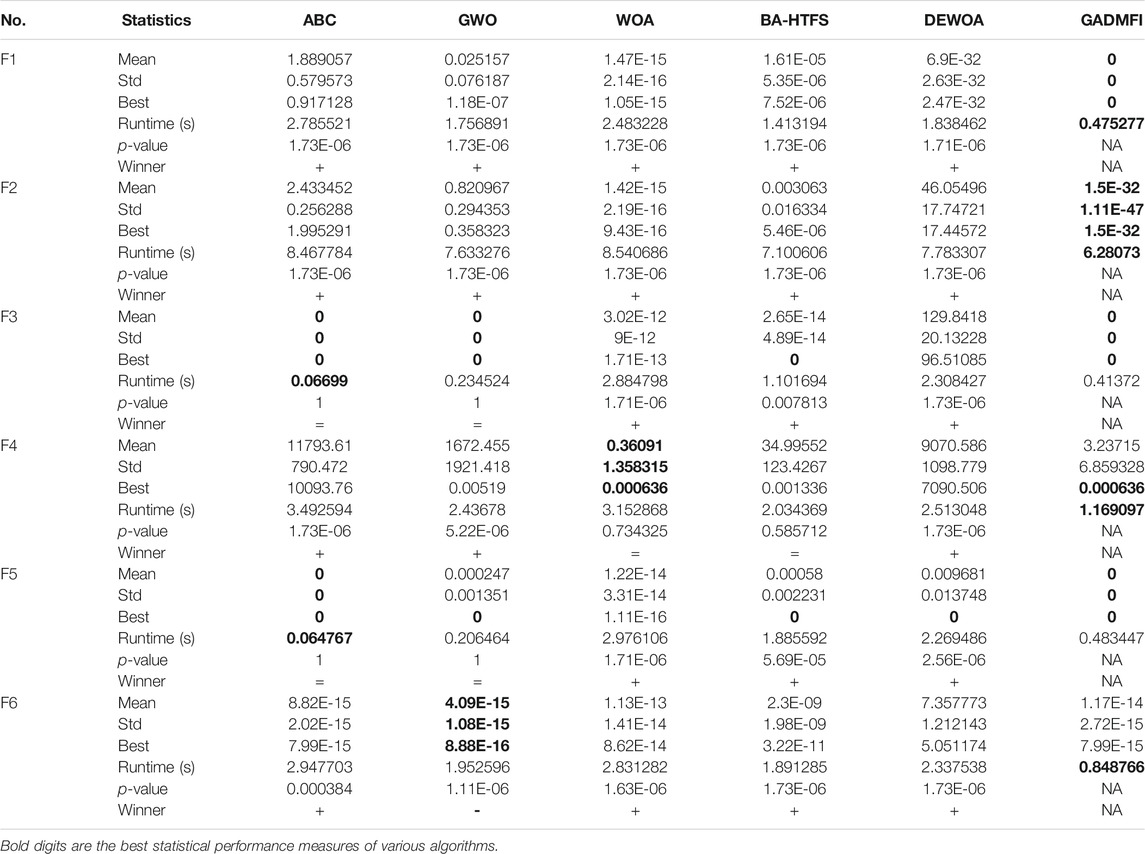
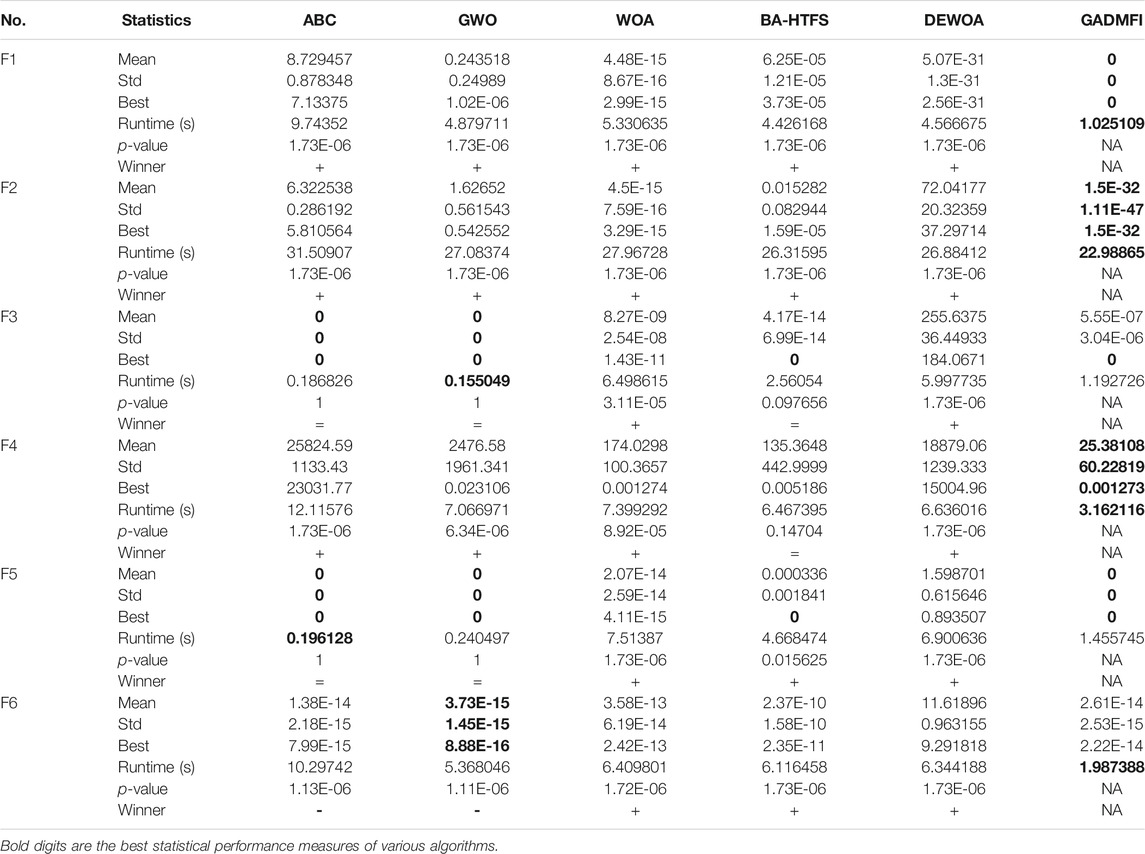
In order to validate the performance of the algorithm, a set of benchmark functions are selected from Civicioglu (2013), which are shown in Table 3, including low-dimensional, multi-dimensional, unimodal (U), multimodal (M), separable (S), and non-separable (N) functions. Advanced meta-heuristics are employed for qualitative and quantitative comparison using the benchmark problems. They are ABC, the grey wolf optimizer (GWO) (Mirjalili et al., 2014), the whale optimization algorithm (WOA) (Mirjalili and Lewis, 2016), the bat algorithm with triangle-flipping strategy (BA-HTFS) (Cai et al., 2017), and Hybrid DE-WOA Algorithm (DEWOA) (Wang et al., 2019c). In addition, the Wilcoxon Signed-Rank Test was used for pairwise comparisons, with the statistical significance value $\alpha =0.05$ . The null hypothesis ${\text{H}}_0$ for this test is as follows: there is no difference between the median of the solution between the two algorithms. The experimental computer is Intel(R) Core (TM) i9-10900F CPU @ 3.7GHZ and its RAM is 16.0 GHz.

TABLE 3

TABLE 3. The basic information of the six benchmark functions.

Parameters Setting

MaXFEs for 30, 50, and 100-dimensional benchmarks are set as $D\ast 10000$ , which means that when $\text{FEs}$ reach $\text{MaxFEs}$ , the optimization algorithms will be terminated. In addition, private parameters of methods taking part in the comparison from the corresponding references are set as in Table 4.

TABLE 4

TABLE 4. The private parameters of the algorithms.

Performance Analysis

The performance of an optimization method should be evaluated in convergence accuracy, speed, and robustness. Therefore, the mean, best, and standard deviation of the objective values based on 30 independent runs from three dimensions 30, 50, and 100 are utilized in the quantitative analysis in Tables 5–7, and several typical qualitative graphs are shown in Figure 3.

TABLE 5

TABLE 5. The statistics data of 30 runs of the benchmarks of 30 dimensions.

TABLE 6

TABLE 6. The statistics data of 30 runs of the benchmarks of 50 dimensions.

TABLE 7

TABLE 7. The statistics data of 30 runs of the benchmarks of 100 dimension.

FIGURE 3

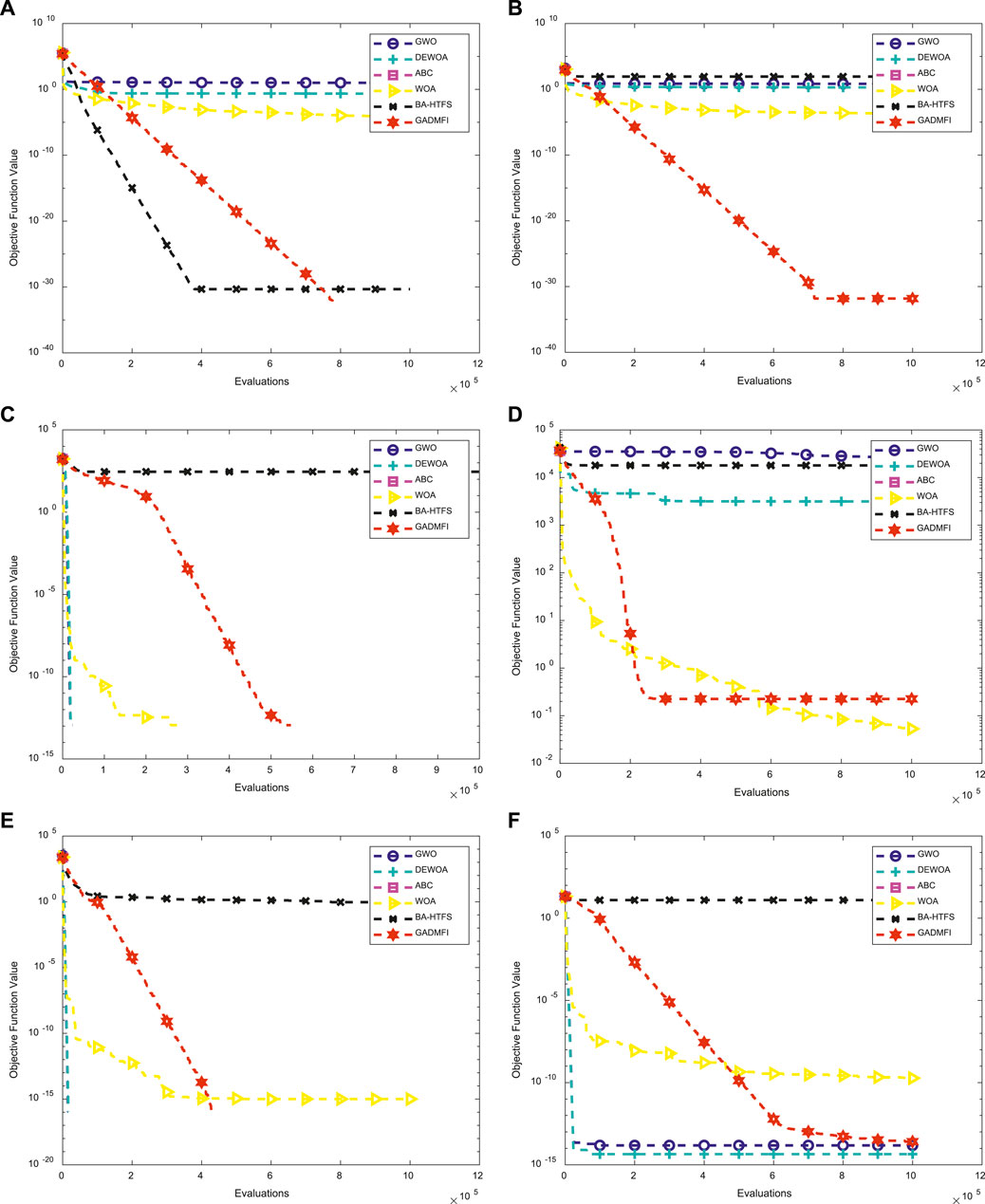
FIGURE 3. Evolution curves of six functions of 100 dimensions are shown. As can be seen, the convergence curve of the GADMFI shows superior exploration and exploitation abilities. (A) The curve presents a straight line, which shows that when dealing with unimodal problems, the proposed DMFI has the potential to explore a promising area. (B–F) With multiple local minima, it stays at approximately constant speed until it converges, which again confirms the role of DMFI.

In Tables 5–7, the optimal values of the indicators including “mean”, “Std”, and “best” are bold among the six comparative algorithms. Winner = 1, 0, and −1 mean GADMFI is obviously superior, equivalent, and inferior to other methods with $\alpha =0.05$ . “NA” refers to not available. First of all, it can be seen that, as the dimension size increases, the performance of the algorithm does not change greatly. It can be observed from best that except for F6, none performs better than the proposed GADMFI in terms of the global search. This is attributed to the collaboration of mechanisms of the proposed algorithm. From mean and Std, it can be seen that GADMFI is the most stable and GWO, secondly, which benefits from DMFI has the ability to be directed fine-grained to develop near the current optimal population. From Runtime, the running time of GADMFI is the shortest in most problems, and it comes from the algorithm maintaining the traditional framework of RCGAs. As can be obtained from Winner, only in F6, problem is inferior to ABC, and F6 of 100 dimensions is inferior to GWO, but the difference is very small.

In Figure 3, evolution curves of six functions of 100 dimensions are shown. As can be seen, the convergence curve of the GADMFI shows superior exploration and exploitation abilities. In F1, the curve presents a straight line, which shows that when dealing with unimodal problems, the proposed DMFI has the potential to explore a promising area. In F2–F6 with multiple local minima, it stays at approximately constant speed until it converges, which again confirms the role of DMFI.

In summary, the proposed GADMFI has outstanding performance for the benchmark problems.

Simulation Results and Discussion on Dynamic Economic Dispatch With Plug-In Electric Vehicles Problem

In this section, in order to verify the reliability of the proposed algorithm and constraint handling method, three scenarios and six cases are considered, as described in Table 8, as follows: Scenario A: only units, Scenario B: units with disorderly PEVs, Scenario C: units with orderly PEVs. Case I: only 5 units, Case II: only 10 units, Case III: 5 units with disorderly PEVs, Case IV:10 units with disorderly PEVs, Case V: 5 units with orderly PEVs, and Case VI: 10 units with orderly PEVs. It is worth noting that PEV and transmission loss are all considered in all cases. The population size of the algorithm is 100, $P_c$ is 0.7, and $P_m$ is 0.3. $\text{MaxFEs}$ is set to $\text{D}*10000$ , $\text{D}$ represents the dimension of the decision variable; that is, for Cases I-II; $\text{D}=\text{N*}24$ , for Cases III-VI; $\text{D}=\left(\text{N}+1\right)\text{*}24$ , and in the study, T is set as 24. In addition, in order to avoid contingency, each case is run independently 30 times. The optimization is implemented in the MATLAB ^®2019b on an Intel(R) Core (TM) i9-10900K CPU @ 3.70 GHz with RAM is 16.0 GHz personal computer.

TABLE 8

TABLE 8. Six cases in three scenarios designed to verify the performance of GADMFI in DED with PEVs.

Scenario A: Only Units Without Plug-In Electric Vehicles

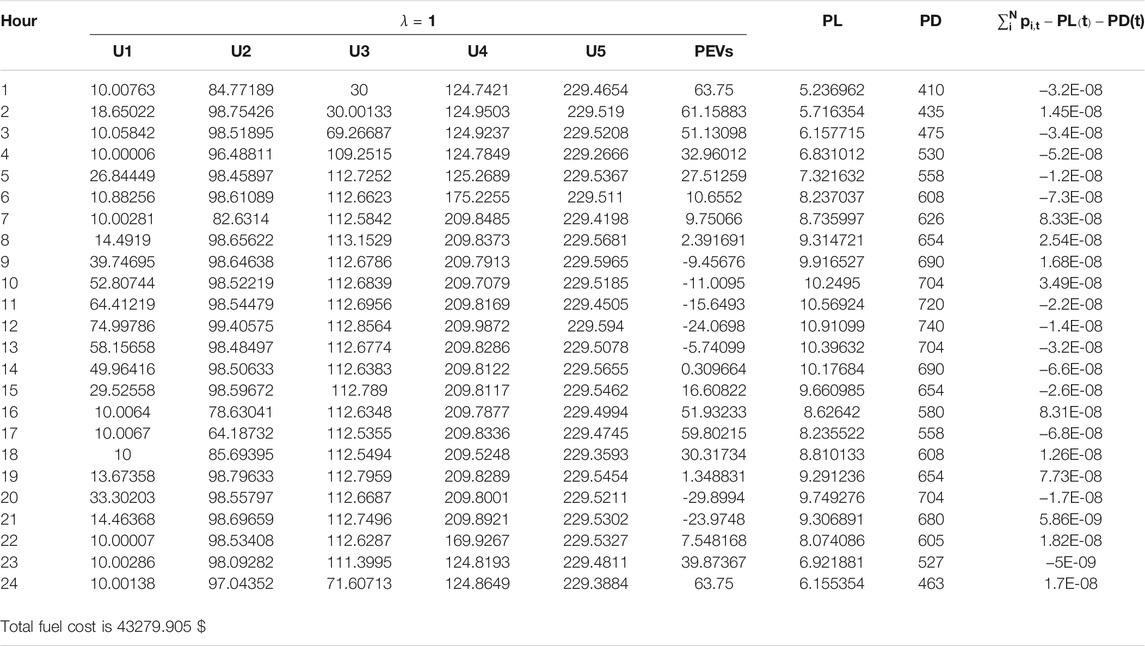
The data of Cases I-II are derived from (Basu, 2008; Mohammadi-ivatloo et al., 2012; Qian et al., 2020), including predicted power demand ( $\text{P}$ D), unit information, and B coefficients in transmission loss. Fuel costs and constraint violations are counted in Table 9 and are compared with the current popular literature, including the new enhanced harmony search (NEHS), the artificial immune system (AIS), the hybrid DE and sequential quadratic programming (DE-SQP), the hybrid PSO and sequential quadratic programming (PSO-SQP), the efficient fitness-based differential evolution algorithm (EFDE), the hybrid seeker optimization algorithm (SOA) and sequential quadratic programming method (SOA-SQP), the simulated annealing (SA), a hybrid genetic algorithm and bacterial foraging approach (HCRO), and the improved bacterial foraging algorithm (IBFA).

TABLE 9

TABLE 9. Specific results of several algorithms for solving the DED without PEVs problem.

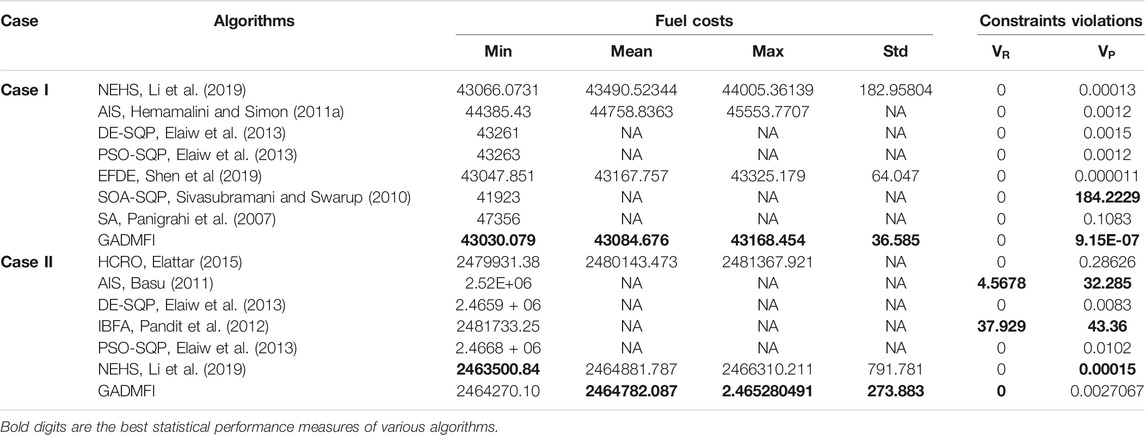
In Table 9, the minimum, average, maximum, and standard deviation of fuel cost of 30 independent trials are presented, as well as the number of violations of unit ramp rate limits and the power balance constraint. Here, the minimum value of each statistic is bold in black font. the constraint violation amount is greater than one and is bold in red font, indicating that the solution is not feasible. For constrained optimization problems, judging the quality of a solution must first meet the conditions of a feasible solution and then evaluate the value of the objective function. Obviously, in the two cases, the proposed constraint processing technology can efficiently repair infeasible solutions. In addition, compared with other algorithms in the literature, except for the minimum value in Case II, it is slightly inferior to NEHS, and GADMFI shows extremely high superiority.

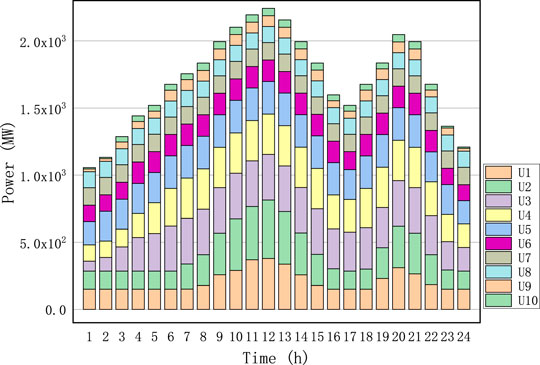
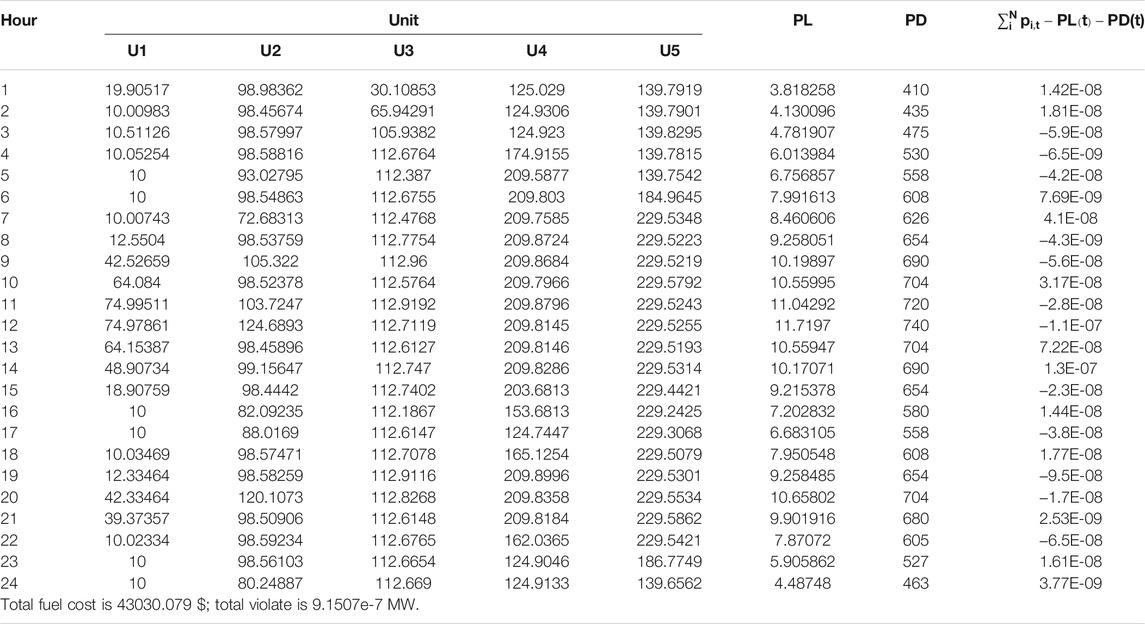
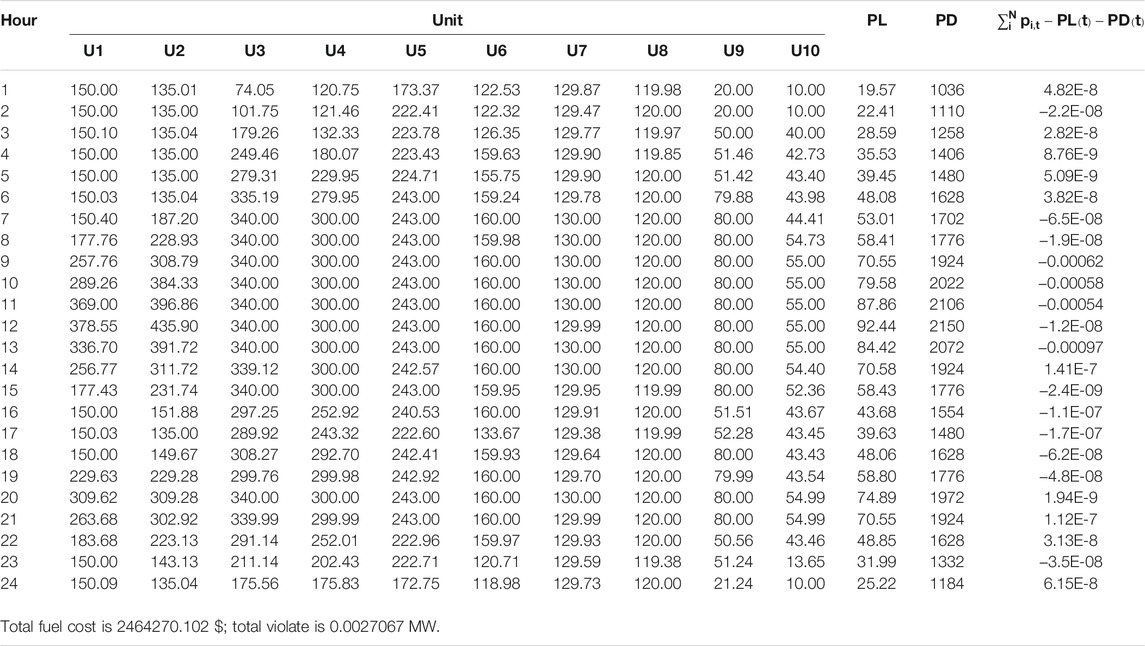
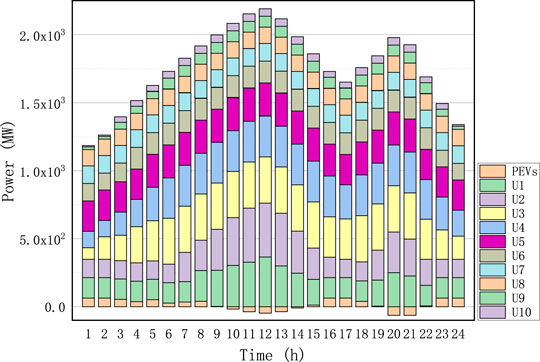
In order to clearly show the output of each unit, the stacked histogram of 10 units is drawn. The impact of the ramp rate limit on the output of the unit can be clearly seen in Figure 4; that is, the power difference between two adjacent moments within the smaller ranges and the optimal solution of 30 trails for Cases I-II are shown in Tables 10-11, as well as the transmission loss ( $\text{PL}$ ) and the amount of violation.

FIGURE 4

FIGURE 4. The power output of the only 10-unit power system.

TABLE 10

TABLE 10. The optimal solution information for Case I: only 5-unit power system.

TABLE 11

TABLE 11. The optimal solution information for Case II: only 10-unit power system.

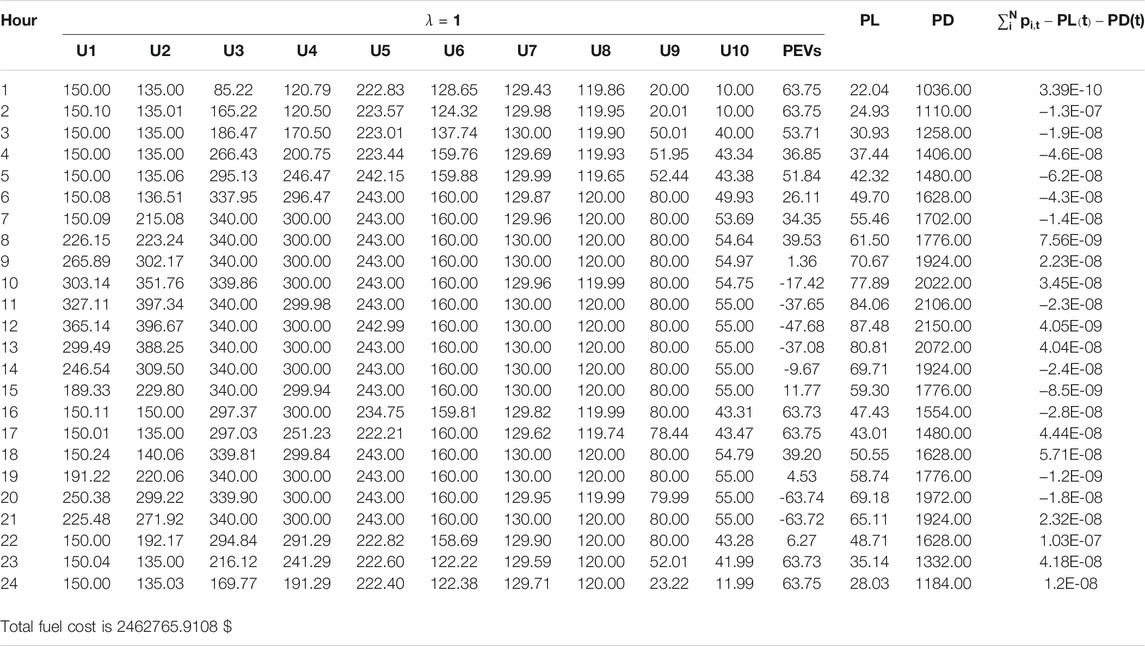
Scenarios B and C: Units With Plug-In Electric Vehicles

A total of 50,000 PEVs are assumed to be integrated into the 5- and 10-unit power systems, and the daily average traveling distance and expected power demand of a PEV are 32.88 miles and 8.22 kWh, respectively (Saber and Venayagamoorthy, 2011). The total power necessity for PEVs is 411 MW and is expected to be met by power generation. The state of charge SOC is 50%; the number of PEVs that can provide V2G/G2V service is 50000/36125; the average battery capacity is 15 kWh; the charging efficiency and the discharge efficiency are both 85%; and available PEVs are 20% (Yang et al., 2017b). In that way, the maximum discharge power $P_{PEV,disc}^{max}=-\mathrm{50,000}\text{*}15\text{KWh*}85\text{\%*}20\text{\%*}50\text{\%}=-63.75\text{KW}$ , and the maximum charge power $P_{PEV,char}^{max}=36125\text{*}15\text{KWh}/85\text{\%*}20\text{\%*}50\text{\%}=+63.75\text{KW}$ . λ = 0 means that electric vehicles are not managed; that is, for Cases III-IV, λ> 0 means that electric vehicles are orderly managed, that is, Cases V-VI. Comparing scenarios B and C and determining $\lambda$ , $f_1$ , and $f_2$ in 30 trials are counted in Table 12.

TABLE 12

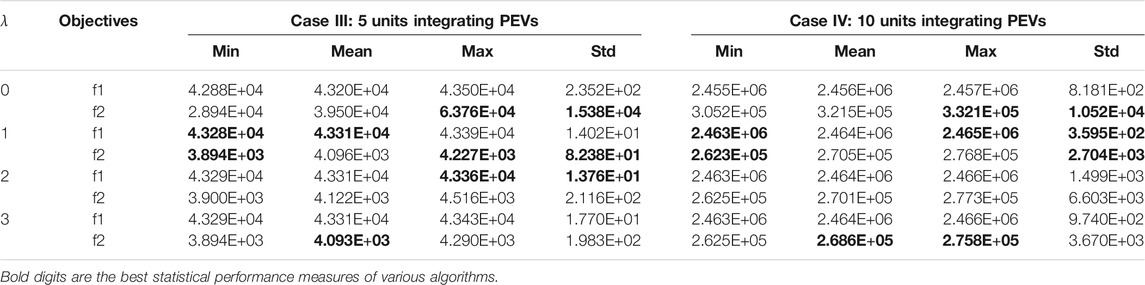
TABLE 12. Statistics of 30 trials in Scenario B, units with disorderly PEVs, and Scenario C, units without orderly PEVs with different $\lambda$ .

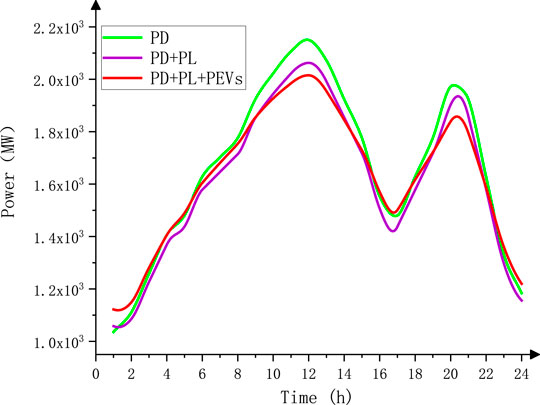
In the column of Max and Std, the larger value is marked in red, indicating that the quality of the solution is poor and unstable, which reflects that the grid fluctuates greatly when electric vehicles are not managed, and further, in λ = 1, 2, 3, when the balance effect is best for $f_1$ and $f_2$ , λ = 1; therefore, in Scenario C, λ is set to 1, and the decision variables are listed in Tables 13 and 14 for Cases V-VI. The output of units and PEVs for Case VI is drawn in Figure 5.

FIGURE 5

FIGURE 5. The power output of the 10 units with an orderly PEVs power system.

TABLE 13

TABLE 13. The optimal solution information for Case V: the 5 units with orderly PEVs.

TABLE 14

TABLE 14. The optimal solution information for Case VI: the 10 units with orderly PEVs.

From Eqs 15, 16, plug-in electric vehicles are effectively managed by the proposed strategy $f_2$ , that is, during peak demand periods, discharge through G2V and charge during trough periods by V2G. In addition, from the perspective of $\text{PL}$ at various times, it is larger than or close to $P_{PEV}$ , so transmission loss should be considered in DED; otherwise, a few decisions may cause mistakes. In order to describe this effect more clearly, PD and PL and $P_{PEV}$ are plotted in Figure 6. It can be seen that the magnitude of the loss is close to the maximum output power of electric vehicles, and the management strategy of electric vehicles has been proved to be effective; that is, it plays the role of cutting peaks and filling valleys.

FIGURE 6

FIGURE 6. The demand considering the loss and PEVs for Case VI.

Conclusion

In view of the impact of plug-in electric vehicles on the power grid, and the complexity of dynamic economic dispatch considering the valve-point effect and transmission loss, this study integrates PEVs into DED and proposes a novel genetic algorithm: GADMFI, a simple and yet efficient constraint handling method aiming at power balance constraints. In three scenarios with two scales, only units, units with disorderly PEVs, and units with orderly PEVs, a horizontal and vertical comparison was carried out. The results show that GADMFI has an excellent performance in dealing with multi-modal, high-dimensional, and large-scale problems such as DED. At the same time, the proposed constraint handling method guarantees the feasibility of solutions and the design of target $f_2$ had achieved the effect of adaptive peak clipping and valley filling.

Data Availability Statement

The author selected the following statement: the data analyzed in this study is subject to the following licenses/restrictions: commercial data. Requests to access these datasets should be directed toemwueWFuZ0BzaWF0LmFjLmNu.

Author Contributions

WY: writing-original draft preparation, data curation. ZP: writing-original draft preparation, investigation. WF: writing-original draft preparation. MM: supervision, visualization, writing-reviewing and Editing.

Funding

This work was financially supported by the National Natural Science Foundation of China (nos. 52077213, 620033326), the Scientific and Technological Project of Henan Province (nos. 202102110281, 202102110282), the Program for Innovative Research Team (in Science and Technology) in University of Henan Province (no. 20IRTSTHN016).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdelaziz, A. Y., Kamh, M. Z., Mekhamer, S. F., and Badr, M. A. L. (2008). A Hybrid HNN-QP Approach for Dynamic Economic Dispatch Problem. Electric Power Syst. Res. 78, 1784–1788. doi:10.1016/j.epsr.2008.03.011

CrossRef Full Text | Google Scholar

Akopov, A. S., Beklaryan, L. A., Thakur, M., and Verma, B. D. (2019). Parallel Multi-Agent Real-Coded Genetic Algorithm for Large-Scale Black-Box Single-Objective Optimisation. Knowledge-Based Syst. 174, 103–122. doi:10.1016/j.knosys.2019.03.003

CrossRef Full Text | Google Scholar

Ali, M. Z., Awad, N. H., Suganthan, P. N., Shatnawi, A. M., and Reynolds, R. G. (2018). An Improved Class of Real-Coded Genetic Algorithms for Numerical Optimization✰. Neurocomputing 275, 155–166. doi:10.1016/j.neucom.2017.05.054

CrossRef Full Text | Google Scholar

Basu, M. (2011). Artificial Immune System for Dynamic Economic Dispatch. Int. J. Electr. Power Energ. Syst. 33, 131–136. doi:10.1016/j.ijepes.2010.06.019

CrossRef Full Text | Google Scholar

Basu, M. (2008). Dynamic Economic Emission Dispatch Using Nondominated Sorting Genetic Algorithm-II. Int. J. Electr. Power Energ. Syst. 30, 140–149. doi:10.1016/j.ijepes.2007.06.009

CrossRef Full Text | Google Scholar

Behera, S., Behera, S., and Barisal, A. K. (2019). “Ieee. Dynamic Economic Load Dispatch with Plug-In Electric Vehicles Using Social Spider Algorithm,” in Proceedings of the 2019 3rd International Conference on Computing Methodologies and Communication (New York: IEEE), 489–494.

Google Scholar

Cai, X., Wang, H., Cui, Z., Cai, J., Xue, Y., and Wang, L. (2017). Bat Algorithm with triangle-flipping Strategy for Numerical Optimization. Int. J. Mach. Learn. Cyber. 9, 199–215. doi:10.1007/s13042-017-0739-8

CrossRef Full Text | Google Scholar

Chakraborty, P., Roy, G. G., Panigrahi, B. K., Bansal, R. C., and Mohapatra, A. (2012). Dynamic Economic Dispatch Using harmony Search Algorithm with Modified Differential Mutation Operator. Electr. Eng. 94, 197–205. doi:10.1007/s00202-011-0230-6

CrossRef Full Text | Google Scholar

Chuang, Y.-C., Chen, C.-T., and Hwang, C. (2015). A Real-Coded Genetic Algorithm with a Direction-Based Crossover Operator. Inf. Sci. 305, 320–348. doi:10.1016/j.ins.2015.01.026

CrossRef Full Text | Google Scholar

Chuang, Y.-C., Chen, C.-T., and Hwang, C. (2016). A Simple and Efficient Real-Coded Genetic Algorithm for Constrained Optimization. Appl. Soft Comput. 38, 87–105. doi:10.1016/j.asoc.2015.09.036

CrossRef Full Text | Google Scholar

Civicioglu, P. (2013). Backtracking Search Optimization Algorithm for Numerical Optimization Problems. Appl. Maths. Comput. 219, 8121–8144. doi:10.1016/j.amc.2013.02.017

CrossRef Full Text | Google Scholar

D’Angelo, G., and Palmieri, F. G. G. A. (2021). A Modified Genetic Algorithm with Gradient-Based Local Search for Solving Constrained Optimization Problems. Inf. Sci. 547, 136–162. doi:10.1016/j.ins.2020.08.040

CrossRef Full Text | Google Scholar

Deep, K., and Thakur, M. (2007). A New Crossover Operator for Real Coded Genetic Algorithms. Appl. Maths. Comput. 188, 895–911. doi:10.1016/j.amc.2006.10.047

CrossRef Full Text | Google Scholar

Elaiw, A. M., Xia, X., and Shehata, A. M. (2013). Hybrid DE-SQP and Hybrid PSO-SQP Methods for Solving Dynamic Economic Emission Dispatch Problem with Valve-point Effects. Electric Power Syst. Res. 103, 192–200. doi:10.1016/j.epsr.2013.05.015

CrossRef Full Text | Google Scholar

Elattar, E. E. (2015). A Hybrid Genetic Algorithm and Bacterial Foraging Approach for Dynamic Economic Dispatch Problem. Int. J. Electr. Power Energ. Syst. 69, 18–26. doi:10.1016/j.ijepes.2014.12.091

CrossRef Full Text | Google Scholar

Fang, N., Zhou, J., Zhang, R., Liu, Y., and Zhang, Y. (2014). A Hybrid of Real Coded Genetic Algorithm and Artificial Fish Swarm Algorithm for Short-Term Optimal Hydrothermal Scheduling. Int. J. Electr. Power Energ. Syst. 62, 617–629. doi:10.1016/j.ijepes.2014.05.017

CrossRef Full Text | Google Scholar

Hemamalini, S., and Simon, S. P. (2011). Dynamic Economic Dispatch Using Artificial Bee colony Algorithm for Units with Valve-point Effect. Euro. Trans. Electr. Power 21, 70–81. doi:10.1002/etep.413

CrossRef Full Text | Google Scholar

Hemamalini, S., and Simon, S. P. (2011). Dynamic Economic Dispatch Using Artificial Immune System for Units with Valve-point Effect. Int. J. Electr. Power Energ. Syst. 33, 868–874. doi:10.1016/j.ijepes.2010.12.017

CrossRef Full Text | Google Scholar

Iyer, V. H., Mahesh, S., Malpani, R., Sapre, M., and Kulkarni, A. J. (2019). Adaptive Range Genetic Algorithm: A Hybrid Optimization Approach and its Application in the Design and Economic Optimization of Shell-And-Tube Heat Exchanger. Eng. Appl. Artif. Intelligence 85, 444–461. doi:10.1016/j.engappai.2019.07.001

CrossRef Full Text | Google Scholar

Kwak, N. S., and Lee, J. (2016). An Enhancement of Selection and Crossover Operations in Real-Coded Genetic Algorithm for Large-Dimensionality Optimization. J. Mech. Sci. Technol. 30, 237–247. doi:10.1007/s12206-015-1227-2

CrossRef Full Text | Google Scholar

Li, Z., Zou, D., and Kong, Z. (2019). A harmony Search Variant and a Useful Constraint Handling Method for the Dynamic Economic Emission Dispatch Problems Considering Transmission Loss. Eng. Appl. Artif. Intelligence 84, 18–40. doi:10.1016/j.engappai.2019.05.005

CrossRef Full Text | Google Scholar

Mei, P., Wu, L., Zhang, H., and Liu, Z. (2019). A Hybrid Multi-Objective Crisscross Optimization for Dynamic Economic/Emission Dispatch Considering Plug-In Electric Vehicles Penetration. Energies 12, 3847. doi:10.3390/en12203847

CrossRef Full Text | Google Scholar

Mellal, M. A., and Williams, E. J. (2020). Cuckoo Optimization Algorithm with Penalty Function and Binary Approach for Combined Heat and Power Economic Dispatch Problem. Energ. Rep. 6, 2720–2723. doi:10.1016/j.egyr.2020.10.004

CrossRef Full Text | Google Scholar

Mirjalili, S., and Lewis, A. (2016). The Whale Optimization Algorithm. Adv. Eng. Softw. 95, 51–67. doi:10.1016/j.advengsoft.2016.01.008

CrossRef Full Text | Google Scholar

Mirjalili, S., Mirjalili, S. M., and Lewis, A. (2014). Grey Wolf Optimizer. Adv. Eng. Softw. 69, 46–61. doi:10.1016/j.advengsoft.2013.12.007

CrossRef Full Text | Google Scholar

Mohammadi-ivatloo, B., Rabiee, A., and Ehsan, M. (2012). Time-varying Acceleration Coefficients IPSO for Solving Dynamic Economic Dispatch with Non-smooth Cost Function. Energ. Convers. Manage. 56, 175–183. doi:10.1016/j.enconman.2011.12.004

CrossRef Full Text | Google Scholar

Nakane, T., Lu, X., and Zhang, C. (2020). A Search History-Driven Offspring Generation Method for the Real-Coded Genetic Algorithm. Comput. Intell. Neurosci. 2020, 8835852. doi:10.1155/2020/8835852

PubMed Abstract | CrossRef Full Text | Google Scholar

Naqvi, F. B., Yousaf Shad, M., and Khan, S. (2020). A New Logistic Distribution Based Crossover Operator for Real-Coded Genetic Algorithm. J. Stat. Comput. Simulation 91, 817–835. doi:10.1080/00949655.2020.1832093

CrossRef Full Text | Google Scholar

Niu, Q., Zhang, H., Li, K., and Irwin, G. W. (2014). An Efficient harmony Search with New Pitch Adjustment for Dynamic Economic Dispatch. Energy 65, 25–43. doi:10.1016/j.energy.2013.10.085

CrossRef Full Text | Google Scholar

Pan, S., Jian, J., and Yang, L. (2018). A Hybrid MILP and IPM Approach for Dynamic Economic Dispatch with Valve-point Effects. Int. J. Electr. Power Energ. Syst. 97, 290–298. doi:10.1016/j.ijepes.2017.11.004

CrossRef Full Text | Google Scholar

Pandit, N., Tripathi, A., Tapaswi, S., and Pandit, M. (2012). An Improved Bacterial Foraging Algorithm for Combined Static/dynamic Environmental Economic Dispatch. Appl. Soft Comput. 12, 3500–3513. doi:10.1016/j.asoc.2012.06.011

CrossRef Full Text | Google Scholar

Panigrahi, C. K., Chattopadhyay, P. K., Chakrabarti, R. N., and Basu, M. (2007). Simulated Annealing Technique for Dynamic Economic Dispatch. Electric Power Components Syst. 34, 577–586. doi:10.1080/15325000500360843

CrossRef Full Text | Google Scholar

Picek, S., Jakobovic, D., and Golub, M. (2013). Ieee. On the Recombination Operator in the Real-Coded Genetic Algorithms. Ieee Congress Evol. Comput. 2013, 3103–3110.

Google Scholar

Picek, S., Jakobovic, D., and Golub, M. (2013). On the Recombination Operator in the Real-Coded Genetic Algorithms. IEEE Congress Evol. Comput. 2013, 3103–3110. doi:10.1109/CEC.2013.6557948

CrossRef Full Text | Google Scholar

Qian, S., Wu, H., and Xu, G. (2020). An Improved Particle Swarm Optimization with Clone Selection Principle for Dynamic Economic Emission Dispatch. Soft Comput. 24, 15249–15271. doi:10.1007/s00500-020-04861-4

CrossRef Full Text | Google Scholar

Ravikumar Pandi, V., and Panigrahi, B. K. (2011). Dynamic Economic Load Dispatch Using Hybrid Swarm Intelligence Based harmony Search Algorithm. Expert Syst. Appl. 38, 8509–8514. doi:10.1016/j.eswa.2011.01.050

CrossRef Full Text | Google Scholar

Saber, A. Y., and Venayagamoorthy, G. K. (2011). Plug-in Vehicles and Renewable Energy Sources for Cost and Emission Reductions. IEEE Trans. Ind. Electron. 58, 1229–1238. doi:10.1109/tie.2010.2047828

CrossRef Full Text | Google Scholar

Sawyerr, B. A., Adewumi, A. O., and Ali, M. M. (2014). Real-coded Genetic Algorithm with Uniform Random Local Search. Appl. Maths. Comput. 228, 589–597. doi:10.1016/j.amc.2013.11.097

CrossRef Full Text | Google Scholar

Sawyerr, B. A., Ali, M. M., and Adewumi, A. O. (2011). A Comparative Study of Some Real-Coded Genetic Algorithms for Unconstrained Global Optimization. Optimization Methods Softw. 26, 945–970. doi:10.1080/10556788.2010.491865

CrossRef Full Text | Google Scholar

Shen, X., Zou, D., Duan, N., and Zhang, Q. (2019). An Efficient Fitness-Based Differential Evolution Algorithm and a Constraint Handling Technique for Dynamic Economic Emission Dispatch. Energy, 186. doi:10.1016/j.energy.2019.07.131

CrossRef Full Text | Google Scholar

Sivasubramani, S., and Swarup, K. S. (2010). Hybrid SOA-SQP Algorithm for Dynamic Economic Dispatch with Valve-point Effects. Energy 35, 5031–5036. doi:10.1016/j.energy.2010.08.018

CrossRef Full Text | Google Scholar

Tang, P.-H., and Tseng, M.-H. (2013). Adaptive Directed Mutation for Real-Coded Genetic Algorithms. Appl. Soft Comput. 13, 600–614. doi:10.1016/j.asoc.2012.08.035

CrossRef Full Text | Google Scholar

Tehzeeb-ul-Hassan, H., Alquthami, T., Butt, S. E., Tahir, M. F., and Mehmood, K. (2020). Short-term Optimal Scheduling of Hydro-thermal Power Plants Using Artificial Bee colony Algorithm. Energ. Rep. 6, 984–992. doi:10.1016/j.egyr.2020.04.003

CrossRef Full Text | Google Scholar

Thakur, M., Meghwani, S. S., and Jalota, H. (2014). A Modified Real Coded Genetic Algorithm for Constrained Optimization. Appl. Maths. Comput. 235, 292–317. doi:10.1016/j.amc.2014.02.093

CrossRef Full Text | Google Scholar

Wang, J., Zhang, M., Ersoy, O. K., Sun, K., and Bi, Y. (2019). An Improved Real-Coded Genetic Algorithm Using the Heuristical Normal Distribution and Direction-Based Crossover. Comput. Intell. Neurosci. 2019, 4243853. doi:10.1155/2019/4243853

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Cheng, Z., Ersoy, O. K., Zhang, P., Dai, W., and Dong, Z. (2018). Improvement Analysis and Application of Real-Coded Genetic Algorithm for Solving Constrained Optimization Problems. Math. Probl. Eng. 2018, 1–16. doi:10.1155/2018/5760841

CrossRef Full Text | Google Scholar

Wang, Y., Zhou, J., Lu, Y., Qin, H., and Wang, Y. (2011). Chaotic Self-Adaptive Particle Swarm Optimization Algorithm for Dynamic Economic Dispatch Problem with Valve-point Effects. Expert Syst. Appl. doi:10.1016/j.eswa.2011.04.236

CrossRef Full Text | Google Scholar

Wang, Y., Yang, Z., Mourshed, M., Guo, Y., Niu, Q., and Zhu, X. (2019). Demand Side Management of Plug-In Electric Vehicles and Coordinated Unit Commitment: A Novel Parallel Competitive Swarm Optimization Method. Energ. Convers. Manage. 196, 935–949. doi:10.1016/j.enconman.2019.06.012

CrossRef Full Text | Google Scholar

Wang, Z. Y., Li, Y. R., and Tang, Y. Q. (2019). “Ieee. An Efficient Hybrid DE-WOA Algorithm for Numerical Function Optimization,” in Ieee 28th International Symposium on Industrial Electronics (New York: Ieee; 2019), 2629–2634.

Google Scholar

Yang, Z., Li, K., and Foley, A. (2015). Computational Scheduling Methods for Integrating Plug-In Electric Vehicles with Power Systems: A Review. Renew. Sustain. Energ. Rev. 51, 396–416. doi:10.1016/j.rser.2015.06.007

CrossRef Full Text | Google Scholar

Yang, Z., Li, K., Niu, Q., and Xue, Y. (2017). A Comprehensive Study of Economic Unit Commitment of Power Systems Integrating Various Renewable Generations and Plug-In Electric Vehicles. Energ. Convers. Manage. 132, 460–481. doi:10.1016/j.enconman.2016.11.050

CrossRef Full Text | Google Scholar

Yang, Z., Li, K., Niu, Q., and Xue, Y. (2017). A Novel Parallel-Series Hybrid Meta-Heuristic Method for Solving a Hybrid Unit Commitment Problem. Knowledge-Based Syst. 134, 13–30. doi:10.1016/j.knosys.2017.07.013

CrossRef Full Text | Google Scholar

Yang, Z., Li, K., Niu, Q., Xue, Y., and Foley, A. (2014). A Self-Learning TLBO Based Dynamic Economic/environmental Dispatch Considering Multiple Plug-In Electric Vehicle Loads. J. Mod. Power Syst. Clean. Energ. 2, 298–307. doi:10.1007/s40565-014-0087-6

CrossRef Full Text | Google Scholar

Yuan, X., Wang, L., Zhang, Y., and Yuan, Y. (2009). A Hybrid Differential Evolution Method for Dynamic Economic Dispatch with Valve-point Effects. Expert Syst. Appl. 36, 4042–4048. doi:10.1016/j.eswa.2008.03.006

CrossRef Full Text | Google Scholar

Zou, D., Li, S., Kong, X., Ouyang, H., and Li, Z. (2018). Solving the Dynamic Economic Dispatch by a Memory-Based Global Differential Evolution and a Repair Technique of Constraint Handling. Energy 147, 59–80. doi:10.1016/j.energy.2018.01.029

CrossRef Full Text | Google Scholar