
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 08 June 2021
Sec. Smart Grids
Volume 9 - 2021 | https://doi.org/10.3389/fenrg.2021.693252
This article is part of the Research Topic Advanced Optimization and Control for Smart Grids with High Penetration of Renewable Energy Systems View all 49 articles
To reliably evaluate the practical performance and to undertake optimal control of PV systems, a precise PV cell parameter extraction–based accurate modeling of PV cells is extremely crucial. However, its inherent high nonlinear and multimodal characteristics usually hinder conventional optimization methods to obtain a fast and satisfactory performance. Besides, insufficient current–voltage (I–V) data provided by manufacturers cannot guarantee high accuracy and flexibility of PV cell parameter extraction under various operation scenarios. Hence, this article proposes a novel parameter extraction strategy by data prediction–based meta-heuristic algorithm (DPMhA). An extreme learning machine (ELM) is adopted to predict output I–V data from measured data, which can provide a more reliable fitness function to meta-heuristic algorithms (MhAs). Consequently, MhAs can undertake a more stable search for optimal solution through extended I–V data; thus, PV cell parameters can be obtained with high accuracy and convergence rate. Its effectiveness is validated via three typical PV cell models, that is, single diode model (SDM), double diode model (DDM), and three diode model (TDM). Last, comprehensive case studies illustrate that the DPMhA can considerably enhance the accuracy and effectiveness compared with those without data prediction.
With severe environmental deterioration (Peng et al., 2020), fossil fuel depletion (Yang et al., 2018), severe air pollution (Sun et al., 2020), and increasing concerns on global energy crisis over the past decade (Yang et al., 2018), energy reform and sustainable development have become essential for an environment-friendly society (Wang et al., 2020). Hence, environmental protection and energy conservation are paramount for all countries around the world (Shen et al., 2019), in which exploitation and utilization of various renewable energy technologies, for example, wind (Li et al., 2019; Zhang et al., 2019) and solar (Liu et al., 2020), have been broadly focused. In particular, solar energy is considered to be one of the most sustainable and viable energy sources of the future (Chaibi et al., 2019), such that photovoltaic (PV) system is widely used for solar energy applications thanks to its distinct merits, for example, abundant resources, low cost, and pollution-free (Yang et al., 2016).
Particularly, measured current–voltage (I–V) data–based reliable PV modeling is extremely critical to dynamic behavior analysis of PV systems. Thus far, a series of PV cell modeling methods have been proposed (Jordehi, 2016) to characterize the output of PV systems for better performance analysis and prediction (Youssef et al., 2017), maximum power point tracking (MPPT) (Yang et al., 2019; Yang et al., 2019), and fault diagnosis (Chen et al., 2018). Two equivalent circuit models, single diode model (SDM) (Nunes et al., 2018) and double diode model (DDM) (Abbassi et al., 2018), are extensively adopted for the sake of simplicity, while more complicated triple diode model (TDM) (Qais et al., 2019) is barely investigated because it might increase computation burden. Nevertheless, as the TDM allows a more efficient and accurate analysis of the complex output characteristics of PV systems, this article validates the performance of all three PV models mentioned above. In particular, the accurate extraction of several electrical parameters related to the model is the most basic and critical step of reliable modeling. However, they are unavailable and changeable as insufficient electrical parameters provided by manufacturers and are only experimentally obtained under standard test conditions (STCs) (Xiong et al., 2018). Besides, their values are also time-varying due to degradation and faults of PV cells, which further increases modeling uncertainties. Hence, the aforementioned two shortcomings render parameter extraction thorny to obtain satisfactory results in practical applications.
To tackle such obstacles, the design of numerous methods consists of three main categories, namely, analytical methods (Majdoul et al., 2015; Torabi et al., 2017), deterministic techniques, and meta-heuristic algorithms (MhAs). Analytical methods are based on a series of mathematical calculations and a number of key points on the I–V curve, which owns a high degree of simplicity, but lacks high accuracy in different operating scenarios. Meanwhile, deterministic techniques, including iterative curve fitting (Villalva et al., 2009) and Newtonian-based methods (Li et al., 2017), can yield more accurate results, while they are extremely demanding in terms of model properties. Moreover, they are highly sensitive to initial operation conditions; thus, the inherent high nonlinearity and multimodality of PV systems always make them easy to be trapped at a local optimum. Hence, the limitations of the aforementioned two methods hinder them to maintain a stable and satisfactory performance on PV cell parameter extraction. In contrast, MhAs can effectively avoid these shortcomings thanks to their outstanding merits, such as high flexibility on problem characteristics (Nesmachnow, 2014), easy implementation (Roeva and Fidanova, 2018), and insensitivity to gradient information (Figueroa et al., 2020). Until now, a large number of MhAs are adopted in PV cell parameter extraction (Yang et al., 2020), such as genetic algorithm (GA) (Jervase et al., 2001), differential evolution (DE) (Ishaque and Salam, 2011), particle swarm optimization (PSO) (Ye et al., 2009), artificial bee colony (ABC) (Oliva et al., 2014), whale optimization algorithm (WOA) (Amroune et al., 2019; Dasu et al., 2019), backtracking search algorithm (BSA) (Yu et al., 2018), moth flame optimizer (MFO) (Allam et al., 2016), grey wolf optimization (GWO) (Yang et al., 2017), bird mating optimizer (BMO) (Askarzadeh and Rezazadeh, 2013), water cycle algorithm (WCA) (Kler et al., 2017),wind-driven optimization (WDO) (Derick et al., 2017), fireworks algorithm (FWA) (Babu et al., 2016), and various hybrids.
Except for the improvements focusing on mechanism and structure of algorithms to enhance the optimization performance, one should realize that all modeling techniques heavily rely on the number and accuracy of measured data. However, in order to improve the simulation accuracy, some parameters in the PV system are not provided by the manufacturer and therefore need to be extracted based on the I–V curve. Such low-dimensional data provided by the manufacturer, while saving computational resources, may also cause important data information to be lost during the simulation. Hence, it is imperative to develop effective data processing methods to enrich data samples. Recently, artificial neural network (ANN) (Grondin-Perez et al., 2014; Zhao et al., 2019) and deep learning strategy (Schmidhuber, 2015) show their great effectiveness in data analysis and prediction. This article adopts a learning algorithm called extreme learning machine (ELM) with a single-hidden layer feedforward neural network (SLFN) for output I–V data prediction (Huang et al., 2006), which can provide a more reliable fitness function to MhAs. The main contributions of this article can be summarized as follows:
• The existing MhAs are directly adopted for PV cell parameter extraction via measured I–V data of PV systems, which are easy to be trapped at a low-quality optimum if measured I–V data are inadequate or distributed intensively. In contrast, the proposed data prediction–based MhA (DPMhA) can effectively solve this difficulty since measured I–V data can be extended via ELM-based data prediction.
• Several advanced MhAs with data prediction are applied for parameter extraction of PV cells, which are thoroughly validated via three different kinds of PV models.
• Four case studies show that DPMhA can achieve simulation results with higher precision and stability compared with those only based on measured data.
The rest of this article is organized as follows: PV Cell Modeling and Problem Formulation illustrates mathematical modeling of PV cell and objective function. The overall introduction of data prediction–based MhAs is elaborated in Methodologies. Case study results on different PV models are provided in Case Studies. Last, conclusions are given in Conclusion.
Shockley diode–based equivalent circuits are always deemed as standard PV models, among which three most widely used models, that is, SDM, DDM, and TDM are discussed in this section.
In general, there are minor differences in the model structures of the three models mentioned above, which are also systematically summarized in Supplementary Table S1 for a more detailed presentation.
As demonstrated in Supplementary Table S1,
where T represents the surface temperature; K is the Boltzmann constant, which has a value of
All the other variables are provided in Nomenclature.
The main objective of parameter identification for various PV models is to find suitable parameters so that the model can more accurately describe the output characteristics of the PV system and minimize the errors between the experimentally collected data and the simulation data, which can be evaluated quantitatively by means of an objective function. The root mean square error (RMSE) is chosen here as the objective function, which can be calculated as
where
Error functions
From Table 1, for the sake of minimizing the difference between experimental data and simulated data, objective function
ELM is a simple learning strategy for SLFNs that mainly depends on generalized inverse matrix theory (Huang and Siew, 2005), which randomly initializes the input weight with no adjustment requirement in subsequent operations (Huang et al., 2000; Huang et al., 2006). Besides, output weight is analytically determined by generalized inverse, which only requires a one-step calculation. Hence, compared with other normal feedforward network learning strategies, for example, back-propagation (BP) algorithm, the ELM can significantly enhance robustness, generalization ability, learning speed, and training accuracy. The main operation structure of ELM is demonstrated in Figure 1.
For N different training samples
where
Since SLFNs can approximate training samples with zero errors for any
Hence, the two equations above are rewritten more simply, as follows:
where
When the hidden layer output matrix is column full rank, it yields
where
For a PV cell, output current and voltage can be measured for parameter extraction, while the increase of measured data will lead to a high extraction accuracy. To employ ELM for output I–V data prediction, PV cell voltage and current are regarded as the input and output of ELM, respectively. Therefore, output I–V data prediction of a PV cell can be achieved by ELM with single input and single output, as described by Eqs. 3–9.
Based on prediction data, MhAs can implement a balance between global and local search with an updated fitness function. Due to all optimization, variables are limited within their lower and upper bounds; RMSE (2) is taken as the fitness function, which should also take the prediction data into account, as follows:
where
The overall operation framework of DPMhA mainly consists of three parts, as illustrated in Figure 2. First, measured output I–V data of various PV cells are transferred to the ELM. Second, the ELM is trained by measured data to predict new data; thus, a more reliable fitness function can be established to evaluate the performance of various MhAs. Finally, MhAs implement relevant global exploration and local exploitation to find optimal PV parameters. Particularly, the detailed execution procedure of DPMhA is given in Table 2, in which the main differences between various algorithms are individual roles and searching mechanisms of global exploration and local exploitation.
In this section, several well-established MhAs are utilized for parameter extraction of three PV cell models. In particular, a total of 26 pairs of measured I–V datasets utilized for simulation are acquired from Easwarakhanthan et al. (1986), which are measured on a 57 mm diameter commercial silicon R.T.C. France solar cell under weather condition (G = 1000 W/m2 and T = 33°C). This dataset has been widely used to test the techniques developed for parameter extraction. Many existing studies (Ye et al., 2009)-(Yu et al., 2018) were tested based on these 26 pairs of measured data. To guarantee a fair comparison with them, the proposed GNN is also implemented based on these 26 pairs of measured data. For the sake of verifying the optimization performance of MhAs based on insufficient measurement data, six sets of data were selected from 26 sets of measurement data in different ratios of 50, 60, 70, 80, 90, and 100% of the measurement data. The presented ELM is essentially a simple single-input and single-output network. Therefore, the pairs of measured data are adequate for training the ELM. To provide a reliable fitness function to MhAs, the total number of each dataset and the prediction data are set to be 50, for example, 24 prediction data for 100% dataset. In addition, each MhA is evaluated under two circumstances, that is, without data prediction (i.e., with only selected measured data) and with data prediction. Note that the measured I–V data are not hard to be acquired. But it is difficult to acquire adequate high-accuracy data with a general measuring instrument. Hence, the measured I–V data cannot completely represent the I–V output feature of the PV cell. Besides, the added prediction I–V data can provide a reliable fitness function; thus, the optimization accuracy and convergence stability of each meta-heuristic algorithm can be improved.
The main parameters of meta-heuristic algorithms are the population size and the maximum number of iterations. To guarantee a fair comparison, these two parameters are set to be the same values for all MhAs under each PV model that is designed to be identical, in which their specific parameters (e.g., the maximum velocity in PSO) are set to be the default values. In order to fairly compare the performance of each algorithm, the maximum number of iterations and the population size of each algorithm were set to be the same. Specifically, the maximum number of iterations for each model was 300, while the population sizes for SDM, DDM, and TDM were designed to be 30, 50, and 70, respectively. In addition, each algorithm was run 100 times independently in each PV cell model to obtain statistical results.
Table 3 shows statistical results of the average RMSE obtained by each algorithm with six measured datasets, where symbol “Y” represents MhAs are applied with data prediction and “N” represents the condition that without data prediction. This shows the average RMSE obtained by each MhA with data prediction is significantly smaller than that with only measured data, especially under 50% measured data. For instance, the average RMSE obtained by PSO with data prediction is 82.32% smaller than that without data prediction under 50% measured data, which verifies such data prediction strategy can significantly enhance searching efficiency and optimization accuracy.
Besides, the average RMSE obtained by each algorithm with six inadequate measured datasets and six prediction datasets is demonstrated in Figure 3, which indicates prediction data–based PV parameter extraction for SDM can obtain higher accuracy and stability.
In addition, Figure 4 shows the boxplots of RMSE obtained by various algorithms in the SDM. From Figure 4, it is clear that as the amount of data increases, the outliers of the RMSE obtained by each algorithm decrease. For instance, the RMSE of PSO exists as several outliers under 50% training data, while these outliers disappear as training data increase to 100%. Besides, the range and upper and lower limits of the distribution are smaller under the 100% data than that under the 50% data. This can effectively validate that MhA improves convergence stability and searching ability based on the increased amount of ELM data predicted.
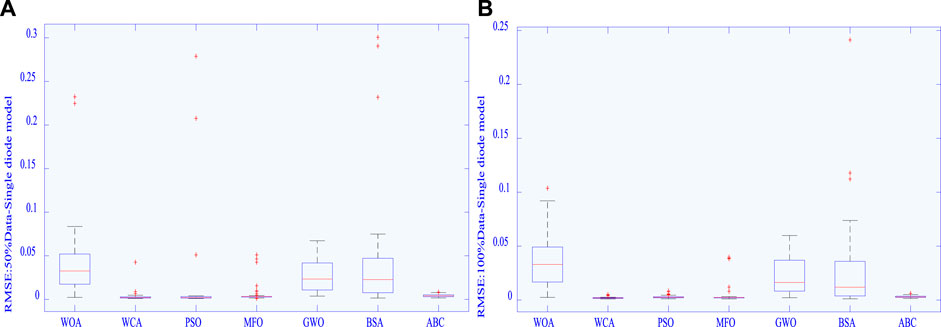
FIGURE 4. Boxplot of RMSE obtained by various algorithms in different data for the SDM: (A) 50% data and (B) 100% data.
Figure 5 plot I–V and P–V curves obtained by the best algorithm (i.e., algorithm can obtain the minimum RMSE) under 50% training data and 100% training data for the SDM, respectively. Note that WCA and MFO can achieve the minimum RMSE under 50% training data and 100% training data, respectively. It is not difficult to find that the model curves obtained from both WCA and MFO based on data prediction are in high agreement with the actual data, which can effectively demonstrate their superiority in PV cell parameter extraction.
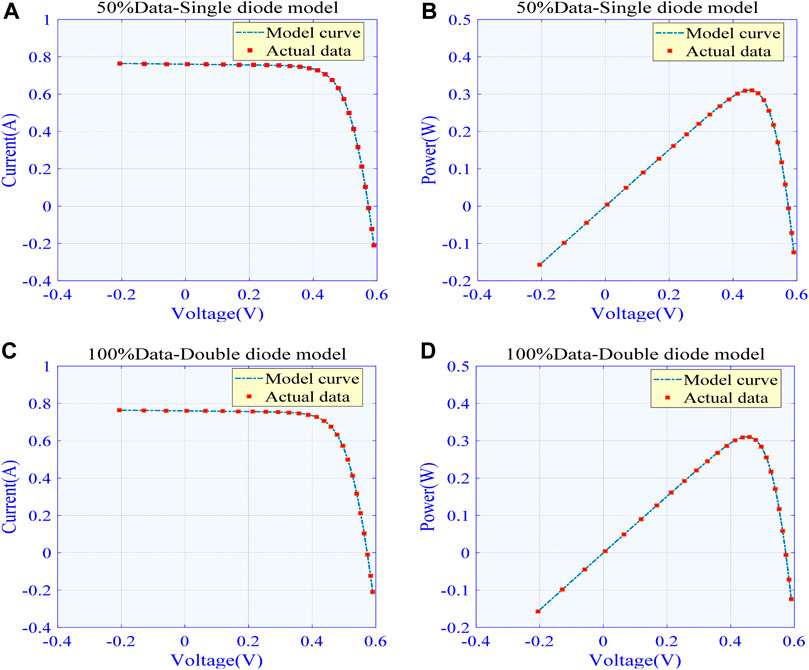
FIGURE 5. Comparison between actual data and model curve obtained by the best algorithm in different training data for SDM: (A)I-V curve in 50% training data (B)P-V curve in 50% training data (C)I-V curve in 100% training data and (D)I-V curve in 100% training data.
Besides, Figure 6 provides convergence of each algorithm under different training data. It can be seen that WOA tends to converge prematurely at the initial stage, and PSO has difficulty in obtaining high-quality optimal solutions with 50% of the training data. Besides, most algorithms can hardly achieve stable and efficient convergence due to inadequate data, along with unsatisfactory convergence accuracy. In contrast, the increase of training data helps them to gradually find high-quality solutions with higher convergence stability and searching efficiency as 100% data-based algorithms can better balance local exploitation and global exploration.
The average RMSE of the DDM obtained over 100 runs by the different MhAs with six measurement datasets is shown in Table 4, which demonstrates that increased prediction data generated by the ELM can effectively improve calculation accuracy. For example, the average RMSE obtained by the GWO algorithm with data prediction is 48.19% lower than that without data prediction under 50% measured data scenario. This illustrates that the data prediction–based meta-algorithm can achieve highly increased stability in finding quality solution through increasing the amount of dataset with a desired solution accuracy; thus, such novel strategy can output desirable results when accuracy and reliability are both taken into consideration in the DDM.
Figure 7 compares the average RMSE obtained by each algorithm under six inadequately measured datasets with that obtained under six prediction datasets in the DDM. One can easily find that each algorithm can find the global optimum more easily when experimental data are expanded by prediction data, upon which optimal values of those unknown parameters can be determined in a more accurate and stable way.
Boxplot of various algorithms is shown in Figure 8, upon which one can easily find that algorithms under 100% training data have fewer outliers and smaller upper/lower bounds in RMSE compared with that under 50% data. This indicates that increase of training data from data-based prediction can effectively enhance the quality of solution and stabilize global searching ability in PV cell parameter extraction.
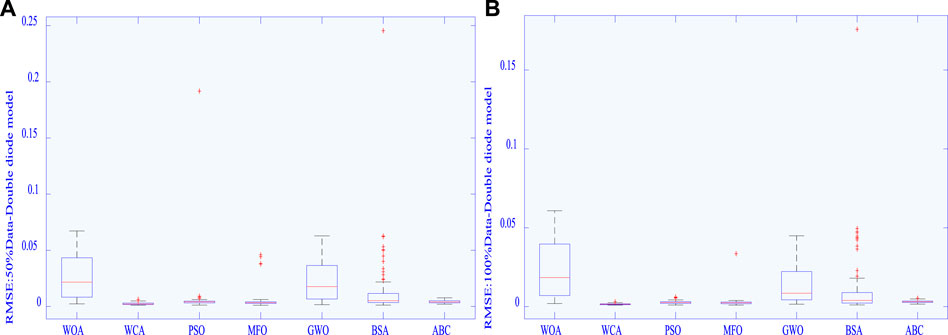
FIGURE 8. Boxplot of RMSE obtained by various algorithms in different data for the DDM: (A) 50% data and (B) 100% data.
Figure 9 plot I–V and P–V curves acquired based on the best data prediction–based MhA (WCA) and actual data under 50% training data and 100% training data, respectively. This indicates that the model curves obtained by WCA are highly consistent with the actual data.
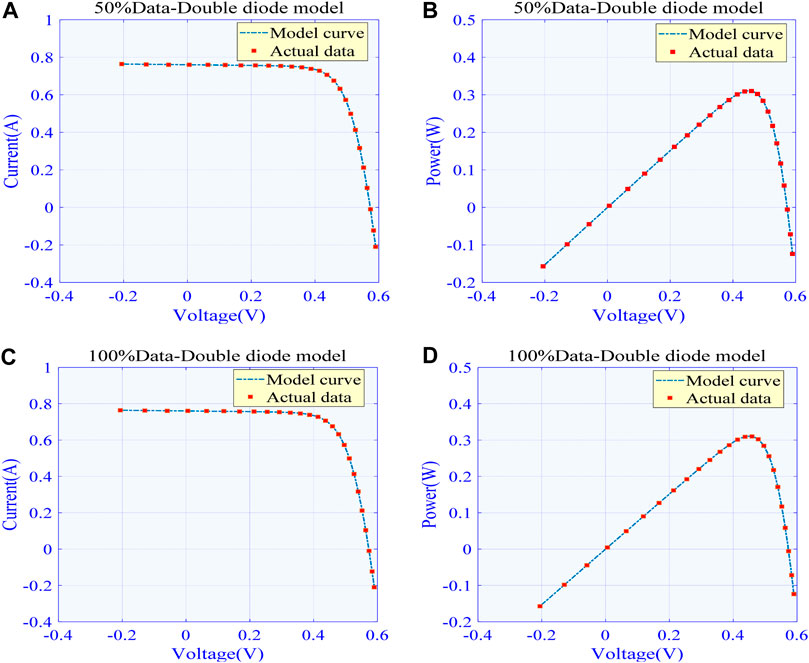
FIGURE 9. Comparison between actual data and model curve acquired by the best algorithm in different training data for DDM: (A)I-V curve in 50% training data (B)P-V curve in 50% training data (C)I-V curve in 100% training data and (d) I-V curve in 100% training data.
Moreover, Figure 10 provides convergence of all algorithms with data prediction, which illustrates that convergence speed of WOA is low and GWO tends to fall into a local optimum with 50% of the training data. On the contrary, convergence under 100% training data verifies that they can more stably find a better solution, especially for GWO.
Table 5 presents the average RMSE obtained by each algorithm with six different measured datasets, which reveals that data prediction–based algorithms still outperform those based on measured data. For example, the average RMSE obtained by PSO with data prediction is 61.06% lower than that without data prediction under 80% measured data. Hence, data prediction–based algorithms own the most satisfactory performance in terms of the accuracy of the solution for the TDM.
Figure 11 shows the comparison of the average RMSE of each algorithm under six inadequate measured datasets with that obtained under six prediction datasets in the TDM. It shows that the average RMSE obtained by WOA decreases by about 25% via data prediction, which verifies the effectiveness of data prediction in solution quality improvement.
Figure 12 presents the boxplot of different MhAs, while Figure 13 show the best algorithm (WCA) and the I–V and P–V curves obtained with the actual data under different datasets, verifying the accuracy of the extracted PV cell parameters. Figure 12 clearly shows that the increase in the volume of data can significantly reduce the RMSE outliers achieved by each algorithm, while lowering the upper/lower limits. Hence, solution precision and stability can be greatly enhanced by increasing the amount of experimental data.
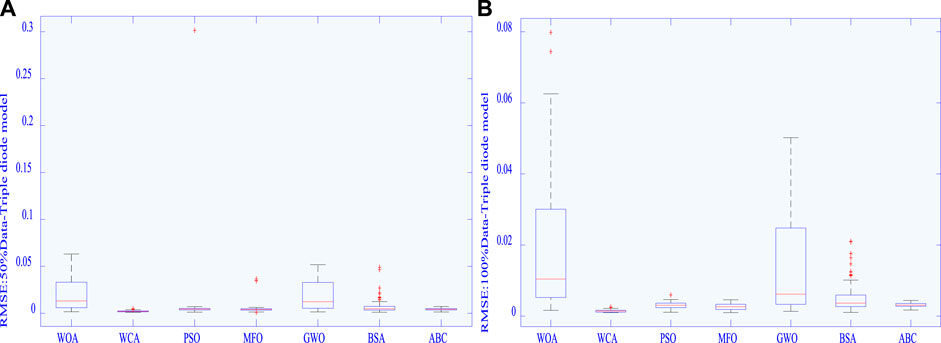
FIGURE 12. Boxplot of RMSE obtained by various algorithms in different data for the TDM: (A) 50% data and (B) 100% data.
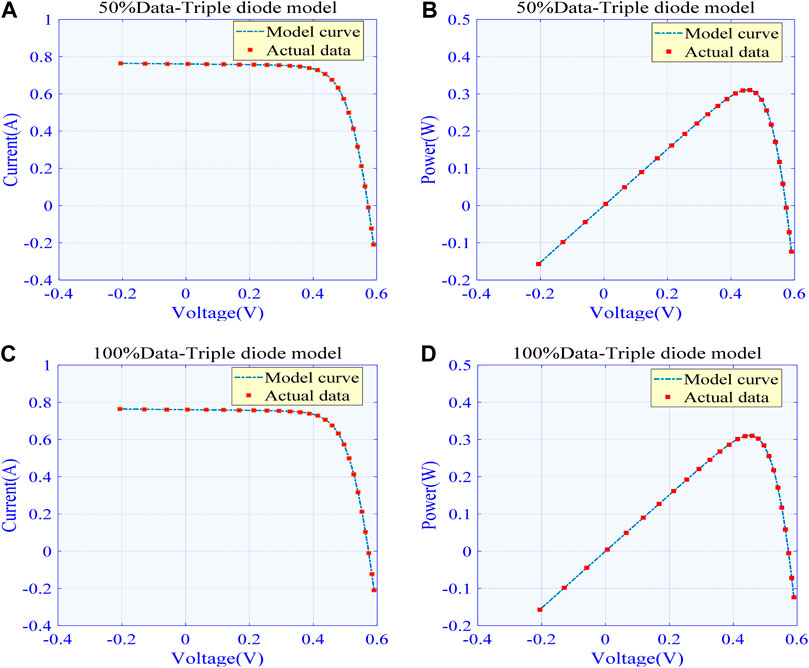
FIGURE 13. Comparison between actual data and model curve obtained by the best algorithm in different training data for TDM: (A)I-V curve in 50% training data (B)P-V curve in 50% training data (C)I-V curve in 100% training data and (D)I-V curve in 100% training data.
Last, Figure 14 provides convergence of all algorithms with data prediction, which shows that 100% training data–based algorithms can achieve a proper trade-off between local exploitation and global exploration, while 50%-based algorithms are easy to be trapped at a local optimum.
The radars of the average RMSE obtained by each MhA with six groups of data at different scales are provided in Supplementary Figure S1, Supplementary Figure S2, and Supplementary Figure S3, where symbol “+” represents MhAs with data prediction, which provides a more explicit illustration of stability of each algorithm with data prediction for PV cell parameter extraction in each model. One can see that the average RMSE obtained by each algorithm with data prediction is smaller compared with that obtained without data prediction at different scales of data. This effectively verifies the outstanding reliability of DPMhA for PV cell parameter extraction.
This article proposes a novel PV cell parameter extraction strategy is developed for three different PV cell models. The main three contributions/innovations in this article can be summarized as follows:
• ELM-based data prediction allows MhAs to perform a more stable search for optimal solution for identification of PV cell parameter with inadequate measured output I–V data.
• Three different types of PV cell models are adopted to reliably verify the practical enhancements and general feasibility of the strategy of DPMhA for PV cell parameter extraction.
• Case studies demonstrate that DPMhAs can considerably improve the accuracy, robustness, and convergence rate of PV cell parameter extraction compared with those only based on original measured output I–V data.
Case studies show that ELM-based MhAs can effectively improve optimization accuracy and convergence stability compared with original MhAs utilizing untrained measured I–V data. Although the convergence stability of MhAs can be improved by extending the data through the ELM, the optimization accuracy of some MhAs still needs to be improved in some conditions due to the error between the generated artificial data and the real measurement data. Hence, the next work will aim to handle this issue by introducing some advanced neural networks with excellent generalization.
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
BL was responsible for the design and revision of the thesis proposal, HC was responsible for writing the introduction and model presentation, and TT was responsible for writing the simulation experiments and simulation analysis.
This work was jointly supported by the Research and Development Start-Up Foundation of Shantou University (NTF19016).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.693252/full#supplementary-material
Abbassi, R., Abbassi, A., Jemli, M., and Chebbi, S. (2018). Identification of Unknown Parameters of Solar Cell Models: A Comprehensive Overview of Available Approaches. Renew. Sust. Energ. Rev. 90, 453–474. doi:10.1016/j.rser.2018.03.011
Allam, D., Yousri, D. A., and Eteiba, M. B. (2016). Parameters Extraction of the Three Diode Model for the Multi-Crystalline Solar Cell/module Using Moth-Flame Optimization Algorithm. Energ. Convers. Manag. 123, 535–548. doi:10.1016/j.enconman.2016.06.052
Amroune, M., Bouktir, T., and Musirin, I. (2019). Power System Voltage Instability Risk Mitigation via Emergency Demand Response-Based Whale Optimization Algorithm. Prot. Control. Mod. Power Syst. 4 (25). doi:10.1186/s41601-019-0142-4
Askarzadeh, A., and Rezazadeh, A. (2013). Extraction of Maximum Power Point in Solar Cells Using Bird Mating Optimizer-Based Parameters Identification Approach. Solar Energy 90, 123–133. doi:10.1016/j.solener.2013.01.010
Babu, T. S., Ram, J. P., Sangeetha, K., Laudani, A., and Rajasekar, N. (2016). Parameter Extraction of Two Diode Solar PV Model Using Fireworks Algorithm. Solar Energy 140, 265–286. doi:10.1016/j.solener.2016.10.044
Chaibi, Y., Allouhi, A., Salhil, M., and El-jouni, A. (2019). Annual Performance Analysis of Different Maximum Power Point Tracking Techniques Used in Photovoltaic Systems. Prot. Control. Mod. Power Syst. 4 (4), 171–180. doi:10.1186/s41601-019-0129-1
Chen, Z., Han, F., Wu, L., Yu, J., Cheng, S., Lin, P., et al. (2018). Random Forest Based Intelligent Fault Diagnosis for PV Arrays Using Array Voltage and String Currents. Energ. Convers. Manag. 178, 250–264. doi:10.1016/j.enconman.2018.10.040
Dasu, B., Sivakumar, M., and Srinivasarao, R. (2019). Interconnected Multi-Machine Power System Stabilizer Design Using Whale Optimization Algorithm. Prot. Control. Mod. Power Syst. 4 (4), 13–23. doi:10.1186/s41601-019-0116-6
Derick, M., Rani, C., Rajesh, M., Farrag, M. E., Wang, Y., and Busawon, K. (2017). An Improved Optimization Technique for Estimation of Solar Photovoltaic Parameters. Solar Energy 157, 116–124. doi:10.1016/j.solener.2017.08.006
Easwarakhanthan, T., Bottin, J., and Bouhouch, I. (1986). Nonlinear Minimization Algorithmfor Determining the Solar Cell Parameters with Microcomputers. Int. J. Solar Energ. 4 (1), 1–12. doi:10.1080/01425918608909835
Figueroa, O. R., Castellanos, M. Q., Montes, E. M., and Schütze, O. (2020). Metaheuristics to Solve Grouping Problems: A Review and a Case Study. Swarm Evol. Comput. 53, 100643. doi:10.1016/j.solener.2016.10.044
Grondin-Perez, B., Roche, S., Lebreton, C., Benne, M., Damour, C., and Kadjo, J.-J. A. (2014). Mechanistic Model versus Artificial Neural Network Model of a Single-Cell PEMFC. Eng 06 (8), 418–426. doi:10.4236/eng.2014.68044
Huang, G. B., Chen, Y. Q.., and Babri, H. A. (2000). Classification Ability of Single Hidden Layer Feedforward Neural Networks. IEEE Trans. Neural Networks 11 (3), 799–801. doi:10.1109/72.846750
Huang, G. B., and Siew, C. K. (2005). Extreme Learning Machine with Randomly Assigned RBF Kernels. Int. J. Inf. Tech. 11 (1), 1–8. doi:10.1109/ICARCV.2004.1468985
Huang, G. B., Zhu, Q. Y., and Siew, C. K. (2006). Extreme Learning Machine: Theory and Applications. Neurocomputing 70 (1-3), 489–501. doi:10.1016/j.neucom.2005.12.126
Humada, A. M., Hojabri, M., Mekhilef, S., and Hamada, H. M. (2016). Solar Cell Parameters Extraction Based on Single and Double-Diode Models: A Review. Renew. Sust. Energ. Rev. 56, 494–509. doi:10.1016/j.rser.2015.11.051
Ishaque, K., and Salam, Z. (2011). An Improved Modeling Method to Determine the Model Parameters of Photovoltaic (PV) Modules Using Differential Evolution (DE). Solar Energy 85 (9), 2349–2359. doi:10.1016/j.solener.2011.06.025
Ishaque, K., Salam, Z., Taheri, H., and Shamsudin, A. (2011). A Critical Evaluation of EA Computational Methods for Photovoltaic Cell Parameter Extraction Based on Two Diode Model. Solar Energy 85 (9), 1768–1779. doi:10.1016/j.solener.2011.04.015
Jervase, J. A., Bourdoucen, H., and Al-lawati, A. (2001). Solar Cell Parameter Extraction Using Genetic Algorithms. Meas. Sci. Technol. 12, 1922–1925. doi:10.1088/0957-0233/12/11/322
Jordehi, A. R. (2016). Parameter Estimation of Solar Photovoltaic (PV) Cells: a Review. Renew. Sust. Energ. Rev. 61, 354–371. doi:10.1016/j.rser.2016.03.049
Khanna, V., Das, B. K., Bisht, D., Vandana, , , and Singh, P. K. (2015). A Three Diode Model for Industrial Solar Cells and Estimation of Solar Cell Parameters Using PSO Algorithm. Renew. Energ. 78, 105–113. doi:10.1016/j.renene.2014.12.072
Kler, D., Sharma, P., Banerjee, A., Rana, K. P. S., and Kumar, V. (2017). PV Cell and Module Efficient Parameters Estimation Using Evaporation Rate Based Water Cycle Algorithm. Swarm Evol. Comput. 35, 93–110. doi:10.1016/j.swevo.2017.02.005
Li, G. D., Li, G. Y., and Zhou, M. (2019). Model and Application of Renewable Energy Accommodation Capacity Calculation Considering Utilization Level of Interprovincial Tie-Line. Prot. Control. Mod. Power Syst. 4 (4), 1–12. doi:10.1186/s41601-019-0115-7
Li, W., Paul, M. C., Rolley, M., Sweet, T., Gao, M., Siviter, J., et al. (2017). A Scaling Law for Monocrystalline PV/T Modules with CCPC and Comparison with Triple Junction PV Cells. Appl. Energ. 202, 755–771. doi:10.1016/j.apenergy.2017.05.182
Liu, J., Yao, W., Wen, J., Fang, J., Jiang, L., He, H., et al. (2020). Impact of Power Grid Strength and PLL Parameters on Stability of Grid-Connected DFIG Wind Farm. IEEE Trans. Sustain. Energ. 11 (1), 545–557. doi:10.1109/tste.2019.2897596
Majdoul, R., Abdelmounim, E., Aboulfatah, M., Touati, A. W., Moutabir, A., and Abouloifa, A. (2015). “Combined Analytical and Numerical Approach to Determine the Four Parameters of the Photovoltaic Cells Models,” in International Conference on Electrical and InformationTechnologies (Marrakech, Morocco). 263–268.
Nesmachnow, S. (2014). An Overview of Metaheuristics: Accurate and Efficient Methods for Optimisation. Ijmheur 3 (4), 320–347. doi:10.1504/ijmheur.2014.068914
Nunes, H. G. G., Pombo, J. A. N., Mariano, S. J. P. S., Calado, M. R. A., and Felippe de Souza, J. A. M. (2018). A New High Performance Method for Determining the Parameters of PV Cells and Modules Based on Guaranteed Convergence Particle Swarm Optimization. Appl. Energ. 211, 774–791. doi:10.1016/j.apenergy.2017.11.078
Oliva, D., Cuevas, E., and Pajares, G. (2014). Parameter Identification of Solar Cells Using Artificial Bee Colony Optimization. Energy 72, 93–102. doi:10.1016/j.energy.2014.05.011
Peng, X., Yao, W., Yan, C., Wen, J., and Cheng, S. (2020). Two-stage Variable Proportion Coefficient Based Frequency Support of Grid-Connected DFIG-WTs. IEEE Trans. Power Syst. 35 (2), 962–974. doi:10.1109/tpwrs.2019.2943520
Qais, M. H., Hasanien, H. M., and Alghuwainem, S. (2019). Identification of Electrical Parameters for Three-Diode Photovoltaic Model Using Analytical and Sunflower Optimization Algorithm. Appl. Energ. 250, 109–117. doi:10.1016/j.apenergy.2019.05.013
Ram, J. P., Manghani, H., Manghani, D. S., Babu, T. S., Miyatake, M., Rajasekar, N., et al. (2018). Analysis on Solar PV Emulators: A Review. Renew. Sust. Energ. Rev. 81, 149–160. doi:10.1016/j.rser.2017.07.039
Roeva, O., and Fidanova, S. (2018). Comparison of Different Metaheuristic Algorithms Based on Intercriteria Analysis. J. Comput. Appl. Math. 340, 615–628. doi:10.1016/j.cam.2017.07.028
Schmidhuber, J. (2015). Deep Learning in Neural Networks: An Overview. Neural Networks 61, 85–117. doi:10.1016/j.neunet.2014.09.003
Shen, Y., Yao, W., Wen, J., He, H., and Jiang, L. (2019). Resilient Wide-Area Damping Control Using GrHDP to Tolerate Communication Failures. IEEE Trans. Smart Grid 10 (3), 2547–2557. doi:10.1109/tsg.2018.2803822
Sun, K., Yao, W., Fang, J., Ai, X., Wen, J., and Cheng, S. (2020). Impedance Modeling and Stability Analysis of Grid-Connected DFIG-Based Wind Farm with a VSC-HVDC. IEEE J. Emerg. Sel. Top. Power Electron. 8, 1375–1390. doi:10.1109/JESTPE.2019.2901747
Torabi, K. E., Eddine, I. A., Obbadi, A., Errami, A., Rmaily, R., Sahnoun, S., et al. (2017). Parameters Estimation of the Single and Double Diode Photovoltaic Models Using a Gauss-Seidel Algorithm and Analytical Method: A Comparative Study. Energ. Convers. Manag. 148, 1041–1054. doi:10.1016/j.solener.2016.10.044
Villalva, M. G., Gazoli, J. R., and Filho, E. R. (2009). Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electron. 24, 1198–1208. doi:10.1109/tpel.2009.2013862
Wang, Q., Yao, W., Fang, J., Ai, X., Wen, J., Yang, X., et al. (2020). Dynamic Modeling and Small Signal Stability Analysis of Distributed Photovoltaic Grid-Connected System with Large Scale of Panel Level DC Optimizers. Appl. Energ. 259, 114132. doi:10.1016/j.apenergy.2019.114132
Xiong, G., Zhang, J., Shi, D., and He, Y. (2018). Parameter Extraction of Solar Photovoltaic Models Using an Improved Whale Optimization Algorithm. Energ. Convers. Manag. 174, 388–405. doi:10.1016/j.enconman.2018.08.053
Yang, B., Jiang, L., Wang, L., Yao, W., and Wu, Q. H. (2016). Nonlinear Maximum Power Point Tracking Control and Modal Analysis of DFIG Based Wind Turbine. Int. J. Electr. Power Energ. Syst. 74, 429–436. doi:10.1016/j.ijepes.2015.07.036
Yang, B., Wang, J., Zhang, X., Yu, T., Yao, W., Shu, H., et al. (2020). Comprehensive Overview of Meta-Heuristic Algorithm Applications on PV Cell Parameter Identification. Energ. Convers. Manag. 208, 112595. doi:10.1016/j.enconman.2020.112595
Yang, B., Yu, T., Shu, H., Dong, J., and Jiang, L. (2018). Robust Sliding-Mode Control of Wind Energy Conversion Systems for Optimal Power Extraction via Nonlinear Perturbation Observers. Appl. Energ. 210, 711–723. doi:10.1016/j.apenergy.2017.08.027
Yang, B., Yu, T., Shu, H., Zhang, Y., Chen, J., Sang, Y., et al. (2018). Passivity-based Sliding-Mode Control Design for Optimal Power Extraction of a PMSG Based Variable Speed Wind Turbine. Renew. Energ. 119, 577–589. doi:10.1016/j.renene.2017.12.047
Yang, B., Yu, T., Zhang, X., Li, H., Shu, H., Sang, Y., et al. (2019). Dynamic Leader Based Collective Intelligence for Maximum Power Point Tracking of PV Systems Affected by Partial Shading Condition. Energ. Convers. Manag. 179, 286–303. doi:10.1016/j.enconman.2018.10.074
Yang, B., Zhang, X., Yu, T., Shu, H., and Fang, Z. (2017). Grouped Grey Wolf Optimizer for Maximum Power Point Tracking of Doubly-Fed Induction Generator Based Wind Turbine. Energ. Convers. Manag. 133, 427–443. doi:10.1016/j.enconman.2016.10.062
Yang, B., Zhong, L., Zhang, X., Shu, H., Yu, T., Li, H., et al. (2019). Novel Bio-Inspired Memetic Salp Swarm Algorithm and Application to MPPT for PV Systems Considering Partial Shading Condition. J. Clean. Prod. 215, 1203–1222. doi:10.1016/j.jclepro.2019.01.150
Ye, M. Y., Wang, X. D., and Xu, Y. S. (2009). Parameter Extraction of Solar Cells Using Particle Swarm Optimization. J. Appl. Phys. 105 (9), 094502–094508. doi:10.1063/1.3122082
Youssef, A., El-Telbany, M., and Zekry, A. (2017). The Role of Artificial Intelligence in Photo-Voltaic Systems Design and Control: a Review. Renew. Sust. Energ. Rev. 78, 72–79. doi:10.1016/j.rser.2017.04.046
Yu, K., Liang, J. J., Qu, B. Y., Cheng, Z., and Wang, H. (2018). Multiple Learning Backtracking Search Algorithm for Estimating Parameters of Photovoltaic Models. Appl. Energ. 226, 408–422. doi:10.1016/j.apenergy.2018.06.010
Zhang, H., Lu, Z., Hu, W., Wang, Y., Dong, L., and Zhang, J. (2019). Coordinated Optimal Operation of Hydro-Wind-Solar Integrated Systems. Appl. Energ. 242, 883–896. doi:10.1016/j.apenergy.2019.03.064
Zhao, Y., Pei, J., and Chen, H. (2019). Multi-layer Radial Basis Function Neural Network Based on Multi-Scale Kernel Learning. Appl. Soft Comput. 82, 105541. doi:10.1016/j.asoc.2019.105541
ABC artificial bee colony
AIS artificial immune system
ANN artificial neural network
BP back-propagation
BSA backtracking search algorithm
DDM double diode model
DE differential evolution
DPMhA data prediction–based meta-heuristic algorithm
ELM extreme learning machine
FWA fireworks algorithm
GA genetic algorithm
GWO grey wolf optimization
I–V current–voltage
MFO moth flame optimizer
MhA meta-heuristic algorithm
MPPT maximum power point tracking
PSO particle swarm optimization
PV photovoltaic
P-V power–voltage
RMSE root mean square error
SDM single diode model
SLFN single-hidden layer feedforward neural network
STC standard test condition
SSA salp swarm algorithm
TDM three diode model
WOA whale optimization algorithm
WCA water cycle algorithm
WDO wind-driven optimization
Keywords: parameter extraction, PV cell, data prediction, meta-heuristic algorithm, extreme learning machine
Citation: Li B, Chen H and Tan T (2021) PV Cell Parameter Extraction Using Data Prediction–Based Meta-Heuristic Algorithm via Extreme Learning Machine. Front. Energy Res. 9:693252. doi: 10.3389/fenrg.2021.693252
Received: 10 April 2021; Accepted: 26 April 2021;
Published: 08 June 2021.
Edited by:
Bo Yang, Kunming University of Science and Technology, ChinaReviewed by:
Feixiong Chen, Fuzhou University, ChinaCopyright © 2021 Li, Chen and Tan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tian Tan, MTl0dGFuQHN0dS5lZHUuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.