Numerical Study on Discharging Characteristics of Entangled Cluster of Particles in Particle Bed

To better understand the flow features of the particle cluster in a particle bed, discharging of the particle entangled cluster is simulated by the discrete element method (DEM). The particle entangled cluster is composed of eight particles connected by rigid bonds, and the simulated entangled cluster models are divided into two types: axisymmetric u-particles and distorted z-particles. The simulation starts with the closed discharge outlet, and the bonded clusters with different IDs are randomly added from the entrance section. The particles fall freely and accumulate freely in the particle bed. The discharge hole opens after all the particles are stationary for a period. Then, the particles are discharged from the particle bed under gravity. The discharging process has time-dependent bulk-movement behavior. There is not much mixing between layers on the boundary. The vertical end not only makes the packing loose but also intensifies the interaction between particles due to entanglement. Consequently, the discharge features of particle entangled clusters of different included angles were quantified. The results show that the particle discharging speeds depend on the entanglement angle (α of u-particles and η of z-particles) and discharging outlet diameter. A large included angle may play the role of retarding or inhibiting the discharging flow rate. Therefore, the entanglement of particle components also always plays the key role of retarding the discharge.

Introduction

The effects of geometric shape (elongation and symmetry) on the packing of granular materials, such as the assembled rods and entangled materials, are important issues in non-spherical particle flow dynamics, e.g., fibers (Rodey et al., 2005). The entangled particles may cause geometric interpenetration and interlockings (Brown et al., 2012). Also, the entangled shape, e.g., Z-shape (Murphy et al., 2016), may affect the packing and building of freestanding structures. The mostly and commonly studied shapes are always tetrahedral (Gui et al., 2017; Gui et al., 2018) and superellipsoids (Liu et al., 2018). More complex shapes, such as Mickey Mouse colloids (Wolters et al., 2015), 3D stars (Zhao et al., 2016), pear-shapes (Smeets et al., 2014), and orthogonal rods (3DX) (Blaak and Mulder, 1998), have also been studied to explore the effect of non-convexity on dense packing during the compression/shaking process. Therefore, it is common interest of researchers in vast fields to explore the effects of geometric shapes on flow dynamics of particle assemblies.

On the contrary, since the last century, nuclear power plants have made great progress in the unremitting efforts of many experts and scholars. The United States, Germany, China, and South Africa have conducted a lot of related experimental and theoretical studies on nuclear power plants (Caram and Hong, 1991; Particle Bed Modular Reactor Limited, 1999; Kadak and Ballinger, 2004; Rycroft et al., 2006). Tsinghua University developed the world’s first high-temperature gas-cooled reactor (HTR-10) in 2003 and successfully generated electricity. HTR is considered an advanced reactor type that can meet the requirements of fourth-generation nuclear energy systems. The particle flow of the reactor is a slow particle flow driven by gravity and has the characteristics of macro discontinuity and micro randomness. Therefore, many mechanical problems in the motion of ball flow still need to be studied.

The discrete element method (DEM) was proposed by Cundall (Cundall, 1971; Cundall and Strack, 1979). The main idea is to use simple mechanical models such as springs, dampers, and friction pairs to simulate normal and tangential forces during contact and collision between particles. In the DEM model, according to Newton’s second law, the motion control equation of each particle is divided into two parts: translation and rotation. The discrete element method belongs to the deterministic model, which contains all the kinematics information of the particles, so it is widely used in many particle studies.

Because of the inherent safety of the fourth-generation reactor, even if an accident occurs, the temperature inside the reactor will not exceed the limit temperature of the particles (Jiang et al., 2019). At present, the particle flow based on the DEM is mainly concentrated on spherical particles (Gui et al., 2016; Wu et al., 2016; Gui et al., 2017), and there is not much research on non-spherical ones. This paper studies the motion of non-spherical particles in a cone-shaped funnel. The research on non-spherical particles is now focused on the separation and mixing of multiple components in the drum (Alberto and Francesco, 2005; Mack et al., 2011; Chen et al., 2016). Arbitrary convex bodies are easier to implement in experiments (Mack et al., 2011), but in numerical simulations, it is relatively simple to use the particle entangled cluster to simulate non-spherical particles due to theoretical limitations (Chen et al., 2016). This paper also uses this method.

Numerical Methods

Numerical Models

The equations for each element are expressed, respectively, as follows:

$m_i\frac{d{V}_i}{dt}={\displaystyle \sum _{j=1}^n{F}_{ji}^C}+F_i^g\hspace{0.17em},(1)$

$I_i\frac{d{w}_i}{dt}={\displaystyle \sum _{j=1}^n{r}_{ij}}\times F_{ji}^C\hspace{0.17em},(2)$

$F_{ji}^{cn}=-k_n\cdot \Delta {\chi }_{ij}^n+{\beta }_n\cdot V_{ji}^n\hspace{0.17em},(3)$

$F_{ji}^{ct}=-k_t\cdot \Delta {\chi }_{ij}^t+{\beta }_t\cdot V_{ji}^t\hspace{0.17em},(4)$

${\left|F_{ji}^{ct}\right|}_{\max }\le \mu \left|F_{ji}^{cn}\right|\hspace{0.17em},(5)$

where m_i, V_i, I_i, and w_i denote the mass, translational velocity, moment of inertia, and rotational velocities of the element i. $F_{ji}^C$ represents the contact force from the element j to i, and r_ij is the vector pointing from the element j to i. On the contrary, n and t denote the normal and tangential components, respectively. k and β are the elastic constant and viscoelastic damping constant coefficients, respectively, while $\Delta \chi$ and V denote the overlap distance and relative velocity of two particles, respectively. µ is the friction coefficient.

It should be noted that the tangential overlap is truncated to fulfill Eq. 5. k_n, k_t, β_n, and β_t are calculated as follows (Alberto and Francesco, 2005; Ai et al., 2011):

$k_n=\frac{4}{3}{Y}^{\text{*}}\sqrt{R^{\text{*}}\Delta {\chi }_{ij}^n}\hspace{0.17em},(6)$

${\beta }_n=-2\sqrt{\frac{5}{6}}\beta \sqrt{2Y^{\text{*}}\sqrt{R^{\text{*}}\Delta {\chi }_{ij}^n}{m}^{\text{*}}}\ge 0\hspace{0.17em},(7)$

$k_{\text{t}}=8G^{\text{*}}\sqrt{R^{\text{*}}\Delta {\chi }_{ij}^n}\hspace{0.17em},(8)$

${\beta }_{\text{t}}=-2\sqrt{\frac{5}{6}}\beta \sqrt{8G^{\text{*}}\sqrt{R^{\text{*}}\Delta {\chi }_{ij}^n}{m}^{\text{*}}}\ge 0\hspace{0.17em},(9)$

where parameters Y^*, R^*, m^*, and G^* represent the equivalent Young’s modulus, equivalent radius, equivalent mass, and equivalent shear modulus, respectively, and they are calculated from the material properties of elements i and j as follows:

$\frac{1}{Y^{\text{*}}}=\frac{(1-v_i^2)}{Y_i}+\frac{(1-v_j^2)}{Y_j}\hspace{0.17em},(10)$

$\frac{1}{R^{\text{*}}}=\frac{1}{R_i}+\frac{1}{R_j}\hspace{0.17em},(11)$

$\frac{1}{m^{\text{*}}}=\frac{1}{m_i}+\frac{1}{m_j}\hspace{0.17em},(12)$

$\beta =\frac{\ln \left(e\right)}{\sqrt{{\ln }^2\left(e\right)+{\pi }^2}}\hspace{0.17em},(13)$

$\frac{1}{G^{\text{*}}}=\frac{2-v_i}{G_i}+\frac{2-v_j}{G_j}\hspace{0.17em},(14)$

where $e$ in Eq. 13 represents the Poisson ratio.

And for entangled particles, the equations are expressed as follows:

$\{\begin{array}{l}M\frac{dV}{dt}={\displaystyle \sum _{j=1}^n{\mathbf{F}}_j^C}+{\mathbf{F}}^g\\ I\frac{d\omega }{dt}={\displaystyle \sum _{j=1}^n{\mathbf{R}}_{Cj}\times {\mathbf{F}}_j^C}\end{array}\hspace{0.17em},(15)$

where R_cj is the position vector from the centroid of the particle entangled cluster to the jth element sphere. n is the element ordinal of particle cluster. The DEM model used in this paper has been verified by previous experiments and simulations (Ge and Gui, 2019; Ge et al., 2020).

The parameters used in current simulation are listed in Table 1.

TABLE 1

TABLE 1. Particle shape parameters used in simulation cases.

Simulation Conditions

The geometry of the particle bed is based on the particle bed experimental setup, and the material properties of particles are also derived from the same test facility. The simulated particle bed has a diameter of 1.8 m and a height of 4 m. A bonded multi-particle model is composed of eight element spheres of radius R = 15 mm. The bonded multi-particle model has the same total volume as the real core particle with a diameter (d_e) of 60 mm in the high-temperature gas-cooled reactor (HTGR). And two different aspect ratios (δ=2:6 and 3:4) are simulated, respectively. It means that the former consists of six element spheres in the horizontal direction and two spheres at the vertical end, while the latter consists of four spheres in the horizontal direction and three spheres at the vertical end. To study the effect of entanglement on particle discharging, the simulated particle models are divided into two types: distorted z-particles and axisymmetric u-particles.

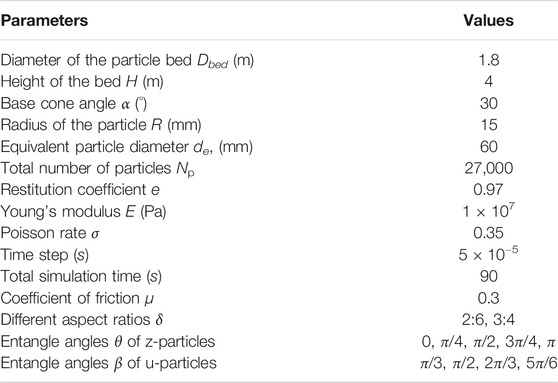
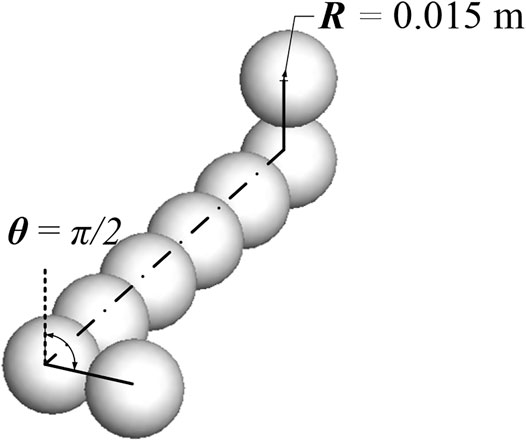
For z-particles, five entangle angles θ = 0, π/4, π/2 (Figure 1), 3π/4, and π have been simulated. In contrast, four entangle angles β = π/3 (Figure 2), π/2, 2π/3, and 5π/6 of u-particles are also simulated.

FIGURE 1

FIGURE 1. Shape of particles with entangle angle θ = π/2 of z-particles.

FIGURE 2

FIGURE 2. Shape of particles with entangle angle β = π/3 of u-particles.

Simulation Results and Discussions

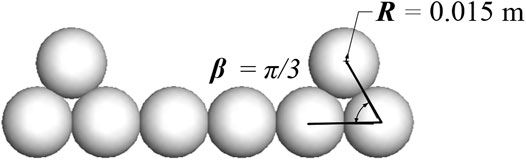
Snapshots of particle discharge when aspect δ = 2:6, β = π/3 at t = 5 s are shown in Figure 3. As can be seen from the figure, the flow of the particle entangled cluster, like the spherical particle flow, has also the bulk-movement behavior.

FIGURE 3

FIGURE 3. Snapshots of particle discharge when aspect δ = 2:6, β = π/3 at t = 5 s.

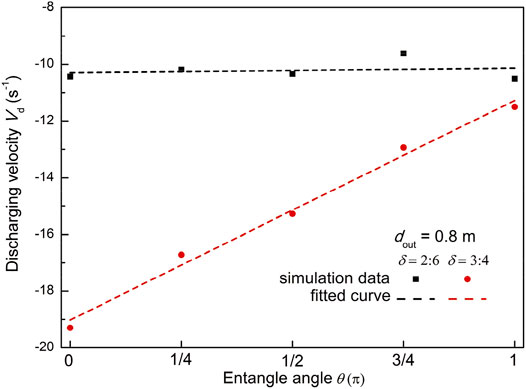
Different from the spherical particle flow, the instantaneous discharge of the particle entangled cluster is significantly less. It shows that the entanglement effect can significantly reduce the discharging velocity.

From the clouds in front, quantitative analysis of the particle discharging speeds depends on the entanglement angle (β and θ) and aspect ratio (δ), as shown below. The number of particles staying in the particle bed at time t is calculated and shown in Figure 4 and Figure 5 to quantitatively analyze the influence of these parameters (Figure 6 and Figure 7). Firstly, the influence of the included angle θ of z-particles on the number of resident particles is shown in Figure 4 with d_out = 0.8 m, respectively. On the contrary, the influence of angle θ of u-particles on the number of resident particles is shown in Figure 5 at fixed included angles of β with d_out = 0.9 m, respectively. It is clearly seen that the numbers of resident particles are always decreasing with time, while the rate of decrease is reduced as the included angle β becomes larger. In other words, a large included angle may play the role of retarding or inhibiting the discharge flow rate. Therefore, the entanglement of particle components also plays the role of retarding the discharge.

FIGURE 4

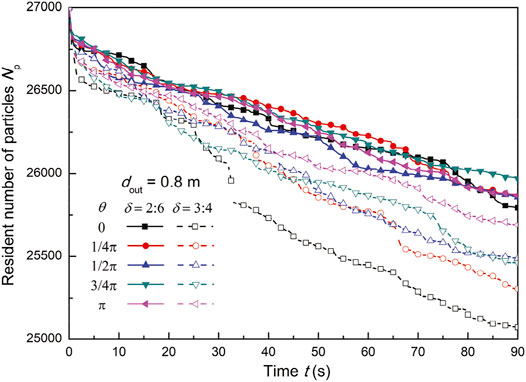
FIGURE 4. Number of resident particles with different included angles θ of z-particles when d_out = 0.8 m.

FIGURE 5

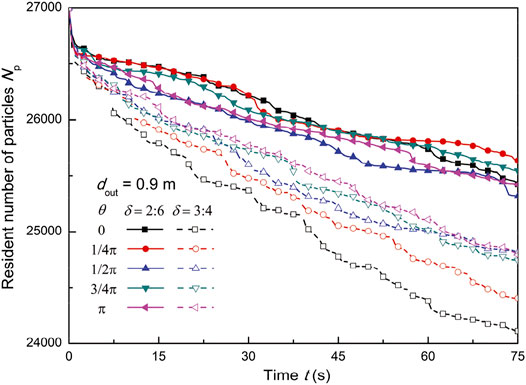
FIGURE 5. Number of resident particles with different included angles θ of z-particles when d_out = 0.9 m.

FIGURE 6

FIGURE 6. Discharging velocity with different included angles θ of z-particles when d_out = 0.8 m.

FIGURE 7

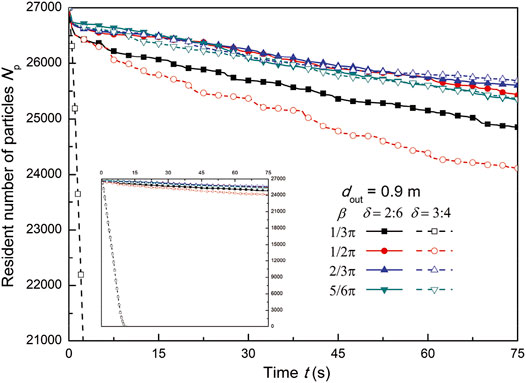
FIGURE 7. Number of resident particles with different included angles β of u-particles when d_out = 0.9 m.

Obviously, the decline rate of δ = 3:4 is much faster than that of δ = 2:6. The increase of vertical end enhances the entanglement but also reduces the packing density. These two trends affect the degree of mechanical entanglement of particles at the same time (Gravish et al., 2012). It can be seen that compared with δ = 3:4, when δ = 2:6, the particle clusters are more resistant to separation.

And when δ = 2:6, the differences between the included angles θ are not great; on the contrary, when δ = 3:4, the differences between the angles θ are great (Figure 6). This is because with the increase of vertical end, the angle changes resulting in sharp changes in the collision situation. When δ = 3:4, the simulation has a very obvious velocity changing rule: as the angle θ increases, the discharging velocity also increases.

As in Figure 4, the trends shown in Figure 5 are the same. Only because of the increase of the discharging outlet, the value of the discharge velocity increases. And when δ changes, the discharging velocity difference among different angles θ also increases significantly.

It is worth pointing out that, at β = π/3, multiple particles become triangle and will not relate to each other; the particles will be discharged soon (Figure 7).

Conclusion

This work used the DEM to obtain the discharging characteristics of particle clusters with different entangle angles in particle bed–type of HTGR. The effects of entanglement angle and aspect ratio on the characteristics of particle flow are studied in this paper.

Overall, the results indicate the characteristics of the particle entangled cluster flow as follows:

1) The entanglement of particle components plays the role of retarding the discharge. And increasing the discharge outlet will also increase the discharging velocity.

2) The entanglement and packing density affect the degree of mechanical entanglement of particles at the same time. The increase of vertical end may decrease or increase discharge speed. In the research example in this paper, the increase of vertical end is to improve the discharging velocity.

3) Once the particle entangled clusters form a closed loop, there will be no entanglement between them, so the discharge velocity will be greatly increased.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

NG conceptualized the idea. XH and LG performed data analysis, and XH and XY performed formal analysis. XH, LG, NG, and XY validated the results. LG and NG performed the methodology and investigation. XH wrote the original draft. XY visualized the results. JT and SJ obtained resources and supervised the work. XY, JT, and SJ reviewed and edited the paper. SJ involved in research project administration and funding acquisition.

Funding

The authors are grateful for the support of this research by the National Science and Technology Major Project (2011ZX06901-003) and the fund of Nuclear Power Technology Innovation Centre (Grant Nos. HDLCXZX-2020-HD-022 and HDLCXZX-2021-ZH-024).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge the conference ICONE-2020 and ASME for use of all or any part of the following ASME conference paper - ‘Numerical Study on Discharging Characteristics of Pebble Cluster Flow in Pebble Bed’.

References

Ai, J., Chen, J.-F., Rotter, J. M., and Ooi, J. Y. (2011). Assessment of Rolling Resistance Models in Discrete Element Simulations. Powder Tech. 206, 269–282. doi:10.1016/j.powtec.2010.09.030

CrossRef Full Text | Google Scholar

Alberto, D. R., and Francesco, P. D. (2005). An Improved Integral Non-linear Model for the Contact of Particles in Distinct Element Simulations. Chem. Eng. Sci. 60, 1303–1312. doi:10.1016/j.ces.2004.10.004

CrossRef Full Text | Google Scholar

Blaak, R., and Mulder, B. M. (1998). Phase Diagram of Onsager Crosses. Phys. Rev. E 58, 5873–5884. doi:10.1103/physreve.58.5873

CrossRef Full Text | Google Scholar

Brown, E., Nasto, A., Athanassiadis, A. G., and Jaeger, H. M. (2012). Strain-stiffening in Random Packings of Entangled Granular Chains. Phys. Rev. Lett. 108, 108302. doi:10.1103/physrevlett.108.108302

PubMed Abstract | CrossRef Full Text | Google Scholar

Caram, H., and Hong, D. C. (1991). Random-walk Approach to Granular Flows. Phys. Rev. Lett. 67 (7), 828–831. doi:10.1103/physrevlett.67.828

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, H., Zhao, X. G., Xiao, Y. G., Liu, Y. L., and Liu, Y. (2016). Radial Mixing and Segregation of Granular Bed Bi-dispersed Both in Particle Size and Density within Horizontal Rotating Drum. Trans. Nonferrous Met. Soc. China 26, 527–535. doi:10.1016/s1003-6326(16)64110-9

CrossRef Full Text | Google Scholar

Cundall, P. A. (1971). “A Computer Model for Simulating Progressive Large Scale Movements in Blocky Rock System,” in Proceedings of the Symposium of the International Society for Rock Mechanics.

Google Scholar

Cundall, P. A., and Strack, O. D. L. (1979). A Discrete Numerical Model for Granular Assemblies. Géotechnique 29 (1), 47–65. doi:10.1680/geot.1979.29.1.47

CrossRef Full Text | Google Scholar

Ge, L., and Gui, N. (2019). Effects of Aspect Ratio and Component Ratio on Binary-Mixed Discharging Particle Flow in Hoppers. Powder Tech. 355, 320–332. doi:10.1016/j.powtec.2019.07.045

CrossRef Full Text | Google Scholar

Ge, L., Gui, N., Yang, X., Tu, J., and Jiang, S. (2020). Effects of Volumetric Fraction and Included Angle of Composite Particles on the Discharge of Binary Mixtures in Hoppers. Particuology 51, 80–90. doi:10.1016/j.partic.2019.10.003

CrossRef Full Text | Google Scholar

Gravish, N., Franklin, S. V., Hu, D. L., and Goldman, D. I. (2012). Entangled Granular media. Phys. Rev. Lett. 108 (20), 208001. doi:10.1103/physrevlett.108.208001

PubMed Abstract | CrossRef Full Text | Google Scholar

Gui, N., Yang, X., Jiang, S., and Tu, J. (2016). A Soft-Sphere-Imbedded Pseudo-hard-particle Model for Simulation of Discharge Flow of brick Particles. Aiche J. 62 (10), 3562–3574. doi:10.1002/aic.15278

CrossRef Full Text | Google Scholar

Gui, N., Yang, X., Tu, J., and Jiang, S. (2017). Flow fields and Packing States in the Discharge Flow of Noncircular Particles-A SIPHPM Simulation. Particuology 35, 10–21. doi:10.1016/j.partic.2017.01.003

CrossRef Full Text | Google Scholar

Gui, N., Yang, X., Tu, J., and Jiang, S. (2017). Numerical Simulation and Analysis of Mixing of Polygonal Particles in 2D Rotating Drums by SIPHPM Method. Powder Tech. 318, 248–262. doi:10.1016/j.powtec.2017.06.007

CrossRef Full Text | Google Scholar

Gui, N., Yang, X., Tu, J., Jiang, S., and Zhang, Z. (2018). Numerical Simulation of Tetrahedral Particle Mixing and Motion in Rotating Drums. Particuology 39, 1–11. doi:10.1016/j.partic.2017.08.004

CrossRef Full Text | Google Scholar

Jiang, S., Tu, J., Yang, X., and Gui, N. (2019). A Review of Pebble Flow Study for Pebble Bed High Temperature Gas-Cooled Reactor. Exp. Comput. Multiph. Flow 1, 159–176. doi:10.1007/s42757-019-0006-1

CrossRef Full Text | Google Scholar

Kadak, A. C., and Ballinger, R. G. (2004). MIT Modular Particle Bed Reactor (MPBR)/2nd International Topical Meeting on High Temperature Reactor Technology. Beijing.

Google Scholar

Liu, L., Yu, Z., Jin, W., Yuan, Y., and Li, S. (2018). Uniform and Decoupled Shape Effects on the Maximally Dense Random Packings of Hard Superellipsoids. Powder Tech. 338, 67–78. doi:10.1016/j.powtec.2018.06.033

CrossRef Full Text | Google Scholar

Mack, S., Langston, P., Webb, C., and York, T. (2011). Experimental Validation of Polyhedral Discrete Element Model. Powder Tech. 214, 431–442. doi:10.1016/j.powtec.2011.08.043

CrossRef Full Text | Google Scholar

Murphy, K. A., Reiser, N., Choksy, D., Singer, C. E., and Jaeger, H. M. (2016). Freestanding Loadbearing Structures with Z-Shaped Particles. Granul. Matter 18, 26. doi:10.1007/s10035-015-0600-2

CrossRef Full Text | Google Scholar

Particle Bed Modular Reactor Limited (1999). PBMR Safety Analysis Report, 001929-207/4, Rev B. South Africa: PBMR.

Google Scholar

Rodey, D., Fivel, M., and Dendievel, R. (2005). Discrete Modeling of the Mechanics of Entangled Materials. Phys. Rev. Lett. 95, 108004. doi:10.1103/PhysRevLett.95.108004

PubMed Abstract | CrossRef Full Text | Google Scholar

Rycroft, C. H., Grest, G. S., Landry, J. W., and Bazant, M. Z. (2006). Analysis of Granular Flow in a Particle-Bed Nuclear Reactor. Phys. Rev. E 74 (2), 021306. doi:10.1103/physreve.74.021306

CrossRef Full Text | Google Scholar

Smeets, B., Odenthal, T., Keresztes, J., Vanmaercke, S., Van Liedekerke, P., Tijskens, E., et al. (2014). Modeling Contact Interactions between Triangulated Rounded Bodies for the Discrete Element Method. Comp. Methods Appl. Mech. Eng. 277, 219–238. doi:10.1016/j.cma.2014.04.017

CrossRef Full Text | Google Scholar

Wolters, J. R., Avvisati, G., Hagemans, F., Vissers, T., Kraft, D. J., Dijkstra, M., et al. (2015). Self-assembly of "Mickey Mouse" Shaped Colloids into Tube-like Structures: Experiments and Simulations. Soft Matter 11, 1067–1077. doi:10.1039/c4sm02375g

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, H., Gui, N., Yang, X., Tu, J., and Jiang, S. (2016). Effects of Particle Size and Region Width on the Mixing and Dispersion of Particles in Two Region Particle Bed. Granular Matter 18, 76. doi:10.1007/s10035-016-0672-7

CrossRef Full Text | Google Scholar

Zhao, Y., Liu, K., Zheng, M., Bares, J., Dierichs, K., Menges, A., et al. (2016). Packings of 3D Stars: Stability and Structure. Granul. Matter 18, 24. doi:10.1007/s10035-016-0606-4

CrossRef Full Text | Google Scholar