Data-Driven Machine Learning for Fault Detection and Diagnosis in Nuclear Power Plants: A Review

Data-driven machine learning (DDML) methods for the fault diagnosis and detection (FDD) in the nuclear power plant (NPP) are of emerging interest in the recent years. However, there still lacks research on comprehensive reviewing the state-of-the-art progress on the DDML for the FDD in the NPP. In this review, the classifications, principles, and characteristics of the DDML are firstly introduced, which include the supervised learning type, unsupervised learning type, and so on. Then, the latest applications of the DDML for the FDD, which consist of the reactor system, reactor component, and reactor condition monitoring are illustrated, which can better predict the NPP behaviors. Lastly, the future development of the DDML for the FDD in the NPP is concluded.

Introduction

Nuclear Energy Development

Nuclear energy is of continuous interest as it can meet increasing energy demands of the world environmentally friendly (Jamil et al., 2016). On the one hand, nuclear power plants (NPPs) consist of many complex systems and components. On the other hand, NPPs are also highly dynamic and non-linear (Peng et al., 2018). In addition, the latest advances come to the further Generation IV NPPs (Yao et al., 2020). In particular, further NPPs greatly emphasize the economics, safety, and reliability over the previous NPPs (Locatelli et al., 2013).

This future of the NPP necessitates the high performance of the fault diagnosis and detection (FDD) in the nuclear industry (Oluwasegun and Jung, 2020). First, the FDD can be adopted in the reactor systems, components, and conditions. Later, it allows the reactor systems and components to be fully optimally used to their lifetime before the maintenance or disposal. Meanwhile, the FDD can reflect the current conditions and enable further prediction of possible malfunctions (Li et al., 2020). Therefore, an accurate and efficient FDD is of great importance to ensure the economics, safety, and reliability of the NPP.

Fault Detection and Diagnosis in NPP

To achieve its goal, the nuclear industry has increased popularity in adapting the FDD techniques (Rezaeianjouybari and Shang, 2020). And the research process of the FDD methods in the NPP can be described as follows.

First, the traditional FDD approach in the NPP belongs to the hardware redundancy method (Betta and Pietrosanto, 2000). For example, the same quantity can be measured by several sensors, and the voting scheme is also introduced for the sensor fault. However, the hardware redundancy principle can hardly suitable for other reactor systems and components (Lu and Upadhyaya, 2005). Thus, it comes to the limit checking method. Usually, it is adopted to monitor the specified parameter of the NPP to see whether the parameter exceeds the predefined value or not (Jamil et al., 2016). Nevertheless, it can only detect the fault when it exceeds a certain value, which could ignore the incipient fault stage. Additionally, the FDD method based on the analytical redundancy can overcome the disadvantages of both the hardware redundancy and limit checking approach (Nguyen et al., 2020). Meanwhile, it can predict the incipient anomalies, optimize the operation schedule, reduce the maintenance cost, and improve safety at the same time. Hence, the FDD method based on the analytical redundancy is of emerging interest in the NPP in these years.

Currently, the FDD methods based on the analytical redundancy can be basically classified into three main types: physic model-based, reliability-based, and data-driven methods (Wang et al., 2020). For the physic model-based techniques, the mathematical models are proposed to describe the research objects. Moreover, the reliability-based approaches adapt the probability theory and knowledge-based statics while it requires prior experience or knowledge of the system (Ma and Jiang, 2011; Jamil et al., 2016). However, it is not suitable for real industrial applications like the NPP as it is highly dynamic and non-linear (Zhao and Wang, 2018). At last, the data-driven approaches require no prior experience of the NPP and just only need the previous data for the model training (Betta and Pietrosanto, 2000; Razavi-Far et al., 2009; Wang et al., 2020). In recent years, it is a promising technique and of interest for the FDD in the NPP (Moshkbar-Bakhshayesh and Ghofrani, 2013; Ren et al., 2016; Utah and Jung, 2020; Nguyen et al., 2020).

Data-Driven Machine Learning Method

The data-driven approaches tend to be more suitable and able to predict without a prior knowledge of the NPP. At the same time, it potentially achieves high accuracy with low economic cost. Combined with the machine learning (ML) algorithms, the data-driven techniques have drawn increasing attention for the FDD in the NPP in the past decades (Ma and Jiang, 2011; Mandal et al., 2017a, b; Wang et al., 2020).

At present, the data-driven machine learning (DDML) methods, including the neural network, support vector machine (SVM), dimension reduction learning (DRL), ensemble learning (EL) or random tree (RT), regression approaches, and so on, have been applied to predict the NPP behaviors (Jamil et al., 2016; Saeed et al., 2020). Nevertheless, few researches concern with the state-of-the-art progress and future trends for both the DDML approach for the FDD and the NPP (Bartlett and Uhrig, 1992; Ma and Jiang, 2011; Moshkbar-Bakhshayesh and Ghofrani, 2013).

Especially, Bartlett and Uhrig (1992) briefly presented the artificial neural network (ANN) method for the FDD in the NPP. However, it only concerns the ANN method. In 2011, Ma and Jiang (2011) considered six areas of applications of the FDD in the NPP. Moreover, the transient diagnosis in the NPP was illustrated with the ANN approach (Moshkbar-Bakhshayesh and Ghofrani, 2013). However, there are either the specified component (system) or the outdated techniques in the available research. As the DDML techniques in the NPP sharp a lot in recent years (Rezaeianjouybari and Shang, 2020; Yao et al., 2020; Saeed et al., 2020), there exists a gap in the current state-of–the-art of the DDML techniques for the FDD in the NPP. In this review, the current classifications, principles, characteristics, and applications of the FDD in the NPP, followed by the discussion on the future development of the DDML method for the NPP state prediction, will be illustrated.

Scope of This Review

Compared with the physic model-based and reliability-based techniques, the data-driven methods have the superior advantage in the trade-off between the safety, reliability, and economics of the NPP. In addition, it has been considered as a promising future FDD direction from the encouraging results made by the recent studies. However, to the best of our knowledge, there still lacks research on comprehensive reviewing the state-of–the-art progress on the DDML for the FDD in the nuclear industry. Therefore, this review focuses on elaborating the DDML in the NPP, introducing the applications of the DDML in the NPP and illustrating the future development. In section “Overview of the DDML for FDD in NPP,” principles and characteristics of the DDML for the FDD are discussed, including the supervised learning type, unsupervised learning type, and reinforcement learning type. Section “Development of DDML for FDD in NPP” shows the applications and further development of the DDML for the FDD. Section “Conclusion” explains the conclusions and remarks on the DDML for the FDD. It should be noted that this review would emphasize the DDML for the FDD in the nuclear industry.

Overview of the DDML for FDD in NPP

Generally, the DDML for the FDD in the NPP can be classified into several types. First, these types include supervised learning, unsupervised learning, and reinforcement learning by the principle of the learning type. Second, these can be sorted into regression, instance-based learning, neural network, deep learning, dimension reduction, and kernel-based learning algorithms by the algorithm type. In addition, the detailed classifications of DDML for FDD in NPP are as shown in Figure 1. As for the DDML, it is of emerging interest for the FDD in the NPP. Hence, it is necessary to be illustrated in detail. Finally, the research profile of the DDML for the FDD in the NPP is described as follows.

FIGURE 1

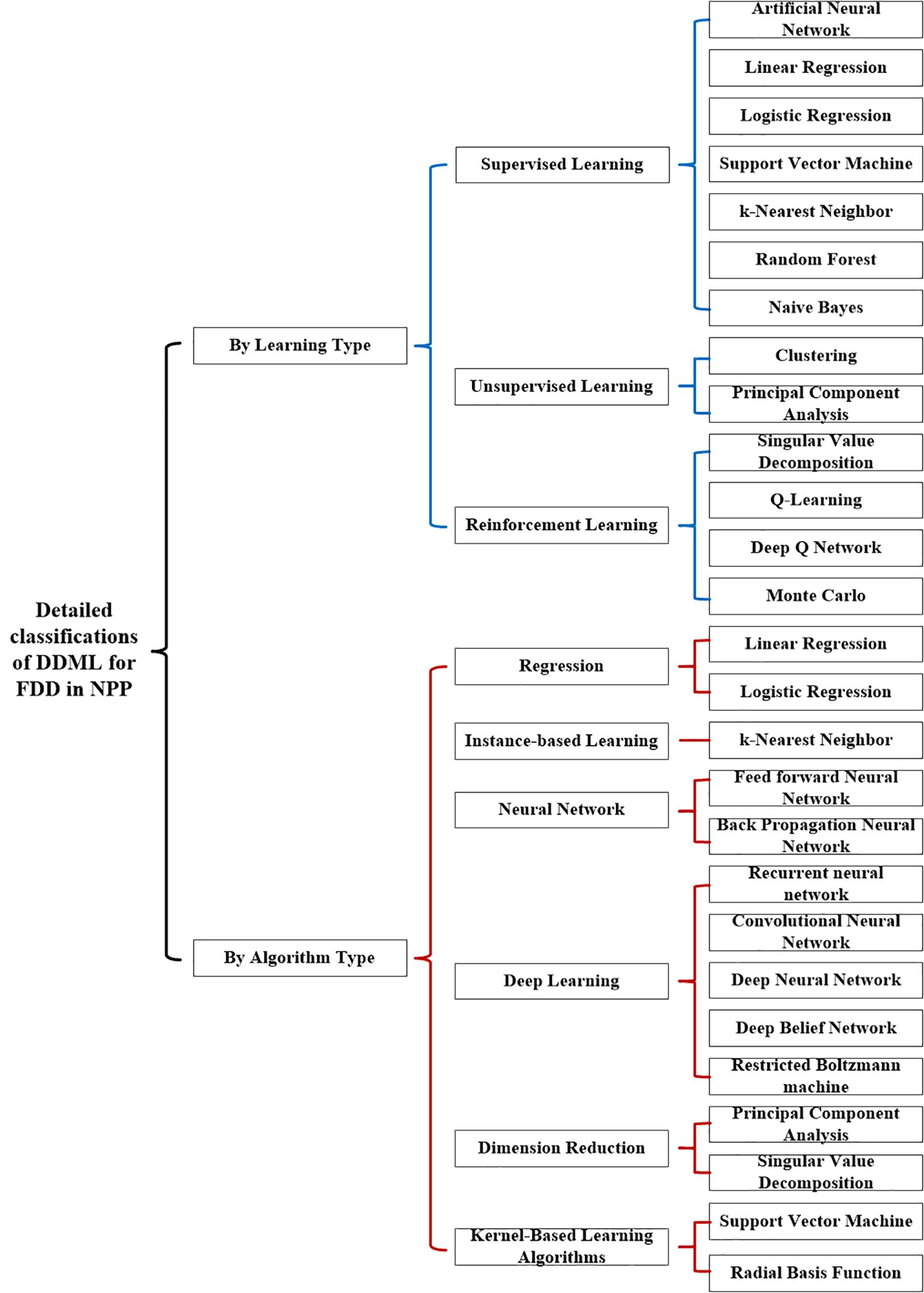
Figure 1. Detailed classifications of data-driven machine learning (DDML) for the fault diagnosis and detection (FDD) in the nuclear power plant (NPP).

Supervised Learning Method

In Table 1, the ANN method, linear regression, logistic regression, SVM, k-nearest neighbor (kNN), RT, and naive Bayes (NB) for the FDD in the NPP belong to the supervised learning approaches.

TABLE 1

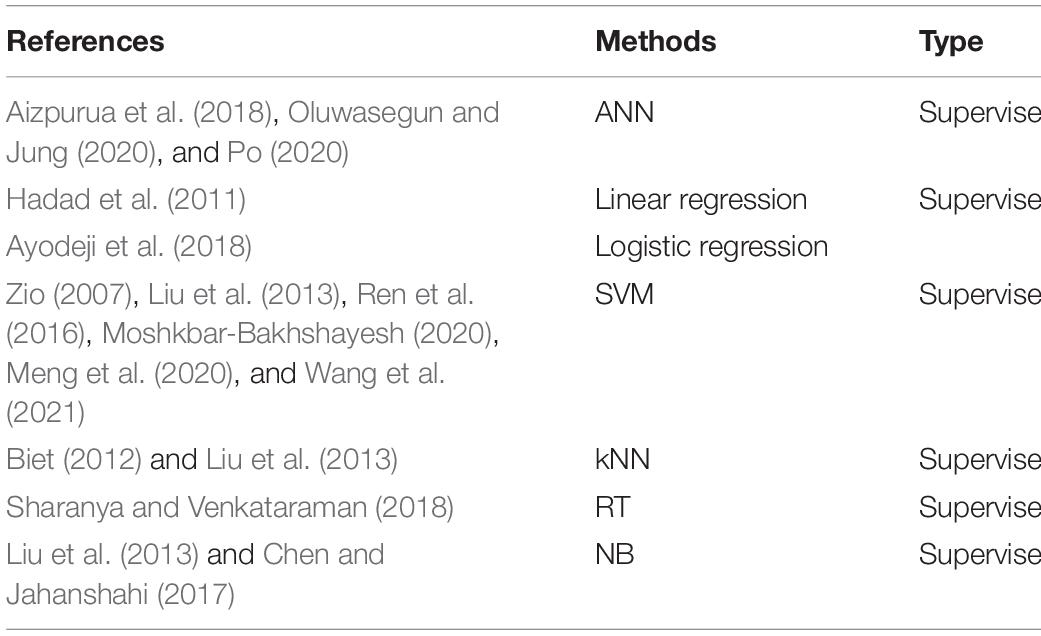
Table 1. Status of the data-driven machine learning (DDML) of the supervised learning method for the fault diagnosis and detection (FDD) in the nuclear power plant (NPP).

Artificial Neural Network Approach

A typical ANN is constructed by three parts: the structure (the input signal, hidden layer, and output), learning algorithm (update the synaptic weights), and activation function. For example, the ANN approaches are taken for the FDD in the NPP like the control rod drive system and accident prevention system (Aizpurua et al., 2018; Po, 2020; Oluwasegun and Jung, 2020) as shown in Figure 2. In Figure 2, the input signals x₁, x₂, …, x_n are the control rod step number, coil current data, vibration data, coolant temperature, etc. They correspond to each synaptic weight w₁, w₂, …, w_n, respectively. After the procession of the summing junction and the activation function φ(⋅), the output y(k) is obtained. Additionally, the ANN approach can quickly adjust to new problems. However, it requires a lot of data for the training and it is hard to select the meta parameters.

FIGURE 2

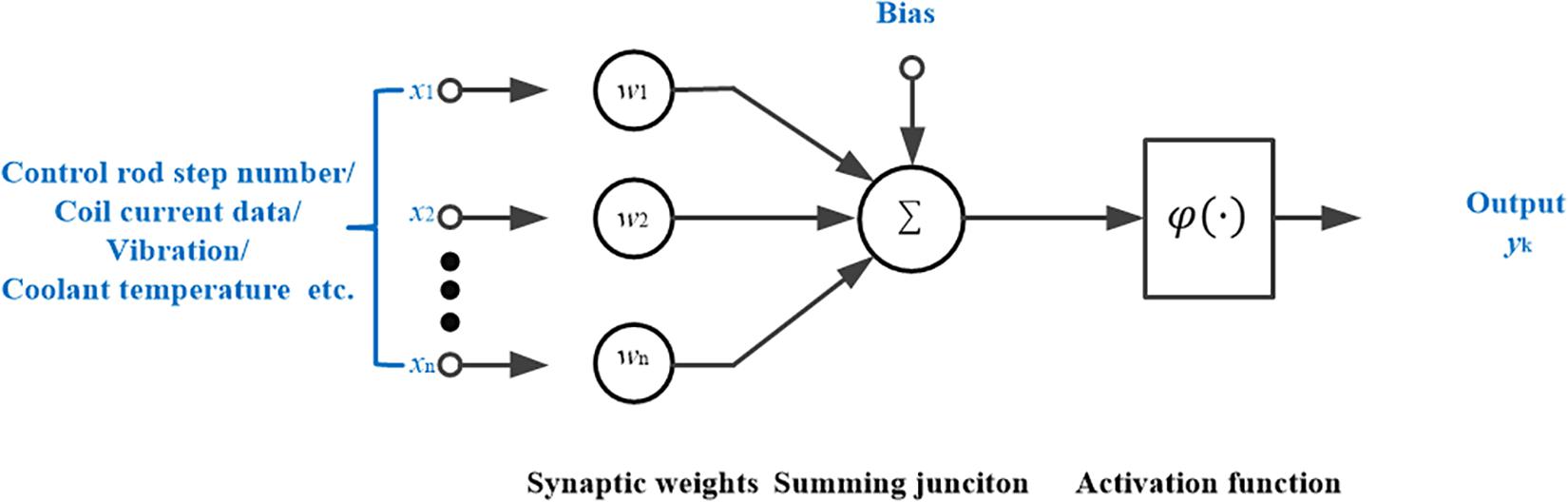
Figure 2. The artificial neural network (ANN) approach for the fault diagnosis and detection (FDD) in the nuclear power plant (NPP).

Regression Algorithm

Especially, the linear regression assumes that the dependent variable obeys a Gaussian distribution, whereas the logistic regression assumes that the dependent variable follows a Bernoulli distribution. Based on the linear regression, the logistic regression introduces non-linear factors through the Sigmoid function. For instance, Hadad et al. (2011) performed a linear regression analysis to evaluate the network performance in the NPP. In 2018, Ayodeji et al. (2018) combined the logistic regression with the SVM for the incipient fault diagnosis in the NPP. In particular, the regression algorithm is direct and fast while it also needs to handle the abnormal value.

Support Vector Machine Method

The basic idea of the SVM learning is to solve the separation hyperplane that can correctly divide the training dataset. In Figure 3A, the formula represents the separating hyperplane. In addition, w is the normal vector to the hyperplane with a magnitude w. The parameter b/w is the offset amount between the hyperplane and the origin. Furthermore, the two hyperplanes wx − b = 1 and wx − b = − 1 are the margins of two classifies. Overall, the distance between the two margins is 2/w. For a linearly separable dataset, there are infinitely such hyperplanes (i.e., perceptrons), whereas the separating hyperplane with the largest geometric interval is the only one. It has the largest geometric interval while the efficiency may not be high.

FIGURE 3

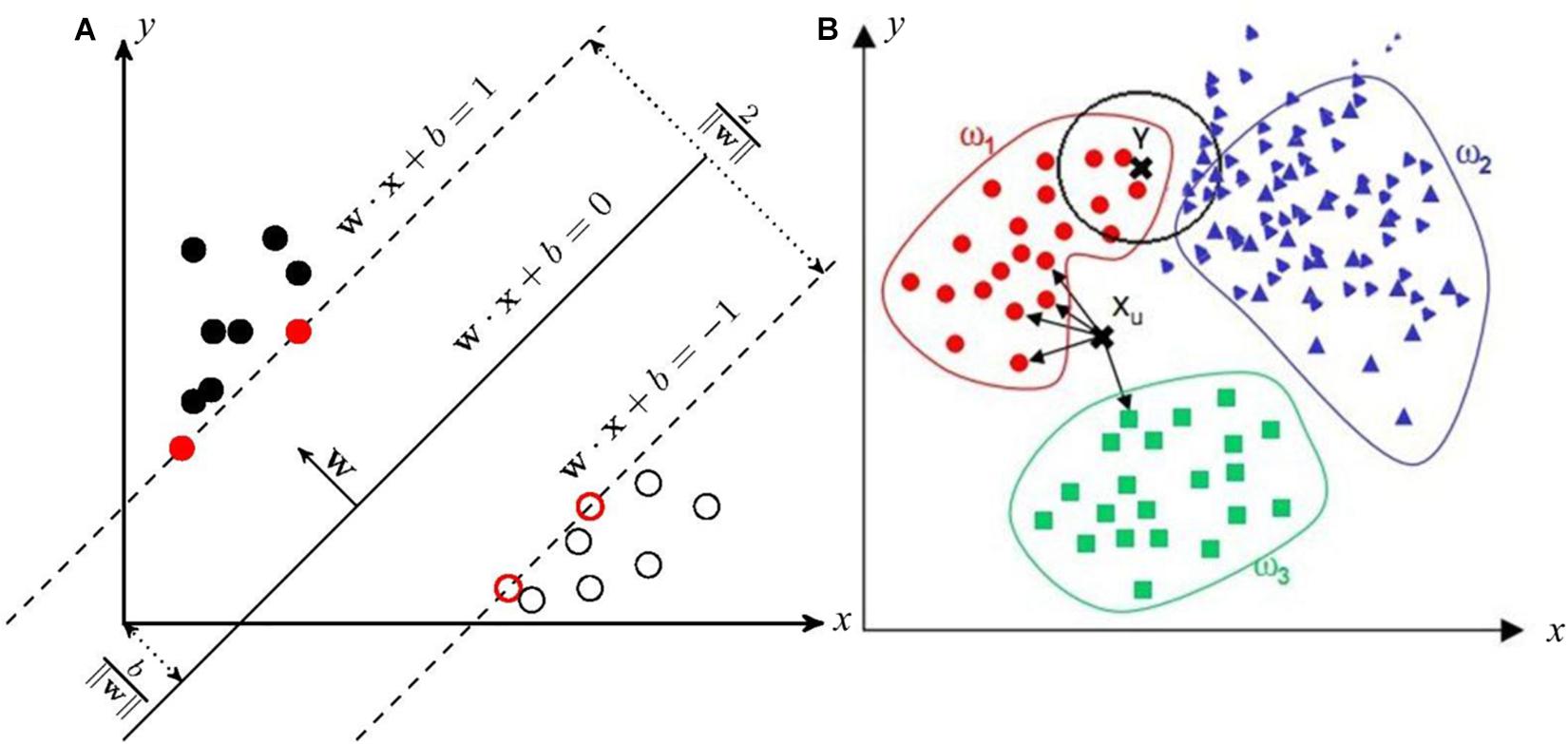
Figure 3. The support vector machine (SVM) and k-nearest neighbor (kNN) method for the fault diagnosis and detection (FDD) in the nuclear power plant (NPP). (A) SVM (B) kNN.

For the FDD in the NPP, Zio (2007) applied the SVM in the anomalies and malfunctions occurring in the feedwater system. Then, Liu et al. (2013) developed the SVM for monitoring the components of NPPs. In addition, Ren et al. (2016) proposed the SVM with sparse representation. Furthermore, Moshkbar-Bakhshayesh (2020) utilized the SVM for the control rod system. Meanwhile, Meng et al. (2020) combined the SVM and objective function method for the loose parts. At last, Wang et al. (2021) adopted the SVM together with the principal component analysis (PCA) and clustering algorithm for the sensor faults in the NPP.

k-Nearest Neighbor Technique

The principle of the kNN technique is described in Figure 3B. In the prediction of point x_u in Figure 3B, four neighboring samples belong to the category c₁ and only one neighboring sample belongs to the category c₂. Hence, the point x_u is classified as the category c₁. But from the visual observation, it should be more reasonable to divide into circular classification. According to this situation, a weight such as ω₁,ω2, and ω₃ can be also added to the distance measurement. First, Liu et al. (2013) coupled the kNN technique with the SVM for monitoring the components of NPPs. Biet (2012) conducted the rotor FDD with the kNN technique and feature section in the NPP. On the one hand, the advantages of this algorithm are simple, easy to understand, and without modeling and training. And it is suitable for multi-classification problems. On the other hand, the shortcomings of this algorithm include the lazy algorithm and a large amount of calculation when classifying the test samples.

Random Tree Approach

The RT approach contains two parts, one is “random” and the other is “tree.” It is based on the decision tree (DT). It can produce very high-dimensional (many features) data without dimensionality reduction or feature selection. And Sharanya and Venkataraman (2018) carried out the RT for the FDD of the coolant tower in the NPP. Meanwhile, it can judge the importance of features. However, the RT has been shown to overfit in some noisy classification or regression problems.

Naive Bayes Method

The NB is a classification method based on the Bayes’ theorem and the independence assumption of characteristic conditions. For this technique, Liu et al. (2013) combined the NB with SVM for components in the NPP. In 2017, Chen and Jahanshahi (2017) carried out the FDD of thermocouples with the naive Bayes method in the NPP. It is fast, easy to train, and has good performance. Meanwhile, it may fall short when the input variables are related.

Unsupervised and Reinforcement Learning Method

Then, the DDML methods of the unsupervised learning type for the FDD in the NPP include the clustering (Baraldi et al., 2013; Li et al., 2020; Wang et al., 2021) and PCA (Ayodeji et al., 2018; Ling et al., 2020; Yu et al., 2020; Wang et al., 2021) techniques as shown in Table 2.

TABLE 2

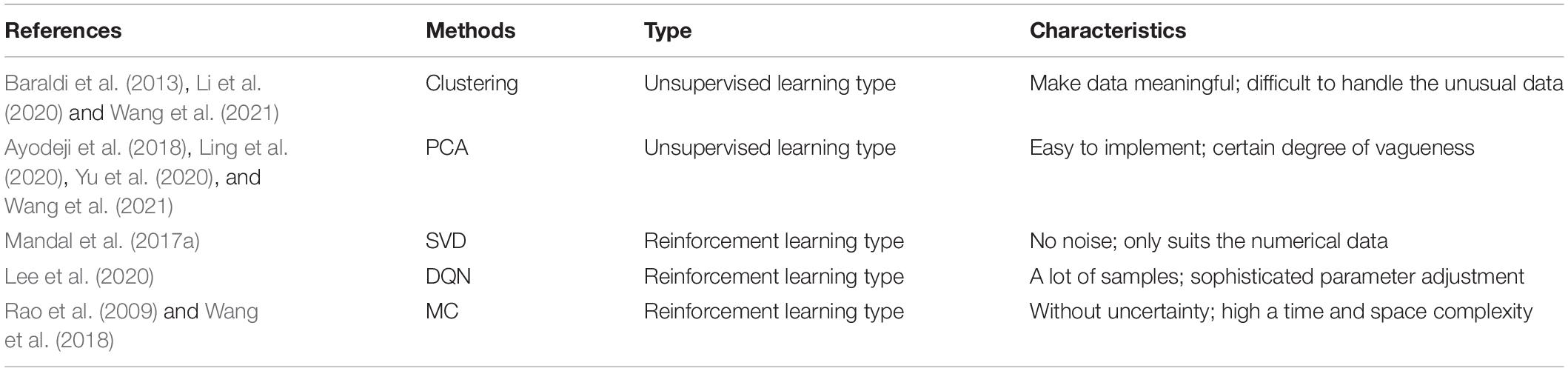
Table 2. Status of the data-driven machine learning (DDML) of the unsupervised and reinforcement learning method for the fault diagnosis and detection (FDD) in the nuclear power plant (NPP).

Afterward, the DDML research of the reinforcement learning type gradually developed in Table 2. The DDML such as the singular value decomposition (SVD) (Mandal et al., 2017a), deep Q learning network (DQN) (Lee et al., 2020), and Monte Carlo (MC) (Rao et al., 2009; Wang et al., 2018) are adopted by the NPP.

Clustering

Clustering algorithm refers to the classification of a group of targets. Compared with other groups of the targets, the same group of the targets are more similar to each other. In 2013, Baraldi et al. (2013) adopted the clustering technique for the FDD of the pressurizer. Later, Li et al. (2020) proposed a clustering algorithm for the transient detection in the NPP. Furthermore, Wang et al. (2021) utilized the clustering algorithm together with the SVM and PCA for the sensor anomalies in the NPP. This algorithm can make the data meaningful. Meanwhile, the results with this algorithm become difficult to interpret for the unusual datasets.

Principal Component Analysis Approach

The PCA approach is a kind of the dimensionality reduction method, which pursues the purpose of using less information to summarize or describe the data. In 2018, Ayodeji et al. (2018) operated the PCA with the radial basis function (RBF) for the transient scenarios in the NPP. Then, Yu et al. (2020) detected the sensor faults with the PCA approach. Afterward, Ling et al. (2020) presented the FDD of the reactor coolant system in the NPP. Lastly, Wang et al. (2021) utilized the PCA together with the clustering algorithm and SVM for the sensor anomalies in the NPP. The main operation of the PCA approach is eigenvalue decomposition, which is easy to implement. Conversely, the meaning of each feature dimension of the principal component has a certain degree of vagueness, which is not as explanatory as the original sample feature.

Singular Value Decomposition Method

The SVD method also belongs to the dimensionality reduction means. It is to decompose a large matrix into a form that is easy to handle. For the FDD in the NPP, Mandal et al. (2017a) introduced the SVD method to the thermocouple sensors. This algorithm can simplify the data, remove the noise, and hence improve the algorithm results. In contrast, it only suits the numerical data.

Deep Q Learning Network Technique

The DQN algorithm is a method of approximating the Q learning through a neural network. In 2020, Lee et al. (2020) focused on developing the algorithm for converting all the currently manual activities in the NPP power-increase process to autonomous operations. Among them, the DQN algorithm is included. For the DQN algorithm, it can produce a large number of samples. Conversely, the DQN algorithm may not necessarily converge and require sophisticated parameter adjustment.

Monte Carlo Method

The MC method has its inherent capability in simulating the actual process and random behavior of the system. First, Rao et al. (2009) carried out the probabilistic safety assessment with the MC method in the NPP. Then, Wang et al. (2018) explored the cyber-attack scenarios with the MC method in the NPP. It can eliminate uncertainty in reliability modeling while this algorithm requires a high time and space complexity.

Algorithm Type Method

In the past decades, the DDML studies can be classified into regression, instance-based learning, neural network, deep learning, dimension reduction, and kernel-based learning algorithms and they are shown in Table 3. Especially, the DDML of the deep learning type is popular for the FDD in the NPP recently. In addition, it is one of the recent advancements in the ANN (Peng et al., 2018). Furthermore, the deep learning type includes the recurrent neural network (RNN) (Moshkbar-Bakhshayesh and Ghofrani, 2013; Ling et al., 2020; Rezaeianjouybari and Shang, 2020), convolutional neural network (CNN) (Chen and Jahanshahi, 2017; Yao et al., 2020; Chae et al., 2020), deep neural network (DNN) (Mo et al., 2007; Chae et al., 2020; Miki and Demachi, 2020; Rezaeianjouybari and Shang, 2020; Saeed et al., 2020; Utah and Jung, 2020), deep belief network or dynamic Bayesian network (DBN) (Mandal et al., 2017b; Peng et al., 2018; Oh and Lee, 2020; Vaddi et al., 2020; Zhao et al., 2020), and restricted Boltzmann machine (RBM) (Rezaeianjouybari and Shang, 2020).

TABLE 3

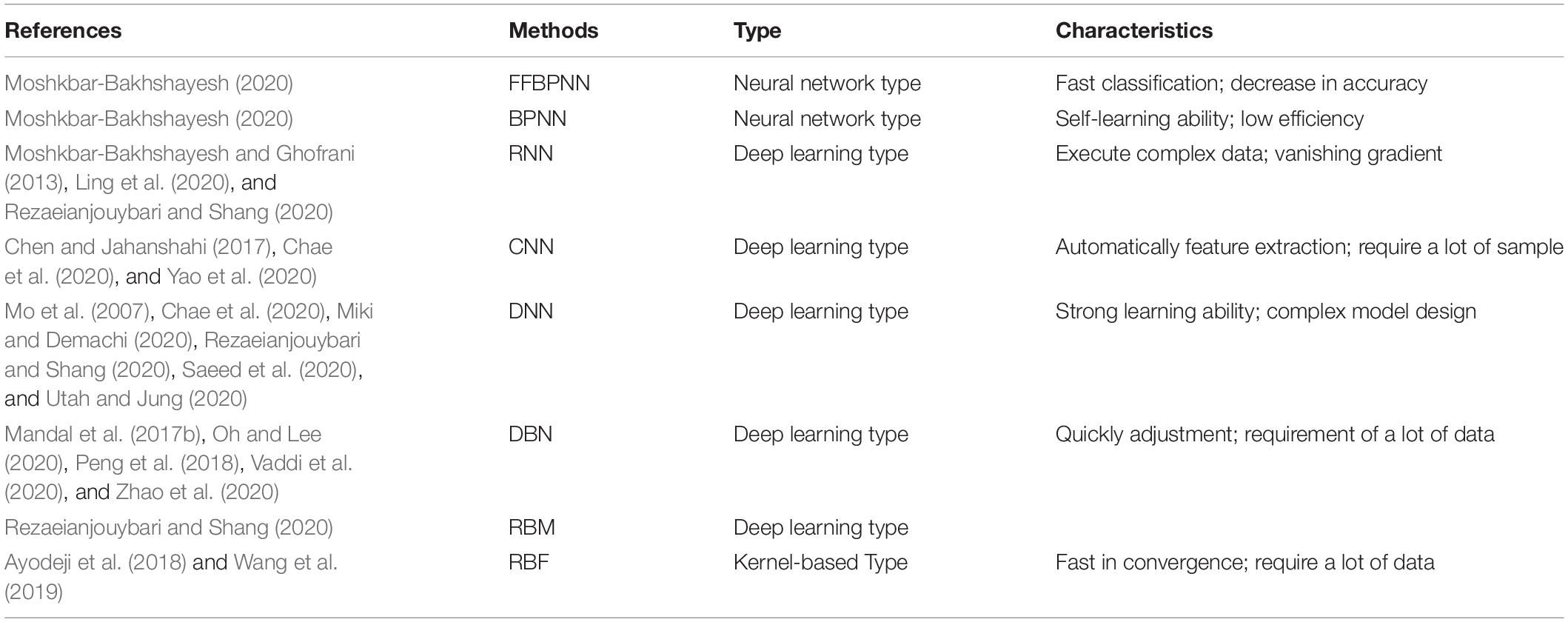
Table 3. Status of the data-driven machine learning (DDML) of the algorithm type method for the fault diagnosis and detection (FDD) in the nuclear power plant (NPP).

Recurrent Neural Network Approach

The biggest difference between the RNN approach and the traditional neural network is that each time it will bring the previous output result to the next hidden layer and train together. In 2013, Moshkbar-Bakhshayesh and Ghofrani (2013) studied the advanced approaches, which include the RNN approach for the transient diagnosis in the NPP. Then, Rezaeianjouybari and Shang (2020) reviewed the RNN algorithm and DNN technique for the prognostics and health management (PHM) in the NPP. Afterward, Ling et al. (2020) presented the RNN approach and PCA for the FDD in the reactor coolant system in the NPP. Especially, the RNN has the ability to learn and execute complex data conversion over a long period of time. It also may cause the problem of the vanishing gradient.

Convolutional Neural Network Method

The CNN algorithm is iteratively trained with a certain model to extract the features. It has been adopted for crack detection (Chen and Jahanshahi, 2017), sensor fault conditions (Yao et al., 2020), and pipe corrosion (Chae et al., 2020). Additionally, the advantages of the CNN algorithm are that it can automatically perform the feature extraction and has no pressure on the high-dimensional data processing. Meanwhile, it needs to adjust the parameters need and requires a large size of the sample.

Deep Neural Network Technique

The DNN technique has been proposed for the transient detection (Mo et al., 2007), PHM (Rezaeianjouybari and Shang, 2020), fault state detection of the solenoid operated valves (Utah and Jung, 2020), and the novel fault scheme (Saeed et al., 2020) in the NPP. In addition, Chae et al. (2020) combined the long–short term memory (LSTM) network with the SVM and CNN approach to diagnose the pipe corrosion in the NPP. Finally, the LSTM network, which is an RNN approach, was also applied for the bear fault in the NPP (Miki and Demachi, 2020). It has a strong learning ability while the model design is complex.

Deep Belief Network and RBM Method

The DBN method is a major method of the Bayesian network (BN). It was applied to classify the fault data of the thermocouple sensors (Mandal et al., 2017b), accident prediction (Peng et al., 2018), operation failure of the high temperature gas-cooled reactor (Zhao et al., 2020), loss of coolant accident (LOCA) identity (Oh and Lee, 2020) and cybersecurity threats (Vaddi et al., 2020) in the NPP. Lastly, the DBN can be seen as a stack of the RBM (Rezaeianjouybari and Shang, 2020). The DBN and RBM method belong to the neural network (NN) method. Hence, the pros and cons of the two techniques are the same as the ANN approach.

Other Techniques

For the kernel-based type approach, the above SVM comes to the first place. Followed with the SVM, the RBF was adopted for the transients monitoring (Ayodeji et al., 2018; Wang et al., 2019). It is fast in convergence while it requires a lot of data. In addition, Moshkbar-Bakhshayesh (2020) investigated the feed-forward back-propagation neural network (FFBPNN), backpropagation neural network (BPNN), DT and SVM for the uncontrolled withdrawal of control rods in the NPP. The advantages and disadvantages of these methods are shown in Table 3.

Development of DDML for FDD in NPP

Currently, huge achievements have already been made in its applications to predict the behaviors of the NPP. Therefore, there is a need to summarize the latest applications of the DDML in the NPP. It can also open future prospects to improve the accuracy of the FDD and have insights into the underlying mechanisms.

Furthermore, the DDML is a promising area with a flexible and efficient fitting algorithm. It does not underlie physical knowledge. Tables 4–6 summarize the approaches taken by a wide range of authors recently. Generally, the DDML for the FDD in the NPP can be classified into three areas: (1) reactor system, (2) reactor component, and (3) reactor condition monitoring.

TABLE 4

Table 4. Latest applications of the data-driven machine learning (DDML) for the fault diagnosis and detection (FDD) of the nuclear power plant (NPP) system.

TABLE 5

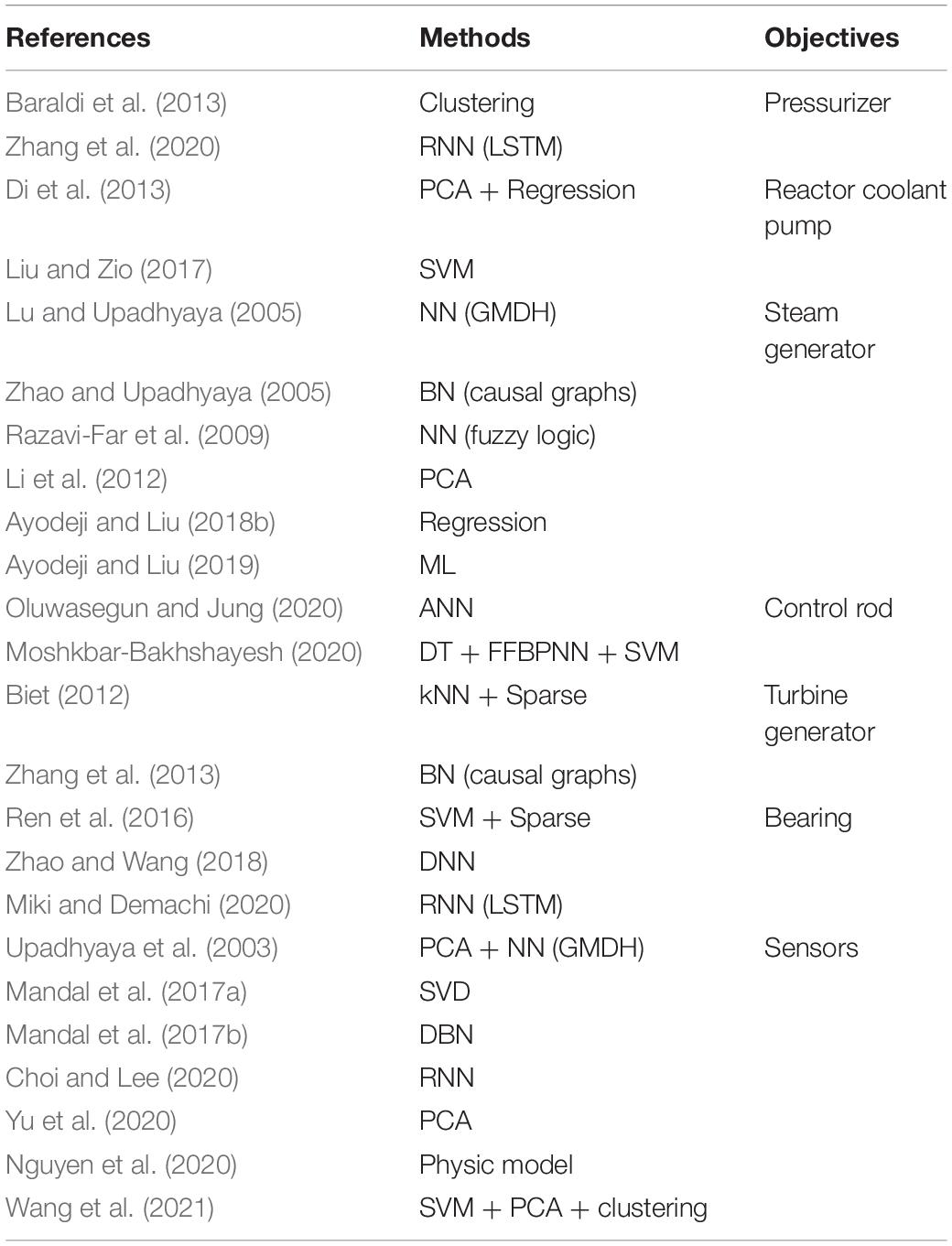
Table 5. Latest applications of the data-driven machine learning (DDML) for the fault diagnosis and detection (FDD) of the nuclear power plant (NPP) component.

TABLE 6

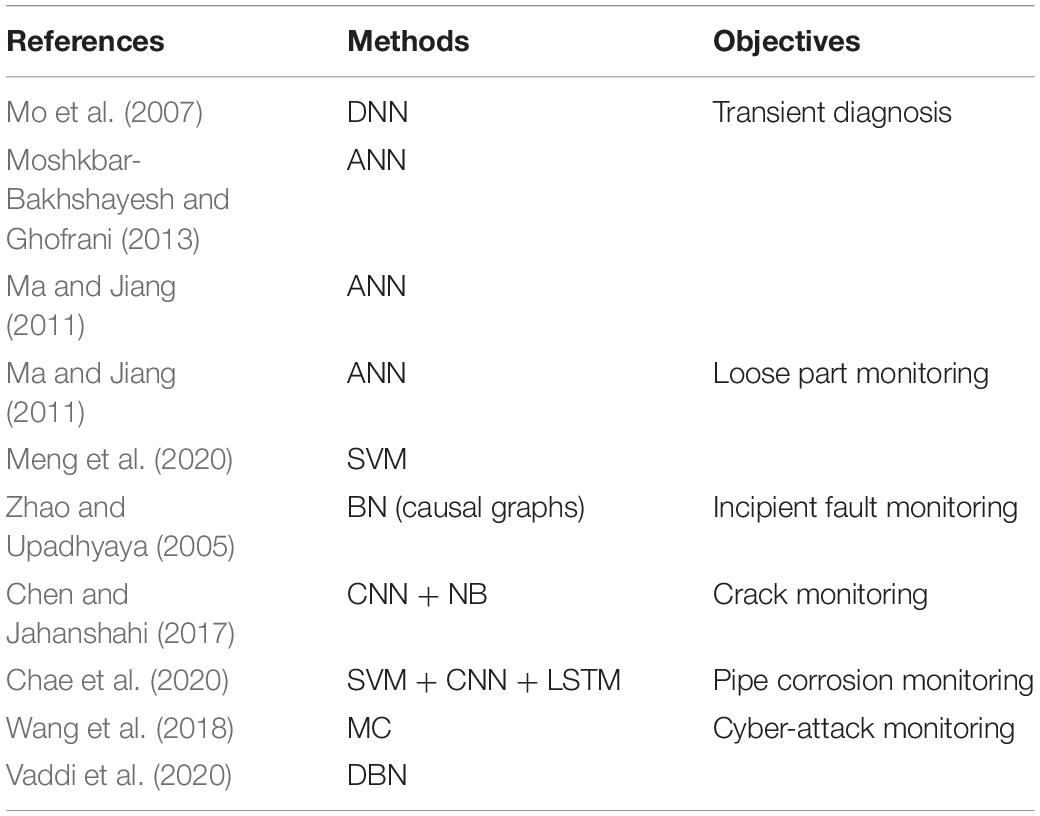
Table 6. Latest applications of the data-driven machine learning (DDML) for the fault diagnosis and detection (FDD) of the nuclear power plant (NPP) condition monitoring.

Latest Applications of DDML for FDD in the NPP System

As shown in Table 4, the DDML has been utilized for the FDD in the reactor coolant system (Ayodeji and Liu, 2018a; Farber and Cole, 2020), secondary loop system (Dong and Zhang, 2020), instrumentation control system (Holbert and Lin, 2012), and feedwater system (Zio, 2007) in the NPP.

First, Ayodeji and Liu (2018a) proposed the SVM for the incipient fault conditions of the reactor coolant system in the pressurized water reactor. In addition, Farber and Cole (2020) combined the ANN with the physical model-based method for the loss of coolant accident (LOCA) of the reactor coolant system. Then, Dong and Zhang (2020) presented the causality graphs, which belong to the BN approach for the secondary loop system in the NPP. Afterward, Holbert and Lin (2012) integrated the fuzzy logic, which is a kind of the NN techniques for the instrumentation control system in the NPP. At last, Zio (2007) utilized the SVM approach for the feedwater system of a boiling water reactor.

Latest Applications of DDML for FDD in the NPP Component

In Table 5, the reactor components, which include the pressurizer (Baraldi et al., 2013; Zhang et al., 2020), reactor coolant pump (Di et al., 2013; Liu and Zio, 2017), steam generator (Lu and Upadhyaya, 2005; Zhao and Upadhyaya, 2005; Razavi-Far et al., 2009; Li et al., 2012; Ayodeji and Liu, 2018b, 2019), control rod (Moshkbar-Bakhshayesh, 2020; Oluwasegun and Jung, 2020), turbine generator (Biet, 2012; Zhang et al., 2013), bearing (Ren et al., 2016; Zhao and Wang, 2018; Miki and Demachi, 2020), and sensors (Upadhyaya et al., 2003; Mandal et al., 2017a, b; Choi and Lee, 2020; Nguyen et al., 2020; Yu et al., 2020; Wang et al., 2021) are captured by different modeling techniques.

Initially, Baraldi et al. (2013) tested the clustering for the FDD in the pressurizer in the NPP. Later, Zhang et al. (2020) applied the LSTM for the water lever prediction of the pressurizer. For the reactor coolant pump, Di et al. (2013) conducted the FDD for the reactor coolant pump with the PCA and kernel-based regression method. Finally, Liu and Zio (2017) predicted the leakage from the reactor coolant pump with the SVM.

However, Lu and Upadhyaya (2005) adopted the group method of data handling method (GMDH), which is a kind of the NN approach for modeling the interrelationship of the U-tube steam generator (UTSG). Zhao and Upadhyaya (2005) presented the causal graphs for a pressurized water reactor. Razavi-Far et al. (2009) detected the faults of the steam generator using the fuzzy logic technique. Meanwhile, the PCA (Li et al., 2012) and support vector regression (Ayodeji and Liu, 2018b) are also adopted for the FDD of the steam generator.

For the control rod, Oluwasegun and Jung (2020) provided the health monitoring with the ANN approach. Meanwhile, Moshkbar-Bakhshayesh (2020) predicted the uncontrolled withdrawal of control rods transient with the DT, FFBPNN, and SVM. In addition, Biet (2012) recoded the rotor faults of the turbine generator with the kNN and sparse. However, Zhang et al. (2013) developed the causal graphs for the FDD of the turbine generator. Furthermore, the SVM plus sparse, DNN, and LSTM approaches for the FDD of the roller bearing were also proposed, respectively (Ren et al., 2016; Zhao and Wang, 2018; Miki and Demachi, 2020). Lastly, various techniques, including the PCA, GMDH, SVD, DBN, RNN, and clustering, are carried out for the sensor faults correspondingly in the NPP as shown in Table 4 (Upadhyaya et al., 2003; Mandal et al., 2017a, b; Choi and Lee, 2020; Nguyen et al., 2020; Yu et al., 2020; Wang et al., 2021).

Latest Applications of DDML for FDD in the NPP Condition Monitoring

To satisfy the reliability, safety, and economics of the NPP, the condition identification of the NPP is expected to become increasingly popular as shown in Table 6 (Moshkbar-Bakhshayesh and Ghofrani, 2013).

For the transient monitoring, Mo et al. (2007) proposed the DNN for the NPP. Furthermore, the ANN method for the transient monitoring in the NPP is mainly reviewed (Moshkbar-Bakhshayesh and Ghofrani, 2013; Ma and Jiang, 2011). Additionally, the ANN and SVM approaches have been adopted for the loose part monitoring (Ma and Jiang, 2011; Meng et al., 2020). Meanwhile, the causal graphs are also utilized for the incipient fault monitoring (Zhao and Upadhyaya, 2005). Moreover, Chen and Jahanshahi (2017) detected cracks on the underwater metallic surfaces from the nuclear inspection videos with the CNN and NB techniques. Furthermore, three approaches, including the SVM, CNN, and LSTM, are combined for the flow-accelerated corrosion of the pipe in the NPP (Chae et al., 2020). Especially, the new threats of the cyber-attack scenarios in the NPP are identified with the MC and DBN methods (Wang et al., 2018; Cyber threats: Vaddi et al., 2020).

Further Development of DDML for FDD in NPP

The DDML is of emerging interest in the FDD in the NPP. As mentioned above, significant efforts have already been taken in the prediction of the NPP behaviors. The future development of the DDML for the FDD in the NPP can be concluded based on the latest applications of the DDML for the FDD in the NPP as described in sections “Latest Applications of DDML for FDD of NPP System” to “Latest Applications of DDML for FDD of NPP Condition Monitoring.”

Combination of DDML and Physic Model-Based Approach

For the DDML, the training data input and the results output. Hence, it is commonly regarded as a “black box.” Although the physic model-based techniques are difficult to be proposed to describe the research objects, it still has its advantages. However, the combination of the DDML and physic model-based approach can help better understanding of the physical process (Farber and Cole, 2020). Furthermore, the DDML can be illustrated the experiment data clearly if the physic model-based approach functions. It should be noted that the hybrid of the DDML and physic model-based approach may attribute to higher computational resources. Nevertheless, it can provide reasonable and accurate insights into the physical processes.

Hybrid of Different Time-Scale Methods

In Tables 4–6, various methods for the FDD of the reactor systems, reactor components, and reactor condition monitoring are illustrated generally. Among them, there are hybrid of two or more techniques (Upadhyaya et al., 2003; Di et al., 2013; Ren et al., 2016; Chae et al., 2020; Moshkbar-Bakhshayesh, 2020; Wang et al., 2021). In particular, the time scale of the physical process of each object differs, which corresponds to its suitable methods for the FDD. Especially, the hybrid of the two or more methods for the FDD can be a superior solution for the evolution of the NPP. By this hybrid, it can present both the short-time and long-time behaviors of the NPP.

Sparse Data Treatment

Due to the safety, reliability, and economic issues, there is usually a lack of the experiment data of the FDD in the NPP. For a reactor system, reactor component, and reactor condition monitoring, not every parameter or data can be obtained. Therefore, there is a need for the DDML approach that is suitable for the sparse data. Special DDML can meet the urgent requirement properly.

Accurate and Fast Simulations

From the above treatment, the experiment data are hardly obtained under some conditions. Hence, the simulations are commonly performed to generate the training data (Wang et al., 2020; Yu et al., 2020). An accurate and fast simulation can understand the system, component, or condition with relatively acceptable computation cost. Detailed simulations are costly. One solution is to create a database of the historic results for the simulations and then train the DDML model. Later, DDML can also contribute to the experiment design for reasonable relatively fewer experiments.

Conclusion

In this paper, the state-of-the-art progress on the DDML for the FDD in the nuclear industry, which is an emerging interest on both the DDML approach for the FDD and the NPP, is reviewed. The main conclusions are obtained.

First, the DDML for the FDD in the NPP, which includes the supervised learning type, unsupervised learning type, and so on, are classified clearly with their characteristics, which help a comprehensive overview of the DDML.

1. Then, principles of various DDML for the FDD in the NPP, in particular, the DDML of the supervised learning type and deep learning type are explained in detail.

2. Furthermore, the latest applications of the DDML for the FDD, which consist of the reactor system, reactor component, and reactor condition monitoring are illustrated.

Lastly, the future development of the DDML for the FDD in the NPP is concluded. Considering the accuracy, complexity, and computation amount, the combination of the DDML and physic model-based approach, hybrid of different time-scale methods, accurate, and fast simulations are the future trends for the FDD in the NPP.

Compared with the physic model-based and reliability-based techniques, the DDML have superior advantages in the trade-off between the safety, reliability, and economics of the NPP. With the advancement of the information technologies and ML algorithms, together with the hybrid of the various approaches in different time scales, the DDML is to be a promising technique for the advanced NPP modeling in the future.

Data Availability Statement

All datasets presented in this study are included in the article/supplementary material.

Author Contributions

GH illustrated and summarized the fault diagnosis and detection in the nuclear power plant. TZ dedicated his time to classifications and principles of the algorithms. QL designed the whole architecture and provided the required resources. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Sichuan Science and Technology Project (Grant No. 2020YFSY0031). It was also partially supported by the National Science Foundation for Young Scientists of China (Grant No. 61703385).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Aizpurua, J. I., McArthur, S. D., Stewart, B. G., Lambert, B., and Cross, C. J. (2018). Adaptive power transformer lifetime predictions through machine learning and uncertainty modeling in nuclear power plants. IEEE Trans. Ind. Electron. 66, 4726–4737. doi: 10.1109/tie.2018.2860532

CrossRef Full Text | Google Scholar

Ayodeji, A., and Liu, Y. K. (2018a). Support vector ensemble for incipient fault diagnosis in nuclear plant components. Nucl. Eng. Technol. 50, 1306–1313. doi: 10.1016/j.net.2018.07.013

CrossRef Full Text | Google Scholar

Ayodeji, A., and Liu, Y. K. (2018b). SVR optimization with soft computing algorithms for incipient SGTR diagnosis. Ann. Nucl. Energy 121, 89–100. doi: 10.1016/j.anucene.2018.07.011

CrossRef Full Text | Google Scholar

Ayodeji, A., and Liu, Y. K. (2019). PWR heat exchanger tube defects: trends, signatures and diagnostic techniques. Prog. Nucl. Energy 112, 171–184. doi: 10.1016/j.pnucene.2018.12.017

CrossRef Full Text | Google Scholar

Ayodeji, A., Liu, Y. K., and Xia, H. (2018). Knowledge base operator support system for nuclear power plant fault diagnosis. Prog. Nucl. Energy 105, 42–50. doi: 10.1016/j.pnucene.2017.12.013

CrossRef Full Text | Google Scholar

Baraldi, P., Di Maio, F., and Zio, E. (2013). Unsupervised clustering for fault diagnosis in nuclear power plant components. Int. J. Comput. Intelligence Syst. 6, 764–777. doi: 10.1080/18756891.2013.804145

CrossRef Full Text | Google Scholar

Bartlett, E. B., and Uhrig, R. E. (1992). Nuclear power plant status diagnostics using an artificial neural network. Nucl. Technol. 97, 272–281. doi: 10.13182/nt92-a34635

CrossRef Full Text | Google Scholar

Betta, G., and Pietrosanto, A. (2000). Instrument fault detection and isolation: state of the art and new research trends. IEEE Trans. Instrum. Meas. 49, 100–107. doi: 10.1109/19.836318

CrossRef Full Text | Google Scholar

Biet, M. (2012). Rotor faults diagnosis using feature selection and nearest neighbors rule: application to a turbogenerator. IEEE Trans. Ind. Electron. 60, 4063–4073. doi: 10.1109/tie.2012.2218559

CrossRef Full Text | Google Scholar

Chae, Y. H., Kim, S. G., Kim, H. M., Kim, J. T., and Seong, P. H. (2020). A methodology for diagnosing FAC induced pipe thinning using accelerometers and deep learning models. Ann. Nucl. Energy 143:107501. doi: 10.1016/j.anucene.2020.107501

CrossRef Full Text | Google Scholar

Chen, F. C., and Jahanshahi, M. R. (2017). NB-CNN: deep learning-based crack detection using convolutional neural network and Naïve Bayes data fusion. IEEE Trans. Ind. Electron. 65, 4392–4400. doi: 10.1109/tie.2017.2764844

CrossRef Full Text | Google Scholar

Choi, J., and Lee, S. J. (2020). A sensor fault-tolerant accident diagnosis system. Sensors 20:5839. doi: 10.3390/s20205839

PubMed Abstract | CrossRef Full Text | Google Scholar

Di, M. F., Baraldi, P., Zio, E., and Seraoui, R. (2013). Fault detection in nuclear power plants components by a combination of statistical methods. IEEE Trans. Reliab. 62, 833–845. doi: 10.1109/tr.2013.2285033

CrossRef Full Text | Google Scholar

Dong, C., and Zhang, Q. (2020). The cubic dynamic uncertain causality graph: a methodology for temporal process modeling and diagnostic logic inference. IEEE Trans. Neural Netw. Learn. Syst. 31, 4239–4253. doi: 10.1109/tnnls.2019.2953177

PubMed Abstract | CrossRef Full Text | Google Scholar

Farber, J. A., and Cole, D. G. (2020). Detecting loss-of-coolant accidents without accident-specific data. Prog. Nucl. Energy 128:103469. doi: 10.1016/j.pnucene.2020.103469

CrossRef Full Text | Google Scholar

Hadad, K., Pourahmadi, M., and Majidi-Maraghi, H. (2011). Fault diagnosis and classification based on wavelet transform and neural network. Prog. Nucl. Energy 53, 41–47. doi: 10.1016/j.pnucene.2010.09.006

CrossRef Full Text | Google Scholar

Holbert, K. E., and Lin, K. (2012). Nuclear power plant instrumentation fault detection using fuzzy logic. Sci. Technol. Nucl. Installations 2012:421070.

Google Scholar

Jamil, F., Abid, M., Haq, I., Khan, A. Q., and Iqbal, M. (2016). Fault diagnosis of Pakistan research Reactor-2 with data-driven techniques. Ann. Nucl. Energy 90, 433–440. doi: 10.1016/j.anucene.2015.12.023

CrossRef Full Text | Google Scholar

Lee, D., Arigi, A. M., and Kim, J. (2020). Algorithm for Autonomous Power-Increase Operation Using Deep Reinforcement Learning and a Rule-Based System. Piscataway, NJ: IEEE.

Google Scholar

Li, F., Upadhyaya, B. R., and Perillo, S. R. (2012). Fault diagnosis of helical coil steam generator systems of an integral pressurized water reactor using optimal sensor selection. IEEE Trans. Nucl. Sci. 59, 403–410. doi: 10.1109/tns.2012.2185509

CrossRef Full Text | Google Scholar

Li, X., Fu, X. M., Xiong, F. R., and Bia, X. M. (2020). Deep learning-based unsupervised representation clustering methodology for automatic nuclear reactor operating transient identification. Knowl. Based Syst. 204:106178. doi: 10.1016/j.knosys.2020.106178

CrossRef Full Text | Google Scholar

Ling, J., Liu, G. J., Li, J. L., Chen, X. C., and You, D. D. (2020). Fault prediction method for nuclear power machinery based on Bayesian PPCA recurrent neural network model. Nucl. Sci. Techniques 31:75.

Google Scholar

Liu, J., and Zio, E. (2017). SVM hyperparameters tuning for recursive multi-step-ahead prediction. Neural Comput. Appl. 28, 3749–3763. doi: 10.1007/s00521-016-2272-1

CrossRef Full Text | Google Scholar

Liu, J., Seraoui, R., Vitelli, V., and Zio, E. (2013). Nuclear power plant components condition monitoring by probabilistic support vector machine. Ann. Nucl. Energy 56, 23–33. doi: 10.1016/j.anucene.2013.01.005

CrossRef Full Text | Google Scholar

Locatelli, G., Mancini, M., and Todeschini, N. (2013). Generation IV nuclear reactors: current status and future prospects. Energy Policy 61, 1503–1520. doi: 10.1016/j.enpol.2013.06.101

CrossRef Full Text | Google Scholar

Lu, B., and Upadhyaya, B. R. (2005). Monitoring and fault diagnosis of the steam generator system of a nuclear power plant using data-driven modeling and residual space analysis. Ann. Nucl. Energy 32, 897–912. doi: 10.1016/j.anucene.2005.02.003

CrossRef Full Text | Google Scholar

Ma, J., and Jiang, J. (2011). Applications of fault detection and diagnosis methods in nuclear power plants: a review. Prog. Nucl. Energy 53, 255–266. doi: 10.1016/j.pnucene.2010.12.001

CrossRef Full Text | Google Scholar

Mandal, S., Santhi, B., Sridhar, S., Vinolla, K., and Swaminathan, P. (2017a). A novel approach for fault detection and classification of the thermocouple sensor in nuclear power plant using singular value decomposition and symbolic dynamic filter. Ann. Nucl. Energy 103, 440–453. doi: 10.1016/j.anucene.2017.01.043

CrossRef Full Text | Google Scholar

Mandal, S., Santhi, B., Sridhar, S., Vinolla, K., and Swaminathan, P. (2017b). Nuclear power plant thermocouple sensor-fault detection and classification using deep learning and generalized likelihood ratio test. IEEE Trans. Nucl. Sci. 64, 1526–1534.

Google Scholar

Meng, J., Su, Y., and Xie, S. (2020). Loose parts detection method combining blind deconvolution with support vector machine. Ann. Nucl. Energy 149:107782. doi: 10.1016/j.anucene.2020.107782

CrossRef Full Text | Google Scholar

Miki, D., and Demachi, K. (2020). Bearing fault diagnosis using weakly supervised long short-term memory. J. Nucl. Sci. Technol. 57, 1091–1100. doi: 10.1080/00223131.2020.1761473

CrossRef Full Text | Google Scholar

Mo, K., Lee, S. J., and Seong, P. H. (2007). A dynamic neural network aggregation model for transient diagnosis in nuclear power plants. Prog. Nucl. Energy 49, 262–272. doi: 10.1016/j.pnucene.2007.01.002

CrossRef Full Text | Google Scholar

Moshkbar-Bakhshayesh, K. (2020). Prediction of unmeasurable parameters of NPPs using different model-free methods based on cross-correlation detection of measurable/unmeasurable parameters: a comparative study. Ann. Nucl. Energy 139:107232. doi: 10.1016/j.anucene.2019.107232

CrossRef Full Text | Google Scholar

Moshkbar-Bakhshayesh, K., and Ghofrani, M. B. (2013). Transient identification in nuclear power plants: a review. Prog. Nucl. Energy 67, 23–32. doi: 10.1016/j.pnucene.2013.03.017

CrossRef Full Text | Google Scholar

Nguyen, T. N., Downar, T., and Vilim, R. (2020). A probabilistic model-based diagnostic framework for nuclear engineering systems. Ann. Nucl. Energy 149:107767. doi: 10.1016/j.anucene.2020.107767

CrossRef Full Text | Google Scholar

Oh, C., and Lee, J. I. (2020). Real time nuclear power plant operating state cognitive algorithm development using dynamic Bayesian network. Reliab. Eng. Syst. Saf. 198:106879. doi: 10.1016/j.ress.2020.106879

CrossRef Full Text | Google Scholar

Oluwasegun, A., and Jung, J. C. (2020). The application of machine learning for the prognostics and health management of control element drive system. Nucl. Eng. Technol. 52, 2262–2273. doi: 10.1016/j.net.2020.03.028

CrossRef Full Text | Google Scholar

Peng, B. S., Xia, H., Liu, Y. K., Yang, B., Guo, D., Zhu, S. M., et al. (2018). Research on intelligent fault diagnosis method for nuclear power plant based on correlation analysis and deep belief network. Prog. Nucl. Energy 108, 419–427. doi: 10.1016/j.pnucene.2018.06.003

CrossRef Full Text | Google Scholar

Po, L. C. (2020). Conceptual design of an accident prevention system for light water reactors using artificial neural network and high-speed simulator. Nucl. Technol. 206, 505–513. doi: 10.1080/00295450.2019.1641877

CrossRef Full Text | Google Scholar

Rao, K. D., Gopika, V., Rao, V. S., Kushwaha, H. S., Verma, A. K., Srividya, A., et al. (2009). Dynamic fault tree analysis using Monte Carlo simulation in probabilistic safety assessment. Reliab. Eng. Syst. Saf. 94, 872–883. doi: 10.1016/j.ress.2008.09.007

CrossRef Full Text | Google Scholar

Razavi-Far, R., Davilu, H., Palade, V., and Lucas, C. (2009). Model-based fault detection and isolation of a steam generator using neuro-fuzzy networks. Neurocomputing 72, 2939–2951. doi: 10.1016/j.neucom.2009.04.004

CrossRef Full Text | Google Scholar

Ren, L., Lv, W., Jiang, S., and Xiao, Y. (2016). Fault diagnosis using a joint model based on sparse representation and SVM. IEEE Trans. Instrum. Meas. 65, 2313–2320. doi: 10.1109/tim.2016.2575318

CrossRef Full Text | Google Scholar

Rezaeianjouybari, B., and Shang, Y. (2020). Deep learning for prognostics and health management: state of the art, challenges, and opportunities. Measurement 163:107929. doi: 10.1016/j.measurement.2020.107929

CrossRef Full Text | Google Scholar

Saeed, H. A., Peng, M. J., Wang, H., and Zhang, B. W. (2020). Novel fault diagnosis scheme utilizing deep learning networks. Prog. Nucl. Energy 118:103066. doi: 10.1016/j.pnucene.2019.103066

CrossRef Full Text | Google Scholar

Sharanya, S., and Venkataraman, R. (2018). “Empirical analysis of machine learning algorithms in fault diagnosis of coolant tower in nuclear power plants,” in International Conference on Computational Vision and Bio Inspired Computing, November 29, (Cham).

Google Scholar

Upadhyaya, B. R., Zhao, K., and Lu, B. (2003). Fault monitoring of nuclear power plant sensors and field devices. Prog. Nucl. Energy 43, 337–342. doi: 10.1016/s0149-1970(03)00046-5

CrossRef Full Text | Google Scholar

Utah, M. N., and Jung, J. C. (2020). Fault state detection and remaining useful life prediction in AC powered solenoid operated valves based on traditional machine learning and deep neural networks. Nucl. Eng. Technol. 52, 1998–2008. doi: 10.1016/j.net.2020.02.001

CrossRef Full Text | Google Scholar

Vaddi, P. K., Pietrykowski, M. C., Kar, D., Diao, X., and Zhao, Y. (2020). Dynamic Bayesian networks based abnormal event classifier for nuclear power plants in case of cyber security threats. Prog. Nucl. Energy 128:103479. doi: 10.1016/j.pnucene.2020.103479

CrossRef Full Text | Google Scholar

Wang, H., Peng, M. J., Hines, J. W., Zheng, G. Y., Liu, Y. K., Upadhyaya, B. R., et al. (2019). A hybrid fault diagnosis methodology with support vector machine and improved particle swarm optimization for nuclear power plants. ISA Trans. 95, 358–371. doi: 10.1016/j.isatra.2019.05.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., Peng, M. J., Yu, Y., Saeed, H., Hao, C.-M., Liu, Y. K., et al. (2021). Fault identification and diagnosis based on KPCA and similarity clustering for nuclear power plants. Ann. Nucl. Energy 150:107786. doi: 10.1016/j.anucene.2020.107786

CrossRef Full Text | Google Scholar

Wang, H., Peng, M., Xu, R., Ayodeji, A., and Xia, H. (2020). Remaining useful life prediction based on improved temporal convolutional network for nuclear power plant valves. Front. Energy Res. 8:584463.

Google Scholar

Wang, W., Cammi, A., Di, M. F., Lorenzi, S., and Zio, E. (2018). A monte carlo-based exploration framework for identifying components vulnerable to cyber threats in nuclear power plants. Reliab. Eng. Syst. Saf. 175, 24–37. doi: 10.1016/j.ress.2018.03.005

CrossRef Full Text | Google Scholar

Yao, Y., Wang, J., Long, P., Xie, M., and Wang, J. (2020). Small-batch-size convolutional neural network based fault diagnosis system for nuclear energy production safety with big-data environment. Int. J. Energy Res. 44, 5841–5855. doi: 10.1002/er.5348

CrossRef Full Text | Google Scholar

Yu, Y., Peng, M. J., Wang, H., Ma, Z. G., and Li, W. (2020). Improved PCA model for multiple fault detection, isolation and reconstruction of sensors in nuclear power plant. Ann. Nucl. Energy 148:107662. doi: 10.1016/j.anucene.2020.107662

CrossRef Full Text | Google Scholar

Zhang, J., Wang, X., Zhao, C., Bai, W., Shen, J., Li, Y., et al. (2020). Application of cost-sensitive LSTM in water level prediction for nuclear reactor pressurizer. Nucl. Eng. Technol. 52, 1429–1435.

Google Scholar

Zhang, Q., Dong, C., Cui, Y., and Yang, Z. (2013). Dynamic uncertain causality graph for knowledge representation and probabilistic reasoning: statistics base, matrix, and application. IEEE Trans. Neural Netw. Learn. Syst. 25, 645–663.

Google Scholar

Zhao, K., and Upadhyaya, B. R. (2005). Adaptive fuzzy inference causal graph approach to fault detection and isolation of field devices in nuclear power plants. Prog. Nucl. Energy 46, 226–240.

Google Scholar

Zhao, L., and Wang, X. (2018). A Deep Feature Optimization Fusion Method for Extracting Bearing Degradation Features. Piscataway, J: IEEE.

Google Scholar

Zhao, Y., Tong, J., Zhang, L., and Wu, G. (2020). Diagnosis of operational failures and on-demand failures in nuclear power plants: an approach based on dynamic Bayesian networks. Ann. Nucl. Energy 138:107181.

Google Scholar

Zio, E. (2007). A support vector machine integrated system for the classification of operation anomalies in nuclear components and systems. Reliab. Eng. Syst. Saf. 92, 593–600.

Google Scholar

Nomenclature