The Sabatier Principle in Electrocatalysis: Basics, Limitations, and Extensions

The Sabatier principle, which states that the binding energy between the catalyst and the reactant should be neither too strong nor too weak, has been widely used as the key criterion in designing and screening electrocatalytic materials necessary to promote the sustainability of our society. The widespread success of density functional theory (DFT) has made binding energy calculations a routine practice, turning the Sabatier principle from an empirical principle into a quantitative predictive tool. Given its importance in electrocatalysis, we have attempted to introduce the reader to the fundamental concepts of the Sabatier principle with a highlight on the limitations and challenges in its current thermodynamic context. The Sabatier principle is situated at the heart of catalyst development, and moving beyond its current thermodynamic framework is expected to promote the identification of next-generation electrocatalysts.

Introduction

Electrocatalysis is gaining widespread attention as a critical technology to enhance the sustainability of human society. Core technology for the hydrogen economy, such as fuel cells and water electrolysis, rely on efficient electrocatalysts to perform the interconversion between water and hydrogen (Mehta and Cooper, 2003). The electrochemical synthesis of next-generation fuels, derived from atmospheric CO₂ rather than from fossil fuels, is also under intensive investigation (Zhang et al., 2018). Even the carbon footprint of the artificial nitrogen cycle can be improved using electrocatalysis, because the Haber-Bosch process used to synthesize ammonia and chemical fertilizers requires vast amounts of hydrogen, which are mainly produced from fossil fuels (Smith et al., 2020). Therefore, the development of electrocatalysts, especially those based on earth-abundant elements, is currently a central topic in chemistry and energy research.

However, the parameter space to search for new catalytic materials is massive. For example, oxides, such as the dimensionally stable anodes in the chlor-alkali industry (Karlsson and Cornell, 2016) or the iridium oxides in electrolyzers (Carmo et al., 2013), are a widely used family of catalysts. Based on the periodic table of elements, a chemist may choose from approximately 40 elements with which to make a single metal oxide. However, if the material candidates are expanded to binary, ternary, or even more complex mixed oxides, the possibility of materials expands massively (40⁴ > 2 million), especially if dopants are considered. Furthermore, every elemental composition has multiple possible atomic orientations in the bulk and the surface (Ulissi et al., 2017). Surface reconstruction, which can potentially occur during catalysis, are an additional contribution to the huge parameter space of materials (Fabbri et al., 2017; Li et al., 2019), leading to a combinatorial explosion of the possible candidate materials. In order to identify next-generation catalysts within this massive parameter space, a design principle which connects the chemical structure to catalytic activity is needed.

Nowadays, this role is fulfilled by the Sabatier principle (Sabatier, 1913; Che, 2013). This principle states that “an ideal catalyst must bind to the reactant at an intermediate strength which is neither too weak nor too strong.” This concept is based on the notion that if the bond is too weak, the catalyst and the reactant will hardly interact with each other, whereas if the bond is too strong, the reactant will not desorb from the catalyst surface, effectively inhibiting further reactions. This principle was first proposed in 1913 by the Nobel laureate, Paul Sabatier, based on empirical observations (Sabatier, 1913; Che, 2013). At that time, there was no method to directly obtain the binding energy, and therefore, other experimentally accessible parameters, such as hydride (Trasatti, 1972) or chelate formation energies (Rootsaert and Sachtler, 1960), were used to quantitatively assess the interaction between the catalyst and the reactant. A century later, however, it is now the norm to directly evaluate the binding energy of intermediate states using in silico computation (Nørskov et al., 2004; Rossmeisl et al., 2005; Rossmeisl et al., 2007b). In particular, the widespread accessibility of density functional theory (DFT) has made it almost every-day practice to predict the activity of a potential candidate prior to performing actual experiments (Greeley et al., 2006). Recent computational studies are further supplemented by machine-learning techniques to reduce computational costs (Back et al., 2019a,b; Li et al., 2020; Ulissi et al., 2016, 2017). In the following section, we will provide a brief, conceptual overview of the Sabatier principle in its current form, which has been widely employed to evaluate catalysts in silico. In section “CHALLENGES OF THE SABATIER PRINCIPLE AND APPROACHES FORWARD,” its challenges and limitations will be highlighted, along with ongoing approaches to overcome these bottlenecks. The main question addressed in this review is “what is the (theoretical) requirement for active electrocatalysts?”, not “which material satisfies these conditions?” For the reader with an interest in the progress of state-of-the-art materials, we would like to recommend several excellent reviews published recently (Xiao et al., 2015; Tahir et al., 2017; Song et al., 2020; Theerthagiri et al., 2020).

The Sabatier Principle and its Thermodynamic Interpretation

The Ideal Free-Energy Landscape

The free-energy difference between the initial (reactant) and final (product) states is defined by thermodynamics and is independent of the actual catalyst. When the applied electrode potential (U) is the same as the half-cell potential U₀, the free energies of the reactant and product are equal, and the system is in equilibrium. The reaction can proceed once the electrode potential is shifted away from the half-cell potential, such that the free energy of the product state becomes lower than that of the reactants. The difference between the applied potential and the half-cell potential is known as the applied overpotential, η = U – U₀. A positive overpotential is required for anodic (oxidation) processes, such as the chlorine evolution reaction (CER), whereas a negative overpotential is necessary for cathodic (reduction) reactions, such as the hydrogen evolution reaction (HER). However, the word “overpotential” is used to refer to absolute values in the following sections for simplicity, and hence “a larger overpotential” should be interpreted as the reaction becoming more thermodynamically favorable.

Within this framework, the role of the catalyst is to tune the free-energy landscape between the reactant and the product in a way that is beneficial for the catalytic process (Koper, 2011b). For a two-step reaction, such as the CER (Trasatti, 1987; Exner, 2020b) or HER (Gerischer and Gerischer, 1956; Parsons, 1958; Nørskov et al., 2005; Zeradjanin et al., 2016; Exner, 2020e), there is only one reaction intermediate, whose free energy depends on the catalyst surface to which it is adsorbed to (Figure 1A; Koper, 2011b, 2013a). The free energy of this reaction intermediate with respect to the reactant at equilibrium potential is denoted as ΔG_RI. Currently, the general consensus of an ideal free-energy landscape is one where this reaction intermediate has the same free energy as the reactant and the product at equilibrium. In other words, ΔG_RI = 0 is the criterion for an ideal catalyst (Koper, 2011b, 2013a; Laursen et al., 2012), and ΔG_RI can be considered as a “descriptor” for catalytic activity (Greeley and Nørskov, 2007; Peterson and Nørskov, 2012; Dubouis and Grimaud, 2019).

FIGURE 1

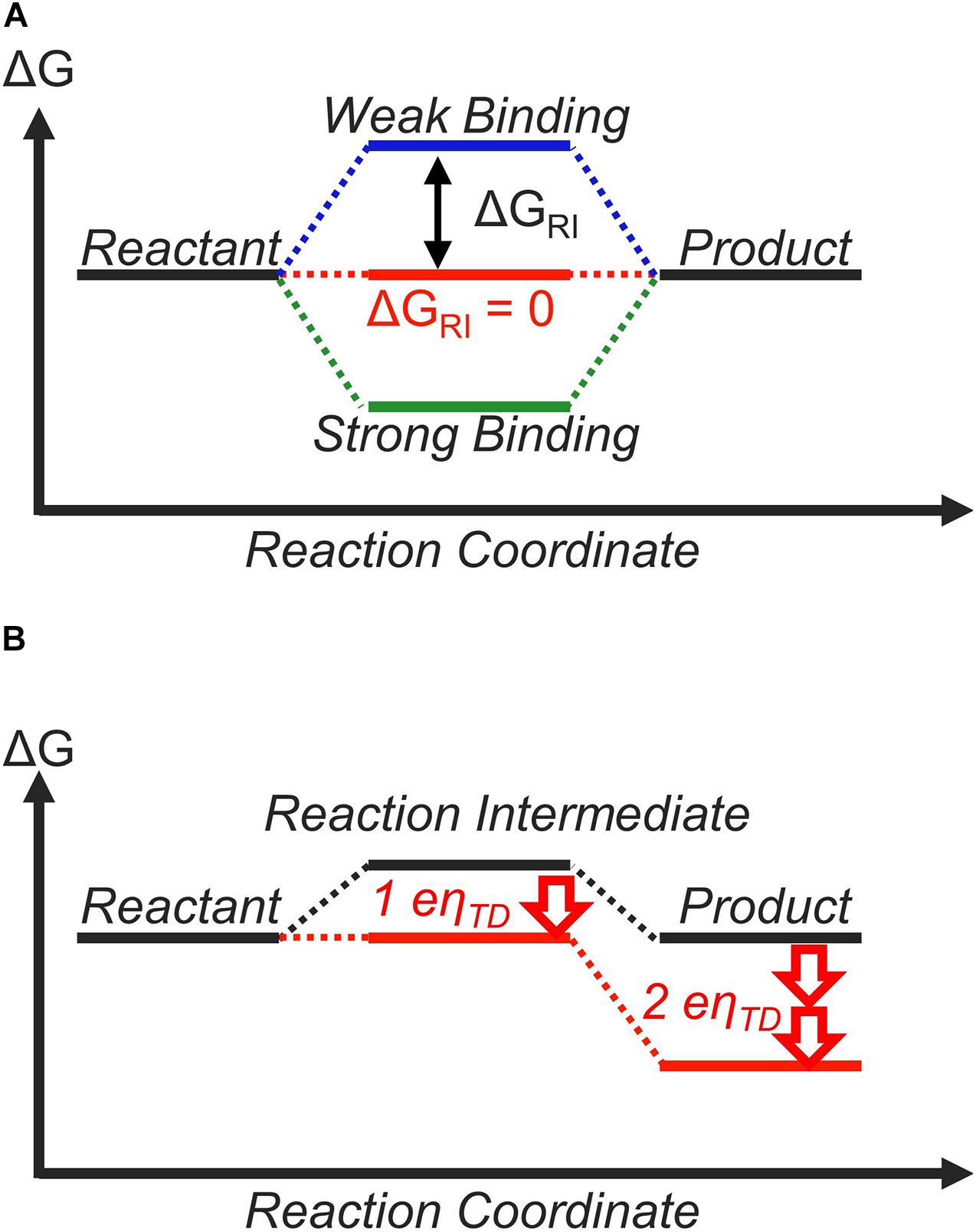
Figure 1. The thermodynamic free-energy landscape of a catalytic reaction with one reaction intermediate. (A) indicates the free-energy landscape for different binding strengths (ΔG_RI) of the reaction intermediate. (B) shows the free-energy landscape for a catalyst that binds the reaction intermediate weakly (ΔG_RI > 0 at equilibrium, black). By applying an overpotential of η = η_TD, all elementary reaction steps become thermoneutral or downhill in free energy (red).

The reason behind why thermoneutral bonding (ΔG_RI = 0) is considered ideal is shown in Figure 1. If the reaction intermediate is bound too weakly (ΔG_RI > 0), the first step is thermodynamically unfavorable (Figure 1A, blue lines). On the other hand, if the intermediate is bound too strongly (ΔG_RI < 0), the second step is thermodynamically unfavorable (Figure 1B, green lines). If we assume that the efficiency of the overall reaction is determined by the most thermodynamically unfavorable step, a thermoneutral landscape where no elementary step is thermodynamically unfavorable corresponds to the ideal situation (Figure 1A, red lines). This is often discussed quantitatively using the concept of the thermodynamic overpotential (η_TD), introduced by Nørskov, Rossmeisl, and co-workers (Nørskov et al., 2004). η_TD is defined as the minimum overpotential necessary to make all elementary reaction steps either thermoneutral or exergonic (Rossmeisl et al., 2005; Rossmeisl et al., 2007b). A smaller value of η_TD implies higher activity, and η_TD is commonly used to compare and rationalize the activity of various materials. In the case of a two-step reaction, η_TD = |ΔG_RI|/e with e = elementary charge, and therefore, a thermoneutral landscape (ΔG_RI = 0) yields η_TD = 0 V. For this reason, the thermodynamically ideal catalyst is sometimes referred to as the “zero overpotential catalyst” (Koper, 2011b, 2013a; Craig et al., 2019). This discussion is based on purely thermodynamic considerations and does not explicitly differentiate between outer-sphere and inner-sphere electron transfer mechanisms. However, all electrocatalytic reactions involve the rearrangement of chemical bonds, suggesting they can be considered as inner-sphere processes (Bard, 2010; Schmickler and Santos, 2010).

Nowadays, the free-energy landscape of an electrocatalyst can be calculated using computational techniques, such as density functional theory (DFT). Nørskov and co-workers introduced the computational hydrogen electrode (CHE) model, which substitutes the free energy of an electron-proton pair with that of half a hydrogen molecule at U = 0 V vs. RHE (reversible hydrogen electrode) (Nørskov et al., 2004). Using this method, it is possible to determine the free energies of reaction intermediates as a function of the applied electrode potential and pH by a posteriori analysis. Once the free energies of reaction intermediates are determined by DFT at zero electrode potential and pH zero conditions, they can be shifted to any electrochemical condition based on the CHE model (Calle-Vallejo and Koper, 2012). In principle, this method can also be used to determine the free energies of charged reaction intermediates (Craig et al., 2019), although in practice, most studies focus on non-charged intermediates (Calle-Vallejo and Koper, 2012) due to the large computational errors for charged intermediate states on solid surfaces. Regardless of these limitations, the CHE model and the thermodynamic overpotential (η_TD) are by far the most popular way to evaluate electrocatalytic activity in silico. To date, many experimental trends have been rationalized and new materials have been identified based on this simple framework (Hinnemann et al., 2005; Greeley et al., 2006; Diaz-Morales et al., 2016; Seitz et al., 2016).

Practical Application and Linear Scaling Relationships

From a thermodynamic viewpoint, the free-energy landscape should be completely flat at equilibrium to obtain the ideal catalyst. This notion holds true even when the mechanism involves more than two elementary steps. In practice, however, it is much easier to tune the landscape for two-electron transfer reactions, such as the HER and CER, compared to reactions which transfer more electrons, such as the oxygen evolution and reduction reactions (OER and ORR: 2 H₂O ↔ O₂ + 4H⁺ + 4e^–). This is reflected in the experimental literature, as some HER/HOR catalysts, such as Pt, are so active that practically no overpotential is visible in the cyclic voltammogram and the current density increases exponentially as soon as an overpotential is applied (Auinger et al., 2011; Durst et al., 2014). Other examples include a Pd-based catalyst which also exhibits almost no overpotential to catalyze the two-electron transfer reaction between CO₂ and formic acid (Kortlever et al., 2015a). In contrast, even the most active OER/ORR catalysts require overpotentials of several hundred mV to obtain current densities in the order of mA/cm² (Suntivich et al., 2011a, b; Diaz-Morales et al., 2016; Seitz et al., 2016; Chen et al., 2017). The reason why it is difficult to realize thermodynamically ideal catalysts for reactions with more than two electrons transferred has been rationalized due to the so-called scaling relationships, which impose physical limitations on how the free-energy landscape can be tuned. Let us take the OER as an example.

The OER is a four-electron process, in which water molecules are transformed into gaseous oxygen according to equation (1):

$$2\mathrm{H}{}_2\mathrm{O}{}_{(\mathrm{aq})}\to \mathrm{O}{}_{2(\mathrm{g})}+4\mathrm{H}{}^{+}+4\mathrm{e}{}^{-},\mathrm{U}{}_0=1.23\mathrm{V}\mathrm{vs}.\mathrm{RHE}(1)$$

Rossmeisl et al. (2005, 2007b) calculated the OER free-energy landscape according to a pathway, which assumes the OH, O, and OOH adsorbates as reaction intermediates. Each step was assumed to proceed via concerted proton-electron transfer steps. This was originally due to technical reasons, namely to maintain charge neutrality (cf. Section “Stepwise Proton-Electron Transfer and Charged Intermediates”) (Rossmeisl et al., 2005, 2007b), but this mechanism is still adopted in the recent literature (Halck et al., 2014; Busch et al., 2016; Dickens and Nørskov, 2017; Hajiyani and Pentcheva, 2018).

$$\mathrm{H}{}_2\mathrm{O}{}_{(\mathrm{l})}+\mathrm{S}\to \text{S-OH}+\text{H}{}^{+}+\text{e}{}^{-}\mathit{\hspace{1em}\hspace{1em}\hspace{1em}}\mathrm{\Delta }\mathrm{G}{}_1(2)$$

$$\mathrm{S}-\mathrm{OH}\to \text{S-O}+\text{H}{}^{+}+\text{e}{}^{-}\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} }\mathrm{\Delta }\mathrm{G}{}_2(3)$$

$$\mathrm{S}-\mathrm{O}+\mathrm{H}{}_2\mathrm{O}{}_{(\mathrm{l}}{}_{)}\to \text{S-OOH}+\text{H}{}^{+}+\text{e}{}^{-}\mathit{\hspace{1em}\hspace{1em}\hspace{1em} }\mathrm{\Delta }\mathrm{G}{}_3(4)$$

$$\mathrm{S}-\mathrm{OOH}\to \mathrm{S}+\mathrm{O}{}_{2(\text{g})}+\text{H}{}^{+}+\text{e}{}^{-}\mathit{\hspace{1em}}\mathrm{\Delta }\mathrm{G}{}_4(5)$$

In equations (2) – (5), S denotes the active site of an OER catalyst. In order to realize an ideal catalyst, every step must be thermoneutral at the equilibrium potential. In other words, when the free-energy change of the i^th step is denoted as ΔG_i, the criterion of a thermodynamically ideal catalyst is: ΔG₁ = ΔG₂ = ΔG₃ = ΔG₄ = 0 eV at U = 1.23 V vs. RHE (Figure 2, blue lines). This results in ΔG₁ = ΔG₂ = ΔG₃ = ΔG₄ = 1.23 eV at U = 0 V vs. RHE (Figure 2, black lines), which corresponds to the usual conditions of DFT calculations within the CHE framework.

FIGURE 2

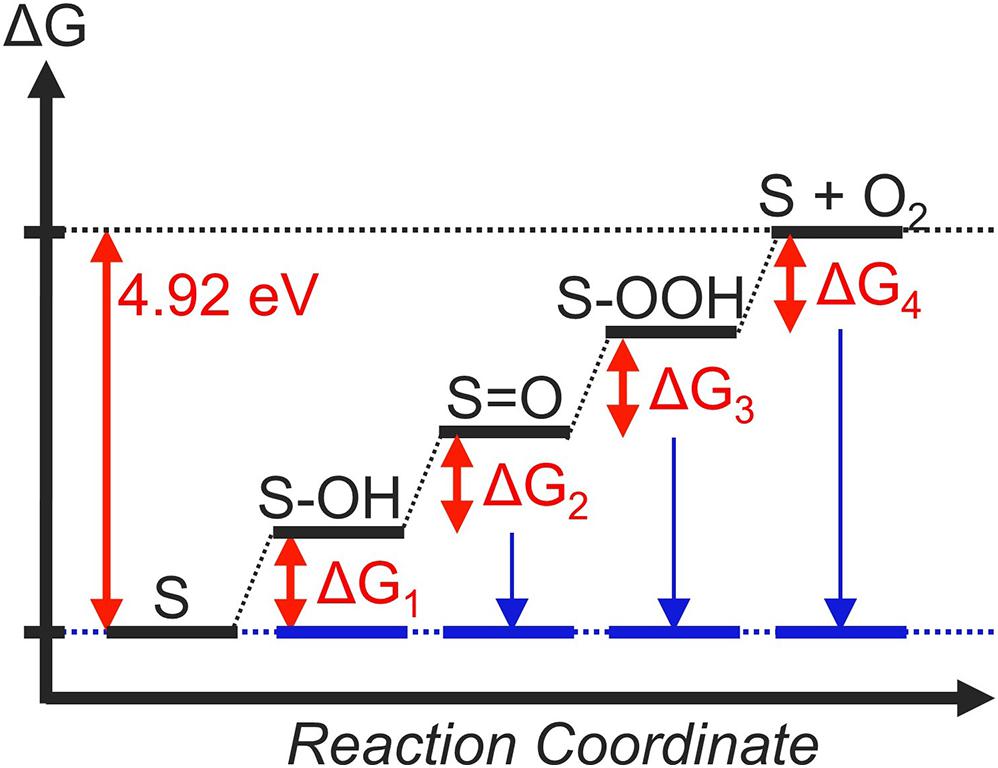
Figure 2. The thermodynamic landscape of an ideal OER catalyst at U = 0 V (black lines) and U = 1.23 V (blue lines). Relative energies are indicated in red letters.

In reality however, no electrode material that fulfills the requirements of a thermodynamically ideal catalyst has been identified so far. This is because the binding energies of structurally similar intermediates are difficult to tune independently. For example, the binding energies of the OH and OOH adsorbates are known to exhibit a linear correlation. This relationship is often referred to as a linear scaling relationship (Man et al., 2011; Viswanathan et al., 2012), and is given by equation (6):

$$\mathrm{\Delta }G{}_2+\mathrm{\Delta }G{}_3=3.2\text{eV}(6)$$

The number 3.2 eV is the value that has been reported for planar metal oxides (Rossmeisl et al., 2005; Man et al., 2011; Viswanathan et al., 2012). The values in more recent studies span a range of about 2.8 eV – 3.4 eV (Calle-Vallejo et al., 2013; Viswanathan and Hansen, 2014; Tao et al., 2019; Exner, 2020a), suggesting that different classes of materials may follow different scaling relationships.

In any case, the scaling relationship directly implies that a thermodynamically ideal catalyst cannot be realized. For example, if a certain electrocatalyst exhibits ideal thermodynamics for the second step (ΔG₂ = 1.23 eV at U = 0 V), the scaling relationships indicate that the third step cannot be thermodynamically ideal due to: ΔG₃ = 3.2 eV – 1.23 eV = 1.97 eV (Figure 3A, green line). On the other hand, setting ΔG₃ to 1.23 eV leads to a scenario where ΔG₂ is unfavorable (Figure 3B, blue line). In other words, optimizing either ΔG₂ or ΔG₃ leads to the other deviating from the thermodynamic ideal. If the most thermodynamic unfavorable reaction step dictates catalytic activity, the best compromise is to distribute the free-energy penalty from the scaling relationship into equal parts; that is, ΔG₂ = ΔG₃ = 3.2 eV / 2 = 1.6 eV (Man et al., 2011). In this case, the thermodynamic overpotential amounts to η_TD = 1.60 V – 1.23 V = 0.37 V (Figure 3A, red line), which is significantly smaller than η_TD = 1.97 V – 1.23 V = 0.74 eV which results by making either the second step or third step thermodynamically ideal (Figure 3A, blue and green lines). In terms of the volcano plot, electrocatalysts with optimum ΔG₂ or ΔG₃ are located at the leg of the volcano because they bind the O adsorbate either too strongly or too weakly, respectively, such that the other step becomes thermodynamically prohibitive. This leads to a minimum thermodynamic overpotential, also denoted as minimum theoretical overpotential, of 0.37 V for the OER (Figure 3B). This value is roughly consistent with the experimental overpotential necessary to reach a current density of 10 mA/cm², a benchmark for the solar-cell community (Suntivich et al., 2011b; Diaz-Morales et al., 2016; Seitz et al., 2016). However, some recent materials have overpotentials below 200 mV to sustain of 10 mA/cm² (Kim et al., 2017; Su et al., 2018; Retuerto et al., 2019; Hao et al., 2020), indicating that η_TD is not necessarily a quantitatively accurate descriptor of electrocatalytic activity (Exner, 2021a). This discrepancy is most likely because the thermodynamic overpotential and the experimental overpotential have different definitions, and thus have no direct physical correlation: while η_TD is a purely thermodynamic indicator of activity based on the free-energy landscape at equilibrium (zero overpotential), the experimental overpotential η must be evaluated at some non-zero current density, and is thus always influenced by the kinetics. However, the concept of η_TD does offer at least a qualitative explanation why the OER is a more difficult process compared to the HER and other two-electron processes, where the thermodynamics is not restrained by any scaling relationships.

FIGURE 3

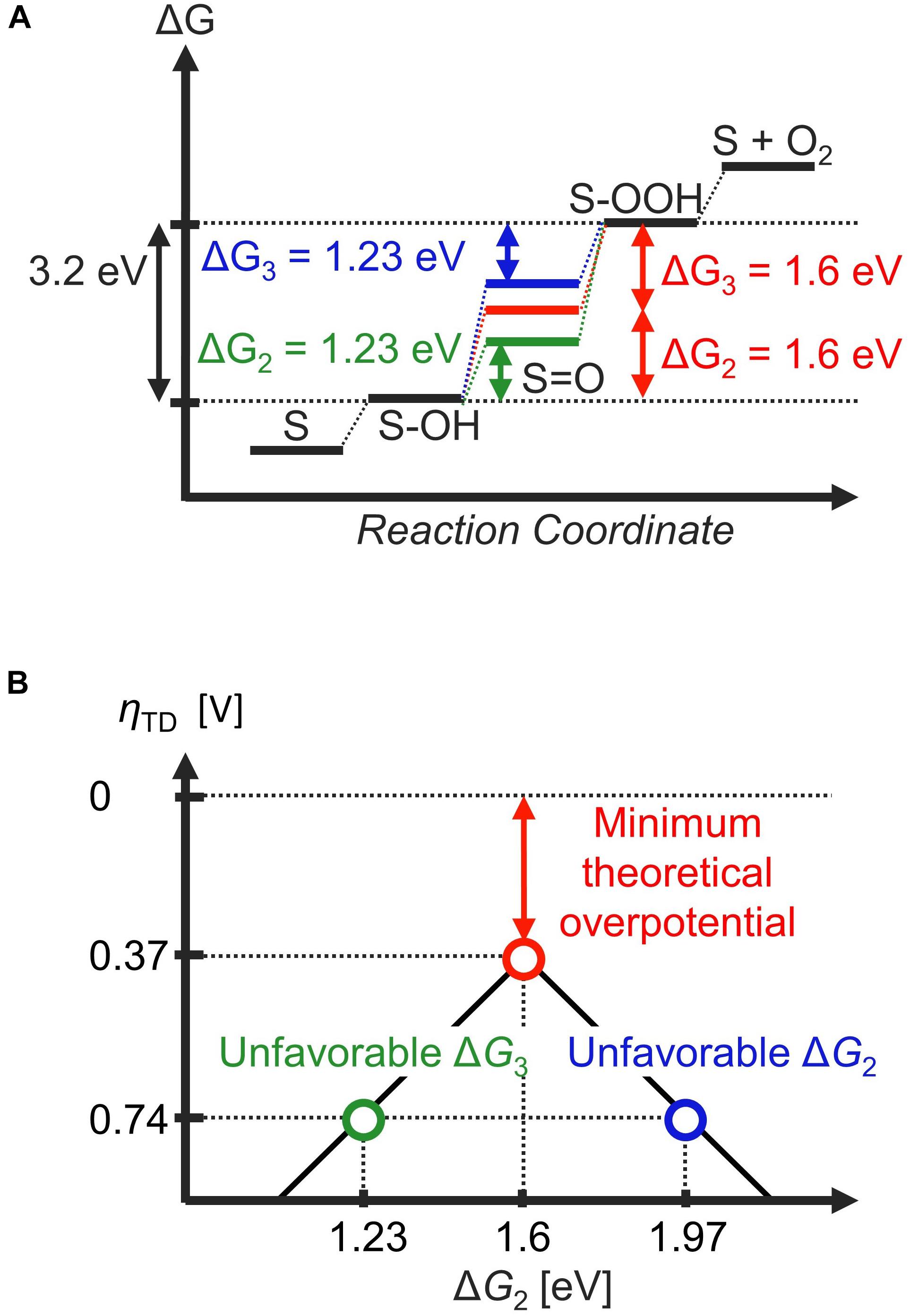
Figure 3. The effect of the scaling relation on the thermodynamic free-energy landscape for the oxygen evolution reaction (OER), assuming the participation of OH, O, and OOH adsorbates within the catalytic cycle. (A) Due to the linear scaling relationship between the OH and OOH adsorbates (ΔG₂ + ΔG₃ = 3.2 eV), it is not possible to adjust both ΔG₂ and ΔG₃ to 1.23 eV simultaneously (blue and green pathways). The minimum thermodynamic (theoretical) overpotential is realized when ΔG₂ = ΔG₃ = 1.6 eV; that is, the free-energy penalty due to the scaling relations is shared equally between these two elementary steps. (B) The thermodynamic overpotential is plotted as a function of ΔG₂ in the form of a volcano plot.

Examples for the Application of the Sabatier Principle in Practice

The Sabatier principle and its thermodynamic interpretation have been successfully applied for the development of new catalysts. For example, Greeley et al. used ΔG_RI to screen alloy catalysts for the HER (Greeley et al., 2006), and identified a Bi-Pt surface alloy with higher electrocatalytic activity than platinum. Similarly, Hinnemann et al. (2005) identified MoS₂ nanoparticles as a potential HER electrocatalyst by applying the Sabatier principle in its thermodynamic form. The work of Seitz et al. is another example, where the highly active IrO_x/SrIrO₃ catalyst for the OER was predicted based on the framework of scaling relations and η_TD discussed in the previous section (Seitz et al., 2016). These works, among others, contributed to the fact that in silico screening procedures became extremely popular in electrocatalysis and, nowadays, are broadly used for the discovery of catalytic materials (Yao et al., 2019; Yang et al., 2020).

More recently, the rise of data science has promoted the usage of the Sabatier principle for materials’ screening (Basdogan et al., 2020a; Toyao et al., 2020). For example, Ulissi et al. used a neural network-based surrogate model to reduce the number of explicit DFT calculations by an order of magnitude, allowing them to extensively screen active sites for CO₂ reduction (Ulissi et al., 2017). Machine-learning has also been beneficial to obtain more accurate binding energies across wider configurations (Back et al., 2019a).

Application of the Sabatier Principle to Enzymes, Molecular Catalysts, and Beyond

The Sabatier principle has also been successfully applied to enzymes and homogeneous catalysts. For example, biological OER and ORR enzymes were compared with their artificial counterparts, and their higher activity was rationalized by their lower η_TD (Rossmeisl et al., 2007a; Kjaergaard et al., 2010). These enzymes deviate from the linear scaling relationships reported for planar metal oxides (Man et al., 2011). Therefore, this finding has stimulated various studies aiming to find strategies to break scaling relations (Li and Sun, 2016; Pegis et al., 2017; Huang et al., 2019). However, breaking the scaling relationship in itself is not a sufficient condition to realize active materials, because it does not guarantee a lower η_TD as the recent literature has shown (Govindarajan et al., 2018; Exner, 2020f; Piqué et al., 2020).

More recently, Kari et al. (2018) demonstrated experimentally that enzymes also follow a Sabatier-type trend. The Michaelis-Menten constant K_m is a quantitative measure of the substrate-enzyme interaction and was used as a substitute for the binding energy to construct volcano plots of various cellulases. The maximum rate was observed at intermediate values of K_m, suggesting that an intermediate interaction strength between the catalyst and the reactant may also be important to enhance enzymatic activity.

Scaling relations and volcano plots have also been introduced into the field of organometallic chemistry. For example, the thermodynamics of Suzuki coupling catalysts was rationalized based on linear scaling relationships and free-energy changes (Busch et al., 2015, 2016; Wodrich et al., 2018). Catalysts known to be active from experiments appear near the top of the volcano plot, suggesting the Sabatier principle may also help in the understanding of organometallic catalysts.

The Sabatier principle was also transferred to the field of lithium-ion batteries in order to study the intercalation of lithium-ions into spinel lithium titanate electrodes (Exner, 2018, 2019e). While the conventional Sabatier principle only considers activity by analyzing binding energies, stability was introduced as a second performance parameter to rationalize experimental trends by the construction of activity-stability volcano plots. The volcano plots indicate that an intermediate lithium binding strength is the best compromise between enhanced energy density while maintaining stability, thus building a bridge between the catalysis and battery science communities (Exner, 2018, 2019e). This may be the reason why the idea of an intermediate binding strength in conjunction with the volcano notion has found entrance for the screening of electrode materials in batteries (Pande and Viswanathan, 2019). The advanced framework of activity-stability volcano curves can also be employed to electrocatalytic processes such as the CER (Exner, 2019a).

Challenges of the Sabatier Principle and Approaches Forward

The simplicity of the Sabatier principle and its thermodynamic interpretation has led to its widespread application so far. At the same time, however, this simplicity implies limitations where theory does not match with experiments. This can be due to issues at multiple levels.

For example, the binding energy estimated from the CHE model may not reflect the true binding energy without a more extensive treatment of factors such as solvation or the effective electrochemical potential in the double layer. In this case, the discrepancy between theory and experiments is a matter of accuracy which can be resolved by sufficient technical advancement. The Sabatier principle itself is not the problem if a more accurate binding energy can yield predictions consistent with experiments.

In other cases, the issue may be rooted deeper in the theory. For example, the Sabatier principle has its basis on the thermodynamics because the binding energy is in essence an equilibrium constant between the adsorption and desorption of a reactant. However, thermodynamics alone cannot explain how quickly electron-transfer reactions occur. Conventionally, kinetic factors such as activation barrier heights are assumed to scale universally with the thermodynamics. However, if this assumption is not valid, activity trends can no longer be predicted from thermodynamic criteria such as the thermodynamic overpotential, binding energies, or scaling relations. This is an issue which is beginning to attract more attention, stimulating recent microkinetic studies (Ooka and Nakamura, 2019; Exner, 2020c,e) which have attempted to expand the Sabatier principle (Exner, 2019d, 2021b) by the incorporation of overpotential and kinetic factors.

Finally, there are some chemical processes which the Sabatier principle does not consider at all. The Sabatier principle predicts the intrinsic activity of a material, but in some cases, the observed electrocatalytic behavior is not purely due to the intrinsic activity. For example, mass transport is well known to influence electrode kinetics, such as in the case of the CO₂ reduction reaction (Ringe et al., 2020). The electrochemically active surface area is another consideration which cannot be determined by DFT calculations due to the usage of simplified slab models.

Proper comparison between theoretical and experimental activities requires calculation of the full free-energy landscape including the kinetics, which is computationally expensive. This is the reason why theoretical and experimental activities are often evaluated at the level of material trends by comparing the thermodynamics (theory) with the kinetics (experiment). A more rigorous and critical verification based on a direct quantitative comparison would be beneficial to improve the accuracy of theoretical predictions. In the following sections, we have attempted to sort the existing challenges of the Sabatier principle and the CHE model in order to provide a guideline of possible approaches beyond the current thermodynamic framework.

Challenges to Accurately Predict the Binding Energy

Influence of the Electrolyte: Beyond the CHE Model

Electrocatalysis is in general a phenomenon which is also dependent on the electrolyte. The most famous example for pH dependence may be the HER on platinum, which is more active in acid compared to alkaline conditions (Sheng et al., 2010). However, the CHE model treats the electrolyte ion concentrations of protons and hydroxides based on the Nernst equation, and thus, the thermodynamic overpotential η_TD is independent of the pH. As η_TD is the common theoretical measure for electrocatalytic activity, this is a direct contradiction with experiments. Other ions besides protons and hydroxides in the electrolyte may also influence electrocatalytic activity (Xue et al., 2018; Garcia et al., 2019; Shinagawa et al., 2019), yet such factors are not considered in the CHE model.

Although the influence of the electrolyte can be ascribed to multiple factors, at least part of the reason is due to the binding energy being electrolyte dependent. The electrolyte determines the double-layer structure surrounding the adsorbate (Ledezma-Yanez et al., 2017), which has direct implications on the stability of intermediates on the electrode.

The double layer structure is also influenced by the electrochemical potential, and thus the binding energy may also deviate from the Nernstian behavior assumed in the CHE model when the electrode potential or pH is changed (Hörmann et al., 2019, 2020). There are several recent studies which have attempted to explain the pH dependence of Pt in the HER by considering the binding energies to be pH dependent (Kunimatsu et al., 2007; Sheng et al., 2010, 2015; Zheng et al., 2016; Ledezma-Yanez et al., 2017; Zhu et al., 2020). Yet, such effects are not considered in most theoretical studies, which tacitly assume the binding energy to be a material-specific value which is pH independent (Nørskov et al., 2005, 2009).

The above-highlighted challenges could potentially be overcome if the electrolyte solution, consisting of all ions and solvent molecules, is explicitly modeled in the theoretical framework. This, however, requires computationally expensive ab initio molecular dynamics (AIMD) simulations (Kenmoe et al., 2018; Sakong and Groß, 2020). The cell sizes that can be treated by AIMD (Groß, 2020) so far are too small to simulate the dependency of binding energies on electrolyte concentrations (Groß, 2020). Although a steep increase in the computational power is needed to accurately determine the binding energies as a function of electrolyte composition, the effect of the electrolyte solution on the binding energy of an intermediate is significant, nonetheless. For example, explicit consideration of a solvent bilayer was found to change the DFT-obtained binding energy of adsorbed hydroxyl (OH_ads) on Pt(111) by −0.5 eV, and assuming the same solvation configuration for different metals resulted in errors exceeding 0.2 eV (He et al., 2017). This is the same order of magnitude compared to typical DFT errors (Nørskov et al., 2009), indicating that proper modeling of solvation within the available methods is indispensable for the computational design of electrocatalysts.

Currently, continuum solvation models such as Vaspsol (Mathew et al., 2014, 2019), COSMO (Klamt and Schüürmann, 1993), or Jaguar (Bochevarov et al., 2013) are commonly used to describe solvation at the electrode/electrolyte interface (Abidi et al., 2020; Basdogan et al., 2020b; Groß, 2020). However at least in the case of the intermediates relevant to the ORR and CO₂ reduction reactions on Cu, Au, and Pt, the widely used continuum solvation models did not improve the accuracy of binding energies compared to the respective calculations in vacuum (Heenen et al., 2020). Due to the complexity and computational costs of AIMD, solvation models by the inclusion of machine-learning techniques have been developed (Basdogan et al., 2020b), which are a promising alternative to continuum solvation models.

Another shortcoming of the CHE model refers to the fact that this approach relies on a canonical ensemble, in which the charge is fixed. Experimental conditions, however, correspond to a grand canonical ensemble where the electrode potential is fixed instead of the charge. Recent progress in this field put forth grand canonical models beyond the CHE method (Hansen and Rossmeisl, 2016; Hörmann et al., 2019, 2020; Abidi et al., 2020), allowing the electrode potential to be explicitly included into the DFT calculations (Govind Rajan et al., 2020; Groß, 2020). Yet, a limitation of this approach is that the outcome may severely depend on the chosen value for the proton/hydrogen work function, for which values between 3.9 eV and 4.7 eV have been reported in the literature (Busch et al., 2020; Bhattacharyya et al., 2021).

Influence of Surface Charge

Another challenge in the accurate evaluation of the binding energy is the influence of the surface charge density on the electrode. Adsorbates on the electrode surface are usually charged due to the partial charge transfer in the chemisorption process. For instance, halogen ions adsorbed to a metal surface still carry a significant fraction of its negative charge after adsorption (Ávila et al., 2020) leading to the formation of surface dipole moments. The free energy of these surface dipoles depends on the local electric field, which is further modulated by the electrode surface charge. Therefore, the binding energy of reaction intermediates usually depends on the electrode surface charge. Furthermore, the electrode surface charge determines the local reaction conditions, such as the reactant concentration and the driving force at the reaction plane, thus having a pronounced effect on electrocatalytic activity. A recent example is the peroxodisulfate reduction on Pt, which has been shown to be inhibited when the surface charge density is negative (Martnez-Hincapié et al., 2018). This result could be explained by incorporating effects of the electrochemical double layer on electron transfer kinetics described using the Marcus–Hush–Chidsey theory (Zhang and Huang, 2020).

In order to incorporate double layer effects, an explicit model of the interface between the electrode and the electrolyte is necessary. When a reaction intermediate is adsorbed to the electrode surface, this is usually concurrent with the desorption of a solvent molecule. The displacement of the solvent molecule is rarely modeled explicitly due to the fact that conventional DFT studies are commonly performed in vacuum or with implicit solvation models. However, it has been proposed that this process is a possible origin of the pH-dependent HER activity of Pt (Sheng et al., 2015; Zheng et al., 2016; Ledezma-Yanez et al., 2017). If the chemisorbed intermediate possesses a dipole moment such as OH_ads, this intermediate contributes to the electrical field at the electrode surface (Ávila et al., 2020). The electrical field is dependent on the coverage of the intermediates, which is in turn dependent on the electrochemical potential, thus making the modeling of the double layer’s potential dependency a non-trivial task.

The normal potential of zero charge (PZC) is defined for ideally polarizable electrodes, at which variation of the metal potential only alters the distribution of the electron spillover without resulting in electron transfer from or onto ions and molecules in the solution. This is not the case for electrocatalytic interfaces, at which ions and molecules may adsorb onto the electrode surface, forming chemical bonds. The chemisorption dramatically changes the structure of the electric double layer. One known effect is associated with surface dipole moments that arise from partially charged chemisorbates. The chemisorption-induced surface dipole moments generate a significant potential drop on the electrode surface. This additional surface potential drop will change the surface charging behavior of the electrode, resulting in a second PZC in the potential region where chemisorption occurs.

In the case of Pt (111) in 0.1 M HClO₄, the normal PZC is around 0.3 V vs RHE, and shifting the electrode potential to more positive potentials should lead to an increase in the surface charge (Figure 4A). However, at potentials above 0.6 V vs. RHE, water dissociation leads to the chemisorption of negatively charged OH^–, forming an inward surface dipole moment (Figure 4B, the direction of a dipole moment is from negative to positive charge). This effectively neutralizes the potential-dependent increase of the surface charge, resulting in a nonmonotonic surface charging relation as can be seen from the second PZC in the OH_ads potential region (Huang et al., 2016b; Huang et al., 2018).

FIGURE 4

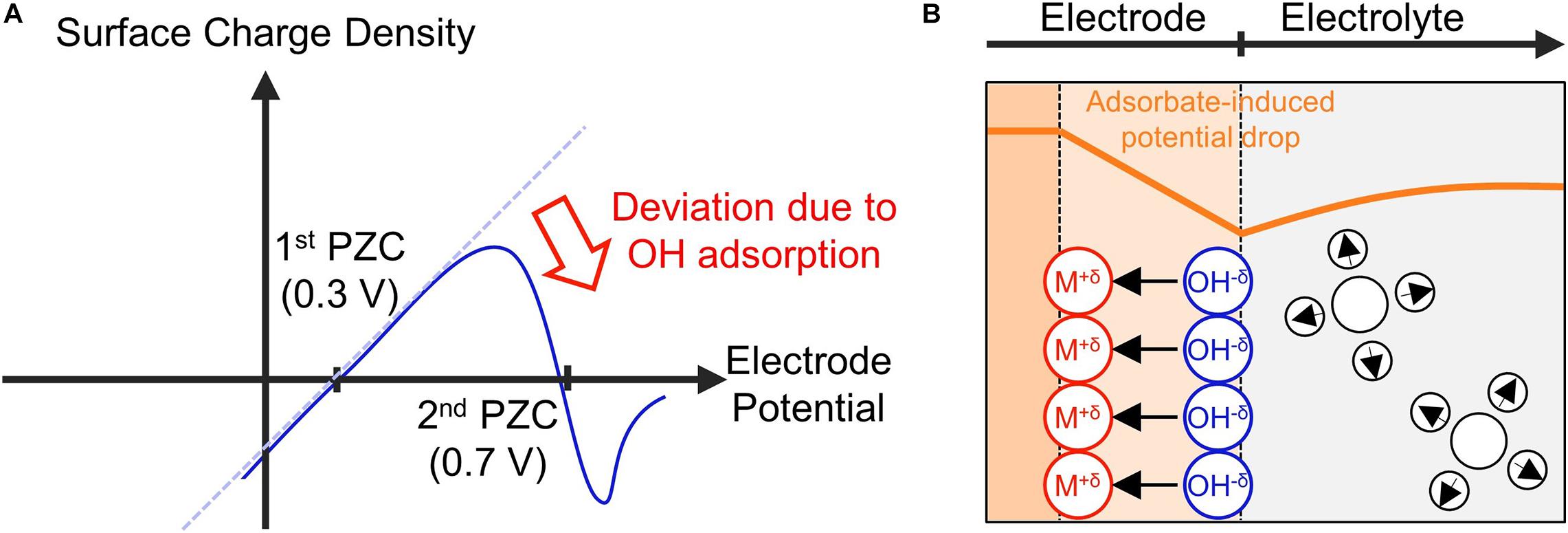
Figure 4. Schematic illustrations of (A) the surface charge density with respect to the potential and (B) the structure of the electrode – electrolyte interface near the second PZC.

In general, when there is a net dipole change upon displacing the solvent with an adsorbate, there is a possibility for a second PZC, and therefore, this phenomenon is most likely not unique to the combination of platinum and OH intermediates (Frumkin and Petrii, 1975; Martnez-Hincapié et al., 2018). In addition to the ORR (Huang et al., 2016a; Zhang et al., 2019; Zhou et al., 2020), the double layer model above has been used successfully to model the formic acid oxidation (Zhu and Huang, 2019), and peroxodisulfate reduction (PDSR) reactions (Zhang and Huang, 2020) at Pt(111).

Stepwise Proton-Electron Transfer and Charged Intermediates

Another challenge to obtain accurate binding energies is the involvement of charged intermediate species. The CHE model avoids charged intermediates by assuming that the proton and electron are always transferred together in a single step, also denoted as concerted proton-electron transfer (CPET). This is partially justified because the CPET mechanism is in general thermodynamically more favorable compared to stepwise proton-electron transfer (SPET) (Hammes-Schiffer and Stuchebrukhov, 2010; Warren et al., 2010; Koper, 2013c). However, there is experimental evidence suggesting decoupled electron-proton transfer steps are involved in reactions such as CO₂ reduction on copper (Kortlever et al., 2015b) and gold (Wuttig et al., 2016), or the ORR on gold (Rodriguez and Koper, 2014). If so, this implies that some intermediates are charged, and evaluating their free energies accurately is necessary to construct the free-energy landscape for the electrocatalytic process. In fact, from a purely thermodynamic standpoint, the pH dependence of many electrocatalytic reactions already suggests the participation of SPET within the reaction mechanism (Hammes-Schiffer and Stuchebrukhov, 2010; Koper, 2013b; Sakaushi et al., 2020). Furthermore, the theoretical model by Koper suggests SPET may even be beneficial in some cases because modulating the driving force of electrochemical and non-electrochemical steps separately may lead to higher activity or selectivity (Koper, 2013b). The pH dependent selectivity regulation of nitrite reduction on MoS₂ is a direct support to this theoretical model (He et al., 2018, 2020). SPET pathways have also been proposed for other electrocatalytic processes, including the OER and ammonia oxidation reaction (Katsounaros et al., 2016; Saveleva et al., 2018; Exner and Over, 2019).

To date, the energetics of SPET pathways has been assessed theoretically for some molecular catalysts, and it has been shown that charged intermediates are indeed preferred during reactions such as CO₂ reduction (Göttle and Koper, 2017) or the OER (Craig et al., 2019). Thorough treatment of CPET and SPET pathways by quantum chemical considerations can be found in the works of Hammes-Schiffer and coworkers, who have developed computational protocols for the calculation of concerted or decoupled proton-electron transfers for biological enzymes and bio-inspired molecules (Goings and Hammes-Schiffer, 2020; Sayfutyarova and Hammes-Schiffer, 2020; Warburton et al., 2020). Although direct calculation of charged intermediates using DFT tends to be avoided due to their large errors, moving beyond the conventional picture of uncharged intermediate states within the CHE model is of particular importance to the electrocatalysis community. First steps for molecular catalysts have been made, whereas the description of charged species on solid-state surfaces is still in its early stages (Kastlunger et al., 2018; Lindgren et al., 2020).

Coverage Dependence of the Binding Energy

When evaluating the binding energy of intermediate species, it is also important to account for the chemical environment of the adsorbate. For example, the hydrogen binding energy on Pt(111) was shown to shift from strong-binding to weak-binding when the coverage was increased (Skúlason et al., 2010). The hydrogen binding energy also increases with the coverage of CO on metals such as Cu or Mo, which has been used to explain why Cu favor CO₂ reduction of HER when the two are in competition (Zhang et al., 2014). The CER on RuO₂(110) is another example which is influenced by the coverage (Exner et al., 2016). The active site under typical CER conditions consists of a surface oxygen atom, O_ads, on which chloride anions from the electrolyte solution adsorb under formation of an OCl_ads precursor (Exner et al., 2014). The binding strength of chlorine to the underlying oxygen atoms is stronger if there is a neighboring OH group instead of an oxygen atom, due to the attractive interaction between the adsorbed chlorine and the neighboring hydrogen atom in the OH group.

In order to calculate the binding energy more accurately, it is desirable to resolve not only the active site but also its surrounding environment under typical reaction conditions. One approach is to use DFT to construct surface Pourbaix diagrams (Hansen et al., 2008; Sumaria et al., 2018; Vinogradova et al., 2018). These diagrams indicate the thermodynamically most favorable surface structure as a function of the applied electrode potential and pH (Gossenberger et al., 2020), and by assuming that this surface corresponds to the active surface, it is possible to predict the coverage of intermediates and adsorbates. However, this approach is purely thermodynamic in nature, and cannot be used if the surface structure in experiments deviates from the most energetically favorable one. The gap between thermodynamics and kinetics is discussed in detail in the following section, and some of the methods discussed therein may allow the construction of more accurate Pourbaix diagrams which include not only thermodynamic but also kinetic information.

Thermodynamics and Kinetics

The BEP Relationship

The previous section has focused on challenges to obtain accurate binding energies. However, even if the free energy of reaction intermediates could be obtained without any error, there is still a conceptual gap between the Sabatier principle and the activity in real experiments. This is because the traditional interpretation of the Sabatier principle is based on pure thermodynamic considerations, whereas experiments always contain the influence of kinetics.

A framework based on pure thermodynamic considerations has historically been rationalized by the Brønsted (Bell) – Evans – Polanyi (BEP) relationship, which states that the free-activation energy (ΔG_RI^#) is linearly correlated with the reaction free energy (ΔG_RI) (Bligaard et al., 2004; Cheng et al., 2008). In other words, ΔG_RI^# = βΔG_RI, where β denotes the so-called BEP coefficient (0 < β < 1) (Van Santen et al., 2009).

An example for a two-electron reaction, such as the HER, is shown in Figure 5. For a weak-binding catalyst (Figure 5A), the first step should have a higher transition-state free energy compared to the second because the first step is uphill in free energy. In contrast, for a strong-binding catalyst (Figure 5B), the BEP relation predicts that the second elementary reaction step would have a higher transition-state free energy than the first step. The optimum situation corresponds to a thermoneutral catalyst (Figure 5C) because in this case, the transition-state free energies of both elementary reactions are at the same height, and the highest transition state within the entire landscape would be lower than that of the weak-binding and strong-binding catalysts. In general, the positive nature of β ensures that a thermodynamically unfavorable step would have unfavorable kinetics due to a higher transition state. Based on this logic, the thermodynamically ideal (zero-overpotential) catalyst should also be the kinetically optimum catalyst, in agreement with the discussion in Section 2.1. Following the pioneering work of Parsons from the 1950s (Parsons, 1951, 1958), the reaction intermediates preceding the highest transition state can be considered to be in quasi-equilibrium, and the rate of the entire reaction (Figure 5) is governed by the free energy difference between the intermediate with smallest free energy and the transition state with highest free energy (Exner et al., 2018).

FIGURE 5

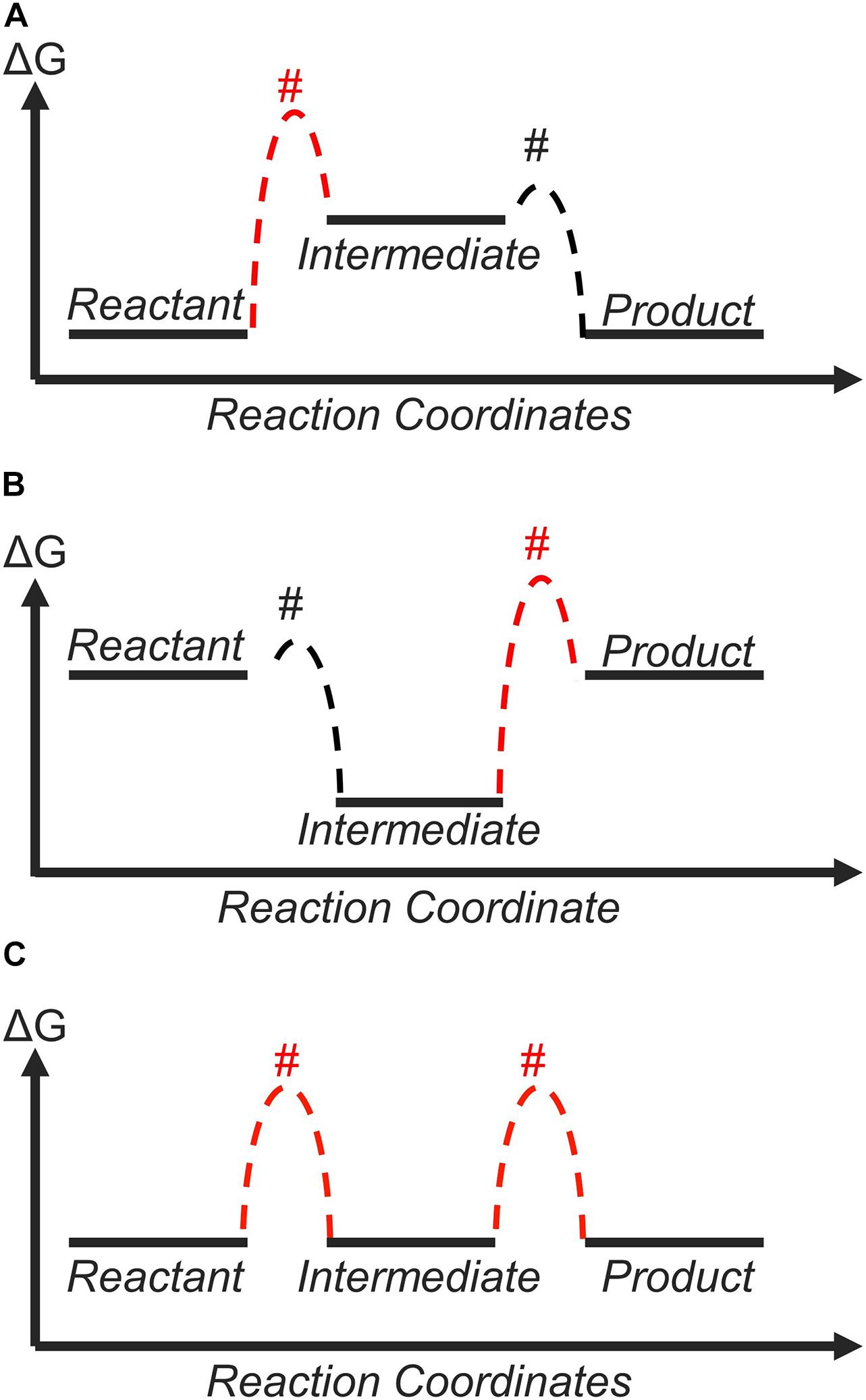
Figure 5. The free-energy landscape of a two-step electrocatalytic process in equilibrium. The heights of transition states indicated by # were drawn assuming a constant BEP coefficient: (A) weak-binding catalyst; (B) strong-binding catalyst; (C) thermoneutral catalyst. The highest transition state, shown in red, occurs at the reaction step with the least favorable thermodynamics. Therefore, the thermodynamically ideal catalyst (C) should also be the kinetically ideal catalyst.

On the other hand, there are examples in the literature where the binding energy and the activity do not seem to correlate. For example, thermodynamic DFT calculations analyzed in terms of the BEP relationship for the ORR predict an activity trend of Pt > Ir > Rh, although the experimental trend is Pt > Rh > Ir (Figure 6A; Zhou et al., 2020). This discrepancy persists despite the experiments being performed using single crystals and even after diffusion effects are compensated, suggesting that the binding energy alone cannot predict the activity of electrocatalysts. A discrepancy between theory and experiment is observed even within different single crystal facets of Pt (Figure 6B; Gómez-Marín et al., 2014). There are also examples where the activity trend is reversed when the overpotential is increased; that is, a material which is less active than another electrocatalyst at low overpotentials can become more active at large overpotentials (Exner, 2019d). These discrepancies are mainly because the experimental activity is evaluated by the current density (kinetics) whereas theoretical trends are evaluated based on the thermodynamics (cf. Section “The Ideal Free-Energy Landscape”) (Exner, 2021b).

FIGURE 6

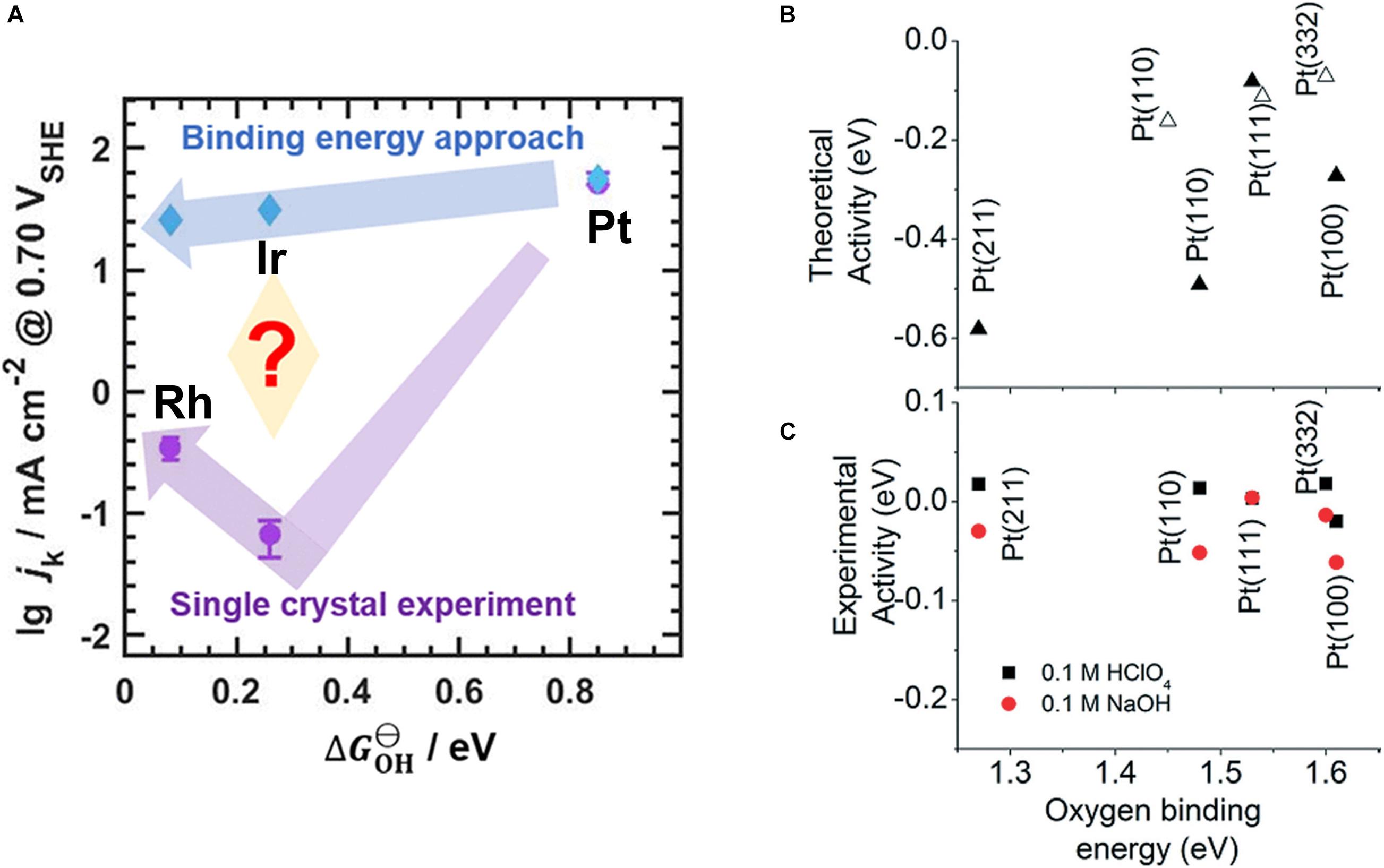
Figure 6. (A) Theoretical (blue) and experimental (purple) ORR activity trends on Pt, Ir, and Rh single-crystal (111) rotating disk electrodes. (B,C) A theoretical and experimental volcano plot of ORR on different facets of platinum. Reproduced from Zhou et al. (2020) and Gómez-Marín et al. (2014) with permission. Copyright 2020 American Chemical Society, 2014 Royal Society of Chemistry.

Validity of the BEP Relationship

First, it is important to note that the BEP relationship is in direct contradiction to the Marcus theory of electron transfer, and therefore, in some cases, it does not depict the free-energy landscape accurately. Although the BEP relationship states a linear relationship between the free energy of activation and the reaction free energy (ΔG_RI^# = βΔG_RI), the Marcus theory states a quadratic relationship (ΔG_RI^# = $\frac{{\left(\lambda +\mathrm{\Delta }{G}_{\text{RI}}\right)}^2}{4\lambda }$). This is a direct consequence of how these two theories modeled the free-energy landscape: while Brønsted, Evans, and Polanyi assumed the free energy to be a linear function of the reaction coordinate, Marcus assumed it to be quadratic. As these assumptions are fundamental to both theories, the applicability of these theories depends on the validity of these presumptions, which should ideally be tested on a system-by-system basis. As a general guideline, the discrepancy between the two is less apparent near equilibrium as the non-linearity, predicted by the Marcus theory, is less important. However, the predictions from the two theories diverge when the overpotential is increased. The most iconic example is the Marcus inverted region (Hammes-Schiffer, 2009; Parada et al., 2019), where once the overpotential is increased beyond a certain point, the free energy of activation starts to increase. This corresponds to a negative BEP coefficient, which is a direct contradiction to the assumption of 0 < β < 1.

As for the value of the BEP coefficient, β = 0.5 is a frequent assumption, although there is no physical basis for why β should be 0.5 or why it should be independent of the material (Koper, 2011a; Akhade et al., 2018). There is also no basis for why β should be constant throughout the various elementary steps of a multistep electrocatalytic reaction. β = 0.5 is only a convenient assumption for theoretical analysis and should be treated as such.

Overpotential Effects on the BEP Relationship

So far, the entire discussion connecting thermodynamic and kinetics via the BEP relationship is based on the free-energy landscape at equilibrium (zero overpotential). Experimentally, however, electrocatalytic turnover can only be observed if a non-zero overpotential is applied to make the overall reaction exergonic (cf. Section “The Ideal Free-Energy Landscape”). Therefore, there is a discrepancy in the condition between theory (η = 0) and experiments (η > 0) (Exner, 2019a, 2020c,b).

How can the applied overpotential be introduced in the analysis of the free-energy changes (thermodynamics) within the reaction mechanism? For a two-electron process, Exner suggested analyzing the potential dependency of the reaction intermediates in the free-energy landscape, |ΔG_RI(η)| (Exner, 2019d, 2021b). |ΔG_RI(η)| is an overpotential-dependent activity descriptor, reaching its maximum at the overpotential η_target that fulfills |ΔG_RI(η_target)| = 0 eV. As a consequence, thermoneutral bonding of the reaction intermediate at the targeted overpotential, η_target, has been identified as a design criteria for active electrocatalysts (Exner, 2020d). This is in contrast to the conventional approach which aims for thermoneutral bonding at zero overpotential (cf. Section “The Ideal Free-Energy Landscape”), and has been coined as the extended Sabatier principle (Exner, 2021b).

Accounting for the overpotential dependency in predicting activity trends appears to be especially important for the evaluation of active catalysts located near the top of the volcano plot (Exner, 2020a). The conventional volcano analysis with the thermodynamic overpotential as the activity descriptor predicts IrO₂ > RuO₂ in both CER and OER (Briquet et al., 2017; Krishnamurthy et al., 2018), although once the overpotential dependence of the free-energy landscape is considered, the experimental activity trend of RuO₂ > IrO₂ could be reproduced (Exner, 2020d). This suggests that the link between the thermodynamics and kinetics via the BEP relationship should not be set at η = 0 V, but rather at the target overpotential (η > 0 V) based on typical reaction conditions in experiments. While the targeted overpotential may be about 50 – 100 mV for a two-electron process such as the HER and CER, a larger value of 300 – 400 mV is more realistic for sluggish four-electron processes such as the OER (Exner, 2019c).

A major consequence of the extended Sabatier principle is the shift in the optimum binding energy with increasing driving force (Exner, 2019d, 2020c). In Section “The BEP Relationship,” it was demonstrated that the thermodynamically ideal free-energy landscape for a two-electron process is one which is completely flat at equilibrium (ΔG_RI = 0 eV at η = 0 V). However, this may no longer be ideal if an overpotential is applied. The criterion for the optimum landscape according to the overpotential-dependent description refers to thermoneutral bonding of the reaction intermediate at the target overpotential (Exner, 2020c). Applying the CHE scheme, the free energy of the reaction intermediate at zero overpotential is described by the relation ΔG_RI = e|η_target| > 0 eV, and hence the optimum binding energy of the reaction intermediate shifts to weak bonding with increasing overpotential (Figure 7), in which ΔG_RI of about 100 – 200 meV has been recognized as the ideal situation for a two-electron process. It is noteworthy that only the extended Sabatier principle can explain the high activities of Pt (ΔG_RI = 0.21 eV), MoS₂ (ΔG_RI = 0.20 eV), and Mo₂C (ΔG_RI = 0.13 eV) in the HER (Tang and Jiang, 2016; Handoko et al., 2019; Lindgren et al., 2020) as well as the high activity of RuO₂ (ΔG_RI = 0.13 eV) in the CER (Exner, 2019b, 2021b). In contrast, the conventional Sabatier approach would not consider these materials as highly active electrocatalysts, because they are not located at the top (ΔG_RI = 0 eV) of the volcano plot at η = 0 V.

FIGURE 7

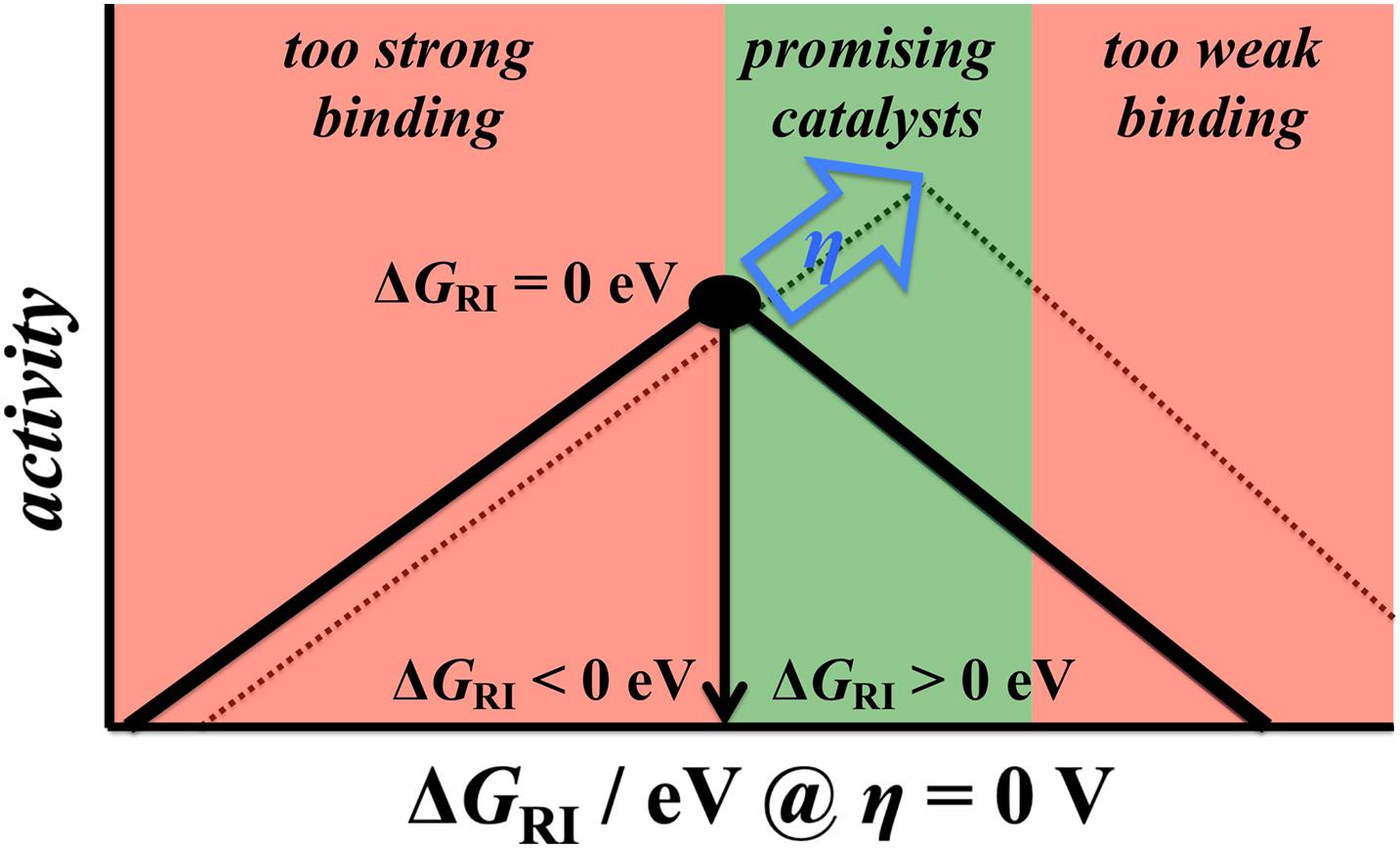
Figure 7. The extended Sabatier principle purports a positive shift of the reaction intermediate’s optimum binding energy with increasing driving force for a two-electron process. As such, electrocatalysts that bind the intermediate slightly weakly (by about 100 – 200 meV) are the most promising materials. Reproduced from Exner (2020c) with permission. Copyright 2020 John Wiley and Sons.

So far, the overpotential dependence for the free energy of the reaction intermediate relating to a simple two-electron process has been discussed. In case of a four-electron process, the situation is more complex since three reaction intermediates need to be considered in the analysis (cf. Section “Practical Application and Linear Scaling Relationships”). The common approach to assess electrocatalytic activity for multiple-electron processes relies on the notion of the thermodynamic overpotential, η_TD, assuming that the highest free-energy change at the equilibrium potential governs the catalytic performance. It was already recognized by Calle-Vallejo and coworkers that the assessment of a single free-energy change to approximate electrocatalytic activity is too simplistic (Govindarajan et al., 2018; Piqué et al., 2020). These authors put forth an alternate activity descriptor, the electrochemical-step symmetry index (ESSI), which in contrast to η_TD analyzes the entire free-energy landscape at zero overpotential. As such, the ESSI is a more balanced activity descriptor than η_TD and provides better results in the sorting of highly active electrocatalysts (Exner, 2020f; Piqué et al., 2020). Yet, the ESSI does not contain any overpotential effects in its framework. Recently, Exner derived an overpotential-dependent activity descriptor for multiple-electron processes, denoted G_max(η) (Exner, 2020g). In a similar fashion to the descriptor |ΔG_RI(η)| for a two-electron process, G_max(η) analyzes the thermodynamics of the reaction intermediates at the target overpotential, but at the same time makes use of the free-energy span model (Kozuch and Shaik, 2011; Kozuch, 2012) by assessing the free-energy difference between the intermediate with smallest free energy and the intermediate with highest free energy in the free-energy landscape. This is achieved by a dedicated procedure of renumbering the electron-proton transfer steps with increasing overpotential, as illustrated in Figure 8.

FIGURE 8

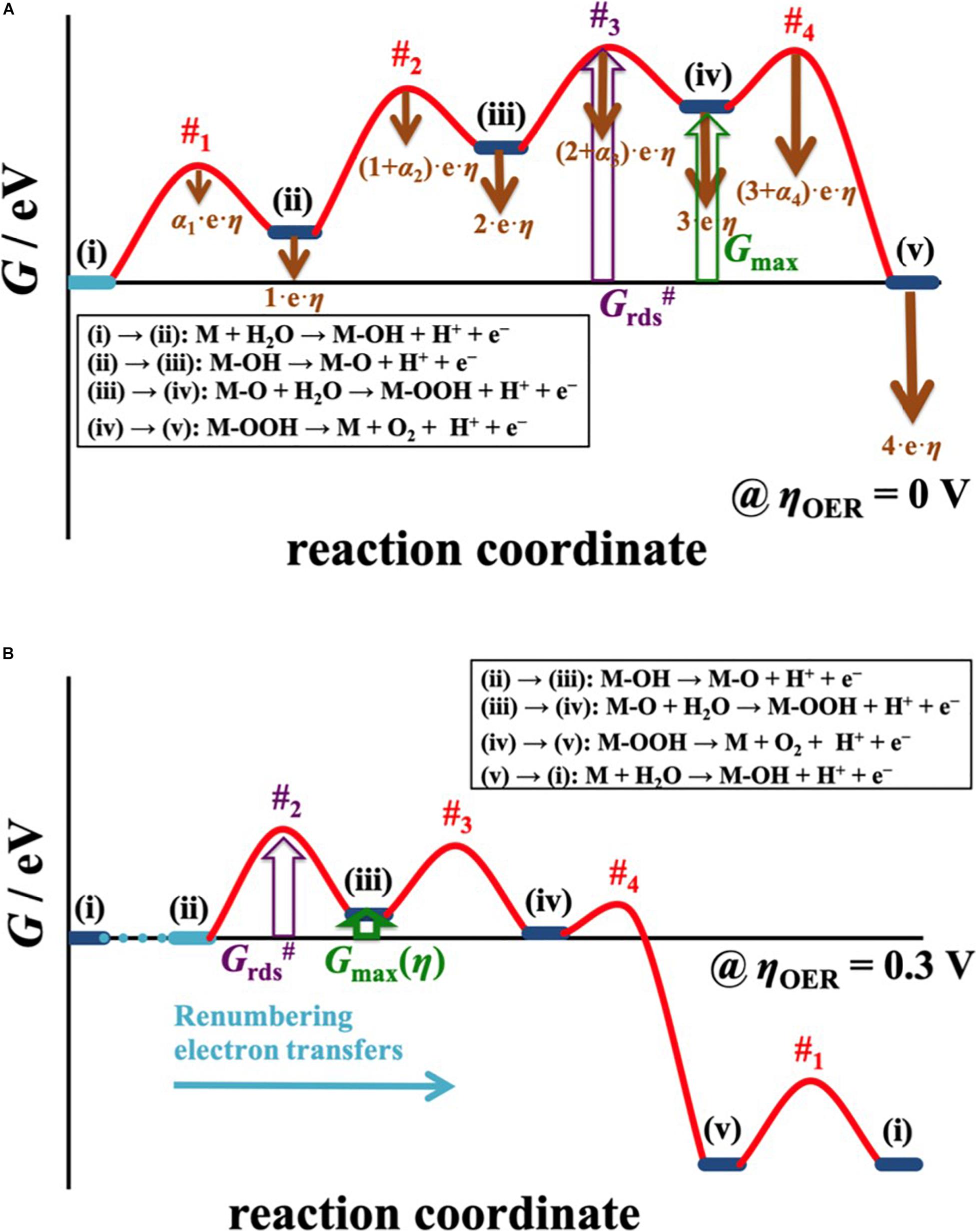
Figure 8. (A) The free-energy span model is applied to determine the distance between the intermediate with smallest free energy and the intermediate with highest free energy in the OER landscape, described by the descriptor G_max. By accounting for the overpotential dependency of the elementary reaction steps, indicated by brown arrows in a), the free-energy diagram is translated to an applied overpotential of 300 mV in (B) to evaluate G_max(η). Herein, the electron-proton transfer steps are renumbered in that the reaction always commences from the intermediate with smallest free energy. The peculiarity of the overpotential-dependent descriptor G_max(η), albeit of thermodynamic nature, is that this activity measure directly scales with the kinetics of the reaction, which is governed by the transition state with highest free energy (G_rds^#) in the free-energy diagram. Reproduced with permission from Exner (2020g). Copyright 2020 American Chemical Society.

The concept of G_max(η) as activity descriptor goes far beyond the assessment of a single free-energy change, as encountered with η_TD. It is noteworthy that the application of G_max(η) to OER electrocatalysts predicts that the volcano apex is situated at about ΔG₂ = 1.40 eV (Exner, 2020g). Following the discussion in Section “Practical Application and Linear Scaling Relationships,” the thermodynamic analysis at zero overpotential in terms of η_TD purports ΔG₂ = 1.60 eV as the optimum situation in the OER, indicating a shift of the volcano top by about 200 meV. Thus, the displacement of the volcano apex with increasing driving force is in the same order of magnitude as observed for a two-electron process (Figure 7), whereas the direction of the shift is toward stronger bonding of the oxygen adsorbate (smaller value of ΔG₂). The move of the volcano top to stronger oxygen bonding is further corroborated by a unifying screening approach which considers not only binding energies but also the applied overpotential, rate-determining steps, and catalytic symmetry, and reports ΔG₂ = 1.30 eV as the optimum situation at an OER overpotential of 400 meV (Exner, 2019c).

Consideration of the applied overpotential for the approximation of electrocatalytic activity by the thermodynamics is of crucial importance when analyzing free-energy changes to comprehend trends in a class of materials. The concept of the extended Sabatier principle by connecting the thermodynamics to the kinetics at the target overpotential of the reaction is recognized as a valuable tool to distinguish between active and inactive electrode materials, particularly since it has been shown that the approximation of electrocatalytic activity by a single free-energy change, as encountered with the notion of η_TD, is insufficient (Exner, 2021c). Yet, this framework cannot entirely close the gap between theory and model experiments. This is also related to the fact that the kinetics is only partly covered in this theory, motivating the following discussion on kinetic effects.

Kinetic Effects Beyond the BEP Relationship

Under the assumption that the reaction intermediates preceding the transition state with highest free energy are in quasi-equilibrium (Parsons, 1951, 1958), the rate of an electrocatalytic process is governed by the transition state with the highest free energy in the free-energy landscape (cf. Figure 8). It should be noted that the transition-state free energy consists of a coverage term [(i) → (iii) in Figure 8A] as well as a free-energy barrier [(iii) → #₃ in Figure 8A], in which the transition state with highest free energy can change upon increasing the overpotential (cf. Figure 8B). However, such a switch in the transition state with highest free energy cannot be predicted solely by thermodynamic considerations, leading to potential discrepancies between thermodynamics and kinetics.

The transition state with highest free energy in the free-energy landscape is connected with the experimentally measurable current density, governing electrocatalytic activity (Parsons, 1951, 1958; Exner et al., 2018). Experiments commonly assess the relation between the current and electrode potential by measuring the Tafel plot, in which the applied overpotential is depicted as a function of the logarithm of the current density. This graph facilitates quantifying the so-called Tafel slope (Hu et al., 2004; Guidelli et al., 2014; Shinagawa et al., 2015), which is a measure for the electrocatalyst’s sensitivity to the applied electrode potential. The Tafel slope, b, indicates by how many mV the applied overpotential needs to be enhanced to yield an increase of the current density by one order of magnitude:

$$b=\frac{\partial \eta }{\partial {\log }_{10}j}(7)$$

In equation (7), η and j denote the applied overpotential and current density, respectively. Some catalysts are extremely sensitive to the applied overpotential. For instance, a Tafel slope of 40 mV/dec. is obtained for HER on Pt in acid at low overpotentials, whereas the Tafel slope increases to about 120 mV/dec. at higher overpotentials. In alkaline solutions, a single Tafel slope with b = 120 mV/dec. is observed (Sheng et al., 2010). In general, a smaller Tafel slope is desirable because a slight increase in the overpotential can significantly increase the current and thus, the observed electrocatalytic activity.

The different Tafel slopes of 40 mV/dec. and 120 mV/dec. can be ascribed to differences in the location of the highest transition state in the free-energy landscape (Parsons, 1951, 1958). The Tafel slope can be expressed in terms of the apparent transfer coefficient, β, which is given by Exner et al. (2018):

$$b=\frac{RT\ln 10}{F\beta }=\frac{59}{\beta }\mathrm{mV}/\mathrm{dec}(8)$$

In case of β = 0.5, the Tafel slope amounts to 120 mV/dec., whereas for β = 1.5 a Tafel slope of 40 mV/dec. is obtained. This finding directly indicates that different transition states govern the rate of the HER over platinum in acidic or alkaline environment at small overpotentials. The apparent transfer coefficient is related to the transfer coefficient for the highest transition state (α) and the number of electrochemical reaction steps consisting of a charge transfer preceding it (n) as follows:

$$\beta =n+\alpha (9)$$

Commonly, the assumption α = 0.5 is used, even if deviations from this notion have been reported in the literature (Fang and Liu, 2014; Rojas-Carbonell et al., 2018; Exner and Over, 2019). Now, it becomes clear that n = 0 results in β = ½, and thus b = 120 mV/dec., whereas n = 1 yields ß = 1.5 and b = 40 mV/dec. As a result, when the first or second elementary reaction step governs the rate, the Tafel slope amounts to 120 mV/dec. or 40 mV/dec., respectively. It shall be noted that these different Tafel slopes can be obtained even if the thermodynamic landscape is the same, which is illustrated in Figure 9 for a two-electron process.

FIGURE 9

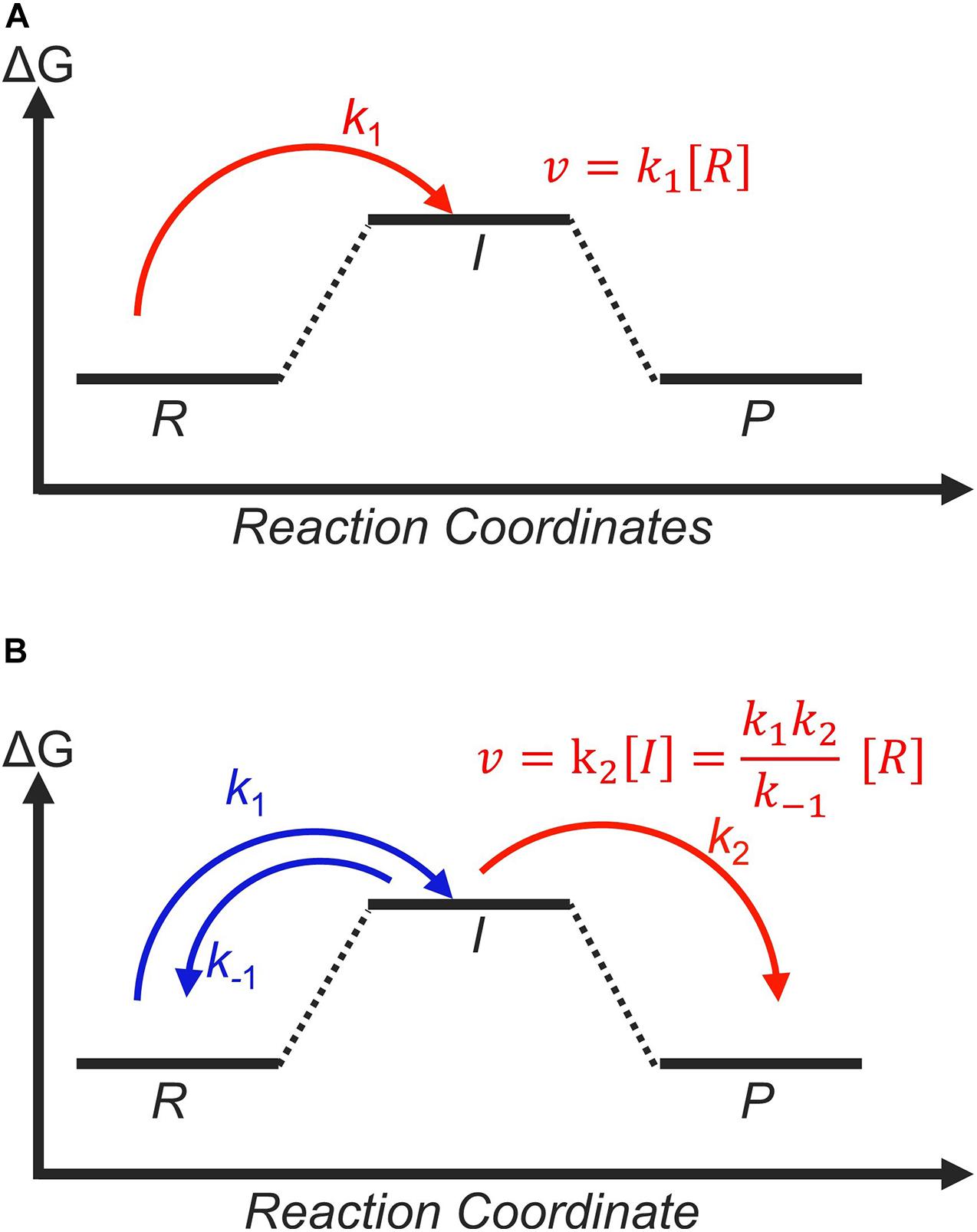
Figure 9. Catalysts with the same thermodynamic free-energy landscapes can still yield different experimental activities, depending on whether the first (A) or the second (B) step determines the catalytic rate. This is governed by the transition state with highest free energy, indicated in red. The corresponding rate equation are shown in both panels, with [R] and [I] corresponding to the concentrations of the reactant and intermediate, respectively. Rate constants are according to usual nomenclature, where k₁ is for the formation of the intermediate, k₂ is for the formation of the product, and negative signs indicate reverse reactions.

Recently, there have been several attempts to bridge the gap between the thermodynamics and kinetics, at least for two-electron processes such as the HER. For example, a microkinetic study by Koper has explicitly shed light on the relationship between thermodynamic and kinetic free-energy landscapes, and has shown how the thermodynamic landscape may overestimate the catalytic rate due to unfavorable kinetics (Koper, 2013a). A recent study by Ooka and Nakamura demonstrates that the optimum binding energy in terms of maximizing reaction rates may not be thermoneutral as expected from the traditional thermodynamic framework (cf. Section “The Ideal Free-Energy Landscape”). Instead, the optimum binding energy is dependent on the kinetic rate constants, and higher rates are achieved if the binding energy of the reaction intermediate shifts to weak or strong bonding with increasing driving force (Ooka and Nakamura, 2019). Exner has taken the analysis one step further to propose the direction of the binding energy’s shift by combining microkinetics with the characteristics of the free-energy diagram in electrocatalysis, pointing out that a shift to strong bonding can be fairly excluded (Exner, 2020e). Rather, displacement of the optimum binding energy to weak bonding is observed for a two-electron process, coinciding with the theory of the extended Sabatier principle (cf. Section “Validity of the BEP Relationship”) (Exner, 2019d, 2020c). In addition to these and many other studies based on microkinetic considerations in the steady-state approximation (Wang et al., 2009; Holewinski and Linic, 2012; Marshall and Vaisson-Béthune, 2015; Shinagawa et al., 2015; Tao et al., 2019; Mefford et al., 2020; Tichter et al., 2020; Zhang et al., 2020), Dauenhauer and coworkers directly calculated the time-dependent kinetics of electrochemical processes, proposing that an oscillation in the driving force may lead to an enhancement in the reaction rate compared to the steady state (Ardagh et al., 2019; Shetty et al., 2020). This is because temporal oscillations allow a single catalytic material to exhibit multiple free-energy landscapes, which promote different parts of the reaction.

Chemical Processes Outside the Scope of the Sabatier Principle

Finally, in this section, we will consider factors which influence the observed electrocatalytic performance in ways which are beyond the scope of the Sabatier principle. The Sabatier principle is useful to predict the intrinsic activity of a material. However, in some cases, the intrinsic activity is not the limiting factor of the catalysis.

Mass Transport and Reactant Availability

A prominent example where mass transport and reactant availability significantly influence the observed electrocatalytic reaction is CO₂ reduction (Gattrell et al., 2006; Ooka et al., 2017; Lum and Ager, 2018). It has been demonstrated both experimentally and theoretically that the availability of CO₂, protons, and other electrolyte ions at the electrode heavily influences the selectivity of this reaction (Hori et al., 1989; Murata and Hori, 1991; Varela et al., 2016; Pérez-Gallent et al., 2017; Ringe et al., 2020). While it is difficult to understand the effect of each ion directly from experiments, it is possible to resolve trends of different ions qualitatively using theoretical approaches (Ringe et al., 2019). This requires multi-scale modeling bridging different time and length scales, which accounts for factors such as surface charging, the potential of zero charge, and the double layer capacitance (cf. Section “Challenges to Accurately Predict the Binding Energy”).

Another difficulty of CO₂ reduction is the change of the pH during the reaction. For example, the bicarbonate ion inside the electrolyte, either added intentionally or formed as a result from the equilibrium with CO₂, acts as a pH buffer, thus influencing the pH (Gattrell et al., 2006; Gupta et al., 2006). The buffering effect changes as the reaction progresses because there is a gradual accumulation of products inside the reactor. Although gaseous products, such as CO, CH₄, and C₂H₄, have no buffering capacity, oxygenated products such as HCOOH and acetate also have protonation equilibria of their own, and hence are expected to influence the pH. As CO₂ reduction is known to be highly sensitive to the pH (Bumroongsakulsawat and Kelsall, 2014; Schouten et al., 2014; Gao et al., 2015; Birdja et al., 2019), this effect would directly impact electrocatalytic activity and selectivity. It is possible to steer the selectivity of electrochemical reactions by manipulating the local concentrations of substrates, as has been shown experimentally in the case of CO₂ reduction vs. HER (Ooka et al., 2017) or the CER vs. OER (Vos et al., 2018; Wintrich et al., 2019).

Surface Area

The surface area and the availability of active sites on the electrocatalyst surface are other factors which influences the observed activity in ways independent from the intrinsic activity. Although the number of active sites can be estimated theoretically from simplified slab models, there is no direct access to the electrochemically active surface area. From an experimental point of view, the surface area is a critical factor to design new electrodes because the activity is usually evaluated based on the geometric area. For this reason, many reports of active materials are based on porous substrates, such as carbon felt or Pt/Ti mesh, compared with glassy carbon or conductive glass substrates (Park et al., 2012; Xie et al., 2017; Kang et al., 2019).

The surface area may also indirectly influence diffusion at the vicinity of the electrode as a rough surface would disrupt the diffusion layer. Although most studies so far assume the concentration of chemical species within the diffusion layer to be dependent only on the distance from the electrode, a more accurate prediction may be obtained by taking the roughness of the electrode into account (Pajkossy and Nyikos, 1989; Louch and Pritzker, 1993; Kant, 1994). This is especially important for cascade reaction systems, where the intermediate must reach the next catalyst before it diffuses into the bulk solution (Lum and Ager, 2018; Gurudayal et al., 2019). So far, both the electrochemically active surface area and the roughness of the electrode are difficult to describe using DFT, indicating another limitation for the comparison between experiment and theory, which is particularly pronounced when surface blocking or roughness effects govern electrocatalytic activity.

Conclusion

The present review has summarized the key concepts of the Sabatier principle, which is widely used today to guide catalyst development. From traditional materials science to the most advanced machine learning studies, there is a general consensus that the binding energy of reaction intermediates is a critical parameter to predict electrocatalytic activity. This descriptor-based approach has also been recently transferred to the surrounding fields of homogeneous catalysis and enzyme catalysis.

Since the concept of the binding energy and the Sabatier principle are central in the current electrocatalysis theory, it is important to highlight not only its usefulness, but also its challenges and shortcomings in a critical light. This may help not only to prevent misleading analyses, but also to clarify what steps need to be taken next. To this end, we have attempted to accentuate at which level issues can arise. Some matters are technical in nature and can be overcome if the accuracy of binding energy calculations is enhanced. On the other hand, some aspects are not an issue of computational accuracy and are more fundamental in nature, such as the bridge between the thermodynamics and kinetics by the Brønsted – Evans – Polanyi relationship or the influence of electrolyte, surface charging and mass transport effects, which require the application of multi-scale frameworks. While the simplicity of the CHE model has led to its widespread success and application, more comprehensive approaches which include a grand canonical description of the electrochemical double layer as well as an explicit treatment of the overpotential and its influence on kinetic barriers may be the next step forward. Increasing the model complexity can be promoted considering the emergence of new techniques such as machine learning, which can be used to reduce computational costs.

The theoretical advancement based on the CHE model and the Sabatier principle in its thermodynamic form has been a major driving force behind the advancement of electrocatalysis in the last fifteen years. Building upon and expanding our current framework is critical to promote the identification of next-generation electrocatalysts, and to realize a truly sustainable society.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

HO is grateful to the support from the RIKEN Special Postdoctoral Researcher Program and to the grant-in-aid for scientific research (No. 20K15387) from the Japan Society for the Promotion of Science. JH appreciates the support from the National Natural Science Foundation of China (No. 21802170). KE gratefully acknowledges funding from the Alexander von Humboldt Foundation. KE is associated with the CRC/TRR247: “Heterogeneous Oxidation Catalysis in the Liquid Phase” (Project number 388390466-TRR 247). KE is associated with the RESOLV Cluster of Excellence, funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC 2033 – 390677874 – RESOLV. The contribution of KE is based upon the work from COST Action 18234, supported by COST (European Cooperation in Science and Technology).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Abidi, N., Lim, K. R. G., Seh, Z. W., and Steinmann, S. N. (2020). Atomistic modeling of electrocatalysis: are we there yet? WIRES Comput. Mol. Sci. doi: 10.1002/wcms.1499 [Epub ahead of print],

CrossRef Full Text | Google Scholar

Akhade, S. A., Nidzyn, R. M., Rostamikia, G., and Janik, M. J. (2018). Using brønsted-evans-polanyi relations to predict electrode potential-dependent activation energies. Catal. Tod. 312, 82–91. doi: 10.1016/j.cattod.2018.03.048

CrossRef Full Text | Google Scholar

Ardagh, M. A., Abdelrahman, O. A., and Dauenhauer, P. J. (2019). Principles of dynamic heterogeneous catalysis: surface resonance and turnover frequency response. ACS Catal. 9, 6929–6937. doi: 10.1021/acscatal.9b01606

CrossRef Full Text | Google Scholar

Auinger, M., Katsounaros, I., Meier, J. C., Klemm, S. O., Biedermann, P. U., Topalov, A. A., et al. (2011). Near-surface ion distribution and buffer effects during electrochemical reactions. Phys. Chem. Chem. Phys. 13, 16384–16394. doi: 10.1039/C1CP21717H

PubMed Abstract | CrossRef Full Text | Google Scholar

Ávila, M., Juárez, M. F., and Santos, E. (2020). Role of the partial charge transfer on the chloride adlayers on Au (100). ChemElectroChem 7, 4269–4282. doi: 10.1002/celc.202001228

CrossRef Full Text | Google Scholar

Back, S., Tran, K., and Ulissi, Z. W. (2019a). Toward a design of active oxygen evolution catalysts: insights from automated density functional theory calculations and machine learning. ACS Catal. 9, 7651–7659. doi: 10.1021/acscatal.9b02416

CrossRef Full Text | Google Scholar

Back, S., Yoon, J., Tian, N., Zhong, W., Tran, K., and Ulissi, Z. W. (2019b). Convolutional neural network of atomic surface structures to predict binding energies for high-throughput screening of catalysts. J. Phys. Chem. Lett. 10, 4401–4408. doi: 10.1021/acs.jpclett.9b01428

PubMed Abstract | CrossRef Full Text | Google Scholar

Bard, A. J. (2010). Inner-sphere heterogeneous electrode reactions. Electrocatalysis and photocatalysis: the challenge. J. Am. Chem. Soc. 132, 7559–7567. doi: 10.1021/ja101578m

PubMed Abstract | CrossRef Full Text | Google Scholar

Basdogan, Y., Groenenboom, M. C., Henderson, E., De, S., Rempe, S. B., and Keith, J. A. (2020a). Machine learning-guided approach for studying solvation environments. J. Chem. Theory Comput. 16, 633–642. doi: 10.1021/acs.jctc.9b00605

PubMed Abstract | CrossRef Full Text | Google Scholar

Basdogan, Y., Maldonado, A. M., and Keith, J. A. (2020b). Advances and challenges in modeling solvated reaction mechanisms for renewable fuels and chemicals. WIRES Comput. Mol. Sci. 10:e1446. doi: 10.1002/wcms.1446

CrossRef Full Text | Google Scholar

Bhattacharyya, K., Poidevin, C., and Auer, A. A. (2021). Structure and reactivity of IrO X nanoparticles for the oxygen evolution reaction in electrocatalysis: an electronic structure theory study. J. Phys. Chem. C 125, 4379–4390. doi: 10.1021/acs.jpcc.0c10092

CrossRef Full Text | Google Scholar

Birdja, Y. Y., Pérez-Gallent, E., Figueiredo, M. C., Göttle, A. J., Calle-Vallejo, F., and Koper, M. T. (2019). Advances and challenges in understanding the electrocatalytic conversion of carbon dioxide to fuels. Nat. Energ. 4, 732–745. doi: 10.1038/s41560-019-0450-y

CrossRef Full Text | Google Scholar

Bligaard, T., Nørskov, J. K., Dahl, S., Matthiesen, J., Christensen, C. H., and Sehested, J. (2004). The Brønsted–Evans–polanyi relation and the volcano curve in heterogeneous catalysis. J. Catal. 224, 206–217. doi: 10.1016/j.jcat.2004.02.034

CrossRef Full Text | Google Scholar

Bochevarov, A. D., Harder, E., Hughes, T. F., Greenwood, J. R., Braden, D. A., Philipp, D. M., et al. (2013). Jaguar: a high-performance quantum chemistry software program with strengths in life and materials sciences. Int. J. Quantum Chem. 113, 2110–2142. doi: 10.1002/qua.24481

CrossRef Full Text | Google Scholar

Briquet, L. G., Sarwar, M., Mugo, J., Jones, G., and Calle-Vallejo, F. (2017). A new type of scaling relations to assess the accuracy of computational predictions of catalytic activities applied to the oxygen evolution reaction. ChemCatChem 9, 1261–1268. doi: 10.1002/cctc.201601662

CrossRef Full Text | Google Scholar

Bumroongsakulsawat, P., and Kelsall, G. (2014). Effect of solution pH on CO: formate formation rates during electrochemical reduction of aqueous CO2 at Sn cathodes. Electrochim. Acta 141, 216–225. doi: 10.1016/j.electacta.2014.07.057

CrossRef Full Text | Google Scholar

Busch, M., Halck, N. B., Kramm, U. I., Siahrostami, S., Krtil, P., and Rossmeisl, J. (2016). Beyond the top of the volcano?–A unified approach to electrocatalytic oxygen reduction and oxygen evolution. Nano Energ. 29, 126–135. doi: 10.1016/j.nanoen.2016.04.011

CrossRef Full Text | Google Scholar

Busch, M., Laasonen, K., and Ahlberg, E. (2020). Method for the accurate prediction of electron transfer potentials using an effective absolute potential. Phys. Chem. Chem. Phys. 22, 25833–25840. doi: 10.1039/D0CP04508J

PubMed Abstract | CrossRef Full Text | Google Scholar

Busch, M., Wodrich, M. D., and Corminboeuf, C. (2015). Linear scaling relationships and volcano plots in homogeneous catalysis–revisiting the suzuki reaction. Chem. Sci. 6, 6754–6761. doi: 10.1039/C5SC02910D

PubMed Abstract | CrossRef Full Text | Google Scholar

Calle-Vallejo, F., and Koper, M. T. (2012). First-principles computational electrochemistry: achievements and challenges. Electrochim. Acta 84, 3–11. doi: 10.1016/j.electacta.2012.04.062

CrossRef Full Text | Google Scholar

Calle-Vallejo, F., Martnez, J., Garcá-Lastra, J., Abad, E., and Koper, M. (2013). Oxygen reduction and evolution at single-metal active sites: comparison between functionalized graphitic materials and protoporphyrins. Surf. Sci. 607, 47–53. doi: 10.1016/j.susc.2012.08.005

CrossRef Full Text | Google Scholar

Carmo, M., Fritz, D. L., Mergel, J., and Stolten, D. (2013). A comprehensive review on PEM water electrolysis. Int. J. Hyd. Energ. 38, 4901–4934. doi: 10.1016/j.ijhydene.2013.01.151

CrossRef Full Text | Google Scholar

Che, M. (2013). Nobel prize in chemistry 1912 to sabatier: organic chemistry or catalysis? Catal. Tod. 218, 162–171. doi: 10.1016/j.cattod.2013.07.006

CrossRef Full Text | Google Scholar

Chen, X., Yu, L., Wang, S., Deng, D., and Bao, X. (2017). Highly active and stable single iron site confined in graphene nanosheets for oxygen reduction reaction. Nano Energ. 32, 353–358. doi: 10.1016/j.nanoen.2016.12.056

CrossRef Full Text | Google Scholar

Cheng, J., Hu, P., Ellis, P., French, S., Kelly, G., and Lok, C. M. (2008). Brønsted- evans- polanyi relation of multistep reactions and volcano curve in heterogeneous catalysis. J. Phys. Chem. C 112, 1308–1311. doi: 10.1021/jp711191j

CrossRef Full Text | Google Scholar

Craig, M. J., Coulter, G., Dolan, E., Soriano-López, J., Mates-Torres, E., Schmitt, W., et al. (2019). Universal scaling relations for the rational design of molecular water oxidation catalysts with near-zero overpotential. Nat. Commun. 10, 1–9. doi: 10.1038/s41467-019-12994-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Diaz-Morales, O., Raaijman, S., Kortlever, R., Kooyman, P. J., Wezendonk, T., Gascon, J., et al. (2016). Iridium-based double perovskites for efficient water oxidation in acid media. Nat. Commun. 7, 1–6. doi: 10.1038/ncomms12363

PubMed Abstract | CrossRef Full Text | Google Scholar

Dickens, C. F., and Nørskov, J. K. (2017). A theoretical investigation into the role of surface defects for oxygen evolution on RuO2. J. Phys. Chem. C 121, 18516–18524. doi: 10.1021/acs.jpcc.7b03481

CrossRef Full Text | Google Scholar

Dubouis, N., and Grimaud, A. (2019). The hydrogen evolution reaction: from material to interfacial descriptors. Chem. Sci. 10, 9165–9181. doi: 10.1039/C9SC03831K

PubMed Abstract | CrossRef Full Text | Google Scholar

Durst, J., Siebel, A., Simon, C., Hasche, F., Herranz, J., and Gasteiger, H. (2014). New insights into the electrochemical hydrogen oxidation and evolution reaction mechanism. Energ. Environ. Sci. 7, 2255–2260. doi: 10.1039/C4EE00440J

CrossRef Full Text | Google Scholar

Exner, K. S. (2018). Activity–stability volcano plots for the investigation of nano-sized electrode materials in lithium-ion batteries. ChemElectroChem 5, 3243–3248. doi: 10.1002/celc.201800838

CrossRef Full Text | Google Scholar

Exner, K. S. (2019a). Activity-stability volcano plots for material optimization in electrocatalysis. ChemCatChem 11, 3234–3241. doi: 10.1002/cctc.201900500

CrossRef Full Text | Google Scholar

Exner, K. S. (2019b). Beyond the traditional volcano concept: overpotential-dependent volcano plots exemplified by the chlorine evolution reaction over transition-metal oxides. J. Phys. Chem. C 123, 16921–16928. doi: 10.1021/acs.jpcc.9b05364

CrossRef Full Text | Google Scholar

Exner, K. S. (2019c). Design criteria for oxygen evolution electrocatalysts from first principles: introduction of a unifying material-screening approach. ACS Appl. Energ. Mater. 2, 7991–8001. doi: 10.1021/acsaem.9b01480

CrossRef Full Text | Google Scholar

Exner, K. S. (2019d). Is thermodynamics a good descriptor for the activity? Re-investigation of Sabatier’s principle by the free energy diagram in electrocatalysis. ACS Catal. 9, 5320–5329. doi: 10.1021/acscatal.9b00732

CrossRef Full Text | Google Scholar

Exner, K. S. (2019e). Recent advancements towards closing the gap between electrocatalysis and battery science communities: the computational lithium electrode and activity–stability volcano plots. ChemSusChem 12, 2330–2344. doi: 10.1002/cssc.201900298

PubMed Abstract | CrossRef Full Text | Google Scholar

Exner, K. S. (2020a). Comparison of the conventional volcano analysis with a unifying approach: material screening based on a combination of experiment and theory. J. Phys. Chem. C 124, 822–828. doi: 10.1021/acs.jpcc.9b10860

CrossRef Full Text | Google Scholar

Exner, K. S. (2020b). Design criteria for the competing chlorine and oxygen evolution reactions: avoid the OCl adsorbate to enhance chlorine selectivity. Phys. Chem. Chem. Phys. 22, 22451–22458. doi: 10.1039/D0CP03667F

PubMed Abstract | CrossRef Full Text | Google Scholar

Exner, K. S. (2020c). Does a Thermoneutral Electrocatalyst correspond to the apex of a volcano plot for a simple two-electron process? Angew. Chem. Int. Ed. 22, 10236–10240. doi: 10.1002/anie.202003688

PubMed Abstract | CrossRef Full Text | Google Scholar

Exner, K. S. (2020d). Overpotential-dependent volcano plots to assess activity trends in the competing chlorine and oxygen evolution reactions. ChemElectroChem 7, 1448–1455. doi: 10.1002/celc.202000120

CrossRef Full Text | Google Scholar

Exner, K. S. (2020e). Paradigm change in hydrogen electrocatalysis: the volcano’s apex is located at weak bonding of the reaction intermediate. Int. J. Hyd. Energ. 45, 27221–27229. doi: 10.1016/j.ijhydene.2020.07.088

CrossRef Full Text | Google Scholar

Exner, K. S. (2020f). Recent progress in the development of screening methods to identify electrode materials for the oxygen evolution reaction. Adv. Funct. Mater. 30:2005060. doi: 10.1002/adfm.202005060

CrossRef Full Text | Google Scholar

Exner, K. S. (2020g). A universal descriptor for the screening of electrode materials for multiple-electron processes: beyond the thermodynamic overpotential. ACS Catal. 10, 12607–12617. doi: 10.1021/acscatal.0c03865

CrossRef Full Text | Google Scholar

Exner, K. S. (2021a). Boosting the stability of RuO2 in the acidic oxygen evolution reaction by tuning oxygen-vacancy formation energies: a viable approach beyond noble-metal catalysts? ChemElectroChem 8, 46–48. doi: 10.1002/celc.202001465

CrossRef Full Text | Google Scholar

Exner, K. S. (2021b). Hydrogen electrocatalysis revisited: weak bonding of adsorbed hydrogen as design principle for active electrode materials. Curr. Opin. Electrochem. 26:100673. doi: 10.1016/j.coelec.2020.100673

CrossRef Full Text | Google Scholar

Exner, K. S. (2021c). Why approximating electrocatalytic activity by a single free-energy change is insufficient. Electrochim. Acta 375:137975. doi: 10.1016/j.electacta.2021.137975

CrossRef Full Text | Google Scholar

Exner, K. S., Anton, J., Jacob, T., and Over, H. (2014). Controlling selectivity in the chlorine evolution reaction over RuO2-based catalysts. Angew. Chem. Int. Ed. 53, 11032–11035. doi: 10.1002/anie.201406112

PubMed Abstract | CrossRef Full Text | Google Scholar

Exner, K. S., Anton, J., Jacob, T., and Over, H. (2016). Full kinetics from first principles of the chlorine evolution reaction over a RuO2 (110) model electrode. Angew. Chem. Int. Ed. 55, 7501–7504. doi: 10.1002/anie.201511804

PubMed Abstract | CrossRef Full Text | Google Scholar

Exner, K. S., and Over, H. (2019). Beyond the rate-determining step in the oxygen evolution reaction over a single-crystalline IrO2 (110) model electrode: kinetic scaling relations. ACS Catal. 9, 6755–6765. doi: 10.1021/acscatal.9b01564

CrossRef Full Text | Google Scholar

Exner, K. S., Sohrabnejad-Eskan, I., and Over, H. (2018). A universal approach to determine the free energy diagram of an electrocatalytic reaction. ACS Catal. 8, 1864–1879. doi: 10.1021/acscatal.7b03142

CrossRef Full Text | Google Scholar

Fabbri, E., Nachtegaal, M., Binninger, T., Cheng, X., Kim, B.-J., Durst, J., et al. (2017). Dynamic surface self-reconstruction is the key of highly active perovskite nano-electrocatalysts for water splitting. Nat. Mater. 16, 925–931. doi: 10.1038/nmat4938

PubMed Abstract | CrossRef Full Text | Google Scholar

Fang, Y.-H., and Liu, Z.-P. (2014). Tafel kinetics of electrocatalytic reactions: from experiment to first-principles. ACS Catal. 4, 4364–4376. doi: 10.1021/cs501312v

CrossRef Full Text | Google Scholar

Frumkin, A., and Petrii, O. (1975). Potentials of zero total and zero free charge of platinum group metals. Electrochim. Acta 20, 347–359. doi: 10.1016/0013-4686(75)90017-1

CrossRef Full Text | Google Scholar

Gao, D., Wang, J., Wu, H., Jiang, X., Miao, S., Wang, G., et al. (2015). pH effect on electrocatalytic reduction of CO2 over Pd and Pt nanoparticles. Electrochem. Commun. 55, 1–5. doi: 10.1016/j.elecom.2015.03.008

CrossRef Full Text | Google Scholar

Garcia, A. C., Touzalin, T., Nieuwland, C., Perini, N., and Koper, M. T. (2019). Enhancement of oxygen evolution activity of nickel oxyhydroxide by electrolyte alkali cations. Angew. Chem. Int. Ed. 58, 12999–13003. doi: 10.1002/anie.201905501

PubMed Abstract | CrossRef Full Text | Google Scholar

Gattrell, M., Gupta, N., and Co, A. (2006). A review of the aqueous electrochemical reduction of CO2 to hydrocarbons at copper. J. Electroanal. Chem. 594, 1–19. doi: 10.1016/j.jelechem.2006.05.013

CrossRef Full Text | Google Scholar

Gerischer, R., and Gerischer, H. (1956). Über die Katalytische Zersetzung Von Wasserstoffsuperoxyd an metallischem platin. Z. Phys. Chem. 6, 178–200. doi: 10.1524/zpch.1956.6.3_4.178

CrossRef Full Text | Google Scholar

Goings, J. J., and Hammes-Schiffer, S. (2020). Nonequilibrium dynamics of proton-coupled electron transfer in proton wires: concerted but asynchronous mechanisms. ACS Cent. Sci. 6, 1594–1601. doi: 10.1021/acscentsci.0c00756

PubMed Abstract | CrossRef Full Text | Google Scholar

Gómez-Marín, A. M., Rizo, R., and Feliu, J. M. (2014). Oxygen reduction reaction at Pt single crystals: a critical overview. Catal. Sci. Technol. 4, 1685–1698. doi: 10.1039/C3CY01049J

CrossRef Full Text | Google Scholar

Gossenberger, F., Juarez, F., and Groß, A. (2020). Sulfate, bisulfate, and hydrogen co-adsorption on Pt (111) and Au (111) in an electrochemical environment. Front. Chem. 8:634. doi: 10.3389/fchem.2020.00634

PubMed Abstract | CrossRef Full Text | Google Scholar

Göttle, A. J., and Koper, M. T. (2017). Proton-coupled electron transfer in the electrocatalysis of CO2 reduction: prediction of Sequential Vs. Concerted pathways using DFT. Chem. Sci. 8, 458–465. doi: 10.1039/C6SC02984A

PubMed Abstract | CrossRef Full Text | Google Scholar

Govind Rajan, A., Martirez, J. M. P., and Carter, E. A. (2020). Why do we use the materials and operating conditions we use for heterogeneous (Photo) electrochemical water splitting? ACS Catal. 10, 11177–11234. doi: 10.1021/acscatal.0c01862

CrossRef Full Text | Google Scholar

Govindarajan, N., García-Lastra, J. M., Meijer, E. J., and Calle-Vallejo, F. (2018). Does the breaking of adsorption-energy scaling relations guarantee enhanced electrocatalysis? Curr. Opin. Electrochem. 8, 110–117. doi: 10.1016/j.coelec.2018.03.025

CrossRef Full Text | Google Scholar

Greeley, J., Jaramillo, T. F., Bonde, J., Chorkendorff, I., and Nørskov, J. K. (2006). Computational high-throughput screening of electrocatalytic materials for hydrogen evolution. Nat. Mater. 5, 909–913. doi: 10.1038/nmat1752

PubMed Abstract | CrossRef Full Text | Google Scholar

Greeley, J., and Nørskov, J. K. (2007). Large-scale, density functional theory-based screening of alloys for hydrogen evolution. Surf. Sci 601, 1590–1598. doi: 10.1016/j.susc.2007.01.037

CrossRef Full Text | Google Scholar

Groß, A. (2020). “Theory of solid/electrolyte interfaces,” in Surface and Interface Science: Volume 8: Interfacial Electrochemistry, ed. K. Wandelt (Weinheim: Wiley-VCH Verlag GmbH & Co. KGaA).

Google Scholar

Guidelli, R., Compton, R. G., Feliu, J. M., Gileadi, E., Lipkowski, J., Schmickler, W., et al. (2014). Defining the transfer coefficient in electrochemistry: an assessment (Iupac Technical Report). Pure Appl. Chem. 86, 245–258. doi: 10.1515/pac-2014-5026

CrossRef Full Text | Google Scholar

Gupta, N., Gattrell, M., and MacDougall, B. (2006). Calculation for the cathode surface concentrations in the electrochemical reduction of CO2 in KHCO3 solutions. J. Appl. Electrochem. 36, 161–172. doi: 10.1007/s10800-005-9058-y

CrossRef Full Text | Google Scholar

Gurudayal, D. P., Malani, S., Lum, Y., Haussener, S., and Ager, J. W. (2019). Sequential cascade electrocatalytic conversion of carbon dioxide to C–C coupled products. ACS Appl. Energ. Mater. 2, 4551–4559. doi: 10.1021/acsaem.9b00791

CrossRef Full Text | Google Scholar

Hajiyani, H., and Pentcheva, R. (2018). Surface termination and composition control of activity of the CoxNi1–xFe2O4 (001) surface for water oxidation: insights from DFT + U calculations. ACS Catal. 8, 11773–11782. doi: 10.1021/acscatal.8b00574

CrossRef Full Text | Google Scholar

Halck, N. B., Petrykin, V., Krtil, P., and Rossmeisl, J. (2014). Beyond the volcano limitations in electrocatalysis–oxygen evolution reaction. Phys. Chem. Chem. Phys. 16, 13682–13688. doi: 10.1039/C4CP00571F

PubMed Abstract | CrossRef Full Text | Google Scholar

Hammes-Schiffer, S. (2009). Theory of proton-coupled electron transfer in energy conversion processes. Acc. Chem. Res. 42, 1881–1889. doi: 10.1021/ar9001284

PubMed Abstract | CrossRef Full Text | Google Scholar

Hammes-Schiffer, S., and Stuchebrukhov, A. A. (2010). Theory of coupled electron and proton transfer reactions. Chem. Rev. 110, 6939–6960. doi: 10.1021/cr1001436

PubMed Abstract | CrossRef Full Text | Google Scholar

Handoko, A. D., Steinmann, S. N., and Seh, Z. W. (2019). Theory-guided materials design: two-dimensional mxenes in electro-and photocatalysis. Nanoscale Horiz. 4, 809–827. doi: 10.1039/C9NH00100J

CrossRef Full Text | Google Scholar

Hansen, H. A., Rossmeisl, J., and Nørskov, J. K. (2008). Surface pourbaix diagrams and oxygen reduction activity of Pt, Ag and Ni (111) surfaces studied by DFT. Phys. Chem. Chem. Phys. 10, 3722–3730. doi: 10.1039/B803956A

PubMed Abstract | CrossRef Full Text | Google Scholar

Hansen, M. H., and Rossmeisl, J. (2016). pH in grand canonical statistics of an electrochemical interface. J. Phys. Chem. C 120, 29135–29143. doi: 10.1021/acs.jpcc.6b09019

CrossRef Full Text | Google Scholar

Hao, S., Liu, M., Pan, J., Liu, X., Tan, X., Xu, N., et al. (2020). Dopants fixation of ruthenium for boosting acidic oxygen evolution stability and activity. Nat. Commun. 11, 1–11. doi: 10.1038/s41467-020-19212-y

PubMed Abstract | CrossRef Full Text | Google Scholar

He, D., Li, Y., Ooka, H., Go, Y. K., Jin, F., Kim, S. H., et al. (2018). Selective electrocatalytic reduction of nitrite to dinitrogen based on decoupled proton–electron transfer. J. Am. Chem. Soc. 140, 2012–2015. doi: 10.1021/jacs.7b12774

PubMed Abstract | CrossRef Full Text | Google Scholar

He, D., Ooka, H., Kim, Y., Li, Y., Jin, F., Kim, S. H., et al. (2020). Atomic-scale evidence for highly selective electrocatalytic N- N coupling on metallic MoS2. Proc. Natl. Acad. Sci. U.S.A. 117, 31631–31638. doi: 10.1073/pnas.2008429117

PubMed Abstract | CrossRef Full Text | Google Scholar

He, Z.-D., Hanselman, S., Chen, Y.-X., Koper, M. T. M., and Calle-Vallejo, F. (2017). Importance of solvation for the accurate prediction of oxygen reduction activities of pt-based electrocatalysts. J. Phys. Chem. Lett. 8, 2243–2246. doi: 10.1021/acs.jpclett.7b01018

PubMed Abstract | CrossRef Full Text | Google Scholar

Heenen, H. H., Gauthier, J. A., Kristoffersen, H. H., Ludwig, T., and Chan, K. (2020). Solvation at metal/water interfaces: an Ab initio molecular dynamics benchmark of common computational approaches. J. Chem. Phys. 152:144703. doi: 10.1063/1.5144912

CrossRef Full Text | Google Scholar

Hinnemann, B., Moses, P. G., Bonde, J., Jørgensen, K. P., Nielsen, J. H., Horch, S., et al. (2005). Biomimetic hydrogen evolution: MoS2 nanoparticles as catalyst for hydrogen evolution. J. Am. Chem. Soc. 127, 5308–5309. doi: 10.1021/ja0504690

PubMed Abstract | CrossRef Full Text | Google Scholar

Holewinski, A., and Linic, S. (2012). Elementary mechanisms in electrocatalysis: revisiting the ORR tafel slope. J. Electrochem. Soc. 159:H864. doi: 10.1149/2.022211jes

CrossRef Full Text | Google Scholar

Hori, Y., Murata, A., and Takahashi, R. (1989). Formation of hydrocarbons in the electrochemical reduction of carbon dioxide at a copper electrode in aqueous solution. J. Chem. Soc. 85, 2309–2326. doi: 10.1039/F19898502309

CrossRef Full Text | Google Scholar

Hörmann, N. G., Andreussi, O., and Marzari, N. (2019). Grand canonical simulations of electrochemical interfaces in implicit solvation models. J. Chem. Phys. 150:041730. doi: 10.1063/1.5054580

CrossRef Full Text | Google Scholar

Hörmann, N. G., Marzari, N., and Reuter, K. (2020). Electrosorption at metal surfaces from first principles. NPJ Comput. Mater. 6, 1–10. doi: 10.1038/s41524-020-00394-4

CrossRef Full Text | Google Scholar

Hu, J.-M., Zhang, J.-Q., and Cao, C.-N. (2004). Oxygen evolution reaction on IrO2-based DSA type electrodes: kinetics analysis of tafel lines and EIS. Int. J. Hyd. Energ. 29, 791–797. doi: 10.1016/j.ijhydene.2003.09.007

CrossRef Full Text | Google Scholar

Huang, J., Malek, A., Zhang, J., and Eikerling, M. H. (2016a). Non-monotonic surface charging behavior of platinum: a paradigm change. J. Phys. Chem. C 120, 13587–13595. doi: 10.1021/acs.jpcc.6b03930

CrossRef Full Text | Google Scholar

Huang, J., Zhang, J., and Eikerling, M. (2016b). Theory of electrostatic phenomena in water-filled Pt nanopores. Faraday Disc. 193, 427–446. doi: 10.1039/C6FD00094K

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, J., Zhang, J., and Eikerling, M. (2018). Unifying theoretical framework for deciphering the oxygen reduction reaction on platinum. Phys. Chem. Chem. Phys. 20, 11776–11786. doi: 10.1039/C8CP01315B

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, Z.-F., Song, J., Dou, S., Li, X., Wang, J., and Wang, X. (2019). Strategies to break the scaling relation toward enhanced oxygen electrocatalysis. Matter 1, 1494–1518. doi: 10.1016/j.matt.2019.09.011

CrossRef Full Text | Google Scholar

Kang, Y. S., Jo, S., Choi, D., Kim, J. Y., Park, T., and Yoo, S. J. (2019). Pt-Sputtered Ti mesh electrode for polymer electrolyte membrane fuel cells. Int. J. Precis 6, 271–279. doi: 10.1007/s40684-019-00077-6

CrossRef Full Text | Google Scholar

Kant, R. (1994). Can one electrochemically measure the statistical morphology of a rough electrode? J. Phys. Chem. 98, 1663–1667. doi: 10.1021/j100057a020

CrossRef Full Text | Google Scholar

Kari, J., Olsen, J. P., Jensen, K., Badino, S. F., Krogh, K. B., Borch, K., et al. (2018). Sabatier principle for interfacial (Heterogeneous) enzyme catalysis. ACS Catal. 8, 11966–11972. doi: 10.1021/acscatal.8b03547

CrossRef Full Text | Google Scholar

Karlsson, R. K., and Cornell, A. (2016). Selectivity between oxygen and chlorine evolution in the chlor-alkali and chlorate processes. Chem. Rev. 116, 2982–3028. doi: 10.1021/acs.chemrev.5b00389

PubMed Abstract | CrossRef Full Text | Google Scholar

Kastlunger, G., Lindgren, P., and Peterson, A. A. (2018). Controlled-potential simulation of elementary electrochemical reactions: proton discharge on metal surfaces. J. Phys. Chem. C 122, 12771–12781. doi: 10.1021/acs.jpcc.8b02465

CrossRef Full Text | Google Scholar

Katsounaros, I., Chen, T., Gewirth, A. A., Markovic, N. M., and Koper, M. T. (2016). Evidence for decoupled electron and proton transfer in the electrochemical oxidation of ammonia on Pt (100). J. Phys. Chem. Lett. 7, 387–392. doi: 10.1021/acs.jpclett.5b02556

PubMed Abstract | CrossRef Full Text | Google Scholar

Kenmoe, S., Lisovski, O., Piskunov, S., Bocharov, D., Zhukovskii, Y. F., and Spohr, E. (2018). Water adsorption on clean and defective anatase Tio2 (001) nanotube surfaces: a surface science approach. J. Phys. Chem. B 122, 5432–5440. doi: 10.1039/C9CP06584A

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, J., Shih, P.-C., Tsao, K.-C., Pan, Y.-T., Yin, X., Sun, C.-J., et al. (2017). High-performance pyrochlore-type yttrium ruthenate electrocatalyst for oxygen evolution reaction in acidic media. J. Am. Chem. Soc. 139, 12076–12083. doi: 10.1021/jacs.7b06808

PubMed Abstract | CrossRef Full Text | Google Scholar

Kjaergaard, C. H., Rossmeisl, J., and Nørskov, J. K. (2010). Enzymatic versus inorganic oxygen reduction catalysts: comparison of the energy levels in a free-energy scheme. Inorg. Chem. 49, 3567–3572. doi: 10.1021/ic900798q

PubMed Abstract | CrossRef Full Text | Google Scholar

Klamt, A., and Schüürmann, G. (1993). COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. II 5, 799–805. doi: 10.1039/P29930000799

CrossRef Full Text | Google Scholar

Koper, M. T. (2011a). Structure sensitivity and nanoscale effects in electrocatalysis. Nanoscale 3, 2054–2073. doi: 10.1039/C0NR00857E

PubMed Abstract | CrossRef Full Text | Google Scholar

Koper, M. T. (2011b). Thermodynamic theory of multi-electron transfer reactions: implications for electrocatalysis. J. Electroanal. Chem. 660, 254–260. doi: 10.1016/j.jelechem.2010.10.004

CrossRef Full Text | Google Scholar

Koper, M. T. (2013a). Analysis of electrocatalytic reaction schemes: distinction between rate-determining and potential-determining steps. J. Solid State Electrochem. 17, 339–344. doi: 10.1007/s10008-012-1918-x

CrossRef Full Text | Google Scholar

Koper, M. T. (2013b). Theory of multiple proton–electron transfer reactions and its implications for electrocatalysis. Chem. Sci. 4, 2710–2723. doi: 10.1039/C3SC50205H

CrossRef Full Text | Google Scholar

Koper, M. T. (2013c). Theory of the transition from sequential to concerted electrochemical proton–electron transfer. Phys. Chem. Chem. Phys. 15, 1399–1407. doi: 10.1039/c2cp42369c

PubMed Abstract | CrossRef Full Text | Google Scholar

Kortlever, R., Balemans, C., Kwon, Y., and Koper, M. T. (2015a). Electrochemical CO2 reduction to formic acid on a Pd-based formic acid oxidation catalyst. Catal. Tod. 244, 58–62. doi: 10.1016/j.cattod.2014.08.001

CrossRef Full Text | Google Scholar

Kortlever, R., Shen, J., Schouten, K. J. P., Calle-Vallejo, F., and Koper, M. T. (2015b). Catalysts and reaction pathways for the electrochemical reduction of carbon dioxide. J. Phys. Chem. Lett. 6, 4073–4082. doi: 10.1021/acs.jpclett.5b01559

PubMed Abstract | CrossRef Full Text | Google Scholar

Kozuch, S. (2012). A refinement of everyday thinking: the energetic span model for kinetic assessment of catalytic cycles. WIRES Comput. Mol. Sci. 2, 795–815. doi: 10.1002/wcms.1100

CrossRef Full Text | Google Scholar

Kozuch, S., and Shaik, S. (2011). How to conceptualize catalytic cycles? The energetic span model. Acc. Chem. Res. 44, 101–110. doi: 10.1021/ar1000956

PubMed Abstract | CrossRef Full Text | Google Scholar

Krishnamurthy, D., Sumaria, V., and Viswanathan, V. (2018). Maximal predictability approach for identifying the right descriptors for electrocatalytic reactions. J. Phys. Chem. Lett. 9, 588–595. doi: 10.1021/acs.jpclett.7b02895

PubMed Abstract | CrossRef Full Text | Google Scholar

Kunimatsu, K., Senzaki, T., Samjeské, G., Tsushima, M., and Osawa, M. (2007). Hydrogen adsorption and hydrogen evolution reaction on a polycrystalline Pt electrode studied by surface-enhanced infrared absorption spectroscopy. Electrochim. Acta 52, 5715–5724. doi: 10.1016/j.electacta.2006.12.007

CrossRef Full Text | Google Scholar

Laursen, A. B., Varela, A. S., Dionigi, F., Fanchiu, H., Miller, C., Trinhammer, O. L., et al. (2012). Electrochemical hydrogen evolution: Sabatier’s principle and the volcano plot. J. Chem. Educ. 89, 1595–1599. doi: 10.1021/ed200818t

CrossRef Full Text | Google Scholar

Ledezma-Yanez, I., Wallace, W. D. Z., Sebastián-Pascual, P., Climent, V., Feliu, J. M., and Koper, M. T. (2017). Interfacial water reorganization as a pH-dependent descriptor of the hydrogen evolution rate on platinum electrodes. Nat. Energ. 2, 1–7. doi: 10.1038/nenergy.2017.31

CrossRef Full Text | Google Scholar

Li, Y., Du, X., Huang, J., Wu, C., Sun, Y., Zou, G., et al. (2019). Recent progress on surface reconstruction of earth-abundant electrocatalysts for water oxidation. Small 15:1901980. doi: 10.1002/smll.201901980

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., and Sun, Q. (2016). Recent advances in breaking scaling relations for effective electrochemical conversion of CO2. Adv. Energ. Mater. 6:1600463. doi: 10.1021/jp077210j

CrossRef Full Text | Google Scholar

Li, Z., Achenie, L. E., and Xin, H. (2020). An adaptive machine learning strategy for accelerating discovery of perovskite electrocatalysts. ACS Catal. 10, 4377–4384. doi: 10.1021/acscatal.9b05248

CrossRef Full Text | Google Scholar

Lindgren, P., Kastlunger, G., and Peterson, A. A. (2020). A challenge to the G ∼0 interpretation of hydrogen evolution. ACS Catal. 10, 121–128. doi: 10.1021/acscatal.9b02799

CrossRef Full Text | Google Scholar

Louch, D. S., and Pritzker, M. D. (1993). Transport to rough electrode surfaces: part 2: perturbation solution for two-dimensional steady state transport to an arbitrary surface under mixed diffusion-kinetic control. J. Electroanal. Chem. 346, 211–237. doi: 10.1016/0022-0728(93)85014-8

CrossRef Full Text | Google Scholar

Lum, Y., and Ager, J. W. (2018). Sequential catalysis controls selectivity in electrochemical CO2 reduction on Cu. Energ. Environ. Sci. 11, 2935–2944. doi: 10.1039/C8EE01501E

CrossRef Full Text | Google Scholar

Man, I. C., Su, H.-Y., Calle-Vallejo, F., Hansen, H. A., Martinez, J. I., Inoglu, N. G., et al. (2011). Universality in oxygen evolution electrocatalysis on oxide surfaces. ChemCatChem 3, 1159–1165. doi: 10.1002/cctc.201000397

CrossRef Full Text | Google Scholar

Marshall, A. T., and Vaisson-Béthune, L. (2015). Avoid the quasi-equilibrium assumption when evaluating the electrocatalytic oxygen evolution reaction mechanism by tafel slope analysis. Electrochem. Commun. 61, 23–26. doi: 10.1016/j.elecom.2015.09.019

CrossRef Full Text | Google Scholar

Martnez-Hincapié, R., Climent, V., and Feliu, J. M. (2018). Peroxodisulfate reduction as a probe to interfacial charge. Electrochem. Commun. 88, 43–46. doi: 10.1016/j.elecom.2018.01.012

CrossRef Full Text | Google Scholar

Mathew, K., Kolluru, V. C., Mula, S., Steinmann, S. N., and Hennig, R. G. (2019). Implicit self-consistent electrolyte model in plane-wave density-functional theory. J. Chem. Phys. 151:234101. doi: 10.1063/1.5132354

CrossRef Full Text | Google Scholar

Mathew, K., Sundararaman, R., Letchworth-Weaver, K., Arias, T., and Hennig, R. G. (2014). Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways. J. Chem. Phys. 140:084106. doi: 10.1063/1.4865107

CrossRef Full Text | Google Scholar

Mefford, J. T., Zhao, Z., Bajdich, M., and Chueh, W. C. (2020). Interpreting Tafel behavior of consecutive electrochemical reactions through combined thermodynamic and steady state microkinetic approaches. Energ. Environ. Sci. 13, 622–634. doi: 10.1039/C9EE02697E

CrossRef Full Text | Google Scholar

Mehta, V., and Cooper, J. S. (2003). Review and analysis of PEM fuel cell design and manufacturing. J. Power Sources 114, 32–53. doi: 10.1016/S0378-7753(02)00542-6

CrossRef Full Text | Google Scholar

Murata, A., and Hori, Y. (1991). Product selectivity affected by cationic species in electrochemical reduction of CO2 and CO at a Cu electrode. Bull. Chem. Soc. Jpn. 64, 123–127. doi: 10.1246/bcsj.64.123

PubMed Abstract | CrossRef Full Text | Google Scholar

Nørskov, J. K., Bligaard, T., Logadottir, A., Kitchin, J., Chen, J. G., Pandelov, S., et al. (2005). Trends in the exchange current for hydrogen evolution. J. Electrochem. Soc. 152:J23. doi: 10.1149/1.1856988

CrossRef Full Text | Google Scholar

Nørskov, J. K., Bligaard, T., Rossmeisl, J., and Christensen, C. H. (2009). Towards the computational design of solid catalysts. Nat. Chem. 1, 37–46. doi: 10.1038/nchem.121

PubMed Abstract | CrossRef Full Text | Google Scholar

Nørskov, J. K., Rossmeisl, J., Logadottir, A., Lindqvist, L., Kitchin, J. R., Bligaard, T., et al. (2004). Origin of the overpotential for oxygen reduction at a fuel-cell cathode. J. Phys. Chem. B 108, 17886–17892. doi: 10.1021/jp047349j

CrossRef Full Text | Google Scholar

Ooka, H., Figueiredo, M. C., and Koper, M. T. (2017). Competition between hydrogen evolution and carbon dioxide reduction on copper electrodes in mildly acidic media. Langmuir 33, 9307–9313. doi: 10.1021/acs.langmuir.7b00696

PubMed Abstract | CrossRef Full Text | Google Scholar

Ooka, H., and Nakamura, R. (2019). Shift of the optimum binding energy at higher rates of catalysis. J. Phys. Chem. Lett. 10, 6706–6713. doi: 10.1021/acs.jpclett.9b01796

PubMed Abstract | CrossRef Full Text | Google Scholar

Pajkossy, T., and Nyikos, L. (1989). Diffusion to fractal surfaces? II. Verification of theory. Electrochim. Acta 34, 171–179. doi: 10.1016/0013-4686(89)87082-3

CrossRef Full Text | Google Scholar

Pande, V., and Viswanathan, V. (2019). Computational screening of current collectors for enabling anode-free lithium metal batteries. ACS Energy Lett. 4, 2952–2959. doi: 10.1021/acsenergylett.9b02306

CrossRef Full Text | Google Scholar

Parada, G. A., Goldsmith, Z. K., Kolmar, S., Rimgard, B. P., Mercado, B. Q., Hammarström, L., et al. (2019). Concerted proton-electron transfer reactions in the marcus inverted region. Science 364, 471–475. doi: 10.1126/science.aaw4675

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, S., Lee, J.-W., and Popov, B. N. (2012). A review of gas diffusion layer in PEM fuel cells: materials and designs. Int. J. Hyd. Energ. 37, 5850–5865. doi: 10.1016/j.ijhydene.2011.12.148

CrossRef Full Text | Google Scholar

Parsons, R. (1951). General equations for the kinetics of electrode processes. Trans. Faraday Soc. 47, 1332–1344. doi: 10.1039/TF9514701332

CrossRef Full Text | Google Scholar

Parsons, R. (1958). The rate of electrolytic hydrogen evolution and the heat of adsorption of hydrogen. Trans. Faraday Soc. 54, 1053–1063. doi: 10.1039/TF9585401053

CrossRef Full Text | Google Scholar

Pegis, M. L., Wise, C. F., Koronkiewicz, B., and Mayer, J. M. (2017). Identifying and breaking scaling relations in molecular catalysis of electrochemical reactions. J. Am. Chem. Soc. 139, 11000–11003. doi: 10.1021/jacs.7b05642

PubMed Abstract | CrossRef Full Text | Google Scholar

Pérez-Gallent, E., Marcandalli, G., Figueiredo, M. C., Calle-Vallejo, F., and Koper, M. T. (2017). Structure-and potential-dependent cation effects on CO reduction at copper single-crystal electrodes. J. Am. Chem. Soc. 139, 16412–16419. doi: 10.1021/jacs.7b10142

PubMed Abstract | CrossRef Full Text | Google Scholar

Peterson, A. A., and Nørskov, J. K. (2012). Activity descriptors for CO2 electroreduction to methane on transition-metal catalysts. J. Phys. Chem. Lett. 3, 251–258. doi: 10.1021/jz201461p

CrossRef Full Text | Google Scholar

Piqué, O., Illas, F., and Calle-Vallejo, F. (2020). Designing water splitting catalysts using rules of thumb: advantages, dangers and alternatives. Phys. Chem. Chem. Phys. 22, 6797–6803. doi: 10.1039/D0CP00896F

PubMed Abstract | CrossRef Full Text | Google Scholar

Retuerto, M., Pascual, L., Calle-Vallejo, F., Ferrer, P., Gianolio, D., Pereira, A. G., et al. (2019). Na-doped ruthenium perovskite electrocatalysts with improved oxygen evolution activity and durability in acidic media. Nat. Commun. 10, 1–9. doi: 10.1038/s41467-019-09791-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Ringe, S., Clark, E. L., Resasco, J., Walton, A., Seger, B., Bell, A. T., et al. (2019). Understanding cation effects in electrochemical CO2 reduction. Energ. Environ. Sci. 12, 3001–3014. doi: 10.1039/C9EE01341E

CrossRef Full Text | Google Scholar

Ringe, S., Morales-Guio, C. G., Chen, L. D., Fields, M., Jaramillo, T. F., Hahn, C., et al. (2020). Double layer charging driven carbon dioxide adsorption limits the rate of electrochemical carbon dioxide reduction on gold. Nat. Commun. 11, 1–11. doi: 10.1038/s41467-019-13777-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Rodriguez, P., and Koper, M. T. (2014). Electrocatalysis on gold. Phys. Chem. Chem. Phys. 16, 13583–13594. doi: 10.1039/C4CP00394B

PubMed Abstract | CrossRef Full Text | Google Scholar

Rojas-Carbonell, S., Artyushkova, K., Serov, A., Santoro, C., Matanovic, I., and Atanassov, P. (2018). Effect of pH on the activity of platinum group metal-free catalysts in oxygen reduction reaction. ACS Catal. 8, 3041–3053. doi: 10.1021/acscatal.7b03991

CrossRef Full Text | Google Scholar

Rootsaert, W., and Sachtler, W. (1960). Interaction of formic acid vapour with tungsten. Z. Phys. Chem. 26, 16–26. doi: 10.1524/zpch.1960.26.1_2.016

CrossRef Full Text | Google Scholar

Rossmeisl, J., Dimitrievski, K., Siegbahn, P., and Nørskov, J. K. (2007a). Comparing electrochemical and biological water splitting. J. Phys. Chem. C 111, 18821–18823.

Google Scholar

Rossmeisl, J., Logadottir, A., and Nørskov, J. K. (2005). Electrolysis of water on (Oxidized) metal surfaces. Chem. Phys. 319, 178–184. doi: 10.1016/j.chemphys.2005.05.038

CrossRef Full Text | Google Scholar

Rossmeisl, J., Qu, Z.-W., Zhu, H., Kroes, G.-J., and Nørskov, J. K. (2007b). Electrolysis of water on oxide surfaces. J. Electroanal. Chem. 607, 83–89. doi: 10.1016/j.jelechem.2006.11.008

CrossRef Full Text | Google Scholar

Sabatier, P. (1913). La Catalyse en Chimie Organique, Encyclopédie de Science Chimique Appliquée. Dunham, QC: Ch. Béranger.

Google Scholar

Sakaushi, K., Kumeda, T., Hammes-Schiffer, S., Melander, M. M., and Sugino, O. (2020). Advances and challenges for experiment and theory for multi-electron multi-proton transfer at electrified solid–liquid interfaces. Phys. Chem. Chem. Phys. 22, 19401–19442. doi: 10.1039/D0CP02741C

PubMed Abstract | CrossRef Full Text | Google Scholar

Sakong, S., and Groß, A. (2020). Water structures on a Pt (111) electrode from Ab initio molecular dynamic simulations for a variety of electrochemical conditions. Phys. Chem. Chem. Phys. 22, 10431–10437.

Google Scholar

Saveleva, V. A., Wang, L., Teschner, D., Jones, T., Gago, A. S., Friedrich, K. A., et al. (2018). Operando evidence for a universal oxygen evolution mechanism on thermal and electrochemical iridium oxides. J. Phys. Chem. Lett. 9, 3154–3160. doi: 10.1021/acs.jpclett.8b00810

PubMed Abstract | CrossRef Full Text | Google Scholar

Sayfutyarova, E. R., and Hammes-Schiffer, S. (2020). Excited state molecular dynamics of photoinduced proton-coupled electron transfer in anthracene–phenol–pyridine triads. J. Phys. Chem. Lett. 11, 7109–7115. doi: 10.1021/acs.jpclett.0c02012

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmickler, W., and Santos, E. (2010). Interfacial Electrochemistry. Berlin: Springer Science & Business Media.

Google Scholar

Schouten, K. J. P., Gallent, E. P., and Koper, M. T. (2014). The influence of pH on the reduction of CO and CO2 to hydrocarbons on copper electrodes. J. Electroanal. Chem. 716, 53–57. doi: 10.1016/j.jelechem.2013.08.033

CrossRef Full Text | Google Scholar

Seitz, L. C., Dickens, C. F., Nishio, K., Hikita, Y., Montoya, J., Doyle, A., et al. (2016). A highly active and stable IrOx/SrIrO3 catalyst for the oxygen evolution reaction. Science 353, 1011–1014. doi: 10.1126/science.aaf5050

PubMed Abstract | CrossRef Full Text | Google Scholar

Sheng, W., Gasteiger, H. A., and Shao-Horn, Y. (2010). Hydrogen oxidation and evolution reaction kinetics on platinum: acid Vs Alkaline electrolytes. J. Electrochem. Soc. 157:B1529. doi: 10.1149/1.3483106

CrossRef Full Text | Google Scholar

Sheng, W., Zhuang, Z., Gao, M., Zheng, J., Chen, J. G., and Yan, Y. (2015). Correlating hydrogen oxidation and evolution activity on platinum at different pH with measured hydrogen binding energy. Nat. Commun. 6, 1–6. doi: 10.1038/ncomms6848

PubMed Abstract | CrossRef Full Text | Google Scholar

Shetty, M., Walton, A., Gathmann, S. R., Ardagh, M. A., Gopeesingh, J., Resasco, J., et al. (2020). The catalytic mechanics of dynamic surfaces: stimulating methods for promoting catalytic resonance. ACS Catal. 10, 12666–12695. doi: 10.1021/acscatal.0c03336

CrossRef Full Text | Google Scholar

Shinagawa, T., Garcia-Esparza, A. T., and Takanabe, K. (2015). Insight on tafel slopes from a microkinetic analysis of aqueous electrocatalysis for energy conversion. Sci. Rep. 5:13801. doi: 10.1038/srep138012015

CrossRef Full Text | Google Scholar

Shinagawa, T., Obata, K., and Takanabe, K. (2019). Switching of kinetically relevant reactants for the aqueous cathodic process determined by mass-transport coupled with protolysis. ChemCatChem 11, 5961–5968. doi: 10.1002/cctc.201901459

CrossRef Full Text | Google Scholar

Skúlason, E., Tripkovic, V., Björketun, M. E., Gudmundsdottir, S., Karlberg, G., Rossmeisl, J., et al. (2010). Modeling the electrochemical hydrogen oxidation and evolution reactions on the basis of density functional theory calculations. J. Phys. Chem. C 114, 18182–18197. doi: 10.1021/jp1048887

CrossRef Full Text | Google Scholar

Smith, C., Hill, A. K., and Torrente-Murciano, L. (2020). Current and future role of haber–bosch ammonia in a carbon-free energy landscape. Energ. Environ. Sci. 13, 331–344. doi: 10.1039/C9EE02873K

CrossRef Full Text | Google Scholar

Song, J., Wei, C., Huang, Z.-F., Liu, C., Zeng, L., Wang, X., et al. (2020). A review on fundamentals for designing oxygen evolution electrocatalysts. Chem. Soc. Rev. 49, 2196–2214. doi: 10.1039/C9CS00607A

PubMed Abstract | CrossRef Full Text | Google Scholar

Su, J., Ge, R., Jiang, K., Dong, Y., Hao, F., Tian, Z., et al. (2018). Assembling ultrasmall copper-doped ruthenium oxide nanocrystals into hollow porous polyhedra: highly robust electrocatalysts for oxygen evolution in acidic media. Adv. Mater. 30:1801351. doi: 10.1002/adma.201801351

PubMed Abstract | CrossRef Full Text | Google Scholar

Sumaria, V., Krishnamurthy, D., and Viswanathan, V. (2018). Quantifying confidence in DFT predicted surface pourbaix diagrams and associated reaction pathways for chlorine evolution. ACS Catal. 8, 9034–9042. doi: 10.1021/acscatal.8b01432

CrossRef Full Text | Google Scholar

Suntivich, J., Gasteiger, H. A., Yabuuchi, N., Nakanishi, H., Goodenough, J. B., and Shao-Horn, Y. (2011a). Design principles for oxygen-reduction activity on perovskite oxide catalysts for fuel cells and metal–air batteries. Nat. Chem. 3, 546–550. doi: 10.1038/nchem.1069

PubMed Abstract | CrossRef Full Text | Google Scholar

Suntivich, J., May, K. J., Gasteiger, H. A., Goodenough, J. B., and Shao-Horn, Y. (2011b). A perovskite oxide optimized for oxygen evolution catalysis from molecular orbital principles. Science 334, 1383–1385. doi: 10.1126/science.1212858

PubMed Abstract | CrossRef Full Text | Google Scholar

Tahir, M., Pan, L., Idrees, F., Zhang, X., Wang, L., Zou, J.-J., et al. (2017). Electrocatalytic oxygen evolution reaction for energy conversion and storage: a comprehensive review. Nano Energ. 37, 136–157. doi: 10.1016/j.nanoen.2017.05.022

CrossRef Full Text | Google Scholar

Tang, Q., and Jiang, D.-E. (2016). Mechanism of hydrogen evolution reaction on 1T-MoS2 from first principles. ACS Catal. 6, 4953–4961. doi: 10.1021/acscatal.6b01211

CrossRef Full Text | Google Scholar

Tao, H. B., Zhang, J., Chen, J., Zhang, L., Xu, Y., Chen, J. G., et al. (2019). Revealing energetics of surface oxygen redox from kinetic fingerprint in oxygen electrocatalysis. J. Am. Chem. Soc. 141, 13803–13811. doi: 10.1021/jacs.9b01834

PubMed Abstract | CrossRef Full Text | Google Scholar

Theerthagiri, J., Lee, S. J., Murthy, A. P., Madhavan, J., and Choi, M. Y. (2020). Fundamental aspects and recent advances in transition metal nitrides as electrocatalysts for hydrogen evolution reaction: a review. Curr. Opin. Solid State Mater. Sci. 24:100805. doi: 10.1016/j.cossms.2020.100805

CrossRef Full Text | Google Scholar

Tichter, T., Schneider, J., and Roth, C. (2020). Finite heterogeneous rate constants for the electrochemical oxidation of Vo2+ at glassy carbon electrodes. Front. Energ. Res. 8:155. doi: 10.3389/fenrg.2020.00155

CrossRef Full Text | Google Scholar

Toyao, T., Maeno, Z., Takakusagi, S., Kamachi, T., Takigawa, I., and Shimizu, K. (2020). Machine learning for catalysis informatics: recent applications and prospects. ACS Catal. 10, 2260–2297. doi: 10.1021/acscatal.9b04186

CrossRef Full Text | Google Scholar

Trasatti, S. (1972). Work function, electronegativity, and electrochemical behaviour of metals: III. Electrolytic hydrogen evolution in acid solutions. J. Electroanal. Chem. Interfacial Electrochem. 39, 163–184. doi: 10.1016/S0022-0728(72)80485-6

CrossRef Full Text | Google Scholar

Trasatti, S. (1987). Progress in the understanding of the mechanism of chlorine evolution at oxide electrodes. Electrochim. Acta 32, 369–382. doi: 10.1016/0013-4686(87)85001-6

CrossRef Full Text | Google Scholar

Ulissi, Z. W., Singh, A. R., Tsai, C., and Nørskov, J. K. (2016). Automated discovery and construction of surface phase diagrams using machine learning. J. Phys. Chem. Lett. 7, 3931–3935. doi: 10.1021/acs.jpclett.6b01254

PubMed Abstract | CrossRef Full Text | Google Scholar

Ulissi, Z. W., Tang, M. T., Xiao, J., Liu, X., Torelli, D. A., Karamad, M., et al. (2017). Machine-learning methods enable exhaustive searches for active bimetallic facets and reveal active site motifs for CO2 reduction. ACS Catal. 7, 6600–6608. doi: 10.1021/acscatal.7b01648

CrossRef Full Text | Google Scholar

Van Santen, R. A., Neurock, M., and Shetty, S. G. (2009). Reactivity theory of transition-metal surfaces: a Brønsted- evans- polanyi linear activation energy- free-energy analysis. Chem. Rev. 110, 2005–2048. doi: 10.1021/cr9001808

PubMed Abstract | CrossRef Full Text | Google Scholar

Varela, A. S., Ju, W., Reier, T., and Strasser, P. (2016). Tuning the catalytic activity and selectivity of Cu for CO2 electroreduction in the presence of halides. ACS Catal. 6, 2136–2144. doi: 10.1021/acscatal.5b02550

CrossRef Full Text | Google Scholar

Vinogradova, O., Krishnamurthy, D., Pande, V., and Viswanathan, V. (2018). Quantifying confidence in DFT-predicted surface pourbaix diagrams of transition-metal electrode–electrolyte interfaces. Langmuir 34, 12259–12269. doi: 10.1021/acs.langmuir.8b02219

PubMed Abstract | CrossRef Full Text | Google Scholar

Viswanathan, V., and Hansen, H. A. (2014). Unifying solution and surface electrochemistry: limitations and opportunities in surface electrocatalysis. Top. Catal. 57, 215–221. doi: 10.1007/s11244-013-0171-6

CrossRef Full Text | Google Scholar

Viswanathan, V., Hansen, H. A., Rossmeisl, J., and Nørskov, J. K. (2012). Universality in oxygen reduction electrocatalysis on metal surfaces. ACS Catal. 2, 1654–1660. doi: 10.1021/cs300227s

CrossRef Full Text | Google Scholar

Vos, J. G., Wezendonk, T. A., Jeremiasse, A. W., and Koper, M. T. (2018). MnOx/IrOx as selective oxygen evolution electrocatalyst in acidic chloride solution. J. Am. Chem. Soc. 140, 10270–10281. doi: 10.1021/jacs.8b05382

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J. X., Uribe, F. A., Springer, T. E., Zhang, J., and Adzic, R. R. (2009). Intrinsic kinetic equation for oxygen reduction reaction in acidic media: the double tafel slope and fuel cell applications. Faraday Disc. 140, 347–362. doi: 10.1039/B802218F

PubMed Abstract | CrossRef Full Text | Google Scholar

Warburton, R. E., Hutchison, P., Jackson, M. N., Pegis, M. L., Surendranath, Y., and Hammes-Schiffer, S. (2020). Interfacial field-driven proton-coupled electron transfer at graphite-conjugated organic acids. J. Am. Chem. Soc. 142, 20855–20864. doi: 10.1021/jacs.0c10632

PubMed Abstract | CrossRef Full Text | Google Scholar

Warren, J. J., Tronic, T. A., and Mayer, J. M. (2010). Thermochemistry of proton-coupled electron transfer reagents and its implications. Chem. Rev. 110, 6961–7001. doi: 10.1021/cr100085k

PubMed Abstract | CrossRef Full Text | Google Scholar

Wintrich, D., Öhl, D., Barwe, S., Ganassin, A., Möller, S., Tarnev, T., et al. (2019). Enhancing the selectivity between oxygen and chlorine towards chlorine during the anodic chlorine evolution reaction on a dimensionally stable anode. ChemElectroChem 6, 3108–3112. doi: 10.1002/celc.201900784

CrossRef Full Text | Google Scholar

Wodrich, M. D., Sawatlon, B., Busch, M., and Corminboeuf, C. (2018). On the generality of molecular volcano plots. ChemCatChem 10, 1586–1591. doi: 10.1002/cctc.201701709

CrossRef Full Text | Google Scholar

Wuttig, A., Yaguchi, M., Motobayashi, K., Osawa, M., and Surendranath, Y. (2016). Inhibited proton transfer enhances Au-catalyzed CO2-to-fuels selectivity. Proc. Natl. Acad. Sci. U.S.A. 113, E4585–E4593. doi: 10.1073/pnas.1602984113

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiao, P., Chen, W., and Wang, X. (2015). A review of phosphide-based materials for electrocatalytic hydrogen evolution. Adv. Energ. Mater. 5:1500985. doi: 10.1002/aenm.201500985

CrossRef Full Text | Google Scholar

Xie, C., Wang, Y., Yan, D., Tao, L., and Wang, S. (2017). In situ growth of cobalt at cobalt-borate core–shell nanosheets as highly-efficient electrocatalysts for oxygen evolution reaction in alkaline/neutral medium. Nanoscale 9, 16059–16065. doi: 10.1039/C7NR06054H

PubMed Abstract | CrossRef Full Text | Google Scholar

Xue, S., Garlyyev, B., Watzele, S., Liang, Y., Fichtner, J., Pohl, M. D., et al. (2018). Influence of alkali metal cations on the hydrogen evolution reaction activity of Pt, Ir, Au, and Ag electrodes in alkaline electrolytes. ChemElectroChem 5, 2326–2329. doi: 10.1002/celc.201800690

CrossRef Full Text | Google Scholar

Yang, T., Zhou, J., Song, T. T., Shen, L., Feng, Y. P., and Yang, M. (2020). High-throughput identification of exfoliable two-dimensional materials with active basal planes for hydrogen evolution. ACS Energy Lett. 5, 2313–2321. doi: 10.1021/acsenergylett.0c00957

CrossRef Full Text | Google Scholar

Yao, S., Zhang, X., Chen, A., Zhang, Z., Jiao, M., and Zhou, Z. (2019). Algorithm screening to accelerate discovery of 2d metal-free electrocatalysts for hydrogen evolution reaction. J. Mat. Chem. A 7, 19290–19296. doi: 10.1039/C9TA06286F

CrossRef Full Text | Google Scholar

Zeradjanin, A. R., Grote, J.-P., Polymeros, G., and Mayrhofer, K. J. (2016). A critical review on hydrogen evolution electrocatalysis: re-exploring the volcano-relationship. Electroanalysis 28, 2256–2269. doi: 10.1002/elan.201600270

CrossRef Full Text | Google Scholar

Zhang, J., Tao, H. B., Kuang, M., Yang, H. B., Cai, W., Yan, Q., et al. (2020). Advances in thermodynamic-kinetic model for analyzing the oxygen evolution reaction. ACS Catal. 10, 8597–8610. doi: 10.1021/acscatal.0c01906

CrossRef Full Text | Google Scholar

Zhang, L., and Huang, J. (2020). Understanding surface charge effects in electrocatalysis. Part I: peroxodisulfate reduction at Pt (111). J. Phys. Chem. C 124, 16951–16960. doi: 10.1021/acs.jpcc.0c02824

CrossRef Full Text | Google Scholar

Zhang, W., Hu, Y., Ma, L., Zhu, G., Wang, Y., Xue, X., et al. (2018). Progress and perspective of electrocatalytic CO2 reduction for renewable carbonaceous fuels and chemicals. Adv. Sci. 5:1700275. doi: 10.1002/advs.201700275

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Zhang, J., and Huang, J. (2019). Potential-dependent volcano plot for oxygen reduction: mathematical origin and implications for catalyst design. J. Phys. Chem. Lett. 10, 7037–7043.

Google Scholar

Zhang, Y.-J., Sethuraman, V., Michalsky, R., and Peterson, A. A. (2014). Competition between CO2 reduction and H2 evolution on transition-metal electrocatalysts. ACS Catal. 4, 3742–3748. doi: 10.1021/cs5012298

CrossRef Full Text | Google Scholar

Zheng, J., Sheng, W., Zhuang, Z., Xu, B., and Yan, Y. (2016). Universal dependence of hydrogen oxidation and evolution reaction activity of platinum-group metals on pH and hydrogen binding energy. Sci. Adv. 2:e1501602. doi: 10.1021/jacs.0c01104

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, D., Wei, J., He, Z.-D., Xu, M.-L., Chen, Y., and Huang, J. (2020). Combining single crystal experiments and microkinetic modeling in disentangling thermodynamic, kinetic and double-layer factors influencing oxygen reduction. J. Phys. Chem. C 124, 13672–13678. doi: 10.1021/acs.jpcc.0c01621

CrossRef Full Text | Google Scholar

Zhu, S., Qin, X., Yao, Y., and Shao, M. (2020). pH-dependent hydrogen and water binding energies on platinum surfaces as directly probed through surface-enhanced infrared absorption spectroscopy. J. Am. Chem. Soc. 142, 8748–8754.

Google Scholar

Zhu, X., and Huang, J. (2019). Modeling electrocatalytic oxidation of formic acid at platinum. J. Electrochem. Soc. 167:013515. doi: 10.1149/2.0152001JES

CrossRef Full Text | Google Scholar