- 1Department of Electric Power Engineering, Norwegian University of Science and Technology, Trondheim, Norway
- 2Department of Industrial Engineering, University of Trento, Trento, Italy
The exponential rise of renewable energy sources and microgrids brings about the challenge of guaranteeing frequency stability in low-inertia grids through the use of energy storage systems. This paper reviews the frequency response of an ac power system, highlighting its different time scales and control actions. Moreover, it pinpoints main distinctions among high-inertia interconnected systems relying on synchronous machines and low-inertia systems with high penetration of converter-interfaced generation. Grounded on these concepts and with a set of assumptions, it derives algebraic equations to rate an energy storage system providing inertial and primary control. The equations are independent of the energy storage technology, robust to system nonlinearities, and rely on parameters that are typically defined by system operators, industry standards, or network codes. Using these results, the authors provide a step-by-step procedure to size the main components of a converter-interfaced hybrid energy storage system. Finally, a case study of a wind-powered oil and gas platform in the North Sea demonstrates with numerical examples how the proposed methodology 1) can be applied in a practical problem and 2) allows the system designer to take advantage of different technologies and set specific requirements for each storage device and converter according to the type of frequency control provided.
1 Introduction
Planning, design, and operation of ac power systems (ACPSs) are becoming more involved. For instance, conversion from primary sources and storage is performed using not only synchronous machines (SMs) but also converter-interfaced generators (CIGs). Moreover, groups of interconnected loads and distributed energy resources, also known as microgrids (MGs) (IEEE, 2018a; IEEE, 2018b), can form islands and operate independently from the interconnected power system.
From this perspective, energy storage systems (ESSs) can help to balance demand and supply and control frequency, voltage, and power flows in isolated power systems or MGs operating in islanded mode. These features increase not only the stability and security of the system but also its efficiency and asset utilization (Fu et al., 2013; Strbac et al., 2015). Nonetheless, these desired features can be achieved only with the proper sizing of ESSs.
In particular, sizing the components of a converter-interfaced ESS is one of the main challenges in MGs and large ACPSs with high penetration of CIGs, the main reason being the trade-off among key technical characteristics in storage solutions, where no single technology stands out (Koohi-Kamali et al., 2013; Farhadi and Mohammed, 2016; Gallo et al., 2016). For instance, ultracapacitors and flywheels are appropriate for inertia simulation as they offer high power density and efficiency. However, their low energy density and high cost per kWh make them unsuitable for primary and secondary control. Further examples are the several types of batteries and fuel cell technologies. These solutions are well-suited for secondary control because they offer reasonable power and energy densities and cost per kWh. Nevertheless, their lifetime can be extremely reduced if applied in inertia simulation and primary control due to the abrupt current changes and number of charge and discharge cycles required. In summary, there is no one-size-fits-all technology for ESSs, so hybrid solutions are currently becoming the preferred choice not only in transportation but also in ACPS applications (Hemmati and Saboori, 2016).
When considering all that, sizing an ESS to provide inertial and primary frequency control becomes an intricate task. Many researchers have been devoting time to untangle this problem. For MGs, Aghamohammadi and Abdolahinia (2014) optimally sized a battery ESS for primary frequency control considering overloading characteristics and limitation of the state of charge. For that, the authors proposed an iterative procedure based on time-domain simulations that considers the battery permissible overload coefficient and duration. Bijaieh et al. (2020a) and Bijaieh et al. (2020b) presented a control-based approach applying the Hamiltonian surface shaping and power flow control to size the ESS and to address how communication and controller bandwidth can affect the sizing and filtering requirements. For large ACPSs with high penetration of CIGs, Knap et al. (2016) introduced a methodology to size ESSs for the provision of inertial response and primary frequency regulation. In this work, a linearized version of the swing equation was applied to determine the ESS rated power and energy capacity, and it was shown that this converter-interfaced system can achieve similar performance to a conventional peak power plant. Sandelic et al. (2018) focused on primary control and proposed a broader three-stage methodology, which evaluates not only the battery dynamic response and provision of frequency reserves but also the lifetime and economic assessment.
From a system operator or developer point of view, the main limitations in these previous works are the following: 1) the extensive use of time-domain simulations to support their sizing methodology, 2) the assumption that the required ESS technology and model parameters are well-known beforehand, and 3) the linearization of the swing equation to study the frequency-control problem.
For the first limitation, it must be noted that defining the rated active power and energy capacity of an ESS is a multi-stage process involving a techno-economical evaluation as emphasized by Sandelic et al. (2018) and Riboldi et al. (2021). Hence, the analysis of the ESS dynamic response is only one step of the problem, which requires integration into a broad optimization involving several time scales. Nonetheless, an inspection of recent literature reviews on ac MG planning (Gamarra and Guerrero, 2015; Al-Jaafreh and Mokryani, 2019) reveals that conditions for frequency stability are largely overlooked in the problem formulation, and most optimization algorithms consider that matching power demand with generation is the only required dynamic constraint, without imposing minimum requirements on system damping or frequency reserves. This is typically justified by the argument that frequency stability analysis in ACPSs requires computationally demanding simulation models that can turn the optimization into an intractable problem. Therefore, ESS sizing models should be efficient and, if possible, algebraic to be directly incorporated as constraints in larger optimization algorithms.
For the second limitation, system operators of ACPSs are fundamentally interested in specifying the minimum equivalent inertia, damping, deadband, and time delay of equipment supplying inertial response and primary frequency regulation (Duckwitz, 2019). Indeed, in many regulated ACPSs, such as transmission and distribution grids, system operators avoid requiring specific technologies and prefer to limit specifications to functionalities to be provided (ENTSO-E, 2019). For instance, Chang et al. (2013) solved the unit commitment problem for an islanded ACPS with high penetration of CIGs including constraints on frequency reserves using mixed-integer linear programming. For that, the authors determined the minimum system damping empirically relying on the load-frequency sensitivity index. Moreover, frequency stability constraints have also been proposed in planning and operation studies of large ACPSs, such as optimal power flow problems, by Wen et al. (2016); Abhyankar et al. (2017); Geng et al. (2017); and Nguyen et al. (2019).
For the third limitation, it is reported in the literature that the linearized swing equation may underestimate frequency variations during transients (Caliskan and Tabuada, 2015) and, as a consequence, the required damping of an ACPS (Alves et al., 2020). Accordingly, a certain level of robustness must be considered when sizing an ESS to account for nonlinear effects, especially in low-inertia systems.
Considering this context, the contributions of this work are threefold: 1) It offers an updated literature review of the frequency response of ACPSs, highlighting the different time scales of the frequency-control problem and the main distinctions among traditional systems, MGs and large systems with high penetration of CIGs. 2) Based on the type of frequency control being supplied by a converter-interfaced ESS, it proposes an algebraic method to calculate the rated energy of its energy storage (ES) devices and the rated power of its converters. The proposed method is robust to system nonlinearities and based on parameters typically defined by system operators, industry standards, or network codes. 3) It provides a step-by-step systematic procedure to size the main components of hybrid ESSs independently from the technologies used in the ES devices and requiring knowledge of few ACPS parameters.
2 Materials and Methods
2.1 Frequency Control in ac Power Systems
The principles of frequency control in ACPSs can be understood by analyzing a simplified model of a flywheel spinning at a rated angular frequency
Equation 1 is obtained by applying Newton’s second law of motion to this simplified flywheel model. The moment of inertia
The representation of an ACPS as an equivalent rotating mass and Eq. 1, also referred to as the swing equation, was already applied in the interwar period by Doherty and Nickle (1927) and reported in many classical power systems books such as Concordia (1951); Grainger and Stevenson (1994); Kimbark (1995); Kundur et al. (1994); and Machowski et al. (2008). Moreover, limitations of this model have been discussed in the last 40 years (Tavora and Smith, 1972; Caliskan and Tabuada, 2015). Mainly, a proper transient analysis of an ACPS must include voltage dynamics, which requires very detailed models and knowledge of the network topology and characteristics, time delays of controllers, and so on (Dörfler and Bullo, 2012). This level of detail is often not available during the planning phases of ACPSs and, still today, the swing equation model is a useful concept to evaluate the frequency response in the early design of a project (Delille et al., 2012; Egido et al., 2015; Riboldi et al., 2020) or in operation planning (Chang et al., 2013; Ahmadi and Ghasemi, 2014; Wen et al., 2016).
It is convenient to normalize and express the balance of torques in Eq. 1 as a balance of power. The normalization starts by dividing Eq. 1 by the rated apparent power of the system
The above equation contains two variables that are not yet normalized, namely, ω and
The dynamics from Eq. 3 is better understood when rearranging it and defining a state centered at the rated angular frequency, i.e.,
When inspecting Eq. 4 and assuming that
In traditional interconnected ACPSs with high inertia
• Inertial control is physically embedded in SMs because their rotors are flywheels providing the inertial effect required to oppose frequency variations. In other words,
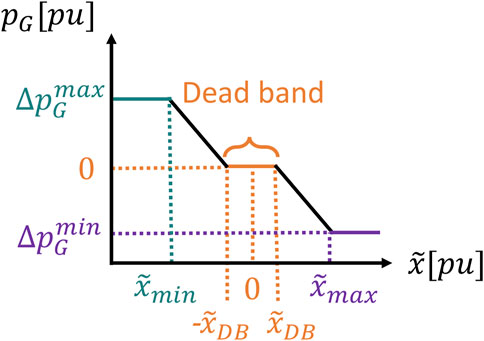
• Primary control is offered by generators or loads sensing frequency deviations from the rated value and automatically adjusting their active power accordingly. This control scheme is known as frequency-droop control (IEEE, 2018a) or frequency sensitivity mode (FSM) (EU Commission Regulation, 2016). The slope of the FSM curve (solid black line) shown in Figure 1 represents the value of
• Secondary control is provided by a central controller typically in a dispatch center and requires communication infrastructure. When a frequency deviation is detected in the system and after a pre-defined time delay, this controller remotely changes the active power setpoint of generators or loads to match the power demand, i.e., make
In MGs and ACPSs with high penetration of CIGs, where inertia may be low (
• Inertial control is usually implemented in grid-forming units (Vandoorn et al., 2013) using virtual inertia emulation (D’Arco and Suul, 2013; Fang et al., 2019). In this case, the value of
• Primary control is provided by grid-forming and grid-following units using the frequency-droop mechanism (Vandoorn et al., 2013) akin to interconnected ACPSs. However, the reaction time is a fraction of a second because the bandwidth of a CIG controller is at least one order of magnitude larger than that of traditional turbine governors and motor drives (Fang et al., 2019).
• Secondary control is provided by grid-following units (Vandoorn et al., 2013). Considering that a MG may contain a large number of small units, manual operation can become unfeasible and automatic dispatch coordinated by a central unit, such as a MG controller, may be necessary. The reaction time of secondary control is typically faster than that in traditional ACPSs, from a couple of minutes in a large system with high penetration of CIGs (ENTSO-E, 2019) to a couple of seconds in a MG (dos Santos Alonso et al., 2019; Brandao et al., 2019).
The dynamic behavior of the average system frequency after an active power imbalance is similar for high- and low-inertia ACPSs, despite their differences, and can be divided in three periods (Eto et al., 2018):
1. Arrest: It starts immediately after the imbalance occurs. If there is lack of generation
2. Rebound: It starts immediately after the nadir/zenith is reached. During this period, the primary control is fully activated and will bring the frequency to a new equilibrium condition. This settling point is below the rated value when
3. Recovery: It starts after the settling point is reached and secondary control is activated. Primary control does not have the capacity to restore the frequency to its rated value after an imbalance. Hence, the system frequency remains at the settling point until the secondary control is activated. In traditional high-inertia systems, the frequency is often restored to its rated value slowly due to practical limitations and to avoid counteraction of inertial control. However, when secondary control is fast, the rebound period can be considerably shortened and even eliminated [i.e.,
Figure 2 illustrates the three control actions and the three periods following a perturbation caused by lack of generation. Even though the three periods following an active power imbalance are similar for both high- and low-inertia ACPSs, their energy management strategies for frequency control may differ considerably.
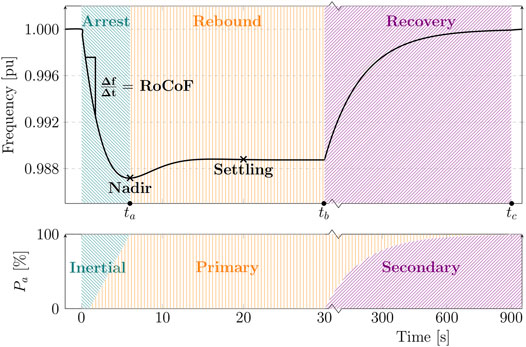
FIGURE 2. Three periods of frequency variation (arrest, rebound, and recovery) and control actions (inertial, primary, and secondary) following a perturbation caused by lack of generation.
During the arrest period, a high-inertia system relies on the rotating masses of SMs as their main energy buffer. In other words, the kinetic energy is drained from or stored into the rotor of SMs limiting the RoCoF and bounding the nadir or zenith. This energy exchange happens “automatically” without any dedicated power or control equipment because the rotor of an SM is electromagnetically coupled to its stator and, hence, the ACPS. For low-inertia systems, on the contrary, the energy buffer formed by rotating masses may not be large enough to guarantee the stable operation after a large power imbalance. In such cases, CIGs must participate as FFRs and support the system by either supplying or absorbing energy during the arrest period. The dc-link capacitor of CIGs could be considered an obvious candidate for storing the additional FFR energy. However, for power systems applications in the MW range, the required capacitance or voltage values become so high such that this solution becomes unfeasible with current technology. Therefore, an additional ESS must be sized specifically for this purpose (Milano et al., 2018).
As mentioned earlier, primary reserves are responsible for bringing the frequency from its extreme values to an acceptable settling point during the rebound phase. In traditional high-inertia systems, some generators are selected to operate with spare up and down power capacity and form FCRs. Commonly, those are dispatchable and fast-acting generating units, such as those in gas and hydropower plants, and have a large energy buffer in the form of chemical or potential energy. However, low-inertia systems may not have the necessary power or energy reserves for primary frequency control. This is because CIGs are typically connected to renewable energy sources operating in maximum power point tracking. Those have no available power up capacity and have limited down capacity. Moreover, as is the case with FFRs, the dc-link capacitor of CIGs is not designed to store the energy amount required by FCRs. In summary, an ESS must be sized to provide the energy and power capacity demanded by FCRs in low-inertia systems.
The main goal of this paper is, thus, establishing a procedure for sizing an ESS’s power and energy capacities according to its expected use (inertial control or FFRs, primary control or FCRs, or both) based on parameters that are 1) typically defined by system operators, industry standards, or network codes, 2) independent of the energy storage technology, and 3) robust to system nonlinearities. It is worth mentioning, though, that sizing the ESS for secondary control or FRRs is outside the scope of this paper. In addition, the procedure presented in the following sections assumes that a thorough stability analysis was carried out beforehand in the ACPS where the ESS will perform frequency control. This stability analysis must include measurement and actuation time delays, nonlinearities and, as a result, select or at least restrict the possible values of M and D. This type of assessment is typically a task of the transmission system operator in large and regulated ACPSs. However, this responsibility might be debatable in smaller and unregulated systems such as MGs. A detailed discussion about this topic is outside the scope of this paper, but it is worth highlighting that if
Additional information about frequency control in high-inertia ACPSs is discussed by Kundur et al. (1994); Machowski et al. (2008); and Sauer et al. (2017). The main characteristics and challenges of low-inertia systems are reviewed by Vandoorn et al. (2013); Eto et al. (2018); Milano et al. (2018); Fang et al. (2019); dos Santos Alonso et al. (2019); and Brandao et al. (2020).
Lastly, tertiary control and generator rescheduling are further alternatives to frequency control. They are long-term, slow-response strategies based on communication infrastructure and/or electricity markets that are outside the scope of this paper. A throughout description of the European approach to these strategies is given by EU Commission Regulation (2015), while the North American approach is summarized by Eto et al. (2018).
2.2 Sizing of the Converter-Interfaced ESS Elements
This section includes the proposed procedure to size the energy capacity of the ES device and the rated power of an ES converter providing inertial or primary frequency control. Based on this initial estimation and selected references from the literature, it describes a methodology to dimension the remaining ESS power unit components.
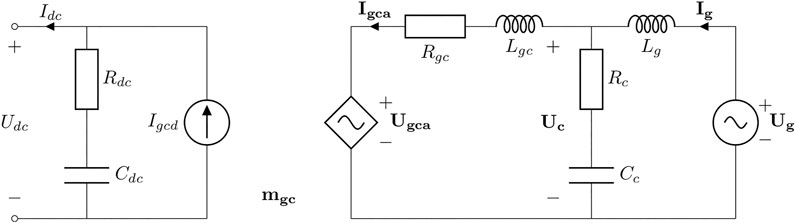
Figure 3 presents an overview of the main elements of a converter-interfaced ESS, namely, the power and control units. In general terms, the power unit can be further subdivided into the ES device and its converter, the dc link, and the grid converter and its LC filter.
2.2.1 The ES Device and Its Converter
This section proposes a method to calculate the ES converter rated power
The calculation of
Using this framework, algebraic expressions of
1. Constant inertia and damping during the interval 0 ≤ t < tc:
2. Primary control linearly takes over the inertial control during the interval
3. The frequency nadir and zenith are bounded: The frequency nadir and zenith are enforced by either a proper combination of inertia, damping, and primary control delays or the actuation of extreme control actions such as automatic generation curtailment or load shedding (EU Commission Regulation, 2017; Eto et al., 2018).
In this case, the normalized angular speed error
4. Only primary control is active during the interval
5. The settling point is bounded: After a power imbalance, the primary control is capable of driving the angular frequency back from the frequency zenith or nadir to within an acceptable steady-state frequency deviation
6. Secondary control linearly takes over during the interval
Using assumption 2,
The energy required by the inertial control
To define the worst-case value for
In short, a bound for
Note that
2.2.2 The dc Link
The main goal of this section is to define the rated capacitance
Typically,
The value of
Finally,
In the approximation of Eqs. 22–24, it is assumed that
2.2.3 The Grid Converter and Its LC Filter
This section discusses briefly the sizing of the grid converter and recommends references for the design of the LC filter. Figure 4 shows a schematic representation of the grid converter, the dc link, and the LC filter.
Contractual and grid code requirements have to be taken into consideration when defining the rated apparent power of the grid converter. Among those requirements, one can mention minimum reactive power injection capacity, short-term overload, and low-voltage ride through capability (EU Commission Regulation, 2016; IEEE, 2018a). However, a relatively simple and common practice in the industry is adopted in this paper. It uses a defined or required power factor λ. The rated apparent power of the converter,
This practice generally limits the equipment size and cost. Nevertheless, it does not necessarily guarantee unsaturated operation for systems with high penetration of CIGs and MGs. In such cases, the grid converter sizing may have to consider the compensation of harmonic distortions and the definition of
Once
1. Calculate the converter side inductance
2. Choose the step-up transformer series inductance
3. Select the filter capacitance
4. Check if the filter resonance frequency
5. Calculate the filter damping resistance
For that, the following equations can be used as guidelines:
where
It is worth emphasizing that the design of an LCL filter is iterative. Failure to comply with requirements implies restarting the whole process and changing the initial assumptions, i.e.,
Finally, alternative topologies to the one presented in Figure 3 and Figure 4 are possible. Nonetheless, the principles discussed earlier in this section can also be applied to more complex solutions. For instance, ES devices using different technologies may be connected in parallel, such as ultracapacitors and batteries. The hybridization is possible because the requirements for each type of frequency control (inertial and primary) are set independently, as discussed in section 2.2.1. This also allows control strategies to operate in parallel and ES converters to share the same dc link, grid converter, and LC filter in a hybrid solution, which may help to reduce equipment costs, volume, and weight (Rocabert et al., 2019). Not least, ESSs may require more complex and robust configurations for the grid converter and consider aspects such as operating costs, efficiency, reliability, power quality, and others, as discussed by Xavier et al. (2019). However, note that these considerations will not affect the rated energy of ES devices nor the rated power of their converters, which are the variables being focused in the procedure presented in this paper.
3 Results
This section presents a case study with numerical examples demonstrating how the method and equations presented in the previous section are applied to size the main components of a hybrid, converter-interfaced ESS supplying primary and secondary frequency control to an ACPS, supported by inertial control of traditional synchronous generators.
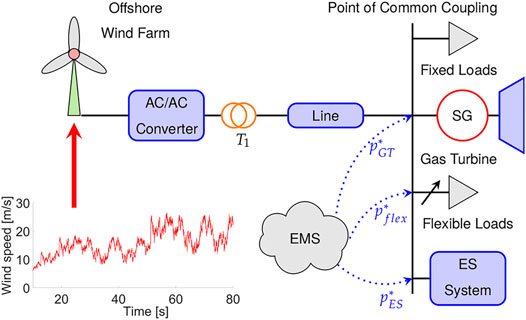
3.1 Case Study: A Wind-Powered Offshore Platform in the North Sea
The system used as a reference is depicted in Figure 5 and represents an isolated ACPS of an offshore oil and gas platform in the North Sea.
This installation operates at
An initial techno-economical study of this installation (Riboldi et al., 2020) suggests that a reduction of up to 30% of its annual CO2 emissions is possible when connecting it to a
Nevertheless, a high number of start–stop and load-change cycles are known to be the main drivers of PEM devices’ deterioration and performance decay (Pei et al., 2008). To avoid that, PEM fuel cells and electrolyzers are assigned to secondary control only and their load ramp rate is restricted to 0–100% in 120 s. The latter is also the value assumed for the recovery period
Further on the topic primary control, it is important to mention that electric loads of this platform are divided into two groups: fixed
Hence, the water injection system can also be considered a short-term ESS that is capable of offering primary frequency control to the ACPS. When assuming that 20% of the installed flexible load can be used for primary frequency control, the following damping coefficient is obtained:
Finally, the load demand was obtained from the platform’s supervisory control and data acquisition (SCADA) system for one representative week with a sampling period of 1 s. Figure 6 presents the histogram of this dataset, which is fit by a normal distribution when ignoring outliers below 0.6 pu. The distribution gives a load variation of
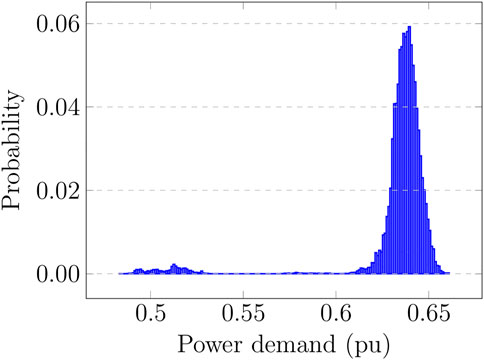
FIGURE 6. Histogram of the platform active power demand showing an average load of 0.6377 pu and a maximum variation of 0.0428 pu with 99.9% of probability when outliers below 0.6 pu are ignored.
Thus, the ES device responsible for primary control should provide the following additional damping:
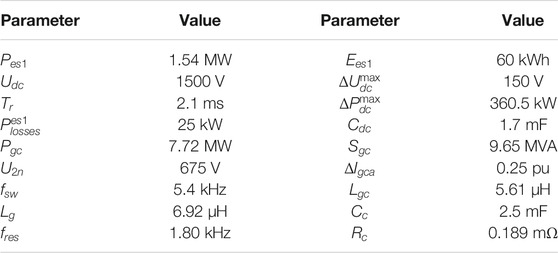
Table 1 presents a summary of the installation parameters and the ESS requirements listed above.

TABLE 1. Parameters of the ACPS of an offshore oil and gas platform in the Norwegian continental shelf and the requirements for its converter-interfaced ESS.
3.2 Sizing of the Energy Storage System
Applying Eqs. 8, 16 using the values from Table 1, the rated power
The most suitable ES device is chosen based on the calculated
To define
The next step in the procedure is defining
The final step is calculating the components of the LC filter. For the sake of brevity, this design is not presented in this paper. The recommended procedure and references are listed in section 2.2.3. Nonetheless, the algorithm for calculating the LC filter is available for the reader in Alves (2021). The grid converter’s switching frequency is adopted as
Table 2 presents a summary of the parameters obtained above for the ESS providing primary control in the case study installation.
3.3 Sizing Validation
To validate the calculations presented in section 3.2, a surrogate model of the case study installation was implemented in MATLAB Simulink R2018a. It has the level of details required to represent the frequency dynamics of the installation and to validate the proposed sizing of the ES device responsible for primary frequency control. It includes all main elements represented in Figure 5, namely, the turbo-generators, the fixed and flexible loads, the wind farm and its transmission line, the ESS, and the EMS. Figure 7 gives an overview of these elements in Simulink.
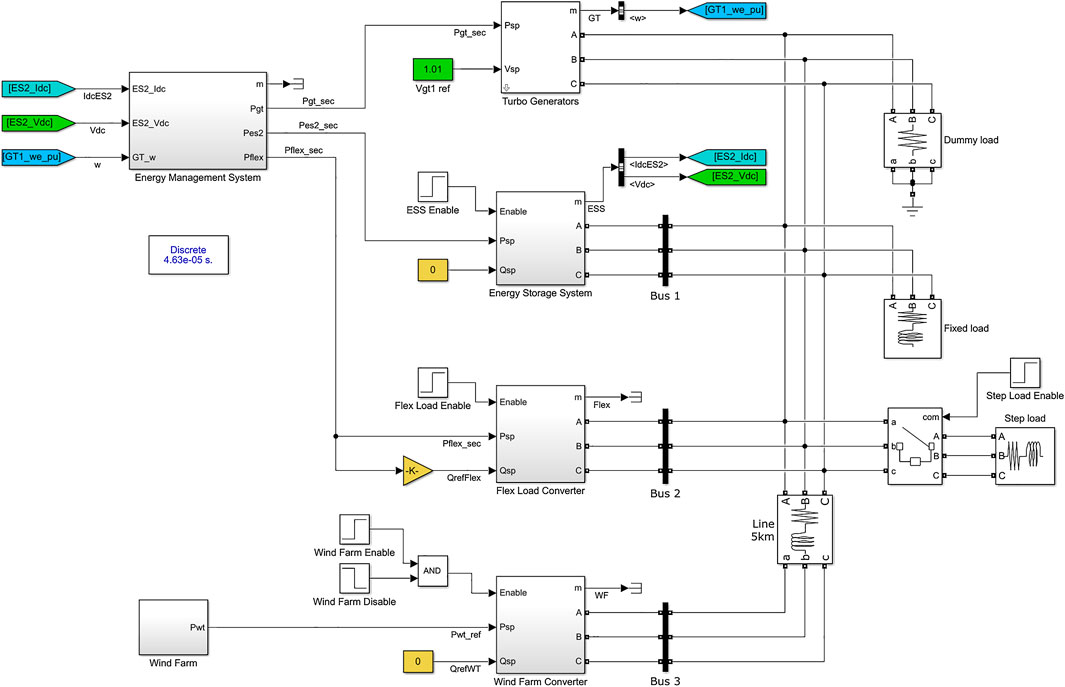
FIGURE 7. Overview of the MATLAB Simulink model used to validate the proposed sizing of the energy storage device responsible for primary control in the case study.
The model was implemented using blocks of the Simscape Electrical Specialized Power Systems toolbox complemented by an open library developed by the authors (Alves, 2020). The latter includes a generalized nonlinear droop controller that is presented in Figure 8. This block is used as the main primary frequency controller in the turbo-generators, ESSs, and flexible load subsystems with their parameters as presented in Table 3. Moreover, the secondary control is implemented in the EMS subsystem using a nonlinear integral controller from the open library with anti-windup and hold functionalities. To minimize CO2 emissions, the EMS gives priority for changes in the ESS setpoint when the secondary control is active. The re-dispatch of turbo-generators happens only when the limits of fuel cells or electrolyzers are reached, and those may be considered a supplementary FRR.
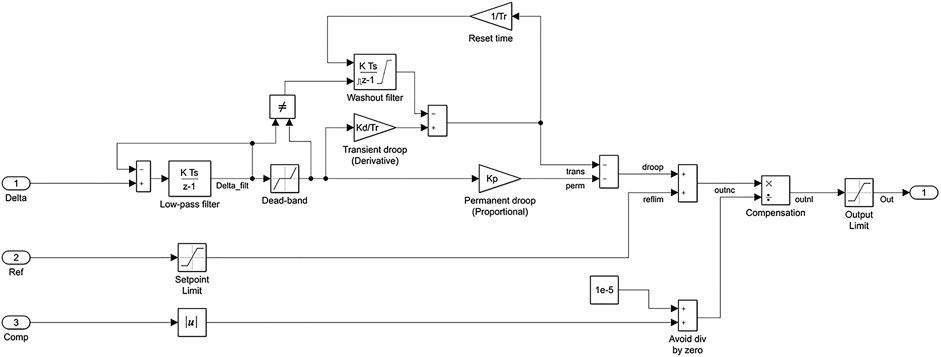
FIGURE 8. Generalized nonlinear droop controller with deadband, permanent droop (proportional gain), transient droop (derivative gain), output compensation, setpoint, and output limitation.
It should be emphasized that it is not the goal of this model to validate the design of the grid converter, its controllers, or its LC filter nor to evaluate harmonics or possible power quality problems. Moreover, the validation of the fuel cell and electrolyzer stack size and their required
To create the power imbalance required for checking the ESS sizing, a load of
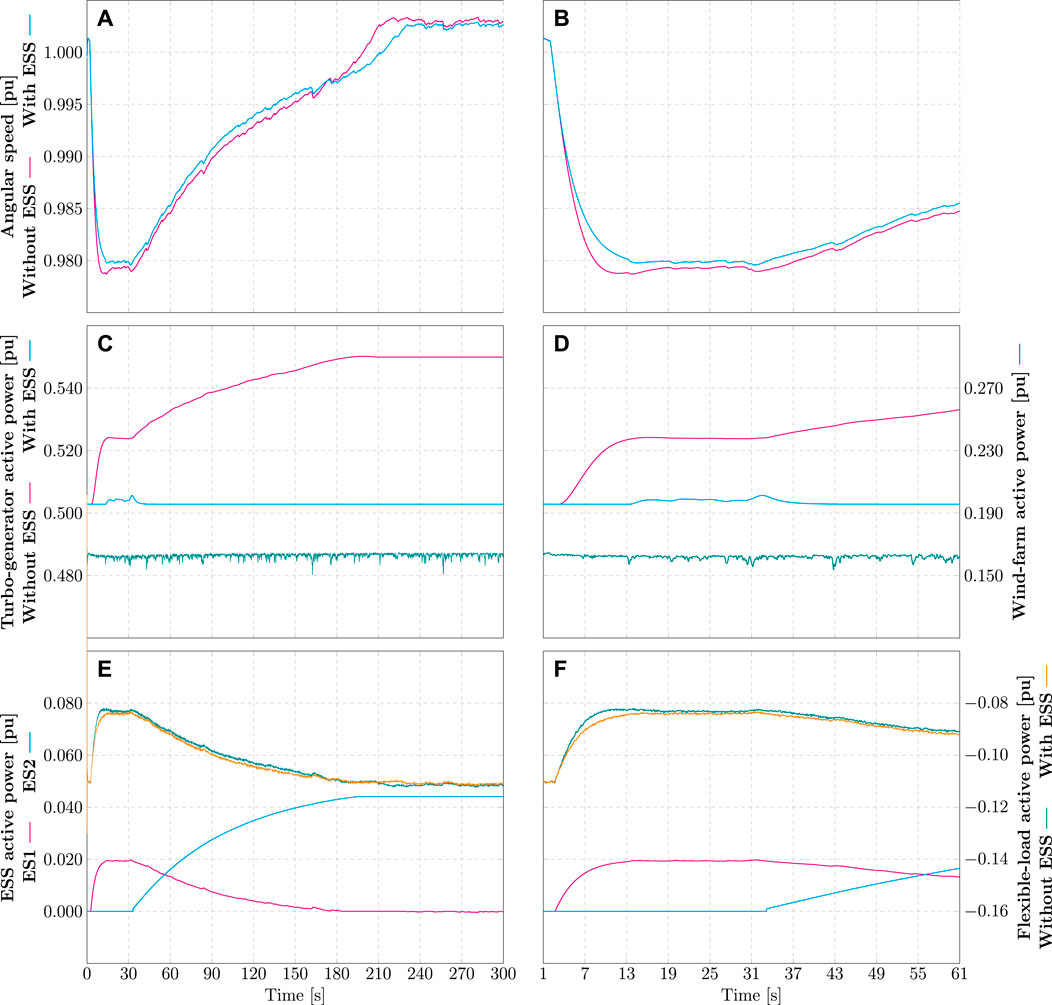
FIGURE 9. Case study behavior during a load increase of
From a frequency-control standpoint, a closer look at Figures 9A,B reveals that the angular speed behaves similarly in both cases, i.e., with and without the ESS. The minor deviations among the cases are explained by the different deadbands and actuation delays of the turbo-generator and the ESS. Indeed, the smaller deadband and actuation delay of the converter-interfaced ESS make its performance slightly superior, achieving a higher nadir (0.9796 pu) than the turbine governor (0.9787 pu) and a smaller steady-state error (0.25 vs. 0.28%) after secondary control is deactivated. This better performance is reflected in the results seen in Figures 9E,F, which show a marginal reduction of the flexible-load active power deviation from its original setpoint while the primary control is active. Foremost, Figures 9C,D corroborate the idea proposed in section 3.2, i.e., a properly sized battery ESS would allow turbo-generators to operate at a constant setpoint when a 3 MW load variation happens suddenly while respecting the load ramp-rate limit of the PEM fuel cell, as shown in Figures 9E,F.
From a sizing perspective, the ES device responsible for primary control (battery system) delivered a peak active power of 0.0197 pu or 1.38 MW and consumed 29.4 kWh of energy. The latter was calculated by trapezoidal numerical integration of the curve ES1 in Figure 9E using a step of 100 ms. When compared to the calculated values
At this point, it is important to recap that the energy of the ES device responsible for primary control is dependent on 1) the damping

FIGURE 10. Case study behavior during the wind farm disconnection under full production (
Figures 10A,C,E show the whole transient lasting 540 s, whereas Figures 10B,D,F zoom in its first minute. From a frequency-control point of view, Figure 10B suggests that the angular speed behaves similarly with and without the ESS during the arrest and rebound periods. However, a closer look at Figure 10A reveals that the dynamics of the recovery period in Cases 3 and 4 are distinct. This happens because the secondary controller acts differently in these two simulations.
In Case 3, the turbo-generator is the sole contributor to the FRR, and as seen in Figure 10C, its active power increases exponentially in the recovery period. As a consequence, the angular speed deviation decreases exponentially, until it reaches the deadband of the droop controller.
In Case 4, there are two sources for the FRR: the hydrogen-based ESS (preferential) and the turbo-generator (supplementary). Hence, the secondary controller ramps up the PEM fuel cell (ES2) until it reaches its rated power, as seen in Figure 10E. At the same time, the angular speed deviation decreases, and as a consequence, the droop controller reduces the turbo-generator active power, as shown in Figures 10A,C. When the ES2 limit is hit, the secondary controller starts increasing the turbo-generator active power. However, the latter is also reduced by its droop controller because the angular speed is still decreasing. These adversarial contributions continue until the deadband of the turbo-generator droop controller is reached. After that, only the secondary controller is active and the angular speed deviation decreases exponentially, until it reaches the deadband of the ES2 droop controller.
From a sizing frame of reference, the peak active power delivered by the battery system was 1.54 MW and the energy supplied was 95.6 kWh. The peak active power was limited by the nonlinear droop controller and matches the value defined in section 3.2. On the contrary, the energy obtained in the simulation is more than three times larger than the calculated value. Naturally, this happens because the parameters of the 3 and 12 MW load-increase events are disparate.
By inspection of Figure 10A, one will note that the frequency limit
4 Conclusions
This paper reviewed the frequency response theory in ac power systems, highlighting the different time periods (arrest, rebound, recovery) and control actions (inertial, primary, secondary) of the frequency-control problem. It also highlighted the main distinctions among traditional high-inertia systems relying on synchronous machines and low-inertia systems such as those with high penetration of converter-interfaced generation and microgrids. Grounded on these concepts and some assumptions, it derived analytical equations to rate the energy capacity and active power required by an energy storage system for providing inertial and primary control to an ac power system. The proposed equations rely on parameters typically defined by system operators, industry standards, or network codes, namely, the steady-state and transient frequency ranges, the maximum rate of change of frequency, and the desired equivalent moment of inertia and damping coefficient. Note that these parameters are independent of the technologies or topologies used in the energy storage devices and converters.
Using these results, this work also provided a step-by-step systematic procedure to initially size the remaining components of a converter-interfaced hybrid energy storage system connected to three-phase ac systems, i.e., the shared dc link and the grid converter and its LC filter. Finally, a case study of a wind-powered oil and gas platform in the North Sea was presented. It demonstrated with numerical examples how the proposed equations and the step-by-step procedure can be applied in a practical problem, where simulations in MATLAB Simulink validated the algebraic calculations and showed they slightly oversize energy storage devices. Not least, the case study demonstrated that the proposed method allows the system designer to take advantage of different energy storage technologies and set specific requirements for each storage device and converter in a hybrid system according to the type of frequency-control action being provided and requirements set by industry standards and grid codes.
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: at https://zenodo.org/record/4601067 (doi 10.5281/zenodo.4384697).
Author Contributions
EA and ET conceptualized the idea. EA and DM developed the software and performed the formal analysis and investigation. EA developed the methodology, validated the results, curated the data, wrote the original draft, and produced figures and tables. ET acquired the funding, supervised and administrated the project. DM and ET reviewed and edited this paper.
Funding
This research was funded by the Research Council of Norway under the program PETROMAKS2, grant number 281986, project “Innovative Hybrid Energy System for Stable Power and Heat Supply in Offshore Oil and Gas Installation (HES-OFF),” and through the PETROSENTER scheme, under the “Research Centre for Low-Emission Technology for Petroleum Activities on the Norwegian Continental Shelf” (LowEmission), grant number 296207.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
ABB (2016). Technical Data for Vacuum Cast Coil Dry-Type Transformers. Zaragoza, Spain. Tech. Rep. 1LES100021-ZD.
Abhyankar, S., Geng, G., Anitescu, M., Wang, X., and Dinavahi, V. (2017). Solution Techniques for Transient Stability‐constrained Optimal Power Flow - Part I. IET Generation, Transm. Distribution 11, 3177–3185. doi:10.1049/iet-gtd.2017.0345
Aghamohammadi, M. R., and Abdolahinia, H. (2014). A New Approach for Optimal Sizing of Battery Energy Storage System for Primary Frequency Control of Islanded Microgrid. Int. J. Electr. Power Energ. Syst. 54, 325–333. doi:10.1016/j.ijepes.2013.07.005
Ahmadi, H., and Ghasemi, H. (2014). Security-Constrained Unit Commitment With Linearized System Frequency Limit Constraints. IEEE Trans. Power Syst. 29, 1536–1545. doi:10.1109/TPWRS.2014.2297997
Akhil, A. A., Huff, G., Currier, A. B., Kaun, B. C., Rastler, D. M., Chen, S. B., et al. (2015). DOE/EPRI Electricity Storage Handbook in Collaboration with NRECA. Sandia National Laboratories, Tech. Rep. SAND2015-1002.
Al-Jaafreh, M. A., and Mokryani, G. (2019). Planning and Operation of LV Distribution Networks: A Comprehensive Review. IET Energ. Syst. Integ. 1, 133–146. doi:10.1049/iet-esi.2019.0013
Alves, E. F., Bergna, G., Brandao, D. I., and Tedeschi, E. (2020). Sufficient Conditions for Robust Frequency Stability of AC Power Systems. IEEE Trans. Power Syst. 1, 1. doi:10.1109/TPWRS.2020.3039832
Alves, E. F. (2021). Efantnu/hybrid-ess-design: Review 1 Release. version v1.1Zenodo. doi:10.5281/zenodo.4601067
Alves, E., Sanchez, S., Brandao, D., and Tedeschi, E. (2019). Smart Load Management with Energy Storage for Power Quality Enhancement in Wind-Powered Oil and Gas Applications. Energies 12, 2985. doi:10.3390/en12152985
Beres, R. N., Wang, X., Blaabjerg, F., Liserre, M., and Bak, C. L. (2016a). Optimal Design of High-Order Passive-Damped Filters for Grid-Connected Applications. IEEE Trans. Power Electron. 31, 2083–2098. doi:10.1109/TPEL.2015.2441299
Beres, R. N., Wang, X., Liserre, M., Blaabjerg, F., and Bak, C. L. (2016b). A Review of Passive Power Filters for Three-Phase Grid-Connected Voltage-Source Converters. IEEE J. Emerg. Sel. Top. Power Electron. 4, 54–69. doi:10.1109/JESTPE.2015.2507203
Bijaieh, M. M., Weaver, W. W., and Robinett, R. D. (2020a). Energy Storage Power and Energy Sizing and Specification Using HSSPFC. Electronics 9, 638. doi:10.3390/electronics9040638
Bijaieh, M. M., Weaver, W. W., and Robinett, R. D. (2020b). Energy Storage Requirements for Inverter-Based Microgrids Under Droop Control in D-Q Coordinates. IEEE Trans. Energ. Convers. 35, 611–620. doi:10.1109/TEC.2019.2959189
Brandao, D. I., Araujo, L. S., Alonso, A. M. S., dos Reis, G. L., Liberado, E. V., and Marafao, F. P. (2020). Coordinated Control of Distributed Three- and Single-Phase Inverters Connected to Three-Phase Three-Wire Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 8, 3861, 3877. doi:10.1109/JESTPE.2019.2931122
Brandao, D. I., Ferreira, W. M., Alonso, A. M. S., Tedeschi, E., and Marafao, F. P. (2020). Optimal Multiobjective Control of Low-Voltage AC Microgrids: Power Flow Regulation and Compensation of Reactive Power and Unbalance. IEEE Trans. Smart Grid 11, 1239–1252. doi:10.1109/TSG.2019.2933790
Caliskan, S. Y., and Tabuada, P. (2015). “Uses and Abuses of the Swing Equation Model,” in 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, December 15–December 18, 2015, 6662–6667. doi:10.1109/CDC.2015.7403268
Chang, G. W., Chuang, C.-S., Lu, T.-K., and Wu, C.-C. (2013). Frequency-regulating Reserve Constrained Unit Commitment for an Isolated Power System. IEEE Trans. Power Syst. 28, 578–586. doi:10.1109/TPWRS.2012.2208126
Channegowda, P., and John, V. (2010). Filter Optimization for Grid Interactive Voltage Source Inverters. IEEE Trans. Ind. Electron. 57, 4106–4114. doi:10.1109/TIE.2010.2042421
D’Arco, S., and Suul, J. A. (2013). Virtual Synchronous Machines — Classification of Implementations and Analysis of Equivalence to Droop Controllers for Microgrids. PowerTech (Grenoble, France: IEEE), 1–7. doi:10.1109/PTC.2013.6652456
Delille, G., Francois, B., and Malarange, G. (2012). Dynamic Frequency Control Support by Energy Storage to Reduce the Impact of Wind and Solar Generation on Isolated Power System's Inertia. IEEE Trans. Sustain. Energ. 3, 931–939. doi:10.1109/TSTE.2012.2205025
Devold, H. (2013). Oil and Gas Production Handbook: An Introduction to Oil and Gas Production, Transport, Refining and Petrochemical Industry (Oslo: ABB). (Accessed July 17, 2020).
DNV-GL (2016). Joint Industry Project: Wind-Powered Water Injection. Høvik, Norway, Tech. rep., DNV-GL.
Doherty, R. E., and Nickle, C. A. (1927). Synchronous Machines-III Torque-Angle Characteristics Under Transient Conditions. Trans. Am. Inst. Electr. Eng. XLVI, 1–18. doi:10.1109/T-AIEE.1927.5061336
Dörfler, F., and Bullo, F. (2012). Synchronization and Transient Stability in Power Networks and Nonuniform Kuramoto Oscillators. SIAM J. Control. Optim. 50, 1616–1642. doi:10.1137/110851584
dos Santos Alonso, A. M., Carlos Afonso, L., Brandao, D. I., Tedeschi, E., and Marafao, F. P. (2019). “Considerations on Communication Infrastructures for Cooperative Operation of Smart Inverters,” in 2019 IEEE 15th Brazilian Power Electronics Conference and 5th IEEE Southern Power Electronics Conference COBEP/SPEC). (Santos, Brazil: IEEE). doi:10.1109/COBEP/SPEC44138.2019.9065382
Duckwitz, D. (2019). Power System Inertia: Derivation of Requirements and Comparison of Inertia Emulation Methods for Converter-Based Power Plants. PhD thesis. Kassel (Germany): University of Kassel.
Egido, I., Sigrist, L., Lobato, E., Rouco, L., and Barrado, A. (2015). An Ultra-capacitor for Frequency Stability Enhancement in Small-Isolated Power Systems: Models, Simulation and Field Tests. Appl. Energ. 137, 670–676. doi:10.1016/j.apenergy.2014.08.041
Entso-E, (2019). Fast Frequency Reserve – Solution to the Nordic Inertia Challenge. Tech. rep., Entso-e.
Erickson, R. W., and Maksimović, D. (2001). Fundamentals of Power Electronics. 2 edn. Springer. doi:10.1007/b100747
Eto, J. H., Undrill, J., Roberts, C., Mackin, P., and Ellis, J. (2018). Frequency Control Requirements for Reliable Interconnection Frequency Response. Lawrence Berkeley National Laboratory, Tech. Rep. LBNL-2001103.
EU Commission Regulation (2015). Guideline on Capacity Allocation and Congestion managementTech. Rep. Brussels, Belgium: European Union. EU 2015/1222 Online. (Accessed July 17, 2020).
EU Commission Regulation (2017). Guideline on Electricity Transmission System OperationTech. Rep. Brussels, Belgium: European Union. EU 2017/1485Online. (Accessed July 17, 2020).
EU Commission Regulation (2016). Network Code on Requirements for Grid Connection of Generators. EU 2016/631. Tech. Rep. Brussels, Belgium: European Union. Online. (Accessed July 17, 2020).
Fang, J., Li, H., Tang, Y., and Blaabjerg, F. (2019). On the Inertia of Future More-Electronics Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 7, 2130–2146. doi:10.1109/JESTPE.2018.2877766
Farhadi, M., and Mohammed, O. (2016). Energy Storage Technologies for High-Power Applications. IEEE Trans. Ind. Applicat. 52, 1953–1961. doi:10.1109/TIA.2015.2511096
Fu, Q., Hamidi, A., Nasiri, A., Bhavaraju, V., Krstic, S. B., and Theisen, P. (2013). The Role of Energy Storage in a Microgrid Concept: Examining the Opportunities and Promise of Microgrids. IEEE Electrific. Mag. 1, 21–29. doi:10.1109/MELE.2013.2294736
Gallo, A. B., Simões-Moreira, J. R., Costa, H. K. M., Santos, M. M., and Moutinho dos Santos, E. (2016). Energy Storage in the Energy Transition Context: A Technology Review. Renew. Sustain. Energ. Rev. 65, 800–822. doi:10.1016/j.rser.2016.07.028
Gamarra, C., and Guerrero, J. M. (2015). Computational Optimization Techniques Applied to Microgrids Planning: A Review. Renew. Sustain. Energ. Rev. 48, 413–424. doi:10.1016/j.rser.2015.04.025
Geng, G., Abhyankar, S., Wang, X., and Dinavahi, V. (2017). Solution Techniques for Transient Stability‐constrained Optimal Power Flow - Part II. IET Generation, Transm. Distribution 11, 3186–3193. doi:10.1049/iet-gtd.2017.0346
Grainger, J. J., and Stevenson, W. D. (1994). Power System Analysis. New York, NY: McGraw-Hill Series in Electrical and Computer Engineering McGraw-Hill.
Hemmati, R., and Saboori, H. (2016). Emergence of Hybrid Energy Storage Systems in Renewable Energy and Transport Applications - A Review. Renew. Sustain. Energ. Rev. 65, 11–23. doi:10.1016/j.rser.2016.06.029
IEC (2019). IEC 61892:2019 Mobile and Fixed Offshore Units - Electrical Installations. Geneva, Switzerland: IEC.
IEEE (2018a). IEEE 1547-2018 - IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. New York, NY: IEEE.
IEEE (2018b). IEEE 2030.8-2018 IEEE Standard for the Testing of Microgrid Controllers. New York, NY: IEEE.
Infineon Technologies (2020). Power and Sensing Selection Guide 2020. Tech. rep., Infineon Technologies Austria AG.
Jalili, K., and Bernet, S. (2009). Design of LCL Filters of Active-Front-End Two-Level Voltage-Source Converters. IEEE Trans. Ind. Electron. 56, 1674–1689. doi:10.1109/TIE.2008.2011251
Kimbark, E. W. (1995). Power System Stability. New York, NY: IEEE Press Power Systems Engineering Series, IEEE Press.
Knap, V., Chaudhary, S. K., Stroe, D.-I., Swierczynski, M., Craciun, B.-I., and Teodorescu, R. (2016). Sizing of an Energy Storage System for Grid Inertial Response and Primary Frequency Reserve. IEEE Trans. Power Syst. 31, 3447–3456. doi:10.1109/TPWRS.2015.2503565
Koohi-Kamali, S., Tyagi, V. V., Rahim, N. A., Panwar, N. L., and Mokhlis, H. (2013). Emergence of Energy Storage Technologies as the Solution for Reliable Operation of Smart Power Systems: A Review. Renew. Sustain. Energ. Rev. 25, 135–165. doi:10.1016/j.rser.2013.03.056
Kundur, P., Balu, N. J., and Lauby, M. G. (1994). Power System Stability and Control. The EPRI Power System Engineering. New York, NY: McGraw-Hill.
Liserre, M., Blaabjerg, F., and Dell’Aquila, A. (2004). Step-by-step Design Procedure for a Grid-Connected Three-phase PWM Voltage Source Converter. Int. J. Electron. 91, 445–460. doi:10.1080/00207210412331306186
Machowski, J., Bialek, J. W., and Bumby, J. R. (2008). Power System Dynamics: Stability and Control. 2nd edn. Chichester, U.K: Wiley.
Malesani, L., Rossetto, L., Tenti, P., and Tomasin, P. (1995). AC/DC/AC PWM Converter with Reduced Energy Storage in the DC Link. IEEE Trans. Ind. Applicat. 31, 287–292. doi:10.1109/28.370275
Marchgraber, J., Alács, C., Guo, Y., Gawlik, W., Anta, A., Stimmer, A., et al. (2020). Comparison of Control Strategies to Realize Synthetic Inertia in Converters. Energies 13, 3491. doi:10.3390/en13133491
Milano, F., Dorfler, F., Hug, G., Hill, D. J., and Verbic, G. (2018). “Foundations and Challenges of Low-Inertia Systems,” in 2018 Power Systems Computation Conference (PSCC). Dublin: IEEE, 1–25. doi:10.23919/PSCC.2018.8450880
Muhlethaler, J., Schweizer, M., Blattmann, R., Kolar, J. W., and Ecklebe, A. (2013). Optimal Design of LCL Harmonic Filters for Three-Phase PFC Rectifiers. IEEE Trans. Power Electron. 28, 3114–3125. doi:10.1109/TPEL.2012.2225641
Nguyen, N., Almasabi, S., Bera, A., and Mitra, J. (2019). Optimal Power Flow Incorporating Frequency Security Constraint. IEEE Trans. Ind. Appl. 55, 6508–6516. doi:10.1109/TIA.2019.2938918
Pei, P., Chang, Q., and Tang, T. (2008). A Quick Evaluating Method for Automotive Fuel Cell Lifetime. Int. J. Hydrogen Energ. 33, 3829–3836. doi:10.1016/j.ijhydene.2008.04.048
Peña-Alzola, R., Liserre, M., Blaabjerg, F., Sebastián, R., Dannehl, J., and Fuchs, F. W. (2013). Analysis of the Passive Damping Losses in LCL-Filter-Based Grid Converters. IEEE Trans. Power Electron. 28, 2642–2646. doi:10.1109/TPEL.2012.2222931
Riboldi, L., Alves, E. F., Pilarczyk, M., Tedeschi, E., and Nord, L. O. (2020). “Innovative Hybrid Energy System for Stable Power and Heat Supply in Offshore Oil & Gas Installation (HES-OFF): System Design and Grid Stability,” in 30th European Symposium on Computer Aided Process Engineering (ESCAPE30). Milano, Italy: Elsevier.
Riboldi, L., Alves, E. F., Pilarczyk, M., Tedeschi, E., and Nord, L. O. (2021). Optimal Design of a Hybrid Energy System for the Supply of Clean and Stable Energy to Offshore Installations. Front. Energ. Res. doi:10.3389/fenrg.2020.607284
Rocabert, J., Capo-Misut, R., Munoz-Aguilar, R. S., Candela, J. I., and Rodriguez, P. (2019). Control of Energy Storage System Integrating Electrochemical Batteries and Supercapacitors for Grid-Connected Applications. IEEE Trans. Ind. Applicat. 55, 1853–1862. doi:10.1109/TIA.2018.2873534
Rockhill, A. A., Liserre, M., Teodorescu, R., and Rodriguez, P. (2011). Grid-Filter Design for a Multimegawatt Medium-Voltage Voltage-Source Inverter. IEEE Trans. Ind. Electron. 58, 1205–1217. doi:10.1109/TIE.2010.2087293
Sanchez, S., Tedeschi, E., Silva, J., Jafar, M., and Marichalar, A. (2017). Smart Load Management of Water Injection Systems in Offshore Oil and Gas Platforms Integrating Wind Power. IET Renew. Power Generation 11, 1153–1162. doi:10.1049/iet-rpg.2016.0989
Sandelic, M., Stroe, D.-I., and Iov, F. (2018). Battery Storage-Based Frequency Containment Reserves in Large Wind Penetrated Scenarios: A Practical Approach to Sizing. Energies 11, 3065. doi:10.3390/en11113065
Sarjeant, W., Clelland, I., and Price, R. (2001). Capacitive Components for Power Electronics. Proc. IEEE 89, 846–855. doi:10.1109/5.931475
Sauer, P. W., Pai, M. A., and Chow, J. H. (2017). Power System Dynamics and Stability: With Synchrophasor Measurement and Power System Toolbox. 2nd Edn. Hoboken, NJ: Wiley.
Siemens, (2020). SINACON PV Photovoltaic Central Inverter Technical Data. Erlangen, Germany, Tech. Rep. SIDS-B10020-00-7600, Siemens AG.
Siemens, (2017). The GEAFOL Neo: The Optimum Foundation for Power Distribution. Erlangen, Germany, Tech. Rep. EMTR-B10021-00-7600, Siemens AG.
Strbac, G., Hatziargyriou, N., Lopes, J. P., Moreira, C., Dimeas, A., and Papadaskalopoulos, D. (2015). Microgrids: Enhancing the Resilience of the European Megagrid. IEEE Power Energ. Mag. 13, 35–43. doi:10.1109/MPE.2015.2397336
Tavora, C. J., and Smith, O. J. M. (1972). Characterization of Equilibrium and Stability in Power Systems. IEEE Trans. Power Apparatus Syst. Pas- 91, 1127–1130. doi:10.1109/TPAS.1972.293468
Tenti, P., Costabeber, A., Mattavelli, P., Marafao, F. P., and Paredes, H. K. M. (2014). Load Characterization and Revenue Metering Under Non-Sinusoidal and Asymmetrical Operation. IEEE Trans. Instrum. Meas. 63, 422–431. doi:10.1109/TIM.2013.2280480
Vandoorn, T. L., Vasquez, J. C., De Kooning, J., Guerrero, J. M., and Vandevelde, L. (2013). Microgrids: Hierarchical Control and an Overview of the Control and Reserve Management Strategies. IEEE Ind. Electron. Mag. 7, 42–55. doi:10.1109/MIE.2013.2279306
Wen, Y., Li, W., Huang, G., and Liu, X. (2016). Frequency Dynamics Constrained Unit Commitment With Battery Energy Storage. IEEE Trans. Power Syst. 31, 5115–5125. doi:10.1109/TPWRS.2016.2521882
Xavier, L. S., Amorim, W. C. S., Cupertino, A. F., Mendes, V. F., do Boaventura, W. C., and Pereira, H. A. (2019). Power Converters for Battery Energy Storage Systems Connected to Medium Voltage Systems: A Comprehensive Review. BMC Energy 1, 7. doi:10.1186/s42500-019-0006-5
Xu, J., and Xie, S. (2018). LCL-resonance Damping Strategies for Grid-Connected Inverters with LCL Filters: A Comprehensive Review. J. Mod. Power Syst. Clean. Energ. 6, 292–305. doi:10.1007/s40565-017-0319-7
Nomenclature
ACPS ac power system
CIG converter-interfaced generator
EMS energy management system
ES energy storage
ESS energy storage system
FCRs frequency containment reserves
FFRs fast frequency reserves
FRRs frequency restoration reserves
FSM frequency sensitivity mode
MG microgrid
RoCoF rate of change of frequency
PEM proton exchange membrane
SCADA supervisory control and data acquisition
SM synchronous machine
Keywords: low-inertia systems, energy storage, inertial control, primary control, frequency stability, power system design
Citation: Alves EF, Mota DdS and Tedeschi E (2021) Sizing of Hybrid Energy Storage Systems for Inertial and Primary Frequency Control. Front. Energy Res. 9:649200. doi: 10.3389/fenrg.2021.649200
Received: 04 January 2021; Accepted: 22 April 2021;
Published: 28 May 2021.
Edited by:
Hong Fan, Shanghai University of Electric Power, ChinaCopyright © 2021 Alves, Mota and Tedeschi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Erick Fernando Alves, ZXJpY2suZi5hbHZlc0BudG51Lm5v
 Erick Fernando Alves
Erick Fernando Alves Daniel dos Santos Mota
Daniel dos Santos Mota Elisabetta Tedeschi
Elisabetta Tedeschi