Optimal Operation of Isolated Micro-Grids-cluster Via Coalitional Energy Scheduling and Reserve Sharing

Microgrids (MG) cluster are isolated from the utility grid but they have the potential to achieve better techno-economic performance by using joint energy and reserve sharing among MGs. This paper proposes a techno-economic framework for the optimal operation of isolated MGs-cluster by scheduling cooperative energy sharing and real-time reserve sharing for ancillary services based on the cooperative game theory. In the day-ahead scheduling, a coalitional sharing scheme is formulated as an adjustable robust optimization (ARO) problem to optimally schedule the energy and reserves of distributed generators (DGs) and energy storage systems (ESSs), thereby responding to the uncertainties of photovoltaic systems, wind turbines, and loads. These uncertainties are the main reason for power system imbalance which is mitigated by regulating the frequency in real-time and a dynamic droop control process is used to realize the reserves in a distributed manner. This control process is embedded into the ARO problem, which is formulated as an affine ARO problem and then transformed into a deterministic optimization problem that is solved by off-shore solvers Apart from the reduction in the operation cost, the frequency restoration can be improved jointly, resulting in the coupled techno-economic contribution of the MGs in the coalition. The contribution of each MG is quantified using shapely value, a cooperative game approach. Simulations are conducted for a case study with 4 MGs and the results demonstrate the merits of the proposed cooperative scheduling scheme.

1 Introduction

Due to the interconnection of distributed energy resources (DERs), e.g., wind turbines (WTs), photovoltaic (PV) modules, distributed generators (DGs) (Ma et al., 2016; Hamidi et al., 2017; Lara et al., 2018) and energy storage systems (ESSs), microgrids (MGs) have been playing a crucial role in the development of smart grid technology. MGs are capable of operating in both isolated and grid-connected modes (Faisal et al., 2018; Lv et al., 2016). Other than ensuring the power balancing status among local DERs and loads, MGs can also exchange power flexibly with external systems (Vahedipour-Dahraie et al., 2020), e.g., the utility grid and other MGs. By developing a more efficient and resilient MGs-cluster, these exchanges cover not only conventional energy sources but also emerging ancillary services, especially for isolated MGs-cluster with high penetration of schedulable DERs (Pourghasem et al., 2019).

The optimal operation of isolated MGs was generally investigated considering the uncertainty of schedulable DERs using stochastic optimization (Hu et al., 2016; Shi et al., 2019) and robust optimization (Ghahramani et al., 2019; Liu et al., 2019). In a grid-connected mode, the MGs-cluster is created by connecting them and the distribution network (Luo et al., 2020). Due to cluster formation and grid-connection, each MG utilizes the local grid resources (Lv and Ai, 2016; Ghadi et al., 2019; Mostafa et al., 2020), as well as those of other MGs (Lv and Ai, 2016; Gao et al., 2017; Ali et al., 2019; Toutounchi et al., 2019).

Regarding the coalitional operation of an MGs-cluster, an energy management problem was extended to a multi-MG in (Liu et al., 2018; Purage et al., 2019) to minimize the cost. The amount of production cannot be controlled in uncontrollable energy sources; therefore, in (Purage et al., 2019), a controllable distributed energy re-source (CDER) was presented such as DGs and ESS where the production amount can be controlled by the energy management system. Energy management approaches for the utilization of energy resources in MGs-cluster and the grid were presented in (Zhang and Xu, 2018). This approach successfully decreases the volume of energy acquired from the grid which significantly increases the MG profit. In (Aktas et al., 2017), a stochastic bi-level model that provided an effective solution for the coordinated operation of the MGs-cluster was proposed. In (Simões et al., 2016), a strategy was recommended for the exchange of information between MGs-cluster to enhance the coordination among the MGs to increase the profit and reduce the operational cost of each member of the cluster. In (Xie et al., 2017), an economic-probabilistic model was presented for the balanced exchange of energy between the MGs-cluster by controlling the energy resources and loads of the MGs.

The stability of the power system is achieved when the generation and load are in equilibrium. However, due to the possibility of errors in the day-ahead forecasted outputs of PV, WT, and load demand, the real-time outputs exhibit fluctuations in the frequency. The scheduling of the controllable DER (CDER) output must be readjusted according to the output of the PV, WT, and load demand to achieve frequency stability (Lin et al., 2018). The isolated MGs-cluster requires a robust frequency regulation that depends on the three-level hierarchical energy management system, i.e., primary, secondary, and tertiary control level (Pinzón et al., 2018). The primary control level is focused on the automatic voltage and frequency control of the inverter-interfaced DERs (IIDERs) (Castilla et al., 2019). For secondary control, researchers have implemented the droop-based control method to model the frequency security in energy management (EM) problem. It should be noted that the dependence of IIDERs on MG frequency is insubstantial, however, to keep the power sharing strategy more secure from over-heating risks, the more advanced P-f droop control method is used (Arani and Mohamed, 2017). The highest control level is the tertiary control when primary and secondary levels are insufficient for frequency excursions; this is executed by the MGs-cluster control center (MGCCC) (Basso et al., 2012). For reserve sharing, a linear quadratic regulator-based technique is used to control the CDERs instead of the traditional proportional-integral derivative-based controller (Ketabi et al., 2017). The fluctuations of the renewable energy sources (RES) significantly influence reserve sharing in the MG and the existing droop control method should be modified to handle RES uncertainty (Liu et al., 2018).

In (Rokrok et al., 2018), a contributing factor was introduced for reserve sharing among MGs and the grid to ensure that the system is in equilibrium with the load demand and that the economic impact due to reserve sharing is distributed among the MGs. Further-more, ancillary services regarding frequency support and voltage regulation could be potentially introduced by MGs (Anvari-Moghaddam et al., 2017).

The existing literature indicates that: 1) previous studies on MGs-cluster have mostly considered energy collaboration, reserve cooperation, and economic benefits; besides, the MGs-cluster are connected to the distribution network. However, power system constraints were not considered and their effect on power quality was neglected; the quality is affected due to the transient nature of PVs and WTs because imbalances in the power supply and demand occur. 2) To maintain the power system in equilibrium, market-based regulation services are provided by different MGs in a cluster; however, the coordination of these services and the provision of economic benefits for the MGs have not been considered.

To address these problems, we propose a scheduling model for energy sharing and reserve sharing for ancillary services to achieve the optimal operation of isolated MGs-cluster. The main contributions of this paper are twofold.

(1) A techno-economic framework is proposed for the optimal operation of isolated MGs-cluster by scheduling cooperative energy sharing and real-time reserve sharing for ancillary services based on the cooperative game theory.

(2) An economic subsidy sharing between MGs-cluster members is achieved by determining the Shapley values of the coordinated distribution of economic benefits. In the coalitional operation of the MGs-clusters, the Shapley values are used to allocate economic benefits to individual MGs

2 Coalitional Scheduling of Isolated Microgrids-Cluster

2.1 Isolated Microgrids-Cluster System

The typical structure of MGs-cluster is shown in Figure 1, it includes multiple interconnected MGs. Each MG consists of DGs, WTs, PVs, ESSs, and loads, which are managed by the corresponding MG control center (MGCC). The MGCC is responsible for information acquisition from the respective MG and information exchange with the external systems. All MGs are integrated into a ring configuration with NB buses and NL lines; this represents the MGs-cluster that is supported by the MGCCC. The MGCCC is responsible for the secure and efficient operation of the MGs-cluster by providing energy and ancillary services, e.g., regulation of reserves and sharing among MGs across multiple scheduling and control processes.

FIGURE 1

FIGURE 1. Typical structure of MGs-Cluster.

2.2 Operating Process of Microgrids-Cluster

Generally, the operating process of the MGs-cluster includes day-ahead scheduling and reserve sharing for real-time frequency regulation (see Figure 2). In the day-ahead scheduling, the forecasted power output of PVs, WTs, and loads (Li et al., 2018; Ullah et al., 2019), as well as the technical information of DGs and ESS, are sent to the MGCCC by each MGCC. After receiving the information, the MGCCC implements the joint energy and reserve optimization to optimally schedule the energy and reserve of the DGs and ESSs in each MGCC; besides, the energy exchange and reserve sharing among MGs for each day is determined. The scheduling plan is sent to each MGCC after the joint energy and reserve optimization. In each operating period, the outputs of the DGs and ESSs are adjusted by the corresponding MGCC according to the day-ahead scheduling plan and in response to the actual power outputs of PVs, WTs, and loads. In this way, the day-ahead scheduling is done by MGCC that includes the power output of DGs and ESSs. The real-time adjustment of the DGs and ESSs is implemented in a distributed manner using a droop control method (Xiao et al., 2017). However, the transient nature of the WT, PV, and load demand is not entirely predictable; therefore, the forecasted information rarely matches the real-time data. To maintain the stability of the MG, real-time scheduling is a challenging task; therefore, the MGCC and the MGCCC coordinate energy and reserve sharing (Xiao et al., 2017). When the load demand is lower than the power generation, the MG can provide excess energy and reserve energy to other MGs and the MGCCC provides economic compensation to that MG. On the other hand, when an MG has a shortage of energy, the MGCCC arranges for other MGs to pro-vide energy to the respective MG. In this way, energy and reserves can be shared and exchanged within the MGs-cluster in real-time for frequency regulation.

FIGURE 2

FIGURE 2. Energy sharing and reserve sharing of isolated MGs-Cluster.

Consequently, this paper proposes to address the technical aspect of the framework by doing frequency regulation and economic aspect by addressing the energy and reserve sharing within the MGs-cluster. Therefore, we propose a techno-economic framework for optimal operation of isolated MGs-cluster. Formulations for energy and reserve scheduling for single MG are given in the next section. The coalition scheduling and reserve sharing formulation is discussed in Section 4. Details of the economic model are presented in Section 5.

3 Energy and Reserve Scheduling for Single Microgrids

3.1 Objective Function

The energy and reserve scheduling problem is formulated as an affine adjustable robust optimization problem, where the uncertainties of PVs, WTs, and loads are depicted as a robust set and mitigated by the DGs and ESSs in the real-time frequency regulation. The objective of the MG scheduling is to minimize the total operating cost (OC) of the DGs and ESSs, which is shown in Equation 1:

${\mathit{C}}^{\mathit{n}}={\displaystyle \sum }_{\mathit{t}=1}^{\mathit{T}}\{{\displaystyle \sum }_{\mathit{g}=1}^{{\mathit{N}}_{\mathit{G}}^{\mathit{n}}}({\mathit{C}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{t},\mathit{E}}+{\mathit{C}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{t},\mathit{R}})+{\displaystyle \sum }_{\mathit{k}=1}^{{\mathit{N}}_{\mathit{B}}^{\mathit{n}}}({\mathit{C}}_{\mathit{B},\mathit{k}}^{\mathit{n},\mathit{t},\mathit{E}}+{\mathit{C}}_{\mathit{B},\mathit{k}}^{\mathit{n},\mathit{t},\mathit{R}})\}\mathit{ }(1)$

where $C_{G,g}^{n,t,E}$ and $C_{G,g}^{n,t,R}$ are the DG OC in the case of energy and reserve sharing for the gth DG in the nth MG during the tth time interval. n = 1, 2, ..., $N_{MG}$ , and $N_{MG}$are the number of MGs; g = 1, 2,...,$N_G^n$, and $N_G^n$ are the number of DGs in the nth MG. $C_{B,k}^{n,t,E}$ and $C_{B,k}^{n,t,R}$ are the ESS OC in case of energy and reserve sharing for the tth ΔESS in the nth MG during the tth time interval respectively. k = 1, 2, ...,$N_B^n$, and are the number of ESSs in the nth MG. The details on each item is explained in Section 4.3.

3.2 Constraints of Day-Ahead Operation

In the day-ahead operation, the constraints concerning the DGs and ESSs are as follows:

${\mathit{p}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{min}}\le {\mathit{p}}_{\mathit{G},\mathit{g},\mathit{f}}^{\mathit{n},\mathit{t}}\le {\mathit{p}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{max}}(2)$

$\mathit{Ram}{\mathit{p}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{dn}}\le ({\mathit{p}}_{\mathit{G},\mathit{g},\mathit{f}}^{\mathit{n},\mathit{t}}-{\mathit{p}}_{\mathit{G},\mathit{g},\mathit{f}}^{\mathit{n},\mathit{t}-1})\le \mathit{Ram}{\mathit{p}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{up}}(3)$

$0\le {\mathit{p}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{d},\mathit{n},\mathit{t}}\le {\left({\mathit{p}}_{\mathit{B},\mathit{k}}^{\mathit{d},\mathit{n}}\right)}^{\mathit{max}}(4)$

$0\le {\mathit{p}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{c},\mathit{n},\mathit{t}}\le {\left({\mathit{p}}_{\mathit{B},\mathit{k}}^{\mathit{c},\mathit{n}}\right)}^{\mathit{max}}(5)$

${\mathit{E}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{n},\mathit{t}}={\mathit{E}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{n},\mathit{t}-1}+({\mathit{p}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{c},\mathit{n},\mathit{t}}{\mathit{\eta }}_{\mathit{k}}^{\mathit{c},\mathit{n}}-\frac{{\mathit{p}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{d},\mathit{n},\mathit{t}}}{{\mathit{\eta }}_{\mathit{k}}^{\mathit{d},\mathit{n}}})(6)$

${\mathit{E}}_{\mathit{B},\mathit{k}}^{\mathit{n},\mathit{min}}\le {\mathit{E}}_{\mathit{B},\mathit{k}}^{\mathit{n},0}\le {\mathit{E}}_{\mathit{B},\mathit{k}}^{\mathit{n},\mathit{max}}(7)$

To minimize the OC, the DGs must operate under the constraints defined in Equations 2, 3. The maximum and minimum outputs of the gth DG in the nth MG are $p_{G,g}^{n,max}$ and $p_{G,g}^{n,min}$respectively whereas the ramp-down and ramp-up rate limits are $Ram{p}_{G,g}^{n,dn}$ and$Ram{p}_{G,g}^{n,up}$, respectively. In constraints (4)–(5), the maximum charging and discharging power of the kth ESS are ${\left(p_{B,k}^{c,n}\right)}^{max}$ and ${\left(p_{B,k}^{d,n}\right)}^{max}$ , respectively. The energy level at the end of the tth time interval is $E_{B,k}^{n,t}$ . ${\eta }_k^{c,n}$ and ${\eta }_k^{d,n}$ are the charging and discharging efficiencies, and $E_{B,k}^{n,max}$ and $E_{B,k}^{n,min}$ are the maximum and minimum capacities of the kth ESS, where$p_{G,g,f}^{n,t}$ and $p_{B,k,f}^{n,t}$ are the base-point power output of the gth DG and kth ESS in the nth MG in the tth time.

3.3 Constraints for Real Time Operation.

To minimize the OC in real-time, the following constraints must be satisfied. The constraints concerning DGs and ESSs are as follows:

${\mathit{p}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{min}}\le {\mathit{p}}_{\mathit{G},\mathit{g},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{G},\mathit{g},\mathit{q}}^{\mathit{n},\mathit{t}}\le {\mathit{p}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{max}}(9)$

$\mathit{Ram}{\mathit{p}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{dn}}\le \left({\mathit{p}}_{\mathit{G},\mathit{g},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{G},\mathit{g},\mathit{q}}^{\mathit{n},\mathit{t}}\right)-({\mathit{p}}_{\mathit{G},\mathit{g},\mathit{f}}^{\mathit{n},\mathit{t}-1}+\mathit{\Delta }{\mathit{p}}_{\mathit{G},\mathit{g},\mathit{q}}^{\mathit{n},\mathit{t}-1})\le \mathit{Ram}{\mathit{p}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{up}}(10)$

${\mathit{R}}_{\mathit{G},\mathit{g},\mathit{q}}^{\mathit{n},\mathit{t}}\ge \mathit{\Delta }{\mathit{p}}_{\mathit{G},\mathit{g},\mathit{q}}^{\mathit{n},\mathit{t}}(11)$

${\mathit{R}}_{\mathit{G},\mathit{g},\mathit{q}}^{\mathit{n},\mathit{t}}\le -\mathit{\Delta }{\mathit{p}}_{\mathit{G},\mathit{g},\mathit{q}}^{\mathit{n},\mathit{t}}(12)$

$0\le {\mathit{p}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{d},\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{B},\mathit{k},\mathit{q}}^{\mathit{d},\mathit{n},\mathit{t}}\le {\left({\mathit{p}}_{\mathit{B},\mathit{k}}^{\mathit{d},\mathit{n}}\right)}^{\mathit{max}}(13)$

$0\le {\mathit{p}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{c},\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{B},\mathit{k},\mathit{q}}^{\mathit{c},\mathit{n},\mathit{t}}\le {\left({\mathit{p}}_{\mathit{B},\mathit{k}}^{\mathit{c},\mathit{n}}\right)}^{\mathit{max}}(14)$

${\mathit{R}}_{\mathit{B},\mathit{k},\mathit{q}}^{\mathit{n},\mathit{t}}\ge \mathit{\Delta }{\mathit{p}}_{\mathit{B},\mathit{k},\mathit{q}}^{\mathit{n},\mathit{t}}(15)$

${\mathit{R}}_{\mathit{B},\mathit{k},\mathit{q}}^{\mathit{n},\mathit{t}}\le -\mathit{\Delta }{\mathit{p}}_{\mathit{B},\mathit{k},\mathit{q}}^{\mathit{n},\mathit{t}}(16)$

${\mathit{E}}_{\mathit{B},\mathit{k}}^{\mathit{n},\mathit{t}}={\mathit{E}}_{\mathit{B},\mathit{k}}^{\mathit{n},\mathit{t}-1}+({\mathit{p}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{c},\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{B},\mathit{k},\mathit{q}}^{\mathit{c},\mathit{n},\mathit{t}}){\mathit{\eta }}_{\mathit{k}}^{\mathit{c},\mathit{n}}-\frac{{\mathit{p}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{d},\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{B},\mathit{k},\mathit{q}}^{\mathit{d},\mathit{n},\mathit{t}}}{{\mathit{\eta }}_{\mathit{k}}^{\mathit{d},\mathit{n}}}(17)$

${\mathit{E}}_{\mathit{B},\mathit{k}}^{\mathit{n},\mathit{min}}\le {\mathit{E}}_{\mathit{B},\mathit{k}}^{\mathit{n},0}\le {\mathit{E}}_{\mathit{B},\mathit{k}}^{\mathit{n},\mathit{max}}(18)$

The constraint Equation 9 represents the power capacity limit of DGs, where $\Delta p_{G,g,q}^{n,t}$ is the change in the qth control level in the gth DG output in the nth MG in the tth time. The index $q\mathit{ϵ}Q$ denotes that the hierarchical control level is equal to the pri (primary) and sec (secondary) control level. The constraints Equations 11, 12, 15, 16 are the limits of the primary and secondary upward/downward reserve of the DGs and ESSs respectively. $\Delta p_{B,k,q}^{d,n,t}$ is the change in the qth control level in the kth ESS output in the nth MG in the tth time. $R_{G,g,q}^{n,t}$ and $R_{B,k,q}^{n,t}$ are define in 4.3.

3.4 Real-Time Frequency Regulation

Normally, the primary control, secondary control, and tertiary control are the hierarchical control approach involve in the frequency regulation of MGs-Cluster. As shown in Figure 1, the primary control level, the VSI-based CDER units alleviate the frequency excursions by adjusting their active power outputs in proportion to the frequency excursions (Rezaei and Kalantar, 2015). The primary control has fast response speed and the time scale is between 0.1 ms and 1ms (Wu et al., 2020). However due to inherent errors of the droop controllers, the MG frequency may be stabilizes at a value which may be distinctive to the reference frequency. In such case, the secondary control level, the MGCC can restore the frequency to its reference value by readjusting the active power set-points (Guo et al., 2014). Worth mentioning that, the restoration function should be carried out subject to the MG economic and environmental targets (Li et al., 2019).The response speed of the secondary control is slower than the primary control and the time scale is between 100 ms and 1s (Feng et al., 2017). The tertiary control level is responsible for should coordinate each MG through MGCCC to share active power among them and also regulate the system (de Azevedo et al., 2017; Feng et al., 2017). The tertiary is generally at the slowest level of control and the time scale is in the range of several seconds to minutes (Mohamed et al., 2017).The detailed steady-state model of the droop control function that is shown in Figure 3 is described in (Rezaei and Kalantar, 2015). Furthermore, the control functions corresponding to internal voltage and current controllers have been neglected in the steady state. Worth to be noted, it is assumed that MG is in the steady-state and all the transients and oscillating modes have been died down. The frequency depends on the behavior of the droop-controlled inverter-interfaced DGs and ESSs, as defined in Equations 19, 20 (Rezaei and Kalantar, 2015) where,$\mathit{ }{m}_{pg}$and $m_{p,k}$ are frequency droop control gain of VSI base DG and ESS and ${\omega }_c$ = 8 kHz The Equation 21 ensures that the frequency remains within secure limits; $\mathit{\Delta }{f}_{q,max}^{n,t}$ is the frequency excursion limit.

$\mathit{\Delta }{\mathit{f}}_{\mathit{q}}^{\mathit{n},\mathit{t}}={\mathit{m}}_{\mathit{pg}}.(\mathit{\Delta }{\mathit{P}}_{\mathit{G}.\mathit{g},\mathit{f}}^{\mathit{n},\mathit{t}}-\mathit{\Delta }{\mathit{p}}_{\mathit{G},\mathit{g},\mathit{q}}^{\mathit{n},\mathit{t}})(19)$

$\mathit{\Delta }{\mathit{f}}_{\mathit{q}}^{\mathit{n},\mathit{t}}={\mathit{m}}_{\mathit{p},\mathit{k}}.(\mathit{\Delta }{\mathit{P}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{n},\mathit{t}}-\mathit{\Delta }{\mathit{p}}_{\mathit{B},\mathit{k},\mathit{q}}^{\mathit{n},\mathit{t}})(20)$

$\left|\mathit{\Delta }{\mathit{f}}_{\mathit{q}}^{\mathit{n},\mathit{t}}\right|\le \mathit{\Delta }{\mathit{f}}_{\mathit{q},\mathit{max}}^{\mathit{n},\mathit{t}}(21)$

The frequency depends on the behavior of the droop-controlled inverter-interfaced DGs and ESSs at the primary and secondary control levels. It is noteworthy that, at the primary level, the control functions are processed instantaneously in a few seconds, hence the MGCC does not have enough time to change the base set points of the CDERs. Therefore, $\mathit{\Delta }{P}_{G,g,f}^{n,t}$,$\mathit{ }\mathit{\Delta }{p}_{B,k,f}^{n,t}$ = 0 for all q = pri. (Rezaei and Kalantar, 2015). In contrast, at the secondary control level, the MGCC has more freedom to restore its frequency within its available reserve capacity (Ding et al., 2016). Moreover, if the required energy is not sufficient to restore the frequency, the MGCC has to move to the tertiary control level and purchase energy from another member of the MGs-cluster.

FIGURE 3

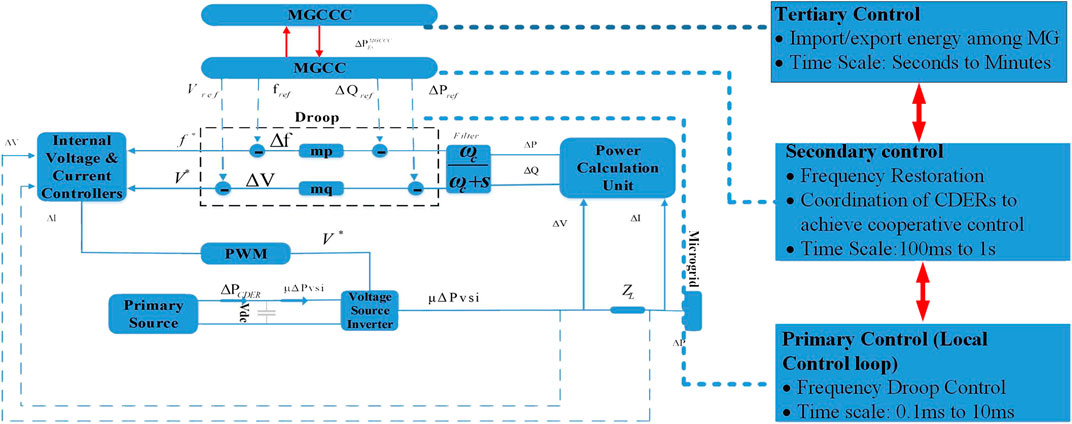
FIGURE 3. The steady-state block diagram of the droop controlled VSI-based CDER unit hierarchical frequency control (Rezaei and Kalantar, 2015).

4 Coalitional Scheduling and Reserve Sharing

4.1 Energy Sharing Among Microgrids

The MGCC tries to schedule its DGs and ESSs to match demand and supply within the MG. The MGCCC supervises the MGCC to schedule the DGs and ESSs for energy sharing when other MGs power generation reaches the capacity constraints. Extending the problem Equations 1–21, the day-ahead energy sharing within MGs-cluster is to minimize the energy exchange cost. Equation 22 shows the amount of energy that an MG can exchange (import/export) with the MGCCC. If the value of $p_{Ex,f}^{n,t}$ is positive, it means MGCC will sell energy to MGCCC. On the other hand, if its value is negative MGCC will buy energy from MGCCC. Equation 23 represents the hourly power balances. The power flow constraint between 2 MGs is expressed in Equation 24 (Rezaei et al., 2018). The overall energy exchange must be zero for isolated MGs-cluster as shown in Equation 25.

${\mathit{p}}_{\mathit{Ex},\mathit{f}}^{\mathit{n},\mathit{t}}=({\mathit{p}}_{\mathit{W},\mathit{w},\mathit{f}}^{\mathit{n},\mathit{t}}+{\mathit{p}}_{\mathit{PV},\mathit{s},\mathit{f}}^{\mathit{n},\mathit{t}}+{\mathit{p}}_{\mathit{G},\mathit{g},\mathit{f}}^{\mathit{n},\mathit{t}}+{\mathit{p}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{n},\mathit{t}})-{\mathit{p}}_{\mathit{L},\mathit{f}}^{\mathit{n},\mathit{t}}(22)$

${\displaystyle \sum }_{\mathit{g}=1}^{{\mathit{N}}_{\mathit{G}}^{\mathit{n}}}{\mathit{p}}_{\mathit{G},\mathit{g},\mathit{f}}^{\mathit{n},\mathit{t}}+{\displaystyle \sum }_{\mathit{k}=1}^{{\mathit{N}}_{\mathit{B}}^{\mathit{n}}}{\mathit{p}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{n},\mathit{t}}+{\displaystyle \sum }_{\mathit{w}=1}^{{\mathit{N}}_{\mathit{W}}^{\mathit{n}}}{\mathit{p}}_{\mathit{W},\mathit{w},\mathit{f}}^{\mathit{n},\mathit{t}}+{\displaystyle \sum }_{\mathit{s}=1}^{{\mathit{N}}_{\mathit{PV}}^{\mathit{n}}}{\mathit{p}}_{\mathit{PV},\mathit{s},\mathit{f}}^{\mathit{n},\mathit{t}}+{\mathit{p}}_{\mathit{Ex},\mathit{f}}^{\mathit{n},\mathit{t}}-{\mathit{p}}_{\mathit{L},\mathit{f}}^{\mathit{n},\mathit{t}}=0(23)$

$\mathit{L*}(\left({\displaystyle \sum }_{\mathit{g}=1}^{{\mathit{N}}_{\mathit{G}}^{\mathit{n}}}{\mathit{p}}_{\mathit{G},\mathit{g},\mathit{f}}^{\mathit{n},\mathit{t}}+{\displaystyle \sum }_{\mathit{k}=1}^{{\mathit{N}}_{\mathit{B}}^{\mathit{n}}}{\mathit{p}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{n},\mathit{t}}\right)+({\displaystyle \sum }_{\mathit{w}=1}^{{\mathit{N}}_{\mathit{W}}^{\mathit{n}}}{\mathit{p}}_{\mathit{W},\mathit{w},\mathit{f}}^{\mathit{n},\mathit{t}}+{\displaystyle \sum }_{\mathit{w}=1}^{{\mathit{N}}_{\mathit{W}}^{\mathit{n}}}{\mathit{p}}_{\mathit{W},\mathit{w},\mathit{f}}^{\mathit{n},\mathit{t}}+{\displaystyle \sum }_{\mathit{s}=1}^{{\mathit{N}}_{\mathit{PV}}^{\mathit{n}}}{\mathit{p}}_{\mathit{PV},\mathit{s},\mathit{f}}^{\mathit{n},\mathit{t}})-\left({\mathit{p}}_{\mathit{L},\mathit{f}}^{\mathit{n},\mathit{t}}\right)\le {\mathit{p}}_{\mathit{L}}^{\mathit{max}}(24)$

${\displaystyle \sum }_{\mathit{n}=1}^{\mathit{N}}{\mathit{p}}_{\mathit{Ex},\mathit{f}}^{\mathit{n},\mathit{t}}=0(25)$

Where, $p_{Ex,f}^{n,t}$ is the scheduled energy sharing among the MGs, where, L represents an $N_L$*($N_B$-1) matrix of the power transfer distribution factor and explain in detail in (Rezaei et al., 2018).

4.2 Reserve Sharing Among Microgrids

In real-time operation, the MGCC utilizes its reserve to address its mismatch first and then participates in reserve sharing to keep the power system in equilibrium; this is defined in Equation 26. The power balance in real-time after reserve sharing is shown in Equation 27 and the power flow constraint between 2 MGs is defined in Equation 28. The sum of the exchanged energy in the isolated MGs-cluster must be equal to zero as shown in Equation 29.

$\mathit{\Delta }{\mathit{p}}_{\mathit{Ex}}^{\mathit{n},\mathit{t}}=(\mathit{\Delta }{\mathit{p}}_{\mathit{W},\mathit{w}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{s},\mathit{PV}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{B},\mathit{k}}^{\mathit{n},\mathit{t}})\mathit{ }-\mathit{\Delta }{\mathit{p}}_{\mathit{L}}^{\mathit{n},\mathit{t}}(26)$

${\displaystyle \sum }_{\mathit{w}=1}^{{\mathit{N}}_{\mathit{W}}^{\mathit{n}}}({\mathit{p}}_{\mathit{W},\mathit{w},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{W},\mathit{w}}^{\mathit{n},\mathit{t}})+{\displaystyle \sum }_{\mathit{s}=1}^{{\mathit{N}}_{\mathit{PV}}^{\mathit{n}}}\left({\mathit{p}}_{\mathit{PV},\mathit{s},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{PV},\mathit{s}}^{\mathit{n},\mathit{t}}\right)+({\mathit{p}}_{\mathit{Ex},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{Ex}}^{\mathit{n},\mathit{t}})-({\mathit{p}}_{\mathit{L},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{L}}^{\mathit{n},\mathit{t}})=0(27)$

$\mathit{L*}\left(\left({\mathit{p}}_{\mathit{G},\mathit{g},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{G},\mathit{g},\mathit{q}}^{\mathit{n},\mathit{t}}\right)+({\mathit{p}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{E},\mathit{k},\mathit{q}}^{\mathit{n},\mathit{t}})\right)+({\mathit{p}}_{\mathit{W},\mathit{w},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{W},\mathit{w}}^{\mathit{n},\mathit{t}})+({\mathit{p}}_{\mathit{PV},\mathit{s},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{PV},\mathit{s}}^{\mathit{n},\mathit{t}})$

$-({\mathit{p}}_{\mathit{L},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{L}}^{\mathit{n},\mathit{t}})\le ({\mathit{p}}_{\mathit{L}}^{\mathit{max}}+\mathit{\Delta }{\mathit{p}}_{\mathit{L}}^{\mathit{max}})(28)$

${\displaystyle \sum }_{\mathit{n}=1}^{\mathit{N}}({\mathit{p}}_{\mathit{Ex},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{Ex}}^{\mathit{n},\mathit{t}})=0(29)$

where $\Delta p_{Ex}^{n,t}$ is the reserve sharing among the MGs and $\mathit{\Delta }{p}_{G,g}^{n,t}$ and $\Delta p_{B,k}^{n,t}$ are the power levels of the DG and ESS that participate in the primary and secondary frequency control.

4.3 Microgrid Component Modeling

The MG energy management system usually solves the day-ahead dispatch problem, which is subject to the power balance constraint of the MG and the operational constraints of the MG components. To enable the formulation of this dispatch problem, the cost functions, and the operational constraints of all the MG components are developed in the following paragraphs. The MG generally consists of DGs, ESSs, WTs, PVs, etc. The objective of optimizing the schedule of an MG is to reduce the overall OC, which contains the operational expenses of the DGs and ESSs, as well as the exchange energy cost between the MGs. The basic cost function corresponding to the energy and reserve cost of DGs and ESSs are given as follows:

${\mathit{C}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{t}}\left({\mathit{p}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{t}}\right)={\mathit{a}}_{\mathit{G},\mathit{g}}^{\mathit{n}}\left({\mathit{p}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{t}}\right)+{\mathit{b}}_{\mathit{G},\mathit{g}}^{\mathit{n}}(30)$

${\mathit{C}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{t},\mathit{R}}={\displaystyle \sum }_{\mathit{q}\mathrm{ϵ}\mathit{Q}}{\mathit{c}}_{\mathit{G},\mathit{g},\mathit{q}}^{\mathit{n},\mathit{R}}.\mathit{ }{\mathit{R}}_{\mathit{G},\mathit{g},\mathit{q}}^{\mathit{n},\mathit{t}}(31)$

${\mathit{C}}_{\mathit{B},\mathit{k}}^{\mathit{n},\mathit{t},\mathit{E}}={\mathit{a}}_{\mathit{B},\mathit{k}}^{\mathit{n}}\left|{\mathit{p}}_{\mathit{B},\mathit{k}}^{\mathit{n},\mathit{t}}\right|(32)$

${\mathit{C}}_{\mathit{B},\mathit{k}}^{\mathit{n},\mathit{t},\mathit{R}}={\displaystyle \sum }_{\mathit{q}\mathrm{ϵ}\mathit{Q}}({\mathit{c}}_{\mathit{B},\mathit{k},\mathit{q}}^{\mathit{n},\mathit{R}}.{\mathit{R}}_{\mathit{B},\mathit{k},\mathit{q}}^{\mathit{n},\mathit{t}})(33)$

The basic OC of DGs in case of the energy $C_{G,g}^{n,t,E}$ and reserve $C_{G,g}^{n,t,R}$ cost is defined in Equations 30, 31, where $p_{G,g}^{n,t}$ and $R_{G,g,q}^{n,t}$ are the active power output and reserve of the gth DG. The $a_{G,g}^n$ and $b_{G,g}^n$ are the OC coefficients and $c_{G,g,q}^{n,R}$ is the reserve cost of the gth DG at control level q. The OC of the ESS in case of the energy $C_{B,k}^{n,t,E}$ and reserve $C_{B,k}^{n,t,R}$ cost is expressed in Equations 32, 33, where $p_{B,k}^{n,t}$ and $R_{G,g,q}^{n,t}$ are the charging and discharging power and reserve of the kth ESS. $c_{B,k}^n$ is the OC coefficient and $c_{B,k,q}^{n,R}$ is the reserve cost of the kth ESS at control level q.

In the day-ahead scheduling, the MGCC schedules its DGs and ESSs within its capacity constraints to match demand and supply in the MG power system as shown in Equation 34; if the MGCC is not able to match the load and power generation, the MGCCC is responsible for energy sharing from other MGs, as follows:

${\displaystyle \sum }_{\mathit{g}=1}^{{\mathit{N}}_{\mathit{G}}^{\mathit{n}}}{\mathit{p}}_{\mathit{G},\mathit{g},\mathit{f}}^{\mathit{n},\mathit{t}}+{\displaystyle \sum }_{\mathit{B}=1}^{{\mathit{N}}_{\mathit{E}}^{\mathit{n}}}{\mathit{p}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{n},\mathit{t}}+{\displaystyle \sum }_{\mathit{w}=1}^{{\mathit{N}}_{\mathit{W}}^{\mathit{n}}}{\mathit{p}}_{\mathit{W},\mathit{w},\mathit{f}}^{\mathit{n},\mathit{t}}+{\displaystyle \sum }_{\mathit{s}=1}^{{\mathit{N}}_{\mathit{PV}}^{\mathit{n}}}{\mathit{p}}_{\mathit{s},\mathit{PV},\mathit{f}}^{\mathit{n},\mathit{t}}-{\mathit{p}}_{\mathit{L},\mathit{f}}^{\mathit{n},\mathit{t}}\ge 0(34)$

The uncertain nature of PVs and WTs makes it a challenging task to obtain real power output values. Therefore, errors exist in the forecasted value; hence, the real power outputs of PVs and WTs are presented as a sum of the forecast values and errors:

${\mathit{p}}_{\mathit{W},\mathit{w}}^{\mathit{n},\mathit{t}}\in [{\mathit{p}}_{\mathit{W},\mathit{w},\mathit{f}}^{\mathit{n},\mathit{t}}-\mathit{\Delta }{\mathit{p}}_{\mathit{W},\mathit{w}}^{\mathit{n},\mathit{t}},{\mathit{p}}_{\mathit{W},\mathit{w},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{W},\mathit{w}}^{\mathit{n},\mathit{t}}](35)$

${\mathit{p}}_{\mathit{PV},\mathit{s}}^{\mathit{n},\mathit{t}}\in [{\mathit{p}}_{\mathit{PV},\mathit{s},\mathit{f}}^{\mathit{n},\mathit{t}}-\mathit{\Delta }{\mathit{p}}_{\mathit{PV},\mathit{s}}^{\mathit{n},\mathit{t}},{\mathit{p}}_{\mathit{PV},\mathit{s},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{PV},\mathit{s}}^{\mathit{n},\mathit{t}}](36)$

Where, $p_{W,w}^{n,t}$ , $p_{W,w,f}^{n,t}$ , and $\Delta p_{W,w}^{n,t}$ are the actual power, forecast power, and forecast errors of the wth WT in nth MG in tth time. $p_{PV,s}^{n,t}$ , $p_{PV,s,f}^{n,t}$; $\Delta p_{PV,s}^{n,t}$ are the actual Power, forecast Power, and forecast errors of the sth PV in nth MG in tth time.

Likewise, the load demand $p_L^{n,t}$ is expressed as follows:

${\mathit{p}}_{\mathit{L}}^{\mathit{n},\mathit{t}}\in [{\mathit{p}}_{\mathit{L},\mathit{f}}^{\mathit{n},\mathit{t}}-\mathit{\Delta }{\mathit{p}}_{\mathit{L}}^{\mathit{n},\mathit{t}},{\mathit{p}}_{\mathit{L},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{L}}^{\mathit{n},\mathit{t}}](37)$

Where,$p_L^{n,t}$, $p_{L,f}^{n,t}$ and $\Delta p_L^{n,t}$ are the actual load, the forecasted load, and forecast error respectively during the tth time interval, which is displayed in Equation 37.

The discrepancy in the power values ${\varphi }^{n,t}$of the nth MG due to the forecast error is defined as follows:

${\varphi }^{\mathit{n},\mathit{t}}={\mathit{p}}_{\mathit{L}}^{\mathit{n},\mathit{t}}-{\displaystyle \sum }_{\mathit{g}=1}^{{\mathit{N}}_{\mathit{G}}^{\mathit{n}}}{\mathit{p}}_{\mathit{G},\mathit{g},\mathit{f}}^{\mathit{n},\mathit{t}}\mathit{ }-{\displaystyle \sum }_{\mathit{k}=1}^{{\mathit{N}}_{\mathit{B}}^{\mathit{n}}}{\mathit{p}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{n},\mathit{t}}-{\displaystyle \sum }_{\mathit{w}=1}^{{\mathit{N}}_{\mathit{W}}^{\mathit{n}}}{\mathit{p}}_{\mathit{W},\mathit{w}}^{\mathit{n},\mathit{t}}-{\displaystyle \sum }_{\mathit{s}=1}^{{\mathit{N}}_{\mathit{PV}}^{\mathit{n}}}{\mathit{p}}_{\mathit{PV},\mathit{s}}^{\mathit{n},\mathit{t}}(38)$

And

${\mathit{p}}_{\mathit{L},\mathit{max}}^{\mathit{n},\mathit{t}}={\mathit{p}}_{\mathit{L},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{L}}^{\mathit{n},\mathit{t}}(39)$

${\mathit{p}}_{\mathit{W},\mathit{w},\mathit{max}}^{\mathit{n},\mathit{t}}={\mathit{p}}_{\mathit{W},\mathit{w},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{W},\mathit{w}}^{\mathit{n},\mathit{t}}(40)$

${\mathit{p}}_{\mathit{PV},\mathit{s},\mathit{max}}^{\mathit{n},\mathit{t}}={\mathit{p}}_{\mathit{PV},\mathit{s},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{PV},\mathit{s}}^{\mathit{n},\mathit{t}}(41)$

${\mathit{p}}_{\mathit{L},\mathit{min}}^{\mathit{n},\mathit{t}}={\mathit{p}}_{\mathit{L},\mathit{f}}^{\mathit{n},\mathit{t}}-\mathit{\Delta }{\mathit{p}}_{\mathit{L}}^{\mathit{n},\mathit{t}}(42)$

${\mathit{p}}_{\mathit{W},\mathit{w},\mathit{min}}^{\mathit{n},\mathit{t}}={\mathit{p}}_{\mathit{W},\mathit{w},\mathit{f}}^{\mathit{n},\mathit{t}}-\mathit{\Delta }{\mathit{p}}_{\mathit{W},\mathit{w}}^{\mathit{n},\mathit{t}}(43)$

${\mathit{p}}_{\mathit{PV},\mathit{s},\mathit{min}}^{\mathit{n},\mathit{t}}={\mathit{p}}_{\mathit{PV},\mathit{s},\mathit{f}}^{\mathit{n},\mathit{t}}-\mathit{\Delta }{\mathit{p}}_{\mathit{PV},\mathit{s}}^{\mathit{n},\mathit{t}}(44)$

where $p_{L,max}^{n,t}$, $p_{W,w,max}^{n,t}$, and $p_{PV,s,max}^{n,t}$ are the maximum values of $p_L^{n,t}$, $p_{W,w}^{n,t}$, and $p_{PV,s}^{n,t}$, respectively. $p_{L,min}^{n,t}$ ,$p_{W,w,min}^{n,t}$, and $p_{PV,s,min}^{n,t}$are the corresponding minimum values. It is evident in Equations 39–44 that ${\varphi }^{n,t}$ is an interval number and the maximum and minimum values are obtained as follows:

${\varphi }_{\mathit{max}}^{\mathit{n},\mathit{t}}={\displaystyle \sum }_{\mathit{w}=1}^{{\mathit{N}}_{\mathit{W}}^{\mathit{n}}}\mathit{\Delta }{\mathit{p}}_{\mathit{W},\mathit{w}}^{\mathit{n},\mathit{t}}+{\displaystyle \sum }_{\mathit{s}=1}^{{\mathit{N}}_{\mathit{PV}}^{\mathit{n}}}\mathit{\Delta }{\mathit{p}}_{\mathit{PV},\mathit{s}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{L}}^{\mathit{n},\mathit{t}}(45)$

${\varphi }_{\mathit{min}}^{\mathit{n},\mathit{t}}=-{\displaystyle \sum }_{\mathit{w}=1}^{{\mathit{N}}_{\mathit{W}}^{\mathit{n}}}\mathit{\Delta }{\mathit{p}}_{\mathit{W},\mathit{w}}^{\mathit{n},\mathit{t}}-{\displaystyle \sum }_{\mathit{s}=1}^{{\mathit{N}}_{\mathit{PV}}^{\mathit{n}}}\mathit{\Delta }{\mathit{p}}_{\mathit{PV},\mathit{s}}^{\mathit{n},\mathit{t}}-\mathit{\Delta }{\mathit{p}}_{\mathit{L}}^{\mathit{n},\mathit{t}}(46)$

The differences between the forecasted and real-time values due to the uncertain nature of PVs, WTs, and load demand might result in instability in the power system; therefore, the MGCC tries to utilize the reserve resources to maintain a stable power system. A new approach for real-time OPF was introduced in (Reddy and Bijwe, 2016) by using the ‘best-fit’ participation factors (PFs) of each power source. The term ${\varphi }^{n,t}$ represents the power imbalance to the base point solution; the PF that provides the power source for each reserve is shown in Equations 47, 48. The actual outputs of the DGs and ESSs can be determined with Equations 49, 50. The MGCC will try to balance the uncertainty with its available resources as shown in Equation 51 and if the MG reserve resource hits the capacity constraints, the MGCCC is responsible for reserve sharing from other MGs.

$\mathit{P}{\mathit{F}}_{\mathit{G},\mathit{g}}^{\mathit{n}}=\frac{\mathit{ }{\mathit{p}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{t},}}{{{\displaystyle \sum }}_{\mathit{g}=1}^{{\mathit{N}}_{\mathit{G}}^{\mathit{n}}}\mathit{ }{\mathit{p}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{t}}+{{\displaystyle \sum }}_{\mathit{k}=1}^{{\mathit{N}}_{\mathit{B}}^{\mathit{n}}}{\mathit{p}}_{\mathit{B},\mathit{k}}^{\mathit{n},\mathit{t}}}(47)$

$\mathit{P}{\mathit{F}}_{\mathit{B},\mathit{k}}^{\mathit{n}}=\frac{\mathit{ }{\mathit{p}}_{\mathit{E},\mathit{k}}^{\mathit{n},\mathit{t},}}{{{\displaystyle \sum }}_{\mathit{g}=1}^{{\mathit{N}}_{\mathit{G}}^{\mathit{n}}}\mathit{ }{\mathit{p}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{t}}+{{\displaystyle \sum }}_{\mathit{k}=1}^{{\mathit{N}}_{\mathit{B}}^{\mathit{n}}}{\mathit{p}}_{\mathit{B},\mathit{k}}^{\mathit{n},\mathit{t}}}(48)$

$\mathit{ }{\mathit{p}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{t}}={\mathit{p}}_{\mathit{G},\mathit{g},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{P}{\mathit{F}}_{\mathit{G},\mathit{g}}^{\mathit{n}}{\varphi }^{\mathit{n},\mathit{t}}(49)$

$\mathit{ }{\mathit{p}}_{\mathit{E},\mathit{k}}^{\mathit{n},\mathit{t}}={\mathit{p}}_{\mathit{E},\mathit{k},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{P}{\mathit{F}}_{\mathit{B},\mathit{k}}^{\mathit{n}}{\varphi }^{\mathit{n},\mathit{t}}(50)$

${\displaystyle \sum }_{\mathit{g}=1}^{{\mathit{N}}_{\mathit{G}}^{\mathit{n}}}\left({\mathit{p}}_{\mathit{G},\mathit{g},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{t}}\right)+{\displaystyle \sum }_{\mathit{k}=1}^{{\mathit{N}}_{\mathit{B}}^{\mathit{n}}}({\mathit{p}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{B},\mathit{k}}^{\mathit{n},\mathit{t}})+{\displaystyle \sum }_{\mathit{w}=1}^{{\mathit{N}}_{\mathit{W}}^{\mathit{n}}}({\mathit{p}}_{\mathit{W},\mathit{w},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{W},\mathit{w}}^{\mathit{n},\mathit{t}})+{\displaystyle \sum }_{\mathit{s}=1}^{{\mathit{N}}_{\mathit{PV}}^{\mathit{n}}}\left({\mathit{p}}_{\mathit{s},\mathit{PV},\mathit{f}}^{\mathit{n},\mathit{t}}\right)$

$+{\displaystyle \sum }_{\mathit{s}=1}^{{\mathit{N}}_{\mathit{PV}}^{\mathit{n}}}({\mathit{p}}_{\mathit{s},\mathit{PV},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{s},\mathit{PV}}^{\mathit{n},\mathit{t}})-({\mathit{p}}_{\mathit{L},\mathit{f}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{L}}^{\mathit{n},\mathit{t}})\ge 0(51)$

5 Economic Model

5.1 Cooperative Game-Based Energy and Reserve Sharing

The coalitional game for the energy and reserve sharing model is denoted as {N, υ, φ}. The MGs-cluster is denoted by ϰ where the number of MGs is N. Therefore, $2^N$ possible alliances can cooperate for N MG. Furthermore, a 4-MG game comprises 16 possible alliances, including an empty alliance {∅} and the grand alliance {N}. υ denotes the characteristic function for a random alliance S ⊂ $2^N$ and φ is the vector of payment to be allocated to individual MGs (Li et al., 2018).

The MGs-cluster coalitional operation that is used to quantify the economic benefit is based on the coalitional characteristic function. To achieve equal distribution of benefits/turn over to each member of the cluster, an allocation framework is adopted. In the cooperative environment, the power exchange should consider energy sharing and the MG can provide reserve sharing for ancillary services to other members of the cluster. The MGCCC is responsible for the determination of the optimal energy and reserve sharing. The benefit function π_S is formulated as follows:

${\mathit{\pi }}_{\mathit{s}}=-{\mathit{C}}_{\mathit{S}}=-{\displaystyle \sum }_{\mathit{n}=1}^{\mathit{S}}{\mathit{C}}^{\mathit{n}}=-{\displaystyle \sum }_{\mathit{n}=1}^{\mathit{S}}{\displaystyle \sum }_{\mathit{t}=1}^{\mathit{T}}\{{\displaystyle \sum }_{\mathit{g}=1}^{{\mathit{N}}_{\mathit{G}}^{\mathit{n}}}({\mathit{C}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{E}}+{\mathit{C}}_{\mathit{G},\mathit{g}}^{\mathit{n},\mathit{R}})+{\displaystyle \sum }_{\mathit{k}=1}^{{\mathit{N}}_{\mathit{B}}^{\mathit{n}}}({\mathit{C}}_{\mathit{B},\mathit{k}}^{\mathit{n},\mathit{E}}+{\mathit{C}}_{\mathit{B},\mathit{k}}^{\mathit{n},\mathit{R}})\}\mathit{ }(52)$

where the total OC of the MGs-cluster is denoted by $C_{\mathcal{S}}$ and S is the number of MGs in this coalition.${\varphi }^t$ represents the total power mismatch in terms of:

${\varphi }^{\mathit{t}}={\displaystyle \sum }_{\mathit{n}=1}^{\mathit{S}}\mathit{ }{\varphi }^{\mathit{n},\mathit{t}}={\displaystyle \sum }_{\mathit{n}=1}^{\mathit{S}}\{{\mathit{p}}_{\mathit{L}}^{\mathit{n},\mathit{t}}-\mathit{ }{\displaystyle \sum }_{\mathit{g}=1}^{{\mathit{N}}_{\mathit{G}}^{\mathit{n}}}\mathit{ }{\mathit{p}}_{\mathit{G},\mathit{g},\mathit{f}}^{\mathit{n},\mathit{t},}-{\displaystyle \sum }_{\mathit{k}=1}^{{\mathit{N}}_{\mathit{B}}^{\mathit{n}}}{\mathit{p}}_{\mathit{B},\mathit{k},\mathit{f}}^{\mathit{n},\mathit{t}}-{\displaystyle \sum }_{\mathit{w}=1}^{{\mathit{N}}_{\mathit{W}}^{\mathit{n}}}{\mathit{p}}_{\mathit{W},\mathit{w}}^{\mathit{n},\mathit{t}}-{\displaystyle \sum }_{\mathit{s}=1}^{{\mathit{N}}_{\mathit{PV}}^{\mathit{n}}}{\mathit{p}}_{\mathit{PV},\mathit{s}}^{\mathit{n},\mathit{t}}\}(53)$

Equations 45, 46 indicate that the overall power mismatches with the maximum and minimum values are defined as:

${\varphi }_{\mathit{max}}^{\mathit{t}}={\displaystyle \sum }_{\mathit{n}=1}^{\mathit{S}}\{\mathit{ }{\displaystyle \sum }_{\mathit{w}=1}^{{\mathit{N}}_{\mathit{W}}^{\mathit{n}}}\mathit{\Delta }{\mathit{p}}_{\mathit{W},\mathit{w}}^{\mathit{n},\mathit{t}}+{\displaystyle \sum }_{\mathit{s}=1}^{{\mathit{N}}_{\mathit{PV}}^{\mathit{n}}}\mathit{\Delta }{\mathit{p}}_{\mathit{PV},\mathit{s}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{L}}^{\mathit{n},\mathit{t}}\}(54)$

${\varphi }_{\mathit{min}}^{\mathit{t}}=-{\displaystyle \sum }_{\mathit{n}=1}^{\mathit{S}}\{\mathit{ }{\displaystyle \sum }_{\mathit{w}=1}^{{\mathit{N}}_{\mathit{W}}^{\mathit{n}}}\mathit{\Delta }{\mathit{p}}_{\mathit{W},\mathit{w}}^{\mathit{n},\mathit{t}}+{\displaystyle \sum }_{\mathit{s}=1}^{{\mathit{N}}_{\mathit{PV}}^{\mathit{n}}}\mathit{\Delta }{\mathit{p}}_{\mathit{PV},\mathit{s}}^{\mathit{n},\mathit{t}}+\mathit{\Delta }{\mathit{p}}_{\mathit{L}}^{\mathit{n},\mathit{t}}\}(55)$

Therefore, the proposed model of energy sharing scheduling and real-time reserve sharing for the isolated MGs-cluster is defined as follows:

$\mathbf{max}\mathit{ }{\mathit{\pi }}_{\mathcal{S}}\left(\mathit{x}.\mathit{u}\right) \mathbf{o}\mathbf{r}\mathbf{ min}\mathit{ }{\mathit{C}}_{\mathcal{S}}\left(\mathit{x}.\mathit{u}\right)(56)$

$\mathbf{s}.\mathbf{t} \mathit{G}\left(\mathit{x}.\mathit{u}\right)=0(57)$

$\mathit{H}\left(\mathit{x}.\mathit{u}\right)\le 0(58)$

where $x$ is the vector of the decision variables, including $p_{G,g}^{n,t}$ and $p_{B,k}^{n,t}$, where $\left(n=\mathrm{1,2},\dots \dots \dots ,N\right)$. The uncertain variables of the MGs-cluster are denoted by$u$ and consist of $p_{W,w}^{n,t}$, $p_{PV,s}^{n,t}$, and $p_L^{n,t}$. $G\left(x.u\right)$ are the equality constraints, which include Equations 6, 17, 19, 20, 22, 23, 25–27, 29, 51 whereas $H\left(x.u\right)$are the inequality constraints, comprised of Equations 2–5, 7, 9–21, 24, 28, 34–38, 46–50, 53–54. Note that “max${\pi }_{\mathcal{S}}\left(x.u\right)$” is equivalent to “min$C_{\mathcal{S}}\left(x.u\right)$” based on Equation 1.

To solve the optimization problem that is shown in Equations 46–48, the uncertain variables have to be determined. One of the best approaches to solve this problem is the affine ARO (Kumar et al., 2017). The off-shore solvers used is CPLEX.

5.2 Profit Distribution Between Microgrids-Cluster

In a coalitional game, every alliance S aims to ensure that each member of the game obtains an economic benefit; thus, the characteristic function of each MG union is represented by $v\left(\mathcal{S}\right)$. Due to the coalition of MGs, it is essential to determine the characteristic function of each union, which indicates that each member makes a profit due to the coalitional mode. The characteristic function is defined as follows:

$\mathit{v}\left(\mathcal{U}\right)={\mathit{\pi }}_{\mathcal{U}}-{\displaystyle \sum }_{\mathit{\omega }\mathrm{ϵ}\mathcal{S}}{\mathit{\pi }}_{\mathit{\omega }}(59)$

where $\omega$ is a single MG in the coalition $\mathcal{S}$. When the MGs operate without the coalition mode, the entire profits acquired by the MGs are ${\displaystyle \sum }_{\omega \mathit{ϵ}\mathcal{S}}{\pi }_{\omega }$. The proposed scheduling model for energy sharing and real-time reserve sharing for MGs-cluster in the coalitional game is super-additive (Kumar et al., 2017) as follows:

$\mathit{v}\left(\mathcal{S}\right)-\mathit{v}\left(\mathcal{U}\right)={\mathit{\pi }}_{\mathcal{S}}-{\displaystyle \sum }_{\mathit{\omega }\mathrm{ϵ}\mathcal{S}}{\mathit{\pi }}_{\mathit{\omega }}+{\mathit{\pi }}_{\mathcal{U}}-{\displaystyle \sum }_{\mathit{\omega }\mathrm{ϵ}\mathcal{U}}{\mathit{\pi }}_{\mathit{\omega }}={\mathit{\pi }}_{\mathit{S}}+{\mathit{\pi }}_{\mathcal{U}}-{\displaystyle \sum }_{\mathit{\omega }\mathrm{ϵ}\mathcal{S}{{\displaystyle \cup }}^{\text{}}\mathcal{U}}{\mathit{\pi }}_{\mathit{\omega }}\le {\mathit{\pi }}_{\mathcal{S}{{\displaystyle \cup }}^{\text{}}\mathcal{U}}-{\displaystyle \sum }_{\mathit{\omega }\mathrm{ϵ}\mathcal{S}{{\displaystyle \cup }}^{\text{}}\mathcal{U}}{\mathit{\pi }}_{\mathit{\omega }}$

$=\mathit{v}\left(\mathcal{S}{{\displaystyle \cup }}^{\text{}}\mathcal{U}\right)(60)$

This approach is described in Equation 57 and the simulation results verify that the maximum profit is achieved by the alliance in which all MGs in the cluster participated. Hence for equal distribution of profits among all members of the MGs-figure, the Shapley value is the best approach (Anvari-Moghaddam et al., 2017). The Shapley value is formulated for the nth MG as follows:

${\varnothing }_{\mathit{n}}\left(\mathit{v}\right)={\displaystyle \sum }_{\mathit{S}\subseteq \mathcal{N}\left\{\mathit{n}\right\}}\frac{\left|\mathcal{S}\right|!\left(\left|\mathcal{N}\right|-\left|\mathcal{S}\right|-1\right)!}{\left|\mathcal{N}\right|!}\left[\mathit{v}\left(\mathcal{N}{{\displaystyle \cup }}^{\text{}}\left\{\mathit{n}\right\}\right)-\mathit{v}\left(\mathcal{S}\right)\right](61)$

where $\left|\mathcal{N}\right|$ are the total number of MGs and the sum extends over all subsets S of S excluding the nth MG. |$\mathcal{S}$ | is the number of MGs in S . The formula can be interpreted as follows: considering that the coalition is formed 1 MG at a time, each MG demands its contribution v ($\mathcal{S}$ ∪{$n$ }) − v ($\mathcal{S}$ ) as fair compensation; it then uses the average of this contribution over different combinations in which the coalition can be formed. It should be mentioned that the MGCCC is the authorized entity for conducting the benefit distribution.

6 Case Study

6.1 Case Description

A cluster of 4 MGs (see Figure 1) is used as a test system for the proposed model. Each MG comprises 1 DG, 1 ESS,1 WT, and 1 PV. The associated parameters of these components are listed in Table 1. Figure 4 shows the forecast values of the output powers of the WT, PV, and load demands; their forecasting errors are 20%, 10%, and 10% (Li et al., 2018), respectively, Furthermore, the power mismatch among MGs due to unpredictable nature of PVs, WTs, and Load are shown in Figure 5. The service fee imposed by the MGCCC on both the buyer and seller MG is 0.005 $/kW (Sampath et al., 2018).

TABLE 1

TABLE 1. MGs-cluster parameter.

FIGURE 4

FIGURE 4. Forecast values of the power outputs of the (A) WT, (B) PV, and (C) load.

FIGURE 5

FIGURE 5. Power mismatch in MG1, MG2, MG3, MG4.

6.2 Simulation Results and Discussion

Since the MGs-cluster consists of a system of 4 MGs, 16 different alliances can be formed in the coalitional game. The turn-over of the coalition’s MG (1,2,3), MG (1,2,4), MG (1,3,4), MG (2,3,4), and MG (1,2,3,4) are $61.10, $48.40, $48.53, $46.50, and $71.25 respectively, which is calculated by Equation 61 and shown in Table 2 and Figure 6 The maximum obtained profit is $71.25, which is obtained by the coalition MG (1, 2, 3, 4). The results indicate that if all 4 MGs operate in a coordinated and coalitional manner, the combined profit is maximized. The total economic cost of MG4 is $6.64, demonstrating that MG4 compensates for all its expenses by selling its surplus electricity that is worth $64.42 and $33.02 in energy and reserve sharing respectively. To obtain an economic benefit and it also plays its part to keep the isolated MGs-cluster in equilibrium and stable.

TABLE 2

TABLE 2. Operational cost and RC for coalitions of MGs.

FIGURE 6

FIGURE 6. Turnover and EC of MG coalition.

The optimal results of jointed energy and reserve scheduling in term of MG (1,2,3,4) consist of day-ahead scheduling of DGs and ESSs, furthermore, the participation factor (PFs) of DGs and ESSs are shown in Figures 7, 8, respectively The DGs participate in both energy and reserve scheduling but the DG in MG2 operates on a full load, as shown in Figure 7A. Therefore, the respective DG cannot participate in reserve energy as shown in Figure 8A However, as shown in Figure 7B, it is noted that ESSs do not participate in the energy scheduling, specifically MG1, MG2, and MG3, while they focus on participation in reserve energy sharing as presented in Figure 8B, therefore their PFs exceed 0.2 for all time interval. But MG4 will charge and discharge in the first to fourth and the 20th and 24th hour respectively. As a result, the participation of ESS in MG4 is reserve sharing is less than those of MG1, MG2, and MG3 during these time intervals.

FIGURE 7

FIGURE 7. Optimal energy scheduling of the (A) DGs and (B) ESSs.

FIGURE 8

FIGURE 8. Participation factor of (A) DGs and (B) ESSs.

The real-time outputs of all CDERs and the exchanged energy in period 5:00 to 5:15 based on the optimal plan are depicted in Figure 9. The output of the WTs in MG1 decreases from 52.2 kW to 41.76 kW, the DG output increases from 180 kW to 200 kW, the ESS discharges 3.26 kW, and 6.10 kW of reserve energy is purchased from MG3 through MGCCC to compensate for the mismatch. The load increases from 180.81 kW (planned value) to 198.89 kW (real-time value).

FIGURE 9

FIGURE 9. Reserve sharing in the fifth, 12th, and 21st hours.

The real-time outputs of all CDERs and the exchanged energy in period 12:00 to 12:15 based on the optimal plan are shown in subsection Figure 9. The forecast outputs and optimal schedule values are depicted in Figures 4, 7. The WT output in MG1 increases from 70.2 kW (planned value) to 84.24 kW (real-time value), the load increases from 285.03 kW to 313.63 kW, and the PV output increases from 61.92 kW to 68.112 kW. The DG output increases from 182 kW to 200 kW, the ESS discharges 6.19 kW, 8.62 kW of reserve energy is purchased from MG3, and 14.03 kW is purchased from MG4 through MGCCC to compensate for the mismatch.

The real-time outputs of all CDERs and the exchanged energy in period 21:00 to 21:15 based on the optimal plan are shown in subsection Figure 9. The output of the WTs in MG1 increases from 42.1 kW (planned value) to 50.52 kW (real-time value), the load increases from 302.70 kW to 332.97 kW, and the PV output decreases from 1.44 kW to 1.296 kW. Since the DG was scheduled to operate on a full load, it cannot participate in reducing the mismatch. Therefore MG1 purchases 8.49 kW from MG3 and 25.14 kW from MG4 through MGCCC to compensate for the mismatch.

As shown in Figure 10, the frequency of the MGs for periods 5:00–5:15, 12:00–12:15, and 21:00–21:15 are stabilized from 49.89 Hz, 49.88 Hz, and 49.86 Hz–50 Hz respectively, after reserve sharing. Figure 11A depicts the energy sharing and Figure 11B depicts the reserve sharing among the MGs.

FIGURE 10

FIGURE 10. Frequency Restoration in the fifth, 12th, and 21st hours.

FIGURE 11

FIGURE 11. Power exchange among MGs-Cluster MGs.

Using the obtained optimal coalitional energy and reserve scheduling solution for MG (1,2,3,4), we obtain the values of the day-ahead operational cost (DAOC) and Reserve Cost (RC) in term of DGs, ESSs and Power exchange cost (EX) for each MG which are shown in Table 3. Compared with the benefit values for MG1, MG2, MG3, and MG4 presented in Table 2. As presented in Table 2 when MGs operate in isolated mode the turnover in of every MG is null as each MG tries to balance its generation and load as well as DGs also try to follow the load curve in both energy and reserve operation which is shown in Figure 12. In Cooperative mode, each MG tries to balance its generation and load as well to get some benefit by sell surplus energy to other MGs as compare the benefit of MG4 in (Isolated Mode) which is 0$ with the turn-over in (Cooperative Mode) which is 25.56$, the value of such benefit is 25.56$-0$ = 25.56$. The other benefit of the cooperative mode of operation is the smooth curve of DG which in other words reduces the operation cost of DG which is shown in Figure 12.

TABLE 3

TABLE 3. Operational cost and RC for the coalition MG (1, 2, 3, 4).

FIGURE 12

FIGURE 12. Benefits of Coalitional operation of MGs-Cluster.

7 Conclusion

This study proposed a techno-economic framework for the optimal operation of isolated MGs-cluster by scheduling coalitional energy sharing and real-time reserve sharing for ancillary services such as frequency regulation caused by the uncertainty of PVs, WTs, and loads. The coalitional economic benefits of each member of a coalition are determined by shapely. A case study was conducted on the Isolated MGs-cluster and simulation results have been investigated in terms of energy and reserve sharing to stabilize the frequency of cluster power systems in real-time which is the technical aspect of our framework. Furthermore, we verify the effectiveness of the proposed coalitional sharing scheme for the economic operation of a cluster, compared with their isolated operation which explains the economical aspect of our framework. As we are considering the frequency regulation therefore, we consider the active power for the whole system. Therefore, our future research direction is to include the control issues of voltage and reactive power in our system.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

The author HQ is the Ph.D. scholar, who introduced the conceptualization of the idea, implemented the proposed scheme and contributed to concepts with the help of Professor NL and TZ supervised and finalized the proposed research. TW and ZU helped out in manuscript writing, original draft and verified the simulation results in accordance to the investigated case studies. All authors have read and agreed to the published current version of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Aktas, A., Erhan, K., Ozdemir, S., and Ozdemir, E. (2017). Experimental investigation of a new smart energy management algorithm for a hybrid energy storage system in smart grid applications. Elec. Power Syst. Res. 144, 185–196. doi:10.1016/j.epsr.2016.11.022

CrossRef Full Text | Google Scholar

Ali, M. S., Haque, M. M., and Wolfs, P. (2019). A review of topological ordering based voltage rise mitigation methods for LV distribution networks with high levels of photovoltaic penetration. Renew. Sustain. Energy Rev. 103, 463–476. doi:10.1016/j.rser.2018.12.049

CrossRef Full Text | Google Scholar

Anvari-Moghaddam, A., Guerrero, J. M., Vasquez, J. C., Monsef, H., and Rahimi-Kian, A. (2017). Efficient energy management for a grid-tied residential microgrid. IET Gener. Transm. Distrib. 11 (11), 2752–2761. doi:10.1049/iet-gtd.2016.1129

CrossRef Full Text | Google Scholar

Arani, M. F. M., and Mohamed, Y. A.-R. I. (2017). Dynamic droop control for wind turbines participating in primary frequency regulation in microgrids. IEEE Trans. Smart Grid. 9 (6), 5742–5751. doi:10.1109/tsg.2017.2696339

CrossRef Full Text | Google Scholar

Basso, T., Hambrick, J., and DeBlasio, D. (2012). “Update and review of IEEE P2030 smart grid interoperability and IEEE 1547 interconnection standards”, in IEEE PES innovative smart grid technologies (ISGT). (Washington, DC, United States: IEEE), 1–7.

Google Scholar

Castilla, M., de Vicuña, L. G., and Miret, J. (2019). “Control of power converters in AC microgrids,” in Microgrids design and implementation. (Switzerland: Springer), 139–170.

CrossRef Full Text | Google Scholar

de Azevedo, R., Cintuglu, M. H., Ma, T., and Mohammed, O. A. (2017). Multiagent-based optimal microgrid control using fully distributed diffusion strategy. IEEE Trans. Smart Grid. 8 (4), 1997–2008. doi:10.1109/tsg.2016.2587741

CrossRef Full Text | Google Scholar

Ding, T., Bie, Z., Bai, L., and Li, F. (2016). Adjustable robust optimal power flow with the price of robustness for large-scale power systems. IET Gener. Transm. Distrib. 10 (1), 164–174. doi:10.1049/iet-gtd.2015.0561

CrossRef Full Text | Google Scholar

Faisal, M., Hannan, M. A., Ker, P. J., Hussain, A., Mansor, M. B., and Blaabjerg, F. (2018). Review of energy storage system technologies in microgrid applications: issues and challenges. IEEE Access. 6, 35143–35164. doi:10.1109/access.2018.2841407

CrossRef Full Text | Google Scholar

Feng, X., Shekhar, A., Yang, F., Hebner, E. R., and Bauer, P. (2017). Comparison of hierarchical control and distributed control for microgrid. Elec. Power Compon. Syst. 45 (10), 1043–1056. doi:10.1080/15325008.2017.1318982

CrossRef Full Text | Google Scholar

Gao, H., Liu, J., Wang, L., and Wei, Z. (2017). Decentralized energy management for networked microgrids in future distribution systems. IEEE Trans. Power Syst. 33(4), 3599–3610. doi:10.1109/tpwrs.2017.2773070

CrossRef Full Text | Google Scholar

Ghadi, M. J., Ghavidel, S., Rajabi, A., Azizivahed, A., Li, L., and Zhang, J. (2019). A review on economic and technical operation of active distribution systems. Renew. Sustain. Energy Rev. 104, 38–53. doi:10.1016/j.rser.2019.01.010

CrossRef Full Text | Google Scholar

Ghahramani, M., Nazari-Heris, M., Zare, K., and Mohammadi-Ivatloo, B. (2019). Energy and reserve management of a smart distribution system by incorporating responsive-loads/battery/wind turbines considering uncertain parameters. Energy. 183, 205–219. doi:10.1016/j.energy.2019.06.085

CrossRef Full Text | Google Scholar

Guo, F., Wen, C., Mao, J., and Song, Y.-D. (2014). Distributed secondary voltage and frequency restoration control of droop-controlled inverter-based microgrids. IEEE Trans. Ind. Electron. 62 (7), 4355–4364. doi:10.1109/TIE.2014.2379211

Google Scholar

Hamidi, A., Nazarpour, D., and Golshannavaz, S. (2017). Multiobjective scheduling of microgrids to harvest higher photovoltaic energy. IEEE Trans. Ind. Inf. 14 (1), 47–57. doi:10.1109/tii.2017.2717906

CrossRef Full Text | Google Scholar

Hu, W., Wang, P., and Gooi, H. B. (2016). Toward optimal energy management of microgrids via robust two-stage optimization. IEEE Trans. Smart Grid. 9 (2), 1161–1174. doi:10.1109/tsg.2016.2580575

CrossRef Full Text | Google Scholar

Ketabi, A., Rajamand, S., and Shahidehpour, M. (2017). Accurate power sharing for parallel DGs in microgrid with various-type loads. Energy Equip. Syst. 5 (1), 27–41. doi:10.22059/ees.2017.60847

Google Scholar

Kumar, D., Zare, F., and Ghosh, A. (2017). DC microgrid technology: system architectures, AC grid interfaces, grounding schemes, power quality, communication networks, applications, and standardizations aspects. IEEE Access. 5, 12230–12256. doi:10.1109/access.2017.2705914

CrossRef Full Text | Google Scholar

Lara, J. D., Olivares, D. E., and Canizares, C. A. (2018). Robust energy management of isolated microgrids. IEEE Syst. J. 13 (1), 680–691. doi:10.1109/JSYST.2018.2828838

Google Scholar

Li, Y., Zhao, T., Wang, P., Gooi, H. B., Wu, L., Liu, Y., et al. (2018). Optimal operation of multimicrogrids via cooperative energy and reserve scheduling. IEEE Trans. Ind. Inf. 14 (8), 3459–3468. doi:10.1109/tii.2018.2792441

CrossRef Full Text | Google Scholar

Li, Z., Cheng, Z., Liang, J., Si, J., Dong, L., and Li, S. (2019). Distributed event-triggered secondary control for economic dispatch and frequency restoration control of droop-controlled AC microgrids. IEEE Trans. Sustainable Energy. 11 (3), 1938–1950. doi:10.1109/tste.2019.2946740

CrossRef Full Text | Google Scholar

Lin, P., Jin, C., Xiao, J., Li, X., Shi, D., Tang, Y., et al. (2018). A distributed control architecture for global system economic operation in autonomous hybrid AC/DC microgrids. IEEE Trans. Smart Grid. 10 (3), 2603–2617. doi:10.1109/tsg.2018.2805839

CrossRef Full Text | Google Scholar

Liu, T., Tan, X., Sun, B., Wu, Y., and Tsang, D. H. (2018). Energy management of cooperative microgrids: a distributed optimization approach. Int. J. Electr. Power Energy Syst. 96, 335–346. doi:10.1016/j.ijepes.2017.10.021

CrossRef Full Text | Google Scholar

Liu, Z., Yi, Y., Yang, J., Tang, W., Zhang, Y., Xie, X., et al. (2019). Optimal planning and operation of dispatchable active power resources for islanded multi-microgrids under decentralised collaborative dispatch framework. IET Gener. Transm. Distrib. 14 (3), 408–422. doi:10.1049/iet-gtd.2019.0796

CrossRef Full Text | Google Scholar

Luo, L., Abdulkareem, S. S., Rezvani, A., Miveh, M. R., Samad, S., Aljojo, N., et al. (2020). Optimal scheduling of a renewable based microgrid considering photovoltaic system and battery energy storage under uncertainty. J. Energy Storage. 28, 101306. doi:10.1016/j.est.2020.101306

CrossRef Full Text | Google Scholar

Lv, T., and Ai, Q. (2016). Interactive energy management of networked microgrids-based active distribution system considering large-scale integration of renewable energy resources. Appl. Energy. 163, 408–422. doi:10.1016/j.apenergy.2015.10.179

CrossRef Full Text | Google Scholar

Lv, T., Ai, Q., and Zhao, Y. (2016). A bi-level multi-objective optimal operation of grid-connected microgrids. Elec. Power Syst. Res. 131, 60–70. doi:10.1016/j.epsr.2015.09.018

CrossRef Full Text | Google Scholar

Ma, L., Liu, N., Zhang, J., Tushar, W., and Yuen, C. (2016). Energy management for joint operation of CHP and PV prosumers inside a grid-connected microgrid: a game theoretic approach. IEEE Trans. Ind. Inf. 12 (5), 1930–1942. doi:10.1109/tii.2016.2578184

CrossRef Full Text | Google Scholar

Mohamed, A. A., Elsayed, A. T., Youssef, T. A., and Mohammed, O. A. (2017). Hierarchical control for DC microgrid clusters with high penetration of distributed energy resources. Elec. Power Syst. Res. 148, 210–219. doi:10.1016/j.epsr.2017.04.003

CrossRef Full Text | Google Scholar

Mostafa, M. H., Aleem, S. H. A., Ali, S. G., Abdelaziz, A. Y., Ribeiro, P. F., and Ali, Z. M. (2020). Robust energy management and economic analysis of microgrids considering different battery characteristics. IEEE Access. 8, 54751–54775. doi:10.1109/access.2020.2981697

CrossRef Full Text | Google Scholar

Pinzón, A. M. O., da Silveira, P. M., and Baghzouz, Y. (2018). “Simulation of microgrid hierarchical control”, in 18th international conference on harmonics and quality of power (ICHQP). (Ljubljana, Slovenia: IEEE), 1–6.

Google Scholar

Pourghasem, P., Sohrabi, F., Abapour, M., and Mohammadi-Ivatloo, B. (2019). Stochastic multi-objective dynamic dispatch of renewable and CHP-based islanded microgrids. Elec. Power Syst. Res. 173, 193–201. doi:10.1016/j.epsr.2019.04.021

CrossRef Full Text | Google Scholar

Purage, M. I. S. L., Krishnan, A., Foo, E. Y., and Gooi, H. B. (2019). Cooperative bidding-based robust optimal energy management of multimicrogrids. IEEE Trans. Ind. Inf. 16 (9), 5757–5768. doi:10.1109/tii.2019.2955991

CrossRef Full Text | Google Scholar

Reddy, S. S., and Bijwe, P. (2016). Day-ahead and real time optimal power flow considering renewable energy resources. Int. J. Electr. Power Energy Syst. 82, 400–408. doi:10.1016/j.ijepes.2016.03.033

CrossRef Full Text | Google Scholar

Rezaei, N., Ahmadi, A., Khazali, A. H., and Guerrero, J. M. (2018). Energy and frequency hierarchical management system using information gap decision theory for islanded microgrids. IEEE Trans. Ind. Electron. 65 (10), 7921–7932. doi:10.1109/tie.2018.2798616

CrossRef Full Text | Google Scholar

Rezaei, N., and Kalantar, M. (2015). Stochastic frequency-security constrained energy and reserve management of an inverter interfaced islanded microgrid considering demand response programs. Int. J. Electr. Power Energy Syst. 69, 273–286. doi:10.1016/j.ijepes.2015.01.023

CrossRef Full Text | Google Scholar

Rokrok, E., Shafie-Khah, M., and Catalão, J. P. (2018). Review of primary voltage and frequency control methods for inverter-based islanded microgrids with distributed generation. Renew. Sustain. Energy Rev. 82, 3225–3235. doi:10.1016/j.rser.2017.10.022

CrossRef Full Text | Google Scholar

Sampath, L., Krishnan, A., Eddy, Y., and Gooi, H. B. (2018). Robust optimal energy and reserve management of multiple-microgrids via cooperative bidding. arXiv preprint arXiv:1812.00177.

Google Scholar

Shi, Z., Liang, H., Huang, S., and Dinavahi, V. (2019). Multistage robust energy management for microgrids considering uncertainty. IET Gener. Transm. Distrib. 13 (10), 1906–1913. doi:10.1049/iet-gtd.2018.6594

CrossRef Full Text | Google Scholar

Simões, M. G., Busarello, T. D. C., Bubshait, A. S., Harirchi, F., Pomilio, J. A., and Blaabjerg, F. (2016). Interactive smart battery storage for a PV and wind hybrid energy management control based on conservative power theory. Int. J. Contr. 89 (4), 850–870. doi:10.1080/00207179.2015.1102971

CrossRef Full Text | Google Scholar

Toutounchi, A. N., Seyedshenava, S., Contreras, J., and Akbarimajd, A. (2019). A stochastic bilevel model to manage active distribution networks with multi-microgrids. IEEE Systems J. 13 (4), 4190–4199. doi:10.1109/jsyst.2018.2890062

CrossRef Full Text | Google Scholar

Ullah, Z., Wang, S., Radosavljević, J., and Lai, J. (2019). A solution to the optimal power flow problem considering WT and PV generation. IEEE Access. 7, 46763–46772. doi:10.1109/access.2019.2909561

CrossRef Full Text | Google Scholar

Vahedipour-Dahraie, M., Rashidizadeh-Kermani, H., Anvari-Moghaddam, A., and Siano, P. (2020). Flexible stochastic scheduling of microgrids with islanding operation complemented by optimal offering strategies. CSEE J. Power Energy Sys. [Epub ahead of print]. doi:10.17775/cseejpes.2019.02560

CrossRef Full Text | Google Scholar

Wu, X., Xu, Y., He, J., Wang, X., Vasquez, J. C., and Guerrero, J. M. (2020). Pinning-based hierarchical and distributed cooperative control for AC microgrid clusters. IEEE Trans. Power Electron. 35 (9), 9867–9887. doi:10.1109/tpel.2020.2972321

CrossRef Full Text | Google Scholar

Xiao, H., Du, Y., Pei, W., and Kong, L. (2017). Coordinated economic dispatch and cost allocation of cooperative multi-microgrids. J. Eng. 2017 (13), 2363–2367. doi:10.1049/joe.2017.0753

CrossRef Full Text | Google Scholar

Xie, J. Z., Chen, S., and Yang, Z. (2017). Multicast middleware for performance and topology analysis of multimedia grids. J. Eng. 2017 (6), 212–219. doi:10.1049/joe.2017.0090

CrossRef Full Text | Google Scholar

Zhang, W., and Xu, Y. (2018). Distributed optimal control for multiple microgrids in a distribution network. IEEE Trans. Smart Grid. 10 (4), 3765–3779. doi:10.1109/tsg.2018.2834921

CrossRef Full Text | Google Scholar