Implementation of Ion Exchange Processes for Carbon Dioxide Mineralization Using Industrial Waste Streams

Sequestration of CO₂ within stable mineral carbonates (e.g., CaCO₃) represents an attractive emission reduction strategy because it offers a leakage-free alternative to geological storage of CO₂ in an environmentally benign form. However, the pH of aqueous streams equilibrated with gaseous streams containing CO₂ (pH < 4) are typically lower than that which is required for carbonate precipitation (pH > 8). Traditionally, alkalinity is provided by a stoichiometric reagent (e.g., NaOH) which renders these processes environmentally hazardous and economically unfeasible. This work investigates the use of regenerable ion-exchange materials to induce alkalinity in CO₂-saturated aqueous solutions such that the pH shift required for mineralization occurs without the need for stoichiometric reagents. Na⁺-H⁺ exchange isotherms (at [H⁺] = 10⁻⁸–10⁻¹ M) and rates were measured for 13X and 4A zeolites and TP-207 and TP-260 organic exchange resins in batch equilibrium and fixed-bed exchange experiments, respectively. At solutions equilibrated with CO₂ at 1.0 atm (pH = 3.9), H⁺ exchange capacities for the materials were similar (1.7–2.4 mmol H⁺/g material) and resulted in pH increases from 3.9 to greater than 8.0. Multi-component mixtures using Ca²⁺ and Mg²⁺ cations (at 10⁻³–10⁻¹ M) in CO₂-saturated water were used to probe competitive ion exchange. The presence of divalent cations in solution inhibited H⁺ exchange, reducing capacities to as low as 0.2 mmol H⁺/g for both resins and zeolites. Dynamic H⁺ exchange capacities in fixed-bed ion exchange columns were similar to equilibrium values for resins (∼1.5 mmol/g) and zeolites (∼0.8 mmol/g) using inlet solutions that were equilibrated with gaseous streams of CO₂ at 1.0 atm. However, exchange kinetics were limited by intraparticle diffusion as indicated by the increased rate parameters with increasing inlet flow rates (20–160 cm³ min⁻¹). Experimental calcite precipitation from mixing the alkaline CO₃²⁻-rich water solution obtained from the ion-exchange column with a simulated liquid waste stream solution achieved thermodynamic maximum yields. The results from these studies indicate that ion exchange processes can be used as an alternative to the addition of stoichiometric bases to induce alkalinity for the precipitation of CaCO₃, thereby opening a pathway toward sustainable and economic mineralization processes.

Introduction

From 1975 to 2018, atmospheric CO₂ levels have dramatically increased from 250 to 410 ppm. The International Energy Outlook reported that world energy carbon dioxide (CO₂) emissions would reach 35 gigatons CO₂ equivalent (Gt CO₂e) by 2020 (IEA, 2020b). Of these emissions, thirty-two percent (17.8 Gt CO₂^e) have been generated during primary energy consumption of oil and gas in the transportation and industrial sectors (IEA, 2019; IEA, 2020a). In the United States, transportation emissions (totaling 1.9 Gt CO₂e in 2018 Nyquist and Ruys, 2009; IEA, 2019) are generated via distributed sources and must be mitigated via direct air capture technology, industrial power generation [1.0 Gt CO₂e in 2018 from direct combustion of fossil fuels for energy (Nyquist and Ruys, 2009; IEA, 2019)] can be considered as point sources of CO₂. In addition to non-electric power generation, oil and gas production operations (i.e., refineries, onshore oil and natural gas production, and natural gas processing) contribute greater than 10% [0.34 Gt CO₂e per year (Sofia Plagakis, 2013; Allen, 2016; U.S. Department of Energy, 2019)] of emissions associated with the oil and gas sector.

Post-combustion capture of CO₂ [e.g., from power plants using amine-based processes (Kim et al., 2016; El Hadri et al., 2017; Kar et al., 2019)] and storage in geological formations (CCS) is the current state-of-the-art for CO₂ emissions mitigation. Decades of process optimization (Cohen et al., 2012; Mores et al., 2014; Bui et al., 2014) and large theoretical storage capacities in the United States (Drage et al., 2012; Armstrong and Styring, 2015; Zhang et al., 2016) make amine-based CCS processes particularly effective for large point source emitters [e.g., fossil fuel fired power plants (Manzolini et al., 2015; Dutcher et al., 2015; Rao and Rubin, 2020)]. However, large energy demands [>0.36 MWh per ton CO₂ captured for streams with less than 12% CO₂ (Dutcher et al., 2015; Liu et al., 2019)], high capital costs of large amine plants (Dutcher et al., 2015; Oh et al., 2018; Baseline Survey, 2019), and high operating expenses (e.g., for pipeline transportation and for storage site monitoring) are barriers for the use of amine-based processes in the oil and gas sector where emissions are more dilute and/or distributed [e.g., less than 3% CO₂ in flare gases from refineries, petrochemical plants, and natural gas wells (Chaikittisilp et al., 2011; Choi et al., 2011a; Choi et al., 2011b)]. Thus, the low carbon future envisioned to combat climate change will require new technologies for CO₂ emissions mitigation from primary energy users and during oil and gas recovery.

Sequestration of CO₂ as a solid carbonate (i.e., mineralization) is an alternative emission mitigation strategy opposed to post-combustion capture of CO₂. CO₂ is captured as a stable carbonate solid (usually in the form of calcium or magnesium carbonates) via chemical reaction with Ca/Mg ions in alkaline aqueous solutions (Seifritz, 1990; Azdarpour et al., 2014). Mineralization-based CO₂ capture and storage involve inherently lower energy processes because the CO₂ capture and storage occur without requiring a separate removal/concentration step (i.e., absorption from a vapor phase). These processes also exploit the favorable thermodynamics of carbonate precipitation reactions (ΔG = -1129.1 kJ/mol for calcite precipitation). By avoiding the CO₂ capture steps, mineralization-based approaches can be applied across a wide range of CO₂ concentrations (i.e., atmospheric concentrations to 100 vol. % CO₂) and temperatures (i.e., ambient to ∼90 °C) without increasing energy requirements [i.e., associated with large heat duties for thermal swing amine-based processes (Zhang et al., 2016)]. These processes are also insensitive to the impurities in CO₂-containing streams (e.g., hydrocarbons and H₂S). Thus, mineralization approaches represent an attractive alternative to CCS for CO₂ emission mitigation in the oil and gas sector because reduced process complexity and broad operating conditions enable modularity with few unit operations (i.e., process intensification) and flexibility in fulfilling carbon management goals across diverse locations and settings without the need for transport infrastructure (e.g., pipelines, compression stations, etc.).

CO₂ mineralization (e.g., as calcium carbonate) occurs via the following reaction

${\mathrm{Ca}}^{2+}\left(\mathrm{aq}\right)+{\mathrm{CO}}_3^{2-}\left(\mathrm{aq}\right)\to {\mathrm{CaCO}}_3\left(\text{s}\right)(1)$

The speciation reactions that describe the CO₂–H₂O system are written as:

${\mathrm{CO}}_2\left(\text{g}\right)+{\text{H}}_2\text{O}\rightleftharpoons {\mathrm{CO}}_2\left(\mathrm{aq}\right)+{\text{H}}_{2}O\rightleftharpoons {\text{H}}_2{\mathrm{CO}}_3\left(\mathrm{aq}\right)(2)$

${\text{H}}_2{\mathrm{CO}}_3\left(\mathrm{aq}\right)\rightleftharpoons {\text{H}}^{+}\left(\mathrm{aq}\right)+{\mathrm{HCO}}_3^{-}\left(\mathrm{aq}\right)(3)$

${\mathrm{HCO}}_3^{-}\left(\mathrm{aq}\right)\rightleftharpoons {\text{H}}^{+}\left(\mathrm{aq}\right)+{\mathrm{CO}}_3^{2-}\left(\mathrm{aq}\right)(4)$

In general, the concentration of CO₃²⁻ anions (and thus, the extent of carbonate precipitation) depends on pH (e.g., in water, CO₃²⁻ is the dominant carbon species at pH > 10.33 (King and Farlow, 2000; Cerozi and Fitzsimmons, 2016), so the mineralization strategy described above requires sources of Ca/Mg ions and alkalinity. Approximately 22 billion barrels of liquid-waste water, known as produced water (PW), is produced during oil and gas extraction yearly (Guerra et al., 2011; Roach et al., 2013; Dastgheib et al., 2014; Scanlon et al., 2020;). The vast majority of PW is injected for disposal, resulting in only 0.6% of PW utilized for beneficial reuse (Guerra et al., 2011; Dastgheib et al., 2014; Scanlon et al., 2020). After separation of organic components, PW is rich in primarily Na⁺, Ca²⁺, Mg²⁺ and Cl⁻ ions (0.050–3.0 M) (Blondes et al., 2018). These high cation concentrations make PW viable sources of cations for mineralization processes. However, these streams are typically produced at 4 < pH < 7 (with bicarbonate, HCO₃⁻, as the predominant species) (Blondes et al., 2018). The addition of caustic soda (NaOH) to increase the pH of these streams would render mineralization processes uneconomical because of the costs and hazards of using NaOH. Previous studies have explored the use of alkaline solid wastes (i.e., combustion fly ashes and slags) (Teir et al., 2007; Said et al., 2013; Chang et al., 2017; Humbert and Castro-Gomes, 2019), however, this still involves the use of a stoichiometric reagent whose production occurs in much lower abundance (130 million tons per year) (Federal Highway Administration, 2016; Humbert and Castro-Gomes, 2019) compared to CO₂ emissions from oil and gas processes (2.9 billion tons per year).

In this work, we investigate the use of ion exchange (IEX) processes as an alternative method to induce alkalinity for the precipitation of CaCO₃ using wastewater streams. Exposing CO₂-saturated solutions (pH = 3.9) to regenerable IEX materials can shift the pH to >10.0, thereby creating favorable conditions for CO₂-mineralization reactions. Ion exchange occurs between an electrolyte solution and similarly charged ions immobilized in an IEX material through a stoichiometric, reversible IEX reaction. Previous research has shown the reversible exchange of H⁺ and Na⁺ ions in a solution using clay minerals (Avena and De Pauli, 1998; Klein et al., 2010; Robin et al., 2015). H⁺-Na⁺ ion exchange is described by:

${\text{H}}^{+}+ {\text{R}}^{\text{Na}}\leftrightarrow {\mathrm{ R}}^{\text{H}}+{\mathrm{Na}}^{+}(5)$

where ${\text{R}}^{\mathrm{Na}/H}$ is the IEX material in either sodium or proton form and H⁺ and Na⁺ are ions in solution. Protons in solution are introduced by dissolving CO₂ (pCO₂ = 1.0 atm; pH 3.9) into water according to Eqs. 2–4. As protons are removed from the solution via ion exchange, the equilibria of reactions 2‒4 shifts toward the formation of CO₃²⁻ ions. (Druckenmiller and Maroto-Valer, 2005) The resulting solution after IEX is an alkaline, CO₃²⁻-rich solution that can be used for CaCO₃ precipitation without the addition of caustic soda. The regeneration energy requirement for CO₂ capture using solid IEX materials is significantly lower than that of dry solid adsorbent and aqueous amine-based processes due to the absence of heat requirement since the process uses a concentrated sodium chloride waste stream to regenerate the materials (as described in this work) (Rao and Rubin, 2020).

IEX technology is commonly used to purify solutions by removing the dissolved ions by electrostatic sorption into IEX materials of various physical forms (Harland, 1994; Nasef, 2008). All zeolites can serve as IEX materials because of their specific structural features. However, for practical applications, high-alumina zeolites, or zeolites with Si/Al ratios in the range of 1–5 (Flanigen et al., 2010), are preferred for IEX applications because of the large number of acid sites (Inglezakis, 2005). IEX and selectivity in zeolites are mainly affected by the properties of the exchangeable cations, the concentration of the solution, the presence of other cations and the characteristics of the zeolite such as channels and Si/Al ratios (Kirov and Filizova, 2012). Type A and Type X zeolites have high affinities for proton exchange in solutions of pH 3.9–7 because of their small Si/Al ratios (Munthali et al., 2014), making them suitable materials for a pH swing process. IEX resins contain functionalized ionizable groups placed along their polymer-backbone chains and are classified depending on the functional group into weakly (WAC) and strongly (SAC) acidic materials. The high H⁺ affinity of WAC resins makes it advantageous to use instead of SAC resins because they can be regenerated using weakly acidic feeds. The pKa of the functional groups on WAC resins are generally greater than 2, whereas SAC resins generally require concentrated acids (pH < 2) because of the functional group’s smaller pKa values (Kunin and Vassiliou, 1963; Leaković et al., 2000; Guo et al., 2013; Maul et al., 2014; Víctor-Ortega et al., 2017).

This work aims to identify commercially available IEX materials capable of shifting the pH of CO₂-saturated solutions for subsequent precipitation as carbonates. Commercially available WAC resins (TP-207, TP-260) and synthetic zeolites (Type 4A, Type 13X) were selected to quantify exchange capacities and kinetic exchange parameters. These resins and synthetic zeolites were selected because of their weakly acidic functional groups and small Si/Al ratios (1.0 for Type 4A and 1.24 for Type 13X), respectively. IEX was studied across a range of H⁺ concentrations from HCl and CO₂ batch solutions to determine the effect of proton and anion concentrations on the exchange capacities of these materials. Equilibrium IEX isotherms were developed for materials and compared with competitive ions to determine the process design and configuration. IEX kinetic constants and capacities are quantified using simple linear driving force (LDF) models for dynamic IEX experiments performed by column exchange. Materials were regenerated to quantify working capacities and kinetics. Furthermore, CO₂ mineralization was performed using simulated PW streams as the source for calcium ions (Otton and Kharaka, 2003; Roach et al., 2013; Dastgheib et al., 2014; Blondes et al., 2018) and the effluent solution compositions from the IEX columns. Geochemical modeling to rapidly estimate the propensity of formation of minerals in solution (e.g., CaCO₃) was performed using Gibbs Energy Minimization (GEM) software (Kulik et al., 2012; Wagner et al., 2012). The work presented herein demonstrates these processes by identifying suitable materials and process parameters and by presenting possible strategies for integration with various processes related to the oil and gas sector.

Materials and Methods

Materials

Sodium chloride (NaCl, >99.0%), calcium chloride dihydrate (CaCl₂∙2 H₂O, >99.0%), calcium sulfate dihydrate (CaSO₄∙2 H₂O, >99.0%), ferric chloride hexahydrate (FeCl₃∙6 H₂O, >99.0%), potassium chloride (KCl, >99.0%) and magnesium chloride hexahydrate (MgCl₂∙6 H₂O, >99.0%) were all purchased from Fisher Chemicals. 70% (w/w) nitric acid (HNO₃) and 12.5% (w/w) hydrochloric acid (HCl) solutions were purchased from Sigma Aldrich. High purity carbon dioxide (CO₂, 99.99%, Airgas) cylinders were used as the source for the preparation of CO₂-saturated solutions. All chemicals were used as received unless otherwise stated. Commercially available synthetic zeolites (4A and 13X; 8–12 mesh; Fisher Chemicals) and sodium-form chelating cation exchange resins (Lewatit TP 207 (iminodiacetate functional groups) and Lewatit TP 260 (aminomethyl phosphonate functional groups); Sigma Aldrich) were used for IEX experiments. Cation exchange resins were preconditioned using 2 N HCl (Sigma Aldrich), 1 N NaOH (Sigma Aldrich), and washed with ultra-pure water (Milli-Q, resistance of 18.2 MΩ cm⁻¹) to remove any contaminants and ensure resins are Na⁺-form at saturation (Seggiani et al., 2006).

Chemical analysis of ion-exchange materials (Supplementary Table S1) was performed by electron dispersion spectroscopy (EDS; Nova 230 model) with a 10 kV accelerating voltage and a working distance of 5 mm. Brunauer-Emmett-Teller (BET) surface areas were calculated from N₂ adsorption-desorption isotherms, measured at 77 K with a Micrometrics ASAP 2020 Plus I system. Before measurements, samples were degassed at 1 × 10⁻³ Torr, and 573 K. Pore size distributions were calculated from the adsorption branches of the isotherms using the Barrett-Joyner-Halenda (BJH) model. Bulk porosities and densities were measured using helium pycnometry (AccuPyc II 1340, Micrometrics) after drying the materials at 65°C for 3 h. Additionally, particle size distributions were measured using static light scattering (SLS; LS13–320, Beckman Coulter Static Light Scattering) with water and sonication being used to ensure particle dispersion. A summary of material properties is shown in Supplementary Table S2.

Batch Equilibrium Ion-Exchange Experiments

Single component IEX experiments using HCl and CO₂-saturated solutions (pCO₂ = 1.0 atm, pH = 3.9) were performed to determine Na⁺-H⁺ exchange isotherms. Aqueous solutions with 0.001, 0.010, 0.1, 0.25, and 0.5 M of HCl were prepared by diluting 12.5% (w/w) HCl with ultra-pure water (18.2 MΩ cm⁻¹). CO₂-saturated solutions were prepared by bubbling CO₂ into ultra-pure water at 25 °C, where [CO2] = 0.0334 M according to Henry’s law (KH = 30 L atm mol⁻¹), resulting in a saturation pH of 3.9 (Bhaduri et al.). CO₂ was bubbled until a stable pH of 3.9 was read using a pH electrode (Thermo Scientific Orion Versa Star). Exchange capacities for divalent cations were measured using 0.001, 0.010, 0.1, 0.25, 0.5, and 1 M of CaCl₂ and MgCl₂ separately, prepared in ultra-pure water. All experiments were performed using a solid/liquid ratio of 0.003 g/ml and at 25°C unless otherwise stated. All batch equilibrium experiments were performed using tightly sealed conical centrifuge tubes of equal dimensions and shaken continuously using a Corning LSE orbital shaker for four days. Solutions from all batch equilibrium experiments were sampled at 5, 10, 30, 60, 100, 180, and 240 min, and every 24 h afterward for cation concentration analysis by inductively coupled plasma–optical emission spectroscopy (ICP-OES; Avio 200 ICP Optical Emission Spectrometer, Perkin Elmer) to ensure equilibrium was achieved. Samples were filtered through a 0.2-micron Corning filter and diluted in 5% (w/w) HNO₃ (prepared by diluting 70% HNO₃ in ultra-pure water).

Equilibrium was established when cation concentrations in solution were invariant with time. Equilibrium exchange capacities (EC; mmol/g) were calculated by

$\mathit{EC}=\frac{\left(C_0-C_f\right)\cdot V}{W}(6)$

where $C_f$ and $C_o$ are final and initial cation concentrations in solution, respectively, $V$ is the solution volume, and $W$ is the mass of solid.

Competitive IEX was performed using the following solutions (summarized in Supplementary Tables S3–S6) containing Na-Ca, Na-Mg, Mg-Ca, HCl-NaCl and CO₂-NaCl (saturated CO₂ in solution at pCO₂ = 1.0 atm). Binary Na-Ca and Na-Mg solutions contained a fixed concentration of 1 M NaCl with CaCl₂ and MgCl₂ concentrations varying from 0.001 to 1 M. Binary Ca-Mg solutions contained equimolar concentrations of each cation varying from 0.001 to 1 M. Binary HCl-NaCl experiments consisted of a fixed concentration of 1 M HCl (pH = 0.2) for resin experiments and 0.1 M HCl (pH = 1.0) for zeolite experiments with varying NaCl concentrations from 0.001 to 1 M. Ternary IEX experiments (summarized in Supplementary Table S7) were performed in solutions composed of CO₂-NaCl-CaCl₂ to further quantify competitive exchange between H⁺, Na⁺, and Ca²⁺. Solutions were equilibrated with CO₂ at 1.0 atm with CaCl₂ concentrations varied from 0.001 to 1 M and NaCl concentrations at 0.1, 0.5 and 1.0 M.

Fixed Bed Ion-Exchange Experiments

An IEX column apparatus was constructed to study the dynamic ion exchange performance for the IEX materials. A schematic of the apparatus is shown in Supplementary Figure S1. Liquid feed was introduced into a glass tube (3.5 cm inner diameter) using a BioLogic LP peristaltic pump. Fixed beds of IEX material (performed using bed volumes of 134.7 cm³ [14 cm height] unless otherwise stated) were held in place using quartz wool. Flow-rate studies using an inlet CO₂-saturated solution (pCO₂ = 1.0 atm, pH 3.9) were performed at 20, 40, 60, 120 and 160 cm³ min⁻¹ (ccm) until the effluent pH (or cation concentration) was equivalent to that of the inlet. Effluent samples were collected at intervals of 5 min during the first hour and 30 min thereafter. Collected effluent samples were analyzed using a pH meter and ICP-OES. The breakthrough curves developed are presented as the normalized effluent H⁺ concentration (Eq. 7) as a function of the number of normalized bed volumes (NBV) processed (Eq. 8). NBV is defined as liquid flowrate, Q (ml/min) divided by IEX material bed volume (BV; cm³) multiplied by time, t (min).

$\mathit{Normalized}\mathit{\hspace{0.17em}}\mathit{Effluent}\mathit{\hspace{0.17em}}\mathit{Concentration}=\frac{C_{\mathrm{effluent}}}{C_{\mathrm{inlet}}}(7)$

$\mathrm{NBV}=\frac{Q\cdot t}{\mathrm{BV}}(8)$

The effect of inlet CO₂ concentrations on the H⁺ exchange was performed using TP-207 (134.7 cm³; 14 cm height; 40 ccm) at the following CO₂ inlet concentrations: 1.0 atm/pH 3.9, 0.5 atm/pH 4.1, 0.25 atm/pH 4.2 and 0.1.0 atm/pH 4.4. Samples were collected at the same intervals described previously and analyzed using a pH meter and ICP-OES.

Regeneration Experiments

Regeneration of IEX materials was performed using 0.001, 0.010, 0.10, and 1 M NaCl solutions. Regeneration efficiency (RE) of IEX materials is defined by:

$\mathrm{RE}=\left(1-\frac{{\mathrm{EC}}_{\text{H}}-{\mathrm{EC}}_{\mathrm{Na}}}{{\mathrm{EC}}_{\text{H}}}\right)\times 100(9)$

where EC_H and EC_Na are the exchange capacities of H⁺ and Na⁺, respectively, determined from single component exchange experiments. Fixed-bed IEX regeneration experiments (12.4 cm³; 1.5 cm inner diameter and 7 cm bed length; 40 ccm) were performed using an inlet CO₂-saturated solution (pCO₂ = 1.0 atm, pH 3.9) to exhaust the column to the saturation limit and subsequently regenerated using an inlet solution composed of 0.7 M NaCl at pH 9.9 (representative of the solution composition following mineralization in this process). Three cycles were performed for each IEX material used in this study.

Analytical Models for Dynamic Ion-Exchange Processes

Mathematical models that relate the properties of the material and the experimental conditions to the concentration-time profiles in the effluent of a fixed bed (i.e., a breakthrough curve) were used to quantify the rate and maximum exchange capacity from dynamic IEX experiments. Combining the partial differential equation that arises from the mass balance on the cation in a fixed bed with an ordinary differential equation that represents a linear exchange rate leads to a simple, two parameter equation [the exchange rate parameter (kK) and the maximum exchange capacity$\left(q_s\right)$] that describes the breakthrough curve (see the SI for the detailed derivation). These parameters can be regressed from breakthrough curve data using nonlinear least squares fitting (Chowdhury et al., 2014).

The rate parameter (kK) reflects resistance to exchange at three length scales: 1) diffusion of cations in the bulk liquid phase to the solid surface, 2) diffusion within solid phase pores, and 3) ion exchange at the anionic site. Diffusion resistances can be determined from known engineering correlations [see SI (IEA, 2019; IEA, 2020a)], and these resistances can be summed in series (similar to electrical resistances) according to Eq. 10 (Ruthven, 1984):

$\frac{1}{kK}=\frac{R_p}{3k_f}+\frac{R_p^2}{15{\epsilon }_p{D}_p}+\frac{1}{k_{ex}}(10)$

where R_p is the radius of the ion exchanger particles, D_p is the effective diffusivity of the incoming cation inside the pores of the solids, k_f is the mass transfer coefficient for fluid film mass, k_ex rate of exchange at the anionic site, and ɛ_p is the porosity of the solid particles. The distribution parameter (K) is the ratio of the concentration of the cation in the solid phase to that in the fluid phase at equilibrium.

Carbon Dioxide Mineralization Using Simulated Produced Water and Ion Exchange Solutions

CO₂ mineralization experiments were performed using the effluents collected from dynamic IEX experiments described in Fixed Bed Ion-Exchange Experiments. Simulated produced water samples (see Supplementary Table S9 for compositions) were mixed with IEX effluents at varying volume ratios within a 1 L beaker, and solid precipitates were collected after 6 h. Volume ratios, $V_R$, are defined as:

$V_R=V_{PW}/\left(V_{PW}+V_{IEX}\right)(11)$

where $V_{IEX}$ represents the volume of IEX solution of the effluent stream from the IEX column and $V_{PW}$ represents the volume of simulated PW.

The IEX effluent and produced water solutions were continuously stirred for 4 h to ensure the CO₂ mineralization reaction had occurred. After precipitation, two separate samples of the supernatant were analyzed via ICP-OES and pH measurements. Both samples were filtered through a 0.2-micron Corning filter and the ICP-OES sample was diluted in 5% (w/w) HNO₃ (prepared by diluting 70% HNO₃ in ultra-pure water). The solid was collected from the solution via vacuum filtration and dried at 60 °C for 24 h prior to analysis. Powder X-ray diffraction (XRD) patterns of the precipitated phases were obtained on an X-Ray diffractometer (Panalytical X’Pert Pro X-ray Powder Diffractometer) using Cu Kα radiation of 1.5410 Å to identify the phases in the precipitated solids. Scanning electron microscopy (SEM; Nova 230; 5 kV accelerating voltage and a working distance of 5 mm) and EDS was used to quantify elemental composition at the surface of the solids.

Thermodynamic Modeling of Precipitation Products

The activities and speciation of aqueous components were calculated using GEMSelektor, version 3.4, which includes a native GEM (Gibbs energy minimization) solver (Kulik et al., 2012; Wagner et al., 2012), a built-in NAGRA-PSI “Kernel”, and the slop98.dat and Cemdata18 thermodynamic databases (Johnson et al., 1992; Hummel et al., 2002; Thoenen et al., 2007; Lothenbach et al., 2019). Thermodynamic data for the solid phases are shown in Supplementary Table S10, and thermodynamic data for aqueous species/complexes and gases are shown in Supplementary Tables S11, S12, respectively. Thermodynamic data for nesquehonite (MgCO_3.3H₂O) (Robie and Hemingway, 1995), hydromagnesite (Mg₅(CO₃)₄(OH)₂·4H₂O) (Galvez-Martos et al., 2018), dolomite ((Ca_0.5Mg_0.5)CO₃) (Galvez-Martos et al., 2018), monohydrocalcite (CaCO₃.H₂O) (Robie and Hemingway, 1995), and an iron-calcium carbonate solid-solution model ((Ca,Fe)CO₃) (Di Lorenzo et al., 2017) were included in the simulations. Thermodynamic data for metastable nesquehonite and hydromagnesite were included as potential magnesium carbonate phases, opposed to “natural” mineral thermodynamic data to represent the short-term precipitation time. The dolomite phase was chosen to represent partial calcium replacement by magnesium within CaCO₃. The (Ca,Fe)CO₃ non-ideal solution model was developed in a CaO-MgO-FeOOH-CO₂ system to represent iron (II) replacement within the CaCO₃ structure in the presence of magnesium (Di Lorenzo et al., 2017).

The activity of any relevant ion species is described within GEMS using the Truesdell-Jones modification of the extended Debye-Hückel equation that is applicable for ionic strengths ($I$, mol/L) less than 2 mol/L (see Eq. 12) (Helgeson et al., 1981):

$\log {\gamma }_i=\frac{-A{z}_i^2\sqrt{I}}{1+\dot{a}B\sqrt{I}}+b_{\gamma }I+\log \frac{X_{jw}}{X_w}(12)$

where, ${\gamma }_i$ and $z_i$ are the activity coefficient and charge of the $i^{\mathit{th}}$ aqueous species respectively, $A$ and $B$ are temperature- and pressure-dependent coefficients, $I$ is the molar ionic strength, $X_{jw}$ is the molar quantity of water, and $X_w$ is the total molar amount of the aqueous phase. A common ion size parameter, $\dot{a}$ (3.72 Å) and short-range interaction parameter, $b_{\gamma }$ (0.064 kg mol⁻¹), are used as constants for the NaCl background electrolyte (Helgeson et al., 1981). NaCl was selected as the dominant electrolyte throughout this study to simulate the IEX product solution compositions and pH shown in Supplementary Table S8 because of constantly larger NaCl concentration in solution. Solution compositions in the simulations used the V_R ratios as described by Eq. 11 using the solutions shown in Supplementary Tables S8–S9.

Results and Discussion

Non-competitive H⁺ and Na⁺ Uptake from DI Water

To demonstrate the feasibility of pH shift using TP-207 (R-1), TP-260 (R-2), 4A (Z-1), and 13X (Z-2), increasing amounts of these materials were added to 20 ml of CO₂-saturated DI water (pCO₂ = 1.0 atm; pH = 3.9). 13X and 4A exhibited maximum pH increases to 8.8 and 9.8, respectively, at solid loading ratios of 0.15 g/g, while the two organic resins increased the solution pH to ∼11 at ratios of 0.35 (Figure 1A) within 48 h (Supplementary Figure S2). To further quantify the maximum H⁺ exchange (i.e., non-competitive) at equilibrium pH values similar to those for a CO₂-saturated solution (pH ∼ 4), H⁺-Na⁺ exchange isotherms (Figure 1B) were collected for the resins and zeolites in DI water. Exchange isotherms were the same using HCl and CO₂-saturated solutions, indicating that there is negligible counter ion (i.e., Cl⁻, HCO₃⁻ or CO₃²⁻) effect. H⁺ exchange capacities at solution equilibrium concentrations of 10^–4 M H⁺ (pH ∼ 3.9, similar to CO₂-saturated water) range from 1.7 to 2.4 mmol H⁺ (g material)⁻¹ (circled in Figure 1B), with the organic resins exhibiting higher uptake capacities than the zeolites under more acidic solutions (pH < 4; [H⁺] > 10⁻⁴ M). These data demonstrate the ability of these ion exchange materials to sufficiently shift the pH of aqueous solutions to conditions that favor carbonate precipitation (i.e., pH from 3.9 to >10) via compact flow processes (i.e., 50 g of material required to increase the pH of 1 L of water from 4 to 10; described in more detail in Dynamic Ion Exchange).

FIGURE 1

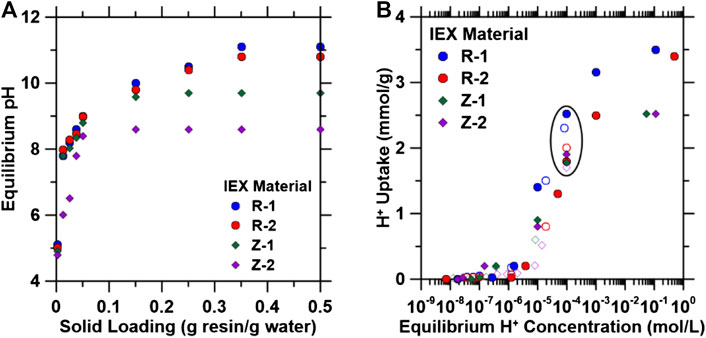
FIGURE 1. (A) Changes in the pH of saturated carbon dioxide (CO₂₎ solutions (pCO₂ = 1.0 atm; initial pH = 3.9) using various amounts of ion exchange (IEX) materials (i.e., 0.010–10 g of IEX material were added to 20 ml of the CO₂-saturated solution). (B) H⁺ exchange isotherms for organic IEX resins and zeolites in DI water. Batch exchange experiments were conducted using HCl (closed symbols) and CO₂ (open symbols) as a source of H⁺ ions. HCl isotherms were developed by varying HCl concentrations from 0.001 to 1 M. CO₂ isotherms were developed by varying mass load at fixed volume of carbonated water at initial pCO₂ = 1.0 atm. Circled area represents the equilibrium H⁺ capacities at 10⁻⁴ M H⁺ (pH ∼ 3.9, similar to CO₂ saturated water).

Na⁺ exchange experiments were subsequently performed on the materials tested in Figure 1 using 0.001–1 M NaCl solutions to probe the reversibility (i.e., regeneration) of this exchange. Na⁺ exchange isotherms (Figure 2A) exhibit similar forms as H⁺ exchange isotherms, with maximum regeneration capacity achieved at Na⁺ concentrations greater than 0.1 M. To quantify the extent of regeneration, materials at the 10⁻⁴ M concentration point on the isotherms in Figure 1B were subsequently exposed to 1 M NaCl solutions [i.e., the typical minimum concentration in produced and waste water streams (Blondes et al., 2018)], and the H⁺ and Na⁺ exchange capacities of these materials are shown in Figure 2B, indicating near complete reversibility of the exchange. Regeneration efficiencies were calculated from these values (using Eq. 9), and for all exchange materials, >95% regeneration was achieved. Multi-cycle experiments under flowing conditions (described in Regeneration Experiments) were conducted to further quantify the regenerability and stability of these IEX materials. Thus, the results indicate that these IEX materials are promising candidates for the regenerable pH shift process presented herein and that they can be regenerated using industrial wastewater streams (e.g., produced water).

FIGURE 2

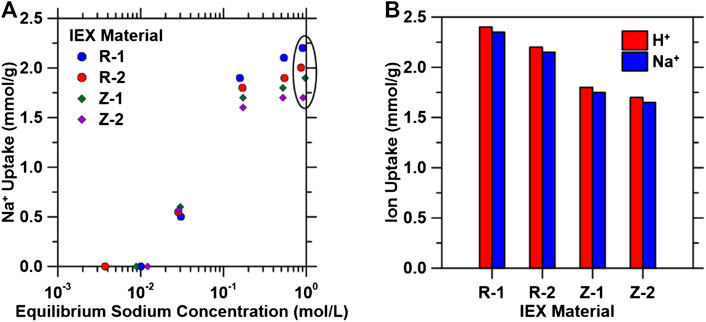
FIGURE 2. (A) Regeneration isotherms of ion exchange materials using initial [H⁺] of 10⁻⁴ M at varying equilibrium NaCl concentrations within the range 0.001 < [NaCl] < 1 M. (B) Ion exchange capacities for H⁺ (in equilibrium with 10⁻⁴ M H⁺ in solution) and Na⁺ (in equilibrium with 1 M NaCl in solution) ions for the four ion exchange materials used in this study. Circled area in (A) represents the equilibrium Na⁺ capacities at 1 M Na⁺, where maximum uptake was observed.

Competitive Ion Exchange

Competitive Exchange Between H⁺ and Ca²⁺

Industrial produced water typically contains a variety of ions [in particular, Ca and Mg at 0.1 and 0.05 M respectively (Blondes et al., 2018)]. The organic cation exchange resins used in this study have a high affinity for divalent cations because of the chelating-like functional groups, as they are commonly used for water hardness removal (i.e., removal of Ca and Mg ions from water) (Dinu and Dragan, 2008). Similarly, the zeolites used in this study readily exchange cationic species (e.g., exchange of Na⁺ with Ca²⁺ leads to the formation of zeolite Type 5A from 4A) (Breck, 1974). Thus, these affinities for divalent cations may hinder Na⁺ and H⁺ uptake when using a produced water feed for the pH shift process, so binary component IEX isotherms were generated (Figures 3A,B) using 0.01–1 M CaCl₂ solutions with fixed initial HCl (1 M for resins, 0.1 M for zeolites to avoid dissolution) or CO₂ (equilibration with pCO₂ = 1.0 atm, pH = 3.9) concentrations to quantify the effect of Ca²⁺ exchange on H⁺ uptake capacity. As shown in Figures 3A,B, H⁺ uptake decreased (and final pH decreased; Supplementary Figure S3) with increasing equilibrium calcium concentrations for all materials. These results indicate that a pH swing process using the materials studied herein requires pH shift of a Ca/Mg depleted stream with subsequent mixing with PW in a separate precipitation reactor (as described subsequently in Carbon Dioxide Mineralization of Simulated Produced Water and Ion Exchange Solutions).

FIGURE 3

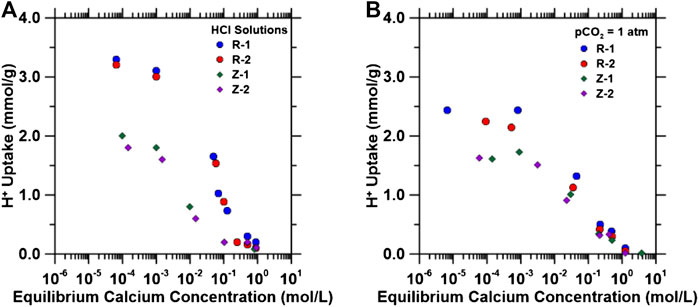
FIGURE 3. H⁺ capacity as a function of equilibrium calcium concentrations (0.001–1.0 M CaCl₂) in solution in (A) 1 mol/L HCl for resins, 0.1 mol/L HCl for zeolites, and (B) aqueous solutions equilibrated with pCO₂ = 1.0 atm (initial pH = 3.9) using a solid/liquid ratio of 0.003 g/ml.

Competitive Exchange Between Na⁺ and Ca²⁺ or Mg²⁺

Selectivity of IEX materials for divalent cations over monovalent cations during the regeneration step was further probed using a binary mixture of NaCl-CaCl₂ and NaCl-MgCl₂. These solutions contained a fixed concentration of 1 M NaCl and CaCl₂ or MgCl₂ concentrations in a range from 0.001 to 1 M. Supplementary Figures S4A,B show the single component calcium and magnesium isotherms, respectively. Figures 4A,B shows the ratio of the exchange capacity (Eq. 6) for Ca and Mg in the presence of 1 M NaCl (EC_Ca-Na and EC_Mg-Na) to that for single component Ca and Mg exchange (EC_Ca and EC_Mg). These exchange capacity ratios are >0.9 across the entire experimentally tested range and approach 1.0 for concentrations of Mg and Ca found in typical PW. At ambient temperature and low concentrations of cations, the extent of exchange is a function of ion’s valence, radius, and activity. However, at a higher concentration of the incoming cation, the effect of valence in ion exchange is weakened, and ions with lower valence have higher exchange potential (Wachinski, 2017). As shown in Figure 4, IEX material regeneration must be accomplished with PW that is deficient of divalent cations due to the larger divalent cation uptake.

FIGURE 4

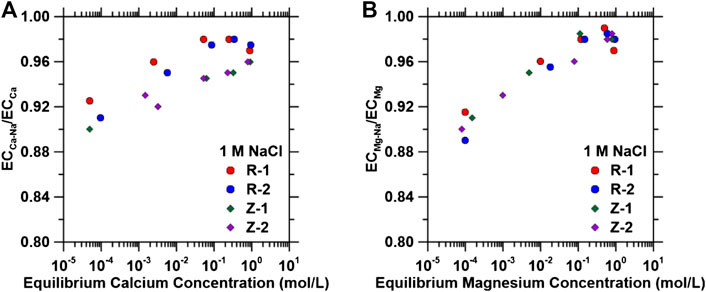
FIGURE 4. Effect of 1 M NaCl on (A) calcium and (B) magnesium normalized exchange capacities of ion exchange materials as a function of equilibrium concentrations.

H⁺ Exchange in the Presence of Na⁺ and Ca²⁺

The effect on H⁺ uptake capacity in a ternary system composed of CO₂-NaCl-CaCl₂ was quantified to examine the effect of high NaCl concentrations on the H⁺ capacities. In systems containing large NaCl concentrations and small CaCl₂ concentrations (i.e., typical produced waters), Ca²⁺ cation uptake may be inhibited because of the larger concentration gradient of the monovalent cations present (Galvez-Martos et al., 2018). Figure 5 shows the effect of Ca²⁺ on H⁺ capacities.

FIGURE 5

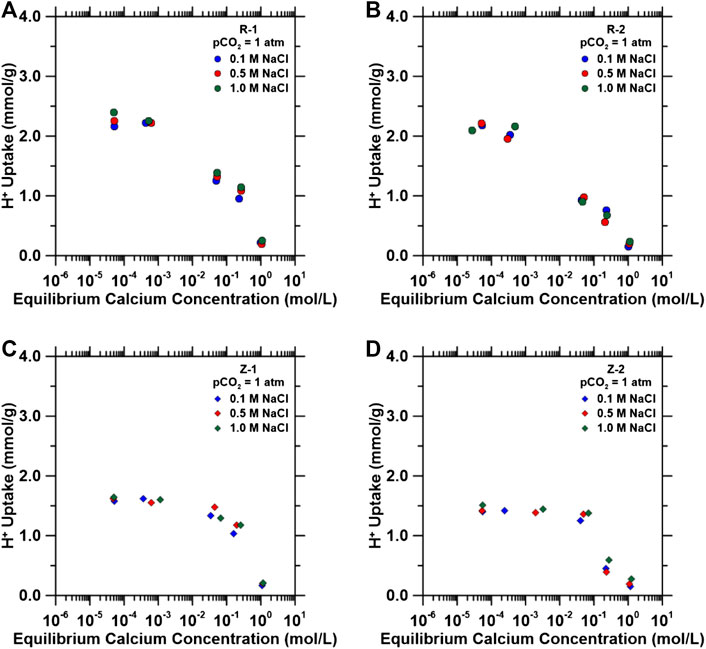
FIGURE 5. H⁺ inhibition in ternary systems composed of fixed pCO₂ = 1.0 atm and variable NaCl concentration as a function of equilibrium calcium concentration in solution for (A) R-1, (B) R-2, (C) Z-1 and (D) Z-2. H⁺ uptake capacities were quantified using varying CaCl₂ solutions (0.01–1 M), fixed pCO₂ = 1.0 atm, and varying background NaCl solutions (0.1–1 M). Background NaCl concentrations remained the same in solution before and after H⁺ exchange.

For each material and consistent with the results shown in Competitive Exchange Between H⁺and Ca²⁺, increasing equilibrium calcium concentrations decreases H⁺ uptake despite the additional presence of background Na⁺ cations in solution. Both types of materials exhibited similar divalent cation uptake, and, in this regard, there is no clear advantage to choose one material over another.

These results confirm the requirement of removal of divalent cations from PW prior to the pH shift step. In the overall process (as later described in Process Design), produced water streams will be mixed with basic (pH > 10), CO₂-saturated effluents from the IEX columns to induce precipitation of CaCO₃. The residual liquid after precipitation, which is rich in Na and Mg but depleted of Ca, will be processed via nanofiltration and reverse osmosis to remove Mg and produce a Na-rich stream for IEX column regeneration. The Na-depleted stream from the effluent of regeneration can then be saturated with CO₂ for the pH swing process to produce alkaline solutions for precipitation. Thus, this configuration ensures utilization of the entire PW stream while minimizing the need for fresh DI water streams.

Dynamic Ion Exchange

Fixed bed exchange experiments were conducted to determine the impact of transport phenomena on exchange capacities and to quantify exchange rates so that IEX columns can be sized for various process conditions (e.g., column contact times and feed pH). The performance of the fixed-bed columns (i.e., determination of parameters $kK$ and $q_s$) were quantified using the LDF models described in Fixed Bed Ion-Exchange Experiments (and in the SI). The breakthrough curves (Supplementary Figures S4–S6; Figure 6) are presented as the normalized effluent H⁺ concentration as a function of the number of NBV as defined in Fixed Bed Ion-Exchange Experiments (Eq. 8).

FIGURE 6

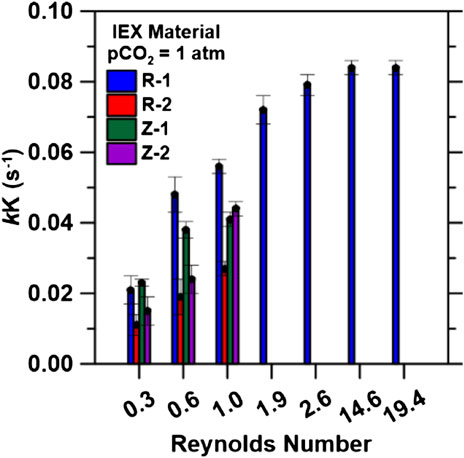
FIGURE 6. Regressed rate parameters, kK (s⁻¹), using inlet pCO₂ = 1.0 atm at all inlet flow rates. Bed volumes of 134.7 cm³ (3.5 cm column diameter) were used for Reynolds numbers 0.3−1.0. Bed volume was increased to 279 cm³ (3.5 cm column diameter) for Reynolds numbers 1.9 to 2.6. Bed volume of 51.2 cm³ (1.27 cm column diameter) was used for Reynold numbers 14.6 and 19.4.

Effects of Flowrate on H⁺ Uptake Capacities and Rates

Flowrate is an important parameter to evaluate the efficiency of ion exchange materials in a continuous process because contact time and column hydrodynamics [i.e., Reynolds number (Re)] can impact IEX capacities and rates (Cooper, 1965; Barros et al., 2004; Borba et al., 2006; Chatterjee et al., 2018). The effect of varying flow rate on H⁺ saturation capacities and ion exchange rate parameters were probed using saturated CO₂ (1.0 atm CO₂; pH = 3.9) feed solutions at flow rates ranging from 20–160 ccm (Re 0.3–19.4). Experimental saturation capacities were quantified when the outlet H⁺ concentration was equivalent to 95% of the inlet H⁺ concentration. The second order LDF model (Supplementary Equation S2) was used to quantify the rate parameter (kK in Eq. 10). (Bohart and Adams, 1920) IEX resins had larger capacities compared to zeolites, which is consistent with the exchange isotherms described previously. However, shown in Supplementary Figure S6, saturation capacities (mmol H⁺/g) achieved in the flow experiments (1.45 for R-1, 1.44 mmol/g for R-2, 0.91 mmol/g for Z-1 and 0.75 mmol/g for Z-2 at BV = 134.7 cm³) were lower compared to the equilibrium values determined from the isotherms (Figure 1B) and decreased with increasing inlet flow rate. It has previously been reported that increasing flow rates reduces contact times with the IEX solid resulting in decrease in saturation capacities (and smaller values compared to equilibrium capacities) because of insufficient diffusion of solute into the pores of the IEX solid, consequently limiting the number of active sites or ionic groups in contact with the solute for ion exchange (Baker et al., 1954; Aksu and Gönen, 2004; Han et al., 2006; El-Kamash, 2008; El-Kamash, 2008; Mondal, 2009; Guo et al., 2013; Bhaumik et al., 2013; Jang and Lee, 2016; Malik et al., 2018).

Additional breakthrough tests (Supplementary Figure S5E,F) using bed volumes of 279 cm³ (height 29 cm, diameter 3.5 cm), 51.2 cm³ (height 29 cm, diameter 1.27 cm) and inlet flow rates of 120 and 160 ccm for R-1 were conducted to probe the IEX process at higher Re (>1.0). Re = 1.0 (∼1.35) and Re = 1.9 (∼1.75). Increasing bed volume (from 134.7 to 279 cm³ for Re = 1.9 and 2.6) increased H⁺ capacities to 1.71 mmol/g (Supplementary Figure S6), closer to its equilibrium capacity (2.4 mmol/g). This increase in saturation capacity can be explained by the increase in contact time and the expansion of the mass transfer zone due to the increase in ion exchange sites available along the larger bed length (Golie and Upadhyayula, 2016; Mazur et al., 2016; Chatterjee et al., 2018; Jin et al., 2018). Furthermore, as shown in Figure 7, increasing flowrate led to an increase in kK for all materials. The regressed rate parameter increased significantly with an increase in flow rate (20–60 ccm) from 0.021 to 0.056 s⁻¹ for R-1, from 0.011 to 0.027 s⁻¹ for R-2, 0.023 to 0.041 s⁻¹ for Z-1 and 0.015 to 0.044 s⁻¹ for Z-2, demonstrating the overall system kinetics is dominated by external mass transfer in the column (Aksu and Gönen, 2004; Ostroski et al., 2011; Bhaumik et al., 2013; Puerta-Falla et al., 2017; Gouran-Orimi et al., 2018). Under convective mixing, the ion-exchange rate increases as the mixing speed increases (in this case the flow rate), and the resistance of the boundary layer that surrounds the ion exchange materials weakens (Dyer and Gettins, 1970). When diffusion is the rate-controlling step, then the rate-controlling diffusion process may not be within the micropores themselves but, instead, limited by the transport via a near-static boundary layer that is inserted between the external solution and the crystalline surface (Townsend, 1991). This process is described as a film or boundary-layer diffusion. However, increasing flow rates up to 160 ccm, from 60 ccm, for R-1 using pCO₂ = 1.0 atm displayed minimal changes to the rate parameter kK (∼0.075 s⁻¹), indicating decreased influence of film diffusion limitations. Additionally, increasing Re by reducing the column diameter at 120 and 160 ccm (Re 14.6 and 19.4, respectively) showed no changes in the rate parameter (0.084 s⁻¹). At this point, k represents intraparticle diffusion rates that will define the kinetics of the IEX process and can be used to design the process at the appropriate flow rates as discussed in Process Design.

FIGURE 7

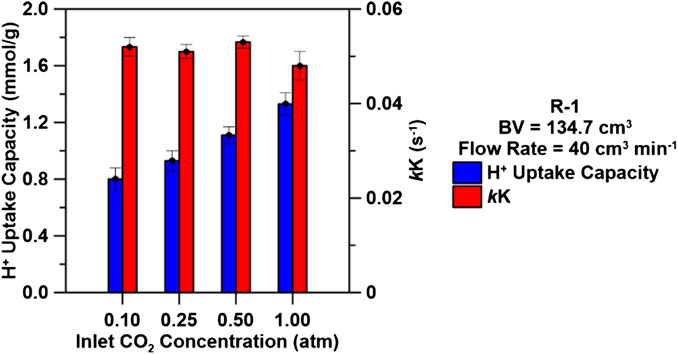
FIGURE 7. H⁺ uptake capacities (mmol/g) and regressed rate parameter, kK, (s⁻¹) for R-1 at varying carbon dioxide inlet concentrations using a bed volume of 134.7 cm³ and an inlet flow rate of 40 cm³ min⁻¹.

Effect of Inlet Concentration on H⁺ Uptake Capacities

CO₂ concentrations by volume from point sources are about 3% for natural gas-fired power plants, 12% for coal-fired power plants and iron and steel mills, 20% for cement plants, and >90% from ammonia, ethanol, and hydrogen plants (Florin et al., 2010). An increase in inlet concentrations for IEX processes lead to higher uptake capacities and faster breakthrough time because of the large concentration gradient produced (Chowdhury et al., 2014). Therefore, breakthrough curves at varying inlet CO₂ concentrations (0.10, 0.25, 0.50, and 1.0 atm CO₂) were collected for R-1 IEX resin (the IEX material with the highest H⁺ uptake capacity) to probe this effect under flowing conditions.

Breakthrough curves were collected for R-1 at CO₂ concentrations from 0.10 to 1.0 atm (10–100%) to quantify its effect on saturation capacities and breakthrough time using an inlet flow rate of 40 ccm and a bed volume of 134.7 cm³. The breakthrough time decreased as CO₂ influent concentration increased from 0.10 to 1.0 atm and H⁺ uptake capacities decreased with decreasing inlet CO₂ concentrations, as shown in Supplementary Figure S7; Figure 8. The maximum uptake capacity was achieved using an initial CO₂ concentration of 1.0 atm at 1.33 mmol/g with minimal changes to the kinetic rate parameter kK (∼0.050 s⁻¹). The driving force for ion exchange is the concentration difference between the solute on the sorbent and the solute in the solution (Aksu and Gönen, 2004; El-Kamash, 2008; Bhaumik et al., 2013). A high concentration difference provides a high driving force for the ion exchange process, which may explain why higher H⁺ uptake capacities were obtained using larger CO₂ inlet concentrations. Additionally, at larger inlet CO₂ concentrations, binding sites are rapidly filled with sorbate H⁺ which results in a decrease in breakthrough time. Maximizing H⁺ uptake capacities across all concentrations can be performed by increasing bed-depth as discussed in Effects of Flowrate on H⁺Uptake Capacities and Rates.

FIGURE 8

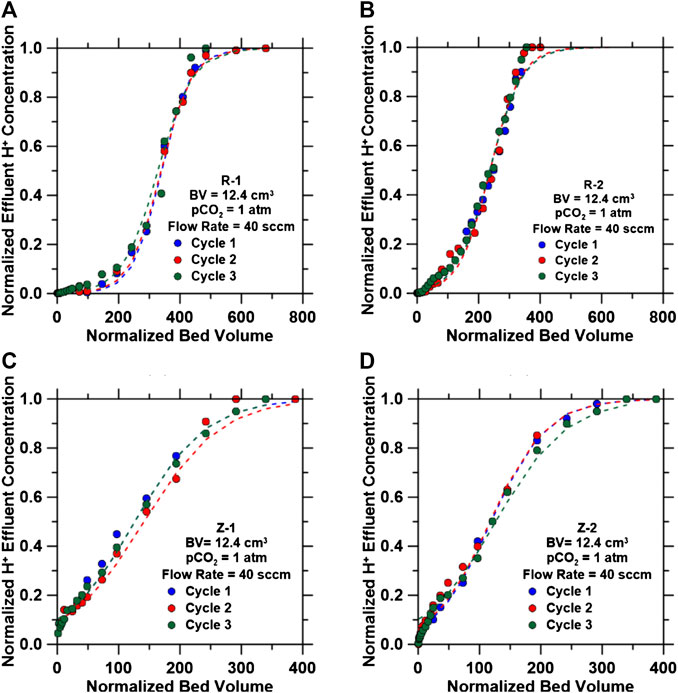
FIGURE 8. Breakthrough curves for the H⁺ exchange reaction for three cycles after regenerating with an inlet composition of 0.7 M NaCl at a pH 9.9. Breakthrough curves developed using inlet flow rates of 40 ccm and pCO₂ = 1.0 atm for (A) R-1, (B) R-2, (C) Z-1 and (D) Z-2. Dashed lines represent Bohart-Adams model predictions for breakthrough curves.

Regeneration and Cycling of Ion Exchange Materials

Cycle-to-cycle stability of IEX materials were studied via successive H⁺-Na⁺ exchange cycles, as shown in Figure 6 (at BV of 12.4 cm³, flow rate of 40 ccm, H+ exchange pH = 3.9, and Na + exchange inlet concentrations of 0.7 M NaCl/pH 9.9). Regeneration for all IEX materials was achieved within 100 normalized bed volumes for each cycle, when the effluent pH was equivalent to the inlet pH, as shown in Supplementary Figure S8. Breakthrough curves for all three cycles for each IEX material are shown in Figure 6 with their respective exchange parameters shown in Supplementary Table S13. The breakthrough time for each material was almost constant for each of their respective cycles, resulting in identical H⁺ uptake capacities and rate parameter kK values (Supplementary Table S13).

The four IEX materials studied displayed similar H⁺ uptake capacities after three cycles using a regenerant feed composed of 0.7 M NaCl at a pH 9.9, which is representative of the solution following the mineralization step of this process (discussed in Carbon Dioxide Mineralization of Simulated Produced Water and Ion Exchange Solutions). Regeneration time for the IEX resins can be reduced using higher pH solutions as is done industrially with caustic soda (Kunin and Vassiliou, 1963; Maul et al., 2014; Víctor-Ortega et al., 2017). More cycles will be necessary to identify the point at which the IEX materials begin to reduce in H⁺ uptake capacities.

Carbon Dioxide Mineralization of Simulated Produced Water and Ion Exchange Solutions

Simulated CO₃²⁻-rich water with the same Na⁺ and CO₃²⁻ concentrations as the IEX columns was mixed with simulated produced water solutions at varying volumetric ratios, V_R (Eq. 11). As shown in Supplementary Table S8, R-1 displayed a larger pH swing, with a final solution pH 11.1, compared to the other IEX materials. Therefore, thermodynamic simulations were performed to predict phase formation and calcite yield using R-1 compositions as a function of different volume fractions (V_R), shown in Figure 9A.

FIGURE 9

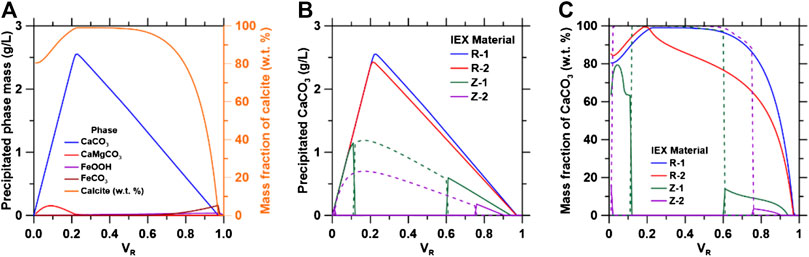
FIGURE 9. (A) Simulated phase formation and purity of calcite in alkaline conditions; (B) CaCO₃ formation and (C) purity of calcite formed as a function of varying volume fractions for the four ion exchange solutions studied. The dashed lines for zeolitic materials represent aragonite phase formation.

As shown in Figure 9A, CaCO₃ formation changes with varying volume ratio due to increasing [Ca]:[CO₂] ratio in solution. CaCO₃ formation is maximized when the [Ca]:[CO₂] ratio was 1:1, which occurs at a V_R of 0.23. R-1 solutions produce the largest quantities of CaCO₃ and highest purities of calcite as shown in Figures 9B,C, respectively, because of the higher initial pH,.

For zeolitic solutions, aragonite formation is dominant between volume ratios of 0.2–0.6 because large [Ca]/[Fe] ratios are required to favor calcite formation (Di Lorenzo et al., 2017), with goethite as the primary contaminant. The reduction of the initial pH reduces goethite formation which decreases the [Ca]/[Fe] in solution to a point where it enters the miscibility gap of the (Fe,Ca)CO₃ solid solution model used (Di Lorenzo et al., 2017). The FeCO₃ end-member forms preferentially but at low quantities which causes aragonite to form in place of calcite. CaCO₃ precipitation decreases at V_R > 0.25 for ion exchange materials because of the lower initial pH and reduction of aqueous CO₂, reducing the activity of CO₃²⁻ in solution.

To validate the thermodynamic simulations, experiments were performed using R-1 solutions because of the larger predicted mass and purity of CaCO₃ precipitated. The dominant phase formed from volume fractions 0.2–0.6 was calcite with goethite as the primary contaminant as shown in the XRD patterns (Figure 10A). At V_R = 0.1, monohydrocalcite (MHC) was the primary phase that formed during mineralization (Supplementary Figure S9A) as it requires a solution containing [Mg]/[Ca] > 0.2 and [CO₂]/[Ca] > 1 to form (Nishiyama et al., 2013; Rodriguez-Blanco et al., 2014; Blue et al., 2017). When V_R = 0.1, the [Mg]/[Ca] and [CO₂]/[Ca] were 0.44 and 2.54, respectively, which are within the parameters required for MHC formation. At V_R > 0.18, the [CO₂]/[Ca] < 1.0 thus, MHC did not form after this point.

FIGURE 10

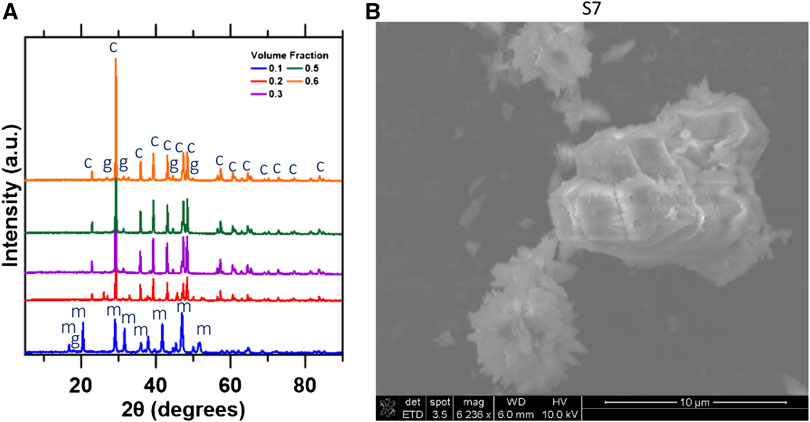
FIGURE 10. (A) XRD diffraction patterns identifying present phases over varying volume ratios. c, calcite, g, goethite and m, monohydrocalcite; (B) SEM image of calcite synthesizes at a volume fraction of 0.7.

The SEM image (Figure 10B) of calcite precipitated at V_R = 0.3 displays the stable rhombohedral structure expected of calcite formation (Kralj et al., 2004). The rhombohedral structure was observed for V_R values of 0.2–0.6. At V_R = 0.1, the stable rod-like structure for MHC was dominant, as shown in Supplementary Figure S9B. EDS analysis at the surface was performed to quantify CaCO₃ purity. As shown in Supplementary Table S14, experimental results are consistent with thermodynamic simulations performed for across the volume fractions studied.

The experimental data and simulated mass balances showed good agreement. Simulated goethite was within 0.3 mass % of the experimental values throughout. Within the range 0.2 < V_R < 0.6, simulated calcite was within 2 mass % of the experimental values. Significant CaCO₃ differences was observed for V_R = 0.1 because simulations predicted 9.9 mass% of potential CaMgCO₃ phase formation. CaMgCO₃ phases were not detected in XRD patterns across all volume ratios leading to differences in the mass of magnesium detected and simulated, implying either the small magnesium content is not detectable by XRD or the magnesium is adsorbed at the surface of the solid.

The precipitated mass of calcite increased and decreased, shown in Figure 11A, following the molar ratios of [Ca]:[CO₃^2-], where <5% difference between simulated and experimental values were observed. The pH was observed to decrease as the V_R increased as shown in Figure 11B, because of the increasing dilution of the alkaline IEX solution by produced water. The pH buffering effect of carbonate ions is observed up to V_R = 0.43, where pH = 9.6. A significant drop in pH may be the result of increased goethite formation in the system, consuming additional [OH⁻] provided by the IEX column. Additionally, simulated pH values were in good agreement with the experimental results as they were within 0.1–0.3 pH units. Concentrations of cations increased as the PW ratio increased, shown in Figure 11C. However, calcium concentrations observed a postponed rise due to calcite formation. Iron concentrations do not increase significantly until V_R = 0.46. The available iron at V_R < 0.46 was converted into goethite resulting in [Fe] < 2.3 × 10⁻⁶ mmol/L. When V_R > 0.46, the iron concentration rose rapidly due to decreasing [OH⁻] as the alkalinity provided by the IEX solution decreased. The accurate thermodynamic predictions shown from the experimental results and simulations are significant as they can further be used to predict phase formations and CaCO₃ yields for the IEX process using different compositions of PW or of other brine compositions (e.g., desalination brine discharge). CaCO₃ yields will be significantly affected by total Ca²⁺ concentrations, whereas purities will significantly be affected by total Mg²⁺ and Fe^2+/3+ concentrations as the results have shown.

FIGURE 11

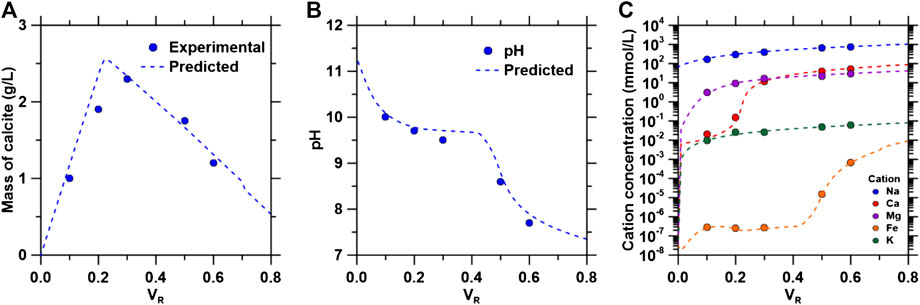
FIGURE 11. (A) Yield of precipitated calcite, (B) final pH of solution after precipitation and (C) cation concentrations in solution following precipitation as a function of volume ratios. The “filled’ circle represent experimental data and the dotted lines represent simulation results.

Process Design

The results from these studies indicate that ion exchange processes can be used as an alternative to the addition of stoichiometric bases to induce alkalinity for the precipitation of CaCO₃. A process flow diagram for the industrial scale setup is shown in Figure 12. CO₂ from flue gas (pCO₂ = 0.12 atm) is combined with fresh water to provide H⁺ in solution (pH 4.4) that is used as the inlet solution for the IEX columns. Minor acidic impurities in the flue gas (e.g., sulfur) are not expected to substantially impact the process performance (e.g., H⁺ exchange capacities). The carbonate-rich effluent of the columns (pH > 10) is mixed with the calcium-rich produced water in a precipitation reaction to produce CaCO₃. Following separation of the solids, the remaining solution undergoes a nanofiltration step for the removal of the remaining divalent cations in solution that would inhibit regeneration of the IEX columns (e.g., Ca²⁺, Mg²⁺ and Fe^2+/3+ cations preferably exchanging at the exchanging sites instead of Na⁺ cations). Performance studies of nanofiltration membranes are required to quantify the compositions of these cations following this step as they may decrease IEX performance (e.g., regeneration capacities and cycles). A reverse osmosis step is implemented for the continuous production of fresh water that is used in the first step of the IEX process and for simultaneous concentration of sodium cations in solution used for regeneration of IEX columns. The pH in both retentate and permeate streams of the reverse-osmosis step would have to be monitored as this can effect regeneration time and CO₂ absorption. The retentate is transferred to the IEX columns for regeneration, where a larger pH would result in a faster regeneration time. The permeate is utilized for the initial carbonation step, where a larger pH would result in larger CO₂ absorption, inducing a change in V_R where CaCO₃ yields are maximized. High calcium carbonate yields (1-ton CO₂/day) can be achieved by utilizing a CO₂ mass flow rate = 69.2 kg/min, a produced water flow rate = 57.8 L/min and a total bed volume = 0.05 m³. The cycling and regeneration efficiency of these IEX materials discussed earlier make this a viable alternative process for CO₂ mineralization at standard temperature and pressure.

FIGURE 12

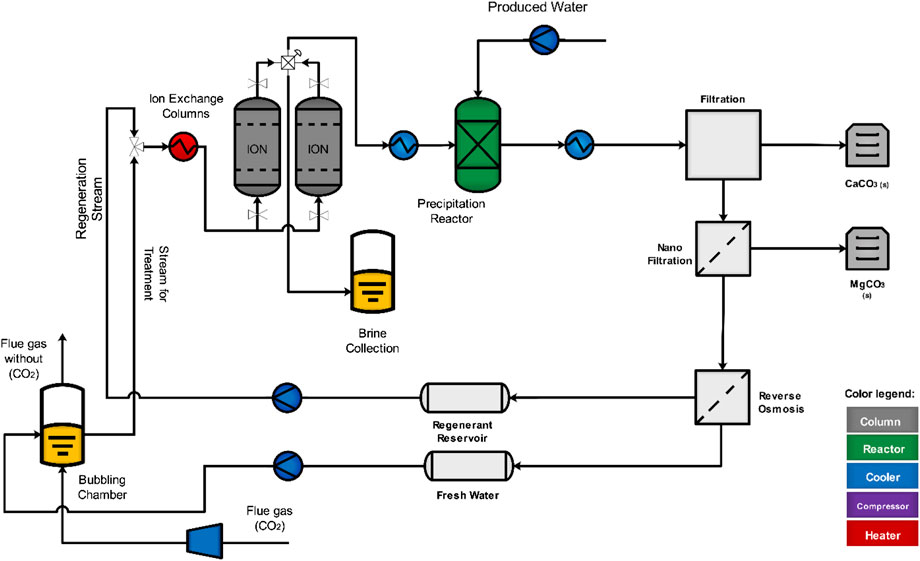
FIGURE 12. Process flow diagram for industrial scale setup of ion exchange for carbon dioxide mineralization.

Conclusion

Our initial discoveries show that the ion exchange process can be used to induce alkalinity through the system to a degree where precipitation is favored. The results from these studies indicate that ion exchange processes can be used as an alternative to the addition of stoichiometric inorganic bases (e.g., sodium hydroxide) to induce alkalinity for the consequent precipitation of CaCO₃. Batch equilibrium isotherms showed larger H⁺ uptake capacities for IEX resins compared to zeolites. For all materials in all conditions, H⁺ uptake increased with a decrease in divalent cation concentrations in solution. Inhibition of H⁺ exchange is likely the result of the larger field strength of divalent cations. Results identified that an inlet stream for the IEX process must be absent of divalent cations in solution. Dynamic IEX experiments showed changes in uptake capacities due to contact time and changes in kinetic bulk parameters due to changes in flow rate implying external diffusion limitations. Capacities for zeolites were smaller than those for IEX resins; H⁺ uptake may be hindered by the porous structure of zeolites. IEX materials were shown to be regenerable using simulated produced water feeds following mineralization.

CO₂ mineralization experiments followed thermodynamic predictions with regards to phase formations and concentrations of cations in solutions. Experimental calcite yields were 2.3 g/L for cation exchange resins with the formation of goethite (an iron-hydroxide phase, FeOOH) as the primary contaminant phase (99% calcite, 1% goethite). Yields calculated via simulations were 2.6 g/L for the resin, indicating that the experimental process was able to achieve thermodynamic maximum production of calcite. Calcite was the dominant phase for volume ratios 0.2–0.6, with goethite as the primary contaminant phase. These results indicate high purity of calcite formation and volume ratios required to achieve these purities. The high calcium carbonate yields (1 ton CO₂/day utilizing a produced water flow rate = 57.8 L/min and a total bed volume = 0.05 m³) obtained for the materials examined and the successful operation at standard temperature and pressure conditions support their potential for industrial implementation.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

SB, AA, and DP conducted experiments and analyzed data. SB, DP, and DS wrote and edited the manuscript. BW and RR edited the manuscript. DS, ELP, GS, and BW conceived the technological concept and directed the research.

Funding

This work was supported by the United States Department of Energy under Award Number DE-FE0031705.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2020.610392/full#supplementary-material.

References

Allen, D. T. (2016). Emissions from oil and gas operations in the United States and their air quality implications. J. Air Waste Manag. Assoc. 66 (6), 549–575. doi:10.1080/10962247.2016.1171263

PubMed Abstract | CrossRef Full Text | Google Scholar

Aksu, Z., and Gönen, F. (2004). Biosorption of phenol by immobilized activated sludge in a continuous packed bed: prediction of breakthrough curves. Process Biochem. 39 (5), 599–613. doi:10.1016/S0032-9592(03)00132-8

CrossRef Full Text | Google Scholar

Armstrong, K., and Styring, P. (2015). Assessing the potential of utilization and storage strategies for post-combustion CO2 emissions reduction. Front. Energy Res. 3, 1–8. doi:10.3389/fenrg.2015.00008

CrossRef Full Text | Google Scholar

Avena, M. J., and De Pauli, C. P. (1998). Proton adsorption and electrokinetics of an argentinean montmorillonite. J. Colloid Interface Sci. 202 (1), 195–204. doi:10.1006/jcis.1998.5402

CrossRef Full Text | Google Scholar

Azdarpour, A., Asadullah, M., Junin, R., Manan, M., Hamidi, H., and Daud, A. R. M. (2014). Carbon dioxide mineral carbonation through PH-swing process: a review. Energy Procedia 61, 2783–2786, doi:10.1016/j.egypro.2014.12.311

CrossRef Full Text | Google Scholar

Baker, J. M., Gehrke, C.W., and Affsprung, H. E. (1954). An ion-exchange resin-contact time method for the study of inorganic equilibria in milk, J. Dairy Sci. 37 (12), 1409–1415. doi:10.3168/jds.S0022-0302(54)91425-3

CrossRef Full Text | Google Scholar

Barros, M. A. S. D., Silva, E. A., Arroyo, P. A., Tavares, C. R. G., Schneider, R. M., Suszek, M., et al. (2004). Removal of Cr(III) in the fixed bed column and batch reactors using as adsorbent zeolite NaX. Chem. Eng. Sci. 59 (24), 5959–5966. doi:10.1016/j.ces.2004.07.040

CrossRef Full Text | Google Scholar

Baseline Survey (2019). Baseline studies overview. Available at: https://netl.doe.gov/node/7512 (Accessed November 4, 2020).

Google Scholar

Bhaduri, G. A., Alamiry, M. A. H., and Šiller, L. (2015). Nickel nanoparticles for enhancing carbon capture. J. Nanomater. 2015, 1–13. doi:10.1155/2015/581785

CrossRef Full Text | Google Scholar

Bhaumik, M., Setshedi, K., Maity, A., and Onyango, M. S. (2013). Chromium(VI) removal from water using fixed bed column of polypyrrole/Fe₃O₄ nanocomposite. Separ. Purif. Technol. 110, 11–19. doi:10.1016/j.seppur.2013.02.037

CrossRef Full Text | Google Scholar

Blondes, M., Engle, M., Kharaka, Y., Reidy, M., Saraswathula, V., Thordsen, J., et al. (2018). Geological survey national produced waters geochemical database (ver. 2.3, January 2018). Reston, VI: U.S. Geological Survey Data Release.

Google Scholar

Blue, C. R., Giuffre, A., Mergelsberg, S., Han, N., De Yoreo, J. J., and Dove, P. M. (2017). Chemical and physical controls on the transformation of amorphous calcium carbonate into crystalline CaCO₃ polymorphs. Geochem. Cosmochim. Acta 196, 179–196. doi:10.1016/j.gca.2016.09.004

CrossRef Full Text | Google Scholar

Bohart, G. S., and Adams, E. Q. (1920). Some aspects OF the behavior OF charcoal with respect to CHLORINE.1. J. Am. Chem. Soc. 42 (3), 523–544. doi:10.1021/ja01448a018

CrossRef Full Text | Google Scholar

Borba, C. E., Guirardello, R., Silva, E. A., Veit, M. T., and Tavares, C. R. G. (2006). Removal of nickel(II) ions from aqueous solution by biosorption in a fixed bed column: experimental and theoretical breakthrough curves. Biochem. Eng. J. 30 (2), 184–191. doi:10.1016/j.bej.2006.04.001

CrossRef Full Text | Google Scholar

Breck, D. (1974). Zeolite molecular sieves: structure, chemistry and use. New York, NY: John Wiley & Sons Inc.

Google Scholar

Bui, M., Gunawan, I., Verheyen, V., Feron, P., Meuleman, E., and Adeloju, S. (2014). Dynamic modelling and optimisation of flexible operation in post-combustion CO2 capture plants—a review. Comput. Chem. Eng. 61, 245–265. doi:10.1016/j.compchemeng.2013.11.015

CrossRef Full Text | Google Scholar

Cerozi, B. D. S., and Fitzsimmons, K. (2016). The effect of PH on phosphorus availability and speciation in an aquaponics nutrient solution. Bioresour. Technol. 219, 778–781. doi:10.1016/j.biortech.2016.08.079

PubMed Abstract | CrossRef Full Text | Google Scholar

Chaikittisilp, W., Kim, H.-J., and Jones, C. W. (2011). Mesoporous alumina-supported amines as potential steam-stable Adsorbents for capturing CO2 from simulated flue gas and ambient air. Energy Fuels 25 (11), 5528–5537. doi:10.1021/ef201224v

CrossRef Full Text | Google Scholar

Chang, R., Kim, S., Lee, S., Choi, S., Kim, M., and Park, Y. (2017). Calcium carbonate precipitation for CO2 storage and utilization: a review of the carbonate crystallization and polymorphism. Front. Energy Res. 5, 2–12. doi:10.3389/fenrg.2017.00017

CrossRef Full Text | Google Scholar

Chatterjee, S., Mondal, S., and De, S. (2018). Design and scaling up of fixed bed adsorption columns for lead removal by treated laterite. J. Clean. Prod. 177, 760–774. doi:10.1016/j.jclepro.2017.12.249

CrossRef Full Text | Google Scholar

Choi, S., Drese, J. H., Eisenberger, P. M., and Jones, C. W. (2011a). Application of amine-tethered solid sorbents for direct CO2 capture from the ambient air. Environ. Sci. Technol. 45 (6), 2420–2427. doi:10.1021/es102797w

PubMed Abstract | CrossRef Full Text | Google Scholar

Choi, S., Gray, M. L., and Jones, C. W. (2011b). Amine-tethered solid adsorbents coupling high adsorption capacity and regenerability for CO₂ capture from ambient air. ChemSusChem 4 (5), 628–635. doi:10.1002/cssc.201000355

PubMed Abstract | CrossRef Full Text | Google Scholar

Chowdhury, Z. Z., Hamid, S. B. A., and Zain, S. M. (2014). Evaluating design parameters for breakthrough curve analysis and kinetics of fixed bed columns for Cu(II) cations using lignocellulosic wastes. BioResources 10 (1), 732–749. doi:10.15376/biores.10.1.732-749

CrossRef Full Text | Google Scholar

Cohen, S. M., Rochelle, G. T., and Webber, M. E. (2012). Optimizing post-combustion CO2 capture in response to volatile electricity prices. Inter. J. Greenhouse Gas Contr. 8, 180–195. doi:10.1016/j.ijggc.2012.02.011

CrossRef Full Text | Google Scholar

Cooper, R. S. (1965). Slow particle diffusion in ion exchange columns. Ind. Eng. Chem. Fund. 4 (3), 308–313. doi:10.1021/i160015a012

CrossRef Full Text | Google Scholar

Dastgheib, S. A., Knutson, C., and Yang, Y. (2014). Produced water from CO2-EOR in the Illinois basin. Energy Procedia 63, 6878–6886. doi:10.1016/j.egypro.2014.11.722

CrossRef Full Text | Google Scholar

Di Lorenzo, F., Burgos-Cara, A., Ruiz-Agudo, E., Putnis, C. V., and Prieto, M. (2017). Effect of ferrous iron on the nucleation and growth of CaCO 3 in slightly basic aqueous solutions. CrystEngComm 19 (3), 447–460. doi:10.1039/C6CE02290A

CrossRef Full Text | Google Scholar

Dinu, M. V., and Dragan, E. S. (2008). Heavy metals adsorption on some iminodiacetate chelating resins as a function of the adsorption parameters. React. Funct. Polym. 68 (9), 1346–1354. doi:10.1016/j.reactfunctpolym.2008.06.011

CrossRef Full Text | Google Scholar

Drage, T. C., Snape, C. E., Stevens, L. A., et al. (2012). Materials challenges for the development of solid sorbents for post- combustion carbon capture. J. Mater. Chem. 22 (7), 2815–2823. doi:10.1039/C2JM12592G

CrossRef Full Text | Google Scholar

Druckenmiller, M. L., and Maroto-Valer, M. M. (2005). Carbon sequestration using brine of adjusted PH to form mineral carbonates. Fuel Process. Technol. 86 (14), 1599–1614. doi:10.1016/j.fuproc.2005.01.007

CrossRef Full Text | Google Scholar

Dutcher, B., Fan, M., and Russell, A. G. (2015). Amine-based CO2 capture technology development from the beginning of 2013-a review. ACS Appl. Mater. Interfaces 7 (4), 2137–2148. doi:10.1021/am507465f

PubMed Abstract | CrossRef Full Text | Google Scholar

Dyer, A., and Gettins, R. B. (1970). The mobility of cations in synthetic zeolites with the faujasite framework — III: self-diffusion of cations into X and Y zeolites from non-aqueous solutions. J. Inorg. Nucl. Chem. 32 (7), 2401–2410. doi:10.1016/0022-1902(70)80523-1

CrossRef Full Text | Google Scholar

El Hadri, N., Quang, D. V., Goetheer, E. L. V., and Abu Zahra, M. R. M. (2017). Aqueous amine solution characterization for post-combustion CO2 capture process. Appl. Energy 185, 1433–1449. doi:10.1016/j.apenergy.2016.03.043

CrossRef Full Text | Google Scholar

El-Kamash, A. M. (2008). Evaluation of zeolite A for the sorptive removal of Cs+ and Sr2+ ions from aqueous solutions using batch and fixed bed column operations. J. Hazard Mater. 151 (2), 432–445. doi:10.1016/j.jhazmat.2007.06.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Federal Highway Administration (2016). Blast furnace slag - material description - user guidelines for waste and Byproduct materials in pavement construction - FHWA-RD-97-148. Available at: https://www.fhwa.dot.gov/publications/research/infrastructure/structures/97148/bfs1.cfm#:∼:text=It%20is%20estimated%20that%20approximately,annually%20in%20the%20United%20States.&text=Almost%20all%20of%20the%20blast,of%20this%20slag%20is%20ACBFS (Accessed August 4, 2020).

Google Scholar

Flanigen, E. M., Broach, R. W., and Wilson, S. T. (2010). Zeolites in industrial separation and catalysis. Hoboken, NJ: John Wiley & Sons, 1–26. doi:10.1002/9783527629565.ch1

CrossRef Full Text | Google Scholar

Florin, N. H., Blamey, J., and Fennell, P. S. (2010). Synthetic CaO-based sorbent for CO₂ capture from large-point sources. Energy Fuel. 24 (8), 4598–4604. doi:10.1021/ef100447c

CrossRef Full Text | Google Scholar

Galvez-Martos, J.-L., Elhoweris, A., Morrison, J., and Al-horr, Y. (2018). Conceptual design of a CO2 capture and utilisation process based on calcium and magnesium rich brines. J. CO₂ Utilizat. 27, 161–169. doi:10.1016/j.jcou.2018.07.011

CrossRef Full Text | Google Scholar

Golie, W. M., and Upadhyayula, S. (2016). Continuous fixed-bed column study for the removal of nitrate from water using chitosan/alumina composite. J. Water Process Engin. 12, 58–65. doi:10.1016/j.jwpe.2016.06.007

CrossRef Full Text | Google Scholar

Gouran-Orimi, R., Mirzayi, B., Nematollahzadeh, A., and Tardast, A. (2018). Competitive adsorption of nitrate in fixed-bed column packed with bio-inspired polydopamine coated zeolite. J. Environ. Chem. Engin. 6 (2), 2232–2240. doi:10.1016/j.jece.2018.01.049

CrossRef Full Text | Google Scholar

Guerra, K., Dahm, K., and Dundorf, S. (2011). Oil and gas produced water management and beneficial use in the western United States. Reclamation Managing Water in the West 157, 1–113.

Google Scholar

Guo, H., Ren, Y., Sun, X., Xu, Y., Li, X., Zhang, T., et al. (2013). Removal of Pb2+ from aqueous solutions by a high-efficiency resin. Appl. Surf. Sci. 283, 660–667. doi:10.1016/j.apsusc.2013.06.161

CrossRef Full Text | Google Scholar

Han, R., Zou, W., Li, H., Li, Y., and Shi, J. (2006). Copper(II) and lead(II) removal from aqueous solution in fixed-bed columns by manganese oxide coated zeolite. J. Hazard Mater. 137 (2), 934–942. doi:10.1016/j.jhazmat.2006.03.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Harland, C. E. (1994). Ion exchange. Cambridge, UK: Royal Society of Chemistry. doi:10.1039/9781847551184

CrossRef Full Text | Google Scholar

Helgeson, H. C., Kirkham, D. H., and Flowers, G. C. (1981). Theoretical prediction of the thermodynamic behavior of aqueous electrolytes by high pressures and temperatures; IV, calculation of activity coefficients, osmotic coefficients, and apparent molal and standard and relative partial molal properties to 600 degrees C and 5kb. Am. J. Sci. 281 (10), 1249–1516. doi:10.2475/ajs.281.10.1249

CrossRef Full Text | Google Scholar

Humbert, P. S., and Castro-Gomes, J. (2019). CO2 activated steel slag-based materials: a review. J. Clean. Prod. 208, 448–457. doi:10.1016/j.jclepro.2018.10.058

CrossRef Full Text | Google Scholar

Hummel, W., Berner, U., Curti, E., Pearson, F., and Thoenen, T. (2002). Nagra/PSI chemical thermodynamic data base 01/01. doi:10.1524/ract.2002.90.9-11_2002.805

CrossRef Full Text | Google Scholar

IEA (2019). Global energy and CO₂ status report 2019–analysis. Available at: https://www.iea.org/reports/global-energy-co2-status-report-2019 (Accessed August 12, 2020).

Google Scholar

IEA (2020a). Global CO2 emissions in 2019–analysis in 2019. Available at: https://www.iea.org/articles/global-co2-emissions-in-2019 (Accessed August 12, 2020).

Google Scholar

IEA (2020b). Global energy and CO2 emissions in 2020–global energy review 2020–analysis. Available at: https://www.iea.org/reports/global-energy-review-2020/global-energy-and-co2-emissions-in-2020 (Accessed August 12, 2020).

Google Scholar

Inglezakis, V. J. (2005). The concept of “capacity” in zeolite ion-exchange systems. J. Colloid Interface Sci. 281 (1), 68–79. doi:10.1016/j.jcis.2004.08.082

PubMed Abstract | CrossRef Full Text | Google Scholar

Jang, J., and Lee, D. S. (2016). Enhanced adsorption of cesium on PVA-alginate encapsulated prussian blue-graphene oxide hydrogel beads in a fixed-bed column system. Bioresour. Technol. 218, 294–300. doi:10.1016/j.biortech.2016.06.100

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, Y., Teng, C., Yu, S., Song, T., Dong, L., Liang, J., et al. (2018). Batch and fixed-bed biosorption of Cd(II) from aqueous solution using immobilized pleurotus ostreatus spent substrate. Chemosphere 191, 799–808. doi:10.1016/j.chemosphere.2017.08.154

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, J. W., Oelkers, E. H., and Helgeson, H. C. (1992). SUPCRT92: a software package for calculating the standard molal thermodynamic properties of minerals, gases, aqueous species, and reactions from 1 to 5000 bar and 0 to 1000°C. Comput. Geosci. 18 (7), 899–947. doi:10.1016/0098-3004(92)90029-Q

CrossRef Full Text | Google Scholar

Kar, S., Goeppert, A., and Prakash, G. K. S. (2019). Integrated CO₂ capture and conversion to formate and methanol: connecting two threads. Acc. Chem. Res. 52 (10), 2892–2903. doi:10.1021/acs.accounts.9b00324

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, S., Shi, H., and Lee, J. Y. (2016). CO2 absorption mechanism in amine solvents and enhancement of CO2 capture capability in blended amine solvent. Inte. J. Greenhouse Gas Contr. 45, 181–188. doi:10.1016/j.ijggc.2015.12.024

CrossRef Full Text | Google Scholar

King, D. W., and Farlow, R. (2000). Role of carbonate speciation on the oxidation of Fe(II) by H2O2. Mar. Chem. 70 (1), 201–209. doi:10.1016/S0304-4203(00)00026-8

CrossRef Full Text | Google Scholar

Kirov, G., and Filizova, L. (2012). Cationic hydration impact on zeolite formation and properties: а review and discussion. Geokhim., Mineral. Petrol 49, 65–82.

Google Scholar

Klein, A. R., Baldwin, D. S., Singh, B., and Silvester, E. (2010). Salinity-induced acidification in a wetland sediment through the displacement of clay-bound iron (II). Environ. Chem. 7, 413–421. doi:10.1071/EN10057

CrossRef Full Text | Google Scholar

Kralj, D., Kontrec, J., Brecević, L., Falini, G., and Nöthig-Laslo, V. (2004). Effect of inorganic anions on the morphology and structure of magnesium calcite. Chem. Eur J. 10 (7), 1647–1656. doi:10.1002/chem.200305313

CrossRef Full Text | Google Scholar

Kulik, D. A., Wagner, T., Dmytrieva, S. V., Kosakowski, G., Hingerl, F. F., Chudnenko, K. V., et al. (2012). GEM-selektor geochemical modeling package: revised algorithm and GEMS3K numerical kernel for coupled simulation codes. Berlin, Germany: Springer. doi:10.1007/s10596-012-9310-6

CrossRef Full Text | Google Scholar

Kunin, R., and Vassiliou, B. (1963). Regeneration of carboxylic cation exchange resins with carbon dioxide. Ind. Eng. Chem. Prod. Res. Dev. 2 (1), 1–3. doi:10.1021/i360005a001

CrossRef Full Text | Google Scholar

Leaković, S., Mijatović, I., Cerjan-Stefanović, Š., and Hodžić, E. (2000). Nitrogen removal from fertilizer wastewater by ion exchange. Water Res. 34 (1), 185–190. doi:10.1016/S0043-1354(99)00122-0

CrossRef Full Text | Google Scholar

Liu, S., Gao, H., He, C., and Liang, Z. (2019). Experimental evaluation of highly efficient primary and secondary amines with lower energy by a novel method for post-combustion CO2 capture. Appl. Energy 233‒234, 443–452. doi:10.1016/j.apenergy.2018.10.031

PubMed Abstract | CrossRef Full Text | Google Scholar

Lothenbach, B., Kulik, D. A., Matschei, T., Balonis, M., Baquerizo, L., Dilnesa, B., et al. (2019). Cemdata18: a chemical thermodynamic database for hydrated portland cements and alkali-activated materials. Cement Concer Res. 115, 472–506. doi:10.1016/j.cemconres.2018.04.018

CrossRef Full Text | Google Scholar

Malik, D. S., Jain, C. K., and Yadav, A. K. (2018). Heavy metal removal by fixed-bed column – a review. ChemBioEng Rev. 5 (3), 173–179. doi:10.1002/cben.201700018

CrossRef Full Text | Google Scholar

Manzolini, G., Sanchez Fernandez, E., Rezvani, S., Macchi, E., Goetheer, E. L. V., and Vlugt, T. J. H. (2015). Economic assessment of novel amine based CO2 capture technologies integrated in power plants based on European benchmarking task force methodology. Appl. Energy 138, 546–558. doi:10.1016/j.apenergy.2014.04.066

CrossRef Full Text | Google Scholar

Maul, G. A., Kim, Y., Amini, A., Zhang, Q., and Boyer, T. H. (2014). Efficiency and life cycle environmental impacts of ion-exchange regeneration using sodium, potassium, chloride, and bicarbonate salts. Chem. Eng. J. 254, 198–209. doi:10.1016/j.cej.2014.05.086

CrossRef Full Text | Google Scholar

Mazur, L. P., Pozdniakova, T. A., Mayer, D. A., Boaventura, R. A., and Vilar, V. J. (2016). Design of a fixed-bed ion-exchange process for the treatment of rinse waters generated in the galvanization process using laminaria hyperborea as natural cation exchanger. Water Res. 90, 354–368. doi:10.1016/j.watres.2015.12.027

PubMed Abstract | CrossRef Full Text | Google Scholar

Mondal, M. K. (2009). Removal of Pb(II) ions from aqueous solution using activated tea waste: adsorption on a fixed-bed column. J. Environ. Manag. 90 (11), 3266–3271. doi:10.1016/j.jenvman.2009.05.025

CrossRef Full Text | Google Scholar

Mores, P. L., Godoy, E., Mussati, S. F., and Scenna, N. J. (2014). A NGCC power plant with a CO2 post-combustion capture option. Optimal economics for different generation/capture goals. Chem. Eng. Res. Des. 92 (7), 1329–1353. doi:10.1016/j.cherd.2013.11.013

CrossRef Full Text | Google Scholar

Munthali, M., Elsheikh, M., Johan, E., and Matsue, N. (2014). Proton adsorption selectivity of zeolites in aqueous media: effect of Si/Al ratio of zeolites. Molecules 19 (12), 20468–20481. doi:10.3390/molecules191220468

PubMed Abstract | CrossRef Full Text | Google Scholar

Nasef, M. (2008). Polymer grafting and crosslinking. Hoboken, NJ: John Wiley & Sons, 233–272. doi:10.1002/9780470414811.ch10

CrossRef Full Text | Google Scholar

Nishiyama, R., Munemoto, T., and Fukushi, K. (2013). Formation condition of monohydrocalcite from CaCl2–MgCl2–Na₂CO₃ solutions. Geochem. Cosmochim. Acta 100, 217–231. doi:10.1016/j.gca.2012.09.002

CrossRef Full Text | Google Scholar

Nyquist, S., and Ruys, J. (2009). CO2 abatement: exploring options for oil and natural gas companies. New York, NY: McKinsey & Company.

Google Scholar

Oh, S.-Y., Yun, S., and Kim, J.-K. (2018). Process integration and design for maximizing energy efficiency of a coal-fired power plant integrated with amine-based CO2 capture process. Appl. Energy 216, 311–322. doi:10.1016/j.apenergy.2018.02.100

CrossRef Full Text | Google Scholar

Ostroski, I. C., Borba, C. E., Silva, E. A., Arroyo, P. A., Guirardello, R., and Barros, M. A. S. D. (2011). Mass transfer mechanism of ion exchange in fixed bed columns. J. Chem. Eng. Data 56 (3), 375–382. doi:10.1021/je100568n

CrossRef Full Text | Google Scholar

Otton, J. K., and Kharaka, Y. K. (2003). Environmental impacts of Petroleum production: initial results from the osage-skiatook petroleum environmental research sites, Osage County, OK: Diane Publishing. doi:10.3133/wri034260

CrossRef Full Text | Google Scholar

Puerta-Falla, G., Balonis, M., Falzone, G., Bauchy, M., Neithalath, N., and Sant, G. (2017). Monovalent ion exchange kinetics of hydrated calcium-alumino layered double hydroxides. Ind. Eng. Chem. Res. 56 (1), 63–74. doi:10.1021/acs.iecr.6b03474

CrossRef Full Text | Google Scholar

Rao, A. B., and Rubin, E. S. (2020). A technical, economic, and environmental assessment of amine-based CO2 capture technology for power plant Greenhouse gas control. Environ. Sci. Technol. 44 (5), 330. doi:10.1021/es0158861

CrossRef Full Text | Google Scholar

Roach, R. W., Carr, R. S., Howard, C. L., and Cain, B. W. (1993). AN assessment OF produced water impacts IN the galveston bay system, 38.

Google Scholar

Robie, R., and Hemingway, B. (1995). Thermodynamic properties of minerals and related substances at 298.15 K and 1 bar (105 pascals) pressure and at higher temperatures. San Bernardino County, CA: U.S Geological Survey Bulletin. doi:10.3133/b1452

CrossRef Full Text | Google Scholar

Robin, V., Tertre, E., Beaufort, D., Regnault, O., Sardini, P., and Descostes, M. (2015). Ion exchange reactions of major inorganic cations (H+, Na+, Ca2+, Mg2+ and K+) on beidellite: experimental results and new thermodynamic database. Toward a better prediction of contaminant mobility in natural environments. Appl. Geochem. 59, 74–84. doi:10.1016/j.apgeochem.2015.03.016

CrossRef Full Text | Google Scholar

Rodriguez-Blanco, J. D., Shaw, S., Bots, P., Roncal-Herrero, T., and Benning, L. G. (2014). The role of Mg in the crystallization of monohydrocalcite. Geochem. Cosmochim. Acta 127, 204–220. doi:10.1016/j.gca.2013.11.034

CrossRef Full Text | Google Scholar

Ruthven, D. M. (1984). Principles of adsorption and adsorption processes. Hoboken, NJ: WileyAvailable at: https://www.wiley.com/en-us/Principles+of+Adsorption+and+Adsorption+Processes-p-9780471866060 (Accessed August 12, 2020).

Google Scholar

Said, A., Mattila, H.-P., Järvinen, M., and Zevenhoven, R. (2013). Production of precipitated calcium carbonate (PCC) from steelmaking slag for fixation of CO2. Appl. Energy 112, 765–771. doi:10.1016/j.apenergy.2012.12.042

CrossRef Full Text | Google Scholar

Scanlon, B. R., Reedy, R. C., Xu, P., Engle, M., Nicot, J. P., Yoxtheimer, D., et al. (2020). Can we beneficially reuse produced water from oil and gas extraction in the U.S.? Sci. Total Environ. 717, 137085. doi:10.1016/j.scitotenv.2020.137085

PubMed Abstract | CrossRef Full Text | Google Scholar

Seggiani, M., Vitolo, S., and D’Antone, S. (2006). Recovery of nickel from orimulsion fly ash by iminodiacetic acid chelating resin. Hydrometallurgy 81 (1), 9–14. doi:10.1016/j.hydromet.2005.09.005

CrossRef Full Text | Google Scholar

Seifritz, W. (1990). CO₂ disposal by means of silicates. Nature 345 (6275), 486. doi:10.1038/345486b0

CrossRef Full Text | Google Scholar

Sofia Plagakis (2013). ource of Greenhouse gas emissions, EPA data reveals. Washington, DC: Center for Effective Government Available at: https://www.foreffectivegov.org/oil-and-gas-production-major-source-of-greenhouse-gas-emissions-epa-data-reveals (Accessed August 4, 2020).

Google Scholar

Teir, S., Eloneva, S., Fogelholm, C.-J., and Zevenhoven, R. (2007). Dissolution of steelmaking slags in acetic acid for precipitated calcium carbonate production. Energy 32 (4), 528–539. doi:10.1016/j.energy.2006.06.023

CrossRef Full Text | Google Scholar

Thoenen, T., Hummel, W., Berner, U., and Curti, E. (2007). The PSI/nagra chemical thermodynamic database 12/07; villigen PSI. Villigen, Switzerland: Paul Scherrer Institut.

Google Scholar

Townsend, R. P. (1991). “Chapter 10 ion exchange in zeolites,” in Studies in surface science and catalysis. Introduction to zeolite science and practice. Editors H. van Bekkum, E. M. Flanigen, and J. C. Jansen (Amsterdam, Netherlands: Elsevier), Vol. 58, 359–390. doi:10.1016/S0167-2991(08)63608-3

CrossRef Full Text | Google Scholar

U.S. Department of Energy (2019). Natural gas flaring and venting: state and federal regulatory Overview. Trends, and impacts.

Google Scholar

Víctor-Ortega, M. D., Ochando-Pulido, J. M., and Martínez-Ferez, A. (2017). Impacts of main parameters on the regeneration process efficiency of several ion exchange resins after final purification of olive mill effluent. Separ. Purif. Technol. 173, 1–8. doi:10.1016/j.seppur.2016.08.037

CrossRef Full Text | Google Scholar

Wachinski, A. M. (2017). Environmental ion exchange: principles and design. 2nd Edn. Boca Raton, London, New York: CRC Press, Taylor & Francis Group.

Google Scholar

Wagner, T., Kulik, D. A., Hingerl, F. F., and Dmytrieva, S. V. (2012). Gem-selektor geochemical modeling package: TSolMod library and data interface for multicomponent phase models. Cancer Mineral. 50 (5), 1173–1195. doi:10.3749/canmin.50.5.1173

CrossRef Full Text | Google Scholar

Zhang, W., Liu, H., Sun, Y., Cakstins, J., Sun, C., and Snape, C. E. (2016). Parametric study on the regeneration heat requirement of an amine-based solid adsorbent process for post-combustion carbon capture. Appl. Energy 168, 394–405 doi:10.1016/j.apenergy.2016.01.049

CrossRef Full Text | Google Scholar