To the Calculation of the Average Value of the Volume Fraction of the Key Bulk Component at the Intermediate Stage of Mixing With an Inclined Bump

The aim of this work is to develop a stochastic method for calculating the average value of the volume fraction of a key bulk component at an intermediate stage of mixing with an inclined bump based on the energy method. The specified characteristic is used to assess the quality of the granular mixture when choosing a criterion in the form of a heterogeneity coefficient of the product obtained at the corresponding stage of operation of the gravitational apparatus. This equipment is designed to produce a mixture of solid dispersed components in a ratio of 1/10 or more. At the same time, at each stage of mixing, two types of mixing devices (brush elements and inclined bump surfaces) work. A distinctive feature of the application of the energy method is to obtain an analytical relationship for the desired characteristics of the process of mixing bulk materials, taking into account their physical and mechanical properties and a set of structural and operational parameters of the apparatus. The calculation of the increment angles of reflection of rarefied flows of bulk components after interaction with the bump surface is proposed. The differential distribution functions of the number of particles of these components over the states of macrosystems are taken into account. The basis is the results of stochastic modeling of mixing of flowing media with brushes. The effectiveness of the intermediate stage of mixing with the bump using the coefficient of heterogeneity of the granular mixture is analyzed. The influence of the most significant design parameters of the gravitational apparatus and its operating modes on the quality of the intermediate mixture in comparison with the results for the initial and final steps is investigated. It has been established that this class of parameters includes the angular velocity of rotation of the drum, the angle of inclination of the bump to the horizontal, the pitch of screw winding, and a comprehensive indicator of the deformation of the brush elements. For example, an increase in the last complex indicator by 0.05 units leads to a decrease in the inhomogeneity coefficient by (0.15–0.80%) in the studied range of the angular velocity of rotation of the drums. In addition, the consequence of this is a decrease of 0.5 s⁻¹ for the value of the angular velocity of the mixing drum, which corresponds to the minimum value for the specified quality criterion of the mixture. The latter fact allows under the selected conditions ensuring a reduction in energy costs for the expended power drives of the mixing drums. The results of the work, confirmed by experimental studies, predict rational ranges of change of significant process parameters using the criteria for the best mixing of components proposed by the authors earlier.

Introduction

The urgency of the problem of mixing loose components is explained by the diversity of the purpose of the mixtures obtained for the needs of various industries and the agroindustrial complex. At the same time, the tasks of obtaining homogeneous composites, whose properties are imposed by strict regulated consumer requirements in the field of thermal and nuclear energy, are of particular relevance. In addition, the heterogeneity of the mixture of solid dispersed media, intended further for the production of rubber products, glass, porcelain, asphalt concrete, and so on, significantly reduces the quality of the finished product and affects the overall production indicators of energy and resource efficiency. Factors such as humidity and especially pronounced adhesive properties of the components being mixed make it difficult to solve this problem and lead to additional costs in processing these materials. The development of methods for mixing bulk components in a regulatory ratio of 1:10 or more, in particular, actively used in glass and foundry, requires the designers of the appropriate equipment to perform a system–structural analysis of this process.

The basis of this analysis is a theoretical prediction of the efficiency of the mixing process at each stage. The gravitational method for obtaining a free-flowing mixture with the specified ratio of components in the finished product proposed in Zaitzev et al. (2016) implies the presence of three mixing stages on trays with two steps in each. In this case, the first step involves the use of additional mixing elements in the form of brushes, and the second, fender surfaces.

The aim of the work is to develop a method for calculating the average value for the volume fraction of the key bulk component at the intermediate stage of gravity mixing using an inclined bump stop surface. This characteristic of the mixing process is necessary in assessing the quality of the mixture with a regulatory ratio of 1:10 components, as an indicator of the effectiveness of the intermediate stage of the process under study. The proposed expression for the desired characteristic of the key component was obtained on the basis of the stochastic approach (Klimontovich, 2014; Kapranova et al., 2016), taking into account the results of modeling the formation of rarefied streams of solid dispersed materials. The stochastic modeling of the studied process of mixing bulk solids in rarefied flows is based on the energy method (Klimontovich, 2014), tested by the authors when describing the kinetics of a non-equilibrium energetically open macrosystem (Kapranova et al., 2016). This method allows one to build the distribution of particle density of each mixed component according to the characteristic parameter of the studied technological operation. In this case, the particle sizes, the densities of their substances, and dissipative effects when interacting with the mixing elements of the apparatus, its design parameters, and the regulatory parameters of the finished mixture are taken into account. Various variations of stochastic modeling methods are known (Johnson et al., 1962; Kendall and Stuart, 1967; Mizonov et al., 2016; Rosato et al., 2016; Zhuang et al., 2016; Alsayyad et al., 2018), in particular, cell-based (Mizonov et al., 2016) in the framework of the theory of the AA Markov process, time series (Johnson et al., 1962; Kendall and Stuart, 1967), cybernetic, and so on. In contrast to them, the method proposed for use (Klimontovich, 2014) allows one to obtain an analytical representation of the result, which is essential when constructing an engineering methodology for calculating the designed mixer of bulk materials.

At the same time, at the first step for the stage of intermediate mixing, it is supposed to use brush elements on a rotating drum (Kapranova et al., 2015, 2016; Kapranova and Verloka, 2018a). At the second step, a fencing surface is used (Kapranova and Verloka, 2016, 2017; Kapranova et al., 2018a; Verloka et al., 2018) for impact interaction with rarefied flows of mixed materials formed after scattering by brushes. The indicated expression uses the function for the volume fraction of the key component, depending on the reflection angles of each of the two bulk materials from the baffle surface (Verloka et al., 2018). In addition, the latter function takes into account the previously proposed method for calculating volume fractions (Kapranova and Verloka, 2018b; Kapranova et al., 2018b; Kapranova A. B. et al., 2020) for mixed portions of components that correspond to the intermediate stage of this process (Kapranova et al., 2019a). Note that a convenient criterion for assessing the quality of a mixture in this case is its heterogeneity coefficient, which is determined by the traditional one and is estimated on the basis of the proposed models of the authors (Kapranova and Verloka, 2018b; Kapranova et al., 2018b; Kapranova A. B. et al., 2020) at various stages of mixing: the first (Verloka et al., 2018), intermediate (Kapranova and Verloka, 2017; Kapranova et al., 2019a), and final (Kapranova et al., 2019b).

Theory

Description of the Gravitational Principle of Mixing Bulk Components by Additional Mixing Elements

Let the gravitational apparatus require a loose mixture of two components (i = 1, 2) with the ratio of their volumes Ω_{1, nϑ}/Ω_{2, nϑ} = α_{1, nϑ}/α_{2, nϑ}, where Ω_iτ and α_iτ are, respectively, the volume and volume fraction of component i at stage τ for $\tau =\overline{1,n_{\vartheta }}$. Moreover, the notation for the subscript i is as follows: “1” is the transporting component; “2” is the key, then let the condition α_{1, nϑ}≪α_{2, nϑ} be fulfilled. The gravitational principle of mixing bulk components is implemented using a set of inclined trays located at an angle μ_ϑ when it is counted from the vertical wall of the apparatus body to the bottom surface of the tray. The alternate location of the trays on opposite sides of the vertical walls of the apparatus at different levels provides a transition from one mixing stage to another. A feature of the proposed method of mixing in a gravitational apparatus is the use at the intermediate stage (Figures 1A–C) of auxiliary mixing elements, which allow us to divide the process of intermediate mixing of bulk components into two steps. Schematic diagrams of these steps are shown in Figure 1A. The first step of mixing at its intermediate stage involves spreading from tray 5 layers of granular materials with the help of brush elements 8 ($j=\overline{1,n_b}$), mounted on the cylindrical drum 7 along counter-propagating helical lines of constant pitch k = 1, 2 (Figures 1B,C). The second step is the impact interaction with the inclined baffle surface 9 formed in the first step of the torches of bulk components. Note that further modeling takes into account the discharge of loose components i = 1, 2 from each of the deformed brush elements 8 ($j=\overline{1,n_b}$), fixed on the cylindrical surface of drum 7 along oncoming helical lines k = 1, 2.

FIGURE 1

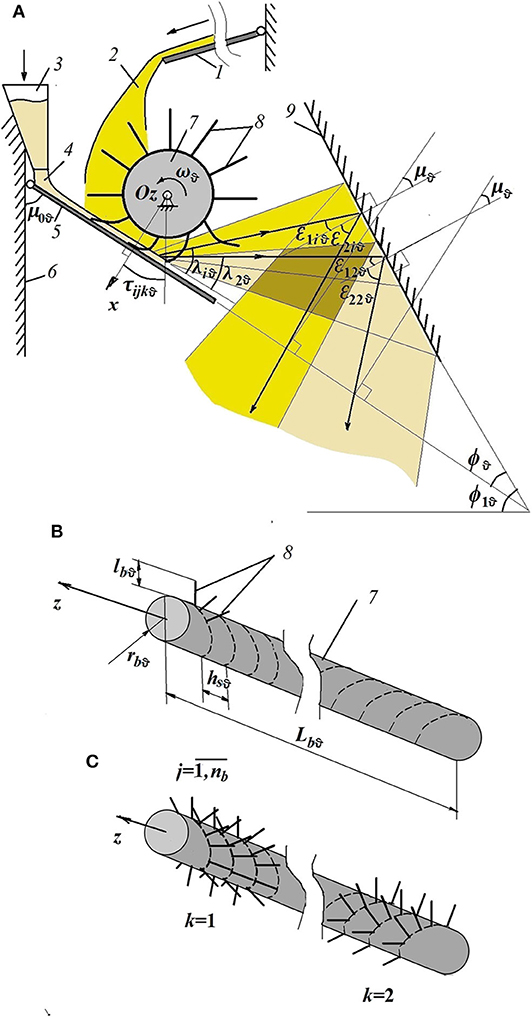
Figure 1. Conditional schemes: (A) for the intermediate stage of mixing (τ = ϑ) of bulk components (i = 1, 2) in the gravitational apparatus when their flows interact with the brush elements $j=\overline{1,n_b}$ (step 1) and the bump surface (step 2): 1—inclined tray; 2—the flow of the granular mixture after the stage τ = ϑ−1 with the preliminary composition of two components (i = 1, 2) in the ratio of their volumes Ω_{1, ϑ−1}/Ω_{2, ϑ −1} = α_{1, ϑ −1}/α_{2, ϑ −1}; 3—hopper dispenser; 4—the flow of the key loose component (i = 2) with the volume (Ω_{2, ϑ} − Ω_{2, ϑ−1}) corresponding to the increment of the fraction of this component Δα_{2, ϑ} = α_{2, ϑ}−α_{2, ϑ −1}; 5—inclined tray; 6—wall of the housing; 7—drum; 8—brush elements; 9—bump surface; (B) for drum 7; (C) for drum 7 and brush elements 8. The copyright holder of the patents referenced here is Yaroslavl State Technical University, Yaroslavl, Russia.

It is assumed that at the intermediate stage ϑ for τ = 1, …, ϑ−1, ϑ, ϑ + 1, …, n_ϑ for gravitational mixing (Figure 1A), two streams 2 and 4 are fed vertically to the inclined tray into the gap between drum 7 with brush element 8 and the specified tray 5. One stream 2 is a loose mixture obtained in the previous stage at τ = ϑ−1 for the gravitational mixing process and has a preliminary composition with two components (i = 1, 2) in the ratio of their volumes Ω_{1, ϑ−1}/Ω_{2, ϑ−1} = α_{1, ϑ−1}/α_{2, ϑ−1}. Another stream 4 is supplied to the indicated inclined tray 5 and consists of only one (key) component i = 2. The volume of this stream 4 is equal to the difference in volumes Ω_{2, ϑ} − Ω_{2, ϑ−1} and corresponds to the increment of the fraction of this component Δα_{2, ϑ} = α_{2, ϑ} − α_{2, ϑ−1} at the stage ϑ. To calculate the value of Δα_{2, ϑ}, we use the recurrence relation proposed by the authors of Kapranova and Verloka (2016) and tested in Kapranova and Verloka (2018b), Kapranova et al. (2018b), and Kapranova A. B. et al. (2020). In this calculation, the principle of mixing equal volumes at stage ϑ is taken into account when Ω_{1, ϑ−1} + Ω_{2, ϑ−1} = Ω_{2, ϑ}. Let a particle of granular material i have a spherical shape, diameter $D_{Si}={n_{di}}^{-1}\sum _{g=1}^{n_{di}}{d}_{ig}$ averaged over fractions, and substance density ρ_Si. Here it is indicated that d_ig = (d_{ig, max} + d_{ig, min})/2 is the average particle diameter of the fraction фракции $=\overline{1,n_{di}}$; n_di is the number of fractions for the material component i; d_{ig, max} and d_{ig, min} are the maximum and minimum values of the particle diameters in each selected fraction g.

The Main Features of Modeling the Process of Formation of Rarefied Flows of Loose Components by Brush Elements

Initially, we consider the process of formation of rarefied flows of bulk components (i = 1, 2, Figure 1A) after their discharge by deformed brush elements 8 ($j=\overline{1,n_b}$), mounted on rotating drum 7 along oncoming helical lines k = 1, 2 (Figure 1C). The application of the stochastic approach in the framework of the energy method (Klimontovich, 2014) to simulate a random process of mixing granular media at the indicated first step (Kapranova and Verloka, 2018a; Kapranova A. B. et al., 2020) involves considering the motion of a spherical particle of material i in a phase volume with the element dΦ_ijkϑ = dv_xijkϑdv_yijkϑ at the intermediate stage ϑ.

Here, the Hamilton parameters are chosen as phase variables as the components of the velocity (v_xijkϑ, v_yijkϑ) for the center of mass of the indicated particle in the Cartesian coordinate plane Oxy perpendicular to the axis of rotation of the drum Oz (Figures 1A–C).

Then, the transition to polar coordinates (r_ijkϑ, θ_ijkϑ) when the angular coordinate θ_ij is counted from the abscissa axis Ox leads to the next change in the representation phase volume element $d{\Phi }_{ijk\vartheta }={-{\omega }_{\vartheta }}^2{r}_{ijk\vartheta }d{r}_{\text{i}\text{j}\text{k}\vartheta }d{\theta }_{ijk\vartheta }$. The specified axis Ox is perpendicular to the surface of tray 5, along which the layers of granular components slide into the gap between tray 5 and drum 7 with brush elements 8.

It is believed that particle collisions after interacting with brush elements 8 of counter-helical lines k = 1, 2 are significant and can be considered as large-scale fluctuations in the state of the particle macrosystem of each bulk component i = 1, 2. This fact suggests that the indicated macrosystem i has an influx of energy from the outside, that is, energetically open (Kapranova and Verloka, 2018a). The states of such systems are described according to approach (Klimontovich, 2014) using the Fokker–Planck-type kinetic equation with a random Langevin source when choosing the ordering criterion for these states in the form of the Lyapunov S-theorem of the function (Klimontovich, 2014). Using the energy representation of the kinetic equation of the Fokker–Planck type with respect to the distribution function for the states of the macrosystem of particles (i = 1, 2), we restrict ourselves to the stationary solution of this equation obtained at the time of stochasticization of the macrosystem i similarly (Kapranova and Verloka, 2018a; Verloka et al., 2018).

In the case of the energy openness of this macrosystem i, the general form of the obtained stationary solution can be represented depending on the energy of a single particle E_ijkϑ. In this case, two types of energy parameters are introduced with the introduction of two types of energy parameters: E_0ijkϑ and E_fijkϑ are, respectively, the energy of the macrosystem at the indicated time and the loss of this energy due to interparticle collisions, as large-scale fluctuations states. Then we have

$\begin{array}{ll}{h}_{ijk\vartheta }=A_{ijk\vartheta }\text{exp}\left[\frac{-E_{ijk\vartheta }}{E_{0ijk\vartheta }}+E_{fijk\vartheta }^2/{(2E_{ijk\vartheta })}^2\right].& (1)\end{array}$

Note that in Kapranova and Verloka (2018a), based on Klimontovich (2014), an analysis was made of possible stationary solutions of the Fokker–Planck-type kinetic equation in the energy representation from the standpoint of dividing the parameters of the random process of mixing bulk components into optimizing and control ones. In expression (1), the constant A_ijkϑ, taking into account the form Φ_ijk, is determined by the normalization equation of the form

$\begin{array}{ll}{\displaystyle {\int }_{{\Phi }_{ijk\vartheta }}{h}_{ijk\vartheta }d{\Phi }_{ijk\vartheta }=1.}& (2)\end{array}$

The dependence of the energy E_ijkϑ(r_ijkϑ, θ_ijkϑ) for the motion of a spherical particle of material i in the phase volume with the element dΦ_ijkϑ is constructed by analogy with Kapranova and Verloka (2018a) in the form

$\begin{array}{ll}{E}_{ijk\vartheta }\left(r_{ijk\vartheta },{\theta }_{ijk\vartheta }\right)={\mu }_{1\vartheta }{\theta }_{ijk\vartheta }^2+{\mu }_{2ijk\vartheta }({\theta }_{ijk\vartheta })r_{ijk\vartheta }^2.& (3)\end{array}$

Here, the values of the coefficient μ_1ϑ and the functions μ_2ijkϑ(θ_ijkϑ) are determined by the physicomechanical properties of the mixed components and brush elements, as well as by the set of design and operating parameters of the gravity mixer, the choice of which is described in Kapranova A. B. et al. (2020).

The main structural parameters include the following (Figures 1A,B): r_bϑ and L_bϑ are radius and length of the drum; l_bϑ and h_sϑ are the length of the brush elements and the pitch of their screw winding; the following parameters are included in the operating parameters: ω_ϑ is angular velocity of rotation of the drum; h_0ϑ is the height of the gap between tray 5 and the surface of drum 7. Expression (3) takes into account the nature of free motion for particles of material i, provided that they have random angular momenta at the moment of elastic interaction with the brush element j for screw winding k at the intermediate mixing stage ϑ. Then, according to (1), an analytical expression can be obtained for the differential distribution function h_ijkϑ(τ_ijkϑ) for the number of particles of material i over the spread angle τ_ijkϑ by the brush element j for screw winding k in accordance with the definition:

$\begin{array}{ll}{h}_{ijk\vartheta }\left({\tau }_{ijk\vartheta }\right)\equiv N_{ijk\vartheta }^{-1}d{N}_{ijk\vartheta }/d{\tau }_{ijk\vartheta }.& (4)\end{array}$

In this case, the search for the explicit form of the energy parameters E_0ijkϑ and E_fijkϑ for the random process of mixing bulk components is determined by solving the system of equations. This system includes equations: energy balance (Kapranova et al., 2015, 2018a; Kapranova and Verloka, 2018a) and conservation of flows (Kapranova and Verloka, 2018a), taking into account large-scale fluctuations of states of macrosystem i, when the collisions of particles of various materials are most significant after scattering with a brush element j corresponding to the opposite screw windings at k = 1 and k = 2.

It follows from expressions (1) to (4) that the general form of the desired function h_ijkϑ(τ_ijkϑ) for the formation of sparse flows of loose components (i =1, 2) after they are dumped by deformed brush elements ($j=\overline{1,n_b}$) fixed on rotating drums along oncoming helical lines k = 1, 2 can be represented in the form:

$\begin{array}{l}{h}_{ijk\vartheta }\left({\tau }_{ijk\vartheta }\right)=b_{0ijk\vartheta }\left(\text{}\text{erf}\left\{b_{1ijk\vartheta }\left[1+b_{2ijk\vartheta }{\left({\tau }_{ijk\vartheta }-{\phi }_{ijk\vartheta }\right)}^2\text{}\right]\right\}\text{}\right)\\ -\text{erf}\left(\left(b_{1ijk\vartheta }\right)\right)\times \text{exp}\left[b_{3ijk\vartheta }\text{}\left({\tau }_{ijk\vartheta }-{\phi }_{ijk\vartheta }\right){\text{}}^2\right]\text{}.& (5)\end{array}$

The coefficients b_lijkϑ, l = 0, 1, 2, 3 from expression (5) depend on the design and operating parameters of the gravity mixer, as well as the physicomechanical characteristics of the mixed materials and brush elements; φ_ijkϑ is the characteristic angle determined by the bending geometry of the deformed brushes.

The Main Features of Modeling the Mixing of Granular Materials After Impact Interaction With an Inclined Bump Surface

At the second step of the intermediate stage ϑ for mixing granular materials (Kapranova and Verloka, 2016, 2018b), it is proposed to use bump surface 9 (Figures 1A–C) installed so that the formed rarefied flows of bulk components (i = 1, 2) after discharge by deformed brush elements 8 ($j=\overline{1,n_b}$) from oncoming helical lines k = 1, 2 of the rotating drum 7 experienced impact interaction with bump surface 9. After this impact interaction, new rarefied flows of granular components are formed having corresponding reflection angles γ_ijkϑ, which are measured from the normal to bump surface 9. These new rarefied flows have intersection areas in which additional mixing of loose components takes place. The bulk mixture obtained at the intermediate stage falls onto the lower inclined tray located on the opposite side of the body of the gravitational apparatus and slides along it, proceeding to the next mixing stage τ = ϑ+1. The general form of the differential distribution function H_ijkϑ(γ_ijkϑ) for the number of particles of material i according to the angle of reflection γ_ijkϑ from the chipper according to the results of Kapranova and Verloka (2016, 2018b) depends on the representation (5) for the function h_ijkϑ(τ_ijkϑ)

$\begin{array}{l}{H}_{ijk\vartheta }({\gamma }_{ijk\vartheta })=B_{0ijk\vartheta }\left(\text{erf}\left\{B_{1ijk\vartheta }\left[1+B_{2ijk\vartheta }{B}_{4ijk\vartheta }\left({\gamma }_{ijk\vartheta }\right)\right]\right\}\right)\\ -\text{erf}\left(\left(B_{1ijk\vartheta }\right)\right)\times \text{exp}\left[B_{3ijk\vartheta }{B}_{4ijk\vartheta }\left({\gamma }_{ijk\vartheta }\right)\right].& (6)\end{array}$

The coefficients B_lijkϑ, l = 0, 1, 2, 3 from expression (6) are also determined by the designing and operating parameters of the studied process and physicomechanical properties for the mixed components and brush elements. The functional dependence B_4ijkϑ(γ_ijkϑ) is defined by the geometric relation from Kapranova and Verloka (2018b) between the characteristic angles τ_ijkϑ and γ_ijkϑ.

Having made the transition to the averaged values for the angles of incidence ε_1ikϑ on the bump suface 9 of rarefied flows, which are described using the function h_ijkϑ(τ_ijkϑ), and the reflection angles ${\epsilon }_{2ik\vartheta }={n_b}^{-1}\sum _{j=1}^{n_b}{\gamma }_{ijk\vartheta }$ from this bump element 9 in terms of the number of deformed brush elements j for each component i mixed, we obtain from (6) the following representation for the desired function W_ijkϑ(ε_2ikϑ).

We pass to the averaged values for the angles of incidence ε_1ikϑ on the bump suface 9 of rarefied flows, which are described using the function h_ijkϑ(τ_ijkϑ), and the reflection angles ${\epsilon }_{2ik\vartheta }={n_b}^{-1}\sum _{j=1}^{n_b}{\gamma }_{ijk\vartheta }$ from this bump element 9 in terms of the number of deformed brush elements j for each component i mixed. We obtain from (6) the following representation for the desired function W_ijkϑ(ε_2ikϑ):

$\begin{array}{l}{W}_{ijk\vartheta }({\epsilon }_{2ik\vartheta })=B_{0ijk\vartheta }\left(\text{erf}\left\{B_{1ijk\vartheta }\left[1+B_{2ijk\vartheta }{\beta }_{4ijk\vartheta }\left({\epsilon }_{2ik\vartheta }\right)\right]\right\}\right)\\ -\text{erf}\left(\left(B_{1ijk\vartheta }\right)\right)\times \text{exp}\left[B_{3ijk\vartheta }{\beta }_{4ijk\vartheta }\left({\epsilon }_{2ik\vartheta }\right)\right]& (7)\end{array}$

where the functional dependence β_4ijkϑ(ε_2ikϑ), in contrast to B_4ijkϑ(γ_ijkϑ) from (6), is also determined by the recovery coefficients for particles of the mixed components i. Additionally, the assumption is made that the values ε_2i1ϑ = ε_2i2ϑ ≡ ε_2iϑ are equal due to the symmetrical arrangement of the screw windings of the brush elements 8 on the surface of the mixing drum 7 (Figure 1A). This assumption allows us to further omit the subscript k in the notation ε_2iϑ for the reflection angles of the particles of material i. The preservation of the indicated index k when designating the function W_ijkϑ(ε_2ikϑ) ≡ W_ijkϑ(ε_2iϑ) is explained by taking into account when it calculates particle collisions from rarefied flows of mixed components formed when interacting with brush elements from symmetric screw windings.

Therefore, taking into account (7), the complete non-equilibrium distribution functions R_ikϑ(ε_2iϑ) for the number of particles of component i, depending on the described reflection angles ε_2iϑ, take the form

$\begin{array}{ll}{R}_{ik\vartheta }\left({\epsilon }_{2i\vartheta }\right)={\displaystyle \prod _{j=1}^{n_b}{W}_{ijk\vartheta }\left({\epsilon }_{2i\vartheta }\right)}.& (8)\end{array}$

Using expression (8), the function Ψ_ϑ(ε_21ϑ, ε_22ϑ) is determined for the volume fraction of the key component (i = 2) obtained at the intermediate stage (τ = ϑ) for the process of mixing bulk materials after averaging over the number of symmetrical screw windings k for brush elements

$\begin{array}{l}{\Psi }_{\vartheta }\left({\epsilon }_{21\vartheta },{\epsilon }_{22\vartheta }\right)=\\ \frac{1}{2}{\displaystyle \sum _{k=1}^2\frac{{\rho }_{S1}{R}_{1k\vartheta }\left({\epsilon }_{21\vartheta }\right)+{\rho }_{S2}{\displaystyle {\sum }_{\tau =1}^{\vartheta -1}{\alpha }_{2,\tau }{R}_{2k\vartheta }\left({\epsilon }_{22\vartheta }\right)}}{{\rho }_{S1}{R}_{1k\vartheta }\left({\epsilon }_{21\vartheta }\right)+{\rho }_{S2}{\displaystyle {\sum }_{\tau =1}^{\vartheta }{\alpha }_{2,\tau }{R}_{2k\vartheta }\left({\epsilon }_{22\vartheta }\right)}}}.& (9)\end{array}$

Here, according to the recurrence relation proposed by the authors of Kapranova and Verloka (2016), the value of the volume fraction of the key component α_{2, τ} at an arbitrary mixing stage τ depends on the ratio of the volume fractions of bulk components at the final stage α_{1, nϑ}/α_{2, nϑ}

$\begin{array}{ll}{\alpha }_{2,\tau }={\alpha }_{1,1}\{(\tau -1)[\left({\alpha }_{2,n_{\vartheta }}-1\right)/2+1]-1\}.& (10)\end{array}$

Note that in formula (10) it is assumed that the volume fractions of the transporting component (i = 1) are equal at the initial (τ = 1) and final (τ = n_ϑ) mixing stages α_{1, 1} = α_{1, nϑ}. In addition, expression (9) contains values for the densities of substances ρ_Si corresponding to each component i.

Assessment of the Quality of a Mixture of Bulk Components After an Intermediate Stage of Their Gravitational Mixing

It is proposed to evaluate the quality of the bulk mixture obtained at the intermediate stage (τ = ϑ) using the criterion in the form of the inhomogeneity coefficient K_Cϑ, %, which is calculated using expression (9) for the function Ψ_ϑ(ε_21ϑ, ε_22ϑ), according to the following formula:

$\begin{array}{ll}{K}_{C\vartheta }=100{\left(\frac{\langle {\Psi }_{\vartheta }{}^2\rangle }{{\langle {\Psi }_{\vartheta }\rangle }^2}-1\right)}^{1/2}& (11)\end{array}$

where 〈Ψ_ϑ〉 and $\langle {{\Psi }_{\vartheta }}^2\rangle$ are the values, respectively, for the average of the fraction of the key component (i = 2) and the average of the square of the specified fraction from (9)

$\begin{array}{l}\langle {\Psi }_{\vartheta }\rangle ={\displaystyle \prod _{i=1}^2{(2{\epsilon }_{2i\vartheta }+\Delta {\epsilon }_{2i\vartheta }/2)}^{-1}}{\displaystyle {\int }_{{\epsilon }_{22\vartheta }}^{{\epsilon }_{22\vartheta }+\Delta {\epsilon }_{22\vartheta }/2}}\\ d{\epsilon }_{22\vartheta }{\displaystyle {\int }_{{\epsilon }_{21\vartheta }}^{\Delta {\epsilon }_{21\vartheta }+\Delta {\epsilon }_{21\vartheta }/2}{\Psi }_{\vartheta }\left({\epsilon }_{21\vartheta },{\epsilon }_{22\vartheta }\right)d{\epsilon }_{21\vartheta },}& (12)\end{array}$

$\begin{array}{l}\langle {\Psi }_{\vartheta }{}^2\rangle ={\displaystyle \prod _{i=1}^2{(2{\epsilon }_{2i\vartheta }+\Delta {\epsilon }_{2i\vartheta }/2)}^{-1}}\times {\displaystyle {\int }_{{\epsilon }_{22\vartheta }}^{{\epsilon }_{22\vartheta }+\Delta {\epsilon }_{22\vartheta }/2}}\\ d{\epsilon }_{22\vartheta }{\displaystyle {\int }_{{\epsilon }_{21\vartheta }}^{\Delta {\epsilon }_{21\vartheta }+\Delta {\epsilon }_{21\vartheta }/2}{\left[{\Psi }_{\vartheta }\left({\epsilon }_{21\vartheta },{\epsilon }_{22\vartheta }\right)\right]}^2}d{\epsilon }_{21\vartheta }.& (13)\end{array}$

In expressions (12) and (13), the calculation of the maximum values for the reflection angles ε_2iϑ of each of the bulk components (i = 1, 2) from bump surface 9 (Figure 1A) at the studied intermediate stage (τ = ϑ) of their mixing is carried out, taking into account their increments ε_2iϑ. The increment data ε_2iϑ is calculated using the geometric relationship for the relationship between the reflection angles ε_2iϑ, the scattering λ_iϑ, and the spread τ_ijkϑ

$\begin{array}{l}\Delta {\epsilon }_{2i\vartheta }=2\{\left[u_{1\vartheta }\left({\varphi }_{1\vartheta }\right)-{\lambda }_{i\vartheta }\right]u_{4i\vartheta }\left({\varphi }_{1\vartheta }\right)tg\left(\frac{\Delta {\lambda }_{i\vartheta }}{2}\right)\\ \frac{1+tg\left({\lambda }_{i\vartheta }\right)tg\left(\frac{\Delta {\lambda }_{i\vartheta }}{2}\right)}{1-tg\left({\lambda }_{i\vartheta }\right)tg\left(\frac{\Delta {\lambda }_{i\vartheta }}{2}\right)}-\frac{\Delta {\lambda }_{i\vartheta }{u}_{4i\vartheta }\left({\varphi }_{1\vartheta }\right)}{2}\}& (14)\end{array}$

where u_1ϑ(ϕ_1ϑ)=ϕ−ϕ_1ϑ−μ₀; u_2ϑ(ϕ_1ϑ)=u_1ϑ(ϕ_1ϑ)+ϕ/2; u_3ϑ(ϕ_1ϑ)=ϕ_1ϑ+μ_0ϑ; u_4iϑ(ϕ_1ϑ)=p_1iϑ(ϕ_1ϑ)u_2ϑ(ϕ_1ϑ) sin(μ_ϑ); u_5iϑ(ϕ_1ϑ)=L_i/h_i−ctg[u_3ϑ(ϕ_1ϑ)−π/2]; p_1iϑ(ϕ_1ϑ) = {[1−u_2ϑ(ϕ_1ϑ)]u_5ϑ(ϕ_1ϑ)}/{2u_5ϑ(ϕ_1ϑ)[1−u_5ϑ(ϕ_1ϑ)]}; p_2iϑ(ϕ_1ϑ) = [u_5iϑ(ϕ_1ϑ)+u_2ϑ(ϕ_1ϑ)]/cos(u_3ϑ(ϕ_1ϑ)−π/2); where μ_0ϑ is the angle of inclination of tray 5 to the vertical. At the same time, for the intermediate mixing stage ϑ, we used the functional relationship k_viϑ=k_viϑ(ϕ_1ϑ, μ_ϑ, L_iϑ, h_iϑ) between the recovery coefficient k_viϑ≡sin ε_2iϑ/sin ε_1iϑ and geometric parameters. The following notation is used here for which the following notation is used: ϕ_1ϑ is the angle of inclination of bump surface 9 to the horizontal planes; μ_ϑ is the characteristic angle between the perpendiculars to bump surface 9 and tray 5; L_iϑ is the width of the dispersion of particles of component i along tray 5; h_iϑ is the height between this tray 5 and bump surface 9 at the point of impact interaction of the averaged flow of component i.

Thus, when describing the relationship between the scattering angle τ_ijkϑ from the brushes 8 and the reflection angle ε_2iϑ from bump surface 9 (Kapranova and Verloka, 2016; Verloka et al., 2018), the recovery coefficient k_viϑ is used, which characterizes the directions of the averaged velocities of rarefied flows of each component (i = 1, 2) at impact on bump surface 9 and when they are reflected from it.

In expression (14), the averaged values ${\lambda }_{\text{i}\vartheta }={{(2n}_b)}^{-1}\sum _{k=1}^2\sum _{j=1}^{n_b}{\lambda }_{ijk\vartheta }$ by the number of deformed brush elements j for scattering angles λ_ijkϑ for particles of components (i = 1, 2) from the surface of tray 5 under the mixing drum 7 in their rarefied flows (Figures 1A,C) formed after scattering by the indicated brush elements 8 ($j=\overline{1,n_b}$) screw winding k. In this case, the following approximation is taken when calculating the increments for the scattering angles $\Delta {\lambda }_{i\vartheta }={{(2n}_b)}^{-1}{\sum }_{k=1}^2{\sum }_{j=1}^{n_b}{\Delta \tau }_{ijk\vartheta }$. Here, the increments of the scattering angles τ_ijkϑ are determined from the equations of equality of flows of loose components i with the number of particles N_ik at the entrance to the gap between tray 5 and drum 7 for interaction with the brush elements 8 of the screw winding k for $N_i=\sum _{k=\mathbf{\text{1}}}^{\mathbf{\text{2}}}{N}_{ik}$ as follows:

$\begin{array}{l}{\displaystyle \sum _{i=1}^2{N}_{ik}}={(2{\tau }_{ijk\vartheta }+\Delta {\tau }_{ijk\vartheta }/2)}^{-1}{\displaystyle \sum _{i=1}^2{{\displaystyle \int }}_{{\tau }_{ijk\vartheta }}^{{\tau }_{ijk\vartheta }+\Delta {\tau }_{ijk\vartheta }/2}}\\ {\displaystyle \prod _{j=1}^{n_b}{h}_{ijk\vartheta }\left({\tau }_{ijk\vartheta }\right)}d{\tau }_{ijk\vartheta },& (15)\end{array}$

So, both quantities 〈Ψ_ϑ〉, $\langle {{\Psi }_{\vartheta }}^2\rangle$ from expressions (11–13) are calculated using the differential distribution functions R_ikϑ(ε_2iϑ) for the number of particles of each component i after interacting with bump surface 9 (Kapranova and Verloka, 2016) by angle of reflection ε_2iϑ for the direction of the average particle velocity i. In this case, the results of the stochastic model of the formation of rarefied flows by brush elements (Kapranova and Verloka, 2018a; Verloka et al., 2018) are used for the differential distribution functions h_ijkϑ(τ_ijkϑ) for the number of particles of component i after they are scattered by each brush element j over the spread angle τ_ijkϑ. Note that when calculating the integrals on the right-hand sides of expressions (12), (13), we used the Maclaurin expansion of the following function $f_{i\vartheta }\left({\epsilon }_{2i\vartheta }\right)\text{\hspace{0.17em}\hspace{0.17em}}=\text{\hspace{0.17em}\hspace{0.17em}}1/\left\{{\beta }_{0i\vartheta }\text{\hspace{0.17em}\hspace{0.17em}}+\text{\hspace{0.17em}\hspace{0.17em}}{\beta }_{1i\vartheta }\exp \left[{\displaystyle {\sum }_{j=1}^{n_b}{\beta }_{2i\vartheta }}{({\beta }_{3i\vartheta }\text{\hspace{0.17em}\hspace{0.17em}}+\text{\hspace{0.17em}\hspace{0.17em}}{\beta }_{4i\vartheta }{\epsilon }_{2i\vartheta })}^2\right]\right\}$ in their integrands up to terms of order $\text{O}({{\epsilon }_{2\text{i}\vartheta }}^2)$, where the coefficients ${\beta }_{ri\vartheta };r=\overline{1,4}$ depend on the design parameters and the physical mechanical properties of bulk materials.

Results and Discussion

Thus, we have proposed a method for calculating the dependence Ψ_ϑ(ε_21ϑ, ε_22ϑ) for the volume fraction of the key component (i = 2) obtained at the intermediate stage (τ = ϑ) for the process of mixing bulk materials after averaging over the number of symmetrical screw winding k for brush elements 8 (Figures 1A–C) according to expression (9). This technique allows us to describe the dependence of the heterogeneity coefficient of the resulting mixture K_Cϑ, % at the indicated intermediate stage in various ranges of changes for the main process parameters in accordance with expression (11).

Let us trace this dependence by the example of mixing two loose components (semolina GOST 7022-97 for i = 1 and natural sand GOST 8736-93 for i = 2) with comparable values of particle diameters averaged over fractions D_Si and true densities of the substance ρ_Si, a mixture of which imitates toxic compounds used in various chemical industries ($D_{S1}=4.0\times {10}^{-4}$ m; $D_{\text{S}2}=1.5\times {10}^{-4}$ m; ${\rho }_{S1}=1.44\times {10}^3$ kg/m³; ${\rho }_{S1}=1.525\times {10}^3$ kg/m³). In an experimental study of the particle size distribution of the mixed components according to the GOST 4403-91 methodology, two sets of sieves with nominal hole sizes were used: (1) 6.7 × 10⁻⁴ m; 5.0 × 10⁻⁴ m; 3.5 × 10⁻⁴ m; 2.5 × 10⁻⁴ m; (2) 5.0 × 10⁻⁴ m; 3.5 × 10⁻⁴ m; 2.5 × 10⁻⁴ m; 5.6 × 10⁻⁵ m. The percentage of particles was found from the total mass of component i, taking into account the particle size distribution for semolina GOST 7022-97 (i = 1): 81.0%—fractions with a diameter $d_{11}=(3.5-6.7)\times {10}^{-4}$ m; 19.0%—$d_{12}=(2.5-3.5)\times {10}^{-4}$ m; for natural sand GOST 8736-93 (i = 2): 0.8%—$d_{21}=(3.5-5.0)\times {10}^{-4}$ m; 8.7%—$d_{22}=(2.5-3.5)\times {10}^{-4}$ m; 87.5%—$d_{23}=(0.56-2.5)\times {10}^{-4}$ m and 3%—for the diameter $d_{24}<5.6\times {10}^{-5}$ m. When calculating the average diameter of the bulk component, only fractions whose content in the mixture exceeded 10% were taken into account.

The values of the additional characteristics of the physicomechanical properties of the working materials and brush elements are, respectively, equal to k_v1ϑ = 0.1587; k_v2ϑ = 0.1853 for the recovery coefficients when the particles hit the bump; $k_u=5.0\times {10}^{-4}$ kg × m/rad for the angular stiffness of brushes 8 (Figures 1A–C). In this case, the regulatory ratio for the proportions of components i after performing the final mixing stage τ = n_ϑ should be α_{1, nϑ}/α_{2, nϑ} = 1/10. Note that the above values for the recovery coefficients k_vϑ upon impact of particles on the bump were determined by the method proposed by the authors (Kapranova et al., 2013). The established functional dependence is applied between the sought coefficient, the average experimental value for the angle of reflection of the particle flux from the bump surface, the given angle of inclination of the bump, and some geometric parameters of the model unit.

Preliminary studies of the authors (Kapranova and Verloka, 2018b; Kapranova A. B. et al., 2020) showed that the following characteristics are of particular interest in choosing the most rational ranges for changing the parameters of the studied process at the intermediate stage (τ = ϑ): angular velocity of rotation ω_ϑ for drum 7; the angle of inclination of bump surface 9 to the horizontal plane ϕ_1ϑ; the pitch of the screw winding h_sϑ of the brush elements 8 on the surface of drum 7; and complex indicator Δ_ϑ = l_bϑ/h_0ϑ. The last parameter Δ_ϑ reflects the degree of deformation of the brush elements of length l_bϑ in the gap height h_0ϑ between drum 7 and tray 5.

In addition, according to Verloka and Kapranova (2018), Kapranova and Verloka (2018b), and Kapranova et al. (2019b), it is sufficient to achieve the specified regulatory ratio 1/10 to perform three stages of mixing (initial τ=1, intermediate τ = ϑ = 2 and final τ = n_ϑ = 3), because an increase in the number of stages to n_ϑ=10 does not lead to a significant difference in the quality indicators of the mixture. Note that the preliminary selection of the variation limits for the described basic parameters from the set {ω_ϑ, ϕ_1ϑ, Δ_ϑ, h_sϑ} is determined by the analysis of the comparative simulation results of the differential distribution function h_ijkϑ(τ_ijkϑ) for the number of particles of material i by the spread angle τ_ijkϑ by brush element j for screw winding k from the expression (4). In particular, according to (Kapranova and Verloka, 2018a; Kapranova A. B. et al., 2020), the criterion for the best mixing of the components is the condition for the approximation of characteristic angles ${\sigma }_{ik\vartheta }^{\text{e}\text{x}}$ for the maxima of the total differential distribution functions $F_{ik\vartheta }({\sigma }_{ik\vartheta })={\prod }_{j=1}^{n_b}{h}_{ijk\vartheta }({\tau }_{\text{i}j\text{k}\vartheta })$ for the number of particles of both components (i = 1, 2) over the average scattering angle σikϑ, as well as the shape of the curves for the indicated functions F_ikϑ(σ_ikϑ). When using this condition in the form ${\sigma }_{1k\vartheta }^{\text{e}\text{x}}={\sigma }_{2k\vartheta }^{\text{e}\text{x}}$ for the following values of the design parameters for the mixing process under study ($r_{b2}=3.0\times {10}^{-2}$ m; $l_{b2}=4.5\times {10}^{-2}$ m; $L_{b2}=1.85\times {10}^{-1}$ m; μ₀₂=1.3083 rad) and its additional characteristics ($L_{12}=2.8\times {10}^{-1}$ m; $L_{22}=2.4\times {10}^{-1}$ m; $h_{12}=8.0\times {10}^{-2}$ m; $h_{22}=6.0\times {10}^{-2}$ m; μ₂ = 0.7071 rad), the preliminary limits of variation of the main characteristic parameters in experimental studies are chosen as ω_ϑ = (44−51) s⁻¹; ϕ_1ϑ = (0.87−1.04) rad; Δ_ϑ = (1.49−1.62); $h_{s\vartheta }=(1.59-1.61)\times {10}^{-2}$ m, taking into account the deformation of the brush elements ($j=\overline{1,n_b}$) with a total number n_b = 3 with rotation of the drum by an angle π/2 rad. It is indicated here: r_bϑ and L_bϑ are radius and length of the drum; l_bϑ and h_sϑ are the length of the brush elements and the pitch of their helical winding.

When performing the experimental part of the research (Verloka and Kapranova, 2018), a patented method was used to assess the quality of the granular mixture based on pixel analysis of photographs of experimental samples by calculating the position of the “threshold hue” (Zaisev et al., 2017) based on Petrov et al. (2012) using an open access software product Mixan (2015). In particular, according to Zaisev et al. (2017), the experimental value of the inhomogeneity coefficient for the mixing stage ϑ was calculated using the formula

$\begin{array}{ll}{K}_{C\vartheta ,ex}=\left(\frac{100}{C_{\vartheta }}\right){\left({(n_{q\vartheta }-1)}^{-1}{\displaystyle \sum _{q=1}^{n_{q\vartheta }}{(C_{2\vartheta q}-C_{\vartheta })}^2}\right)}^{\frac{1}{2}}.& (16)\end{array}$

Formula (16) contains the notation: C_ϑ and C_2ϑq values, respectively, for the “ideal” fraction of the key component (i = 2) in the mixture and the proportion of this component in the selected sample; n_qϑ is the number of samples. The C_2ϑq fraction data are determined by the ratio of the number of pixels of a certain shade of gray for the key component in the sample to the total number of pixels for this material. Values C_2ϑq are sorted in a histogram on a scale for shades of gray within (0–255) units. Based on the coordinates of the centers of gravity for the areas of the histograms corresponding to the components of the resulting granular mixture, the abscissa of the middle of the segment between the indicated centers is calculated. The coordinate set in this way on the scale of shades of gray corresponds to the “threshold hue” (Zaisev et al., 2017).

Comparison of theoretical and experimental (Verloka and Kapranova, 2018) results at the intermediate stage of mixing (τ = ϑ=2) for the dependence of the heterogeneity coefficient K_C2(ω₂), % for mixture of the semolina GOST 7022-97, and natural sand GOST 8736-93 in the ratio of their volume fractions α_{1, nϑ}/α_{2, nϑ}=1/10 are shown, respectively, in Figures 2A–C for various values of the complex exponent Δ_ϑ=Δ₂ and the following choice of ϕ₁₂ = 0.96 rad; $h_{s2}=1.6\times {10}^{-2}$ m.

FIGURE 2

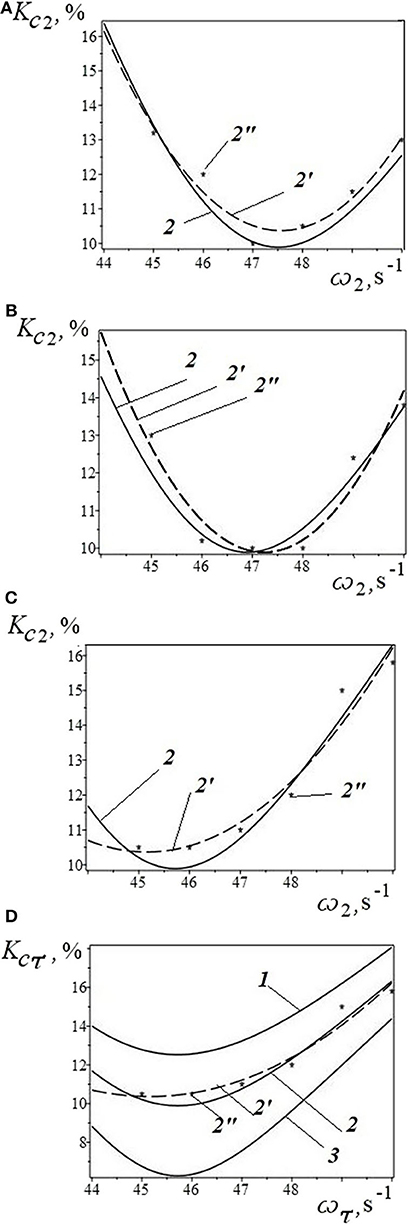
Figure 2. The dependence of the heterogeneity coefficient K_Cτ(ω_τ) (%) for a mixture of semolina GOST 7022-97 and natural sand GOST 8736-93 in the ratio of their volume fractions α_{1, nϑ}/α_{2, nϑ}= 1/10: (A–C) K_C2(ω₂) (%) for the intermediate mixing stage (τ = ϑ = 2); (D) for three stages of mixing (τ = 1, 2, 3), (A) Δ₂ = 1.45; (B) Δ₂ = 1.5; (C,D) Δ₂ = Δ_τ = 1.6; 1—τ = 1; 2—τ = 2; 3—τ = 3; 2—theory, 2′—regression curves (A): $K_{C2}({\omega }_2)=1040-43.3{\omega }_2+0.46{{\omega }_2}^2$; (B): K_C2(ω₂) = 1261−53ω₂+0.56 ${{\omega }_2}^2$; (C,D): K_C2(ω₂) = 520−22 $.5{\omega }_2+0.25{{\omega }_2}^2$, 2″ are the experimental points for K_{C2, ex} (Verloka and Kapranova, 2018); ϕ₁₂ = 0.96 rad; $h_{s2}=1.6\times {10}^{-2}$ m.

Moreover, the relative error of the data of theory and experiment (Verloka and Kapranova, 2018) does not exceed (5–7%). We note that the best convergence of the indicated results is noted at Δ₂ = 1.5 (Figure 2B, graph 2 and experimental points 2″) under conditions of obtaining the highest quality mixture (K_C2=9.8% for theory and K_{C2, ex}=10.1% for experiment) when the angular velocity is reached, a drum with brush elements equal to ω₂ = 47 s⁻¹. Note that the analysis of the dependence K_Cnϑ(Δ_nϑ), performed in Kapranova et al. (2019b), confirms the obtained result of achieving the highest quality mixture (Figure 2B, graph 2 and experimental points 2″) at ω₂ = 47 s⁻¹, if the value Δ₂ = Δ_nϑ = (1.49−1.52). Additionally, Figure 2D shows the theoretical results for K_Cτ(ω_τ), % at all mixing stages (τ = 1, 2, 3) according to the data for the initial (Kapranova and Verloka, 2018b) and final (Kapranova et al., 2019b) stages of obtaining this mixture with Δ₂ = 1.6.

An increase in Δ_τ for every 0.05 unit leads to a shift of the graph families K_Cτ(ω_τ) to the left along the abscissa axis (Figure 2D, graphs 1–3) with a decrease not only in the minimum values of the inhomogeneity coefficients K_{C1, min}>K_{C2, min}>K_{C3, min} in the range (5.9−12.9)%, but also in the corresponding values of ω₁<ω₂<ω₃ within (45.6−45.8) s⁻¹. The latter fact makes it possible under these conditions to guarantee a reduction in energy costs for the expended capacities of the mixing drum drives 7 (Figures 1A–C).

Key Findings and Results

Here are the main conclusions and results of this study

• A generalization of the results of stochastic modeling of the formation of rarefied flows of bulk components in the case of an intermediate stage (τ = ϑ) of their gravitational mixing in the given ratios of 1/10 or more is carried out, taking into account the method of dosing for the key (i = 2) and transporting (i = 1) components according to Kapranova and Verloka (2016) [expression (10), section Assessment of the Quality of a Mixture of Bulk Components After an Intermediate Stage of Their Gravitational Mixing] for the implementing in two steps:

1) with the help of brush elements ($j=\overline{1,n_b}$) (Kapranova and Verloka, 2018a; Verloka et al., 2018; Kapranova A. B. et al., 2020) provided that the latter are fixed on oncoming helical lines (k = 1, 2), a cylindrical mixing drum [expression (5), section The Main Features of Modeling the Process of Formation of Rarefied Flows of Loose Components by Brush Elements];

2) after impact interaction with an inclined baffle surface (Kapranova and Verloka, 2016, 2018b) [expressions (7), (8), section The Main Features of Modeling the Mixing of Granular Materials After Impact Interaction With an Inclined Bump Surface].

• A method for calculating the volume fraction of the key component (i = 2) obtained at the intermediate stage (τ=ϑ) for the process of mixing bulk materials [expression (9), section 2.3]. In particular, the calculation method is based on the specified generalization of the results of stochastic modeling (Kapranova and Verloka, 2016, 2018a,b; Verloka et al., 2018; Kapranova A. B. et al., 2020) taking into account the method of dispensing the key (i = 2) and transporting [(i = 1) components according to Kapranova and Verloka (2016); expression (10), section Assessment of the Quality of a Mixture of Bulk Components After an Intermediate Stage of Their Gravitational Mixing].

• Expressions (12) and (13) are obtained for calculating the values, respectively, for the average of the fraction of the key component (i = 2) and the average of the square of the specified fraction. These expressions allow, in the case of an intermediate stage (τ = ϑ), gravitational mixing of bulk materials in the given ratios 1/10 or more. These expressions allow a quality assessment of the mixture according to the criterion of heterogeneity (11) (section 2.4). In this case, the basis for the calculation is the indicated generalization of the results of the authors' models, taking into account the scattering angles from deformed brush elements and the scattering angles of the flows of granular components in and angles of reflection from an inclined baffle.

• These generalizations of the results of the authors' models make it possible

1) to identify the most significant parameters of the structure and its operation modes (angular velocity of rotation of the drum, angle of inclination of the chipper to the horizontal, pitch of screw winding, and a comprehensive indicator of the deformation of brush elements; section Assessment of the Quality of a Mixture of Bulk Components After an Intermediate Stage of Their Gravitational Mixing);

2) to predict rational ranges of their changes (section Assessment of the Quality of a Mixture of Bulk Components After an Intermediate Stage of Their Gravitational Mixing) due to the previously proposed criterion for the best mixing of components (Kapranova and Verloka, 2018a; Kapranova A. B. et al., 2020) in the analysis of the total differential distribution functions for the number of particles of both components on average scattering and reflection angles.

• An example is the process of mixing of two components (semolina GOST 7022-97 and natural sand GOST 8736-93 in a ratio of 1/10) after an intermediate stage (τ = ϑ = 2, section 2.4) of gravitational mixing with the implementation of two steps (using brushes and an inclined bump surface). These bulk materials mimic the toxic composition for the needs of the chemical industry. The article analyzes the influence of the most significant design parameters and its operation modes on the value of the inhomogeneity coefficient in comparison with the results for the initial (τ = 1) (Kapranova and Verloka, 2018b) and final stages (τ=3) (Kapranova et al., 2019b). In particular, this analysis showed the possibility of reducing energy costs for the consumed power drives of mixing drums by varying the values of their angular speeds of rotation at various stages of the process under study. Moreover, the relative error of the theory data (K_C2 = 9.8%) and experiment [K_{C2, ex} = 10.1% (Verloka and Kapranova, 2018)] does not go beyond (5-7%).

Conclusions

An analytical method has been developed for assessing the quality of a granular mixture, taking into account physical, and mechanical properties and a set of structural and operational parameters of the apparatus based on the energy method in the framework of the stochastic approach. The differential functions of the distribution of the number of particles of these components over the states of the corresponding macrosystems were used. When studying the influence of the most significant parameters of the studied process of mixing solid dispersed materials, a set of relevant characteristics was established (the angular velocity of rotation of the drum, the angle of inclination of the bump to the horizontal, the pitch of the screw winding, a comprehensive indicator of the deformation of the brush elements). Using the example of model mixing of two non-humidified components, comparable in size and density (sand and semolina), the heterogeneity coefficient of the resulting mixture for the intermediate stage was calculated. For this stage, mixing is assumed in equal proportions between the resulting mixture after the initial stage and the new portion of the key component (sand). Note that the calculation of the volume fractions at each of the three stages of gravitational mixing is performed using a recurrent formula from Kapranova and Verloka (2016), so that the ratio of components in the finished product corresponds to the regulatory 1:10 or more. It is shown that an increase in the complex index of deformation of brush elements by 0.05 units leads to a decrease in the coefficient of heterogeneity by (0.15–0.80%) in the studied range of the angular velocity of rotation of the drums. At the same time, the minimum indices of the indicated coefficient correspond to the values of the angular velocity of the mixing drum, reduced by 0.5 s⁻¹. Thus, a reduction in the cost of expended power drives of the mixing drums is achieved by reducing the values of their angular velocities without loss of quality of the resulting mixture. The distinctive features of the application of the obtained results, confirmed by experimental studies, include the possibility of predicting rational ranges of changes in significant parameters of the process under study.

The results of the work can be used in the formation of an engineering method for calculating a new gravity mixer of non-humidified bulk components in predetermined ratios of 1:10 or more with additional mixing elements (brushes and bump stops). In particular, the proposed dependences (14) for incrementing the reflection angles of rarefied flows were used in calculating the performance values of the gravitational apparatus at the corresponding stages of mixing bulk components (Kapranova A. et al., 2020).

Data Availability Statement

All datasets generated for this study are included in the article.

Author Contributions

All authors contributed to manuscript revision, read and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Alsayyad, T., Pershin, V., Pasko, A., and Pasko, T. (2018). Virtual modeling of particles two-step feeding. J. Phys. 1084:012005. doi: 10.1088/1742-6596/1084/1/012005

CrossRef Full Text | Google Scholar

Johnson, N., Kendall, M., and Stuart, A. (1962). Review: the advanced theory of statistics: Volume I (1958): Distribution Theory; The Advanced Theory of Statistics: Volume II (1961): Inference and Relationship. J. R. Stat. Soc. Ser. D 12, 138–142. doi: 10.2307/2987065

CrossRef Full Text | Google Scholar

Kapranova, A., Verloka, I., and Bahaeva, D. (2020). “Factors of increasing the performance of the bulk material mixer of the gravity type,” in Proceedings of EECE 2019. EECE 2019. Lecture Notes in Civil Engineering, Vol. 70, eds B. Anatolijs, V. Nikolai, and S. Vitalii (Cham: Springer), 337–347. doi: 10.1007/978-3-030-42351-3_30

CrossRef Full Text | Google Scholar

Kapranova, A., Verloka, I., Bahaeva, D., Tarshis, M., and Cherpitsky, S. (2019a). “To the calculation of the average value of the volume fraction of the key bulk component at the intermediate stage of mixing with an inclined bump,” in Bridging Science with Technology: 12^th European Congress of Chemical Engineering/5^th European Congress of Applied Biotechnology – ECCE12/ECAB5 (Florence) 2015–2016.

Kapranova, A., Verloka, I., Bahaeva, D., Tarshis, M., Cherpitsky, S., and Sidorov, V. (2019b). “Investigation of the heterogeneity coefficient of the loose mixture at the final stage of mixing in a gravitational apparatus,” in Proceedings of the International Conference on Innovative Applied Energy - IAPE,19 14–15 March, 2019. (Oxford). Available online at: http://www.iape-conference.org/Downloads/Proceedings/Proceedings%20of%20IAPE'19.pdf

Kapranova, A. B., Bakin, M. N., Lebedev, A. E., and Zaisev, A. I. (2013). Evaluation parameter recovery of shock interacting flows of solid dispersion media with a sloping baffle [Otsenka parametra vosstanovleniya udarno-vzaimodeystvuyuikh potokov tverdykh dispersnykh sred s naklonnym otboynikom] Russian Journal of Chemistry and Chemical Technology [Izvestiya vysshikh uchebnykh zavedeniy]. Seriya 56, 111–113. Available online at: https://www.elibrary.ru/item.asp?id=20160954

Kapranova, A. B., Bakin, M. N., and Verloka, I. I. (2018a). Simulation of the quality criterion of a mixture in a drum-belt apparatu. Chem. Petrol. Eng. 54, 287–297. doi: 10.1007/s10556-018-0477-0

CrossRef Full Text | Google Scholar

Kapranova, A. B., Bakin, M. N., Verloka, I. I., and Zaitzev, A. I. (2015). Methods for describing the motion of solid dispersed media in various planes for sections of a mixing drum. [Sposoby opisaniya dvizheniya tverdykh dispersnykh sred v razlichnykh ploskostyakh dlya secheniy smesitel'nogo barabana]. Vestn. TGTY Her TGTY. 58, 296–304. doi: 10.17277/vestnik.2015.02.pp.296-304

CrossRef Full Text | Google Scholar

Kapranova, A. B., and Verloka, I. I. (2016). On the assessment of the content of the key component after shock dispersion of bulk materials at the initial stage of batch mixing. [Ob otsenke soderzhaniya klyuchevogo komponenta posle udarnogo rasseivaniya sypuchikh materialov na nachal'nom etape portsionnogo smeshivaniya]. Vestn. IGEY Her IGEY. 3, 78–83. doi: 10.17588/2072-2672.2016.3.078-083

CrossRef Full Text | Google Scholar

Kapranova, A. B., and Verloka, I. I. (2017). The study of the volume fraction of key component in the second phase of the portion mixing by means of the device of gravity type. J. Chem. Eng. Process Technol. 8:59. doi: 10.4172/2157-7048-C1-009

CrossRef Full Text | Google Scholar

Kapranova, A. B., and Verloka, I. I. (2018a). Stochastic description of the formation of flows of particulate components in apparatuses with brush elements. Theor. Found. Chem. Eng. 52, 1004–1018. doi: 10.1134/S0040579518050330

CrossRef Full Text | Google Scholar

Kapranova, A. B., and Verloka, I. I. (2018b). On the features of estimating the coefficient of inhomogeneity of a loose mixture during the operation of a gravitational device. J. Chem. Eng. Process Technol. 9:53. doi: 10.4172/2157-7048-C3-018

CrossRef Full Text | Google Scholar

Kapranova, A. B., Verloka, I. I., and Bahaeva, D. D. (2020). “About preparation of the analytical platform for creation of a cyber-physical system of industrial mixture of loose components,” in Cyber-Physical Systems: Advances in Design and Modelling. Studies in Systems, Decision and Control, Vol. 259, eds A. Kravets, A. Bolshakov, and M. Shcherbakov (Cham: Springer), 81–91. doi: 10.1007/978-3-030-32579-4_7

CrossRef Full Text | Google Scholar

Kapranova, A. B., Verloka, I. I., Lebedev, A. E., and Zaitzev, A. I. (2016). The model of dispersion of particles during their flow from chipping the surface. Czas. Tech. Mech. 113, 145–150. doi: 10.4467/2353737XCT.16.102.5501t

CrossRef Full Text | Google Scholar

Kapranova, A. B., Verloka, I. I., Yakovlev, P. A., and Bahaeva, D. D. (2018b). Investigation of the quality of mixture at the first stage of work of the gravitational type apparatus. [Issledovaniye kachestva smesi na pervoy stadii raboty apparata gravitatsionnogo tipa]. Rossiyskiy Khimicheskiy Zhurnal 62, 48–50. Available online at: https://elibrary.ru/item.asp?id=36290375

Kendall, M. G., and Stuart, A. (1967). The Advanced Theory of Statistics, Vol. 2. Inference and Relationship, 4th ed, Hafner, 690.

Google Scholar

Klimontovich, Y. L. (2014). Turbulent Motion and Chaos Structure: A New Approach to the Statistical Theory of Open Systems. LENAND, Moscow.

Mixan (2015). Available online at: https://pa2311.blogspot.com/2015/06/mixan-244.html (accessed May 29, 2020).

Mizonov, V., Balagurov, I., Berthiaux, H., and Gatumel, C. (2016). Gatumel Markov chain model of mixing kinetics for ternary mixture of dissimilar particulate solids. Particuology 31, 80–86. doi: 10.1016/j.partic.2016.05.006

CrossRef Full Text | Google Scholar

Petrov, A. A., Lebedev, A. E., Zaisev, A. I., and Kapranova, A. B. (2012). Express-method for assessing the uniformity of mixtures of bulk materials [Ekspress-metod otsenki odnorodnosti smesey sypuchikh materialov] Russian Journal of Chemistry and Chemical Technology [Izvestiya vysshikh uchebnykh zavedeniy]. Seriya 55, 88–90. Available online at: https://www.elibrary.ru/item.asp?id=17858196

Rosato, A. D., Zuo, L., Blackmore, D., et al. (2016). Tapped granular column dynamics: simulations, experiments and modeling. Comput. Particle Mech. 3, 333–348. doi: 10.1007/s40571-015-0075-2

CrossRef Full Text | Google Scholar

Verloka, I., and Kapranova, A. (2018). “Three-stage gravitational method for mixing bulk components. [Trekhstadiynyy gravitatsionnyy sposob smeshivaniya sypuchikh komponentov],” in 71st All-Russian. scientific and technical conf. Nuclear Technology University Students, Undergraduates and Graduate Students with International Participation (April 18, 2018): Sat Conf.: In 3 hours. Part 2 [Electronic resource] (Yaroslavl), 27–29.

Verloka, I., Kapranova, A., Tarshis, M., and Cherpitsky, S. (2018). Stochastic modeling of bulk components batch mixing process in gravity apparatus. Int. J. Mech. Eng. Technol. 9, 438–444. Available online at: http://www.iaeme.com/IJMET/issues.asp?JType=IJMET&amp;VType=9&amp;IType=2

Zaisev, A. I., Lebedev, A. E., Kapranova, A. B., Verloka, I. I., Badaev, N. V., Vatagin, A. A., et al. (2017). A Method for Determining the Coefficient of Heterogeneity of a Mixture of Difficult to Separate Bulk Materials. Patent 2620387 Russian Federation, G01N1/28. Bull. N. 15.

Zaitzev, A. I., Lebedev, A. E., Kapranova, A. B., and Verloka, I. I. (2016). Gravity-Type Bulk Solids Mixer. Patent 2586126 Russian Federation, IPC B01F3/18.

Zhuang, Y., Chen, X., and Liu, D. (2016). Stochastic bubble developing model combined with Markov process of particles for bubbling fluidized beds. Chem. Eng. J. 291, 206–214. doi: 10.1016/j.cej.2016.01.095

CrossRef Full Text | Google Scholar