Coordinated Operation of Gas and Electricity Systems for Flexibility Study

The increased interdependencies between electricity and gas systems driven by gas-fired power plants and gas electricity-driven compressors necessitates detailed investigation of such interdependencies, especially in the context of an increased share of renewable energy sources. In this paper, the value of an integrated approach for operating gas and electricity systems is assessed. An outer approximation with equality relaxation (OA/ER) method is used to deal with the optimization class of the mixed-integer non-linear problem of the integrated operation of gas and electricity systems. This method significantly improved the efficiency of the solution algorithm and achieved a nearly 40% reduction in computation time compared to successive linear programming. The value of flexibility technologies, including flexible gas compressors, demand-side response, battery storage, and power-to-gas, is quantified in the operation of integrated gas and electricity systems in GB 2030 energy scenarios for different renewable generation penetration levels. The modeling demonstrates that the flexibility options will enable significant cost savings in the annual operational costs of gas and electricity systems (up to 21%). On the other hand, the analysis carried out indicates that deployment of flexibility technologies appropriately supports the interaction between gas and electricity systems.

1. Introduction

The share of variable Renewable Energy Sources (RES) in the power generation mix is increasing significantly in Great Britain (GB) to meet de-carbonization targets (National Grid Plc, 2016). Gas plants are expected to contribute to the management of the variability of renewable energy generation, which consequently will increase the interaction between gas and electricity systems and increase challenges associated with the management of gas storage and linepack in the gas transmission system. Therefore, operating the gas and electricity systems as an integrated energy system is increasingly important.

Battery storage, Demand-Side Response (DSR), power-to-gas (P2G), and flexible compressors can enhance the system flexibility needed to support more cost-effective balancing of electricity demand and supply. Furthermore, these options can participate in the provision of various ancillary services, including reserve and frequency regulation (Qadrdan et al., 2017b). Battery storage facilitates the integration of wind into the grid through managing variation of the peak plants, such as gas-fired plants. The employment of DSR helps to deal with the variability of RES better, as energy consumption can be shifted, which can act as a virtual power plant (Ameli et al., 2017a,b). Furthermore, P2G technologies would make use of a surplus of renewable electricity by producing hydrogen via electrolyzers that would be injected into the gas system or stored in hydrogen storage facilities. Afterward, the hydrogen can be transported to the demand centers or provided to Combined Cycle Gas Turbines (CCGTs) to produce free-carbon electricity. In the gas system, flexible gas compressors improve gas delivery to the demand centers through changing the gas flow direction. Several studies, such as Troy et al. (2012) and Pudjianto et al. (2014), have evaluated the role of flexibility options in addressing the electricity balancing challenges caused by RES.

From whole energy system perspectives, by taking flexibilities into account, the interaction of gas and electricity systems was studied in Correa-Posada and Sanchez-Martin (2015), He et al. (2017), Zlotnik et al. (2017), Qadrdan et al. (2017a), Ameli et al. (2017c,d), and Wu et al. (2019). Zlotnik et al. (2017) developed coordinated modeling of interdependent gas and electricity systems for day-ahead scheduling of power dispatch and gas compressor operation. The efficiency of the model was validated by improvement in system operation and cost reduction. In Ameli et al. (2017d), the role of multi-directional compressors as one of the options in making the gas system more flexible was investigated in different operation methodologies of gas and electricity systems. It was demonstrated that increased flexibility in the gas system is beneficial for the whole energy system. In Sheikhi et al. (2015), an integrated demand-side response framework as a part of a smart energy hub was proposed. In this framework, the customer can modify the use of gas or electricity based on the gas and electricity prices. It was shown that this approach offers benefits for both customers and utilities in terms of costs and profits. In Yang et al. (2019), the coordination of different P2G conversions, including electrolysis and Steam Methane Reforming (SMR), and gas-fired plants in an integrated operation of gas and electricity networks was proposed. It was shown how this combined model can improve energy efficiency and reduce carbon emissions compared to the power-to-hydrogen-to-methane-to-pipeline approach. From a modeling point of view, it was not mentioned in detail how this optimization problem may be solved. In He et al. (2017), coordinated scheduling of gas and electricity systems considering P2G was investigated. Furthermore, another study (Akhtari and Baneshi, 2019) showed how the excess electricity generated by renewables can be used in the electrolysis process to produce hydrogen. The proposed method was tested in five different cities, and a decrease in carbon emissions was reported. In Wu et al. (2019), a hybrid multi-objective optimization approach was developed for the operation of integrated energy systems considering gas and electricity. In this approach, the price of electricity and cooling demands are considered. The results indicated fair treatment for all the players in the integrated energy system. In Zeng et al. (2016), a bi-directional energy flow between gas and electricity systems was proposed to realize high penetration of renewables and an increase in system flexibility. The effectiveness of the proposed method (i.e., solved by the Newton-Raphson method) was analyzed on an IEEE-9 test system and a 7-node gas system. In Correa-Posada and Sanchez-Martin (2015), a coupled model of natural gas and power systems aimed at providing energy adequacy was presented. Non-linear equations and constraints were linearized to solve a Mixed-Integer Linear Programming (MILP) problem. A weak point of this study was that linearizing the non-linearities piecewise causes a significant increase in the probability of data loss. In Gil et al. (2016), two coupling methodologies for gas and electricity markets in a European regulatory framework were presented. The first methodology was based on maximizing the profit of the electricity market, and the second approach was based on minimizing the operational cost of the natural gas system. It was demonstrated that if the modeling is accurate, the difference between these two methodologies may be negligible. In addition, in Zlotnik et al. (2017), different coordinated scheduling scenarios of natural gas and power systems were presented. The Unit Commitment (UC) problem of the generation units was not considered. This was done in order to reduce the model complexity by preventing binary variables in the optimization procedure, which may lead to inaccuracy. The authors of Deane et al. (2017) built and applied an integrated electricity and gas model for the European Union system. In this research, gas supply interruption scenarios were derived to examine the impacts on power system operation. As an example, it was shown that interruption of the Russian gas supply to the EU enhanced the average gas price by 28% and the electricity price by 12%. In Sardou et al. (2018), the role of microgrid aggregators in a coordinated operation strategy for gas and electricity systems was investigated. In Zhang et al. (2016), the role of demand response in providing energy balance was considered. A coordinated MILP strategy for natural gas and power systems was proposed. In this strategy, the power system was optimized, and then the natural gas constraints were checked for the feasibility of the solution. It was shown that this model increased the social welfare of the scenarios. However, through linearizing the gas flow equation piecewise, the complexity of the model is reduced, and accuracy may be lost. In the literature, different methods have been applied to linearize the general gas flow and propose a MILP formulation for the operation of a gas network (Correa-Posadaa and Sanchez-Martin, 2014; He et al., 2017; HU et al., 2017; Sirvent et al., 2017). Although piecewise linearization affects the time required to solve the problem considerably, the accuracy of each method (i.e., ability to find the optimal solution) significantly relies on the generating segments. On the other hand, some methods are not scalable and can only be used for a problem of a predetermined size (Correa-Posadaa and Sanchez-Martin, 2014).

The coupling of the binary variables representing the On/Off states of generating units and non-linear equations of gas flow in pipes and compressor power consumption makes the optimization of the integrated operation of gas and electricity systems a Mixed-Integer Non-Linear Programming (MINLP) problem, which is complex and challenging to solve from the computational perspective (Floudas, 1995). In order to deal with the aforementioned complexity in solving the MINLP problem, several algorithms, such as Generalized Benders Decomposition (GBD), Outer Approximation (OA), Outer Approximation with Equality Relaxation (OA/ER), and generalized cross decomposition, have been developed (Floudas, 1995). Deterministic methods, such as Lagrangian Relaxation (LR) (Ongsakul and Petcharaks, 2004) and Benders Decomposition (BD) (Nasri et al., 2016), and also heuristic methods, such as an evolutionary algorithm (Chung et al., 2011) have been applied to solve MINLP problems in power systems. In Shabanpour-Haghighi and Seifi (2015), a solving technique based on a modified teaching–learning method for optimal power flow taking electricity, gas, and heat into account was proposed. This method was evaluated and compared with conventional evolutionary algorithms to highlight the effectiveness of the method. In He et al. (2017), co-optimization scheduling of gas and electricity systems was proposed. A decomposition method was applied to solve the electricity system sub-problem and gas system sub-problem separately.

The OA approach, which is the fundamental technique in this study, has been implemented in a few studies for dealing with the Unit Commitment (UC) problem (Yang et al., 2017) with AC power flow (Castillo et al., 2016) as well as security-constrained UC (Dai et al., 2016). The OA/ER decomposition method solves a binary relaxed primal problem [Non-Linear Problem (NLP)] and a relaxed master problem (MILP). The OA/ER decomposition method copes with non-linear inequalities and consequently creates sequences of lower and upper bounds. In the OA/ER approach, the non-linear equalities are converted to linear inequalities based on their associated Lagrangian multipliers. It is worth mentioning that the integrated operation of gas and electricity systems is solved by Successive Linear Programming (SLP) (Default solver of Xpress FICO, 2013) and investigated from different aspects in a few papers, such as Qadrdan et al. (2017a) and Ameli et al. (2017d). The MINLP problem of integrated operation of gas and electricity is non-convex, which implies the potential existence of multiple local optima.

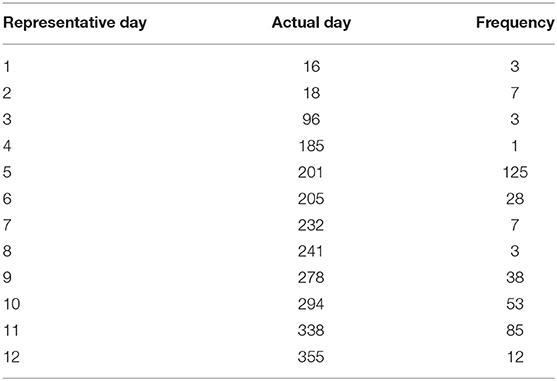
Hence, in this paper, in order to deal with the complexity of the above-mentioned model, a solution algorithm is implemented based on the OA/ER approach to model the integrated operation of gas and electricity systems. The efficiency of this decomposition method is validated by comparing the computational performance in terms of optimization time and objective function with the SLP method. Furthermore, the role and value of the flexibility options, including DSR, electricity storage, flexible gas plants, P2G, and multi-directional compressors, in the cost-effective operation of the integrated systems for intact and contingency configurations (i.e., gas supply interruption) on a 2030 GB system are investigated. In this regard, to evaluate the sensitivity of the renewable penetration level to the flexibility options, different renewable generation and gas supply development scenarios in the presence of different installed capacities of flexibility options are defined to quantify the operation of the energy systems. To model the entire year, a demand clustering method is developed to reduce the size of the optimization problem, so that, through this method, the entire year is represented by 12 days.

2. Gas and Electricity Systems Including a Flexibility Operational Model

2.1. Formulation of Electricity System Operation

The constraints governing the electricity system over the time horizon ($t\in {T}$) are represented by equations (1)–(11). These constraints include: minimum and maximum power generation limits for generators (1), Minimum Stable Generation (MSG) for thermal generators (2), maximum limit for power generation and provision of reserve by thermal generators (3), Minimum Up/Down Time (MUT/MDT) of generators (4)–(5), ramp up/down limits of generators (6), start-up cost of generators (7) (8), minimum reserve requirement (including the unserved reserve) (9) (Ameli et al., 2019), capacity of power transmission lines (10), and power balance at each time step (11).

$\begin{array}{ll}{\text{P}}_i^{\text{min}}\le P_{i,t}\le {\text{P}}_i^{\text{max}},\forall i\in {G}-{K},t\in {T}& (1)\end{array}$

$\begin{array}{ll}{P}_{i,t}\ge {\sigma }_{i,t}·{\text{P}}_i^{\text{min}},\forall i\in {K},t\in {T}& (2)\end{array}$

$\begin{array}{ll}{P}_{i,t}+r_{i,t}\le {\sigma }_{i,t}·{\text{P}}_i^{\text{max}},\forall i\in {K},t\in {T}& (3)\end{array}$

$\begin{array}{ll}{\sigma }_{i,\acute{t}}-{\sigma }_{i,\acute{t}-1}\le {\sigma }_{i,t};\acute{t}=\left[t-{\Gamma }_i^{\text{up}}+1,t-1\right],\forall i\in {K},t\in {T}& (4)\end{array}$

$\begin{array}{ll}{\sigma }_{i,\acute{t}-1}-{\sigma }_{i,\acute{t}}\le 1-{\sigma }_{\text{i},\text{t}};\acute{t}=\left[t-{\Gamma }_i^{\text{down}}+1,t-1\right],\forall i\in {K},t\in {T}& (5)\end{array}$

$\begin{array}{ll}|P_{i,t}-P_{i,t-1}|\le {\mu }_i,\forall i\in {K},t\in {T}& (6)\end{array}$

$\begin{array}{ll}{w}_{i,t}^{\text{su}}\ge {\text{C}}_i^{\text{su}}·({\sigma }_{i,t}-{\sigma }_{i,t-1}),\forall i\in {K},t\in {T}& (7)\end{array}$

$\begin{array}{ll}{w}_{i,t}^{\text{su}}\ge 0,\forall i\in {K},t\in {T}& (8)\end{array}$

$\begin{array}{ll}\begin{array}{c}{\displaystyle \sum _{i=1}^{{K}}}{r}_{i,t}+{\displaystyle \sum _{p=1}^{{P}}}{r}_{p,t}^{\text{pump}}+u{r}_t\ge {\displaystyle \underset{i\in {K}}{max}}({\text{P}}_i^{\text{max}})+\alpha ·{\displaystyle \sum _{b=1}^{{B}}}{P}_{b,t}^{\text{wind}},\forall t\in {T}\end{array}& (9)\end{array}$

$\begin{array}{ll}{P}_{x,t}^{\text{line}}\le {{\text{P}}_x}^{\text{line},\text{max}},\forall x\in {{L}}_e,t\in {T}& (10)\end{array}$

$\begin{array}{ll}\begin{array}{c}{\displaystyle \sum _{i=1}^{{G}}}{P}_{i,t}+{\displaystyle \sum _{b=1}^{{B}}}{P}_{b,t}^{\text{wind}}+{\displaystyle \sum _{p=1}^{{P}}}\left(P_{p,t}^{\text{pump},\text{with}}-P_{p,t}^{\text{pump},\text{inj}}\right)\\ ={\displaystyle \sum _{b=1}^{{B}}}\left({\text{P}}_{b,t}^{\text{eload}}+P_{b,t}^{\text{ecomp}}-P_{b,t}^{\text{eshed}}\right),\forall t\in {T}\end{array}& (11)\end{array}$

where

2.2. Formulation of Gas System Operation

The operation of the gas system over the time horizon ($t\in {T}$) is modeled via constraints for gas flow along a pipe (12) (Osiadacz, 1987) (detailed formulation is presented in Ameli et al., 2019), power consumption by the compressors (14), changes in the gas system linepack (15), minimum and maximum pressure limits (16), and gas balance at each node and time step (17). In order to model a bi-directional gas flow, in the gas flow equation in (12), the term ${Q_{x,t}^{\text{avg}}}^{1.854}$ is replaced by $Q_{x,t}^{\text{avg}}·|Q_{x,t}^{\text{avg}}{|}^{0.854}$ (13).

$\begin{array}{ll}\begin{array}{c}{\left(p_{x,t}^{\text{in}}\right)}^2-{\left(p_{x,t}^{\text{out}}\right)}^2=\frac{18.43\text{ L}{\text{e}}_x}{{\left({\eta }_x^{\text{pipe}}\right)}^2·{\text{D}}_x^{4.848}}{Q_{x,t}^{\text{avg}}}^{1.854},\forall x\in {{L}}_g\end{array}& (12)\end{array}$

$\begin{array}{ll}\begin{array}{c}{\left(p_{x,t}^{\text{in}}\right)}^2-{\left(p_{x,t}^{\text{out}}\right)}^2=\frac{18.43\text{ L}{\text{e}}_x}{{\left({\eta }_x^{\text{pipe}}\right)}^2·{\text{D}}_x^{4.848}}{Q}_{x,t}^{\text{avg}}·|Q_{x,t}^{\text{avg}}{|}^{0.854},\\ \forall x\in {{L}}_g,t\in {T}\end{array}& (13)\end{array}$

$\begin{array}{ll}{P}_{x,t}^{\text{comp}}=\frac{\beta .Q_{x,t}^{\text{comp}}}{{\eta }^{\text{comp}}}.\left[{\left(\frac{p_{x,t}^{\text{dis}}}{p_{x,t}^{\text{suc}}}\right)}^{(1/\beta )}-1\right],\forall x\in {C},t\in {T}& (14)\end{array}$

$\begin{array}{ll}\begin{array}{c}{L}_{x,t}=L_{x,t-1}+{\displaystyle \underset{\partial L_{x,t}}{{\displaystyle \underbrace{{\displaystyle {\int }_{t-1}^t}(Q_{x,\tau -1}^{\text{in}}-Q_{x,\tau -1}^{\text{out}}).d\tau }}}},\forall x\in {{L}}_g,t\in {T}\end{array}& (15)\end{array}$

$\begin{array}{ll}{\text{p}}_x^{\text{min}}\le p_{x,t}\le {\text{p}}_x^{\text{max}},\forall x\in {M},t\in {T}& (16)\end{array}$

$\begin{array}{l}{Q}_{x,t}^{\text{supp}}+\left({\displaystyle \sum _{w=1}^{{W}}}{\text{M}}_{w,x}^{\text{flow}}·Q_{w,t}\right)+\left(Q_{x,t}^{\text{gstor},\text{with}}-Q_{x,t}^{\text{gstor},\text{inj}}\right)\\ +\left({\displaystyle \sum _{c=1}^{{C}}}{\text{M}}_{c,x}^{\text{comp}}·Q_{c,t}^{\text{comp}}-{\displaystyle \sum _{c=1}^{{C}-{{C}}_e}}{\text{M}}_{c,x}^{\text{ecomp}}·{\zeta }_{c,t}\right)\\ =\left({\text{Q}}_{x,t}^{\text{gload}}+Q_{x,t}^{\text{gen}}-Q_{x,t}^{\text{gshed}}\right),\forall x\in {M},t\in {T}& (17)\end{array}$

where

2.3. Coupling Components

The gas and electricity systems are coupled via gas-fired generators and electrically driven compressors. The electric power consumption of electrically driven compressors and the gas required for power generation are calculated by (14) and (18), respectively.

$\begin{array}{ll}{Q}_{x,t}^{\text{gen}}={\nu }_g{\displaystyle \sum _{i=1}^{{K}}}{\text{M}}_{x,i}^{\text{conn}}·\frac{P_{i,t}}{{\eta }_i},\forall x\in {M},t\in {T}& (18)\end{array}$

where

2.4. Flexibility Options Modeling

2.4.1. Battery Storage

The operational characteristics of battery storage are modeled using equations (19)–(23) (Pudjianto et al., 2014; Ameli et al., 2020). A round trip efficiency of 80% is assumed for the battery storage. In this case, the reserve requirements and power balance equations of (9) and (11) are changed to (24) and (25), respectively. It is worth mentioning that, since the model is a least-cost optimization and attempts to minimize the cost, when an optimal solution is achieved, no simultaneous charge and discharge is happening.

$\begin{array}{l}{E}_{b,t}^{\text{estor}}=E_{b,t-1}^{\text{estor}}+\left({\eta }^{\text{estor}}.P_{b,t}^{\text{estor},\text{with}}-P_{b,t}^{\text{estor},\text{inj}}\right)·\text{ts},\\ \forall b\in {B},t\in {T}& (19)\end{array}$

$\begin{array}{ll}{P}_{b,t}^{\text{estor},\text{inj}}\le {\text{P}}_b^{\text{inj},\text{max}},\forall b\in {B},t\in {T}& (20)\end{array}$

$\begin{array}{ll}{P}_{b,t}^{\text{estor},\text{with}}\le {\text{P}}_b^{\text{with},\text{max}},\forall b\in {B},t\in {T}& (21)\end{array}$

$\begin{array}{ll}{E}_{b,t}^{\text{estor}}\le {\text{E}}_b^{\text{max}},\forall b\in {B},t\in {T}& (22)\end{array}$

$\begin{array}{ll}{P}_{b,t}^{\text{estor},\text{inj}}·\text{ts}+r_{b,t}^{\text{estor}}·\text{ts}\le E_{b,t-1}^{\text{estor}},\forall b\in {B},t\in {T}& (23)\end{array}$

$\begin{array}{l}{\displaystyle \sum _{i=1}^{{K}}}{r}_{i,t}+{\displaystyle \sum _{i=1}^{{P}}}{r}_{i,t}^{\text{pump}}+{\displaystyle \sum _{b=1}^{{B}}}{r}_{b,t}^{\text{estor}}+u{r}_t\ge {\displaystyle \underset{i\in {K}}{max}}({\text{P}}_i^{\text{max}})\\ +\alpha ·{\displaystyle \sum _{b=1}^{{B}}}{P}_{b,t}^{\text{wind}},\forall t\in {T}& (24)\end{array}$

$\begin{array}{ll}\begin{array}{l}{\displaystyle \sum _{i=1}^{{G}}{P}_{i,t}+{\displaystyle \sum _{b=1}^{{B}}{P}_{b,t}^{\text{wind}}}+{\displaystyle \sum _{i=1}^{{P}}\left(P_{i,t}^{\text{pumb,with}}-P_{i,t}^{\text{pumb,inj}}\right)}}\hfill \\ ={\displaystyle \sum _{b=1}^{{B}}({\text{P}}_{b,t}^{\text{eload}}+P_{b,t}^{\text{ecomp}}-P_{b,t}^{\text{eshed}}}\hfill \\ -P_{b,t}^{\text{estor,with}}+P_{b,t}^{\text{estor,inj}}),\forall t\in {T}\hfill \end{array}& (25)\end{array}$

where

2.4.2. Demand-Side Response (DSR)

A set of generic DSR constraints are implemented in the proposed model: the maximum amount of load that could be shifted (26), the change in load profile due to DSR (27), and temporal shifting of demand while considering potential losses (28) through the presented efficiency, as shifting demand could require an increase in overall energy consumption (Pudjianto et al., 2014). In the presence of DSR, (11) is replaced by (29).

$\begin{array}{ll}{P}_{b,t}^{\text{dneg}}\le \psi ·{\text{P}}_{b,t}^{\text{eload}},\forall b\in {B},t\in {T}& (26)\end{array}$

$\begin{array}{ll}{P}_{b,t}^{\text{dsr}}={\text{P}}_{b,t}^{\text{eload}}-P_{b,t}^{\text{dneg}}+P_{b,t}^{\text{dpos}},\forall b\in {B},t\in {T}& (27)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{t=1}^{{T}}}{P}_{b,t}^{\text{dneg}}\le {\eta }^{\text{dsr}}·{\displaystyle \sum _{t=1}^{{T}}}{P}_{b,t}^{\text{dpos}},\forall b\in {B}& (28)\end{array}$

$\begin{array}{ll}\begin{array}{c}{\displaystyle \sum _{i=1}^{{G}}}{P}_{i,t}+{\displaystyle \sum _{b=1}^{{B}}}{P}_{b,t}^{\text{wind}}+{\displaystyle \sum _{i=1}^{{P}}}\left(P_{i,t}^{\text{pump},\text{with}}-P_{i,t}^{\text{pump},\text{inj}}\right)\\ ={\displaystyle \sum _{b=1}^{{B}}}\left(P_{b,t}^{\text{dsr}}+P_{b,t}^{\text{ecomp}}-P_{b,t}^{\text{eshed}}\right),\forall t\in {T}\end{array}& (29)\end{array}$

where

2.4.3. Power-to-Gas (P2G)

Equations (30)–(32) describe the modeling of the P2G option with an efficiency of 70% (ITM Power, 2013). In (30), the energy content of hydrogen production by electrolyzer to its equivalent natural gas volume is presented. The amount of electricity used for hydrogen production is limited to the capacity of the electrolyzer (31). The amount of hydrogen that can be injected into the gas pipelines cannot exceed the maximum allowance (32). In this case, (11) and (17) are changed to (33) and (34), respectively.

$\begin{array}{ll}{P}_{b,t}^{\text{e}\to {\text{H}}_2}·\text{ts}=\nu {\displaystyle \sum _{x=1}^{{M}}}{\text{M}}_{b,x}^{\text{bus},\text{node}}·{\eta }^{\text{P}2\text{G}}·Q_{x,t}^{{\text{H}}_2\to \text{g}},\forall b\in {B},t\in {T}& (30)\end{array}$

$\begin{array}{ll}{P}_{b,t}^{\text{e}\to {\text{H}}_2}\le {\text{P}}_b^{\text{e}\to {\text{H}}_2^{\max }},\forall b\in {B},t\in {T}& (31)\end{array}$

$\begin{array}{ll}{Q}_{x,t}^{{\text{H}}_2\to \text{g}}\le \Omega ·Q_{x,t}^{\text{available}},\forall x\in {M},t\in {T}& (32)\end{array}$

$\begin{array}{ll}\begin{array}{c}{\displaystyle \sum _{i=1}^{{G}}}{P}_{i,t}+{\displaystyle \sum _{b=1}^{{B}}}{P}_{b,t}^{\text{wind}}+{\displaystyle \sum _{i=1}^{{P}}}\left(P_{i,t}^{\text{pump},\text{with}}-P_{i,t}^{\text{pump},\text{inj}}\right)\\ ={\displaystyle \sum _{b=1}^{{B}}}\left({\text{P}}_{b,t}^{\text{eload}}+P_{b,t}^{\text{ecomp}}-P_{b,t}^{\text{eshed}}+P_{b,t}^{\text{e}\to {\text{H}}_2}\right),\forall t\in {T}\\ \end{array}& (33)\end{array}$

$\begin{array}{l}{Q}_{x,t}^{\text{supp}}+\left({\displaystyle \sum _{w=1}^{{W}}}{\text{M}}_{w,x}^{\text{flow}}·Q_{w,t}\right)+\left(Q_{x,t}^{\text{gstor},\text{with}}-Q_{x,t}^{\text{gstor},\text{inj}}\right)\\ +\left({\displaystyle \sum _{c=1}^{{C}}}{\text{M}}_{c,x}^{\text{comp}}·Q_{c,t}^{\text{comp}}-{\displaystyle \sum _{c=1}^{{C}-{{C}}_e}}{\text{M}}_{c,x}^{\text{ecomp}}·{\zeta }_{c,t}\right)\\ =\left({\text{Q}}_{x,t}^{\text{gload}}+Q_{x,t}^{\text{gen}}-Q_{x,t}^{\text{gshed}}\right)-Q_{x,t}^{{\text{H}}_2\to \text{g}},\forall x\in {M},t\in {T}& (34)\end{array}$

where

2.4.4. Multi-Directional Compressors

Flexible multi-directional compressor stations can enhance flexibility and enable the gas system to deal with growing variability through optimally redirecting the gas flow. Detailed modeling of these units is presented in Ameli et al. (2017d).

3. Modeling Methodology

Figure 1 illustrates the structure of the model. The model minimizes the total operational cost of the gas and electricity systems, simultaneously. In the gas system, (a) cost of supply, (b) cost of unserved gas demand, and (c) cost of storage facilities and in the electricity system, (a) cost of power generation, (b) emission penalties, (c) unserved reserve, (d) cost of unserved electricity demand, and (e) start-up cost of the generators are taken into account (35).

$\begin{array}{ll}\begin{array}{l}Z={\displaystyle \sum _{t=1}^{{T}}({\displaystyle \sum _{i=1}^{{G}}\left({\text{C}}_i^{\text{fuel}}+{\text{C}}_i^{\mathrm{var}}\right).P_{i,t}\cdot \text{ts}+}{\displaystyle \sum _{i=1}^{{K}}{\text{C}}_i^{\text{em}}\cdot e_{i,t}}}\hfill \\ +\left({\text{C}}^{\text{ur}}.u{r}_t\cdot \text{ts}\right)+{\displaystyle \sum _{b=1}^{{B}}{\text{C}}^{\text{eshed}}.P_{b,t}^{\text{eshed}}\cdot \text{ts}+{\displaystyle \sum _{i=1}^{{K}}{w}_{i,t}^{\text{su}}}}\hfill \\ +{\displaystyle \sum _{x=1}^{{Y}}{\text{C}}^{\text{gas}}.Q_{x,t}^{\text{supp}}+{\displaystyle \sum _{x=1}^{{M}}{\text{C}}^{\text{gshed}}.Q_{x,t}^{\text{gshed}}}}\hfill \\ +{\displaystyle \sum _{x=1}^{{{S}}_g}\left({\text{C}}^{\text{gstor,with}}.Q_{x,t}^{\text{gstor,with}}-{\text{C}}^{\text{gstor,inj}}.Q_{x,t}^{\text{gstor,inj}}\right)})\hfill \end{array}& (35)\end{array}$

where

FIGURE 1

Figure 1. Rolling planning structure of the gas and electricity system model.

3.1. Temporal Structure of the Model

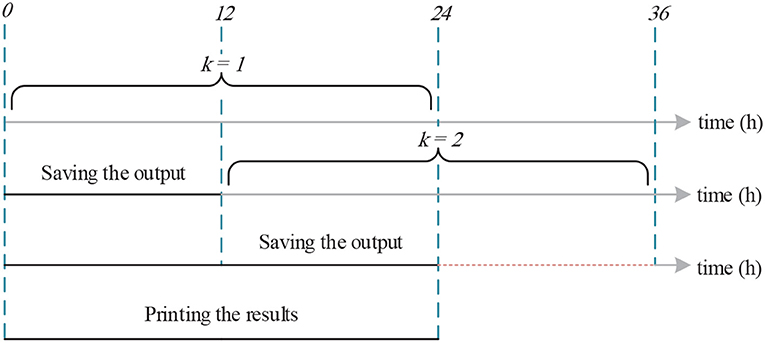
The operation of the gas and electricity systems is optimized using a day-ahead rolling planning approach. After solving the optimization problem for each iteration (i.e., 24 h), solutions representing the state of the system, e.g., On/Off states of the thermal generating units, linepack, and storage for the first 12 h of the iteration are saved (Figure 2). This is carried out in order to decrease the “end-of-optimization” effect and to model the storage facilities and unit commitment approach more realistically. Afterward, the solution of the state variables is used in time-dependent constraints when considering the following 24 h.

FIGURE 2

Figure 2. Twelve-hours output saving strategy.

3.2. OA/ER Decomposition Method

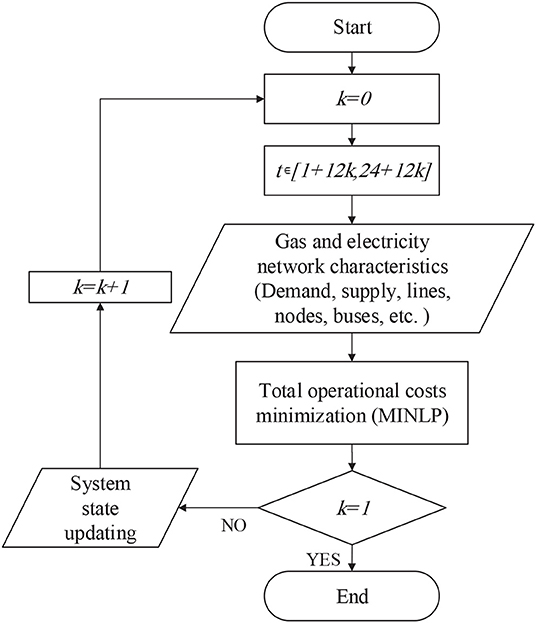
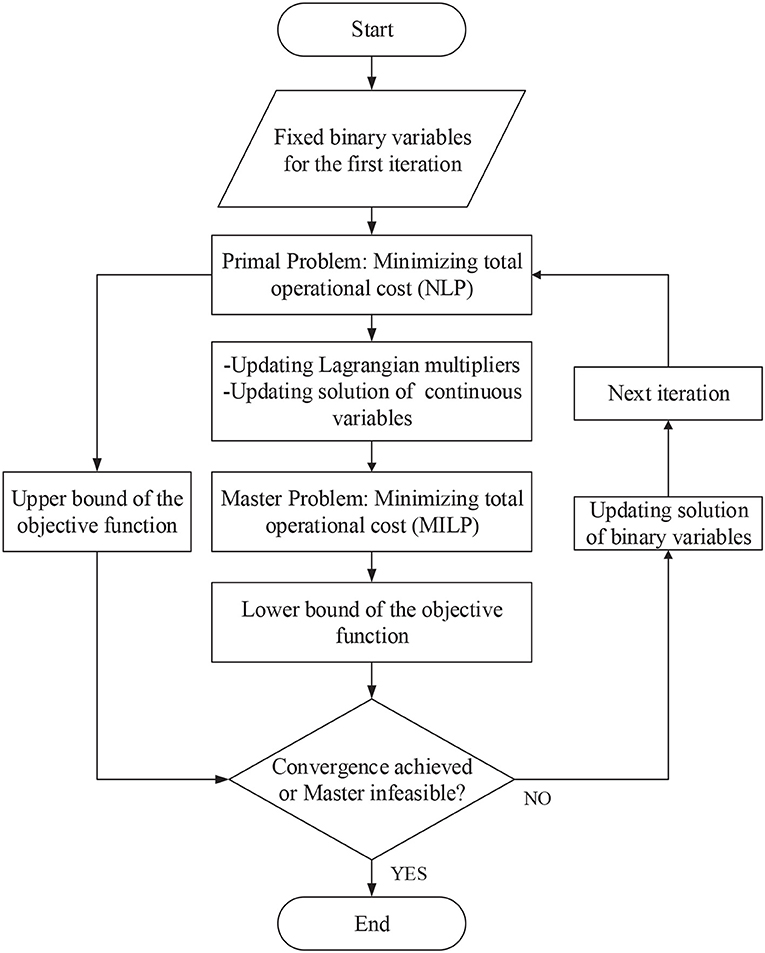
The MINLP problem of the integrated operation of gas and electricity systems is solved using the OA/ER method. The structure of the OA/ER approach is presented in Figure 3. This structure represents the block “Total operational costs minimization” in Figure 1.

FIGURE 3

Figure 3. Structure of OA/ER decomposition method.

In each iteration, an upper bound and a lower bound of the objective function are generated to solve the MILNP problem. The upper bound is obtained from the primal problem, and the lower bound is obtained from the master problem. In the primal problem, the binary variables are fixed. The upper bound and the Lagrangian multipliers associated with the non-linear equality constraints are provided from the primal as input to the master problem. The master problem is derived through relaxing the non-linear equalities to linear inequalities via the use of the Lagrangian multipliers obtained in the primal problem. The master problem provides information about the lower bound and the updated values for binary variables that will be used in the next iteration of the primal problem. The lower bound and upper bound sequences converge as the iterations proceed. A detailed description of this approach is presented in Ameli et al. (2019).

For the sake of simplification, the sets of continuous variables and integer variables in the objective function of the electricity system are defined as:

$\begin{array}{l}\text{X}=\left[P_{i,t},P_{b,t}^{\text{eshed}},e_{i,t},u{r}_t\right],\forall i\in {G},b\in {B},t\in {T}\\ \text{Y}=\left[w_{i,t}^{\text{su}}\right],\forall i\in {K},t\in {T}.\end{array}$

the sets of variables in the objective function of the gas system are defined as:

$\begin{array}{l}\text{U}=\left[Q_{x,t}^{\text{supp}},Q_{x,t}^{\text{gstorwith}},Q_{x,t}^{\text{gstorinj}},\partial L_{l,t},Q_{x,t}^{\text{gshed}}\right],\\ \forall x\in {M},l\in {{L}}_g,t\in {T}.\end{array}$

and the sets of variables in (12) and (14) are presented by:

$\begin{array}{l}\text{S}=\left[p_{x,t}^{\text{in}},p_{x,t}^{\text{out}},Q_{x,t}^{\text{avg}}\right],\forall x\in {{L}}_g,t\in {T}\\ \text{T}=\left[Q_{x,t}^{\text{comp}},p_{x,t}^{\text{dis}},p_{x,t}^{\text{suc}}\right],\forall x\in {C},t\in {T}.\end{array}$

In this regard, in the objective function, f(X) is representing the cost of the continuous variables in the electricity system, g(Y) is representing the cost of the integer variables in the electricity system, h(U) is representing the cost of the continuous variables in the gas system, q(S) is representing the gas flow equation, and r(T) is representing the compressor power consumption.

3.2.1. Primal Problem

In the primal problem, the binary variables of $w_{i,t}^{\text{su}}$ are given as fixed values. Therefore, the MINLP function in (35) is converted to NLP (36). For the first iteration, initial values based on the optimization (using Xpress SLP solver FICO, 2013) described in Ameli et al. (2017d), were given as the values for g(Y^*)⁽¹⁾. The * represents the values that are input to the problem. This selection of initial values makes the convergence process faster. For the next iteration of the primal problem, the fixed values of binary variables are provided subsequently by the master problem.

$\begin{array}{ll}{Z}_{\text{primal}}^{(\rho )}=f\left({\text{X}}^{(\rho )}\right)+h\left({\text{U}}^{(\rho )}\right)+g\left({\text{Y}}^{*(\rho )}\right),\forall \rho \in {F}& (36)\end{array}$

where ${F}$ is the total number iterations. At iteration ρ, if the primal problem is feasible, then information on the continuous variables in the gas system h(U^*(ρ)) and in the electricity system f(X^*(ρ)) is provided as input to the master problem. Additionally, the Lagrangian multipliers of the non-linear equations ${\lambda }_{q(\text{S})}^{(\rho )}$ and ${\lambda }_{r(\text{T})}^{(\rho )}$ are calculated and given as input to the master problem. If the primal problem is infeasible, a feasibility problem considering penalties would be solved to identify the feasible points.

The elements of the ${\Phi }_{q(\text{S})}^{(\rho )}$ and ${\Phi }_{r(\text{T})}^{(\rho )}$ matrices are presented in (37). These matrices provide information regarding the sign of the relaxed inequalities of the non-linear equations in the master problem.

$\begin{array}{l}{\varphi }_{q(\text{S})}^{(\rho )}=\left\{\begin{array}{cc}-1& \text{if }{\lambda }_{q(\text{S})}^{(\rho )}<0\\ \\ +1& \text{if }{\lambda }_{q(\text{S})}^{(\rho )}>0\\ \\ 0& \text{if }{\lambda }_{q(\text{S})}^{(\rho )}=0\\ \end{array}\right\}\\ \text{and }{\varphi }_{r(\text{T})}^{(\rho )}=\left\{\begin{array}{cc}-1& \text{if }{\lambda }_{r(\text{T})}^{(\rho )}<0\\ \\ +1& \text{if }{\lambda }_{r(\text{T})}^{(\rho )}>0\\ \\ 0& \text{if }{\lambda }_{r(\text{T})}^{(\rho )}=0\\ \end{array}\right\}& (37)\end{array}$

3.2.2. Master Problem

The master problem formulation is presented by equations (38)-(43). In (38), the objective function of the master problem is presented. In (39), variable ξ is introduced to constrain the linearized objective function of the primal at the solution points of continuous variables. However, since the objective function is linear, it can be expressed as in (39).

$\begin{array}{ll}{Z}_{\text{master}}^{(\rho )}=g\left({\text{Y}}^{(\rho )}\right)+\xi ,\forall \rho \in {F}& (38)\end{array}$

$\begin{array}{ll}\xi \ge f\left({\text{X}}^{*(\rho )}\right)+h\left({\text{U}}^{*(\rho )}\right),\forall \rho \in {F}& (39)\end{array}$

The non-linear equalities of gas flow equation (12) and compressor power consumption (14) are relaxed to inequalities of (40) and (41), respectively.

$\begin{array}{ll}\begin{array}{l}{\Phi }_{q\left(\text{S}\right)}^{(\rho )}·\left(q\left({\text{S}}^{*(\rho )}\right)+\left[\nabla q\left({\text{S}}^{*(\rho )}\right)\right]·{\left[{\text{S}}^{(\rho )}-{\text{S}}^{*(\rho )}\right]}^T\right)\\ \le 0,\forall \rho \in {F}\end{array}& (40)\end{array}$

$\begin{array}{ll}\begin{array}{l}{\Phi }_{r\left(\text{T}\right)}^{(\rho )}·\left(r\left({\text{T}}^{*(\rho )}\right)+\left[\nabla r\left({\text{T}}^{*(\rho )}\right)\right]·{\left[{\text{T}}^{(\rho )}-{\text{T}}^{*(\rho )}\right]}^T\right)\\ \le 0,\forall \rho \in {F}\end{array}& (41)\end{array}$

In each iteration, the objective function of the master problem should be between the current objective function of the primal (upper bound) and the previous objective value of the master (lower bound) in order to proceed with convergence of the problem (42). The optimization is terminated when (43) is met or the master problem is infeasible, where ϵ is the convergence bound.

$\begin{array}{ll}{Z}_{\text{master}}^{(\rho -1)}\le Z_{\text{master}}^{(\rho )}\le Z_{\text{primal}}^{(\rho )},\forall \rho \in {F}& (42)\end{array}$

$\begin{array}{ll}|Z_{\text{master}}^{(\rho )}-Z_{\text{primal}}^{(\rho )}|\le ϵ,\forall \rho \in {F}& (43)\end{array}$

4. Case Studies

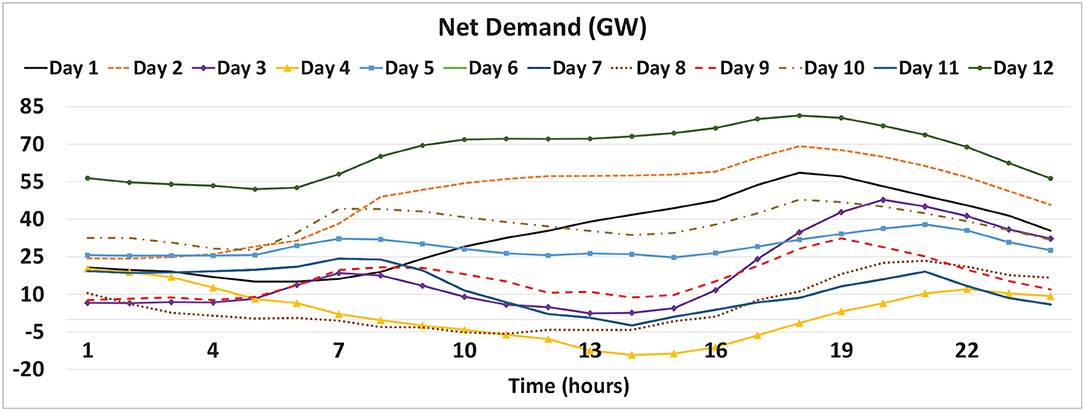
The operation of a GB gas and electricity system with large penetration of wind generation is modeled for twelve representative days characterizing possible conditions for net electricity demand within the year in 2030.

The efficiency of the OA/ER decomposition method approach for solving the optimal operation problem of gas and electricity systems is assessed by comparing it to the commercial XPRESS SLP solver.

The efficacy of the flexibility options, namely (a) battery storage (EStor), (b) demand-side response (DSR), (c) Power-to-Gas (P2G), and (d) multi-directional compressors (Multi), to address electricity supply-demand balancing challenges is evaluated and compared to a reference (Ref) case in which no particular measure was considered to facilitate efficient integration of a large penetration of renewable generation.

4.1. GB Gas and Electricity Systems

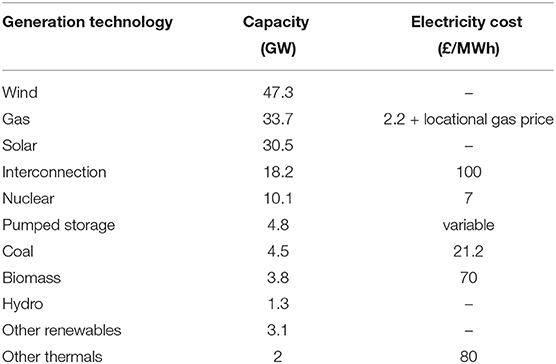
The power generation mix in this study is shown in Table 1 and is based on the year 2030 of the “Gone Green” scenario of the National Grid (National Grid Plc, 2016). For gas-fired plants, variation in the cost of electricity production (2.2 /MWh) depending on the fuel price is taken into account.

TABLE 1

Table 1. Generation mix in GB 2030.

The updated version of the GB 62-node National Transmission System (NTS) gas network (Qadrdan et al., 2010) and a 29-busbar electricity transmission system (Ameli et al., 2017d) are modeled. The data presented in Ameli et al. (2017d) are used as the base for hourly wind generation and non-electric gas demand in 2030. The gas demand for power generation is determined endogenously by (18). The electricity peak demand is assumed to be 85 GW, which is driven by the electrification of segments of the heat and transport sectors.

In the optimization problems of integrated operation of gas and electricity systems, about 43,000 variables including 3,500 binary variables are determined in each 24 h.

4.2. Demand Clustering Strategy

Due to the complexity of modeling the integrated operation of gas and electricity systems, it is computationally challenging to analyze the system for an entire year with an hourly time step (8,760 time steps in total). Instead, the net electricity demand profiles (i.e., renewable electricity generation deducted from electricity demand) for a number of characteristic days are selected, which represent the combination of electricity demand and renewable electricity generation. The clustering algorithm is presented in this section. At the beginning for each day, an equal weight of $\frac{1}{365}$ is considered. The net demand clustering algorithm is described as follows.

• Step 1: Calculating the distance between different net demand profiles through (44), where k is the counter.

$\begin{array}{ll}{\Delta }_{i,j}=\sqrt{{\displaystyle \sum _{t=1}^{{T}}}{\left(P_{i,t}^{\text{net}}-P_{j,t}^{\text{net}}\right)}^2},k={{N}}_{\text{pr}},\forall i,j\in {H}& (44)\end{array}$

• Step 2: Finding the two closest profiles.

$\begin{array}{ll}\forall i,j\in {H}:{\Delta }_{i^{*},j^{*}}=\text{mi}{\text{n}}_{i\ne j}{\Delta }_{i,j}& (45)\end{array}$

• Step 3: Comparing the frequency of occurrence of the profiles in order to delete the profile with less frequency.

• Step 4: The frequency of the deleted profile is added to the closest profile, and k = k − 1.

$\begin{array}{l}\text{if }{\varpi }_{i^{*}}\ge {\varpi }_{j^{*}}\to \text{profile }{j}^{*}\text{is deleted}\\ \to {\varpi }_i={\varpi }_{i^{*}}+{\varpi }_{j^{*}},\\ \text{if }{\varpi }_{i^{*}}<{\varpi }_{j^{*}}\to \text{profile }{i}^{*}\text{is deleted}\\ \to {\varpi }_j={\varpi }_{i^{*}}+{\varpi }_{j^{*}}.\end{array}$

• Step 5: If $k={{N}}_{\text{dp}}$ then terminate. Otherwise, return to step 1.

where,

In Figure 4, the net electricity demand profiles selected by the clustering algorithm are presented. The actual days in the year and the frequency of occurrence of the representative profiles are provided in Table 2. Some of the profiles that occur less frequently pose unique characteristics, e.g., Day 4 occurs only once in the whole year and represents a summer day in which a significant amount of electricity is generated by RES; therefore, net electricity demand is negative during most hours of the day.

FIGURE 4

Figure 4. Net demand profiles after the demand clustering strategy.

TABLE 2

Table 2. Representative days for the entire year.

4.3. Description of Flexibility Case Studies

To investigate the role and value of the flexibility options in supporting the cost-effective operation of gas and electricity systems, different combinations of available flexibility and level of wind generation penetration are considered. For each flexibility option, two different levels considered: low 4 GW installed capacity and high 12 GW installed capacity. For wind generation, three different levels of installed capacity, i.e., 23.6, 47.3, and 70.9 GW, are assumed.

5. Results and Discussions

5.1. Computational Performance of the OA/ER Approach

The optimization problem was run on a computer with a 3.20 GHz Intel(R) Xeon(R) processor and 16 GB of RAM. The computational performance of the proposed OA/ER decomposition method was benchmarked against the SLP algorithm of Xpress solver (FICO, 2013). The employment of the OA/ER decomposition method significantly improved the efficiency of the solution algorithm, achieving a nearly 40% reduction in the computation time compared to the SLP method. In addition, the solution of the optimization (i.e., operational cost) was slightly improved. A summary of the computational characteristics for a day is presented in Table 3.

TABLE 3

Table 3. Computational performance for optimization of a day through different solving approaches.

5.2. Performance of Flexibility Options in the Electricity System

5.2.1. Impacts of Increased Flexibility on Generation Dispatch

Figure 5 shows how the use of flexibility options affects the electricity outputs of different generation technologies through the change in electricity production with respect to the Ref Case. The application of flexibility options enhances the ability of the system to absorb more electricity from renewable sources. Consequently, due to more electricity being supplied from renewables, compared to the Ref case, the power from the expensive option (interconnection) as well as coal (i.e., characterized by high emissions) is reduced. Furthermore, the share of gas-fired plants increases to complement variable renewable generation. In Figure 5A, the significant role of high installation of DSR in accommodating more gas-fired plants is presented. This is due to the fact that, since the wind penetration is low, gas plants play the main part in supplying demand, and by shifting the demand optimally, around 5 TWh more electricity is provided by the gas-fired plants. Due to the small penetration of wind, electricity storage and P2G have a small impact on the electricity produced by different types of generators. In Figure 5B, although more electricity is absorbed by the grid, the gas plants are generating more. This is due to the fact that according to (23), the electricity storage is contributing to providing a reserve, and hence gas plants participate more in the supply-demand balance. Figure 5C shows that, due to the flexibility provided by electricity storage through optimal charging and discharging, the contribution of gas-fired plants and hydro is reduced. In P2G cases, the increased absorption of electricity from wind is primarily used for hydrogen production. Furthermore, to support the operation of the gas system during peak periods, up to 2.6 TWh/yr additional electricity, mainly from hydro (i.e., limited in the Ref case because of transmission congestion), is used for producing and injecting hydrogen into the gas system. As can be seen in Figures 5B,C, more electricity from hydrogen-based CCGTs is produced compared to the Ref case (up to 0.8 TWh/yr), which leads to less emissions from gas-fired plants.

FIGURE 5

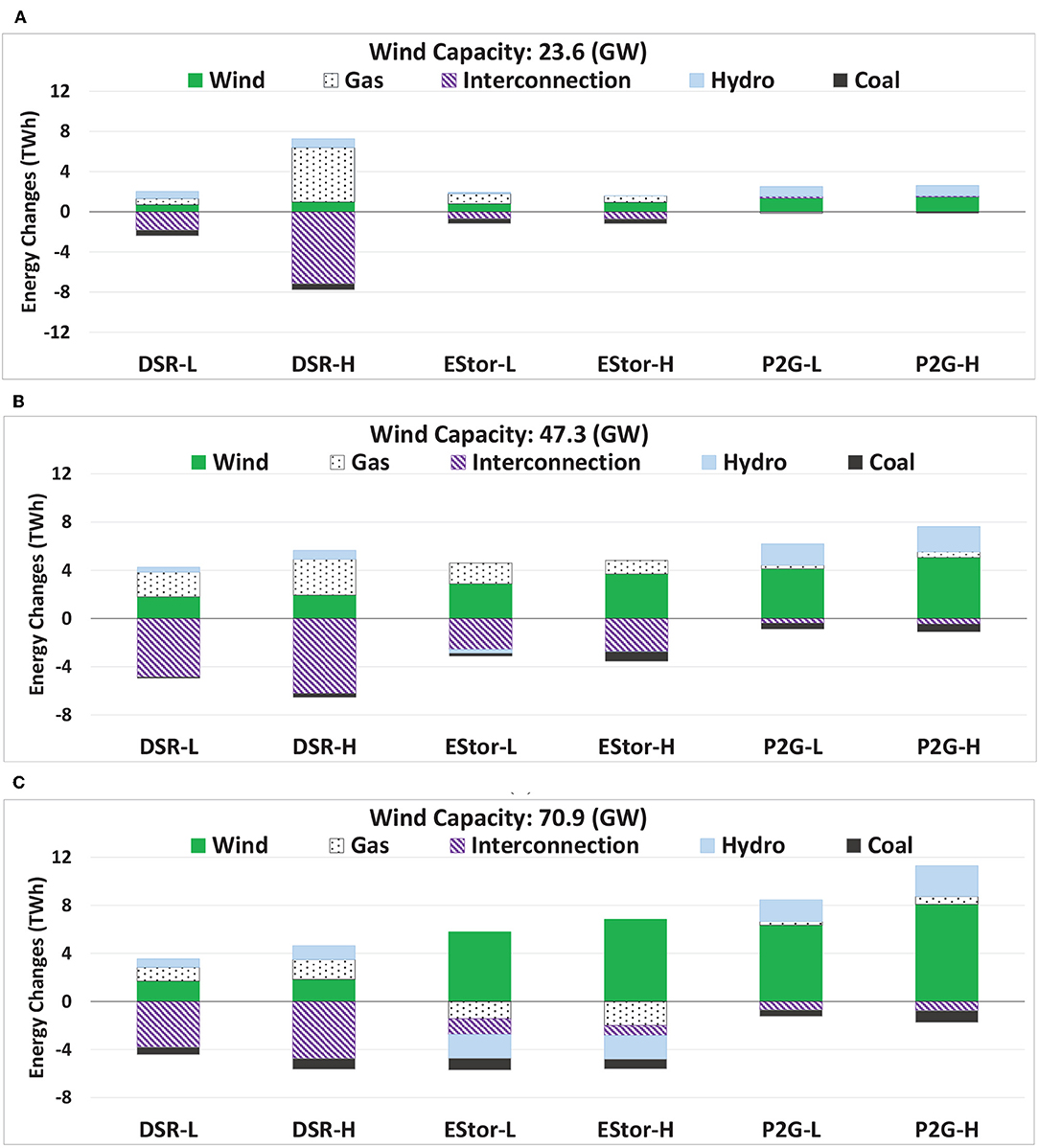
Figure 5. Annual energy changes for different installed capacities of wind (compared to the Ref case): (A) 23.6 GW, (B) 46.7 GW, and (C) 70.9 GW.

It is shown that when increasing the penetration level of wind to the system, electricity storage plays a significant role in changing the power dispatch from different technologies. As presented in Figure 5A, this is demonstrated by integrating more wind into the system while decreasing the electricity from coal and interconnection and reducing the share of renewables, and there are decreases in all other generation technologies at higher shares of wind. For other flexibility options for all wind penetration levels, the generation from wind, gas-fired, and hydro plants increases, while the production of interconnectors and coal plants decreases. In P2G cases, the hydrogen produced through the excess of wind is injected into the gas pipelines as well as being used as a fuel for gas-fired plants.

5.2.2. Wind Curtailment

As expected, the increased level of flexibility reduces wind curtailment. The highest reductions in wind curtailment are achieved in the P2G and EStor cases. The annual reduction of wind curtailment is presented in Figure 6A.

FIGURE 6

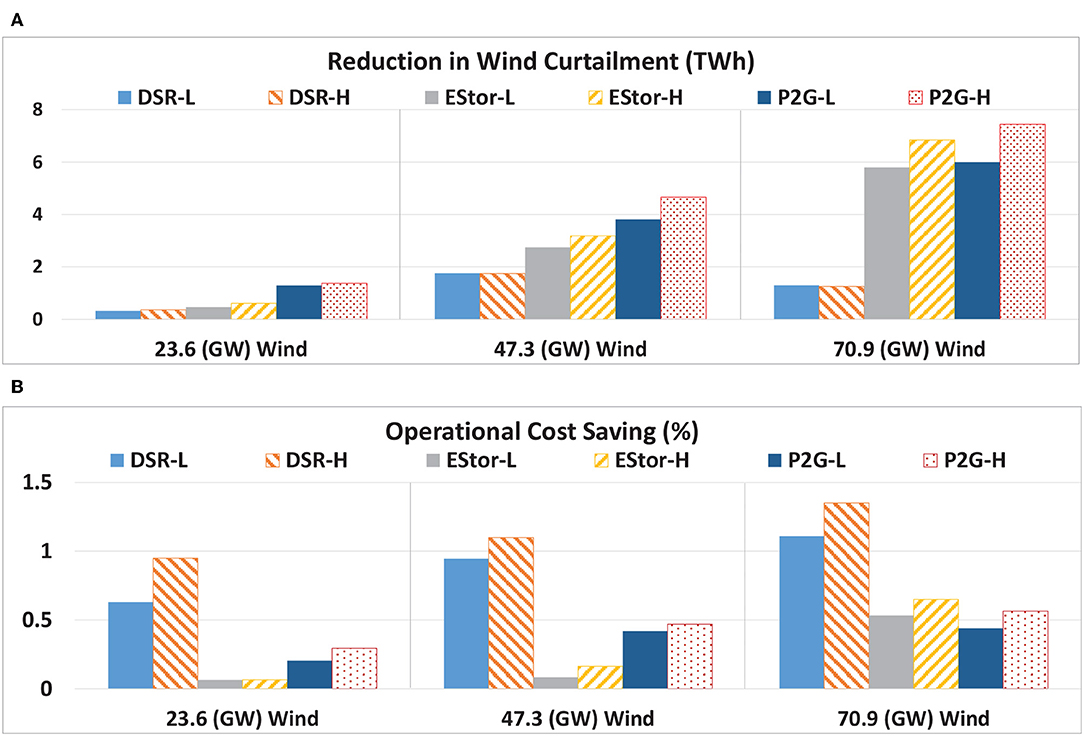
Figure 6. (A) Cumulative wind curtailment reduction, and (B) annual operational cost savings of gas and electricity systems compared to the Ref case.

5.2.3. Operational Costs

In Figure 6B, the annual gas and electricity operational cost savings compared to the Ref case are presented for different levels of wind penetration and the application of different flexibility options. The total operational costs of gas and electricity systems for the Ref case are shown in Table 4.

TABLE 4

Table 4. Total operational costs in the Ref case.

The value of flexibility options increases when the penetration of wind generation increases. In DSR cases, due to the flexibility provided, demand is shifted mainly from peaks to off-peaks, which results in a significant decrease in electricity importation (Figure 5). As a result, the largest cost savings are achieved in DSR cases. Overall, the enhanced flexibility provided by DSR, electricity storage, and P2G increases the efficiency of system operation by reducing the challenges caused by RES.

It is worth mentioning that in the DSR modeling, the demand satisfaction constraints (i.e., related to customer behavior) is not taken into account (Pudjianto et al., 2014), and it is assumed that the part of demand that is flexible can be shifted when it is required by the system operator. In a case where demand satisfaction constraints should be considered, the cost savings would be lower.

5.3. Performance of Flexibility Options in the Gas System

If flexibility in the gas system is enhanced through multi-directional gas compressors, it is possible to deliver more gas to the gas plants. Consequently, the supply through coal decreases, and therefore the overall emissions and the total operational costs of the systems reduce. Figure 7 demonstrates that enhancing the flexibility of the gas infrastructure in the integrated operation of gas and electricity systems increases the generation by gas-fired power plants and reduce wind curtailment, while the production from coal characterized by high emissions reduces. This delivers prevention of about 300 kilotonnes of CO₂ production.

FIGURE 7

Figure 7. Change in annual electricity generation in the Multi case in respect to the Ref case.

It is worth mentioning that since there is enough gas supply to the system, under normal conditions, the multi-directional gas compressors do not play a major role in improving the operation of the system. This flexibility can enhance the energy system resiliency. Therefore, to highlight the role of multi-directional gas compressors, a stressed condition of the energy system considering two characteristics is derived: (a) when an increase in demand in morning hours coincides with a reduction in wind generation, as presented in Figure 8A, and (b) when gas supply capacities in the St Fergus, Bacton, and Easington gas terminals are constrained (Figure 8B).

FIGURE 8

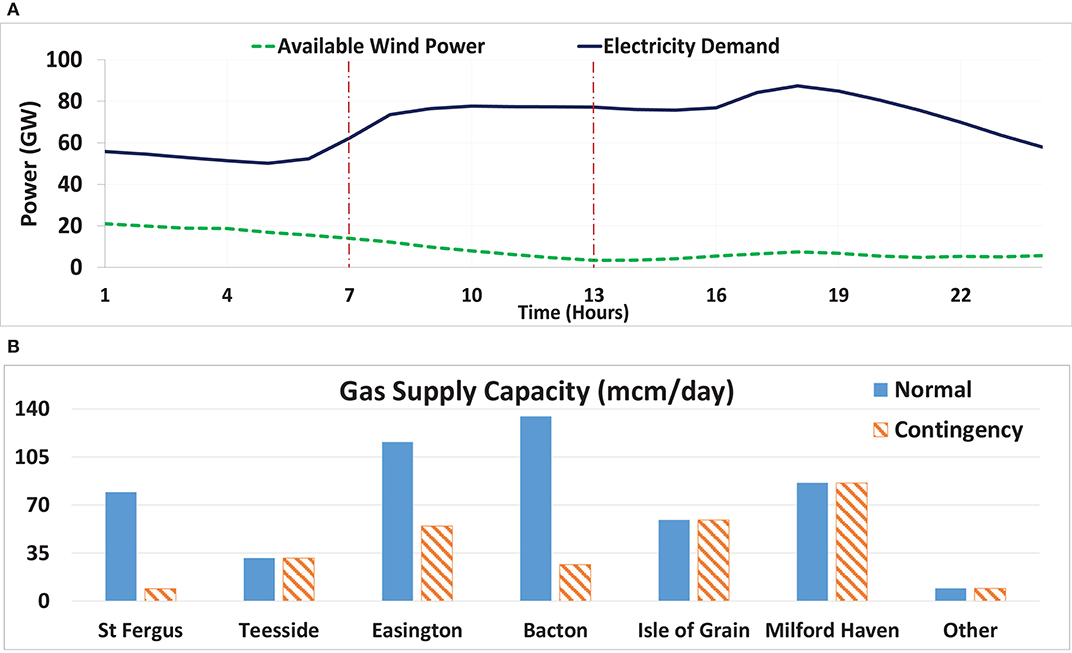
Figure 8. (A) Electricity demand and available wind, and (B) gas terminal capacity on the day of supply interruption (other refers to Barrow, Burton point, and Theddlethrope).

5.3.1. Power Dispatch

The employment of flexibility options enables an effective balancing of electricity supply and demand during gas supply interruption and therefore reduces the need to import electricity (which is assumed to be at highest cost) or coal plants, which are characterized by high emissions. As seen in Figure 9, electricity from interconnectors and coal is reduced by up to 36 and 50 GWh compared to the Ref case in the two stress conditions, respectively. Hence, more accommodation of wind energy is facilitated, which leads to cost savings for both natural gas and power systems.

FIGURE 9

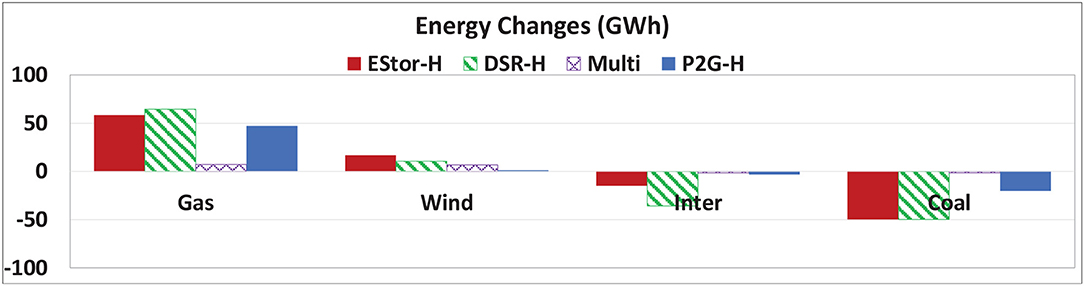
Figure 9. Change in the electricity in presence of different flexibility options during the day of gas supply interruption compared to the Ref case.

5.3.2. Gas Compressor Performance

Multi-directional compressors play a key role in mitigating the impacts of gas supply interruption by redirecting gas flows and maintaining gas supply to gas-fired power plants that would be otherwise be affected by the supply interruption. As is presented in Figure 10A, in the Multi case, especially in the morning hours when a demand increase and a sudden wind drop coincide, the compressors operate more frequently to redirect the gas flow direction. In other cases, the compressor performance is almost the same as the Ref case, as the changes are small. This is due to the fact that, in these cases, the flexibility of the gas system infrastructure is not enhanced.

FIGURE 10

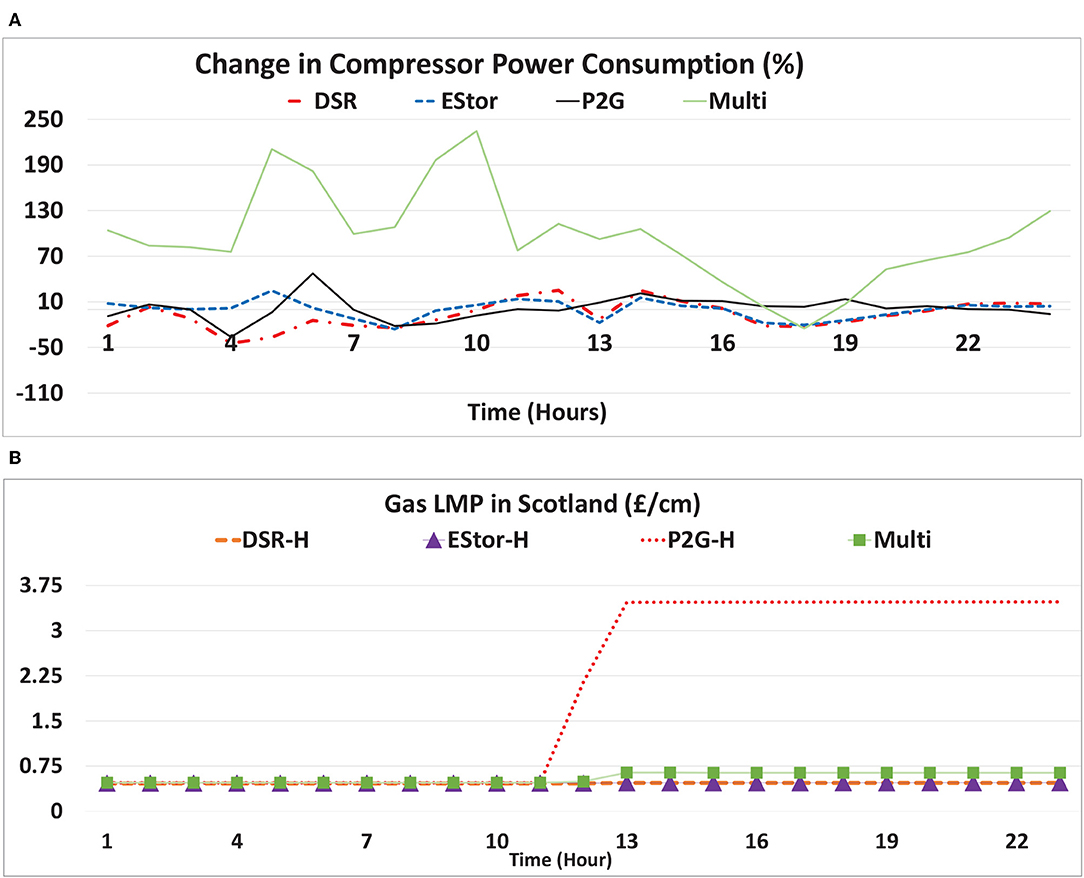
Figure 10. (A) Change in power consumed by the gas compressors on the day of supply interruption compared to the Ref case, and (B) gas LMP in Scotland on the day of supply interruption.

5.3.3. Locational Marginal Price of Gas

As was discussed, the large penetration of RES increases the interaction of gas and electricity networks. Therefore, changes in the level of wind generation will significantly influence the operation of the gas system. In the case of no interruption of gas supply, since there is still enough gas to meet the demand, gas Locational Marginal Prices (LMP) are around the gas price (0.35 £/cm). The gas system security will be impacted, particularly during interruption in the gas supply system. The index considered for the gas system security is the amount of non-served gas demand. In the Ref case, the gas supply interruption causes a loss of 0.033 mcm of gas demand. This results in a significant increase in the gas LMP, especially in Scotland after 11:00 a.m., when both gas and electricity demand are high (Figure 10B). The gas LMP in Scotland in the Ref case after 11 h is equal to the assumed Value of Lost Load (VoLL) (11.1 £/cm Chaudry et al., 2008). The use of flexibility options prevents gas load shedding during the supply interruption. As is shown in Figure 10B, the use of DSR and battery storage minimize the impact of the gas supply interruption on the gas LMP (0.46 £/cm). In the Multi case, the gas LMP is 0.72 £/cm, which indicates the efficacy of multi-directional compressors in gas delivery to demand centers. P2G prevents gas load shedding by producing hydrogen and injecting it into the gas system. However, the LMPs are high (3.4 £/cm) given that the wind generation is low and hydrogen injection therefore cannot help significantly to obviate the gas system congestion.

Overall, the modeling demonstrates that the investment in flexibility in gas infrastructure will be driven by increased requirements for flexibility in the electricity system. This will require closer coordination of operation and investment in both systems in order to facilitate cost-effective de-carbonization of the electricity system.

On the other hand, the case studies indicate that enhancing flexibility in gas and electricity networks could reduce the dependency between gas and electricity systems by addressing demand-supply balancing challenges as well as gas supply interruptions.

6. Conclusion

An outer approximation with equality relaxation method is proposed to effectively solve the optimization problem of the operation of integrated gas and electricity systems. The modeling approach developed is applied to demonstrate the benefits of an integrated approach to the operation of interdependent gas and electricity systems.

In addition, the modeling indicates that significant cost savings and corresponding emissions reduction can be achieved through enhancing the flexibility of the gas infrastructure. The value of different flexibility options (battery storage, demand-side response, power-to-gas, and multi-directional compressors) for the operation of gas and electricity systems were investigated for various scenarios representing different levels of wind generation penetration. It was demonstrated that flexibility options would enhance the ability of the system to accommodate wind generation and simultaneously reduce the operating cost of the gas and electricity systems by up to 21%.

It was demonstrated that during sudden drops in wind generation as well as gas supply interruptions, the flexibility options play important roles in enhancing the efficiency of system operation and the security of gas supply. The ability of the flexibility options to reduce the interaction between gas and electricity networks in an integrated strategy highlights the importance of reforming the current regulatory and market framework to coordinate operation and investment in both systems for a cost-effective transition to lower-carbon energy systems.

Future work will involve modeling of investment in different flexibility options and emission constraints in order to identify the optimal portfolio of these technologies that would achieve carbon targets at minimum whole-system costs. Furthermore, integrated analysis of local and national infrastructures will be important for considering alternative evolution pathways of the gas and electricity infrastructures.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

HA conducted the modelings and run the optimization as well as writing the paper. MQ and GS provided the guidance as well as contributing in writing the paper. All authors contributed to the article and approved the submitted version.

Funding

The authors gratefully acknowledge the SysFlex project, which has received funding from the European Union's Horizon 2020 research and innovation program under award number 773505 as well as the EPSRC-funded program Integrated Development of Low-Carbon Energy Systems (IDLES) under award number EP/R045518/1.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Akhtari, M. R., and Baneshi, M. (2019). Techno-economic assessment and optimization of a hybrid renewable co-supply of electricity, heat and hydrogen system to enhance performance by recovering excess electricity for a large energy consumer. Energy Convers. Manag. 188, 131–141. doi: 10.1016/j.enconman.2019.03.067

CrossRef Full Text | Google Scholar

Ameli, H., Abbasi, E., Ameli, M. T., and Strbac, G. (2017a). A fuzzy-logic based control methodology for secure operation of a microgrid in interconnected and isolated modes. Int. Trans. Electric. Energy Syst. 27:e2389. doi: 10.1002/etep.2389

CrossRef Full Text | Google Scholar

Ameli, H., Ameli, M. T., and Hosseinian, S. H. (2017b). Multi-stage frequency control of a microgrid in the presence of renewable energy units. Electric Power Comp. Syst. 45, 159–170. doi: 10.1080/15325008.2016.1247389

CrossRef Full Text | Google Scholar

Ameli, H., Qadrdan, M., and Strbac, G. (2017c). Techno-economic assessment of battery storage and power-to-gas: a whole-system approach. Energy Proc. 142, 841–848. doi: 10.1016/j.egypro.2017.12.135

CrossRef Full Text | Google Scholar

Ameli, H., Qadrdan, M., and Strbac, G. (2017d). Value of gas network infrastructure flexibility in supporting cost effective operation of power systems. Appl. Energy 202, 571–580. doi: 10.1016/j.apenergy.2017.05.132

CrossRef Full Text | Google Scholar

Ameli, H., Qadrdan, M., and Strbac, G. (2019). Coordinated operation strategies for natural gas and power systems in presence of gas-related flexibilities. IET Energy Syst. Integr. 1, 3–13. doi: 10.1049/iet-esi.2018.0047

CrossRef Full Text | Google Scholar

Ameli, H., Qadrdan, M., Strbac, G., and Ameli, M. T. (2020). Investing in flexibility in an integrated planning of natural gas and power systems. IET Energy Syst. Integr. 2, 101–111 doi: 10.1049/iet-esi.2019.0065

CrossRef Full Text | Google Scholar

Castillo, A., Laird, C., Silva-Monroy, C. A., Watson, J. P., and O'Neill, R. P. (2016). The unit commitment problem with ac optimal power flow constraints. IEEE Trans. Power Syst. 31, 4853–4866. doi: 10.1109/TPWRS.2015.2511010

CrossRef Full Text | Google Scholar

Chaudry, M., Jenkins, N., and Strbac, G. (2008). Multi-time period combined gas and electricity network optimisation. Electric Power Syst. Res. 78, 1265–1279. doi: 10.1016/j.epsr.2007.11.002

CrossRef Full Text | Google Scholar

Chung, C. Y., Yu, H., and Wong, K. P. (2011). An advanced quantum-inspired evolutionary algorithm for unit commitment. IEEE Trans. Power Syst. 26, 847–854. doi: 10.1109/TPWRS.2010.2059716

CrossRef Full Text | Google Scholar

Correa-Posada, C. M., and Sanchez-Martin, P. (2015). Integrated power and natural gas model for energy adequacy in short-term operation. IEEE Trans. Power Syst. 30, 3347–3355. doi: 10.1109/TPWRS.2014.2372013

CrossRef Full Text | Google Scholar

Correa-Posadaa, C. M., and Sanchez-Martin, P. (2014). Gas network optimization: a comparison of piecewise linear models. Chem. Eng. Sci. 30, 1–24.

Google Scholar

Dai, C., Wu, L., and Wu, H. (2016). A multi-band uncertainty set based robust scuc with spatial and temporal budget constraints. IEEE Trans. Power Syst. 31, 4988–5000. doi: 10.1109/TPWRS.2016.2525009

CrossRef Full Text | Google Scholar

Deane, J., Ciaráin, M. O., and Gallachóir, B. O. (2017). An integrated gas and electricity model of the EU energy system to examine supply interruptions. Appl. Energy 193, 479–490. doi: 10.1016/j.apenergy.2017.02.039

CrossRef Full Text | Google Scholar

FICO (2013). Fico Xpress Optimisation Suite. San Jose, CA.

Floudas, C. A. (1995). Nonlinear and Mixed-Integer Optimization: Fundamentals and Applications. Oxford, UK: Oxford University Press.

Google Scholar

Gil, M., Duenas, P., and Reneses, J. (2016). Electricity and natural gas interdependency: comparison of two methodologies for coupling large market models within the european regulatory framework. IEEE Trans. Power Syst. 31, 361–369. doi: 10.1109/TPWRS.2015.2395872

CrossRef Full Text | Google Scholar

He, C., Wu, L., Liu, T., and Shahidehpour, M. (2017). Robust co-optimization scheduling of electricity and natural gas systems via admm. IEEE Trans. Sustain. Energy 8, 658–670. doi: 10.1109/TSTE.2016.2615104

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, Y., Lian, H., Bie, Z., and Zhou, B. (2017). Unified probabilistic gas and power flow. J. Mod. Power Syst. Clean Energy 5, 400–411. doi: 10.1007/s40565-017-0284-1

CrossRef Full Text | Google Scholar

ITM Power (2013). Report and Financial Statements. Technical report, Sheffield, United Kingdom.

Nasri, A., Kazempour, S. J., Conejo, A. J., and Ghandhari, M. (2016). Network-constrained ac unit commitment under uncertainty: a benders decomposition approach. IEEE Trans. Power Syst. 31, 412–422. doi: 10.1109/TPWRS.2015.2409198

CrossRef Full Text | Google Scholar

National Grid Plc (2016). UK Future Energy Scenarios, GB Gas and Electricity Transmission. Technical Report July, Warwick, United Kingdom.

Ongsakul, W., and Petcharaks, N. (2004). Unit commitment by enhanced adaptive lagrangian relaxation. IEEE Trans. Power Syst. 19, 620–628. doi: 10.1109/TPWRS.2003.820707

CrossRef Full Text | Google Scholar

Osiadacz, A. (1987). Simulation and Analysis of Gas Networks. Houston, TX: Gulf Publishing Company.

Google Scholar

Pudjianto, D., Aunedi, M., Djapic, P., and Strbac, G. (2014). Whole-systems assessment of the value of energy storage in low-carbon electricity systems. IEEE Trans. Smart Grid 5, 1098–1109. doi: 10.1109/TSG.2013.2282039

CrossRef Full Text | Google Scholar

Qadrdan, M., Ameli, H., Strbac, G., and Jenkins, N. (2017a). Efficacy of options to address balancing challenges: integrated gas and electricity perspectives. Appl. Energy 190, 181–190. doi: 10.1016/j.apenergy.2016.11.119

CrossRef Full Text | Google Scholar

Qadrdan, M., Chaudry, M., Wu, J., Jenkins, N., and Ekanayake, J. (2010). Impact of a large penetration of wind generation on the GB gas network. Energy Policy 38, 5684–5695. doi: 10.1016/j.enpol.2010.05.016

CrossRef Full Text | Google Scholar

Qadrdan, M., Cheng, M., Wu, J., and Jenkins, N. (2017b). Benefits of demand-side response in combined gas and electricity networks. Appl. Energy 192, 360–369. doi: 10.1016/j.apenergy.2016.10.047

CrossRef Full Text | Google Scholar

Sardou, I. G., Khodayar, M. E., and Ameli, M. T. (2018). Coordinated operation of natural gas and electricity networks with microgrid aggregators. IEEE Trans. Smart Grid 9, 199–210. doi: 10.1109/TSG.2016.2547965

CrossRef Full Text | Google Scholar

Shabanpour-Haghighi, A., and Seifi, A. R. (2015). Simultaneous integrated optimal energy flow of electricity, gas, and heat. Energy Convers. Manag. 101, 579–591. doi: 10.1016/j.enconman.2015.06.002

CrossRef Full Text | Google Scholar

Sheikhi, A., Bahrami, S., and Ranjbar, A. M. (2015). An autonomous demand response program for electricity and natural gas networks in smart energy hubs. Energy 89, 490–499. doi: 10.1016/j.energy.2015.05.109

CrossRef Full Text | Google Scholar

Sirvent, M., Kanelakis, N., GeiSSler, B., and Biskas, P. (2017). Linearized model for optimization of coupled electricity and natural gas systems. J. Mod. Power Syst. Clean Energy 5, 364–374. doi: 10.1007/s40565-017-0275-2

CrossRef Full Text | Google Scholar

Troy, N., Flynn, D., and O'Malley, M. (2012). Multi-mode operation of combined-cycle gas turbines with increasing wind penetration. IEEE Trans. Power Syst. 27, 484–492. doi: 10.1109/TPWRS.2011.2163649

CrossRef Full Text | Google Scholar

Wu, Q. H., Qin, Y. J., Wu, L. L., Zheng, J. H., Li, M. S., Jing, Z. X., et al. (2019). Optimal operation of integrated energy systems subject to the coupled demand constraints of electricity and natural gas. CSEE J. Power Energy Syst. 6, 1–14. doi: 10.17775/CSEEJPES.2018.00640

CrossRef Full Text | Google Scholar

Yang, L., Jian, J., Dong, Z., and Tang, C. (2017). Multi-cuts outer approximation method for unit commitment. IEEE Trans. Power Syst. 32, 1587–1588. doi: 10.1109/TPWRS.2016.2584862

CrossRef Full Text | Google Scholar

Yang, Z., Gao, C., and Zhao, M. (2019). Coordination of integrated natural gas and electrical systems in day-ahead scheduling considering a novel flexible energy-use mechanism. Energy Convers. Manag. 196, 117–126. doi: 10.1016/j.enconman.2019.05.109

CrossRef Full Text | Google Scholar

Zeng, Q., Fang, J., Li, J., and Chen, Z. (2016). Steady-state analysis of the integrated natural gas and electric power system with bi-directional energy conversion. Appl. Energy 184, 1483–1492. doi: 10.1016/j.apenergy.2016.05.060

CrossRef Full Text | Google Scholar

Zhang, X., Shahidehpour, M., Alabdulwahab, A., and Abusorrah, A. (2016). Hourly electricity demand response in the stochastic day-ahead scheduling of coordinated electricity and natural gas networks. IEEE Trans. Power Syst. 31, 592–601. doi: 10.1109/TPWRS.2015.2390632

CrossRef Full Text | Google Scholar

Zlotnik, A., Roald, L., Backhaus, S., Chertkov, M., and Andersson, G. (2017). Coordinated scheduling for interdependent electric power and natural gas infrastructures. IEEE Trans. Power Syst. 32, 600–610. doi: 10.1109/TPWRS.2016.2545522

CrossRef Full Text | Google Scholar