The Effect of Different Branch Angles and Different Branch Pipe Sizes on the Onset Law of Liquid Entrainment

The T-junction has been extensively employed in nuclear power plant systems. To ensure the normal operation of nuclear power plant, the onset point of T-junction liquid entrainment requires in-depth studies. Existing studies have been conducted on the onset point of liquid entrainment, whereas most of them are for small branch pipes. This study primarily discussed the onset law of large branch pipe. Moreover, the effects of branch angle and size on the onset point of liquid entrainment were analyzed by comparing it with other branch pipe sizes in this study. This study demonstrated that the effect of branch angle on the onset point of entrainment complies with that of other sizes, i.e., because that the decrease in the inertial force in the vertical direction acting on the liquid phase by the gas phase with the decrease in the angle, hence, the onset requires larger Fr_g under the identical h_bwith the decrease in the angle between the branch pipe and the horizontal direction. Moreover, by comparing the onset point law of liquid entrainment exhibiting different branch pipe sizes, the effect of branch pipe size on the onset was reported in this study that the smaller branch pipe requires the greater gas velocity in the presence of onset. We found that there is different flow resistance of different sizes of branch pipe, small branch has larger flow resistance, in order to remedy the flow resistance, the gas dynamic head decreases, thereby causing the Bernoulli effect weaker; the onset of liquid entrainment requires larger V_3g.

Introduction

The T-junction has been broadly applied in the industry, and it is also critical to the nuclear industry. Two examples of this technology are the inlet piping of the Fourth Stage Automatic Depressurization System (ADS-4) of the AP1000 (Schulz, 2006) and the header-feeder system of CANDU (Kowalski and Hanna, 1989). On the whole, the T-junction refers to a major horizontal pipe with an inclined branch pipe. The liquid entrainment is that liquid phase acts as the discontinuous phase, while gas phase serves as the continuous phase; liquid phase can be entrained into the branch pipe by the gas phase (Zuber, 1980). In 1980, Zuber (Zuber, 1980) published a technical report on a small break water loss accident, suggesting that in the occurrence of the reactor LOCA accident, liquid entrainment is more likely to occur; due to the effect of gravity, the gas-liquid two-phase flows in the major horizontal pipe exhibits stratified flow. In the presence of the liquid entrainment, it is more likely to cause the nuclear reactor meltdown. The more liquid phase is entrained, the less coolant will be left in the core (Wang et al., 2011). Accordingly, the study on liquid entrainment is critical to engineering.

Liquid phase entrainment reflects the Bernoulli effect. When there exists a pressure difference between the gas phase in the branch pipe and in the main pipe, then, the liquid phase overcomes gravity by the action of the gas phase pressure difference (Smoglie and Reimann, 1986; Smoglie et al., 1987) and is carried out of the branch pipe.

The study on liquid phase entrainment complies with the onset of liquid entrainment. Thus, the study on onset point of liquid entrainment appears to be essential. Numerous scholars have long conducted a lot of studies on the liquid entrainment onset phenomenon, they have made several achievements. Different scholars have conducted a series of studies on the onset, there is exhibiting two parts, one is different branch pipe sizes and another one is different branch pipe angles.

In the study on onset, the size of branch pipe is defined below. On the whole, a branch pipe with the diameter to main pipe diameter ratio <0.2 is defined as a small branch pipe, while the ratio over or =0.2 is defined as a large branch pipe (Meng, 2015). Moreover, branch pipe angle refers to the angle between the branch pipe and the horizontal direction (Lee et al., 2007).

The studied conducted by Yonomoto and Tasaka (1991) and Lee et al. (2007) suggested that the entrainment onset phenomenon is associated with the vortex of the branch pipe entrance. Lee et al. (2007) and Lee et al. (2006) analyzed the onset phenomenon of the liquid entrainment of small branch pipes (the branch pipe diameter d: 16 mm and 24.8 mm, the horizontal main pipe diameter D: 184 mm). Besides, Lee et al. obtained the law of small branch pipes with different angles (the angle θ: 30°, 60°, 90°). The study by Lee et al. suggested that onset of liquid entrainment is primarily correlated with the gas phase, Froude number and the dimensionless air chamber height h_b/d. Besides, the air chamber height h_b of onset point rises with the increase in gas phase Froude number. Many other scholars have built some mathematical models that have been successfully applied for various analysis programs (e.g., RELAP5 Ransom et al., 2001 and CATHARE Maciaszek and Micaelli, 1990). However, Bartley et al. (2008) studied the entrainment process of the inclined branch pipe on the flat wall surface; he found that the onset point of the liquid phase entrainment was independent of the inclination angle. Wang et al. (2011) and Smoglie et al. (1987) assessed the entrainment onset of small branch pipes with horizontal, vertical upward and vertical downward directions by ignoring the viscosity and surface tension of the fluid. Furthermore, Cho et al. (2004), Cho and Jeun (2004), Cho and Jeun (2007), and Welter et al. (2004) also made outstanding contributions to the study on the onset of liquid entrainment.

Lu et al. (2018) have conducted a study on large branch pipe (D = 80 mm, d = 56 mm) with different angles. In the research conducted by Lu et al., the entrainment onset correlation was developed. They demonstrated that the gas phase Fr at the onset of liquid entrainment decreases with an increase in the branch angle θ (Lu et al., 2018).

There are considerable studies on the onset of liquid entrainment, whereas most of the studies are about small branch pipe. Many researchers (Welter et al., 2004; Meng et al., 2014a,b) found that the onset entrainment of small branch pipes is different from large branch pipes, whereas the study on large branch pipes remains rare. Also, fewer studies have been conducted on the effect of size and angle on the onset of liquid entrainment, but branch pipes of different sizes and different angles are ubiquitous in engineering. Accordingly, it is necessary to study large branch pipes and the effect of size and angle on the onset of liquid entrainment.

Method

Experimental Content

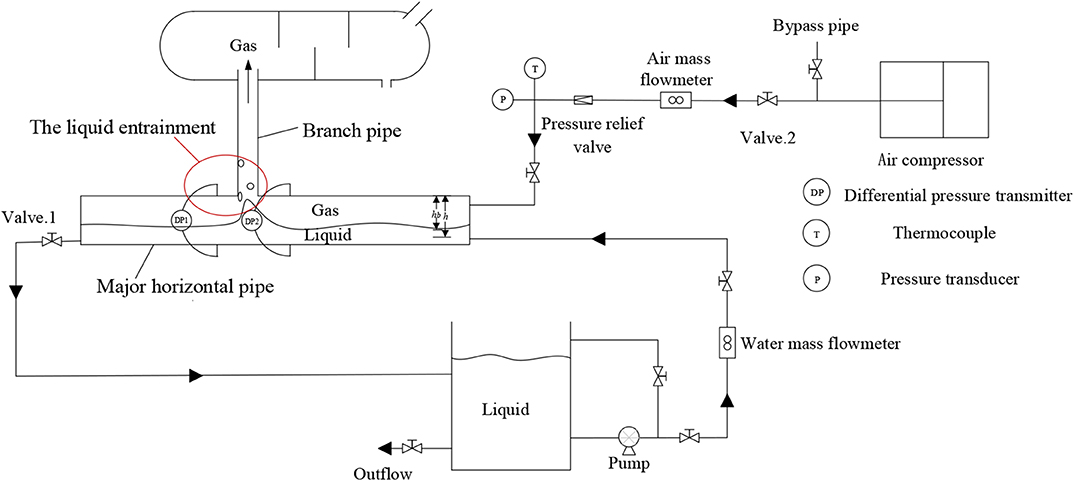
As shown in Figure 1, when gas-liquid two-phase flows in the pipeline, the distance between the interface of the gas-liquid two-phase and the entrance center of branch pipe refers to h. Under the regulated liquid level and gas flow in the major horizontal pipe, when the liquid level and the gas flow rate reach the certain value, the gas phase begins to carry the liquid phase into the branch pipe, at which time h is equated with a critical value h_b, and the h_b denotes the height of the onset of entrainment. If the liquid level continues to be elevated, h will decrease, and the amount of liquid phase carried by the gas phase will increase. The test section used throughout this study is a T-junction with a main pipe inner diameter of 80 mm and a branch pipe inner diameter of 31 mm. The total length of the test bench is 2,570 mm, of which the upstream is 1,730 mm and the downstream is 840 mm. In the experimental pipeline, the working medium of the gas phase is air, and liquid working medium is water. For stratified flow inside the major horizontal pipe, the means of visualization were combined with quantitative and qualitative methods to analyze the liquid entrainment of different branch pipe (d/D = 0.3875) angles.

FIGURE 1

Figure 1. Schematic diagram of the experimental facility and the liquid entrainment of T-junction.

The study on this experiment is about that onset entrainment of large branch pipe and the effect of branch angle and branch pipe size on the onset of liquid entrainment. The study on the onset point of liquid entrainment involves: When the onset entrainment occurs at different angles, analyzing the flow condition and corresponding parameters of two-phase working medium, and ascertaining the effects of various factors (air chamber height, gas velocity, branch pipe angle, etc.) on the onset point of liquid entrainment according to the experimental data; compared with previous study on the onset point of liquid entrainment exhibiting different branch pipe sizes to analyze the effect of different branch pipe sizes on the onset point of liquid entrainment with certain parameters.

Experimental Facility

The schematic diagram of the experimental facility used in this study is illustrated in Figure 1. The experimental facility primarily consists of three sub-systems: (1) water supply system, (2) gas supply system, and (3) Experimental section.

The water supply system: the water supply system consists of a centrifugal pump with a maximum flow rate of 4 m³/h and turbine flowmeter (Model: LWGY-15C, Shanghai Automation Instrumentation Co., Ltd., China, Accuracy: 1.0%) with a measurement range of 0–5 m³/h. The water flowed into the T-junction experimental section via a 40 mm diameter stainless steel pipeline. The gas supply system: the gas supply system consists of a roots blower. A vortex flowmeter (Model: Prowirl200, Endress+Hauser AG, Switzerland, Accuracy: 0.5%) exhibits a measurement range of 0–200 kg/h. The gas was transported into the T-junction test section via a 40 mm diameter stainless steel pipeline. The experimental section: the length of horizontal upstream pipe is 1,730 mm, the length of horizontal downstream pipe is 840 mm, and the length of branch pipe reaches 700 mm. The T-junction experimental section took polymethyl methacrylate (PMMA) acrylic plastic as the material to more effectively observe the onset point of liquid entrainment and analysis of the onset point of entrainment mechanism. Other experimental facilities: the pressure difference transmitter (Accuracy: 0.05%) with a measurement range of 0–0.17 kPa is used to measure the water level in the major horizontal pipe. The temperature was measured by K-Thermocouple (Accuracy: 0.5°C) with a measurement range of 0–350°C. The entrance of the experimental section was provided with a partition board to ensure that the gas-liquid two-phase flow in the pipeline is stratified. During the experiment, the water level in the major horizontal pipe was regulated by adjusting the valve at downstream of the experiment section.

In this study, the thermocouple was adopted to measure the gas temperature and get the density of the gas based on the gas temperature. The pressure difference between the bottom of the main pipe and the two phases interface was measured with a pressure difference sensor. Based on this pressure difference, the liquid phase height of the pipeline was obtained, and then the air chamber height was calculated. A vortex flowmeter was adopted to measure the gas phase flow. For the analysis of uncertainty, the following formula was adopted (Liu, 2000; Hu, 2002; Liang et al., 2005; Luo, 2007; Ni, 2009):

$\begin{array}{ll}{U}_B=\frac{{\Delta }_{ins}}{C}& (1)\end{array}$

Where Δ_ins is the measurement error, C = $\sqrt{3}$. Δ_ins includes both Δ_mea and Δ_NI, Δ_mea is the instrumentation measurement error, Δ_NI is the error in NI acquisition systems. After calculation, three types of uncertainty were obtained (gas temperature 0.3°C, pressure difference 0.07 Pa, gas flow 0.6 m³/h). The primary analysis parameter in the experiment is the Froude number, the formula for Froude number is expressed as:

$\begin{array}{ll}F{r}_g=\frac{V_{3g}}{\sqrt{gd}}& (2)\end{array}$

Where V_3g(the gas phase velocity at the branch pipe entrance) denotes the gas flow. Thus, the relative uncertainty of the Froude number is 0.015.

The experimental process:

(1). Opening the pump and blower to make the gas-liquid two-phase fluid enter the experimental section.

(2). Regulating the valve1 to make the water level in the major horizontal pipe reaches the level at which the onset of liquid entrainment can occur.

(3). Recording the experimental data (the water level in major horizontal pipe, the gas flow) then.

(4). Keeping the liquid flow constant, altering the gas flow by regulating the valve2 and repeating the experiment step (2)-(3).

(5). Turning off the pump and blower when sufficient experimental data were obtained.

(6). Changing the branch angle, repeating the experiment step (1)-(5).

Data processing:

Key parameters of existing studies about the onset point of liquid entrainment were almost the same (θ: the branch pipe angle, h_b: the air chamber height of liquid entrainment onset, d: the inner diameter of branch pipe, V: the gas flow rate, etc.). Accordingly, the experimental data were also processed here according to these parameters.

During the experiment, the effect of branch angle on onset entrainment was found correlated with the water level and the balance of gravity and inertial forces. The Fr denotes a dimensionless number that represents the ratio of inertial force to gravity. Besides, the air chamber height h_b can represent the water level. Thus, the experimental parameters used in the research regarding the effect of branch angle on the onset point of liquid entrainment are Fr_g and the dimensionless air chamber height h_b/d of the branch pipe. Moreover, the effect of branch size on onset entrainment was found correlated with the water level and the gas phase velocity. The experimental parameters in the research regarding the effect of branch size on the onset point of liquid entrainment used are the gas phase velocity V_3g at the branch pipe entrance and the air chamber height h_b.

Results

Based on the study of Lee et al. (2007) and Lu et al. (2018), we obtained the experimental data of other pipe sizes. As shown in Table 1 of the Appendix, we presented our experimental data and the data of other pipe sizes. Our analysis is based on these data.

The Effect of Branch Angle

We analyze the effect of branch angle on the onset of liquid phase entrainment by drawing upon the comparison of the results of Lee et al. (2007) and Lu et al. (2018). As shown in Figure 2C, given the experimental data acquired, Fr_g (ρ_g/Δρ)^0.5 with h_b/d relationship curves were plotted in this study. As showed in the experimental data: at constant θ value, the air chamber height h_b of the onset of liquid entrainment increases with Fr_g increase; under the identical air chamber height, the onset of liquid entrainment requires larger Fr_g when the angle of the branch decreases in the horizontal direction.

FIGURE 2

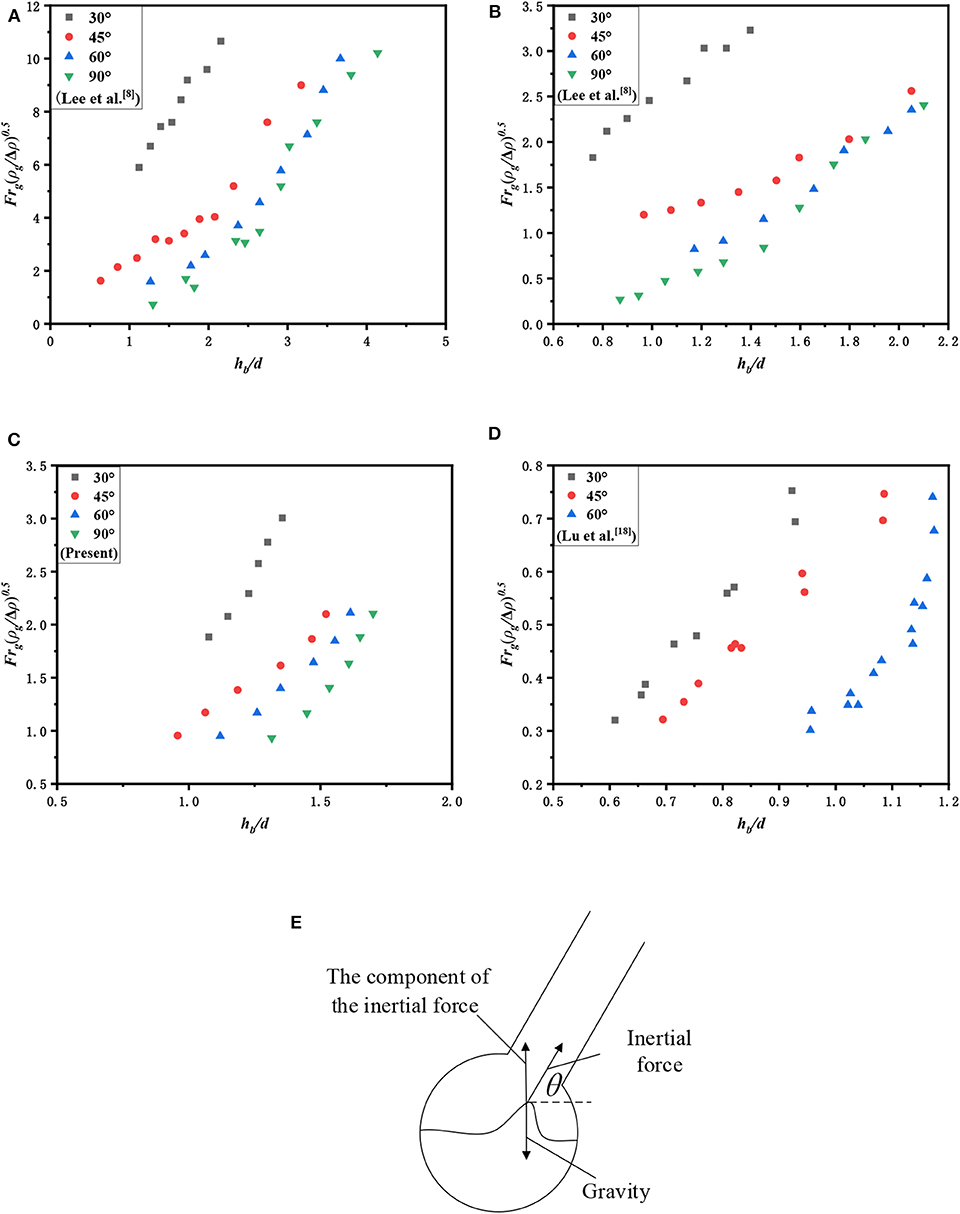
Figure 2. Comparison of entrainment onset data at different branch angles (Lee et al., 2007; Lu et al., 2018) (A) d = 16 mm, (B) d = 24.8 mm, (C) d = 31 mm, and (D) d = 56 mm (E) diagram of force balance.

As shown in Figures 2A,B,D, there are experimental data to curves of the other three branches. By comparing the experimental data, the onset point law of liquid entrainment of all branch sizes with the variation of angle is consistent. At constant θ, the Bernoulli effect increases with Fr_g increase, and therefore the gas phase exerts a greater inertial force on the liquid phase in the presence of the onset. Besides, the water level requirement in the main pipe will be reduced, accordingly, the air chamber height h_b of the onset of liquid entrainment increases with Fr_g increase.

As shown in Figure 2E, under the identical water level, the component of the inertial force in vertical direction will be smaller with the same Fr_g when the angle of the branch decreases. According to the balance of forces, to achieve the presence of the onset of liquid entrainment, a greater inertial force is required to overcome gravity; thus, it requires larger Fr_g. Lastly, the result presents that the h_b of the onset increases with Fr_g increase.

The Effect of Branch Pipe Size

As shown in Figures 3A–D, respectively, under the fixed angle, the relationship curves of the gas phase velocity V_3g with the air chamber height h_b were plotted. The data indicate the laws as follows: the air chamber height h_bat the onset of liquid entrainment increases with the increase in gas velocity V_3g; at the identical air chamber height, the smaller the branch pipe diameter, the greater the gas phase velocity will be generally required for the onset. The explanation for the law that h_b rises with the increase in V_3g has been stated in the previous section and will not be repeated here. Under the identical air chamber height, the gas phase velocity at the onset of liquid entrainment increases with the decrease in branch pipe diameter, the explanation for which are as follows:

FIGURE 3

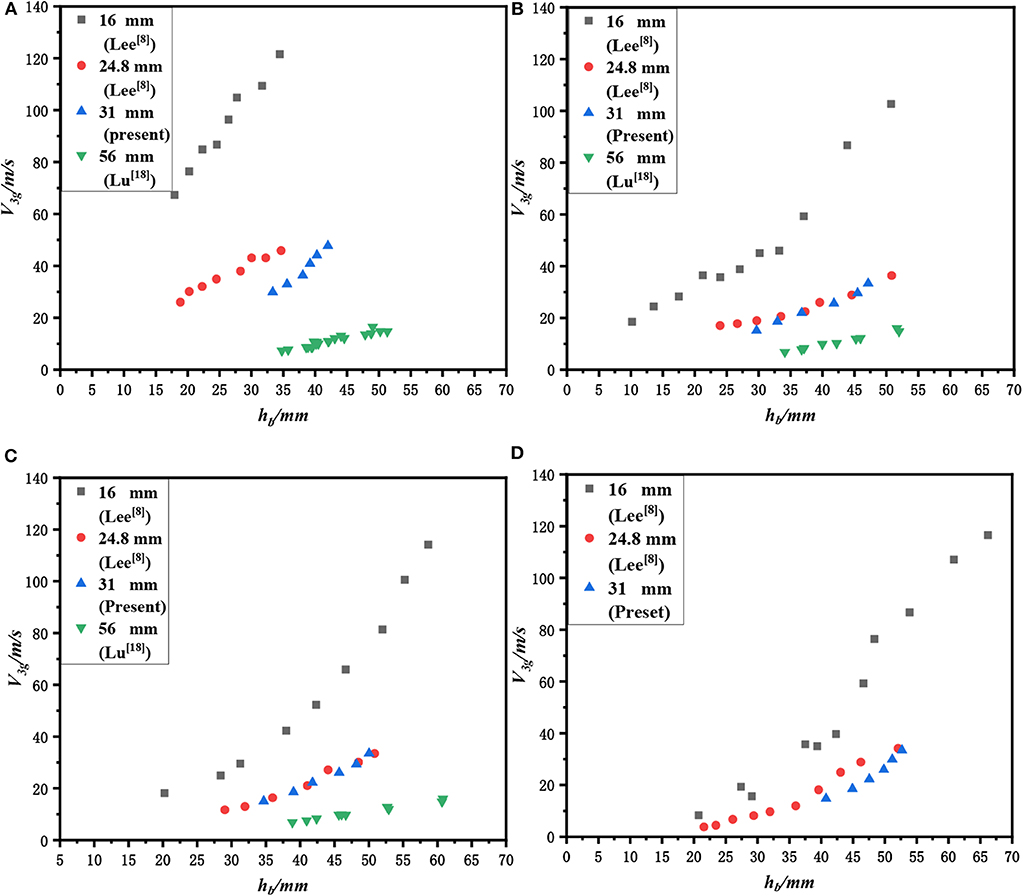
Figure 3. Comparison of entrainment onset data at different branch sizes (Lee et al., 2007; Lu et al., 2018) (A) Branch angle: 30°, (B) Branch angle: 45°, (C) Branch angle: 60°, and (D) Branch angle: 90°.

In accordance with fluid mechanics, the flow resistance of a pipe is inversely proportional to the diameter of the pipe; accordingly, the smaller the pipe diameter, the greater the flow resistance will be (Kong, 1992). Moreover, the force exploited to balance the flow resistance is exerted by the dynamic head of the gas. When the flow resistance of a fluid under the identical entrance conditions in the pipe is greater, the dynamic head loss of the gas will be comparatively larger, the Bernoulli's equation is expressed as

$\begin{array}{ll}{P}_1+\rho g{h}_1+\frac{\rho {v_1}^2}{2}=P_2+\rho g{h}_2+\frac{\rho {v_2}^2}{2}\text{=}C& (3)\end{array}$

where P denotes the fluid static pressure, ρ is the fluid density, v is the fluid velocity and $\frac{\rho v^2}{2}$ is the dynamic pressure, and h is the fluid location. In this study, h exerts almost no effect; thus, the Bernoulli's equation is expressed as:

$\begin{array}{ll}{P}_1+\frac{\rho {v_1}^2}{2}=P_2+\frac{\rho {v_2}^2}{2}=C& (4)\end{array}$

The Bernoulli's equation reveals that when the smaller the dynamic pressure, the larger the static pressure will be. In this study, under the same branch pipe entrance air velocity, the flow resistance of the gas-phase fluid varies with branch diameter, the diameter of is 16 mm leads to the maximum flow resistance, and the diameter of 56 mm leads to the minimum flow resistance. According to the mentioned principle, under the identical air chamber height and the identical entrance air velocity, when the branch pipe is smaller, the fluid resistance will be larger, the loss of dynamic pressure will rise, the static pressure P will increase; as a result, the pressure difference between the gas-liquid interface and the branch pipe will decrease. Accordingly, the liquid entrainment onset is difficult to occur, and the onset point of liquid entrainment requires higher gas phase velocity V_3g.

Conclusion

In this study, the mechanism of onset was observed by a visualized experimental facility.

The effect of branch angle on the law of onset is studied in this paper. This study found that the onset point law of entrainment with the angle change is consistent. With the decrease in the angle between the branch pipe and the horizontal direction, the onset requires larger Fr_g under the identical h_b. The component of the inertial force in the vertical direction will be smaller with the same Fr_g when the angle of the branch becomes smaller, according to the balance of forces, to make the onset of liquid entrainment occur there must have a greater Fr_g.

Under θ as a constant value, the study regarding the effect of the branch pipe size on the onset of liquid entrainment reported that the onset of smaller branch pipe requires larger V_3g with the identical air chamber height. Since the flow resistance of different branches is different, the smaller branch has greater flow resistance, and the gas dynamic head helps remedy the flow resistance, thereby causing the Bernoulli effect weaker; subsequently, the onset of liquid entrainment requires larger V_3g.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

XL participated in the experimental process, and he processed and analyzed the experimental data to sum up the law. GS sorted out the material and provided some useful opinions on the experimental process and data processing. PL, JG, and NG helped to build the experimental facility and carried out the experiment. ZM guided the whole process of the research and provided suggestions for experiments and data processing.

Funding

The work was financed by a grant from the National Natural Science Foundation of China (No. 11605032).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2020.00095/full#supplementary-material

References

Bartley, J. T., Soliman, H. M., and Sims, G. E. (2008). Experimental investigation of the onsets of gas and liquid entrainment from a small branch mounted on an inclined wall. Int. J. Multiph. Flow 34, 905–915. doi: 10.1016/j.ijmultiphaseflow.2008.04.003

CrossRef Full Text | Google Scholar

Cho, Y. J., Ahn, S.-H., and In-Goo Kim/KINS. (2004). Development of Horizontal Off-Take Model for Application to Reactor Headers of CANDU Type Reactors. Karlsruhe: US Nuclear Regulatory Commission.

Google Scholar

Cho, Y. J., and Jeun, G. D. (2004). Modeling of liquid entrainment and vapor pull-through in header-feeder pipes of CANDU. Nucl. Eng. Technol. 36, 142–152.

Google Scholar

Cho, Y. J., and Jeun, G. D. (2007). A study of the liquid entrainment and vapor pull-through in an angled branch line. Nucl Technol. 158, 366–377. doi: 10.13182/NT07-A3848

CrossRef Full Text | Google Scholar

Hu, X. (2002). On the uncertainty of measurement. Phys. Testing Chem. Analysis B Chem. Analysis 38, 406– 409.

Google Scholar

Kong, L. (1992). Engineering fluid mechanics. Beijing: China Electric Power Press. 84–85. (in Chinese).

Google Scholar

Kowalski, J., and Hanna, B. (1989). “Studies of two-phase flow distribution in a CANDU-type header/feeder system,” in Fourth international topical meeting on nuclear reactor thermal-hydraulics (NURETH-4). Proceedings. Vol. 1. Washington, DC.

Google Scholar

Lee, J. Y., Hwang, G. S., Kim, M., and No, H. C. (2006). Experimental analysis of off-take phenomena at the header–feeder system of CANDU. Ann. Nuclear Energy 33, 1–12. doi: 10.1016/j.anucene.2005.09.002

CrossRef Full Text | Google Scholar

Lee, J. Y., Hwang, S. H., Kim, M., and Park, G. C. (2007). Onset condition of gas and liquid entrainment at an inclined branch pipe on a horizontal header. Nucl. Eng. Design 237, 1046–1054. doi: 10.1016/j.nucengdes.2007.01.002

CrossRef Full Text | Google Scholar

Liang, K., Jiao, T., Li, S., Luo, X., Chen, J., Liu, W., et al. (2005). Measurement uncertainty in analytical data processing. Anal. Testing Technol. 11, 149–152.

Google Scholar

Liu, Z. (2000). Uncertainty and Its Practice. Beijing: Standards Press of China.

Google Scholar

Lu, Z., Meng, Z., Gu, N., Wang, J., Nian, F., Wang, J., et al. (2018). Development of correlations for liquid entrainment through a large-scale inclined branch pipe connected to the main horizontal pipe. Exp. Thermal Fluid Sci. 96, 128–136. doi: 10.1016/j.expthermflusci.2018.03.007

CrossRef Full Text | Google Scholar

Luo, G. (2007). Serches of the uncertainty A and the uncertainty B. Metrol. Measur. Technique 34, 42-43.

Google Scholar

Maciaszek, T., and Micaelli, J. (1990). CATHARE phase separation modeling for small breaks in horizontal pipes with stratified flow. Nuclear Eng. Design 124, 247–256. doi: 10.1016/0029-5493(90)90295-9

CrossRef Full Text | Google Scholar

Meng, Z. (2015). Research of entrainment at t-junction in large advanced PWR (doctoral thesis). Xi'an Jiaotong University, Xian, China.

Google Scholar

Meng, Z., Dong, B., Wang, L., Fu, X., Tian, W., Yang, Y., Su, G., et al. (2014a). Experimental research of liquid entrainment through ADS-4 in AP1000. Ann. Nuclear Energy 72, 428–437. doi: 10.1016/j.anucene.2014.06.012

CrossRef Full Text | Google Scholar

Meng, Z., Dong, B., Wang, L., Fu, X., Tian, W., Yang, Y., Su, G., et al. (2014b). Experimental and theoretical investigation of liquid entrainment through small-scaled ADS-4 in AP1000. Exp. Thermal Fluid Sci. 57, 177–187. doi: 10.1016/j.expthermflusci.2014.04.022

CrossRef Full Text | Google Scholar

Ni, Y. (2009). Evaluation of Practical Measurement Uncertainty. Beijing: China Metrology Press.

Google Scholar

Ransom, V. H. J., Trapp, J., and Wagner, R. (2001). “RELAP5/MOD3. 3 code manual volume IV: models and correlations,” in Information Systems Laboratories (Washington, DC: Division of Systems Research Office of Nuclear Regulatory Research).

Google Scholar

Schulz, T. L. (2006). Westinghouse AP1000 advanced passive plant. Nucl. Eng. Design 236, 1547–1557. doi: 10.1016/j.nucengdes.2006.03.049

CrossRef Full Text | Google Scholar

Smoglie, C., and Reimann, J. (1986). Two-phase flow through small branches in a horizontal pipe with stratified flow. Int. J. Multiphase Flow 12, 609–625. doi: 10.1016/0301-9322(86)90063-7

CrossRef Full Text | Google Scholar

Smoglie, C., Reimann, J., and Müller, U. (1987). Two phase flow through small breaks in a horizontal pipe with stratified flow. Nucl. Eng. Design 99, 117–130. doi: 10.1016/0029-5493(87)90114-2

CrossRef Full Text | Google Scholar

Wang, W., Su, G. H., Qiu, S. Z., and Tian, W. X. (2011). Thermal hydraulic phenomena related to small break LOCAs in AP1000. Progress in Nuclear Energy53, 407–419. doi: 10.1016/j.pnucene.2011.02.007

CrossRef Full Text | Google Scholar

Welter, K., Wu, Q., You, Y., Abel, K., McCreary, D., Bajorek, S. M., et al. (2004). Experimental investigation and theoretical modeling of liquid entrainment in a horizontal tee with a vertical-up branch. Int. J. Mult. Flow 30, 1451–1484. doi: 10.1016/j.ijmultiphaseflow.2004.08.001

CrossRef Full Text | Google Scholar

Yonomoto, T., and Tasaka, K. (1991). Liquid and gas entrainment to a small break hole from a stratified two-phase region. Int. J. Mult. Flow 17, 745–765. doi: 10.1016/0301-9322(91)90054-7

CrossRef Full Text | Google Scholar

Zuber, N. (1980). Problems in Modeling of Small Break LOCA. Technical Report. Washington, DC: Nuclear Regulatory Commission, Div. of Reactor Safety Research. doi: 10.1615/ICHMT.1982.AdvCourHeatTransfNucReactSaf.20

CrossRef Full Text | Google Scholar

Nomenclature