Multi-Factorial Comparison for 24 Distinct Transposition Models for Inclined Surface Solar Irradiance Computation in the State of Palestine: A Case Study

Solar energy industries require an accurate estimation of global solar irradiation particularly on inclined planes. This improves the accuracy of the sizing procedures and optimizes the performance of the solar energy platforms as photovoltaic modules and flat-plate solar collectors. A variety of the transposition models have been developed and reportedly determine incidences of solar irradiance on an inclined surface. However, there is a gap in the literature regarding identifying the most promising transposition model, particularly for the Middle East and North Africa region (MENA). Therefore, this article serves two main objectives. Firstly, it compares comprehensively 24 different transposition models. Several statistical methods are used to quantify the performance of the tilted surface transposition models. Furthermore, the transposition models are compared with real, hourly measured time-series data for several Palestinian cities to identify the promising and most accurate model. The analysis was carried out on three bases: annually, monthly, and a clearness index. The transposition models prove their ability to represent the measured data during the annual and monthly analyses, but they all failed to achieve complacency in the clearness index (K_tK_t) for the clear sky condition (K_t > 0.78). Secondly, the article advises a reliable and accurate transposition model for the area of the MENA for clear sky conditions. The proposed model was tested for the sites under investigation, and it produces significantly better performance than the candidate transposition models.

Introduction

Accurate meteorological data, particularly different components of solar radiation, are mandatory for the different stages of the solar energy project, such as design, sizing, performance evaluation, and implementation phases. However, there is a lack of accurate data for the global solar irradiance on titled surfaces for the MENA region, particularly Palestine state. The transposition models could compensate for the deficiency in the measured solar irradiance data. They estimate the global solar radiation with acceptable accuracy (Ulgen and Hepbasli, 2004; Noorian et al., 2008; Chwieduk, 2009; Besharat et al., 2013; Escobedo et al., 2014; Pandey and Katiyar, 2014; Horváth and Csoknyai, 2015; Tuomiranta and Ghedira, 2015; Michael et al., 2016; Vasar et al., 2016; Moretón et al., 2017; Zhang et al., 2017; Pérez-Burgos et al., 2018). The transposition models in general depend on the measured values of horizontal irradiance (Idh) and the global horizontal irradiance (Ih) to compute the global solar irradiance on a tilted surface. Moreover, they could be used to optimize the tilt and azimuth of Photovoltaic (PV) arrays (Yadav and Chandel, 2013; Camelia and Dorin, 2014; Khatib et al., 2015; Hafez et al., 2017; Raptis et al., 2017), which boost the conversion efficiency of PVs and allows accurate tracking for maximum power point under different operating conditions.

Recently, many transposition models are developed and reported for estimating the hourly global solar radiation on inclined surfaces. These models, as the literature claimed, could predict solar irradiation with sufficient accuracy (Ulgen and Hepbasli, 2004; Noorian et al., 2008; Tuomiranta and Ghedira, 2015; Michael et al., 2016; Moretón et al., 2017; Zhang et al., 2017). However, it is difficult to identify a promising transposition model that could be considered as a reference. The literature shows a major difference between the transposition model output and the measured data. In general, the transposition model, as the literature claimed, is site dependent. This also is obvious in Table A1, where list of recommended models for various countries is shown. Moreover, a discrepancy is quite obvious in the literature. For example, the isotropic model is claimed in Reindl et al. (1990a) to be the least efficient for the hourly diffusion of radiation on tilted surfaces. However, Table A1 in the appendix shows the contrary; here, the isotropic model is adopted as a transposition model for diffuse solar irradiance on inclined plane for different countries.

Solar energy software shows the significance of transposition model accuracy. These simulation programs are developed by commercial and governmental bodies for facilitating the sizing, design, and economical/dynamic evaluation of solar energy projects. Their performance is solely transposition model dependent. Thus, uncertainty and/or inaccurate estimations of solar irradiance result in economic and technical inconveniences. Table A2 tabulates the widely used solar energy software, including the software name, the country, and the transposition model used for developing.

Recently, several databases, such as NASA-SSE¹ SOLARGIS², Meteoblue AG³, HELIOS⁴, European Solar Radiation Atlas (ESRA)⁵, Satel-Light⁶, and Meteonorm⁷, have begun to provide different components of solar irradiances, such as Ih, Idh, and It, freely to users in a simplified manner. However, these databases face the same limitation as solar energy evaluating software; they principally depend on a transposition model. They use different models to compute the sky-diffuse and ground-reflected components of the solar irradiance on inclined surfaces. For example, the HelioClim3 database uses a Muneer model for the sky-diffuse and isotropic model for ground-reflected components⁸. Therefore, it is necessary to identify the most reliable, applicable, and accurate transposition model, which has the objective of determining the most reliable database and solar energy software.

The literature lacks clear comparative studies between the different transportation models. Usually, the literature has a peer-to-peer comparison between a proposed and an existing model. This comparison usually focuses on the ability of the proposed model to fit the measured data for a particular site and specific time span (Yadav and Chandel, 2013; Camelia and Dorin, 2014; Khatib et al., 2015; Hafez et al., 2017; Raptis et al., 2017). Therefore, this article introduces a comprehensive and statistically authenticated comparison between 24 different transposition models to identify the most promising candidate for the MENA region and the Palestine state in particular. The article addresses different problems of the widely used transposition models, such as site dependency and the mechanism for forecasting global solar irradiance on inclined surface. The analysis was carried out on three bases: annually, monthly, and a clearness index. The transposition models are compared with real, hourly measured time-series data over the course of 15 months (June 2017 to August 2018) of the selected cities to identify the promising and most accurate model. The article also advises a simple and robust transportation model for estimating the solar irradiance of inclined surface for clear sky. The MENA region enjoys a clear sky scenario, K_t > 0.78, for a high percentage of daylight hours.

The article has several contributions:

1. Identifying the most accurate models for representing the sky-diffuse solar irradiance under different sky conditions, and Palestinian territories are used as a case study. Consequently, the appropriate solar energy software/database could be easily determined for the study case and the similar geographical sites.

2. Advising a model that achieves better performance in predicating climatic data for clear sky than the reported transposition models. A clear sky scenario, K_t > 0.78, represents a high percentage of daylight hours for the region of the MENA.

Data And Methodology

The research methodology commenced by discussing the studied sites and the data control. This was to confirm the validity and applicability of the obtained results. Then, the transposition models concerned were highlighted. Finally, the methodology section introduces the statistical tools used for evaluating each transposition model individually.

Data and Studied Sites

Six different cities in the Palestine state were used for assessing the feasibility of these models. The location and geographical data for these cities are illustrated in Figure 1 and Table 1. These cities are selected to represent different characteristics of the Palestine State. For example, Rafah and Gaza depict the terrains with relatively long coasts, Hebron and Nablus represent territories surrounded with mountains, and Jericho and Tulkarm represent the terrains with valleys and plains, respectively. The analysis carried out in thiss research is generic. It could therefore act as a valuable reference for similar territories.

FIGURE 1

Figure 1. The cities concerned in the Palestine State (circled green). [source: https://www.dreamstime.com/stock-illustration-state-palestine-political-map-designated-capital-east-jerusalem-claiming-west-bank-gaza-strip-borders-image74413499].

TABLE 1

Table 1. Geographical data for selected cities.

The three components, I_bt, I_dt, and I_rt, of the global inclined solar irradiance It were determined from the measured values of I_t, I_h, and I_dh. Three pyranometers were used for values of I_t, I_h, and I_dh. Idh is usually obtained from an eye shaded pyranometer. This research used the data recorded from 7th June 2017 up to 12th September 2018 for Rafah, Gaza, Hebron, Jericho, Nabuls, and Tulkarm. The data of global, sky-diffuse horizontal, and global for tilt angle 30° south-facing pyranometers were recorded. A specimen of these measurements and calculations are presented graphically in Figure 2 for horizontal and 30° south-facing planes for the four cities during the day of 21st November 2017.

FIGURE 2

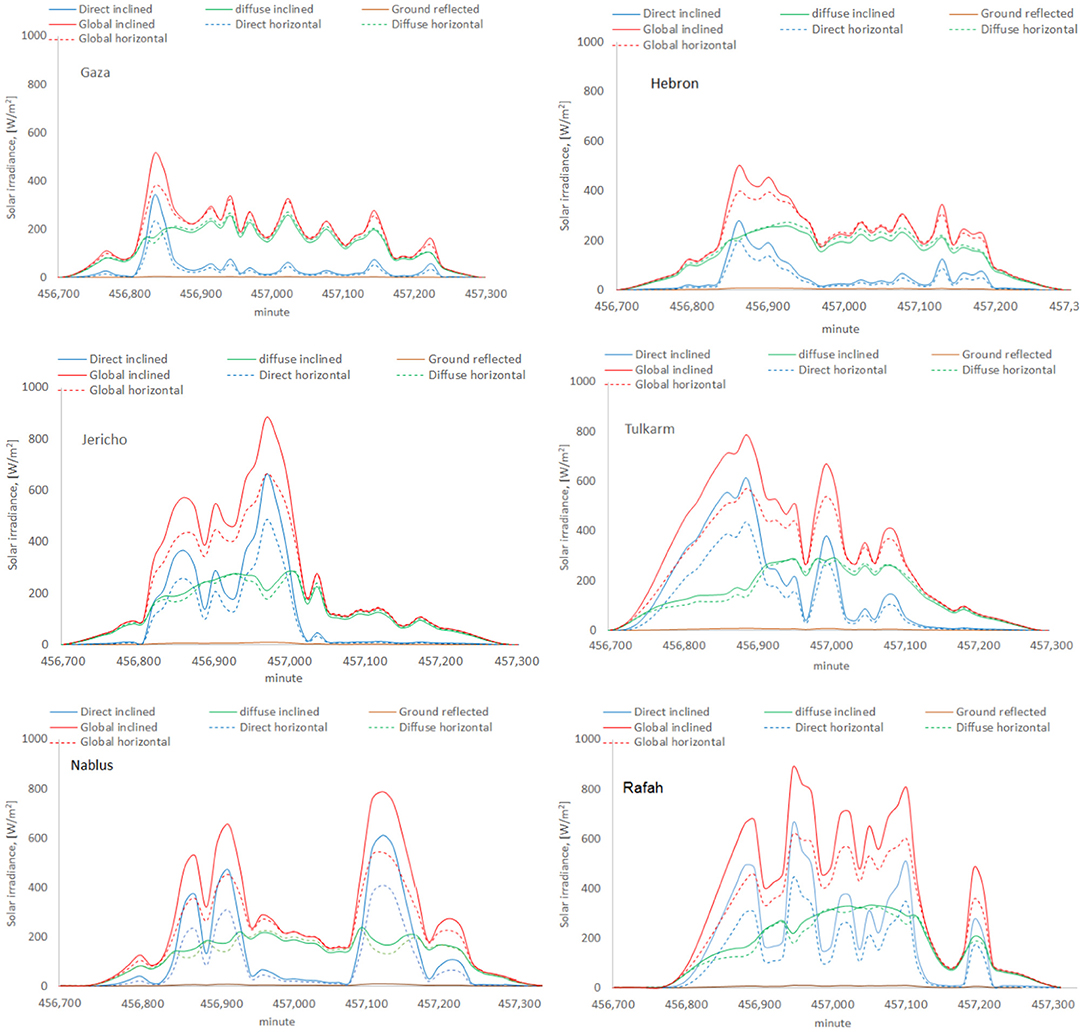
Figure 2. Fifteen-minute time-series measurements and estimated solar radiation components for Gaza, Hebron, Jericho, Tulkarm, Nablus, and Rafah on November 21st, 2017.

Figure 2 shows that the city of Rafah receives more solar irradiance than other cities. Jericho has the highest peak. Each city has distinctive solar irradiance patterns despite the small geographical zone of them (Figure 1). The global inclined irradiance is more than the horizontal one, which is attributed to the reflected component. Figure 2 shows that Gaza and Hebron have high degree of similarity. The data in the article have passed a quality control by many solar energy research centers in Gaza Strip and West Bank Universities (such as An-Najah National University, Polytechnic University, University of Palestine, The Palestinian Energy & Environment Research Center, and many others). The data are also authorized to be used by the Palestinian Central Bureau of Statistics, and they are handled by local researchers.

Transposition Models Under Concern

Transposition models require data of I_h and I_dh to estimate the global solar irradiance on a tilted surface (I_t). I_h is usually measured via a pyranometer. A pyranometer could be used also for measuring I_dh by shading its eye. This is to eliminate the direct beam component by mounting a small shading disk on the pyranometer. I_h has two components, direct beam (I_bh) and sky-diffuse (I_dh), as given by Nassar (2006); Duffie and Beckman (2013); Bilbao et al. (2014); Alsadi and Nassar (2016),

$\begin{array}{ll}{I}_h=I_{bh}+I_{dh}& (1)\end{array}$

The direct normal solar irradiance (I_DN) is given by

$\begin{array}{ll}{I}_{DN}=\frac{I_{bh}}{cos{\theta }_z}& (2)\end{array}$

Transposition models usually convert solar irradiance on a horizontal plane to that on a tilted one. Thus, the global irradiance for a tilted surface, I_t, at a slope angle (β) from the horizontal is given by Nassar (2006)

$\begin{array}{ll}{I}_t=I_{bt}+I_{dt}+I_{rt}& (3)\end{array}$

Equation (3) could be arranged in terms of the available data I_bh and I_dh by Nassar (2006), Duffie and Beckman (2013)

$\begin{array}{ll}{I}_t=I_{bh}{R}_b+I_{dh}{R}_d+I_h{R}_r& (4)\end{array}$

The transposition factor R_b could be given as a function of geometrical parameters of the inclined surface and the position of the sun by Nassar (2006), Duffie and Beckman (2013)

$\begin{array}{ll}{R}_b=max\left(0,\frac{cos{\theta }_i}{cos{\theta }_z}\right)& (5)\end{array}$

where θ_i, θ_z are the solar incidence and zenith angles, respectively. Similarly, R_r is the transposition factor for ground-reflected solar irradiance. It is given by

$\begin{array}{ll}{R}_r=p_g\frac{1-cos\beta }{2}& (6)\end{array}$

ρ_g is the albedo radiation factor, which is alternatively themed for the ground reflectivity. It is generally assumed to equal 0.2 (Moretón et al., 2017). For a ground covered with a layer of water or with plants having glossy leaves, the reflection of such radiation is usually anisotropic. The ground transposition factor R_r is given by Temps and Coulson (1977)

$\begin{array}{ll}{R}_r=p_g|cos\psi |\left(\frac{1-cos\beta }{2}\right)\left[1+{sin}^2\left(\frac{{\theta }_z}{2}\right)\right]& (7)\end{array}$

where ψ is the surface azimuth angle. The diffuse irradiance is due to scattering of the solar radiation by the different components of the atmosphere. Therefore, it has naturally a non-uniform distribution throughout the sky. However, some models consider diffuse irradiance to be uniform and isotropic. Other models try to depict the scattering processing by adding to the isotropic background, the diffuse irradiance coming from the circumsolar region and the horizon band. Therefore, the models for estimating I_dt, and hence the transposition models, could be divided into two groups: isotropic and anisotropic. The anisotropic group is further divided depending on the region and/or the band used in considering I_dt (Gracia and Huld, 2013).

Isotropic Models

The isotropic models assume that the intensity of diffuse sky radiation is uniform over the sky hemisphere. Hence, the diffuse radiation depends only on the transposition factor R_d. Equations (5)–(7) could be used for determining R_b and R_r for these groups (Liu and Jordan, 1963; Temps and Coulson, 1977; Jimenez and Castro, 1986; Koronakis, 1986; Tian et al., 2001; Badescu, 2002; Nassar, 2006; Psiloglou and Kambezidis, 2009; Duffie and Beckman, 2013; Gracia and Huld, 2013; Bilbao et al., 2014; Lave et al., 2015; Alsadi and Nassar, 2016). This group includes several models:

1. Liu and Jordan model, 1963 (Liu and Jordan, 1963),

$\begin{array}{ll}{R}_d=\left(\frac{1+cos\beta }{2}\right)& (8)\end{array}$

2. Korokanis model, 1986 (Koronakis, 1986),

$\begin{array}{ll}{R}_d=\left(\frac{2+cos\beta }{3}\right)& (9)\end{array}$

3. Jimenez & Castro model, 1986 (Jimenez and Castro, 1986),

$\begin{array}{ll}{R}_d=\left(\frac{1+cos\beta }{5}\right)& (10)\end{array}$

The transposition factor R_b of Jimenezvand Castro model is given by (Jimenez and Castro, 1986)

$\begin{array}{ll}{R}_b=0.8\frac{cos{\theta }_i}{cos{\theta }_z}& (11)\end{array}$

4. Tian model, 2001 (Tian et al., 2001),

$\begin{array}{ll}{R}_d=1-\left(\frac{\beta }{180}\right)& (12)\end{array}$

where β is given in degree

5. Badescu model, 2002 (Badescu, 2002),

$\begin{array}{ll}{R}_d=\frac{(3+cos2\beta )}{4}& (13)\end{array}$

Anisotropic Models

The anisotropic models assume the anisotropy of the diffuse sky radiation in the circumsolar region and the horizon in addition to the isotropic diffuse component. This group is relatively more accurate than isotropic models. Therefore, around 19 models of this group are considered in this comparative study. These include:

6. Bugler model, 1977 (Bugler, 1977),

$\begin{array}{ll}{R}_d=\frac{1+cos\beta }{2}+0.05\frac{I_{bh}}{I_d}{R}_b& (14)\end{array}$

7. Temps-Coulson model, 1977 (Temps and Coulson, 1977),

$\begin{array}{ll}{R}_d=\left({cos}^2\frac{\beta }{2}\right)(1+{cos}^2{\theta }_i{sin}^3{\theta }_z)\left(1+{sin}^3\frac{\beta }{2}\right)& (15)\end{array}$

8. Steven and Unsworth model, 1979 (Steven and Unsworth, 1980),

$\begin{array}{ll}{R}_d=0.143\left(sin\beta -\beta cos\beta -\pi {sin}^2\frac{\beta }{2}\right)+{cos}^2\frac{\beta }{2}& (16)\end{array}$

9. Hay model, 1979 (Hay, 1979),

$\begin{array}{ll}{R}_d=F_{Hay}{R}_b(1-F_{Hay})\left(\frac{1+cos\beta }{2}\right)& (17)\end{array}$

where $F_{Hay}=\left(\frac{{\text{I}}_{bh}}{{\text{I}}_{ext}}\right)$ is Hay's sky-clarity factor

10. Klucher model, 1979 (Klucher, 1979),

$\begin{array}{ll}{R}_d=\left({cos}^2\frac{\beta }{2}\right)\left(1+{f_{k}cos}^2{\theta }_i{sin}^3{\theta }_z\right)\left(1+f_k{sin}^3\left(\frac{\beta }{2}\right)\right)& (18)\end{array}$

where $f_k=1-{\left(\frac{I_{dh}}{I_h}\right)}^2$

11. Modified Steven and Unsworth model, 1980 (Steven and Unsworth, 1979),

$\begin{array}{ll}{R}_d=0.51R_b+\frac{1+cos\beta }{2}-\frac{1.74}{1.26\pi }\left[sin\beta -\beta cos\beta -\pi {sin}^2\frac{\beta }{2}\right]& (19)\end{array}$

12. Willmot model, 1982 (Willmot, 1982),

$\begin{array}{ll}{R}_d=\frac{I_{bn}{R}_b}{I_0}+C_{\beta }\left(1+\frac{I_{bn}}{I_{sc}}\right)& (20)\end{array}$

where: $Ibn=\frac{{\text{I}}_{\text{b}}}{cos{\theta }_{\text{z}}}$, $C_{\beta }=1.01150.20293\beta 0.080823{\beta }^2$, β is in radians, and I_sc = 1367W/m²

13. Ma-Iqbal model, 1983 (Ma, 1983),

$\begin{array}{ll}{R}_d=k_t{R}_b(1-k_t)\left(\frac{1+cos\beta }{2}\right)& (21)\end{array}$

where k_t is the clearness index $k_t=\frac{I_h}{I_{ext}}$

14. Skartveit-Olseth model, 1986 (Skartveit and Olseth, 1986),

$\begin{array}{ll}{R}_d=F_{Hay}{R}_b+Zcos\beta +(1-F_{Hay}-Z){cos}^2\left(\frac{\beta }{2}\right)& (22)\end{array}$

where Z = max [(0.3−2F_Hay), 0 ].

Equations (17) and (22) show that the Skartveit-Olseth model is evolved from the Hay model. Therefore, the performances of these models are forecasted to have a high degree of similarity.

15. Gueymard model, 1987 (Gueymard, 1986),

$\begin{array}{ll}{R}_d=(1-N_g)R_{d0}+N_g{R}_{d1}& (23)\end{array}$

where N_g, R_do and R_d1 are given by

$\begin{array}{ll}{N}_g=max\left[min(Y,1),0\right]& (24)\end{array}$

$\begin{array}{ll}Y=\{\begin{array}{ll}6.6667\frac{I_{dh}}{I_h}-1.4167\hfill & if\left(\frac{I_{dh}}{I_h}\right)\le 0.227\hfill \\ 1.2121\frac{I_{dh}}{I_h}-0.1758\hfill & otherwise\hfill \end{array}& (25)\end{array}$

$\begin{array}{l}{R}_{d0}=exp(a_0+a_{1}cos\theta +a_2{cos}^2\theta +a_3{cos}^3\theta )\\ +F(\beta )G(\gamma )& (26)\end{array}$

where coefficients a_i are a function of the solar elevation angle in γ degrees,

$\begin{array}{ll}{a}_0=0.8973.364{\gamma }^{\prime }+3.96{\gamma \prime }^{2}1.909{\gamma \prime }^3& (27)\end{array}$

$\begin{array}{l}{a}_1=4.44812.962{\gamma }^{\prime }+34.601{{\gamma }^{\prime }}^{2}48.784{{\gamma }^{\prime }}^3\\ +27.511{{\gamma }^{\prime }}^4& (28)\end{array}$

$\begin{array}{l}{a}_2=2.77+9.164{\gamma }^{\prime }18.876{\gamma \prime }^2\\ +23.7764{\gamma \prime }^{3}13.041{\gamma \prime }^4& (29)\end{array}$

$\begin{array}{ll}{a}_3=0.3120.217{\gamma }^{\prime }0.805{\gamma \prime }^2+0.318{\gamma \prime }^3& (30)\end{array}$

where γ′ = 0.01γ

$\begin{array}{ll}F(\beta )=\frac{10.2249{sin}^2\beta +0.1231sin2\beta +0.0342sin4\beta }{10.2249}& (31)\end{array}$

$\begin{array}{ll}G(\gamma )=0.4080.323{\gamma }^{\prime }+0.384{\gamma }^{\prime 2}-0.17{\gamma }^{\prime 3}& (32)\end{array}$

$\begin{array}{ll}{R}_{d1}=\frac{1+cos\beta }{2}-\frac{\frac{1}{\pi }(\beta cos\beta -sin\beta )+\left(\frac{1-cos\beta }{2}\right)}{\left(1+\frac{3}{2b}\right)}& (33)\end{array}$

where b = 1.5

16. Modified Bugler model, 1988 (Hay and McKay, 1988),

$\begin{array}{ll}{R}_d=\left(1-0.05\frac{I_{bh}}{I_d}\right)\frac{1+cos\beta }{2}+0.05\frac{I_{bh}}{I_d}{R}_b& (34)\end{array}$

17. Perez model, 1988 (Perez and Scott, 1983; Perez and Stewart, 1983; Perez and Arbogast, 1985; Perez et al., 1986, 1987a,b, 1990a,b),

The Perez model is subjected to continuous revisions. This is to improve its performance capabilities and fit the measured data more accurately (Perez and Scott, 1983; Perez and Stewart, 1983; Perez and Arbogast, 1985; Perez et al., 1986, 1987a,b, 1990a,b). In this research study, two versions of the perez models are investigated: Perez model 1988 and1990. Perez model 1988, is given by

$\begin{array}{ll}{R}_d=F_1\frac{a}{b}+(1-F_1)\left(\frac{1+cos\beta }{2}\right)+F_{1}sin\beta & (35)\end{array}$

where a, b, F₁, and F₂ are given by

$\begin{array}{ll}a=max(0,cos{\theta }_i)& (36)\end{array}$

$\begin{array}{ll}b=max(cos{85}^o,sin\gamma )& (37)\end{array}$

$\begin{array}{ll}{F}_1=F_{11}(\epsilon )+F_{12}(\epsilon \Delta )+F_{13}(\epsilon ){\theta }_z& (38)\end{array}$

$\begin{array}{ll}{F}_2=F_{21}(\epsilon )+F_{22}(\epsilon \Delta )+F_{23}(\epsilon \Delta ){\theta }_z& (39)\end{array}$

where $\epsilon =\frac{\frac{I_h}{I_{dh}}+1.041{\theta }_z^3}{1+1.041{\theta }_z^3}$ and Δ$=M\frac{I_{dh}}{I_{ext}}$, θ_z is in radians, and M is the optical air mass.

Perez published many versions of the F_ij coefficients for different locations. Table A3 tabulates the F_ij coefficients for Perezs model 1988.

18. Perez model, 1990 (Perez and Scott, 1983; Perez and Stewart, 1983; Perez and Arbogast, 1985; Perez et al., 1986, 1987a,b, 1990a,b),

Perez model 1990 reported in the literature (Perez et al., 1987a,b) has the same equations as Perez model 1988, Equation (35)–(39). However, the values of F_ij coefficients, and thus F_ij coefficients, differ from those in Table A3. Table A4 gives the F_ij coefficients for Perezs model 1993.

19. Modified Ma-Iqbal model, 1990 (Kasten, 1966),

$\begin{array}{ll}{R}_d=k_t^{\prime }{R}_b+(1-k_t\prime )\left(\frac{1+cos\beta }{2}\right)& (40)\end{array}$

Where $k_t\prime$ and the optical air mass, M are given, respectively, by

$\begin{array}{ll}{k}_t^{\prime }=\frac{k_t}{1.031exp\left(\frac{-1.4}{0.9+\frac{9.4}{M}}\right)+0.1}& (41)\end{array}$

$\begin{array}{ll}M={\left[cos{\theta }_z+0.15{(93.885-{\theta }_z)}^{-1.253}\right]}^{-1}& (42)\end{array}$

k_t is as given by Equation (21)

20. Muneer model, 1990 (Muneer, 1990, 1997; Muneer et al., 2004),

$\begin{array}{ll}{R}_d=TM(1-F_M)+F_M{R}_b& (43)\end{array}$

$\begin{array}{l}TM=\left(\frac{1+cos\beta }{2}\right)\\ +\frac{2b}{\pi (3+2b)}\left(sin\beta -\beta cos\beta -\pi {sin}^2\left(\frac{\beta }{2}\right)\right)& (44)\end{array}$

F_M is a composite clearness function. For shaded surface or overcast sky conditions F_M = 0 and b = 2.5, while for clear sky and partly cloudy sky conditions F_M = F_Hay and F_Hay could be determined by solving the following quadratic equation

$\begin{array}{ll}{F}_{Hay}^2+0.404F_{Hay}+\left(\frac{0.987b}{\pi (3+2b)}-0.0197\right)=0.0& (45)\end{array}$

21. HDKR model, 1990 (Reindl et al., 1990a,b):

$\begin{array}{ll}{R}_d=F_{Hay}{R}_b+(1-F_{Hay})\left(\frac{1+cos\beta }{2}\right)\left[1+f{sin}^3\left(\frac{\beta }{2}\right)\right]& (46)\end{array}$

where $f=\sqrt{\left(\frac{I_{bh}}{I_h}\right)}$

22. Hay model, 1993 (Hay, 1993):

$\begin{array}{ll}{R}_d=F_{Hay}\prime R_b+\left(1-{F^{\prime }}_{Hay}\right)co{s}^2\left(\frac{\beta }{2}\right)& (47)\end{array}$

Where $F_{Hay}\prime =\frac{I_{bh}}{I_{sc}}$

This late model of Hay 1993 is the modified version of Hay's 1979. However, Hay's factor F_Hay in Equation (47) is normalized to the maximum value of solar irradiance, I_sc.

23. Modified Olmo model, 1999 (Olmo et al., 1999),

$\begin{array}{ll}{R}_d=exp(-k_t({\theta }_i^2-{\theta }_z^2))f_c^{\prime }& (48)\end{array}$

where θ_i and θ_z (in radians) are the incidence and solar zenith angles, respectively, k_t is the hourly clearness index, and the ρ_g is albedo of the underlying surface. The function $f_c\prime$ is given by

$\begin{array}{ll}{f}_c\prime =\{\begin{array}{ll}1-{\rho }_{g}co{s}^3\frac{{\theta }_i}{2}\hfill & if0\le k_t\le 0.35\hfill \\ 1-{\rho }_{g}sin\frac{{\theta }_i}{2}\hfill & if0.35\le k_t\le 0.65\hfill \\ 1\hfill & otherwise\hfill \end{array}& (49)\end{array}$

24. CIBSE model, 2008 (CIBSE, 2008),

This is a modification of Klucher model, where the diffuse horizontal radiation was corrected:

$\begin{array}{ll}{I}^{\prime }{}_{dh}=I_{dh}x{f}_{\beta }\left(1-k_b\right)+k_b{R}_b& (50)\end{array}$

where k_b and f_β are given by

$\begin{array}{ll}{k}_b=\frac{I_{bh}}{{ϵ}_j{I}_{ext}}& (51)\end{array}$

$\begin{array}{l}{f}_{\beta }=[co{s}^2\frac{\beta }{2}+\left\{\frac{2c}{\pi \left(3+2c\right)}\right\}x\left\{sin\beta -\frac{\text{πβ}}{180}\right\}cos\beta \\ -\pi si{n}^2\frac{\beta }{2}]& (52)\end{array}$

ϵ_j is the correction to mean solar distance on day j, and c is a constant. The values for constant c are as follows: Shadow surface: c = 5.73, Sunlit surface under overcast sky: c = 1.68, and Sunlit surface under non-overcast sky: c = −0.62.

Transposition Models Assessment

Four different statistical methods are used to assess the potential of the transposition models. This is to identify the most reliable and accurate model, particularly for the area under concern. RMSE, MBE, PAD, and t-stat are the tools of the comparison. Furthermore, the outputs of the different transposition models are compared with measured values to visualize the fitting ability of each model. RMSE, MBE, PAD, and t-stat are defined by Alsadi and Nassar (2016),

$\begin{array}{ll}RMSE={\left[\frac{1}{n}{\displaystyle \sum _{i=1}^n}{(I_{i,c}-I_{i,m})}^2\right]}^{1/2}& (53)\end{array}$

$\begin{array}{ll}MBE=\frac{1}{n}{\displaystyle \sum _{i=1}^n}(I_{i,c}-I_{i,m})& (54)\end{array}$

$\begin{array}{ll}PAD(\%)=\frac{100}{n}{\displaystyle \sum _{i=1}^n}\frac{|I_{i,c}-I_{i,m}|}{I_{i,c}}& (55)\end{array}$

$\begin{array}{ll}t-stat={\left[\frac{(n-1){MBE}^2}{{RMSE}^2-{MBE}^2}\right]}^{1/2}& (56)\end{array}$

The statistical methods Equations (53)–(56) could provide a logical pattern for comparing the different models. The Equations (53)–(56) indicates that the smaller values of RMSE, PAD, and t-stat the more accurate the transposition models are. The Equations (53)–(56) show that the results of RMSE, PAD, and t-stat are positive, while MBE produce ± values according to the deviation of the estimate from the measured values. The most promising transposition model should have the smallest values for RMSE, MBE, PAD, and t-stat simultaneously. However, they may not agree simultaneously on single transposition model (Khan and Ahmad, 2012). Therefore, the graphical comparison is introduced to show visually the correlation between the measured values and the output of each model.

Results and Discussion

The analysis is carried according to three bases: annual, monthly, and a clearness index. This diversity in the analysis widens the comparison and thus increases the feasibility and reliability of the conducted results.

All Sky Conditions (Annual) Base Analysis

The evaluation was carried out on an hourly basis for almost 1 year's worth of data records. The sky-diffuse solar irradiance on a 30° tilted south-facing surface was determined from measured horizontal data using the 24 models and compared with the semi-measured data for a tilted surface during the same period. Table 2 tabulates the statistical analysis results of the 24 considered transposition models for Hebron city.

TABLE 2

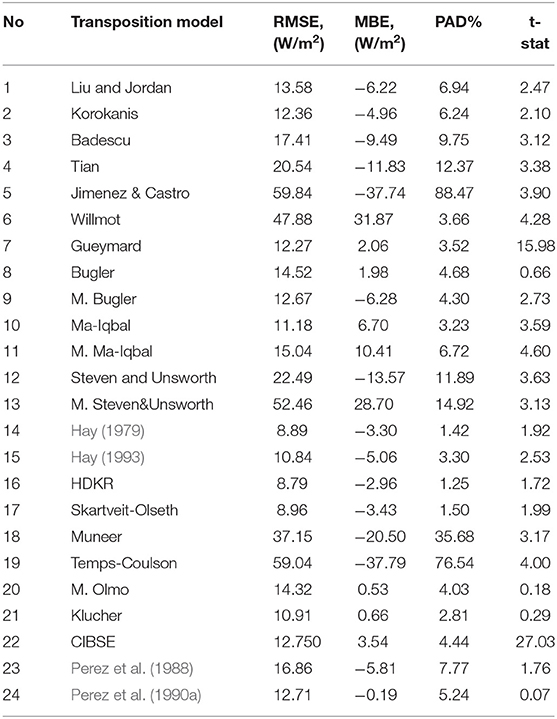
Table 2. Results of the transposition models, for Hebron city for a tilted angle of 30° south facing.

Skartveit-Olseth and HDKR are the most promising candidates according to RMSE. For t-stat, Perez 1990 has the best performance; however, HDKR is a reliable candidate. According to MBE, Perez 1990 is the most accurate model for Herbon city. It is clear from Table 2 that there is a difficulty for a model to achieve the best performance according to the different comparison statistical tools simultaneously. It could be concluded that HDKR model produces the better overall performance than the others for Herbon city. The table mandates the application of an additional comparison tool in order to confirm the feasibility and applicability of a definite transposition model. This tool could be the graphical comparison between the model output and the measured data (Padovan and Del-Col, 2010; Besharat et al., 2013).

In the graphical comparison, Figure 3, the red line represents the locus of the ideal transposition model. Therefore, the quality of a transposition model performance is evaluated via the shape of the distribution of blue dots around the red line. The average of the blue dots should be as close as possible to the red line for a reliable transposition model. Figure 3 shows that the majority of transposition model could produce reasonable accuracy in predicting I_dt for Herbon city. However, HDKR, Skartveit-Olseth, and Hay 1979 are the most promising models. Meanwhile, Jimenez and Castro, Muneer, Temps-Coulson, and M. Steven deviated significantly from the measured values.

FIGURE 3

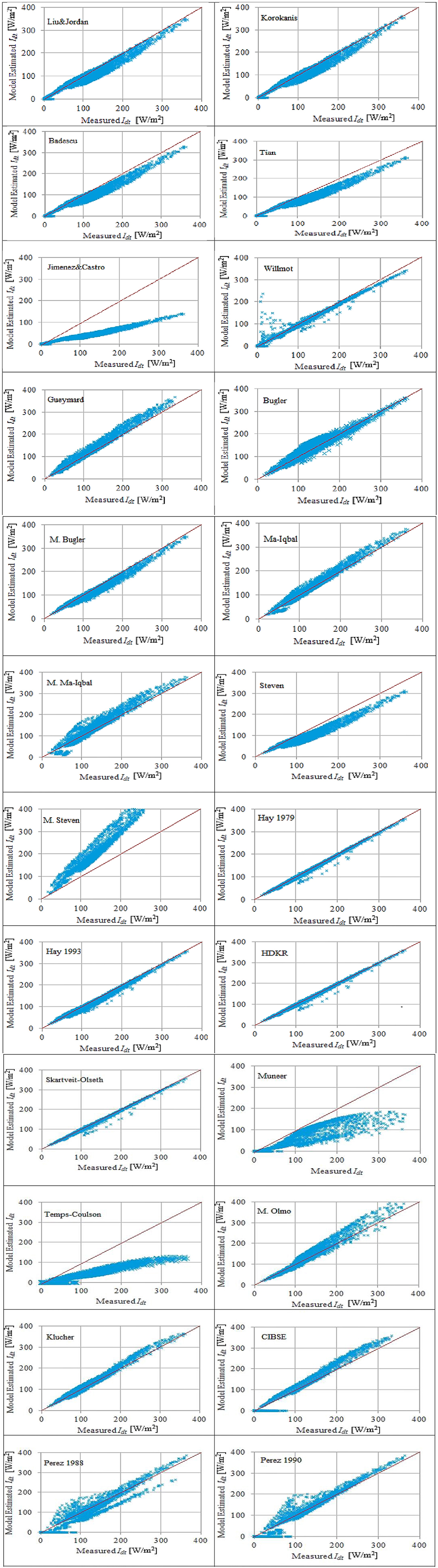
Figure 3. Sky-diffused solar irradiance estimation vs. measures for south-facing 30° tilt angle inclined surface in Herbon city for 24 models during all sky conditions (8,700 points depicted in the graph) (blue dot), y = x relation (red line).

It could be concluded from Table 2 and Figure 3 that HDKR could be considered as the reference transposition model for Herbon city.

Table 2 shows that t-stat is the least efficient comparison tool as it diverges from the remaining tools. Moreover, the graphical comparison, Figure 3, validates the deficiency of t-stat. The authors, when assessing the transposition models in the other cities concerned, found again that t-stat could not identify the promising model. Therefore, it could be concluded that t-stat is not recommended for identifying a transposition model for particular zone. This, however, differs from the conclusion in reference (Togrul, 1989), which recommends adopting t-stat as the standard tool for determining the best transposition model. Also, MBE fails to identify the appropriate transposition model for a specific city/zone. Table 2 and Figure 3 validate this finding. Therefore, RMSE and PAD are only considered in the remaining research as the authenticated comparative tools. The results of RMSE and PAD of different transposition models for different cities under investigations are given in Table 3.

TABLE 3

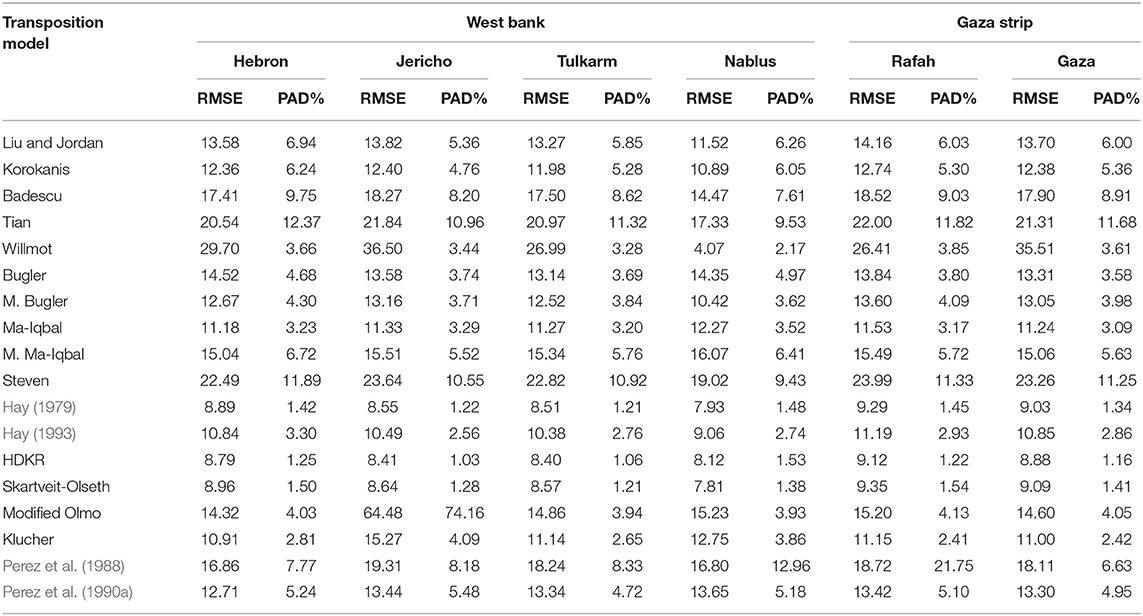
Table 3. RMSe and PAD of transposition models considered cities for a surface tilted 30° south facing.

Table 3 shows that there is coherent between RMSE and PAD. For a transposition model they converge simultaneously to optimal solutions. They could therefore also identify the quality of the transposition model at the same time. The bold numbers in Table 3 show the best solution. HDKR is the most promising solution for 83% of territories under concern. Again, Hay 1979 and Skartveit-Olseth produced comparable performance to HDKR at the majority of the cities under concern. Skartveit-Olseth produced better results than HDKR at Nablus. The preferred transposition models for Gaza, Rafah, Jericho, Tulkram, and Nablus are shown in Figure 4, where a visual comparison between estimated and measured values of I_dt for these cities is shown.

FIGURE 4

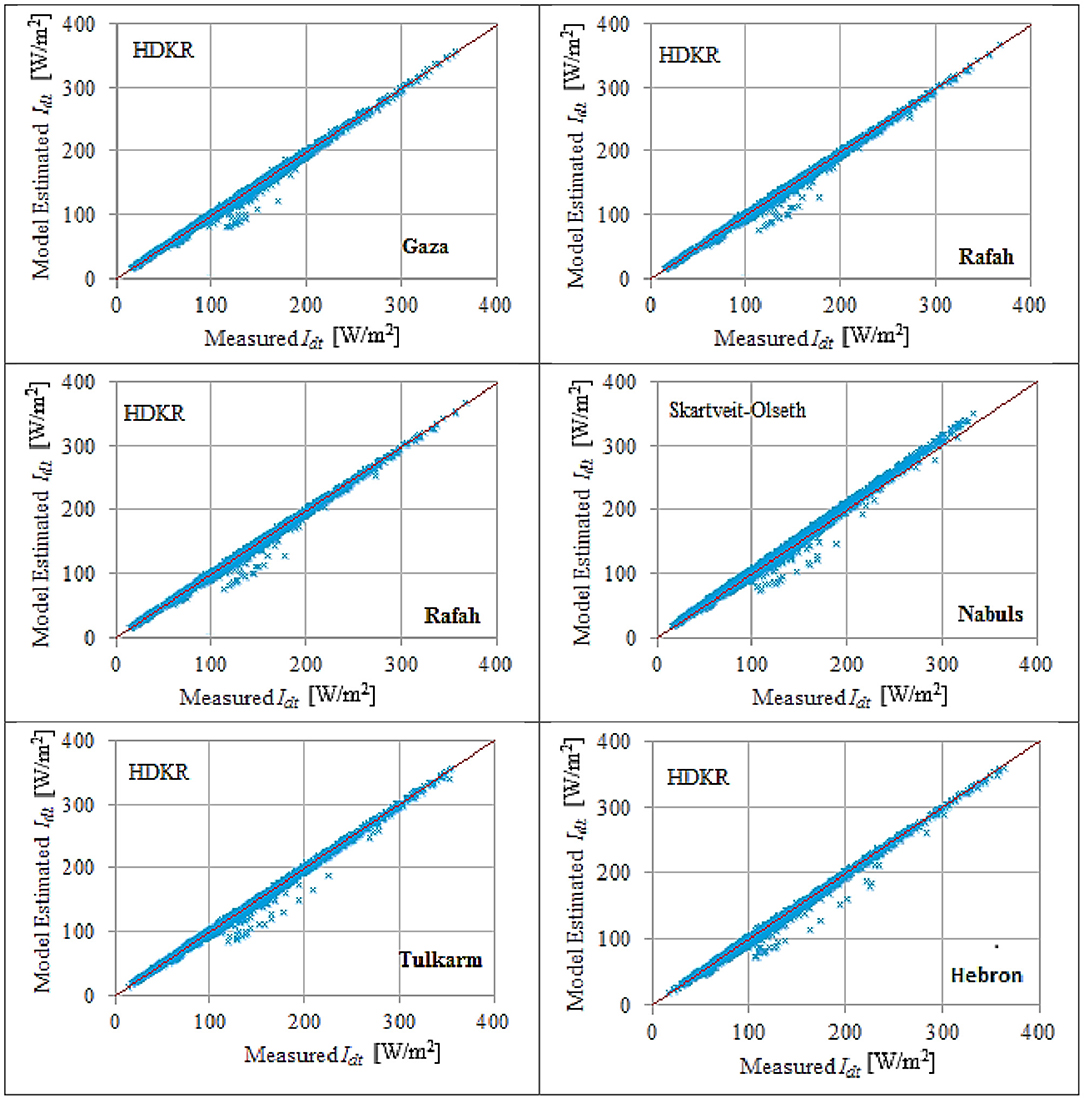
Figure 4. The most accurate diffuse-sky solar irradiance transposition models for the considered cities (8,700 points depicted in the graph) (blue dot), y = x relation (red line).

Figure 4 shows that HDKR model is the most accurate for majority of cities under concern except Nablus where the Stratveit-Olseth model is the most accurate model.

Monthly Based Analysis

The monthly based approach was adopted to improve the accuracy of the obtained results. PAD was the tool used in the monthly based analysis to differentiate between the different transposition models. Again, the analysis was carried out from August 2017 until September 2018 for six different cities in the Palestine State. Table 4 shows the most promising transposition model for the different cities during each month.

TABLE 4

Table 4. The monthly preferred model for each city from August 2017 until September 2018.

Table 4 confirms the annually based analysis, as HDKR is the most promising candidate at different sites except Nablus, where Skartveit-Olseth model is preferred. However, there was some disparity in the behavior of the models over the months. The similarity between Rafah and Gaza is attributed to same climatological conditions for the two cities.

Clearness Index (K_t) Based Analysis

This analysis assesses the ability of the different transposition models in manipulating solar irradiance for different sky conditions. The sky conditions are classified into three scenarios (Burgess et al., 2011): overcast, intermediate, and clear conditions. The clearness index, k_t, usually differentiated between the different conditions the sky. For example, overcast condition clearness index is below 0.3, k_t < 0.3, while for intermediate conditions the clearness index is between 0.3 and 0.78 0.3 ≤ k_t ≤ 0.78, and clearness index is more than 0.78, k_t > 0.78 for clear conditions. The RMSE and PAD were calculated for all cities under different values of k_t. The most accurate models having the lowest value of the RMSE and PAD are given in Table 5.

TABLE 5

Table 5. The best transposition models For different Kt.

Table 5 again shows that there is no single transposition model that could produce an accurate estimation for the global solar irradiance on a titled plane and its component for different sky conditions, even for the same city. HDKR produced a satisfactory performance for intermediate sky condition for all cities except Nablus. However, for overcast and clear conditions, HDKR deviated from the optimal performance. The Perez model is possibly preferred for a clear sky, while Hay is preferable for overcast.

Table 5 shows that all cities except Nablus and Tulkram have the same best models: Hay 1979, HDKR, and Perez 1900 for clear, intermediate, and overcast sky conditions, respectively. This could be attributed to the latitudes of Nablus and Tulkram, as shown in Figure 1 and Table 1. These two cities are relatively far from the remaining cities.

The preferred models, Table 5, are subjected to the graphical comparison with the measured data for Hebron Figure 5 and Nablus Figure 6. Hebron and Nablus represent the two extremes.

FIGURE 5

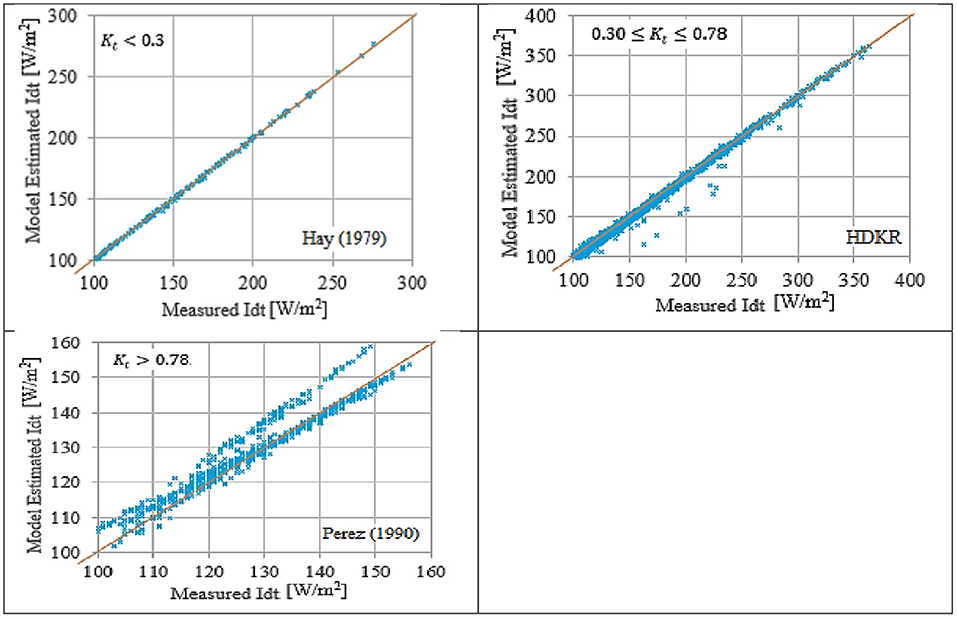
Figure 5. Preferred transposition model for different sky conditions for Hebron city (8,700 points depicted in the graph) (blue dot), y = x relation (red line).

FIGURE 6

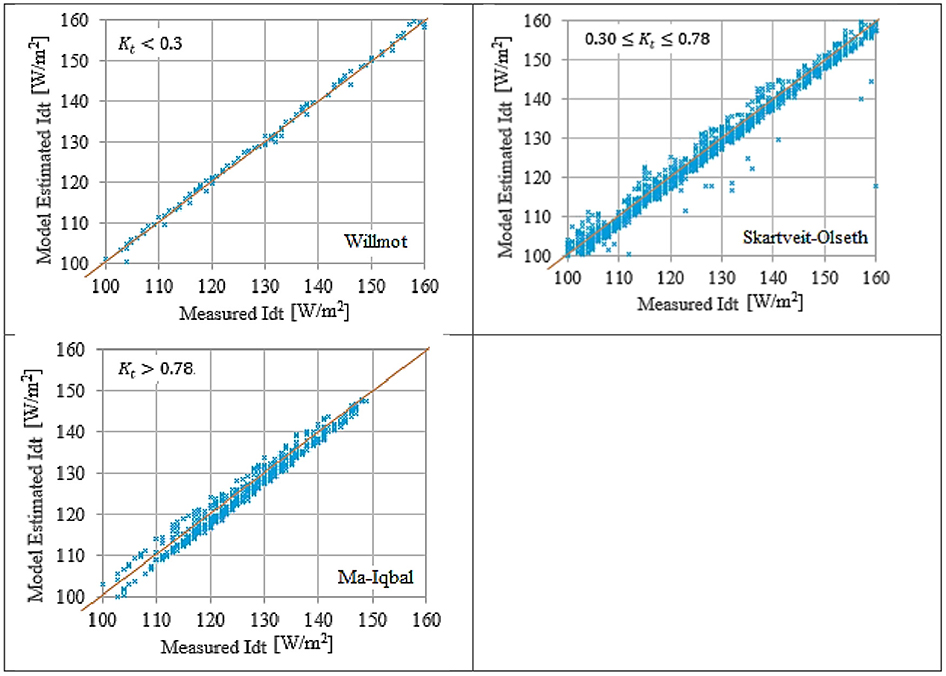
Figure 6. Preferred transposition model for different sky conditions for Nablus city (8,700 points depicted in the graph) (blue dot), y = x relation (red line).

Figures 5, 6 show the preferred models have satisfactory prediction capabilities for the measured data. However, for clear sky, kt > 0.78, the prediction capabilities of Perez 1990 and Ma-Iqbal were not adequate.

Perez 1990 and Ma-Iqbal models were the preferred models for Hebron and Nablus, respectively, for kt > 0.78, Table 5. However, their performances in the graphical comparison were not efficient. Moreover, kt > 0.78 represents the most dominant weather conditions in the area of MENA and Palestine State. Therefore, an adequate and robust transposition model is advised in this research for kt > 0.78.

Advised Transposition Model For Clear Sky, K_T > 0.78

The proposed model is basically a modification of the Muneer model. It is realized by increasing the share of the isotropic term in Equations (41) and (42). Different regression methods are used for developing the proposed model. Then, a refining is carried out to the model via trial and error technique. The proposed model is given by

$\begin{array}{ll}{R}_d=T_{Mp}(1-F_p)+F_p{R}_b& (57)\end{array}$

$\begin{array}{l}{T}_{Mp}=\left\{16.7362+\frac{17.5317}{{\left[1+exp\left(\frac{0.97-\beta }{0.1689}\right)\right]}^{0.008}}\right\}\\ +\frac{2b}{\pi \left(3+2b\right)}\left(sin\beta -\beta cos\beta -\pi {sin}^2\left(\frac{\beta }{2}\right)\right)& (58)\end{array}$

F_b is as mentioned before a composite clearness function. It is equal to F_Hay, which is obtained from Equation (42) and is given in radians.

Table 6 tabulates the performance of the proposed model is compared against the best models for the different cities under investigations for clear sky conditions, k_t > 0.78. RMSE and PAD are used as the comparison tools.

TABLE 6

Table 6. The best and Proposed model For clear sky Kt > 0.78.

Table 6 shows that the proposed model is better at predicating sky-diffused solar irradiance on a titled surface for a clear sky than reported transposition models. There is around 600% reduction in the values of RMSE and PAD. This indicates that the proposed model outputs are similar to the measured values. Table 6 corroborates the reliability and functionality of the proposed model. The feasibility of the proposed model is validated further via a graphical comparison with the measured data, as shown in Figure 7.

FIGURE 7

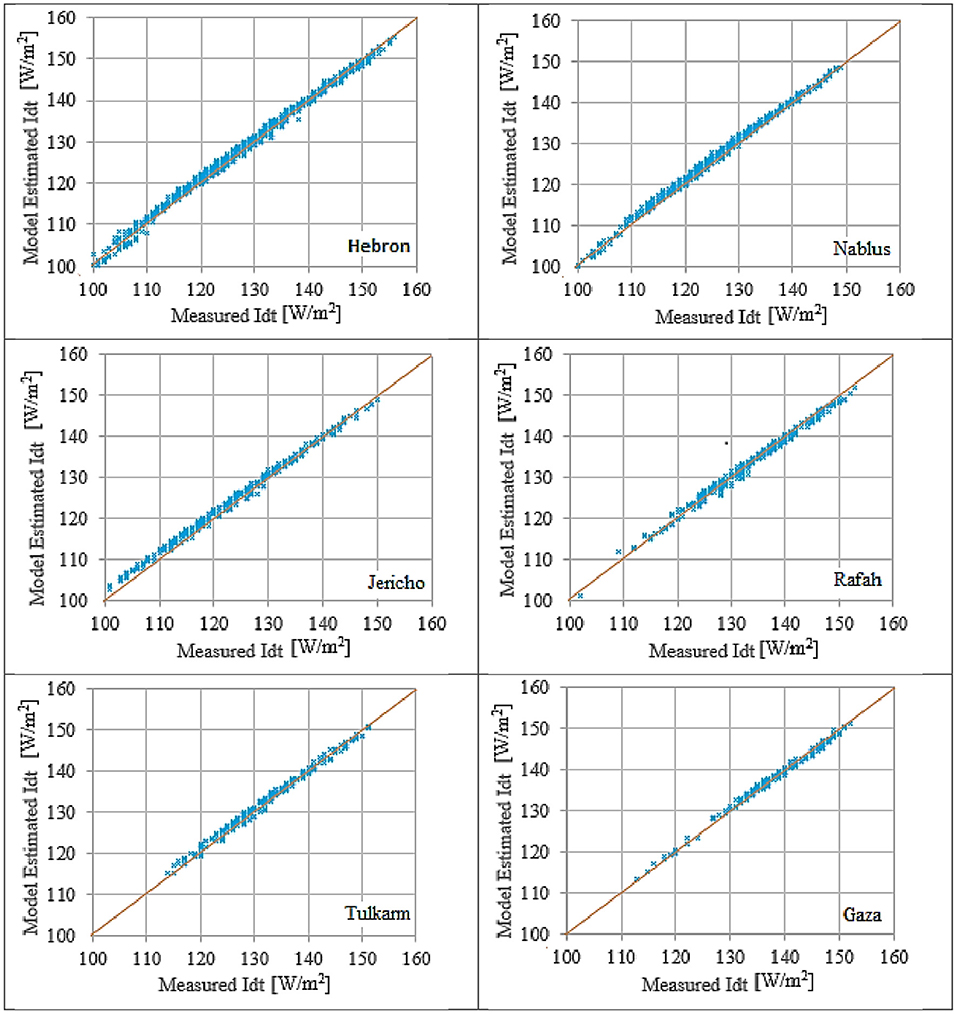
Figure 7. The behavior of the modified Muneer model for clear sky condition K_t > 0.78 (8,700 points depicted in the graph) (blue dot), y = x relation (red line).

Figure 7 shows the applicability of the proposed model in predicting global diffused solar irradiance on a titled surface. It fits the measured data efficiently.

Comparing Figures 5–7 reveals the evaluated quality of the proposed model. It produces much higher quality than even the best models. This model could be considered as a reference for Palestine city under investigations for this 30° south-facing inclined surface. Moreover, the feasibility of the proposed model is examined in other cities for the same climatological conditions. It again produces the best performance for clear sky condition, k_t > 0.78.

Conclusion

The transposition model is a basic element in the solar energy conversion systems. It generates the data of the incidence of different solar irradiance components on inclined surfaces. These data are mandatory for the phases of design, sizing, and implementation of a solar energy project.

Solar energy software is usually developed according to specific transposition model. Moreover, the databases employ transposition models to generate the different solar irradiance data. Therefore, evaluating the performance of the dominant transposition models is elementary in determining the appropriate database and solar software.

This article compared comprehensively 24 different transposition models. The comparison is multi-factorial; it includes statistical and graphical phases. In the statistical part, four different methods—RMSE, MBE, PAD, and t-stat—were used to identify the most promising transposition model. In the graphical, the outputs of the transposition models were compared with the measured data to visualize the accuracy of the different models. Moreover, the comparison was carried out on three bases: annual, monthly, and a clearing index. Climatological data over 15 months (June 2017 to August 2018) of six different cities in the Palestine State were used to identify the potential of these 24 models, thus identifying the most accurate model for this region.

The results reveal a number of conclusions:

1. The Transposition model is site dependent; it is therefore difficult to adopt one model for entire zone/region with diverse climatological conditions. This conclusion complies with the literature (Kasten, 1966; Bugler, 1977; Hay, 1979, 1993; Klucher, 1979; Steven and Unsworth, 1979, 1980; Willmot, 1982; Ma, 1983; Perez and Scott, 1983; Perez and Stewart, 1983; Perez and Arbogast, 1985; Gueymard, 1986; Perez et al., 1986, 1987a,b, 1988, 1990a,b; Skartveit and Olseth, 1986; Hay and McKay, 1988; Muneer, 1990, 1997; Reindl et al., 1990b; Olmo et al., 1999; Tian et al., 2001; Badescu, 2002; Muneer et al., 2004; CIBSE, 2008; Padovan and Del-Col, 2010; Khan and Ahmad, 2012). Moreover, the accuracy of the transposition model varies according to the sky clearness, as the model could produce the best performance for overcast sky, but it suffered from deteriorated performance under clear sky conditions, Table 5.

2. The HDKR model showed a relatively better performance than the others for depicting the sky-diffuse inclined solar irradiance for a majority of Palestinian cities. For Nablus, however, the Skartveit-Olseth model produced a better overall performance than the other candidate models. It produced 3.4% higher than the HDKR model.

3. A majority of the investigated models suffered from inefficient performances for clear sky conditions, k_t >0.78, which represents the majority of climatological conditions in the MENA; a robust, efficient, and reliable transposition model is therefore proposed in this article for k_t >0.78. The proposed model, as shown in Table 6, Figures 5–7, produced a better performance than the best models for different the Palestine terrains under investigation.

4. It is difficult to identify a single software that could be used for the different cities in the entire region as these software are developed according to single transposition model, Table A2 in the appendix. A number of these are recommended for investigating the performance of solar energy projects in the Palestine state, such as HOMER, Energypro, and PVdesignPro. Matlab Simulink is appropriate for clear sky conditions, k_t >0.78.

It is worth mentioning that further investigations are required for assessing the feasibility of the studied transposition models and the proposed model for other tilt and azimuth surface angles.

Data Availability Statement

All datasets generated for this study are included in the article/Supplementary Material.

Author Contributions

YN conceptualized the project and carried out the analysis. AH performed the editing. SA performed the data collection and graphical presentation.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2019.00163/full#supplementary-material

Footnotes

1. ^Satellite Solar Radiation Data. Available online at: http://www.eosweb.larc.nasa.gov/sse/.

2. ^SOLAR GIS. Available online at: http://www.solargis.info/index.html.

3. ^Meteoblue AG - Switzerland. Available online: http://www.meteoblue.com

4. ^HELIOS. Available online: http://www.helios.ies-def.upm.es/.

5. ^ESRA. The European Solar Radiation Atlas. Available online: https://www.scribd.com/document/142793445/The-European-Solar-Radiation-Atlas-Esra-1.

6. ^Global radiation data based on satellite images. Available online: http://www.satellight.com.

7. ^http://www.meteonorm.com/

8. ^http://www.soda-pro.com/web-services/radiation/helioclim-3-archives-for-free/info

References

Alsadi, S., and Nassar, Y. (2016). Correction of the ASHRAE clear-sky model parameters based on solar radiation measurements in the Arabic countries. Int. J. Renew. Energy Technol. Res. 5, 1–16. Available online at: http://ijretr.org (accessed November 02, 2019).

Google Scholar

Badescu (2002). 3D isotropic approximation for solar diffuse irradiance on tilted surfaces. Renew. Energy 26, 221–223. doi: 10.1016/S0960-1481(01)00123-9

CrossRef Full Text | Google Scholar

Besharat, F., Dehghan, A., and Faghih, A. (2013). Empirical models for estimating global solar radiation: a review and case study. Renew. Sustain. Energy Rev. 21, 798–821. doi: 10.1016/j.rser.2012.12.043

CrossRef Full Text | Google Scholar

Bilbao, J., Román, R., and De Miguel, A. (2014). “Measurements and model evaluations of direct normal irradiance in central Spain,” in Conference EuroSun 2014 (Aix-les-Bains). doi: 10.18086/eurosun.2014.08.03

CrossRef Full Text | Google Scholar

Bugler, J. (1977). The determination of hourly insolation on an inclined plane using a diffuse irradiance model based on hourly measured global horizontal insolation. Solar Energy 19, 477–491. doi: 10.1016/0038-092X(77)90103-7

CrossRef Full Text | Google Scholar

Burgess, P., Vahdati, M., Davies, D., and Philip, S. (2011). “Development of A virtual pyranometer for solar energy monitoring,” in TSBE Eng. Conference (Whiteknights: TSBE Centre, University of Reading). Available online at: http://www.reading.ac.uk/tsbe/ (accessed November 02, 2019).

Google Scholar

Camelia, S., and Dorin, S. (2014) Optimum tilt angle for flat plate collectors all over the World – A declination dependence formula comparisons of three solar radiation models. Energy Conv. Manag. 81, 133–143. doi: 10.1016/j.enconman.2014.02.016

CrossRef Full Text | Google Scholar

Chwieduk, A. (2009). Recommendation on modelling of solar energy incident on a building envelope. Renew. Energy 34, 736–741. doi: 10.1016/j.renene.2008.04.005

CrossRef Full Text | Google Scholar

CIBSE (2008). CIBSE Guide J. London: Chartered Institution of Building Services Engineers.

Google Scholar

Duffie, J., and Beckman, W. (2013). Solar Engineering of Thermal Processes, 4th Edn. Hoboken, NJ: John Wiley & Sons, Inc.

Google Scholar

Escobedo, J., Souza, A., and Martins, D. (2014). An assessment of the diffuse radiation models for prediction on hourly global radiation on tilted surface. Nativa 2, 23–31. doi: 10.14583/2318-7670.v02n01a05

CrossRef Full Text | Google Scholar

Gracia, A., and Huld, T. (2013). Performance Comparison of Different Models for the Estimation of Global Irradiance on Inclined Surfaces, Report EUR 26075. Brussels: European Commission; Joint Research Centre; Institute for Energy and Transport.

Gueymard, C. (1986). An anisotropic solar irradiance model for tilted surfaces and its comparison with selected engineering algorithms. Solar Energy 38, 367–386. doi: 10.1016/0038-092X(87)90009-0

CrossRef Full Text | Google Scholar

Hafez, A., Soliman, A., El-Metwally, K., and Ismail, I. (2017). Tilt and azimuth angles in solar energy applications – a review. Renew. Sustain. Energy Rev. 77, 147–168. doi: 10.1016/j.rser.2017.03.131

CrossRef Full Text | Google Scholar

Hay, J. (1979). Study of Shortwave Radiation on Non-horizontal Surfaces, Downs View: Atmospheric Environment Service. Canadian Climate Centre Report.

Google Scholar

Hay, J. (1993). Calculating solar radiation for inclined surfaces: practical approaches. Renew. Energy 3, 373–380. doi: 10.1016/0960-1481(93)90104-O

CrossRef Full Text | Google Scholar

Hay, J., and McKay, D. (1988). Final Report IEA Task IX-Calculation of Solar Irradiances for Inclined Surfaces: Verification of Models Which Use Hourly and Daily Data. Technical Report. International Energy Agency Solar Heating and Cooling Programme.

Horváth, M., and Csoknyai, T. (2015). Evaluation of solar energy calculation methods for 45o inclined, south facing surface. Energy Proc. 78, 465–470. doi: 10.1016/j.egypro.2015.11.700

CrossRef Full Text | Google Scholar

Jimenez, J., and Castro, Y. (1986). National Assembly of Geophysics and Geodesy, Vol. II, 805.

Kasten, F. (1966). A new table and approximate formula for relative optical air mass. Arch. Meteoral. Geophys. Bioklimatal. Series B 14, 206–223. doi: 10.1007/BF02248840

CrossRef Full Text | Google Scholar

Khan, M., and Ahmad, M. (2012). Estimation of global solar radiation using clear sky radiation in Yemen. J Eng. Sci. Technol. Rev. 5, 12–19. doi: 10.25103/jestr.052.03

CrossRef Full Text | Google Scholar

Khatib, T., Mohamed, A., Mahmoud, M., and Sopian, K. (2015). Optimization of the tilt angle of solar panels for Malaysia. Energy Sources 37, 606–613. doi: 10.1080/15567036.2011.588680

CrossRef Full Text | Google Scholar

Klucher, T. (1979). Evaluation of models to predict insolation on tilted surfaces. Solar Energy 23, 111–114. doi: 10.1016/0038-092X(79)90110-5

CrossRef Full Text

Koronakis, P. (1986). On the choice of the angle of tilt for south facing solar collectors in the Athens basin area. Solar Energy 36, 217–225. doi: 10.1016/0038-092X(86)90137-4

CrossRef Full Text | Google Scholar

Lave, M., Hayes, M., Pohl, A., and Hansen, C. (2015). Evaluation of global horizontal irradiance to plane-of-array irradiance models at locations across the united states. IEEE J. Photovolt. 5, 597–606. doi: 10.1109/JPHOTOV.2015.2392938

CrossRef Full Text | Google Scholar

Liu, B., and Jordan, R. (1963). The long-term average performance of flat-plate solar energy collectors. Solar Energy 7, 53–74. doi: 10.1016/0038-092X(63)90006-9

CrossRef Full Text | Google Scholar

Ma, C. (1983). Statistical comparison of models for estimating solar radiation on inclined surfaces. Solar Energy 31, 313–317. doi: 10.1016/0038-092X(83)90019-1

CrossRef Full Text | Google Scholar

Michael, S., Okundamiya, J., Emagbetere, O., and Emmanuel, A. (2016). Evaluation of various global solar radiation models for Nigeria. Int. J. Green Energy 13, 505–512. doi: 10.1080/15435075.2014.968921

CrossRef Full Text | Google Scholar

Moretón, R., Lorenzo, E., Pinto, A., Muñoa, J., and Narvarte, L. (2017). From broadband horizontal to effective inplane irradiation: a review of modelling and derived uncertainty for PV yield prediction. Renew. Sustain. Energy Rev. 78, 886–903. doi: 10.1016/j.rser.2017.05.020

CrossRef Full Text | Google Scholar

Muneer, T. (1990). Solar radiation models for Europe. Build. Serv. Eng. Res. Technol. 11, 153–163. doi: 10.1177/014362449001100405

CrossRef Full Text | Google Scholar

Muneer, T. (1997) Solar Radiation and Daylight Models for the Energy Efficient Design of Buildings. Oxford; Boston, MA: Architectural Press. 197–200.

Muneer, T., Gueymard, C., and Kambezidis, H. (2004). “Hourly slope irradiation and illuminance,” in Solar Radiation and Daylight Models, ed G. M. Alam (Oxford: Butterworth-Heinemann), 143–221. doi: 10.1016/B978-075065974-1/50012-7

CrossRef Full Text

Nassar, Y. (2006). Solar Energy Engineering Active Applications. Libya: Sebha University.

Google Scholar

Noorian, A., Moradi, I., and Kamali, G. (2008). Evaluation of 12 models to estimate hourly diffuse irradiation on inclined surfaces. Renew. Energy 33, 1406–1412. doi: 10.1016/j.renene.2007.06.027

CrossRef Full Text | Google Scholar

Olmo, F., Vida, J., Foyo, I., Castro-Diez, Y., and Alados-Arboledas, L. (1999). Prediction of global irradiance on inclined surfaces from horizontal global irradiance. Energy 24, 689–704. doi: 10.1016/S0360-5442(99)00025-0

CrossRef Full Text | Google Scholar

Padovan, A., and Del-Col, D. (2010). Measurement and modelling of solar irradiance components on horizontal and tilted planes. Solar Energy 84, 2068–2084. doi: 10.1016/j.solener.2010.09.009

CrossRef Full Text | Google Scholar

Pandey, C., and Katiyar, A. (2014). Hourly solar radiation on inclined surfaces. Sust. Energy Technol. Assess. 6, 86–92. doi: 10.1016/j.seta.2014.01.007

CrossRef Full Text | Google Scholar

Perez, R., and Arbogast, C. (1985). “Climatology of an anisotropic diffuse sky radiation model for slopes,” in Proceedings ISES Word Congress (Montreal, QC). doi: 10.1016/B978-0-08-033177-5.50470-1

CrossRef Full Text | Google Scholar

Perez, R., Arbogast, C., Seals, P., and Scott, J. (1986). An anisotropic hourly diffuse radiation model for sloping surfaces: description, performance validation, site dependency evaluation. Solar Energy 36, 487–497. doi: 10.1016/0038-092X(86)90013-7

CrossRef Full Text | Google Scholar

Perez, R., and Scott, J. (1983). “A two-parameter description of the sky hemisphere,” in Proceedings of ISES/AMS Fifth Conference on Atmospheric Radiation, Baltimore, MD (Boston: American Meteorological Society), 322–325.

Google Scholar

Perez, R., Seals, R., Ineichen, P., and Menicucci, D. (1987b). A new simplified version of the Perez diffuse irradiance model for tilted surfaces. Solar Energy 39, 22l−231. doi: 10.1016/S0038-092X(87)80031-2

CrossRef Full Text | Google Scholar

Perez, R., Seals, R., Ineichen, P., Stewart, R., and Michalsky, J. (1990a). Modelling daylight availability and irradiance components from direct and global irradiance. Solar Energy 44, 271–289. doi: 10.1016/0038-092X(90)90055-H

CrossRef Full Text | Google Scholar

Perez, R., Seals, R., and Stewart, R. (1987a). “Modelling irradiance on tilted planes: a simpler version of the Perez model: US-wide climatic/environmental evaluation,” in Advances in Solar Energy Technology ISES World Congress, Ham burg. (New York, NY: Pergamon Press), 3784–3788. doi: 10.1016/B978-0-08-034315-0.50698-4

CrossRef Full Text | Google Scholar

Perez, R., Seals, R., Zelenka, A., and Ineichen, P. (1990b). Climatic evaluation of models that predict hourly direct irradiance from hourly global irradiance: prospects for performance improvements. Solar Energy 44, 99–108. doi: 10.1016/0038-092X(90)90071-J

CrossRef Full Text | Google Scholar

Perez, R., and Stewart, R. (1983). “An anisotropic model for diffuse radiation incident on slopes of different orientations and possible applications to CPCs,” in Proceeding of ASES Minneapolis. (Minneapolis, MN), 883–888.

Google Scholar

Perez, R., Stewart, R., and Guertin, T. (1988). Sandia National Laboratories Contractor Report SAND88-7030 Oct. (1988). The Development and veriFication of the Perez Diffuse Radiation Model. Albuquerque, NM. doi: 10.2172/7024029

CrossRef Full Text | Google Scholar

Pérez-Burgos, A., Díez-Mediavilla, M., Alonso-Tristán, C., and Dieste-Velasco, M. (2018). Retrieval of monthly average hourly values of direct and diffuse solar irradiance from measurements of global radiation in Spain. J. Renew. Sustain. Energy 10:023707. doi: 10.1063/1.5016926

CrossRef Full Text | Google Scholar

Psiloglou, B., and Kambezidis, H. (2009). Estimation of the ground albedo for the Athens area, Greece. J. Atmos. Solar Terrestr. Phys. 71, 943–954. doi: 10.1016/j.jastp.2009.03.017

CrossRef Full Text | Google Scholar

Raptis, P., Kazadzis, S., Psiloglou, B., Kouremeti, N., Kosmopoulos, P., and Kazantzidis, A. (2017). Measurements and model simulations of solar radiation at tilted planes, towards the maximization of energy capture. Energy 130, 570–580. doi: 10.1016/j.energy.2017.04.122

CrossRef Full Text | Google Scholar

Reindl, D., Beckman, W., and Duffie, J. (1990a). Diffuse fraction correlations. Solar Energy 45, 1–7. doi: 10.1016/0038-092X(90)90060-P

CrossRef Full Text | Google Scholar

Reindl, D., Beckman, W., and Duffie, J. (1990b). Evaluation of hourly tilted surface radiation models. Solar Energy 45, 9–17. doi: 10.1016/0038-092X(90)90061-G

CrossRef Full Text | Google Scholar

Skartveit, A., and Olseth, J. (1986). Modelling slope irradiance at high latitudes. Solar Energy 36, 333–344. doi: 10.1016/0038-092X(86)90151-9

CrossRef Full Text | Google Scholar

Steven, M., and Unsworth, M. (1979). The diffuse solar irradiance of slopes under cloudless skies. Quart. J. Roy. Meteorol. Soc. 105, 593–602. doi: 10.1002/qj.49710544507

CrossRef Full Text | Google Scholar

Steven, M., and Unsworth, M. (1980). The angular distribution and interception of diffuse solar radiation below overcast skies. Quart. J. Roy. Meteorol. Soc. 106, 57–61. doi: 10.1002/qj.49710644705

CrossRef Full Text | Google Scholar

Temps, R., and Coulson, K. (1977). Solar radiation incident upon slopes of different orientation. Solar Energy 19, 179–184. doi: 10.1016/0038-092X(77)90056-1

CrossRef Full Text | Google Scholar

Tian, Y., Davies-Colley, R., Gong, P., and Thorrold, B. (2001). Estimating solar radiation on slopes of arbitrary aspect. Agric. Forest Meteorol. 109, 67–74. doi: 10.1016/S0168-1923(01)00245-3

CrossRef Full Text | Google Scholar

Togrul, I. (1989). Comparison of statistical performance of seven sunshine based models for Elazig, Turkey. Chim. Acta Turcicam. 1, 26–37.

Google Scholar

Tuomiranta, A., and Ghedira, H. (2015). “Evaluation of decomposition and transposition models for irradiance data conversion under a hot desert climate,” in 3rd International Conference Energy and Meteorology (Boulder, CO).

Google Scholar

Ulgen, K., and Hepbasli, A. (2004). Solar radiation models. Part 1: a review. Energy Sourc. 26, 507–520. doi: 10.1080/00908310490429696

CrossRef Full Text | Google Scholar

Vasar, C., Prostean, O., and Prostean, G. (2016). Evaluating solar radiation on tilted surfaces – a study case in Timis (Romania). IOP Conf. Ser. Mater. Sci. Eng. 106:012026. doi: 10.1088/1757-899X/106/1/012026

CrossRef Full Text | Google Scholar

Willmot, C. (1982). On the climatic optimization of the tilt and azimuth of flat-plate solar collectors. Solar Energy 28, 205–216. doi: 10.1016/0038-092X(82)90159-1

CrossRef Full Text | Google Scholar

Yadav, A., and Chandel, S. S. (2013). Tilt angle optimization to maximize incident solar radiation: a review. Renew. Sust. Energy Rev. 23, 503–513. doi: 10.1016/j.rser.2013.02.027

CrossRef Full Text | Google Scholar

Zhang, J., Zhao, L., Deng, S., Xu, W., and Zhang, Y. (2017). A critical review of the models used to estimate solar radiation. Renew. Sustain. Energy Rev. 70, 314–329. doi: 10.1016/j.rser.2016.11.124

CrossRef Full Text | Google Scholar

Nomenclature