A Combined Bi-objective Optimization and Bayesian Framework to Postulate Pharmacometric Compartmental Models

Recently, some applications of Process Systems Engineering to physiology and clinical medicine make use of compartmental analysis to represent transport of material in biological processes. One of the first steps of this analysis is to generate a set of plausible models that describe the system under study. In a previous work, we have proposed an optimization framework to support this task using a superstructure approach which inherently considers the different feasible flows between any pair of compartments. In this work, we extend such a framework to a bi-objective optimization that allows evaluating the trade-off between model fitness and complexity. To discriminate among the different models in the Pareto frontier, we employ a Bayesian metric which is approximated using a Markov Chain Monte Carlo sampling. We present a case study related to an immuno-oncology agent pharmacokinetics to demonstrate the advantages and limitations of the proposed approach.

Introduction

It is recognized that Process System Engineering can play a relevant role in addressing the problem of delivering appropriate treatment to patients (Rao et al., 2017). In order to achieve this, pharmacometric models to support the design of individualized therapies are needed. Compartment models are usually employed to represent drug absorption and disposition in biological systems.

For instance, Savoca et al. (2018) propose a physiologically-based diffusion- compartment model for the simulation of melatonin pharmacokinetics. Nacu and Pistikopoulos (2017) utilize a compartmental model for the drug distribution and drug effect of intravenous anesthesia. They develop control schemes to deal with inter- and intra-patient variability. Pavurala and Achenie (2013) present compartmental models in the study of drug release, absorption, and transit in order to test hypothesis regarding drug delivery mechanisms. They carry out a comparative study on different cimetidine tablet formulations and used the developed framework to determine optimal dosages. Sresht et al. (2011) employ a first-order compartmental model to study the side effects of cisplatin therapy. A model is developed for the cytotoxicity of cisplantin to predict cancer cells survival when subjected to a given dose of the chemotherapeutic agent. One of the main challenges still remaining in pharmacometrics is to identify the appropriate model to describe the experimental data. In a previous work, we proposed a super-structure optimization framework in order to support the model builder in elucidating plausible compartmental models. Here, we extend that framework to provide a better control of over-fitting and to permit the quantitative assessment of the existing trade-off between model complexity (i.e., number of estimated parameters and compartments) and accuracy. To do so, we develop a bi-objective optimization, which involves maximizing a fitness metric, log-likelihood, and minimizing the number of the model's active parameters, simultaneously. In addition, to discriminate the different models comprising the Pareto frontier we propose the use of a Bayesian metric that quantifies and thus allows comparing different models adequacy.

Bi-objective Optimization Model

Here, we extend the model presented by Laínez-Aguirre et al. (2017) to include binary variables to control the number of unknown parameters. The underlying idea of this model is to inherently consider all possible flows between any pair of compartments. The different types of flows are represented by set s in this model. Figure 1 shows a schematic representation of two compartments i and i′. The model determines the s connectivity relations that are active between any pair of compartments.

FIGURE 1

Figure 1. Schematic representation of the super-structure for a compartmental model.

The optimization model is comprised of four group of equations, namely, (i) the mass balances, (ii) the predictions, (iii) the equations to control the number of unknown parameters, and (iv) the objective functions. They are briefly discussed next.

Mass Balances

The Transportation Phenomena Among Compartments Must Satisfy the Material Balance Expressed in Equation (1).

$\begin{array}{ll}\frac{d}{dt}{Â}_i(t)=k_i^0+{\displaystyle \sum _s}{\displaystyle \sum _{i\ne i^{\prime }}}{k}_{s{i}^{\prime }i}^T{Â}_{i^{\prime }}^{e1s}{Â}_i^{e2s}-{\displaystyle \sum _s}{\displaystyle \sum _{i\ne i^{\prime }}}{k}_{si{i}^{\prime }}^T{Â}_i^{e1s}{Â}_{i^{\prime }}^{e2s}\forall i\notin Ī& (1)\end{array}$

This equation enforces that the change rate of the material amount (Â_i[g]) in compartment i to be equal to the difference between the input transfers from an external source ($k_i^0$ [kg/h]) and from other compartments i′($k_{s{i}^{\prime }i}^T$ [kg/h]), and the transfers from compartment i to other compartment i′($k_{si{i}^{\prime }}^T$[kg/h]). The material elimination can be contemplated as a transfer from compartment i to a dummy compartment i′. This dummy compartment is represented by the unitary set Ī. Please, note that each type of flow rate s comprises a pair of associated parameters e_1s and e_2s. They denote the power to which the material amount in the origin and destination compartment is to be raised in the mass balance equation, respectively.

Predictions

The material balances drive the predictions for the experimental data. Since the relationship to estimate such predictions can vary significantly depending on the experimental exercise, the generic Equation (2) is used to represent their formulation. This equation must be adjusted for each case study. Here, $\widehat{\text{y}}(t)$ [kg or kg/m³] is the vector of predicted values for the experimental observations, while f is a function relating the material amount in the compartments to the predicted values.

$\begin{array}{ll}ŷ(t)=f\left({Â}_i(t),\dots \mathrm{\text{,}}{Â}_I(t)\right)& (2)\end{array}$

Unknown Parameters

Equations (3) to (4) control the number of parameters in the model. In these equations, $X_{s{i}^{\prime }i}$ is a binary variable which takes the value of 1 if $k_{s{i}^{\prime }i}^T$active model parameter. Equation (3) forces parameter $k_{s{i}^{\prime }i}^T$to be 0 when it is not active, otherwise its value is within the limits $k_{s{i}^{\prime }i}^{Min}$and $k_{s{i}^{\prime }i}^{Max}$.

$\begin{array}{ll}{k}_{sii\stackrel{´}{}}^{min}{X}_{sii\stackrel{´}{}}\le k_{sii\stackrel{´}{}}^T\le k_{sii\stackrel{´}{}}^{max}{X}_{sii\stackrel{´}{}}\forall s\text{, }i\text{, }i\stackrel{´}{}\ne i& (3)\end{array}$

$\begin{array}{ll}P={\displaystyle \sum _s}{\displaystyle \sum _i}{\displaystyle \sum _{i^{\prime }\ne i}}{X}_{sii\stackrel{́}{}}& (4)\end{array}$

The Fitness Function

The model utilizes the log-likelihood as fitness function. Assuming that the experimental error is a zero-mean Gaussian process with covariance matrix V, the log-likelihood function can be expressed as the first term in the right hand side of Equation (5). The covariance matrix V can be represented as a constant diagonal matrix for homoscedastic errors; while, correlation functions can be used when heteroscedasticity is considered (Rasmussen and Williams, 2006). In order to control the over-fitting phenomenon, in this work we don't use a regularization term. Instead a bi-objective optimization is formulated. The objective functions are the log-likelihood Z and the total number of active parameters P.

$\begin{array}{ll}Z=\text{ln}N([y_1,\mathrm{...},y_n]|[{\widehat{y}}_1,\mathrm{...},{\widehat{y}}_n],V)& (5)\end{array}$

Then, the compartmental model can be mathematically posed as follows:

$\begin{array}{l}{\displaystyle \underset{X,Y}{\text{Min}}}\left\{-Z,P\right\}\end{array}$

subject to Equations (1) to (5)

where the sets X and Y denote the model binary and continuous variables, respectively. To deal with the optimization of the resulting set of differential equations, orthogonal collocation on finite elements is employed. The interested reader is referred to Cuthrell and Biegler (1987) for details about this methodology. With regard to the bi-objective optimization, the ϵ-constraint method (Messac et al., 2003) is used to generate the Pareto frontier. This is achieved by imposing a limit in the number of active unknown parameter $k_{si{i}^{\prime }}^T$, as shown in Equation (6). In this equation $\bar{P}$ is an integer representing the upper limit imposed to P.

$\begin{array}{ll}P\le \bar{P}& (6)\end{array}$

Model Discrimination

A Pareto frontier is obtained as result from the optimization model described in the previous section. Such frontier provides a set of non-dominated plausible models. To discriminate and select the most adequate model from the set, we will use the Bayesian methodology proposed by Blau et al. (2008). The authors suggest to obtain and use for each model under evaluation the posterior probability distribution of the unknown parameters.

$\begin{array}{ll}p(M_n|D)=\frac{L(M_n|D)p(M_n)}{{\displaystyle \sum _n}L(M_n|D)p(M_n)}& (7)\end{array}$

Equation (7) is the application of the Bayes' theorem by considering that each model M_n is an alternative to explain the experimental data. In this equation, p(M_n|D) is the posterior probability quantifying the belief that model M_n explains the data D, p(M_n) is the prior probability for model M_n, and L(M_n|D) is the likelihood associated with model M_n given the data D. Blau et al. (2008) propose to calculate this likelihood as follows:

$\begin{array}{ll}L(M_n|D)={\displaystyle \underset{k_n^T}{\int }}L(k_n^T|D)p(k_n^T|D){\text{d}K}_n^T& (8)\end{array}$

This is the average likelihood of the model n unknown parameters given the data D [Equation (5)] over the posterior probability distribution of those parameters. To approximate L(M_n|D) in Equation (8), we will employ a Markov Chain Monte Carlo (MCMC) sampling method. Computing p(M_n|D) will allow us to rank the compartmental models represented in the Pareto frontier.

The overall proposed methodology is summarized in the flow diagram depicted in Figure 2.

FIGURE 2

Figure 2. Flow diagram summarizing the proposed methodology.

Computational Study

To demonstrate the capabilities and limitations of the proposed approach, a case study related to the pharmacokinetics of an oncological therapeutic agent, Cyclophosphamide (CY), is reported. CY is activated in the body to hydroxy-cyclophosphamide (HCY), which is then metabolized to Carboxyethylphosphoramide mustard (CEPM) (McDonald et al., 2003).

We employ the data published for 20 patients as obtained from the clinical study carried out by Salinger et al. (2006) to postulate some plausible models by using the proposed approach. In their study, blood was sampled over 16 h to measure plasma concentrations of CEPM and HCY. This data was collected by administering an initial intravenous infusion of 45 mg CY per kg body weight (Dose₁) during approximately 1 h. The experimental data is listed in Laínez-Aguirre et al. (2017).

For this case study, we consider in the optimization model a maximum of four potential compartments and one dummy compartment for the elimination processes. The rates that are considered for the material flows are shown in Table 1. Four elements each including four collocation points corresponding to the roots of a Legendre polynomial are utilized for the orthogonal collocation. The model was implemented in GAMS (Rosenthal, 2011) and consists of a Mixed Integer Nonlinear Program (MINLP) with 880 equations, 781 continuous variables, and 52 binary variables. The total CPU time for its solution was limited to 8 h using the solvers CONOPT3, CPLEX and SBB on an Intel i7 at 2.67 GHz computer. The MCMC has been implemented using the R (R Development Core Team, 2008) software and its package MCMCpack (Martin et al., 2011). DAE models have been coded in C++ and integrated with R using the Rccp package. The convergence of the MCMC approach has been assessed using both the average likelihood plot and trace plots for the parameters (Cosma and Evers, 2010).

TABLE 1

Table 1. Type of flows considered in the compartmental model.

Figure 3 depicts the Pareto frontier obtained after applying the proposed optimization model to the Cyclophosphamide pharmacokinetic data. The Pareto frontier could include models with less than four unknown parameters. Nevertheless, such models are not relevant from the applicability standpoint given their low data fitness. Figure 3 shows that there is a significant improvement when moving from a four to a five parameter model. As expected the error decreases as we increase the model complexity. However, the higher the total number of unknown parameters that are included in the model, the more significant the impact of overfitting becomes. For this reason, the Pareto frontier has been truncated at nine unknown parameters.

FIGURE 3

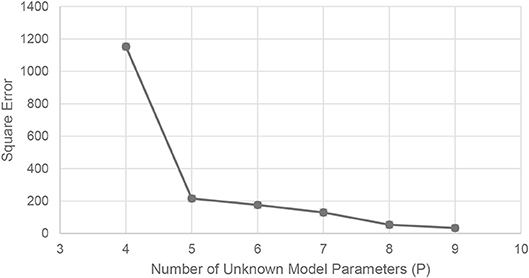
Figure 3. Pareto frontier from the bi-objective optimization. Each point represents a different compartmental model.

The additional reduction in the square error by adding an extra parameter at this point is less than 1.5% of the error resulting from the four-parameter model.

Figure 4 shows an schematic of the six parameter compartment model and its equations are listed in Equation (9), while the seven parameter compartment model is depicted in Figure 5 and expressed in Equation (10). One can notice that the structure of these two models are very similar. They only differ in that the seven parameter model includes a second order flow originating from the CEPM to the HCY compartment. This extra flow/parameter results in an error reduction of 26%.

$\begin{array}{l}\frac{d{\widehat{A}}_1}{dt}=k_0-k_{13}{\widehat{A}}_1^2+k_{31}{\widehat{A}}_3-k_{e1}{\widehat{A}}_1\\ \frac{d{\widehat{A}}_3}{dt}=k_{13}{\widehat{A}}_1^2-k_{31}{\widehat{A}}_3-k_{34}{\widehat{A}}_3^2+k_{43}{\widehat{A}}_3{\widehat{A}}_4-k_{e3}{\widehat{A}}_3\\ \frac{d{\widehat{A}}_4}{dt}=k_{34}{\widehat{A}}_3^2-k_{e4}{\widehat{A}}_4\\ k_0=\left\{\begin{array}{ll}Dos{e}_1/\text{h},\hfill & \text{if\hspace{0.17em}\hspace{0.17em}0h}\le \text{t}\le 1\text{h}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\right\}\\ {\widehat{A}}_1(0)=0;{\widehat{A}}_3(0)=0;{\widehat{A}}_4(0)=0& (9)\end{array}$

$\begin{array}{l}\frac{d{\widehat{A}}_1}{dt}=k_0-k_{13}{\widehat{A}}_1^2+k_{31}{\widehat{A}}_3-k_{e1}{\widehat{A}}_1\\ \frac{d{\widehat{A}}_3}{dt}=k_{13}{\widehat{A}}_1^2-k_{31}{\widehat{A}}_3-k_{34}{\widehat{A}}_3^2+k_{43}{\widehat{A}}_3{\widehat{A}}_4-k_{e3}{\widehat{A}}_3\\ \frac{d{\widehat{A}}_4}{dt}=k_{34}{\widehat{A}}_3^2-k_{43}{\widehat{A}}_3{\widehat{A}}_4-k_{e4}{\widehat{A}}_4\\ k_0=\left\{\begin{array}{ll}Dos{e}_1/\text{h},\hfill & \text{if\hspace{0.17em}\hspace{0.17em}0h}\le \text{t}\le 1\text{h}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\right\}\\ {\widehat{A}}_1(0)=0;{\widehat{A}}_3(0)=0;{\widehat{A}}_4(0)=0& (10)\end{array}$

We then apply to these two models the Bayesian discrimination method- ology previously described. A random walk Metropolis algorithm is employed which has been implemented in the MCMCpack package of the R software. A total of 100 × 10³ samples are drawn from the posterior probability distribution for the unknown parameters of each model. We assume that the model prior distribution is uniform between these two models [i.e., p(M₆) = p(M₇) = 0.5). Likewise, a non-informative prior probability distribution is utilized for the parameters. The resulting posterior probabilities are 7.07 × 10⁻⁸⁰ and 1 for the six-parameter and seven-parameter model, respectively. Based on this metric, the model depicted in Figure 5 describes more accurately the Cyclophosphamide pharmacokinetic data. By comparing the structures of the most likely mathematical models, the model builder can gain insights about the pharmacokinetics of the drug (e.g., linearity vs. non-linearity, multicompartment behavior, absorption vs. elimination rates).

FIGURE 4

Figure 4. Compartmental model with six unknown parameters.

FIGURE 5

Figure 5. Compartmental model with seven unknown parameters.

Concluding Remarks

In this work a combined bi-objective optimization and Bayesian model discrimination approach is proposed to tackle the problem of postulating compartmental models. We extend a previous super-structure model, which allows evaluating and discriminating simultaneously a significant number of potential compartmental models in a straight-forward manner. Equations are added to control the resulting model complexity. The mathematical model is posed as a bi-objective optimization that maximizes the fitness metric, while minimizing the total number of unknown parameters. The optimization provides a Pareto frontier, which is comprised by a set of non-dominated plausible models. To discriminate and select the most adequate model from this set, the Bayesian methodology proposed by Blau et al. (2008) is employed. The posterior distributions required by this evaluation are obtained using a Markov Chain Monte Carlo sampling.

A case study related to Cyclophosphamide pharmacokinetics is presented. In this exercise, the selection of the compartmental model has been driven completely by the experimental data. We would like to point out that we do not intend to suggest that the resulting model is a final model for this problem. Instead, we believe that the proposed methodology could deliver valuable insights to practitioners to support the process of building new models that explain experimental data.

To address the computational expense of solving the proposed model decomposition techniques can be applied. This is part of our ongoing work.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Blau, G., Lasinski, M., Orcun, S., Hsu, S.-H., Caruthers, J., Delgass, N., et al. (2008). High fidelity mathematical model building with experimental data: a Bayesian approach. Comput. Chem. Eng. 32, 971–989. doi: 10.1016/j.compchemeng.2007.04.008

CrossRef Full Text | Google Scholar

Cosma, I. A., and Evers, L. (2010). Markov Chains and Monte Carlo Methods. Lecture Notes. Cape Town: African Institute for Mathematical Sciences.

Google Scholar

Cuthrell, J. E., and Biegler, L. T. (1987). On the optimization of differential-algebraic process systems. AIChE J. 33, 1257–1270.

Google Scholar

Laínez-Aguirre, J. M., Gary, B., and Luis, P. (2017). Building pharmacokinetic compartmental models using a superstructure approach. Comput. Chem. Eng. 107, 92–99. doi: 10.1016/j.compchemeng.2017.05.027

CrossRef Full Text | Google Scholar

Martin, A. D., Quinn, K. M., and Park, J. H. (2011). Markov Chain Monte Carlo (MCMC) package. J. Stat. Softw. 42. Available online at: http://www.jstatsoft.org/

McDonald, G. B., Slattery, J. T., Bouvier, M. E., Ren, S., Batchelder, A. L., Kalhorn, T. F., et al. (2003). Cyclophosphamide metabolism, liver toxicity, and mortality following hematopoietic stem cell transplantation. Blood 101, 2043–2048. doi: 10.1182/blood-2002-06-1860

PubMed Abstract | CrossRef Full Text | Google Scholar

Messac, A., Ismail-Yahaya, A., and Mattson, C. A. (2003). The normalized normal constraint method for generating the pareto frontier. Struct. Multidiscipl. Optimization 25, 86–98. doi: 10.1007/s00158-002-0276-1

CrossRef Full Text | Google Scholar

Nacu, I., and Pistikopoulos, E. N. (2017). Modeling, estimation and control of the anaesthesia process. Comput. Chem. Eng. 107, 318–332. doi: 10.1016/j.compchemeng.2017.02.016

CrossRef Full Text | Google Scholar

Pavurala, N., and Achenie, L. E. K. (2013). A mechanistic approach for modeling oral drug delivery. Comput. Chem. Eng. 57, 196–206. doi: 10.1016/j.compchemeng.2013.06.002

CrossRef Full Text | Google Scholar

R Development Core Team (2008). R: A Language and Environment for Statistical Computing. R Development Core Team: Vienna.

PubMed Abstract

Rao, R. T., Scherholz, M. L., Hartmanshenn, C., and Bae, S.-A, Androulakis, I. P. (2017). On the analysis of complex biological supply chains: From process systems engineering to quantitative systems pharmacology. Comput. Chem. Eng. 107, 100–110. doi: 10.1016/j.compchemeng.2017.06.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Rasmussen, C. E., and Williams, C. K. I. (2006). Gaussian Processes for Machine Learning. Cambridge, MA: MIT Press.

Google Scholar

Rosenthal, R. E. (2011). GAMS - A User's Guide. Washington, DC: GAMS Development Corporation.

Google Scholar

Salinger, D. H., McCune, J. S., Ren, A. G., Shen, D. D., Slattery, J. T., Phillips, B., et al. (2006). Real-time dose adjustment of cyclophos- phamide in a preparative regimen for hematopoietic cell transplant: a Bayesian pharmacokinetic approach. Clin. Cancer Res. 12, 4888–4898. doi: 10.1158/1078-0432.CCR-05-2079

CrossRef Full Text | Google Scholar

Savoca, A., Mistraletti, G., and Manca, D. (2018). A physiologically- based diffusion-compartment model for transdermal administration—the melatonin case study. Comput. Chem. Eng. 113, 115–124. doi: 10.1016/j.compchemeng.2018.03.008

CrossRef Full Text | Google Scholar

Sresht, V., Bellare, J. R., and Gupta, S. K. (2011). Modeling the cytotoxicity of Cisplatin. Indust. Eng. Chem. Res. 50, 12872–12880. doi: 10.1021/ie102360e

CrossRef Full Text | Google Scholar