Effect of Nuclear Motion on Charge Transport in Fullerenes: A Combined Density Functional Tight Binding—Density Functional Theory Investigation

Fullerene-based materials are widely used as acceptor and electron transport layer materials in organic and planar perovskite solar cells. Modeling of electronic properties such as band alignment and charge transport for these applications is typically done using optimized geometries. Here, we estimate the effects of nuclear motions on band structure, and electron and hole transport in two prototypical fullerenes, C60 and C70. We model the dynamics in solid fullerenes using Density Functional Tight Binding and we use the Density Functional Theory based Projection of Monomer Orbitals on Dimer Orbitals (DIPRO) approach to estimate the effects on the charge transfer integral in the Marcus approximation. We show that room-temperature molecular dynamics cause a shift and spread of frontier orbital energies on the order of 0.1 eV, which leads to an increase by more than a factor of two in the Marcus exponent, and can cause a decrease by up to orders of magnitude in the overlap integral, leading, in most cases, to an overall decrease in the charge transport rate.

Introduction

Fullerene-based materials remain the preferred acceptor materials in bulk heterojunction (BHJ) organic solar cells (OSC) (Lee et al., 2008; Park et al., 2009; Cowan et al., 2010; Ganesamoorthy et al., 2017), and fullerenes are efficient electron transport layer materials in planar perovskite solar cells (PSC) (Liang et al., 2015; Nie et al., 2015; Gil-Escrig et al., 2016). Indeed, fullerene-based perovskite solar cells have now achieved power conversion efficiencies (PCE) exceeding 20% which are competitive with PCEs achieved with titania-based cells (Jiang et al., 2017) while being more suitable for large-area production. While addends to the buckyball have to be employed in OSCs to control the BHJ morphology (PCBM is the famous example), bare C60 and C70 [or their mix (Lin et al., 2018)] work well in PSCs (Brédas et al., 2009; Ameri et al., 2013). Fullerenes with addends can also be used in PSCs to control film morphology and band alignment with the perovskite and they also have a significant effect on the charge transport (Pal et al., 2017).

Critical electronic properties of fullerenes in these applications include band alignment with the organic donor or the perovskite, which determines charge separation rate at the interface, and the electron transport rate in bulk and across grain boundaries. The band alignment is controlled by the position of the LUMO (lowest unoccupied molecular orbital), which is centered on the buckyball, even when addends are used (Pal et al., 2017). The LUMO must be lower in energy than the LUMO of the organic donor or the conduction band minimum (CBM) of the perovskite, to provide sufficient driving force for charge separation, where the charge transfer rate can be approximated with the Marcus equation:

$\begin{array}{rc}{\omega }_{ij}=\frac{|J_{ij}{|}^2}{\hslash }\sqrt{\frac{\pi }{\lambda k_{B}T}}exp\left[-\frac{{(\Delta G_{ij}+\lambda )}^2}{4\lambda k_B}\right]& (1)\end{array}$

where ω_ij is the charge transfer rate between states i and j, λ is the reorganization energy, ΔG_ij is the driving force (difference in Gibbs free energies between the two states), k_B is Boltzmann constant, and T is the temperature. J_ij is the overlap integral between the wavefunctions of states i and j: 〈ψ_i|V_ij|ψ_j〉, where V_ij is the coupling (Coulomb interaction) term. The driving force can be approximated by the differences between corresponding single electron state energies. In general, a larger driving force leads to more efficient charge separation at the price of a lower open circuit voltage V_oc. It is therefore important to optimize the driving force so that it is large enough to provide efficient charge separation but as small as possible to reduce voltage loss. Selection of a particular fullerene (optimal for a given donor) is part of such optimization. The driving force is also important for charge transport in bulk fullerenes, in which case i and j are LUMO (for electron transport) or HOMO (for hole transport) orbitals centered on different molecules. ΔG_ij in this case is non-zero due to reorganization effects as electrons occupy and de-occupy orbitals. The overlap integral J_ij strongly depends on mutual position of molecules.

Ab initio modeling can be used to estimate the LUMO level as well as the reorganization energy; this is relatively easy at the molecular level but is also feasible for solid fullerenes (Ching et al., 1991; Xue et al., 2017). Typically, ab initio models of charge transfer consider equilibrium geometries. Finite temperature nuclear motions are, however, expected to affect the band alignment. Indeed, we have previously shown that room-temperature nuclear dynamics cause changes in LUMO of dyes and polymers by tenths of an eV (Manzhos et al., 2012a,b, 2013; Manzhos, 2013). This can have significant effects on charge separation, especially in interfaces with small driving forces designed for high voltage, as well as on bulk charge transport, via Equation (1). Further, molecular units in organic solids such as fullerenes, which are bound by van der Waals (vdW) forces, can be relatively mobile (Pal et al., 2017). This is expected to have a drastic effect on the overlap integral. Note that as Equation (1) depends (strongly) non-linearly on ΔG_ij and on intermolecular separation, the effects of nuclear motions will not in general average out.

In this work, we study the effects of room-temperature nuclear motions on band structure of C60 and C70 and on electron and hole transport in these fullerenes. We consider transport in bulk, as effects of microstructure are still not feasible to compute ab initio. We perform approximate ab initio (using Density Functional Tight Binding) molecular dynamics and compute expectation values of key quantities entering Equation (1). We show that nuclear motions have a strong effect on both the overlap integral and the exponent in the Marcus equation as well as on the overall charge transport rate, which can become several-fold smaller once the effects of nuclear motions are included.

Methods

Density Functional Theory (DFT) (Hohenberg and Kohn, 1964; Kohn and Sham, 1965) calculations on molecules and dimers for calculating the transfer integral were performed in Gaussian 09 (Frisch et al., 2016) using the 6–31+g(d,p) basis set. The ΔG and reorganization energy were calculated as described in the previous work (Pal et al., 2017). Namely, ΔG estimated from the difference in the redox potentials of the neutral and charged systems: $\Delta G=E_{ox(red)}^{+(-)}-E_{ox(red)}^0$, where $E_{ox(red)}^{+(-)}$ and $E_{ox(red)}^0$ were the oxidation (reduction) potential of ionic and neutral molecules. These potentials were computed as E_ox(red) = E⁺⁽⁻⁾ − E⁰, where E⁺, E⁻, and E⁰ were the energies of the cation, anion, and neutral molecules (Dardenne et al., 2015). The redox potentials were computed with the ωB97XD functional (Chai and Head-Gordon, 2008), as it was reported that a large fraction of exact exchange is desired to accurately compute them (Dardenne et al., 2015; Chen and Manzhos, 2016; Sk et al., 2016). The reorganization energy was calculated using the equation $\lambda ={\lambda }_1+{\lambda }_2=(E_{+(-)}^{*}-E_{+(-)})+(E^{*}-E)$, where $E_{+(-)}^{*}$ is ion energy at the geometry of the neutral molecule, E₊₍₋₎ is ion energy at its optimized geometry, E* is the energy of the neutral molecule at ion's geometry, and E is the energy of the neutral molecule at its optimized geometry. This was done with the B3LYP functional (Becke, 1993).

The transfer integral was computed by DFT/DIPRO (DImer PROjection) approach included in the VOTCA-CTP module (Baumeier et al., 2010; Rühle et al., 2011). The PBE functional (Perdew et al., 1996) was used for transfer integral calculations for computational efficiency (Baumeier et al., 2010). We previously showed (Pal et al., 2017) that this approach results in electron transfer rate for C60 in good agreement with available experimental and computational data reported elsewhere (Günes et al., 2007; Grzegorczyk et al., 2010; Ferguson et al., 2011; Nardes et al., 2012, 2014; Arntsen et al., 2013; Pelzer et al., 2017).

Solid state calculations and ab initio molecular dynamics were performed using the Self-Consistent Charge Density Functional Tight Binding (SCC-DFTB) method (Elstner et al., 1998) in DFTB+ (Aradi et al., 2007). The 3ob-3-1 Slater-Koster parameter set and DFTB3 capability were used (Gaus et al., 2011). Dispersion interactions were modeled with the UFF (universal force field) (Rappé et al., 1992). We previously showed that (dispersion-corrected) DFTB computes molecular and solid-state structures of fullerenes in good agreement with experiment and (dispersion-corrected) DFT, see (Pal et al., 2017, 2018; Lin et al., 2018) for corresponding benchmarks. Specifically, while the DFTB parameterization causes an underestimation of the absolute value of the bandgap, molecular and solid structures as well as relative changes in electronic structure sufficiently reproduce those computed with DFT (Pal et al., 2017, 2018; Lin et al., 2018).

Simulation cells consisted of 8 C60 or C70 molecules. Initial structures were taken from known bcc and hcp structures for C60 and C70, respectively (Quo et al., 1991; Soldatov et al., 2001). The Brillouin zone was sampled at the Gamma point which was sufficient due to the size of the cells (more than 17 Å in each dimension). Molecular dynamics simulations were performed using the Berendsen thermostat/barostat with a time constant of 100 fs at room temperature (300 K). First 100 ps were used for equilibration, and the following 900 ps were used for data analysis. Intermolecular (based on center of mass) distances as well as HOMO and LUMO energy levels were collected during the trajectory.

Results

Effect of Nuclear Motions on Band Structure and Driving Force

The simulation cells of C60 and C70 are shown in Figure 1. The distributions of HOMO and LUMO energy levels for the two fullerenes are shown in Figure 2. The HOMO and LUMO energies at the equilibrium geometry as well as their expectation values over the MD (molecular dynamics) trajectories are listed in Table 1. The expectation values over the trajectories differ from the values at the equilibrium geometry by about 0.1 eV; this is equivalent to an amount of change in ΔG, which was previously associated with changes in electron transfer rate by about a factor of 2 (Koops et al., 2009; Santos et al., 2010). The distributions are broad on the order of 0.1 eV with respect to their expectation value (3σ width, where the standard deviations are about σ = 0.02 eV). The distribution of the exponential of the Marcus equation is shown in Figure 3; it is computed as

$\begin{array}{rc}E=exp\left[-\frac{{(\Delta E^{\prime }-\Delta E^{″}+\Delta G_{eq}+\lambda )}^2}{4\lambda k_{B}T}\right]& (2)\end{array}$

where ΔE′ and ΔE″ are deviations from the equilibrium-geometry levels for neighboring molecular units. The values of reorganization energies for electron and hole transport are listed in Table 1.

FIGURE 1

Figure 1. The simulations cells of C60 (left) and C70 (right).

FIGURE 2

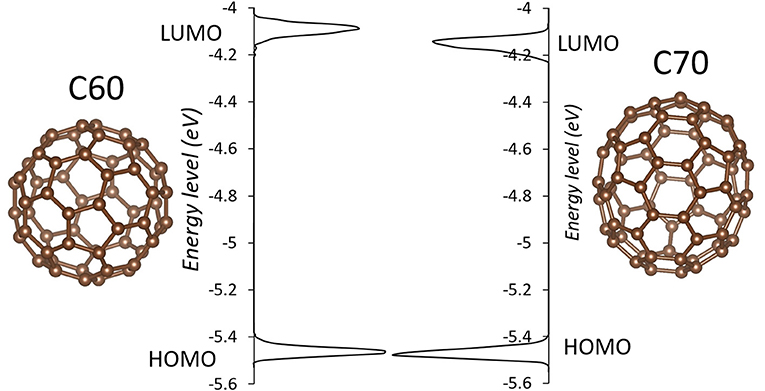
Figure 2. The distributions of HOMO and LUMO levels in C60 (left) and C70 (right) during molecular dynamics in solid state. Individual molecules are shown next to respective plots.

TABLE 1

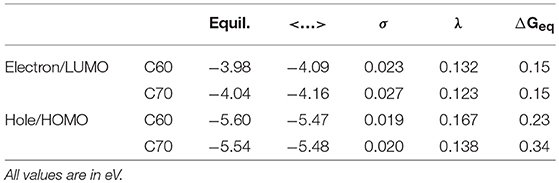
Table 1. HOMO and LUMO energies at the equilibrium geometry (“Equil.”), their expectation values over MD trajectories (“ < …>”), standard deviations of HOMO and LUMO distributions over MD trajectories (“σ”) as well as reorganization energies λ and driving forces ΔG_eq for electron and hole transport in C60 and C70.

FIGURE 3

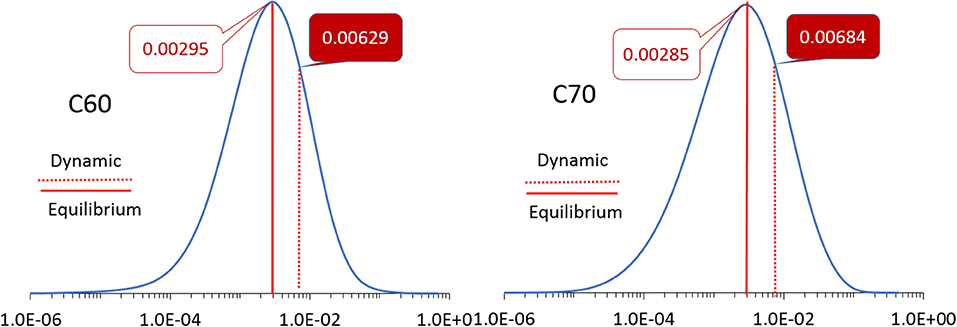
Figure 3. The distributions of the values of the exponent in the Marcus equation (Equation 2) for C60 (left) and C70 (right). The values at the equilibrium geometry and expectation values over molecular dynamics trajectories are indicated by solid and dotted red lines, respectively, with corresponding numbers as inserts. Note the logarithmic scale of the abscissa.

The expectation value of this distribution for C60 and C70 for electron transport (i.e., based on LUMO) is 0.0063 and 0.0068, respectively, compared to values at the equilibrium geometry of 0.0030 and 0.0029, respectively. This change is due to both the different expectation values of LUMO over MD trajectories from their equilibrium values (Table 1) as well as the finite width of the distribution which has a strong effect on E due to the strongly non-linear dependence of E on orbital energies. A similar effect is seen for hole transport (based on HOMO): the expectation value of E over the trajectories for C60 is 2.02 × 10⁻⁴ vs. the equilibrium value of 1.08 × 10⁻⁴ and for C70, 4.85 × 10⁻⁷ vs. the equilibrium value of 1.11 × 10⁻⁷.

Effect of Nuclear Motions on the Overlap Integral and Charge Transfer Rate

Molecular dynamics causes a distribution of inter-molecular separation of C60, C70 units. These distributions (of distances between centers of mass) are shown in Figure 4. The equilibrium geometry C60-C60 and C70-C70 nearest neighbor distances are 9.3 and 11.3 Å, respectively. The distributions have a strong effect on the overlap integral. The overlap integrals as a function of the inter-molecular distance are also shown in Figure 4. The strongly non-linear dependence of the integral on the distance leads to a strong effect of nuclear motions on the overlap integral; for C60, while the value of $J_{ij}^2$ for electron/hole transport at the equilibrium inter-molecular distance is 0.045/0.258 eV, its expectation value over the MD trajectory is 0.0023/2.15 × 10⁻⁶ eV. For C70, these numbers are 0.151/0.002 and 0.0010/0.0012 eV, respectively. Figure 4 was computed by changing the inter-molecular distance starting from nearest C60 and C70 dimers as they are positioned in the crystal at a specific orientation. At selected distances, we computed overlap integrals at other molecular orientations. Not surprisingly, given the strong sensitivity of the overlap integral, different orientations resulted in changes in J_{e, h} of more than an order of magnitude. It is not feasible to fully sample and average the curves in Figure 4 for all possible orientations. Nevertheless, Figure 4 still clearly demonstrates the strong effect of nuclear dynamics on the charge transfer integral and thereby on the rate.

FIGURE 4

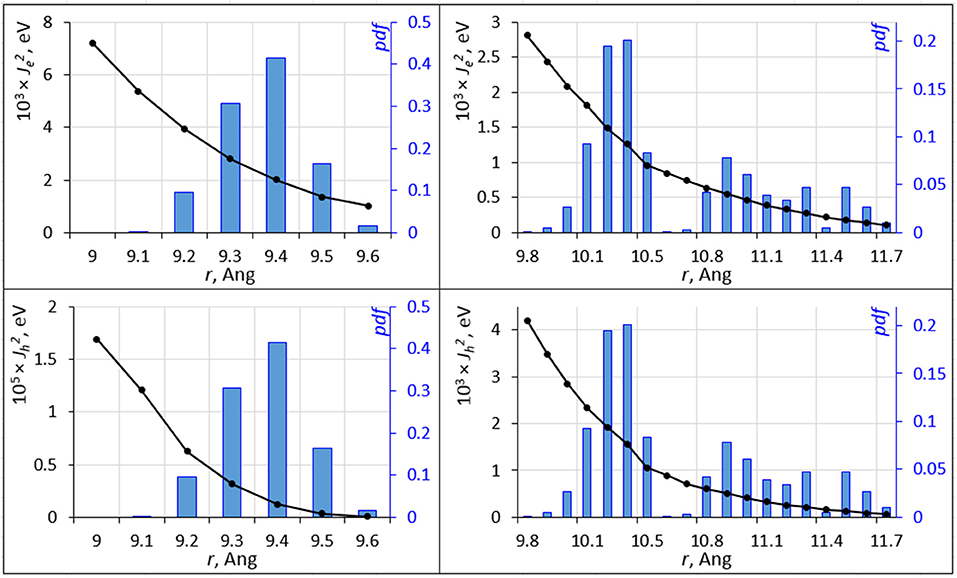
Figure 4. The squared electron transfer integrals (left ordinate axis) for electrons ($J_e^2$, top panels) and holes ($J_h^2$, bottom panels) for C60 (left panels) and C70 (right panels) are shown as black lines vs. intermolecular distance r. The probability density function (pdf ) of r is shown as blue histogram (right ordinate axis).

We also observed that the distributions in HOMO and LUMO energies were uncorrelated with the distribution in inter-molecular distances. This is demonstrated in Figure 5. This was not unexpected in a vdW material like fullerene, where the intramolecular vibrational modes (mostly responsible for HOMO, LUMO changes) have little coupling to inter-molecular motion. The absence of significant correlation permits estimating the expected charge transfer rate with the effect of nuclear motions 〈ω_ij〉 as

$\begin{array}{rc}\langle {\omega }_{ij}\rangle =\frac{\langle |J_{ij}{|}^2\rangle }{\hslash }\sqrt{\frac{\pi }{\lambda k_{B}T}}\times \langle E\rangle & (3)\end{array}$

where the angular brackets denote expectation values (averages over MD trajectories), e.g., 〈E〉 is the expectation value of the Marcus exponent, Equation (2). The resulting average electron and hole transfer rates for C60 were 6.75 × 10¹¹ and 1.79 × 10⁷ s⁻¹, respectively, and for C70 are 3.32 × 10¹¹ and 2.69 × 10⁷ s⁻¹, respectively. Except for hole transport in C70 (where the equilibrium-geometry charge-transfer integral is very low leading to a very low equilibrium-geometry rate), these rates were significantly lower than the rates computed at the equilibrium geometry, which for C60 were 6.24 × 10¹² and 1.15 × 10¹² s⁻¹, respectively, and for C70 were 2.10 × 10¹³ and 1.16 × 10⁷ s⁻¹, respectively. Rates can thus change by orders of magnitude. Specifically, for hole transport in C70, a significantly higher <E> than its equilibrium value outweighs the dynamic lowering of J_ij, resulting in a computed expectation value for the rate which is higher than its (very low) computed equilibrium value.

FIGURE 5

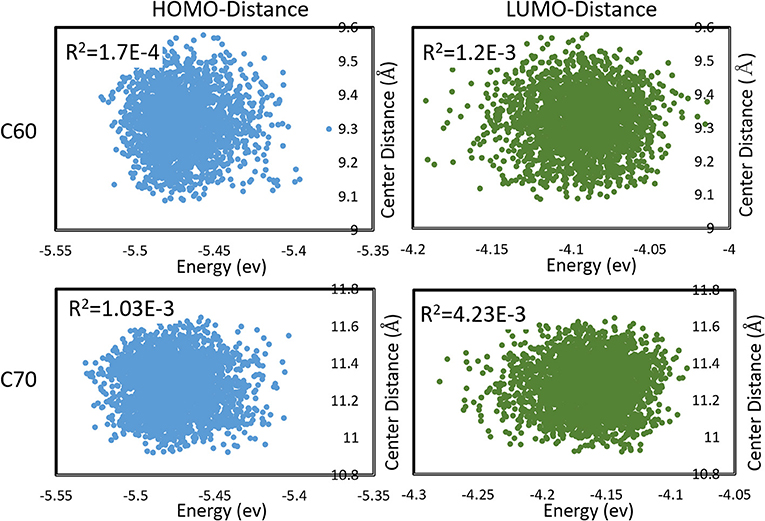
Figure 5. Correlations between HOMO, LUMO energies, and intermolecular distances (between centers of mass) during molecular dynamics in C60 and C70. Pearson R² coefficients are also shown.

The rate calculations are very sensitive, due to a very sensitive dependence of the overlap integral on small changes in geometry or orbital distribution as well as due to the exponential dependence on ΔG and the reorganization energy. We therefore believe that such data are reliable mostly on the trend basis.

Conclusions

In this work, we considered effects due to room-temperature atomic and molecular motions on charge transfer rates in solid C60 and C70. We modeled solid C60 and C70 using Density Functional Tight Binding and performed DFTB MD to estimate effects of dynamics on components of the Marcus equation. Room-temperature molecular dynamics cause a spread of frontier orbital energies on the order of 0.1 eV which leads to a distribution of driving forces to charge transfer and an increase by more than a factor of two in the Marcus exponent. We also computed a decrease, in some cases by orders of magnitude, in the expectation value of the overlap integral, leading to an overall decrease in the charge transport rate in most cases.

Considering the high degree of sensitivity of the rates to various approximations (the DIPRO approximation and the level of ab initio treatment within it, the approximate treatment of vdW interactions responsible for the structure of the solid, the classical MD used to model dynamics and the structures used for rate calculations, etc.), the numeric results are likely only semi-quantitative at best. This might have led e.g., to the very low expectation values of hole transfer rates vs. equilibrium geometry rate. Nevertheless, the qualitative trends are likely trustworthy, and they consistently point to a strong effect of nuclear dynamics already at room temperature on the electron and hole transport rate.

The effect of nuclear dynamics should therefore be included when feasible. The calculations are not routine and are multi-stepped, involving solid state MD calculations, dimer generation, and DIPRO model application. We have shown here that effects on the charge transfer integral and on the exponent of the Marcus equation are largely uncorrelated, which significantly simplifies such estimates. Development of approximate schemes, which would allow routine inclusion of dynamics effect on the Marcus rate, is therefore desired, especially those considering orientation distributions of molecules which were not fully considered here. Hopefully this work will help encourage such development.

Author Contributions

SM: conceptualization, project guidance, and text; SA: DFTB calculations and data analysis; AP: charge transport calculations; KY: advisor to SA. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the Ministry of Education of Singapore. KY was supported by MEXT as Priority Issue on Post-K computer (Development of new fundamental technologies for high-efficiency energy creation, conversion/storage and use).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Prof. Yutaka Matsuo and Dr. Il Jeon of the University of Tokyo for discussions.

References

Ameri, T., Li, N., and Brabec, C. J. (2013). Highly efficient organic tandem solar cells: a follow up review. Energy Environ. Sci. 6, 2390–2413. doi: 10.1039/c3ee40388b

CrossRef Full Text | Google Scholar

Aradi, B., Hourahine, B., and Frauenheim, T. (2007). DFTB+, a sparse matrix-based implementation of the DFTB method. J. Chem. Phys. A 111, 5678–5684. doi: 10.1021/jp070186p

PubMed Abstract | CrossRef Full Text | Google Scholar

Arntsen, C., Reslan, R., Hernandez, S., Gao, Y., and Neuhauser, D. (2013). Direct delocalization for calculating electron transfer in fullerenes. Int. J. Quantum Chem. 113, 1885–1889. doi: 10.1002/qua.24409

CrossRef Full Text | Google Scholar

Baumeier, B., Kirkpatrick, J., and Andrienko, D. (2010). Density-functional based determination of intermolecular charge transfer properties for large-scale morphologies. Phys. Chem. Chem. Phys. 12, 11103–11113. doi: 10.1039/c002337j

PubMed Abstract | CrossRef Full Text | Google Scholar

Becke, A. D. (1993). A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 98, 1372–1377. doi: 10.1063/1.464304

CrossRef Full Text | Google Scholar

Brédas, J. L., Norton, J. E., Cornil, J., and Coropceanu, V. (2009). Molecular understanding of organic solar cells: the challenges. Acc. Chem. Res. 42, 1691–1699. doi: 10.1021/ar900099h

PubMed Abstract | CrossRef Full Text | Google Scholar

Chai, J. D., and Head-Gordon, M. (2008). Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 128:084106. doi: 10.1063/1.2834918

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., and Manzhos, S. (2016). Voltage and capacity control of polyaniline based organic cathodes: an ab initio study. J. Power Sources 336, 126–131. doi: 10.1016/j.jpowsour.2016.10.066

CrossRef Full Text | Google Scholar

Ching, W. Y., Huang, M. Z., Xu, Y. N., Harter, W. G., and Chan, F. T. (1991). First-principles calculation of optical properties of C 60 in the fcc lattice. Phys. Rev. Lett. 67, 2045–2048. doi: 10.1103/PhysRevLett.67.2045

CrossRef Full Text | Google Scholar

Cowan, S. R., Roy, A., and Heeger, A. J. (2010). Recombination in polymer-fullerene bulk heterojunction solar cells. Phys. Rev. B 82:245207. doi: 10.1103/PhysRevB.82.245207

CrossRef Full Text | Google Scholar

Dardenne, N., Blase, X., Hautier, G., Charlier, J. C., and Rignanese, G. M. (2015). Ab initio calculations of open-cell voltage in li-ion organic radical batteries. J. Phys. Chem. C 119, 23373–23378. doi: 10.1021/acs.jpcc.5b07886

CrossRef Full Text | Google Scholar

Elstner, M., Porezag, D., Jungnickel, G., Elsner, J., Haugk, M., Frauenheim, T., et al. (1998). Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 58, 7260–7268. doi: 10.1103/PhysRevB.58.7260

CrossRef Full Text | Google Scholar

Ferguson, A. J., Kopidakis, N., Shaheen, S. E., and Rumbles, G. (2011). Dark carriers, trapping, and activation control of carrier recombination in neat P3HT and P3HT: PCBM blends. J. Phys. Chem. C 115, 23134–23148. doi: 10.1021/jp208014v

CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2016). Gaussian 09, Revision D.01. Wallingford, CT: Gaussian, Inc.

Google Scholar

Ganesamoorthy, R., Sathiyan, G., and Sakthivel, P. (2017). Fullerene based acceptors for efficient bulk heterojunction organic solar cell applications. Solar Energy Mater. Solar Cells 161, 102–148. doi: 10.1016/j.solmat.2016.11.024

CrossRef Full Text | Google Scholar

Gaus, M., Cui, Q., and Elstner, M. (2011). DFTB3: extension of the self-consistent-charge density-functional tight-binding method (SCC-DFTB). J. Chem. Theory Comput. 7, 931–948. doi: 10.1021/ct100684s

PubMed Abstract | CrossRef Full Text | Google Scholar

Gil-Escrig, L., Momblona, C., Sessolo, M., and Bolink, H. J. (2016). Fullerene imposed high open-circuit voltage in efficient perovskite based solar cells. J. Mater. Chem. A 4, 3667–3672. doi: 10.1039/C5TA10574A

CrossRef Full Text | Google Scholar

Grzegorczyk, W. J., Savenije, T. J., Dykstra, T. E., Piris, J., Schins, J. M., and Siebbeles, L. D. (2010). Temperature-independent charge carrier photogeneration in P3HT– PCBM blends with different morphology. J. Phys. Chem. C 114, 5182–5186. doi: 10.1021/jp9119364

CrossRef Full Text | Google Scholar

Günes, S., Neugebauer, H., and Sariciftci, N. S. (2007). Conjugated polymer-based organic solar cells. Chem. Rev. 107, 1324–1338. doi: 10.1021/cr050149z

PubMed Abstract | CrossRef Full Text | Google Scholar

Hohenberg, P., and Kohn, W. (1964). Inhomogeneous electron gas. Phys. Rev. 136, B864–B871. doi: 10.1103/PhysRev.136.B864

CrossRef Full Text | Google Scholar

Jiang, Q., Chu, Z., Wang, P., Yang, X., Liu, H., Wang, Y., et al. (2017). Planar-structure perovskite solar cells with efficiency beyond 21%. Adv. Mater. 29:1703852. doi: 10.1002/adma.201703852

PubMed Abstract | CrossRef Full Text | Google Scholar

Kohn, W., and Sham, L. J. (1965). Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138. doi: 10.1103/PhysRev.140.A1133

CrossRef Full Text | Google Scholar

Koops, S. E., O'Regan, B. C., Barnes, P. R., and Durrant, J. R. (2009). Parameters influencing the efficiency of electron injection in dye-sensitized solar cells. J. Am. Chem. Soc. 131, 4808–4818. doi: 10.1021/ja8091278

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J. K., Ma, W. L., Brabec, C. J., Yuen, J., Moon, J. S., Kim, J. Y., et al. (2008). Processing additives for improved efficiency from bulk heterojunction solar cells. J. Am. Chem. Soc. 130, 3619–3623. doi: 10.1021/ja710079w

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, P. W., Chueh, C. C., Williams, S. T., and Jen, A. K. Y. (2015). Roles of fullerene-based interlayers in enhancing the performance of organometal perovskite thin-film solar cells. Adv. Energy Mater. 5:1402321. doi: 10.1002/aenm.201402321

CrossRef Full Text | Google Scholar

Lin, H.-S., Jeon, I., Xiang, R., Seo, S., Lee, J.-W., Li, C., et al. (2018). Achieving high efficiency in solution-processed perovskite solar cells using C60/C70 mixed fullerenes. ACS Appl. Mater. Interfaces 10, 39590–39598. doi: 10.1021/acsami.8b11049

PubMed Abstract | CrossRef Full Text | Google Scholar

Manzhos, S. (2013). Effects of nuclear vibrations on the energetics of polythiophene: quantized energy molecular dynamics. Aust. J. Chem. 66, 1021–1028. doi: 10.1071/CH13112

CrossRef Full Text | Google Scholar

Manzhos, S., Segawa, H., and Yamashita, K. (2012a). Effect of nuclear vibrations, temperature, and orientation on injection and recombination conditions in amino-phenyl acid dyes on TiO₂. Proc. SPIE 8438:843814. doi: 10.1117/12.921133

CrossRef Full Text | Google Scholar

Manzhos, S., Segawa, H., and Yamashita, K. (2012b). The effect of ligand substitution and water co-adsorption on the adsorption dynamics and energy level matching of amino-phenyl acid dyes on TiO₂. Phys. Chem. Chem. Phys. 14, 1749–1755. doi: 10.1039/C2CP23039A

PubMed Abstract | CrossRef Full Text | Google Scholar

Manzhos, S., Segawa, H., and Yamashita, K. (2013). Effect of nuclear vibrations, temperature, co-adsorbed water, and dye orientation on light absorption, charge injection and recombination conditions in organic dyes on TiO₂. Phys. Chem. Chem. Phys. 15, 1141–1147. doi: 10.1039/C2CP43448B

PubMed Abstract | CrossRef Full Text | Google Scholar

Nardes, A. M., Ayzner, A. L., Hammond, S. R., Ferguson, A. J., Schwartz, B. J., and Kopidakis, N. (2012). Photoinduced charge carrier generation and decay in sequentially deposited polymer/fullerene layers: bulk heterojunction vs. planar interface. J. Phys. Chem. C 116, 7293–7305. doi: 10.1021/jp212390p

CrossRef Full Text | Google Scholar

Nardes, A. M., Ferguson, A. J., Wolfer, P., Gui, K., Burn, P. L., Meredith, P., et al. (2014). Free carrier generation in organic photovoltaic bulk heterojunctions of conjugated polymers with molecular acceptors: planar versus spherical acceptors. ChemPhysChem 15, 1539–1549. doi: 10.1002/cphc.201301022

PubMed Abstract | CrossRef Full Text | Google Scholar

Nie, W., Tsai, H., Asadpour, R., Blancon, J. C., Neukirch, A. J., Gupta, G., et al. (2015). High-efficiency solution-processed perovskite solar cells with millimeter-scale grains. Science 347, 522–525. doi: 10.1126/science.aaa0472

PubMed Abstract | CrossRef Full Text | Google Scholar

Pal, A., Arabnejad, S., Yamashita, K., and Manzhos, S. (2018). Influence of the aggregate state on band structure and optical properties of C60 computed with different methods. J. Chem. Phys. 148:204301. doi: 10.1063/1.5028329

PubMed Abstract | CrossRef Full Text | Google Scholar

Pal, A., Wen, L. K., Jun, C. Y., Jeon, I., Matsuo, Y., and Manzhos, S. (2017). Comparative density functional theory–density functional tight binding study of fullerene derivatives: effects due to fullerene size, addends, and crystallinity on band structure, charge transport and optical properties. Phys. Chem. Chem. Phys. 19, 28330–28343. doi: 10.1039/C7CP05290A

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, S. H., Roy, A., Beaupre, S., Cho, S., Coates, N., Moon, J. S., et al. (2009). Bulk heterojunction solar cells with internal quantum efficiency approaching 100%. Nat. Photon. 3, 297–302. doi: 10.1038/nphoton.2009.69

CrossRef Full Text | Google Scholar

Pelzer, K. M., Vázquez-Mayagoitia, Á., Ratcliff, L. E., Tretiak, S., Bair, R. A., Gray, S. K., et al. (2017). Molecular dynamics and charge transport in organic semiconductors: a classical approach to modeling electron transfer. Chem. Sci. 8, 2597–2609. doi: 10.1039/C6SC04547B

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi: 10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Quo, Y., Karasawa, N., and Goddard, W. A. III. (1991). Prediction of fullerene packing in C60 and C70 crystals. Nature 351, 464–467. doi: 10.1038/351464a0

CrossRef Full Text | Google Scholar

Rappé, A. K., Casewit, C. J., Colwell, K. S., Goddard, I. I. I. W. A, and Skiff, W. M. (1992). UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 114, 10024–10035. doi: 10.1021/ja00051a040

CrossRef Full Text | Google Scholar

Rühle, V., Lukyanov, A., May, F., Schrader, M., Vehoff, T., and, Kirkpatrick, J., et al. (2011). Microscopic simulations of charge transport in disordered organic semiconductors. J. Chem. Theory Comput. 7, 3335–3345. doi: 10.1021/ct200388s

PubMed Abstract | CrossRef Full Text | Google Scholar

Santos, T. D., Morandeira, A., Koops, S., Mozer, A. J., Tsekouras, G., Dong, Y., et al. (2010). Injection limitations in a series of porphyrin dye-sensitized solar cells. J. Phys. Chem. C 114, 3276–3279. doi: 10.1021/jp908401k

CrossRef Full Text | Google Scholar

Sk, M. A., Chen, Y., and Manzhos, S. (2016). Orbital order switching in molecular calculations using GGA functionals: qualitative errors in materials modeling for electrochemical power sources and how to fix them. Chem. Phys. Lett. 659, 270–276. doi: 10.1016/j.cplett.2016.07.047

CrossRef Full Text | Google Scholar

Soldatov, A. V., Roth, G., Dzyabchenko, A., Johnels, D., Lebedkin, S., Meingast, C., et al. (2001). Topochemical polymerization of C70 controlled by monomer crystal packing. Science 293, 680–683. doi: 10.1126/science.1061434

PubMed Abstract | CrossRef Full Text | Google Scholar

Xue, H. T., Boschetto, G., Krompiec, M., Morse, G. E., Tang, F. L., and Skylaris, C. K. (2017). Linear-scaling density functional simulations of the effect of crystallographic structure on the electronic and optical properties of fullerene solvates. Phys. Chem. Chem. Phys. 19, 5617–5628. doi: 10.1039/C6CP08165G

PubMed Abstract | CrossRef Full Text | Google Scholar