Thermal Energy Processes in Direct Steam Generation Solar Systems: Boiling, Condensation and Energy Storage – A Review

Direct steam generation coupled is a promising solar-energy technology, which can reduce the growing dependency on fossil fuels. It has the potential to impact the power-generation sector as well as industrial sectors where significant quantities of process steam are required. Compared to conventional concentrated solar power systems, which use synthetic oils or molten salts as the heat transfer fluid, direct steam generation offers an opportunity to achieve higher steam temperatures in the Rankine power cycle and to reduce parasitic losses, thereby enabling improved thermal efficiencies. However, its practical implementation is associated with non-trivial challenges, which need to be addressed before such systems can become more economically competitive. Specifically, important thermal-energy processes take place during flow boiling, flow condensation and thermal-energy storage, which are highly complex, multi-scale and multi-physics in nature, and which involve phase-change, unsteady and turbulent multiphase flows in the presence of conjugate heat transfer. This paper reviews our current understanding and ability to predict these processes, and the knowledge that has been gained from experimental and computational efforts in the literature. In addition to conventional steam-Rankine cycles, the possibility of implementing organic Rankine cycle power blocks, which are relevant to lower operating temperature conditions, are also considered. This expands the focus beyond water as the working fluid, to include refrigerants also. In general, significant progress has been achieved in this space, yet there remain challenges in our capability to design and to operate high-performance and low-cost systems effectively and with confidence. Of interest are the flow regimes, heat transfer coefficients and pressure drops that are experienced during the thermal processes present in direct steam generation systems, including those occurring in the solar collectors, evaporators, condensers and relevant energy storage schemes during thermal charging and discharging. A brief overview of some energy storage options are also presented to motivate the inclusion of thermal energy storage into direct steam generation systems.

Introduction

During the past few decades, the demand for energy, particularly related to electricity production and the production of thermal energy in industries around the world, has been steadily growing, and is projected to continue to do so. Rankine or organic Rankine cycle (ORC) type thermal power systems allow for the production of high pressure superheated steam or vapour (in the case of an ORC), which can be used to generate electrical energy, and/or thermal energy if configured for cogeneration (Freeman et al., 2015, 2017). In their simplest form such cycles consist of four basic processes. Heat is transferred to a working substance in a boiler unit to produce superheated vapour, downstream of which the vapour is converted into mechanical power in a turbine, which is then converted into electrical power by a generator. The vapour leaving the turbine is condensed, and the condensate is pumped back to the boiler, first by a condensate pump and then possibly by a feed-water pump (Martha, 2012). In the case of a Rankine cycle power plant, water (steam) is used as the working fluid, whereas in ORC power plants, a large variety of refrigerants can be suitable working fluids (Freeman et al., 2017), which lends advantages to these plants in some cases (Markides, 2015). Different heat sources can be used including the heat from combustion of fossil fuels, nuclear reactions, or solar thermal energy. Regardless of the working fluid, fuel and operating conditions, these power cycles operate with boiling and condensation in order to meet the demands for higher cooling or heating rates (Mudawar, 2013; Kharangate and Mudawar, 2017).

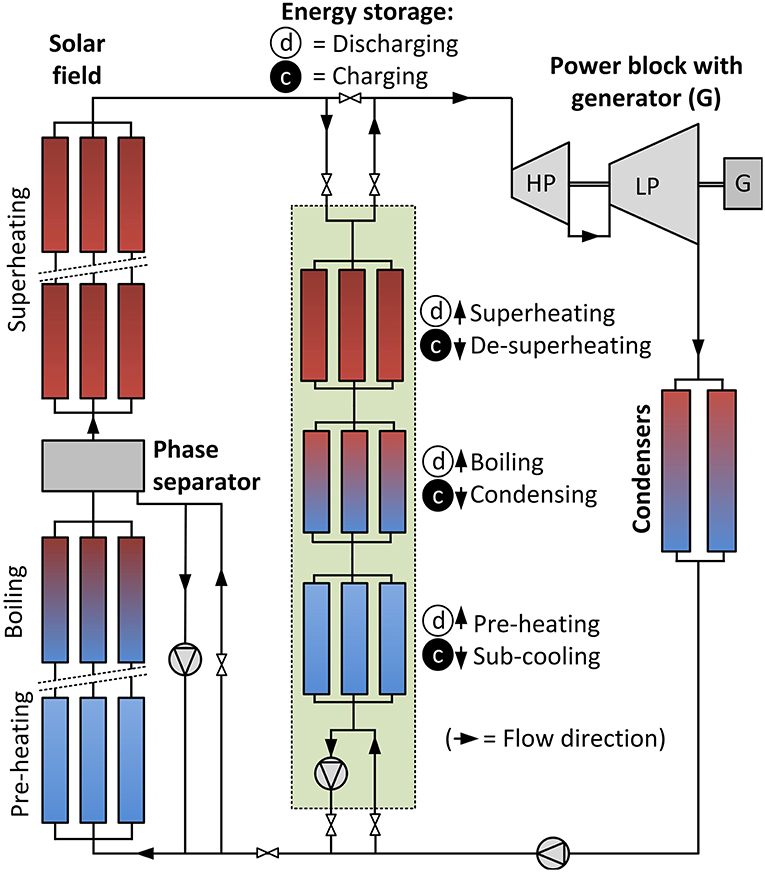
Concerns arising from the environmental impacts of fossil-fuel power generation and the finite nature of these resources have acted as drivers for the development of renewable energy technologies such as concentrated solar power (CSP) plants (Islam et al., 2018). An alternative option to conventional CSP systems, is direct steam generation (DSG). In the case of a steam-Rankine cycle, such a system operates with water which is used directly as the heat transfer fluid (HTF) in the solar receivers, and which also acts as the working fluid in the thermodynamic power-cycle (Hirsch et al., 2014) as is represented in a simplistic example of such a system type (Birnbaum et al., 2010) in Figure 1.

FIGURE 1

Figure 1. Example of a direct steam generation system architecture with energy storage.

In this particular design, the solar field is operated in a recirculation mode. The preheating, evaporating and superheating sections are used to produce steam (or superheated vapour in an ORC) directly. The high-pressure steam/vapour is fed to the high pressure turbine, followed by, for instance, a low pressure turbine, a condenser and a liquid pump. Thermal energy storage can be provided as indicated where different stages of energy charging and discharging can be accommodated, depending on the particular architecture (other architectures and thermal energy storage options also exist as will be discussed later in the article). During energy charging, heat is passed to the energy storage media from the working fluid resulting, in for instance, the desuperheating, condensation and subcooling of a portion of the high pressure steam/vapour. During discharging, the flow of the working fluid in the energy storage sections is altered, and the high pressure steam/vapour from the solar field is either replaced or complemented by steam/vapour production in the energy storage sections. In this mode, heat is passed from the energy storage media to the working fluid in stages that preheat, evaporate and superheat the working fluid. It is thus interesting to note that evaporation or flow boiling occurs in both the solar field and during the discharge mode in the energy storage section, while condensation occurs in both the condensers as well as during energy the charging mode in the energy storage section.

The use of a single fluid (water or refrigerant) for both functions (heat transfer fluid and working fluid) can overcome some of the problems faced by conventional CSP plants: (1) significantly higher steam temperatures in the case of water can be achieved, which has a direct influence on the thermal efficiency; and (2) secondary heat exchangers are not required between the solar field and the power block, thus reducing parasitic frictional/pressure losses and thermal inertia. The increase in thermal performance and the reduction in the number of heat transfer system components can significantly reduce the power generation cost if the system is correctly designed using suitable materials, while the associated reduction in thermal inertia can vastly improve part-load performance and operational flexibility, including start-up times and load-following capabilities.

However, some arising challenges need to be addressed, including the development of more sophisticated thermal-storage schemes and overcoming the inherent unsteadiness of cycle operation introduced at the solar receivers due to flow instabilities, variations of diurnal irradiance, cloud coverage or ambient conditions. Such variations have a detrimental effect on the steam/vapour temperature stability (Birnbaum et al., 2011), operating conditions of the turbine affecting its lifetime, and flow stability in the solar receivers.

Reviews and studies are available on DSG solar receivers and collector fields (Zarza et al., 2004; Bouvier et al., 2015; Xu and Wiesner, 2015; Liu et al., 2016b; Giglio et al., 2017; Li et al., 2017), control strategies (Valenzuela et al., 2006; Eck and Hirsch, 2007; Aurousseau et al., 2016; Guo et al., 2017), transient behaviour and operation modelling (Lippke, 1996; Biencinto et al., 2016), cycle and performance analyses (Montes et al., 2009; Fraidenraich et al., 2013; Elsafi, 2015a) comparisons between DSG and other types of plants (Feldhoff et al., 2012; Rovira et al., 2013; Sanz-Bermejo et al., 2014), and energy storage (Bayón et al., 2010; Seitz et al., 2013).

An updated overview of our current knowledge and the state of the art for the thermal energy processes during boiling and condensation in DSG systems is lacking in the literature. As mentioned, flow boiling and flow condensation are present in several solar-system components including the energy storage sections. In order for all of these processes to be adequately modelled and understood, a firm foundation in the thermo-hydraulic behaviour of the working fluid is required. For this purpose, the paper is divided into the following sections: two-phase flow regime maps, flow boiling, flow condensation, and energy storage options. For flow boiling and condensation, attention is given to developments and trends as obtained from experimental data as well as computational research, especially for flows in circular tube and pipes, while for energy storage, the emphasis is predominantly on thermal energy storage methods, along with a brief comparison with other energy storage options to motivate an appreciation why thermal energy storage could be advantageous from a cost perspective.

Two-Phase Flow Regimes

At a particular operating condition, the prevailing two-phase flow regime has an impact on the heat transfer and pressure drop performance during boiling/evaporation and condensation in the various system components mentioned earlier. Several flow regimes (or patterns) are encountered in boiling and condensation. Flow regime information provides important insight into the thermo-hydraulic phenomena that are occurring, such as how the two phases are distributed and interacting with each other. Flow regimes in horizontal two-phase flow boiling depend mainly on the surface tension and the gravitational forces, along with other parameters such as the surface roughness, tube inclination, flow geometry and thermo-physical properties of the fluid. This information is crucial for accurate heat transfer and pressure drop predictions, as well as the prediction of structural-related phenomena such as vibrations and local temperature variations at tube walls.

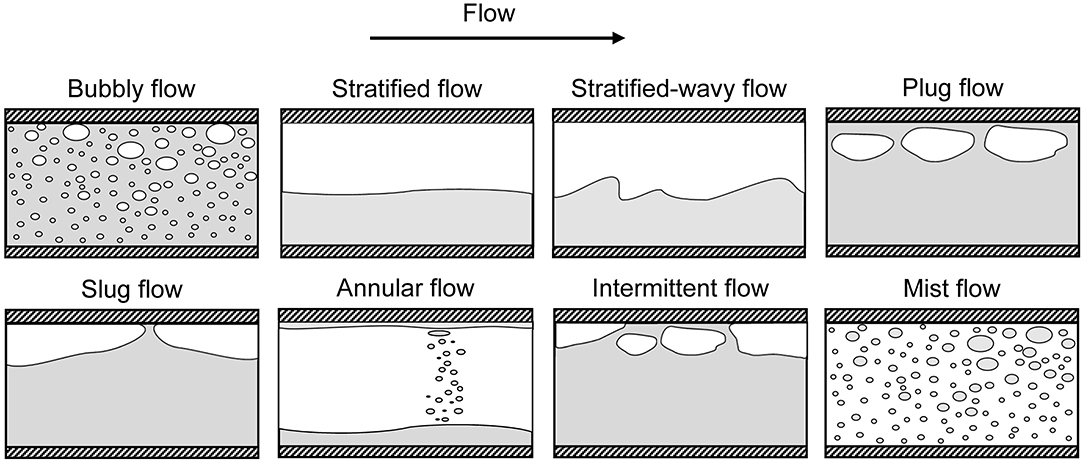
Flow patterns have been categorised as follows: bubbly, stratified, stratified-wavy, plug (or elongated bubble), slug, annular, intermittent and mist. A visualisation of the occurring flow regimes during flow boiling in horizontal tubes is shown in Figure 2. Both evaporation and condensation phase-change processes, have a major influence on the flow regimes (Kandlikar, 2002). Besides no entrainment of liquid droplets (Kim et al., 2012) and no dry-out occurring in the condensation process (Bejan and Kraus, 2003), it has been reported that the flow regimes during in-tube condensation are very similar to those of evaporation. The saturated vapour condenses on the tube wall and a thin condensate coating is formed all around the tube wall. For instance, the top of the tube is dry in the stratified flow of the evaporation process, but wet in the stratified flow of the condensation process.

FIGURE 2

Figure 2. Illustrations of flow regimes for flow boiling showing liquid (grey) and vapour (white).

In order to determine the prevailing flow regime at a particular operating condition, several flow regime maps have been developed. A thorough review about the fundamentals and applications of flow pattern maps is reported in the study of Cheng et al. (2008b). Other reviews also exist, such as by Kandlikar (2002) for flow boiling in minichannels. In general, different flow regime maps exist depending on the operating conditions. Thus, there is no universal flow regime map for all types of multiphase flows. Some flow regime maps published in the literature include the Baker (1954), Hewitt and Roberts (1969), Taitel and Dukler (1976), Barnea (1987), Steiner (1993), Kattan et al. (1998a), Hajal et al. (2003), Coleman and Garimella (2003), Wojtan et al. (2005a), Mandhane et al. (1974), and Cheng et al. (2008a) flow regime maps. All of these maps were developed for horizontal flow.

Figure 3A for instance, shows the Kattan et al. (1998a) and Hajal et al. (2003) flow pattern maps for R134a at a particular heat flux and tube diameter. It indicates under which conditions the different flow regimes can be expected for that fluid. Hajal et al. (2003) modified the Kattan et al. (1998a) flow pattern map, which was originally developed for evaporating and adiabatic flows, to represent flow patterns of condensing flows in a horizontal tube. It can be noted in Figure 3A that all the flow boundaries are the same for both evaporation and condensation, except the transition boundary labelled “Wavy,” which describes the transition between annular and stratified wavy flow (the boundary for evaporation is slightly tinted red in Figure 3A). The difference is due to the presence of dry-out in evaporation processes and its absence in condensation processes (Thome, 2005). For R22 for instance, Figure 3B provides a link between the predicted and measured evaporation heat transfer coefficients and the flow pattern maps of Wojtan et al. (2005a), where the red line in Figure 3C shows the operational mass flux. It can be observed that the modifications by Wojtan et al. (2005a) to the model by Kattan et al. (1998a) led to a better prediction of the “Wavy” patterns as confirmed by the experiments, where the transition between the intermittent and annular flow can be observed.

FIGURE 3

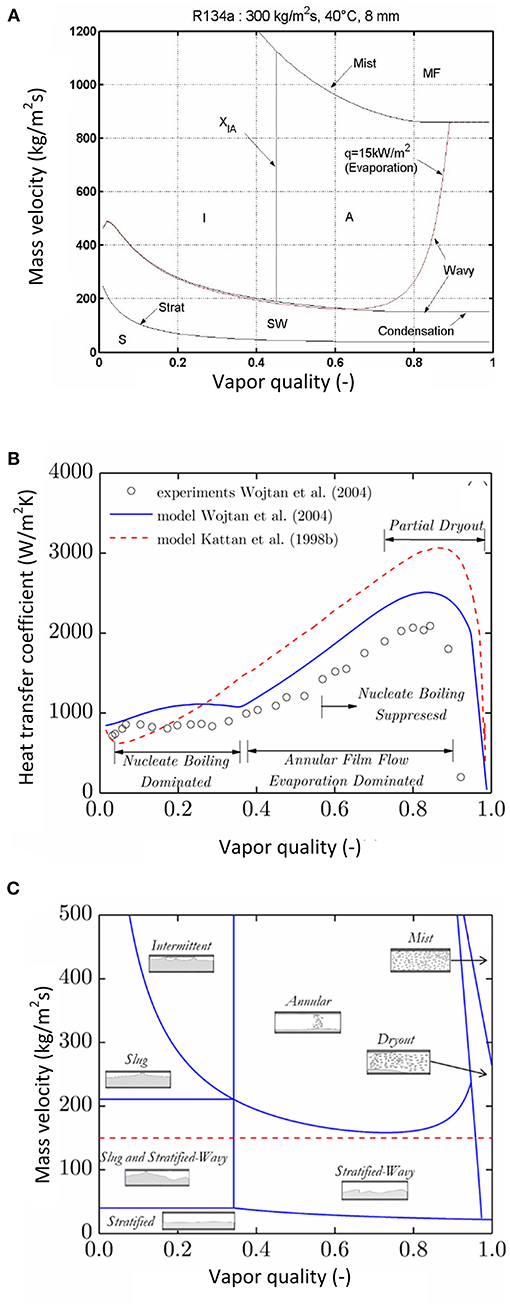
Figure 3. (A) Comparison between flow pattern transition boundaries of condensation and evaporation. Reproduced from a public access source. (Thome, 2005). (“S”, stratified; “SW”, stratified wavy; “I”, intermittent; “A”, annular; “MF”, mist flow) (B) Predicted heat transfer coefficients of the Kattan et al. (1998b) and Wojtan et al. (2005b) models plotted against the experiments of Wojtan (2004) (C) Generated flow pattern map by Wojtan et al. (2005a), for evaporating R22 at G = 150 kg/m²s, T_sat = 5°C, D = 13.84 mm and q″ = 3.6 kW/m².

A comparison between the Hajal et al. (2003) and Wojtan et al. (2005a) flow pattern maps which were proposed for flow boiling, was done by Garbai and Sánta (2012). The intermittent, annular, stratified wavy and stratified flow regimes are common to both flow pattern maps, whereas mist and slug flows are only present on the Wojtan et al. (2005a) map. Garimella et al. (2002) studied flow patterns of condensing flows of R134a in circular tubes and presented a criterion for the transition between intermittent and non-intermittent flows. Martín-Callizo et al. (2010) investigated the flow patterns associated with flow boiling of R134a experimentally and observed the isolated bubbly, confined bubbly, slug, churn, slug annular, annular and mist flows. They compared intermittent and non-intermittent flow patterns to the transition criterion proposed by Garimella et al. (2002). The experimental data of flow boiling tally with the transition criterion for condensation. Martín-Callizo et al. (2010) added that surface tension forces become significant in small diameter tubes and in flows whose Bond number tends to 1, and therefore the characteristics of flow boiling and flow condensation become similar.

Bejan and Kraus (2003) compared their refrigerant evaporation data with the Mandhane et al. (1974) flow pattern map. Although this flow pattern map is based on the Baker (1954) map with a much larger set of data range for water-air flow, it presented systematic errors. These problems arose because the properties of refrigerants differ from those of air. The errors are expected to be greater in condensation since the vapour density of refrigerants at condensation temperatures is larger than that at evaporation temperatures.

Several flow maps were used for the investigation of flow boiling in collector tubes of CSP applications. For instance, the map by Taitel and Dukler (1976) was used by Sun et al. (2015) and Odeh et al. (2000) to determine the flow pattern transitions. The flow map of Kattan et al. (1998a) was used by Frein et al. (2018). Elsafi (2015b) utilised the Wojtan et al. (2005a) map for evaluating their experimental data. Müller (1991) used the Steiner (1993) map to perform preliminary predictions of flow patterns in a parabolic trough power plant's absorber tube. Pye (2008) used the Barnea (1987) map to address the effects of tube inclinations.

Probabilistic methods for determining the flow regime also exist. Canière et al. (2010) found that the probabilistic flow mapping approach leads to an accurate and objective determination of the flow patterns, and thus, more accurate flow pattern maps, which is not the case in visual observations of flow. A drawback of such methods is that it requires the determination of probability function parameters for a large set of conditions since the approach is intrinsically not suitable to be used outside its proposed condition range (Canière, 2009).

Flow Boiling

In DSG, flow boiling occurs in the solar field within circular tubes which are in the order of magnitude of a few centimetres. Figure 4A gives a representation of the collector and reflector types that have the most relevance to DSG. These are parabolic trough, Fresnel and central receiver type lay-outs. For the first two, flow boiling occurs in horizontal flow, while in the latter, flow boiling could occur in vertical and horizontal flow, depending on the heat collector design. Solar tracking occurs by adjusting the orientation of the reflector surfaces. In the energy storage units, depending on their design, boiling during energy discharge could occur in several flow inclination and in flow passages that may or may not be circular, and in flow passages which could range in scale from micro-channels to macro-scale channels. Therefore, a wide range of geometric conditions are of importance to a holistic view of flow boiling in DSG.

FIGURE 4

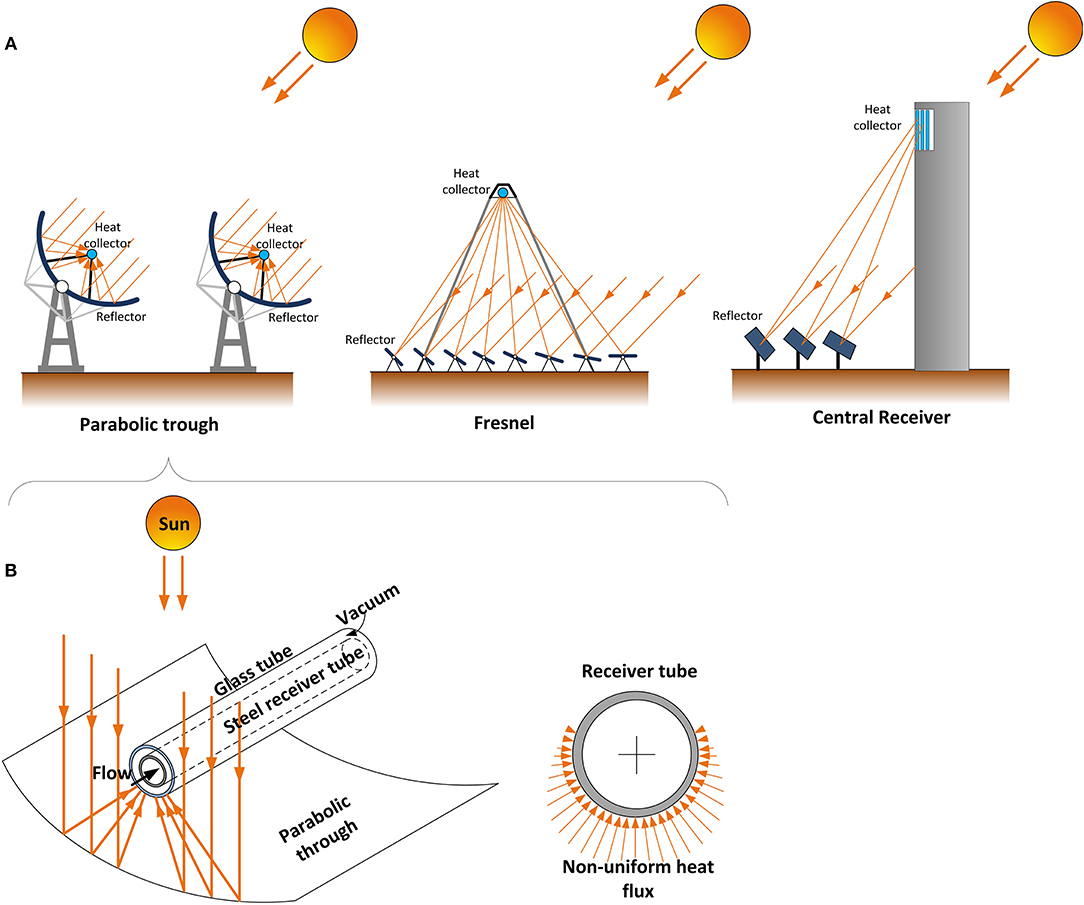
Figure 4. (A) Collector types in which flow boiling occurs during horizontal flow for parabolic trough and Fresnel collector and horizontal/vertical for central receivers. (B) Illustration of non-uniform heat flux on the collector tube in a parabolic trough solar collector.

Experimental Studies of Flow Boiling

Experimental In-tube Flow Boiling Heat Transfer Correlations

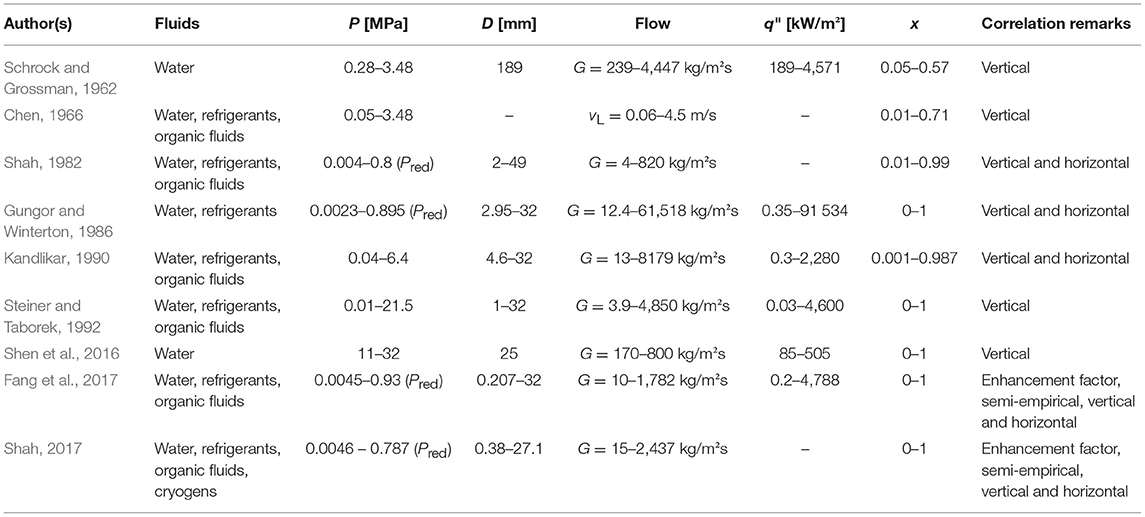
Table 1 lists the most recent and some of the key correlations that have been developed throughout the years, which claim to cover the flow boiling heat transfer of water/steam in tubes. In the table, P refers to pressure, D to diameter, G to mass flux, v_L to fluid velocity, q” to heat flux, and x to vapour quality. Some are discussed in more detail below in relation to other flow boiling works. Due to the complex nature of these correlations, only simplified equations are presented to aid the discussion. Interested readers are referred to the original texts for a full description of the correlations development and structure of the several intermediate variable groupings needed to execute the correlation calculations.

TABLE 1

Table 1. Flow boiling heat transfer correlations for straight and smooth tubes validated for water.

One of the earliest efforts to deduce a generally applicable two-phase heat transfer coefficient (h_TP) correlation was done by Chen (1966) and was applicable to several fluids in vertical flows. The total convective coefficient is defined as a superposition of the nucleate (h_NB) and convective boiling (h_CB) heat transfer coefficients. The Dittus-Boelter correlation was used for the convective part that is analogous with the liquid-only heat transfer coefficient, whereas the Forster-Zuber pool boiling correlation was incorporated as the nucleate term. A term based on the two-phase Reynolds number, F, was added to the convective part and a bubble-growth suppression factor S was included in the nucleate term. The general form is expressed as:

$\begin{array}{ll}{h}_{\text{TP}}=h_{\text{NB}}S+h_{\text{CB}}F& (1)\end{array}$

where F is a function of the empirically modified Lockhart-Martinelli parameter incorporating a momentum-analogy analysis. S is an empirical function of the two-phase Reynolds number.

Although it was validated and recommended by many authors, the correlation is reported to over-estimate the effect of nucleation (Kandlikar, 1990). The reason for the overestimation can be attributed to the fact that the Forster-Zuber's pool boiling correlation is validated with data obtained for a narrow range of experimental conditions. Moreover, the correlation is only valid for vapour qualities lower than 0.7 and solely for vertical tubes (Bertsch et al., 2009).

The Shah (1982) correlation was developed with a large experimental database from various studies and improved the Chen (1966) correlation for boiling in both horizontal and vertical flow passages. This was done by means of assigning a Froude number criterion that determines if the tube wall is wetted or not, depending on the flow orientation. An asymptotic-like approach is used, where mainly the largest of the nucleate or convective term was included in the calculation. The Dittus-Boelter correlation is used to obtain h_l, which is multiplied by factor ψ:

$\begin{array}{ll}{h}_{\text{TP}}=\psi h_{\text{l}}& (2)\end{array}$

Amongst others, ψ is dependent on the Froude number (Fr), the boiling number (Bo) and the convection number (Co) which is used for determining if the boiling is taking place in the purely nucleate, bubble suppression or purely convective regions. Later, Gungor and Winterton (1986) simplified the Shah (1982) correlation to reduce the amount of calculations needed, by discarding the convection number and instead employing an asymptotic approach with the two boiling mechanisms.

Kandlikar (1990) proposed a correlation that was developed from an extensive database of existing two-phase flow data. In addition to the methods used by Gungor and Winterton (1986) and Shah (1982), Kandlikar (1990) used the fluid-specific data to determine a new fluid-dependent parameter (F_fl): used to address nucleate boiling. The correlation also superimposes convective and nucleate boiling terms and takes the following form:

$\begin{array}{ll}{h}_{\text{TP}}=h_{\text{l}}\left[C_{1}C{o}^{C_2}{(25Fr)}^{C_5}+C_{3}B{o}^{C_4}{F}_{\text{fl}}\right]& (3)\end{array}$

Information on C₁to C₅ can be found in the original text.

More recently, Bertsch et al. (2009) developed a composite correlation that solves the Chen (1966) correlation's accuracy problem for small-diameter tubes. Steiner and Taborek (1992) proposed a semi-phenomenological flow boiling heat transfer correlation for vertical flows with the asymptotic approach.

The most recent milestone in two-phase heat transfer coefficient prediction came with the flow pattern-based models, some advantages of which have been mentioned earlier in the text. Kattan et al. (1998b) developed a heat transfer model for in-tube flow boiling in horizontal smooth tubes that incorporates the flow patterns, flow stratification and the partial dry-out in annular flow. With the incorporation of flow regimes in heat transfer prediction, the local peaks of heat transfer coefficients with respect to the vapour quality could be observed, where good predictive capabilities were reported at high vapour qualities (>85%) (Kattan et al., 1998b). Zhang et al. (2016e) modified the Kattan et al. (1998b) model to include the subcooling effects at the inlet which are observed in thermosiphon natural circulation loops.

Of significant importance to direct steam generation systems is the literature related to the flow boiling correlations for water heat transfer and pressure drop from the last two decades. It is mainly composed of boiling in mini- and micro-scale (or other compact heat exchangers) (Saisorn and Wongwises, 2012; Cheng, 2016), critical heat flux (Ong and Thome, 2011; Fang et al., 2015; Konishi and Mudawar, 2015), microgravity (Kattan et al., 1998b; Zhang et al., 2016e) and nuclear phenomena (Santini et al., 2016; Gou et al., 2017). Since the work of Steiner and Taborek (1992), only recent heat transfer correlations that are deduced for water flow boiling in conventional diameter tubes and channels (hydraulic diameters larger than 3 mm Kandlikar and Grande (2003) are proposed by Shen et al. (2016), Fang et al. (2017), and Shah (2017).

The Shen et al. (2016) correlation for non-post-dry-out conditions takes the form of:

$\begin{array}{ll}{h}_{\text{TP}}=h_{\text{l}}\left[0.0338{\left(\frac{1}{X_{\text{tt}}}\right)}^{0.0199}{\left(\frac{P}{P_{\text{cr}}}\right)}^{0.555}{\left(\frac{G}{G_{\text{max}}}\right)}^{-0.671}{q^{″}}^{0.97}\right]& (4)\end{array}$

where h_l is based on an adjusted Dittus-Boelter equation, X_tt is the Lockhart-Martinelli parameter, P_cr is the critical pressure and G_max is the maximum mass flux in their dataset.

The Fang et al. (2017) correlation takes the following form, expressed as a Nusselt number:

$\begin{array}{ll}N{u}_{\text{TP}}=F_{\text{fl}}{M}^{-0.18}B{o}^{0.98}F{r}^{0.48}B{d}^{0.72}{\left(\frac{{\rho }_{\text{l}}}{{\rho }_{\text{g}}}\right)}^{0.29}{\left[ln\left(\frac{{\mu }_{\text{lf}}}{{\mu }_{\text{lw}}}\right)\right]}^{-1}Y& (5)\end{array}$

with F_fl also being a fluid dependent parameter, M being the molecular mass, Bd the Bond number, ρ_l and ρ_g the liquid and vapour densities, μ_lf and μ_lw the liquid flow viscosity and the liquid wall viscosity, and Y a parameter that is dependent on the Prantl number.

The Shah (2017) correlation is expressed as follows and is an extension of the Shah (1982) correlation briefly described in Equation (2):

$\begin{array}{ll}{h}_{\text{TP}}=\psi h_{\text{l}}(2.1-0.008W{e}_{\text{GT}}-110Bo)& (6)\end{array}$

with We_GT being the Webber number based on the vapour mass flow.

These correlations have mainly empirical or semi-empirical forms, while the flow patterns are not taken into consideration. Moreover, the Shen et al. (2016) correlation is only valid for vertical tubes and for a narrow data range. Although, the Fang et al. (2017) and the Shah (2017) correlations claim to cover water flow boiling heat transfer in conventional size tubes and channels, none of the three correlations have been experimentally validated for saturated flow boiling heat transfer of water in smooth tubes.

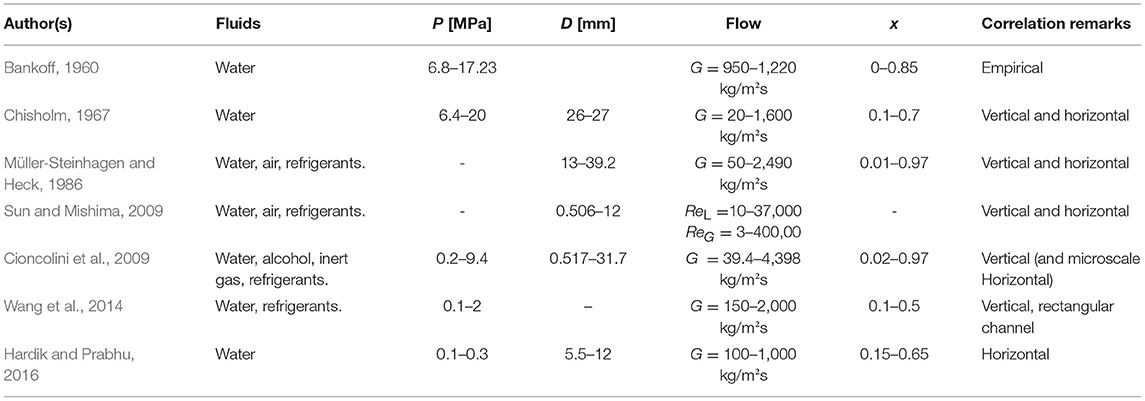
A similar situation exists for the pressure drop correlations. Since the Müller-Steinhagen and Heck (1986) correlation from 1986, only four prediction methods claim to cover water flow boiling pressure-drop data in conventional-sized and plain channels, namely the Sun and Mishima (2009), Cioncolini et al. (2009), Wang et al. (2014), and Hardik and Prabhu (2016) correlations. Interested readers are referred to the original texts for the expressions of the correlations, which vary significantly in format from one to the other. It is important to note that none of these methods are constructed by taking flow patterns and transitions into consideration. Cioncolini et al. (2009) correlated the empirical data from various studies only for annular flow in vertical tubes (horizontal flows were only investigated for microchannels). Also, no studies have been performed thus far that experimentally validate the Cioncolini et al. (2009) correlation's use for predicting the water/steam boiling pressure drop in tubes of practical sizes in the order of a centimetre. Moreover, the Sun and Mishima (2009) method is mainly proposed for micro- and small-diameter channels. Several studies exist that evaluate this correlation for water/steam boiling pressure drop. Wang et al. (2014) found a 54% mean deviation from their water flow boiling pressure drop data in a 2 mm by 40 mm narrow rectangular channel. Hardik and Prabhu (2016) found a 59% deviation from their water flow boiling pressure drop data in horizontal tubes. In both of these studies, the Müller-Steinhagen and Heck (1986) and Chisholm (1967) correlations showed better prediction accuracy (<40%) compared to the correlation proposed by Sun and Mishima (2009). Table 2 lists some two-phase pressure drop correlations for water/steam.

TABLE 2

Table 2. Flow boiling pressure drop correlations for straight and smooth tubes validated for water.

A first perspective on the reasons why the existing correlations (two-phase heat transfer or pressure drop) cannot be reliably extrapolated to water/steam applications is because they are developed for refrigerant flow boiling with a relatively low saturation temperature. As reported by Charnay et al. (2014), the research on two-phase flow boiling of refrigerants mainly focuses on saturation temperatures between −20°C and 40°C. Most of these values correspond to reduced pressures between 0.05 and 0.5. The critical pressures of common refrigerants vary between approximately 35 and 70 bar. These two-phase heat transfer correlation values range far from the critical pressure of water (220 bar). At this point, the finding by Cooper (1984) states that fluids exhibit similar thermo-physical properties at the same reduced pressures. Thus, at different values of reduced pressure, the heat transfer can be affected as the density and the viscosity of the liquid phase increases while the opposite trend will hold for the vapour phase. Hence, the liquid phase velocity increases, while the vapour phase velocity reduces (the slip ratio drops). Moreover, the surface tension increases and the gravity starts to play a less significant role in shaping the particular flow pattern (Charnay et al., 2014). None of the proposed correlations address these issues.

The flow boiling research that is specifically related to water/steam systems, is mostly confined to critical heat flux and subcooled flow boiling (Weisman and Pei, 1983) correlations for both macro- and micro-channels (Thome, 2004; Karayiannis and Mahmoud, 2017). In macrochannels that are used in nuclear applications, the saturated boiling is not desired due to safety reasons (Hewitt, 1982). In microchannels, saturated flow boiling can induce flow instabilities and reversals (Kaya et al., 2013). Since the mechanisms of subcooled and saturated flow boiling are different, an extrapolation covering the two is prone to errors.

Saturated flow boiling of water also requires high mass flow rates, due to the high latent heat of water. A high mass flow rate is crucial for having a longer annular flow region in the tube. However, higher mass flow rates also translates to higher pressure drops. Due to this constraint, larger diameter tubes need to be employed. The size considerations bring out a new issue for the existing predictive methods, since most of the two-phase flow boiling research is performed for refrigeration applications, where mainly smaller tube sizes (<10 mm) are used. From a hydrodynamics aspect, extrapolating small-diameter heat transfer and pressure drop data to larger diameters is an unreliable method due to several aspects of the flow boiling phenomenon that will need to be considered, such as the changing surface tension, shear stresses at the liquid-vapour interface (Dobson et al., 1993), the nucleate and convective heat transfer contribution ratio (convective heat transfer decreases at flow boiling in larger diameters) and the changing Reynolds number (Copetti et al., 2011).

Considerations on Flow Boiling Under High Radiative Heat Flux

Accurate control of the flow patterns is needed when designing a collector tube for concentrated solar power (CSP) applications. Of significant interest is the non-uniform nature of the incident heat flux on the collector tube in a parabolic trough solar collector as is illustrated in Figure 4B. Due to the high heat flux, large temperature variations can occur at the tube circumference between the wetted and dried out regions making a controlled annular flow regime crucial. The findings of Ajona et al. (1996) showed that temperature differences of 50 K occur at the circumference of a stainless steel tube of a collector accommodating stratified flow, where annular flow leads to 3 K difference only. A large temperature gradient at the tube circumference can lead to bending of the tube or breaking of the vacuum space glass casing (Odeh et al., 2000; Abedini-Sanigy et al., 2015). Moreover, the occurrence of slug flow is possible under high radiative heat fluxes, which can in turn can bring issues such as undesirable flow transitions (Odeh et al., 2000) with high circumference temperature oscillations that can lead to local dry-out spots (Ghajar, 2005), and vibrations (Al-Hashimy et al., 2016) that can lead to the physical damaging of brittle systems such as the CSP collector's glass components.

Research related to two-phase flow in CSP collectors is scarce. Odeh et al. (2000) developed a hydrodynamic model to evaluate the flow patterns and the pressure drop in a direct steam generation collector. The flow pattern investigation was based on the map provided by Taitel and Dukler (1976). The pressure drop was based on the Lockhart-Martinelli parameter and the Olujic (1985) model for low-velocity (typical for CSP) boiling pressure drop. Lobón et al. (2014) developed a simulation model to study the dynamic behaviour of a parabolic-trough solar system for direct steam generation. Their model could predict the temperature and pressure gradient distributions in the tube with an error of less than 6% and 4–12%, respectively. Elsafi (2015b) found a strong match (RMSE of 2.2%) between the measurements and the flow map of Wojtan et al. (2005a). However, his modelling approach did not address the transient conditions inside a collector tube.

Kumar and Reddy (2018) compared two-phase flow correlations for thermo-hydraulic modelling of direct steam generation (DSG) in a solar parabolic trough collector (PTC) system. They assessed the validity of existing two-phase heat transfer and pressure drop correlations for a range of local temperature and pressure measurements obtained for DSG in a PTC test rig (DISS facility in Almeria, Spain) by Lobón et al. (2014) The facility consists of 13 parabolic-trough collectors connected in series, with a total length of 700 m where the collector tubes have an inner diameter of 25 mm. The tested correlations for heat transfer were those of Gungor and Winterton (1986), Shah (1982), and Wojtan et al. (2005b), whereas for the pressure drop the Lockhart and Martinelli (1949), Grönnerud (1972), and Quibén et al. (2009) correlations were used. The temperature and pressure gradient profiles predicted by the correlations had an RMSE of <2.10% and <0.57%, respectively, when compared with the measurements.

Although the measurements of Lobón et al. (2014) and the predictions done by the simulation of Kumar and Reddy agree fairly well, the aforementioned correlations used in the model of Kumar and Reddy (2018) do not consider the non-uniform heat flux, that is typically encountered at solar collector tubes due to the uneven solar flux and receiver structure (Ajona et al., 1996; Shen et al., 2014; De Sá et al., 2018; Lin et al., 2018). Shen et al. (2014) studied the convective heat transfer of molten salt in a circular collector tube subject to non-uniform heat flux. Their measurements led to a new correction parameter, which was added to their single-phase Nusselt number correlation.

Another important aspect is the choice of the collector tube diameter. Employing smaller tubes has the advantage of higher heat transfer coefficients, lower thermal losses to the environment, and easier control of the annular flow pattern. However, using smaller tubes dramatically increases the pressure drop penalty, leading to a higher pumping power requirement and increases the need for a better quality concentrator, which can increase the cost. Moreover, flow instabilities and flow reversals may occur and negatively affect the performance of an evaporator with small diameter tubes subject to high heat fluxes (Kaya et al., 2014; Zhou et al., 2015). Although Odeh et al. (2000) concluded that using larger diameter tubes holds more advantages than disadvantages, the risk of flow stratification needs to be addressed.

Numerical Modelling of Flow Boiling

Inasmuch as CSP with DSG is a viable alternative for electricity generation, certain factors are essential for consideration during system design, installation, usage and maintenance. Given the challenges associated with experimental work in terms of cost and time, a number of modelling approaches have been developed to generate data but also to serve as design tools.

Flow Boiling Modelling Methods and Governing Equations

Two-phase flow can be modelled at different scales, including system scale, macroscale, mesoscale, and microscale, where each scale allows for the determination of particular flow features. Most computational fluid dynamic (CFD) codes model the fluid flow at macroscale level, whereby the fluid is considered as a continuum. A two-phase fluid flow may be solved using either the single fluid flow or the two-fluid flow approach. Unlike the two-fluid flow approach which considers each phase separately, the single fluid model solves only one set of conservation equations of mass, momentum and energy governing the fluid flow as follows:

$\begin{array}{l}\frac{\partial \rho }{\partial t}+\nabla ·\left(\rho \text{u}\right)=0\\ \frac{\partial \rho \text{u}}{\partial t}+\nabla ·\left(\rho \text{uu}\right)=-\nabla P+\nabla ·\tau +\rho \text{g}+F_{\sigma },& (7)\end{array}$

and

$\begin{array}{l}\frac{\partial (\rho c_{\text{P}}T)}{\partial t}+\nabla \left[\text{u}(\rho c_{\text{P}}T+P)\right]=\nabla .(k\nabla T)+Se+W\end{array}$

Here ρ represents density, t is time, u represents the velocity vector, τ is the stress tensor, g is the gravity vector, F_σ is the surface tension force, c_P is the specific heat, T is temperature, k is the thermal conductivity, Se is the energy source term and W is work.

The surface tension force, F_σ can be determined using the continuum surface stress (CSS) method (Lafaurie et al., 1994) or the continuum surface force (CSF) method (Brackbill et al., 1992; Yang et al., 2008). With CSF this is expressed as follows with subscripts l and g referring to liquid and vapor, respectively:

$\begin{array}{ll}{F}_{\sigma }={\sigma }_{lg}\frac{{\rho }_{\text{l}}{F}_{\text{l}}{\kappa }_{\text{g}}\nabla F_{\text{g}}+{\rho }_{\text{g}}{F}_{\text{g}}{\kappa }_{\text{l}}\nabla F_{\text{l}}}{0.5({\rho }_{\text{l}}+{\rho }_{\text{g}})}& (8)\end{array}$

where F_l and F_g are the volume fractions, σ_lg is the tension force along the liquid-vapour interface, and κ_l and κ_g represent the liquid and vapour curvature, respectively:

$\begin{array}{ll}{\kappa }_{\text{l}}=\frac{\Delta F_{\text{l}}}{|\nabla F_{\text{l}}|}{\kappa }_{\text{g}}=\frac{\Delta F_{\text{g}}}{|\nabla F_{\text{g}}|}& (9)\end{array}$

At the interfacial surface where both phases are present in almost equal proportion (that is κ_l = κ_g, ∇F_l = ∇F_g), the surface tension force can be rewritten:

$\begin{array}{ll}{F}_{\sigma }=2{\sigma }_{\text{lg}}\frac{\rho {\kappa }_{\text{g}}\nabla F_{\text{g}}}{{\rho }_{\text{l}}+{\rho }_{\text{g}}}& (10)\end{array}$

The dynamic boundary condition equation is used to express the unit normal to the surface of the cell close to the wall, hence modifying the interface curvature close to the wall:

$\begin{array}{ll}\vec{n}={\vec{n}}_{\text{w}}cos{\theta }_{\text{w}}+{\vec{m}}_{\text{w}}sin{\theta }_{\text{w}}& (11)\end{array}$

Here ${\vec{m}}_w$ and ${\vec{n}}_w$ are the unit vectors tangential and normal to the interface, respectively. θ_w is often referred to as the contact angle (Faghri and Zhang, 2006).

The Navier-Stokes equations are, however, not solved directly in most turbulent flow cases. A direct numerical simulation (DNS) would require a very fine computational domain and a very small time step size, which are well-beyond the present computing capabilities. Close to DNS, large-eddy simulation (LES) resolves the large-scale motions of the flow while the small-scale ones are modelled. However, the LES approach remains computationally expensive. Instead, the Reynolds-averaged Navier-Stokes approaches, which consist of decomposing a flow variable ϕ into a mean, φ and a fluctuating component, ϕ′ as shown below, are employed in most turbulent flows:

$\begin{array}{ll}\varphi =\overline{\varphi }+{\varphi }^{\prime }.& (12)\end{array}$

Considering a constant density, such a decomposition leads to the following Reynolds-averaged Navier-Stokes equations:

$\begin{array}{l}\frac{\partial {\overline{u}}_{\text{j}}}{\partial x_{\text{i}}}=0;\\ \rho \frac{\partial {\overline{u}}_{\text{j}}}{\partial t}+\rho {\overline{u}}_{\text{i}}\frac{\partial {\overline{u}}_{\text{j}}}{\partial x_{\text{i}}}=-\frac{\partial \overline{p}}{\partial x_{\text{j}}}+\frac{\partial }{\partial x_{\text{i}}}\left[\mu \frac{\partial {\overline{u}}_{\text{j}}}{\partial x_{\text{i}}}-\rho \overline{u^{\prime }{u}_j{}^{\prime }}\right]& (13)\end{array}$

where μ refers to the viscosity.

A turbulence model is thus needed to close the set of governing fluid flow equations and to cater for the turbulence effects of the flow. A wide range of turbulence models, including standard k−ε, realisable k−ε, standard k−ω and shear-stress transport (SST) k−ω models, are available in the literature.

It must be pointed out that while solving an incompressible flow, a pressure-velocity coupling method is required because pressure does not have its own transport equation. A method is then required to correct both the pressure and the velocity fields while satisfying the continuity equations. The different methods that allow these particular corrections include the SIMPLE algorithm, the SIMPLEC algorithm, and the PISO method.

The interface between the two phases of the two-phase fluid flow can be localised using either an interface capturing or interface reconstruction method. Three popular techniques are the front tracking (FT), the level-set (LS), and the volume of fluid (VOF) method. Figure 5A shows the reconstruction of an interface using the FT, LS, and VOF methods. In these methods, a marker function is reconstructed or advected directly to determine the fluid properties (χ) at a particular point, x. It is given by:

$\begin{array}{ll}\chi \left(x\right)=\{\begin{array}{cc}1,& ifthechosenprimaryphaseisatx;\\ 0,& ifthesecondaryphaseisatx.\end{array}& (14)\end{array}$

FIGURE 5

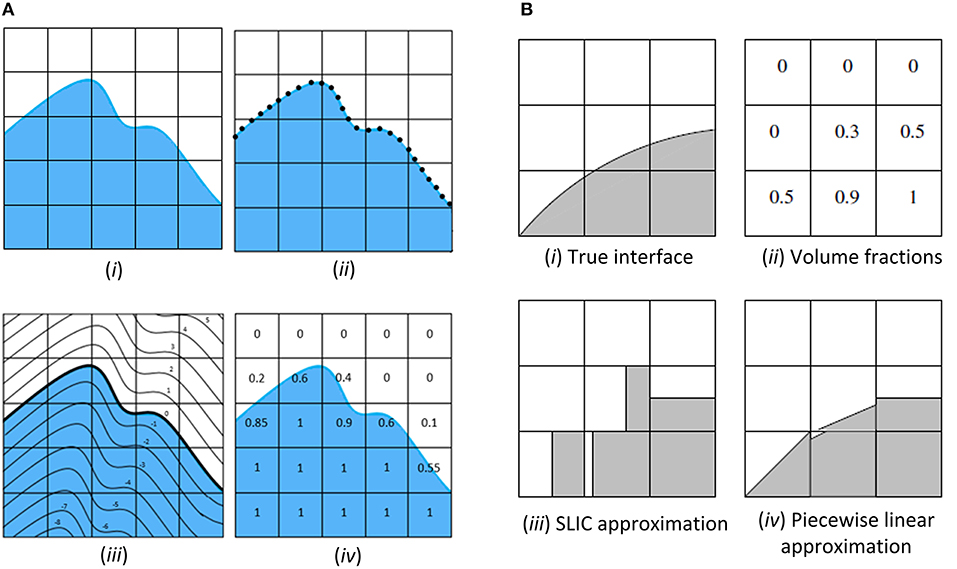
Figure 5. (A) (i) Example of an interface. (ii) FT method employs connected marker points to represent the interface. (iii) The zero iso-level curve represents the interface in LS method. (iv) In VOF, volume fractions are defined in each cell to indicate the position of the interface. (B) The interface (i) is represented as volume fractions as shown in (ii) by VOF methods. The interface is approximated by SLIC in (iii) and PLIC in (iv).

The FT method is an interface tracking method whereby the interface is represented by connected marker points which are advected in an Lagrangian manner. A major drawback of this method is that it does not handle topological changes of the interface, such as merging of two interfaces or a rupture of a film. Therefore, an additional algorithm needs to be implemented in order to cater for topological changes.

The LS and the VOF methods are based on the interface capturing formulation. Originally developed by Osher and Sethian (1988), the LS method employs a continuous marker function to represent the distance of a particular point from the interface. The LS method is widely employed due to its simplicity and its ability to handle topological changes of the interface. However, this method does not preserve mass and therefore a mass correction algorithm is necessary.

On the other hand, a significant advantage of the VOF method is its ability to preserve mass accurately. It also accounts for topological changes of the interface and it can easily be extended from a two-dimensional to a three-dimensional Cartesian mesh. The VOF method keeps track of a colour function C, which is defined as the average value of the marker function χ(x, y), in each computational cell. The function C is calculated as follows in a two-dimensional domain (x, y):

$\begin{array}{l}C=\frac{1}{\Delta x\Delta y}{\displaystyle {\int }_V\chi \left(x,y\right)dxdy}\\ =\{\begin{array}{l}1,ifthereferencefluidisinthecell;\\ 0,ifthereferencefluidisnotinthecell;\\ 0<C<1,ifthereisaninterfaceinthecell.& (15)\end{array}\end{array}$

where V is the volume of the computational cell. The density, viscosity and thermal conductivity of the two-phase fluid flow are then, respectively determined as:

$\begin{array}{l}\rho =C{\rho }_1+(1-C){\rho }_2,\\ \mu =C{\mu }_1+(1-C){\mu }_2,& (16)\end{array}$

and

$\begin{array}{l}k=C{k}_1+(1-C)k_2,\end{array}$

where ρ₁, μ₁, k₁ are the properties of the reference fluid and ρ₂, μ₂, k₂ are those of the secondary fluid.

VOF is a also a commonly used method in CFD (Magnini et al., 2013). Although VOF is conservative in nature, special care is needed to track the interface between phases correctly. The interface reconstruction techniques of the VOF method can be classified into donor-acceptor schemes, high-order differencing schemes and line techniques. These techniques can further be categorised into the Hirt and Nichols method, the flux-corrected transport (FCT) method, the compressive interface capturing scheme for arbitrary meshes (CICSAM), the modified high resolution interface capturing (HRIC) method, the simple line interface calculation (SLIC) method, and the piecewise linear interface calculation (PLIC) method. Rudman (1997) investigated the accuracy and efficiency of SLIC, Hirt & Nichols, FCT-VOF and PLIC methods as proposed by Youngs (1982) and concluded that the latter method outperforms the others. Figure 5B illustrates the reconstruction of an interface using the SLIC and PLIC methods, whereby the accuracy of the PLIC approach is noted.

The liquid-vapour interface (F_l + F_v = 1) can be tracked or captured by solving the volume fraction continuity equation for both phases, which is given as:

$\begin{array}{ll}\text{Liquid phase}:\frac{\partial F_{\text{l}}}{\partial t}+div\left(F_{\text{l}}\text{u}\right)=-\frac{{\dot{m}}_{\text{lg}}}{{\rho }_{\text{l}}}& (17)\end{array}$

$\begin{array}{ll}\text{Vapour phase}:\frac{\partial F_{\text{v}}}{\partial t}+div\left(F_{\text{v}}\text{u}\right)=-\frac{{\dot{m}}_{\text{lv}}}{{\rho }_{\text{v}}}& (18)\end{array}$

When F_g = 1 (that is F_l = 0), the region is entirely vapour and when F_l = 1 (that is F_g = 0) in which the region is entirely liquid. The mass flow rate of the phase change and the heat generation per unit volume is calculated based on the temperature field obtained during the process. ṁ_e is the mass transfer rate of evaporation, which is given in terms of the heat generaton per unit volume (Q) and the latent heat of vapourisation (LH):

$\begin{array}{ll}{\dot{m}}_{lg}=\frac{Q}{LH}& (19)\end{array}$

The mass transfer rate of evaporation is given by Lee (1980) as follows:

$\begin{array}{ll}{\dot{m}}_{lg}=\frac{{r_{\text{lg}}\rho }_{\text{l}}{F}_{\text{l }}(T_1-T_{\text{sat}})}{T_{\text{sat}}}(T_1\ge T_{\text{sat}})& (20)\end{array}$

$\begin{array}{ll}{\dot{m}}_{lg}=\frac{{r_{\text{gl}}\rho }_{\text{g}}{F}_{\text{g }}(T_1-T_{\text{sat}})}{T_{\text{sat}}}(T_1<T_{\text{sat}})& (21)\end{array}$

where r_lg and r_gl are rates of evaporation and condensation, respectively.

The fluid properties are defined by the mixture of the two-phases:

$\begin{array}{r}{\rho ={\rho }_{\text{l}}F}_{\text{l}}+{\rho }_{\text{g}}{F}_{\text{g}}\\ {\mu ={\mu }_{\text{l}}F}_{\text{l}}+{\mu }_{\text{g}}{F}_{\text{g}}\\ c_{\text{p}}=\frac{1}{\rho }({{\rho }_{\text{l}}{c_{\text{p}}}_{\text{l}}{F}_{\text{l}}+\rho }_{\text{g}}{c_{\text{p}}}_{\text{g}}{F}_{\text{g}})\\ k{=k_{\text{l}}F}_{\text{l}}+k_{\text{g}}{F}_{\text{g}}\\ c_{\text{p}}T=\frac{{\rho }_{\text{l}}{F}_{\text{l}}{E}_{\text{l}}+{\rho }_{\text{g}}{F}_{\text{g}}{E}_{\text{g}}}{{\rho }_{\text{l}}{F}_{\text{l}}+{\rho }_{\text{g}}{F}_{\text{g}}}\\ E_{\text{l}}=C_{\text{g},\text{l}}(T-298.15),E_{\text{g}}=C_{\text{g},\text{g}}(T-298.15)& (22)\end{array}$

where temperature, T, is expressed with Kelvin as unit and 298.15 K chosen as the reference temperature.

The Eulerian multiphase model can also be used to solve flow boiling problem numerically. It successfully models multiple separate but interacting phases. However, it is deficient in modelling streamwise periodic flow with constant mass flow rate, non-viscous flow and solidification and melting flow. The number of secondary phases that can be modelled depends on computational power and the convergence behaviour. It is not commonly used due to its complexity. The model governing conservation equations are quite different from that which is used in the VOF model in which each of the conservation equations are solved per phase (that is the continuity and the momentum equation) and thereafter coupled together using the pressure and the interphase exchange coefficients except for the energy equation.

Numerical Modelling of the Heat Transfer Coefficients

Magnini et al. (2013) simulated flow boiling in a microchannel to investigate the phase interface, the variation in the local heat transfer coefficient at the heated wall, the hydrodynamics of elongated bubbles during evaporation, and the flow and thermal phenomena in the channel with R113 using the volume of fluid (VOF) method. Liquid film evaporation was observed to be the dominant heat transfer mechanism. Guo et al. (2016) considered annular flow boiling in microchannels and observed that the heat transfer coefficient was initially high after which it decrease to constant value even as the Graetz number (Gz) decreased. Lorenzini and Joshi (2015) studied flow boiling for non-uniform heat flux in a silicon microchannel.

In the numerical analysis of the saturated flow regime for the slug flow regime in a microchannel, Magnini and Thome (2016) observed that the heat transfer coefficient was found to observe a direct relationship with the bubble frequency. Zhang et al. (2016g) observed that at low inlet subcooling temperatures of 10 and 40 K, the heat transfer coefficient was significantly increased with a reduced pressure drop along the channel. Lee et al. (2016) computed the heat transfer coefficient of GaN-on-SiC semiconductors devices for the various flow regimes. For the bubbly flow regime, an increase in mass flux suppressed nucleate boiling growth, which consequentially decreased the heat transfer coefficient. However, in the annular flow regime where convective boiling is the prevailing mechanism of heat transfer, the heat transfer coefficient was observed to increase with mass flux.

Zhang and Jia (2016) studied the heat and mass transfer behaviour of liquid nitrogen and flow patterns evolution during flow boiling in minichannels and microchannels by using a coupled volume of fluid (VOF)/level-set method in a three-dimensional domain. They found that the heat transfer coefficient strongly depends on the flow pattern and that the heat transfer coefficient continues to increase along the flow direction as the flow patterns develop.

Numerical Modelling of the Pressure Drop

In power and process industries, the design of any plant requires accurate prediction of the pressure. For two-phase flow, the total pressure drop can be expressed as the summation of the pressure drops due to acceleration as a result of the phase change, friction, gravitational force and sudden expansion or contraction at the entrance or exit region (Kandlikar et al., 2005):

$\begin{array}{ll}\Delta P_{\text{Total}}=\Delta P_{\text{accel}}+\Delta P_{\text{frict}}+\Delta P_{\text{grav}}+\Delta P_{\text{in}-\text{out}}& (23)\end{array}$

In a macrochannel, acceleration pressure drop strongly depends on the superficial void fraction (Tibiriçá and Ribatski, 2013). Pressure drop behaviour follows the same trend in both microchannels and macrochannels, however correlations developed for macrochannel pressure drop cannot be used to predict microchannel behaviour because of the different relative importance of forces acting on the flow and the differences in the behaviour of the fluid (Copetti et al., 2011). The presence of a wide range of flow regimes as a result of varying physical conditions along the heated channel, complicates the computation of pressure drop along the length.

Tibiriçá and Ribatski (2013) attribute the reasons for the differences in the results on pressure drop by different authors on to inadequate information about the roughness ratio of the inner surface of the channels, inadequate knowledge of the experimental conditions, lacking experimental result validation using single-phase flow pressure drop and energy balance, as well as poor and inconsistent assumptions during evaluation. However, discussed below are the observations from different numerical simulations by various researchers.

Large pressure drops have been identified as one of the key problems in two-phase heat sinks. However, Fang et al. (2010) introduced the concept of vapour-escape mechanism to mitigate pressure drop comparable to single-phase flows in microchannel without compromising the high heat transfer coefficient associated with the phase change process. They considered numerical analysis of two-phase flow boiling in a vapour-venting microchannel using a VOF method for interface capturing. Without the vapour-venting mechanism, the internal volume of the channel becomes rapidly filled and clogged with vapour, acting like fouling layer and drastically reducing the cross section of channel available for liquid flow. The presence of vapour bubbles filling the channel section increase the pressure drop in a channel, a further reason why pressure drop is higher in microchannel as compared to macrochannel.

Mukherjee and Kandlikar (2005) performed numerical simulations to study the influence of inlet constriction on bubble growth in flow boiling. The study highlighted that pressure drop varies inversely with the channel diameter. Yang et al. (2008) observed relatively large fluctuations in the pressure drop along the channel length as more bubbles were generated and coalesced, and more Significant pressure drop and volume fraction decreases were experienced when flow wave valleys reached the channel exit. Also, an increase in both pressure drop and volume fraction was observed as heat flux increased.

Wei et al. (2011) performed a numerical investigation on subcooled flow boiling under swing motion to predict bubble behaviour. Results showed large pressure drop fluctuation for swing motion but an insignificant fluctuation for motionless conditions. Magnini et al. (2013) studied the heat transfer and hydrodynamics associated with elongated bubbles during flow boiling. They observed that the pressure drop increased as the Reynolds and the capillary number increased.

Liu et al. (2016a) considered subcooled flow boiling at constant heat flux with deposited fouling layer. They discovered that the pressure drop increased significantly with an increase in inlet velocity. Lee et al. (2016) studied GaN-on-SiC semiconductor microchannel coolers devices with high heat flux, focusing on the heat transfer and flow phenomena. They compared the effect of tapered channel design (45° tapered) with an un-tapered channel design at varying mass fluxes. It was demonstrated that half of the entire pressure drop occurred at the entrance of an un-tapered microchannel due to sudden contraction. Bahreini et al. (2017) considered a vertical minichannel and found that the pressure drop increased as the Reynolds number of the liquid at the inlet increased under both microgravity and non-microgravity conditions for subcooled flow boiling under conjugate heat transfer conditions.

Modelling of Steam Generation Process Inside a Solar Collector Tube

Table 3 summarises numerical studies performed on solar collector tubes, some for steam generation. All of these studies considered parabolic trough solar collectors. Of special interest are the studies that start to consider non-uniform heat flux boundary conditions. In general, though, this is still lacking in many studies, specifically lab-scale experimental work, probably due to the difficulty in replicating such thermal boundary conditions. For this reason, numerical simulations that do consider non-uniform heat flux are becoming more important.

TABLE 3

Table 3. Numerical studies on solar collector tubes.

Flow Condensation

In condensing power plants, the exhaust steam is discharged into the condenser, which allows the steam to expand to a relatively low pressure, increasing the cycle efficiency. In non-condensing power plants, the steam discharged from the turbine is at atmospheric pressure or a pressure slightly higher than atmospheric pressure. Thus, condensing power plants have two significant advantages. Firstly, a greater amount of energy is derivable per kilogram of steam. In addition, since the steam condenses in the condenser, it can be recycled and recirculated to the boiler with the help of a pump. This water recycling is especially important in areas with water shortages, quite unlike non-condensing power plants, which discharge the steam into the atmosphere and require a fresh supply of water to be pumped into the boiler from a nearby stream or river (Chanda and Mukhopaddhyay, 2016; Woodruff et al., 2016).

The low temperature loss of heat is the main reason that power plant efficiency is pegged around 45%. Based on the second law of thermodynamics, the heat loss in the condenser cannot be avoided (Gara, 1995). A temperature difference between the inlet temperature of the steam turbine and that of the condenser exhaust is required for heat to be converted into mechanical energy. Better conversion can be achieved in two ways: either by increasing the turbine inlet steam temperature or by decreasing the temperature at the outlet of the turbine (condenser temperature) (Breeze, 2014).

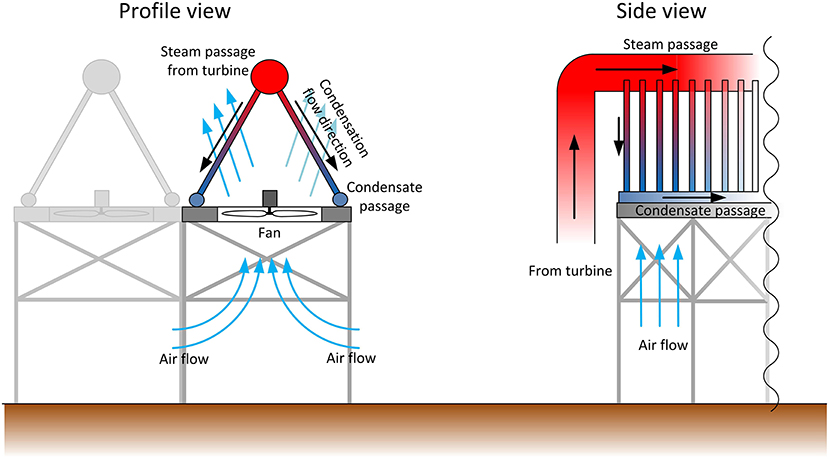
Regions with high direct normal irradiance are generally dry and arid. This necessitates the use of air cooled condensers opposed to water-cooled condensers. Figure 6 shows a representation of the lay-out of an A-frame type air cooled condenser. Low density steam from the turbine is distributed into two banks of tubes inclined in a downward direction. Air is passed over the tubes via fans to sustain the condensation process inside the condenser tubes at a desired rate. The condenser tubes may also be vertical or even horizontal depending on the condenser design, but almost always makes use of circular tubes. Other flow passage geometries may however exist in thermal storage units, depending on their design. As with flow boiling, a wide range of applicable operating condition and flow passage geometries and size ranges exist for condensation in DSG systems.

FIGURE 6

Figure 6. Schematic layout of an A-frame type air cooled condenser.

Experimental and Modelling Studies in Simplified Geometries

It is not always economical and feasible to conduct two-phase phenomena experiments in full scale conditions. To overcome this, numerical methods and experimental work on simplified geometries are conducted to better understand the heat transfer and pressure drop phenomena. Extensive reviews of condensation work have been conducted by Dalkilic and Wongwise (2009) and Lips and Meyer (2011).

Correlations based on experimental data are widely used to predict the characteristic parameters like pressure drop and heat transfer coefficient in multiphase systems. During recent years many researchers worked on the development of experimental correlations for the prediction of pressure drop and heat transfer coefficient for condensing flows. The developed correlations considered the dominant parameters such as: working fluid, characteristic length, heat flux, saturation temperature, flow regime, mass flux, and phase quality. Tables 4, 5 present a summary of the most applicable correlations published in literature for condensation pressure drop and heat transfer coefficients, respectively. Some of them are discussed briefly below, but interested readers are referred to the original texts for full description of the various correlations.

TABLE 4

Table 4. Experimental correlations for condensation heat transfer coefficient.

TABLE 5

Table 5. Experimental correlations for pressure drop in two-phase and/or condensing flows.

The Cavallini et al. (2006) heat transfer coefficient correlation, which similarly represents the basis of many other correlations or portions of several other correlations, uses the following two equations to make predictions in the temperature difference dependence regime and the temperature difference independence regimes, respectively:

$\begin{array}{l}{h}_{\text{TP},\text{A}}=h_{\text{l}}[11.128x^{0.8170}{\left(\frac{{\rho }_{\text{l}}}{{\rho }_{\text{g}}}\right)}^{0.3685}{\left(\frac{{\mu }_{\text{l}}}{{\mu }_{\text{g}}}\right)}^{0.2363}\\ {\left(1-\frac{{\mu }_{\text{g}}}{{\mu }_{\text{l}}}\right)}^{2.144}{\mathrm{Pr}}_1^{-0.100}]& (24)\end{array}$

$\begin{array}{ll}{h}_{\text{TP},\text{D}}=\left[h_{\text{TP},\text{A}}{\left(\frac{J_{\text{g}}^{\text{T}}}{J_{\text{g}}}\right)}^{0.8}-h_{\text{strat}}\right]\left(\frac{J_{\text{g}}}{J_{\text{g}}^{\text{T}}}\right)+h_{\text{strat}}& (25)\end{array}$

where Pr is the Prandtl number, h_strat is the stratified flow regime heat transfer coefficient, J_g is the transmission parameter, and $J_{\text{g}}^{\text{T}}$ is the transition dimensionless gas velocity.

The Shah (2016a) heat transfer coefficient correlation aims to present a comprehensive approach and covers both vertical, horizontal and inclined flows, and incorporate improvements from earlier correlations including portions of the Cavallini et al. (2006) heat transfer coefficient correlation. Shah uses the Webber number to differentiate between different flow regimes and offers different equations formats for each. Interested readers are referred to the original text for a full description of the equations.

In conjunction with experimental work, a significant effort is being made to supplement experimental data with numerical data as is shown in Table 6. Similar governing equations and modelling approaches, as discussed earlier in the flow boiling section, are also applicable to flow condensation. As with flow boiling, different working fluids, mass fluxes, geometries and boundary conditions have been considered. However, most of the available numerical in-tube condensation models are for the annular flow regime because this flow pattern delivers the highest heat transfer coefficient and persists over a large section of the tube length.

TABLE 6

Table 6. Summary of computational condensation studies.

Ganapathy et al. (2012, 2013) compared numerically predicted two-phase frictional pressure drop and two-phase Nusselt number with prior empirical correlations and concluded that the predictions of the proposed numerical model are of reasonably good accuracy. Yu et al. (2018) used the numerically determined film heat transfer coefficient to calculate the heat transfer coefficient of zeotropic mixtures. Qiu et al. (2015) compared numerically determined heat transfer coefficients and frictional pressure drops using different turbulence models and concluded that the Reynolds stress model gave the best results because of its ability to cater for anisotropic turbulent flows. The authors also showed that numerical results of the heat transfer coefficient and the frictional pressure drop are closer to experimental values when entrainment effects are considered.

Kim and Mudawar (2012) proposed a theoretical control-volume-based model for annular flow condensation in rectangular microchannels. They highlighted the complexities of modelling annular flow. Later, Park et al. (2013) modified the theoretical model of Kim and Mudawar (2012) to predict heat transfer coefficient in a vertical circular tube under the influence of gravity. Lee et al. (2013) employed the theoretical model with the modifications by Park et al. (2013) to model annular flow condensation in microgravity.

Da Riva and co-workers (Da Riva and Del Col, 2009, 2011, 2012; Da Riva et al., 2010a, 2011, 2012; Del Col et al., 2014) conducted a series of extensive numerical studies on annular flow condensation of R134a in a 1 mm inner diameter horizontal minichannel. In all of their studies, they adopted a steady three-dimensional VOF model to analyse the influence of gravity, turbulence and surface tension on the flow. More recently, Kharangate et al. (2016) successfully captured the interfacial behaviour of the latter flow pattern, including its waviness.

Many researchers prefer a turbulent model to a laminar one for modelling this combination of flow types. In their studies, Da Riva and co-workers investigated the use of both the laminar and the turbulent models in the liquid film, while keeping the turbulent model for the vapour core and reported the impacts of each computational approaches. For the laminar liquid film approach, the authors modified the standard k−ω model so that the values of the turbulent viscosity are set to zero and the actual value given by the k−ω model in the liquid and vapour phase, respectively. Regarding the turbulent liquid film approach, the two-equation shear stress transport (SST) k−ω turbulence model is employed throughout the computational domain. The laminar liquid film approach accurately predicts the condensation heat transfer coefficients for low mass fluxes only. On the other hand, the turbulent liquid film approach accurately predicts correctly at high mass fluxes but over-predicts at low mass fluxes.

Although experimental studies show an influence of mass flux on the heat transfer coefficient, the laminar computational approach does not exhibit this. This may be the reason why researchers choose the turbulent computational approach. Da Riva et al. (2012) stated the causes of over-prediction of heat transfer coefficient by the turbulent model, as firstly the model predicts the transition to turbulence at low Reynolds number and secondly, the turbulent Prandtl number used during numerical simulations should be higher than 0.85 to decrease the turbulent thermal conductivity and hence avoid over-predictions. They stated that the very weak effect of mass flux on the heat transfer coefficient by the laminar liquid film approach is due to the large stratification of condensate by the latter approach and therefore the contribution of the tube bottom to the global cross-sectional heat flux is negligible.

Numerical simulations of vertical condensation flow were conducted by Lee (1980) and Kharangate et al. (2016). While Lee (1980) investigated vertical down-flow, Kharangate et al. (2016) studied condensation of FC-72 in vertical upward flow. Similar to Lee et al. (2015), Kharangate et al. (2016) simulated transient two-dimensional condensing flows in an axisymmetric computational domain. In both studies (Lee et al., 2015; Kharangate et al., 2016), local values of the heat transfer coefficient and the wall temperature have been under-predicted and over-predicted in the upstream and downstream regions of the tube, respectively. Bahreini et al. (2017) studied the effect of gravity on the flow boiling inside a vertical tube under conjugate heat transfer. The results showed that the heat transfer coefficient increased as gravity decreased, while the pressure drop showed the reverse behaviour.

Following the studies of Da Riva and co-workers, Zhang and co-workers (Zhang and Li, 2016; Zhang et al., 2016a,b) simulated condensing flows of R410a in horizontal mini/micro-tubes. They investigated the effect of saturation temperature on film thickness and heat transfer coefficient. The three-dimensional steady-state simulations revealed the formation of vortices during the condensation. In Zhang et al. (2016c,d); Zhang et al. (2017) the heat transfer enhancement in round, flattened tubes and microfin tubes was investigated. When compared to a round tube with a hydraulic diameter of 3.78 mm, the flattened tubes with aspect ratios of 3.07, 4.23, and 5.39 resulted in higher heat transfer coefficients. The numerical results presented by Zhang et al. (2017) showed microfin tubes with larger helical angles enhanced the heat transfer coefficient. The authors achieved good agreement of numerically determined heat transfer coefficients and pressure drops with empirical correlations (Zhang and Li, 2016; Zhang et al., 2016a,b,c,d).

It is noted from Table 6 that the boundary condition imposed at the wall of the tube is either defined in terms of temperature or heat flux. In their investigations, Da Riva and co-workers applied a constant wall temperature such that T_sat−T_wall = 10 C, while Lee (1980) and Kharangate et al. (2016) applied an axial variation of wall heat flux using a user-defined function in Fluent. Da Riva and Del Col (2011) stated that a constant wall temperature instead of a constant heat flux should be imposed since it reflects the actual operation of condensers, whereby the condensing refrigerant is being cooled by means of a secondary fluid.

Full-Scale Investigations

As discussed earlier, the condensation phenomenon has been investigated by many researchers, however, the majority of them were conducted at lab scale. From a practical point of view there should be a link between the outcomes of the experimental studies and their applicability in real situations. As an example, new multi-effect distillation units are being designed using tilted tubes for the evaporator and condenser sections. Such an approach probably came from the results of the previous research works on the condensation of steam and refrigerants inside (Caruso and Maio, 2014; Cao et al., 2017) and outside (Nada and Hussein, 2016) of tubes, all of which were done at lab scale.

Another approach is to conduct research on actual systems and apparatus, to thoroughly understand the phenomena related with real operating conditions and scales. To do so, some researchers performed experiments on industrial scales (Wu et al., 2015; Chen et al., 2017a). Mazed et al. (2018) performed an experimental study on condensation of steam inside a pressure vessel prototyped from a real thermonuclear reactor. The results showed that the condensation regime is governed by the water temperature, downstream pressure and the steam mass flow rate. They also found that the stable condensation regime requires a minimum mass flow rate per passage of about 2.5 g/s for a water temperature of 10°C; and that this critical steam flow rate increased with the increase in the water temperature.

In another work, Berrichon et al. (2016) built an experimental set-up to study reflux condensation at sub-atmospheric pressure based on the actual scale of heat exchangers in power plants. They observed that the condensation heat transfer coefficient for the reflux condensation was lower than the co-current flows, which could be due to the thicker condensate film in the co-current flows. They also proposed an analytical method based on the diffusion layer theory, momentum balance and combination of heat and mass transfer for the prediction of the condensation heat transfer coefficient. Milovanovic et al. (2012) proposed a method for the prediction of reliability in real condensation thermal electric power plants. Their modified algorithm was able to evaluate the reliability of reference thermal power plant system and also present the optimised operating conditions for the other nominal powers.

Rusowicz et al. (2017) proposed a two-dimensional steady-state numerical model to predict the fluid flow and the heat transfer in an operating two-tube pass condenser in a 50 MW power plant. The model considered the tube bundle in the condenser to be porous. The flow was modelled using the conservation equations of mass, momentum and air mass fraction, which were solved using the upwind Petrov-Galerkin finite element method. The results of the numerical model, which was validated against measured cooling water temperatures, demonstrated the distributions of velocity, pressure and inert gases. In this way, the regions of high pressure and high air concentration were identified in the condenser.

The flow in real condensers is, however, three-dimensional and hence, three-dimensional models are needed to capture the full flow details (Rusowicz et al., 2017). Roy et al. (2001) reported a quasi-three-dimensional steady-state steady-flow model to investigate the influence of air in-leakage on the efficiency of a condenser in a 750 MW power unit. The model, which was based on the conservation equations for mass, momentum, energy and air mass fraction, also accounted for the ejection of air. The model was validated and agreed well with measured cooling water inlet and outlet temperature data.

Laskowski (2012) employed the Buckingham Π theorem to derive two non-dimensional parameters, which depend on measured parameters including, the temperature difference between the inlet and outlet of the heat exchanger, mass flow rate, gravity, steam pressure, and the area of the heat exchanger. A linear relationship between the two derived parameters was established using measured data of a steam condenser in a 200 MW power plant. The relation showed good agreement with measured data. Bracco et al. (2009) derived three steady-state mathematical models based on the number of transfer units effectiveness method to determine the influence of the air inlet temperature on the condenser performance.

Recently, Li et al. (2018b) performed data-driven modelling of an air-cooled condenser in a 660 MW power plant. They investigated the optimal operating fan frequency to a maximum power gain. It was seen that an increase in the fan frequency increases the heat transfer on the air side, despite a rise in power consumption. In addition, Li et al. (2018b) claimed that the performance of the plant degrades with time and therefore the performance of a plant differs from the design specifications of the manufacturer. Hence, real operating data should be used to adjust off-design models.

Medica-Viola et al. (2018) presented a numerical model coupled with four heat transfer coefficient algorithms in order to calculate the steam saturation pressure in a condenser for a 210 MW power plant. The four heat transfer coefficient algorithms included a physical algorithm for dropwise condensation with blowing effect, a physical algorithm for dropwise condensation without blowing effect, an empirical algorithm for dropwise condensation and a physical algorithm for film-wise condensation. The model was validated against actual measurements and the physical heat transfer coefficient algorithm for dropwise condensation without blowing effect was observed to be the most accurate one. The heat transfer coefficient algorithm based on film-wise condensation was the least accurate one.

Li et al. (2018b), whilst focusing on air-cooled condensers, reviewed the challenge of employing numerical simulation, highlighting that the analysis of the distribution of the temperature and fluid fields in multiple scales (from fin, to fan, to fan clusters, to fan island, etc.) may provide useful information on how to improve the condenser design itself. However, the computational approach remains expensive and time-consuming (Yang et al., 2012; Chen et al., 2016a,b, 2017b; Kumar et al., 2016; Kong et al., 2017).

As reported by Rusowicz et al. (2017), condensers flow parameters vary not only in two directions in the cross-sectional plane of the tube bundle, but also along the bundle. Thus, due to the three-dimensional nature of the flow, a three-dimensional model is the one that most adequately describes processes occurring in the condenser. However, as mentioned by Saari et al. (2014), such a model is complex and requires many parameters and long calculation times, which is why two-dimensional models are most often used for assessing the power condenser performance. Moreover, in the case of DSG, time-varying fluctuations also will need to be included.

Efforts to Improve Efficiency

Much research has been conducted on improvement to the efficiency of power plants. This has led to proposals for new configurations and cycle architectures (Wu et al., 2012; Zhang and Zhang, 2013; Mcgrail et al., 2017), suggestions for improving the efficiency of the two-phase phenomena in power plants, such as boiling (Nie et al., 2017; Tian et al., 2017; Ahmadpour et al., 2018) and condensation (Yoo et al., 2018), as well as recommendations for improving the overall efficiency of plant through operation in cogeneration mode (Das and M. Al-Abdeli, 2017; Gvozdenaca et al., 2017; Moradi et al., 2017).

Combined Cycles

Early attempts were aimed at improving the overall efficiency of power plants by using the high-pressure, high-temperature vapour stream at the outlet section of the turbine (Rao, 2012). To do so, combined heat and power (CHP) systems were introduced. While the conventional method of producing usable heat and power separately has a typical overall of combined (i.e., electrical plus thermal) efficiency of 45%, CHP systems can operate at levels as high as 80% (Rao, 2012; Li et al., 2014).

The condensation process is one of the major causes of losses in power plants. During the past few years, significant efforts have been made to improve condensation efficiency by focusing on novel ideas such as using enhanced surfaces (Zhao et al., 2016), imposing inclination angles (Würfel et al., 2003; Meyer et al., 2014; Adelaja et al., 2016; Noori Rahim Abadi et al., 2018b,c), developing new cycles or improving the condensation process in the thermal cycles (Matsuda, 2014; Zhang et al., 2016h; Bao et al., 2017b), and proposing new cross-sectional geometries (Chiou et al., 1994; Chen et al., 2014; Kang et al., 2017; Mahvi et al., 2018).

One way of increasing the efficiency of cogeneration plants is to optimise the condensation process (Wang et al., 2016; Bao et al., 2018). Li et al. (2014) proposed a design procedure for the condensation temperature in CHP systems based on an ORC prime mover. They found a threshold condensation temperature at which the efficiency of the system reached a maximum. The results for a particular case showed that, through the proper design of the condensation temperature, the annual power output could be increased by 50%.

In other work, Bao et al. (2017b) proposed a novel two-stage condensation Rankine cycle to improve the power-generation efficiency. The results showed that the thermal efficiency, net power output, and energy efficiency of the new proposed cycle increased by 42.9, 45.3, and 52.3%, respectively. Bao et al. (2017a) extended their work by examining the number of condensation stages for seven different cycles in power-generation systems for liquefied natural gas cold energy recovery. They considered three main parameters of electricity in their study: production cost, net power output and annual net income. Based on the chosen objective function, different results were obtained and the two-stage condensation system showed the best performance.

Furthermore, Pantaleo et al. (2017, 2018) investigated solar-biomass combined systems, with Joule/Brayton top and ORC bottoming cycles and thermal storage and found that the hybridisation with biomass allows for significant performance improvements, enabled by the higher temperatures compared to conventional CSP, as well as cost savings due to the reduction in the required size of the solar field.

Optimisation of Operating Conditions

In addition to attempts to improve the efficiency of power plants by modifying their thermal cycles, much research has focused on condensation mechanisms and their characteristics. A better understanding of the condensation process and the dominant parameters will lead to power plants being designed with higher efficiency and lower cost. Some of the main parameters of the condensation phenomenon that have been studied are discussed below.

Recently, Dalkilic and Wongwise (2009) performed an extensive literature review on enhanced tubes. They focused on various passive enhancement techniques, such as rough surfaces, twisted-tape inserts and microfin tubes. They concluded that the study of the condensation heat transfer mechanism was still unlimited. Orejon et al. (2017) conducted experiments to study the simultaneous drop-wise and film-wise condensation of water on completely hydrophilic silicon micropillars with different pillar densities. They found that the condensation mechanism was directly dependant on the spacing between the pillars. Research also revealed that the simultaneous drop-wise and film-wise condensations had a higher heat transfer coefficient compared to the single drop-wise or film-wise mode. Li et al. (2018a) investigated the performance of different enhanced surfaces for the in-tube convective condensation of R410a.

Another approach to improve the condensation process is to impose a proper inclination angle based on the operating conditions. Meyer and co-workers (Lips and Meyer, 2012a,b,c,d; Meyer et al., 2014; Oliviera et al., 2016; Adelaja et al., 2017; Ewim et al., 2018; Meyer and Ewim, 2018) conducted extensive experimental investigations to study the possibility of heat transfer enhancement during the condensation of R134a inside a smooth tube. They found an optimum inclination angle region between −30° and −15° (downward flow), depending on the operating conditions. In addition to the refrigerants, some research has been conducted on steam condensation inside inclined tubes, which is widely seen in conventional power plants (Ren et al., 2014; Wang et al., 2017). Caruso et al. (2013) conducted experiments to study the effect of the inclination angle on the in-tube condensation of steam-air mixture. Wang and Du (2000) experimentally and analytically studied steam condensation in long, smooth tubes. They considered different parameters in their investigation, such as steam mass flow rate, tube diameter, and inclination angle. They found that the inclination angle affected the condensation heat transfer mainly by stratifying the fluids and thinning the liquid film. A successful optimisation of the operating conditions was also performed for the condensing flow of R134a inside an inclined smooth tube by Noori Rahim Abadi et al. (2018a).

Conjugate Heat-Transfer Phenomena

Although much promising research has been conducted on condensation in power plants, this phenomenon is often seen in combination with other two-phase phenomena like pool and convective boiling. In these cases, the conjugate heat transfer (Mathie and Markides, 2013; Mathie et al., 2013) should be considered to better analyse the thermal performance of two-phase processes in power plants. Such a method is vital to satisfy the demand for high cooling and heat rates in power plants (Wu et al., 2010; Minocha et al., 2016; Noori Rahim Abadi et al., 2018c).

Nie et al. (2017) studied the conjugate condensation of high-pressure steam inside a tube and atmospheric pool boiling outside a tube experimentally. This configuration is widely seen in many power plants, particularly in passive heat-removal systems. The results showed that the increase in pressure, mass velocity and steam quality caused an increase in the wall temperature and heat flux. Moreover, the condensation heat transfer coefficient increased as the steam quality and mass flux increased, but decreased with saturation pressure. Bahreini et al. (2017) numerically studied the effect of gravity on flow boiling inside a vertical tube under conjugate heat transfer. The results showed that the heat transfer coefficient increased as gravity decreased, while the pressure drop showed the reverse behaviour. They also found that increasing the inlet mass flux changed the flow regime to bubbly flow, which consequently led to a lower heat transfer coefficient.

Energy Storage Options

For DSG technology to offer a feasible, affordable and dispatchable renewable energy solution, either directly for process heat via steam provision, or for power generation via CSP, the important issue of energy storage must be addressed. Energy storage is needed to bridge the temporal mismatch between solar energy availability and demand, notably during periods of low solar irradiance, and at night. The storage scheme must provide the ability to charge and discharge efficiently, be economical to construct and operate, and be sustainable and environmentally safe to implement.

In DSG plants, several suitable energy storage solutions exist and could include thermal energy storage (TES) and non-TES options. In CSP applications, when generating electrical power, in addition to possible onsite TES storage options that have the advantage of a lower cost, the generated electrical energy can also be stored downstream of the CSP plant, presenting additional opportunities for improvements to the plant's capacity factor and other wider energy system services. Therefore, depending on the application of DSG technology, both thermal and/or other storage can be relevant.

For this purpose, in the interest of presenting an overview of the possible impact that TES can have on DSG plants and levelised costs, a brief discussion on other storage methods that can be viewed as rival energy storage options should be considered.

Energy storage often suffers from being narrowly defined. Electrical energy storage (EES) technologies, which both charge and discharge electricity, are only a subset of energy storage, albeit a high-profile one. Heat and electricity are of course not equivalent in a thermodynamic sense, as while electricity can be converted wholly into heat, the converse is not true. Direct comparisons between TES and EES can be challenging as a result. If the desired output is electricity, a store which charges using heat will need to store more energy than one which charges with electricity. If a CSP plant has an average thermal-to-electrical efficiency of around 20%, its thermal store will need to store about five times more energy than a battery with a 98% electrical-to-electrical efficiency. Crucially, however, this does not mean that the thermal store is necessarily larger or more expensive than the battery, and in fact the converse is often true, as sensible heat storage can be one of the cheapest ways of storing energy (<10 $/kWh_th for sensible-heat TES and up to 20–50 $/kWh_th for other forms of TES) while thermochemical energy storage (TCS) can be one of the most compact (Brandon et al., 2016). Levelised costs for TES can be an order of magnitude cheaper than batteries, which have levelised costs in the range $260–780 per MWh of electricity delivered (Lazard, 2017).

CSP with integrated TES is an example of a generation-integrated energy storage (GIES) system, as identified by Garvey et al. (2015). Hydroelectric power plants are another GIES example, with the exception of run-of-river plants that cannot hold up the flow of water (Ardizzon et al., 2014). In CSP, the incoming solar radiation is captured and stored as heat in a thermal storage medium such as a molten salt (Sioshansi and Denholm, 2010; Pelay et al., 2017), which can then be converted to electricity on demand via a steam Rankine cycle. The thermal efficiency of various power plant technologies, including solar-driven Rankine cycles have been discussed by Markides (2013). An equivalently-sized solar PV system with battery EES first produces electricity from sunlight, then converts it to electrochemical energy for storage, before finally converting back to electricity when this is required (plus there are other DC-AC conversion steps). A GIES system avoids the intermediate step of producing electricity before storage, and thereby reduces the number of transformations required. This can bring benefits in terms of avoiding energy losses and the cost of additional power-conversion hardware (Garvey et al., 2015).

A DSG CSP plant can also function as a GIES system, through storage of the steam itself in a steam accumulator, or by storage of the sensible and latent heat in thermal stores. The system complexity and cost is likely to be higher than that for conventional CSP with sensible thermal storage, however. Further studies are required to quantify the trade-off between the higher efficiency that a DSG CSP plant can achieve and the higher costs and complexity. A DSG CSP plant can also act as a non-GIES system and deliver electricity directly, for subsequent storage using an EES system such as batteries or pumped hydroelectric storage. Again, further work is required to evaluate the whole-system costs and benefits of such an approach, though it seems likely that the overall cost of dispatchable energy will be higher than that for conventional CSP with storage.

In the light of this, we give an overview on thermal options in the next section, followed there-after by brief a discussion on other energy storage options.

Thermal Energy Storage

Solar thermal powered cycles have the advantage of being able to receive energy stored thermally and converting it into electricity when needed. In broad terms thermal energy storage (TES) can be classified into sensible, latent and thermochemical storage (Weinstein et al., 2015).

Indeed, existing non-DSG CSP plants are already reliant on some of these storage methods to provide bulk energy storage. In such plants, typically at least two flow loops are required which operate with different fluids. The one (colder) loop contains the power block and is operated on Rankine-related thermodynamic cycles using steam, while the other (warmer) loop contains a single-phase liquid which is used to transport thermal energy from the solar field to the energy storage systems and to the power block loop via heat exchangers. Gil et al. (2010) and Medrano et al. (2010) present reviews on best practices for high-temperature TES for power generation, providing a summary of various available materials and technologies that can be used for electricity generation in solar power plants and which can accompany TES systems. The merits and the demerits of each one were comprehensively discussed. Several architectures and thermal control mechanisms exist (González-Roubaud et al., 2017). The warmer loop typically uses thermal oils (Biencinto et al., 2014; Boukelia et al., 2015) or molten salts (Olivares, 2012; Flueckiger et al., 2013). TES consisting of liquid thermocline schemes (Qin et al., 2012; Flueckiger et al., 2013; Mostafavi Tehrani et al., 2017), liquid two-tank schemes (Bauer et al., 2013), and sensible solid media storage schemes (Niyas et al., 2015; Tiskatine et al., 2017) are also used and are sized to provide suitable amounts of thermal storage.

In order to implement thermal storage schemes for DSG cycles, alternative storage system concepts and architectures are required. This is necessary because a single HTF (steam/water) is present in a unified flow loop system between the solar field, the power block and the condenser(s), as is shown in Figure 1. When considering possible thermal energy storage schemes, notably both the technical and economic feasibility of the scheme must be considered (Mostafavi Tehrani et al., 2017).

Based on existing technology and proposals from literature, the most noteworthy storage options include direct steam accumulation systems, indirect sensible heat storage systems, and indirect latent heat storage systems.

Steam accumulation TES is based on a concept where wet steam from the solar field is fed into a steam buffer drum, which acts as an energy storage module (González-Roubaud et al., 2017). Saturated liquid water is used as the energy storage medium while saturated steam is fed directly to a turbine, or through an additional heating section to produce superheated vapour. For DSG, this is a direct energy storage method because the energy is stored directly in the HTF (water). Additional heating can be done by means of a solar field, or by means of a secondary thermal energy storage medium. Discharge from the steam accumulator is facilitated by a drop in pressure (Stevanovic et al., 2012) in the accumulator (which results in a decrease of the remaining saturated liquid temperature), which forces the saturated liquid to partially flash into saturated steam. The energy is thus actually stored as sensible energy as the temperature of the saturated liquid changes. Several configurations exist, ranging from a simple steam accumulator, an accumulator that also serves as a phase separator, integrated internal sensible, and latent heat storage (Steinmann and Eck, 2006). Without external superheating of the steam before the power block, such schemes suffer from low thermal efficiency and pressure glide during energy discharge. Thus, a major disadvantage of steam accumulation systems, is the low associated thermal efficiency of the power block due to the relatively low inlet temperature at the turbine.

By utilising the sensible thermal response of secondary heat storage media, this limitation can partially be addressed. In these indirect energy storage methods, energy is stored not in the water or steam itself, but in a secondary medium or media. During discharge, when utilising sensible TES, the thermal response of the storage medium can be used to preheat the water, generate steam, and to superheat the steam (Seitz et al., 2013). This, however, results in several heat transfer limitations due to the mismatch between the enthalpy-temperature profile of the storage medium and that of the water/steam as is shown in Figure 7A. Therefore, the combination of sensible energy storage with latent heat storage (Laing et al., 2011) is recommended to improve the enthalpy-temperature profile match for charging and discharging operation as is shown in Figure 7B. When combined with latent storage schemes (discussed in more detail later), sensible heat is normally only used during discharge operation for preheating of liquid water and/or superheating of the steam.

FIGURE 7

Figure 7. Temperature-enthalpy diagram for charging and discharging using: (A) a sensible storage medium only, and (B) a sensible storage medium for pre-heating and superheating, and a latent storage medium for steam generation.

The inclusion of TES, however, complicates the operation of the power plant and requires modifications to the cycle architecture compared to those of fuel fired power plants (Birnbaum et al., 2010). A significant implication is the adjustment of the steam saturation pressure during charging and discharging modes to allow heat to flow to and from the storage medium as is shown in Figure 7B. The reduction of saturation pressure during discharging causes the power block to operate on part-load conditions and thermodynamically also results in a reduction of the thermal efficiency of the system. There are ways to minimise this impact (Seitz et al., 2013), but requires careful relative sizing of the storage sections.

For sensible TES, solid or liquid media are preferred due to their relatively high energy densities compared to gas media. Solid TES media are generally less expensive than liquid media, but suffer from gliding discharge temperatures. Liquid thermocline and two-tank liquid TES schemes (Zaversky et al., 2017) do address this to some extent by providing more stable HTF outlet temperatures, but require more expensive storage and circulation systems.

Solids such as high temperature concrete, ceramics, rock beds, sand, fly ash and soil are suitable due to their ability to be used in simple designs and to be operated in a wide temperature range (Navarro et al., 2012; Meffre et al., 2015; Niyas et al., 2015; Tiskatine et al., 2017). They are also relatively inexpensive, thermally and chemically stable, non-flammable, and non-toxic.

Sensible TES using solids often utilise packed beds (Kuravi et al., 2013; Bruch et al., 2014) which can be modelled as porous media (Andreozzi et al., 2012) or flow channel passages within volumes containing the storage medium (Buscemi et al., 2018), or combinations with thermocline liquid storage tanks (Mostafavi Tehrani et al., 2017). During charging, the temperature of the storage media is increased by heat transfer from the interfacing fluid, while during discharging heat is transfered back into the interfacing fluid. Heat absorption and release occurs internally via thermal conduction. Packed beds have also been proposed for thermal (hot and/or cold) storage in pumped-heat schemes (White et al., 2014, 2016; Mctigue et al., 2018) that will be presented further down in the next section.

High charging and discharging rates, and high energy storage densities are desired. This requires materials which have relatively high thermal conductivities, high densities and high specific heat capacities. Comparisons have been made on the transient behaviour of storage modules with the HTF in channels within different cast-able solids such as concrete and cast steel (Niyas et al., 2015) where it has been shown that the charging and discharging rate can only be well controlled via the HTF flow rate if the solid has a high thermal conductivity. For high temperature storage, the inclusion of thermal conductivity enhancement powders, such as copper, into cement-like material has been shown to increase both the thermal conductivity and the specific heat capacity (Yuan et al., 2015). The placement (number) and size (diameter) of the flow passages are also important (Bai and Xu, 2011) and have also been under investigation in order to optimise the charging and discharging rates (Hua et al., 2017) and when optimised in terms of overall cost (Jian et al., 2015). The inclusion of longitudinal fins in shell-and-tube type configurations within concrete storage media are also used to increase the charging and discharging rates (Rao et al., 2018).

The ability of a solid sensible TES medium to sustain constant discharge rates are, however, still a challenge which requires the optimisation of classical volume-to-point heat flow problems (Dan and Bejan, 1998). Thermal cycling (Alonso et al., 2016) of embedded pipe systems is also of significant importance. Moisture content and thermal expansion coefficient mismatches in high-temperature concrete can be problematic during commissioning stages, but when handled properly, can be overcome (Laing et al., 2011). On the other hand, packed beds, where the HTF flows through a porous medium volume filled with solids TES media, do not suffer from excessive thermal stress but can result in significant frictional pressure drop in the HTF flowing through the storage module (Singh et al., 2006). Such geometries are also likely not investigated well for flow boiling or flow condensation. The inclusion of a thermo-chemical energy storage section at the outlet of the HTF can also be used to improve the outflow temperature of the HTF (Ströhle et al., 2017).

Compared to sensible TES using solid media, sensible TES using liquids is relatively more mature due to its use in thermal oil and molten salt non-DSG CSP systems. Suitable storage media include binary salt mixtures using components such as NaNO₃ and KNO₃ (Bauer et al., 2013; Fernández et al., 2015; Parrado et al., 2016; González-Roubaud et al., 2017) and thermal oils. These liquids are acceptable because of their thermo-physical properties, thermal stability in their applicable temperature operating ranges, as well as their metallic corrosive properties.

In these liquid TES schemes, heat exchangers may be used to transfer heat to and from between the HTF and the thermal storage medium. On the working fluid side, this allows for the use of flow passages which better resemble the flow geometries that are covered in literature related to flow boiling and flow condensation, as have been discussed earlier in this article. The use of pumped hot liquids is enables constant steam temperatures and sustain energy rates, both of which are required in DSG. As mentioned, such schemes are often used for pre-heating of water and superheating of steam in conjunction with latent energy storage. Different storage architectures exist which may employ one (Mostafavi Tehrani et al., 2017), two (Wu et al., 2016) or three liquid tanks (Seitz et al., 2013). During charging in schemes with more than one tank, liquid is pumped from a cold tank and heated in heat exchangers to one hot tank or to two tanks (one intermediate warm tank and one hot tank). The reverse occurs during discharging. The use of an intermediate tank can be useful to reduce exergy destruction by better matching the differences in the specific heats of liquid water during pre-heating and that of steam during superheating, but it results in more complicated and expensive systems requiring more pumps.

The use of latent energy storage is, however, recommended if achieving a better thermal match with the enthalpy-temperature profile of the water/steam during the charging and discharging modes is desired. During charging, heat transfer from condensing steam is transferred to the storage medium causing a phase change to occur, while during discharging the reverse occurs to result in steam production. Liquid-solid phase change materials (PCMs) are preferred because of their high latent heat of fusion and the relatively small volumetric expansion and contraction during phase transitions. The most significant advantages of latent TES using PCMs are the high associated energy storage densities (Wang et al., 2012) and the ability to charge and discharge energy at relatively constant phase change temperatures. Beyond high latent heat, a good PCM should have a relatively low cost, high availability, high thermal conductivity, and suitable melting temperature.

The phase-change temperature should be matched as closely as possible to the saturation temperature of the steam at the desired pressure. For Rankine type cycles this temperature should be approximately between 310°C and 350°C (Abujas et al., 2016) which makes some metal alloys such as Mg-Zn (Weinstein et al., 2015), inorganic salts such as NaNO₃ and KNO₃, and salt mixtures (Zhang et al., 2015) suitable choices. Challenges associated with PCMs are, however, the relatively higher material cost, low thermal conductivities of non-metal PCMs, density changes, property stability during long term cycles, subcooling, phase segregation and corrosion (Vasu et al., 2017). Even though metal alloys have high volumetric heat capacity and thermal conductivities, they are relatively expensive (Weinstein et al., 2015) compared to KNO₃ and NaNO₃, with NaNO₃ being the least expensive (Vasu et al., 2017).

A promising integration scheme of latent TES in DSG plants is the adoption of a three-stage thermal storage architecture where preheating, steam production and superheating is done sequentially in different sections (see Figure 1) and where PCMs play a central role (Tamme et al., 2008; Garcia et al., 2016). As mentioned, pre-heating and superheating can be done via sensible heat, and is desired because of the lower associated material cost. For typical operating pressures, approximately two thirds of the stored energy is required for steam generation (Laing et al., 2011), but there are several suggested concepts to reduce the quantity of PCMs needed and to ultimately lower the initial investment costs. These include the use of intermediate sensible TES liquid tanks, steam-side modifications by using superheated steam and saturated water recirculation and by using continuous steam-pressure reductions in the superheated stream (Seitz et al., 2013). Other architectures also exist in which sensible and latent heat storage is integrated, such as with the inclusion of PCM within the sensible liquid TES systems.

Irrespective of the storage system architecture, a thermal interface is needed between the HTF and the PCM. This can take the form of a multi-tube scheme where the HTF is passed through the PCM volume (Tao et al., 2012; Wang et al., 2012; Seddegh et al., 2015; Fornarelli et al., 2016; Pirasaci and Goswami, 2016; Meng and Zhang, 2017), or PCM encapsulations surrounded by the HTF. Examples of the latter are packed beds with PCM encapsulations (Peng et al., 2014; Wu et al., 2016; Zhang et al., 2016f) or PCM tube bundles (Ghoneim, 1989; Pirasaci and Goswami, 2016). Pirasaci and Goswami (2016) characterised the impact of tube bundle diameters and the steam/water flow rate for an NaCl-MgCl₂ eutectic PCM mixture.

Several numerical simulation studies on the use of PCM as the energy storage medium have been conducted (Michels and Pitz-Paal, 2007; Guo and Zhang, 2008; Tao et al., 2012, 2014; Wang et al., 2012; Guo et al., 2013; Sciacovelli et al., 2015; Seddegh et al., 2015; Fornarelli et al., 2016; Kargar et al., 2018). Xu et al. (2015) provides a comprehensive review on the model description and numerical approach on previous studies that utilised a one-dimensional numerical model for spherical PCM capsules and those that used two-dimensional thermocline modelling in latent heat TES schemes. In their work, a cost-effective design for PCM TES system was identified by ensuring that the system cut-off temperature and the PCM melting temperature are the same. This design was said to significantly reduce the volume of the storage tank, the amount of PCM required and the cost of constructing the system. Several other authors have numerically modelled thermal energy storage modules. Different techniques have been utilised to solve the transient phase-change process numerically. Similar behaviour has been obtained for the solidification and melting of the PCM using the specified governing heat transfer mechanisms. However, the computational cost and time still remains challenging as the melting and solidification numerical simulations only converge using small time steps (Pirasaci and Goswami, 2016). Hence, it becomes essential to develop simple numerical techniques that require little computational time. It is important to note that charging and discharging of the TES occurs during condensation and boiling, respectively, of the working fluid. It thus requires relatively complex models to incorporate the dominant physics associated with such operating processes.

As with sensible TES, the charging and discharging rates of latent TES is of paramount importance. During discharging, the PCMs progressively solidify from the thermal interface region away from the HTF as described by the Stephan problem. The low thermal conductivity of inorganic salt PCMs results in a significant challenge in this regard due to diminishing heat transfer rates as the phase-change fronts move further away from the HTF and the associated increase of the thermal conduction resistance of the solid phase layer increases. To overcome this, several enhancement techniques have been investigated. These include extended surfaces using fins (Guo and Zhang, 2008; Sciacovelli et al., 2015), micro encapsulations and the use of composite PCM mixtures such as the inclusion of nano-particles or using expanded foams to create form-stable composites (Zhao et al., 2010; Khalifa et al., 2015; Abujas et al., 2016; Zhang et al., 2016f). The use of form-stable composites is a good option because it results in significantly higher effective thermal conductivities and produces stable thermo-physical properties under thermal cycling. Both metal foams (Bhagat and Saha, 2016) and expanded graphite foams are suitable. Compared to the use of metal fins, such as aluminium and steel, protruding into the PCM volume, the use of expanded graphite foams can dramatically reduce charging and discharging times. Graphite foams do, however exhibit lower energy densities (Abujas et al., 2016). Another important implication is the choice of material paring where the resistance of the encapsulation material against corrosion by the phase change material is important as has been highlighted by Riuz-Cabanas et al. (Ruiz-Cabañas et al., 2017).

Other Energy Storage Options

It is important to determine the relative cost positioning of TES in terms of rival energy storage methods. For this purpose a brief discussion on other energy storage options is presented to offer a more balanced view of the possible impact of TES in DSG.

In CSP applications for power generation, a wide range of technologies are available for electrical energy storage downstream of the CSP plant. Although not directly related to the core theme of this paper, any TES option must be competitive with respect to alternative electrical storage options if it is to stand a realistic possibility of practical implementation, so we provide here some limited information on the latter as a benchmark for comparison and as a means of defining targets for further TES technology development, from both performance and cost perspectives.

Many authors have surveyed the electrical energy storage landscape, with notable technology reviews in Chen et al. (2009), Luo et al. (2015), and cost assessments by Zakeri and Syri (2015) and Schmidt et al. (2017), while a range of institutions have provided detailed guides to available technologies and costs (Rastler, 2010; Akhil et al., 2013; IRENA, 2017). Relevant technologies include electrochemical energy storage (e.g., lithium ion, sodium sulphur, lead acid, and flow batteries, amongst others) as well as thermomechanical energy storage (e.g., compressed air, pumped thermal, liquid air, pumped hydro and other gravitational storage technologies, amongst others).

The wide range of services that energy storage systems can provide, and the variety of scales and locations at which they can be used, mean that multiple criteria must be used to evaluate the fit of any given technology to its use. Metrics for technology performance must include the capital and levelised costs of storing energy and delivering power, but lifetime, roundtrip efficiency, degradation and response time can significantly affect the overall project economics. For instance, technologies such as pumped hydroelectric storage and compressed air energy storage may have lifetimes of many decades, whereas lead-acid or lithium-ion technologies may require replacement batteries within a few years (Akhil et al., 2013). Power and energy density, both in terms of volume and mass, are highly relevant in applications such as electric vehicles and distributed energy storage in homes, but less so in grid-scale installations. Safety is also key, as each technology brings its own hazards, from high temperatures and pressures to flammable, unstable or toxic materials (Lloyd's Register Foundation, 2017). Further considerations include materials issues and security of supply, safe disposal, and lifecycle energy and emissions.

Thermomechanical energy storage technologies that can store and discharge electricity over 1–24 h (or longer) at megawatt scale or above are well suited to bulk electricity storage and specifically in the context of integrating large-scale intermittent renewable generation such as CSP. Two relevant technologies that are at the commercial or near-commercial stage in the short term are shown in the upper-right quadrant of Figure 8, namely pumped hydroelectric storage (PHS) (Deane et al., 2010; Rehman et al., 2015) and compressed air energy storage (CAES) (Allen et al., 1985; Rogers et al., 2014; Budt et al., 2016).

FIGURE 8

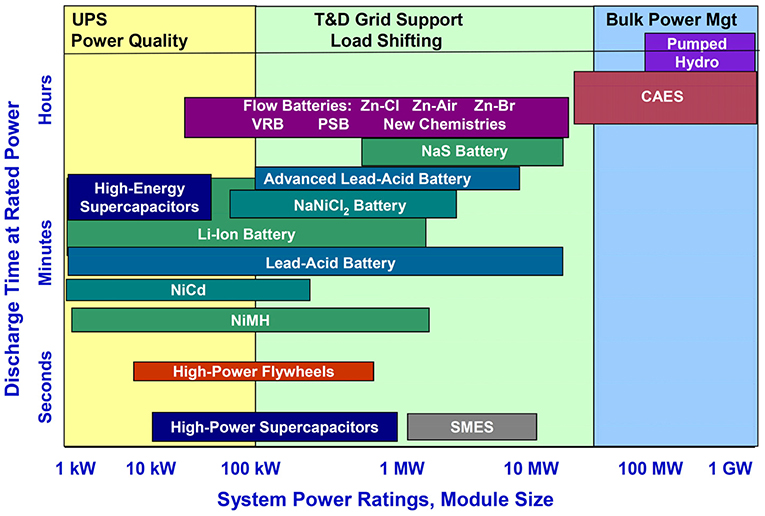
Figure 8. Approximate ranges of power ratings and discharge durations of EES technologies, from a public access report (Akhil et al., 2013).

Three main variants of CAES exist, with each handling the heat produced during compression (charging) differently. Diabatic systems release the heat to the environment and then use an external heat source, for example combustion of natural gas, during the discharge process (Crotogino et al., 2001). Adiabatic systems store the heat of compression in thermal storage (Bullough et al., 2004; Barbour et al., 2015), while isothermal systems aim to carry out the compression and subsequent expansion at close to ambient temperature (Fong et al., 2010; Li et al., 2011). Storage of the high pressure air can take place in caverns (He et al., 2017), aboveground pressure vessels (Liu et al., 2014), or underwater (Pimm and Garvey, 2009; Mas and Rezola, 2016).

Emerging technologies such as liquid air energy storage (LAES) (Morgan et al., 2015; Antonelli et al., 2017; Sciacovelli et al., 2017; Highview Power, 2018), pumped thermal energy storage (PTES) (White et al., 2013; Mctigue et al., 2015; Benato and Stoppato, 2018), and power-to-gas approaches (Belderbos et al., 2015; Mazza et al., 2018) are also under investigation. Georgiou et al. (2018) provide a comparison between LAES and PTES also considering the size of plant and further identify the compression and expansion processes, and the associated components (see Mathie et al., 2014; Willich et al., 2017 for a discussion of piston-expander performance), as highly important for overall system performance, while Farres-Antunez et al. (2018) identify a promising hybridisation of the two systems. These technologies operate at suitable scales and typically have long lifetimes, while a range of flow battery chemistries have been proposed for multi-hour storage but typically at smaller scales (Ponce De León et al., 2006; Alotto et al., 2014). They can in some cases compete with the deferral of electricity generation using TES for directly-generated steam.

Power-to-gas and associated technologies tend to operate best at longer timescales and typically with lower roundtrip efficiencies, whereas technologies such as supercapacitors, flywheels and superconducting magnetic energy storage are primarily suited to short-duration storage, and so are of less interest for this specific purpose but can be employed closer to the point of use. Load-shifting at the point of consumption (such as thermal storage in the fabric of buildings and chilled-water air conditioning systems) and demand-side response (DSR) technologies are also available and can provide similar flexibility to the wider energy system (Strbac et al., 2012).

For bulk energy storage, the cost of storage capacity tends to dominate over the cost of rated power, as a result of the longer storage durations. Technologies such as pumped hydro with roundtrip efficiencies of 70–80% are able to compete in this application thanks to their low capital costs per unit of stored energy. Similarly, response time is less critical than it would be for frequency regulation or power quality services, where near-instantaneous delivery of power is required.

Figure 9 presents the current and projected future performance of EES technologies in terms of roundtrip efficiency and capital costs (IRENA, 2017), while also showing the marginal cost and storage efficiency of conventional onsite TES employing molten salts (Mehos et al., 2017). For TES, storage efficiency represents the ratio of thermal energy returned from storage to that supplied during charging, analogous to the electrical roundtrip efficiency. The subsequent losses during the conversion of heat to electricity affect the amount of energy which must be stored, and hence the capital cost of the store, but not the storage efficiency, as these losses are incurred regardless of when storage takes place. It can be seen that the current TES technology delivers higher efficiency than even the future EES systems, while only a few EES systems achieve lower capital costs. It is worth noting that the comparison in Figure 9 does not take into account the lifetime of the systems, and a focus on installation cost alone is not sufficient when the desire is to minimise overall lifetime costs (World Energy Council, 2016).

FIGURE 9

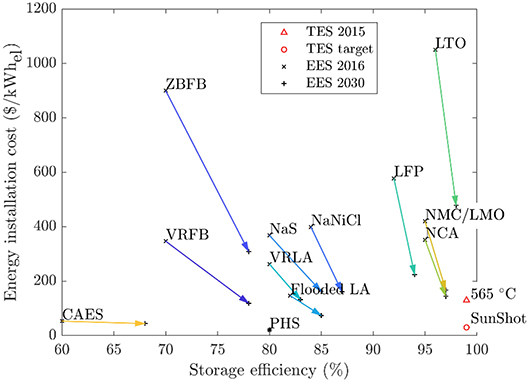
Figure 9. Capital costs and storage efficiencies for EES and TES technologies now and in the future from a public access reports (IRENA, 2017; Mehos et al., 2017). The cost of TES at 565°C is converted to a cost per kWh of electrical storage by assuming a 20% thermal-to-electric conversion efficiency. The U.S. Dept. of Energy SunShot target specifies 15 $/kWhth and a 50% conversion efficiency. IRENA (2017) contains further details on the EES technologies and on the acronyms used.

The positioning of TES for a CSP plant with DSG on this chart is the subject of ongoing work. It remains to be seen whether the expected efficiency improvement from the move to direct steam generation is sufficient to outweigh the additional cost and complexity incurred to store both latent and sensible heat. In energy systems where the daytime peak generation aligns with peak demand, the need for storage at a CSP plant may be limited, but for other applications, the ability to store and dispatch power is a crucial consideration.

Conclusions

In this article, we considered direct steam generation systems as applied for concentrated solar power generation and process steam production. In these systems, important thermal-energy processes take place during flow boiling, flow condensation and energy storage. Our understanding and ability to predict these processes have been reviewed, covering both experimental and computational efforts in the literature. In general, these are highly complex, multi-scale and multi-physics processes that involve phase-change phenomena, inherently unsteady and turbulent multiphase flows in the presence of conjugate heat transfer, and therefore many challenges remain in the rational design of high-performance and low-cost systems, and in their optimal operation. An overview was supplied of the use of flow regime maps to assist with the better understanding modelling and predicting heat transfer coefficients and pressure drops during flow boiling and condensation. The transitions between flow regimes are, however, complicated and depend on several parameters including the flow passage scale, flow passage geometry, thermal boundary conditions, and fluid properties. As such, a singular flow pattern map is not yet in existence. Flow boiling was discussed in terms of experimental and numerical investigation of the heat transfer coefficients and pressure drops. Several experimentally-based correlations exist, but there is still a need to consider the influence of non-uniform heat flux conditions, especially at high heat fluxes on the collector tubes, amongst others. Likewise, flow condensation was considered both from an experimental point of view as well as from a numerical modelling point of view. An overview of the energy storage options of interest to DSG was also presented. For thermal energy storage, steam accumulation, sensible thermal energy storage and latent energy storage was covered. Some other energy storage options including electric energy storage, was also discussed. Areas for further exporation include he impact that transient solar irradiance has on the heat transfer and pressure drop performance of the collector tubes and the stability of the system as a whole, and the improvement, optimisation and enhancement of the energy discharge rates from the energy storage sections. The use of numerical techniques to model the heat transfer and pressure drop behaviour of a variety of working fluids during flow boiling in the solar collectors, flow condensation in the condensers, and during thermal-energy storage (charge and discharge) has experienced significant progress in recent years with promising improvements; nevertheless, complementary experimental work to generate data of practical interest or for the purpose of model development and validation, on both lab-scale or full-scale components, remains vital. In the latter case, for comparison with modern advanced three-dimensional space and time-resolved codes, the need for equivalent space and time-resolved data is of particular importance.

Author Contributions

JD: compiler and co-author of some of the text; DJ, AlK, EO, MS, SL, SN, VV, AA, MD, AbK, SO, OO, ME, MiD, and JM: co-author of some of the text; CM: corresponding author and co-author of some of the text.

Funding

This work was supported by the Department for International Development (DFID) through the Royal Society-DFID Africa Capacity Building Initiative and by the UK Engineering and Physical Sciences Research Council (EPSRC) [grant numbers EP/P004709/1 and EP/J006041/1]. Data supporting this publication can be obtained on request from Y2VwLWxhYkBpbXBlcmlhbC5hYy51aw==.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Abedini-Sanigy, M. H., Ahmadi, F., Goshtasbirad, E., and Yaghoubi, M. (2015). Thermal stress analysis of absorber tube for a parabolic collector under quasi-steady state condition. Energy Proc. 69, 3–13. doi: 10.1016/j.egypro.2015.03.002

CrossRef Full Text | Google Scholar

Abujas, C. R., Jové, A., Prieto, C., Gallas, M., and Cabeza, L. F. (2016). Performance comparison of a group of thermal conductivity enhancement methodology in phase change material for thermal storage application. Renew. Energy 97, 434–443. doi: 10.1016/j.renene.2016.06.003

CrossRef Full Text | Google Scholar

Adelaja, A. O., Dirker, J., and Meyer, J. P. (2016). Convective condensation heat transfer of r134a in tubes at different inclination angles. Int. J. Green Energy 13, 812–821. doi: 10.1080/15435075.2016.1161633

CrossRef Full Text | Google Scholar

Adelaja, A. O., Dirker, J., and Meyer, J. P. (2017). Experimental study of the pressure drop during condensation in an inclined smooth tube at different saturation temperatures. Int. J. Heat Mass Transfer 105, 237–251. doi: 10.1016/j.ijheatmasstransfer.2016.09.098

CrossRef Full Text | Google Scholar

Ahmadpour, A., Noori Rahim Abadi, S. M. A., and Meyer, J. P. (2018). Numerical investigation of pool boiling on a staggered tube bundle for different working fluids. Int. J. Multiphase Flow 104, 89–102. doi: 10.1016/j.ijmultiphaseflow.2018.03.008

CrossRef Full Text | Google Scholar

Ajona, M. J., Herrmann, J. I., Sperduto, U., and Farinha, F. (1996). “Main achievements within ARDISS advanced receiver for direct solar stream production in parabolic trough solar power plant project,” in Proceedings of 8th International Symposium on Solar Thermal Concentrating Technology (Cologne), 33–753.

Akers, W. W., Deans, H. A., and Crosser, O. K. (1959). Condensation heat transfer within horizontal tubes. Chem. Eng. Progr. Symp. Series 55, 171–176.

Google Scholar

Akhil, A. A., Huff, G., Currier, A. B., Kaun, B. C., Rastler, D. M., Chen, S. B., et al. (2013). DOE/EPRI Electricity Storage Handbook in Collaboration With NRECA, Report SAND2013, Albuquerque, NM.

Google Scholar

Al-Hashimy, Z. I., Al-Kayiem, H. H., and Time, R. W. (2016). Experimental investigation on the vibration induced by slug flow in horizontal pipe. ARPN J. Eng. Appl. Sci. 11, 12134–12139.

Google Scholar

Allen, R. D., Doherty, T. J., and Kannberg, L. D. (1985). Summary of Selected Compressed Air Energy Storage Studies. Pacific Northwest Laboratory, Operated for the U.S. Department of Energy by Battelle Memorial Institute. Available online at: www.osti.gov

Alonso, M. C., Vera-Agullo, J., Guerreiro, L., Flor-Laguna, V., Sanchez, M., and Collares-Pereira, M. (2016). Calcium aluminate based cement for concrete to be used as thermal energy storage in solar thermal electricity plants. Cement Concrete Res. 82, 74–86. doi: 10.1016/j.cemconres.2015.12.013

CrossRef Full Text | Google Scholar

Alotto, P., Guarnieri, M., and Moro, F. (2014). Redox flow batteries for the storage of renewable energy: a review. Renew. Sust. Energy Rev. 29, 325–335. doi: 10.1016/j.rser.2013.08.001

CrossRef Full Text | Google Scholar

Ananiev, E. P., Boyko, L. D., and Kruzhilin, G. N. (1961). Heat transfer in the presence of steam condensation in a horizontal tube. Int. Dev. Heat Transfer 290–295.

Andreozzi, A., Buonomo, B., Manca, O., Mesolella, P., and Tamburrino, S. (2012).Numerical investigation on sensible thermal energy storage with porous media for high temperature solar systems. J. Phys. Conf. Series 395:2150. doi: 10.1088/1742-6596/395/1/012150

CrossRef Full Text

Antonelli, M., Barsali, S., Desideri, U., Giglioli, R., Paganucci, F., and Pasini, G. (2017). Liquid air energy storage: potential and challenges of hybrid power plants. Appl. Energy 194, 522–529. doi: 10.1016/j.apenergy.2016.11.091

CrossRef Full Text | Google Scholar

Ardizzon, G., Cavazzini, G., and Pavesi, G. (2014). A new generation of small hydro and pumped-hydro power plants: advances and future challenges. Renew. Sust. Energy Rev. 31, 746–761. doi: 10.1016/j.rser.2013.12.043

CrossRef Full Text | Google Scholar

Aurousseau, A., Vuillerme, V., and Bezian, J. J. (2016). Control systems for direct steam generation in linear concentrating solar power plants - a review. Renew. Sust. Energy Rev. 56, 611–630. doi: 10.1016/j.rser.2015.11.083

CrossRef Full Text | Google Scholar

Bahreini, M., Ramiar, A., and Ranjbar, A. A. (2017). Numerical simulation of subcooled flow boiling under conjugate heat transfer and microgravity condition in a vertical mini channel. Appl. Thermal Eng. 113, 170–185. doi: 10.1016/j.applthermaleng.2016.11.016

CrossRef Full Text | Google Scholar

Bai, F., and Xu, C. (2011). Performance analysis of a two-stage thermal energy storage system using concrete and steam accumulator. Appl. Thermal Eng. 31, 2764–2771. doi: 10.1016/j.applthermaleng.2011.04.049

CrossRef Full Text | Google Scholar

Baker, O. (1954). Simultaneous flow of oil and gas. Oil Gas J. 53, 185–190.

Google Scholar

Bankoff, S. G. (1960). A variable density single-fluid model for two-phase flow with particular reference to steam-water flow. J. Heat Transfer 82, 265–265. doi: 10.1115/1.3679930

CrossRef Full Text | Google Scholar

Bao, J., Lin, Y., Zhang, R., Zhang, N., and He, G. (2017a). Effects of stage number of condensing process on the power generation systems for lng cold energy recovery. Appl. Thermal Eng. 126, 566–582. doi: 10.1016/j.applthermaleng.2017.07.144

CrossRef Full Text | Google Scholar

Bao, J., Lin, Y., Zhang, R., Zhang, N., and He, G. (2017b). Strengthening power generation efficiency utilizing liquefied natural gas cold energy by a novel two-stage condensation rankine cycle (Tcrc) system. Energy Conver. Manage. 143, 312–325. doi: 10.1016/j.enconman.2017.04.018

CrossRef Full Text | Google Scholar

Bao, J., Zhang, R., Lin, Y., Zhang, N., Zhang, X., and He, G. (2018). The effect of the arrangements for compression process and expansion process on the performance of the two-stage condensation rankine cycle. Energy Conver. Manage. 159, 299–311. doi: 10.1016/j.enconman.2017.12.094

CrossRef Full Text | Google Scholar

Barbour, E., Mignard, D., Ding, Y., and Li, Y. (2015). Adiabatic compressed air energy storage with packed bed thermal energy storage. Appl. Energy 155, 804–815. doi: 10.1016/j.apenergy.2015.06.019

CrossRef Full Text | Google Scholar

Barnea, D. (1987). A unified model for predicting flow-pattern transitions for the whole range of pipe inclinations. Int. J. Multiphase Flow 13, 1–12. doi: 10.1016/0301-9322(87)90002-4

CrossRef Full Text | Google Scholar

Bauer, T., Pfleger, N., Breidenbach, N., Eck, M., Laing, D., and Kaesche, S. (2013). Material aspects of solar salt for sensible heat storage. Appl. Energy 111, 1114–1119. doi: 10.1016/j.apenergy.2013.04.072

CrossRef Full Text | Google Scholar

Bayón, R., Rojas, E., Valenzuela, L., Zarza, E., and León, J. (2010). Analysis of the experimental behaviour of a 100 kw <inf>th</inf>latent heat storage system for direct steam generation in solar thermal power plants. Appl. Thermal Eng. 30, 2643–2651. doi: 10.1016/j.applthermaleng.2010.07.011

CrossRef Full Text | Google Scholar

Bejan, A., and Kraus, A. D. (2003). Heat Transfer Handbook. Hoboken, NJ: John Wiley & Sons.

Google Scholar

Belderbos, A., Delarue, E., and D'haeseleer, W. (2015). “Possible role of power-to-gas in future energy systems,” in 12th International Conference On The European Energy Market (EEM), (Lisbon:IEEE), 19–22.

Google Scholar

Benato, A., and Stoppato, A. (2018). Pumped thermal electricity storage: a technology overview. Thermal Sci. Eng. Progr. 6, 301–315. doi: 10.1016/j.tsep.2018.01.017

CrossRef Full Text | Google Scholar

Berrichon, J. D., Louahlia-Gualous, H., Bandelier, P., Marion, M., and Bariteau, N. (2016). Local heat transfer during reflux condensation at subatmospheric pressure and with and without non-condensable gases for power plant application. Int. Commun. Heat Mass Transfer 76, 117–126. doi: 10.1016/j.icheatmasstransfer.2016.05.026

CrossRef Full Text | Google Scholar

Bertsch, S. S., Groll, E. A., and Garimella, S. V. (2009). A composite heat transfer correlation for saturated flow boiling in small channels. Int. J. Heat Mass Transfer 52, 2110–2118. doi: 10.1016/j.ijheatmasstransfer.2008.10.022

CrossRef Full Text | Google Scholar

Bhagat, K., and Saha, S. K. (2016). Numerical analysis of latent heat thermal energy storage using encapsulated phase change material for solar thermal power plant. Renew. Energy 95, 323–336. doi: 10.1016/j.renene.2016.04.018

CrossRef Full Text | Google Scholar

Biencinto, M., González, L., and Valenzuela, L. (2016). A quasi-dynamic simulation model for direct steam generation in parabolic troughs using trnsys. Appl. Energy 161, 133–142. doi: 10.1016/j.apenergy.2015.10.001

CrossRef Full Text | Google Scholar

Biencinto, M., González, L., Zarza, E., Díez, L. E., and Muñoz-Antón, J. (2014). Performance model and annual yield comparison of parabolic-trough solar thermal power plants with either nitrogen or synthetic oil as heat transfer fluid. Energy Conver. Manage. 87, 238–249. doi: 10.1016/j.enconman.2014.07.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Birnbaum, J., Eck, M., Fichtner, M., Hirsch, T., Lehmann, D., and Zimmermann, G. (2010). A direct steam generation solar power plant with integrated thermal storage. J. Solar Energy Eng. Transac. 132, 0310141–0310145. doi: 10.1115/1.4001563

CrossRef Full Text | Google Scholar

Birnbaum, J., Feldhoff, J. F., Fichtner, M., Hirsch, T., Jöcker, M., Pitz-Paal, R., et al. (2011). Steam temperature stability in a direct steam generation solar power plant. Solar Energy 85, 660–668. doi: 10.1016/j.solener.2010.10.005

CrossRef Full Text | Google Scholar

Bohdal, T., Charun, H., and Sikora, M. (2011). Comparative investigations of the condensation of r134a and r404a refrigerants in pipe minichannels. Int. J. Heat Mass Transfer 54, 1963–1974. doi: 10.1016/j.ijheatmasstransfer.2011.01.005

CrossRef Full Text | Google Scholar

Boiko, L. D., and Kruzhilin, G. N. (1965). Heat transfer in vapor condensation in a tube. Izvestiya Akademii Nauk Sssr, Energetika I Transport 128, 113–128.

Boukelia, T. E., Mecibah, M. S., Kumar, B. N., and Reddy, K. S. (2015). Investigation of solar parabolic trough power plants with and without integrated TES (thermal energy storage) and FBS (fuel backup system) using thermic oil and solar salt. Energy 88, 292–303. doi: 10.1016/j.energy.2015.05.038

CrossRef Full Text | Google Scholar

Bouvier, J. L., Michaux, G., Salagnac, P., Nepveu, F., Rochier, D., and Kientz, T. (2015). Experimental characterisation of a solar parabolic trough collector used in a micro-CHP (micro-cogeneration) system with direct steam generation. Energy 83, 474–485. doi: 10.1016/j.energy.2015.02.050

CrossRef Full Text | Google Scholar

Bracco, S., Caligaris, O., and Trucco, A. (2009). Mathematical models of air-cooled condensers for thermoelectric units. Wit Transac. Ecol. Environ. 121, 399–410. doi: 10.2495/ESU090351

CrossRef Full Text | Google Scholar

Brackbill, J., Kothe, D. B., and Zemach, C. (1992). A continuum method for modeling surface tension'. J. Comput. Phys. 100, 335–354. doi: 10.1016/0021-9991(92)90240-Y

CrossRef Full Text | Google Scholar

Brandon, N. P., Edge, J. S., Aunedi, M., Barbour, E., Bruce, P., Chakrabarti, B. K., et al. (2016). UK Research Needs in Grid Scale Energy Storage Technologies. The Energy SUPERSTORE. Available online at: www.energysuperstore.org

Breeze, P. (2014). Power Generation Technologies. Oxford: Elsevier ltd.

Google Scholar

Bruch, A., Fourmigué, J. F., and Couturier, R. (2014). Experimental and numerical investigation of a pilot-scale thermal oil packed bed thermal storage system for CSP power plant. Solar Energy 105, 116–125. doi: 10.1016/j.solener.2014.03.019

CrossRef Full Text | Google Scholar

Budt, M., Wolf, D., Span, R., and Yan, J. (2016). A review on compressed air energy storage: basic principles, past milestones and recent developments. Appl. Energy 170, 250–268. doi: 10.1016/j.apenergy.2016.02.108

CrossRef Full Text | Google Scholar

Bullough, C., Gatzen, C., Jakiel, C., Koller, M., Nowi, A., and Zunft, S. (2004). Advanced Adiabatic Compressed Air Energy Storage for the Integration of Wind Energy. London: Wind Energy.

Google Scholar

Buscemi, A., Panno, D., Ciulla, G., Beccali, M., and Lo Brano, V. (2018). Concrete thermal energy storage for linear fresnel collectors: exploiting the south mediterranean's solar potential for agri-food processes. Energy Conver. Manage. 166, 719–734. doi: 10.1016/j.enconman.2018.04.075

CrossRef Full Text | Google Scholar

Canière, H. (2009). Flow Pattern Mapping of Horizontal Evaporating Refrigerant Flow Based On Capacitive Void Fraction Measurements. Ghent: Ghent University.

Google Scholar

Canière, H., Bauwens, B., T'joen, C., and Depaepe, M. (2010) “Capacitive void fraction measurements probabilistic flow pattern mapping of horizontal refrigerant flow,” in 14th International Heat Transfer Conference (Washington, DC), 903–912.

Cao, S., Xu, J., Li, Y., and Yan, Y. (2017). Condensation heat transfer of r245fa in a shell-tube heat exchanger at slightly inclined angles. Int. J. Thermal Sci. 115, 197–209. doi: 10.1016/j.ijthermalsci.2017.01.029

CrossRef Full Text | Google Scholar

Caruso, G., Maio, D., and Naviglio, A. (2013). Film condensation in inclined tubes with non-condensable gases: an experimental study on the local heat transfer coefficient. Int. Commun. Heat Mass Transfer 45, 1–10. doi: 10.1016/j.icheatmasstransfer.2013.04.010

CrossRef Full Text | Google Scholar

Caruso, G., and Maio, D. V. D. (2014). Heat and mass transfer analogy applied to condensation in the presence of noncondensable gases inside inclined tubes. Int. J. Heat Mass Transfer 68, 401–414. doi: 10.1016/j.ijheatmasstransfer.2013.09.049

CrossRef Full Text | Google Scholar

Cavallini, A., Col, D. D., Doretti, L., Matkovic, M., Rossetto, L., Zilio, C., et al. (2006). Condensation in horizontal smooth tubes: a new heat transfer model for heat exchanger design. Heat Transfer Eng. 27, 31–38. doi: 10.1080/01457630600793970

CrossRef Full Text | Google Scholar

Cavallini, A., Col, D. D., Matkovic, M., and Rossetto, L. (2009). Frictional pressure drop during vapour-liquid flow in minichannels: modelling and experimental evaluation. Int. J. Heat Fluid Flow 30, 131–139. doi: 10.1016/j.ijheatfluidflow.2008.09.003

CrossRef Full Text | Google Scholar

Cavallini, A., and Zecchin, R. (1974). “A dimensionless correlation for heat transfer in forced convection condensation,” in Proceeding of Fifth International Heat Transfer Conference (Tyoko).

Google Scholar

Chanda, P., and Mukhopaddhyay, S. (2016). Operation and Maintenance of Thermal Power Stations. Springer India.

Charnay, R., Bonjour, J., and Revellin, R. (2014). Flow boiling characteristics of r-245fa in a minichannel at medium saturation temperatures: flow patterns and flow pattern maps. Int. J. Heat Fluid Flow 46, 1–16. doi: 10.1016/j.ijheatfluidflow.2013.12.002

CrossRef Full Text

Chen, H., Cong, T. N., Yang, W., Tan, C., Li, Y., and Ding, Y. (2009). Progress in electrical energy storage system: a critical review. Progr. Nat. Sci. 19, 291–312. doi: 10.1016/j.pnsc.2008.07.014

CrossRef Full Text | Google Scholar

Chen, H., Pan, P., Chen, X., Wang, Y., and Zhao, Q. (2017a). Fouling of the flue gas cooler in a large-scale coal-fired power plant. Appl. Thermal Eng. 117, 698–707. doi: 10.1016/j.applthermaleng.2017.02.048

CrossRef Full Text | Google Scholar

Chen, H. T., Chiu, Y. J., Tseng, H. C., and Chang, J. R. (2017b). Effect of domain boundary set on natural convection heat transfer characteristics for vertical annular finned tube heat exchanger. Int. J. Heat Mass Transfer 109, 668–682. doi: 10.1016/j.ijheatmasstransfer.2017.02.043

CrossRef Full Text | Google Scholar

Chen, H. T., Lin, Y. S., Chen, P. C., and Chang, J. R. (2016a). Numerical and experimental study of natural convection heat transfer characteristics for vertical plate fin and tube heat exchangers with various tube diameters. Int. J. Heat Mass Transfer 100, 320–331. doi: 10.1016/j.ijheatmasstransfer.2016.04.039

CrossRef Full Text | Google Scholar

Chen, I. Y., Yang, K.-S., Chang, Y. J., and Wang, C.-C. (2001). Two-phase pressure drop of air-water and r-410a in small horizontal tubes. Int. J. Multiphase Flow 27, 1293–1299. doi: 10.1016/S0301-9322(01)00004-0

CrossRef Full Text | Google Scholar

Chen, J. C. (1966). A correlation for boiling heat transfer of saturated fluids in convective flow. Ind. Eng. Chem. Process Des. Dev. 5, 322–329. doi: 10.1021/i260019a023

CrossRef Full Text | Google Scholar

Chen, L., Yang, L., Du, X., and Yang, Y. (2016b). A novel layout of air-cooled condensers to improve thermo-flow performances. Appl. Energy 165, 244–259. doi: 10.1016/j.apenergy.2015.11.062

CrossRef Full Text | Google Scholar

Chen, S., Yang, Z., Duan, Y., Chen, Y., and Wu, D. (2014). Simulation of condensation flow in a rectangular microchannel. Chem. Eng. Process. 76, 60–69. doi: 10.1016/j.cep.2013.12.004

CrossRef Full Text | Google Scholar

Chen, Y., Wu, J., Shi, M., and Peterson, G. (2008). Numerical simulation for steady annular condensation flow in triangular microchannels. Int. Commun. Heat Mass Transfer 35, 805–809. doi: 10.1016/j.icheatmasstransfer.2008.03.001

CrossRef Full Text | Google Scholar

Cheng, L. (2016). “Flow boiling heat transfer with models in microchannels,” in Microchannel Phase Change Transport Phenomena (Oxford: Butterworth-Heinemann), 141–191.

Google Scholar

Cheng, L., Ribatski, G., Moreno, T. Q., and Thome, J. R. (2008a). New prediction methods for Co₂ evaporation inside tubes, Part 1-a two-phase flow pattern map and a flow pattern based phenomenological model for two-phase flow frictional pressure drops. Int. J. Heat Mass Transfer 51, 111–124. doi: 10.1016/j.ijheatmasstransfer.2007.04.002

CrossRef Full Text | Google Scholar

Cheng, L., Ribatski, G., and Thome, J. R. (2008b). Two-phase flow patterns and flow-pattern maps: fundamentals and applications. Appl. Mech. Rev. 61:0508021-05080228. doi: 10.1115/1.2955990

CrossRef Full Text | Google Scholar

Cheng, Z. D., He, Y. L., Cui, F. Q., Xu, R. J., and Tao, Y. B. (2012). Numerical simulation of a parabolic trough solar collector with nonuniform solar flux conditions by coupling FVM and MCRT method. Solar Energy 86, 1770–1784. doi: 10.1016/j.solener.2012.02.039

CrossRef Full Text | Google Scholar

Cheng, Z. D., He, Y. L., Xiao, J., Tao, Y. B., and Xu, R. J. (2010). Three-dimensional numerical study of heat transfer characteristics in the receiver tube of parabolic trough solar collector. Int. Commun. Heat Mass Transfer 37, 782–787. doi: 10.1016/j.icheatmasstransfer.2010.05.002

CrossRef Full Text | Google Scholar

Chiou, J.-S., Yang, S.-A., and Chen, C. O.-K. (1994). Laminar film condensation inside a horizontal elliptical tube. Appl. Math. Model. 18, 340–346. doi: 10.1016/0307-904X(94)90358-1

CrossRef Full Text | Google Scholar

Chisholm, D. (1967). A theoretical basis for the lockhart-martinelli correlation for two-phase flow. Int. J. Heat Mass Transfer 10, 1767–1778. doi: 10.1016/0017-9310(67)90047-6

CrossRef Full Text | Google Scholar

Cioncolini, A., Thome, J. R., and Lombardi, C. (2009). Unified macro-to-microscale method to predict two-phase frictional pressure drops of annular flows. Int. J. Multiphase Flow 35, 1138–1148. doi: 10.1016/j.ijmultiphaseflow.2009.07.005

CrossRef Full Text | Google Scholar

Coleman, J. W., and Garimella, S. (2003). Two-phase flow regimes in round, square and rectangular tubes during condensation of refrigerant r134a. Int. J. Refriger. 26, 117–128. doi: 10.1016/S0140-7007(02)00013-0

CrossRef Full Text | Google Scholar

Cooper, M. G. (1984). Heat flow rates in saturated nucleate pool boiling-a wide-ranging examination using reduced properties. Adv. Heat Transfer 16, 157–239. doi: 10.1016/S0065-2717(08)70205-3

CrossRef Full Text | Google Scholar

Copetti, J. B., Macagnan, M. H., Zinani, F., and Kunsler, N. L. F. (2011). Flow boiling heat transfer and pressure drop of r-134a in a mini tube: an experimental investigation. Exp. Thermal Fluid Sci. 35, 636–644. doi: 10.1016/j.expthermflusci.2010.12.013

CrossRef Full Text | Google Scholar

Crotogino, F., Mohmeyer, K.-U., and Scharf, R. (2001). “Huntorf CAES more than 20 years of successful operation,” in Solution Mining Research Institute (SMRI) Spring Meeting (Orlando, FL), 351–357.

Google Scholar

Da Riva, E., Bortolin, S., and Del Col, D. (2011). “Condensation in a square minichannel: application of The VOF Method,” in 3rd Micro And Nano Flows Conference (Thessaloniki).

Google Scholar

Da Riva, E., and Del Col, D. (2009). “Numerical simulation of condensation in a minichannel,” in ASME 2nd Micro/Nanoscale Heat And Mass Transfer International Conference, (Shanghai), 139–145.

Google Scholar

Da Riva, E., and Del Col, D. (2011). Effect of gravity during condensation of R134a in a circular minichannel. Microgr. Sci. Technol. 23, 87–97. doi: 10.1007/s12217-011-9275-4

CrossRef Full Text | Google Scholar

Da Riva, E., and Del Col, D. (2012). Numerical simulation of laminar liquid film condensation in a horizontal circular minichannel. J. Heat Transfer 134, 1–8. doi: 10.1115/1.4005710

CrossRef Full Text | Google Scholar

Da Riva, E., Del Col, D., and Cavallini, A. (2010a). “Modelling of condensation in a circular minichannel by means of the VOF method,” 14th International Heat Transfer Conference (Washington, DC), 205–213.

Google Scholar

Da Riva, E., Del Col, D., Cavallini, A., and Garimella, S. (2010b). “Simulation of condensation in a circular minichannel: application of VOF method and turbulence model,” International Refrigeration And Air Conditioning Conference, 12–15 Purdue (West Lafayette, IN), 1160.

Google Scholar

Da Riva, E., Del Col, D., Garimella, S. V., and Cavallini, A. (2012). The importance of turbulence during condensation in a horizontal circular minichannel. Int. J. Heat Mass Transfer 55, 3470–3481. doi: 10.1016/j.ijheatmasstransfer.2012.02.026

CrossRef Full Text | Google Scholar

Dalkilic, A. S., and Wongwise, S. (2009). Intensive literature review of condensation inside smooth and enhanced tubes. Int. J. Heat Mass Transfer 52 3409–3426. doi: 10.1016/j.ijheatmasstransfer.2009.01.011

CrossRef Full Text | Google Scholar

Dan, N., and Bejan, A. (1998). Constructal tree networks for the time-dependent discharge of a finite-size volume to one point. J. Appl. Phys. 84, 3042–3050. doi: 10.1063/1.368458

CrossRef Full Text | Google Scholar

Das, B. K., and M. Al-Abdeli, Y. (2017). Optimisation of stand-alone hybrid chp systems meeting electric and heating loads. Energy Conver. Manage. 153, 391–408. doi: 10.1016/j.enconman.2017.09.078

CrossRef Full Text | Google Scholar

De Sá, A. B., Pigozzo Filho, V. C., Tadrist, L., and Passos, J. C. (2018). Direct steam generation in linear solar concentration: experimental and modeling investigation – a review. Renew. Sust. Energy Rev. 90, 910–936. doi: 10.1016/j.rser.2018.03.075

CrossRef Full Text | Google Scholar

Deane, J. P., Ó Gallachóir, B. P., and Mckeogh, E. J. (2010). Techno-economic review of existing and new pumped hydro energy storage plant. Renew. Sust. Energy Rev. 14, 1293–1302. doi: 10.1016/j.rser.2009.11.015

CrossRef Full Text | Google Scholar

Del Col, D., Bortolato, M., Azzolin, M., and Bortolin, S. (2014). Effect of inclination during condensation inside a square cross section minichannel. Int. J. Heat Mass Transfer. 78, 760–777. doi: 10.1016/j.ijheatmasstransfer.2014.06.078

CrossRef Full Text | Google Scholar

Dobson, M. K., Wattelet, J. P., and Chato, J. C. (1993). Optimal Sizing of Two-Phase Heat Exchangers. Urbana, IL: Air Conditioning and Refrigeration Center, University of Illinois, Mechanical & Industrial Engineering Department.

Google Scholar

Eck, M., and Hirsch, T. (2007). Dynamics and control of parabolic trough collector loops with direct steam generation. Solar Energy 81, 268–279. doi: 10.1016/j.solener.2006.01.008

CrossRef Full Text | Google Scholar

Elsafi, A. M. (2015a). Exergy and exergoeconomic analysis of sustainable direct steam generation solar power plants. Energy Conver. Manage. 103, 338–347. doi: 10.1016/j.enconman.2015.06.066

CrossRef Full Text | Google Scholar

Elsafi, A. M. (2015b). On thermo-hydraulic modeling of direct steam generation. Solar Energy 120, 636–650. doi: 10.1016/j.solener.2015.08.008

CrossRef Full Text | Google Scholar

Ewim, D. R. E., Meyer, J. P., and Noori Rahim Abadi, S. M. A. (2018). Condensation heat transfer coefficients in an inclined smooth tube at low mass fluxes. Int. J. Heat Mass Transfer 123, 455–467. doi: 10.1016/j.ijheatmasstransfer.2018.02.091

CrossRef Full Text | Google Scholar

Faghri, A., and Zhang, Y. (2006). Transport Phenomena in Multiphase Systems. Burlington, MA: Academic Press.

Google Scholar

Fang, C., David, M., Rogacs, A., and Goodson, K. (2010). Volume of fluid simulation of boiling two-phase flow in a vapor-venting microchannel. Front. Heat Mass Transfer 1:013002. doi: 10.5098/hmt.v1.1.3002

CrossRef Full Text | Google Scholar

Fang, X., Wu, Q., and Yuan, Y. (2017). A general correlation for saturated flow boiling heat transfer in channels of various sizes and flow directions. Int. J. Heat Mass Transfer 107, 972–981. doi: 10.1016/j.ijheatmasstransfer.2016.10.125

CrossRef Full Text | Google Scholar

Fang, X., Zhou, Z., and Wang, H. (2015). Heat transfer correlation for saturated flow boiling of water. Appl. Thermal Eng. 76, 147–156. doi: 10.1016/j.applthermaleng.2014.11.024

CrossRef Full Text | Google Scholar

Farres-Antunez, P., Xue, H., and White, A. J. (2018). Thermodynamic analysis and optimisation of a combined liquid air and pumped thermal energy storage cycle. J. Energy Storage 18, 90–102. doi: 10.1016/j.est.2018.04.016

CrossRef Full Text | Google Scholar

Feldhoff, J. F., Schmitz, K., Eck, M., Schnatbaum-Laumann, L., Laing, D., Ortiz-Vives, F., et al. (2012). Comparative system analysis of direct steam generation and synthetic oil parabolic trough power plants with integrated thermal storage. Solar Energy 86, 520–530. doi: 10.1016/j.solener.2011.10.026

CrossRef Full Text | Google Scholar

Fernández, A. G., Ushak, S., Galleguillos, H., and Pérez, F. J. (2015). Thermal characterisation of an innovative quaternary molten nitrate mixture for energy storage in csp plants. Solar Energy Mater Solar Cells 132, 172–177. doi: 10.1016/j.solmat.2014.08.020

CrossRef Full Text | Google Scholar

Flueckiger, S. M., Yang, Z., and Garimella, S. V. (2013). Review of molten-salt thermocline tank modeling for solar thermal energy storage. Heat Transfer Eng. 34, 787–800. doi: 10.1080/01457632.2012.746152

CrossRef Full Text | Google Scholar

Fong, D. A., Crane, S. E., and Berlin, E. P. (2010). Compressed air energy storage system utilizing two-phase flow to facilitate heat exchange. United States Patent Application 20100326069.

Fornarelli, F., Camporeale, S. M., Fortunato, B., Torresi, M., Oresta, P., Magliocchetti, L., et al. (2016). CFD analysis of melting process in a shell-and-tube latent heat storage for concentrated solar power plants. Appl. Energy 164, 711–722. doi: 10.1016/j.apenergy.2015.11.106

CrossRef Full Text | Google Scholar

Fraidenraich, N., Oliveira, C., Vieira Da Cunha, A. F., Gordon, J. M., and Vilela, O. C. (2013). Analytical modeling of direct steam generation solar power plants. Solar Energy 98, 511–522. doi: 10.1016/j.solener.2013.09.037

CrossRef Full Text | Google Scholar

Freeman, J., Hellgardt, K., and Markides, C. N. (2015). An assessment of solar-powered organic Rankine cycle systems for combined heating and power in UK domestic applications. Appl. Energy 138, 605–620. doi: 10.1016/j.apenergy.2014.10.035

CrossRef Full Text | Google Scholar

Freeman, J., Hellgardt, K., and Markides, C. N. (2017). Working fluid selection and electrical performance optimisation of a domestic solar-ORC combined heat and power system for year-round operation in the UK. Appl. Energy 186, 291–303. doi: 10.1016/j.apenergy.2016.04.041

CrossRef Full Text | Google Scholar

Frein, A., Motta, M., Berger, M., and Zahler, C. (2018). Solar DSG plant for pharmaceutical industry in jordan: modelling, monitoring and optimization. Solar Energy 173, 362–376. doi: 10.1016/j.solener.2018.07.072

CrossRef Full Text | Google Scholar

Ganapathy, H., Shooshtari, A., Choo, K., Dessiatoun, S., and Alshehhi, M.M.M.O. (2012). “Numerical analysis of condensation of R134a in a single microchannel,” in ASME International Mechanical Engineering Congress And Exposition (Houston, TX), 2971–2980.

Google Scholar

Ganapathy, H., Shooshtari, A., Choo, K., Dessiatoun, S., and Alshehhi, M.M.M.O. (2013). Volume of fluid-based numerical modeling of condensation heat transfer and fluid flow characteristics in microchannels. Int. J. Heat Mass Transfer 65, 62–72. doi: 10.1016/j.ijheatmasstransfer.2013.05.044

CrossRef Full Text | Google Scholar

Gara, P. (1995). Handbook of Industrial Power and Steam Systems. Englewood Cliffs, NJ: Fairmont Press, Incorporated.

Garbai, L., and Sánta, R. (2012). “Flow pattern map for in tube evaporation and condensation,” in 4th International Symposium On Exploitation Of Renewable Energy Sources (Subotica: Express).

Google Scholar

Garcia, P., Vuillerme, V., Olcese, M., and El Mourchid, N. (2016). “Design and modelling of an innovative three-stage thermal storage system for direct steam generation CSP plants,” in SOLARPACES 2015: International Conference on Concentrating Solar Power and Chemical Energy Systems, AIP Conference Proceedings (Cape Town).

Google Scholar

García-Valladares, O., and Velázquez, N. (2009). Numerical simulation of parabolic trough solar collector: improvement using counter flow concentric circular heat exchangers. Int. J. Heat Mass Transfer 52, 597–609. doi: 10.1016/j.ijheatmasstransfer.2008.08.004

CrossRef Full Text | Google Scholar

Garimella, S., Killion, J. D., and Coleman, J. W. (2002). Experimentally validated model for two-phase pressure drop in the intermittent flow regime for circular microchannels. J. Fluids Eng. Transac. ASME 124, 205–214. doi: 10.1115/1.1428327

CrossRef Full Text | Google Scholar

Garvey, S. D., Eames, P. C., Wang, J. H., Pimm, A. J., Waterson, M., Mackay, R. S., et al. (2015). On generation-integrated energy storage. Energy Policy 86, 544–551. doi: 10.1016/j.enpol.2015.08.001

CrossRef Full Text | Google Scholar

Georgiou, S., Shah, N., and Markides, C. N. (2018). A thermo-economic analysis and comparison of pumped-thermal and liquid-air electricity storage systems. Appl. Energy 226, 1119–1133. doi: 10.1016/j.apenergy.2018.04.128

CrossRef Full Text | Google Scholar

Ghajar, A. J. (2005). Non-boiling heat transfer in gas-liquid flow in pipes: a tutorial. J. Brazil. Soc. Mech. Sci. Eng. 27, 46–73. doi: 10.1590/S1678-58782005000100004

CrossRef Full Text | Google Scholar

Ghoneim, A. A. (1989). Comparison of theoretical models of phase-change and sensible heat storage for air and water-based solar heating systems. Solar Energy 42, 209–220. doi: 10.1016/0038-092X(89)90013-3

CrossRef Full Text | Google Scholar

Giglio, A., Lanzini, A., Leone, P., Rodrïguez Garcïa, M. M., and Zarza Moya, E. (2017). Direct steam generation in parabolic-trough collectors: a review about the technology and a thermo-economic analysis of a hybrid system. Renew. Sust. Energy Rev. 74, 453–473. doi: 10.1016/j.rser.2017.01.176

CrossRef Full Text | Google Scholar

Gil, A., Medrano, M., Martorell, I., Lázaro, A., Dolado, P., Zalba, B., et al. (2010). State of the art on high temperature thermal energy storage for power generation. Part 1-Concepts, Materials and modellization. Renew. Sust. Energy Rev. 14, 31–55. doi: 10.1016/j.rser.2009.07.035

CrossRef Full Text | Google Scholar

González-Roubaud, E., Pérez-Osorio, D., and Prieto, C. (2017). Review of commercial thermal energy storage in concentrated solar power plants: steam vs. Molten Salts. Renew. Sust. Energy Rev. 80, 133–148. doi: 10.1016/j.rser.2017.05.084

CrossRef Full Text | Google Scholar

Gou, J., Ma, H., Yang, Z., and Shan, J. (2017). An assessment of heat transfer models of water flow in helically coiled tubes based on selected experimental datasets. Ann. Nuclear Energy 110, 648–667. doi: 10.1016/j.anucene.2017.07.015

CrossRef Full Text | Google Scholar

Grönnerud, R. (1972). Investigation of Liquid Hold-Up Flow-Resistance and Heat Transfer in Circulation Type Evaporators, Part Iv: Two-Phase Flow Resistance in Boiling Refrigerants (Freudenstadt), 127–138.

Gungor, K. E., and Winterton, R. H. S. (1986). A general correlation for flow boiling in tubes and annuli. Int. J. Heat Mass Transfer 29, 351–358. doi: 10.1016/0017-9310(86)90205-X

CrossRef Full Text | Google Scholar

Guo, C., and Zhang, W. (2008). Numerical simulation and parametric study on new type of high temperature latent heat thermal energy storage system. Energy Conver. Manage. 49, 919–927. doi: 10.1016/j.enconman.2007.10.025

CrossRef Full Text | Google Scholar

Guo, S., Li, H., Zhao, J., Li, X., and Yan, J. (2013). Numerical simulation study on optimizing charging process of the direct contact mobilized thermal energy storage. Appl. Energy 112, 1416–1423. doi: 10.1016/j.apenergy.2013.01.020

CrossRef Full Text | Google Scholar

Guo, S., Liu, D., Chen, X., Chu, Y., Xu, C., Liu, Q., et al. (2017). Model and control scheme for recirculation mode direct steam generation parabolic trough solar power plants. Appl. Energy 202, 700–714. doi: 10.1016/j.apenergy.2017.05.127

CrossRef Full Text | Google Scholar

Guo, Z., Haynes, B. S., and Fletcher, D. F. (2016). Numerical simulation of annular flow boiling in microchannels. J. Comput. Multiphase Flows 8, 61–82. doi: 10.1177/1757482X16634205

CrossRef Full Text | Google Scholar

Gvozdenaca, D., Urošević, B. G., Menke, C., Urošević, D., and Bangviwat, A. (2017). High efficiency cogeneration: chp and non-chp energy. Energy 135, 269–278. doi: 10.1016/j.energy.2017.06.143

CrossRef Full Text | Google Scholar

Hajal, J. E., Thome, J. R., and Cavallini, A. (2003). Condensation in horizontal tubes, part 1: two-phase flow pattern map. Int. J. Heat Mass Transfer 46, 3349–3363. doi: 10.1016/S0017-9310(03)00139-X

CrossRef Full Text | Google Scholar

Hardik, B. K., and Prabhu, S. V. (2016). Boiling pressure drop and local heat transfer distribution of water in horizontal straight tubes at low pressure. Int. J. Thermal Sci. 110, 65–82. doi: 10.1016/j.ijthermalsci.2016.06.025

CrossRef Full Text | Google Scholar

He, W., Luo, X., Evans, D., Busby, J., Garvey, S., Parkes, D., et al. (2017). Exergy storage of compressed air in cavern and cavern volume estimation of the large-scale compressed air energy storage system. Appl. Energy 208, 745–757. doi: 10.1016/j.apenergy.2017.09.074

CrossRef Full Text | Google Scholar

Heo, J., and Yun, R. (2015). Prediction of co₂ condensation heat transfer coefficient in a tube. Int. J. Thermal Sci. 89, 254–263. doi: 10.1016/j.ijthermalsci.2014.11.021

CrossRef Full Text | Google Scholar

Hewitt, G. (1982). Multiphase Science and Technology, Volume 1. Berlin: Hemisphere Pub. Corp.

Google Scholar

Hewitt, G. F., and Roberts, D. N. (1969). Studies of Two-Phase Flow Patterns by Simultaneous X-ray and Flash Photography. Atomic Energy Research Establishment, Harwell, Report No. Aere-M 2159.

Highview Power (2018). RE: Highview Power Launches World's First Grid-Scale Liquid Air Energy Storage Plant. Available online at: https://www.highviewpower.com/news_announcement/world-first-liquid-air-energy-storage-plant/ (accessed June 22, 2018).

Hirsch, T., Feldhoff, J. F., Hennecke, K., and Pitz-Paal, R. (2014). Advancements in the field of direct steam generation in linear solar concentrators-a review. Heat Transfer Eng. 35, 258–271. doi: 10.1080/01457632.2013.825172

CrossRef Full Text | Google Scholar

Hossain, M. A., Afroz, H. M. M., and Miyara, A. (2015). Two-phase frictional multiplier correlation for the prediction of condensation pressure drop inside smooth horizontal tube. Proc. Eng. 105, 64–72. doi: 10.1016/j.proeng.2015.05.008

CrossRef Full Text | Google Scholar

Hua, Y. C., Zhao, T., and Guo, Z. Y. (2017). Transient thermal conduction optimization for solid sensible heat thermal energy storage modules by the monte carlo method. Energy 133, 338–347. doi: 10.1016/j.energy.2017.05.073

CrossRef Full Text | Google Scholar

Iqbal, O., and Bansal, P. (2012). In-tube condensation heat transfer of co₂ at low temperatures in a horizontal smooth tube. Int. J. Refriger. 35, 270–277. doi: 10.1016/j.ijrefrig.2011.10.015

CrossRef Full Text | Google Scholar

IRENA (2017). Electricity Storage and Renewables: Costs and Markets to 2030. Abu Dhabi: International Renewable Energy Agency. Available online at: www.irena.org.

Islam, M. T., Huda, N., Abdullah, A. B., and Saidur, R. (2018). A comprehensive review of state-of-the-art concentrating solar power (CSP) technologies: current status and research trends. Renew. Sust. Energy Rev. 91, 987–1018. doi: 10.1016/j.rser.2018.04.097

CrossRef Full Text | Google Scholar

Jian, Y., Falcoz, Q., Neveu, P., Bai, F., Wang, Y., and Wang, Z. (2015). Design and optimization of solid thermal energy storage modules for solar thermal power plant applications. Appl. Energy 139, 30–42. doi: 10.1016/j.apenergy.2014.11.019

CrossRef Full Text | Google Scholar

Kandlikar, S., Garimella, S., Li, D., Colin, S., and King, M. R. (2005). Heat Transfer and Fluid Flow In Minichannels and Microchannels. Oxford: Elsevier.

Google Scholar

Kandlikar, S. G. (1990). A general correlation for saturated two-phase flow boiling heat transfer inside horizontal and vertical tubes. J. Heat Transfer 112, 219–219. doi: 10.1115/1.2910348

CrossRef Full Text | Google Scholar

Kandlikar, S. G. (2002). Two-phase flow patterns, pressure drop, and heat transfer during boiling in minichannel flow passages of compact evaporators. Heat Transfer Eng. 23, 5–23. doi: 10.1080/014576302753249570

CrossRef Full Text | Google Scholar

Kandlikar, S. G., and Grande, W. J. (2003). Evolution of microchannel flow passages-thermohydraulic performance and fabrication technology. Heat Transfer Eng. 24, 3–17. doi: 10.1080/01457630304040

CrossRef Full Text | Google Scholar

Kang, Y., Davies, W. A., Hrnjak, P., and Jacobi, A. M. (2017). Effect of inclination on pressure drop and flow regimes in large flattened-tube steam condensers. Appl. Thermal Eng. 123, 498–513. doi: 10.1016/j.applthermaleng.2017.05.062

CrossRef Full Text | Google Scholar

Karayiannis, T. G., and Mahmoud, M. M. (2017). Flow boiling in microchannels: fundamentals and applications. Appl. Thermal Eng. 115, 1372–1397. doi: 10.1016/j.applthermaleng.2016.08.063

CrossRef Full Text | Google Scholar

Kargar, M. R., Baniasadi, E., and Mosharaf-Dehkordi, M. (2018). Numerical analysis of a new thermal energy storage system using phase change materials for direct steam parabolic trough solar power plants. Solar Energy 170, 594–605. doi: 10.1016/j.solener.2018.06.024

CrossRef Full Text | Google Scholar

Kattan, N., Thome, J. R., and Favrat, D. (1998a). Flow boiling in horizontal tubes-part i: development of a diabatic two-phase flow pattern map. J. Heat Transfer 120, 140–147. doi: 10.1115/1.2830037

CrossRef Full Text | Google Scholar

Kattan, N., Thome, J. R., and Favrat, D. (1998b). Flow boiling in horizontal tubes: part 3-development of a new heat transfer model based on flow pattern. J. Heat Transfer 120, 156–165. doi: 10.1115/1.2830039

CrossRef Full Text | Google Scholar

Kaya, A., Özdemir, M. R., Keskinöz, M., and Koşar, A. (2014). The effects of inlet restriction and tube size on boiling instabilities and detection of resulting premature critical heat flux in microtubes using data analysis. Appl. Thermal Eng. 65, 575–587. doi: 10.1016/j.applthermaleng.2014.01.062

CrossRef Full Text | Google Scholar

Kaya, A., Özdemir, R. M., and Kosar, A. (2013). High mass flux flow boiling and critical heat flux in microscale. Int. J. Thermal Sci. 65, 70–78. doi: 10.1016/j.ijthermalsci.2012.10.021

CrossRef Full Text | Google Scholar

Khalifa, A., Tan, L., Date, A., and Akbarzadeh, A. (2015). Performance of suspended finned heat pipes in high-temperature latent heat thermal energy storage. Appl. Thermal Eng. 81, 242–252. doi: 10.1016/j.applthermaleng.2015.02.030

CrossRef Full Text | Google Scholar

Kharangate, C. R., Lee, H., Park, I., and Mudawar, I. (2016). Experimental and computational investigation of vertical upflow condensation in a circular tube. Int. J. Heat Mass Transfer 95, 249–263. doi: 10.1016/j.ijheatmasstransfer.2015.11.010

CrossRef Full Text | Google Scholar

Kharangate, C. R., and Mudawar, I. (2017). Review of computational studies on boiling and condensation. Int. J. Heat Mass Transfer 108, 1164–1196. doi: 10.1016/j.ijheatmasstransfer.2016.12.065

CrossRef Full Text | Google Scholar

Kim, S.-M., and Mudawar, I. (2013). Universal approach to predicting heat transfer coefficient for condensing mini/micro-channel flow. Int. J. Heat Mass Transfer 56, 238–250. doi: 10.1016/j.ijheatmasstransfer.2012.09.032

CrossRef Full Text | Google Scholar

Kim, S. M., Kim, J., and Mudawar, I. (2012). Flow condensation in parallel micro-channels–part 1: experimental results and assessment of pressure drop correlations. Int. J. Heat Mass Transfer 55, 971–983. doi: 10.1016/j.ijheatmasstransfer.2011.10.013

CrossRef Full Text | Google Scholar

Kim, S. M., and Mudawar, I. (2012). Theoretical model for annular flow condensation in rectangular micro-channels. Int. J. Heat Mass Transfer 55, 958–970. doi: 10.1016/j.ijheatmasstransfer.2011.10.014

CrossRef Full Text | Google Scholar

Kim, Y., Choi, J., Kim, S., and Zhang, Y. (2015). Effects of mass transfer time relaxation parameters on condensation in a thermosyphon. J. Mech. Sci. Technol. 29, 5497–5505. doi: 10.1007/s12206-015-1151-5

CrossRef Full Text | Google Scholar

Kong, Y., Wang, W., Huang, X., Yang, L., Du, X., and Yang, Y. (2017). Direct dry cooling system through hybrid ventilation for improving cooling efficiency in power plants. Appl. Thermal Eng. 119, 254–268. doi: 10.1016/j.applthermaleng.2017.03.067

CrossRef Full Text | Google Scholar

Konishi, C., and Mudawar, I. (2015). Review of flow boiling and critical heat flux in microgravity. Int. J. Heat Mass Transfer 80, 469–493. doi: 10.1016/j.ijheatmasstransfer.2014.09.017

CrossRef Full Text | Google Scholar

Kumar, A., Joshi, J. B., Nayak, A. K., and Vijayan, P. K. (2016). 3D CFD simulations of air cooled condenser-II: natural draft around a single finned tube kept in a small chimney. Int. J. Heat Mass Transfer 92, 507–522. doi: 10.1016/j.ijheatmasstransfer.2015.07.136

CrossRef Full Text | Google Scholar

Kumar, B. N., and Reddy, K. S. (2018). Comparison of two-phase flow correlations for thermo- hydraulic modeling of direct steam generation in a solar parabolic trough collector system. J. Thermal Sci. Eng. Appl. 10, 1–10. doi: 10.1115/1.4038988

CrossRef Full Text | Google Scholar

Kuravi, S., Trahan, J., Goswami, Y., Jotshi, C., Stefanakos, E., and Goel, N. (2013). Investigation of a high-temperature packed-bed sensible heat thermal energy storage system with large-sized elements. J. Solar Energy Eng. Transac. ASME 135:041008. doi: 10.1115/1.4023969

CrossRef Full Text | Google Scholar

Lafaurie, B., Nardone, C., Scardovelli, R., Zaleski, S., and Zanetti, G. (1994). Modelling merging and fragmentation in multiphase flows with surfer. J. Comput. Phys. 113, 134–147. doi: 10.1006/jcph.1994.1123

CrossRef Full Text | Google Scholar

Laing, D., Bahl, C., Bauer, T., Lehmann, D., and Steinmann, W. D. (2011). Thermal energy storage for direct steam generation. Solar Energy 85, 627–633. doi: 10.1016/j.solener.2010.08.015

CrossRef Full Text | Google Scholar

Laskowski, R. M. (2012). A mathematical model of a steam condenser in off-design operation. J. Power Technol. 92, 101–108.

Google Scholar

Lazard (2017). Lazard's Levelized Cost of Storage Analysis — version 3.0. Available online at: www.lazard.com

Lee, H., Agonafer, D. D., Won, Y., Houshmand, F., Gorle, C., Asheghi, M., et al. (2016). Thermal modeling of extreme heat flux microchannel coolers for GaN-on-SiC semiconductor devices. J. Electronic Packag. 138:010907. doi: 10.1115/1.4032655

CrossRef Full Text | Google Scholar

Lee, H., Kharangate, C. R., Mascarenhas, N., Park, I., and Mudawar, I. (2015). Experimental and computational investigation of vertical downflow condensation. Int. J. Heat Mass Transfer 85, 865–879. doi: 10.1016/j.ijheatmasstransfer.2015.02.037

CrossRef Full Text | Google Scholar

Lee, H., Mudawar, I., and Hasan, M. M. (2013). Experimental and theoretical investigation of annular flow condensation in microgravity. Int. J. Heat Mass Transfer 61, 293–309. doi: 10.1016/j.ijheatmasstransfer.2013.02.010

CrossRef Full Text | Google Scholar

Lee, H. J., and Lee, S. Y. (2001). Pressure drop correlations for two-phase fow within horizontal rectangular channels with small heights. Int. J. Multiphase Flow 27, 783–796. doi: 10.1016/S0301-9322(00)00050-1

CrossRef Full Text | Google Scholar

Lee, W. H. (1980). $“Pressure iteration scheme for two-phase flow modeling,” in Multiphase Transport Fundamentals, Reactor Safety, Applications 1, ed T. N. Veziroglu (Washington, DC: Hemisphere Publishing), 407–431.

Google Scholar

Li, J., Pei, G., Ji, J., Bai, X., Li, P., and Xia, L. (2014). Design of the ORC (Organic Rankine Cycle) condensation temperature with respect to the expander characteristics for domestic CHP (Combined Heat and Power) applications. Energy 77, 579–590. doi: 10.1016/j.energy.2014.09.039

CrossRef Full Text | Google Scholar

Li, L., Sun, J., and Li, Y. (2017). Thermal load and bending analysis of heat collection element of direct-steam-generation parabolic-trough solar power plant. Appl. Thermal Eng. 127, 1530–1542. doi: 10.1016/j.applthermaleng.2017.08.129

CrossRef Full Text | Google Scholar

Li, P. Y., Loth, E., Simon, T. W., Van De Ven, J. D., and Crane, S. E. (2011). Compressed Air Energy Storage for Offshore Wind Turbines. Las Vegas: International Fluid Power Exhibition.

Google Scholar

Li, W., Tang, W., Chen, J., Zhu, H., Kukulka, D. J., He, Y., et al. (2018a). Convective condensation in three enhanced tubes with different surface modifications. Exp. Thermal Fluid Sci. 97, 79–88. doi: 10.1016/j.expthermflusci.2018.04.011

CrossRef Full Text | Google Scholar

Li, X., Wang, N., Wang, L., Yang, Y., and Maréchal, F. (2018b). Identification of optimal operating strategy of direct air-cooling condenser for rankine cycle based power plants. Appl. Energy 209, 153–166. doi: 10.1016/j.apenergy.2017.10.081

CrossRef Full Text | Google Scholar

Lin, M., Reinhold, J., Monnerie, N., and Haussener, S. (2018). Modeling and design guidelines for direct steam generation solar receivers. Appl. Energy 216, 761–776. doi: 10.1016/j.apenergy.2018.02.044

CrossRef Full Text | Google Scholar

Lippke, F. (1996). Direct steam generation in parabolic trough solar power plants: numerical investigation of the transients and the control of a once-through system. J. Solar Energy Eng. Transac. ASME 118, 9–14.

Google Scholar

Lips, S., and Meyer, J. P. (2011). Two-phase flow in inclined tubes with specific reference to condensation: a review. Int. J. Multiphase Flow 37, 845–859. doi: 10.1016/j.ijmultiphaseflow.2011.04.005

CrossRef Full Text | Google Scholar

Lips, S., and Meyer, J. P. (2012a). Effect of gravity forces on heat transfer and pressure drop during condensation of R134a. Microgr. Sci. Technol. 24, 157–164. doi: 10.1007/s12217-011-9292-3

CrossRef Full Text | Google Scholar

Lips, S., and Meyer, J. P. (2012b). Experimental study of convective condensation in an inclined smooth tube. Part I: inclination effect on flow pattern and heat transfer coefficient. Int. J. Heat Mass Transfer 55, 395–404. doi: 10.1016/j.ijheatmasstransfer.2011.09.033

CrossRef Full Text | Google Scholar

Lips, S., and Meyer, J. P. (2012c). Experimental study of convective condensation in an inclined smooth tube. Part II: inclination effect on pressure drops and void fractions. Int. J. Heat Mass Transfer 55, 405–412. doi: 10.1016/j.ijheatmasstransfer.2011.09.034

CrossRef Full Text | Google Scholar

Lips, S., and Meyer, J. P. (2012d). Stratified flow model for convective condensation in an inclined tube. Int. J. Heat Fluid Flow 36, 83–91. doi: 10.1016/j.ijheatfluidflow.2012.03.005

CrossRef Full Text | Google Scholar

Liu, J., Zhang, X., Xu, Y., Chen, Z., Chen, H., and Tan, C. (2014). Economic analysis of using above ground gas storage devices for compressed air energy storage system. J. Thermal Sci. 23, 535–543. doi: 10.1007/s11630-014-0738-y

CrossRef Full Text | Google Scholar

Liu, X., Zhang, X., Lu, T., Mahkamov, K., Wu, H., and Mirzaeian, M. (2016a). Numerical simulation of sub-cooled boiling flow with fouling deposited inside channels. Appl. Thermal Eng. 103, 434–442. doi: 10.1016/j.applthermaleng.2016.04.041

CrossRef Full Text | Google Scholar

Liu, Y., Chen, Q., Hu, K., and Hao, J. H. (2016b). Flow field optimization for the solar parabolic trough receivers in direct steam generation systems by the variational principle. Int. J. Heat Mass Transfer 102, 1073–1081. doi: 10.1016/j.ijheatmasstransfer.2016.06.083

CrossRef Full Text | Google Scholar

Liu, Z., Sunden, B., and Wu, H. (2015). Numerical modeling of multiple bubbles condensation in subcooled flow boiling. J. Thermal Sci. Eng. Appl. 7, 1–9. doi: 10.1115/1.4029953

CrossRef Full Text | Google Scholar

Liu, Z., Sunden, B., and Yuan, J. (2012). VOF modeling and analysis of filmwise condensation between vertical parallel plates. Heat Transfer Res. 43, 47–68. doi: 10.1615/HeatTransRes.2012004376

CrossRef Full Text | Google Scholar

Lloyd's Register Foundation (2017). Foresight Review of Energy Storage. Available online at: http://www.lrfoundation.org.uk/publications/foresight-energy-storage-download.aspx

Lobón, D. H., Baglietto, E., Valenzuela, L., and Zarza, E. (2014). modeling direct steam generation in solar collectors with multiphase CFD. Appl. Energy 113, 1338–1348. doi: 10.1016/j.apenergy.2013.08.046

CrossRef Full Text | Google Scholar

Lockhart, R. W., and Martinelli, R. C. (1949). Proposed correlation of data for isothermal two-phase, two-component flow in pipes. Chem. Eng. Progr. 45, 39–48.

Google Scholar

Lorenzini, D., and Joshi, Y. K. (2015). “CFD analysis of flow boiling in a silicon microchannel with non-uniform heat flux,” in 13th ASME International Conference on Nanochannels Microchannels and Minichannels Collocated With the ASME International Technical Conference and Exhibition on Packaging and Integration of Electronic and Photonic Microsystems, paper 48098 (San Francisco, CA).

Google Scholar

Luo, X., Wang, J., Dooner, M., and Clarke, J. (2015). Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 137, 511–536. doi: 10.1016/j.apenergy.2014.09.081

CrossRef Full Text | Google Scholar

Magnini, M., Pulvirenti, B., and Thome, J. R. (2013). Numerical investigation of hydrodynamics and heat transfer of elongated bubbles during flow boiling in a microchannel. Int. J. Heat Mass Transfer 59, 451–471. doi: 10.1016/j.ijheatmasstransfer.2012.12.010

CrossRef Full Text | Google Scholar

Magnini, M., and Thome, J. R. (2016). Computational study of saturated flow boiling within a microchannel in the slug flow regime. J Heat Transfer 138:021502. doi: 10.1115/1.4031234

CrossRef Full Text | Google Scholar

Mahvi, A. J., Rattner, A. S., and Jennifer Lin, S. G. (2018). Challenges in predicting steam-side pressure drop and heat transfer in air-cooled power plant condensers. Appl. Thermal Eng. 133, 396–406. doi: 10.1016/j.applthermaleng.2018.01.008

CrossRef Full Text | Google Scholar

Mandhane, J. M., Gregory, G. A., and Aziz, K. (1974). A flow pattern map for gas-liquid flow in horizontal pipes. Int. J. Multiphase Flow 1, 537–553. doi: 10.1016/0301-9322(74)90006-8

CrossRef Full Text | Google Scholar

Markides, C. N. (2013). The role of pumped and waste heat technologies in a high-efficiency sustainable energy future for the UK. Appl. Thermal Eng. 53, 197–209. doi: 10.1016/j.applthermaleng.2012.02.037

CrossRef Full Text | Google Scholar

Markides, C. N. (2015). Low-concentration solar-power systems based on organic Rankine cycles for distributed-scale applications: overview and further developments. Front. Energy Res. 3:47. doi: 10.3389/fenrg.2015.00047

CrossRef Full Text | Google Scholar

Martha, G. F. (2012). Thermal Power Plant Performance Analysis. London: Springer-Verlag.

Google Scholar

Martín-Callizo, C., Palm, B., Owhaib, W., and Ali, R. (2010). Flow boiling visualization of r-134a in a vertical channel of small diameter. J. Heat Transfer 132, 1–8. doi: 10.1115/1.4000012

CrossRef Full Text

Mas, J., and Rezola, J. M. (2016). Tubular design for underwater compressed air energy storage. J. Energy Storage 8, 27–34. doi: 10.1016/j.est.2016.08.006

CrossRef Full Text | Google Scholar

Mathie, R., and Markides, C. N. (2013). Heat transfer augmentation in unsteady conjugate thermal systems - Part I: semi-analytical 1-D framework. Int. J. Heat Mass Transfer 56, 802–818. doi: 10.1016/j.ijheatmasstransfer.2012.08.023

CrossRef Full Text | Google Scholar

Mathie, R., Markides, C. N., and White, A. J. (2014). A framework for the analysis of thermal losses in reciprocating compressors and expanders. Heat Transf. Eng. 35, 1435–1449. doi: 10.1080/01457632.2014.889460

CrossRef Full Text | Google Scholar

Mathie, R., Nakamura, H., and Markides, C. N. (2013). Heat transfer augmentation in unsteady conjugate thermal systems - Part II: applications. Int. J. Heat Mass Transfer 56, 819–833. doi: 10.1016/j.ijheatmasstransfer.2012.09.017

CrossRef Full Text | Google Scholar

Matsuda, K. (2014). Low heat power generation system. Appl. Thermal Eng. 70, 1056–1061. doi: 10.1016/j.applthermaleng.2014.03.037

CrossRef Full Text | Google Scholar

Mazed, D., Frano, R. L., Aquaro, D., Serra, D. D., Sekachev, I., and Olcese, M. (2018). Experimental investigation of steam condensation in water tank at subatmospheric pressure. Nuclear Eng. Design 335, 241–254. doi: 10.1016/j.nucengdes.2018.05.025

CrossRef Full Text | Google Scholar

Mazza, A., Bompard, E., and Chicco, G. (2018). Applications of power to gas technologies in emerging electrical systems. Renew. Sust. Energy Rev. 92, 794–806. doi: 10.1016/j.rser.2018.04.072

CrossRef Full Text | Google Scholar

Mcgrail, B. P., Jenks, J. J., Abrams, W. P., Motkuri, R. K., Phillips, N. R., Veldman, T. G., et al. (2017). A non-condensing thermal compression power generation system. Energy Proc. 129, 1041–1046. doi: 10.1016/j.egypro.2017.09.240

CrossRef Full Text | Google Scholar

Mctigue, J. D., Markides, C. N., and White, A. J. (2018). Performance response of packed-bed thermal storage to cycle duration perturbations. J. Energy Storage 19, 379–392. doi: 10.1016/j.est.2018.08.016

CrossRef Full Text | Google Scholar

Mctigue, J. D., White, A. J., and Markides, C. N. (2015). Parametric studies and optimisation of pumped thermal electricity storage. Appl. Energy 137, 800–811. doi: 10.1016/j.apenergy.2014.08.039

CrossRef Full Text | Google Scholar

Medica-Viola, V., Pavković, B., and Mrzljak, V. (2018). Numerical model for on-condition monitoring of condenser in coal-fired power plants. Int. J. Heat Mass Transfer 117, 912–923. doi: 10.1016/j.ijheatmasstransfer.2017.10.047

CrossRef Full Text | Google Scholar

Medrano, M., Gil, A., Martorell, I., Potau, X., and Cabeza, L. F. (2010). State of the art on high-temperature thermal energy storage for power generation. Part 2-Case Studies. Renew. Sust. Energy Rev. 14, 56–72. doi: 10.1016/j.rser.2009.07.036

CrossRef Full Text | Google Scholar

Meffre, A., Py, X., Olives, R., Bessada, C., Veron, E., and Echegut, P. (2015). High-temperature sensible heat-based thermal energy storage materials made of vitrified mswi fly ashes. Waste Biomass Valorizat. 6, 1003–1014. doi: 10.1007/s12649-015-9409-9

CrossRef Full Text | Google Scholar

Mehos, M., Turchi, C., Vidal, J., Wagner, M., Ma, Z., Ho, C., et al. NREL (2017). Concentrating Solar Power gen3 Demonstration Roadmap. National Renewable Energy Laboratory. Available online at: www.nrel.gov

Meng, Z. N., and Zhang, P. (2017). Experimental and numerical investigation of a tube-in-tank latent thermal energy storage unit using composite PCM. Appl. Energy 190, 524–539. doi: 10.1016/j.apenergy.2016.12.163

CrossRef Full Text | Google Scholar

Meyer, J. P., Dirker, J., and Adelaja, A. O. (2014). Condensation heat transfer in smooth inclined tubes for r134a at different saturation temperatures. Int. J. Heat Mass Transfer 70, 515–525. doi: 10.1016/j.ijheatmasstransfer.2013.11.038

CrossRef Full Text | Google Scholar

Meyer, J. P., and Ewim, D. R. E. (2018). Heat transfer coefficients during the condensation of low mass fluxes in smooth horizontal tubes. Int. J. Multiphase Flow 99, 485–499. doi: 10.1016/j.ijmultiphaseflow.2017.11.015

CrossRef Full Text | Google Scholar

Michels, H., and Pitz-Paal, R. (2007). Cascaded latent heat storage for parabolic trough solar power plants. Solar Energy 81, 829–837. doi: 10.1016/j.solener.2006.09.008

CrossRef Full Text | Google Scholar

Milovanovic, Z. N., Knezevic, D., Milasinovic, A., Dumonjic-Milovanovic, S. R., and Ostojic, D. (2012). Modified method for reliability evaluation of condensation thermal electric power plant. J. Safety Eng. 1, 57–67. doi: 10.5923/j.safety.20120104.02

CrossRef Full Text | Google Scholar

Minocha, N., Joshi, J. B., Nayak, A. K., and Vijayan, P. K. (2016). 3D CFD simulation of passive decay heat removal system under boiling conditions: role of bubble sliding motion on inclined heated tubes. Chem. Eng. Sci. 145, 245–265. doi: 10.1016/j.ces.2016.02.015

CrossRef Full Text | Google Scholar

Montes, M. J., Abánades, A., and Martínez-Val, J. M. (2009). Performance of a direct steam generation solar thermal power plant for electricity production as a function of the solar multiple. Solar Energy 83, 679–689. doi: 10.1016/j.solener.2008.10.015

CrossRef Full Text | Google Scholar

Moradi, S., Ghaffarpour, R., Ranjbar, A. M., and Mozaffari, B. (2017). Optimal integrated sizing and planning of hubs with midsize/large chp units considering reliability of supply. Energy Conver. Manage. 148, 974–992. doi: 10.1016/j.enconman.2017.06.008

CrossRef Full Text | Google Scholar

Morgan, R., Nelmes, S., Gibson, E., and Brett, G. (2015). Liquid air energy storage – analysis and first results from a pilot scale demonstration plant. Appl. Energy 137, 845–853. doi: 10.1016/j.apenergy.2014.07.109

CrossRef Full Text | Google Scholar

Moser, K. W., Webb, R. L., and Na, B. (1998). A new equivalent reynolds number model for condensation in smooth tubes. J. Heat Transfer 120, 410–416. doi: 10.1115/1.2824265

CrossRef Full Text | Google Scholar

Mostafavi Tehrani, S. S., Taylor, R. A., Nithyanandam, K., and Shafiei Ghazani, A. (2017). Annual comparative performance and cost analysis of high temperature, sensible thermal energy storage systems integrated with a concentrated solar power plant. Solar Energy 153, 153–172. doi: 10.1016/j.solener.2017.05.044

CrossRef Full Text | Google Scholar

Mudawar, I. (2013). Recent advances in high-flux, two-phase thermal management. J. Thermal Sci. Eng. Appl. 5:021012. doi: 10.1115/1.4023599

CrossRef Full Text | Google Scholar

Mukherjee, A., and Kandlikar, S. G. (2005). Numerical simulation of growth of a vapor bubble during flow boiling of water in a microchannel. Microfluidics Nanofluidics 1, 137–145. doi: 10.1007/s10404-004-0021-8

CrossRef Full Text | Google Scholar

Müller, M. (1991). Test loop for research on direct steam generation in parabolic trough power plants. Sol. Energy Mater. 24, 222–230. doi: 10.1016/0165-1633(91)90062-P

CrossRef Full Text | Google Scholar

Müller-Steinhagen, H., and Heck, K. (1986). A simple friction pressure-drop correlation for 2-phase flow in pipes. Chem. Eng. Process. 20, 297–308. doi: 10.1016/0255-2701(86)80008-3

CrossRef Full Text | Google Scholar

Nada, S. A., and Hussein, H. M. S. (2016). General semi-empirical correlation for condensation of vapor on tubes at different orientations. Int., J. Thermal Sci. 100, 391–400. doi: 10.1016/j.ijthermalsci.2015.10.023

CrossRef Full Text | Google Scholar

Navarro, M. E., Martínez, M., Gil, A., Fernández, A. I., Cabeza, L. F., Olives, R., et al. (2012). Selection and characterization of recycled materials for sensible thermal energy storage. Solar Energy Mater. Solar Cells 107, 131–135. doi: 10.1016/j.solmat.2012.07.032

CrossRef Full Text | Google Scholar

Nie, Z., Bi, Q., Shiyilei, Lv, H., and Guo, Y. (2017). Experimental study on condensation of high-pressure steam in a horizontal tube with pool boiling outside. Int. J. Heat Mass Transfer 108, 2523–2533. doi: 10.1016/j.ijheatmasstransfer.2017.01.006

CrossRef Full Text | Google Scholar

Niyas, H., Prasad, L., and Muthukumar, P. (2015). Performance investigation of high-temperature sensible heat thermal energy storage system during charging and discharging cycles. Clean Technol. Environ. Policy 17, 501–513. doi: 10.1007/s10098-014-0807-7

CrossRef Full Text | Google Scholar

Noori Rahim Abadi, S. M. A., Mehrabi, M., and Meyer, J. P. (2018a). Prediction and optimization of condensation heat transfer coefficients and pressure drops of R134a inside an inclined smooth tube. Int. J. Heat Mass Transfer 124, 953–966. doi: 10.1016/j.ijheatmasstransfer.2018.04.027

CrossRef Full Text | Google Scholar

Noori Rahim Abadi, S. M. A., Meyer, J. P., and Dirker, J. (2018b). Effect of inclination angle on the condensation of R134a inside an inclined smooth tube. Chem. Eng. Res. Design 132, 346–357. doi: 10.1016/j.cherd.2018.01.044

CrossRef Full Text | Google Scholar

Noori Rahim Abadi, S. M. A., Meyer, J. P., and Dirker, J. (2018c). Numerical simulation of condensation inside an inclined smooth tube. Chem. Eng. Sci. 182, 132–145. doi: 10.1016/j.ces.2018.02.043

CrossRef Full Text | Google Scholar

Odeh, S. D., Behnia, M., and Morrison, G. L. (2000). Hydrodynamic analysis of direct steam generation solar collectors. J. Solar Energy Eng. 122, 14–14. doi: 10.1115/1.556273

CrossRef Full Text | Google Scholar

Olivares, R. I. (2012). The thermal stability of molten nitrite/nitrates salt for solar thermal energy storage in different atmospheres. Solar Energy 86, 2576–2583. doi: 10.1016/j.solener.2012.05.025

CrossRef Full Text | Google Scholar

Olivier, J. A., Liebenberg, L., Kedzierski, M. A., and Meyer, J. P. (2004). Pressure drop during refrigerant condensation inside horizontal smooth, helical microfin, and herringbone microfin tubes. J. Heat Transfer 126, 687–696. doi: 10.1115/1.1795240

CrossRef Full Text | Google Scholar

Oliviera, S. P., Meyer, J. P., Paepe, M. D., and Kerpel, K. D. (2016). The influence of inclination angle on void fraction and heat transfer during condensation inside a smooth tube. Int. J. Multiphase Flow 80, 1–14. doi: 10.1016/j.ijmultiphaseflow.2015.10.015

CrossRef Full Text | Google Scholar

Olujic, Z. (1985). Predicting two phase flow friction loss in horizontal pipes. Chem. Eng. 92, 45–50.

Google Scholar

Ong, C. L., and Thome, J. R. (2011). Macro-to-microchannel transition in two-phase flow: part 2 - flow boiling heat transfer and critical heat flux. Exp. Thermal Fluid Sci. 35, 873–886. doi: 10.1016/j.expthermflusci.2010.12.003

CrossRef Full Text | Google Scholar

Orejon, D., Shardt, O., Gunda, N. S. K., Ikuta, T., Takahashi, K., Takata, Y., et al. (2017). Simultaneous dropwise and filmwise condensation on hydrophilic microstructured surfaces. Int. J. Heat Mass Transfer 114, 187–197. doi: 10.1016/j.ijheatmasstransfer.2017.06.023

CrossRef Full Text | Google Scholar

Osher, S., and Sethian, J. A. (1988). Fronts propagating with curvature-dependent speed: algorithms based on hamilton-jacobi formulations. J. Comput. Phys. 79, 12–49. doi: 10.1016/0021-9991(88)90002-2

CrossRef Full Text | Google Scholar

Pantaleo, A. M., Camporeale, S. M., Sorrentino, A., Miliozzi, A., Shah, N., and Markides, C. N. (2017). Solar/biomass hybrid cycles with thermal storage and bottoming ORC: System integration and economic analysis. Energy Proc. 2017, 724–731. doi: 10.1016/j.egypro.2017.09.105

CrossRef Full Text | Google Scholar

Pantaleo, A. M., Camporeale, S. M., Sorrentino, A., Miliozzi, A., Shah, N., and Markides, C. N. (2018). Hybrid solar-biomass combined Brayton/organic Rankine-cycle plants integrated with thermal storage: techno-economic feasibility in selected Mediterranean areas. Renew. Energy. doi: 10.1016/j.renene.2018.08.022. [Epub ahead of print].

CrossRef Full Text | Google Scholar

Park, I., Kim, S. M., and Mudawar, I. (2013). Experimental measurement and modeling of downflow condensation in a circular tube. Int. J. Heat Mass Transfer 57, 567–581. doi: 10.1016/j.ijheatmasstransfer.2012.10.060

CrossRef Full Text | Google Scholar

Parrado, C., Marzo, A., Fuentealba, E., and Fernández, A. G. (2016). 2050 LCOE improvement using new molten salts for thermal energy storage in CSP plants. Renew. Sust. Energy Rev. 57, 505–514. doi: 10.1016/j.rser.2015.12.148

CrossRef Full Text | Google Scholar

Pelay, U., Luo, L., Fan, Y., Stitou, D., and Rood, M. (2017). Thermal energy storage systems for concentrated solar power plants. Renew. Sust. Energy Rev. 79, 82–100. doi: 10.1016/j.rser.2017.03.139

CrossRef Full Text | Google Scholar

Peng, H., Dong, H., and Ling, X. (2014). Thermal investigation of PCM-based high temperature thermal energy storage in packed bed. Energy Conver. Manage. 81, 420–427. doi: 10.1016/j.enconman.2014.02.052

CrossRef Full Text | Google Scholar

Pimm, A., and Garvey, S. (2009). Analysis of flexible fabric structures for large-scale subsea compressed air energy storage. J. Phys.: Conference Series 181:012049. doi: 10.1088/1742-6596/181/1/012049

CrossRef Full Text | Google Scholar

Pirasaci, T., and Goswami, D. Y. (2016). Influence of design on performance of a latent heat storage system for a direct steam generation power plant. Appl. Energy 162, 644–652. doi: 10.1016/j.apenergy.2015.10.105

CrossRef Full Text | Google Scholar

Ponce De León, C., Frías-Ferrer, A., González-García, J., Szánto, D. A., and Walsh, F. C. (2006). Redox flow cells for energy conversion. J. Power Sources 160, 716–732. doi: 10.1016/j.jpowsour.2006.02.095

CrossRef Full Text | Google Scholar

Pye, J. D. (2008). Modelling of the Compact Linear Fresnel Reflector. Sydney, NSW: University of New South Wales.

Google Scholar

Qin, F. G. F., Yang, X., Ding, Z., Zuo, Y., Shao, Y., Jiang, R., et al. (2012). Thermocline stability criterions in single-tanks of molten salt thermal energy storage. Appl. Energy 97, 816–821. doi: 10.1016/j.apenergy.2012.02.048

CrossRef Full Text | Google Scholar

Qiu, G., Cai, W., Wu, Z., Yao, Y., and Jiang, Y. (2015). Numerical simulation of forced convective condensation of propane in a spiral tube. J. Heat Transfer 137, 1–9. doi: 10.1115/1.4029475

CrossRef Full Text | Google Scholar

Qiu, G., Wu, Z., Jiang, Y., Li, S., and Cai, W. (2014a). “Numerical simulation of condensation of upward flow in a vertical pipe,” in ASME 4th Joint Us-European Fluids Engineering Division Summer Meeting (Chicago). V01dt32a003.

Google Scholar

Qiu, G. D., Cai, W. H., Li, S. L., Wu, Z. Y., Jiang, Y. Q., and Yao, Y. (2014b). Numerical simulation on forced convective condensation of steam upward flow in a vertical pipe. Adv. Mech. Eng. 6:589250. doi: 10.1155/2014/589250

CrossRef Full Text | Google Scholar

Quibén, J. M., Cheng, L., Da Silva Lima, R. J., and Thome, J. R. (2009). Flow boiling in horizontal flattened tubes: part II - flow boiling heat transfer results and model. Int. J. Heat Mass Transfer 52, 3645–3653. doi: 10.1016/j.ijheatmasstransfer.2008.12.033

CrossRef Full Text | Google Scholar

Rao, A. D. (2012). Combined Cycle Systems for Near-Zero Emission Power Generation. Cambridge: Woodhead Publishing Ltd.

Google Scholar

Rao, C. R. C., Niyas, H., and Muthukumar, P. (2018). Performance tests on lab–scale sensible heat storage prototypes. Appl. Thermal Eng. 129, 953–967. doi: 10.1016/j.applthermaleng.2017.10.085

CrossRef Full Text | Google Scholar

Rastler, D. (2010). Electricity Energy Storage Technology Options: A White Paper Primer on Applications, Costs, and Benefits. Palo Alto, CA: Electric Power Research Institute.

Google Scholar

Rehman, S., Al-Hadhrami, L. M., and Alam, M. M. (2015). Pumped hydro energy storage system: a technological review. Renew. Sust. Energy Rev. 44, 586–598. doi: 10.1016/j.rser.2014.12.040

CrossRef Full Text | Google Scholar

Ren, B., Zhang, L., Xu, H., Cao, J., and Tao, Z. (2014). Experimental study on condensation of steam/air mixture in a horizontal tube. Exp. Thermal Fluid Sci. 58, 145–155. doi: 10.1016/j.expthermflusci.2014.06.022

CrossRef Full Text | Google Scholar

Rogers, A., Henderson, A., Wang, X., and Negnevitsky, M. (2014). “compressed air energy storage: thermodynamic and economic review,” in IEEE Power & Energy Society General Meeting (Washington DC).

Google Scholar

Roldán, M. I., Valenzuela, L., and Zarza, E. (2013). Thermal analysis of solar receiver pipes with superheated steam. Appl. Energy 103, 73–84. doi: 10.1016/j.apenergy.2012.10.021

CrossRef Full Text | Google Scholar

Rovira, A., Montes, M. J., Varela, F., and Gil, M. (2013). Comparison of heat transfer fluid and direct steam generation technologies for integrated solar combined cycles. Appl. Thermal Eng. 52, 264–274. doi: 10.1016/j.applthermaleng.2012.12.008

CrossRef Full Text | Google Scholar

Roy, R. P., Ratisher, M., and Gokhale, V. K. (2001). A computational model of a power plant steam condenser. J. Energy Resources Technol. Transac. ASME 123, 81–91. doi: 10.1115/1.1348336

CrossRef Full Text | Google Scholar

Rudman, M. (1997). Volume-tracking methods for interfacial flow calculations'. Int. J. Numerical Methods Fluids 24, 671–691. doi: 10.1002/(SICI)1097-0363(19970415)24:7<671::AID-FLD508>3.0.CO;2-9

CrossRef Full Text | Google Scholar

Ruiz-Cabañas, F. J., Jové, A., Prieto, C., Madina, V., Fernández, A. I., and Cabeza, L. F. (2017). Materials selection of steam-phase change material (pcm) heat exchanger for thermal energy storage systems in direct steam generation facilities. Solar Energy Mater. Solar Cells 159, 526–535. doi: 10.1016/j.solmat.2016.10.010

CrossRef Full Text | Google Scholar

Rusowicz, A., Laskowski, R., and Grzebielec, A. (2017). The numerical and experimental study of two passes power plant condenser. Thermal Sci. 21, 353–362. doi: 10.2298/TSCI150917011R

CrossRef Full Text | Google Scholar

Saari, J., Kaikko, J., Vakkilainen, E., and Savolainen, S. (2014). Comparison of power plant steam condenser heat transfer models for on-line condition monitoring. Appl. Thermal Eng. 62, 37–47. doi: 10.1016/j.applthermaleng.2013.09.005

CrossRef Full Text | Google Scholar

Saisorn, S., and Wongwises, S. (2012). A critical review of recent investigations on flow pattern and heat transfer during flow boiling in micro-channels. Front. Heat Mass Transfer 3:3007. doi: 10.5098/hmt.v3.1.3007

CrossRef Full Text | Google Scholar

Santini, L., Cioncolini, A., Butel, M. T., and Ricotti, M. E. (2016). Flow boiling heat transfer in a helically coiled steam generator for nuclear power applications. Int. J. Heat Mass Transfer 92, 91–99. doi: 10.1016/j.ijheatmasstransfer.2015.08.012

CrossRef Full Text | Google Scholar

Sanz-Bermejo, J., Gallardo-Natividad, V., Gonzalez-Aguilar, J., and Romero, M. (2014). Comparative system performance analysis of direct steam generation central receiver solar thermal power plants in megawatt range. J. Solar Energy Eng. Transac. ASME 136:010908. doi: 10.1115/1.4026279

CrossRef Full Text | Google Scholar

Schmidt, O., Hawkes, A., Gambhir, A., and Staffell, I. (2017). The future cost of electrical energy storage based on experience rates. Nat. Energy 6:17110. doi: 10.1038/nenergy.2017.110

CrossRef Full Text | Google Scholar

Schrock, V. E., and Grossman, L. M. (1962). Forced convection boiling in tubes. Nuclear Sci. Eng. 12, 474–481. doi: 10.13182/NSE62-A26094

CrossRef Full Text | Google Scholar

Sciacovelli, A., Gagliardi, F., and Verda, V. (2015). Maximization of performance of a pcm latent heat storage system with innovative fins. Appl. Energy 137, 707–715. doi: 10.1016/j.apenergy.2014.07.015

CrossRef Full Text | Google Scholar

Sciacovelli, A., Vecchi, A., and Ding, Y. (2017). Liquid air energy storage (laes) with packed bed cold thermal storage – from component to system level performance through dynamic modelling. Appl. Energy 190, 84–98. doi: 10.1016/j.apenergy.2016.12.118

CrossRef Full Text | Google Scholar

Seddegh, S., Wang, X., and Henderson, A. D. (2015). Numerical investigation of heat transfer mechanism in a vertical shell and tube latent heat energy storage system. Appl. Therm. Eng. 87, 698–706. doi: 10.1016/j.applthermaleng.2015.05.067

CrossRef Full Text | Google Scholar

Seitz, M., Cetin, P., and Eck, M. (2013). Thermal storage concept for solar thermal power plants with direct steam, generation. Energy Procedia 49, 993–1002. doi: 10.1016/j.egypro.2014.03.107

CrossRef Full Text | Google Scholar

Shah, M. M. (1982). “Chart correlation for saturated boiling heat transfer: equations and further study,” in Semiannual Meeting Of The American Society Of Heating, Refrigerating And Air-Conditioning Engineers (Toronto, ON).

Google Scholar

Shah, M. M. (2016a). Comprehensive correlations for heat transfer during condensation in conventional and mini/micro channels in all orientations. Int. J. Refrigerat. 67, 22–41. doi: 10.1016/j.ijrefrig.2016.03.014

CrossRef Full Text | Google Scholar

Shah, M. M. (2016b). A correlation for heat transfer during condensation in horizontal mini/micro channels. Int. J. Refrigerat. 64, 187–202. doi: 10.1016/j.ijrefrig.2015.12.008

CrossRef Full Text | Google Scholar

Shah, M. M. (2016c). Prediction of heat transfer during condensation of carbon dioxide in channels. Appl. Therm. Eng. 93, 192–199. doi: 10.1016/j.applthermaleng.2015.09.016

CrossRef Full Text | Google Scholar

Shah, M. M. (2017). Unified correlation for heat transfer during boiling in plain mini/micro and conventional channels. Int. J. Refrigerat. 74, 606–626. doi: 10.1016/j.ijrefrig.2016.11.023

CrossRef Full Text | Google Scholar

Shen, X., Lu, J., Ding, J., and Yang, J. (2014). Convective heat transfer of molten salt in circular tube with nonuniform heat flux. Exp. Therm. Fluid Sci. 55, 6–11. doi: 10.1016/j.expthermflusci.2014.02.015

CrossRef Full Text | Google Scholar

Shen, Z., Yang, D., Xie, H., Nie, X., Liu, W., and Wang, S. (2016). Flow and heat transfer characteristics of high-pressure water flowing in a vertical upward smooth tube at low mass flux conditions. Appl. Therm. Eng. 102, 391–401. doi: 10.1016/j.applthermaleng.2016.03.150

CrossRef Full Text | Google Scholar

Singh, R., Saini, R. P., and Saini, J. S. (2006). Nusselt number and friction factor correlations for packed bed solar energy storage system having large sized elements of different shapes. Solar Energy 80, 760–771. doi: 10.1016/j.solener.2005.07.001

CrossRef Full Text | Google Scholar

Sioshansi, R., and Denholm, P. (2010). The value of concentrating solar power and thermal energy storage. IEEE Trans. Sustain. Energy 1, 173–183. doi: 10.1109/TSTE.2010.2052078

CrossRef Full Text | Google Scholar

Steiner, D. (1993). Strömungssieden Gesättigter Flüssigkeiten. Düsseldorf, Vdi-Wärmeatlas.

Steiner, D., and Taborek, J. (1992). Flow boiling heat transfer in vertical tubes correlated by an asymptotic model. Heat Transf. Eng. 13, 43–69. doi: 10.1080/01457639208939774

CrossRef Full Text | Google Scholar

Steinmann, W. D., and Eck, M. (2006). Buffer storage for direct steam generation. Solar Energy 80, 1277–1282. doi: 10.1016/j.solener.2005.05.013

CrossRef Full Text | Google Scholar

Stevanovic, V. D., Maslovaric, B., and Prica, S. (2012). Dynamics of steam accumulation. Appl. Therm. Eng. 37, 73–79. doi: 10.1016/j.applthermaleng.2012.01.007

CrossRef Full Text | Google Scholar

Strbac, G., Aunedi, M., Pudjianto, D., Djapic, P., Teng, F., and Sturt, A. (2012). Strategic Assessment of the Role and Value of Energy Storage Systems in the UK. Carbon Trust, Energy Futures Lab, Imperial College London.

Ströhle, S., Haselbacher, A., Jovanovic, Z. R., and Steinfeld, A. (2017). Upgrading sensible-heat storage with a thermochemical storage section operated at variable pressure: an effective way toward active control of the heat-transfer fluid outflow temperature. Appl. Energy 196, 51–61. doi: 10.1016/j.apenergy.2017.03.125

CrossRef Full Text | Google Scholar

Sun, J., Liu, Q., and Hong, H. (2015). Numerical study of parabolic-trough direct steam generation loop in recirculation mode: characteristics, performance and general operation strategy. Energy Conv. Manage. 96, 287–302. doi: 10.1016/j.enconman.2015.02.080

CrossRef Full Text | Google Scholar

Sun, L., and Mishima, K. (2009). Evaluation analysis of prediction methods for two-phase flow pressure drop in mini-channels. Int. J. Multiphase Flow 35, 47–54. doi: 10.1016/j.ijmultiphaseflow.2008.08.003

CrossRef Full Text | Google Scholar

Taitel, A. E., and Dukler, Y. (1976). A model for predicting flow regime transitions in horizontal and near horizontal gas liquid flow. Aiche J. 22, 47–55. doi: 10.1002/aic.690220105

CrossRef Full Text | Google Scholar

Tamme, R., Bauer, T., Buschle, J., Laing, D., Müller-Steinhagen, H., and Steinmann, W. D. (2008). Latent heat storage above 120°c for applications in the industrial process heat sector and solar power generation. Int. J. Energy Res. 32, 264–271. doi: 10.1002/er.1346

CrossRef Full Text | Google Scholar

Tao, Y. B., He, Y. L., and Qu, Z. G. (2012). Numerical study on performance of molten salt phase change thermal energy storage system with enhanced tubes. Solar Energy 86, 1155–1163. doi: 10.1016/j.solener.2012.01.004

CrossRef Full Text | Google Scholar

Tao, Y. B., Li, M. J., He, Y. L., and Tao, W. Q. (2014). Effects of parameters on performance of high temperature molten salt latent heat storage unit. Appl. Therm. Eng. 72, 48–55. doi: 10.1016/j.applthermaleng.2014.01.038

CrossRef Full Text | Google Scholar

Thome, J. R. (2004). Boiling in microchannels: a review of experiment and theory. Int. J. Heat. Fluid Flow 25, 128–139. doi: 10.1016/j.ijheatfluidflow.2003.11.005

CrossRef Full Text | Google Scholar

Thome, J. R. (2005). Condensation in plain horizontal tubes: recent advances in modelling of heat transfer to pure fluids and mixtures. J. Brazil. Soc. Mech. Sci. Eng. 27, 23–30. doi: 10.1590/S1678-58782005000100002

CrossRef Full Text | Google Scholar

Thome, J. R., Hajal, J. E., and Cavallini, A. (2003). Condensation in horizontal tubes, part 2: new heat transfer model based on flow regimes. Int. J. Heat.Mass Transfer 46, 3365–3387. doi: 10.1016/S0017-9310(03)00140-6

CrossRef Full Text | Google Scholar

Tian, Y., Zhang, K., Wang, N., Cui, Z., and Cheng, L. (2017). Numerical study of pool boiling heat transfer in a large-scale confined space. Appl. Therm. Eng. 118, 188–198. doi: 10.1016/j.applthermaleng.2017.02.110

CrossRef Full Text | Google Scholar

Tibiriçá, C. B., and Ribatski, G. (2013). Flow boiling in micro-scale channels-synthesized literature review. Int. J. Refriger. 36, 301–324. doi: 10.1016/j.ijrefrig.2012.11.019

CrossRef Full Text | Google Scholar

Tijani, A. S., and Bin Roslan, A. M. S. (2016). Simulation analysis of thermal losses of parabolic trough solar collector in malaysia using computational fluid dynamics. Procedia Technol. 15, 842–849. doi: 10.1016/j.protcy.2014.09.058

CrossRef Full Text | Google Scholar

Tiskatine, R., Oaddi, R., Ait El Cadi, R., Bazgaou, A., Bouirden, L., Aharoune, A., et al. (2017). Suitability and characteristics of rocks for sensible heat storage in csp plants. Solar Energy Mater. Solar Cells 169, 245–257. doi: 10.1016/j.solmat.2017.05.033

CrossRef Full Text | Google Scholar

Valenzuela, L., Zarza, E., Berenguel, M., and Camacho, E. F. (2006). Control scheme for direct steam generation in parabolic troughs under recirculation operation mode. Solar Energy 80, 1–17. doi: 10.1016/j.solener.2005.09.009

CrossRef Full Text | Google Scholar

Vasu, A., Hagos, F. Y., Noor, M. M., Mamat, R., Azmi, W. H., Abdullah, A. A., et al. (2017). Corrosion effect of phase change materials in solar thermal energy storage application. Renew. Sustain. Energy Rev. 76, 19–33. doi: 10.1016/j.rser.2017.03.018

CrossRef Full Text | Google Scholar

Wang, B., and Du, X. (2000). study on laminar film-wise condensation for vapour flow in an inclined small/mini-diameter tube. Int. J. Heat Mass Transfer 43, 1859–1868. doi: 10.1016/S0017-9310(99)00256-2

CrossRef Full Text | Google Scholar

Wang, C., Wang, H., Li, X., and Gao, P. (2014). Experimental study of saturated boiling heat transfer and pressure drop in vertical rectangular channel. Nuclear Eng. Design 273, 631–643. doi: 10.1016/j.nucengdes.2014.03.053

CrossRef Full Text | Google Scholar

Wang, J., Wang, B., Wu, W., Li, X., and Shi, W. (2016). Performance analysis of an absorption-compression hybrid refrigeration system recovering condensation heat for generation. Appl. Thermal Eng. 108, 54–65. doi: 10.1016/j.applthermaleng.2016.07.100

CrossRef Full Text | Google Scholar

Wang, P., Liu, D. Y., and Xu, C. (2013). Numerical study of heat transfer enhancement in the receiver tube of direct steam generation with parabolic trough by inserting metal foams. Appl. Energy 102, 449–460. doi: 10.1016/j.apenergy.2012.07.026

CrossRef Full Text | Google Scholar

Wang, S., Faghri, A., and Bergman, T. L. (2012). A comparison study of sensible and latent thermal energy storage systems for concentrating solar power applications. Numer. Heat Transfer Part A Applications 61, 860–871. doi: 10.1080/10407782.2012.672887

CrossRef Full Text | Google Scholar

Wang, Y., Mu, X., Shen, S., and Zhang, W. (2017). Heat transfer characteristics of steam condensation flow in vacuum horizontal tube. Int. J. Heat Mass Transfer 108, 128–135. doi: 10.1016/j.ijheatmasstransfer.2016.12.006

CrossRef Full Text | Google Scholar

Wei, J. H., Pan, L. M., Chen, D. Q., Zhang, H., Xu, J. J., and Huang, Y. P. (2011). Numerical simulation of bubble behaviors in subcooled flow boiling under swing motion. Nuclear Eng. Design 241, 2898–2908. doi: 10.1016/j.nucengdes.2011.05.008

CrossRef Full Text | Google Scholar

Weinstein, L. A., Loomis, J., Bhatia, B., Bierman, D. M., Wang, E. N., and Chen, G. (2015). Concentrating solar power. Chem. Rev. 115, 12797–12838. doi: 10.1021/acs.chemrev.5b00397

PubMed Abstract | CrossRef Full Text | Google Scholar

Weisman, J., and Pei, B. S. (1983). Prevision du flux thermique critique dans un ecoulement avec ebullition a faible qualite. Int. J. Heat Mass Transfer 26, 1463–1477. doi: 10.1016/S0017-9310(83)80047-7

CrossRef Full Text

White, A., Mctigue, J., and Markides, C. (2014). Wave propagation and thermodynamic losses in packed-bed thermal reservoirs for energy storage. Appl. Energy 130, 648–657. doi: 10.1016/j.apenergy.2014.02.071

CrossRef Full Text | Google Scholar

White, A., Parks, G., and Markides, C. N. (2013). Thermodynamic analysis of pumped thermal electricity storage. Appl. Thermal Eng. 53, 291–298. doi: 10.1016/j.applthermaleng.2012.03.030

CrossRef Full Text | Google Scholar

White, A. J., Mctigue, J. D., and Markides, C. N. (2016). Analysis and optimisation of packed-bed thermal reservoirs for electricity storage applications. Proc. Inst. Mech. Eng. A 230, 739–754. doi: 10.1177/0957650916668447

CrossRef Full Text | Google Scholar

Willich, C., Markides, C. N., and White, A. J. (2017). An investigation of heat transfer losses in reciprocating devices. Appl. Ther. Eng. 111, 903–913. doi: 10.1016/j.applthermaleng.2016.09.136

CrossRef Full Text | Google Scholar

Wojtan, L. (2004). Experimental and Analytical Investigation of Void Fraction and Heat Transfer During Evaporation in Horizontal Tubes. Ph.D. Thesis, Department Of Mechanical Engineering,Swiss Federal Institute Of Technology Lausanne, Ch-1015 Lausanne.

Wojtan, L., Ursenbacher, T., and Thome, J. R. (2005a). Investigation of flow boiling in horizontal tubes: part I - a new diabatic two-phase flow pattern map. Int. J. Heat Mass Transfer 48, 2955–2969. doi: 10.1016/j.ijheatmasstransfer.2004.12.012

CrossRef Full Text | Google Scholar

Wojtan, L., Ursenbacher, T., and Thome, J. R. (2005b). Investigation of flow boiling in horizontal tubes: part II - development of a new heat transfer model for stratified-wavy, dryout and mist flow regimes. Int. J. Heat Mass Transfer 48, 2970–2985. doi: 10.1016/j.ijheatmasstransfer.2004.12.013

CrossRef Full Text | Google Scholar

Woodruff, E. B., Lammers, H. B., and Lammers, T. F. (2016). Steam-Plant Operation. New York, NY: McGraw Hill Higher Education.

Google Scholar

World Energy Council (2016). E-Storage: Shifting From Cost to Value. Wind and Solar Applications, World Energy Resources Report. Available online at: www.worldenergy.org

Wu, J., Bi, Q., and Zhou, C. (2015). Experimental study on circulation characteristics of secondary passive heat removal system for chinese pressurized water reactor. Appl. Thermal Eng. 77, 106–112. doi: 10.1016/j.applthermaleng.2014.12.014

CrossRef Full Text | Google Scholar

Wu, M., Xu, C., and He, Y. (2016). Cyclic behaviors of the molten-salt packed-bed thermal storage system filled with cascaded phase change material capsules. Appl. Thermal Eng. 93, 1061–1073. doi: 10.1016/j.applthermaleng.2015.10.014

CrossRef Full Text | Google Scholar

Wu, W.-F., Long, X.-P., Yu, X.-L., and Feng, Q.-K. (2012). A new power generation method utilizing a low grade heat source. J. Zhejiang Univ. Sci. A 13, 140–145. doi: 10.1631/jzus.A1100152

CrossRef Full Text | Google Scholar

Wu, X., Yan, C., Meng, Z., Chen, K., Song, S., Yang, Z., et al. (2010). Investigation of characteristics of passive heat removal system based on the assembled heat transfer tube. Nuclear Eng. Technol. 48, 1321–1329. doi: 10.1016/j.net.2016.08.007

CrossRef Full Text | Google Scholar

Würfel, R., Kreutzer, T., and Fratzscher, W. (2003). Turbulence transfer processes in adiabatic and condensing film flow in an inclined tube. Chem. Eng. Technol. 26, 439–448. doi: 10.1002/ceat.200390067

CrossRef Full Text | Google Scholar

Xu, B., Li, P., and Chan, C. (2015). Application of phase change materials for thermal energy storage in concentrated solar thermal power plants: a review to recent developments. Appl. Energy 160, 286–307. doi: 10.1016/j.apenergy.2015.09.016

CrossRef Full Text | Google Scholar

Xu, R., and Wiesner, T. F. (2015). Closed-form modeling of direct steam generation in a parabolic trough solar receiver. Energy 79, 163–176. doi: 10.1016/j.energy.2014.11.004

CrossRef Full Text | Google Scholar

Yang, L. J., Wang, M. H., Du, X. Z., and Yang, Y. P. (2012). Trapezoidal array of air-cooled condensers to restrain the adverse impacts of ambient winds in a power plant. Appl. Energy 99, 402–413. doi: 10.1016/j.apenergy.2012.06.006

CrossRef Full Text | Google Scholar

Yang, Z., Peng, X. F., and Ye, P. (2008). Numerical and experimental investigation of two phase flow during boiling in a coiled tube. Int. J. Heat Mass Transfer 51, 1003–1016. doi: 10.1016/j.ijheatmasstransfer.2007.05.025

CrossRef Full Text | Google Scholar

Yoo, J. M., Kang, J. H., Yun, B. J., Hong, S. W., and Jeong, J. J. (2018). Improvement of the melcor condensation heat transfer model for the thermal-hydraulic analysis of a pwr containment. Prog. Nuclear Energy 104, 172–182. doi: 10.1016/j.pnucene.2017.09.012

CrossRef Full Text | Google Scholar

Youngs, D. L. (1982). Time-Dependent Multi-Material Flow With Large Fluid Distortion,Numerical Methods for Fluid Dynamics. Academic Press.

Yu, J., Jiang, Y., Cai, W., and Li, F. (2018). Numerical investigation on flow condensation of zeotropic hydrocarbon mixtures in a helically coiled tube. Appl. Thermal Eng. 134, 322–332. doi: 10.1016/j.applthermaleng.2018.02.006

CrossRef Full Text | Google Scholar

Yuan, H., Shi, Y., Lu, C., Xu, Z., Ni, Y., and Lan, X. (2015). Enhanced performance of high temperature aluminate cementitious materials incorporated with cu powders for thermal energy storage. Cement Concrete Composites 55, 139–144. doi: 10.1016/j.cemconcomp.2014.08.006

CrossRef Full Text | Google Scholar

Zakeri, B., and Syri, S. (2015). Electrical energy storage systems: a comparative life cycle cost analysis. Renew. Sust. Energy Rev. 42, 569–596. doi: 10.1016/j.rser.2014.10.011

CrossRef Full Text | Google Scholar

Zarza, E., Valenzuela, L., León, J., Hennecke, K., Eck, M., Weyers, H. D., et al. (2004). Direct steam generation in parabolic troughs: final results and conclusions of the diss project. Energy 29, 635–644. doi: 10.1016/S0360-5442(03)00172-5

CrossRef Full Text | Google Scholar

Zaversky, F., Pérez De Zabalza Asiain, J., and Sánchez, M. (2017). Transient response simulation of a passive sensible heat storage system and the comparison to a conventional active indirect two-tank unit. Energy 139, 782–797. doi: 10.1016/j.energy.2017.07.156

CrossRef Full Text | Google Scholar

Zhang, J., and Li, W. (2016). Numerical study on heat transfer and pressure drop characteristics of R410a condensation in horizontal circular mini/micro-tubes. Can. J. Chem. Eng. 94, 1809–1819. doi: 10.1002/cjce.22554

CrossRef Full Text | Google Scholar

Zhang, J., Li, W., and Minkowycz, W. (2016a). Numerical simulation of condensation for R410a at a different saturation temperature in mini/micro tubes. Numerical Heat Transfer Part A Appl. 69, 825–840. doi: 10.1080/10407782.2015.1090844

CrossRef Full Text | Google Scholar

Zhang, J., Li, W., and Minkowycz, W. (2016b). Numerical simulation of condensation for R410a at varying saturation temperatures in mini/micro tubes. Numerical Heat Transfer Part A Appl. 69, 464–478. doi: 10.1080/10407782.2015.1081029

CrossRef Full Text | Google Scholar

Zhang, J., Li, W., and Minkowycz, W. (2017). Numerical simulation of r410a condensation in horizontal microfin tubes. Numerical Heat Transfer Part A Appl. 71, 361–376. doi: 10.1080/10407782.2016.1243934

CrossRef Full Text | Google Scholar

Zhang, J., Li, W., and Sherif, S. (2016c). A numerical study of condensation heat transfer and pressure drop in horizontal round and flattened minichannels. Int. J. Thermal Sci. 106, 80–93. doi: 10.1016/j.ijthermalsci.2016.02.019

CrossRef Full Text | Google Scholar

Zhang, J., Li, W., Shih, T. I. P., Zhang, Y., Shi, Y., and Niu, Y. (2016d). “Heat transfer and pressure drop characteristics of condensation for R410a in a 3.78 mm circular tube under normal and micro gravity,” ASME Heat Transfer Summer Conference (Washington, DC), Ht2016–7045.

Google Scholar

Zhang, L., Hua, M., Zhang, X., Yu, Z., and Mei, R. (2016e). Visualized investigation of gas–liquid stratified flow boiling of water in a natural circulation thermosyphon loop with horizontal arranged evaporator. Int. J. Heat Mass Transfer 102, 980–990. doi: 10.1016/j.ijheatmasstransfer.2016.06.089

CrossRef Full Text | Google Scholar

Zhang, P., and Jia, H. W. (2016). Evolution of flow patterns and the associated heat and mass transfer characteristics during flow boiling in mini-/micro-channels. Chem. Eng. J. 306, 978–991. doi: 10.1016/j.cej.2016.08.034

CrossRef Full Text | Google Scholar

Zhang, P., Ma, F., and Xiao, X. (2016f). Thermal energy storage and retrieval characteristics of a molten-salt latent heat thermal energy storage system. Appl. Energy 173, 255–271. doi: 10.1016/j.apenergy.2016.04.012

CrossRef Full Text | Google Scholar

Zhang, P., Xiao, X., Meng, Z. N., and Li, M. (2015). Heat transfer characteristics of a molten-salt thermal energy storage unit with and without heat transfer enhancement. Appl. Energy 137, 758–772. doi: 10.1016/j.apenergy.2014.10.004

CrossRef Full Text | Google Scholar

Zhang, S., Yuan, W., Tang, Y., Chen, J., and Li, Z. (2016g). Enhanced flow boiling in an interconnected microchannel net at different inlet subcooling. Appl. Thermal Eng. 104, 659–667. doi: 10.1016/j.applthermaleng.2016.05.117

CrossRef Full Text | Google Scholar

Zhang, X., Wu, L., Wang, X., and Ju, G. (2016h). Comparative study of waste heat steam SRC, ORC and S-ORC power generation systems in medium-low temperature. Appl. Thermal Eng. 106, 1427–1439. doi: 10.1016/j.applthermaleng.2016.06.108

CrossRef Full Text | Google Scholar

Zhang, X.-R., and Zhang, Y. (2013). Experimental investigation on heat recovery from condensation of thermal power plant exhaust steam by a CO₂ vapor compression cycle. Int. J. Energy Res. 37, 1908–1916. doi: 10.1002/er.3018

CrossRef Full Text | Google Scholar

Zhao, C. Y., Lu, W., and Tian, Y. (2010). Heat transfer enhancement for thermal energy storage using metal foams embedded within phase change materials (PCMS). Solar Energy 84, 1402–1412. doi: 10.1016/j.solener.2010.04.022

CrossRef Full Text | Google Scholar

Zhao, F., Liang, Y., Cheng, H., Jiangb, L., and Qu, L. (2016). Highly efficient moisture-enabled electricity generation from graphene oxide frameworks. Energy Environ. Sci. 9, 912–916. doi: 10.1039/C5EE03701H

CrossRef Full Text | Google Scholar

Zhou, J., Wang, S., Gao, L., Zhao, L., and Pang, L. (2015). Study on flow instability inside multiple parallel pipes of direct steam generation. Energy Proc. 69, 259–268. doi: 10.1016/j.egypro.2015.03.030

CrossRef Full Text | Google Scholar