Hydration and proton conductivity of ionomers: the model case of sulfonated aromatic polymers

The hydration of proton-conducting ionomers is described in terms of a simplified model, where only osmotic and elastic contributions to the Gibbs free energy of hydration are considered. Although only two physically meaningful parameters are used – the deformation parameter, inversely proportional to the elastic modulus of the ionomer, and the free volume parameter – simulated hydration isotherms are in good agreement with the experiment. The proton mobility u inside the electrolyte solution of the ionomer is calculated from the proton conductivity determined at various hydration numbers. Its variation with the proton concentration c reveals the percolation threshold of hydrated nanometric channels and the tortuosity of the membrane. Above the percolation threshold, a power law u ~ c⁻³ is observed, in agreement with the “universal” law for 3-dimensional percolation. The proton conductivity σ shows at 100°C a maximum of 0.2 S/cm at a hydration number ~90. The σ = f(c) plot allows to predict, which hydration conditions are necessary for a desired area specific resistance.

Introduction

Polymer electrolytes are a fascinating class of materials with many promising applications, especially in the field of energy and environment (Armand, 1994; Meyer, 1998; Fergus, 2010, 2012; Couture et al., 2011; Hou et al., 2011; Li et al., 2011; Merle et al., 2011; Wang et al., 2011; Di Vona and Knauth, 2013; Hickner, 2013). One can mention ion exchange membranes, and a major application concerns separation membranes for electrochemical energy technologies, such as lithium polymer batteries and polymer electrolyte fuel cells.

Whereas polymer electrolytes for lithium batteries must work in absence of water to avoid corrosion and decomposition reactions, polymer electrolytes used in fuel cells and redox flow batteries contain significant amounts of water in hydrated nanometric domains that assure the proton or anion conduction inside a matrix made by the polymer backbones (Springer et al., 1991; Zawodzinski et al., 1993; Kreuer, 2001; Kreuer et al., 2004; Smitha et al., 2005; Diat and Gebel, 2008; Peckham et al., 2008; Hickner, 2012; Wu et al., 2013). Such polymers with a micro-phase separation between hydrated ionic conducting domains and electronically insulating polymer domains are also called ionomers.

Given the particular ion conduction mechanism, the water content of ionomers bears a particular importance (Zawodzinski et al., 1993; Gebel, 2000; Paddison, 2003; Mauritz and Moore, 2004; Majsztrik et al., 2007; Freger, 2009; Wu et al., 2011, 2013; Kumar et al., 2013; Yan et al., 2013). It fosters on one hand the ionic conductivity, but reduces on the other hand the mechanical and dimensional stability of the ionomer, because the high dielectric constant of water diminishes the Van der Waals interactions between macromolecular chains that determine the elastic properties of the ionomer (Alberti et al., 2008). The loss of dimensional stability is detrimental for the application in electrochemical energy technologies, because the swelling or shrinkage observed during changes of hydration might lead to delamination of metal electrodes in contact with the ionomers. This is particularly true in the case of fuel cells, where transients between high and low humidity conditions are observed during on-off cycles.

Water-uptake measurements of an ionomer are thus among the most important characterizations to be performed; the determination of the ionic conductivity as function of the hydration of the ionomer is also fundamental (Casciola et al., 2006; Peckham et al., 2008; Knauth and Di Vona, 2012; Di Vona et al., 2013; Knauth et al., 2013).

It is therefore tempting to analyze the interdependence of hydration and ionic conductivity also by theoretical means and to predict these properties using simple concepts and analytical equations, if available (Knauth and Di Vona, 2012; Narducci et al., 2014).

The following text is an attempt to present recent achievements made by our group for the phenomenological description of hydration and ionic conductivity of ionomers and their relationship. We will take as practical examples sulfonated poly-ether-ether-ketone (SPEEK) and sulfonated polyphenylsulfone (SPPSU) for which numerous experimental properties have been published over the years (Bauer et al., 2000; Rikukawa and Sanui, 2000; Li et al., 2003; Robertson et al., 2003; Roziere and Jones, 2003; Xing et al., 2004; Reyna-Valencia et al., 2006; Di Vona et al., 2009, 2010; Sgreccia et al., 2010; Wu et al., 2011; Hou et al., 2012; Knauth et al., 2013) but the discussed relations are also valid for other ionomers.

Hydration Properties

The hydration equilibrium of an ionomer is governed by the Gibbs free energy of hydration that contains several contributions (Choi et al., 2005; Freger, 2009; Knauth et al., 2014; Narducci et al., 2014):

$\mathrm{\Delta }{G}_{\mathrm{hydration}}=\mathrm{\Delta }{G}_{\mathrm{osmotic}}+\mathrm{\Delta }{G}_{\mathrm{elastic}}+\mathrm{\Delta }{G}_{\mathrm{interface}}+\mathrm{\Delta }{G}_{\mathrm{electrostatic}}$ (1)

The driving force for the hydration is the osmotic pressure difference of water between the membrane and the environment (ΔG_osmotic). The osmotic pressure π is related to the concentration of the electrolyte solution inside the ionomer and the outside water activity a(H₂O) (given for example by the relative humidity RH):

$\mathrm{\pi }=\frac{RT}{V_0}\ln \left(\frac{a\mathrm{(}{\mathrm{H}}_{\mathrm{2}}\mathrm{O)}}{x_{\mathrm{0,el}}}\right)$ (2)

In this equation, x_0,el is the water molar fraction in the electrolytic solution; R is the gas constant, T the absolute temperature, and V₀ the molar volume of water.

The osmotic driving force is counterbalanced by the elastic forces (ΔG_elastic) that hold the polymer together and which can be expressed by the elastic modulus E of the ionomer. In the elastic domain of the ionomer, a linear relation exists between the deformation pressure P (taken as equal to the osmotic pressure) and the volume strain (Lazare et al., 1956):

$P=\frac{V_{\mathrm{wet}}-V_{\mathrm{dry}}}{V_{\mathrm{dry}}}E$ (3)

This relation is the tridimensional equivalent of the one-dimensional Hooke’s law for elastic solids.

The wet volume V_wet is the sum of the volumes of the internal electrolyte solution and of the polymer backbone, which contains the fixed sulfonate anions and is considered incompressible. The dry volume V_dry is the sum of the polymer backbone volume and the accessible open volume between macromolecular chains, called the “free volume” V_free. This free volume can be estimated using Bondi’s equation (Bondi, 1964). In most polymers, it is considered to be between 10 and 25% of the dry molar volume.

Other contributions to the Gibbs free energy of hydration can be taken into account, including an interfacial energy term (ΔG_interface), due to the interface curvature of the hydrated domains inside the ionomer (Choi et al., 2005; Freger, 2009) and an electrostatic term (ΔG_{electrostatic}), due to the presence of electrically charged groups inside the ionomer (Lazare et al., 1956; Eikerling and Berg, 2011). These contributions are, however, more difficult to estimate. The interfacial term depends on the shape of the hydrophilic domains. In general, these are assumed to have a cylindrical or spherical shape but this depends on the amount of water present and the type of polymer (Gebel, 2000; Diat and Gebel, 2008). In absence of a complete analysis, the interface term, although reputedly related to the Schröder paradox (Freger, 2009), is thus difficult to assess. The electrostatic term, which can be written analytically only with the simplified linearized Poisson–Boltzmann equation (Kortüm, 1965; Hamann et al., 2007), can be described in general only numerically, as done for instance in the early work by Gregor and coworkers (Lazare et al., 1956). These two terms are thus difficult to express in an analytical form and hard to predict.

We use in the following a description of the hydration of ionomers based on the equivalence between the osmotic pressure term and the elastic term. We thus assume that the osmotic pressure π and the deformation pressure P are identical.

The volume of the inner electrolyte solution can be written as the sum of the molar volumes of water and of protons present in the electrolyte. The latter being negligible, we can write:

$V_{\mathrm{el}}={\displaystyle \sum _i}{n}_i{V}_i\approx n_0{V}_0$ (4)

A linear relationship can be postulated between V_el and the thermodynamic osmotic pressure π (Gregor, 1951):

$V_{\mathrm{el}}=a\mathrm{\pi }\mathrm{+}b$ (5)

The parameters a and b depend upon the specific ionomer considered. Using the previous considerations, we can identify in Eq. 5:

$a=\frac{V_{\mathrm{dry}}}{E}\mathrm{and}b=V_{\mathrm{free}}$ (6)

We will in the following call a “deformation parameter” and b “free volume parameter.”

A change of the mole number of water n₀ changes V_el in Eq. 4, but also in Eq. 5 by a modification of the osmotic pressure π in Eq. 2. The equilibrium water-uptake n_0,eq can then be found graphically or numerically: it is the simultaneous solution of Eqs 4 and 5. As we use consistently molar quantities, n_0,eq is directly equal to the hydration number λ, also called the water-uptake coefficient, defined as:

$n_{\mathrm{0,eq}}=\mathrm{\lambda }=\frac{n\mathrm{(}{\mathrm{H}}_{\mathrm{2}}\mathrm{O)}}{n\mathrm{(S}{\mathrm{O}}_{\mathrm{3}}\mathrm{H)}}=\frac{\mathrm{WU}}{\mathrm{IEC}\times \text{M(}{\mathrm{H}}_{\mathrm{2}}\mathrm{O)}}$ (7)

The water-uptake WU is obtained from the polymer mass in wet and dry conditions. The ion exchange capacity IEC is expressed in mol/g and M(H₂O) is the molar mass of water in g/mol. Using Eqs 4–6, we can give an analytical expression for the water-uptake coefficient:

$\mathrm{\lambda }\approx \frac{V_{\mathrm{dry}}}{E\cdot V_0}\mathrm{\pi }+\frac{V_{\mathrm{free}}}{V_0}$ (8)

In principle, the advantage of this approach is that it allows the prediction of water-uptake data based on only two physically relevant parameters: the deformation parameter, inversely proportional to the elastic modulus of the ionomer, and the free volume parameter, which is related to the available open space and can be estimated using Bondi’s equation. The model assumes thermodynamic ideality, i.e., all activity coefficients are set to unity and partial volumes identified to the molar volume.

We will now check the reliability of the model prediction by confronting them with experimental hydration isotherms for SPEEK without cross-links and with some reticulation (Knauth et al., 2014). In this case, the deformation parameters were determined from the experimental elastic modulus (~1.1 GPa for cross-linked and ~0.6 GPa for uncross-linked SPEEK) and its dry volume (0.275 L/mol) giving values of a = 7.5 × 10⁻⁵ and 1.5 × 10⁻⁴ L/(kg.mol), respectively. The free volume parameter can be estimated from Bondi’s equation using tabulated atomic or group contributions (Bondi, 1964) giving b = 0.13 L/mol.

Figure 1 shows experimental hydration isotherms and modeling based on the analytical equations for SPEEK with and without cross-linking sulfone bridges. The overall agreement between experiments and simulation is quite good, given that no fitting parameters were used, but only two physically meaningful constants.

FIGURE 1

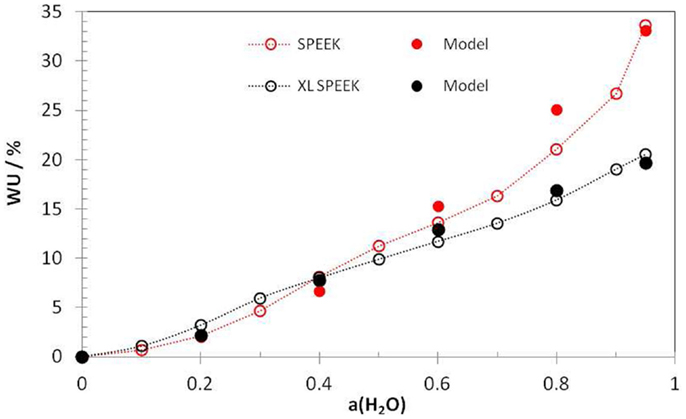
Figure 1. Experimental water-uptake isotherms (open symbols) for uncross-linked (IEC = 2.5 eq/kg) and cross-linked SPEEK (XL, degree of cross-linking = 0.45, IEC = 1.5 eq/kg) and model results using Eqs 2, 4, and 5 (full symbols). The deformation parameter was taken as 1.5 × 10⁻⁴ (SPEEK) or 7.5 × 10⁻⁵ (XL SPEEK) L mol⁻¹ bar⁻¹ and the free volume parameter as 0.13 L/mol in both cases. From Knauth et al. (2014).

We can recognize that the curves of cross-linked and uncross-linked ionomers do intersect at a relative humidity value around 40%. At higher humidity, the cross-linked ionomer shows a lower water uptake, as expected. However, more surprisingly, the hydration at lower humidity is higher for the cross-linked than for the uncross-linked ionomer. This is in fact a general finding observed for many other ionomers, see for example (Di Vona et al., 2009, 2010). Actually, the XL sample does not take up more water at low RH, but it loses less. In cross-linked ionomers, the deformation is permanently fixed and conformational changes observed during hydration are impossible; there are, thus, lower changes in hydration number between high and low humidity. In other words, the ionomer with the higher stiffness is less sensible to changes of relative humidity.

Figure 2 shows water-uptake data for sulfonated polyphenylsulfone (SPPSU) with high degree of sulfonation (IEC = 3.56 eq/kg) and after a cross-linking treatment (IEC = 2.35 eq/kg, corresponding to a degree of crosslinking ~0.7). The calculation was done with a deformation parameter 2 × 10⁻⁴ L/(mol.bar) (SPPSU) and 10⁻⁴ L/(mol.bar) (XL-SPPSU) and a constant free volume parameter of 0.1 L/mol, which can be obtained from Bondi’s equation. Again, the change made by XL is mainly the reduced deformation parameter due to the larger elastic modulus. The agreement between model and experiment is again quite good, at high humidity especially for the XL ionomer. This is probably related to the fact that XL ionomers have a larger stiffness so that they are better described by an elastic model.

FIGURE 2

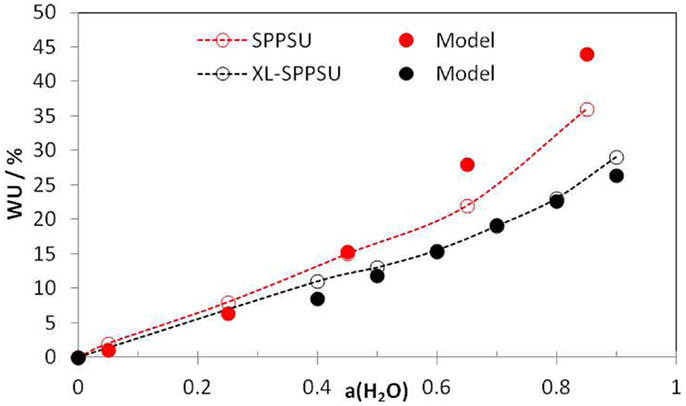
Figure 2. Experimental water-uptake isotherms (open symbols) for uncross-linked (IEC = 3.56 eq/kg) and cross-linked SPPSU (XL, degree of cross-linking ~0.7, IEC = 2.35 eq/kg) and model results using Eqs 2, 4, and 5 (full symbols). The deformation parameter was taken as 2 × 10⁻⁴ (SPPSU) or 10⁻⁴ (XL SPPSU) L mol⁻¹ bar⁻¹ and the free volume parameter as 0.1 L/mol in both cases. From Knauth et al. (2014).

In order to verify that hypothesis, let us check also the water uptake in liquid water and the existence of a Schröder paradox in some of our samples, i.e., differences between the water-uptake measured in liquid water and that in saturated water vapor, which should be identical according to equilibrium thermodynamics. Several explanations for the Schröder paradox have been brought forward over the years, including slow changes of conformation of the ionomers [kinetic effect (Alberti et al., 2008)] or the interface curvature of hydrated domains [thermodynamic effect (Freger, 2009)]. Figure 3 shows a comparison of water uptake at high humidity, water uptake in liquid water and model data for SPEEK ionomers with various IEC and degrees of cross-linking. One can clearly observe that the Schröder paradox is only apparent for the highest IEC = 2.5 eq/kg. XL ionomers do not show significant differences between water uptake in water vapor or liquid water and the model data are in good agreement. This seems to indicate that the appearance of a Schröder paradox is related to an ionomer with low stiffness and to irreversible plastic deformation of the ionomer in water, whereas in stiffer ionomers with high elastic modulus only elastic deformation is observed, which is well described by our elastic model.

FIGURE 3

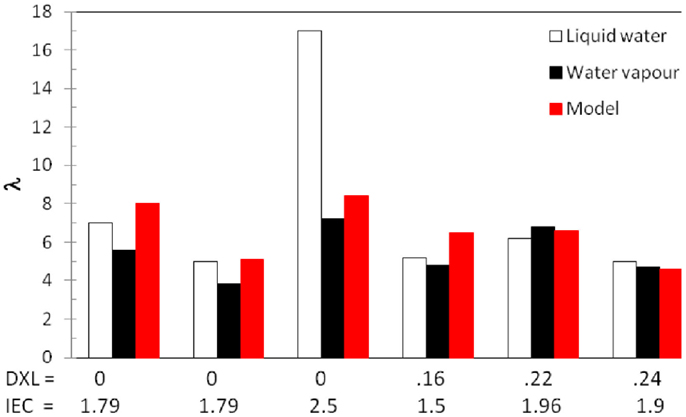
Figure 3. Hydration numbers (λ) in liquid water and water vapor [a(H₂O) = 0.95] for SPEEK with various degrees of cross-linking (DXL) and ionic exchange capacities (IEC/eq.kg⁻¹) and comparison with model. One notices a good agreement of the data except for uncross-linked SPEEK with the largest IEC.

Given that the durability of ionomers decreases with repeated swelling-drying cycles, a lower difference between water uptakes at high and low humidity should reduce the degradation issues for example under fuel-cell operation conditions, especially in electric vehicles with frequent on-off cycles. In that sense, cross-linked ionomers appear particular appealing for this application (Knauth et al., 2014). More discussion of the model assumptions and predictions and more experimental and modeling data for other ionomers, including Nafion, can be found in the reference (Knauth et al., 2014).

Proton Conductivity

High proton conductivity is an even more indispensable property for an ionomer separation membrane. Given the particular conduction mechanism through hydrated nanometric domains, the hydration is of fundamental importance for high proton conduction. The relation between proton conductivity and hydration will be the topic of this part.

Let us first specify that the ionic exchange capacity (IEC) of the ionomer alone is not a pertinent parameter to analyze the proton conductivity, because it does not consider the water content of the ionomer. We will in the following establish the proton concentration as a more relevant parameter. The proton concentration c (in mol/L per liter) is defined using the IEC of the ionomer and its water-uptake WU:

$c=\frac{\mathrm{IEC}\cdot d}{\mathrm{WU}}$ (9)

d is the solution density, taken as 1 kg/L. The relation of the proton concentration c with the hydration number λ (also called water-uptake coefficient) can be written:

$\mathrm{\lambda }=\frac{1000\cdot d}{\mathrm{M(}{\mathrm{H}}_{\mathrm{2}}\mathrm{O)}\cdot c}$ (10)

These equations assume a full dissociation of the acidic groups; although this is certainly correct for super-acids at high water content, deviations from full dissociation will occur at lower hydration and are reflected in a large change of the apparent proton mobility (see below).

The proton conductivity σ can be written as function of the proton concentration c:

$\mathrm{\sigma }=F\cdot u\cdot c$ (11)

u is the apparent proton mobility inside the nanometric hydrated channels, which can now be calculated using the measured proton conductivity and the measured (or calculated, see above) water uptake. Figure 4 shows the dependence of the apparent proton mobility on the proton concentration at 25 and 100°C. The very strong mobility dependence is characteristic of an electrolyte, where the proton dissociation depends on the hydration. Similar curves can for example be found for acetic acid solutions (Hamann et al., 2007). The difference between values at 25 and 100°C decreases with decreasing concentration, simply because the activation energy decreases when the solution gets more diluted and the Grotthuss structural diffusion mechanism becomes dominant (Kreuer et al., 2004).

FIGURE 4

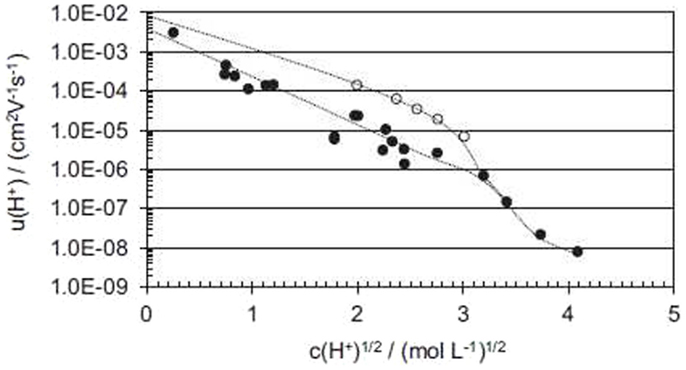
Figure 4. Apparent proton mobility in SPEEK ionomers as function of the square root of the proton concentration (Di Vona et al., 2013). The open dots were determined at 100°C, the closed dots at 25°C.

The very strong change of mobility observed in Figure 2 at √c ≈ 3 (corresponding according to Eq. 10 to λ ~ 6) can be related to the percolation threshold of the hydrated channels. A similar percolation threshold has been found by molecular dynamics for SPEEK (Mahajan and Ganesan, 2010a,b). Near the percolation threshold, the concentration dependence of conductivity can be written using a “universal” power law as function of the polymer volume fraction φ (φ_p corresponds to the percolation threshold):

$\mathrm{\sigma }\mathrm{=}{\mathrm{\sigma }}_0{\left(\mathrm{\phi }-{\mathrm{\phi }}_p\right)}^{\mathrm{\alpha }}$ (12)

The critical exponent α = 2 is typical for three-dimensional percolation (Clerc et al., 1990). This law explains well the experimental power law u ~ c⁻³ observed above the percolation threshold, given that the concentration is inversely proportional to the polymer volume fraction.

The linear part of the semi-logarithmic mobility plot in Figure 4 can be extrapolated to c = 0 (infinite dilution). The extrapolated value at 25°C is somewhat lower than the proton mobility in pure water (≈3.6 × 10⁻³ cm²/V.s (Kortüm, 1965)). This is due to the fact that the hydrated domains have only a reduced size (expressed by the “porosity”) and are not straight, but tortuous, so that protons have to move a longer way to cross the membrane as compared to the membrane thickness. These two factors can be taken into account by two phenomenological parameters, called membrane porosity ε and tortuosity τ. The proton mobility can be rescaled using these two parameters:

$u=u_0\cdot \frac{\mathrm{\epsilon }}{\mathrm{\tau }}$ (13)

The ratio ε/τ ~ 0.2 shows a relatively high tortuosity of SPEEK, as discussed previously in the literature (Mahajan and Ganesan, 2010a).

Using the mobility dependence on concentration, the maximum proton conductivity can be computed using Eq. 11: a maximum is expected at high hydration, because the mobility decreases strongly with concentration. Figure 5 shows this dependence for SPEEK at 25 and 100°C; such a plot allows predicting the best conductivity achievable for an ionomer.

FIGURE 5

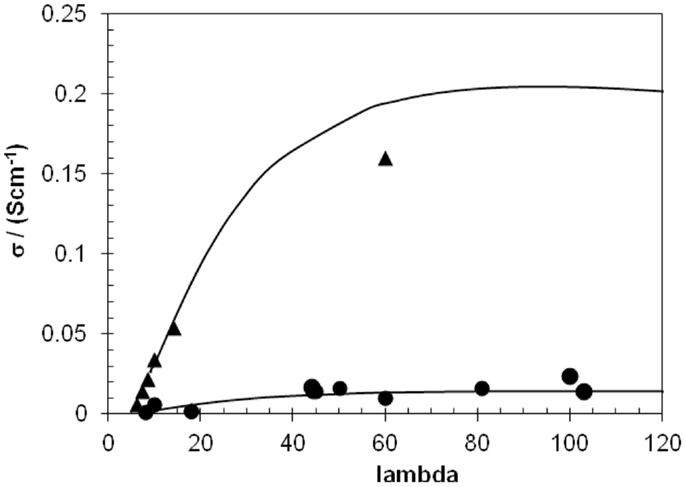
Figure 5. Proton conductivity variation with the hydration number (a) at 25°C (dots), (b) at 100°C (triangles). An intermediate maximum of proton conductivity is observed for hydration numbers around 90. At 100°C, proton conductivity above 0.1 S/cm can be obtained for hydration number 25.

The maximum is observed for a quite high hydration number, about 90, and one may ask if such high values make sense as excessive swelling must be avoided to provide good durability. However, this plot allows also choosing conditions for combined high proton conductivity and acceptable swelling. For example, it allows predicting which hydration conditions are necessary for a desired area specific resistance. At 100°C, proton conductivity above 0.1 S/cm, which is often considered the threshold to be reached by funding agencies, can be attained for a hydration number of 25, which is more compatible with the requirements for low swelling. The excellent properties of XL-SPEEK membranes in fuel cells will be reported soon.

This plot allows also prediction of the area specific resistance of the ionomer under whatever hydration conditions. Given that the hydration itself can be valuably predicted using our simplified hydration model, the potential of a new ionomer can be evaluated based on only few experimental parameters: elastic modulus, dry molar volume, and proton conductivity at low (dry state) and high (in water) humidity.

Conclusion

We have presented a phenomenological model for the description of the hydration of ionomers. This model involves only two parameters, related to physical properties of the ionomer: the deformation parameter can be calculated from the elastic modulus and the dry volume of the ionomer. The free volume parameter can be estimated from the Bondi equation. Experimental and simulated hydration isotherms for SPEEK are in remarkable agreement; another strength of our simple model is that ionomer hydration properties can be predicted. The lower difference between hydration at low and high humidity for cross-linked ionomers should be an asset for higher durability under fuel-cell operation conditions (frequent on-off cycles).

The proton conductivity of ionomers depends very strongly on the hydration. Our approach based on the calculation of the apparent proton mobility, plotted vs. proton concentration, allows the determination of the percolation threshold and the ratio porosity/tortuosity of the ionomer membrane. Furthermore, optimal hydration conditions can be determined where good proton conductivity and acceptable swelling can be realized simultaneously in order to reach the required area specific resistance.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Alberti, G., Narducci, R., and Sganappa, M. (2008). Effects of hydrothermal/thermal treatments on the water-uptake of Nafion membranes and relations with changes of conformation, counter-elastic force and tensile modulus of the matrix. J. Power Sources 178, 575–583. doi:10.1016/j.jpowsour.2007.09.034

CrossRef Full Text | Google Scholar

Armand, M. (1994). The history of polymer electrolytes. Solid State Ionics. 69, 309–319. doi:10.1016/0167-2738(94)90419-7

CrossRef Full Text | Google Scholar

Bauer, B., Jonesb, D. J., Rozièreb, J., Tchicayab, L., Albertic, G., Casciolac, M., et al. (2000). Electrochemical characterisation of sulfonated polyetherketone membranes. J. New Mater. Electrochem. Syst. 3, 93–98.

Google Scholar

Bondi, A. (1964). van der Waals Volumes and Radii. J. Phys. Chem. 68, 441–451. doi:10.1021/j100785a001

CrossRef Full Text | Google Scholar

Casciola, M., Alberti, G., Sganappa, M., and Narducci, R. (2006). On the decay of Nafion proton conductivity at high temperature and relative humidity. J. Power Sources 162, 141–145. doi:10.1016/j.jpowsour.2006.06.023

CrossRef Full Text | Google Scholar

Choi, P., Jalani, N. H., and Datta, R. (2005). Thermodynamics and proton transport in Nafion – II. Proton diffusion mechanisms and conductivity. J. Electrochem. Soc. 152, E123–E130. doi:10.1149/1.1859814

CrossRef Full Text | Google Scholar

Clerc, J. P., Giraud, G., Laugier, J. M., and Luck, J. M. (1990). The AC electrical-conductivity of binary disordered-systems, percolation clusters, fractals and related models. Adv. Phys. 39, 191–308. doi:10.1080/00018739000101501

CrossRef Full Text | Google Scholar

Couture, G., Alaaeddine, A., Boschet, F., and Ameduri, B. (2011). Polymeric materials as anion-exchange membranes for alkaline fuel cells. Prog. Polym. Sci. 36, 1521–1557. doi:10.1016/j.progpolymsci.2011.04.004

CrossRef Full Text | Google Scholar

Di Vona, M. L., and Knauth, P. (2013). Sulfonated aromatic polymers as proton-conducting solid electrolytes for fuel cells: a short review. Int. J. Res. Phys. Chem. Chem. Phys. 227, 595–614. doi:10.1524/zpch.2013.0337

CrossRef Full Text | Google Scholar

Di Vona, M. L., Pasquini, L., Narducci, R., Pelzer, K., Donnadio, A., Casciola, M., et al. (2013). Cross-linked sulfonated aromatic ionomers via SO2 bridges: conductivity properties. J. Power Sources 243, 488–493. doi:10.1016/j.jpowsour.2013.05.127

CrossRef Full Text | Google Scholar

Di Vona, M. L., Sgreccia, E., Licoccia, S., Alberti, G., Tortet, L., and Knauth, P. (2009). Analysis of temperature-promoted and solvent-assisted cross-linking in sulfonated poly(ether ether ketone) (speek) proton-conducting membranes. J. Phys. Chem. B 113, 7505–7512. doi:10.1021/jp9006679

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Di Vona, M. L., Sgreccia, E., Tamilvanan, M., Khadhraoui, M., Chassigneux, C., Knauth, P., et al. (2010). High ionic exchange capacity polyphenylsulfone (SPPSU) and polyethersulfone (SPES) cross-linked by annealing treatment: Thermal stability, hydration level and mechanical properties. J. Memb. Sci. 354, 134–141. doi:10.1016/j.memsci.2010.02.058

CrossRef Full Text | Google Scholar

Diat, O., and Gebel, G. (2008). Proton channels. Nat. Mater. 7, 13–14. doi:10.1038/nmat2091

CrossRef Full Text | Google Scholar

Eikerling, M. H., and Berg, P. (2011). Poroelectroelastic theory of water sorption and swelling in polymer electrolyte membranes. Soft Matter 7, 5976–5990. doi:10.1039/c1sm05273j

CrossRef Full Text | Google Scholar

Fergus, J. W. (2010). Ceramic and polymeric solid electrolytes for lithium-ion batteries. J. Power Sources 195, 4554–4569. doi:10.1016/j.jpowsour.2010.01.076

CrossRef Full Text | Google Scholar

Fergus, J. W. (2012). Ion transport in sodium ion conducting solid electrolytes. Solid State Ionics 227, 102–112. doi:10.1016/j.ssi.2012.09.019

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Freger, V. (2009). Hydration of ionomers and Schroeder’s paradox in nafion. J. Phys. Chem. B 113, 24–36. doi:10.1021/jp806326a

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Gebel, G. (2000). Structural evolution of water swollen perfluorosulfonated ionomers from dry membrane to solution. Polymer 41, 5829–5838. doi:10.1016/S0032-3861(99)00770-3

CrossRef Full Text | Google Scholar

Gregor, H. P. (1951). GIBBS-Donnan equilibria in ion exchange resin systems. J. Am. Chem. Soc. 73, 642–650. doi:10.1021/ja01146a042

CrossRef Full Text | Google Scholar

Hamann, C. H., Hamnett, A., and Vielstich, W. (2007). Electrochemistry, 2nd Edn. Weinheim: Wiley-VCH.

Google Scholar

Hickner, M. A. (2012). Water-mediated transport in ion-containing polymers. J. Polymer. Sci. B Polymer. Phys. 50, 9–20. doi:10.1002/polb.22381

CrossRef Full Text | Google Scholar

Hickner, M. A. (2013). Ion-containing polymers: new energy & clean water. Mater. Today 13, 34–41. doi:10.1016/S1369-7021(10)70082-1

CrossRef Full Text | Google Scholar

Hou, H. Y., Di Vona, M. L., and Knauth, P. (2011). Durability of sulfonated aromatic polymers for proton-exchange-membrane fuel cells. Chem. Sus. Chem. 4, 1526–1536. doi:10.1002/cssc.201000415

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Hou, H. Y., Maranesi, B., Chailan, J.-F., Khadhraoui, M., Polini, R., Di Vona, M. L., et al. (2012). Crosslinked SPEEK membranes: mechanical, thermal, and hydrothermal properties. J. Mater. Res. 27, 1950–1957. doi:10.1557/jmr.2012.151

CrossRef Full Text | Google Scholar

Knauth, P., and Di Vona, M. L. (2012). Sulfonated aromatic ionomers: analysis of proton conductivity and proton mobility. Solid State Ionics. 225, 255–259. doi:10.1016/j.ssi.2012.01.043

CrossRef Full Text | Google Scholar

Knauth, P., Pasquini, L., Maranesi, B., Pelzer, K., Polini, R., and Di Vona, M. L. (2013). Proton mobility in sulfonated PolyEtherEtherKetone (SPEEK): influence of thermal crosslinking and annealing. Fuel Cells 13, 79–85. doi:10.1002/fuce.201200120

CrossRef Full Text | Google Scholar

Knauth, P., Sgreccia, E., and Di Vona, M. L. (2014). Chemomechanics of acidic ionomers: hydration isotherms and physical model. J. Power Sources 267, 692–699. doi:10.1016/j.jpowsour.2014.05.127

CrossRef Full Text | Google Scholar

Kortüm, G. (1965). Treatise on Electrochemistry, 2nd Edn. Amsterdam, NY: Elsevier.

Google Scholar

Kreuer, K. D. (2001). On the development of proton conducting polymer membranes for hydrogen and methanol fuel cells. J. Memb. Sci. 185, 29–39. doi:10.1016/S0376-7388(00)00632-3

CrossRef Full Text | Google Scholar

Kreuer, K. D., Paddison, S. J., Spohr, E., and Schuster, M. (2004). Transport in proton conductors for fuel-cell applications: simulations, elementary reactions, and phenomenology. Chem. Rev. 104, 4637–4678. doi:10.1021/cr020715f

CrossRef Full Text | Google Scholar

Kumar, M., Edwards, B. J., and Paddison, S. J. (2013). A macroscopic model of proton transport through the membrane-ionomer interface of a polymer electrolyte membrane fuel cell. J. Chem. Phys. 138, 13. doi:10.1063/1.4789960

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Lazare, L., Sundheim, B. R., and Gregor, H. P. (1956). A model for cross-linked polyelectrolytes. J. Phys. Chem. 60, 641–648. doi:10.1021/j150539a035

CrossRef Full Text | Google Scholar

Li, L., Zhang, J., and Wang, Y. X. (2003). Sulfonated poly(ether ether ketone) membranes for direct methanol fuel cell. J. Memb. Sci. 226, 159–167. doi:10.1016/j.memsci.2003.08.018

CrossRef Full Text | Google Scholar

Li, X. F., Zhang, H. M., Mai, Z. S., and Zhang, H. Z. I (2011). Vankelecom, Ion exchange membranes for vanadium redox flow battery (VRB) applications. Energy Environ. Sci. 4, 1147–1160. doi:10.1039/c0ee00770f

CrossRef Full Text | Google Scholar

Mahajan, C. V., and Ganesan, V. (2010a). Atomistic simulations of structure of solvated sulfonated poly(ether ether ketone) membranes and their comparisons to nafion: I. Nanophase segregation and hydrophilic domains. J. Phys. Chem. B 114, 8357–8366. doi:10.1021/jp104078h

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Mahajan, C. V., and Ganesan, V. (2010b). Atomistic simulations of structure of solvated sulfonated poly(ether ether ketone) membranes and their comparisons to nafion: II. Structure and transport properties of water, hydronium ions, and methanol. J. Phys. Chem. B 114, 8367–8373. doi:10.1021/jp1040794

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Majsztrik, P. W., Satterfield, M. B., Bocarsly, A. B., and Benziger, J. B. (2007). Water sorption, desorption and transport in Nafion membranes. J. Memb. Sci. 301, 93–106. doi:10.1021/jp7103243

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Mauritz, K. A., and Moore, R. B. (2004). State of understanding of Nafion. Chem. Rev. 104, 4535–4585. doi:10.1021/cr0207123

CrossRef Full Text | Google Scholar

Merle, G., Wessling, M., and Nijmeijer, K. (2011). Anion exchange membranes for alkaline fuel cells: a review. J. Memb. Sci. 377, 1–35. doi:10.1016/j.memsci.2011.04.043

CrossRef Full Text | Google Scholar

Meyer, W. H. (1998). Polymer electrolytes for lithium-ion batteries. Adv. Mater. Weinheim 10, 439. doi:10.1002/(SICI)1521-4095(199804)10:6

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Narducci, R., Di Vona, M. L., and Knauth, P. (2014). Cation-conducting ionomers made by ion exchange of sulfonated poly-ether-ether-ketone: Hydration, mechanical and thermal properties and ionic conductivity. J. Memb. Sci. 465, 185–192. doi:10.1016/j.memsci.2014.03.073

CrossRef Full Text | Google Scholar

Paddison, S. J. (2003). Proton conduction mechanisms at low degrees of hydration in sulfonic acid-based polymer electrolyte membranes. Ann. Rev. Mater. Res. 33, 289–319. doi:10.1146/annurev.matsci.33.022702.155102

CrossRef Full Text | Google Scholar

Peckham, T. J., Schmeissert, J., and Holdcroft, S. (2008). Relationships of acid and water content to proton transport in statistically sulfonated proton exchange membranes: Variation of water content via control of relative humidity. J. Phys. Chem. B 112, 2848–2858. doi:10.1021/jp077218t

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Reyna-Valencia, A., Kaliaguine, S., and Bousmina, M. (2006). Structural and mechanical characterization of poly(ether ether ketone) (PEEK) and sulfonated PEEK films: Effects of thermal history, sulfonation, and preparation conditions. J. Appl. Polymer. Sci. 99, 756–774. doi:10.1002/app.22551

CrossRef Full Text | Google Scholar

Rikukawa, M., and Sanui, K. (2000). Proton-conducting polymer electrolyte membranes based on hydrocarbon polymers. Prog. Polym. Sci. 25, 1463–1502. doi:10.1016/S0079-6700(00)00032-0

CrossRef Full Text | Google Scholar

Robertson, G. P., Mikhailenko, S. D., Wang, K., Xing, P., Guiver, M. D., et al. (2003). Casting solvent interactions with sulfonated poly(ether ether ketone) during proton exchange membrane fabrication. J. Memb. Sci. 219, 113–121. doi:10.1016/S0376-7388(03)00193-5

CrossRef Full Text | Google Scholar

Roziere, J., and Jones, D. J. (2003). Non-fluorinated polymer materials for proton exchange membrane fuel cells. Ann. Rev. Mater. Res. 33, 503–555. doi:10.1146/annurev.matsci.33.022702.154657

CrossRef Full Text | Google Scholar

Sgreccia, E., Chailan, J. F., Khadhraoui, M., Di Vona, M. L., and Knauth, P. (2010). Mechanical properties of proton-conducting sulfonated aromatic polymer membranes: stress-strain tests and dynamical analysis. J. Power Sources 195, 7770–7775. doi:10.1016/j.jpowsour.2009.09.061

CrossRef Full Text | Google Scholar

Smitha, B., Sridhar, S., and Khan, A. A. (2005). Solid polymer electrolyte membranes for fuel cell applications – a review. J. Memb. Sci. 259, 10–26. doi:10.1016/j.memsci.2005.01.035

CrossRef Full Text | Google Scholar

Springer, T. E., Zawodzinski, T. A., and Gottesfeld, S. (1991). Polymer electrolyte fuel-cell model. J. Electrochem. Soc. 138, 2334–2342. doi:10.1149/1.2085971

CrossRef Full Text | Google Scholar

Wang, Y., Chen, K. S., Mishler, J., Cho, S. C., and Adroher, X. C. (2011). A review of polymer electrolyte membrane fuel cells: technology, applications, and needs on fundamental research. Appl. Energy 88, 981–1007. doi:10.1016/j.apenergy.2010.09.030

CrossRef Full Text | Google Scholar

Wu, L., Zhang, Z., Ran, J., Zhou, D., Li, C., and Xu, T. (2013). Advances in proton-exchange membranes for fuel cells: an overview on proton conductive channels (PCCs). Phys. Chem. Chem. Phys. 15, 4870–4887. doi:10.1039/c3cp50296a

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Wu, X. M., Wang, X. W., He, G. H., and Benziger, J. (2011). Differences in water sorption and proton conductivity between nafion and SPEEK. J. Polymer Sci. B Polymer. Phys. 49, 1437–1445. doi:10.1002/polb.22326

CrossRef Full Text | Google Scholar

Xing, P. X., Robertson, G. P., Guiver, M. D., Mikhailenko, S. D., Wang, K., and Kaliaguine, S. (2004). Synthesis and characterization of sulfonated poly(ether ether ketone) for proton exchange membranes. J. Memb. Sci. 229, 95–106. doi:10.1016/j.memsci.2003.09.019

CrossRef Full Text | Google Scholar

Yan, X. M., He, G. H., Wu, X. M., and Benziger, J. (2013). Ion and water transport in functionalized PEEK membranes. J. Memb. Sci. 429, 13–22. doi:10.1016/j.memsci.2012.11.026

CrossRef Full Text | Google Scholar

Zawodzinski, T. A., Springer, T., Davey, J., Jestel, R., Lopez, C., Valerio, J., et al. (1993). A comparative-study of water-uptake by and transport through ionomeric fuel-cell membranes. J. Electrochem. Soc. 140, 1981–1985. doi:10.1149/1.2220749

CrossRef Full Text | Google Scholar