Quantization and sparsity-aware processing for energy-efficient NVM-based convolutional neural networks

Nonvolatile memory (NVM)-based convolutional neural networks (NvCNNs) have received widespread attention as a promising solution for hardware edge intelligence. However, there still exist many challenges in the resource-constrained conditions, such as the limitations of the hardware precision and cost and, especially, the large overhead of the analog-to-digital converters (ADCs). In this study, we systematically analyze the performance of NvCNNs and the hardware restrictions with quantization in both weight and activation and propose the corresponding requirements of NVM devices and peripheral circuits for multiply–accumulate (MAC) units. In addition, we put forward an in situ sparsity-aware processing method that exploits the sparsity of the network and the device array characteristics to further improve the energy efficiency of quantized NvCNNs. Our results suggest that the 4-bit-weight and 3-bit-activation (W4A3) design demonstrates the optimal compromise between the network performance and hardware overhead, achieving 98.82% accuracy for the Modified National Institute of Standards and Technology database (MNIST) classification task. Moreover, higher-precision designs will claim more restrictive requirements for hardware nonidealities including the variations of NVM devices and the nonlinearities of the converters. Moreover, the sparsity-aware processing method can obtain 79%/53% ADC energy reduction and 2.98×/1.15× energy efficiency improvement based on the W8A8/W4A3 quantization design with an array size of 128 × 128.

1 Introduction

Recently, deep neural networks have reached significant accomplishments in many manufacturing and daily life applications. Their impressive ability to learn and extract abstract features has greatly changed the field of artificial intelligence (AI) from what it was before (LeCun et al., 2015). Among the most popular deep neural network models, convolutional neural networks (CNNs) demonstrate vital importance, especially in image processing (Krizhevsky et al., 2017), object detection (Girshick et al., 2014), and acoustic feature extraction (Bi et al., 2015). However, the calculation procedure of CNN requires a large amount of multiply and accumulation (MAC) operations, which are highly energy and time intensive, putting forward critical challenges for CNNs to be implemented on hardware, especially for resource-constrained edge intelligence applications.

To efficiently accelerate hardware neural networks, the computing-in-memory (CIM) approach using nonvolatile memory (NVM) device arrays, including memristors (Lin et al., 2020; Yao et al., 2020; Xue et al., 2021), flash (Guo et al., 2017), phase-change memory (PCM) (Ambrogio et al., 2018), ferroelectric gate field-effect transistors (FeFET) (Jerry et al., 2017), and magnetic RAM (MRAM) (Jain et al., 2018), is receiving extensive attention. Recent studies have successfully demonstrated various hardware implementations of the NVM-based convolutional neural networks (NvCNNs), obtaining orders of magnitude of better energy efficiency compared with Central Processing Unit (CPU)- or Graphics Processing Unit (GPU)-based solutions (Guo et al., 2017; Lin et al., 2020; Yao et al., 2020; Xue et al., 2021). In NVM arrays, the conductance of NVM devices is mapped as the weights, and the voltage signals are mapped as the activations. The output of the MAC can be directly generated through Ohm’s law and Kirchhoff’s current law. The NVM arrays and the periphery circuits together combine into the MAC units to accelerate neural networks with high parallelism and speed.

However, for resource-constrained application circumstances, there are still many requirements for further improving the performance and energy efficiency of NvCNNs. The first is that both the precision of NVM devices and the periphery circuits, which are mainly the analog-to-digital converters (ADCs) and the digital-to-analog converters (DACs), have crucial effects on network performance and energy consumption. For NVM devices, the number of available and stable conductance states of the analog devices is usually limited, making them difficult to map high-precision weights. For ADCs and DACs, the full-scale voltage range (V_FSR) and the limited precision of the convertors will directly affect the sampling and generation of the practical voltage signals in the MAC units. Hardware implementing design with higher-precision devices and converters can usually achieve better network performance, but will also result in larger hardware overhead. Researchers have explored many NVM-based neural networks with limited precision designs in order to ease the hardware burden. Most studies considered low-to-medium-precision quantization (usually 4 bits) (Jacob et al., 2018; Cai et al., 2019; Ma et al., 2019). Other studies on the other hand focused on the binary and ternary quantized conditions (Tang et al., 2017; Qin et al., 2020). However, a thorough analysis combining hardware characteristics and the network quantization method should also be implemented.

The second is that to further conduct specific optimization on the NVM-based neural networks, one should take advantage of their intrinsic characteristics. The sparse characteristics of the parameters in the neural networks widely existed due to the advantages of the rectified linear unit (ReLU) activation function and regularization training methods. Enhancing the sparsity of the weights and the activations can be considered equally as increasing the ratio of high-resistance-state devices and low-amplitude voltage signals in the hardware implementation, which dominate in reducing the energy consumption (Sun et al., 2020). However, the sparsity of the activations can be further utilized to reduce the required ADC precision and the corresponding energy consumption. Some researchers utilize counters or input encoder circuit modules to sense the sparsity of binary input (Ali et al., 2021; Wang et al., 2021; Li et al., 2022). Others recorded the map of the sparsity distribution maps in advance during the network training (Yue et al., 2020; Yue et al., 2021). However, a more versatile and convenient approach to sense the sparsity is expected to further reduce the hardware overhead and energy consumption of NVM-based neural networks.

In this study, we focus on exploring the energy-efficient hardware design of NVM-based convolutional neural networks through the quantization and sparsity-aware processing method. Based on the benchmark of LeNet-5, we thoroughly explore the quantization coeffect of both weight and activation from 1-bit extreme low precision to 8-bit high precision and compare the corresponding hardware burden. The results imply that a combination of 4-bit weight and 3-bit activation is favorable for the optimal compromise between network performance and hardware overhead. To further improve the energy efficiency, we propose an in situ sparsity-aware processing approach in the quantized neural network with the help of an additional row of the memory devices. Impressive enhancement can be obtained through the approach by greatly reducing the ADC energy consumption and improving the energy efficiency of the MAC units especially when the activations are highly sparse and the original ADC hardware burdens are severe.

2 Hardware design of NvCNN

In NVM MAC units, the impressive capability of accelerating the neural networks comes from the highly parallel processing of the MAC operations. However, the precision of the computation is straightly related to the hardware implementation. The quantization, which has been widely used in industry and academia to compress the neural networks (Sze et al., 2017; Deng et al., 2020), is not only intrinsically embedded within the hardware implementation, and require specific discussion to assure the processing accuracy, but also a powerful method to reduce the hardware burden and improve the processing energy efficiency. In this section, we will introduce the hardware design strategy of the quantized CNN on the NVM MAC unit.

2.1 Network structure and the NVM MAC unit

The typical and extensively analyzed LeNet-5 is adopted as the evaluated model in this study (LeCun et al., 1998). The structure of the network is demonstrated in Figure 1A, which is consisted of two convolutional layers with 5 × 5 filters, two average pooling layers with 2 × 2 filters, and three fully connected layers. The ReLU function is used as the activation function of the hidden layers, while the SoftMax function is used for the output layer. Moreover, the Modified National Institute of Standards and Technology database (MNIST) with 28 × 28 handwritten digit images is used as the benchmark (LeCun et al., 1998), which are divided into 60 and 10 k images for the training and testing set respectively.

FIGURE 1

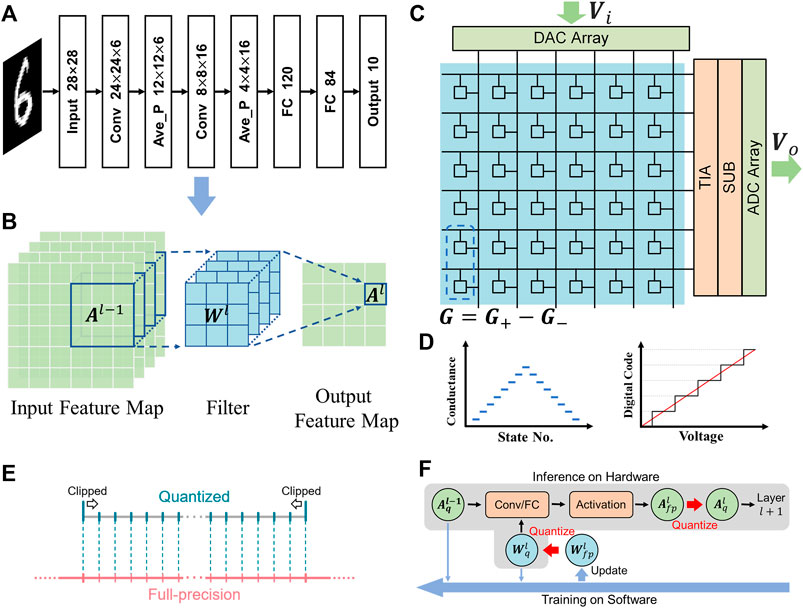
FIGURE 1. (A) The structure of the LeNet-5 model. (B) Schematic of the convolutional layer of CNNs. (C) Schematic of an NVM MAC unit, consisting of the NVM array and the periphery circuits. Each weight is represented by the differential conductance of two memory devices. (D) Schematics of the NVM devices that are limited by the number of available conductance states (left), and DACs/ADCs that possess finite precision within the truncated range (right), leading to the quantization effect on the weight and activation parameters, respectively. (E) Schematic of quantization operation from FP parameters to quantized ones. (F) Schematic of the overall quantization algorithm. The black arrows denote the dataflow direction of the forward propagation as well as the inference phase on the hardware. The blue arrows denote the data flow direction of the backpropagation.

For the hardware design of CNNs, the mapping strategy of the parameters between the convolutional layers, as the representation of the network layers, and the NVM MAC units are illustrated in Figures 1B,C. The input activations A are mapped as the input voltage signals V_i and then conducted into the array columns through DACs. The weights W are mapped as the conductance difference G of the NVM device pairs in the array. The output activations A are mapped as the output voltage signals V_o, which are converted from the row currents I through peripheral circuit modules including trans-impedance amplifiers (TIAs) and subtractors (SUBs). Finally, V_o is sampled by the ADCs and buffered for further processing, and used as the input signals for the next MAC unit. Notably, the ReLU function is automatically embedded within the ADC sampling process. The corresponding mapping relationship between the parameters can be described in the equations as follows:

$\begin{array}{c}{\mathit{G}}^{\mathit{l}}={\mathit{W}}^{\mathit{l}}\cdot G_{\mathrm{range}}/w_{\mathrm{range}}\end{array},(1)$

$\begin{array}{c}{\mathit{V}}^{\mathit{l}}={\mathit{A}}^{\mathit{l}}\cdot V_{\mathrm{range}}/a_{\mathrm{range}}\end{array},(2)$

$\begin{array}{c}{\mathit{A}}^{\mathit{l}}=ReLU\left({\mathit{A}}^{\mathit{l}-1}{\mathit{W}}^{\mathit{l}}\right)\end{array},(3)$

$\begin{array}{c}{\mathit{V}}_{\mathit{o}}=R_t{\mathit{V}}_{\mathit{i}}{\mathit{G}}^{\mathit{l}}\end{array},(4)$

where the superscript l denotes the lth layer and the corresponding device array, the subscript range denotes the distribution range of the corresponding parameters, and R_t denotes the equivalent trans-impedance coefficient of the overall peripheral circuits during the conversion of the current signals to the voltage ones.

2.2 Quantization algorithm

In the hardware implementation of the NVM MAC units, NVM devices used to map the weight parameters are limited by the number of available conductance states, while the DACs/ADCs which generate/sample the voltage signals possess finite precision within the truncated range, will result in quantization effects in mapping the activation parameters, as shown in Figure 1D. Therefore, the quantization of both weights and activations is necessary for the evaluation of the NvCNNs.

In the quantization algorithm, for a full-precision (FP) parameter to be quantized, two primary hyperparameters, the clipping range, and the precision, should be concerned (Figure 1E). The clipping range determines the allowed range of the parameters, meaning that if the value of the FP parameter is out of the range, it will be clipped to the upper or lower boundary of the clipping range accordingly. The precision then determines the allowed number of states, which are usually distributed uniformly within the clipping range.

The overall quantization algorithm is shown in Figure 1F. During the training, two sets of weights should be stored and utilized, that is, the FP weights W_fp and the quantized weights W_q. However, only the quantized activations A_q are buffered and conducted into the next layer. W_q and A_q are used for both forward propagation and backpropagation. W_fp is used to accumulate the small updates of each training iteration, and generate W_q for the next iteration. The training is conducted on the software using the stochastic gradient descent with a batch size of 200 and a learning rate of 0.01.300 iteration cycles are used to ensure the convergence of the network training. Once the training is completed on the software, W_fp can be discarded, and the quantized parameters are transferred onto the hardware for inference applications.

3 Evaluation of network quantization and hardware overhead

As mentioned previously, higher weight precision will bring more demands on the analog performance of the devices, and higher activation precision will lead to more precise converters with larger hardware overhead as well. Constrained by the limited resources of the hardware implementation, the quantized neural networks need to seek a compromise between network performance and hardware overhead. Moreover, the impact of the hardware nonidealities on the network performance should be considered an essential consideration to better guide the design of the hardware neural networks.

3.1 Quantization precision and hardware overhead

The quantization effects of the network parameters on the performance are mainly determined by their clipping range and precision. According to the previous research (Pan et al., 2020), the weight parameters of the networks are centralized around zeros and can be clipped within [−0.25, 0.25] during quantization to obtain better network accuracies. Similar trends can also be observed in the activation parameters. After the ReLU function is applied, negative activations are all truncated to zeros, while the positive ones are mostly centralized around zeros apart from several individual extreme data. As for the activation quantization, traditional methods use the maximum and minimum values of the activations to determine the quantization range. However, such methods will be critically influenced by the extreme data, and discard abundant information on small but major values. Some researchers use nonlinear activation quantization methods to compensate for the extreme values and obtain better performance, but require to generate nonuniform reference signals, which introduce a complex fabrication process and are not friendly for the hardware implementation of ADCs/DACs (Sun et al., 2020). Therefore, a uniform and clipped activation quantization strategy is used to better match the characteristics of ADC/DAC implementations and ease the hardware design.

The lower boundary of the activation clipping range is stationed at 0 in the following analysis due to the utilization of the ReLU function. The effect of the upper boundary of the activation clipping range on the network accuracy is analyzed and shown in Figure 2A. Results demonstrate that either too large or too small upper boundary will result in a decrease in the overall accuracies. The network possesses slightly better overall performance when the upper boundary is set to 2. Thus, the clipping range of activations is fixed at [0, 2] along the following discussion.

FIGURE 2

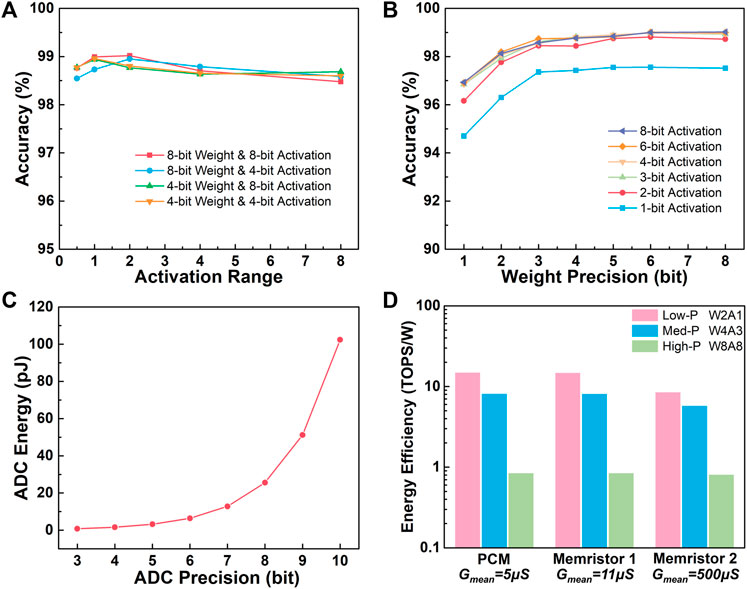
FIGURE 2. (A) The effect of clipped activation range on the network accuracy of the MNIST dataset according to different quantization conditions. (B) The effects of weight and activation quantization on the network accuracy of the MNIST dataset. Especially, the 1-bit weight precision denotes the binary-weight case. (C) The energy consumption of the leading ADCs with respect to their precisions. (D) Evaluation of the overall energy efficiency of the MAC units with 128 × 128 device array according to different quantization precision designs.

The effects of weight and activation quantization precision are illustrated in Figure 2B. In general, the network accuracy tends to saturate at high-precision conditions for either weights or activations but declines obviously with decreasing precisions, especially at 1-bit. Specifically, in the consideration of weight precision, high-precision weights no less than 6-bit show the highest network performance. However, to achieve such high-precision-weight designs, NVM devices require much more tunable states, claiming strict demands in material and device structure design as well as operating strategies (Tang et al., 2019; Xi et al., 2020). Medium-precision weights between 3-bit and 5-bit possess only a small accuracy decline. Moreover, the devices with no more than 3-bit stable and distinguishable states can be relatively easy to obtain through operating methods like pulse stimulation (Chen et al., 2019), current compliance (Chen et al., 2020), and write-verify (Luo et al., 2020), etc. Therefore, medium-precision weight designs are more hardware efficient for application, and the 4-bit weight precision can provide relatively higher network accuracy. Low-precision weights, i.e. binary (1-bit) or ternary (2-bit), result in a large accuracy decline compared to other cases. However, both binary- and ternary-weight designs can be easily represented using a pair of binary devices, which usually possess state-of-the-art switching characteristics including retention, endurance, variation, yield as well as programing simplicity (Huang et al., 2020), thus are more suitable to achieve high reliability.

With respect to the activation precision, the precision of the converters is equivalently considered, as mentioned previously. The energy and area overhead of the converters usually occupy a large portion of the NVM MAC units and become even larger when their precisions are increased. Figure 2C shows the tendency of the typical energy consumption of the leading ADC implements at various precision designs (Murmann, 2021). On the one hand, high-precision activations like 6-bit and 8-bit can obtain the highest performance but at the cost of ultrahigh hardware redundancy. On the other hand, low-precision cases, i.e. 1-bit and 2-bit, are more energy and area efficient but suffer from significant accuracy decline. Our result suggests that 3-bit activation is a better choice to obtain rather high hardware efficiency while still maintaining tolerable accuracy decline. Still, 1-bit-activation design can be more favorable when the constrained resource becomes the most concerning aspect in real world applications, because in this case the energy-intensive converters can be substituted by more compact and efficient circuit modules like transmission gate (TG), voltage comparator, or current sense amplifier (CSA) (Yan et al., 2019).

The comparison of the overall energy efficiency of the MAC unit between various precision designs and NVM device benchmarks (Li et al., 2018; Joshi et al., 2020; Yao et al., 2020) is demonstrated in Figure 2D, according to the circuit module metrics in (Miyahara et al., 2011; Texas Instruments, 2011; Rabuske et al., 2012; Mahdavi et al., 2017; Bchir et al., 2021). Great enhancement in energy efficiency can be observed in the hardware designs with lower precision. The quantization method is further conducted on the LeNet-5, VGG16 (Simonyan and Zisserman, 2014), and ResNet-18 (He et al., 2016) network models using the CIFAR-10 (Krizhevsky and Hinton, 2009) dataset. The performances of the quantized networks are shown in Table 1. The 4-bit-weight and 3-bit-activation design exhibits a relatively low accuracy drop compared with the low-precision quantization, suggesting the potential of improving the energy efficiency in deeper network models.

TABLE 1

TABLE 1. Comparisons of three typical neural networks on the Cifar-10 dataset at different quantization precisions.

In general, medium-precision quantization can obtain the optimal compromise between network accuracy and hardware overhead. Specifically, for LeNet-5, 4-bit-weight and 3-bit-activation design is the most recommended choice, which can acquire 98.82% network accuracy on the MNIST dataset with minor degeneration compared to the 99.08% accuracy of the full-precision one. 2-bit-weight and 1-bit-activation can be favorable for extreme conditions where the accuracy can be sacrificed in exchange for hardware reliability and overhead.

3.2 Evaluation of hardware nonidealities on network performance

For the neural network inference application of the NVM MAC unit, the well-trained parameters need to be transferred to the hardware. However, the hardware implementation of the NVM arrays and periphery circuits inevitably suffered from nonidealities, causing undesired deviations between the ideal and practical parameter values.

Due to the intrinsic stochasticity of the device mechanisms and fabrication process, NVM devices possess unavoidable variation issues in the conductance states, which can usually be simulated using Gaussian distributions (Joshi et al., 2020). Therefore, weight parameters are also affected by such characteristics, and reduce the performance of the hardware network. We define the normalized variation of weight nv_w, which will also be equal to the normalized variation of conductance, in the equation as follows:

$\begin{array}{c}n{\nu }_w={\sigma }_w/w_{\mathrm{range}}={\sigma }_G/G_{\mathrm{range}}\end{array},(5)$

where σ stands for the standard deviation of the parameters. To analyze the effect of different precisions on the network robustness, we extract the maximum acceptable nv_w that can maintain over 90% accuracy of the network as the comparison criterion. As for the effect of weight precisions, the networks trained with lower weight precisions possess significantly enhanced robustness, as demonstrated in Figure 3A, due to the fact that higher-precision weights will suffer from more serious state overlapping problems compared to lower-precision conditions. The results also suggest that the hardware designs with higher weight precision will require extra efforts to suppress the variation of device conductance states.

FIGURE 3

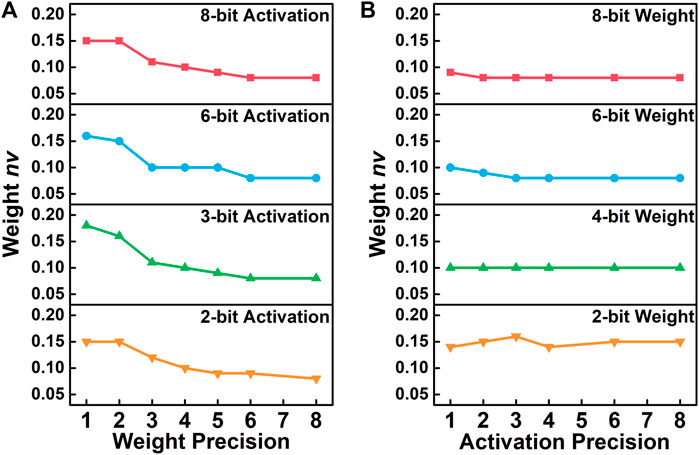
FIGURE 3. The effect of different (A) weight precisions and (B) activation precisions on the network robustness to the weight variation. The maximum acceptable nv_w that can still maintain over 90% network accuracy is used as the comparison criterion to represent the robustness.

As for the effect of activation precisions on the network robustness, the quantization of activation serves as a rounding function on the outputs of MAC, and ought to cover slight deviations of the activations caused by the weight variation. However, the robustness shows no distinct tendency across different activation precisions, as shown in Figure 3B. Such a phenomenon might be explained by the fact that even though low-precision-activation cases have better opportunities to suppress the output deviations, the fatality caused by each error is also more critical. Therefore, due to the two effects canceling each other out, the overall robustness of the weight variation is almost not affected by the activation precision.

Common types of ADCs and DACs usually use a series of weighted resistors or capacitors to achieve the division of the reference voltage. However, the standard manufacturing process will always introduce random deviations in the resistance and capacitance. These nonidealities are usually described in terms of integral nonlinearity (INL) and differential nonlinearity (DNL), which can cause misjudgments during voltage comparison. To evaluate the deviations caused by the converter nonlinearities, a simplified model is analyzed, which randomly introduces variations into the comparison levels of the quantization function. The normalized variation of activation nv_a is defined similarly to the nv_w. In each simulation evaluation, the nv_a are randomly generated but fixed according to each weight filter to better imitate the hardware implement circumstances. As illustrated in Figure 4, the robustness to converter nonlinearities is barely affected by the weight precisions, and only a slight enhancement can be observed by lower weight precision designs. However, the network robustness is significantly improved by the decreased activation precision design. Such phenomena can be explained by the larger gaps between the adjacent states in lower-precision cases. The results also suggest that high-precision activation designs impose much higher requirements on the DAC/ADC hardware implement, which otherwise would result in unfavorable sharp declines in performance.

FIGURE 4

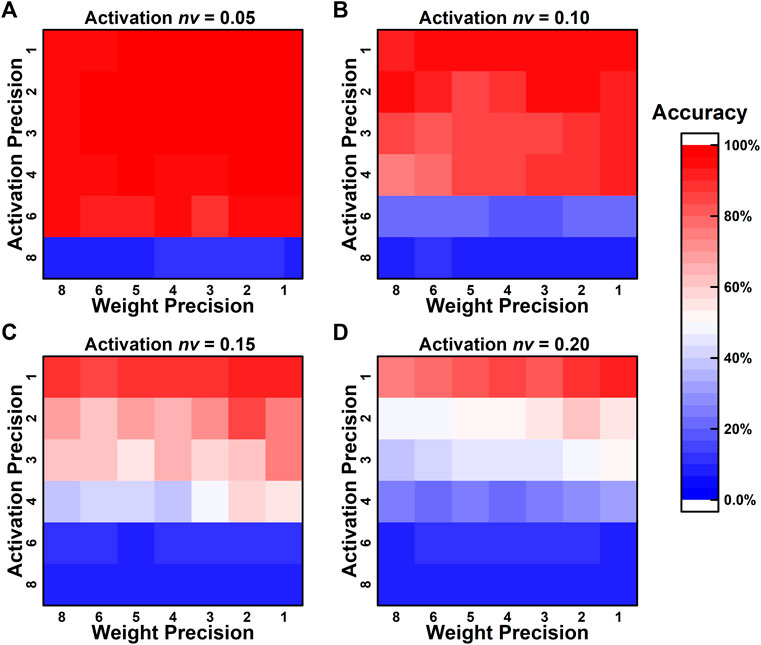
FIGURE 4. The effect of different quantization precisions on network robustness to the activation variation.

4 Sparsity-aware processing method

The aforementioned simulations have evaluated the quantization strategy to achieve proper hardware design that can obtain good network performance at relatively low hardware overhead. However, the quantization operation has inevitably damaged the accuracy of the network anyway, and attempts to further reduce the quantization precision will bring about a more severe accuracy decline, as suggested by the results of the low-precision quantization designs. Therefore, an energy efficiency improvement strategy that is capable of maintaining the accuracy of the MAC operations for the quantized NvCNNs is pursued. Here, we present a novel in situ sparsity-aware processing strategy with the assistance of an additional row of memory devices.

In neural networks, the sparse characteristics of the parameters widely existed due to the utilization of the ReLU activation function and regularization constraint term during the training. The activation cumulative probability distribution of the quantized NvCNN under two representative conditions, that is, the 4-bit-weight-and-3-bit-activation (W4A3) medium-precision design and the 8-bit-weight-and-8-bit-activation (W8A8) high-precision design, are demonstrated in Figures 5A,B, respectively. It can be observed that the activations of the network have demonstrated high sparsity. For instance, in the W4A3 design, over 99% of the total activation values are no greater than 0.25. After the ADC sampling, the maximum activations (activation = 1.75) can be represented as a binary value 111, while the values that equal 0.25 will be expressed as 001, and the values that equal 0 will be expressed as 000. Therefore, these values ≤0.25 can be distinguished from each other by only the lowest bit, which is 2-bit lower than the overall one (from 3 bit to 1 bit). However, the aforementioned evaluation of the activation quantization effect has suggested that the minor extreme data that occupy less than 1% still provide indispensable roles in the network, and cannot be truncated. Similarly, in the W8A8 case, over 97% of the total activation values can be expressed by a precision 4-bit lower than that of the maximum ones (from 8 bit to 4 bit). Therefore, in the NvCNNs, most of the voltage signals that map the activations possess the capability of being sampled with many lower-precision configurations by the precision-reconfigurable ADCs (Yip and Chandrakasan, 2013; Fateh et al., 2015), leading to desirable potential in reducing the energy consumption of the hardware implementation.

FIGURE 5

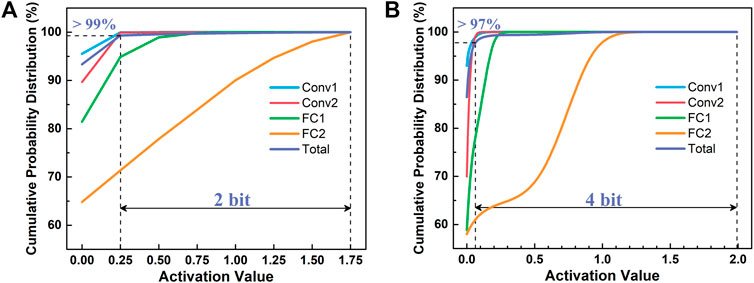
FIGURE 5. The layer-wise and total activation cumulative probability distributions of (A) W4A3 and (B) W8A8 cases, respectively. The activations are highly sparse, and over 99%/97% of the total values can be expressed with precisions 2-bit/4-bit lower than that of the maximum ones for the W4A3/W8A8 case.

The hardware implementing scheme and the flowchart of the proposed sparsity-aware processing algorithm are demonstrated in Figures 6A,B, respectively. The overall strategy of the method is to sense the sparseness of the input signals by predicting the range of the MAC output results, while the range of the MAC output results is predicted through the additional device row so called as the sparsity sensing row. After that, the ADC precision configuration is modulated according to the sensed sparseness of the input signals, and energy efficiency improvement is finally achieved.

FIGURE 6

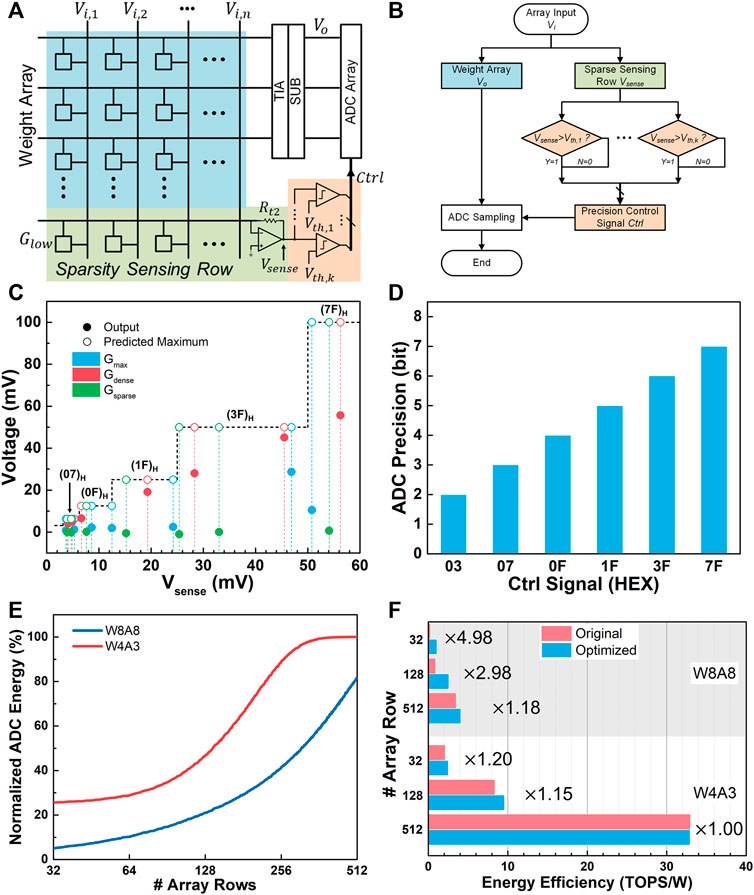
FIGURE 6. Scheme of (A) hardware implementation and (B) the flowchart of the proposed sparse-aware processing method. (C) Simulation results of the sparsity-aware processing circuit design with respect to different V_sense. (D) The configuration of the ADC precision according to different Ctrl signals. (E) The normalized ADC energy consumptions that use the proposed sparsity-aware processing method with respect to the array row sizes. (F) The comparison of the energy efficiency between the optimized MAC units with the sparsity-aware processing method and the original ones under W8A8 (gray) and W4A3 (white) cases.

Concretely, according to Ohm’s law and Kirchhoff’s current law, the output voltages of the sparsity sensing row V_sense and the regular rows for MAC operations V_o can be determined as follows:

$\begin{array}{c}{V}_{\mathrm{sense}}=R_{t2}{G}_{\mathrm{low}}{\displaystyle \sum }_{p=1}^n{V}_{i,p}\end{array},(6)$

$\begin{array}{c}{V}_{o,q}=R_t{\displaystyle \sum }_{p=1}^n{V}_{i,n}{G}_{\mathrm{pq}} \le R_t{G}_{\max }{\displaystyle \sum }_{p=1}^n{V}_{i,p}\end{array},(7)$

where n is the array accumulation number, G_low is the lowest conductance state of the memory devices, G_max stands for the maximum value of G, and R_t2 is similarly defined as the equivalent trans-impedance coefficient of the peripheral circuits of the sparse sensing row. Thus, through V_sense, the overall sparsity of the input signals can be sensed, and the maximum range of the regular MAC outputs V_o can be predicted.

Figure 6C demonstrates the SPICE simulation results of the proposed sparsity-aware processing circuit design of the W8A8 case. The V_sense equivalently reflects the different degrees of the overall sparsity of the inputs. The output values denote the regular output voltages of the MAC operations V_o, while the predicted maximum values are the predicted maximum range of V_o deduced from V_sense. Three typical examples of the device matrixes are evaluated, that is, the G_max with all maximum weights, G_dense with dense and all-positive weight elements, and G_sparse with sparse and random weights on behalf of the practical weight matrixes, respectively. The results demonstrate that under all circumstances, the output values are less than the predicted maximum values, which also proves that the sparsity sensing row can provide accurate estimates of the range of the output voltages.

Here, the thresholds of the V_sense that represent different degrees of the input sparsity and will generate different predicted results (enveloped as the black dotted line), are recorded as Vth, which can be derived as follows:

$\begin{array}{c}{V}_{\mathrm{th},k}=V_{\mathrm{FSR}}\times \frac{1}{2^k}\frac{R_{t2}{G}_{\mathrm{low}}}{R_t{G}_{\max }} , k=\mathrm{1,2,3},···\end{array}(8)$

where Vth,_k stands for the kth threshold voltage. If V_sense is less than the predetermined Vth_,k during the processing, then the kth MSB of the sampling results of the output voltages can be determined to zero. Thus, by comparing the V_sense with the properly prerecorded Vth, we can generate control signals Ctrl for the ADCs to dispense the highest few sampling bits, and modulate the required precision configuration dramatically, as shown in Figure 6D. Eventually, the corresponding energy or time consumption of the highest few bits can be eliminated, and the energy efficiency of the NVM MAC unit can be further improved for the quantized NvCNNs.

To evaluate the effect of the proposed method, the normalized ADC energy consumptions that use the proposed sparsity-aware processing method according to different array sizes are shown in Figure 6E. An impressive reduction in the ADC energy can be observed from the results. With an array row size of 128, the MAC unit can reduce the ADC energy consumption to 47% of the original within the W4A3 design. Since the W8A8 design possesses higher activation sparsity, the energy of the ADCs can even be reduced to around 21%. With an array row size of 512, the proposed sparsity-aware processing method fails in the case of the W4A3 design, but still provides over 18% reduction in the W8A8 condition. It is obvious that such a method cannot fulfill the purpose when the array becomes too large. However, 512 parallel rows have already covered up most advanced MAC chips. Moreover, a larger array size will intensify the parasite effects, and partial readout schemes are expected in extremely large arrays. In the proposed method, higher activation sparsity and lower array row size can both obtain better ADC energy reduction. The former is determined by the characteristics and training methods of the neural networks, while the latter will result in low parallelism of the MAC unit, which introduces a trade-off between the energy reduction and the processing parallelism, and require dedicated design for different application situations.

Notably, apart from the ADC energy reduction, an additional row of memory devices as well as the corresponding periphery circuits are introduced by the sparsity sensing method, which unfavorably increases the overall energy consumption. Using the same circuit module benchmarks as in Section 3 and the devices from Ref (Joshi et al., 2020), we analyze the improvement of the overall energy efficiency of the optimized MAC unit, as shown in Figure 6F. The optimized MAC unit can achieve an overall energy efficiency improvement of 4.98× to 1.18× with the array row size varying from 32 to 512 in the W8A8 design. As for the case of the W4A3 design, despite the relatively low sparsity and the already highly compressed hardware overhead, such a method can still provide 1.20× and 1.15× for the MAC units with 32 × 32 and 128 × 128 array size despite the quantized neural network.

Generally speaking, the proposed sparsity-aware processing method can achieve significant improvement in energy efficiency, especially in the cases when the activations are highly sparse and the original ADC overhead is severe. Higher energy efficiency improvement can be obtained when utilizing devices with lower conductance states. Moreover, such a method can be conducted in situ on the array without additional circuit module designs and is adaptable to many other commonly used input encoding approaches such as serial pulse sequences or modulated-width pulses (Hung et al., 2021). However, there are still some limitations to this method. First, the ratio of the energy reduction is directly related to the sparsity of the activations and the array size, thus, the advantages of the proposed method demand evaluation in the context of the practical applications. Second, this method might not be effective enough when the ADC consumption is not the main constraint of energy efficiency.

5 Conclusion

In conclusion, we have thoroughly studied the quantization coeffect of both weight and activation to the network performance and the corresponding hardware overhead and proposed an in situ sparsity-aware processing method for the energy-efficient hardware neural networks. We find that high-precision (higher than 6-bit) designs are not helpful to further improve the network performance, and will lead to serious hardware redundancy. Moreover, the high-precision designs impose much higher hardware implement requirements on the device variations and nonlinearities of the converters. Medium-precision quantization can obtain the optimal compromise between network accuracy and hardware overhead. For LeNet-5, 4-bit-weight and 3-bit-activation design is recommended as the hardware implementing solution, which can acquire 98.82% network accuracy on the MNIST dataset compared to the 99.08% accuracy of the full-precision one. The low-precision designs can significantly improve the energy efficiency and the robustness of the hardware implementation, but will also introduce relatively high accuracy loss, which makes them more favorable when the hardware reliability and overhead become the most concerning aspect. Moreover, we provided a novel sparsity-aware processing method in situ on the array to further improve the energy efficiency by taking advantage of the neural network sparsity and the device array characteristics. Such a method can reduce the heavy energy consumption of ADCs and achieve additional improvement in energy efficiency especially when the activations are highly sparse and the hardware overhead of ADCs is severe, e.g., 79%/53% ADC energy reduction and 2.98×/1.15× energy efficiency improvement for 8-bit-weight-and-8-bit-activation/4-bit-weight-and-3-bit-activation design with an array size of 128 × 128. However, a thorough evaluation in the context of particular application circumstances is still necessary to fully leverage this method. We believe our strategies and evaluations will provide valuable guidance on the design of hardware implementation of energy-efficient NvCNN for resource-constrained edge intelligence.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

HB proposed the method, conducted the analyses, and prepared the manuscript in this work. YQ and JC assisted in refining the idea and the analyses. LY assisted in the spice simulation analyses. JL and HZ helped with the figures and the manuscript. YL and XM conceived the topic and edited the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This manuscript was supported by the National Key Research and Development Plan of MOST of China (Grant Nos. 2019YFB2205100 and 2021ZD0201201), National Natural Science Foundation of China (Grant Nos. 92064012 and 51732003), Hubei Key Laboratory for Advanced Memories, Hubei Engineering Research Center on Microelectronics, and Chua Memristor Institute.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ali, M., Chakraborty, I., Saxena, U., Agrawal, A., Ankit, A., Roy, K., et al. (2021). A 35.5-127.2 TOPS/W dynamic sparsity-aware reconfigurable-precision compute-in-memory SRAM macro for machine learning. IEEE Solid. State. Circuits Lett. 4, 129–132. doi:10.1109/lssc.2021.3093354

CrossRef Full Text | Google Scholar

Ambrogio, S., Narayanan, P., Tsai, H., Shelby, R. M., Boybat, I., Di Nolfo, C., et al. (2018). Equivalent-accuracy accelerated neural-network training using analogue memory. Nature 558 (7708), 60–67. doi:10.1038/s41586-018-0180-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Bchir, M., Aloui, I., Hassen, N., and Besbes, K. (2021). “Low voltage low power 4 bits digital to analog converter,” in 2021 IEEE 2nd international conference on signal, control and communication (SCC), Tunisia, December 20–22, 2021, 81–85.

CrossRef Full Text | Google Scholar

Bi, M., Qian, Y., and Yu, K. (2015). “Very deep convolutional neural networks for LVCSR,” in Sixteenth annual conference of the international speech communication association, Dresden, Germany, September 6–10, 2015.

CrossRef Full Text | Google Scholar

Cai, Y., Tang, T., Xia, L., Li, B., Wang, Y., Yang, H., et al. (2019). Low bit-width convolutional neural network on rram. IEEE Trans. Comput. Aided. Des. Integr. Circuits Syst. 39 (7), 1414–1427. doi:10.1109/tcad.2019.2917852

CrossRef Full Text | Google Scholar

Chen, J., Lin, C.-Y., Li, Y., Qin, C., Lu, K., Wang, J.-M., et al. (2019). LiSiOX-based analog memristive synapse for neuromorphic computing. IEEE Electron Device Lett. 40 (4), 542–545. doi:10.1109/led.2019.2898443

CrossRef Full Text | Google Scholar

Chen, J., Pan, W.-Q., Li, Y., Kuang, R., He, Y.-H., Lin, C.-Y., et al. (2020). High-precision symmetric weight update of memristor by gate voltage ramping method for convolutional neural network accelerator. IEEE Electron Device Lett. 41 (3), 353–356. doi:10.1109/led.2020.2968388

CrossRef Full Text | Google Scholar

Deng, L., Li, G., Han, S., Shi, L., and Xie, Y. (2020). Model compression and hardware acceleration for neural networks: a comprehensive survey. Proc. IEEE 108 (4), 485–532. doi:10.1109/jproc.2020.2976475

CrossRef Full Text | Google Scholar

Fateh, S., Schönle, P., Bettini, L., Rovere, G., Benini, L., Huang, Q., et al. (2015). A reconfigurable 5-to-14 bit SAR ADC for battery-powered medical instrumentation. IEEE Trans. Circuits Syst. I. 62 (11), 2685–2694. doi:10.1109/tcsi.2015.2477580

CrossRef Full Text | Google Scholar

Girshick, R., Donahue, J., Darrell, T., and Malik, J. (2014). “Rich feature hierarchies for accurate object detection and semantic segmentation,” in Proceedings of the IEEE conference on computer vision and pattern recognition, Columbus, OH, June 23–28, 2014, 580–587.

CrossRef Full Text | Google Scholar

Guo, X., Bayat, F. M., Bavandpour, M., Klachko, M., Mahmoodi, M., Prezioso, M., et al. (2017). “Fast, energy-efficient, robust, and reproducible mixed-signal neuromorphic classifier based on embedded NOR flash memory technology,” in 2017 IEEE international electron devices meeting (IEDM), San Francisco, CA, December 2–6, 2017 (IEEE), 6.5. 1–6.5. 4.

CrossRef Full Text | Google Scholar

He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Deep residual learning for image recognition,” in Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, June 26–July 1, 2016, 770–778.

CrossRef Full Text | Google Scholar

Huang, X.-D., Li, Y., Li, H.-Y., Xue, K.-H., Wang, X., and Miao, X.-S. (2020). Forming-free, fast, uniform, and high endurance resistive switching from cryogenic to high temperatures in W/AlO x/Al 2 O 3/Pt bilayer memristor. IEEE Electron Device Lett. 41 (4), 549–552. doi:10.1109/led.2020.2977397

CrossRef Full Text | Google Scholar

Hung, J.-M., Jhang, C.-J., Wu, P.-C., Chiu, Y.-C., and Chang, M.-F. (2021). Challenges and trends of nonvolatile in-memory-computation circuits for AI edge devices. IEEE Open J. Solid. State. Circuits Soc. 1, 171–183. doi:10.1109/ojsscs.2021.3123287

CrossRef Full Text | Google Scholar

Jacob, B., Kligys, S., Chen, B., Zhu, M., Tang, M., Howard, A., et al. (2018). “Quantization and training of neural networks for efficient integer-arithmetic-only inference,” in Proceedings of the IEEE conference on computer vision and pattern recognition, Salt Lake City, UT, June 18–23, 2018, 2704–2713.

CrossRef Full Text | Google Scholar

Jain, S., Ranjan, A., Roy, K., and Raghunathan, A. (2018). Computing in memory with spin-transfer torque magnetic RAM. IEEE Trans. VLSI. Syst. 26 (3), 470–483. doi:10.1109/tvlsi.2017.2776954

CrossRef Full Text | Google Scholar

Jerry, M., Chen, P.-Y., Zhang, J., Sharma, P., Ni, K., Yu, S., et al. (2017). “Ferroelectric FET analog synapse for acceleration of deep neural network training,” in 2017 IEEE international electron devices meeting (IEDM), San Francisco, CA, December 2–6, 2017 (IEEE), 6.2. 1–6.2. 4.

CrossRef Full Text | Google Scholar

Joshi, V., Le Gallo, M., Haefeli, S., Boybat, I., Nandakumar, S. R., Piveteau, C., et al. (2020). Accurate deep neural network inference using computational phase-change memory. Nat. Commun. 11 (1), 2473. doi:10.1038/s41467-020-16108-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Krizhevsky, A., and Hinton, G. (2009). Learning multiple layers of features from tiny images. Toronto: University of Toronto.

Google Scholar

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2017). ImageNet classification with deep convolutional neural networks. Commun. ACM 60 (6), 84–90. doi:10.1145/3065386

CrossRef Full Text | Google Scholar

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learning. Nature 521 (7553), 436–444. doi:10.1038/nature14539

PubMed Abstract | CrossRef Full Text | Google Scholar

LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). Gradient-based learning applied to document recognition. Proc. IEEE 86 (11), 2278–2324. doi:10.1109/5.726791

CrossRef Full Text | Google Scholar

Li, C., Hu, M., Li, Y., Jiang, H., Ge, N., Montgomery, E., et al. (2018). Analogue signal and image processing with large memristor crossbars. Nat. Electron. 1 (1), 52–59. doi:10.1038/s41928-017-0002-z

CrossRef Full Text | Google Scholar

Li, W., Sun, X., Huang, S., Jiang, H., and Yu, S. (2022). A 40-nm MLC-RRAM compute-in-memory macro with sparsity control, on-chip write-verify, and temperature-independent ADC references. IEEE J. Solid-State Circuits, 1. doi:10.1109/jssc.2022.3163197

CrossRef Full Text | Google Scholar

Lin, P., Li, C., Wang, Z., Li, Y., Jiang, H., Song, W., et al. (2020). Three-dimensional memristor circuits as complex neural networks. Nat. Electron. 3 (4), 225–232. doi:10.1038/s41928-020-0397-9

CrossRef Full Text | Google Scholar

Luo, Y., Han, X., Ye, Z., Barnaby, H., Seo, J.-S., and Yu, S. (2020). Array-level programming of 3-bit per cell resistive memory and its application for deep neural network inference. IEEE Trans. Electron Devices 67 (11), 4621–4625. doi:10.1109/ted.2020.3015940

CrossRef Full Text | Google Scholar

Ma, W., Chiu, P.-F., Choi, W. H., Qin, M., Bedau, D., and Lueker-Boden, M. (2019). “Non-volatile memory array based quantization-and noise-resilient LSTM neural networks,” in 2019 IEEE international conference on rebooting computing (ICRC), San Mateo, CA, November 4–8, 2019 (IEEE), 1–9.

CrossRef Full Text | Google Scholar

Mahdavi, S., Ebrahimi, R., Daneshdoust, A., and Ebrahimi, A. (2017). “A 12bit 800MS/s and 1.37 mW Digital to Analog Converter (DAC) based on novel RC technique,” in 2017 IEEE international conference on power, control, signals and instrumentation engineering (ICPCSI), Chennai, India, September 21–22, 2017 (IEEE), 163–166.

CrossRef Full Text | Google Scholar

Miyahara, M., Lee, H., Paik, D., and Matsuzawa, A. (2011). “A 10b 320 MS/s 40 mW open-loop interpolated pipeline ADC,” in 2011 symposium on VLSI circuits-digest of technical papers, Chennai, India, June 15–17, 2011 (IEEE), 126–127.

Google Scholar

Murmann, B. (2021). ADC performance survey 1997-2021. [Online]. Available at: http://web.stanford.edu/∼murmann/adcsurvey.html (Accessed July 14, 2022).

Google Scholar

Pan, W.-Q., Chen, J., Kuang, R., Li, Y., He, Y.-H., Feng, G.-R., et al. (2020). Strategies to improve the accuracy of memristor-based convolutional neural networks. IEEE Trans. Electron Devices 67 (3), 895–901. doi:10.1109/ted.2019.2963323

CrossRef Full Text | Google Scholar

Qin, Y.-F., Kuang, R., Huang, X.-D., Li, Y., Chen, J., Miao, X.-S., et al. (2020). Design of high robustness BNN inference accelerator based on binary memristors. IEEE Trans. Electron Devices 67 (8), 3435–3441. doi:10.1109/ted.2020.2998457

CrossRef Full Text | Google Scholar

Rabuske, T. G., Nooshabadi, S., and Rodrigues, C. R. (2012). A 54.2 μW 5 MSps 9-bit ultra-low energy analog-to-digital converter in 180 nm technology. Analog. Integr. Circuits Signal Process. 72 (1), 37–46. doi:10.1007/s10470-011-9821-4

CrossRef Full Text | Google Scholar

Simonyan, K., and Zisserman, A. (2014). Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556.

Google Scholar

Sun, H., Zhu, Z., Cai, Y., Chen, X., Wang, Y., and Yang, H. (2020). “An energy-efficient quantized and regularized training framework for processing-in-memory accelerators,” in 2020 25th Asia and South Pacific design automation conference (ASP-DAC), Beijing, China, January 16–19, 2017 (IEEE), 325–330.

CrossRef Full Text | Google Scholar

Sze, V., Chen, Y.-H., Yang, T.-J., and Emer, J. S. (2017). Efficient processing of deep neural networks: a tutorial and survey. Proc. IEEE 105 (12), 2295–2329. doi:10.1109/jproc.2017.2761740

CrossRef Full Text | Google Scholar

Tang, J., Yuan, F., Shen, X., Wang, Z., Rao, M., He, Y., et al. (2019). Bridging biological and artificial neural networks with emerging neuromorphic devices: fundamentals, progress, and challenges. Adv. Mat. 31 (49), 1902761. doi:10.1002/adma.201902761

CrossRef Full Text | Google Scholar

Tang, T., Xia, L., Li, B., Wang, Y., and Yang, H. (2017). “Binary convolutional neural network on RRAM,” in 2017 22nd Asia and South Pacific design automation conference (ASP-DAC), Chiba, Japan, January 13–16, 2020 (IEEE), 782–787.

CrossRef Full Text | Google Scholar

Texas Instruments (2011). Ultra-low-Power, rail-to-rail out, negative rail in, VFB op amp. OPAx835 datasheet, Jan. 2011 [Revised Mar. 2021].

Google Scholar

Wang, L., Ye, W., Dou, C., Si, X., Xu, X., Liu, J., et al. (2021). Efficient and robust nonvolatile computing-in-memory based on voltage division in 2T2R RRAM with input-dependent sensing control. IEEE Trans. Circuits Syst. II. 68 (5), 1640–1644. doi:10.1109/tcsii.2021.3067385

CrossRef Full Text | Google Scholar

Xi, Y., Gao, B., Tang, J., Chen, A., Chang, M.-F., Hu, X. S., et al. (2020). In-memory learning with analog resistive switching memory: a review and perspective. Proc. IEEE 109 (1), 14–42. doi:10.1109/jproc.2020.3004543

CrossRef Full Text | Google Scholar

Xue, C.-X., Hung, J.-M., Kao, H.-Y., Huang, Y.-H., Huang, S.-P., Chang, F.-C., et al. (2021). “A 22nm 4Mb 8b-precision ReRAM computing-in-memory macro with 11.91 to 195.7 TOPS/W for tiny AI edge devices,” in 2021 IEEE international solid-state circuits conference (ISSCC), San Francisco, CA, February 13–22, 2021 (IEEE), 245–247.

Google Scholar

Yan, B., Li, B., Qiao, X., Xue, C.-X., Chang, M. F., Chen, Y., et al. (2019). Resistive memory-based in-memory computing: from device and large-scale integration system perspectives. Adv. Intell. Syst. 1 (7), 1900068. doi:10.1002/aisy.201900068

CrossRef Full Text | Google Scholar

Yao, P., Wu, H., Gao, B., Tang, J., Zhang, Q., Zhang, W., et al. (2020). Fully hardware-implemented memristor convolutional neural network. Nature 577 (7792), 641–646. doi:10.1038/s41586-020-1942-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Yip, M., and Chandrakasan, A. P. (2013). A resolution-reconfigurable 5-to-10-bit 0.4-to-1 V power scalable SAR ADC for sensor applications. IEEE J. Solid-State Circuits 48 (6), 1453–1464. doi:10.1109/jssc.2013.2254551

CrossRef Full Text | Google Scholar

Yue, J., Feng, X., He, Y., Huang, Y., Wang, Y., Yuan, Z., et al. (2021). “A 2.75-to-75.9 TOPS/W computing-in-memory NN processor supporting set-associate block-wise zero skipping and ping-pong CIM with simultaneous computation and weight updating,” in 2021 IEEE international solid-state circuits conference (ISSCC), San Francisco, CA, February 13–22, 2021 (IEEE), 238–240.

Google Scholar

Yue, J., Yuan, Z., Feng, X., He, Y., Zhang, Z., Si, X., et al. (2020). “14.3 A 65nm computing-in-memory-based CNN processor with 2.9-to-35.8 TOPS/W system energy efficiency using dynamic-sparsity performance-scaling architecture and energy-efficient inter/intra-macro data reuse,” in 2020 IEEE international solid-state circuits conference-(ISSCC), San Francisco, CA, February 16–20, 2020 (IEEE), 234–236.

CrossRef Full Text | Google Scholar