- Department of ECE, Purdue University, West Lafayette, IN, United States
Due to the diverse and mobile nature of the deployment environment, smart commodity devices are vulnerable to various spoofing attacks which can allow a rogue device to get access to a large network. The vulnerability of the traditional digital signature-based authentication system lies in the fact that it uses only a key/pin, ignoring the device fingerprint. To circumvent the inherent weakness of the traditional system, various physical signature-based RF fingerprinting methods have been proposed in literature and RF-PUF is a promising choice among them. RF-PUF utilizes the inherent nonidealities of the traditional RF communication system as features at the receiver to uniquely identify a transmitter. It is resilient to key-hacking methods due to the absence of secret key requirements and does not require any additional circuitry on the transmitter end (no additional power, area, and computational burden). However, the concept of RF-PUF was proposed using MATLAB-generated data, which cannot ensure the presence of device entropy mapped to the system-level nonidealities. Hence, an experimental validation using commercial devices is necessary to prove its efficacy. In this work, for the first time, we analyze the effectiveness of RF-PUF on commodity devices, purchased off-the-shelf, without any modifications whatsoever. We have collected data from 30 Xbee S2C modules used as transmitters and released as a public dataset. A new feature has been engineered through PCA and statistical property analysis. With a new and robust feature set, it has been shown that 95% accuracy can be achieved using only ∼1.8 ms of test data fed into a neural network of 10 neurons in 1 layer, reaching
1 Introduction
The fourth industrial revolution, fueled by low-power, high-speed modern communication systems has ushered in a new era of immersive and unprecedented user experience through smart devices. These devices are connected not only with each other but also to the cloud and are popularly known as the Internet of Things (IoT). The global IoT market is experiencing a rapid boost and according to a prediction by Norton, there will be around 21 billion connected devices by 2025 (Symanovich 2019). Researchers are already talking about the Internet of Everything (IoE) which essentially refers to people, data, and smart things connected to form an ecosystem that ensures a better and smarter lifestyle. The diverse application environment of the smart devices has rendered them vulnerable to a wide attacking surface. The weakest point in a network defines its overall security. The resource-limited, user-end devices are the weakest nodes of the IoT networks where a security compromise can provide access to a rogue device that can pose a massive threat to all the connected nodes and user data. So, the question of secure authentication before granting access to a large network is of increasing importance.
Traditional methods such as symmetric-key cryptography and asymmetric-key cryptography use secret private keys or public/private key pairs respectively, for encryption/decryption. Key-based methods require the storage of a secret key in a nonvolatile memory (NVM) or SRAM. However, they are vulnerable to different invasive/semi-invasive key-hacking attacks and side-channel attacks (Kocher et al., 1999; Quisquater and Samyde 2001; Hospodar et al., 2011). Multi-factor authentication (MFA) (Ting et al., 2015; Ometov et al., 2018) requires one or more verification factors (e.g., biometric factor, two-factor code from authentication app, etc.) along with the secret key. The widely-used open authentication (OAuth 2.0) protocol (OAuth 2.0 and OAuth 2022) for current IoT networks suffers from cross-site request forgery (CSRF) attacks (Barth et al., 2008; Siddiqui and Verma 2011). Both OAuth and MFA are inconvenient for large networks as they require manual verification. In addition to these vulnerabilities, the use of digital signatures also puts additional power and area burden which are typically small but could be significant for extremely energy and resource constraint edge devices.
To circumvent this, the idea of radio frequency physical unclonable function (RF-PUF) has been recently proposed (Chatterjee et al., 2019) using physical signature instead of or in addition to the digital signature. The concept of RF-PUF is explained in Figure 1. RF-PUF exploits the inherent device imperfections due to manufacturing process variation and other system-level nonidealities (e.g., LO frequency offset, I-Q mismatch, DC offset, attenuation, fading, Doppler shift, etc.) as unique physical signatures. These signatures are used as features and fed to a neural network at the receiver to train it. Once trained, this network can be employed at the receiver for authentication. RF-PUF does not demand any additional preamble, digital keys, or assistive communication medium for authentication purposes. The absence of an external security key or preamble makes RF-PUF highly resilient to different types of key-hacking attacks and alleviates the need for preamble obfuscation (Chacko 2017). Also, it does not require any secured memory block for key storage. Thus, both power and area overhead is reduced on the resource-constrained edge-node side of an asymmetric IoT network.
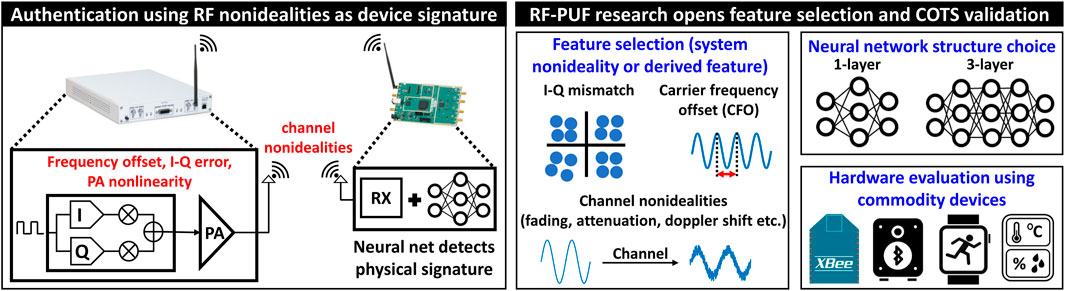
FIGURE 1. The concept of RF-PUF exploits the inherent physical signature embedded in the device which manifests itself as different imperfections, which are used as features to train a neural network at the receiver end for authentication. The challenges involve developing a proper feature set, choosing a proper neural network architecture, and evaluating the concept in real, commodity devices.
In (Chatterjee et al., 2019), the idea of RF-PUF was presented primarily based on simulation data using I-Q samples as features. However, the PUF output is stochastic in nature and it is very hard to accurately capture the device nonidealities in simulation. This calls for addressing the open research needs of experimental validation of RF-PUF and demonstration of high-accuracy on devices found ‘in-the-wild’. In this work, we address both these research problems by 1) analyzing the efficacy of RF-PUF on unmodified commodity devices and 2) introducing effective feature selection to increase RF-PUF accuracy
It has been shown that 95% accuracy can be achieved even with a lightweight, single-layer neural network with 10 neurons and
1.1 Our Contribution
In this work, through thorough statistical analysis of unmodified commodity devices, we have found an optimum feature that improves the accuracy of RF-PUF significantly on a suite of commodity hardware devices leading to
(1) Feature engineering: Principal component analysis has been performed on the existing feature set found in the literature to find the dominant feature. Through moment analysis on the dominant feature (i.e. carrier frequency offset) we demonstrate that the addition of a feature called COV (ratio of standard deviation and mean of carrier frequency offset) significantly helps in achieving high
(2) Highest accuracy achieved with unmodified COTS devices: 30 Xbee S2C modules have been used without the help of any assisting communication preamble or any modification to the devices whatsoever. Using data received over a wireless channel with a suitable feature set and a lightweight neural network, 99.8% accuracy can be achieved which, to our best knowledge, is the highest accuracy using this many commodity COTS devices considering the wireless channel (Section 4.4).
(3) RF-PUF established as a strong PUF: Any distinct PUF class is identified through some properties that make it a separate class. They include constructability, evaluability, uniqueness, reliability, and identifiability. We have explored these properties for RF-PUF in detail, calculated intra-PUF and inter-PUF hamming distances and in an extensive test of 41238000 cases, we have shown that the probability of proper identification of an RF-PUF instance is 0.9987. This is the first time analysis of RF-PUF as a PUF class which experimentally demonstrates RF-PUF as a strong and unique PUF class by itself (Section 6).
(4) Performance evaluation using popular machine learning algorithms and comparison with neural network (NN) based approach. It has been shown that even a lightweight NN with a single hidden layer can handle
(5) Wireless channel variability analysis on the accuracy of RF-PUF and the effect of network depth on accuracy with and without a wireless channel has been presented. Discussion on possible important attack models and the robustness of RF-PUF against such attacks (Section 5.5).
(6) Public Dataset: Our collected data have been released as a public dataset for the whole community to explore and experiment with (Section 3.3).
The rest of the paper is structured as follows: Section 2 provides relevant works on RF fingerprinting and device authentication. Section 3 provides an overview of our experimental setup, data collection, and data processing method. Section 4 presents a new feature set development using statistical analysis and corresponding performance enhancement. Section 5 explores the design space in detail. Section 6 analyzes various PUF properties in the context of RF-PUF. Section 7 discusses possible attack models and the resilience of RF-PUF against them. Finally, section 8 concludes this paper.
2 Related Works
Traditional RF fingerprinting approaches use modulation domain metrics, statistical parameters, transient properties, wavelet-based approaches, etc. In (Brik et al., 2008), authors used various modulation domain metrics such as frequency and IQ offset, magnitude and phase error, sync correlation, etc. to propose a radio device identification method called PARADIS (PAssive RAdiometic Device Identification System). They collected data from 138 Atheros network interface cards (NIC) and tested their proposed methods (SVM-based and kNN-based) on the ORBIT testbed facility (ORBIT 2022). They achieved an error rate of 3% for 138 NIC classification. In (Zhuo et al., 2017) authors have used IQ imbalance-based features for device fingerprinting. Based on simulation data from 5 transmitters and 400 signals from each of them, they have shown that they can achieve
Several fingerprinting methods use transients during device start-up and extract features from them. But before feature extraction, proper detection of the transients is a major challenge and several approaches for that are described in (Shaw and Kinsner 1997; Hall et al., 2003). Authors in (Danev and Capkun 2009) have used data from 50 COTS devices (Tmote Sky sensor) and FFT-based Fisher features to show an accuracy of
There are other works that have used various time and frequency domain properties of individual transmitters for RF fingerprinting (Rasmussen and Capkun 2007; Scanlon et al., 2010; Nguyen et al., 2011; Bihl et al., 2016; Vo-Huu et al., 2016; Peng et al., 2018; Xie et al., 2018). However, both time and frequency domain analysis have their limitations in the form of detecting the start and end of the transients, high oversampling ratios, and the need for fixed preambles to avoid data dependency. MAC layer and other upper layers of the communication protocol have also been used for RF-fingerprinting (Xu et al., 2016a). However, device identifiers in upper layers like IMEI number, IP address, MAC address, etc. can be spoofed (Chomsiri 2007; Kumar et al., 2015; Alotaibi and Elleithy 2016; Wang and Yang 2017). Several statistical parameter-based approaches have also been proposed. For example, authors in (Patel 2015) have used various statistical features to identify 4 Xbee devices. Using a Random Forrest classifier (Pal 2005), they could achieve 97% accuracy for SNR ≥ 10 dB. Another work (Lukacs et al., 2015) has used RF-DNA (Radio Frequency Distinct Native Attribute) dependent RF fingerprinting. RF-DNA uses various statistical features. For a 7 class dataset, authors have achieved an average accuracy of 81% for the MDA/ML classifier. For real-time device authentication, authors in (Bari et al., 2021a) have used a dynamic irregular clustering approach. One attractive feature here is that this algorithm learns incrementally with more input data.
Recently deep learning-based RF fingerprinting has gained popularity. Different types of deep networks (convolutional neural networks or CNN (Albawi et al., 2017; Kim 2017), recurrent neural network or RNN (Medsker and Jain 2001; Liu et al., 2016), generative adversarial networks or GAN (Mao et al., 2017; Creswell et al., 2018), etc.) are being used extensively for RF device identification and authentication. Hanna et al. utilized power amplifier nonlinearity with deep learning to fingerprint RF devices (Hanna and Cabric 2019) using simulation data. In (Sankhe et al., 2020), authors proposed a new method called ORACLE (Optimized Radio clAssification through Convolutional neuraL nEtworks) using the AlexNet-like CNN framework. With data from 16 USRP X310 transmitters, they could achieve 87.13 and 99% accuracy for the static and quasi-static channels respectively. However, wireless data are contaminated with noise and interference, any use of the RF data without processing always posits a risk of huge performance drop in scenarios where environmental nonidealities can go beyond the estimation that was used while designing the network. Processing data, extracting a proper feature set, and unraveling the mystery of the design space can render a robust authentication method that is less vulnerable to environmental factors and provides more flexibility to the designer. That is why RF-PUF performs better than the CNN-based approach as shown in (Bari et al., 2021b). In (Soltani et al., 2020), authors have used multiple deep networks and integrated their outputs to make a final prediction. They collected data from 7 UAVs or drones (DJI M100) and got maximum accuracy of 99% with data augmentation. Using data from 5 USRP devices and bispectrum of the received signal as the feature, authors in (Ding et al., 2018) have achieved 75% accuracy with a custom CNN. Another work (Peng et al., 2020) also used custom CNN with DCTF (Differential Constellation Trace Figure) as features to fingerprint 16 Xbee devices. For SNR ≥ 15 dB, they achieved 90% accuracy. In (Zong et al., 2020), authors have used CNN to identify 5 transmitter devices. Although they achieved 99% accuracy, their dataset is quite small.
A much bigger and more extensive dataset is the DARPA RFMLS dataset, containing data from 10000 devices (Jian et al., 2020). The authors have presented two architecture based on AlexNet and ResNet-50 to perform multiple learning tasks. On this dataset, another group of researchers has used a modified CNN called ADCC (augmented dilated causal convolution network) (Robinson et al., 2020). Apart from these traditional or modified CNN-based methods, there are some works reported in the literature that use GAN. For example, AC-WGAN (Auxiliary Classifier Wasserstein Generative Adversarial Networks) achieves 95% accuracy for UAV classification (Zhao et al., 2018). For a low number of devices (8 USRP B210), authors have achieved 99.9% accuracy using GAN (Roy et al., 2019). Some other prominent works for RF fingerprinting using deep learning are mentioned in (O’Shea and Hoydis 2017; Wang et al., 2017; Wang et al., 2018; Zhang et al., 2019). A detailed review of RF fingerprinting methods can be found in (Xu et al., 2016b; Guo et al., 2019; Jagannath et al., 2022). Our experimental study in this work shows
3 Experimental Setup
3.1 Physical Device Setup
For experimental validation, 30 XBee S2C modules are chosen (IEEE 802.15.4 standard) which is designed for industrial and commercial use. Figure 2A shows the Xbee devices whereas Figure 2B, and Figure 2C show the block diagram and the actual setup. The TX and RX are kept 1 m apart. Using SMA cable, a HackRF One software-defined radio (SDR) module has been connected either to the TX (case 1) or to the RX (case 2) to extract data excluding (case 1) or including (case 2) wireless channel.
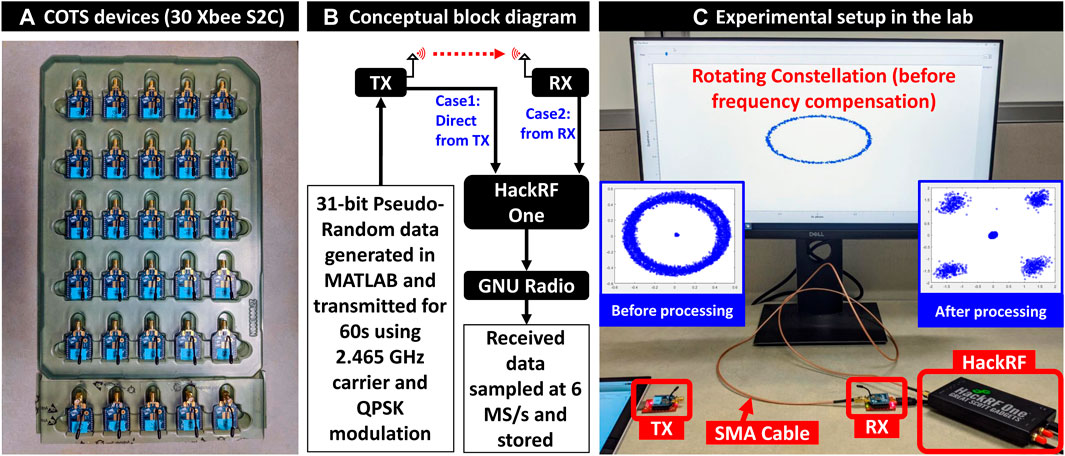
FIGURE 2. (A) Commodity off-the-shelf devices (30 Xbee S2C modules) used as transmitters for data collection. (B) Conceptual experimental setup. (C) Actual experimental setup in the lab. The TX and RX are placed 1 m apart (they are close here for image capturing purposes only) and a HackRF module was used to collect data either from the TX (case 1) or RX (case 2). GNU Radio records the collected data and shows a live constellation (visible on-screen). The rotating constellation is later processed in MATLAB through coarse and fine frequency compensation.
3.2 Data Collection and Filtering Noise
A 31-bit pseudo-random bit sequence (PRBS) is generated in MATLAB and fed to each TX which transmits this data for 60 s with QPSK modulation at 2.465 GHz and 230,400 bps baud rate. These data were captured in a Xbee RX module. Simultaneously, data were also captured by a HackRF one software-defined radio (SDR) module, sampled at 6 MSps, and stored by GNU Radio. The captured data are divided into several frames, each containing a number of samples. From the constellation diagram of the frame data (Figure 3), it is found that some frames have no significant data points and contain only noise as the Xbee devices transmit data intermittently due to their buffer limitation. These blank frames containing only noise were discarded.
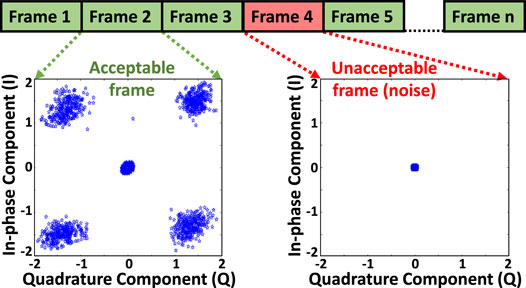
FIGURE 3. Grouping collected data in a number of frames and filtering of data for acceptable frames. This step is required as the Xbee module transmits data on an interval.
3.3 Public Dataset
This dataset contains raw data collected from 30 Xbee S2C transmitters for both cases (excluding and including the channel) in binary format. The total size of the dataset is 155.4 GB (each transmitter data is ∼2.5 GB). It can be downloaded from Sparclab RF-PUF Dataset (Bari and Sen 2022).
4 Feature Extraction
4.1 Initial Feature Set
In our work, CFO and I-Q data are taken as features just as in the original RF-PUF paper (Chatterjee et al., 2019). The previously generated frames are filtered using matched filtering, frequency compensated (both fine and coarse), and finally synchronized using timing recovery. In this process, CFO is found as a byproduct. Along with CFO, the compensated in-phase and quadrature-phase components in four quadrants are used as features. The 9 features (CFO + 4 I-components + 4 Q-components) from each frame and 1,000 frames from each TX lead to a feature set of 9 × 1000. The final feature matrix is a combination of these feature sets from all 30 devices and has a size of 9 × 30000.
4.2 Accuracy With Carrier Frequency Offset and I-Q Features
The whole feature data are divided into 70%, 15%, and 15% respectively for training, validation, and test purposes and fed into a neural network (NN). The performance of the neural network is tested by varying the number of neurons and hidden layers. Figure 4A shows the accuracy of the trained model for different neural networks. The accuracy is less than 75% in all test cases. Since exploring different NN configurations does not provide expected accuracy, our choice here is to: 1) form an improved feature set to be used with the NN 2) use different machine learning (ML) algorithms 3) use more data. We first search for an improved feature set for better accuracy. Later, the effect of more data is shown in subsection 5.1, 5.2 and a comparison of different ML algorithms and NN is discussed in subsection 5.4.
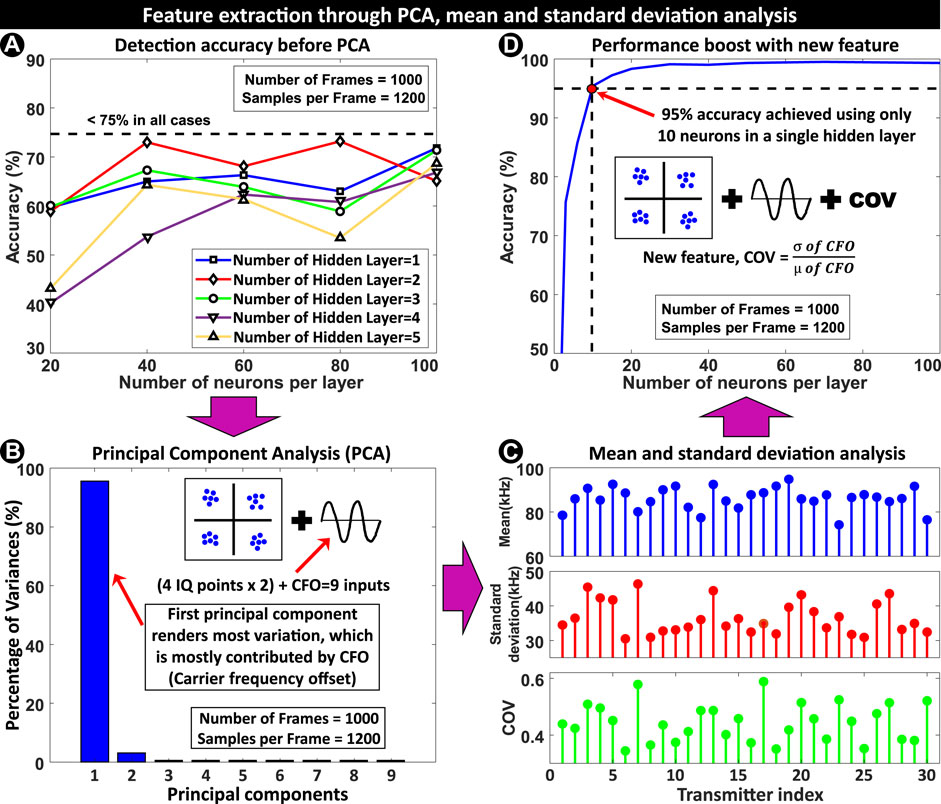
FIGURE 4. (A) Accuracy vs. the number of neurons in each hidden layer. Even after increasing the number of hidden layers, the accuracy remains
4.3 Statistical Analysis
4.3.1 Principal Component Analysis
We start the investigation by performing Principal Component Analysis (PCA) with feature matrix as input (each feature represents one input dimension). Figure 4B shows the principal components and their contribution to the variances. The first principal component (PC) contributes to most of the variances and the input to PC mapping reveals that the CFO is the most dominant feature. So, an in-depth statistical property analysis of the CFO can help in deriving a new feature.
4.3.2 Moment Analysis
Since CFO varies from frame to frame (i.e., with time), it is intuitive to look at the moments of their distribution. Specifically, we want to look at first and second-order moments (mean and variance). Figure 4C shows the absolute values of mean and standard deviation (square root of variance) of CFO. These parameters vary significantly from TX to TX in most cases. And even if for any two TX, the mean is similar, the standard deviation is different, and vice versa. If they can be combined to form a new feature, that can provide significant discrimination among transmitters and lead to much better accuracy. In statistics, the ratio of standard deviation and mean is known as the coefficient of variation. So, using this statistical parameter, we form a new feature named the coefficient of frequency offset variation (COV) which is defined as:
4.4 Performance Using Coefficient of Frequency Offset Variation Feature
COV is included as the 10th feature in our existing feature matrix. From PCA analysis, it is already revealed that the I-Q features contribute to much fewer variances and can be discarded by trading some accuracy. Since our goal is to achieve maximum possible accuracy, we still keep them as features. Also, I-Q values contain channel information, which will help the NN to compensate for the wireless channel (channel effect is explained in subsection 5.5).
After including COV as the 10th feature, our neural network was trained, validated, and tested again with the new feature matrix. Figure 4D shows that the performance of the network has improved drastically. With just a single hidden layer,
5 Evaluation of Design Parameters
5.1 Effect of Number of Samples
Figure 5A shows the plot of detection accuracy versus the number of samples in each frame for different neural networks. The general trend (Bold red arrow) is that, for each NN configuration, detection accuracy improves with the increase in the number of samples (along the x-axis). This is expected because a higher number of samples provide more information and hence better performance. We want to mention that there might be some temporary sporadic drops in accuracy (as in the red line where accuracy slightly drops from 50 to 100 samples), but that does not represent the general trend which clearly shows that more samples translate to better accuracy. Also,
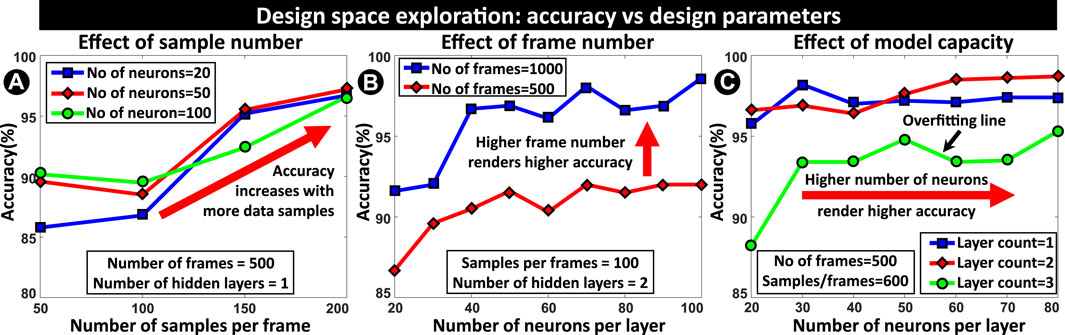
FIGURE 5. (A) Detection accuracy vs. the number of samples per frame for different neural networks which shows a trend of accuracy improvement (indicated by red arrow) with the increase in sample number. (B) Detection accuracy for different frame numbers shows higher frame number renders better performance. (C) Detection accuracy versus the number of neurons per layer. The general trend shows that accuracy improves with the increase in the number of neurons in each layer. Also, accuracy typically improves with more hidden layers until the higher model order causes overfitting and degrades performance.
5.2 Effect of the Number of Frames in Feature Set
Figure 5B shows accuracy versus the number of neurons per layer for two different frame numbers, 500 and 1000. With a higher frame number, the information content of each transmitter device increases. As the NN gets more information about the device, its performance improves and the detection accuracy gets better as shown by the blue (1000 frames) and red lines (500 frames) respectively. We can generalize the previous subsection (sample number effect) and this subsection as this: more data render better performance.
5.3 Effect of the Neural Network Parameters
Figure 5C shows the plots of accuracy versus the number of neurons in each hidden layer. As the number of neurons increases along the x-axis, accuracy, in general, gets better (there might be sporadic peaks or drops as in the case of the blue line with an outlier peak at 30 neurons, but this does not represent a general trend). Also, as the number of hidden layers increases, the network performs better initially (from blue to red line), but later it creates an overfitting problem (the green line) where the model capacity is too large compared to data. This phenomenon directly manifests itself as a degradation in performance. Hence, there is an optimum model capacity up to which accuracy increases, and beyond that accuracy drops.
5.4 Using Simple Machine Learning Algorithm
It has been observed that the COV values vary significantly among different transmitters. When a simple feature displays a significant separation among different classes, it can be modeled with a complex if-else ladder structure. This implies that even simple ML algorithms (e.g. Tree) can show good results. Figure 6A shows that some popular ML algorithm achieves
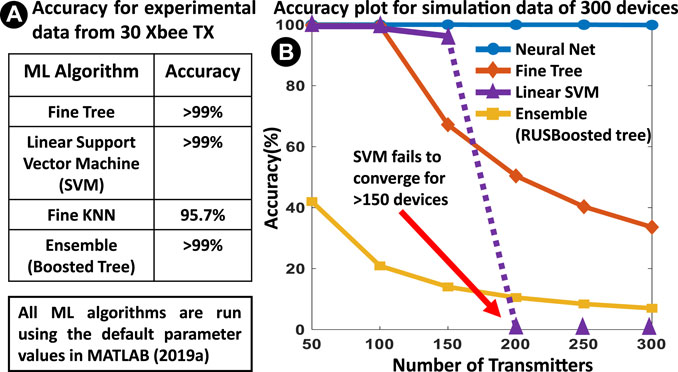
FIGURE 6. (A) Popular ML algorithms show high accuracy for 30 Xbee devices. (B) The accuracy of simple ML networks drops when the number of TX is large, wherein the neural network still holds up with
The true power of the neural network comes into play when the number of TX increases as shown in Figure 6B. For this, features are generated for 300 TX devices following a Gaussian distribution (as in (Chatterjee et al., 2019)) with the same mean and variance as that of the original 30 TX devices, for both inter and intra-class variations. Figure 6B shows that as the number of TX increases, accuracy falls after a certain point (
5.5 Effect of Wireless Channel
So far, nonidealities due to TX were considered and the wireless channel was ignored (TX and RX are connected via SMA cable). But the channel itself adds some nonidealities. Here, the effect of a static wireless channel (1 m of fixed TX-RX separation) has been analyzed. Figure 7 shows accuracy versus neuron number in a single layer, with and without the wireless channel. For iso-accuracy of 95%, wireless channel demands slightly higher model capacity (10 vs. 15 neurons). But when the number of neurons increases
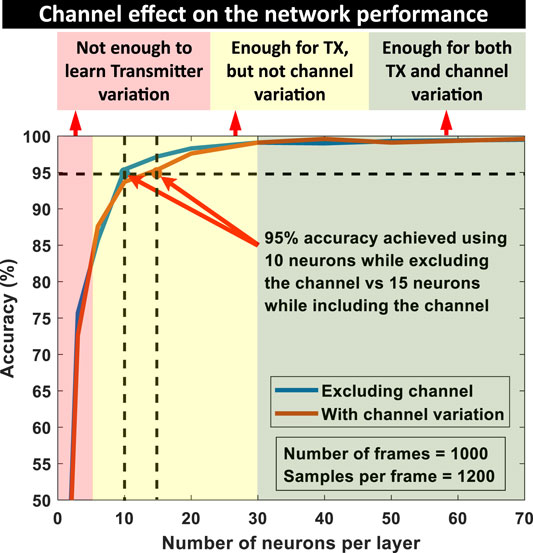
FIGURE 7. Comparison of the network performance in the cases of including and excluding the wireless channel data. The network needs 15 neurons compared to 10 neurons in a hidden layer to achieve 95% accuracy for the case where the channel is considered. But with higher model capacity, both lines converge and the network learns the channel effect on data. d the network learns the channel effect on data. The light red box shows the region where the network fails to learn transmitter variation, light yellow box shows the region where the network learns transmitter variation but fails to learn the variation due to the wireless channel. The light green box shows the region where the network learns both the transmitter and channel variation properly.
In one of our recent works (Bari et al., 2021b), we applied RF-PUF on the ORACLE dataset which contains data for 16 USRP X310 TX for both static and quasi-static (variable TX-RX separation) cases with a channel length varying from 2 to 62 ft. We have shown that RF-PUF achieves 100% accuracy up to 38 ft and
5.6 Computational Complexity of RF-PUF
RF-PUF does not add any additional circuitry on the TX side. Hence there is no extra computational burden at the TX end. On the receiver side, it employs just a multilayer perceptron (MLP) or NN along with the standard receiver. The standard receiver corrects the received signal and in the process discards various system-level nonidealities which are used as features to the NN. Hence, the computational complexity of RF-PUF is that of a neural network. For an n-dimensional input (n = 10 for our case), the training phase (done only once) has a computational complexity on the order of
6 Analysis of PUF Properties
PUF response to a particular challenge is a probabilistic function. In this section, we will determine intra-PUF hamming distance and inter-PUF hamming distance and discuss various PUF properties ((Maes 2013; Plusquellic 2018)) in light of those distances.
6.1 Constructability
A PUF class
6.2 Evaluability
A PUF class
6.3 Inter PUF Distance - Uniqueness
Uniqueness refers to how different each instance of a PUF class
Here,
To calculate HDinter, the first 1000 frames from each of the transmitters are taken. Each frame contains 3600 samples. Our features remain unchanged: CFO, eight I-Q component values, and COV. But after taking 10 features from each of 1000 frames, instead of using them as a feature matrix for each transmitter, the mean values of the features are taken across all the frames. This means that instead of representing each transmitter as a 10 × 1000 feature matrix, it is represented as a 10 × 1 feature vector. The reason for taking the average value across the frames is that the frames have an associated timestamp with them i.e., each frame data are collected from time to time. So, each frame faces slightly different environmental conditions such as heating of the transmitter due to data transmission for a long time, external interference, noise, etc. Averaging the feature values across a large number of frames mitigates the environmental factors, especially noise. Also, taking the first 1000 frames from each transmitter ensures the same initial heating pattern across devices. So the final outcome is that the feature vector for each transmitter has a very similar environmental factor α, which is one of the conditions of inter-chip hamming distance calculation.
After taking the feature vector from each transmitter, the Euclidean distance was calculated in ten-dimensional feature space as hamming distance. For pufm, let us denote CFOm = carrier frequency offset, COVm = coefficient of frequency offset variation, Ik,m = in-phase component in the kth quadrant, and Qk,m = quadrature-phase component in the kth quadrant. Then distance dm,n between pufm and pufn instances is given by:
The inter-chip distances were calculated for each transmitter with respect to all 30 transmitters (including the chip under test), which leads to a 30 × 30 symmetric matrix (upper and lower triangular matrices with same values since dm,n = dn,m = inter-chip distance between pufm and pufn) with a principal diagonal of zeros (self-distance). It is found that the worst-case scenario with minimum distance, HDinter,min = 0.2307, and the best-case scenario with maximum distance, HDinter,max = 10.149.
In literature, often a mean inter-puf distance, μinter, is reported which is the average of all HDinter. The formula is:
Where Npuf is the number of puf instances (Npuf = 30 for us), and Nchal is the number of challenges (Nchal = 1, since we are not varying our challenge). Using this formula, we find that μinter = 3.703.
Figure 8C shows the probability mass function distribution of
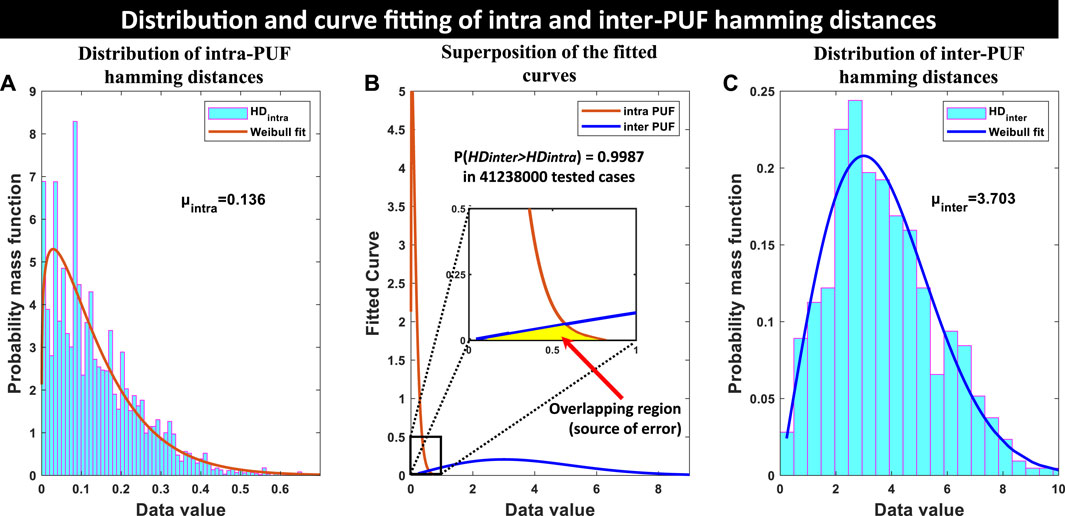
FIGURE 8. Data distribution of (A) intra-PUF hamming distances and (C) inter-PUF hamming distances. Due to skewness, Weibull distribution fitting is a more accurate representation in these cases. (B) The two Weibull curves are superimposed on top of each other. It is seen that there is a very slight overlap (yellow region) between the curves which is shown in a zoomed inset. Although trivial, this overlapping is the source of the detection error.
6.4 Intra PUF Distance–Reliability
PUF responses are in general dependent on various environmental factors that render any PUF instance response as a probabilistic function. This means that a particular PUF instance can provide slightly different values of features based on varying environmental conditions. For authentication purposes, this poses an issue. Reliability refers to how resilient a PUF instance is against environmental factors e.g. noise, interference, temperature, supply voltage, etc.
A measurement metric that is used to represent how reliable a particular instance of a PUF class
Here,
To calculate HDintra, we follow two steps. Let us consider one particular PUF instance pufm. In step 1, the first 1000 frames (frame number 1 to frame number 1000) were taken from pufm, each frame containing 3600 samples. Then mean values of the previously mentioned ten features were taken just as before to represent it as a 10 × 1 feature vector. Let us represent this vector as fv,1. Then in step 2, the first 5 frames are skipped and the next 1000 frames are taken from frame number = 6 to frame number = 1005. Step 1 is repeated here to get the next feature vector fv,2. Then next 1000 frames are taken from frame number = 11 to frame number = 1010 and a feature vector fv,3 is formed. This process is repeated 80 times to form 80 different feature vectors fv,α; α = 1, 2, … , 80. These 10 × 1 feature vectors are stacked together to form a feature vector set fset,m of size 10 × 80 for pufm. The whole process is then repeated for all 30 devices.
The purpose of taking frame-shifted or time-shifted frame groups is to consider the time factor. Each frame has a duration of 0.6 ms, so 5 frames gap in between two frame groups renders a time difference of at least 3 ms (in reality the difference is much larger since the transmitter transmits data for a small time and most of the frames are just noise which are filtered in data pre-processing step). The 80 time-spaced frames, in reality, cover almost half a minute. Our 2.4 GHz clock will have LO drift cycle time in the nanoseconds range. Hence, half-minute data can incorporate significant environmental factors into frame data. So, it can be assumed that the feature vectors fv,α; α = 1, 2, … , 80 in feature vector set fset,m of pufm represents α = 80 different environmental conditions.
Now, for each instance pufm, Euclidean distance is calculated in 10-dimensional feature space among the feature vectors in the feature vector set using Eq. 1. This results in a symmetric matrix of size 80 × 80 with a principal diagonal of zeros. This process is repeated for other transmitters as well. Essentially it gives us 30 matrices of size 80 × 80 for intra-PUF distances. In the best-case scenario, the minimum distance is HDintra,min = 7.23 × 10–5 and in the worst case scenario, the maximum distance is HDintra,max = 0.73.
Figure 8A shows the probability mass function distribution of
Finally, a mean intra-PUF distance, μintra, is calculated which is the average of all HDintra. The formula is:
Where Npuf is the number of puf instances (Npuf = 30 for us), Nchal is the number of challenges (Nchal = 1, since we are not varying our challenge) and α is the number of environmental conditions (α = 80 in our study). Using this formula, it is found that μintra = 0.136.
6.5 Identifiability
In the previous two subsections, both inter-PUF and intra-PUF hamming distances and their mean values: μinter = 3.703 and μintra = 0.136 are calculated. Their comparison shows that μinter > μintra, which establishes that on average the PUF instances can be distinguished from each other. But the mean value does not depict the full story. Figure 8B shows the fitted distribution curves superimposed on each other. The brown curve (intra-PUF distribution) is skewed to the left and the blue curve (inter-PUF distribution) is skewed to the right and they mostly cover different regions. However, there is slight overlapping between them which is shown in the inset as a zoomed version of the overlapping area. Ideally, there should be no overlapping. But in a practical scenario, this overlapping region is the source of detection error.
From the definition of identifiability, a PUF class
In the previous two subsections,
This is a very high probability and close to 1. This proves that RF-PUF has strong identifiability and this property along with reliability, uniqueness, constructability, and evaluability manifests RF-PUF as a distinct PUF class. This is the first-ever experimental validation of RF-PUF as a distinct and strong PUF class by itself.
7 Possible Attack Models on RF-PUF
RF-PUF does not store any digital key and hence, is not susceptible to malicious PUF models which assume that the adversary can have access to all the challenge-response pairs through a built-in logger software/implanted Trojan. However, there is a possibility of a machine learning-based attack that needs to be discussed (Figure 10). For RF-PUF, ML attack is a two-step process:
• Step 1: model/profile the victim TX (Unsupervised)
• Step 2: use that model for spoofing/replay attacks
In step 1, the rogue device tries to learn the feature/parameter values of the victim TX. Unlike the intended RX, this is an unsupervised problem for the attacker. We have utilized k-means clustering to divide the feature map into 30 clusters and compare the predicted and true labels (Figure 9). The process was repeated 1,000 times as k-means isn’t unique without specific conditions. Our analysis shows that clustering achieves
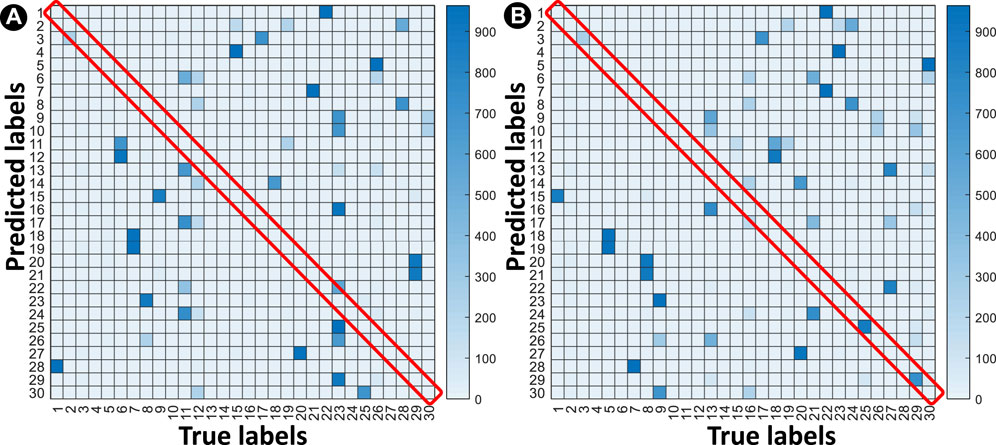
FIGURE 9. Heatmap of unsupervised learning in the attacker using k-means clustering. (A) The worst-case accuracy of 0.09% and (B) the best-case accuracy of 6.8%. Repeated clustering 1000 times shows 3.63% accuracy on average.
If somehow the attacker succeeds in step 1, then in step 2, the attacker needs to produce an RF signal that contains the same imperfections as the victim TX with high accuracy. This requires a high speed and high-resolution circuitry. Figure 10 shows that the physical signature of the transmitter, S, goes through transformation TTX at TX and TRX at RX. The transformations in the attacker are TA, TML1, TML2, and TD respectively. Full transformation for the original device is TRX (TTX(S)) and for the adversary is TRX (TD (TML2 (TML1 (TA (TTX(S)))))). The adversary ML2 framework needs to make these two transformations equal by undoing the effect of its ADC/DAC which requires almost infinite resolution, rendering it practically impossible (typical ADC/DAC are 8/16-bit). This Resolution limitation in ADC/DAC and bandwidth limitation in filters and other RF components also prevent replay attack, which requires the attacker to convert the TX signal in the digital domain, incorporate malicious contents and then transform it back into the RF domain with very high precision. Further analysis of precision requirements for a practical attack will be included in future work. The robustness of RF-PUF against malicious PUF model, ML attack, and replay attack proves its strong candidacy of employment for RF security.
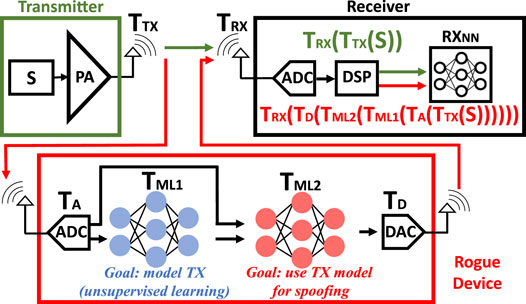
FIGURE 10. ML attack model. Adversary ML networks cannot undo the effect of ADC and DAC which requires extremely high precision and resolution, making the attack impractical.
8 Conclusion
In this work, data collected from off-the-shelf commodity components (30 Xbee modules) were used to develop a new feature called the coefficient of frequency offset variation (COV) through PCA and moment analysis. The new feature leads to 95% accuracy for a single hidden layer with 10 neurons and
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/SparcLab/Sparclab-RF-PUF-Dataset.
Author Contributions
PA prepared an initial framework of 4 Xbee devices for data collection. MB has set up the test environment, prepared and conducted the experiment with 30 Xbee modules in a renewed framework, processed data, performed the statistical analysis, feature engineering, and evaluated performance. BC helped both PA and MB in setting up the experimental framework and data processing as well as guiding with technical feedback. SS supervised the whole work. MB wrote the manuscript while both BC and SS helped in writing the paper, reviewing and updating it as needed.
Funding
This work was supported in part by the National Science Foundation, under Grant 1935573.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Albawi, S., Mohammed, T. A., and Al-Zawi, S. “Understanding of a Convolutional Neural Network,” in 2017 international conference on engineering and technology (ICET) (IEEE), 1–6. doi:10.1109/icengtechnol.2017.8308186
Alotaibi, B., and Elleithy, K. (2016). A New Mac Address Spoofing Detection Technique Based on Random Forests. Sensors 16 (3), 281. doi:10.3390/s16030281
Bari, M. F., and Anowarul Fattah, S. (2020). Epileptic Seizure Detection in EEG Signals Using Normalized IMFs in CEEMDAN Domain and Quadratic Discriminant Classifier. Biomed. Signal Process. Control. 58, 101833. doi:10.1016/j.bspc.2019.101833
Bari, M. F., Chatterjee, B., and Sen, S. (2021a). “DIRAC: Dynamic-IRregulAr Clustering Algorithm with Incremental Learning for RF-Based Trust Augmentation in IoT Device Authentication,” in 2021 IEEE International Symposium on Circuits and Systems (ISCAS) (IEEE), 1–5.
Bari, M. F., Chatterjee, B., Sivanesan, K., Yang, L. L., and Sen, S. (2021b). “High Accuracy RF-PUF for EM Security through Physical Feature Assistance Using Public Wi-Fi Dataset,” in 2021 IEEE MTT-S International Microwave Symposium (IMS), 108–111. doi:10.1109/ims19712.2021.9574917
Bari, M. F., and Sen, S. (2022). Sparclab RF-PUF Dataset,” GitHub. [Online]. Available at: https://github.com/SparcLab/Sparclab-RF-PUF-Dataset (Accessed March 6, 2022).
Barth, A., Jackson, C., and Mitchell, J. C. (2008). “Robust Defenses for Cross-Site Request Forgery,” in Proceedings of the 15th ACM conference on Computer and communications security, 75–88. doi:10.1145/1455770.1455782
Bertoncini, C., Rudd, K., Nousain, B., and Hinders, M. (2012). Wavelet Fingerprinting of Radio-Frequency Identification (Rfid) Tags. IEEE Trans. Ind. Electron. 59 (12), 4843–4850. doi:10.1109/tie.2011.2179276
Bihl, T. J., Bauer, K. W., and Temple, M. A. (2016). Feature Selection for RF Fingerprinting with Multiple Discriminant Analysis and Using ZigBee Device Emissions. IEEE Trans. Inf. Forensics Secur. 11 (8), 1862–1874. doi:10.1109/TIFS.2016.2561902
Brik, V., Banerjee, S., Gruteser, M., and Oh, S. (2008). “Wireless Device Identification with Radiometric Signatures,” in Proceedings of the 14th ACM International Conference on Mobile Computing and Networking (MobiCom ’08) (New York, NY, USA: Association for Computing Machinery), 116–127. doi:10.1145/1409944.1409959
Chacko, J. (2017). “Physical Gate Based Preamble Obfuscation for Securing Wireless Communication,” in International Conference on Computing, Networking and Communications (ICNC), 293–297.
Chatterjee, B., Das, D., Maity, S., and Sen, S. (2019). RF-PUF: Enhancing IoT Security through Authentication of Wireless Nodes Using In-Situ Machine Learning. IEEE Internet Things J. 6 (1), 388–398. doi:10.1109/JIOT.2018.2849324
Chomsiri, T. (2007). “HTTPS Hacking protection,” in 21st International Conference on Advanced Information Networking and Applications Workshops (AINAW’07), 590–594.1
Creswell, A., White, T., Dumoulin, V., Arulkumaran, K., Sengupta, B., and Bharath, A. A. (2018). Generative Adversarial Networks: An Overview. IEEE Signal. Process. Mag. 35 (1), 53–65. doi:10.1109/msp.2017.2765202
Danev, B., and Capkun, S. (2009). “Transient-based Identification of Wireless Sensor Nodes,” in 2009 International Conference on Information Processing in Sensor Networks, 25–36.
Danev, B., Heydt-Benjamin, T. S., and Capkun, S. (2009). “Physical-layer Identification of Rfid Devices,” in USENIX Security Symposium, 199–214.
Ding, L., Wang, S., Wang, F., and Zhang, W. (2018). Specific Emitter Identification via Convolutional Neural Networks. IEEE Commun. Lett. 22 (12), 2591–2594. doi:10.1109/lcomm.2018.2871465
Fredenslund, K. (2022). Computational Complexity of Neural Networks. [Online]. Available at: https://kasperfred.com/series/introduction-to-neural-networks/computational-complexity-of-neural-networks (Accessed March 6, 2022).
Guo, X., Zhang, Z., and Chang, J. (2019). “Survey of mobile Device Authentication Methods Based on Rf Fingerprint,” in IEEE INFOCOM 2019 - IEEE Conference on Computer Communications Workshops (Infocom Wkshps), 1–6. doi:10.1109/infocomwkshps47286.2019.9093755
Hall, J., Barbeau, M., and Kranakis, E. (2003). Detection of Transient in Radio Frequency Fingerprinting Using Signal Phase. Wireless Opt. Commun., 13–18.
Hanna, S. S., and Cabric, D. (2019). “Deep Learning Based Transmitter Identification Using Power Amplifier Nonlinearity,” in 2019 International Conference on Computing, Networking and Communications (HonoluluHI, USA: ICNC), 674–680. doi:10.1109/ICCNC.2019.8685569
Hospodar, G., Gierlichs, B., Mulder, E. D., Verbauwhede, I., and Vandewalle, J. (2011). Machine Learning in Side-Channel Analysis: a First Study. J. Cryptographic Eng. 1 (4), 293. doi:10.1007/s13389-011-0023-x
Huang, N. E. (2014). Hilbert-huang Transform and its Applications, 16. New Jersey: World Scientific.
Huang, Y., and Zheng, H. (2012). “Radio Frequency Fingerprinting Based on the Constellation Errors,” in 2012 18th Asia-Pacific Conference on Communications (APCC), 900–905. doi:10.1109/apcc.2012.6388238
Jian, T., Rendon, B. C., Ojuba, E., Soltani, N., Wang, Z., Sankhe, K., et al. (2020). Deep Learning for Rf Fingerprinting: A Massive Experimental Study. IEEE Internet Things M. 3 (1), 50–57. doi:10.1109/iotm.0001.1900065
Jagannath, A., Jagannath, J., and Kumar, P. S. P. V. (2022). A Comprehensive Survey on Radio Frequency (RF) Fingerprinting: Traditional Approaches, Deep Learning, and Open Challenges. arXiv [Preprint]. doi:10.48550/arXiv.2201.00680
Kennedy, I. O., Scanlon, P., Mullany, F. J., Buddhikot, M. M., Nolan, K. E., and Rondeau, T. W. (2008). “Radio Transmitter Fingerprinting: A Steady State Frequency Domain Approach,” in 2008 IEEE 68th Vehicular Technology Conference, 1–5.
Kim, P. (2017). “Convolutional Neural Network,” in MATLAB Deep Learning: With Machine Learning, Neural Networks and Artificial Intelligence (Berkeley, CA: Apress), 121–147. doi:10.1007/978-1-4842-2845-6_6
Klein, R. W., Temple, M. A., and Mendenhall, M. J. (2009). Application of Wavelet-Based Rf Fingerprinting to Enhance Wireless Network Security. J. Commun. Netw. 11 (6), 544–555. doi:10.1109/jcn.2009.6388408
Kocher, P., Jaffe, J., and Jun, B. (1999). “Differential Power Analysis,” in Annual International Cryptology Conference (Berlin, Heidelberg: Springer), 388–397. doi:10.1007/3-540-48405-1_25
Kumar, K., Kaur, P., and Amritsar, G. N. D. U. (2015). “Vulnerability Detection of International mobile Equipment Identity Number of Smartphone and Automated Reporting of Changed IMEI Number,” in International Journal of Computer Science and Mobile Computing, 527–533.45
Liu, P., Qiu, X., and Huang, X. (2016). Recurrent Neural Network for Text Classification with Multi-Task Learning. arXiv [Preprint]. doi:10.48550/arXiv.1605.05101
Lukacs, M., Collins, P., and Temple, M. (2015). Classification Performance Using 'RF‐DNA' Fingerprinting of Ultra‐wideband Noise Waveforms. Electron. Lett. 51 (10), 787–789. doi:10.1049/el.2015.0051
Maes, R. (2013). Physically Unclonable Functions: Constructions, Properties and Applications. New York: Springer Science & Business Media. doi:10.1007/978-3-642-41395-7
Mao, X., Li, Q., Xie, H., Lau, R. Y., Wang, Z., and Paul Smolley, S. (2017). “Least Squares Generative Adversarial Networks,” in Proceedings of the IEEE international conference on computer vision, 2794–2802. doi:10.1109/iccv.2017.304
Nguyen, N. T., Zheng, G., Han, Z., and Zheng, R. (2011). “Device Fingerprinting to Enhance Wireless Security Using Nonparametric Bayesian Method,” in 2011 Proceedings IEEE INFOCOM, 1404–1412. doi:10.1109/infcom.2011.5934926
OAuth 2.0, OAuth (2022). [Online] Available at: https://oauth.net/2/(Accessed 14Jan, 2022).
Ometov, A., Bezzateev, S., Mäkitalo, N., Andreev, S., Mikkonen, T., and Koucheryavy, Y. (2018). Multi-factor Authentication: A Survey. Cryptography 21 (1), 1. doi:10.3390/cryptography2010001
ORBIT (2022). Open-access Research Testbed for Next-Generation Wireless Networks (Orbit). Available at: https://www.orbit-lab.org/.
O’Shea, T., and Hoydis, J. (2017). An Introduction to Deep Learning for the Physical Layer. IEEE Trans. Cogn. Commun. Netw. 3 (4), 563–575. doi:10.1109/TCCN.2017.2758370
Pal, M. (2005). Random forest Classifier for Remote Sensing Classification. Int. J. remote sensing 26 (1), 217–222. doi:10.1080/01431160412331269698
Patel, H. (2015). “Non-parametric Feature Generation for Rf-Fingerprinting on Zigbee Devices,” in 2015 IEEE Symposium on Computational Intelligence for Security and Defense Applications (CISDA), 1–5. doi:10.1109/cisda.2015.7208645
Peng, L., Hu, A., Zhang, J., Jiang, Y., Yu, J., and Yan, Y. (2018). Design of a Hybrid RF Fingerprint Extraction and Device Classification Scheme. IEEE Internet Things J. 6 (1), 349–360. doi:10.1109/JIOT.2018.2838071
Peng, L., Zhang, J., Liu, M., and Hu, A. (2020). Deep Learning Based Rf Fingerprint Identification Using Differential Constellation Trace Figure. IEEE Trans. Veh. Technol. 69 (1), 1091–1095. doi:10.1109/tvt.2019.2950670
Plusquellic, J. (2018). Physical Unclonable Functions 1. [Online]. Available at: http://ece-research.unm.edu/jimp/HOST/slides/PUF1.pdf (Accessed = Feb 6, 2022).
Quisquater, J.-J., and Samyde, D. (2001). “Electromagnetic Analysis (Ema): Measures and Counter-measures for Smart Cards,” in International Conference on Research in Smart Cards (Berlin, Heidelberg: Springer), 200–210. doi:10.1007/3-540-45418-7_17
Rasmussen, K. B., and Capkun, S. (2007). “Implications of Radio Fingerprinting on the Security of Sensor Networks,” in 2007 Third International Conference on Security and Privacy in Communications Networks and the Workshops-Secure Comm 2007 (IEEE, Sep.), 331–340. doi:10.1109/seccom.2007.4550352
Robinson, J., Kuzdeba, S., Stankowicz, J., and Carmack, J. M. (2020). “Dilated Causal Convolutional Model for Rf Fingerprinting,” in roc. of 10th Annual Computing and Communication Workshop and Conference (CCWC), 0157. doi:10.1109/ccwc47524.2020.9031257P
Roy, D., Mukherjee, T., Chatterjee, M., and Pasiliao, E. (2019). “Detection of Rogue Rf Transmitters Using Generative Adversarial Nets,” in 2019 IEEE Wireless Communications and Networking Conference (WCNC), 1–7. doi:10.1109/wcnc.2019.8885548
Sankhe, K., Belgiovine, M., Zhou, F., Angioloni, L., Restuccia, F., D'Oro, S., et al. (2020). No Radio Left behind: Radio Fingerprinting through Deep Learning of Physical-Layer Hardware Impairments. IEEE Trans. Cogn. Commun. Netw. 6 (1), 165–178. doi:10.1109/TCCN.2019.2949308
Scanlon, P., Kennedy, I. O., and Liu, Y. (2010). Feature Extraction Approaches to RF Fingerprinting for Device Identification in Femtocells. Bell Labs Tech. J. 15 (3), 141–151. doi:10.1002/bltj.20462
Shaw, D., and Kinsner, W. (1997). “Multifractal Modelling of Radio Transmitter Transients for Classification,” in IEEE WESCANEX 97 Communications, Power and Computing. Conference Proceedings, 306–312.
Siddiqui, M. S., and Verma, D. (2011). “Cross Site Request Forgery: A Common Web Application Weakness,” in 2011 IEEE 3rd International Conference on Communication Software and Networks (IEEE), 538–543. doi:10.1109/iccsn.2011.6014783
Soltani, N., Reus-Muns, G., Salehi, B., Dy, J., Ioannidis, S., and Chowdhury, K. (2020). Rf Fingerprinting Unmanned Aerial Vehicles with Nonstandard Transmitter Waveforms. IEEE Trans. Vehicular Technology 69 (12), 15 518–615 531. doi:10.1109/tvt.2020.3042128
Symanovich, S. (2019). The Future of IOT: 10 Predictions about the Internet of Things. Norton, 14. [Online]. Available at: https://us.norton.com/internetsecurity-iot-5-predictions-for-the-future-of-iot.html (Accessed Jan, 2022).
Ting, D. M., Hussain, O., and LaRoche, G. (2015). Systems and Methods for Multi-Factor Authentication. Washington, DC: U.S. Patent and Trademark Office. U.S. Patent No. 9,118,656.
Ur Rehman, S., Sowerby, K., and Coghill, C. (2012). “Rf Fingerprint Extraction from the Energy Envelope of an Instantaneous Transient Signal,” in 2012 Australian Communications Theory Workshop (CTW), 90–95. doi:10.1109/ausctw.2012.6164912
Vo-Huu, T. D., Vo-Huu, T. D., and Noubir, G. (2016). “Fingerprinting Wi-Fi Devices Using Software Defined Radios,” in Proceedings of the 9th ACM Conference on Security & Privacy in Wireless and Mobile Networks, 3–14. doi:10.1145/2939918.2939936
Wang, T., Wen, C.-K., Wang, H., Gao, F., Jiang, T., and Jin, S. (2017). Deep Learning for Wireless Physical Layer: Opportunities and Challenges. China Commun. 14 (11), 92–111. doi:10.1109/cc.2017.8233654
Wang, X., Wang, X., and Mao, S. (2018). RF Sensing in the Internet of Things: A General Deep Learning Framework. IEEE Commun. Mag. 56 (9), 62–67. doi:10.1109/mcom.2018.1701277
Wang, Y., and Yang, J. (2017). “Ethical Hacking and Network Defense: Choose Your Best Network Vulnerability Scanning Tool,” in 2017 31st International Conference on Advanced Information Networking and Applications Workshops (WAINA), 110–113. doi:10.1109/waina.2017.39
Xie, F., Wen, H., Li, Y., Chen, S., Hu, L., Chen, Y., et al. (2018). Optimized Coherent Integration-Based Radio Frequency Fingerprinting in Internet of Things. IEEE Internet Things J. 5 (5), 3967–3977. doi:10.1109/jiot.2018.2871873
Xu, Q., Zheng, R., Saad, W., and Han, Z. (2016a). Device Fingerprinting in Wireless Networks: Challenges and Opportunities. IEEE Commun. Surv. Tutorials. 18, 94–104. doi:10.1109/COMST.2015.2476338
Xu, Q., Zheng, R., Saad, W., and Han, Z. (2016b). Device Fingerprinting in Wireless Networks: Challenges and Opportunities. IEEE Commun. Surv. Tutorials 18 (1), 94–104. doi:10.1109/comst.2015.2476338
Yuan, Y., Huang, Z., Wu, H., and Wang, X. (2014). Specific Emitter Identification Based on Hilbert-Huang Transform‐based Time-Frequency-Energy Distribution Features. IET Commun. 8 (13), 2404–2412. doi:10.1049/iet-com.2013.0865
Zhang, C., Patras, P., and Haddadi, H. (2019). Deep Learning in mobile and Wireless Networking: A Survey. IEEE Commun. Surv. Tutorials 21 (3), 2224–2287. doi:10.1109/comst.2019.2904897
Zhao, C., Chen, C., Cai, Z., Shi, M., Du, X., and Guizani, M. (2018). “Classification of Small Uavs Based on Auxiliary Classifier Wasserstein gans,” in 2018 IEEE Global Communications Conference (GLOBECOM), 206–212. doi:10.1109/glocom.2018.8647973
Zhuo, F., Huang, Y., and chen, J. (2017). Radio Frequency Fingerprint Extraction of Radio Emitter Based on I/q Imbalance. Proced. Computer Sci. 107, 472–477. doi:10.1016/j.procs.2017.03.092
Keywords: IoT, machine learning, physical security, PUF, neural network (NN), radio frequency, RF fingerprinting, Xbee dataset
Citation: Bari MF, Agrawal P, Chatterjee B and Sen S (2022) Statistical Analysis Based Feature Selection Enhanced RF-PUF With
Received: 17 January 2022; Accepted: 14 March 2022;
Published: 25 April 2022.
Edited by:
Yogesh Singh Chauhan, Indian Institute of Technology Kanpur, IndiaReviewed by:
Nikhil Rangarajan, New York University Abu Dhabi, United Arab EmiratesChinmay Chakraborty, Birla Institute of Technology, Mesra, India
Copyright © 2022 Bari , Agrawal , Chatterjee and Sen . This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Md Faizul Bari , bWJhcmlAcHVyZHVlLmVkdQ==
 Md Faizul Bari
Md Faizul Bari  Parv Agrawal
Parv Agrawal  Baibhab Chatterjee
Baibhab Chatterjee  Shreyas Sen
Shreyas Sen