Dynamic charge order from strong correlations in the cuprates

Charge order has been a central focus in the study of cuprate high-temperature superconductors due to its intriguing yet not fully understood connection to superconductivity. Recent advances in resonant inelastic x-ray scattering (RIXS) in the soft x-ray regime have enabled the first momentum-resolved studies of dynamic charge order correlations in the cuprates. This progress has opened a window for a more nuanced investigation into the mechanisms behind the formation of charge order (CO) correlations. This review provides an overview of RIXS-based measurements of dynamic CO correlations in various cuprate materials. It specifically focuses on electron-doped cuprates and Bi-based hole-doped cuprates, where the CO-related RIXS signals may reveal signatures of the effective Coulomb interactions. This aims to explore a connection between two central phenomena in the cuprates: strong Coulomb correlations and CO-forming tendencies. Finally, we discuss current open questions and potential directions for future RIXS studies as the technique continues to improve and mature, along with other probes of dynamic correlations that would provide a more comprehensive picture.

1 Introduction

Cuprate high-temperature superconductors exhibit a variety of emergent phenomena, including antiferromagnetism, superconductivity, charge order, and strange metal phases. Charge order (CO) has been a central focus in the study of cuprates for a long time, with the initial detection of stripe order in La-based cuprates by neutron scattering in 1995 and the first evidences for charge order in Bi-based cuprates coming from scanning tunneling microscopy and spectroscopy (STM/S) measurements (Comin and Damascelli, 2016; Frano et al., 2020; Tranquada et al., 1995; Hoffman et al., 2002; Vershinin et al., 2004; Howald et al., 2003; Abbamonte et al., 2005; Wise et al., 2008; Ghiringhelli et al., 2012; Chang et al., 2012; Comin et al., 2014; da Silva Neto et al., 2014; Tabis et al., 2014; da Silva Neto et al., 2015; da Silva Neto et al., 2016). A significant breakthrough occurred in 2011 when an incommensurate CO, independent of spin modulations, was detected in $\mathrm{Y}{\mathrm{B}\mathrm{a}}_2{\mathrm{C}\mathrm{u}}_3{\mathrm{O}}_{6+\delta }$ (YBCO) (Wu et al., 2011; Ghiringhelli et al., 2012; Chang et al., 2012). One of the original momentum-resolved detections was obtained from resonant inelastic x-ray scattering experiments (RIXS), but in the same work it was shown that a CO peak in momentum space could be detected with energy-integrated resonant x-ray scattering (EI-RXS), where all the scattered photons are counted by a finite area detector without resolving their energy (Ghiringhelli et al., 2012). Soon after the discovery in YBCO, EI-RXS was used to detect CO in the major hole- and electron-doped cuprate families, including YBCO, ${\mathrm{B}\mathrm{i}}_2$${\mathrm{S}\mathrm{r}}_2$${\mathrm{C}\mathrm{u}\mathrm{O}}_{6+\delta }$ (Bi-2201), ${\mathrm{B}\mathrm{i}}_2{\mathrm{S}\mathrm{r}}_2\mathrm{C}\mathrm{a}{\mathrm{C}\mathrm{u}}_2{\mathrm{O}}_{8+\delta }$ (Bi-2212), ${\mathrm{H}\mathrm{g}\mathrm{B}\mathrm{a}}_2$${\mathrm{C}\mathrm{u}\mathrm{O}}_{4+\delta }$ (HgBCO), ${\mathrm{N}\mathrm{d}}_{2-x}{\mathrm{C}\mathrm{e}}_x\mathrm{C}\mathrm{u}{\mathrm{O}}_4$ (NCCO), and ${\mathrm{L}\mathrm{a}}_{2-x}{\mathrm{C}\mathrm{e}}_x\mathrm{C}\mathrm{u}{\mathrm{O}}_4$. (Comin and Damascelli, 2016; Frano et al., 2020; Tranquada et al., 1995; Abbamonte et al., 2005; Ghiringhelli et al., 2012; Chang et al., 2012; Comin et al., 2014; da Silva Neto et al., 2014; Tabis et al., 2014; da Silva Neto et al., 2015; da Silva Neto et al., 2016). Although the original detection in YBCO was performed using RIXS, EI-RXS was chosen for many studies as it allowed the CO to be characterized as a function of temperature, magnetic fields, and doping in a more time efficient manner. However, this approach could not distinguish whether the scattering was elastic (related to static charge modulations) or inelastic (related to dynamic charge correlations). In the last 7 years, technical advances in soft x-ray RIXS improved the energy resolution at the Cu-$L_3$ edge from approximately 130 meV to less than 40 meV (Brookes et al., 2018; Dvorak et al., 2016; Jarrige et al., 2018; Zhou et al., 2022), enabling explorations of dynamic electron correlations near the CO wavevector (Arpaia and Ghiringhelli, 2021; Chaix et al., 2017; da Silva Neto et al., 2018; Arpaia et al., 2019; Yu et al., 2020; Miao et al., 2017; Miao et al., 2019; Li et al., 2020; Lee et al., 2021; Boschini et al., 2021; Huang et al., 2021; Lu et al., 2022; Scott et al., 2023; Arpaia et al., 2023). These measurements have shown that indeed the charge order is not only static, but shows distinct features in the inelastic spectrum. To date, a universal picture of dynamic CO correlations has yet to be established.

Charge order has been observed as short-range, incommensurate correlations, leading to proposals that it can be understood in terms of a Fermi surface instability or a nesting condition (Comin and Damascelli, 2016). This perspective has led many to view CO as a minor peculiarity of the normal state of underdoped cuprates, essentially an accident of the Fermi surface. However, this early astute interpretation lacked the insights into inelastic dynamical charge order correlations that later emerged with the full exploitation of the energy-resolving capability of RIXS measurements. Another view sees CO as a consequence of the strong electron correlations that are at the heart of the cuprate problem (Machida, 1989; Zaanen and Gunnarsson, 1989; Emery and Kivelson, 1993; Huang et al., 2017; Zheng et al., 2017). Given the central role of strong correlations in cuprate physics, we hypothesize, based on the evidence reviewed here, that they should be considered in any attempt to understand dynamic CO correlations.

Indeed, much of the interest in CO arose from early theoretical proposals suggesting that the formation of charge or stripe order is a natural way for the doped Mott insulator to frustrate the tendency toward phase separation (Emery and Kivelson, 1993). While short-range local Hubbard-like interactions would cause spatial phase separation into metallic and insulating regions, long-range Coulomb interactions prevent this long-wavelength phase separation and result in short-wavelength charge fluctuations instead. These fluctuations may manifest as either dynamic CO modes or incommensurate static CO, or both. Despite numerous EI-RXS and RIXS studies on CO in cuprates, connecting CO correlations to the effective Coulomb interactions has been challenging. This review will explore prominent experiments where Cu-$L_3$ RIXS measurements provide insights into how effective Coulomb interactions may relate to CO.

This review does not aim to comprehensively cover the phenomenon of charge ordering in cuprates. Several aspects, such as the CO doping dependence, differences and similarities between cuprate families, and the determination of the CO intra-unit-cell structure, are beyond its scope; for these topics, readers are directed to existing literature (Comin and Damascelli, 2016; Frano et al., 2020; Arpaia and Ghiringhelli, 2021). Instead, this focused review delves specifically into how Coulomb interactions may relate to CO. Additionally, our understanding of CO in the cuprates has evolved significantly over the past 13 years, closely tied to advancements in EI-RXS and RIXS techniques in the soft x-rays. As these techniques improve, they not only expand our knowledge but also reveal new questions and expose current experimental limitations. Therefore, this review also highlights important technical developments, discusses our present limitations, and suggests possible future directions.

2 Discussion

2.1 The cuprate Cu-$L_3$ RIXS spectrum

The Cu-$L_3$ RIXS cross-section in cuprates is extremely rich. It is sensitive to charge order correlations (Comin and Damascelli, 2016; Frano et al., 2020; Tranquada et al., 1995; Hoffman et al., 2002; Vershinin et al., 2004; Howald et al., 2003; Abbamonte et al., 2005; Wise et al., 2008; Ghiringhelli et al., 2012; Chang et al., 2012; Comin et al., 2014; da Silva Neto et al., 2014; Tabis et al., 2014; da Silva Neto et al., 2015; 2016; Arpaia and Ghiringhelli, 2021; Chaix et al., 2017; da Silva Neto et al., 2018; Arpaia et al., 2019; Yu et al., 2020; Miao et al., 2017; Miao et al., 2019; Li et al., 2020; Lee et al., 2021; Boschini et al., 2021; Huang et al., 2021; Lu et al., 2022; Scott et al., 2023; Arpaia et al., 2023), phonons (including studies of electron-phonon coupling and two-phonon processes) (Chaix et al., 2017; Rossi et al., 2019; Lin J. Q. et al., 2020; Peng et al., 2020; Li et al., 2020; Wang et al., 2021; Lee et al., 2021; Lu et al., 2022; Braicovich et al., 2020; Huang et al., 2021; Peng et al., 2022; Scott et al., 2023; 2024), superconducting and pseudo gaps (Suzuki et al., 2018; Merzoni et al., 2024), magnetic excitations (magnon and bi-magnon excitations) (Hill et al., 2008; Braicovich et al., 2010; Le Tacon et al., 2011; Lee et al., 2014; Ishii et al., 2014; Peng et al., 2015; Minola et al., 2015; Fumagalli et al., 2019; Betto et al., 2021), plasmons (Hepting et al., 2018; Lin J. et al., 2020; Nag et al., 2020; Singh et al., 2022; Hepting et al., 2022; Hepting et al., 2023), dd orbital excitations (Sala et al., 2011; Fumagalli et al., 2019), and the charge transfer gap. Within this rich cross-section, static CO appears prominently as an enhancement of the elastic line at in-plane wavevectors along the Cu-O bond direction, i.e., $\mathbf{q}=(\pm q_{CO},0)$ and $\mathbf{q}=(0,\pm q_{CO})$. However, dynamic CO correlations do not appear as a salient feature of the Cu-$L_3$ RIXS energy-loss spectrum. In fact, an agnostic minimal model of the spectrum in the zero to 1 eV range, requires the following five components though not necessarily a dynamic CO feature: (i) a quasi-elastic peak, (ii) the bond-stretching phonon around 70 meV, (iii) two-phonon mode (from the bond-stretching phonon) near 140 meV, (iv) a damped harmonic oscillator representing spin-flip processes in the 100–800 meV range, and (v) a small broad background Scott et al. (2023). The origin of (v) remains unknown, but some possibilities include scattering from extra charge carriers from doping, a Stoner continuum or high energy quasi-circular dynamic correlations (QCDCs), see Figures 1A, B. Beyond those, great caution must be taken when attempting to add additional terms to the curve fitting functions, although other contributions can be inferred, as depicted in Figure 1C. Indeed, subtler features relating to dynamic CO correlations can be detected by performing careful momentum mapping measurements as a function of temperature, as discussed in Section 2.2. Furthermore, an important quantity that can significantly aid in separating overlapping signals in the spectrum is the polarization of the outgoing photon, which provide information to distinguish between charge and spin scattering. This is accomplished in polarimetric RIXS (pol-RIXS), where the scattered photons are analyzed not only in terms of their energy loss but also in terms of their polarization (Braicovich et al., 2014; Minola et al., 2015; Fumagalli et al., 2019; Betto et al., 2021; da Silva Neto et al., 2018; Hepting et al., 2018; Scott et al., 2024). For example, pol-RIXS measurements were used to demonstrate the two-phonon origin of the feature near 140 meV, showing that it appears in the non-cross polarized scattering channel, $\sigma$-${\sigma }^{\prime }$, but not in the cross-polarized channel, $\sigma$-${\pi }^{\prime }$, where the unprimed (primed) symbol refers to the incoming (scattered) photon polarization (Scott et al., 2024). In another example, pol-RIXS measurements show that the damped harmonic oscillator feature, often simply called a “paramagnon” feature, is actually composed of one- and two-magnon processes (Betto et al., 2021). Despite being a very powerful technique which can resolve fundamental aspects of the scattered signals, the current state-of-the-art pol-RIXS technology is inefficient, typically requiring ten times longer acquisition times than standard RIXS. These lengthy acquisition times have led scientists to focus more on standard RIXS measurements rather than pol-RIXS. However, even with these current limitations, many potential pol-RIXS experiments in cuprates and other materials are feasible with existing technology, indicating potential for a wider exploration of pol-RIXS studies. Moreover, as the method becomes more efficient, it will enable new experiments that will undoubtedly uncover important information.

Figure 1

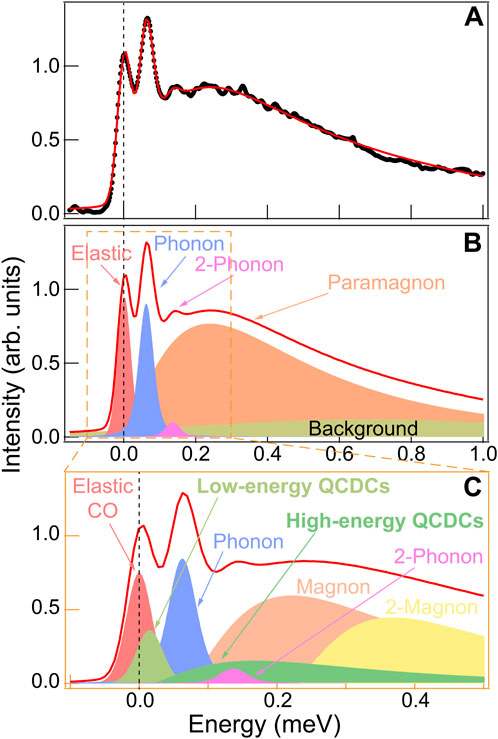
Figure 1. Cuprate Cu-$L_3$ RIXS spectrum of Bi-2212. (A) Example of a RIXS spectrum at $q=0.27$ r. l.u. for $\varphi =0°$. The red line is a fit to the spectrum. (B) Contributions to the fit of (A): a quasi-elastic peak, a phonon peak, a two-phonon peak, a broad paramagnon, and a broad background. (C) Sketch of other possible contributions to the RIXS spectrum of (A): low- and high-energy QCDCs, as well as a magnon and bimagnon peak instead of the broad paramagnon feature. Figures (A, B) are adapted from (Scott et al., 2023). Reprinted with permission from AAAS.

2.2 Dynamic electron correlations near the charge order wavevector

Given the complexity of the RIXS signal discussed above, how can we detect dynamic CO correlations within such a rich spectrum? This is typically accomplished through careful momentum mapping which reveal subtle dynamic features near the charge order wavevector, ${\mathbf{q}}_{CO}$. These features can be broadly categorized into low-energy excitations, below the bond-stretching phonon energy (i.e., $E<70$ meV), and high-energy excitations, spanning the 150–700 meV range. Low-energy features, existing within the same energy range as various phonon branches, have been identified in Bi-2212 (Chaix et al., 2017; Lee et al., 2021; Lu et al., 2022; Scott et al., 2023), Bi-2201 (Li et al., 2020), YBCO (Arpaia et al., 2019; Arpaia et al., 2023), HgBCO (Yu et al., 2020), ${\mathrm{L}\mathrm{a}}_{2-x}{\mathrm{S}\mathrm{r}}_x\mathrm{C}\mathrm{u}{\mathrm{O}}_4$ (Huang et al., 2021), and ${\mathrm{L}\mathrm{a}}_{2-x}{\mathrm{B}\mathrm{a}}_x\mathrm{C}\mathrm{u}{\mathrm{O}}_4$ (Miao et al., 2019), with experimental methodologies varying between studies due to the peculiarities of different materials. For instance, in Bi-based materials, the presence of low-energy CO correlations is inferred through the observation of a softening of the RIXS-measured bond-stretching phonon (Chaix et al., 2017; Lee et al., 2021; Lu et al., 2022; Scott et al., 2023), while in YBCO, the detection of a similar low-energy CO mode was achieved through the careful subtraction of temperature-dependent data (Arpaia et al., 2019; Arpaia et al., 2023). High-energy features, observed in NCCO (da Silva Neto et al., 2018), HgBCO (Yu et al., 2020), and Bi-2212 (Boschini et al., 2021; Scott et al., 2023), overlap with paramagnon excitations and are broader. They are usually detected by examining the momentum-dependence of the RIXS spectrum integrated over an energy window or through meticulous temperature-dependent measurements and background subtraction.

In exploring the relationship between strong electron correlations and CO, high-energy CO features offer valuable insights. These higher energy scales, comparable to the magnetic exchange coupling $J$, are more compatible with strong correlation physics. Perhaps, the clearest realization of the high-energy signal is observed in the electron-doped cuprate NCCO, as discussed in the following section.

2.3 High energy dynamic CO correlations, the case of NCCO

The first indications of CO in electron-doped cuprates came from EI-RXS measurements in NCCO (da Silva Neto et al., 2015). The peak at ${\mathbf{q}}_{CO}$ decreases in intensity with increasing temperature, but, up to 420 K, an onset temperature is not clear in the EI-RXS measurements (da Silva Neto et al., 2015; da Silva Neto et al., 2016), Figures 2A, B. This linear temperature dependence, also observed in Bi-2212 (Boschini et al., 2021), contrasts with typical mean-field-like order parameter behavior. It suggests that dynamic correlations, expected to persist at very high temperatures, significantly contribute to the peak spectral width in the EI-RXS measurements. To analyze the different static and dynamic contributions to this peak, RIXS measurements were employed (da Silva Neto et al., 2018). It was observed that approximately 50% of the low-temperature peak in EI-RXS is composed of dynamic CO correlations, clearly observed in the energy-momentum maps at ${\mathbf{q}}_{CO}$ in the same energy range as the paramagnon excitations, Figures 2C–E. At 300 K, the elastic peak disappears, but dynamic CO correlations remain, Figures 2C,E. Given the overlap between the high-energy feature at ${\mathbf{q}}_{CO}$ and the dispersive paramagnon feature, a natural question arose about whether the scattering was spin-flip or non-spin-flip in nature. The use of pol-RIXS revealed that the enhancement was primarily in the $\sigma$-${\pi }^{\prime }$ channel (cross-polarization) but not in the $\sigma$-${\sigma }^{\prime }$ (non-crossed) channel, indicating a spin-flip scattering process (da Silva Neto et al., 2018), Figure 2F.

Figure 2

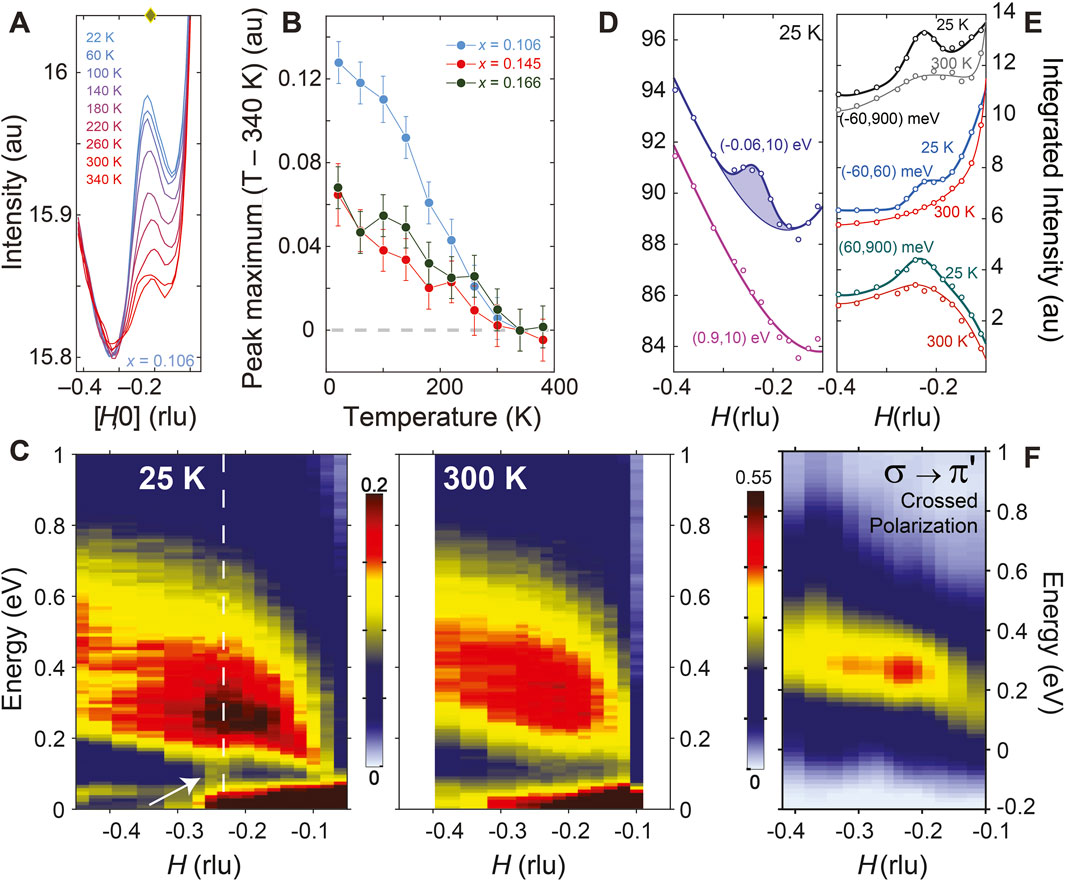
Figure 2. CO correlations in NCCO. (A) Temperature dependence of EI-RXS momentum scans showing the presence of a peak at $q_{CO}$, marked by the yellow diamond. (B) Temperature dependence of the CO peak maximum after subtraction of the 340 K peak maximum, for NCCO at different doping values. (C) Energy-momentum structure of the excitations in NCCO measured with $\sigma$ scattering at 25 and 300 K. The dashed line in marks $q_{CO}$ from the energy-integrated data in panel (A). (D) 25 K RIXS signal integrated over different energy ranges showing that the peak at $q_{CO}$ originates from energies below 900 meV. (E) 25 K RIXS over different energy integration windows for 25 and 300 K. (F) Energy-momentum structure in the $\sigma$-${\pi }^{\prime }$ channel, which is primarily composed of single spin-flip processes. The measurements shown in Figs. (A, C–F), were done on a non-superconducting NCCO $x=0.106$ sample. Figures (A, B) are from (da Silva Neto et al., 2016). Reprinted with permission from AAAS. Figures (C–F) reprinted with permission from (da Silva Neto et al., 2018). Copyright 2018 by the American Physics Society.

At first inspection, the experimental results on NCCO present a puzzle. On one hand, the elastic and inelastic signals appear to be linked since they occur at the same ${\mathbf{q}}_{CO}$ wavevector, which was confirmed for two different dopings, each with distinct ${\mathbf{q}}_{CO}$. On the other hand, the elastic and inelastic signals appear in distinct polarization channels, $\sigma$-${\sigma }^{\prime }$ and $\sigma$-${\pi }^{\prime }$, respectively. However, a resolution was proposed in (da Silva Neto et al., 2018), by noting that that temporal fluctuations of a CO pattern on top of underlying antiferromagnetic correlations require the transfer of charge between neighboring sites with alternating spins. Therefore, some dynamic charge order processes will necessarily involve spin flips.

The existence of dynamic correlations at the $\sigma$-${\pi }^{\prime }$ channel at the same energy scale as $J$ indicates a connection between strong correlation physics and charge order formation. With this rich and detailed phenomenology available, one may ask: what is the simplest Hamiltonian that describes this combined phenomenology? What is the effective Coulomb interaction in that Hamiltonian? A recent theoretical work based on an extended one-band Hubbard model successfully reproduced various aspects of the RIXS experiments on NCCO, including paramagnon dispersion, a plasmonic mode, charge order, the doping dependence of ${\mathbf{q}}_{CO}$, and a significant dynamic CO signal at paramagnon energy scales (Riegler et al., 2023), Figure 3. While model calculations often have to be modified to improve agreement with an experimental aspect at the expense of another, the model in (Riegler et al., 2023) shows excellent simultaneous agreement with all the above-mentioned experimental findings. A key ingredient necessary for this excellent agreement is the existence of a nearest-neighbor Coulomb repulsion $V$ in addition to the onsite repulsion $U$. Within this model, it was found that a moderate $V$ removes the propensity for phase separation with doping, leading to the formation of CO, and associated dynamic correlations, similar to the general mechanism discussed in Section 1. Crucially, the comprehensive and precise experimental RIXS studies provide extensive constraints on the model, naturally increasing confidence in the effective Coulomb interaction obtained from it.

Figure 3

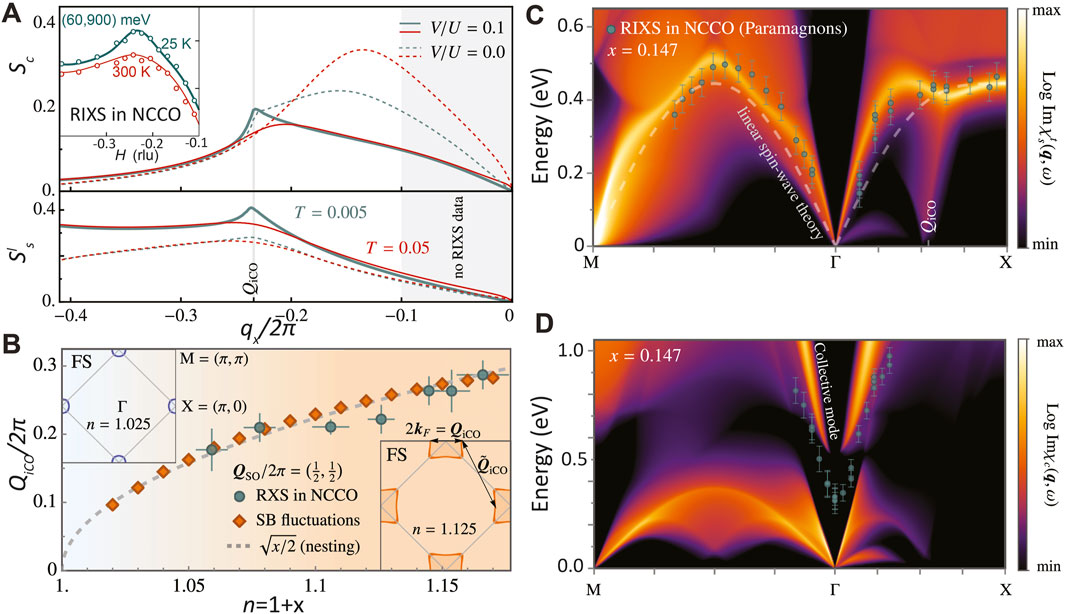
Figure 3. Theory of charge and spins susceptibility in electron-doped cuprates and comparison to RIXS measurements in NCCO. (A) Charge $(S_c)$ and longitudinal $(S_s^l)$ spin-structure factor for $x=0.108$ NCCO as a function of momentum integrated over energy ranges similar to the experiments in (da Silva Neto et al., 2018) (Figure 2E and inset). (B) $q_{CO}$ wavevector inferred from the calculations and compared to EI-RXS data in NCCO (da Silva Neto et al., 2016). (C) Paramagnon dispersion along the high-symmetry directions, which appears as bright lines in the color-coded plot of the transverse spin susceptibility along with RIXS data in NCCO (circles with error bars) obtained from (Lee et al., 2014). (D) Gapped collective mode around the $\mathrm{\Gamma }$-point in the charge susceptibility ${\chi }_c$ along with RIXS data in NCCO from (Lee et al., 2014) displayed by green circles with error bars. Reprinted with permission from (Riegler et al., 2023). Copyright 2023 American Physics Society.

2.4 Quasi-circular dynamic correlations in Bi-2212

To investigate the fingerprints of the effective Coulomb interaction in cuprates, studies of Bi-2212 adopted a new approach. Traditionally, RIXS experiments, constrained by limited synchrotron beam time, focus on the two high-symmetry directions of the 2D in-plane scattering Brillouin zone. However, the $q_x$-$q_y$ structure of the Cu-$L_3$ RIXS cross-section contains signatures of the effective Coulomb interaction, which we review in this section. Before that discussion, however, we will discuss two notable EI-RXS studies that underscore the significance of full in-plane RIXS mapping.

The first study compared EI-RXS measurements of the $q_{CO}$ in Bi-2201 as a function of doping to calculations of the static Lindhard susceptibility (Comin et al., 2014). It was found that along the Cu-O bond direction, the doping dependence of $q_{CO}$ was consistent with the calculation when a pseudogap was included on the Fermi surface Figure 4A. Since the pseudogap itself may result from strong correlations stemming from the parent Mott state, these Lindhard calculations imply a similar origin for the CO. However, as we discuss below, the full 2D static Lindhard calculation shows much stronger intensity along a direction $45°$ away from the static charge order direction Figure 4B, casting doubt on the appropriateness of the Lindhard description.

Figure 4

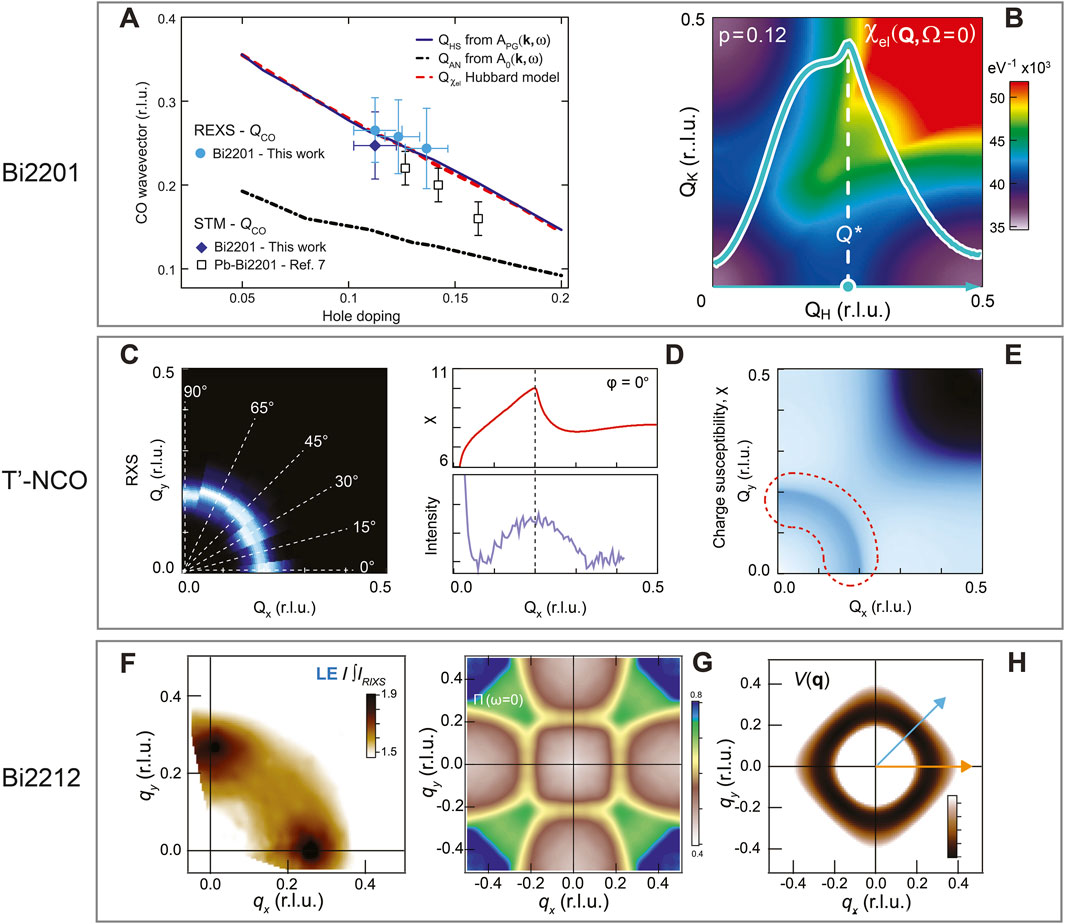
Figure 4. (A) Doping dependence of $q_{CO}$ as determined by EI-RXS and STM on Bi2201 (Comin et al., 2014; Wise et al., 2008). Also shown are evolution of the Fermi surface-derived wavevectors $Q_{AN}$ (antinodal nesting) and $Q_{HS}$ (arc tips) measured from the ARPES spectral function, as well as the doping dependent wavevector $Q_{{\chi }_{el}}$from the calculated Lindhard electronic susceptibility. (B) Static Lindhard susceptibility aclculated for $p=0.12$ doping. The cut along $Q_H$ (full blue line) is overlaid, and the local maximum at $Q_{{\chi }_{el}}\approx 0.26$ is highlighted. (C) EI-RXS measurements of $T^{\prime }$ ${-\mathrm{N}\mathrm{d}}_2$ ${\mathrm{C}\mathrm{u}\mathrm{O}}_4$ over the $q_x$-$q_y$ plane. (D) Comparison of static Lindhard susceptibility and EI-RXS intensity along the $Q_x$ direction. (E) Static Lindhard susceptibility calculated over the full scattering plane. (F) RIXS structure in the $q_x$–$q_y$ plane integrated over ($-0.4,0.9$) eV (LE), normalized to the total fluorescence, i.e., the RIXS spectrum integrated in the ($-\mathrm{4,25}$) eV energy range, at 50 K. (G) Static Lindhard susceptibility calculated for Bi-2212 over the $q_x$-$q_y$ plane. Similar to the calculations for Bi-2201 (B) and $T^{\prime }$ ${-\mathrm{N}\mathrm{d}}_2$ ${\mathrm{C}\mathrm{u}\mathrm{O}}_4$ (E), it shows a maximum intensity along the diagonal direction ($q_x=q_y$). (H) The structure of the calculated Coulomb interaction $V_{\text{eff}}$ calculated using known parameters for Bi-2212. Figures (A, B) from (Comin et al., 2014). Reprinted with permission from AAAS. Figures (C–E) first published in (Kang et al., 2019) by Springer Nature. Figures (F–H) are reproduced from (Boschini et al., 2021). Reference (Boschini et al., 2021) is an open access article licensed under a Creative Commons Attribution 4.0 International License.

The second study focused on $T^{\prime }$${-\mathrm{N}\mathrm{d}}_2$ ${\mathrm{C}\mathrm{u}\mathrm{O}}_4$ thin films with low doping, extending EI-RXS to map the entire $q_x$-$q_y$ plane. Those measurements revealed a quasi-circular ring-like feature, i.e., a nearly constant-radius in-plane pattern (Kang et al., 2019), Figure 4C. Based on a static Lindhard calculation, Figures 4D,E, those results were attributed to low-energy glassy charge modulations that reflect the Fermi surface topology. However, experimentally, EI-RXS could not resolve the energy structure of the scattering, leaving the origin the quasi-circular feature, elastic or inelastic, undetermined.

These two studies lead to an important consideration: Given the well-known Fermi surface in Bi-2212 and the results of the static Lindhard calculations, if a quasi-circular feature were to exist in Bi-2212, it would not originate from a Fermi surface instability, necessitating an alternative explanation. Indeed, RIXS measurements of Bi-2212 found a quasi-circular pattern in the $q_x$-$q_y$ plane at finite inelastic energies, with the same wavevector magnitude, $|\mathbf{q}|=q_{CO}$ as the static CO peak, ${\mathbf{q}}_{CO}$ (Boschini et al., 2021; Scott et al., 2023), Figures 4F, 5. These dynamic correlations with the CO wavelength along all directions in the ${\mathrm{C}\mathrm{u}\mathrm{O}}_2$ plane were termed quasi-circular dynamic correlations (QCDCs). In the original experiment, the RIXS scattering pattern was acquired using an instrument with a medium energy resolution of approximately 800 meV (Boschini et al., 2021), Figure 4F. The results suggested the presence of QCDCs that are broad over the mid-infrared range, approximately from 100 to 900 meV. Furthermore, since static probes like STM have never observed quasi-circles in the scattering patterns of Bi-2212 (Hoffman et al., 2002; Vershinin et al., 2004; Howald et al., 2003; da Silva Neto et al., 2014; Yazdani et al., 2016; Comin and Damascelli, 2016), the existence of a quasi-circle would imply that it is necessarily dynamic. Later, high energy resolution RIXS measurements (approximately 37 meV) tracking the $q_x$-$q_y$ profile of the bond-stretching phonon softening concluded that a similar pattern exists at low energies also (below 70 meV), Figure 5. In Section 2.5 we discuss the phonon-tracking method and the connection between low-energy QCDCs to strange metal behavior (Scott et al., 2023). Before that, however, we discuss how the quasi-circular in-plane pattern provides insights into the origin of charge order and the effective Coulomb interaction (Boschini et al., 2021).

Figure 5

Figure 5. Low-energy QCDCs in Bi-2212 measured using the phonon-tracking method. (A) Energy-momentum structure of the RIXS cross-section at $\varphi =0°$ and $30°$ after subtraction of the elastic line. (B) Location of the phonon peak obtained by fitting the RIXS spectra for different $\varphi$. The solid lines are obtained by fitting the q-dependence of the phonon peak (circles) with a negative Lorentzian function plus a linear background. The shaded regions around the solid lines are generated from the 95% confidence interval obtained for the various fits to the spectra. The solid lines for $\varphi =0°$ and $30°$ in (B) appear as dashed white lines in (A). (C) Momentum-dependence of the RIXS intensity integrated around the elastic line $[-\mathrm{10,10}]$ meV as a function of $\varphi$. (D) Polar plot contrasting M1 (diffusive scattering) and M2 (QCDCs) models (orange and green solid lines) and the experimental data (red symbols). The error bars in (D) are obtained from the fits to the phonon dispersion in Fig. (B). r. l.u., reciprocal lattice units. From (Scott et al., 2023). Reprinted with permission from AAAS.

Given the quasi-circular pattern observed in the experiments, it is natural to ask what many-body description might produce it. Systematically going through different textbook approaches to calculating the charge susceptibility, it was first noted that a static Lindhard calculation strongly deviated from the observed quasi-circular pattern, Figure 4G. Next, to account for the finite energy resolution of the RIXS instruments, the experiments were compared to the dynamic Lindhard susceptibility integrated over an energy window comparable to the experimental resolution. Despite this adjustment, a strong qualitative disagreement persisted. It was further noted that the disagreement remained regardless of the inclusion of a pseudogap in the calculation.

Given the failure of the Lindhard (polarizability) function, directly reflecting the band structure geometry, to capture the most salient features of the experiment, the effective Coulomb interaction was considered. Within the random phase approximation (RPA) formalism, features in the susceptibility may emerge from either peaks in the Lindhard (polarizability) function or from minima in the effective Coulomb interaction. In the extreme case of a featureless polarizability function, as indicated by momentum-resolved electron energy loss spectrosocopy (MEELS) measurements of Bi-2212 (Mitrano et al., 2018; Husain et al., 2019), the RPA susceptibility is dominated by the form of the effective Coulomb interaction, $V_{\text{eff}}$. Using known expressions and experimentally determined parameters (Drozdov et al., 2018; Hwang et al., 2007; Takayanagi et al., 2002), a $V_{\text{eff}}$ was calculated, incorporating both a short-range Hubbard-like component and a long-range potential derived from Poisson’s equation (Becca et al., 1996; Seibold et al., 2000; Caprara et al., 2017; Kivelson et al., 2003). While separately the short-range and long-range components are monotonic functions of $|\mathbf{q}|$, with the former increasing and the latter decreasing, together they form a minimum at an intermediate value inside the scattering Brillouin zone. Remarkably, the minima of $V_{\text{eff}}$, Figure 4H, form a quasi-circular pattern with a radius and shape that closely match the experimentally observed QCDCs (Boschini et al., 2021). In other words, the form of the Coulomb interaction described above captured the most salient aspect of the RIXS mapping—a quasi-circular scattering structure. It also indicated that the same long-range Coulomb interactions necessary to avoid phase separation were key to the appearance of quasi-circular minima in $V_{\text{eff}}$.

A more detailed theoretical model that simultaneously reproduces various aspects of the RIXS on Bi-2212, similar to the one for NCCO, is still being developed. Nevertheless, following the first reports of QCDCs, theoretical works have also observed similar quasi-circular structures, using the same model that reproduced the RIXS measured plasmons in cuprates (Yamase et al., 2021; Bejas et al., 2022). Interestingly, these studies converge on an important conceptual point: the QCDCs are likely the consequence of an effective Coulomb potential that must include long-range interactions.

2.5 Low-energy QCDCs as mediators of strange metal behavior

Recent combined transport and RIXS studies revealed an unexpected link between linear-in-temperature resistivity, which characterizes the strange metal behavior, and charge order (CO) in YBCO (Wahlberg et al., 2021). The linear-in-temperature resistivity (Gurvitch and Fiory, 1987; Martin et al., 1990), often associated with an isotropic scattering rate that depends solely on temperature (i.e., $\propto k_{B}T/\hslash$, sometimes called the Planckian regime) (Grissonnanche et al., 2021; Varma et al., 1989; Aji and Varma, 2007; Patel et al., 2018; Patel and Sachdev, 2019; Phillips et al., 2022; Patel et al., 2023), has been suggested to result from low-energy dynamic CO leading to effective isotropic scattering (Seibold et al., 2021; Caprara et al., 2022). In this scenario, isotropic scattering occurs if collective modes, (i) low in energy and (ii) broad in momentum-space, are available to scatter electrons between any two points on the Fermi surface. Naturally, QCDCs occupying such a large momentum space manifold satisfy the second criterion. Demonstrating the first criterion, that they also exist at low energies, required a new approach based on a phonon-tracking methodology (Scott et al., 2023). This is based on the phenomenology revealed by RIXS measurements on various cuprates, which indicate a softening of the RIXS-measured bond-stretching (BS) phonon peak at ${\mathbf{q}}_{CO}$, i.e., along $q_x$ and $q_y$ (Chaix et al., 2017; Lee et al., 2021; Li et al., 2020; Miao et al., 2019; Lin J. Q. et al., 2020; Peng et al., 2020; Huang et al., 2021; Wang et al., 2021). By tracking the softening of the RIXS-measured BS phonon in the $q_x$-$q_y$ plane, QCDCs were shown to exist at energies below approximately 70 meV (Scott et al., 2023), Figures 5A,B,D. Interestingly, the softening at azimuthal angles close to $45°$ contrasts with the absence of a static CO peak on the elastic line for azimuthal angles away from $0°$, Figure 5C. Overall, these measurements demonstrated the dynamic, low-energy nature of the QCDCs, positioning them as a viable candidate to mediate the isotropic scattering in the strange metal phase.

3 Open questions and future directions

3.1 Enabling technical advancements

Before addressing open questions and future directions, we briefly discuss the key instruments used to obtain the EI-RXS and RIXS results reviewed above, pointing out their key technical characteristics. This section is not intended as a comprehensive review of technical developments, but rather a brief mention of the beamlines from which these studies originated. For a more detailed and recent review of RIXS, we refer readers to (de Groot et al., 2024).

First, in the studies of charge order using EI-RXS in the soft x-rays, the UE-46 beamline at the BESSY II synchrotron (Weschke and Schierle, 2018) and the REIXS beamline at the Canadian Light Source (Hawthorn et al., 2011) were instrumental. At REIXS, measurements were conducted down to 20 K, with the capability to heat the sample stage up to 400 K. The ability to reach high temperatures was crucial for the temperature-dependent studies of electron-doped cuprate (da Silva Neto et al., 2015; 2016), such as the one presented in Figure 2B. Complementarily, the UE-46 beamline allowed access to lower temperatures, down to 10 K, and a second endstation at UE-46 enabled the application of magnetic fields at similar temperatures. These features were pivotal for studying the relationship between charge order and superconductivity (Blanco-Canosa et al., 2014), particularly in low-$T_c$ samples, such as electron-doped cuprates (da Silva Neto et al., 2016).

Second, the evolution of RIXS, as reflected in the results presented above, was driven by advancements in energy resolution at the Cu-$L_3$ edge. Before the developments at the ID32 beamline of the European Synchrotron Radiation Facility, which achieved better than 35 meV resolution (Brookes et al., 2018), the best energy resolution of 130 meV was achieved at the ADRESS beamline of the Swiss Light Source (Ghiringhelli et al., 2006; Strocov et al., 2010) (e.g., (Le Tacon et al., 2011)). Following this significant breakthrough, similar energy resolutions were achieved at the SIX beamline at the National Synchrotron Light Source II at Brookhaven National Laboratory (Dvorak et al., 2016; Jarrige et al., 2018) and the I21 beamline at the Diamond Light Source (Zhou et al., 2022). Additionally, the development of pol-RIXS capabilities at ID32 was crucial for the studies on NCCO shown in Figure 2F. Future application of pol-RIXS are discussed in the next section.

Finally, despite the advancements in energy resolution for Cu-$L_3$ RIXS, achieving these high resolutions comes at the cost of reduced flux, leading to longer measurement times. For some applications, however, a lower energy resolution may suffice for initial measurements. For instance, the first detection of QCDCs (Boschini et al., 2021) was achieved with an energy resolution of 0.8 eV at the qRIXS beamline of the Advanced Light Source at Lawrence Berkeley National Laboratory (Chuang et al., 2022). The balance between energy resolution and flux there allowed for a full in-plane mapping within 12–24 h, whereas at high-resolution beamlines, this time frame typically applies to q-mapping at a single $\varphi$. Thus, there remains significant potential for discovery with instruments operating at resolutions on the order of hundreds of meV.

3.2 Decomposing the high energy CO correlations with polarimetric RIXS

One of the main advantages of the soft x-ray RIXS cross-section is its sensitivity to various degrees of freedom (Ament et al., 2011; Devereaux et al., 2016), but this also presents complications. Despite the success of the phonon-tracking method, the energy profile of the QCDCs, i.e., their energy spectrum, has not been resolved. Thus, although high-energy and low-energy QCDCs appear at the same momenta, it remains possible that they have different origins. Resolving this question requires the ability to decompose the rich RIXS spectrum into its different components. For this, pol-RIXS may be the most effective technique to determine the contributions to the MIR energy scale, as demonstrated in NCCO. However, these experiments are extremely challenging. The most mature state-of-the-art polarimeter, available at the ID32 beamline of the European Synchrotron Radiation Facility, uses a mirror with an average reflection coefficient of about 0.1 (Brookes et al., 2018; Braicovich et al., 2014). Recently, pol-RIXS is also being developed at the I21 beamline at Diamond Light Source, with a similar average reflection coefficient at the Ni-$L_3$ edge already demonstrated Chen et al. (2024). As a result of the low reflection coefficient, polarimetric RIXS requires acquisition times over ten times longer than standard RIXS to achieve comparable statistics. To fit these measurements within a typical five-day beam time, either energy resolution is sacrificed to allow for momentum mapping, as in NCCO da Silva Neto et al. (2018), or momentum mapping is abandoned to obtain high-resolution polarimetric spectra, as demonstrated in the resolution of the 2-phonon mode (Scott et al., 2024). Furthermore, the actual spectral decomposition is not performed directly by the instrument but requires nuanced data processing. Still, there are plenty of cuprate families, doping values, electronic phases and regions of momentum space that remain to be explored with pol-RIXS. Therefore, we believe that one of the most significant future directions for advancements in soft x-ray RIXS instruments will be the development of fast and reliable polarimetry capabilities.

3.3 QCDCs in other cuprates and strain

It is still unclear if QCDCs exist in other cuprate families. One approach to investigate this would be to use the phonon tracking method to map the $q_x$-$q_y$ plane. However, this method may be affected by varying degrees of coupling between QCDCs and the bond-stretching phonon across different families and it would not probe the high-energy sector. Following a Brazovskii framework (Boschini et al., 2021), the effective Coulomb interaction allows charge order domains to appear along any in-plane direction, while the lattice structure and phonon spectrum determine the direction of static charge order. Thus, manipulating the lattice, for example, with uniaxial strain, should compress spectral weight from the QCDC manifold into the more localized static CO peaks. This differential measurement approach could be used to detect QCDCs in other cuprates. On the other hand, a recent study combining uniaxial strain and RIXS on ${\mathrm{L}\mathrm{a}}_{2-x}{\mathrm{S}\mathrm{r}}_x\mathrm{C}\mathrm{u}{\mathrm{O}}_4$ finds that, while the relative intensity of static CO peaks along $q_x$ and $q_y$ is sensitive to uniaxial strain, the energy and intensity of dynamic CO correlations, as well as the softening of the BS mode, remain equal along $q_x$ and $q_y$ Martinelli et al. (2024). This latest result in ${\mathrm{L}\mathrm{a}}_{2-x}{\mathrm{S}\mathrm{r}}_x\mathrm{C}\mathrm{u}{\mathrm{O}}_4$ further indicates a non-trivial relation between static and dynamic CO correlations, similar to the findings in Scott et al. (2023), which highlight different behaviors of static and dynamic CO correlations with $\varphi$, Figure 5.

Despite the recent successful examples of integrating soft x-ray RXS with uniaxial strain (Boyle et al., 2021; Kim et al., 2021; Wang et al., 2022; Gupta et al., 2023; Martinelli et al., 2024), we note that these measurements are extremely challenging for several reasons: (i) technical challenges associated with the integration of the strain devices into the ultra-high-vacuum chambers of the existing RIXS setups, (ii) a high-rate of broken samples upon stress application and (iii) difficulty in precisely determining the effective strain on the sample during the RIXS study. Barring advances in methods for applying uniaxial strain, more efficient RIXS would greatly benefit these studies by allowing for faster cycling of samples. Relatedly, epitaxial strain (Bluschke et al., 2018) and chemical pressure (Ruiz et al., 2022) have been shown to have significant impact on the out-of-plane coupling of the CO in YBCO. How this translates to the in-plane structure of the dynamic charge correlations remains an open question.

3.4 New experimental probes of high energy CO correlations

In recent years, the advent of free-electron lasers (FELs) has enabled the extension of EI-RXS and RIXS into the time domain, providing new insights into the light-induced dynamics and melting of CO in cuprates (Mitrano et al., 2019; Mitrano and Wang, 2020; Bluschke et al., 2024). In particular, two recent time-resolved EI-RXS studies have reported the dynamic competition between superconductivity and CO in YBCO (Wandel et al., 2022; Jang et al., 2022). Both studies show that quenching the superconducting phase with near-infrared (near-IR) light results in a transient non-thermal enhancement of the static CO coherence length and peak intensity. These results provided evidence that superconductivity is intimately intertwined with CO, disrupting its spatial coherence (Wandel et al., 2022), and that the light-driven non-thermal state of cuprates shares close similarity with that reached under the magnetic field (Jang et al., 2022). Regarding the response of CO above $T_c$, it has been shown that the near-IR light excitation further suppresses the CO peak intensity (Wandel et al., 2022). Therefore, while these pioneering studies demonstrate that studying the transient evolution of CO correlations as an exciting new direction, they could not resolve the possibly different behaviors of the static and dynamic contributions at $q_{CO}$. To gain access into the transient evolution of dynamic CO correlations, time-resolved RIXS (TR-RIXS) becomes necessary.

Building up on the recent report of the ultrafast renormalization of the on-site Coulomb interaction in cuprates via time-resolved X-ray absorption (Baykusheva et al., 2022), we highlight the potential of TR-RIXS to investigate $V_{\text{eff}}$ by noting that visible/near-IR light excitations in the normal state of cuprates can transiently change the screening via the generation of hot carriers. Consequently, a change in the screening should affect the local minimum of the effective Coulomb interaction $V_{eff}$ discussed in Section 2.4, thus potentially transiently altering the QCDCs manifold in the $q_x$-$q_y$ plane–this could be detected with TR-RIXS. And while the current energy resolution of the time-resolved RIXS endstations at the Cu-$L_3$ edge ($\sim$100 meV) may not allow tracking the transient evolution of the phonon softening described in Section 2.5, it is certainly sufficient to separate the quasi-static CO peak from the high-energy CO correlations and other underlying collective excitations. Furthermore, the proposed studies would benefit from complementary time- and angle-resolved photoemission spectroscopy (TR-ARPES) experiments. TR-ARPES, which can access light-induced changes in the low-energy electronic band structure with momentum resolution (Boschini et al., 2024), allows the simultaneous measurement of transient changes in the band structure. A combined TR-RIXS and TR-ARPES study would thus allow us to assess the effects of the Lindhard polarizability on the transient response of CO correlations, ultimately determining how much it may contribute to the RIXS signal and/or the emergence of QCDCs.

The experimental strategy discussed above relies on the combination of two experimental probes to obtain direct insights into the momentum transfer $\mathbf{q}$ (RIXS) and the electronic state momentum $\mathbf{k}$ (ARPES) with energy resolution. However, by combining these two momentum-resolved techniques, we would still not be able to identify exactly which electronic states $\mathbf{k}$ are correlated by $q_{CO}$. In this context, the recently proposed development of two-electron coincidence techniques, such as 2e-ARPES (Trützschler et al., 2017; Mahmood et al., 2022) and noise correlation ARPES (Stahl and Eckstein, 2019; Su and Zhang, 2020; Devereaux et al., 2023), may provide direct access to the static and dynamic correlations between two electronic states for the first time. Looking ahead, the successful demonstration and development of these techniques would offer a direct way to quantitatively estimate which electronic states play a role in the emergence of charge correlations in cuprates and in quantum materials in general.

Author contributions

ES: Writing–original draft, Writing–review and editing. AF: Writing–original draft, Writing–review and editing. FB: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. ES was supported by the Alfred P. Sloan Fellowship and the National Science Foundation under Grant No. DMR-2034345. AF was supported by the CIFAR Azrieli Global Scholars program and by the National Science Foundation under Grant No. DMR-2145080. FB was supported by the Natural Sciences and Engineering Research Council of Canada, the Canada Research Chairs Program, the Fonds de recherche du Québec–Nature et Technologies, and the Ministère de l’Économie, de l’Innovation et de l’Énergie - Québec.

Acknowledgments

We thank Kirsty Scott, Matteo Minola and Yu He for the careful reading of the manuscript and insightful comments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The Handling Editor JP declared a past co-authorship/collaboration with the authors.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbamonte, P., Rusydi, A., Smadici, S., Gu, G. D., Sawatzky, G. A., and Feng, D. L. (2005). Spatially modulated ‘Mottness’ in La₂−xBa_xCuO₄. Nat. Phys. 1, 155–158. doi:10.1038/nphys178

CrossRef Full Text | Google Scholar

Aji, V., and Varma, C. M. (2007). Theory of the quantum critical fluctuations in cuprate superconductors. Phys. Rev. Lett. 99, 067003. doi:10.1103/PhysRevLett.99.067003

PubMed Abstract | CrossRef Full Text | Google Scholar

Ament, L. J. P., van Veenendaal, M., Devereaux, T. P., Hill, J. P., and van den Brink, J. (2011). Resonant inelastic x-ray scattering studies of elementary excitations. Rev. Mod. Phys. 83, 705–767. doi:10.1103/revmodphys.83.705

CrossRef Full Text | Google Scholar

Arpaia, R., Caprara, S., Fumagalli, R., De Vecchi, G., Peng, Y. Y., Andersson, E., et al. (2019). Dynamical charge density fluctuations pervading the phase diagram of a Cu-based high-Tc superconductor. Science 365, 906–910. doi:10.1126/science.aav1315

PubMed Abstract | CrossRef Full Text | Google Scholar

Arpaia, R., and Ghiringhelli, G. (2021). Charge order at high temperature in cuprate superconductors. J. Phys. Soc. Jpn. 90, 111005. doi:10.7566/JPSJ.90.111005

CrossRef Full Text | Google Scholar

Arpaia, R., Martinelli, L., Sala, M. M., Caprara, S., Nag, A., Brookes, N. B., et al. (2023). Signature of quantum criticality in cuprates by charge density fluctuations. Nat. Commun. 14, 7198. doi:10.1038/s41467-023-42961-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Baykusheva, D. R., Jang, H., Husain, A. A., Lee, S., TenHuisen, S. F. R., Zhou, P., et al. (2022). Ultrafast renormalization of the on-site coulomb repulsion in a cuprate superconductor. Phys. Rev. X 12, 011013. doi:10.1103/PhysRevX.12.011013

CrossRef Full Text | Google Scholar

Becca, F., Tarquini, M., Grilli, M., and Di Castro, C. (1996). Charge-density waves and superconductivity as an alternative to phase separation in the infinite-u hubbard-holstein model. Phys. Rev. B 54, 12443–12457. doi:10.1103/PhysRevB.54.12443

PubMed Abstract | CrossRef Full Text | Google Scholar

Bejas, M., Zeyher, R., and Greco, A. (2022). Ring-like shaped charge modulations in the t–j model with long-range coulomb interaction. Phys. Rev. B 106, 224512. doi:10.1103/PhysRevB.106.224512

CrossRef Full Text | Google Scholar

Betto, D., Fumagalli, R., Martinelli, L., Rossi, M., Piombo, R., Yoshimi, K., et al. (2021). Multiple-magnon excitations shape the spin spectrum of cuprate parent compounds. Phys. Rev. B 103, L140409. doi:10.1103/PhysRevB.103.L140409

CrossRef Full Text | Google Scholar

Blanco-Canosa, S., Frano, A., Schierle, E., Porras, J., Loew, T., Minola, M., et al. (2014). Resonant x-ray scattering study of charge-density wave correlations in YBa₂Cu₃O_6+x. Phys. Rev. B 90, 054513. doi:10.1103/physrevb.90.054513

CrossRef Full Text | Google Scholar

Bluschke, M., Frano, A., Schierle, E., Putzky, D., Ghorbani, F., Ortiz, R., et al. (2018). Stabilization of three-dimensional charge order in YBa₂Cu₃O_6+x via epitaxial growth. Nat. Commun. 9, 2978. doi:10.1038/s41467-018-05434-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Bluschke, M., Gupta, N. K., Jang, H., Husain, A. A., Lee, B., Kim, M., et al. (2024). “Orbital-selective time-domain signature of nematicity dynamics in the charge-density-wave phase of La₁.₆₅Eu₀.₂Sr₀.₁₅CuO₄,” in Proceedings of the National Academy of Sciences 121.e2400727121

Google Scholar

Boschini, F., Minola, M., Sutarto, R., Schierle, E., Bluschke, M., Das, S., et al. (2021). Dynamic electron correlations with charge order wavelength along all directions in the copper oxide plane. Nat. Commun. 12, 597–598. doi:10.1038/s41467-020-20824-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Boschini, F., Zonno, M., and Damascelli, A. (2024). Time-resolved arpes studies of quantum materials. Rev. Mod. Phys. 96, 015003. doi:10.1103/revmodphys.96.015003

CrossRef Full Text | Google Scholar

Boyle, T. J., Walker, M., Ruiz, A., Schierle, E., Zhao, Z., Boschini, F., et al. (2021). Large response of charge stripes to uniaxial stress in La₁.₄₇₅Nd₀.₄Sr₀.₁₂₅CuO₄. Phys. Rev. Res. 3, L022004. doi:10.1103/PhysRevResearch.3.L022004

CrossRef Full Text | Google Scholar

Braicovich, L., Minola, M., Dellea, G., Le Tacon, M., Moretti Sala, M., Morawe, C., et al. (2014). The simultaneous measurement of energy and linear polarization of the scattered radiation in resonant inelastic soft x-ray scattering. Rev. Sci. Instrum. 85, 115104. doi:10.1063/1.4900959

PubMed Abstract | CrossRef Full Text | Google Scholar

Braicovich, L., Rossi, M., Fumagalli, R., Peng, Y., Wang, Y., Arpaia, R., et al. (2020). Determining the electron-phonon coupling in superconducting cuprates by resonant inelastic x-ray scattering: methods and results on Nd_+XBa_2−xCu₃O_7−δ. Phys. Rev. Res. 2, 023231. doi:10.1103/physrevresearch.2.023231

CrossRef Full Text | Google Scholar

Braicovich, L., van den Brink, J., Bisogni, V., Sala, M. M., Ament, L. J. P., Brookes, N. B., et al. (2010). Magnetic excitations and phase separation in the underdoped La_2−xSr_xCuO₄ superconductor measured by resonant inelastic x-ray scattering. Phys. Rev. Lett. 104, 077002. doi:10.1103/PhysRevLett.104.077002

PubMed Abstract | CrossRef Full Text | Google Scholar

Brookes, N., Yakhou-Harris, F., Kummer, K., Fondacaro, A., Cezar, J., Betto, D., et al. (2018). The beamline ID32 at the esrf for soft x-ray high energy resolution resonant inelastic x-ray scattering and polarisation dependent x-ray absorption spectroscopy. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 903, 175–192. doi:10.1016/j.nima.2018.07.001

CrossRef Full Text | Google Scholar

Caprara, S., Castro, C. D., Mirarchi, G., Seibold, G., and Grilli, M. (2022). Dissipation-driven strange metal behavior. Commun. Phys. 5, 10–17. doi:10.1038/s42005-021-00786-y

CrossRef Full Text | Google Scholar

Caprara, S., Grilli, M., Di Castro, C., and Seibold, G. (2017). Pseudogap and (an)isotropic scattering in the fluctuating charge-density wave phase of cuprates. J. Supercond. Nov. Magnetism 30, 25–30. doi:10.1007/s10948-016-3775-9

CrossRef Full Text | Google Scholar

Chaix, L., Ghiringhelli, G., Peng, Y. Y., Hashimoto, M., Moritz, B., Kummer, K., et al. (2017). Dispersive charge density wave excitations in Bi₂Sr₂CaCu₂O_8+δ. Nat. Phys. 13, 952–956. doi:10.1038/nphys4157

CrossRef Full Text | Google Scholar

Chang, J., Blackburn, E., Holmes, A. T., Christensen, N. B., Larsen, J., Mesot, J., et al. (2012). Direct observation of competition between superconductivity and charge density wave order in YBa₂Cu₃O₆.₆₇. Nat. Phys. 8, 871–876. doi:10.1038/nphys2456

CrossRef Full Text | Google Scholar

Chen, X., Choi, J., Jiang, Z., Mei, J., Jiang, K., Li, J., et al. (2024). “Electronic and magnetic excitations in La₃Ni₂O₇,”. Available at: https://arxiv.org/abs/2401.12657

CrossRef Full Text | Google Scholar

Chuang, Y.-D., Feng, X., Cruz, A., Hanzel, K., Brown, A., Spucces, A., et al. (2022). Momentum-resolved resonant inelastic soft X-ray scattering (qRIXS) endstation at the ALS. J. Electron Spectrosc. Relat. Phenom. 257, 146897. doi:10.1016/j.elspec.2019.146897

CrossRef Full Text | Google Scholar

Comin, R., and Damascelli, A. (2016). Resonant x-ray scattering studies of charge order in cuprates. Annu. Rev. Condens. Matter Phys. 7, 369–405. doi:10.1146/annurev-conmatphys-031115-011401

CrossRef Full Text | Google Scholar

Comin, R., Frano, A., Yee, M. M., Yoshida, Y., Eisaki, H., Schierle, E., et al. (2014). Charge order driven by fermi-arc instability in Bi₂Sr_2−xLa_xCuO_6+δ. Science 343, 390–392. doi:10.1126/science.1242996

PubMed Abstract | CrossRef Full Text | Google Scholar

da Silva Neto, E. H., Aynajian, P., Frano, A., Comin, R., Schierle, E., Weschke, E., et al. (2014). Ubiquitous interplay between charge ordering and high-temperature superconductivity in cuprates. Science 343, 393–396. doi:10.1126/science.1243479

PubMed Abstract | CrossRef Full Text | Google Scholar

da Silva Neto, E. H., Comin, R., He, F., Sutarto, R., Jiang, Y., Greene, R. L., et al. (2015). Charge ordering in the electron-doped superconductor Nd_2−xCe_xCuO₄. Science 347, 282–285. doi:10.1126/science.1256441

PubMed Abstract | CrossRef Full Text | Google Scholar

da Silva Neto, E. H., Minola, M., Yu, B., Tabis, W., Bluschke, M., Unruh, D., et al. (2018). Coupling between dynamic magnetic and charge-order correlations in the cuprate superconductor superconductor Nd_2−xCe_xCuO₄. Phys. Rev. B 98, 161114. doi:10.1103/PhysRevB.98.161114

CrossRef Full Text | Google Scholar

da Silva Neto, E. H., Yu, B., Minola, M., Sutarto, R., Schierle, E., Boschini, F., et al. (2016). Doping-dependent charge order correlations in electron-doped cuprates. Sci. Adv 2, e1600782. doi:10.1126/sciadv.1600782

PubMed Abstract | CrossRef Full Text | Google Scholar

de Groot, F. M. F., Haverkort, M. W., Elnaggar, H., Juhin, A., Zhou, K.-J., and Glatzel, P. (2024). Resonant inelastic x-ray scattering. Nat. Rev. Methods Prim. 4, 45. doi:10.1038/s43586-024-00322-6

CrossRef Full Text | Google Scholar

Devereaux, T. P., Claassen, M., Huang, X.-X., Zaletel, M., Moore, J. E., Morr, D., et al. (2023). Angle-resolved pair photoemission theory for correlated electrons. Phys. Rev. B 108, 165134. doi:10.1103/physrevb.108.165134

CrossRef Full Text | Google Scholar

Devereaux, T. P., Shvaika, A. M., Wu, K., Wohlfeld, K., Jia, C. J., Wang, Y., et al. (2016). Directly characterizing the relative strength and momentum dependence of electron-phonon coupling using resonant inelastic X-ray scattering. Phys. Rev. X 6, 041019. doi:10.1103/PhysRevX.6.041019

CrossRef Full Text | Google Scholar

Drozdov, I. K., Pletikosić, I., Kim, C.-K., Fujita, K., Gu, G. D., Davis, J. C. S., et al. (2018). Phase diagram of Bi₂Sr₂CaCu₂O_8+δ revisited. Nat. Commun. 9, 5210. doi:10.1038/s41467-018-07686-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Dvorak, J., Jarrige, I., Bisogni, V., Coburn, S., and Leonhardt, W. (2016). Towards 10 mev resolution: the design of an ultrahigh resolution soft x-ray rixs spectrometer. Rev. Sci. Instrum. 87, 115109. doi:10.1063/1.4964847

PubMed Abstract | CrossRef Full Text | Google Scholar

Emery, V., and Kivelson, S. (1993). Frustrated electronic phase separation and high-temperature superconductors. Phys. C. Supercond. 209, 597–621. doi:10.1016/0921-4534(93)90581-A

CrossRef Full Text | Google Scholar

Frano, A., Blanco-Canosa, S., Keimer, B., and Birgeneau, R. J. (2020). Charge ordering in superconducting copper oxides. J. Phys. Condens. Matter 32, 374005. doi:10.1088/1361-648X/ab6140

PubMed Abstract | CrossRef Full Text | Google Scholar

Fumagalli, R., Braicovich, L., Minola, M., Peng, Y. Y., Kummer, K., Betto, D., et al. (2019). Polarization-resolved cu L₃-edge resonant inelastic x-ray scattering of orbital and spin excitations in NdBa₂Cu₃O_7−δ. Phys. Rev. B 99, 134517. doi:10.1103/PhysRevB.99.134517

CrossRef Full Text | Google Scholar

Ghiringhelli, G., Le Tacon, M., Minola, M., Blanco-Canosa, S., Mazzoli, C., Brookes, N. B., et al. (2012). Long-range incommensurate charge fluctuations in (Y,Nd)Ba₂Cu₃O_6+x. Science 337, 821–825. doi:10.1126/science.1223532

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghiringhelli, G., Piazzalunga, A., Dallera, C., Trezzi, G., Braicovich, L., Schmitt, T., et al. (2006). SAXES, a high resolution spectrometer for resonant x-ray emission in the 400–1600eV energy range. Rev. Sci. Instrum. 77, 113108. doi:10.1063/1.2372731

CrossRef Full Text | Google Scholar

Grissonnanche, G., Fang, Y., Legros, A., Verret, S., Laliberté, F., Collignon, C., et al. (2021). Linear-in temperature resistivity from an isotropic planckian scattering rate. Nature 595, 667–672. doi:10.1038/s41586-021-03697-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Gupta, N. K., Sutarto, R., Gong, R., Idziak, S. H. J., Hale, H., Kim, Y.-J., et al. (2023). Tuning charge density wave order and structure via uniaxial stress in a stripe-ordered cuprate superconductor. Phys. Rev. B 108, L121113. doi:10.1103/PhysRevB.108.L121113

CrossRef Full Text | Google Scholar

Gurvitch, M., and Fiory, A. T. (1987). Resistivity of La₁.₈₂₅Sr₀.₁₇₅CuO₄ and YBa₂Cu₃O₇ to 1100 k: Absence of saturation and its implications. Phys. Rev. Lett. 59, 1337–1340. doi:10.1103/PhysRevLett.59.1337

PubMed Abstract | CrossRef Full Text | Google Scholar

Hawthorn, D. G., He, F., Venema, L., Davis, H., Achkar, A. J., Zhang, J., et al. (2011). An in-vacuum diffractometer for resonant elastic soft x-ray scattering. Rev. Sci. Instrum. 82, 073104. doi:10.1063/1.3607438

PubMed Abstract | CrossRef Full Text | Google Scholar

Hepting, M., Bejas, M., Nag, A., Yamase, H., Coppola, N., Betto, D., et al. (2022). Gapped collective charge excitations and interlayer hopping in cuprate superconductors. Phys. Rev. Lett. 129, 047001. doi:10.1103/PhysRevLett.129.047001

PubMed Abstract | CrossRef Full Text | Google Scholar

Hepting, M., Boyko, T. D., Zimmermann, V., Bejas, M., Suyolcu, Y. E., Puphal, P., et al. (2023). Evolution of plasmon excitations across the phase diagram of the cuprate superconductor La_2−xSr_xCuO₄. Phys. Rev. B 107, 214516. doi:10.1103/PhysRevB.107.214516

CrossRef Full Text | Google Scholar

Hepting, M., Chaix, L., Huang, E. W., Fumagalli, R., Peng, Y. Y., Moritz, B., et al. (2018). Three-dimensional collective charge excitations in electron-doped copper oxide superconductors. Nature 563, 374–378. doi:10.1038/s41586-018-0648-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Hill, J. P., Blumberg, G., Kim, Y.-J., Ellis, D. S., Wakimoto, S., Birgeneau, R. J., et al. (2008). Observation of a 500 mev collective mode in La_2−xSr_xCuO₄ and Nd₂CuO₄ using resonant inelastic x-ray scattering. Phys. Rev. Lett. 100, 097001. doi:10.1103/PhysRevLett.100.097001

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoffman, J. E., Hudson, E. W., Lang, K. M., Madhavan, V., Eisaki, H., Uchida, S., et al. (2002). A four unit cell periodic pattern of quasi-particle states surrounding vortex cores in Bi₂Sr₂CaCu₂O_8+δ. Science 295, 466–469. doi:10.1126/science.1066974

PubMed Abstract | CrossRef Full Text | Google Scholar

Howald, C., Eisaki, H., Kaneko, N., and Kapitulnik, A. (2003). Coexistence of periodic modulation of quasiparticle states and superconductivity in in Bi₂Sr₂CaCu₂O_8+δ. Proc. Natl. Acad. Sci. 100, 9705–9709. doi:10.1073/pnas.1233768100

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, E. W., Mendl, C. B., Liu, S., Johnston, S., Jiang, H.-C., Moritz, B., et al. (2017). Numerical evidence of fluctuating stripes in the normal state of high-T_c cuprate superconductors. Science 358, 1161–1164. doi:10.1126/science.aak9546

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, H. Y., Singh, A., Mou, C. Y., Johnston, S., Kemper, A. F., van den Brink, J., et al. (2021). Quantum fluctuations of charge order induce phonon softening in a superconducting cuprate. Phys. Rev. X 11, 041038. doi:10.1103/PhysRevX.11.041038

CrossRef Full Text | Google Scholar

Husain, A. A., Mitrano, M., Rak, M. S., Rubeck, S., Uchoa, B., March, K., et al. (2019). Crossover of charge fluctuations across the strange metal phase diagram. Phys. Rev. X 9, 041062. doi:10.1103/PhysRevX.9.041062

CrossRef Full Text | Google Scholar

Hwang, J., Timusk, T., and Gu, G. D. (2007). Doping dependent optical properties of Bi₂Sr₂CaCu₂O_8+δ. J. Phys. Condens. Matter 19, 125208. doi:10.1088/0953-8984/19/12/125208

CrossRef Full Text | Google Scholar

Ishii, K., Fujita, M., Sasaki, T., Minola, M., Dellea, G., Mazzoli, C., et al. (2014). High-energy spin and charge excitations in electron-doped copper oxide superconductors. Nat. Commun. 5, 3714. doi:10.1038/ncomms4714

PubMed Abstract | CrossRef Full Text | Google Scholar

Jang, H., Song, S., Kihara, T., Liu, Y., Lee, S.-J., Park, S.-Y., et al. (2022). Characterization of photoinduced normal state through charge density wave in superconducting YBa₂Cu₃O₆.₆₇. Sci. Adv. 8, eabk0832. doi:10.1126/sciadv.abk0832

PubMed Abstract | CrossRef Full Text | Google Scholar

Jarrige, I., Bisogni, V., Zhu, Y., Leonhardt, W., and Dvorak, J. (2018). Paving the way to ultra-high-resolution resonant inelastic x-ray scattering with the six beamline at NSLS-II. Synchrotron Radiat. News 31, 7–13. doi:10.1080/08940886.2018.1435949

CrossRef Full Text | Google Scholar

Kang, M., Pelliciari, J., Frano, A., Breznay, N., Schierle, E., Weschke, E., et al. (2019). Evolution of charge order topology across a magnetic phase transition in cuprate superconductors. Nat. Phys. 15, 335–340. doi:10.1038/s41567-018-0401-8

CrossRef Full Text | Google Scholar

Kim, H.-H., Lefrançois, E., Kummer, K., Fumagalli, R., Brookes, N. B., Betto, D., et al. (2021). Charge density waves in YBa₂Cu₃O₆.₆₇ probed by resonant x-ray scattering under uniaxial compression. Phys. Rev. Lett. 126, 037002. doi:10.1103/PhysRevLett.126.037002

PubMed Abstract | CrossRef Full Text | Google Scholar

Kivelson, S. A., Bindloss, I. P., Fradkin, E., Oganesyan, V., Tranquada, J. M., Kapitulnik, A., et al. (2003). How to detect fluctuating stripes in the high-temperature superconductors. Rev. Mod. Phys. 75, 1201–1241. doi:10.1103/RevModPhys.75.1201

CrossRef Full Text | Google Scholar

Lee, W. S., Lee, J. J., Nowadnick, E. A., Gerber, S., Tabis, W., Huang, S. W., et al. (2014). Asymmetry of collective excitations in electron- and hole-doped cuprate superconductors. Nat. Phys. 10, 883–889. doi:10.1038/nphys3117

CrossRef Full Text | Google Scholar

Lee, W. S., Zhou, K.-J., Hepting, M., Li, J., Nag, A., Walters, A. C., et al. (2021). Spectroscopic fingerprint of charge order melting driven by quantum fluctuations in a cuprate. Nat. Phys. 17, 53–57. doi:10.1038/s41567-020-0993-7

CrossRef Full Text | Google Scholar

Le Tacon, M., Ghiringhelli, G., Chaloupka, J., Sala, M. M., Hinkov, V., Haverkort, M. W., et al. (2011). Intense paramagnon excitations in a large family of high-temperature superconductors. Nat. Phys. 7, 725–730. doi:10.1038/nphys2041

CrossRef Full Text | Google Scholar

Li, J., Nag, A., Pelliciari, J., Robarts, H., Walters, A., Garcia-Fernandez, M., et al. (2020). Multiorbital charge-density wave excitations and concomitant phonon anomalies in Bi₂Sr₂LaCuO_6+δ. Proc. Natl. Acad. Sci. 117, 16219–16225. doi:10.1073/pnas.2001755117

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, J., Yuan, J., Jin, K., Yin, Z., Li, G., Zhou, K.-J., et al. (2020a). Doping evolution of the charge excitations and electron correlations in electron-doped superconducting La_2−xCe_xCuO₄. npj Quantum Mater. 5, 4. doi:10.1038/s41535-019-0205-9

CrossRef Full Text | Google Scholar

Lin, J. Q., Miao, H., Mazzone, D. G., Gu, G. D., Nag, A., Walters, A. C., et al. (2020b). Strongly correlated charge density wave in La_2−xSr_xCuO₄ evidenced by doping-dependent phonon anomaly. Phys. Rev. Lett. 124, 207005. doi:10.1103/PhysRevLett.124.207005

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, H., Hashimoto, M., Chen, S.-D., Ishida, S., Song, D., Eisaki, H., et al. (2022). Identification of a characteristic doping for charge order phenomena in Bi-2212 cuprates via rixs. Phys. Rev. B 106, 155109. doi:10.1103/physrevb.106.155109

CrossRef Full Text | Google Scholar

Machida, K. (1989). Magnetism in Bi_2+xSr_2−yCuO_6+δ based compounds. Phys. C. Supercond. 158, 192–196. doi:10.1016/0921-4534(89)90316-X

CrossRef Full Text | Google Scholar

Mahmood, F., Devereaux, T., Abbamonte, P., and Morr, D. K. (2022). Distinguishing finite-momentum superconducting pairing states with two-electron photoemission spectroscopy. Phys. Rev. B 105, 064515. doi:10.1103/physrevb.105.064515

CrossRef Full Text | Google Scholar

Martin, S., Fiory, A. T., Fleming, R. M., Schneemeyer, L. F., and Waszczak, J. V. (1990). Normal-state transport properties of Bi_2+xSr_2−yCuO_6+δ crystals. Phys. Rev. B 41, 846–849. doi:10.1103/PhysRevB.41.846

PubMed Abstract | CrossRef Full Text | Google Scholar

Martinelli, L., Biało, I., Hong, X., Oppliger, J., Lin, C., Schaller, T., et al. (2024). “Decoupled static and dynamical charge correlations in La_2−xSr_xCuO₄,”. doi:10.48550/arXiv.2406.15062

CrossRef Full Text | Google Scholar

Merzoni, G., Martinelli, L., Braicovich, L., Brookes, N. B., Lombardi, F., Rosa, F., et al. (2024). Charge response function probed by resonant inelastic x-ray scattering: signature of electronic gaps of YBa₂Cu₃O_7−δ. Phys. Rev. B 109, 184506. doi:10.1103/PhysRevB.109.184506

CrossRef Full Text | Google Scholar

Miao, H., Fumagalli, R., Rossi, M., Lorenzana, J., Seibold, G., Yakhou-Harris, F., et al. (2019). Formation of incommensurate charge density waves in cuprates. Phys. Rev. X 9, 031042. doi:10.1103/PhysRevX.9.031042

CrossRef Full Text | Google Scholar

Miao, H., Lorenzana, J., Seibold, G., Peng, Y. Y., Amorese, A., Yakhou-Harris, F., et al. (2017). Precursor charge density waves in La₁.₈₇₅Ba₀.₁₂₅CuO₄. ArXiv e-prints

Google Scholar

Minola, M., Dellea, G., Gretarsson, H., Peng, Y. Y., Lu, Y., Porras, J., et al. (2015). Collective nature of spin excitations in superconducting cuprates probed by resonant inelastic x-ray scattering. Phys. Rev. Lett. 114, 217003. doi:10.1103/PhysRevLett.114.217003

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitrano, M., Husain, A. A., Vig, S., Kogar, A., Rak, M. S., Rubeck, S. I., et al. (2018). Anomalous density fluctuations in a strange metal. Proc. Natl. Acad. Sci. 115, 5392–5396. doi:10.1073/pnas.1721495115

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitrano, M., Lee, S., Husain, A. A., Delacretaz, L., Zhu, M., de la Peña Munoz, G., et al. (2019). Ultrafast time-resolved x-ray scattering reveals diffusive charge order dynamics in La_2−xBa_xCuO₄. Sci. Adv. 5, eaax3346. doi:10.1126/sciadv.aax3346

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitrano, M., and Wang, Y. (2020). Probing light-driven quantum materials with ultrafast resonant inelastic x-ray scattering. Commun. Phys. 3, 184. doi:10.1038/s42005-020-00447-6

CrossRef Full Text | Google Scholar

Nag, A., Zhu, M., Bejas, M., Li, J., Robarts, H. C., Yamase, H., et al. (2020). Detection of acoustic plasmons in hole-doped lanthanum and bismuth cuprate superconductors using resonant inelastic x-ray scattering. Phys. Rev. Lett. 125, 257002. doi:10.1103/PhysRevLett.125.257002

PubMed Abstract | CrossRef Full Text | Google Scholar

Patel, A. A., Guo, H., Esterlis, I., and Sachdev, S. (2023). Universal theory of strange metals from spatially random interactions. Science 381, 790–793. doi:10.1126/science.abq6011

PubMed Abstract | CrossRef Full Text | Google Scholar

Patel, A. A., McGreevy, J., Arovas, D. P., and Sachdev, S. (2018). Magnetotransport in a model of a disordered strange metal. Phys. Rev. X 8, 021049. doi:10.1103/physrevx.8.021049

CrossRef Full Text | Google Scholar

Patel, A. A., and Sachdev, S. (2019). Theory of a planckian metal. Phys. Rev. Lett. 123, 066601. doi:10.1103/PhysRevLett.123.066601

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, Y., Martinelli, L., Li, Q., Rossi, M., Mitrano, M., Arpaia, R., et al. (2022). Doping dependence of the electron-phonon coupling in two families of bilayer superconducting cuprates. Phys. Rev. B 105, 115105. doi:10.1103/PhysRevB.105.115105

CrossRef Full Text | Google Scholar

Peng, Y. Y., Hashimoto, M., Sala, M. M., Amorese, A., Brookes, N. B., Dellea, G., et al. (2015). Magnetic excitations and phonons simultaneously studied by resonant inelastic x-ray scattering in optimally doped Bi₁.₅Pb₀.₅₅Sr_1.6La0.4CuO_6+δ. Phys. Rev. B 92, 064517. doi:10.1103/PhysRevB.92.064517

CrossRef Full Text | Google Scholar

Peng, Y. Y., Husain, A. A., Mitrano, M., Sun, S. X.-L., Johnson, T. A., Zakrzewski, A. V., et al. (2020). Enhanced electron-phonon coupling for charge-density-wave formation in La₁._8−xEu₀.₂Sr_xCuO_4+δ. Phys. Rev. Lett. 125, 097002. doi:10.1103/PhysRevLett.125.097002

PubMed Abstract | CrossRef Full Text | Google Scholar

Phillips, P. W., Hussey, N. E., and Abbamonte, P. (2022). Stranger than metals. Science 377, eabh4273. doi:10.1126/science.abh4273

PubMed Abstract | CrossRef Full Text | Google Scholar

Riegler, D., Seufert, J., da Silva Neto, E. H., Wölfle, P., Thomale, R., and Klett, M. (2023). Interplay of spin and charge order in the electron-doped cuprates. Phys. Rev. B 108, 195141. doi:10.1103/PhysRevB.108.195141

CrossRef Full Text | Google Scholar

Rossi, M., Arpaia, R., Fumagalli, R., Moretti Sala, M., Betto, D., Kummer, K., et al. (2019). Experimental determination of momentum-resolved electron-phonon coupling. Phys. Rev. Lett. 123, 027001. doi:10.1103/PhysRevLett.123.027001

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruiz, A., Gunn, B., Lu, Y., Sasmal, K., Moir, C. M., Basak, R., et al. (2022). Stabilization of three-dimensional charge order through interplanar orbital hybridization in Pr_xY_1−xBa₂Cu₃O_6+δ. Nat. Commun. 6197, 6197. doi:10.1038/s41467-022-33607-z

CrossRef Full Text | Google Scholar

Sala, M. M., Bisogni, V., Aruta, C., Balestrino, G., Berger, H., Brookes, N. B., et al. (2011). Energy and symmetry of dd excitations in undoped layered cuprates measured by Cu−L₃ resonant inelastic x-ray scattering. New J. Phys. 13, 043026. doi:10.1088/1367-2630/13/4/043026

CrossRef Full Text | Google Scholar

Scott, K., Kisiel, E., Boyle, T. J., Basak, R., Jargot, G., Das, S., et al. (2023). Low-energy quasi-circular electron correlations with charge order wavelength in Bi₂Sr₂CaCu2O_8+δ. Sci. Adv. 9, eadg3710. doi:10.1126/sciadv.adg3710

PubMed Abstract | CrossRef Full Text | Google Scholar

Scott, K., Kisiel, E., Yakhou, F., Agrestini, S., Garcia-Fernandez, M., Kummer, K., et al. (2024). Detection of a two-phonon mode in a cuprate superconductor via polarimetric resonant inelastic x-ray scattering. Phys. Rev. B 109, 125126. doi:10.1103/PhysRevB.109.125126

CrossRef Full Text | Google Scholar

Seibold, G., Arpaia, R., Peng, Y. Y., Fumagalli, R., Braicovich, L., Di Castro, C., et al. (2021). Strange metal behaviour from charge density fluctuations in cuprates. Commun. Phys. 4, 7–6. doi:10.1038/s42005-020-00505-z

CrossRef Full Text | Google Scholar

Seibold, G., Becca, F., Bucci, F., Castellani, C., Di Castro, C., and Grilli, M. (2000). Spectral properties of incommensurate charge-density wave systems. Eur. Phys. J. B - Condens. Matter Complex Syst. 13, 87–97. doi:10.1007/s100510050013

CrossRef Full Text | Google Scholar

Singh, A., Huang, H. Y., Lane, C., Li, J. H., Okamoto, J., Komiya, S., et al. (2022). Acoustic plasmons and conducting carriers in hole-doped cuprate superconductors. Phys. Rev. B 105, 235105. doi:10.1103/PhysRevB.105.235105

CrossRef Full Text | Google Scholar

Stahl, C., and Eckstein, M. (2019). Noise correlations in time-and angle-resolved photoemission spectroscopy. Phys. Rev. B 99, 241111. doi:10.1103/physrevb.99.241111

CrossRef Full Text | Google Scholar

Strocov, V. N., Schmitt, T., Flechsig, U., Schmidt, T., Imhof, A., Chen, Q., et al. (2010). High-resolution soft X-ray beamline ADRESS at the Swiss Light Source for resonant inelastic X-ray scattering and angle-resolved photoelectron spectroscopies. J. Synchrotron Radiat. 17, 631–643. doi:10.1107/S0909049510019862

PubMed Abstract | CrossRef Full Text | Google Scholar

Su, Y., and Zhang, C. (2020). Coincidence angle-resolved photoemission spectroscopy: proposal for detection of two-particle correlations. Phys. Rev. B 101, 205110. doi:10.1103/physrevb.101.205110

CrossRef Full Text | Google Scholar

Suzuki, H., Minola, M., Lu, Y., Peng, Y., Fumagalli, R., Lefrançois, E., et al. (2018). Probing the energy gap of high-temperature cuprate superconductors by resonant inelastic x-ray scattering. npj Quantum Mater. 3, 65. doi:10.1038/s41535-018-0139-7

CrossRef Full Text | Google Scholar

Tabis, W., Li, Y., Le Tacon, M., Braicovich, L., Kreyssig, A., Minola, M., et al. (2014). Charge order and its connection with Fermi-liquid charge transport in a pristine high-Tc cuprate. Nat. Comm. 5, 5875. doi:10.1038/ncomms6875

PubMed Abstract | CrossRef Full Text | Google Scholar

Takayanagi, T., Kogure, M., and Terasaki, I. (2002). Out-of-plane dielectric constant and insulator-superconductor transition in Bi₂Sr₂Dy_1−xEr_xCu₂O₈ single crystals. J. Phys. Condens. Matter 14, 1361–1370. doi:10.1088/0953-8984/14/6/321

CrossRef Full Text | Google Scholar

Tranquada, J. M., Sternlieb, B. J., Axe, J. D., Nakamura, Y., and Uchida, S. (1995). Evidence for stripe correlations of spins and holes in copper oxide superconductors. Nature 375, 561–563. doi:10.1038/375561a0

CrossRef Full Text | Google Scholar

Trützschler, A., Huth, M., Chiang, C.-T., Kamrla, R., Schumann, F. O., Kirschner, J., et al. (2017). Band-resolved double photoemission spectroscopy on correlated valence electron pairs in metals. Phys. Rev. Lett. 118, 136401. doi:10.1103/physrevlett.118.136401

PubMed Abstract | CrossRef Full Text | Google Scholar

Varma, C. M., Littlewood, P. B., Schmitt-Rink, S., Abrahams, E., and Ruckenstein, A. E. (1989). Phenomenology of the normal state of cu-o high-temperature superconductors. Phys. Rev. Lett. 63, 1996–1999. doi:10.1103/physrevlett.63.1996

PubMed Abstract | CrossRef Full Text | Google Scholar

Vershinin, M., Misra, S., Ono, S., Abe, Y., Ando, Y., and Yazdani, A. (2004). Local ordering in the pseudogap state of the high-Tc superconductor Bi₂Sr₂CaCu₂O_8+δ. Science 303, 1995–1998. doi:10.1126/science.1093384

PubMed Abstract | CrossRef Full Text | Google Scholar

Wahlberg, E., Arpaia, R., Seibold, G., Rossi, M., Fumagalli, R., Trabaldo, E., et al. (2021). Restored strange metal phase through suppression of charge density waves in underdoped YBa₂Cu₃O_7−δ. Science 373, 1506–1510. doi:10.1126/science.abc8372

PubMed Abstract | CrossRef Full Text | Google Scholar

Wandel, S., Boschini, F., da Silva Neto, E., Shen, L., Na, M., Zohar, S., et al. (2022). Enhanced charge density wave coherence in a light-quenched, high-temperature superconductor. Science 376, 860–864. doi:10.1126/science.abd7213

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Q., von Arx, K., Horio, M., Mukkattukavil, D. J., Küspert, J., Sassa, Y., et al. (2021). Charge order lock-in by electron-phonon coupling in La₁.₆₇₅Eu₀.₂Sr₀.₁₂₅CuO₄. Sci. Adv. 7, eabg7394. doi:10.1126/sciadv.abg7394

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Q., von Arx, K., Mazzone, D. G., Mustafi, S., Horio, M., Küspert, J., et al. (2022). Uniaxial pressure induced stripe order rotation in La₁.₈₈Sr₀.₁₂CuO₄. Nat. Commun. 13, 1795. doi:10.1038/s41467-022-29465-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Weschke, E., and Schierle, E. (2018). The ue46 pgm-1 beamline at bessy ii. J. large-scale Res. Facil. JLSRF 4, A127. doi:10.17815/jlsrf-4-77

CrossRef Full Text | Google Scholar

Wise, W. D., Boyer, M. C., Chatterjee, K., Kondo, T., Takeuchi, T., Ikuta, H., et al. (2008). Charge-density-wave origin of cuprate checkerboard visualized by scanning tunnelling microscopy. Nat. Phys. 4, 696–699. doi:10.1038/nphys1021

CrossRef Full Text | Google Scholar

Wu, T., Mayaffre, H., Kramer, S., Horvatic, M., Berthier, C., Hardy, W. N., et al. (2011). Magnetic-field-induced charge-stripe order in the high-temperature superconductor YBa₂Cu₃O_y. Nature 477, 191–194. doi:10.1038/nature10345

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamase, H., Bejas, M., and Greco, A. (2021). Electron self-energy from quantum charge fluctuations in the layered t-j model with long-range coulomb interaction. Phys. Rev. B 104, 045141. doi:10.1103/PhysRevB.104.045141

CrossRef Full Text | Google Scholar

Yazdani, A., da Silva Neto, E. H., and Aynajian, P. (2016). Spectroscopic imaging of strongly correlated electronic states. Annu. Rev. Condens. Matter Phys. 7, 11–33. doi:10.1146/annurev-conmatphys-031214-014529

CrossRef Full Text | Google Scholar

Yu, B., Tabis, W., Bialo, I., Yakhou, F., Brookes, N. B., Anderson, Z., et al. (2020). Unusual dynamic charge correlations in simple-tetragonal HgBa₂ CuO_4+δ. Phys. Rev. X 10, 021059. doi:10.1103/PhysRevX.10.021059

CrossRef Full Text | Google Scholar

Zaanen, J., and Gunnarsson, O. (1989). Charged magnetic domain lines and the magnetism of high-Tc oxides. Phys. Rev. B 40, 7391–7394. doi:10.1103/PhysRevB.40.7391

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, B.-X., Chung, C.-M., Corboz, P., Ehlers, G., Qin, M.-P., Noack, R. M., et al. (2017). Stripe order in the underdoped region of the two-dimensional Hubbard model. Science 358, 1155–1160. doi:10.1126/science.aam7127

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, K.-J., Walters, A., Garcia-Fernandez, M., Rice, T., Hand, M., Nag, A., et al. (2022). I21: an advanced high-resolution resonant inelastic X-ray scattering beamline at Diamond Light Source. J. Synchrotron Radiat. 29, 563–580. doi:10.1107/s1600577522000601

PubMed Abstract | CrossRef Full Text | Google Scholar