On the importance of varying device thickness and temperature on the outcome of space-charge-limited current measurements

Space-charge-limited current (SCLC) measurements are commonly employed to characterize charge-transport properties of semiconductors used in next-generation thin-film optoelectronics, such as organic $\pi$-conjugated small molecules and polymers, and metal-halide perovskites. Despite the wide-spread adoption of the method, there is no community-wide consensus around how SCLC measurements should be performed, nor how the data should be analyzed and reported. While it is common to report device characteristics by employing a simplistic analytical model for fitting a single J-V curve obtained from a solitary device at room temperature—sometimes in a very select voltage range—expectedly, such an approach will often not give an accurate picture of the underlying physics. On that account, we here aim to highlight the importance of reporting values extracted from not just a solitary single-carrier device measured at room temperature, but from devices with different thicknesses measured at varying device temperature. We also highlight how the choice of device thickness is especially critical in determining what device and material characteristics can be extracted from SCLC measurements, and how this choice can greatly affect the conclusions drawn about the probed semiconducting material. While other factors could affect the outcome of an SCLC measurement and the subsequent analysis, we hope that the topics covered in this article will result in overall improved charge-transport characterization of thin-film semiconductors and initiate a broader discussion into SCLC metrology at large.

1 Introduction

Space-charge-limited current (SCLC) measurements (Mott and Gurney, 1940; Dacey, 1953; Shockley and Prim, 1953; Rose, 1955), a class of steady-state DC charge-transport measurements, have become near-ubiquitous within the organic and metal-halide perovskite optoelectronics communities as a tool for estimating key characteristics influencing the performance of solar cells and light-emitting diodes: charge-carrier mobilities, defect characteristics, injection properties, and energetic disorder (Poplavskyy and Nelson, 2003; Van Mensfoort and Coehoorn, 2008; Dacuña and Salleo, 2011; Coehoorn and Bobbert, 2012; Röhr et al., 2018b; Kotadiya et al., 2018; 2019; Lee et al., 2018; Shi et al., 2019; Duijnstee et al., 2020; Sajedi Alvar et al., 2020; Duijnstee et al., 2021; Le Corre et al., 2021; Sachnik et al., 2023; Trieb et al., 2023). Some of the appeals of SCLC measurements include the apparent simplicity of the method and the ability to selectively probe either electron or hole transport through careful design of the single-carrier devices used to perform these measurements. However, while these devices are relatively simple to design and fabricate, the interdependence and magnitudes of the probed characteristics not only complicate the analysis of the obtained current density-voltage (J-V) curves (Röhr et al., 2018b), but also determine the limits of what SCLC measurements can realistically probe (Röhr and MacKenzie, 2020; Le Corre et al., 2021; Röhr, 2024).

Single-carrier devices can be designed to exclusively conduct either electrons or holes by carefully matching the electrode work functions with either the conduction- or valence band-edges of the semiconductor, in which case they are often referred to as either electron- or hole-only devices, respectively (Figure 1A). The work function of a conductor, ${\mathit{{\rm X}}}_{\mathrm{c}}$, is defined as the difference between the conductor Fermi energy, $E_{\mathrm{F},\mathrm{c}}$, and the vacuum level, $E_{\text{vac}}$, i.e., ${\mathit{{\rm X}}}_{\mathrm{c}}=E_{\mathrm{F},\mathrm{c}}-E_{\text{vac}}$. The semiconductor work function can be similarly defined as ${\mathit{{\rm X}}}_{\text{sc}}=E_{\mathrm{F},\text{sc}}-E_{\text{vac}}$. The electron affinity, EA, is given as the difference between $E_{\text{vac}}$ and the conduction band edge, $E_{\mathrm{C}}$, and the ionization potential, IP, is given as the difference between $E_{\text{vac}}$ and the valence band edge, $E_{\mathrm{V}}$. The above-mentioned quantities are shown in Figure 1B. When a conductor is brought into contact with a semiconductor, charge carriers will flow between them until an equilibrium is reached ($E_{\mathrm{F},\mathrm{c}}=E_{\mathrm{F},\text{sc}}$). This results in accumulation of charge carriers in the semiconductor near the interface, forming either a positive of negative space-charge layer. If ${\mathit{{\rm X}}}_{\text{sc}}>{\mathit{{\rm X}}}_{\mathrm{c}}\ge \text{EA}$, a negative space-charge layer will be present near the interface and an ohmic (no injection barrier; $q{\varphi }_{\text{inj}}=0$ eV) or near-ohmic ($q{\varphi }_{\text{inj}}>0$ eV) contact for electron injection is formed, depending on whether ${\mathit{{\rm X}}}_{\mathrm{c}}=\text{EA}$ or ${\mathit{{\rm X}}}_{\mathrm{c}}>\text{EA}$ is true (Figure 1B). An analogous situation would result in a positive space-charge layer, and therefore a hole injection contact, namely, when $\text{IP}\ge {\mathit{{\rm X}}}_{\mathit{c}}>{\mathrm{{\rm X}}}_{\text{sc}}$ (Figure 1B). A single-carrier device is achieved when two such interfaces are joined in series (double-interface devices) (Figure 1B), and the total space charge in a single-carrier device arises from the accumulation of charge-carriers as a result of overlap between these two interfaces. This thickness-, temperature, and voltage-dependent space-charge density (Figures 1C–E) is responsible for the occurance of SCLC (Röhr et al., 2017; Röhr and MacKenzie, 2020).

Figure 1

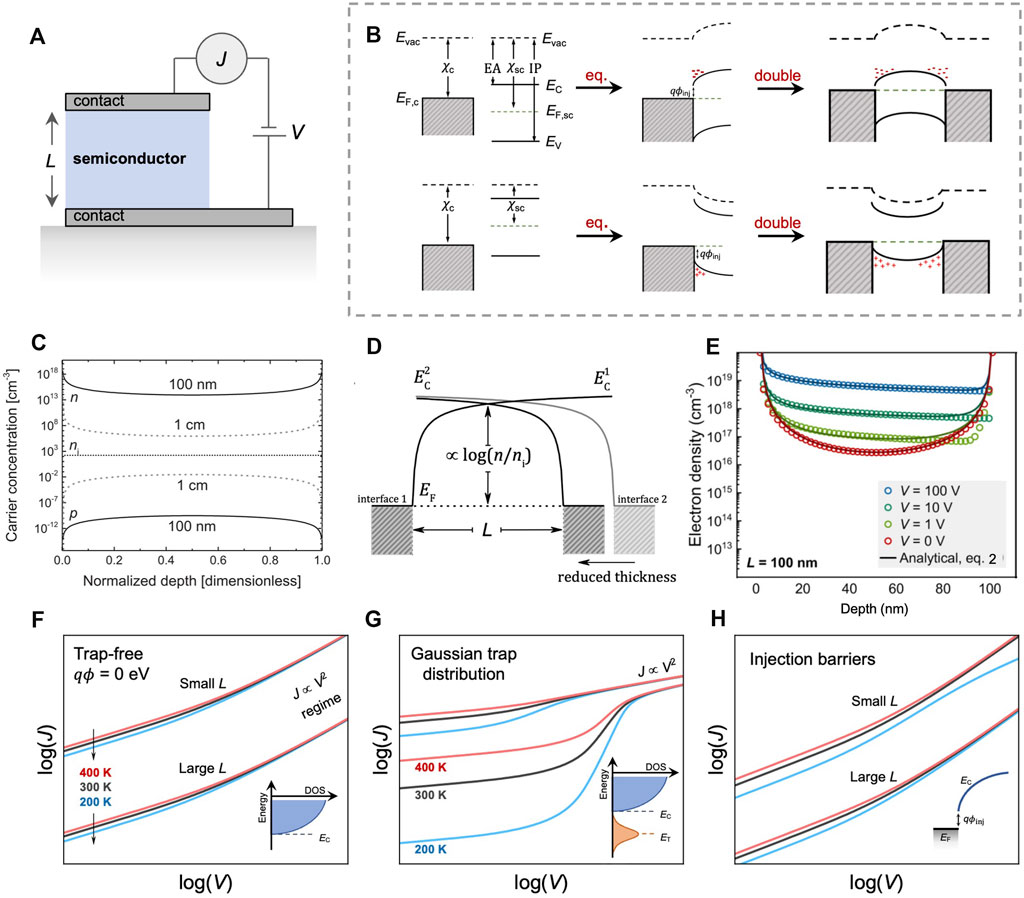
Figure 1. (A), Schematic of a typical sandwich-type single-carrier device, with the probed semiconductor placed between two similar contacts with spacing L. The contact spacing is equal to the semiconductor thickness in this type of device. (B), Energy level diagrams of conductor-semiconductor interfaces, the formation of near-ohmic contacts at equilibrium, and the formation of single-carrier devices. (C), Comparison between background charge-carrier density and intrinsic charge-carrier density in a single-carrier device with either L = 100 nm or L = 1 cm (Röhr et al., 2017). (D), Schematic showing why reducing thickness leads to an increase in charge-carrier density (Röhr et al., 2017). (E), Electron density of an electron-only device under various applied voltages shown in comparison with Eq. 2 (Röhr and MacKenzie, 2020). (F), Conceptual J-V curves from an SCLC measurement where an intrinsic semiconductor is measured, showing the effect from varying device temperature (from 200 K to 400 K) and thickness. The Mott-Gurney law can be employed in the $J\propto V^2$ regime to extract the charge-carrier mobility. (G), Conceptual J-V curves in the case where the semiconductor contains a Gaussian distribution of trap states. (H), Conceptual J-V curves from a device where injection barriers are present but is limiting current flow in the thin device at low temperatures only. The conceptual J-V curves shown in (F–H) were created using a drift-diffusion model. For all the curves, an effective conduction band density of states of 10²⁶ m⁻³ was assumed along with an electron mobility of 10⁻³ cm² V⁻¹ s⁻¹, a dielectric constant of 10, and a band gap of 3 eV. In (F), small L equals 100 nm and large L equals 1000 nm. In (G), small L equals 100 nm and large L equals 200 nm; a deep trap density of 10¹⁷ cm⁻³, at a trap level of 0.85 eV below the conduction band edge, and with a standard deviation of 0.1 eV was added. In (H), small L equals 100 nm and large L equals 500 nm; electron injection barriers of 0.2 eV were added. Calculations were performed at device temperatures of 200 K, 300 K, and 400 K. External resistances were ignored.

Once a single-carrier device is made, SCLC measurements are performed by applying a voltage, V, across the device and measuring the current density, J (Figure 1A). Analyzing the resulting J-V curves can appear to be a relatively simple procedure. In fact, many studies rely on a fitting procedure with a simplistic analytical model, the Mott-Gurney law (Mott and Gurney, 1940), to extract charge-carrier mobilities,

$J=\frac{9}{8}\mu {\epsilon }_0{\epsilon }_{\mathrm{r}}\frac{V^2}{L^3}(1)$

where $\mu$ is either the electron (${\mu }_{\mathrm{n}}$) or hole mobility (${\mu }_{\mathrm{p}}$) dependent on whether electron- or hole-only devices are being measured, ${\epsilon }_0{\epsilon }_{\mathrm{r}}$ is the permittivity, and L is the contact spacing, which equates to the thickness of the semiconductor in a sandwich-type device (Figure 1A). The Mott-Gurney law is a remarkable result: It states that if ${\epsilon }_0{\epsilon }_{\mathrm{r}}$ and L is known, then it is a simple task to fit the model to the J-V data to extract $\mu$ (Figure 1F). However, the Mott-Gurney law describes a highly idealized scenario. Realistically, effects from defects (Figure 1G) and injection barriers (Figure 1H) can greatly influence both the shape and magnitude of the J-V curves in non-trivial ways, leading to significant deviations from the ideal Mott-Gurney behavior (Van Mensfoort and Coehoorn, 2008; Dacuña and Salleo, 2011; Röhr et al., 2018b). In fact, even if an apparent fit with the Mott-Gurney law can be achieved, this does not ensure that the model is a good description of the underlying physics (Röhr et al., 2018a).

Analytical and numerical models exist that attempt to account for the non-ideal behavior described above (Lampert, 1956; Mark and Helfrich, 1962; Murgatroyd, 1970; Dacuña and Salleo, 2011; De Bruyn et al., 2013; Röhr et al., 2018b; Röhr and MacKenzie, 2020; Koopmans et al., 2022). However, to extract meaningful charge-transport characteristics from SCLC data, a “correct” model must be identified for fitting. Identifying a correct model can be difficult, especially when novel materials are being explored and the underlying physics governing charge-transport behavior is not yet understood. Therefore, the default is often to use the simplest model possible that appears to describe a given data set reasonably well. Nonetheless, wrongful characteristics can easily be obtained if the applied model is imprecise in describing the particular material being probed. Fortunately, SCLC data is temperature and device thickness dependent, and will typically show variations corresponding to specific non-idealities influencing charge transport in the material (Dacuña and Salleo, 2011; Röhr et al., 2018b). Examples of this are conceptually shown in Figures 1F–H. Varying the device temperature between each measurement, and measuring a set of devices with different semiconductor thickness, will result in distinct fingerprints in the J-V data that can greatly help in identifying what underlying physics is governing charge transport (Zuo et al., 2017; Röhr et al., 2018b; Shi et al., 2019; Zuo et al., 2019). Although this gives rise to some added complexity during data analysis, the result is a more accurate and trustworthy interpretation.

While the device temperature and thickness dependence on SCLC J-V curves, and how these dependencies can be used during characterization, have been discussed to some length in the literature (Poplavskyy and Nelson, 2003; Dacuña and Salleo, 2011; Röhr et al., 2018b; Kotadiya et al., 2018), less attention has been put towards understanding what the ultimate limits for SCLC measurements truly are. We now understand that there exist temperature and device thickness dependent limits on the minimal doping and trap densities that allow for detection by SCLC measurements (Röhr and MacKenzie, 2020; Le Corre et al., 2021). So while it may appear that a probed semiconductor is not influenced by defects or impurities, it could simply be that the density is below the detection threshold for that particular device at the probed temperature. The same is true for injection barriers (Röhr, 2024). Luckily, simple conditions can now be stated for when these non-idealities are masked (Röhr and MacKenzie, 2020; Le Corre et al., 2021; Röhr, 2024). So while these limits could potentially be considered as a downside of SCLC, they could potentially be used as an additional tool.

Herein, we discuss why J-V curves obtained from SCLC measurements are often highly device thickness and temperature dependent. We subsequently discuss why the choice of device thickness and temperature determines at what threshold which characteristics can be extracted from SCLC measurements. Finally, we present examples where thickness and temperature variation was used to increase the accuracy of fitting procedures, and therefore the accuracy of the data analysis and extracted material and device characteristics.

2 Effects of temperature and thickness on single-carrier devices

The thickness and temperature dependance of SCLC J-V curves can be understood from examining mathematical descriptions of the free, equilibrium/background charge-carrier density inside an intrinsic semiconductor sandwiched by ohmic contacts under zero applied bias (Figures 1C, E). This is the case whether the semiconductor contains defects (either acting as trap sites or as dopants) and/or injection barriers, or not, as defects and injection barriers alter the background charge-carrier density that is responsible for the current flow while also adding their individual temperature dependencies, increasing the overall complexity. We can therefore learn a lot simply from considering how the unaltered, background charge-carrier density varies with thickness and temperature.

In the absence of defects and injection barriers, the total charge-carrier density, $n$, inside a single-carrier device will arise due to several processes. The intrinsic charge-carrier density, $n_{\mathrm{i}}$, arises simply due to statistical mechanics: Some valence electrons will have a non-zero probability of traversing the semiconductor band gap into the conduction band. The background charge-carrier density, $n_{\mathrm{b}}$, arises due to electrons being injected into the semiconductor from the contacts (in the absence of an applied voltage) during Fermi-level equilibration (Figures 1B, C). Finally, charge carriers are injected into the semiconductor in response to an applied voltage, $n_{\text{inj}}$ (Figure 1E). The total charge-carrier density in an intrinsic single-carrier device can therefore be described by, $n=n_{\mathrm{i}}+n_{\mathrm{b}}+n_{\text{inj}}$.

Out of these quantities, $n_{\mathrm{b}}$ is typically very large and will indeed often be larger than $n_{\text{inj}}$ at low voltage and will typically be far in excess of $n_{\mathrm{i}}$ (unless for material with very low band gaps) (Röhr et al., 2017). If that is the case, then we can neglect $n_{\mathrm{i}}$ entirely (Figure 1C) and write, $n=n_{\mathrm{b}}+n_{\text{inj}}$ (Figure 1E) (Van Mensfoort and Coehoorn, 2008; Röhr and MacKenzie, 2020),

$n=\underset{n_{\mathrm{b}}}{\underbrace{\frac{2{\pi }^2{\epsilon }_{\mathrm{r}}{\epsilon }_0{k}_{\mathrm{B}}T}{q^2{L}^2}{\left[{\cos }^2\left(\frac{\pi x}{L}-\frac{\pi }{2}\right)\right]}^{-1}}}+\underset{n_{\text{inj}}}{\underbrace{\frac{3{\epsilon }_{\mathrm{r}}{\epsilon }_{0}V}{4q{L}^{3/2}}{x}^{-1/2}}}(2)$

where, $k_{B}T$ is the thermal energy, $q$ is the elementary charge, and x is the position inside the semiconductor. Given this assumption, the (harmonic) mean, $〈n〉$, of the charge-carrier density Eq. (2) can be described as (Röhr and MacKenzie, 2020),

$〈n〉=\underset{〈n_b〉}{\underbrace{\frac{4{\pi }^2{\epsilon }_{\mathrm{r}}{\epsilon }_0{k}_{\mathrm{B}}T}{q^2{L}^2}}}+\underset{〈n_{\text{inj}}〉}{\underbrace{\frac{9{\epsilon }_{\mathrm{r}}{\epsilon }_{0}V}{8q{L}^2}}}.(3)$

From Eq. (3), it is evident that both the equilibrium charge-carrier density and the injected density are highly influenced by varying the thickness due to the L^-2 terms and that the equilibrium charge-carrier density is additionally affected by temperature via the thermal energy term. Inserting $〈n〉$ into $J=q〈n〉{\mu }_{\mathrm{n}}V/L$, we get (Röhr and MacKenzie, 2020),

$J=4{\pi }^2\frac{k_{\mathrm{B}}T}{q}{\mu }_{\mathrm{n}}{\epsilon }_{\mathrm{r}}{\epsilon }_0\frac{V}{L^3}+\frac{9}{8}{\mu }_{\mathrm{n}}{\epsilon }_{\mathrm{r}}{\epsilon }_0\frac{V^2}{L^3}(4)$

which describes SCLC from the low-voltage regime (first term in Eq. 4) up through the Mott-Gurney regime (second term in Eq. 4). This means that even in a highly idealized case where the semiconductor is not influenced by defects and injection barriers, the J-V response is still influenced by T and L.

3 Impact from trapping

Defects giving rise to trap states can have a profound impact on the current flow in the device as a fraction of the total free charge-carrier density can get immobilized in these states (Hall, 1952; Shockley and Read, 1952; Lampert, 1956; Mark and Helfrich, 1962). A large density of trap states, $N_{\mathrm{t}}$, will result in not only a reduction in the overall current, but also change the shape of the J-V curve and how these curves change with varying T and/or L (Röhr et al., 2018b). It is intuitive that an increase in temperature will increase the probability of charge-carriers escaping said traps (Hall, 1952; Shockley and Read, 1952), resulting in an increase in the current. However, without any knowledge of how $n_{\mathrm{b}}$ varies with L, it would be reasonable to assume that a set density of traps would affect a semiconductor in a single-carrier device in the same manner regardless of how thick this semiconducting layer is; however, this is not the case. As L determines the magnitude of $n_{\mathrm{b}}$, and since the ratio of free to trapped charges is determined by both the trap density and $n_{\mathrm{b}}$, the degree to which trap sites influence the current is therefore also determined by L. Probing devices with different thicknesses can therefore potentially be used as an additional tool for estimating trap states via SCLC.

Besides using thickness variations for characterization, L also determines when traps are entirely screened in the J-V curves. If the background charge-carrier density exceeds the trap density, then the detrimental effects from said traps are diminished. So, while trap states might indeed be present in the semiconductor, even in large quantities, they will sometimes not be observed in the J-V curves, and incorrect conclusions about their presence might be drawn. In fact, it has been shown that a condition for when traps influence a single-carrier device can be derived by noting that $N_{\mathrm{t}}$ must be larger than $〈n_{\mathrm{b}}〉$, $N_{\mathrm{t}}>〈n_{\mathrm{b}}〉$, which yields (Le Corre et al., 2021; Siekmann et al., 2021),

$N_{\mathrm{t}}>\frac{4{\pi }^2{\epsilon }_{\mathrm{r}}{\epsilon }_0{k}_{\mathrm{B}}T}{q^2{L}^2}(5)$

As this quantity is linearly proportional to device temperature and inversely square proportional to the device thickness, we now have qualitative means to understand how varying these quantities will affect whether traps can be observed from the measurement. As an example, we will consider a single-carrier device with L = 200 nm, ${\epsilon }_{\mathrm{r}}=$ 10, and T = 300 K. For such a device, a trap density of $N_{\mathrm{t}}=$ 1.4 $\times$ 10¹⁶ cm⁻³ (as calculated by Eq. 5) or less would be entirely screened by the background charge-carrier density. From this, it is clear that if the effect of trapping is observed in very thin devices, then the density of traps must be very high, as was previously noted by Kotadiya et al., 2019.

This has two rather significant consequences. On the one hand, devices (or experiments) can be designed where the traps are masked, which would allow for a cleaner extraction of the charge-carrier mobility (with Eq. 4 for example,) as traps would not have to be explicitly accounted for during the data analysis. On the other hand, one can accidentally draw the wrongful conclusion that the semiconductor being probed is “trap-free” which could have detrimental impacts on future research into the probed materials and associated devices. However, conducting a series of experiments varying L and T should aid in reducing these wrongful conclusions.

4 Impact from doping and injection barriers

Analogous to the conditions describing when traps are screened in SCLC J-V curves, dopants can similarly be screened if the background charge-carrier density is larger than the density of ionized dopants. Additionally, conditions can be written for the cases where injection barriers, resulting from non-zero injection barriers at the semiconductor/contact interfaces, are no longer influencing the current response.

Dopants are defects that are chosen and incorporated into a semiconductor in a way that ensures that most are thermally ionized at room temperature, i.e., their ionization energies are so low that they are almost guaranteed to grant a charge carrier (e.g., boron dopants in silicon). It is thereby possible to tune the electronic properties of the semiconductor depending on the type of charge carrier introduced. A consequence of dopant ionization energies being so low is that increasing the temperature will not yield any significant additional charge carriers and decreasing the temperature will not result in a significant decrease in the charge-carrier density either (unless the semiconductor is cooled down to very low temperatures). The density of ionized dopants, $N_{\mathrm{D}}$, can therefore typically be considered relatively constant with temperature.

Regardless of the density of ionized dopants being relatively constant with temperature, the device thickness and temperature will still determine when dopants are screened in SCLC J-V curves. Similar to the case of traps, if the background charge-carrier density is exceedingly high, then the effects from said dopants are diminished. A similar condition can therefore be written (Röhr and MacKenzie, 2020),

$N_{\mathrm{D}}>\frac{4{\pi }^2{\epsilon }_{\mathrm{r}}{\epsilon }_0{k}_{\mathrm{B}}T}{q^2{L}^2}(6)$

and the example that was made for the case where the semiconductor contained traps can likewise be made for case where the semiconductor is doped.

In the case of non-ohmic contacts, the temperature dependence can be understood from the effect of having injection barriers at the interfaces, $q{\varphi }_{\text{inj}}$, and how these alter the charge-carrier density occupancy at those interfaces. Taking an electron-only device as an example, we can describe how q${\varphi }_{\text{inj}}$ influences the interface charge-carrier densities via,

$n_{\mathrm{int}}=N_{\mathrm{C}}\exp \left(-\frac{q{\varphi }_{\text{inj}}}{k_{\mathrm{B}}T}\right)(7)$

where $N_{\mathrm{C}}$ is the conduction band effective density of states. We can now set up a similar condition as we did for traps and doping, namely, $n_{\mathrm{int}}<〈n_{\mathrm{b}}〉$ and we can then write the condition for when injection barriers are influencing the device, as a function of L and T, as (Röhr, 2024),

$q{\varphi }_{\text{inj}}>-k_{\mathrm{B}}T\ln \left(\frac{4{\pi }^2{\epsilon }_{\mathrm{r}}{\epsilon }_0{k}_{\mathrm{B}}T}{q^2{L}^2{N}_{\mathrm{C}}}\right).(8)$

Similar to the previous cases, for a device with L = 200 nm, ${\epsilon }_{\mathrm{r}}$ = 10, T = 300 K, and $N_{\mathrm{C}}$ = 10²⁶ m⁻³, injection barriers as large as $\approx$ 0.23 eV would therefore not significantly affect the SCLC J-V curves (as calculated by Eq. 8).

5 Varying thickness and/or temperature to improve SCLC analysis

While the common approach for estimating mobilities using SCLC is to simply fit with the Mott-Gurney law to data from a single device, we and others have used more comprehensive approaches of varying device temperature and measuring devices with different thicknesses to not only improve the accuracy of the analysis but to also obtain characteristics beyond simply the charge-carrier mobility (Wetzelaer et al., 2012; Röhr et al., 2018b). This has been done with both analytical models (including the Mott-Gurney law) and more sophisticated drift-diffusion models. To highlight this, and to hopefully inspire researchers to adopt such approaches, below we focus on a few examples from within the organic electronics communities where important and surprising results were obtained.

In 2018, Kotadiya et al., 2018 employed SCLC measurements, observing transitions from injection-limited to space-charge-limited current, to show that injection from transition-metal oxide hole contacts into a range of organic semiconductors with high ionization potentials can be made ohmic by introducing a thin interlayer of TCTA. To verify this, they measured a large set of hole-only devices where the only variable was the device thickness, and showed that a constant mobility could be extracted for each material, independent of the device thickness (Figure 2A). The following year, Kotadiya et al., 2019 again used SCLC to explore trap states in a large library of semiconducting polymers, small molecules, and fullerene derivatives, using varying device thickness as part of their extensive analysis. They found that hole and electron transport is trap-limited for the investigated materials if they have ionization potentials higher than 6.0 eV and electron affinities smaller than 3.6 eV, respectively (Figures 2B,C). They concluded that these trapping events are caused by water clusters inside the semiconducting films.

Figure 2

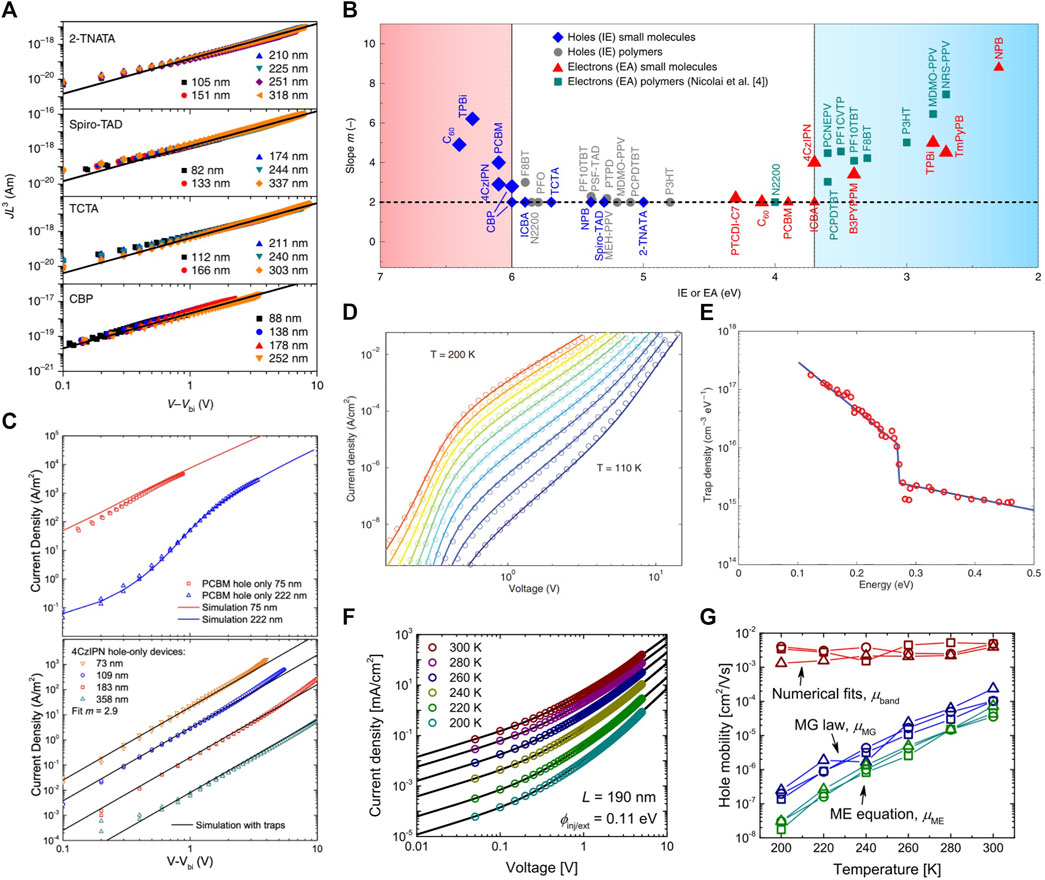
Figure 2. (A), SCLC J-V curves, obtained from four different organic materials with varying device thickness. The y-axis has been corrected to easily show that the curves are thickness independent and that the J-V curves approximate a square-law dependence: $J\propto V^2$ (Kotadiya et al., 2018). (B), Max slope of SCLC curves (m; $J\propto V^m$) as a function of either ionization potential or electron affinity, for a long list of organic semiconductors and fullerene derivatives, showing that trap-free behavior can be observed within an energy window (Kotadiya et al., 2019). (C), Example model fits to SCLC data used to obtain the information shown in (B) (Kotadiya et al., 2019). (D), Fits to J-V curves recorded at various device temperatures (110 K–200 K) obtained from a rubrene crystal sandwiched between two gold contacts (Dacuña and Salleo, 2011). (E), Description of the piecewise, exponential sub-band density of states used to obtain the fits shown in (D) (Dacuña and Salleo, 2011). (F), Fits to SCLC curves at various temperatures (200 K–300 K) for a spiro-OMeTAD single-carrier device. While only the data from the 190 nm device is shown, the model was used to achieve a global fit from data across three sets of thicknesses (115 nm, 190 nm, and 290 nm). Traps and injection barriers had to be explicitly introduced into the model (Röhr et al., 2018b). (G), Mobility values obtained from the data shown in (F) if either analytical or numerical drift-diffusion models were used (Röhr et al., 2018b).

In 2011, Dacuña and Salleo used a drift-diffusion approach to model SCLC data obtained from an organic rubrene single-crystal measured at temperatures varying from 110 K to 200 K (Figure 2D) (Krellner et al., 2007; Dacuña and Salleo, 2011). By fitting their model across the entire range of SCLC data, they were able to conclude that the sub-band density of states is well-modeled by a piecewise exponential function of trap states (Figure 2E). They also showed that while gold contacts were used on either side of the crystal, as one contact was deposited via evaporation while the other was electrostatically laminated, this resulted in two different metal/semiconductor interfaces, thereby resulting in significant contact asymmetry and therefore a built-in voltage that was essential to account for in the low-voltage regime during fitting procedures.

Finally, SCLC measurements have also been employed to investigate hole transport in pristine spiro-OMeTAD (Röhr et al., 2018b), an organic hole-transport material that has historically been used in solid-state dye-sensitized solar cells (Cappel et al., 2012) and which is now commonly used in perovskite solar cells (Kong et al., 2021). We measured a set of hole-only devices with increasing spiro-OMeTAD thickness (115 nm, 190 nm, and 290 nm) across temperatures ranging from 200 K to 300 K (the data from L = 190 nm case are shown in Figure 2F). The data was analyzed with both simple analytical models (Eq. 1 and first term in Eq. 4) and a drift-diffusion model that could explicitly account for trapping, injection barriers, and external resistances. It was shown that while the use of analytical models yielded a highly temperature-dependent “effective” mobility, the band-like mobility obtained from fitting with the drift-diffusion model did not yield as drastic of a temperature dependence while also yielding an overall higher mobility (Figure 2G). This highlights the importance of explicitly accounting for traps and injection barriers when analyzing SCLC data, and how varying both temperature and thickness will aid in this analysis.

6 Conclusion

We here highlighted the importance of not only measuring devices with different thicknesses, but also measuring such devices at varying temperature in order to achieve accurate device and materials characteristics from SCLC measurements. We also highlighted how the choice of device thickness and temperature is critical in determining what characteristics can realistically be extracted from SCLC measurements, and how erroneous conclusions can potentially be drawn about the probed semiconducting material if this is not considered. While this perspective is not extensive in scope, as other factors could affect the outcome of an SCLC measurement and the subsequent analysis, we hope that the topics covered herein will initiate a broader discussion into SCLC metrology while also aiding in improving charge-transport characterization of thin-film semiconductors.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author/s.

Author contributions

AZ: Conceptualization, Writing–review and editing. VL: Conceptualization, Investigation, Writing–review and editing. JR: Conceptualization, Investigation, Supervision, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cappel, U. B., Daeneke, T., and Bach, U. (2012). Oxygen-Induced doping of spiro-MeOTAD in solid-state dye-sensitized solar cells and its impact on device performance. Nano Lett. 12, 4925–4931. doi:10.1021/nl302509q

PubMed Abstract | CrossRef Full Text | Google Scholar

Coehoorn, R., and Bobbert, P. A. (2012). Effects of Gaussian disorder on charge carrier transport and recombination in organic semiconductors. Phys. Status Solidi (a) 209, 2354–2377. doi:10.1002/pssa.201228387

CrossRef Full Text | Google Scholar

Dacey, G. C. (1953). Space-charge limited hole current in germanium. Phys. Rev. 90, 759–763. doi:10.1103/PhysRev.90.759

CrossRef Full Text | Google Scholar

Dacuña, J., and Salleo, A. (2011). Modeling space-charge-limited currents in organic semiconductors: extracting trap density and mobility. Phys. Rev. B 84, 195209. doi:10.1103/PhysRevB.84.195209

CrossRef Full Text | Google Scholar

De Bruyn, P., Van Rest, A. H. P., Wetzelaer, G. A. H., De Leeuw, D. M., and Blom, P. W. M. (2013). Diffusion-limited current in organic metal-insulator-metal diodes. Phys. Rev. Lett. 111, 186801. doi:10.1103/PhysRevLett.111.186801

PubMed Abstract | CrossRef Full Text | Google Scholar

Duijnstee, E. A., Ball, J. M., Le Corre, V. M., Koster, L. J. A., Snaith, H. J., and Lim, J. (2020). Toward understanding space-charge limited current measurements on metal halide perovskites. ACS Energy Lett. 5, 376–384. doi:10.1021/acsenergylett.9b02720

CrossRef Full Text | Google Scholar

Duijnstee, E. A., Le Corre, V. M., Johnston, M. B., Koster, L. J. A., Lim, J., and Snaith, H. J. (2021). Understanding dark current-voltage characteristics in metal-halide perovskite single crystals. Phys. Rev. Appl. 15, 014006. doi:10.1103/PhysRevApplied.15.014006

CrossRef Full Text | Google Scholar

Hall, R. N. (1952). Electron-hole recombination in germanium. Phys. Rev. 87, 387. doi:10.1103/PhysRev.87.387

CrossRef Full Text | Google Scholar

Kong, J., Shin, Y., Röhr, J. A., Wang, H., Meng, J., Wu, Y., et al. (2021). CO2 doping of organic interlayers for perovskite solar cells. Nature 594, 51–56. doi:10.1038/s41586-021-03518-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Koopmans, M., Corre, V., and Koster, L. (2022). SIMsalabim: an open-source drift-diffusion simulator for semiconductor devices. JOSS 7, 3727. doi:10.21105/joss.03727

CrossRef Full Text | Google Scholar

Kotadiya, N. B., Lu, H., Mondal, A., Ie, Y., Andrienko, D., Blom, P. W. M., et al. (2018). Universal strategy for Ohmic hole injection into organic semiconductors with high ionization energies. Nat. Mater 17, 329–334. doi:10.1038/s41563-018-0022-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Kotadiya, N. B., Mondal, A., Blom, P. W. M., Andrienko, D., and Wetzelaer, G.-J. A. H. (2019). A window to trap-free charge transport in organic semiconducting thin films. Nat. Mat. 18, 1182–1186. doi:10.1038/s41563-019-0473-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Krellner, C., Haas, S., Goldmann, C., Pernstich, K. P., Gundlach, D. J., and Batlogg, B. (2007). Density of bulk trap states in organic semiconductor crystals: discrete levels induced by oxygen in rubrene. Phys. Rev. B 75, 245115. doi:10.1103/PhysRevB.75.245115

CrossRef Full Text | Google Scholar

Lampert, M. A. (1956). Simplified theory of space-charge-limited currents in an insulator with traps. Phys. Rev. 103, 1648–1656. doi:10.1103/PhysRev.103.1648

CrossRef Full Text | Google Scholar

Le Corre, V. M., Duijnstee, E. A., El Tambouli, O., Ball, J. M., Snaith, H. J., Lim, J., et al. (2021). Revealing charge carrier mobility and defect densities in metal halide perovskites via space-charge-limited current measurements. ACS Energy Lett. 6, 1087–1094. doi:10.1021/acsenergylett.0c02599

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, H. K. H., Telford, A. M., Röhr, J. A., Wyatt, M. F., Rice, B., Wu, J., et al. (2018). The role of fullerenes in the environmental stability of polymer:fullerene solar cells. Energy Environ. Sci. 11, 417–428. doi:10.1039/C7EE02983G

CrossRef Full Text | Google Scholar

Mark, P., and Helfrich, W. (1962). Space-charge-limited currents in organic crystals. J. Appl. Phys. 33, 205–215. doi:10.1063/1.1728487

CrossRef Full Text | Google Scholar

Mott, N. F., and Gurney, R. W. (1940). Electronic processes in ionic crystals. 2nd Edn.

Google Scholar

Murgatroyd, P. N. (1970). Theory of space-charge-limited current enhanced by Frenkel effect. J. Phys. D. Appl. Phys. 3, 151–156. doi:10.1088/0022-3727/3/2/308

CrossRef Full Text | Google Scholar

Poplavskyy, D., and Nelson, J. (2003). Nondispersive hole transport in amorphous films of methoxy-spirofluorene-arylamine organic compound. J. Appl. Phys. 93, 341–346. doi:10.1063/1.1525866

CrossRef Full Text | Google Scholar

Röhr, J. A. (2024). On injection in intrinsic single-carrier devices. J. Comput. Electron. doi:10.1007/s10825-024-02129-w

CrossRef Full Text | Google Scholar

Röhr, J. A., Kirchartz, T., and Nelson, J. (2017). On the correct interpretation of the low voltage regime in intrinsic single-carrier devices. J. Phys. Condens. Matter 29, 205901. doi:10.1088/1361-648X/aa66cc

PubMed Abstract | CrossRef Full Text | Google Scholar

Röhr, J. A., and MacKenzie, R. C. I. (2020). Analytical description of mixed ohmic and space-charge-limited conduction in single-carrier devices. J. Appl. Phys. 128, 165701. doi:10.1063/5.0024737

CrossRef Full Text | Google Scholar

Röhr, J. A., Moia, D., Haque, S. A., Kirchartz, T., and Nelson, J. (2018a). Exploring the validity and limitations of the Mott–Gurney law for charge-carrier mobility determination of semiconducting thin-films. J. Phys. Condens. Matter 30, 105901. doi:10.1088/1361-648X/aaabad

PubMed Abstract | CrossRef Full Text | Google Scholar

Röhr, J. A., Shi, X., Haque, S. A., Kirchartz, T., and Nelson, J. (2018b). Charge transport in spiro-OMeTAD investigated through space-charge-limited current measurements. Phys. Rev. Appl. 9, 044017. doi:10.1103/PhysRevApplied.9.044017

CrossRef Full Text | Google Scholar

Rose, A. (1955). Space-charge-limited currents in solids. Phys. Rev. 97, 1538–1544. doi:10.1103/PhysRev.97.1538

CrossRef Full Text | Google Scholar

Sachnik, O., Tan, X., Dou, D., Haese, C., Kinaret, N., Lin, K.-H., et al. (2023). Elimination of charge-carrier trapping by molecular design. Nat. Mat. 22, 1114–1120. doi:10.1038/s41563-023-01592-3

CrossRef Full Text | Google Scholar

Sajedi Alvar, M., Blom, P. W. M., and Wetzelaer, G.-J. A. H. (2020). Space-charge-limited electron and hole currents in hybrid organic-inorganic perovskites. Nat. Commun. 11, 4023. doi:10.1038/s41467-020-17868-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, X., Nádaždy, V., Perevedentsev, A., Frost, J. M., Wang, X., Von Hauff, E., et al. (2019). Relating chain conformation to the density of states and charge transport in conjugated polymers: the role of the β -phase in poly(9,9-dioctylfluorene). Phys. Rev. X 9, 021038. doi:10.1103/PhysRevX.9.021038

CrossRef Full Text | Google Scholar

Shockley, W., and Prim, R. C. (1953). Space-charge limited emission in semiconductors. Phys. Rev. 90, 753–758. doi:10.1103/PhysRev.90.753

CrossRef Full Text | Google Scholar

Shockley, W., and Read, W. T. (1952). Statistics of the recombinations of holes and electrons. Phys. Rev. 87, 835–842. doi:10.1103/PhysRev.87.835

CrossRef Full Text | Google Scholar

Siekmann, J., Ravishankar, S., and Kirchartz, T. (2021). Apparent defect densities in halide perovskite thin films and single crystals. ACS Energy Lett. 6, 3244–3251. doi:10.1021/acsenergylett.1c01449

CrossRef Full Text | Google Scholar

Trieb, D., Blom, P. W. M., and Wetzelaer, G. A. H. (2023). Ohmic electron injection into organic semiconductors by solution-processed and evaporated organic interlayers. Adv. Mater. Inter 10, 2202424. doi:10.1002/admi.202202424

CrossRef Full Text | Google Scholar

Van Mensfoort, S. L. M., and Coehoorn, R. (2008). Effect of Gaussian disorder on the voltage dependence of the current density in sandwich-type devices based on organic semiconductors. Phys. Rev. B 78, 085207. doi:10.1103/PhysRevB.78.085207

CrossRef Full Text | Google Scholar

Wetzelaer, G.-J. A. H., Kuik, M., Olivier, Y., Lemaur, V., Cornil, J., Fabiano, S., et al. (2012). Asymmetric electron and hole transport in a high-mobility n -type conjugated polymer. Phys. Rev. B 86, 165203. doi:10.1103/PhysRevB.86.165203

CrossRef Full Text | Google Scholar

Zuo, G., Li, Z., Andersson, O., Abdalla, H., Wang, E., and Kemerink, M. (2017). Molecular doping and trap filling in organic semiconductor host–guest systems. J. Phys. Chem. C 121, 7767–7775. doi:10.1021/acs.jpcc.7b01758

CrossRef Full Text | Google Scholar

Zuo, G., Linares, M., Upreti, T., and Kemerink, M. (2019). General rule for the energy of water-induced traps in organic semiconductors. Nat. Mat. 18, 588–593. doi:10.1038/s41563-019-0347-y

PubMed Abstract | CrossRef Full Text | Google Scholar