
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Electron. Mater , 09 May 2024
Sec. Superconducting Materials
Volume 4 - 2024 | https://doi.org/10.3389/femat.2024.1392760
This article is part of the Research Topic Celebrating 3 Years of Frontiers in Electronic Materials View all 4 articles
Uniaxial stress has proven to be a powerful experimental tuning parameter for effectively controlling lattice, charge, orbital, and spin degrees of freedom in quantum materials. In addition, its ability to manipulate the symmetry of materials has garnered significant attention. Recent technical progress to combine uniaxial stress cells with quantum oscillation and angle-resolved photoemission techniques allowed to study the electronic structure as function of uniaxial stress. This review provides an overview on experimental advancements in methods and examines studies on diverse quantum materials, encompassing the semimetal WTe2, the unconventional superconductor Sr2RuO4, Fe-based superconductors, and topological materials.
Recent years have seen an tremendous interest in uniaxial stress experiments on quantum materials. While hydrostatic pressure alters electronic orbital overlap in all three spatial dimensions, uniaxial pressure explicitly drives anisotropic changes. Therefore, the material’s response can be studied separately for each crystal axis. Often, much larger responses can be obtained with equal amounts of pressures when applied uniaxially. In addition, point group symmetries of crystal structures can be broken.
The perturbation of quantum materials by uniaxial stress has led to a number of important discoveries, for example: It was possible to tune the delicate balance between unconventional superconductivity and competing ordering phenomena in a range of materials. Specifically, the superconducting transition temperature in cuprates was increased by controlling its orthorhombicity (Welp et al., 1992; Takeshita et al., 2004) and charge order was induced in the underdoped regime by uniaxial stress (Kim et al., 2018; Nakata et al., 2022); A dramatic increase in the superconducting Tc with uniaxial stress was also observed in Sr2RuO45, and the material was found to order magnetically at even larger pressures (Grinenko et al., 2021a); The electronic origin of the rotational symmetry breaking in iron-based superconductors, called nematicity, and many of its properties were discovered by anisotropic strain measurements (Chu et al., 2012; Böhmer et al., 2022); Uniaxial pressure also turned out to be a key control parameter for phenomena related to the band-structure topology. For example, transitions between different non-trivial topological phases were induced by uniaxial stress (Mutch et al., 2019; Zhang et al., 2021; Jo et al., 2023a); Extremely large magneto-elastoresistance was observed from WTe2 due to its semi-metallic band structure with different effective masses near the Fermi energy (Jo et al., 2019).
Whereas uniaxial pressure techniques have been available since a long time, they were not intensively used in the study of quantum materials. Recent increased interest was triggered not only by the discovery of various fascinating quantum phenomena but also by new technical developments of stress cells. Apart from standard anvil cells and bending devices, new schemes using thermal contraction (Sunko et al., 2019), turn-screw mechanisms (Tanatar et al., 2010), and in particular piezoelectric devices (Hicks et al., 2014b) were developed. They substantially improve pressure homogeneity and accommodate an ever larger range of experimental probes (Hicks et al., 2014a; Ikeda et al., 2019; Ghosh et al., 2020; Noad et al., 2023), including thermodynamic, transport, spectroscopy, and scattering techniques in environments with low temperatures, high magnetic fields, or in ultra-high vacuum.
Measurements of the electronic structure under in-situ tunable uniaxial pressure are one of the more recent additions. Key insights into the physics of quantum materials can be obtained from spectral function, electronic band structure, and Fermi surface measurements. They provide information for example about effective masses, Fermi velocities, band gaps due to broken symmetries, and surface electronic states. Quantum oscillation measurements and angle-resolved photoemission spectroscopy (ARPES) are standard probes of the electronic structure of quantum materials (Carrington, 2011; Sebastian and Proust, 2015; Hu et al., 2019; Sobota et al., 2021). The technical developments in uniaxial stress cells have therefore been adopted and advanced in recent years in order to combine them with both probes.
Here, we review the current status of uniaxial-stress dependent ARPES and quantum oscillation measurements. We first provide an overview of uniaxial stress devices employed in electronic structure measurements in Chapter II. The following sections present an overview of measurements on several quantum materials. These studies encompass an analysis of strain-induced charge redistribution in WTe2 in Chapter III, the stress-induced Lifshitz transition in Sr2RuO4 in Chapter IV, investigation of nematicity in iron-based superconductors in Chapter V, and explorations of strain-controlled topological phase transitions in Chapter VI.
In general, the deformation of a solid is described in the elastic regime by σij = Cijklϵkl, with σij being the stress tensor, ϵkl the strain tensor and Cijkl the elastic stiffness tensors (Lüthi, 2005). All experimental setups described in this review apply a uniaxial stress to a sample, which in turn strains along all crystallographic directions. Thus, uniaxial pressure results in highly anisotropic strains, which can be quantified by the corresponding Poisson’s ratio
Despite the crucial significance of investigating changes in electronic structure under the influence of uniaxial stress, these studies have only recently gained momentum after experimental challenges were overcome by sophisticated technical developments. Quantum oscillation experiments require low temperatures and high magnetic fields. Uniaxial stress devices based on piezoelectric stacks have been developed for these challenging conditions in recent years (Hicks et al., 2014b) and are now commercially available.
Implementing in-situ tunable uniaxial stress in angle-resolved photoemission spectroscopy (ARPES) experiments presents several additional challenges. Stress devices need to be compatible with the ultra-high vacuum environment; Electric fields distort the trajectories of photoemitted electrons; Most ARPES instruments do not offer electrical contacts at the sample stage; Sample stages are often very small. We present two general types of uniaxial stress devices—mechanical and piezoelectric devices—that overcame these challenges and were successfully used in ARPES experiments. In all devices, the sample is mounted across a gap, the size of which is adjusted either mechanically or by piezoelectric stacks. Sample substrates (Park et al., 2020) can be used in cases where samples require a large force to cleave or when they tend to bend easily during the cleaving process, or if the sample size is smaller than the size of the gap. As a result, samples of varying dimensions and mechanical properties can be studied in these devices either by measuring them in a free-standing configuration or by supporting them with a substrate. The strain due to applied stress is measured optically with microscope images (Sunko et al., 2019; Cai et al., 2020; Hyun et al., 2022), by x-ray diffraction (Zhang et al., 2021), or with strain gauges (Pfau et al., 2019a; Zhang et al., 2021; Hyun et al., 2022; Jo et al., 2023a).
The first type of mechanical devices leverages the concept of differential thermal contraction. The device by Sunko et al. (Sunko et al., 2019) shown in Figure 1A employed a combination of titanium (Ti) and aluminum (Al), which leads to uniaxial compression of the sample platform during cooling. Sample strains of up to −0.6% at temperatures below 40 K were achieved with this device (see Figure 1A for the dimensions of Al and Ti, respectively).
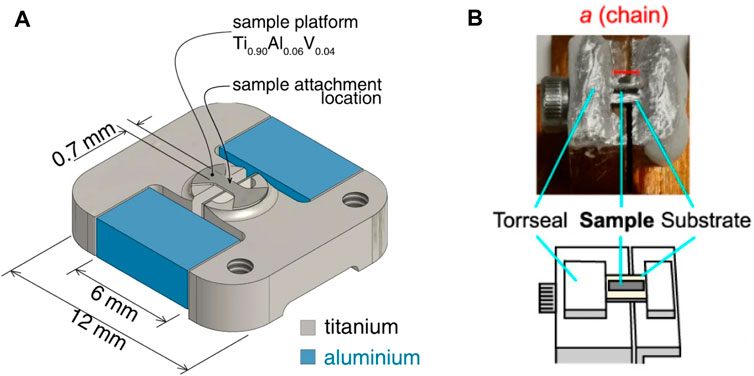
Figure 1. Mechanical uniaxial stress devices. (A) An illustration of the differential thermal contraction strain device. The thermal contraction of aluminum surpasses that of titanium, resulting in uniaxial compression of the sample platform during the cooling process. (This image is from Sunko et.al. 2019 (Sunko et al., 2019). The reference is an Open Access article licensed under a Creative Commons Attribution 4.0 International License.). (B) A screw is employed to apply compression or extension to the substrate, consequently affecting the sample attached to it. (This image is from Peng et.al. 2021 (Zhang et al., 2021). The reference is an Open Access article licensed under a Creative Commons Attribution 4.0 International License.).
The second type of mechanical devices uses screw-turn mechanisms that are adjusted in-situ with a wobble stick (Kim et al., 2011; Zhang et al., 2021; Hyun et al., 2022), which changes the size of the gap [see Figure 1B (Zhang et al., 2021)]. In other devices, the screw was used to induce bending of a substrate to which the sample is affixed (Ricco et al., 2018; Lin et al., 2021; Nicholson et al., 2021). Since these bending cells induce highly non-uniform strains, they do not qualify as true uniaxial stress cells and thus fall outside the scope of this review article on uniaxial stress.
Uniaxial stress devices based on piezoelectric stacks have been used in ARPES set-ups that are equipped with electrical contacts on the sample stage (Pfau et al., 2019b; Cai et al., 2020; Jo et al., 2023a). These devices offer continuous, in-situ, backlash-free stress tuning. The principle design of all of them is based on Ref. (Hicks et al., 2014b) and is adapted to ARPES as shown in Figure 2. In particular, an electric shield surrounds the piezoelectric stacks to shield the high voltage from the photoemitted electrons. Different spring-loaded contact designs are employed depending on the specific sample stage.

Figure 2. Piezoelectric-driven uniaxial stress devices. (A) Schematics of the design for use in ARPES. Reproduced with permission (Pfau et al., 2019b). Copyright 2019 by the American Physics Society. (B) Photograph of the device without (right) and with (left) electrical shielding used in Ref (Pfau et al., 2019a; Pfau et al., 2019b; Pfau et al., 2021a). Reproduced with permission (Pfau et al., 2019a; Pfau et al., 2021a). Copyright 2019 and Copyright 2021 by the American Physics Society. Reference (Pfau et al., 2019b) is an Open Access article licensed under a Creative Commons Attribution 4.0 International License.
With these new techniques, diverse quantum materials have been investigated, unveiling exotic physics. In the following sections, we will discuss each case individually.
As a result of changes in the electronic overlap, the application of uniaxial stress can modify band structures. Stress can influence the curvature of the band, causing changes in the effective mass and the size of the Fermi surface, consequently leading to modifications in carrier density. Changes of the Fermi surface in weakly-correlated systems can be predicted using density functional theory (DFT) and determined experimentally using quantum oscillation measurements. The study by Jo et al. combines these two techniques and showcases the systematic, quantitative tracing of these effects in WTe2 (Jo et al., 2019).
WTe2 is an excellent testbed system to study the influence of uniaxial stress on the electronic structure of quantum materials. It possesses an orthorhombic crystal structure (space group number 31) as shown in Figure 3A. Consequently, the application of uniaxial stress does not lower the material’s crystalline symmetries. While WTe2 undergoes a Lifshitz transition as function of temperature at ≈ 160 K (Wu et al., 2015), no uniaxial stress-induced phase transitions have been observed so far at low temperatures. Note that a superconducting transition occurred upon the application of large hydrostatic pressure (Kang et al., 2015; Pan et al., 2015). However, the paper did not indicate a superconducting phase transition down to 2 K with a maximum of −0.15% of uniaxial stress.
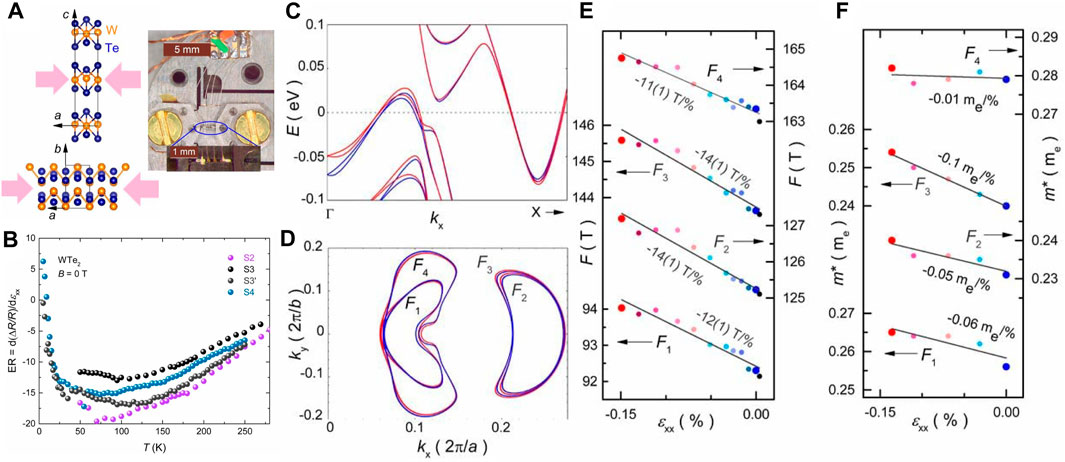
Figure 3. Density functional theory (DFT) results and quantum oscillation analysis under strain. (A) Crystal structure of WTe2. (Left) The top picture shows a view on the ac plane to visualize the layered structure along the c axis. The lower pictures shows the ab plane with distorted zig-zag chains of W atoms in the a direction. A single crystal of WTe2 is mounted on Razorbill CS100 Cryogenic uniaxial stress cell (Piezoelectric device) (right). The electrical current and mechanical stress were applied along the crystallographic a direction, and the magnetic field was applied along the crystallographic c diretion. (B) Elastoresistance of WTe2 was measured in the temperature range of 5 K–270 K, with no applied magnetic field for samples S2, S3, S3′, and S4. It predominantly exhibits negative elastoresistance, with a pronounced upturn observed at low temperatures, specifically below 25 K. (C) Results of DFT band structure calculation along the Γ − X direction without strain (ϵxx = 0%; blue) and with strain (ϵxx = −0.2%; red) applied along the a axis. (D) Strain-induced modification of extremal orbits at kz = 0 from DFT calculation. Blue and red lines refer to the same strain as in (C). Fermi surfaces F1 and F4 correspond to hole bands and F2 and F3 to electron bands. (E) Shubnikov-de-Haas oscillation frequencies of the 4 extremal orbits F1,2,3,4 as a function of strain ϵxx. The numerical values of the slopes are given in the figure. (F) Effective cyclotron masses of the four extremal orbits F1,2,3,4 as a function of strain, with slopes given in the figure. Figure is adapted from Ref. (Jo et al., 2019). Copyright (2019) National Academy of Sciences.
Additionally, the elastoresistance value was found to exceed two at room temperature and exhibited non-monotonic behavior as a function of temperature as shown in Figure 3B. Elastoresistance describes changes in resistance relative to the applied strain (elastoresistance =
In this study, the stress was applied along the crystallographic a-axis using the stress cell shown in Figure 3A. Figures 3C, D depict the results of DFT calculations conducted without (blue) and with (red) a compressive strain of −0.2% along the a-axis. They predict two hole bands and two nearly degenerate electron bands to intersect the Fermi energy. The corresponding four Fermi surface pockets are labeled F1 to F4. As function of strain, slight curvature adjustments in the dispersion are discernible in Figure 3C, while Figure 3D illustrates an evident increase in pocket sizes.
These findings were confirmed through studies of the Shubnikov-de-Haas quantum oscillations. The Fourier transformation of the experimental data revealed four distinct peaks, each corresponding to the crossing of the four bands at the Fermi energy. Additionally, effective masses were extracted from a fit of the temperature-dependent quantum oscillation amplitude with the Lifshitz-Kosevich theory. The experimental results are shown in Figures 3E, F. The frequencies increase upon application of compressive stress, which indicates an expansion in the extremal cross-sectional area of the Fermi surface. The effective masses exhibit an increase under compressive strain with a slope that is strongly band dependent. All of these observations qualitatively agree well with DFT calculations. However, the exact values do not coincide with those measured in experiments. This discrepancy can be attributed to: 1) DFT typically exhibits relative errors in the lattice constant depending on the choice of exchange-correlation functional, and 2) DFT calculations are conducted at 0 K and do not account for finite-temperature effects.
The observation of stress-induced changes in band structure provided crucial insights into the unusual transport properties of WTe2 that exhibits an exceptionally large elastoresistance with a non-monotonic-temperature-dependence. The increase of the size for all Fermi surfaces with compressive strain implies that electrons redistribute between hole-like and electron-like bands at low temperatures. The larger Fermi surfaces also increase significantly both electron and hole carrier densities. As a result, the low-temperature elastoresistance is exceptionally large and positive as observed experimentally. The temperature dependence of the elastoresistance can be captured qualitatively by a low-energy model, which also takes into account the redistribution of charge carriers to bands within kBT. Especially at high temperatures, this includes a heavy hole band below the Fermi energy that could potentially be observed with ARPES. In general, the transport and electronic structure studies point to a strong connection between the elastic and electronic degrees of freedom in WTe2. Due to its small carrier density, the example of WTe2 showcases a novel avenue for manipulating magneto-transport properties through strain in this and related materials.
The quest to understand the unconventional pairing state of the superconductor SrRu2O4 (Mackenzie and Maeno, 2003; Hicks et al., 2014a; Mackenzie et al., 2017; Pustogow et al., 2019; Grinenko et al., 2021b) has been a driving force behind numerous technical advancements in applying controlled uniaxial pressure to bulk materials in the last decade. This pursuit has culminated in a range of modern pressure devices (Hicks et al., 2014b; Barber et al., 2019; Sunko et al., 2019). Conversely, the new technical possibilties have faciliated the discovery of entirely new physics in Sr2RuO4 beyond the one of the superconducting state (Sunko et al., 2019; Li et al., 2022; Noad et al., 2023; Yang et al., 2023). In the following, we will focus on the electronic structure of normal-state Sr2RuO4 under uniaxial pressure. For further reviews on the various aspects of the physics of Sr2RuO4, particularly at ambient pressure, see Refs. (Bergemann et al., 2003; Mackenzie and Maeno, 2003; Mackenzie et al., 2017).
In addition to its unconventional superconductivity, Sr2RuO4 stands out as a correlated metal with a quasi two-dimensional electronic structure which is known in exquisite detail (Mackenzie et al., 1996; Ohmichi et al., 1999; Bergemann et al., 2000; Damascelli et al., 2000; Bergemann et al., 2003; Tamai et al., 2019). This makes Sr2RuO4 one of the best model systems for comparison with theoretical models related to electronic correlations.
Sr2RuO4 belongs to the class of layered Ruddlesden-Popper series (Ruddlesden and Popper, 1958) and exhibits a tetragonal crystal structure. In this structure, the a-b-layers are formed by corner-sharing RuO6 octahedra. The Fermi surface consists of the α, β and γ bands (see Figure 4A), which result from crystal-electric field (CEF) splitting of the 4d manifold of the Ru atom, as well as spin-orbit coupling (SOC). Due to improvements in resolution of ARPES measurements over the years, the effects of correlation-enhanced SOC on the band structure could be visualized and quantified by Tamai et al. (Tamai et al., 2019). The resulting band structure and the orbital character of the bands can be well fitted by a tight-binding model with five hopping parameters t and a SOC strength λSOC (Cobo et al., 2016; Rømer et al., 2019; Tamai et al., 2019). This model provides the basis for understanding the strain-induced changes of the electronic structure.

Figure 4. Fermi surface of Sr2RuO4 in the unstrained and strained condition (with strain applied along the [100] direction of the tetragonal unit cell). (A) Schematic Fermi surfaces of Sr2RuO4 at zero strain (ϵx = ϵy = 0), at intermediate strain (0
Breaking the in-plane tetragonal symmetry has a remarkably strong effect on the band structure, in particular on the γ sheet, as illustrated schematically in Figure 4A. When uniaxial pressure is applied along the [100] direction, Sr2RuO4 experiences a compression along the x-axis with ϵx < 0 and a tension along the y-direction, i.e., ϵy = −νxyϵx > 0 (see Section 2). As a result, upon increasing pressure, the γ sheet becomes compressed along the kx direction, but elongated along the ky direction. At a sufficiently high strain, the γ sheet touches the M point of the Brillouin zone, resulting in a van-Hove singularity (vHs). At this strain value |ϵx − ϵy| = |ϵvHs|, the γ sheet undergoes a so-called Lifshitz transition (Lifshitz, 1960), where its Fermi surface topology changes from a closed configuration (for |ϵx − ϵy| < |ϵvHs|) to an open one (for |ϵx − ϵy| > |ϵvHs|).
Naturally, experimental verification of such a Lifshitz transition is not only interesting by itself, but it also gains significance due to the impact on the physical properties of Sr2RuO4 (Li et al., 2022; Noad et al., 2023). Significant experimental results include a more than two-fold increase in the superconducting critical temperature, Tc, with increasing compression (Steppke et al., 2017) to ϵx, ∼, − 0.45%. Additionally, deviations from the archetypal Fermi-liquid-type T2 temperature dependence of electrical resistivity were observed in a similar strain range (Barber et al., 2018). Experimentally, recent high-precision elastocaloric measurements provided a very detailed thermodynamic map of the phase diagram of Sr2RuO4 as a function of ϵx. The thermodynamic identification of the features of the Lifshitz transition (Li et al., 2022; Noad et al., 2023) and superconductivity clearly demonstrate that maximum Tc occurs at ϵvHS. Presently, it appears likely that this close interrelation is due to the enhanced density of states at the Lifshitz transition and possibly a concomitant increase of electronic correlation strength.
The challenges in probing directly the electronic structure changes at the Lifshitz transition in Sr2RuO4 under large strains were not only related to the specific challenges of ARPES chamber environment, as described in the Section 2, but also related to the elastic properties of Sr2RuO4 (Hicks et al., 2014b; Sunko et al., 2019; Noad et al., 2023). Owing to its high elastic modulus, it is generally hard to apply large strains. In addition, the elastic limit of Sr2RuO4 at room temperature is quite low, only about −0.2% (Barber et al., 2019). This strain is less than the strain needed to reach the vHs. Thus, to probe the Lifshitz transition a device is needed, where some degree of tunability of strain is achieved as the temperature is lowered. This has led Sunko et al. to design the mechanical device, based on the concept of differential thermal expansion (see Section 2).
The great success of their approach is clearly visible in Figure 4B, when comparing the data (Sunko et al., 2019) taken at ϵx = 0 to the data at |ϵx − ϵy| > |ϵvHs|. The change of Fermi surface topology of the γ sheet from a closed to an open contour becomes clearly visible.
Further quantitative results on the evolution of the electronic structure were inferred from ARPES data (Sunko et al., 2019) as a function of varying degrees of strain. In such a passive strain device, the variation was achieved through changes of the sample’s thickness and corresponding variations in the effective strain transfer from the substrate to the top surface of the sample. Among the key results are the following. First, the β sheet responds linearly to strain, whereas the γ sheet shows a strongly non-linear change in particular close to ϵvHs. This is shown in Figure 4C, where the anisotropy of the γ sheet, measured by the parameters ΔkF,M1 and ΔkF,M2 (see Figure 4B), is plotted against the asymmetry of the β sheet, which is taken as a good measure of the anisotropic strain. Second, the Luttinger count of each of the α, β and γ bands remains unchanged with strain (see Figure 4D). This suggests that the Lifshitz transition is solely driven by the distortion of the bands and not by a redistribution of the carriers between the bands.
Tight-binding calculations with hopping parameters t, which change linearly with strain, qualitatively confirm the experimental results. The rate dt/dϵ is taken to be orbital-dependent and results from changes of the Ru-O-Ru bond lengths. Quantitative discrepancies between these calculations and experiments were most pronounced in the evolution of the γ sheet along the ky direction (see Figure 4C). It was suggested that electronic correlations are responsible. This notion is supported by the strong change of the Hall coefficient across the Lifshitz transition (Yang et al., 2023), which points towards a strong change of electron-electron scattering (Zingl et al., 2019) and correlation strength in its proximity. Further ARPES measurements under strain will certainly be useful to understand how correlations are precisely altered through the Lifshitz transition.
Finally, the recent study of the surface states of Sr2RuO4 under strain (Damascelli et al., 2000; Kreisel et al., 2021) by ARPES provided interesting new results (Morales et al., 2023). In contrast to the bulk, the RuO6 octahedra at the surface of Sr2RuO4 are rotated around the c-axis with antiphase on neighboring sites. As a result, the unit cell is enlarged and the Fermi surface significantly reconstructed (Veenstra et al., 2013). The high-quality experimental ARPES data of Abarca Morales et al. (Morales et al., 2023), together with their tight-binding modelling, showed that the strain-induced changes of the surface states can be best understood by only considering changes of the Ru-O-Ru bond lengths rather than by changes in the angles. Thus, the surface of Sr2RuO4 by its own forms an interesting reference system to understand the effect of strain on the electronic structure of quantum materials, where the specific arrangement of transition-metal octahedra plays a key role in the emergent physics.
Nematicity is an electronic instability that breaks rotational symmetry but preserves translational symmetry. It has proven to be a ubiquitous feature of correlated quantum materials and in particular of unconventional superconductors. Nematicity has been studied in great detail in iron-based superconductors (FeSC), which serve as a prototype material class for this instability (Johnston, 2010; Paglione and Greene, 2010; Fisher et al., 2011; Fernandes and Vafek, 2014; Si et al., 2016; Böhmer and Kreisel, 2017; Böhmer et al., 2022). In the FeSCs, nematicty breaks the tetragonal C4 symmetry and yields an order parameter with B2g symmetry. Corresponding anisotropies can be observed in the spin, orbital, and lattice degrees of freedom.
In many FeSCs, the nematic phase is accompanied by a spin-density wave transition at only slightly lower temperatures. Spin fluctuations were therefore suggested to drive an Ising-spin nematic order as a precursor to stripe magnetism (Fang et al., 2008; Xu et al., 2008; Fernandes et al., 2012). The discovery of nematicity without a magnetic order in FeSe (McQueen et al., 2009) promoted the idea of orbital fluctuation as the driving mechanism (Lee et al., 2009; Lv et al., 2009; Chen C.-C. et al., 2010; Onari and Kontani, 2012). Apart from low-energy descriptions, recent studies also explored the interplay of nematicity and electronic correlations in FeSC (Fanfarillo et al., 2017; Hu et al., 2018; Kostin et al., 2018; Lara et al., 2018; Yu et al., 2018; Pfau et al., 2021a; Pfau et al., 2021b; Steffensen et al., 2021; Fanfarillo et al., 2023). Despite extensive studies of nematicity in the FeSCs, there is so far no consensus on its microscopic origin.
The electronic nematic order changes the crystal structure of FeSCs from tetragonal to orthorhombic due to nemato-elastic coupling. An anisotropic strain of B2g symmetry will therefore induce a finite value of the nematic order parameter at all temperatures. A corresponding linear response measurement returns the nematic susceptibility. The resistivity anisotropy is the most prominent observable that has been used as a proxy for the nematic order parameter. The nematic susceptibility extracted from elastoresistivity measurements follows a Curie-Weiss law in a large temperature range above the nematic transition temperature, Tnem, before it decreases inside the nematic phase (Chu et al., 2012). Apart from resistivity, various other transport, thermodynamic, scattering, and spectroscopic probes have been employed in strain-dependent measurements to extract the nematic susceptibility (Böhmer et al., 2014; Kissikov et al., 2018; Cai et al., 2020; Caglieris et al., 2021; Ikeda et al., 2021; Sanchez et al., 2021; Occhialini et al., 2023). The temperature-dependence of the susceptibility is qualitatively very similar in almost all of them. However, it is unclear which observables are a true representation of the nematic order parameter since they probe different aspects of the electronic system. Nematic susceptibility measurements across the doping and substitution phase diagrams of FeSCs reveal growing evidence for a nematic quantum critical point. (Worasaran et al., 2021; Ishida et al., 2022; Palmstrom et al., 2022). If it exists, the consequences for the electronic properties are exciting: The diverging nematic fluctuations can lead to non-Fermi liquid behavior where the quasiparticles on the whole Fermi surface become overdamped (Metzner et al., 2003). At the same time the fluctuations can lead to strong, long-range interactions that promote high-temperature superconductivity (Yamase and Zeyher, 2013; Maier and Scalapino, 2014; Metlitski et al., 2015; Labat and Paul, 2017; Lederer et al., 2017).
The continuous development and sophistication of strain tuning capabilities will be an important factor to resolve the current questions in the field of nematicity in the FeSCs. The recent implementation of uniaxial stress capabilities in ARPES experiments allows to measure the effect of a B2g strain on the electronic structure. A corresponding linear response measurement provides a momentum, orbital, and energy-resolved nematic susceptibility. We will describe in detail how the electronic structure changes inside the nematic state in Section 5.1. This will guide the discussion of ARPES studies under uniaxial pressure in Section 5.2 and Section 5.3.
The Fe 3d orbitals form the low-energy electronic structure and Fermi surface of FeSCs as shown in Figure 5B. The orbitals are split by the tetragonal crystal electric field, which leads to a degeneracy between the dxz and dyz orbitals. This degeneracy is lifted when the material enters the nematic state, which leads to two key signatures in the spectral function that have been observed experimentally with ARPES.
1) The dispersion of the bands that predominantly contain dxz and dyz orbital character changes inside the nematic state. It can be characterized by a nematic band splitting ΔEnem, which is determined from the binding energy difference between the dxz and dyz bands as shown in Figure 5E. This splitting has been characterized in detail with ARPES for both hole and electron bands (Fuglsang Jensen et al., 2011; Kim et al., 2011; Yi et al., 2011; Yi et al., 2012; Nakayama et al., 2014; Suzuki et al., 2015; Watson et al., 2015; Fedorov et al., 2016; Zhang et al., 2016; Watson et al., 2017a; Pfau et al., 2019a; Pfau et al., 2019b; Fedorov et al., 2019; Yi et al., 2019). We highlight the behavior of the hole bands in Figure 5 because they are the focus of the uniaxial stress experiments published so far.
2) Electronic correlations due to the interplay of Coulomb interaction and Hund’s rule coupling split the spectral function into a coherent quasiparticle peak and incoherent Hubbard bands as show in Figure 5C. Hubbard bands have experimentally been observed in FeSe (Evtushinsky et al., 2016; Watson et al., 2017b). The ratio of spectral weight in the Hubbard bands and the quasiparticle peak characterizes quasiparticle coherence or equivalently the degree of electronic localization. Recent ARPES experiments showed that the dxz and dyz orbital have a different degree of quasiparticle coherence inside the nematic phase as sketched in Figure 5F (Pfau et al., 2021a; Pfau et al., 2021b). This effect can be characterized by the spectral weight difference ΔSnem. In general, correlation effects such as enhanced effective masses and the suppression of quasiparticle coherence are strongly orbital dependent in FeSCs (Yi et al., 2017). The observation of the spectral weight anisotropy inside the nematic state reflects this orbital differentiation since the degeneracy of the dxz and dyz is lifted inside the nematic state.
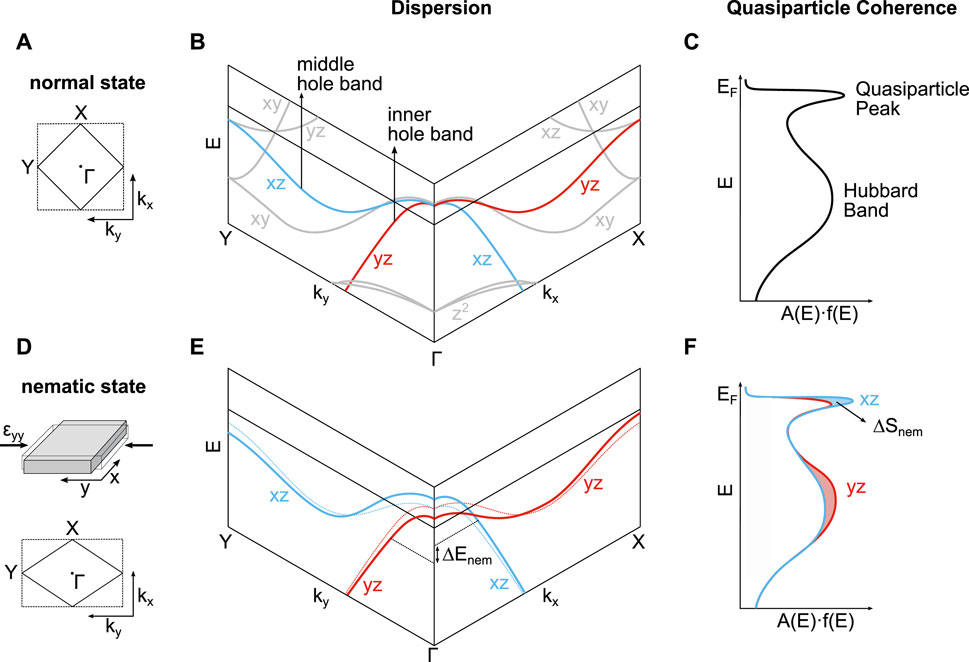
Figure 5. Effects of nematicity on the spectral function. (A) The 1Fe (dashed) and 2Fe (solid) Brillouin zone in the tetragonal state. (B) Sketch of the low energy band structure. While specifics such as band width and chemical potential vary between different FeSCs, the main features are consistent across the family. (C) Over a larger energy range, the spectral function A shows a splitting of the 3d weight into a quasiparticle peak and Hubbard bands. A is multiplied by a Fermi-Dirac distribution f. (D) Brillouin zone in the nematic state. The sketch of the sample indicates the corresponding deformation due to nematicity or due to uniaxial compression along y. (E) Change in dispersion of the two dxz and dyz hole bands in the nematic state. Dashed lines indicate dispersion in normal state for comparison. ΔEnem is the nematic band splitting. (F) Sketch of the observed anisotropy of quasiparticle coherence in nematic state, that can be characterized by ΔSnem (Pfau et al., 2021a; Pfau et al., 2021b). (A–E) have been adapted with permission (Pfau et al., 2021a). Copyright 2021 by the American Physics Society.
The absence of magnetic order made FeSe the ideal candidate to study the effects of nematicity on the electronic structure because band folding due to spin-density wave (SDW) order did not obstruct its signatures. The detailed momentum dependence of ΔEnem and the complex dispersion response at the electron bands was mapped out in detail in FeSe (Nakayama et al., 2014; Shimojima et al., 2014; Suzuki et al., 2015; Watson et al., 2015; Fanfarillo et al., 2016; Fedorov et al., 2016; Watson et al., 2016; Zhang et al., 2016; Watson et al., 2017a; Pfau et al., 2019a; Yi et al., 2019). The anisotropy of quasiparticle coherence inside the nematic phase was revealed in FeSe as well (Pfau et al., 2021b). Comparable measurements of the pristine nematic state for magnetic FeSCs are restricted to a very small temperature window between the nematic and magnetic transition. They are, however, highly desirable to probe whether the microscopic mechanism of nematicity in magnetic and non-magnetic FeSCs is different.
To overcome the interference from SDW order, recent ARPES studies on BaFe2As2 used in-situ tunable uniaxial stress (see Section 2) along the Fe-Fe bond direction applied at a temperature above Tnem = 140 K using a piezoelectric device (Pfau et al., 2019a; Pfau et al., 2021a). By inducing a finite nematic order parameter at all temperatures through B2g strains, this approach allows to study the response of the electronic structure to nematicity without interference of the SDW order.
Figure 6 shows a comprehensive overview of the ARPES results. The uniaxial stress direction is labeled y without loss of generality. Photoemission matrix elements are employed to selectively probe either dxz or dyz orbital character of the inner and the middle hole band. The two spectra for each configuration are taken at a compressed and tensioned state of the sample, respectively. The ARPES data show clear uniaxial stress-induced changes of the electronic structure, that can be identified in the energy distribution curves (EDCs). First, a shift in binding energy ΔE was obtained from the peak maxima (Figure 6A4). Second, a change of the quasiparticle spectral weight ΔS was obtained from the difference in ARPES intensity (Figure 6A3). Both quantities were evaluated along kx and along ky. The associated nematic band splitting and anisotropic quasiparticle coherence is calculated from the antisymmetric component of these observables (Eq. 1) and shown in Figure 7.
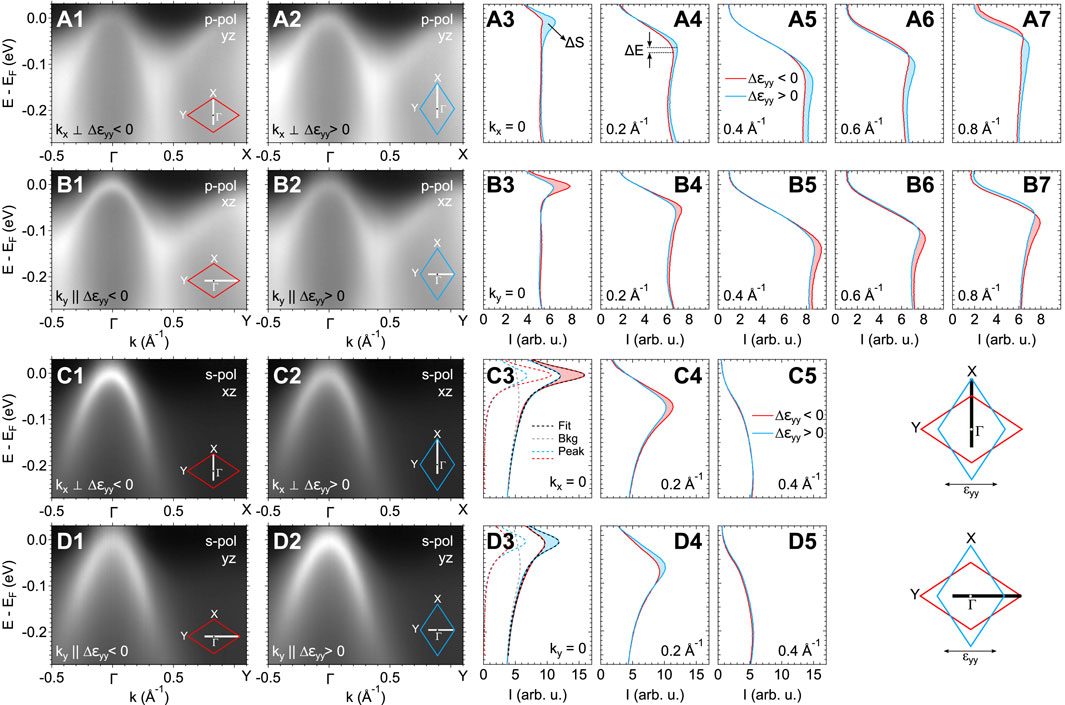
Figure 6. ARPES spectra on BaFe2As2 under uniaxial pressure at 160 K. (A) Spectra taken with p-polarized light, which highlights the middle hole band. It has predominantly dyz character along kx. (A1) is taken with compressive stress applied along y while the sample is tensioned for the spectrum in (A2). (A3–A7) show energy distribution curves (EDCs) extracted from both spectra at the indicated momentum. Each panel compares the compressed with the tensioned state. Stress induced changes of the band dispersion ΔE are obtained from the maximum of the EDCs. The change in quasiparticle spectral weight is indicated by ΔS. (B) same as in (A) but along ky, which leads to photoemisison predominantly from the dxz orbital. (C,D) same as (A,B) but with s-polarized light, which photoemits electrons from the inner hole band. Sketches in the bottom right indicate the measurement geometries with the Brillioun zone for compressive (red) and tensile (blue) stress ϵyy along y. Figures are reproduced with permission Ref. (Pfau et al., 2021a). Copyright 2021 by the American Physics Society.
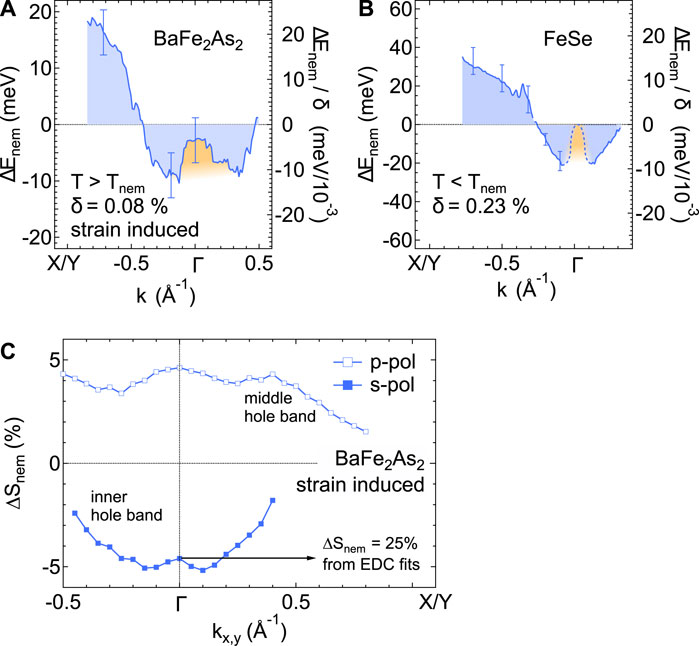
Figure 7. (A) Uniaxial-stress induced nematic band splitting of the middle hole band in BaFe2As2. δ is the orthorhombicity extracted from the measured strain. (B) Equivalent data on FeSe but inside the nematic state. Both materials show the same momentum dependence and overall scale of the nematic band splitting. (C) Uniaxial-stress induced anisotropic quasiparticle coherence in BaFe2As2. It is normalized to the total spectral weight in the measured energy window. The magnitude of the spectral weight response extracted from fits shown in Figure 6C3 is indicated at Γ. (A,B) Reproduced with permission (Pfau et al., 2019a). Copyright 2019, American Physical Society. (C) Reproduced with permission (Pfau et al., 2021a). Copyright 2021, American Physical Society.
The raw data in Figure 6 already show that the response to uniaxial pressure is almost entirely antisymmetric, i.e., it follows a B2g symmetry and therefore corresponds to changes in the spectral function due to a finite nematic order parameter.
Figure 7A shows the momentum-dependent nematic band splitting in BaFe2As2, which can directly be compared to the one obtain for FeSe inside the nematic state (Figure 7B). Both show a sign change between Γ and the Brillouin zone corner. The complex response around Γ is due to an interplay of spin-orbit coupling and nematic band splitting, which has been described in detail in Ref. (Pfau et al., 2019a). The magnitude of the splitting, normalized by the corresponding orthorhombicity δ, is very similar as well. Figure 7C shows the momentum dependence of the strain-induced nematic spectral weight response for the inner and the middle hole band. ΔSnem has the same sign in BaFe2As2 as in FeSe (Pfau et al., 2021b), i.e., the dxz orbital becomes more coherent than the dyz. The size of the response, once normalized to the orthorhombicity, is also on the same order of magnitude. These results suggest that the microscopic mechanism behind nematicity in the non-magnetic FeSe and the magnetic BaFe2As2 is identical.
The nematic band splitting ΔEnem, which is non-zero only below nematic phase transition temperature Tnem, can be interpreted as an order parameter. Its linear strain response and the corresponding nematic susceptibility will detect nematic fluctuations in the charge channel and in an orbital, momentum, and energy-resolved fashion. This knowledge can greatly contribute to current discussions about the microscopic origin of nematicity and about the influence of nematic fluctuations on the strange metal regime. The interpretation of the band shift as an order parameter neglects spin-orbit interaction, which is on the order of a few tens of meV in FeSCs. It leads in principle to a non-linear relationship between the nematic order parameter and the measured band shifts (Fernandes and Vafek, 2014; Pfau et al., 2019a).
Cai et al. performed the first experiments to determine the temperature-dependent nematic susceptibility with ARPES. They measured the strain-response of the dispersion in FeSe0.9S0.1 (Tnem = 65 K) using a piezoelectric device (Cai et al., 2020). Selected ARPES spectra of the inner hole band (α) and the middle hole band (β) as function of the voltage applied to the piezoelectric stacks are shown in Figures 8A, D. The inner hole band is studied around the Brillouin zone center Γ while the middle hole band was studied around the Brillouin zone corner M. Dispersions are extracted from intensity maxima and plotted as function of voltage in Figures 8B, E, respectively. A clear change of the dispersion is detected that varies continuously with uniaxial stress.
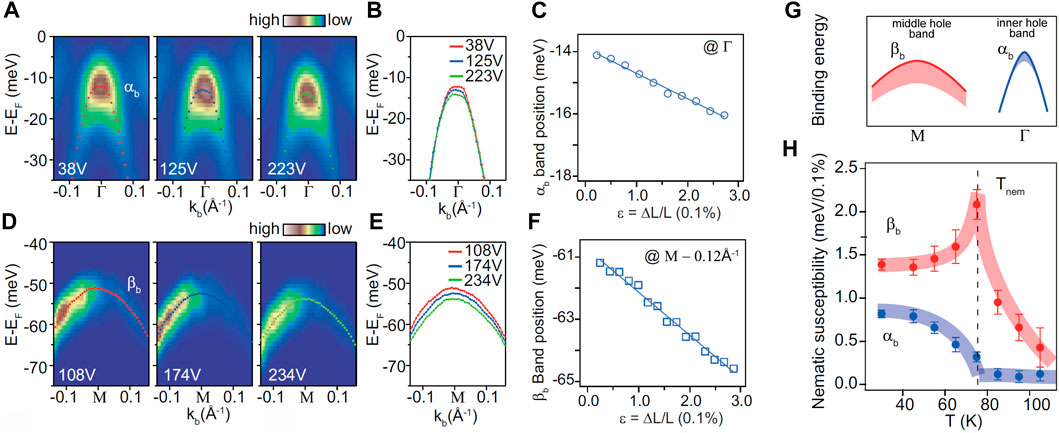
Figure 8. Linear strain response of the dispersion and corresponding nematic susceptibility in FeSe0.9S0.1at 30 K below the nematic transition temperature. (A) ARPES spectra of the inner hole band around the Brillouin center taken at different voltages of the piezo-driven stress device. The points indicate the band position obtained from peak fitting. They are replotted in (B) to illustrate the voltage dependence of the dispersion. (C) The binding energy at Γ follows a linear behavior as function of the strain component ϵ along the pressure direction. (D–F) same as in (A–C) but for the middle hole band measured around the Brillouin zone corner M. (G) Sketch of the measured dispersion and the band shift due to uniaxial stress. (H) Temperature dependence of the nematic susceptibility extracted from the linear response of the band shift. Figures are reproduced with permission (Cai et al., 2020). Copyright 2020, American Physical Society.
The data was quantitatively evaluated as function of strain ϵ, which was measured parallel to the stress direction using microscope images of the gap between the two sample mounting surfaces. The data in Figures 8C, F show that the binding energy is linear as function of ϵ below Tnem (Figures 8C, F). This is in contrast to the hysteresis detected in the spectral weight response due to domain redistribution (not shown). Cai et al. also find a linear response for higher temperatures and across Tnem. Non-linear contributions due to spin-orbit coupling were not observed.
Using the observed linear response, Cai et al. calculated the nematic susceptibility as function of temperature as shown in Figure 8H. Interestingly, the susceptibility is different for the two different bands and momenta. For the middle hole band (β) at a momentum close to M, the nematic susceptibility has a peak at Tnem and resembles a Curie-Weiss behavior. The temperature dependence is qualitatively similar to that from other probes such as resistivity or Raman spectroscopy (Chu et al., 2012; Gallais and Paul, 2016). In contrast, the peak at Tnem is absent in the susceptibility derived from the inner hole band (α) at Γ. The origin of this behavior is unclear so far and possible scenarios include the presence of multiple order parameters at the Brillouin zone center and boundary (Fernandes and Vafek, 2014), or the influence of spin-orbit coupling, which affects the dispersion particularly at Γ (Fernandes and Vafek, 2014; Pfau et al., 2019a). Additionally, the role of the dxy orbital in the formation of nematic order is still debated (Watson et al., 2016; Yi et al., 2019; Rhodes et al., 2022).
Topologically non-trivial materials have attracted significant attention due to their robust, dissipationless electronic states. Controlling these exotic states of matter is crucial for their application. Therefore, topological phase transitions from trivial to non-trivial topological states as well as between different non-trivial states have emerged as a significant research field.
One of the most notable methods to manipulate topological states involves breaking time-reversal symmetry. This can be achieved through the application of a magnetic field or doping with magnetic elements. An early attempt involves the random distribution of magnetic elements on the surface of a topological material (Chen YL. et al., 2010). However, this approach lacks reversibility. A different method employs magnetic topological materials (Andrei Bernevig et al., 2022); however, this approach limits the usable temperature and magnetic field range.
An alternative strategy involves the application of uniaxial stress. Uniaxial stress not only offers reversibility but also provides a means to easily engineer and fine-tune topological phase transitions. This makes it a valuable tool in manipulating the exotic electronic states of topological materials. Topological phase transitions driven by uniaxial and multi-axial strains have been predicted in various materials including Bi2Se3, Cd3As2, ZrTe5, HfTe5, TaSe3, LnPn (Ln = Ce, Pr, Sm, Gd, Yb; Pn = Sb, Bi) and more (Young et al., 2011; Wang et al., 2013; Weng et al., 2014; Duan et al., 2018; Nie et al., 2018). Among them, three different bulk topological materials have been studied with ARPES under uniaxial stress: ZrTe5, HfTe5, and TaSe3. In the following, we will present the results from ARPES studies, which directly visualize the degree of tunability and control of the topological properties with uniaxial stress.
The transition metal pentatellurides ZrTe5 and HfTe5 have an orthorhombic crystal structure (Space group number 63, Cmcm). They are layered materials due to van-der-Waals bonding between Te along the crystallographic b direction. In the late 70’s and early 80’s, these materials received a lot of attention due to peculiar behavior in the resistivity (Okada et al., 1980; DiSalvo et al., 1981; Skelton et al., 1982). Their topological behavior and in particular the prospect of strain tuning topological phase transitions brought them back onto the map of condensed matter research (Chen et al., 2015a; Chen et al., 2015b; Manzoni et al., 2015; Li Qiang et al., 2016; Li Xiang-Bing et al., 2016; Manzoni et al., 2016; Moreschini et al., 2016; Wu et al., 2016; Zheng et al., 2016; Shen et al., 2017; Zhang et al., 2017; Liu et al., 2018; Nair et al., 2018). The band inversion that is responsible for the bulk band gap and the non-trivial topological state is not due to spin-orbit coupling. Instead it is driven by the special nonsymmorphic space group. Specifically, the band inversion at Γ occurs between the zigzag chain Tez-Px and the prism chain dimer Tez-Py states. Both Tez-Px and Tez-Py are initially fourfold degenerate due to the presence of four equivalent Te atoms. However, strong interchain covalent bonding causes each state to split into two, and weak interchain coupling further divides them into singly degenerate states. Consequently, the band inversion occurs between the bonding Ted states with mxz = 1 and the antibonding Tez states with p = −1, resulting in one odd parity state. This change in occupation alters the total parity of the occupied states at Γ, leading to the emergence of the topological state. Hydrostatic pressure does not alter the topological state as long as the interlayer coupling is not strong enough to reverse the band ordering (Weng et al., 2014). In contrast, according to DFT results, uniaxial stress along the crystallographic a axis modifies the energy gap effectively and allows to tune between an STI and WTI state as this material is in the boundary (Mutch et al., 2019). The corresponding phase diagram is shown in Figure 9A.
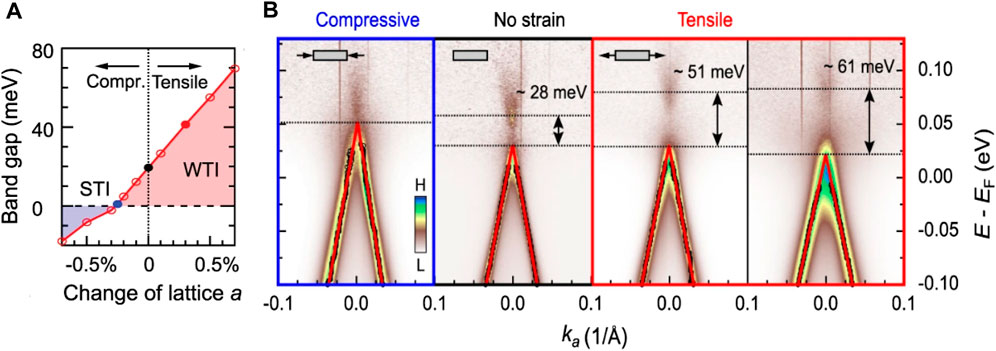
Figure 9. Topological phase transitions in transition-metal pentatellurides. (A) Calculated phase diagram of ZrTe5 with different lattice constants (strain) (Zhang et al., 2021). Blue, black, and red solid circles roughly indicate the experimental values in (B). (B) The ARPES results on ZrTe5 are shown. The bulk band gap changes in size with compressive and tensile strain. With compressive strain, the gap is (nearly) closed, reaching a Dirac semimetal state. With tensile strain, the band gap becomes larger, stabilizing the WTI state. The data are taken with p-polarized photons and normalized by their density of states (DOS). The black markers are extracted from the momentum distribution curve (MDC) peaks, and the red solid lines are the fitting results of the black markers (Zhang et al., 2021). The reference (Zhang et al., 2021) is an Open Access article licensed under a Creative Commons Attribution 4.0 International License.
Zhang et al. performed ARPES measurements under uniaxial stress to visualize the predicted topological phase transition on ZrTe5 (Zhang et al., 2021). They utilized a mechanical stress device as depicted in Figure 1B. The band structure measured under different stress is shown in Figure 9B. The unstrained sample exhibits a bandgap of approximately 28 meV. Upon the application of tensile stress, the bandgap expands and hence the WTI state is stabilized. Under compressive stress, the gap size diminishes and completely disappears, which marks the theoretically-predicted topological phase transition into a Dirac semimetal (DSM) state. Calculations suggest that further compression will lead to a STI phase (Weng et al., 2014; Zhang et al., 2021). The isostructural HfTe5 was predicted to undergo the same topological phase transition as ZrTe5. Jo et al. performed APRES measurements under in-situ tunable stress on HfTe5 using a piezoelectric device (Jo et al., 2023b). The results also indicate a topological phase transition from a WTI to a STI with applied compressive stress. Furthermore, this research highlights that the self-energy of electronic states are strongly impacted by the presence of topological surface states.
TaSe3 is a superconductor with a transition temperature of 2 K (Sambongi et al., 1977). At the same time, it was predicted to host non-trivial topological states (Nie et al., 2018). The possibility of topological superconductivity and Majorana physics renders TaSe3 a particularly exciting material for strain tuning of topological properties. TaSe3 has a monoclinic, quasi one-dimensional crystal structure with chains along the b-axis that are coupled by van-der-Waals interactions. The topological nature is due to a band inversion of Ta d states and Se p states. Spin-orbit interaction leads to a gap opening at the band crossing points.
Initial calculations predicted that TaSe3 undergoes topological transitions as function of strain perpendicular to the chains along the a and c axis (Nie et al., 2018). Subsequent ARPES studies combined with DFT calculations by Lin et al. and Hyun et al. studied topological transitions for strains parallel to the chains along b (Lin et al., 2021; Hyun et al., 2022). Both studies predicted a phase transition sequence from a WTI through a STI towards topological trivial states but differ in their assignment of the zero-stress topological state (see Figure 10). This difference was attributed to internal strains from Se vacancies (Hyun et al., 2022). The pioneering study from Lin et al. used a bending device to apply stress to the sample. The subsequent study by Hyun et al. employed a mechanical uniaxial stress device that is actuated by a screw as described in Section 2. Both ARPES measurements confirm stress-induced changes of the topological properties in TaSe3 as predicted by their DFT calculations.
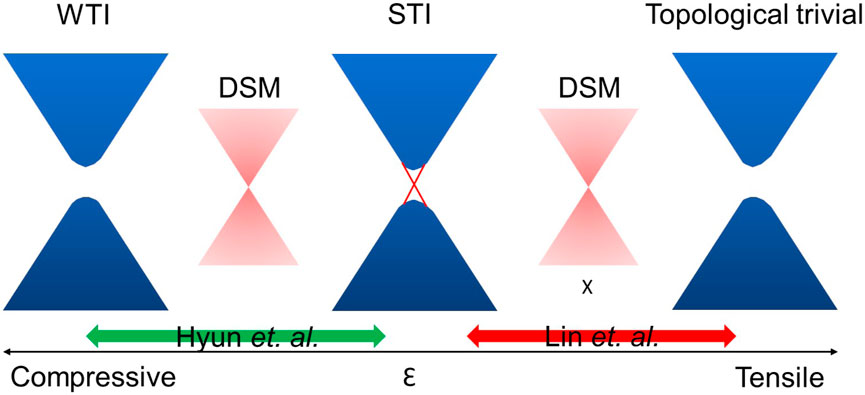
Figure 10. A schematic topological phase diagram of TaSe2 is presented. The green arrow marks the regime studied in reference, (Hyun et al., 2022), while the red arrow marks the regime explored in reference, (Lin et al., 2021). However, in reference (Lin et al., 2021), the Dirac semimetal (DSM) state between STI and trivial insulator was not observed.
The initial experiments have been very successful in showcasing the efficacy of strain-tuning in topological phase transitions. These achievements lay the groundwork for a comprehensive understanding of topological phase transitions in the future.
A key property of quantum materials is their tunability by non-thermal parameters. Changing material properties by in-situ tuning parameters such as electric and magnetic fields or pressure are of particular importance. They circumvent disorder effects induced by chemical doping and substitution and they ease technical application. In the past decade, uniaxial stress tuning uncovered a host of new phenomena and has emerged as a versatile tool in the study of quantum materials. The increased interest was to a large extent driven by technological developments. This is also reflected in the electronic structure measurements under uniaxial pressure that we present here. In particular, the requirements for the photoelectron emission and detection severely limited the implementation of non-thermal tuning in ARPES so far. The adaptation of uniaxial stress cells for photoemission allows for the first time to measure ARPES as function of in-situ tunable stress. There is a push to expand the range of tuning parameters for ARPES even further for example by adding magnetic field tuning (Huang et al., 2023; Ryu et al., 2023). We have discussed how these ARPES measurements, together with quantum oscillation studies, under uniaxial pressure contribute important new insights into fields, such as unconventional superconductivity, correlated electron physics, and topological properties. The examples discussed here demonstrate the importance of these techniques in addressing outstanding questions in the quantum-materials field. Furthermore, these studies not only address existing questions but also pave the way for novel research avenues in quantum materials, in which electronic structure studies under tunable stress will play a crucial role.
Currently, the primary limitations arise from the amount of stress that can be applied to the system. Specifically, when utilizing substrates, they have a constrained elastic response. Looking forward, if we could apply greater uniaxial stress, that would significantly enhance our research capabilities. Another avenue worth pursuing is to improve the spatial resolution via nano-ARPES. Investigating the tuning of strain in two-dimensional materials and their heterostructures could yield fascinating results. Additionally, we could explore new possibilities by broadening the spectrum of stress tensors, including shear forces such as twisting.
NHJ: Writing–original draft, Writing–review and editing. EG: Writing–original draft, Writing–review and editing. HP: Writing–original draft, Writing–review and editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. NHJ acknowledges support from National Science Foundation (NSF) through NSF CAREER grant under Award No. DMR-2337535. HP is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division, under Award Number DE-SC0024135. EG thanks the Max-Planck-Society for financial support.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Andrei Bernevig, B., Felser, C., and Beidenkopf, H. (2022). Progress and prospects in magnetic topological materials. Nature 603, 41–51. doi:10.1038/s41586-021-04105-x
Barber, M. E., Gibbs, A. S., Maeno, Y., Mackenzie, A. P., and Hicks, C. W. (2018). Resistivity in the vicinity of a van hove singularity: sr2ruo4 under uniaxial pressure. Phys. Rev. Lett. 120, 076602. doi:10.1103/physrevlett.120.076602
Barber, M. E., Steppke, A., Mackenzie, A. P., and Hicks, C. W. (2019). Piezoelectric-based uniaxial pressure cell with integrated force and displacement sensors. Rev. Sci. Instrum. 90, 023904. doi:10.1063/1.5075485
Bergemann, C., Julian, S. R., Mackenzie, A. P., NishiZaki, S., and Maeno, Y. (2000). Detailed topography of the fermi surface of sr2ruo4. Phys. Rev. Lett. 84, 2662–2665. doi:10.1103/physrevlett.84.2662
Bergemann, C., Mackenzie, A. P., Julian, S. R., Forsythe, D., and Ohmichi, E. (2003). Quasi-two-dimensional fermi liquid properties of the unconventional superconductor sr2ruo4. Adv. Phys. 52, 639–725. doi:10.1080/00018730310001621737
Böhmer, A. E., Burger, P., Hardy, F., Wolf, T., Schweiss, P., Fromknecht, R., et al. (2014). Nematic susceptibility of hole-doped and electron-doped bafe2as2 iron-based superconductors from shear modulus measurements. Phys. Rev. Lett. 112, 047001. doi:10.1103/physrevlett.112.047001
Böhmer, A. E., Chu, J.-H., Lederer, S., and Yi, M. (2022). Nematicity and nematic fluctuations in iron-based superconductors. Nat. Phys. 18, 1412–1419. doi:10.1038/s41567-022-01833-3
Böhmer, A. E., and Kreisel, A. (2017). Nematicity, magnetism and superconductivity in fese. J. Phys. Condens. Matter 30, 023001. doi:10.1088/1361-648x/aa9caa
Caglieris, F., Wuttke, C., Hong, X. C., Sykora, S., Kappenberger, R., Aswartham, S., et al. (2021). Strain derivative of thermoelectric properties as a sensitive probe for nematicity. npj Quantum Mater. 6, 27. doi:10.1038/s41535-021-00324-7
Cai, C., Han, T. T., Wang, Z. G., Chen, L., Wang, Y. D., Xin, Z. M., et al. (2020). Momentum-resolved measurement of electronic nematic susceptibility in the fese0.9s0.1 superconductor. Phys. Rev. B 101, 180501. doi:10.1103/physrevb.101.180501
Carrington, A. (2011). Quantum oscillation studies of the Fermi surface of iron-pnictide superconductors. Rep. Prog. Phys. 74, 124507. doi:10.1088/0034-4885/74/12/124507
Chen, C.-C., Maciejko, J., Sorini, A. P., Moritz, B., Singh, R. R. P., and Devereaux, T. P. (2010a). Orbital order and spontaneous orthorhombicity in iron pnictides. Phys. Rev. B 82, 100504. doi:10.1103/physrevb.82.100504
Chen, R. Y., Chen, Z. G., Song, X.-Y., Schneeloch, J. A., Gu, G. D., Wang, F., et al. (2015a). Magnetoinfrared spectroscopy of landau levels and zeeman splitting of three-dimensional massless Dirac fermions in ZrTe5. Phys. Rev. Lett. 115, 176404. doi:10.1103/physrevlett.115.176404
Chen, R. Y., Zhang, S. J., Schneeloch, J. A., Zhang, C., Li, Q., Gu, G. D., et al. (2015b). Optical spectroscopy study of the three-dimensional Dirac semimetal ZrTe5. Phys. Rev. B 92, 075107. doi:10.1103/physrevb.92.075107
Chen, Y. L., Chu, J.-H., Analytis, J. G., Liu, Z. K., Igarashi, K., Kuo, H.-H., et al. (2010b). Massive Dirac fermion on the surface of a magnetically doped topological insulator. Science 329, 659–662. doi:10.1126/science.1189924
Chu, J.-H., Kuo, H.-H., Analytis, J. G., and Fisher, I. R. (2012). Divergent nematic susceptibility in an iron arsenide superconductor. Science 337, 710–712. doi:10.1126/science.1221713
Cobo, S., Ahn, F., Eremin, I., and Akbari, A. (2016). Anisotropic spin fluctuations in sr2ruo4: role of spin-orbit coupling and induced strain. Phys. Rev. B 94, 224507. doi:10.1103/physrevb.94.224507
Damascelli, A., Lu, D. H., Shen, K. M., Armitage, N. P., Ronning, F., Feng, D. L., et al. (2000). Fermi surface, surface states, and surface reconstruction in sr2ruo4. Phys. Rev. Lett. 85, 5194–5197. doi:10.1103/physrevlett.85.5194
DiSalvo, F. J., Fleming, R. M., and Waszczak, J. V. (1981). Possible phase transition in the quasi-one-dimensional materials ZrTe5 or HfTe5. Phys. Rev. B 24, 2935–2939. doi:10.1103/physrevb.24.2935
Duan, Xu, Wu, F., Chen, J., Zhang, P., Liu, Y., Yuan, H., et al. (2018). Tunable electronic structure and topological properties of LnPn (Ln= Ce, Pr, Sm, Gd, Yb; Pn= Sb, Bi). Commun. Phys. 1, 71. doi:10.1038/s42005-018-0074-8
Evtushinsky, D. V., Aichhorn, M., Sassa, Y., Liu, Z. H., Maletz, J., Wolf, T., et al. (2016). Direct observation of dispersive lower hubbard band in iron-based superconductor fese. Available at: https://arxiv.org/abs/1612.02313.
Fanfarillo, L., Giovannetti, G., Capone, M., and Bascones, E. (2017). Nematicity at the hund’s metal crossover in iron superconductors. Phys. Rev. B 95, 144511. doi:10.1103/physrevb.95.144511
Fanfarillo, L., Mansart, J., Toulemonde, P., Cercellier, H., Le Fèvre, P., çois Bertran, F., et al. (2016). Orbital-dependent fermi surface shrinking as a fingerprint of nematicity in fese. Phys. Rev. B 94, 155138. doi:10.1103/physrevb.94.155138
Fanfarillo, L., Valli, A., and Capone, M. (2023). Nematic spectral signatures of the hund’s metal. Phys. Rev. B 107, L081114. doi:10.1103/physrevb.107.l081114
Fang, C., Yao, H., Tsai, W.-F., Hu, J. P., and Kivelson, S. A. (2008). Theory of electron nematic order in lafeaso. Phys. Rev. B 77, 224509. doi:10.1103/physrevb.77.224509
Fedorov, A., Yaresko, A., Haubold, E., Kushnirenko, Y., Kim, T., Büchner, B., et al. (2019). Energy scale of nematic ordering in the parent iron-based superconductor bafe2as2. Phys. Rev. B 100, 024517. doi:10.1103/physrevb.100.024517
Fedorov, A., Yaresko, A., Kim, T. K., Kushnirenko, Y., Haubold, E., Wolf, T., et al. (2016). Effect of nematic ordering on electronic structure of fese. Sci. Rep. 6, 36834. doi:10.1038/srep36834
Fernandes, R. M., Chubukov, A. V., Knolle, J., Eremin, I., and Schmalian, J. (2012). Preemptive nematic order, pseudogap, and orbital order in the iron pnictides. Phys. Rev. B 85, 024534. doi:10.1103/physrevb.85.024534
Fernandes, R. M., and Vafek, O. (2014). Distinguishing spin-orbit coupling and nematic order in the electronic spectrum of iron-based superconductors. Phys. Rev. B 90, 214514. doi:10.1103/physrevb.90.214514
Fisher, I. R., Degiorgi, L., and Shen, Z. X. (2011). In-plane electronic anisotropy of underdoped ‘122’ fe-arsenide superconductors revealed by measurements of detwinned single crystals. Rep. Prog. Phys. 74, 124506. doi:10.1088/0034-4885/74/12/124506
Fuglsang Jensen, M., Brouet, V., Papalazarou, E., Nicolaou, A., Taleb-Ibrahimi, A., Le Fèvre, P., et al. (2011). Angle-resolved photoemission study of the role of nesting and orbital orderings in the antiferromagnetic phase of bafe2as2. Phys. Rev. B 84, 014509. doi:10.1103/physrevb.84.014509
Gallais, Y., and Paul, I. (2016). Charge nematicity and electronic Raman scattering in iron-based superconductors. Comptes Rendus Phys. 17, 113–139. iron-based superconductors/ Supraconducteurs à base de fer. doi:10.1016/j.crhy.2015.10.001
Ghosh, S., Brückner, F., Nikitin, A., Grinenko, V., Elender, M., Mackenzie, A. P., et al. (2020). Piezoelectric-driven uniaxial pressure cell for muon spin relaxation and neutron scattering experiments. Rev. Sci. Instrum. 91, 103902. doi:10.1063/5.0025307
Grinenko, V., Ghosh, S., Sarkar, R., Orain, J.-C., Nikitin, A., Elender, M., et al. (2021a). Split superconducting and time-reversal symmetry-breaking transitions in Sr2RuO4 under stress. Nat. Phys. 17, 748–754. doi:10.1038/s41567-021-01182-7
Grinenko, V., Ghosh, S., Sarkar, R., Orain, J.-C., Nikitin, A., Elender, M., et al. (2021b). Split superconducting and time-reversal symmetry-breaking transitions in sr2ruo4 under stress. Nat. Phys. 17, 748–754. doi:10.1038/s41567-021-01182-7
Hicks, C. W., Barber, M. E., Edkins, S. D., Brodsky, D. O., and Mackenzie, A. P. (2014b). Piezoelectric-based apparatus for strain tuning. Rev. Sci. Instrum. 85, 065003. doi:10.1063/1.4881611
Hicks, C. W., Brodsky, D. O., Yelland, E. A., Gibbs, A. S., Bruin, J. A. N., Barber, M. E., et al. (2014a). Strong increase of tc of sr2ruo4 under both tensile and compressive strain. Science 344, 283–285. doi:10.1126/science.1248292
Hu, H., Yu, R., Nica, E. M., Zhu, J.-X., and Si, Q. (2018). Orbital-selective superconductivity in the nematic phase of fese. Phys. Rev. B 98, 220503. doi:10.1103/physrevb.98.220503
Hu, J., Xu, S.-Y., Ni, Ni, and Mao, Z. (2019). Transport of topological semimetals. Annu. Rev. Mater. Res. 49, 207–252. doi:10.1146/annurev-matsci-070218-010023
Huang, J., Yue, Z., Baydin, A., Zhu, H., Nojiri, H., Kono, J., et al. (2023). Angle-resolved photoemission spectroscopy with an in situ tunable magnetic field. Rev. Sci. Instrum. 94, 093902. doi:10.1063/5.0157031
Hyun, J., Jeong, M. Y., Jung, M.-C., Lee, Y., Kim, Y., Jung, S., et al. (2022). Strain-controlled evolution of electronic structure indicating topological phase transition in the quasi-one-dimensional superconductor TaSe3. Phys. Rev. B 105, 115143. doi:10.1103/physrevb.105.115143
Ikeda, M. S., Straquadine, J. A. W., Hristov, A. T., Worasaran, T., Palmstrom, J. C., Sorensen, M., et al. (2019). AC elastocaloric effect as a probe for thermodynamic signatures of continuous phase transitions. Rev. Sci. Instrum. 90, 083902. doi:10.1063/1.5099924
Ikeda, M. S., Worasaran, T., Rosenberg, E. W., Palmstrom, J. C., Kivelson, S. A., and Fisher, I. R. (2021). Elastocaloric signature of nematic fluctuations. Proc. Natl. Acad. Sci. 118, e2105911118. doi:10.1073/pnas.2105911118
Ishida, K., Onishi, Y., Tsujii, M., Mukasa, K., Qiu, M., Saito, M., et al. (2022). Pure nematic quantum critical point accompanied by a superconducting dome. Superconductivity 119, e2110501119. doi:10.1073/pnas.2110501119
Jo, Na H., Ashour, O. A., Shu, Z., Jozwiak, C., Bostwick, A., Ryu, S. H., et al. (2023a). On the effects of strain, defects, and interactions on the topological properties of hfte5. Available at: https://arxiv.org/abs/2303.10836.
Jo, Na H., Ashour, O. A., Shu, Z., Jozwiak, C., Bostwick, A., Ryu, S. H., et al. (2023b) On the effects of strain, defects, and interactions on the topological properties of HfTe5. Available at: https://arxiv.org/abs/2303.10836.
Jo, Na H., Wang, L.-L., Orth, P. P., Bud’ko, S. L., and Canfield, P. C. (2019). Magnetoelastoresistance in WTe2: exploring electronic structure and extremely large magnetoresistance under strain. Proc. Natl. Acad. Sci. 116, 25524–25529. doi:10.1073/pnas.1910695116
Johnston, D. C. (2010). The puzzle of high temperature superconductivity in layered iron pnictides and chalcogenides. Adv. Phys. 59, 803–1061. doi:10.1080/00018732.2010.513480
Kang, D., Zhou, Y., Yi, W., Yang, C., Guo, J., Shi, Y., et al. (2015). Superconductivity emerging from a suppressed large magnetoresistant state in tungsten ditelluride. Nat. Commun. 6, 7804. doi:10.1038/ncomms8804
Kim, H.-H., Souliou, S. M., Barber, M. E., Lefrançois, E., Minola, M., Tortora, M., et al. (2018). Uniaxial pressure control of competing orders in a high-temperature superconductor. Science 362, 1040–1044. doi:10.1126/science.aat4708
Kim, Y., Oh, H., Kim, C., Song, D., Jung, W., Kim, B., et al. (2011). Electronic structure of detwinned BaFe2As2 from photoemission and first principles. Phys. Rev. B 83, 064509. doi:10.1103/physrevb.83.064509
Kissikov, T., Sarkar, R., Lawson, M., Bush, B. T., Timmons, E. I., Tanatar, M. A., et al. (2018). Uniaxial strain control of spin-polarization in multicomponent nematic order of bafe2as2. Nat. Commun. 9, 1058. doi:10.1038/s41467-018-03377-8
Kostin, A., Sprau, P. O., Kreisel, A., Chong, Yi X., Böhmer, A. E., Canfield, P. C., et al. (2018). Imaging orbital-selective quasiparticles in the hund’s metal state of fese. Nat. Mater. 17, 869–874. doi:10.1038/s41563-018-0151-0
Kreisel, A., Marques, C. A., Rhodes, L. C., Kong, X., Berlijn, T., Fittipaldi, R., et al. (2021). Quasi-particle interference of the van hove singularity in sr2ruo4. npj Quantum Mater. 6, 100. doi:10.1038/s41535-021-00401-x
Labat, D., and Paul, I. (2017). Pairing instability near a lattice-influenced nematic quantum critical point. Phys. Rev. B 96, 195146. doi:10.1103/physrevb.96.195146
Lara, B., Valenzuela, B., and Fanfarillo, L. (2018). Nematic pairing from orbital-selective spin fluctuations in fese. npj Quantum Mater. 3, 56. doi:10.1038/s41535-018-0129-9
Lederer, S., Schattner, Y., Berg, E., and Kivelson, S. A. (2017). Superconductivity and non-fermi liquid behavior near a nematic quantum critical point. Proc. Natl. Acad. Sci. 114, 4905–4910. doi:10.1073/pnas.1620651114
Lee, C.-C., Yin, W.-G., and Ku, W. (2009). Ferro-orbital order and strong magnetic anisotropy in the parent compounds of iron-pnictide superconductors. Phys. Rev. Lett. 103, 267001. doi:10.1103/physrevlett.103.267001
Li, Q., Kharzeev, D. E., Zhang, C., Huang, Y., Pletikosić, I., Fedorov, A. V., et al. (2016a). Chiral magnetic effect in ZrTe5. Nat. Phys. 12, 550–554. doi:10.1038/nphys3648
Li, X.-B., Huang, W.-K., Lv, Y.-Y., Zhang, K.-W., Yang, C.-L., Zhang, B.-B., et al. (2016b). Experimental observation of topological edge states at the surface step edge of the topological insulator ZrTe5. Phys. Rev. Lett. 116, 176803. doi:10.1103/physrevlett.116.176803
Li, Y.-S., Garst, M., Schmalian, J., Ghosh, S., Kikugawa, N., Sokolov, D. A., et al. (2022). Elastocaloric determination of the phase diagram of sr2ruo4. Nature 607, 276–280. doi:10.1038/s41586-022-04820-z
Lifshitz, I. (1960). Anomalies of electron characteristics of a metal in the high pressure region. Sov. Phys. JETP 11, 1130.
Lin, C., Ochi, M., Noguchi, R., Kuroda, K., Sakoda, M., Nomura, A., et al. (2021). Visualization of the strain-induced topological phase transition in a quasi-one-dimensional superconductor TaSe3. Nat. Mater. 20, 1093–1099. doi:10.1038/s41563-021-01004-4
Liu, S., Wang, M. X., Chen, C., Xu, X., Jiang, J., Yang, L. X., et al. (2018). Experimental observation of conductive edge states in weak topological insulator candidate HfTe5. Apl. Mater. 6, 121111. doi:10.1063/1.5050847
Lv, W., Wu, J., and Phillips, P. (2009). Orbital ordering induces structural phase transition and the resistivity anomaly in iron pnictides. Phys. Rev. B 80, 224506. doi:10.1103/physrevb.80.224506
Mackenzie, A. P., Julian, S. R., Diver, A. J., McMullan, G. J., Ray, M. P., Lonzarich, G. G., et al. (1996). Quantum oscillations in the layered perovskite superconductor sr2ruo4. Phys. Rev. Lett. 76, 3786–3789. doi:10.1103/physrevlett.76.3786
Mackenzie, A. P., and Maeno, Y. (2003). The superconductivity of sr2ruo4 and the physics of spin-triplet pairing. Rev. Mod. Phys. 75, 657–712. doi:10.1103/revmodphys.75.657
Mackenzie, A. P., Scaffidi, T., Hicks, C. W., and Maeno, Y. (2017). Even odder after twenty-three years: the superconducting order parameter puzzle of sr2ruo4. npj Quantum Mater. 2, 40. doi:10.1038/s41535-017-0045-4
Maier, T. A., and Scalapino, D. J. (2014). Pairing interaction near a nematic quantum critical point of a three-band cuo2 model. Phys. Rev. B 90, 174510. doi:10.1103/physrevb.90.174510
Manzoni, G., Gragnaniello, L., Autès, G., Kuhn, T., Sterzi, A., Cilento, F., et al. (2016). Evidence for a strong topological insulator phase in ZrTe5. Phys. Rev. Lett. 117, 237601. doi:10.1103/physrevlett.117.237601
Manzoni, G., Sterzi, A., Crepaldi, A., Diego, M., Cilento, F., Zacchigna, M., et al. (2015). Ultrafast optical control of the electronic properties of ZrTe5. Phys. Rev. Lett. 115, 207402. doi:10.1103/physrevlett.115.207402
McQueen, T. M., Williams, A. J., Stephens, P. W., Tao, J., Zhu, Y., Ksenofontov, V., et al. (2009). Tetragonal-to-orthorhombic structural phase transition at 90 k in the superconductor fe1.01Se. Phys. Rev. Lett. 103, 057002. doi:10.1103/physrevlett.103.057002
Metlitski, M. A., Mross, D. F., Sachdev, S., and Senthil, T. (2015). Cooper pairing in non-fermi liquids. Phys. Rev. B 91, 115111. doi:10.1103/physrevb.91.115111
Metzner, W., Rohe, D., and Andergassen, S. (2003). Soft fermi surfaces and breakdown of fermi-liquid behavior. Phys. Rev. Lett. 91, 066402. doi:10.1103/physrevlett.91.066402
Morales, E. A., Siemann, G.-R., Zivanovic, A., Murgatroyd, P. A. E., Marković, I., Edwards, B., et al. (2023). Hierarchy of lifshitz transitions in the surface electronic structure of sr2ruo4 under uniaxial compression. Phys. Rev. Lett. 130, 096401. doi:10.1103/physrevlett.130.096401
Moreschini, L., Johannsen, J. C., Berger, H., Denlinger, J., Jozwiak, C., Rotenberg, E., et al. (2016). Nature and topology of the low-energy states in ZrTe5. Phys. Rev. B 94, 081101. doi:10.1103/physrevb.94.081101
Mutch, J., Chen, W.-C., Went, P., Qian, T., Wilson, I. Z., Andreev, A., et al. (2019). Evidence for a strain-tuned topological phase transition in ZrTe5. Sci. Adv. 5, eaav9771. doi:10.1126/sciadv.aav9771
Nair, N. L., Dumitrescu, P. T., Channa, S., Griffin, S. M., Neaton, J. B., Potter, A. C., et al. (2018). Thermodynamic signature of Dirac electrons across a possible topological transition in ZrTe5. Phys. Rev. B 97, 041111. doi:10.1103/physrevb.97.041111
Nakata, S., Yang, P., Barber, M. E., Ishida, K., Kim, H.-H., Loew, T., et al. (2022). Normal-state charge transport in YBa2Cu3O6.67 under uniaxial stress. npj Quantum Mater. 7, 118. doi:10.1038/s41535-022-00532-9
Nakayama, K., Miyata, Y., Phan, G. N., Sato, T., Tanabe, Y., Urata, T., et al. (2014). Reconstruction of band structure induced by electronic nematicity in an fese superconductor. Phys. Rev. Lett. 113, 237001. doi:10.1103/physrevlett.113.237001
Nicholson, C. W., Rumo, M., Pulkkinen, A., Kremer, G., Salzmann, B., Mottas, M.-L., et al. (2021). Uniaxial strain-induced phase transition in the 2D topological semimetal IrTe2. Commun. Mater. 2, 25. doi:10.1038/s43246-021-00130-5
Nie, S., Xing, L., Jin, R., Xie, W., Wang, Z., and Prinz, F. B. (2018). Topological phases in the tase3 compound. Phys. Rev. B 98, 125143. doi:10.1103/physrevb.98.125143
Noad, H. M. L., Ishida, K., Li, Y.-S., Gati, E., Stangier, V. C., Kikugawa, N., et al. (2023) Giant lattice softening at a lifshitz transition in sr2ruo4. Available at: https://arxiv.org/abs/2306.17835.
Occhialini, C. A., Sanchez, J. J., Song, Q., Fabbris, G., Choi, Y., Kim, J.-W., et al. (2023). Spontaneous orbital polarization in the nematic phase of fese. Nat. Mater. 22, 985–991. doi:10.1038/s41563-023-01585-2
Ohmichi, E., Adachi, H., Mori, Y., Maeno, Y., Ishiguro, T., and Oguchi, T. (1999). Angle-dependent magnetoresistance oscillation in the layered perovskite sr2ruo4. Phys. Rev. B 59, 7263–7265. doi:10.1103/physrevb.59.7263
Okada, S., Sambongi, T., and Ido, M. (1980). Giant resistivity anomaly in ZrTe5. J. Phys. Soc. Jpn. 49, 839–840. doi:10.1143/jpsj.49.839
Onari, S., and Kontani, H. (2012). Self-consistent vertex correction analysis for iron-based superconductors: mechanism of coulomb interaction-driven orbital fluctuations. Phys. Rev. Lett. 109, 137001. doi:10.1103/physrevlett.109.137001
Paglione, J., and Greene, R. L. (2010). High-temperature superconductivity in iron-based materials. Nat. Phys. 6, 645–658. doi:10.1038/nphys1759
Palmstrom, J. C., Walmsley, P., Straquadine, J. A. W., Sorensen, M. E., Hannahs, S. T., Burns, D. H., et al. (2022). Comparison of temperature and doping dependence of elastoresistivity near a putative nematic quantum critical point. Nat. Commun. 13, 1011. doi:10.1038/s41467-022-28583-3
Pan, X.-C., Chen, X., Liu, H., Feng, Y., Wei, Z., Zhou, Y., et al. (2015). Pressure-driven dome-shaped superconductivity and electronic structural evolution in tungsten ditelluride. Nat. Commun. 6, 7805. doi:10.1038/ncomms8805
Park, J., Bartlett, J. M., Noad, H. M. L., Stern, A. L., Barber, M. E., König, M., et al. (2020). Rigid platform for applying large tunable strains to mechanically delicate samples. Rev. Sci. Instrum. 91, 083902. doi:10.1063/5.0008829
Pfau, H., Chen, S. D., Hashimoto, M., Gauthier, N., Rotundu, C. R., Palmstrom, J. C., et al. (2021a). Anisotropic quasiparticle coherence in nematic bafe2as2 studied with strain-dependent arpes. Phys. Rev. B 103, 165136. doi:10.1103/physrevb.103.165136
Pfau, H., Chen, S. D., Yi, M., Hashimoto, M., Rotundu, C. R., Palmstrom, J. C., et al. (2019a). Momentum dependence of the nematic order parameter in iron-based superconductors. Phys. Rev. Lett. 123, 066402. doi:10.1103/physrevlett.123.066402
Pfau, H., Rotundu, C. R., Palmstrom, J. C., Chen, S. D., Hashimoto, M., Lu, D., et al. (2019b). Detailed band structure of twinned and detwinned bafe2as2 studied with angle-resolved photoemission spectroscopy. Phys. Rev. B 99, 035118. doi:10.1103/physrevb.99.035118
Pfau, H., Yi, M., Hashimoto, M., Chen, T., Dai, P.-C., Shen, Z.-X., et al. (2021b). Quasiparticle coherence in the nematic state of fese. Phys. Rev. B 104, L241101. doi:10.1103/physrevb.104.l241101
Pustogow, A., Luo, Y., Chronister, A., Su, Y. S., Sokolov, D. A., Jerzembeck, F., et al. (2019). Constraints on the superconducting order parameter in sr2ruo4 from oxygen-17 nuclear magnetic resonance. Nature 574, 72–75. doi:10.1038/s41586-019-1596-2
Rhodes, L. C., Eschrig, M., Kim, T. K., and Watson, M. D. (2022). Fese and the missing electron pocket problem. Front. Phys. 10. doi:10.3389/fphy.2022.859017
Ricco, S., Kim, M., Tamai, A., Walker, S. M. K., Bruno, F. Y., Cucchi, I., et al. (2018). In situ strain tuning of the metal-insulator-transition of Ca2RuO4 in angle-resolved photoemission experiments. Nat. Commun. 9, 4535. doi:10.1038/s41467-018-06945-0
Rømer, A. T., Scherer, D. D., Eremin, I. M., Hirschfeld, P. J., and Andersen, B. M. (2019). Knight shift and leading superconducting instability from spin fluctuations in sr2ruo4. Phys. Rev. Lett. 123, 247001. doi:10.1103/physrevlett.123.247001
Ruddlesden, S. N., and Popper, P. (1958). The compound sr3ti2o7 and its structure. Acta Crystallogr. 11, 54–55. doi:10.1107/s0365110x58000128
Ryu, S. H., Reichenbach, G., Jozwiak, C. M., Bostwick, A., Richter, P., Seyller, T., et al. (2023). magnetoarpes: angle resolved photoemission spectroscopy with magnetic field control. J. Electron Spectrosc. Relat. Phenom. 266, 147357. doi:10.1016/j.elspec.2023.147357
Sambongi, T., Yamamoto, M., Tsutsumi, K., Shiozaki, Y., Yamaya, K., and Abe, Y. (1977). Superconductivity in one-dimensional tase3. J. Phys. Soc. Jpn. 42, 1421–1422. doi:10.1143/JPSJ.42.1421
Sanchez, J. J., Malinowski, P., Mutch, J., Liu, J., Kim, J.-W., Ryan, P. J., et al. (2021). The transport-structural correspondence across the nematic phase transition probed by elasto x-ray diffraction. Nat. Mater. 20, 1519–1524. doi:10.1038/s41563-021-01082-4
Sebastian, S. E., and Proust, C. (2015). Quantum oscillations in hole-doped cuprates. Annu. Rev. Condens. Matter Phys. 6, 411–430. doi:10.1146/annurev-conmatphys-030212-184305
Shen, L., Wang, M. X., Sun, S. C., Jiang, J., Xu, X., Zhang, T., et al. (2017). Spectroscopic evidence for the gapless electronic structure in bulk ZrTe5. J. Electron Spectrosc. Relat. Phenom. 219, 45–52. doi:10.1016/j.elspec.2016.10.007
Shimojima, T., Suzuki, Y., Sonobe, T., Nakamura, A., Sakano, M., Omachi, J., et al. (2014). Lifting of xz/yz orbital degeneracy at the structural transition in detwinned fese. Phys. Rev. B 90, 121111. doi:10.1103/physrevb.90.121111
Si, Q., Yu, R., and Abrahams, E. (2016). High-temperature superconductivity in iron pnictides and chalcogenides. Nat. Rev. Mater. 1, 16017. doi:10.1038/natrevmats.2016.17
Skelton, E. F., Wieting, T. J., Wolf, S. A., Fuller, W. W., Gubser, D. Uo, Francavilla, T. L., et al. (1982). Giant resistivity and X-ray diffraction anomalies in low-dimensional ZrTe5 and HfTe5. Solid state Commun. 42, 1–3. doi:10.1016/0038-1098(82)91016-x
Sobota, J. A., He, Yu, and Shen, Z.-X. (2021). Angle-resolved photoemission studies of quantum materials. Rev. Mod. Phys. 93, 025006. doi:10.1103/revmodphys.93.025006
Steffensen, D., Kreisel, A., Hirschfeld, P. J., and Andersen, B. M. (2021). Interorbital nematicity and the origin of a single electron fermi pocket in fese. Phys. Rev. B 103, 054505. doi:10.1103/physrevb.103.054505
Steppke, A., Zhao, L., Barber, M. E., Scaffidi, T., Jerzembeck, F., Rosner, H., et al. (2017). Strong peak in tc of sr2ruo4 under uniaxial pressure. Science 355, eaaf9398. doi:10.1126/science.aaf9398
Sunko, V., Morales, E. A., Marković, I., Barber, M. E., Milosavljević, D., Mazzola, F., et al. (2019). Direct observation of a uniaxial stress-driven lifshitz transition in sr2ruo4. npj Quantum Mater. 4, 46. doi:10.1038/s41535-019-0185-9
Suzuki, Y., Shimojima, T., Sonobe, T., Nakamura, A., Sakano, M., Tsuji, H., et al. (2015). Momentum-dependent sign inversion of orbital order in superconducting fese. Phys. Rev. B 92, 205117. doi:10.1103/physrevb.92.205117
Takeshita, N., Sasagawa, T., Sugioka, T., Tokura, Y., and Takagi, H. (2004). Gigantic anisotropic uniaxial pressure effect on superconductivity within the CuO2 plane of La1.64Eu0.2Sr0.16CuO4: strain control of stripe criticality. J. Phys. Soc. Jpn. 73, 1123–1126. doi:10.1143/JPSJ.73.1123
Tamai, A., Zingl, M., Rozbicki, E., Cappelli, E., Riccò, S., de la Torre, A., et al. (2019). High-resolution photoemission on sr2ruo4 reveals correlation-enhanced effective spin-orbit coupling and dominantly local self-energies. Phys. Rev. X 9, 021048. doi:10.1103/physrevx.9.021048
Tanatar, M. A., Blomberg, E. C., Kreyssig, A., Kim, M. G., Ni, N., Thaler, A., et al. (2010). Uniaxial-strain mechanical detwinning of 2As2 and BaFe2As2 crystals: optical and transport study. Phys. Rev. B 81, 184508. doi:10.1103/physrevb.81.184508
Veenstra, C. N., Zhu, Z.-H., Ludbrook, B., Capsoni, M., Levy, G., Nicolaou, A., et al. (2013). Determining the surface-to-bulk progression in the normal-state electronic structure of Sr2RuO4 by angle-resolved photoemission and density functional theory. Phys. Rev. Lett. 110, 097004. doi:10.1103/physrevlett.110.097004
Wang, Z., Weng, H., Wu, Q., Dai, Xi, and Fang, Z. (2013). Three-dimensional Dirac semimetal and quantum transport in Cd3As2. Phys. Rev. B 88, 125427. doi:10.1103/physrevb.88.125427
Watson, M. D., Backes, S., Haghighirad, A. A., Moritz, H., Kim, T. K., Coldea, A. I., et al. (2017b). Formation of hubbard-like bands as a fingerprint of strong electron-electron interactions in fese. Phys. Rev. B 95, 081106. doi:10.1103/physrevb.95.081106
Watson, M. D., Haghighirad, A. A., Rhodes, L. C., Hoesch, M., and Kim, T. K. (2017a). Electronic anisotropies revealed by detwinned angle-resolved photo-emission spectroscopy measurements of fese. New J. Phys. 19, 103021. doi:10.1088/1367-2630/aa8a04
Watson, M. D., Kim, T. K., Haghighirad, A. A., Davies, N. R., McCollam, A., Narayanan, A., et al. (2015). Emergence of the nematic electronic state in fese. Phys. Rev. B 91, 155106. doi:10.1103/physrevb.91.155106
Watson, M. D., Kim, T. K., Rhodes, L. C., Eschrig, M., Hoesch, M., Haghighirad, A. A., et al. (2016). Evidence for unidirectional nematic bond ordering in fese. Phys. Rev. B 94, 201107. doi:10.1103/physrevb.94.201107
Welp, U., Grimsditch, M., Fleshler, S., Nessler, W., Downey, J., Crabtree, G. W., et al. (1992). Effect of uniaxial stress on the superconducting transition in YBa2Cu3O7. Phys. Rev. Lett. 69, 2130–2133. doi:10.1103/physrevlett.69.2130
Weng, H., Dai, Xi, and Fang, Z. (2014). Transition-metal pentatelluride ZrTe5 and HfTe5: a paradigm for large-gap quantum spin Hall insulators. Phys. Rev. X 4, 011002. doi:10.1103/physrevx.4.011002
Worasaran, T., Ikeda, M. S., Palmstrom, J. C., Straquadine, J. A. W., Kivelson, S. A., and Fisher, I. R. (2021). Nematic quantum criticality in an fe-based superconductor revealed by strain-tuning. Science 372, 973–977. doi:10.1126/science.abb9280
Wu, R., Ma, J.-Z., Nie, S.-M., Zhao, L.-X., Huang, X., Yin, J.-X., et al. (2016). Evidence for topological edge states in a large energy gap near the step edges on the surface of ZrTe5. Phys. Rev. X 6, 021017. doi:10.1103/physrevx.6.021017
Wu, Y., Jo, Na H., Ochi, M., Huang, L., Mou, D., Bud’ko, S. L., et al. (2015). Temperature-induced lifshitz transition in WTe2. Phys. Rev. Lett. 115, 166602. doi:10.1103/physrevlett.115.166602
Xu, C., Müller, M., and Sachdev, S. (2008). Ising and spin orders in the iron-based superconductors. Phys. Rev. B 78, 020501. doi:10.1103/physrevb.78.020501
Yamase, H., and Zeyher, R. (2013). Superconductivity from orbital nematic fluctuations. Phys. Rev. B 88, 180502. doi:10.1103/physrevb.88.180502
Yang, P.-Ya, Noad, H. M. L., Barber, M. E., Kikugawa, N., Sokolov, D. A., Mackenzie, A. P., et al. (2023). Probing momentum-dependent scattering in uniaxially stressed sr2ruo4 through the hall effect. Phys. Rev. Lett. 131, 036301. doi:10.1103/physrevlett.131.036301
Yi, M., Lu, D., Chu, J.-H., Analytis, J. G., Sorini, A. P., Kemper, A. F., et al. (2011). Symmetry-breaking orbital anisotropy observed for detwinned ba(fe1−xcox)2as2 above the spin density wave transition. Proc. Natl. Acad. Sci. U.S.A. 108, 6878–6883. doi:10.1073/pnas.1015572108
Yi, M., Lu, D. H., Moore, R. G., Kihou, K., Lee, C.-H., Iyo, A., et al. (2012). Electronic reconstruction through the structural and magnetic transitions in detwinned nafeas. New J. Phys. 14, 073019. doi:10.1088/1367-2630/14/7/073019
Yi, M., Pfau, H., Zhang, Y., He, Y., Wu, H., Chen, T., et al. (2019). Nematic energy scale and the missing electron pocket in fese. Phys. Rev. X 9, 041049. doi:10.1103/physrevx.9.041049
Yi, M., Zhang, Y., Shen, Z.-X., and Lu, D. (2017). Role of the orbital degree of freedom in iron-based superconductors. npj Quantum Mater. 2, 57. doi:10.1038/s41535-017-0059-y
Young, S. M., Chowdhury, S., Walter, E. J., Mele, E. J., Kane, C. L., and Rappe, A. M. (2011). Theoretical investigation of the evolution of the topological phase of bi2se3 under mechanical strain. Phys. Rev. B 84, 085106. doi:10.1103/physrevb.84.085106
Yu, R., Zhu, J.-X., and Si, Q. (2018). Orbital selectivity enhanced by nematic order in fese. Phys. Rev. Lett. 121, 227003. doi:10.1103/physrevlett.121.227003
Zhang, P., Noguchi, R., Kuroda, K., Lin, C., Kawaguchi, K., Yaji, K., et al. (2021). Observation and control of the weak topological insulator state in ZrTe5. Nat. Commun. 12, 406. doi:10.1038/s41467-020-20564-8
Zhang, Y., Wang, C., Yu, Li, Liu, G., Liang, A., Huang, J., et al. (2017). Electronic evidence of temperature-induced Lifshitz transition and topological nature in ZrTe5. Nat. Commun. 8, 15512–15519. doi:10.1038/ncomms15512
Zhang, Y., Yi, M., Liu, Z.-K., Li, W., Lee, J. J., Moore, R. G., et al. (2016). Distinctive orbital anisotropy observed in the nematic state of a fese thin film. Phys. Rev. B 94, 115153. doi:10.1103/physrevb.94.115153
Zheng, G., Lu, J., Zhu, X., Ning, W., Han, Y., Zhang, H., et al. (2016). Transport evidence for the three-dimensional Dirac semimetal phase in ZrTe5. Phys. Rev. B 93, 115414. doi:10.1103/physrevb.93.115414
Keywords: strain, uniaxial stress, electronic structure, ARPES, quantum oscillations
Citation: Jo NH, Gati E and Pfau H (2024) Uniaxial stress effect on the electronic structure of quantum materials. Front. Electron. Mater. 4:1392760. doi: 10.3389/femat.2024.1392760
Received: 28 February 2024; Accepted: 19 April 2024;
Published: 09 May 2024.
Edited by:
Indrani Coondoo, University of Aveiro, PortugalReviewed by:
Nikolai Zhigadlo, CrystMat Company, SwitzerlandCopyright © 2024 Jo, Gati and Pfau. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Na Hyun Jo, bmhqb0B1bWljaC5lZHU=; Elena Gati, ZWxlbmEuZ2F0aUBjcGZzLm1wZy5kZQ==; Heike Pfau, aGVpa2UucGZhdUBwc3UuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.