Pair density wave and superconductivity in a kinetically frustrated doped Emery model on a square lattice

The quest to understand the nature of superconductivity in the cuprates has spotlighted the pair density wave (PDW)–a superconducting state characterized by a spatially modulated order parameter. Despite significant advances in understanding PDW properties, conclusively demonstrating its presence in systems pertinent to cuprate superconductors remains elusive. In this study, we present a systematic density-matrix renormalization group study to investigate the Emery model (or the three-band Hubbard model) on two-leg square cylinders with negative electron hopping term t_pp between adjacent oxygen sites. Kinetic frustration - introduced by changing the sign of oxygen-oxygen hopping - leads to a much reduced Cu-Cu antiferromagnetic exchange along with an enlarged charge transfer energy that changes the local properties of the model. At light doping levels, our findings reveal a ground state remarkably consistent with a PDW, exhibiting mutually commensurate superconducting (SC), charge, and spin density wave correlations. Intriguingly, the dominant SC pairing is observed between neighboring oxygen sites, diverging from the expected Cu sites in the positive t_pp case. When the system incorporates moderate near-neighbor interactions, particularly an attractive V_pp between adjacent oxygen sites, the SC correlations become quasi-long-ranged, accompanied by a pronounced divergence in the PDW susceptibility. When the attractive V_pp increases further, the system gives way to an unconventional d-wave superconductivity.

1 Introduction

The Emery model, also known as the three-band Hubbard model, has long been proposed as one of the minimal models to understand the electronic properties of cuprate high-temperature superconductors Zaanen et al. (1985); Emery (1987); Scalettar (1989); Scalettar et al. (1991); White and Scalapino (2015); Huang et al. (2017); Jiang et al. (2023). In this model, a square lattice of copper (Cu) and oxygen (O) atoms in the CuO₂ plane (see Figure 1) is considered, where the Copper sites are represented by a single $3d_{x^2-y^2}$ orbital, while each oxygen site has one active 2p orbital (2p_x or 2p_y). In the hole representation, the model Hamiltonian is defined as

$\begin{array}{ll}\hfill H& =H_k+{\mathrm{\Delta }}_{pd}{\displaystyle \sum _{i\sigma }}{\widehat{p}}_{i\sigma }^{+}{\widehat{p}}_{i\sigma }+U_d{\displaystyle \sum _i}{\widehat{n}}_{i\uparrow }^d{\widehat{n}}_{i\downarrow }^d\hfill \\ \hfill & +U_p{\displaystyle \sum _i}{\widehat{n}}_{i\uparrow }^p{\widehat{n}}_{i\downarrow }^p+V_{pd}{\displaystyle \sum _{\langle ij\rangle }}{\widehat{n}}_i^d{\widehat{n}}_j^p+V_{pp}{\displaystyle \sum _{\langle ij\rangle }}{\widehat{n}}_i^p{\widehat{n}}_j^p.\hfill \end{array}(1)$

$\begin{array}{l}\hfill H_k={\displaystyle \sum _{\langle ij\rangle \sigma }}{t}_{pd}^{ij}\left({\widehat{d}}_{i\sigma }^{+}{\widehat{p}}_{j\sigma }+h.c.\right)+{\displaystyle \sum _{\langle ij\rangle \sigma }}{t}_{pp}^{ij}\left({\widehat{p}}_{i\sigma }^{+}{\widehat{p}}_{j\sigma }+h.c.\right)\end{array}$

FIGURE 1

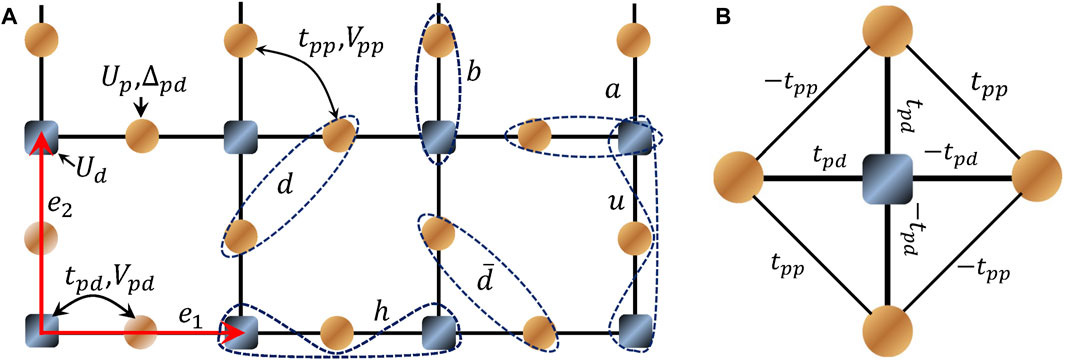
FIGURE 1. Emery model on the square lattice. (A) The squares represent Cu $d_{x^2-y^2}$ orbitals and circles represent O_x/y 2p_x/2p_y orbitals. Periodic (open) boundary condition is imposed in the direction specified by the lattice basis vector e₂ = (0, 1) (e₁ = (1, 0)). The dashed loops represent bonds a, b, d, $\bar{d}$, h and u. (B) Signs of hopping matrix elements in an elementary plaquette in the CuO₂ plane.

Here ${\widehat{d}}_{i\sigma }^{+}$ and ${\widehat{p}}_{j\sigma }^{+}$ create holes with spin-σ on the ith Cu and jth oxygen sites, and ⟨ij⟩ denotes NN sites. ${\widehat{n}}_{i\sigma }^d={\widehat{d}}_{i\sigma }^{+}{\widehat{d}}_{i\sigma }$ and ${\widehat{n}}_{i\sigma }^p={\widehat{p}}_{i\sigma }^{+}{\widehat{p}}_{i\sigma }$ are the number operators for spin-σ at the Cu and O sites, respectively, with the total number operators are defined as ${\widehat{n}}_i^d={\sum }_{\sigma }{\widehat{n}}_{i\sigma }^d$ and ${\widehat{n}}_i^p={\sum }_{\sigma }{\widehat{n}}_{i\sigma }^p$. Δ_pd is the energy difference between having a hole on the Cu and oxygen sites. $t_{pd}^{ij}$ and $t_{pp}^{ij}$ are the hole hopping matrix elements between nearest-neighbor (NN) Cu and oxygen sites and the NN oxygen sites, respectively. U_d and U_p are the on-site Cu and oxygen Coulomb repulsion, and V_pd and V_pp are the NN Cu-O and O-O Coulomb interactions, respectively.

While the Emery model has been proposed as one of the critical frameworks for studying the cuprates superconductors, which captures phenomena like superconductivity, charge, and spin density wave orders Zaanen et al. (1985); Emery (1987); Scalettar (1989); White and Scalapino (2015); Huang et al. (2017); Jiang et al. (2023), it has more recently been extended to investigate the emergence of novel pair density wave (PDW) states Jiang (2023). In a PDW state, the superconducting (SC) order parameter carries finite center-of-mass momentum and varies spatially so that its spatial average vanishes Fulde and Ferrell (1964); Larkin and Ovchinnikov (1965); Berg et al. (2009); Fradkin et al. (2015); Agterberg et al. (2020); Lee (2014); Jian et al. (2020); Lozano et al. (2022). The PDW state has been considered a promising candidate state to understand the physics of cuprates high-temperature superconductors and other strongly correlated systems, where it has been proposed that various phases, including the superconductivity, charge, and spin density wave orders, can emerge by partially melting the PDW state Lee (2014); Fradkin et al. (2015); Agterberg et al. (2020); Himeda et al. (2002). Recently, intense interest in the PDW state has emerged due to experimental observations in cuprate superconductors Bi₂Sr₂CaCu₂O_8+x Hamidian et al. (2016); Ruan et al. (2018); Edkins et al. (2019); Liu et al. (2021) and La_1.875Ba_0.125CuO₄ Agterberg and Tsunetsugu (2008); Li et al. (2007); Berg et al. (2007); Tranquada et al. (2008); Tranquada (2020), Tranquada (2021), kagome superconductor CsV₃Sb₅ Chen H. et al. (2021) and iron-based superconductor Liu et al. (2023).

The realization of a PDW state in microscopic lattice models remains highly nontrivial and usually involves modifying or extending existing frameworks like the Hubbard models to include competing interactions or inhomogeneities that can give rise to spatial modulations Berg et al. (2010); Jaefari and Fradkin (2012); Venderley and Kim (2019); Xu et al. (2019); Peng et al. (2021a,b); Han et al. (2020); Huang et al. (2022); Wu et al. (2023); Jiang and Yao (2023). These include the Kondo-Heisenberg model Berg et al. (2010), the extended Hubbard-Heisenberg model Jaefari and Fradkin (2012), the strong coupling limit of the Holstein-Hubbard model Han et al. (2020); Huang et al. (2022) and generalized t-J and Hubbard models Xu et al. (2019); Venderley and Kim (2019); Peng et al. (2021a), Peng et al. (2021b). More recently, it has also been shown by one of the authors that the PDW ground state can also be realized in the three-band Hubbard model on a two-leg square cylinder Jiang (2023), where the SC correlations are dominant between neighboring Cu sites with $d_{x^2-y^2}$-wave pairing symmetry.

2 Model Hamiltonian and method

In the present work, we consider the Emery model on the square lattice as defined in Figure 1 and Eq. 2 to study whether the same PDW state or distinct SC state emerges upon doping as well as the associated pairing symmetry using the density-matrix renormalization group (DMRG) White (1992), White (1993). The signs of the hopping matrix elements in the related orbital configuration, i.e., Cu $3d_{x^2-y^2}$ orbital and O_x/y 2p_x/2p_y orbitals, of an elementary plaquette centered at a generic Cu site is shown in Figure 1B. It is noted that the sign of $t_{pp}\equiv t_{pp}^{\sigma }-t_{pp}^{\pi }$ is taken to be negative, opposite to that is usually chosen Eskes et al. (1990). The resulting increase in the delocalization energy involving ligand L oxygen orbitals raises the level of the effective charge transfer energy, alters the magnetic exchange among Cu and O, and affects the local symmetry of the ground state orbital configuration. This has a profound impact on the local physics and ground state properties of the system.

Following Ref. White and Scalapino (2015); Jiang (2023), we set t_pd = 1 as the energy unit and take a canonical set of parameters U_d = 8, U_p = 3, Δ_pd = 3 for cuprates White and Scalapino (2015); Armitage et al. (2010); Haule et al. (2014) but negative t_pp = −0.5, and study the ground state properties of this system as a function of V_pd and V_pp. We focus on two-leg cylinders as shown in Figure 1 with width L_y = 2 and length up to L_x = 96, where L_x and L_y are the number of unit cells along the e₁ and e₂ directions, respectively. The total number of sites is N = 3L_xL_y + 2L_y = 3N_u + 2L_y, where N_u is the number of unit cells. The overall hole density of the system is defined as ρ = 1 + δ, where δ = N_h/N_u and N_h denote the hole doping concentration and number of doped holes away from half-filling, respectively. We consider δ = 1/12 and 1/8, and keep up to m = 20,000 states with a typical truncation error ϵ ∼ 10^–10.

3 Results

3.1 Phase diagram

Our main results are summarized in the ground state phase diagram in Figure 2. When V_pp between oxygen sites are not strongly attractive, we find that the ground state of the system is consistent with that of a PDW state with power-law and mutually commensurate SC, charge-density wave (CDW), and spin-density-wave (SDW) correlations. The SC correlations oscillate periodically in real space in such a way that its spatial average vanishes and the PDW ordering wavevector Q ≈ 2πδ is incommensurate. Contrary to the positive t_pp case White and Scalapino (2015); Jiang (2023), our results show that the SC pairing is dominant between adjacent oxygen sites instead of Cu sites. Accordingly, the SC pairing symmetry is consistent with d_xy rather than $d_{x^2-y^2}$ wave. Similar to the single-band Hubbard model on the square lattice Chen Z. et al. (2021); Qu et al. (2022); Peng et al. (2023), the finite electronic attractions V_pd and V_pp, especially V_pp between oxygen sites, can notably enhance the SC correlations while simultaneously suppress the CDW correlations. For modestly strong V_pp interaction, including both repulsion and attraction, the SC correlations become strong enough so that a quasi-long-range PDW order emerges with K_sc < 2 and divergent static PDW susceptibility. When further increasing the attractive V_pp, the system gives way to d-wave superconductivity where the PDW signatures are much suppressed. Interestingly, similar to the PDW phase, the Cooper pairing between adjacent oxygen sites also dominates in the pairing channel and the corresponding pairing symmetry is consistent with the d_xy-wave. For even stronger attractive V_pp, the ground state of the system becomes phase separated.

FIGURE 2

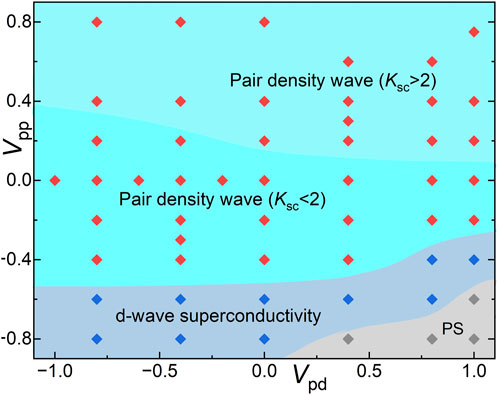
FIGURE 2. Ground state phase diagram of the Emery model on two-leg square cylinders at δ = 1/8. The solid symbols are numerical data points and PS denotes phase separation. The shaded regions are guides for eyes.

3.2 Pair density wave phase

As shown in Figure 2, the majority of the ground state phase diagram is occupied by the PDW phase, where the SC correlations decay as a power-law at long distances and oscillate periodically in real space in such a way that its spatial average vanishes. We provide detailed examples in Figure 3 and Figure 4 for several characteristic sets of parameters. Our conclusions hold for all parameters in the PDW phase in Figure 2.

FIGURE 3

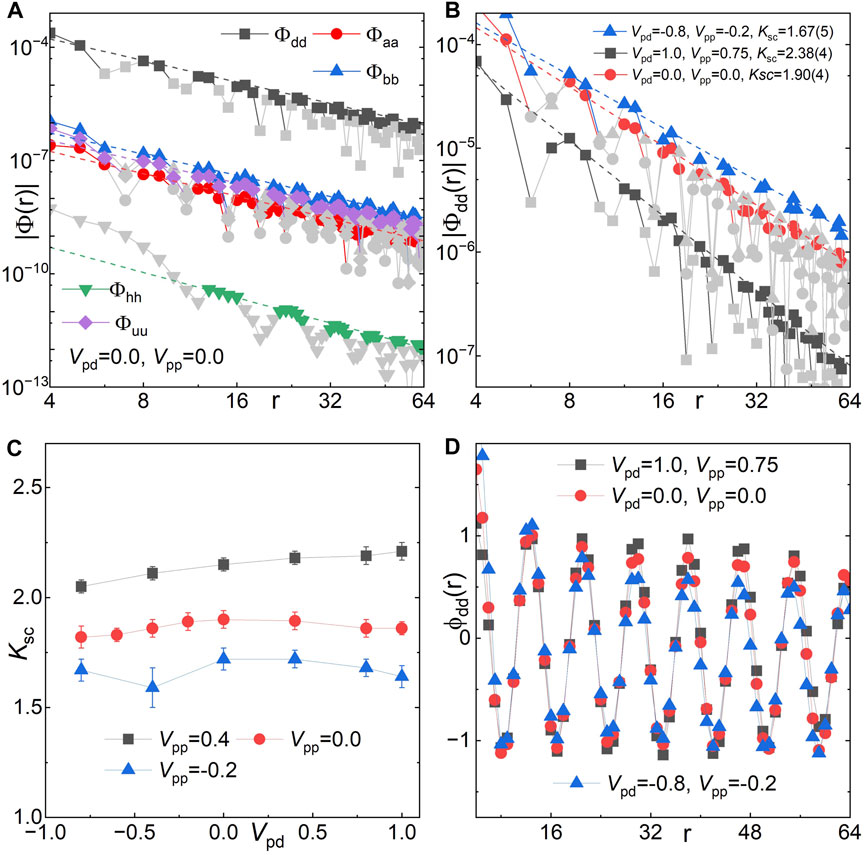
FIGURE 3. Superconducting correlations in the pair density wave phase at δ = 1/8. The magnitude of SC correlations are shown in (A) for Φ(r) at V_pd = V_pp = 0, and in (B) for Φ_dd(r) with different V_pd and V_pp. The dashed lines represent fits to a power-law function $f(r)\sim r^{-K_{sc}}$. Data points far from the envelope and those at short distances are discarded in gray color in the fitting process. (C) Luttinger exponent K_sc as a function of V_pd and V_pp. (D) The normalized functions ϕ_dd(r) = Φ_dd(r)/f_dd(r) reflect the spatial oscillation of Φ_dd(r).

FIGURE 4

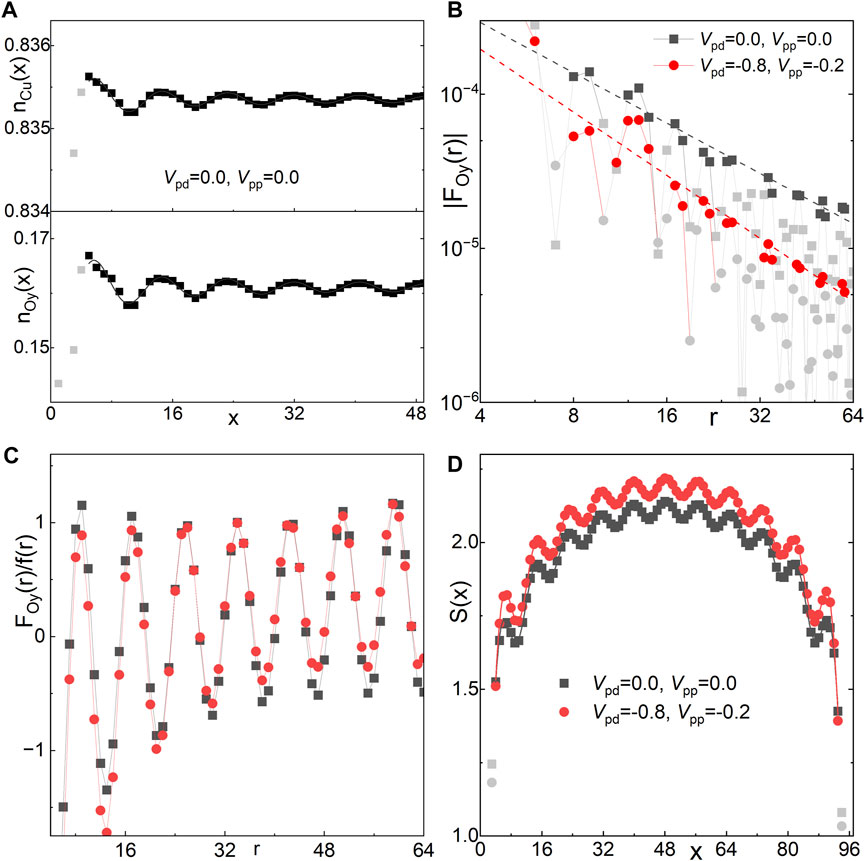
FIGURE 4. Charge density profile, spin-spin correlation and entanglement entropy in the pair density wave phase at δ = 1/8. (A) Charge density profiles n_Cu(x) on the Cu site and n_Oy(x) on the Oy site for V_pd = V_pp = 0. (B) The magnitude of the spin-spin correlation |F(r)| where the dashed lines represent power-law fits $f(r)\sim r^{-K_s}$. (C) The normalized function F(r)/f(r) reflects the spatial oscillation of F(r) in (B). (D) Von Neumann entanglement entropy S(x). Note that a few data points in gray color close to the open ends are excluded to minimize boundary effects.

3.2.1 Superconducting correlations

In order to explore the potential for superconductivity, we have calculated the equal-time spin-singlet SC pair-pair correlations defined as

${\mathrm{\Phi }}_{\alpha \beta }\left(r\right)=⟨{\widehat{\mathrm{\Delta }}}_{\alpha }^{†}\left(x_0,y_0\right){\widehat{\mathrm{\Delta }}}_{\beta }\left(x_0+r,y_0\right)⟩.(2)$

Here, ${\widehat{\mathrm{\Delta }}}_{\alpha }^{†}(x,y)=\frac{1}{\sqrt{2}}[{\widehat{c}}_{(x,y),\uparrow }^{†}{\widehat{c}}_{(x,y)+\alpha ,\downarrow }^{†}-{\widehat{c}}_{(x,y),\downarrow }^{†}{\widehat{c}}_{(x,y)+\alpha ,\uparrow }^{†}]$ is spin-singlet pair creation operator on the bond α = a, b, d, $\bar{d}$, h and u defined in Figure 1A. (x₀, y₀) is a reference bond with x₀ ∼ L_x/4, r is the distance between two bonds in the e₁ direction. We have comprehensively analyzed the various components of the SC correlations. This includes calculations of Φ_aa, Φ_ab, Φ_bb, Φ_dd(r), ${\mathrm{\Phi }}_{d\bar{d}}(r)$, ${\mathrm{\Phi }}_{\bar{d}\bar{d}}(r)$, Φ_hh, Φ_uu and Φ_uh. While the positive t_pp case primarily showcases dominant correlations in Φ_hh and Φ_uu as discussed in Jiang (2023), our results differ significantly for the negative t_pp case. As illustrated in Figure 3A, we observe that the strongest SC correlations are prominently exhibited in Φ_dd(r) and ${\mathrm{\Phi }}_{\bar{d}\bar{d}}(r)$ (not shown). This suggests that the pairing is more dominant between neighboring oxygen sites, rather than Cu sites. Furthermore, even though the pairing symmetry aligns with the d-wave, our findings indicate a shift to the d_xy-wave symmetry in this particular scenario, diverging from the previously understood $d_{x^2-y^2}$-wave. This distinction in d_xy-wave symmetry is characterized by the relationship: ${\mathrm{\Phi }}_{dd}(r)\sim {\mathrm{\Phi }}_{\bar{d}\bar{d}}(r)\sim -{\mathrm{\Phi }}_{d\bar{d}}(r)$.

We have closely examined the spatial distribution of SC correlations, specifically targeting Φ_dd(r). Our findings, based on three representative parameter choices, are depicted in Figure 3D. Here, Φ_dd(r) exhibits clear spatial oscillations as Φ_dd(r) ∼ f(r)ϕ_dd(r) over a vast region of r. In this context, f(r) acts as the envelope, while ϕ_dd(r) gives rise to the spatial oscillation. As we move to longer distances, the envelope function f(r) adheres to a power-law decay $f(r)=A\ast r^{-K_{sc}}$ Kühner et al. (2000). For instance, we derived an exponent K_sc ≈ 2.4 at V_pd = 1.0 and V_pp = 0.75, and K_sc ≈ 1.9 at V_pd = 0 and V_pp = 0, and K_sc ≈ 1.7 at V_pd = −0.8 and V_pp = −0.2. Drawing connections with the established single-band Hubbard model Chen Z. et al. (2021); Qu et al. (2022); Peng et al. (2023) and the positive t_pp Emery model Jiang (2023), we find that diminishing the NN repulsion or amplifying the NN attraction, especially V_pp, can notably enhance SC correlations. This observation is further validated by the K_sc values presented in Figure 3C. More comprehensive results of K_sc for Φ_dd at δ = 1/8 are shown in Figure 3C. These point towards the divergence of the static PDW susceptibility, characterized as ${\chi }_{\mathit{pdw}}\sim T^{-(2-K_{sc})}$ when T → 0. We have also calculated the spin-triplet SC correlations, which are markedly weaker than their spin-singlet counterparts.

The spatial oscillation of the SC correlations Φ(r) is captured by the normalized function ϕ(r), as previously defined. Depictions of ϕ_dd(r) are presented in Figure 3D and align well with the fitting function ϕ_dd(r) ∼ sin(Qr + θ). This pattern resonates with characteristics observed in the PDW state with a vanishing spatial average of ϕ(r) Agterberg et al. (2020). The PDW ordering wavevector appears to be incommensurate as Q ≈ 2πδ with a corresponding wavelength λ_sc ≈ 1/δ. For instance, λ_sc ≈ 8 for δ = 1/8 as evidenced in Figure 3D, whereas λ_sc ≈ 12 for δ = 1/12.

3.2.2 Charge density wave

We have calculated the charge density profile $n_{\alpha }(x,y)=⟨{\widehat{n}}_{\alpha }(x,y)⟩$ and its rung average $n(x)={\sum }_{y=1}^{L_y}{n}_a(x,y)/L_y$ (e.g., Figure 4A) to describe the charge density properties of the system, where α = Cu/O_x/O_y site. Similar with the positive t_pp case Jiang (2023), the spatial oscillation of n_α(x) is also characterized by two ordering wavevectors at Q and 2Q, corresponding to wavelengths λ_Q ≈ 1/δ and λ_2Q ≈ 1/2δ, respectively.

At long distance, the spatial decay of the CDW correlation is dominated by a power-law with an exponent K_c, which can be obtained by fitting the charge density oscillations induced by the cylinder boundaries White et al. (2002).

$\begin{array}{ccc}\hfill n\left(x\right)& =\hfill & A_Q\ast \mathrm{c}\mathrm{o}\mathrm{s}\left(Qx+{\varphi }_1\right)\ast x^{-K_c/2}\hfill \\ +A_{2Q}\ast \mathrm{c}\mathrm{o}\mathrm{s}\left(2Qx+{\varphi }_2\right)\ast x^{-K_c/2}+n_0.\hfill \end{array}(3)$

Here A_Q and A_2Q are amplitudes, ϕ₁ and ϕ₂ are phase shifts and n₀ is the mean density. Examples of the extracted exponents for δ = 1/8 are K_c(Cu)$\approx 1.6$ and K_c(O_y)$\approx 1.7$ for V_pd = 1 and V_pp = 0.75, and K_c(Cu)$\approx 1.7$ and K_c(O_y) = 1.7 for V_pd = V_pp = 0.

3.2.3 Spin-spin correlations

To elucidate the magnetic properties of the ground state, we examine the spin-spin correlation functions $F_{\alpha }(r)=⟨{\vec{S}}_{x_0,y_0}\cdot {\vec{S}}_{x_0+r,y_0}⟩$ where α = Cu/O_x/O_y site. Figure 4C illustrates examples of F(r), based on two representative parameter choices at δ = 1/8. Unlike the dominant spin-spin correlations between Cu sites Jiang (2023), our findings highlight a dominant correlation between oxygen sites in the kinetically frustrated case. Notably, this decays as a power-law, described by $F(r)\sim r^{-K_s}$ over extended distances. The associated Luttinger exponent is K_s(O_y)$\approx 1.1$ for V_pd = V_pp = 0 and K_s(O_y) ≈ 1.3 for V_pd = −0.8 and V_pp = −0.2. In line with the characteristics of a PDW state, F(r) exhibits pronounced spatial oscillations (as seen in the inset of Figure 4C) with a characteristic wavelength, λ_s = 1/δ. This aligns closely with λ_sc, yielding an ordering wavevector Q ≈ 2πδ akin to the SC correlation.

3.2.4 Entanglement entropy

Our findings indicate the presence of multiple gapless modes, encompassing both charge and spin degrees of freedom. These can be characterized by the central charge, c. This charge is derivable from the von Neumann entropy, formulated as: S(x) = −Trρ_xlnρ_x where ρ_x represents the reduced density matrix for a subsystem of length x. For critical systems in 1 + 1 dimensions, described through a conformal field theory, it has been established Calabrese and Cardy (2004); Fagotti and Calabrese (2011) that for an open system of length L_x,

$\begin{array}{ccc}\hfill S\left(x\right)& =\hfill & \frac{c}{6}\ln \left[\frac{4\left(L_x+1\right)}{\pi }\sin \frac{\pi \left(2x+1\right)}{2\left(L_x+1\right)}|\sin k_F|\right]\hfill \\ +\tilde{A}\frac{\sin \left[k_F\left(2x+1\right)\right]}{\frac{4\left(L_x+1\right)}{\pi }\sin \frac{\pi \left(2x+1\right)}{2\left(L_x+1\right)}|\sin k_F|}+\tilde{S},\hfill \end{array}(4)$

where $\tilde{A}$ and $\tilde{S}$ are model dependent fitting parameters, and k_F is the Fermi momentum. Our findings reveal a central charge approximately given by c ≈ 2, with illustrative examples provided in Figure 4D. Specifically, we observed c ≈ 1.95 at V_pd = V_pp = 0 and c ≈ 2.0 at V_pd = −0.8 and V_pp = −0.2 at δ = 1/8. These results point to the presence of both a gapless charge mode and a gapless spin mode.

3.3 d-wave superconductivity

When further increasing the attractive V_pp, the system evolves into a d-wave SC phase. Similar to the PDW phase, we find that Φ_dd(r) in Figure 5A and ${\mathrm{\Phi }}_{\bar{d}\bar{d}}(r)$ (not shown) exhibit the strongest SC correlations, i.e., the pairing is dominant between neighboring oxygen sites instead of Cu sites. The pairing symmetry is also consistent with the d_xy-wave symmetry characterized by the fact ${\mathrm{\Phi }}_{dd}(r)\sim {\mathrm{\Phi }}_{\bar{d}\bar{d}}(r)\sim -{\mathrm{\Phi }}_{d\bar{d}}(r)$.

FIGURE 5

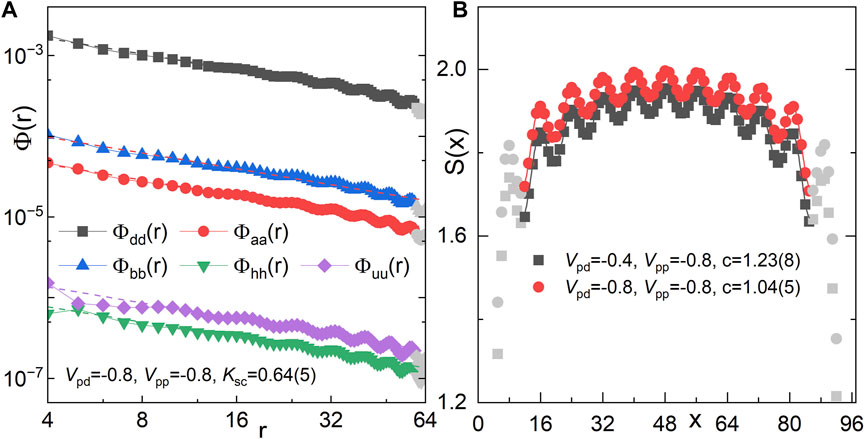
FIGURE 5. Superconducting correlations and entanglement entropy in the d-wave SC phase at δ = 1/8. (A) SC correlations for V_pd = −0.8 and V_pp = −0.8. Dashed lines represent fits to a power-law function $f(r)\sim r^{-K_{sc}}$. (B) Von Neumann entanglement entropy S(x). Note that a few data points in gray color close to open ends are excluded to minimize the boundary effect.

While there are similarities, several significant distinctions can be drawn between the PDW phase and the d-wave SC phase: (1) in the d-wave SC phase, the SC correlations Φ_αβ(r) maintain a consistent sign in real space, as depicted in Figure 5A, and the SC order parameter does not possess finite momentum, (2) the spin-spin correlation functions in this phase are short-ranged and undergo exponential decay, (3) a singular gapless mode with c ≈ 1 is evident, as illustrated in Figure 5B. For instance, the extracted central charge c ≈ 1.04 for V_pd = −0.8 and V_pp = −0.8, and c ≈ 1.2 for V_pd = −0.8 and V_pp = −0.4. Given these observations, our results affirm that the ground state of the d-wave SC phase aligns with the characteristics of a Luther-Emery liquid Emery (1987). This is reminiscent of the single-band Hubbard model on four-leg square cylinders as discussed in prior studies Jiang et al. (2018); Jiang and Devereaux (2019); Jiang Y.-F. et al. (2020); Chung et al. (2020); Jiang H.-C. et al. (2020); Gong et al. (2021); Peng et al. (2023).

4 Summary and discussion

In conclusion, we have extensively investigated the ground state properties of the lightly doped three-band Hubbard model on two-leg square cylinders, specifically focusing on near-neighbor Cu-O and O-O interactions. Our results strongly suggest that the system’s ground state is aligned with the characteristics of a PDW state, showcasing quasi-long-range PDW order and pronounced susceptibility. Several aspects of our findings are unexpected. Within the doped negative t_pp Emery model, Cooper pairing prominently emerges between adjacent oxygen sites rather than between neighboring Cu sites. This stands in stark contrast to the prevailing understanding, where Cooper pairing is believed to be dominant between neighboring Cu sites. It has been postulated that cuprate physics can be encapsulated by a single-band effective Hamiltonian, exclusively encompassing the Cu d holes Zhang and Rice (1988). While the pairing symmetry aligns with the d-wave symmetry, it manifests as d_xy rather than $d_{x^2-y^2}$. This diverges from the $d_{x^2-y^2}$ pairing symmetry characteristic of cuprates Lee et al. (2006); Fradkin et al. (2015).

To understand these results, we return to cluster calculations that determine the relevant parameters t and J of an effective single band model Eskes et al. (1989), Eskes et al. (1990). Specifically, we consider Cu₂O₇ clusters with the same parameters used for DMRG, and compare the results for positive and negative t_pp. Our results are summarized in Table 1. Determining the singlet-triplet energy difference for two holes on the cluster yields an exchange energy J = 0.0179 for t_pp = −0.5, compared to 0.165 if the sign of t_pp is reversed. Largely interpreted as due to an increase in the effective charge transfer energy when ligand delocalization is considered, the effective spin exchange between Cu spins is greatly reduced for negative t_pp. While the dependence on V_pp is negligible, a negative V_pd increases the magnetic exchange for the two-hole ground state configuration. The increase of J for negative V_pd may help to favor stronger hole singlet bonding, promoting stronger SC susceptibilities in Figure 3.

TABLE 1

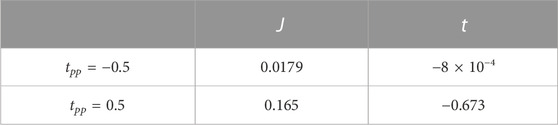
TABLE 1. Effective single band exchange parameter J and NN hopping t determined from Cu₂O₇ clusters for different values of t_pp as indicated. All other parameters are the same as used in the main text.

Calculations for three holes on the same cluster yield the hopping parameter t, defined as the energy difference between the ground and first excited state. For V_pp = V_pd = 0, 2t = −0.673 for t_pp = 0.5 while 2t = −8 × 10⁻⁴ for t_pp = −0.5. These numbers increase slightly for V_pp < 0, but overall a reversed sign of t_pp dramatically affects the magnitude of the NN hopping.

Lastly, the binding of the holes can be examined for the ground state of four holes on the same cluster (see Figure 6). For both t_pp positive and negative, the ground state is a spin-singlet, with Cu spins and O spins both forming singlets. However, the spatial orientation of bound holes on O is different: for t_pp = 0.5, O holes primarily bind to Cu at the ends of the cluster, without substantial hole occupation on the central, bridging oxygen, while for t_pp = −0.5, O holes primarily bind to the central oxygen in a local d_xy configuration with neighboring oxygens. As this might be expected when antiferromagnetic exchange among oxygen becomes dominant over Cu, the predominance of d_xy pairing observed in the phase diagram of Figure 2 may be related to this tendency to bind neighboring O holes.

FIGURE 6

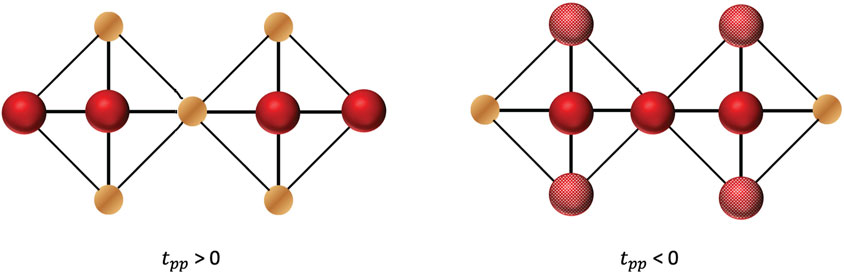
FIGURE 6. Predominant hole distributions for t_pp positive or negative, as indicated. Solid red spheres denote approximately a full hole charge, while shaded red spheres denote an approximate quarter charge.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

H-CJ: Writing–original draft, Writing–review and editing. TD: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences, and Engineering Division, under Contract DE-AC02-76SF00515.

Acknowledgments

We are grateful to Steven Kivelson for insightful discussions and invaluable suggestions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agterberg, D. F., Davis, J. S., Edkins, S. D., Fradkin, E., Van Harlingen, D. J., Kivelson, S. A., et al. (2020). The physics of pair-density waves: cuprate superconductors and beyond. Annu. Rev. Condens. Matter Phys. 11, 231–270. doi:10.1146/annurev-conmatphys-031119-050711

CrossRef Full Text | Google Scholar

Agterberg, D. F., and Tsunetsugu, H. (2008). Dislocations and vortices in pair-density-wave superconductors. Nat. Phys. 639, 639–642. doi:10.1038/nphys999

CrossRef Full Text | Google Scholar

Armitage, N. P., Fournier, P., and Greene, R. L. (2010). Progress and perspectives on electron-doped cuprates. Rev. Mod. Phys. 82, 2421–2487. doi:10.1103/RevModPhys.82.2421

CrossRef Full Text | Google Scholar

Berg, E., Fradkin, E., Kim, E.-A., Kivelson, S. A., Oganesyan, V., Tranquada, J. M., et al. (2007). Dynamical layer decoupling in a stripe-ordered high-T_c superconductor. Phys. Rev. Lett. 99, 127003. doi:10.1103/PhysRevLett.99.127003

PubMed Abstract | CrossRef Full Text | Google Scholar

Berg, E., Fradkin, E., and Kivelson, S. A. (2010). Pair-density-wave correlations in the kondo-heisenberg model. Phys. Rev. Lett. 105, 146403. doi:10.1103/PhysRevLett.105.146403

PubMed Abstract | CrossRef Full Text | Google Scholar

Berg, E., Fradkin, E., Kivelson, S. A., and Tranquada, J. M. (2009). Striped superconductors: how spin, charge and superconducting orders intertwine in the cuprates. New J. Phys. 11, 115004. doi:10.1088/1367-2630/11/11/115004

CrossRef Full Text | Google Scholar

Calabrese, P., and Cardy, J. (2004). Entanglement entropy and quantum field theory. J. Stat. Mech. Theory Exp. 2004, P06002, doi:10.1088/1742-5468/2004/06/p06002

CrossRef Full Text | Google Scholar

Chen, H., Yang, H., Hu, B., Zhao, Z., Yuan, J., Xing, Y., et al. (2021a). Roton pair density wave in a strong-coupling kagome superconductor. Nature 599, 222–228. doi:10.1038/s41586-021-03983-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Z., Wang, Y., Rebec, S. N., Jia, T., Hashimoto, M., Lu, D., et al. (2021b). Anomalously strong near-neighbor attraction in doped 1D cuprate chains. Science 373, 1235–1239. doi:10.1126/science.abf5174

PubMed Abstract | CrossRef Full Text | Google Scholar

Chung, C.-M., Qin, M., Zhang, S., Schollwöck, U., and White, S. R. (2020). Plaquette versus ordinary d-wave pairing in the t′-hubbard model on a width-4 cylinder. Phys. Rev. B 102, 041106. doi:10.1103/PhysRevB.102.041106

CrossRef Full Text | Google Scholar

Edkins, S. D., Kostin, A., Fujita, K., Mackenzie, A. P., Eisaki, H., Uchida, S., et al. (2019). Magnetic field–induced pair density wave state in the cuprate vortex halo. Science 364, 976–980. doi:10.1126/science.aat1773

PubMed Abstract | CrossRef Full Text | Google Scholar

Emery, V. J. (1987). Theory of high-t_c superconductivity in oxides. Phys. Rev. Lett. 58, 2794–2797. doi:10.1103/PhysRevLett.58.2794

PubMed Abstract | CrossRef Full Text | Google Scholar

Eskes, H., Sawatzky, G., and Feiner, L. (1989). Effective transfer for singlets formed by hole doping in the high-tc superconductors. Phys. C. Supercond. 160, 424–430. doi:10.1016/0921-4534(89)90415-2

CrossRef Full Text | Google Scholar

Eskes, H., Tjeng, L. H., and Sawatzky, G. A. (1990). Cluster-model calculation of the electronic structure of cuo: a model material for the high-T_c superconductors. Phys. Rev. B 41, 288–299. doi:10.1103/PhysRevB.41.288

PubMed Abstract | CrossRef Full Text | Google Scholar

Fagotti, M., and Calabrese, P. (2011). Universal parity effects in the entanglement entropy of XX chains with open boundary conditions. J. Stat. Mech. Theory Exp. 2011, P01017, doi:10.1088/1742-5468/2011/01/p01017

CrossRef Full Text | Google Scholar

Fradkin, E., Kivelson, S. A., and Tranquada, J. M. (2015). Colloquium: theory of intertwined orders in high temperature superconductors. Rev. Mod. Phys. 87, 457–482. doi:10.1103/RevModPhys.87.457

CrossRef Full Text | Google Scholar

Fulde, P., and Ferrell, R. A. (1964). Superconductivity in a strong spin-exchange field. Phys. Rev. 135, A550–A563. doi:10.1103/PhysRev.135.A550

CrossRef Full Text | Google Scholar

Gong, S., Zhu, W., and Sheng, D. N. (2021). Robust d-wave superconductivity in the square-lattice t − J model. Phys. Rev. Lett. 127, 097003. doi:10.1103/PhysRevLett.127.097003

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamidian, M. H., Edkins, S. D., Joo, S. H., Kostin, A., Eisaki, H., Uchida, S., et al. (2016). Detection of a cooper-pair density wave in Bi₂Sr₂CaCu₂O_8+x. Nature 532, 343–347. doi:10.1038/nature17411

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, Z., Kivelson, S. A., and Yao, H. (2020). Strong coupling limit of the holstein-hubbard model. Phys. Rev. Lett. 125, 167001. doi:10.1103/PhysRevLett.125.167001

PubMed Abstract | CrossRef Full Text | Google Scholar

Haule, K., Birol, T., and Kotliar, G. (2014). Covalency in transition-metal oxides within all-electron dynamical mean-field theory. Phys. Rev. B 90, 075136. doi:10.1103/PhysRevB.90.075136

CrossRef Full Text | Google Scholar

Himeda, A., Kato, T., and Ogata, M. (2002). Stripe states with spatially oscillating d-wave superconductivity in the two-dimensional t − t′ − J model. Phys. Rev. Lett. 88, 117001. doi:10.1103/PhysRevLett.88.117001

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, E. W., Mendl, C. B., Liu, S., Johnston, S., Jiang, H.-C., Moritz, B., et al. (2017). Numerical evidence of fluctuating stripes in the normal state of high-tc cuprate superconductors. Science 358, 1161–1164. doi:10.1126/science.aak9546

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, K. S., Han, Z., Kivelson, S. A., and Yao, H. (2022). Pair-density-wave in the strong coupling limit of the holstein-hubbard model. npj Quantum Mater 7, 17. doi:10.1038/s41535-022-00426-w

CrossRef Full Text | Google Scholar

Jaefari, A., and Fradkin, E. (2012). Pair-density-wave superconducting order in two-leg ladders. Phys. Rev. B 85, 035104. doi:10.1103/PhysRevB.85.035104

CrossRef Full Text | Google Scholar

Jian, S.-K., Scherer, M. M., and Yao, H. (2020). Mass hierarchy in collective modes of pair-density-wave superconductors. Phys. Rev. Res. 2, 013034. doi:10.1103/PhysRevResearch.2.013034

CrossRef Full Text | Google Scholar

Jiang, H.-C. (2023). Pair density wave in the doped three-band hubbard model on two-leg square cylinders. Phys. Rev. B 107, 214504. doi:10.1103/PhysRevB.107.214504

CrossRef Full Text | Google Scholar

Jiang, H.-C., Chen, S., and Weng, Z.-Y. (2020a). Critical role of the sign structure in the doped mott insulator: Luther-emery versus fermi-liquid-like state in quasi-one-dimensional ladders. Phys. Rev. B 102, 104512. doi:10.1103/PhysRevB.102.104512

CrossRef Full Text | Google Scholar

Jiang, H.-C., and Devereaux, T. P. (2019). Superconductivity in the doped hubbard model and its interplay with next-nearest hopping t. Science 365, 1424–1428. doi:10.1126/science.aal5304

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, H.-C., Weng, Z.-Y., and Kivelson, S. A. (2018). Superconductivity in the doped t-J model: results for four-leg cylinders. Phys. Rev. B 98, 140505. doi:10.1103/PhysRevB.98.140505

CrossRef Full Text | Google Scholar

Jiang, S., Scalapino, D. J., and White, S. R. (2023). Density-matrix-renormalization-group-based downfolding of the three-band hubbard model: the importance of density-assisted hopping. arXiv.

Google Scholar

Jiang, Y.-F., and Yao, H. (2023). Pair density wave superconductivity: a microscopic model in two dimensions. arXiv.

Google Scholar

Jiang, Y.-F., Zaanen, J., Devereaux, T. P., and Jiang, H.-C. (2020b). Ground state phase diagram of the doped hubbard model on the four-leg cylinder. Phys. Rev. Res. 2, 033073. doi:10.1103/PhysRevResearch.2.033073

CrossRef Full Text | Google Scholar

Kühner, T. D., White, S. R., and Monien, H. (2000). One-dimensional bose-hubbard model with nearest-neighbor interaction. Phys. Rev. B 61, 12474–12489. doi:10.1103/PhysRevB.61.12474

CrossRef Full Text | Google Scholar

Larkin, A. I., and Ovchinnikov, Y. N. (1965). Nonuniform state of superconductors. Sov. Phys. JETP 20, 762–770.

Google Scholar

Lee, P. A. (2014). Amperean pairing and the pseudogap phase of cuprate superconductors. Phys. Rev. X 4, 031017. doi:10.1103/PhysRevX.4.031017

CrossRef Full Text | Google Scholar

Lee, P. A., Nagaosa, N., and Wen, X.-G. (2006). Doping a mott insulator: physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85. doi:10.1103/RevModPhys.78.17

CrossRef Full Text | Google Scholar

Li, Q., Hücker, M., Gu, G. D., Tsvelik, A. M., and Tranquada, J. M. (2007). Two-dimensional superconducting fluctuations in stripe-ordered la_1.875 ba_0.125cuo₄. Phys. Rev. Lett. 99, 067001. doi:10.1103/PhysRevLett.99.067001

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, X., Chong, Y. X., Sharma, R., and Davis, J. C. S. (2021). Discovery of a cooper-pair density wave state in a transition-metal dichalcogenide. Science 372, 1447–1452. doi:10.1126/science.abd4607

CrossRef Full Text | Google Scholar

Liu, Y., Wei, T., He, G., Zhang, Y., Wang, Z., and Wang, J. (2023). Discovery of a pair density wave state in a monolayer high-T_c iron-based superconductor. Nature 618, 934–939. doi:10.1038/s41586-023-06072-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lozano, P. M., Ren, T., Gu, G. D., Tsvelik, A. M., Tranquada, J. M., and Li, Q. (2022). Testing for pair density wave order in la_1.875ba_0.125cuo₄. Phys. Rev. B 106, 174510. doi:10.1103/PhysRevB.106.174510

CrossRef Full Text | Google Scholar

Peng, C., Jiang, Y.-F., Devereaux, T. P., and Jiang, H.-C. (2021a). Precursor of pair-density wave in doping kitaev spin liquid on the honeycomb lattice. npj Quantum Mater 6, 64. doi:10.1038/s41535-021-00363-0

CrossRef Full Text | Google Scholar

Peng, C., Jiang, Y.-F., Wang, Y., and Jiang, H.-C. (2021b). Gapless spin liquid and pair density wave of the hubbard model on three-leg triangular cylinders. New J. Phys. 23, 123004. doi:10.1088/1367-2630/ac3a83

CrossRef Full Text | Google Scholar

Peng, C., Wang, Y., Wen, J., Lee, Y. S., Devereaux, T. P., and Jiang, H.-C. (2023). Enhanced superconductivity by near-neighbor attraction in the doped extended hubbard model. Phys. Rev. B 107, L201102. doi:10.1103/PhysRevB.107.L201102

CrossRef Full Text | Google Scholar

Qu, D.-W., Chen, B.-B., Jiang, H.-C., Wang, Y., and Li, W. (2022). Spin-triplet pairing induced by near-neighbor attraction in the extended hubbard model for cuprate chain. Commun. Phys. 5, 257. doi:10.1038/s42005-022-01030-x

CrossRef Full Text | Google Scholar

Ruan, W., Li, X., Hu, C., Hao, Z., Li, H., Cai, P., et al. (2018). Visualization of the periodic modulation of cooper pairing in a cuprate superconductor. Nat. Phys. 1178, 1178–1182. doi:10.1038/s41567-018-0276-8

CrossRef Full Text | Google Scholar

Scalettar, R. (1989). Magnetic and pairing correlations in a three band hubbard model. Phys. C Supercond. its Appl. 162-164, 313–318. doi:10.1016/0921-4534(89)91033-2

CrossRef Full Text | Google Scholar

Scalettar, R. T., Scalapino, D. J., Sugar, R. L., and White, S. R. (1991). Antiferromagnetic, charge-transfer, and pairing correlations in the three-band hubbard model. Phys. Rev. B 44, 770–781. doi:10.1103/PhysRevB.44.770

PubMed Abstract | CrossRef Full Text | Google Scholar

Tranquada, J. M. (2020). Cuprate superconductors as viewed through a striped lens. Adv. Phys. 69, 437–509. doi:10.1080/00018732.2021.1935698

CrossRef Full Text | Google Scholar

Tranquada, J. M. (2021). Topological doping and superconductivity in cuprates: an experimental perspective. Symmetry 13, 2365. doi:10.3390/sym13122365

CrossRef Full Text | Google Scholar

Tranquada, J. M., Gu, G. D., Hücker, M., Jie, Q., Kang, H.-J., Klingeler, R., et al. (2008). Evidence for unusual superconducting correlations coexisting with stripe order in la_1.875ba_0.125cuo₄. Phys. Rev. B 78, 174529. doi:10.1103/PhysRevB.78.174529

CrossRef Full Text | Google Scholar

Venderley, J., and Kim, E.-A. (2019). Evidence of pair-density wave in spin-valley locked systems. Sci. Adv. 5, eaat4698. doi:10.1126/sciadv.aat4698

PubMed Abstract | CrossRef Full Text | Google Scholar

White, S. R. (1992). Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 69, 2863–2866. doi:10.1103/physrevlett.69.2863

PubMed Abstract | CrossRef Full Text | Google Scholar

White, S. R. (1993). Density-matrix algorithms for quantum renormalization groups. Phys. Rev. B 48, 10345–10356. doi:10.1103/PhysRevB.48.10345

PubMed Abstract | CrossRef Full Text | Google Scholar

White, S. R., Affleck, I., and Scalapino, D. J. (2002). Friedel oscillations and charge density waves in chains and ladders. Phys. Rev. B 65, 165122. doi:10.1103/PhysRevB.65.165122

CrossRef Full Text | Google Scholar

White, S. R., and Scalapino, D. J. (2015). Doping asymmetry and striping in a three-orbital cuo₂ hubbard model. Phys. Rev. B 92, 205112. doi:10.1103/PhysRevB.92.205112

CrossRef Full Text | Google Scholar

Wu, Y.-M., Nosov, P. A., Patel, A. A., and Raghu, S. (2023). Pair density wave order from electron repulsion. Phys. Rev. Lett. 130, 026001. doi:10.1103/PhysRevLett.130.026001

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, X. Y., Law, K. T., and Lee, P. A. (2019). Pair density wave in the doped t − j model with ring exchange on a triangular lattice. Phys. Rev. Lett. 122, 167001. doi:10.1103/PhysRevLett.122.167001

PubMed Abstract | CrossRef Full Text | Google Scholar

Zaanen, J., Sawatzky, G. A., and Allen, J. W. (1985). Band gaps and electronic structure of transition-metal compounds. Phys. Rev. Lett. 55, 418–421. doi:10.1103/PhysRevLett.55.418

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, F. C., and Rice, T. M. (1988). Effective Hamiltonian for the superconducting cu oxides. Phys. Rev. B 37, 3759–3761. doi:10.1103/PhysRevB.37.3759

PubMed Abstract | CrossRef Full Text | Google Scholar