- 1Fachbereich Physik, Universität Konstanz, Konstanz, Germany
- 2Department of Physics, University of Basel, Basel, Switzerland
- 3Graduate School of China Academy of Engineering Physics, Beijing, China
Conventional two-dimensional superconductivity is destroyed when the critical in-plane magnetic field exceeds the so-called Pauli limit. Some monolayer transition-metal dichalcogenides lack inversion symmetry and the strong spin-orbit coupling leads to a valley-dependent Zeeman-like spin splitting. The resulting spin-valley locking lifts the valley degeneracy and results in a strong enhancement of the in-plane critical magnetic field. In these systems, it was predicted that the density of states in an in-plane field exhibits distinct mirage gaps at finite energies of about the spin-orbit coupling strength, which arise from a coupling of the electron and hole bands at energy larger than the superconducting gap. In this study, we investigate the impact of a triplet pairing channel on the spectral properties, primarily the mirage gap and the superconducting gap, in the clean limit. Notably, in the presence of the triplet pairing channel, the mirage-gap width is reduced for the low magnetic fields. Furthermore, when the temperature is lower than the triplet critical temperature, the mirage gaps survive even in the strong-field limit due to the finite singlet and triplet order parameters. Our work provides insights into controlling and understanding the properties of spin-triplet Cooper pairs.
1 Introduction
Superconductivity in the presence of magnetism has been a topic of great interest within the scientific community for several decades, and is responsible for many exotic properties. Usually, an external magnetic field destroys superconductivity by aligning the electron spins in the same direction. This is typical in conventional superconductors where Cooper pairs are formed by two electrons with opposite spins. The upper critical field is limited by the Pauli paramagnetic effect Chandrasekhar (1962); Clogston (1962). However, in some superconductors, the Pauli limit can be surpassed by forming Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) states Matsuda and Shimahara (2007) or by creating spin-triplet Cooper pairs so that the parallel-aligned spin configuration in Cooper pairs is not affected by Pauli paramagnetism Aoki et al. (2001); Huy et al. (2007); Aoki and Flouquet (2012). The spin-triplet Cooper pairings are important for spintronics applications Ohnishi et al. (2020) as they can generate and control spin currents. They are also proposed as a possible route to realize topological superconductivity which could be used to build robust quantum computers Frolov et al. (2020). Therefore, understanding the properties of spin-triplet Cooper pairs is of great interest.
The transition-metal dichalcogenides serve as a platform for both exploring spin-triplet pairing physics and surpassing the Pauli limit in high-field superconductivity. It has been predicted that equal-spin triplet pairs can form in a superconducting few-layer 2H-NbSe2 when an in-plane magnetic field is applied Möckli and Khodas (2020). Unlike conventional superconductors, monolayer transition metal dichalcogenides, such as NbSe2, lack in-plane crystal inversion symmetry Frigeri et al. (2004); Smidman et al. (2017); Wickramaratne et al. (2020); Ramires (2022). This results in a spin-orbit interaction that generates an effective out-of-plane magnetic field, causing the electron spins to point out of the plane Xiao et al. (2012); Zhu et al. (2011). Therefore, it is termed as Ising spin-orbit coupling (ISOC) Zhou et al. (2016); Saito et al. (2016); Lu et al. (2015), and the corresponding Ising superconductivity was experimentally found in numerous transition-metal dichalcogenides Lu et al. (2015); Saito et al. (2016); Xi et al. (2016); Xing et al. (2017); Dvir et al. (2018); Costanzo et al. (2018); Lu et al. (2018); de la Barrera et al. (2018); Sohn et al. (2018); Li et al. (2021); Cho et al. (2022); Hamill et al. (2021); Idzuchi et al. (2021); Ai et al. (2021); Kang et al. (2021); Kuzmanović et al. (2022). ISOC is dependent on momentum and has opposite signs at the K and K′ points of the hexagonal Brillouin zone. It prevents the spin directions from being realigned by an externally applied in-plane magnetic field, thus overcoming the Pauli limit to demonstrate high in-plane critical fields Ilić et al. (2017); Kuzmanović et al. (2022).
Ising superconductors subjected to an in-plane magnetic field display unique features in their density of states, notably the emergence of additional half-gaps at finite energies of about the ISOC strength Tang et al. (2021). These newly discovered gaps, called mirage gaps, represent a mirroring of the main superconducting gap and are signatures of the equal-spin triplet finite-energy pairing correlations. Their width is determined by the interplay of the in-plane magnetic field and ISOC. In the previous work, the mirage gaps have only been studied in the context of the singlet pairing channel Tang et al. (2021). However, a recent experiment found that the superconducting gap in a few-layer NbSe2 under an in-plane magnetic field was larger than predictions based solely on the singlet-pairing channel Kuzmanović et al. (2022). This discrepancy was attributed to the existence of a triplet-pairing channel, in which an equal-spin triplet order parameter couples with a singlet one to enhance the critical magnetic field Ilic et al. (2023).
In this work, we investigate the mirage gaps of an Ising superconductor that consists of both singlet and triplet pairing channels Kuzmanović et al. (2022); Ilic et al. (2023). For a fixed temperature, the maximal mirage-gap width by varying the magnetic field decreases with increasing the critical temperature of the triplet pairing channel Tct. When the magnetic field is extremely high and the temperature is lower than Tct, the mirage-gap width remains finite due to the nonvanishing spin-singlet and spin-triplet order parameters. This contrasts with the case without considering the triplet-pairing channel where the mirage gaps always disappear at the critical field for the singlet order parameter Tang et al. (2021).
2 Model and formalism
An Ising superconductor with both a singlet order parameter Δs and an equal-spin triplet order parameter Δt can be described by a Bogoliubov–de Gennes Hamiltonian near the K (K′) valley by neglecting the contribution from Γ point Kuzmanović et al. (2022). By applying an in-plane magnetic field B, the effective Hamiltonian can be written in the Nambu basis
where H0k) is given by
Here, s = +1 corresponds to the valley K and s = −1 to K′. The deviation of the momentum from K or K′ is denoted by p. The Pauli matrices σx, σy, and σz act on the spin space and σ0 is the corresponding unit matrix. The dispersion measured from the chemical potential is ξp = p2/2m − μ. The ISOC strength is denoted by βso. The Zeeman term arising from the in-plane magnetic field in the x-direction is Bxσx which absorbs the factor of gμB/2 containing the Landé g factor and the Bohr magneton μB. Note that the ISOC forces the spins to align out of the plane, whereas the in-plane magnetic field aims to align the spins within the plane. The superconducting order parameter can be written as Kuzmanović et al. (2022); Ilic et al. (2023).
The eigenvalues of the Bogoliubov-de Gennes Hamiltonian are given by
with
The approximation indicates that the mirage-gap width is influenced by the interplay of the singlet and triplet order parameters.
Since the superconducting gap and the ISOC are much smaller compared to the Fermi energy, it allows us to use the formalism of quasiclassical Green’s function Eilenberger (1968); Larkin and Ovchinnikov (1969); Belzig et al. (1999); Kopnin (2001); Eschrig (2015). The structure of the Green’s functions can be written as
The bar operation in the above expression is defined as
The order parameter term
with Δt = (0, isΔt, 0). The Zeeman and ISOC fields are included in the term
The Pauli matrices τ1, τ2, and τ3 act on the Nambu space and τ0 is the corresponding unit matrix. Using the notation
The normalization condition
By combining the Eilenberger equation with
We also find that
and
At very high magnetic field and in the limit of Bx ≫ βso, ϵ, Δs, Δt, one can show that
3 Numerical results
In the numerical calculation, the ISOC strength is set as βso = 7Tcs. In Figure 1A, we plot the singlet (Δs) and triplet (Δt) order parameters versus the in-plane magnetic field Bx by varying the triplet critical temperature Tct at a fixed temperature T. The behavior of the order parameters in the cases of T > Tct and T < Tct will be discussed separately in the following. For the case where T > Tct, with increasing magnetic field, the singlet order parameter Δs decreases and finally vanishes at the critical field. This is attributed to the pair-breaking effect of the magnetic field which tries to align the spins of the spin-singlet Cooper pairs in its direction. On the other hand, the in-plane magnetic field induces the equal-spin triplet pairings which are coupled to the singlet pairings. The triplet order parameter Δt first increases with increasing the in-plane magnetic field since the field attempts to align the spins in the plane which is favorable for the formation of triplet pairs. It then decreases due to its coupling with Δs as seen from the self-consistent gap equations. Finally, both Δs and Δt vanish at the same critical magnetic field for T > Tct. For the case where T < Tct, at small magnetic fields, Δs decreases, and Δt begins to increase in a similar manner to the case where T > Tct. The behavior of both order parameters differ from that of T > Tct case at high magnetic fields. Both Δs and Δt reach saturated values instead of vanishing at a critical field. This is because the triplet order parameter is preserved by the in-plane field as the field favors the formation of triplet pairs. Consequently, Δs does not vanish due to its coupling with Δt.
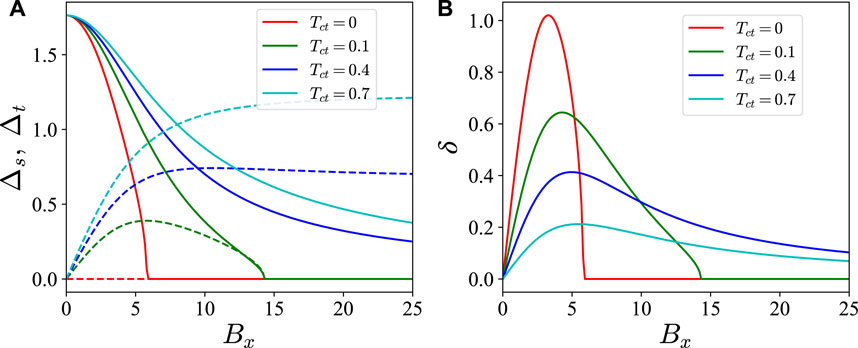
FIGURE 1. (A) Singlet (Δs, solid lines) and triplet (Δt, dashed lines) order parameters versus in-plane magnetic field Bx under different triplet critical temperatures Tct. (B) The mirage-gap width δ versus Bx under different Tct. The temperature is T =0.2. All the quantities are in the units of Tcs.
Figure 1B shows the mirage-gap width δ for different triplet critical temperatures Tct. The maximal mirage-gap width by varying the magnetic field decreases with increasing Tct. The mirage gaps vanish at the critical in-plane field when T > Tct. This is due to the dependence of mirage-gap width on the order parameters which vanish at the critical field. On the other hand, the mirage gaps are finite even at extremely high in-plane fields in the scenarios where T < Tct. This is because the order parameters remain finite in the high field limit at T < Tct.
4 Conclusion
To conclude, we have studied the effect of a triplet pairing channel on the spectral properties of an Ising superconductor. The presence of a triplet order parameter reduces the maximal mirage-gap width by varying the in-plane magnetic field. Notably, at a temperature lower than Tct, both the order parameters and the mirage gap are finite even at very high fields. In contrast, for the case where the temperature is higher than Tct, both the order parameters and the mirage gaps vanish at the critical field. From an experimental standpoint, it is important to note that the intervalley scattering influences both the order parameters, effectively eliminating equal-spin triplet pairing under moderate intervalley disorder Ilic et al. (2023). Our work provides a better understanding about the spin-triplet pairings in Ising superconductors.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
SP: Formal Analysis, Investigation, Methodology, Validation, Writing–original draft, Writing–review and editing. GT: Conceptualization, Formal Analysis, Investigation, Project administration, Writing–original draft, Writing–review and editing. WB: Conceptualization, Formal Analysis, Funding acquisition, Methodology, Supervision, Validation, Writing–review and editing.
Funding
We acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)–Project-ID 443404566—SPP 2244.
Acknowledgments
We acknowledge useful discussions with M. Aprili, C. Bruder, A. Di Bernardo, and D. Nikolić.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ai, L., Zhang, E., Huang, C., Xie, X., Yang, Y., Jia, Z., et al. (2021). Van der Waals ferromagnetic Josephson junctions. Nat. Commun. 12, 6580. doi:10.1038/s41467-021-26946-w
Aoki, D., and Flouquet, J. (2012). Ferromagnetism and superconductivity in uranium compounds. J. Phys. Soc. Jpn. 81, 011003. doi:10.1143/JPSJ.81.011003
Aoki, D., Huxley, A., Ressouche, E., Braithwaite, D., Flouquet, J., Brison, J. P., et al. (2001). Coexistence of superconductivity and ferromagnetism in URhGe. Nature 413, 613–616. doi:10.1038/35098048
Belzig, W., Wilhelm, F. K., Bruder, C., Schön, G., and Zaikin, A. D. (1999). Quasiclassical Green’s function approach to mesoscopic superconductivity. Superlattices Microstruct. 25, 1251–1288. doi:10.1006/spmi.1999.0710
Chandrasekhar, B. S. (1962). A note on the maximum critical field of high-field superconductors. Appl. Phys. Lett. 1, 7–8. doi:10.1063/1.1777362
Cho, C.-w., Lyu, J., An, L., Han, T., Lo, K. T., Ng, C. Y., et al. (2022). Nodal and nematic superconducting phases in NbSe2 monolayers from competing superconducting channels. Phys. Rev. Lett. 129, 087002. doi:10.1103/physrevlett.129.087002
Clogston, A. M. (1962). Upper limit for the critical field in hard superconductors. Phys. Rev. Lett. 9, 266–267. doi:10.1103/PhysRevLett.9.266
Costanzo, D., Zhang, H., Reddy, B. A., Berger, H., and Morpurgo, A. F. (2018). Tunnelling spectroscopy of gate-induced superconductivity in MoS2. Nat. Nanotechnol. 13, 483–488. doi:10.1038/s41565-018-0122-2
de la Barrera, S. C., Sinko, M. R., Gopalan, D. P., Sivadas, N., Seyler, K. L., Watanabe, K., et al. (2018). Tuning Ising superconductivity with layer and spin-orbit coupling in two-dimensional transition-metal dichalcogenides. Nat. Commun. 9, 1427. doi:10.1038/s41467-018-03888-4
Dvir, T., Massee, F., Attias, L., Khodas, M., Aprili, M., Quay, C. H. L., et al. (2018). Spectroscopy of bulk and few-layer superconducting NbSe2 with van der Waals tunnel junctions. Nat. Commun. 9, 598. doi:10.1038/s41467-018-03000-w
Eilenberger, G. (1968). Transformation of Gorkov’s equation for type II superconductors into transport-like equations. Zeitschrift für Physik A Hadrons Nucl. 214, 195–213. doi:10.1007/BF01379803
Eschrig, M. (2015). Spin-polarized supercurrents for spintronics: a review of current progress. Rep. Prog. Phys. 78, 104501. doi:10.1088/0034-4885/78/10/104501
Frigeri, P. A., Agterberg, D. F., Koga, A., and Sigrist, M. (2004). Superconductivity without inversion symmetry: MnSi versus CePt3Si. Phys. Rev. Lett. 92, 097001. doi:10.1103/PhysRevLett.92.097001
Frolov, S. M., Manfra, M. J., and Sau, J. D. (2020). Topological superconductivity in hybrid devices. Nat. Phys. 16, 718–724. doi:10.1038/s41567-020-0925-6
Hamill, A., Heischmidt, B., Sohn, E., Shaffer, D., Tsai, K.-T., Zhang, X., et al. (2021). Two-fold symmetric superconductivity in few-layer NbSe2. Nat. Phys. 17, 949–954. doi:10.1038/s41567-021-01219-x
Huy, N. T., Gasparini, A., de Nijs, D. E., Huang, Y., Klaasse, J. C. P., Gortenmulder, T., et al. (2007). Superconductivity on the border of weak itinerant ferromagnetism in UCoGe. Phys. Rev. Lett. 99, 067006. doi:10.1103/PhysRevLett.99.067006
Idzuchi, H., Pientka, F., Huang, K.-F., Harada, K., Gül, O., Shin, Y. J., et al. (2021). Unconventional supercurrent phase in Ising superconductor Josephson junction with atomically thin magnetic insulator. Nat. Commun. 12, 5332–5338. doi:10.1038/s41467-021-25608-1
Ilić, S., Meyer, J. S., and Houzet, M. (2017). Enhancement of the upper critical field in disordered transition metal dichalcogenide monolayers. Phys. Rev. Lett. 119, 117001. doi:10.1103/PhysRevLett.119.117001
Ilic, S., Meyer, J. S., and Houzet, M. (2023). Spectral properties of disordered ising superconductors with singlet and triplet pairing in in-plane magnetic fields. doi:10.48550/arXiv.2308.02646
Kang, K., Jiang, S., Berger, H., Watanabe, K., Taniguchi, T., Forró, L., et al. (2021). Giant anisotropic magnetoresistance in Ising superconductor-magnetic insulator tunnel junctions. doi:10.48550/arXiv.2101.01327
Kuzmanović, M., Dvir, T., LeBoeuf, D., Ilić, S., Haim, M., Möckli, D., et al. (2022). Tunneling spectroscopy of few-monolayer NbSe2 in high magnetic fields: triplet superconductivity and Ising protection. Phys. Rev. B 106, 184514. doi:10.1103/PhysRevB.106.184514
Larkin, A. I., and Ovchinnikov, Y. N. (1969). Quasiclassical method in the theory of superconductivity. JETP 28, 1200–1205. zh. Eksp. Teor. Fiz. 55, 2262–2272.
Li, J., Song, P., Zhao, J., Vaklinova, K., Zhao, X., Li, Z., et al. (2021). Printable two-dimensional superconducting monolayers. Nat. Mat. 20, 181–187. doi:10.1038/s41563-020-00831-1
Lu, J. M., Zheliuk, O., Leermakers, I., Yuan, N. F. Q., Zeitler, U., Law, K. T., et al. (2015). Evidence for two-dimensional Ising superconductivity in gated MoS2. Science 350, 1353–1357. doi:10.1126/science.aab2277
Lu, J., Zheliuk, O., Chen, Q., Leermakers, I., Hussey, N. E., Zeitler, U., et al. (2018). Full superconducting dome of strong Ising protection in gated monolayer WS2. Proc. Natl. Acad. Sci. U.S.A. 115, 3551–3556. doi:10.1073/pnas.1716781115
Matsuda, Y., and Shimahara, H. (2007). Fulde-Ferrell-Larkin-Ovchinnikov state in heavy fermion superconductors. J. Phys. Soc. Jpn. 76, 051005. doi:10.1143/JPSJ.76.051005
Möckli, D., and Khodas, M. (2020). Ising superconductors: interplay of magnetic field, triplet channels, and disorder. Phys. Rev. B 101, 014510. doi:10.1103/PhysRevB.101.014510
Ohnishi, K., Komori, S., Yang, G., Jeon, K.-R., Olde Olthof, L. A. B., Montiel, X., et al. (2020). Spin-transport in superconductors. Appl. Phys. Lett. 116. doi:10.1063/1.5138905
Ramires, A. (2022). Nonunitary superconductivity in complex quantum materials. J. Phys. Condens. Matter 34, 304001. doi:10.1088/1361-648X/ac6d3a
Saito, Y., Nakamura, Y., Bahramy, M. S., Kohama, Y., Ye, J., Kasahara, Y., et al. (2016). Superconductivity protected by spin-valley locking in ion-gated MoS2. Nat. Phys. 12, 144–149. doi:10.1038/nphys3580
Smidman, M., Salamon, M. B., Yuan, H. Q., and Agterberg, D. F. (2017). Superconductivity and spin–orbit coupling in non-centrosymmetric materials: a review. Rep. Prog. Phys. 80, 036501. doi:10.1088/1361-6633/80/3/036501
Sohn, E., Xi, X., He, W.-Y., Jiang, S., Wang, Z., Kang, K., et al. (2018). An unusual continuous paramagnetic-limited superconducting phase transition in 2D NbSe2. Nat. Mat. 17, 504–508. doi:10.1038/s41563-018-0061-1
Tang, G., Bruder, C., and Belzig, W. (2021). Magnetic field-induced “mirage” gap in an Ising superconductor. Phys. Rev. Lett. 126, 237001. doi:10.1103/PhysRevLett.126.237001
Wickramaratne, D., Khmelevskyi, S., Agterberg, D. F., and Mazin, I. I. (2020). Ising superconductivity and magnetism in NbSe2. Phys. Rev. X 10, 041003. doi:10.1103/PhysRevX.10.041003
Xi, X., Wang, Z., Zhao, W., Park, J.-H., Law, K. T., Berger, H., et al. (2016). Ising pairing in superconducting NbSe2 atomic layers. Nat. Phys. 12, 139–143. doi:10.1038/nphys3538
Xiao, D., Liu, G.-B., Feng, W., Xu, X., and Yao, W. (2012). Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides. Phys. Rev. Lett. 108, 196802. doi:10.1103/PhysRevLett.108.196802
Xing, Y., Zhao, K., Shan, P., Zheng, F., Zhang, Y., Fu, H., et al. (2017). Ising superconductivity and quantum phase transition in macro-size monolayer NbSe2. Nano Lett. 17, 6802–6807. doi:10.1021/acs.nanolett.7b03026
Zhou, B. T., Yuan, N. F. Q., Jiang, H.-L., and Law, K. T. (2016). Ising superconductivity and Majorana fermions in transition-metal dichalcogenides. Phys. Rev. B 93, 180501. doi:10.1103/PhysRevB.93.180501
Keywords: Ising superconductors, spin-orbit coupling, mirage gaps, spin triplet pairing, unconventional superconductivity
Citation: Patil S, Tang G and Belzig W (2023) Spectral properties of a mixed singlet-triplet Ising superconductor. Front. Electron. Mater. 3:1254302. doi: 10.3389/femat.2023.1254302
Received: 06 July 2023; Accepted: 21 August 2023;
Published: 01 September 2023.
Edited by:
Sachio Komori, Nagoya University, JapanReviewed by:
Jianlin Luo, Chinese Academy of Sciences (CAS), ChinaKyung-Hwan Jin, Institute for Basic Science (IBS), Republic of Korea
Copyright © 2023 Patil, Tang and Belzig. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wolfgang Belzig, d29sZmdhbmcuYmVsemlnQHVuaS1rb25zdGFuei5kZQ==
 Sourabh Patil
Sourabh Patil Gaomin Tang
Gaomin Tang Wolfgang Belzig
Wolfgang Belzig